Molecular design and synthesis of bithiophene copolymers for advanced nonlinear optical response

Abstract

In this paper, a series of low band gap bithiophene-based copolymers were designed and synthesized through direct arylation polymerization using a palladium catalyst. The band structures of the five polymers were determined by quantum mechanical calculation employing Density Functional Theory (DFT) in the periodic Boundary Condition (PBC) using the HSE06/6-31G basis set. The polymers were characterized using ¹H NMR, FT-IR, GPC, UV-vis and cyclic voltammetry. The five polymers have an energy gap below 2.95 eV and have broad absorption in the visible region. The experimental results support the theoretical prediction. The fluorescence lifetime of the polymers, P(BT-PH), P(BT-CZ), P(BT-FLN), P(BT-ANT) and P(BT-TPA) was monitored using Time-Correlated Single Photon Counting (TCSPC) in CHCl₃. We report on the third-order nonlinear optical (NLO) properties of the copolymers, which were assessed using the Z-scan method with a nanosecond laser beam at 532 nm. The copolymers P(BT-PH), P(BT-CZ), P(BT-FLN), and P(BT-TPA) were found to have nonlinear absorption coefficients of 3.85 × 10⁻¹⁰, 2.87 × 10⁻¹⁰, 2.99 × 10⁻¹⁰, and 3.01 × 10⁻¹⁰ m W⁻¹, respectively. The polymers exhibit better optical power limiting behavior at 532 nm because of the donor–acceptor scheme. This optical power limiting behavior positions these materials as promising candidates for integration into next-generation photonic devices, including laser protection systems, optical sensors, and nonlinear optical switches.

---

1 Introduction

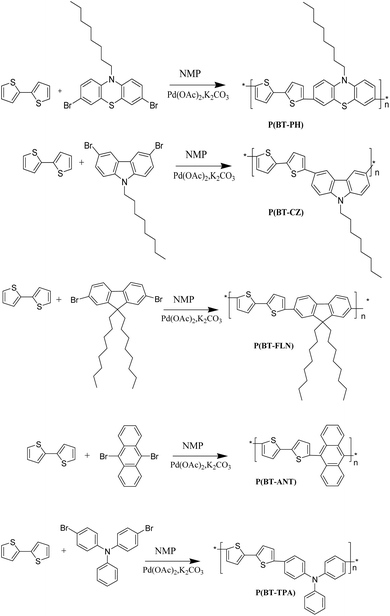
In recent times, there has been a surge in interest in donor–acceptor (D–A) type conducting polymers.^1,2 These polymers offer the advantage of customizable optoelectronic properties, mechanical flexibility, and solution processability, making them highly suitable for the fabrication of optoelectronic devices such as solar cells,^3,4 light-emitting diodes^5,6 and field-effect transistors.^7,8 Especially, organic semiconducting copolymers that integrate heteroatoms like oxygen, nitrogen, or sulfur into their structures are of much interest. These polymers are highly valued for their exceptional electronic, magnetic, and optical properties, which make them promising candidates for various applications. Polythiophene and its derivatives have attracted significant attention in this regard, primarily due to their favorable attributes such as low band gaps and excellent environmental stability.^9–11 Researchers have been exploring ways to fully exploit the potential of polythiophene by modifying its structure through copolymerization with other conjugated building blocks.^12,13 Thiophene, a common building block in polythiophene, has emerged as a particularly promising candidate for copolymerization with a range of monomers, including furan,^14,15 pyrrole,^16,17 phenothiazine,^18,19 benzanthrone²⁰ and benzothiophene.²¹ The present study is aimed at further enhancing the properties of polythiophene-based polymers by incorporating monomers containing electron-rich heteroatoms, such as phenothiazine, carbazole, and triphenylamine, into the bithiophene moiety. This strategic incorporation was expected to broaden the potential applications of the resulting polymers across various fields.

In general, transition metal-catalyzed cross-coupling processes such as the Kumada, Negishi, Stille, and Suzuki types are used to create conjugated polymers.^22–26 These methods often require bifunctional organometallic reagents to preactivate C–H bonds, using hazardous chemicals like butyl lithium that generate toxic byproducts. Direct arylation polymerization (DArP) has become a more effective and safer substitute to get over these restrictions. This approach offers more simplicity, safety, and environmental compatibility by directly coupling aryl halides with heteroarenes, doing away with preactivation procedures.^27–31

This manuscript presents the design and synthesis of five bithiophene-based copolymers, P(BT-PH), P(BT-CZ), P(BT-FLN), P(BT-ANT), and P(BT-TPA) synthesized via the direct arylation polymerization method. These copolymers were obtained by coupling 2,2′-bithiophene (BT) with various dibromo-based acceptor units: 3,7-dibromo-10-octyl phenothiazine (PH), 3,6-dibromo-N-octyl carbazole (CZ), 2,7-dibromo-9,9-dioctyl-9H-fluorene (FLN), 9,10-dibromo anthracene (ANT), and 4,4′-dibromo triphenylamine (TPA). This study highlights the successful synthesis of five low-bandgap copolymers, each incorporating a bithiophene donor segment and one of the above-mentioned dibromo-functionalized acceptor units, offering promising potential for optoelectronic applications. The DFT/B3LYP/6-31G formalism was used to optimize monomers and D-A units. The DFT/B3LYP/6-31G and DFT/HSE06/6-31G methods were used to optimize polymers. Investigations have been done on their thermal, optical, and electrochemical characteristics. In contrast to the B3LYP/6-31G method, the experimental results agree with the theoretical prediction obtained by the HSE06/6-31G method. Using TCSPC in CHCl₃, the fluorescence measurements of every polymer were obtained with high accuracy and lifetime resolution, utilizing a multiexponential decay function.

In recent years, third-order NLO materials with optical power limiting (OPL) capabilities have attracted a lot of attention because of their key function in shielding optical sensors, detectors, and human eyes from impairment caused by intense laser pulses. These materials are also necessary for the creation of photonic limiters, all-optical switches, and optical communication system devices. The need for solution processable, stable, and adjustable polymer-based optical power-limiting materials is urgent due to the increasing use of laser-based technologies in industries like biomedical imaging, defence, aerospace, LiDAR, and optical data storage. Conjugated polymers of the donor–acceptor type are becoming the leaders in this field, especially those with high intramolecular charge transfer and small band gaps. They are perfect for integration into flexible and scalable device architectures due to their capacity to combine high NLO coefficients with desired mechanical and processing characteristics. The present study contributes to this rapidly expanding research area by offering structurally tuneable bithiophene copolymers with demonstrated optical limiting behavior, positioning them as promising candidates for next-generation NLO and photonic systems.

2 Experimental

2.1. Theoretical methodology

The electronic structure and properties of the bithiophene-based D–A copolymers P(BT-PH), P(BT-CZ), P(BT-FLN), P(BT-ANT) and P(BT-TPA) were studied using the quantum mechanical modelling method based on Density Functional Theory (DFT).^32–36 The DFT calculations at two different energy levels, B3LYP and HSE06 (Heyd–Scuseria–Ernzerhof functional), were performed. B3LYP is a widely used functional that combines the Becke three–parameter exchange functional with the Lee–Yang–Parr correlation functional.^37–41 HSE06 is a hybrid functional that incorporates a fraction of Hartree–Fock exchange with the PBE (Perdew–Burke–Ernzerhof) correlation functional. The calculations utilized the 6-31G basis set, which is commonly used for molecular systems and provides a good balance between accuracy and computational cost. The ground state geometries of the oligomers were optimized using DFT at the B3LYP level of theory with the 6-31G basis set. This optimization process involves minimizing the total energy of the system to determine the most stable molecular geometry.

To evaluate excited-state vertical transition energies and oscillator strengths, time-dependent DFT (TD-DFT) calculations were employed. TD-DFT allows for the prediction of electronic excitations and absorption spectra of the polymers.⁴² The electronic properties of the copolymers were further studied using DFT calculations with PBC available in Gaussian 09 quantum chemical codes.⁴¹ PBC allows for the simulation of an infinite periodic lattice, which is essential for modelling extended systems like polymers. DFT/PBC/HSE06/6-31G was identified as a suitable method for predicting the band gap of conjugated polymers compared to DFT/PBC/B3LYP/6-31G.^42,43 The band gap is an important electronic property that determines the material's conductivity and optical properties. The starting unit cell geometries refer to determining the atomic positions and lattice parameters of the unit cell for the polymer under investigation. In this case, the calculations were performed using the HSE06/6-31G theory, a computational method within density functional theory (DFT) that incorporates a hybrid functional.

The central portion of the optimized tetramer (a molecule consisting of four repeating units) was chosen to define the unit cell. This central portion is assumed to represent the bulk properties of the polymer. Once the unit cell geometry is determined, it is assumed to repeat infinitely along the translational vector(s) of the crystal lattice. This assumption simplifies the calculation by treating the system as periodic, allowing for the analysis of its electronic properties within a finite computational space. The band structure represents the energy levels (bands) of electrons in the material as a function of their momentum (wave vector ‘k’) within the Brillouin zone. In this context, the band structure was plotted for the lowest four unoccupied (conduction) bands and highest four occupied (valence) bands. The Brillouin zone boundaries were defined between ‘k = 0’ and ‘k = π/a’, where ‘a’ is the translational vector of the crystal lattice.⁴³ By plotting these bands, one can analyze the electronic structure of the polymer, including its energy bandgap, band dispersion, and density of states.

2.2. Chemical procedures

The detailed reaction schemes for the synthesis of the monomers and polymers are described.

2.2.1 10-n-Octylphenothiazine⁴⁴. A 250 mL flask with two necks contained phenothiazine (10 mmol) and potassium hydroxide (20 mmol) dissolved in 100 mL of DMSO. For thirty minutes, the mixture was stirred. Octyl bromide (55 mmol) was added dropwise to the reaction mixture, which was then stirred for 24 hours at room temperature. After being added to water, the reaction mixture was extracted using dichloromethane and dried using MgSO₄. By purifying the resultant liquid with petroleum ether as an eluent through column chromatography, a colorless liquid was obtained. Yield: 93%, ¹H NMR (400 MHz, CDCl₃): δ 0.87 (t, J = 6.8 Hz, 3H), 1.24–1.43 (m, 10H), 1.77 (m, 2H), 3.80–3.84 (t, J = 7.2 Hz, 2H), 6.83–6.91 (m, 4H), 7.11–7.15 (m, 4H), GCMS: m/z = 311.
2.2.1.1 3,7-Dibromo-10-octylphenothiazine^44,45. 50 mL of dichloromethane was used to dissolve 0.024 mol of 10-n-octylphenothiazine. A syringe was used to introduce 0.05 mol of bromine into the mixture, which was then stirred for 4 hours at room temperature. After adding 20 mL of dilute aqueous NaOH to the reaction mixture, it was allowed to stand for 30 minutes. The organic layer was separated and concentrated after the reaction mixture was extracted three times with dichloromethane and brine. Hexane was used as the eluent in column chromatography to purify the crude product, yielding yellow oil. Yield: 79%, ¹H NMR (400 MHz, CDCl₃): δ 0.86 (t, 3H), 1.14–1.51 (m, 10H), 1.74 (m, 2H), 3.72 (t, 2H), 6.66 (d, 2H), 7.18–7.20 (dd, 2H), 7.24 (d, 2H), LCMS: m/z = 470.

2.2.2 3,6-Dibromocarbazole. After dissolving 100 mmol of carbazole in 150 mL of DMF at 0 °C while stirring, 200 mmol of NBS was added to the solution. The mixture was agitated for two hours at room temperature, the solution was transferred into 500 mL of deionized water, filtered, and washed with water (3 times). The crude product was recrystallized from ethanol. Yield: 88%, ¹H NMR (400 MHz, CDCl₃): δ 8.14 (s, 2H), 8.11 (s, 1H), 7.53 (d, 2H), 7.33 (d, 2H), GCMS: m/z = 322.89.
2.2.2.1 3,6-Dibromo-N-octylcarbazole. Potassium carbonate (40 mmol) was added to 50 mL of anhydrous DMF after 3,6-dibromocarbazole (20 mmol) was dissolved in it. After a one-hour stirring period, 1-bromooctane (30 mmol) was added to the mixture dropwise. The reaction mixture was refluxed for 24 h. After cooling, the mixture was added to water, extracted three times with chloroform, and the combined organic layer was dried over anhydrous magnesium sulphate. Under reduced pressure, the solvent and the unreacted 1-bromooctane were separated, and the residue was purified using column chromatography with a 9 : 1 ratio of hexane: ethyl acetate to yield the compound as a waxy solid. Yield: 80%, ¹H NMR (400 MHz, CDCl₃): δ 8.17 (s, 2H), 7.60–7.52 (d, 2H), 7.30–7.23 (d, 2H), 4.15–4.09 (m, 2H), 2.01–1.97 (m, 1H), 1.35–1.25 (m, 8H), 0.96–0.85 (m, 6H), LCMS: m/z = 435.02.

2.2.3 2,7-Dibromofluorene. Drop by drop, 4 mL of bromine was added to a solution of 9H-fluorene (36 mmol) and iron(III) chloride (1.6 mmol) in CHCl₃ (100 mL) at 0 °C. For twelve hours, the mixture was stirred. It was poured into 50 mL of water after the reaction. NaHCO₃ and NaHSO₃ solution were used to wash the precipitate. After using CHCl₃ to extract the organic layer, anhydrous MgSO₄ was used to dry it. Following filtration, the solvent was extracted using a rotary vacuum evaporator, and the residue was recrystallized from ethanol to produce a white, crystalline product. Yield: 75%, ¹H NMR (400 MHz, CDCl₃): δ 7.66 (s, 2H), 7.60–7.59 (d, 2H), 7.51–7.49 (d, 2H), GCMS: m/z = 321.90.
2.2.3.1 2,7-dibromo-9,9-dioctyl-9H-fluorene⁴⁶. Drop by drop, KOH solution (10 mL, 50%) and 1-Bromooctane (529 mmol) were added to a solution of 2,7-dibromo-9H-fluorene (12 mmol) and tetrabutylammonium bromide (0.0975 mmol) in DMSO (50 mL) under N₂ atmosphere. For two days, the reaction mixture was stirred constantly at 80 °C. The mixture was added to 500 mL of water. Dichloromethane was used to remove the organic layer. The combined organic layer was dried using anhydrous MgSO₄. Reduced pressure was used to extract the solvent. Colorless crystals were obtained by recrystallization of the crude product from hexane. Yield: 89%, ¹H NMR (400 MHz, CDCl₃): δ 7.51 (s, 2H), 7.45 (m, 4H), 1.90 (m, 4H), 1.25–0.86 (m, 24H), 0.83 (t, 6H), LCMS: m/z = 546.15.

2.2.4 9,10-Dibromoanthracene. After combining anthracene (0.056 mol) with acetic acid (300 mL) at room temperature, bromine (0.112 mol) in acetic acid (50 mL) was added dropwise over the course of five minutes. A canary yellow precipitate formed after the reaction was stirred for thirty minutes. After adding 300 mL of water, the suspension was stirred for ten minutes before being filtered and was washed with water. To create the title compound, the yellow solid was vacuum dried for 12 h. Yield: 94%, ¹H NMR (400 MHz, CDCl₃): δ 8.10 (4H, d), 7.35 (4H, d), LCMS: m/z = 336.25.

2.2.5 4,4′-dibromotriphenylamine⁴⁶. NBS (10 mmol) was added in very small portions to a mixture of triphenylamine (10 mmol) in DMF (50 mL). 100 mL of dichloromethane was added to the reaction mixture and stirred for 24 h at room temperature after the color of the solution changed from colorless to light yellow. The mixture was washed with water after the reaction was finished, and the organic layer was separated and dried over MgSO₄. Using a rotary vacuum evaporator, the solvent was evaporated. The crude product was purified using column chromatography over silica gel (hexane: dichloromethane at 5 : 1). Yield: 72%, ¹H NMR (400 MHz, CDCl₃): δ 6.93 (d, 4H), 7.05 (d, 2H), 7.17 (m, 1H), 7.25 (m, 2H), 7.37 (d, 4H). LCMS: m/z = 402.78.

2.2.6 General procedure for polymerization through direct arylation reaction⁴⁷. Dibromo monomer (0.124 mmol), Pd (OAc)₂ (0.012 mmol), and K₂CO₃ (0.31 mmol) were added to a stirred solution of bithiophene (0.124 mmol) in 1.25 mL of N-methylpyrrolidone in a 10 mL Schlenk tube. For five minutes, nitrogen gas was purged through the solution, and the mixture was agitated for 12 h at 80 °C. Methanol was added to the reaction mixture after it had reached room temperature. Following filtration, methanol was used to wash the precipitate. Soxhlet extraction with acetone and methanol was used to purify the polymer for 12 h. The product was separated from methanol by precipitating it using toluene, and vacuum dried.
2.2.6.1 Synthesis of P(BT-PH). Bithiophene (0.124 mmol), 3,7-dibromo-10-octylphenothiazine (0.124 mmol), Pd (OAc)₂ (0.012 mmol), K₂CO₃ (0.31 mmol), and NMP (1.25 mL) were used. Dark green solid. Yield: 75%, UV-visible (THF) λ_max: 428 nm, GPC: Mn = 3350, PDI = 1.37, Td (°C): 317, ¹H NMR (400 MHz, CDCl₃): δ 7–7.21 (m, 5H of bithiophene), 6.72–7.15 (m, ∼6H of phenothiazine), 3.82 (t, 2H, –NCH₂-), 1.92–1.18 (m, ∼12H, aliphatic-H), 0.96 (t, ∼3H, –CH₃).
2.2.6.2 Synthesis of P(BT-CZ). Bithiophene (0.124 mmol), 3,6-Dibromo-N-octylcarbazole (0.124 mmol), Pd (OAc)₂ (0.012 mmol), K₂CO₃ (0.31 mmol), and NMP (1.25 mL) were used. Dark brown solid. Yield: 81%, UV-visible (THF) λ_max: 422 nm, GPC: Mn = 6175, PDI = 1.65, Td(°C): 475, ¹H NMR (400 MHz, CDCl₃): δ 7–7.21 (m, 5H of bithiophene), 7.12–8.5 (m, 6H of carbazole), 4.2 (m, 2H, –NCH₂), 1–1.99 (m, ∼12H, aliphatic-H), 0.98 (t, ∼3H, –CH₃).
2.2.6.3 Synthesis of P(BT-FLN). Bithiophene (0.124 mmol), 2, 7-dibromo-9,9-dioctyl-9H-fluorene (0.124 mmol), Pd (OAc)₂ (0.012 mmol), K₂CO₃ (0.31 mmol), and NMP (1.25 mL) were used. Brown solid. Yield: 79%, UV-visible (THF) λ_max: 411 nm, GPC: Mn = 8534, PDI = 1.53, Td (°C): 476, ¹H NMR (400 MHz, CDCl₃): δ 7–7.21 (m, 5H of bithiophene), 7.38–7.40 (3d, 6H of fluorene), 1.84–1.90 (m, 4H), 1.10–1.20 (m, 20H, aliphatic-H), 0.92 (t, 6H, – CH₃).
2.2.6.4 Synthesis of P(BT-ANT). Bithiophene (0.124 mmol), 9,10-dibromoanthracene (0.124 mmol), Pd(OAc)₂ (0.012 mmol), K₂CO₃ (0.31 mmol), and NMP (1.25 mL) were used. Yellow solid. Yield: 72%, UV-visible (THF) λ_max.: 423 nm, GPC: Mn = 5132, PDI = 1.79, Td (°C): 395, ¹H NMR (400 MHz, CDCl₃): δ 7–7.21 (m, 5H of bithiophene), 7.00–8.35 (d, 8H of anthracene).
2.2.6.5 Synthesis of P(BT-TPA). Bithiophene (0.124 mmol), 4,4′-dibromotriphenylamine (0.124 mmol), Pd (OAc)₂ (0.012 mmol), K₂CO₃ (0.31 mmol), and NMP (1.25 mL) were used. Brown solid. Yield: 74%, UV-visible (THF) λ_max: 421 nm, GPC: Mn = 5586, PDI = 1.23, Td (°C): 441, ¹H NMR (400 MHz, CDCl₃): δ 7–7.21 (m, 5H of bithiophene), δ 6.90–7.35 (d, 10H), 7.15–7.30 (m, 3H).

2.3. Instrumentation

The following experimental techniques were employed for characterization of P(BT-PH), P(BT-CZ), P(BT-FLN), P(BT-ANT), and P(BT-TPA): Fourier Transform Infrared (FT-IR) spectra were obtained using a PerkinElmer Spectrum 100 spectrometer, utilizing KBr pellets. ¹H Nuclear Magnetic Resonance (¹H NMR) spectroscopy was conducted using a Bruker Avance III (400 MHz) spectrometer, with chemical shifts recorded relative to TMS as the internal standard. A Thermo Scientific Evolution 201 UV-visible Spectrophotometer and an Ocean Optics Inc. SD 2000 UV-vis-NIR Ocean Optics Spectrophotometer were used to record the UV-visible absorption and fluorescence emission spectra, respectively. Using dry acetonitrile and Bu₄NPF₆ as the supporting electrolyte, electrochemical experiments were conducted with a BAS Epsilon Electrochemical Analyzer at a quiet time of 2 s and a scan rate of 100 mV s⁻¹. Using a TA Instrument Q 50 thermogravimetric analyzer, thermogravi-metric experiments (TG & DTG) were carried out at a heating rate of 10 °C min⁻¹ under a. Nitrogen atmosphere. By employing Waters GPC with polystyrene standard calibration using THF solution, Gel Permeation Chromatography (GPC) was used to determine the molecular weight and polydispersity index of the copolymers. A Horiba Fluorolog-3 time-correlated single photon counting system (TCSPC) was used to measure the fluorescence lifetime. Using the DAS6 decay analysis program, the data were deconvoluted with exponential decay to yield the fluorescence lifetime values.

The third-order nonlinear susceptibility (χ⁽³⁾) of the copolymers in chloroform was evaluated using Z-scan technique, designed and developed by Sheik Bahae et al.⁴⁸ Nonlinear optical properties of the copolymers were measured using simple and single beam Z-scan technique with nanosecond laser performed with a Q-switched Nd : YAG laser system (Spectra Physics LAB –1760) with pulse width of 7 ns at 10 Hz repetition rate and 532 nm wavelength. In the experiment, a Gaussian laser beam was focused to a narrow waist; its radius (ω_o) was calculated to be 42.56 µm. The sample was moved in the direction of light incidence near the focal spot of the lens with a focal length of 200 mm. The Rayleigh length was estimated to be 10.69 mm, which was much larger than the thickness of either the sample cuvette (1 mm) or the self-assembled films, which is an essential requirement for the validity of the Z-scan theory. CS2 was used as the standard to calibrate the Z-scan system. The transmitted beam energy, reference beam energy and their ratios were measured simultaneously by an energy ratiometer (REj7620, Laser Probe Corp.) having two identical pyroelectric detector heads (Rjp 735). The effects of fluctuations of laser power were reduced by dividing the transmitted power by the power attained at the reference detector; both being measured using identical photo detectors. The data were analysed according to the procedure described by Bahae et al. The nonlinear absorption coefficient was measured by fitting the experimental Z-scan plot with the theoretical plots. Optical power limiting measurements were also carried out to investigate the optical limiting response of the polymer samples. To study the optical limiting property of the polymers, the nonlinear transmission was measured as a function of input intensity.

3 Results and discussion

3.1. Theoretical calculation

Initially, the DFT calculations were performed on the geometries of the bithiophene monomer, the brominated monomers 3,7-dibromo-10-octylphenothiazine (PH), 3,6-dibromo-N-octylcarbazole (CZ), 2,7-dibromo-9,9-dioctyl-9H-fluorene (FLN), 9,10-dibromoanthracene (ANT), and 4,4′-dibromotriphenylamine (TPA), as well as their complementary oligomer units. The Time Dependent Density Functional Theory (TD-DFT) was utilized to calculate the oscillator strength, excitation energy, and absorption maximum of the designed monomers. Table 1 displays the results.

Table 1 Values of E_activation (eV), oscillator strength, and λ_max (nm) of the monomer units obtained by the TD-DFT/B3LYP/6-31G method

Monomer	Optimized geometries of monomers^a	Eactivation^b (eV)	Oscillator strength^b	λma^b (nm)
a Estimated from DFT/B3LYP/6-31G calculation.b Estimated from TD-DFT/B3LYP/6-31G calculation.
2,2′-Bithiophene (BT)		3.98	0.431	312
3,7-Dibromo-10-(octyl)-phenothiazine (PH)		3.96	0.007	315
3,6-dibromo-N-octylcarbazole (CZ)		4.09	0.035	303
2, 7-dibromo-9,9-dioctyl-9H-fluorene (FLN)		4.81	0.171	257
9,10-Dibromo-anthracene (ANT)		3.35	0.068	370
4,4′-dibromo-triphenylamine (TPA)		3.94	0.015	310

---

The B3LYP/6-31G method of Density Functional Theory (DFT) was utilized to investigate the energy levels of monomers and their oligomers. Fig. 1 provides a summary of the results obtained.

Fig. 1 Energy levels of monomers, D−A, and tetramer units of P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA) copolymers.

The energy level diagram revealed the following LUMO levels for BT, PH, CZ, FLN, ANT, and TPA: −0.47, −0.69, −0.61, −0.72, −0.56, and −0.58 eV, in that order. BT−PH, BT−CZ, BT−FLN, BT−ANT, and BT−TPA were found to have LUMO levels of −1.63, −1.39, −1.82, −1.43, and −1.54 eV, respectively. Based on this data, it is evident that HOMO energy levels rise while LUMO levels fall during coupling. The order of the band gaps was BT−FLN > BT−PH > BT−CZ > BT−TPA > BT−ANT. The reduction of band gap was largely influenced by both acceptor strength and geometry.

The band gap reduction observed in the copolymers is primarily attributed to an intramolecular charge transfer phenomenon facilitated by the interaction between the donor (BT) and acceptor (PH, CZ, FLN, ANT, and TPA) moieties. This results in a redistribution of electron density along the polymer backbone, leading to enhanced π-electron delocalization. Additionally, the increased electron delocalization leads to a decrease in the bond length alteration (BLA) of the D−A units.⁴⁹ BLA refers to the distortion or elongation of bonds within the conjugated polymer backbone due to charge redistribution. By minimizing BLA, the copolymer achieves a more uniform distribution of electron density along its structure, thereby reducing the energy required to excite electrons across the band gap. This concept can be further elucidated by examining the frontier orbital distribution of the model compounds, as depicted in Fig. 2.

Fig. 2 Frontier molecular orbital distribution of monomeric unit of BT−PH, BT−CZ, BT−FLN, BT−ANT and BT−TPA.

Polymers were optimized using DFT/HSE06/6-31G and DFT/B3LYP/6-31G methods. The band structure data, ionization potential, and electron affinity of the copolymers are summarized in Table 2.

Table 2 Computational data of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT), and P(BT–TPA) with DFT/HSE06/6-31G^a and DFT/B3LYP/6-31G^b methods

Polymer	HOMO (eV)	IP (eV)	LUMO (eV)	EA (eV)
A comparison of the HOMO–LUMO energy values obtained from DFT/HSE06/6-31G^a DFT/B3LYP/6-31G^b shows a significant difference in the predicted band gaps. The HSE06 functional provides a more accurate and reliable estimation of the band gap for conjugated polymers.
P(BT–PH)	−4.54^a	4.54	−2.02	2.02
	−4.67^b	4.67	−1.76	1.76
P(BT–CZ)	−4.46^a	4.46	−1.78	1.78
	−4.58^b	4.58	−1.53	1.53
P(BT–FLN)	−4.75^a	4.75	−2.27	2.27
	−4.82^b	4.82	−2.30	2.30
P(BT–ANT)	−5.18^a	5.18	−2.24	2.24
	−5.36^b	5.36	−1.96	1.96
P(BT–TPA)	−4.52^a	4.52	−2.28	2.28
	−4.61^b	4.61	−1.74	1.74

---

The band gap values of P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA) copolymers were determined to be 2.90, 3.05, 2.52, 3.39, and 2.86 eV using DFT/B3LYP methods and 2.51, 2.67, 2.48, 2.94, and 2.24 eV using DFT/HSE06 methods, respectively. There is a significant distinction between the band gap values obtained from these two approaches. The method DFT/PBC/HSE06/6-31G is more reliable in predicting the band gap of conjugated polymers than DFT/PBC/B3LYP/6-31G. The first method mentioned, HSE06, employs a screened-hybrid functional to compute the exchange portion of the energy. This approach utilizes an error function screened Coulomb potential, which is fixed to enhance computational efficiency. Screened hybrid functionals, like the HSE method, offer advantages for both finite and extended systems. They are particularly effective in reducing self-interaction errors that commonly arise in systems featuring both localized and delocalized orbitals. In simpler terms, the HSE06 method combines elements of both traditional density functional theory (DFT) and more accurate but computationally intensive methods, such as Hartree-Fock theory.

By incorporating a screened Coulomb potential, this approach achieves a balance between accuracy and computational cost, making it suitable for studying a wide range of systems, including both molecules and extended periodic structures like polymers. HSE06/6-31G theory was used to calculate the ground state unit cell geometries for the Periodic Boundary Condition (PBC). The G09 suite of codes was used to perform the PBC/DFT calculations on IBM power servers. The starting unit cell for the calculations was taken from the central region of the optimized tetramer by assuming that the unit cell was repeated identically an infinite number of times along the translational vector. Fig. 3 displays the PBC/HSE06 optimized unit cell. The length of the translational vector is a crucial parameter in periodic boundary condition (PBC) calculations, as it determines the size of the simulated system along a specific direction. For the polymers P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA), the lengths of the translational vectors were found to be 28.38, 22.31, 31.58, 24.08, and 29.60 Å, respectively. By optimizing the system using the HSE06 level of theory and defining the length of the translational vector, PBC permits band structures in the positive region of the first Brillouin zone (between k = 0 and k = π/a), and the values of the band gap can be calculated. This involves determining the electronic energy levels (bands) along the k-vector for these one-dimensional polymers. In this case, the calculations were performed with 32 k-points, which represent discrete points along the Brillouin zone.^50,51 Fig. 4 displays the band structures of the copolymers P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA). It is evident from the data that all the copolymers are direct band gap polymers, with the lowest band gap occurring at k = 0. The energy levels of bithiophene have been adjusted and rendered suitable for photovoltaic applications through the introduction of acceptor units.

Fig. 3 Unit cell of (a) P(BT−PH), (b) P(BT−CZ), (c) P(BT−FLN), (d) P(BT−ANT), and (e) P(BT−TPA) for the PBC/HSE06/6-31G calculation. The red line represents the translational vector.

Fig. 4 Band structure of (a) P(BT−PH), (b) P(BT−CZ), (c) P(BT−FLN), (d) P(BT−ANT) and (e) P(BT−TPA).

3.2. Polymer synthesis

Scheme 1 summarizes the synthesis of key monomers. The precursor monomer 3,7-dibromo-10-octylphenothiazine was synthesized in two steps starting from phenothiazine. The first step involved alkylation of phenothiazine using 1-bromooctane followed by bromination in 47% HBr. Starting from carbazole, 3,6-dibromo-N-octylcarbazole was prepared by bromination using NBS followed by alkylation. To obtain 2,7-dibromo-9,9-dioctyl-9H-fluorene, 9H-fluorene was treated with iron(III) chloride in CHCl₃ and bromine was added drop by drop, followed by alkylation. The precursor monomers 4,4′-dibromotriphenylamine and 9,10-dibromoanthracene were synthesized by the bromination of triphenylamine and anthracene, respectively. The structure of the monomers was confirmed by ¹H NMR spectra and is depicted in Fig. S1.

Scheme 1 Synthesis of monomer.

The synthesis of copolymers was carried out by an efficient and simple palladium-catalysed direct arylation technique. The bithiophene-based copolymers P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA) attained satisfactory yield by following the synthetic routes outlined in Scheme 2.

Scheme 2 Synthesis of polymers.

In addition to the benefit of reducing toxic by-products, the direct arylation proceeded with a small amount of Pd catalyst (0.012 mmol) in a short reaction time (12 h) compared to conventional polycondensation based on cross-coupling reactions. The copolymers P(BT−PH), P(BT−CZ), P(BT−FLN), P(BT−ANT), and P(BT−TPA) were synthesized through copolymerization of 3,7-dibromo-10-octylphenothiazine (PH), 3,6-dibromo-N-octylcarbazole (CZ), 2,7-dibromo-9,9-dioctyl-9H-fluorene (FLN), 9,10-dibromoanthracene (ANT), and 4,4′-dibromotriphenylamine (TPA) with 2,2′-bithiophene respectively. Here, Pd (OAc)₂ was used as the catalyst, K₂CO₃ as the base, and N-methylpyrrolidone as the solvent at 80 °C for 12 h. The crude copolymers were purified by precipitating in methanol. The precipitate was filtered, followed by Soxhlet extraction using methanol and acetone. The polymers were soluble in common organic solvents such as chloroform, chlorobenzene, THF, and toluene. The reaction in N-methylpyrrolidone (NMP) afforded the polymers in around 70% yield.

The copolymer structures were confirmed by ¹H NMR, FTIR, and GPC analysis. The number average and weight average molecular weights (M_n and (M_w) of the copolymers were determined by GPC analysis. The copolymers showed (M_n a range of 3000–9000 g mol⁻¹ and (M_w) and a range of 4000–14000 g mol⁻¹ with a polydispersity index of 1.2–1.8 using THF as an eluent and polystyrene as the standard. Molecular weight and yield of the copolymers are given in Table 3.

Table 3 Results of direct arylation polymerization

Copolymer	Mn^a	Mw^a	PDI	Yield (%)
a Determined by GPC in THF based on polystyrene standards.
P(BT–PH)	3350	4590	1.37	75
P(BT–CZ)	6175	10189	1.65	81
P(BT–FLN)	8534	13139	1.53	79
P(BT–ANT)	5132	9237	1.79	72
P(BT–TPA)	5586	6926	1.23	74

---

The ¹H NMR spectrum of P(BT–PH), P(BT–CZ), and P(BT–FLN) showed multiplets at the δ 0.8–2.1 region due to alkyl protons. In P(BT–PH) and P(BT–CZ), the peaks corresponding to –NCH₂– protons are observed at δ 3.8–4.1 as triplets. All the copolymers have signals corresponding to aromatic protons and are observed at δ 6.9–7.8 as multiplets. P(BT–FLN) was only slightly soluble in CDCl₃ and showed less intense peaks (Fig. S2–S6).

The FT-IR spectra of the copolymers exhibit characteristic absorptions confirming the incorporation of the designed structural units. The band region 1400–1550 cm⁻¹ is assigned to aromatic/heteroaromatic ring stretching, involving C–C stretching coupled with C–H in-plane bending modes from thiophene and related moieties. Such collective modes are typical in conjugated aromatic systems. The absorption in the 1210–1280 cm⁻¹ region is attributed to ring deformation vibrations of thiophene units, which combine C–C/C–S stretching and C–H in-plane bending. Although a minor C–S contribution may exist, the dominant vibrational character is delocalized aromatic ring motion. For P(BT-PH), the strong bands at 1575 and 1546 cm⁻¹ correspond to aromatic/heteroaromatic ring stretching of the bithiophene and phenothiazine units. The peaks at 2935 and 2860 cm⁻¹ reflect aliphatic C–H stretching, indicative of alkylated phenothiazine substituents. In P(BT-CZ), the 3100 cm⁻¹ band comes from alkenyl C–H stretching, and the 2965 and 2900 cm⁻¹ bands are ascribed to asymmetric C–H stretching in CH₃ and CH₂ groups. The absorption around 1630 cm⁻¹ is consistent with aromatic C–C/C=C stretching in the carbazole–bithiophene backbone. For P(BT-FLN), 2921 and 1370 cm⁻¹ represent aliphatic C–H stretching and bending of the fluorene units. The bands at 809, 851, and 917 cm⁻¹ are C–H out-of-plane bending, and 1064 cm⁻¹ is C–H in-plane bending of phenyl rings, congruent with known fluorene spectra. In P(BT-ANT) and P(BT-TPA), aromatic C–H stretching occurs near 3015–3020 cm⁻¹, and ring stretching modes are observed at 1620–1625 cm⁻¹ and 1540–1545 cm⁻¹, confirming the presence of anthracene and triphenylamine moieties and supporting extended π-conjugation.

3.3. Thermal properties

The onset of degradation and the degradation temperature were determined by thermogravimetric analysis (TGA) in a nitrogen atmosphere at a heating rate of 10 °C min⁻¹. From the TG curve of the synthesized copolymers, it was clear that the polymers showed a single degradation pattern. All the copolymers exhibited high thermal stability, as shown in the TGA curves in Fig. S7. The onset of weight loss temperature for P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) are 300 °C, 425 °C, 451 °C, 363 °C and 425 °C, respectively.

DTG traces showed that the onset of degradation and the degradation temperature of P(BT–PH) were found to be 259 and 317 °C with 4% weight loss at the onset loss point. In P(BT–CZ), the onset of degradation was around 409 °C and the degradation temperature was 475 °C with about 6% weight loss. In the case of P(BT–FLN), P(BT–ANT) and P(BT–TPA) the onset of degradation was around 430 °C, 312 °C and 381 °C and the degradation temperature was 476 °C, 395 °C and 441 °C, respectively with, 7%, 4% and 5% weight loss at the onset loss point. Bithiophene-based polymers have thermal stability much higher than those of homopolymers of phenothiazine,⁵² carbazole⁵³ and fluorene.⁵⁴

3.4. Optical properties

To study the optical absorption, the UV–vis absorption spectra of the polymers P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) in the range of 400 to 800 nm were recorded and are shown in Fig. 5a. The homopolymer, poly(phenothiazine),⁵² poly(carbazole),⁵³ poly(fluorene)⁵⁴ and poly (anthracene)⁵⁵ have low absorption maxima compared to bithiophene-containing copolymers. The insertion of the bithiophene moiety in the polymer backbone has a pronounced influence on the spectroscopic properties of the polymers. The increasing wavelengths of the absorption maxima indicate that the polymers are more conjugated as more thiophene units are added to the structure. The optical band gap of copolymers was determined using Tauc's equation.⁵⁶

Ahν = (hν − E_g)ⁿ (1)

where n is 1/2 for allowed direct transitions, 3/2 for forbidden direct transitions, 2 for allowed indirect transitions, 3 for forbidden indirect transitions. A is absorbance and E_g is band gap corresponding to a particular absorption of photon energy hν.

Fig. 5 (a) UV–visible absorption spectra (b) emission spectra of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA).

For conjugated polymers, which typically exhibit direct allowed transitions, n = 1/2 was used. The direct optical band gap of the polymers was obtained from extrapolating the linear portion of their (Ahν)² versus hν plots to A = 0. The intercept of this extrapolation corresponds to the optical band gap of the polymer.

The onset edge of the lower energy peak of the polymer in THF solution was obtained from the UV–vis absorption data. The band gap of the copolymers, P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) were calculated to be 2.09, 2.14, 2.12, 2.15 and 2.11 eV respectively. Fig. 5b represents the emission spectra of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) in THF medium. The emission peaks of the copolymers are observed at the wavelength range of 515–535 nm. The optical data of the polymers are summarized in Table 4.

Table 4 Optical properties of polymers in THF solution

Polymer	Absorption λmax (nm)	Absorption onset (nm)	Emission λmax (nm)	Eg (eV)
P(BT–PH)	428	592	534	2.09
P(BT–CZ)	422	579	532	2.14
P(BT–FLN)	411	585	517	2.12
P(BT–ANT)	423	577	530	2.15
P(BT–TPA)	421	587	525	2.11

---

3.5. Time-resolved fluorescence measurements

Time-correlated single photon counting (TCSPC) is a highly sensitive technique used to quantify the fluorescence decay of bithiophene-based copolymers. When a laser pulse was used to excite the polymer in the time-resolved fluorescence decay experiment, it started out strongly and quickly began to decay. One of the key advantages of TCSPC is its ability to detect extremely low levels of emission from a sample, even over long-time scales in the nanosecond range. This sensitivity makes TCSPC particularly useful for studying materials with low fluorescence intensity or for detecting subtle changes in fluorescence behavior over time. The type of decay, fluorescence lifetime, and amplitudes of the copolymer were extracted using a fluorescence decay curve derived from the suitably fitted functions acquired from the TCSPC measurement. At 340 nm, the copolymers P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT), and P(BT–TPA) in CHCl₃ were excited. The single exponential fit could not adequately describe the observed decay. Due to the presence of several fluorescing moieties with varying lifetimes, bi-exponential fitting was used to obtain the fluorescence decay curve in the case of bithiophene-based polymers (Fig. 6). The pre-exponential factors are the α1 and α2, and the lifetimes are τ1 and τ2. It was observed that the average lifetimes of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT), and P(BT–TPA) were, respectively, 8.70, 7.02, 6.22, 4.43, and 2.38 ns.

Fig. 6 Biexponential fitted decay curves of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) in CHCl₃ at 340 nm excitation.

One of the key characteristics of fluorescent materials is the quantum yield of fluorescence. It is utilized to evaluate the efficiency of the emission process and assess the suitability of such materials for use as the active elements in optical devices as well as for applications in chemical sensing, bioanalysis, and fluorescence imaging. Various techniques were developed to accurately determine the quantum efficiency. The “absolute” method, which collected the entire spatially distributed fluorescence emission, was applied in this instance.⁵⁷ Using 340 nm as the excitation wavelength, the quantum yield of the copolymers was determined. The quantum yields were determined to be 0.43, 0.39, 0.49, 0.45, and 0.37 for P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT), and P(BT–TPA), respectively, using the same excitation wavelength. The suitability of the copolymers for use as active components in optical devices has been proved by the high quantum efficiency exhibited by all the bithiophene polymers. Table 5 delivers an overview of the quantum yields and the magnitude of the decay times of the bithiophene-based copolymers across the emission wavelength.

Table 5 Fluorescence lifetimes, pre-exponential factors, and quantum yield of P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT) and P(BT–TPA) in CHCl₃ at 340 nm excitation

Polymer	χ^2	τ1 (ns)	α1%	τ2 (ns)	α2%	τav (ns)	ϕ^d
P(BT–PH)	1.16	0.85	96.78	3.26	3.22	8.70	0.43
P(BT–CZ)	1.24	0.63	86.05	2.83	13.95	7.02	0.39
P(BT–FLN)	1.19	0.31	74.14	7.83	25.86	6.22	0.49
P(BT–ANT)	1.11	0.42	95.75	2.41	4.25	4.43	0.45
P(BT–TPA)	0.91	0.12	40.15	0.69	59.85	2.38	0.37

---

3.6. Nonlinear optical properties

The third-order nonlinear susceptibility (χ⁽³⁾) of the copolymers in chloroform was evaluated using the Z-scan technique, designed and developed by Sheik Bahae et al.^58–61 The open-aperture (OA) Z-scan trace of the bithiophene-based copolymers in CHCl₃ at 532 nm is presented in Fig. 7. The open-aperture (OA) Z-scan plots exhibited a normalized transmittance valley-type graph, indicating that they behave as reverse saturable absorption type graph (RSA) with a positive nonlinear absorption coefficient. The third-order nonlinear absorption coefficient (β) and imaginary part of the nonlinear susceptibility (Im χ⁽³⁾) were determined by Z-scan technique under an open aperture configuration (Table 6). The polymers showed large optical nonlinearity due to strong delocalization of π electrons. It is clear from the figure that the nonlinear absorption traces of the copolymers fitted well with the graph derived from the two-photon absorption (TPA) theory. This concludes that TPA is the basic mechanism involved in the nonlinear absorption process.

Fig. 7 Open aperture (OA) Z-scan traces of P(BT–PH), P(BT–CZ) P(BT–FLN) and P(BT–TPA) in CHCl₃ at 79 µJ.

Table 6 Calculated values of nonlinear absorption coefficient and imaginary part of nonlinear susceptibility of P(BT–PH) and P(BT–CZ) at 532 nm

Copolymer	Nonlinear absorption coefficient (β, m W^−1)	Imaginary part of nonlinear susceptibility (Im χ^(3), esu)
P(BT–PH)	3.85 × 10^−10	0.81 × 10^−11
P(BT–CZ)	2.87 × 10^−10	0.62 × 10^−11
P(BT–FLN)	2.99 × 10^−10	0.67 × 10^−11
P(BT–TPA)	3.01 × 10^−10	0.65 × 10^−11

---

The nonlinear absorption coefficient, β, was obtained by fitting the experimental scan plot of the OA measurement to the equation

where, q₀(z,r,t) = βI₀L_eff, with β is the NLA coefficient. I₀ is the incident irradiance at the beam focus (z = 0). The effective sample thickness, L_eff, is given bywhere α is the linear absorption coefficient, and ‘I₀’ is the irradiance at focus.

Also, the imaginary part of the third-order susceptibility (Im χ ⁽³⁾) of copolymers was determined by equation⁵⁹

where n₀ is the linear refractive index of the polymer in chloroform solution, c is the velocity of light in a vacuum, ω is the angular frequency of radiation, which is obtained from the equation ω = 2πc/λ, where λ = 532 nm. The experimentally determined values of β and Im χ⁽³⁾ were found to be in the order of 10⁻¹⁰ m W⁻¹ and 10⁻¹¹ esu respectively. The values implied that the band gaps of the donor–acceptor copolymers P(BT–PH), P(BT–CZ), P(BT–FLN) and P(BT–TPA) were in the semiconducting range. The charge transfer from the donor to the acceptor units results in strong nonlinearity of the copolymers.

The nonlinear absorption coefficient is obtained to be 3.85 × 10⁻¹⁰ and 2.87 × 10⁻¹⁰, 2.99 × 10⁻¹⁰ and 3.01 × 10⁻¹⁰ m W⁻¹ for P(BT–PH), P(BT–CZ) P(BT–FLN) and P(BT–TPA) respectively. There was a slight increase in the β value of P(BT–PH) compared to other bithiophene-based polymers. In addition, the χ⁽³⁾ value was also found to be increased for P(BT–PH). The large optical nonlinearity of P(BT–PH) compared to other polymers was due to the greater acceptor strength of PH than the CZ, FLN and TPA units. In the case of D–A copolymers, nonlinearity is generally due to the charge transfer from donor to acceptor unit, i.e., due to strong delocalization of π electrons. The optical limiting process occurs mainly due to the nonlinear absorption; it is the result of the extent of conjugation, donor–acceptor groups, dimensionality, conformation, and orientation. The optical limiting properties of the copolymers P(BT–PH), P(BT–CZ), P(BT–FLN) and P(BT–TPA) were investigated by the OA Z-scan technique at 532 nm. Fig. 8 presents the transmitted energy of bithiophene-based polymers as a function of input intensity. At low input fluence the output varies linearly with input energy, i.e., polymers obey Beer's law. When the input power reaches the optical limiting threshold, the transmitted energy starts to deviate and show the optical limiting effect.

Fig. 8 Optical limiting curves of P(BT–PH), P(BT–CZ) P(BT–FLN) and P(BT–TPA).

The optical limiting threshold was obtained directly from the optical limiting curves (normalized transmittance vs. power density). The linear portion of the curve at low power was extrapolated, and the point where the transmittance began to deviate significantly from this linear region was identified as the onset of nonlinear absorption. The corresponding power density at this deviation point was taken as the optical limiting threshold. Optical limiting threshold is determined to be 0.21, 0.26, 0.23 and 0.49 GW cm⁻² for P(BT–PH), P(BT–CZ), P(BT–FLN) and P(BT–TPA) respectively. The polymer with a low value of optical limiting threshold is a good optical limiter. All the copolymers exhibited superior optical limiting response, which was due to the donor–acceptor scheme. The P(BT–PH) showed a slightly better optical limiting response than P(BT–CZ), P(BT–FLN) and P(BT–TPA). The copolymers exhibited large optical nonlinearity due to the strong delocalization of π-electrons.

3.7. Conclusion

In conclusion, it was demonstrated theoretically that the band gaps of the conjugated polymers were effectively reduced by the addition of 2,7-dibromo-9,9-dioctyl-9H-fluorene, 4,4′-dibromotriphenyl amine, 3,7-dibromo-10-octyl phenothiazine, 3,6-dibromo-N-octylcarbazole, and 9,10-dibromoanthracene units to the bithiophene unit in accordance with the donor–acceptor concept. The acceptor strength of the PH, CZ, FLN, ANT, and TPA, which aided in the charge transfer from donor to acceptor units, determined the band gap reduction. The polymers P(BT–PH), P(BT–CZ), P(BT–FLN), P(BT–ANT), and P(BT–TPA), synthesized via direct arylation, were characterized using photophysical techniques, including time-resolved fluorescence studies. The synthesized bithiophene-based donor–acceptor copolymers P(BT–PH), P(BT–CZ), P(BT–FLN), and P(BT–TPA) showed significant third-order nonlinear optical (NLO) properties. Their imaginary parts of the third-order nonlinear susceptibility (Im χ³) were in the order of 10⁻¹¹ esu, and their nonlinear absorption coefficients (β) were in the range of 10⁻¹⁰ m W⁻¹. P(BT–PH) had the highest β (3.85 × 10⁻¹⁰ m W⁻¹) and Im χ³ (0.81 × 10⁻¹¹ esu) values of all the polymers under study. This was because the phenothiazine unit was powerful at accepting electrons, which allowed for more effective intramolecular charge transfer. A Superior NLO response and a lower optical limiting threshold (0.21 GW cm⁻²) were the results of this improved charge delocalization in comparison to the other polymers. At 532 nm, all the copolymers exhibited strong optical limiting behavior, mostly because of effective donor–acceptor interactions and good π-electron delocalization. As the input intensity increased, the materials absorbed more light nonlinearly, reducing the transmitted energy and clearly showing optical limiting beyond a certain threshold. Among them, P(BT–PH) performed the best, making these materials promising candidates for real-world applications like laser safety goggles, optical sensors, and protective coatings in photonic and optoelectronic devices, where fast and reliable response to high-intensity light is essential.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting the findings of this article, including spectroscopic, electrochemical, photophysical, and computational results, are provided in the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ra06096f.

Acknowledgements

The authors express their sincere gratitude to Cochin University of Science and Technology (CUSAT) for academic and laboratory support, and to the Kuwait Institute for Scientific Research (KISR), Kuwait, for providing research facilities that significantly contributed to this study.

References

1. T. Liu, J. Heimonen, Q. Zhang, C.-Y. Yang, J.-D. Huang, H.-Y. Wu, M. Antoine Stoeckel, P. A. Tom, V. Pol, Y. Li, S. Y. Jeong, A. Marks, X.-Y. Wang, Y. Puttisong, A. Y. Shimolo, X. Liu, S. Zhang, Q. Li, M. Massetti, W. M. Chen, H. Y. Woo, J. Pei, I. McCulloch, F. Gao, M. Fahlman, R. Kroon and S. Fabiano, Nat. Commun., 2023, 14, 8454.
2. (a) C. S. Sarap, Y. Singh, J. M. Lane and N. Rai, Sci. Rep., 2023, 13, 21587; (b) R. M. Gamini Rajapakse, K. Liyanage, H. Kumara and W. Perera, RSC Adv., 2022, 12, 12089–12115.
3. (a) A. Azeez, Y. Huang, L. Stanly, Z. Kan and S. Karuthedath, EES Sol., 2025, 1, 248–266; (b) Z. Wang, Y. Guo, X. Liu, W. Shu, G. Han, K. Ding, S. Mukherjee, N. Zhang, H. L. Yip, Y. Yi, H. Ade and P. C. Y. Chow, Nat. Commun., 2024, 15, 1212.
4. X. Kong, J. Zhang, L. Meng, C. Sun, S. Qin, C. Zhu, J. Zhang, J. Li, Z. Wei and Y. Li, CCS Chem., 2023, 5, 841–850.
5. (a) M. W. Jeong, J. H. Ma, J. S. Shin, J. S. Kim, G. Ma, T. U. Nam, X. Gu, S. J. Kang, J. Y. Oh and J. Jeong, Sci. Adv., 2023, 9, eadh1504; (b) N. Guan, X. Dai, A. V. Babichev, F. H. Julien and M. Tchernycheva, Chem. Sci., 2017, 8, 7904–7911.
6. Y. Li, Q. Wei, L. Cao, F. Fries, M. Cucchi, Z. Wu, R. Scholz, S. Lenk, B. Voit, Z. Ge and S. Reineke, Front. Chem., 2019, 7, 688.
7. (a) B. Amna and T. Ozturk, J. Mater. Chem. C, 2025, 13, 8354–8424; (b) M. Kim, S. U. Ryu, S. A. Park, K. Choi, T. Kim, D. Chung and T. Park, Adv. Funct. Mater., 2019, 1–25.
8. S. Ren, Z. Wang, W. Zhang, Y. Ding and Z. Yi, Polymers, 2023, 15, 3713.
9. (a) C. Zhang, L. Yao, M. Pu and C. Zhou, RSC Appl. Polym., 2025, 3, 549–573; (b) T. P. Kaloni, P. K. Giesbrecht, G. Schreckenbach and M. S. Freund, Chem. Mater., 2017, 29, 10248–10283.
10. K. Namsheer and C. S. Rout, RSC Adv., 2021, 11, 5659.
11. O. S. Adedoja, E. R. Sadiku and Y. Hamam, J. Inorg. Organomet. Polym. Mater., 2023, 33, 3915–3934.
12. Q. Wang, R. Takita, Y. Kikuzaki and F. Ozawa, J. Am. Chem. Soc., 2010, 132, 11420.
13. S. Tamba, K. Shono, A. Suige and A. Mori, J. Am. Chem. Soc., 2011, 133, 9700.
14. (a) X. Yuan, J. Li, W. Deng, X. Zhou and C. Duan, Chem. Sci., 2025, 16, 14424–14447; (b) S. Ye, V. Lotocki, H. Xu and D. S. Seferos, Chem. Soc. Rev., 2022, 51, 6442–6474.
15. Y. Wang, Y. Cao, X. Zeng, J. Huang and Y.-N. Liu, Ind. Eng. Chem. Res., 2021, 60, 931–938.
16. (a) S. H. Wang, T. W. Wang, H. C. Tsai, P. C. Yang, C. F. Huang and R. H. Lee, RSC Adv., 2020, 10, 9525–9535; (b) M. K. Charyton, T. Reiker, K. Kotwica, H. Zacharias and N. D. Boscher, Mater. Adv., 2023, 4, 2625–2635.
17. T. Reiker, Z. Liu, C. Winter, N. F. Kleimeier, D. Zhang and H. Zacharias, J. Phys. Chem. C, 2021, 125, 5572–5580.
18. (a) M. Ilakiyalakshmi and A. A. Napoleon, RSC Adv., 2024, 14, 8885–8895; (b) R. N. Tezel and I. Kaya, Arab. J. Chem., 2020, 13, 3123–3136.
19. J. Wu, Z. Zeng, Q. Chen, J. Zheng and C. Xu, Polymers, 2019, 96, 1093.
20. R. R. Yue, J. K. Xu, B. Y. Lu, C. C. Liu, Z. J. Zhu and Z. Zhang, Chin. J. Polym. Sci., 2010, 28, 771.
21. Y. Chao, J. Chen, Y.-J. Chiou, P. Kao, J.-L. Wu, C.-T. Chen, L.-H. Chan and R.-J. Jeng, Polymers, 2020, 12, 2964.
22. L. Zani, A. Dessì, D. Franchi, M. Calamante, G. Reginato and A. Mordini, Coord. Chem. Rev., 2019, 392, 77–236.
23. S. Xu, E. H. Kim, A. Wei and E. Negishi, Sci. Technol. Adv. Mater., 2014, 15, 044201.
24. I. D. Kostas, Catalysts, 2021, 11, 473.
25. P. X. T. Rinu, R. M. Philipa and G. Anilkumar, Org. Biomol. Chem., 2023, 21, 6438–6455.
26. W. T. Neo, Q. Ye, Z. Shi, S.-J. Chuaac and J. Xu, Mater. Chem. Front., 2018, 2, 331–337.
27. (a) J. Kimpel, Y. Kim, J. Asatryan, J. Martín, R. Kroon and C. Müller, Chem. Sci., 2024, 15, 7679–7688; (b) N. S. Yuan, H. A. Lin, A. Uva, S. H. Huang and H. Tran, Macromolecules, 2023, 56, 8947–8955.
28. S.-Y. Jang, I.-B. Kim, Y. Kim, D.-H. Lim, H. Kang, M. Heeney and D.-Y. Kim, Adv. Mater., 2022, 43, 2200405.
29. G. E. Castillo and B. C. Thompson, Macro Lett., 2023, 12, 1339–1344.
30. M. Leclerc, S. Brassard and S. Beaupré, Polym. J., 2020, 52, 13–20.
31. L. Ye and B. C. Thompson, J. Polym. Sci., 2022, 60, 393–428.
32. T. van Mourik, M. Bühl and M.-P. Gaigeot, Philos. Trans. R. Soc., A, 2014, 372, 20120488.
33. C. Gustafsson, M. Linares and P. Norman, J. Phys. Chem. A, 2020, 124, 875–888.
34. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
35. K. Kornobis, N. Kumar, P. Lodowski, M. Jaworska, P. Piecuch, J. J. Lutz and P. M. Kozlowski, J. Chem. Theory Comput., 2013, 9, 987.
36. N. Kumar, M. Alfonso-Prieto, C. Rovira, P. Lodowski, M. Jaworska and P. M. Kozlowski, J. Chem. Theory Comput., 2011, 7, 1541.
37. K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089.
38. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
39. F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, J. Phys. Chem., 1995, 99, 16883.
40. J. F. Dobson, G. Vignale and M. P. Das, Electronic Density Functional Theory: Recent Progress and New Directions, Springer Science & Business Media, 2013.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. J. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.02, Gaussian, Inc., Wallingford, CT, 2009.
42. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
43. N. Marom, A. Tkatchenko, M. Rossi, V. V. Gobre, O. Hod, M. Scheffler and L. Kronik, J. Chem. Theory Comput., 2011, 7, 3944.
44. S. Guangyi, Z. Yingping and L. Yongfang, J. Phys. Chem. C, 2008, 112, 12058.
45. A. P. Demchenko, Introduction to Fluorescence Sensing, Springer, Switzerland, 2nd edn, 2015.
46. Y. Zhu, A. R. Rabindranath, T. Beyerlein and B. Tieke, Macromolecules, 2007, 40, 6981.
47. (a) J. Kuwabara, Y. Nohara, S. J. Choi, Y. Fujinami, W. Lu, K. Yoshimura, J. Oguma, K. Suenobu and T. Kanbara, Polym. Chem., 2013, 4, 947–953; (b) S. W. Chang, H. Waters, J. Kettle, Z. R. Kuo, C. H. Li, C. Y. Yu and M. Horie, Macromol. Rapid Commun., 2012, 33, 1927–1932.
48. (a) M. S. Bahae, A. A. Said, T. H. Wei, D. J. Hagan and E. W. Van Stryland, IEEE J. Quantum Electron., 1990, 26, 760; (b) J. Wang, M. S. Bahae, A. A. Said, D. J. Hagen and E. W. V. Stryland, J. Opt. Soc. Am. B, 1994, 11, 1009; (c) A. A. Said, M. S. Bahae, D. J. Hagan, T. H. Wei, J. Wang, J. Young and E. W. V. Stryland, J. Opt. Soc. Am. B, 1992, 9, 405; (d) K. B. Vu, V. V. Vu, H. P. T. Thu, H. N. Giang, N. M. Tam and S. T. Ngo, Synth. Met., 2018, 246, 128–133.
49. (a) S. R. Marder, J. W. Perry, B. G. Tiemann, C. B. Gorman, S. Gilmour, S. L. Biddle and G. Bourhill, J. Am. Chem. Soc., 1993, 115, 2524–2526; (b) M. S. Bahae, A. A. Said and E. W. Van Stryland, Opt. Lett., 1989, 14, 955.
50. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
51. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785; (b) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
52. M. M. Alam and S. A. Jenekhe, Chem. Mater., 2002, 14, 4775.
53. I. L. Vesque, P. O. Bertrand, N. Blouin, M. Leclerc, S. Zecchin, G. Zotti, C. I. Ratcliffe, D. D. Klug, X. Gao, F. Gao and J. S. Tse, Chem. Mater., 2007, 19, 2128.
54. B. Liu, W. L. Yu, Y. H. Lai, W. Huang and B. Liu, Opt. Mater., 2002, 21, 125.
55. K. Rameshbabu, Y. Kim, T. Kwon, J. Yoo and E. Kim, Tetrahedron Lett., 2007, 48, 4755.
56. M. A. Abdullah and Al Hussam, J. Assoc. Arab Univ. Basic Appl. Sci., 2012, 11, 27.
57. R. Zhao, X. Ji, S. Jiang, L. Liu, B. L. Weeks and Z. Zhang, Green Chem., 2011, 13, 1891.
58. M. S. Bahae, A. A. Said and E. W. Van Stryland, Opt. Lett., 1989, 14, 955.
59. M. S. Bahae, A. A. Said, T. H. Wei, D. J. Hagan and E. W. Van Stryland, IEEE J. Quantum Electron., 1990, 26, 760.
60. J. Wang, M. S. Bahae, A. A. Said, D. J. Hagan and E. W. Van Stryland, J. Opt. Soc. Am. B, 1994, 11, 1009.
61. A. A. Said, M. S. Bahae, D. J. Hagan, T. H. Wei, J. Wang, J. Young and E. W. Van Stryland, J. Opt. Soc. Am. B, 1992, 9, 405.

---