 Open Access Article
Open Access ArticleMulti-objective optimization design of microchannel reactors for Fischer–Tropsch synthesis using CFD, GENN, and NSGA-II
Shijie Ren a and
Yuanyang Wang*b
a and
Yuanyang Wang*b
aTaiyuan University of Science and Technology, College of Materials Science and Engineering, College of Energy and Materials Engineering, 66 Waliu Road, Wanbailin District, Taiyuan, Shanxi Province 030024, China. E-mail: renshijie@tyust.edu.cn
bTaiyuan University of Science and Technology, College of Chemical Engineering and Technology, 66 Waliu Road, Wanbailin District, Taiyuan, Shanxi Province 030024, China. E-mail: yywangs@163.com
First published on 8th January 2026
Abstract
In Fischer–Tropsch synthesis processes, microchannel reactors exhibit pronounced process intensification compared with conventional fixed-bed reactors. Computational fluid dynamics was coupled with a surrogate model based on a gradient-enhanced neural network to systematically evaluate the influence of four characteristic geometric variables on the catalytic performance of multi-tubular microchannel reactors. A multi-objective optimization aimed at maximizing C5+ yield and concurrently minimizing the maximum temperature rise was then conducted using the non-dominated sorting genetic algorithm-II. The resulting Pareto frontier was analyzed to identify the solutions that optimally reconcile thermal safety and productivity. The results indicate that, relative to the initial design, the selected optimal configuration reduces ΔTmax by 7.2 °C and increases YC5+ by a factor of 1.86, substantially enhancing reactor performance and providing both a theoretical basis and design reference for pilot-scale demonstration and industrial deployment of Fischer–Tropsch microchannel reactors.
1. Introduction
Non-oil-based carbon resources such as coal, natural gas, and biomass can be converted into clean fuels and high-value chemicals via Fischer–Tropsch synthesis (FTS), thereby alleviating energy shortages, strengthening strategic energy security, and reducing environmental pollution.1 Owing to the strongly exothermic nature of the FTS, microchannel reactors exhibiting superior interphase heat and mass transfer characteristics are employed to effectively suppress thermal runaway and enhance selective hydrocarbon productivity.2 Nevertheless, the micro/millimetric characteristic dimensions preclude intrusive insertion of temperature, concentration, or pressure probes, which inevitably disturbs the flow field; complete spatial profiles of temperature, concentration, and pressure cannot be obtained experimentally, and reactor design therefore is primarily based on computational fluid dynamics (CFD) simulations.3In recent years, CFD has been coupled with optimization algorithms for the design of diverse reactor types. Lee et al.4 rapidly determined the catalyst packing ratio in a four-channel reactor by integrating CFD with a Bayesian envelope optimization algorithm. Teimouri et al.5 embedded a genetically calibrated trimetallic kinetic scheme within a two-dimensional porous-medium CFD model to accurately predict the C5+ distribution in a fixed bed. Na et al.6 employed a CFD-genetic algorithm framework to optimize a zoned catalyst dilution strategy, achieving a significant reduction in temperature rise and an improved yield. Nevertheless, conventional CFD-based design remains a labor-intensive procedure:7 any variation in diameter, length, or thickness necessitates remodeling, remeshing, and re-specification of boundary conditions. When the design space encompasses tens to hundreds of geometric combinations, the “geometry–mesh-solution” cycle becomes computationally prohibitive, and the discrete results yield sparse gradient information for continuous-space optimization.
Gaussian-process regression, radial-basis-function interpolation, and neural networks are routinely employed to construct input–output mappings from limited CFD samples, enabling the resulting surrogate models to replace the CFD solver during the optimization loop and thereby alleviate the associated computational burden. Mishra et al.8 coupled CFD with a deep neural network to enable rapid prediction of local hydrodynamic variables such as bubble number density in a slurry-bed hydrocracking reactor. Qiu et al.9 generated two-dimensional H2 concentration fields from CFD simulations of a methanol steam-reforming fixed bed and subsequently trained a multilayer-perceptron surrogate model to map spatial coordinates to concentration, reducing computational time by 90%. Jung et al.10 performed a dual-objective optimization of reactor volume and maximum temperature difference for a U-cooled microchannel FT process by training an artificial-neural-network surrogate with CFD samples. Ansys has further slashed CFD simulation turnaround times via its cloud-native SimAI platform, which leverages physics-informed AI models trained on legacy simulation datasets to accelerate performance predictions by 10–100 times compared with traditional solvers.11 Collectively, these studies and reports demonstrate that CFD-surrogate coupling constitutes a viable route for mitigating computational intensity in CFD-driven design.12 Surrogate-based modeling enables computationally efficient and quantitative evaluation of the catalytic performance of the microreactor within the bounded geometric design space. Owing to inherent trade-offs among reactor-design variables, multi-objective optimization algorithms must be implemented to identify the Pareto frontier and hence the optimal compromise.10,13 Jiang et al.14 developed a CFD–ANN–NSGA-II framework to optimize the structural parameters of a stirred-tank reactor with high computational efficiency. Zhang et al.15 employed NSGA-II to minimize radial temperature difference and maximize CO conversion, thereby determining the optimal operating conditions of a helium-heated reverse water–gas shift reactor. However, studies on surrogate-assisted multi-objective optimization for Fischer–Tropsch synthesis in multi-tubular microchannel reactors remain unavailable in the open literature.
On the basis of our previously validated CFD model,16 this work presents an integrated framework that combines sensitivity analysis, surrogate modelling and multi-objective optimization for the geometric design of a multi-tubular microchannel reactor for FTS. Latin hypercube sampling (LHS) was used to generate 250 CFD cases within the bounds of the four geometric design variables (RL, RD, RT, RS). A gradient-enhanced neural network (GENN) surrogate model exhibiting the highest predictive accuracy was then constructed, eliminating the need for further computationally intensive simulations. Finally, the GENN surrogate model was integrated with the Non-dominated Sorting Genetic Algorithm II (NSGA-II) algorithm to minimize the maximum temperature rise (ΔTmax) and maximize the C5+ yield (YC5+). The resulting Pareto frontier was analyzed to identify Pareto-optimal solutions that balance thermal stability and productivity, providing a quantitative design basis and optimization strategies for pilot-to-industrial scale-up of multi-tubular microchannel FTS reactors.
2. Reactor model and optimization strategy
2.1 Reactor model
Fig. 1 illustrates the multi-tubular microchannel reactor employed in this study. The reactor consists of seven inner tubes (Tube I) and one outer tube (Tube II). Tube I are axisymmetrically arranged around the central axis of Tube-II, with their ends recessed 30 mm from the corresponding inlet/outlet. The inlet and outlet headers are packed with inert particles to guarantee fully developed laminar flow inside the reactor. Both the inner and outer surfaces of Tube I undergo controlled chemical etching, ultrasonic cleaning and subsequent wash-coating with the active catalytic layer reported in ref. 17, thereby serving simultaneously as catalytic surfaces and mechanical supports. Syngas enters the reactor through the inlet of Tube-II and reacts on the catalytically active surface of Tube I. Reactor fabrication, CFD modelling, validation and flow-field distribution detailed in ref. 16 and 17 are reused here with the same geometric model, mesh, governing equations, kinetics and boundary conditions, with only the dimensions of Tube I treated as parametric variables. Specifically, the CFD model was previously validated in ref. 16, which described a multi-tubular microchannel reactor loaded with Fe-supported catalysts and featuring an identical geometric configuration to that of the present work. Ref. 16 investigated a wide range of operating parameters (inlet temperature: 220–380 °C, pressure: 0.1–2.1 MPa, H2/CO ratio: 1/3–7/3, GHSV: 2000–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1), which fully covers the fixed baseline operating conditions utilized in this study. The simulation results from ref. 16 showed good agreement with experimental data, with mean absolute relative residuals of 11.74% for CO conversion and 0.43% for reactor center temperature, confirming the model's reliability. This consistency in reactor geometry and overlap in operating conditions between ref. 16 and the current study provide robust support for the credibility of the optimized design's simulation results, thereby enhancing the work's reference value for subsequent pilot-scale demonstrations. Geometric design variables including tube length (RL), inner diameter (RD), wall thickness (RT) and inter-tube spacing (RS) are specified in Fig. 1, where RS is established via two one-piece multi-tube locating sleeves positioned inside Tube-II at both ends of the bundle. The corresponding values of each variable are listed in Table 1.
000 h−1), which fully covers the fixed baseline operating conditions utilized in this study. The simulation results from ref. 16 showed good agreement with experimental data, with mean absolute relative residuals of 11.74% for CO conversion and 0.43% for reactor center temperature, confirming the model's reliability. This consistency in reactor geometry and overlap in operating conditions between ref. 16 and the current study provide robust support for the credibility of the optimized design's simulation results, thereby enhancing the work's reference value for subsequent pilot-scale demonstrations. Geometric design variables including tube length (RL), inner diameter (RD), wall thickness (RT) and inter-tube spacing (RS) are specified in Fig. 1, where RS is established via two one-piece multi-tube locating sleeves positioned inside Tube-II at both ends of the bundle. The corresponding values of each variable are listed in Table 1.
2.2 Integrated CFD-surrogate-optimization workflow
A hybrid CFD–GENN–NSGA-II workflow (Fig. 2) is proposed for the high-fidelity design of the multi-tubular microchannel reactor loaded with Fe-supported catalysts for FTS. Reaction kinetics and grid independence have been validated previously in ref. 16 (white block). Three tasks were undertaken in the present study: | ||
| Fig. 2 Hybrid CFD–GENN–NSGA-II workflow for multi-objective optimization of the microchannel reactor for FTS. | ||
(1) Sensitivity analysis (yellow block): the established CFD model was exercised under fixed operating conditions (inlet temperature 340 °C, H2/CO = 2/3, P = 0.7 MPa, GHSV = 8000 h−1) to quantify the individual influence of RL, RD, RT and RS on ΔTmax and YC5+, thereby delimiting the feasible design space.
(2) Surrogate-model construction (blue block): a 250-point LHS design was generated and evaluated by CFD. The data set was randomly split into training (60%), validation (20%) and test (20%) subsets; a GENN surrogate model was then trained to provide rapid estimation of the objective functions across the design space.
(3) Multi-objective optimization (green block): NSGA-II was employed to maximize YC5+ while minimizing ΔTmax, yielding the Pareto frontier and corresponding trade-off solutions.
Geometric modelling was carried out in Ansys SpaceClaim, whereas mesh generation and CFD simulations were performed in Ansys Fluent, which provides practically proven and mature computational capacities for reactive flow research.18 Training of the surrogate model was conducted with SMT (Surrogate Modeling Toolbox) package v.2.9.5,19 and the optimization routine was handled by PyMOO (Multi-Objective Optimization in Python) package v.0.6.1.5.20 All computations and Python scripting were executed on a Dell Precision 7920 Tower workstation (2× Intel Xeon Gold 6258R, 56 cores). Each design cycle was completed in approximately 5 min, corresponding to a ten-fold reduction from the conventional 50 min workflow and substantially improving the computational efficiency of multi-objective optimization of microchannel reactors.
2.3 Surrogate-model selection
Surrogate models were introduced to replace the computationally expensive CFD step and to provide a rapid mapping between design variables and reactor performance. Two candidate surrogates from the SMT library were benchmarked: (i) KRG: a data-efficient Gaussian-process Kriging estimator that simultaneously returns predictive mean and variance, thereby furnishing a built-in metric for adaptive infilling;21 (ii) GENN: a feed-forward network with known adjoint gradients embedded in the loss function, yielding higher-order convergence and superior generalization in a four-dimensional continuous design space for the same sample size.22 The procedure is summarized below:Step 1: sample generation: 250 designs were generated in the 4-D space (RL, RD, RT, RS) by LHS and sequentially solved by CFD, generating y1(YC5+) and y2(ΔTmax) to form the complete data set.
Step 2: data partitioning: the data were randomly partitioned 60%/20%/20% into training, validation and test subsets. The training subset was used to fit the surrogate, the validation subset to monitor generalization error and facilitate hyper-parameter tuning with early stopping, and the test subset to provide an unbiased estimate of predictive accuracy.
Step 3: model training and assessment: KRG and GENN were trained concurrently. Accuracy was quantified by normalized mean absolute error (NMAE) and normalized root-mean-square error (NRMSE), defined in eqn (1) and (2). The model exhibiting the lower validation error was selected for the subsequent optimization loop.
 | (1) |
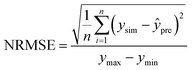 | (2) |
2.4 Optimization strategy
In the previously reported CFD model from ref. 16, products from FTS and WGS were lumped into C1, C3, C5+ and CO2. Maximizing YC5+ was set as the first objective. As FTS is strongly exothermic, previous studies23,24 commonly limit ΔT to 20 °C to mitigate thermal runaway.
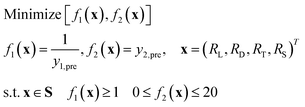 | (3) |
ΔTmax minimization was therefore adopted as the second objective, subject to ΔTmax ≤ 20 °C. The multi-objective problem is formulated as eqn (3), where f1(x) denotes the reciprocal of YC5+ and takes a minimum value of 1, while f2(x) corresponds to ΔTmax; the independent variable x is a four-dimensional design vector, y1,pre and y2,pre are the YC5+ and ΔTmax predicted by the surrogate model, and S refers to the feasible region determined via the sensitivity analysis presented in Section 3.1.
This bi-objective optimization problem was solved using the NSGA-II algorithm implemented in PyMOO The algorithm employs fast non-dominated sorting and crowding distance mechanisms to simultaneously ensure the convergence and diversity of solutions.25 After obtaining the Pareto frontier, the optimal design was selected based on the trade-off principle between temperature rise and product yield.
3. Results and discussion
3.1 Sensitivity analysis of design variables
Local geometric dimensions of the steel tubes composing the reactor directly determine the flow cross-sectional area and channel space velocity, and thus exert a significant influence on reactor performance. Four variables (RL, RD, RT, RS) were selected to characterize the key geometric features. At fixed operating conditions (inlet temperature of 340 °C, operation pressure of 0.7 MPa, H2/CO molar ratio of 2/3, GHSV of 8000 h−1), with the dimensions listed in Table 1 as the baseline, the control variable method was adopted, wherein only one of the four variables was adjusted relative to the base value at a time while the others remained constant. For each variable-adjusted scheme, the reactor performance (e.g. selectivity, temperature, yield) was obtained via CFD simulations, and the results are presented in Fig. 3. Based on these results, the final reasonable ranges of each design variable were determined, and three typical values per variable were selected to generate contour plots (Fig. 4–7) for auxiliary analysis. All these plots share a consistent format, comprising 3D perspective views and 2D sections (axial cross-section of Tube I, plus transverse cross-sections 10 mm inward from Tube I's inlet and outlet), with only the research variables differing across figures. Each variable in Fig. 3 was calculated using eqn (4)–(7).CO conversion rate:
 | (4) |
CO2 selectivity:
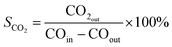 | (5) |
C1, and C5+ selectivity:
 | (6) |
| C5+ yield: YC5+ = XCO × SC5+ × 100% | (7) |
Regarding the geometric variable RL (with typical values of 30, 70, and 120 mm), the results from Fig. 4 indicate that the distribution patterns of all field quantities are consistent across the three parameter levels: increasing RL only expands the catalytic area without altering the channel structure, while the C5+ mass fraction (WC5+) gradually increases along the axial direction with higher values inside the tube than outside. Local XCO increases axially, with SCO2 increasing and SC5+ decreasing in the high-temperature zone at the rear section. Concurrently, the enhanced heat release leads to a simultaneous rise in Tmax, which corresponds to the overall trends in Fig. 3(a). Additionally, as the distance from the center point to the hot spot at the terminal end increases with RL, the temperature difference between Tmax and Tc expands accordingly.
Consequently, the design boundary of RL is defined as [30, 200] mm. This range not only ensures XCO remains at a relatively high level but also prevents excessive decline in SC5+ and temperature runaway:
(1) The lower limit of 30 mm avoids the influence of inlet–outlet backmixing caused by an excessively short reaction channel, which would otherwise lead to component fluctuations and notably low conversion. As presented in Fig. 3(a), YC5+ has decreased to its minimum value at RL 30 mm.
(2) The upper limit of 200 mm covers the main peak range of YC5+. Further extension results in a slowing trend in the variations of XCO and SC5+, while ΔTmax tends to exceed 20 °C. Additionally, the reactor volume and catalyst dosage increase significantly, with the marginal yield gain benefit being far lower than the manufacturing and material costs.
For RD values of 0.5, 2, and 3.5 mm, Fig. 5 reveals notable variations in the distribution of local WC5+, XCO, and temperature. Local WC5+ distribution is highly dependent on RD: at RD = 0.5 mm, WC5+ is only locally elevated at the inlet and then rapidly homogenizes, which is attributed to the combined effect of inlet backmixing and the extremely small inner diameter. By contrast, at RD values of 2 mm and 3.5 mm, WC5+ inside Tube I increases steadily along the axial direction, while that outside remains nearly constant. Local XCO exhibits distinct axial profiles across RD values: it maintains a high level inside Tube I for RD = 0.5 mm, whereas it rises gradually along the axial direction at RD values of 2 mm and 3.5 mm. This discrepancy arises because the 0.5 mm inner diameter is smaller than the default inter-tube spacing (RS = 1 mm). Under laminar flow, the disparity between high central velocity and small RD induces space velocity distribution reversal, altering local reaction extent. In contrast, the local XCO outside Tube I shows similar distribution patterns across the three RD cases. Temperature distributions are broadly consistent: temperature rises axially, and the temperature difference between the outlet center and the area outside Tube I diminishes with increasing RD. At RD = 0.5 mm, outlet tube internal temperature is higher than the external, whereas at 3.5 mm, internal and external temperatures are almost identical, verifying the trend in Fig. 3(b).
Accordingly, the design boundary of RD is defined as [0.5, 4] mm, which encompasses the yield peak while suppressing excessive temperature rise. The rationale for this range is as follows:
(1) Lower limit (0.5 mm): an excessively small inner diameter not only hinders the loading of active components but also tends to cause blockage of the reaction channel.
(2) Upper limit (4 mm): XCO and SC5+ achieve their optimal values within the range of 2.5–3 mm. When RD exceeds 4 mm, the yield decreases continuously, Tmax rises again (increasing the risk of hot spots), and both material consumption and reactor volume increase rapidly. Furthermore, inner diameters greater than 4 mm fall outside the scope of microchannel specifications.
Fig. 6 compares the overall and cross-sectional distribution characteristics of WC5+, XCO, and temperature within the reactor at RT values of 0.25 mm, 1.5 mm, and 6.5 mm. Closer to the reactor outlet, the probability of re-adsorption and hydrogenation of intermediate olefins rises, leading to a corresponding increase in heavy hydrocarbon formation. Within the same cross-section, WC5+ inside Tube I is consistently higher than that outside, and this difference widens as the axial position approaches the outlet. Additionally, WC5+ outside becomes more uniform near the outlet. This is because the stable flow in the 2 mm-diameter inner tube facilitates product accumulation, whereas products generated outside the tube diffuse radially over a large range from the outer wall to the surroundings, which exerts a diluting effect on WC5+. These trends confirm that the channel inside Tube I dominates C5+ formation, with larger RT increasing WC5+ in this channel and thus enhancing C5+ selectivity. Local XCO also increases axially, with uniform cross-sectional distribution at low RT. Increasing RT narrows the spacing outside Tube I and raises space velocity, inducing a distinct radial gradient and thereby reducing the overall XCO. Temperature rises gradually along the axial direction with uniform distribution inside and outside Tube I, attributed to the strong exothermicity of FTS and high axial thermal conductivity of the metal wall. As RT increases, reduced XCO lowers heat release and coupled with metal heat sink and elevated flow velocity synergistically inhibiting temperature rise, which leads to a decrease in the macroscopic temperature level.
Thus, the design boundary of RT is set to [0.25, 6.5] mm, which not only covers the regions where XCO and SC5+ exhibit the highest sensitivity to changes but also avoids the mechano-thermal risks associated with excessively thin walls and diminishing returns caused by overly thick walls.
(1) Lower limit (0.25 mm): a further reduction in wall thickness would result in insufficient radial thermal resistance, making local hotspots unavoidable. It would also lead to inadequate mechanical strength, causing bending or collapse during catalyst loading and under pressure differences, which in turn triggers catalyst layer fracture and flow maldistribution.
(2) Upper limit (6.5 mm): for RT values exceeding 6.5 mm, the negative effect of shortened residence time in the channel outside Tube I on XCO is significantly mitigated. Although further increasing wall thickness expands the external catalytic surface area, its marginal contribution to YC5+ approaches zero. Meanwhile, metal heat capacity and heat conduction paths increase concomitantly, and the temperature profile rises after reaching its minimum at 11 to 15 mm, indicating potential thermal runaway risks for larger RT. Additionally, material consumption and reactor weight increase markedly, which deviates from the microchannel design intent of compactness.
As presented in Fig. 7, three-dimensional contour plots for RS = 0.1 mm, 2.5 mm and 5 mm are compared. The WC5+ distribution shows a pronounced dependence on RS. At RS = 0.1 mm, the narrow inter-tube slit has extremely high flow velocity yet a small gas flow rate, facilitating rapid reactions and the formation of high C5+ concentrations. In contrast, Tube I's 2 mm inner channel and the gap between its outer wall and Tube II's inner wall feature low flow velocity and long residence time, driving steady axial WC5+ accumulation. At RS = 2.5 mm, the inter-tube spacing approximates Tube I's outer diameter and the external space velocity drops sharply, leading to a “high inlet–low outlet” WC5+ profile. At the 40 mm inlet cross-section, WC5+ is uniformly distributed inside Tube I while diffusing outward from its outer wall externally; by the 120 mm cross-section, the distribution homogenizes across both regions. A similar pattern occurs at RS = 5 mm, but external WC5+ remains non-uniform even at the 120 mm outlet cross-section, demonstrating that excessively large spacing reduces the utilization efficiency of catalysts outside Tube I.
Thus, the optimization boundary of RS is set to [0.01, 2.5] mm, which covers the high productivity peak and temperature difference control region, balancing sufficient reaction depth while avoiding thermal accumulation induced by abnormal space velocity from excessively large spacing.
(1) Lower limit (0.01 mm): this corresponds to the narrowest inter-tube slit, featuring the highest cross-sectional flow velocity, a sharp rise in space velocity and extremely short residence time. Both XCO and SC5+ selectivity remain at low levels. Yet the temperature reaches its maximum value in this scenario, rendering the system prone to thermal runaway incidents.
(2) Upper limit (2.5 mm): this matches the inflection point where XCO transitions from a steep decline to a gradual decrease. With further increases in RS, space velocity decreases and heat dissipation weakens, causing wall temperature and central temperature to increase synchronously and elevating thermal runaway risks. Meanwhile, SC5+ decreases monotonically, YC5+ has passed its peak and diminishing returns occur.
3.2 Surrogate model evaluation
Based on the boundary ranges of the four design variables determined in Section 3.1, Latin hypercube sampling was adopted to 250 design points and perform corresponding CFD simulations, establishing a foundational dataset. Of these, 150 samples accounting for 60% were used to train the KRG and GENN models. A further 50 samples representing 20% served as the validation set to iteratively optimize hyperparameters with NMAE and NRMSE as evaluation metrics. The remaining 50 samples making up 20% were reserved as the test set to independently verify the model generalization capability and eliminate overfitting. The final hyperparameters and evaluation metrics are listed in Table 2, and the data distribution and fitting performance are illustrated in Fig. 8. Fig. 8(a) and (b) present the predicted versus simulated value scatter plots and parity checks of KRG for f1(x) and f2(x) respectively, while Fig. 8(c) and (d) show the corresponding results for GENN. Analysis of these plots reveals that GENN yields lower NMAE and NRMSE values than KRG, indicating its higher prediction accuracy. Thus GENN was selected as the surrogate model for subsequent bi-objective optimization.| Model | Hyper-parametera | Parameter description | Value | NMAE | NRMSE |
|---|---|---|---|---|---|
| a All hyperparameters are named following SMT interface functions. Unspecified hyperparameters take the default values of the functions. | |||||
| KRG | poly | Polynomial order that defines the form of the mean function to fit global data trends | Second-order polynomial | 9.27% | 6.36% |
| corr | Type of correlation function that characterizes local data correlation and model smoothness | Squared exponential correlation function | |||
| theta0 | Initial value of correlation function hyperparameter (θ) that initializes model correlation parameters | Four design variables, each initialized to 100 | |||
| theta_bounds | Optimization bounds of θ that constrain parameter range to avoid overfitting and underfitting | [1 × 10−6, 1000] | |||
| hyper_opt | Algorithm for hyperparameter optimization that realizes efficient tuning of model parameters | COBYLA (constrained optimization by linear approximation algorithm) | |||
| GENN | alpha | Learning rate of optimizer that controls parameter update step size to balance convergence | 0.03 (moderate learning rate for stable convergence) | 8.35% | 4.57% |
| hidden_layer_sizes | Number of hidden layers and neurons that determines model fitting capability | [30, 30] (2 hidden layers, 30 neurons per layer) | |||
| num_iterations | Number of optimizer iterations that balances computational cost and prediction accuracy | 1000 (sufficient iterations for model convergence) | |||
| beta1/beta2 | Adam optimizer's momentum decay coefficients that stabilize learning rate scaling | First-order: 0.95, second-order: 0.99 | |||
| lambd | Regularization coefficient that suppresses overfitting by penalizing excessive weights | 0.02 (moderate regularization strength) | |||
| is_normalize | Data normalization flag that improves model training stability and prediction accuracy | True | |||
Fig. 9 further validates the continuous predictive performance of the surrogate model across the entire design space. Fig. 9(a) presents the 1/YC5+ and ΔT distribution of the original 250 high-fidelity samples via scatter plots while Fig. 9(b) shows the GENN prediction results for 2000 Latin hypercube-sampled points within the identical boundary ranges. The predicted results fall within the same physical interval as the original data and achieve smooth transitions in sample-sparse regions without any non-physical oscillations or extrapolation distortions. This confirms that GENN not only accurately reproduces the training samples but also yields a continuous and differentiable predictive profile from discrete sampling points at negligible computational cost. It thus serves as an efficient and reliable fitness evaluation function for subsequent multi-objective optimization, enabling the Pareto frontier solution for the geometric parameters of the microchannel reactor.
3.3 Multi-objective optimization
| Model | Parametera | Parameter description | Value | Remark |
|---|---|---|---|---|
| a All parameters are named following PyMOO interface functions. | ||||
| NSGA II | pop_size | Number of individuals per population generation | 2000 | Balances computational time and result accuracy |
| n_offsprings | Number of offspring generated per generation | 1000 | ||
| Crossover | Crossover operator | prob = 0.7, eta = 5 | Crossover probability and distribution index are 0.7 and 5 respectively | |
| Mutation | Mutation operator | prob = 0.2, eta = 5 | Mutation probability and distribution index are 0.2 and 5 respectively | |
Fig. 11 illustrates the evolution of corresponding geometric parameters after sorting Pareto frontier solutions by increasing 1/YC5+. The geometric characteristics of the leftmost region with high yield and high temperature rise are short channel length, small inner diameter, narrow inter-tube spacing and thin wall thickness. This indicates that small-scale geometries exhibit a pronounced reaction enhancement effect. However, no external heat dissipation is applied and heat removal relies solely on reactant flow, resulting in a high ΔTmax value. As 1/YC5+ increases, RL first rises and then decreases, remaining generally within the range of 90–125 mm. This is the outcome of the continuous trade-off between yield and temperature rise. RD grows gradually, which aligns with the sensitivity analysis results in Section 3.1 where increasing RD within this interval improves YC5+ and reduces ΔTmax. In the left region where ΔT > 9 °C, RT increases rapidly from 1.05 mm to 6 mm, demonstrating that wall thickness plays a dominant role in temperature suppression. Beyond this region where ΔT < 9 °C, further thickening yields minimal cooling effects. RS is only sensitive in the region where YC5+ exceeds 15.4% and ΔT < 9 °C, rising first to 0.7 mm before declining. In all other low-temperature-rise regions, RS takes the minimum value of 0.05 mm. This suggests that adopting a relatively small inter-tube spacing is beneficial for both high yield and low temperature rise simultaneously.
| Design schemes | Design variables/mm | Output results | ||||
|---|---|---|---|---|---|---|
| RL | RD | RT | RS | YC5+/% | ΔT/°C | |
| Initial design | 100 | 2 | 0.5 | 0 | 10.71 | 17.31 |
| S1 | 97.01 | 0.53 | 0.58 | 1.12 | 33.55 | 12.36 |
| S2 | 112.05 | 0.52 | 0.50 | 4.01 | 19.89 | 10.11 |
| S3 | 112.51 | 0.05 | 1.38 | 6.12 | 10.71 | 8.25 |
When selecting the optimal solution, in addition to reaction performance, considerations must be given to manufacturing tolerances, support structure strength and catalyst deactivation temperature limits. Following comprehensive evaluation, Scheme S2 was identified as the final design. The geometric dimensions of this solution were validated via CFD simulations, yielding an actual yield of 18.72% and a temperature rise of 12.87 °C. The relative errors compared with the surrogate model predictions were 6.25% and 0.96% respectively, both falling within the model uncertainty range and confirming the model's reliability. Scheme S2 achieves a 1.86-fold increase in yield while reducing the maximum temperature rise by 7.20 °C, thus laying a foundation for pilot-scale scaling-up and subsequent industrial application.
Since the optimal scheme is obtained under fixed operating conditions, the Pareto frontier will shift when the operating conditions change. Regarding the effects of various operating conditions on YC5+ and ΔTmax of the reactor with initial dimensions, these have been discussed in ref. 16. The operating conditions adopted in this study are those that generate relatively favourable reaction results. However, since YC5+ and ΔTmax do not exhibit a simple monotonic change with variations in operating conditions, it is difficult to directly determine whether the current optimal scheme remains optimal under other operating conditions. An effective strategy is to treat the four operating conditions as design variables and construct an 8-variable input and 2-variable output surrogate model alongside the dimensional variables. Nevertheless, this study is limited by the length of the manuscript and insufficient initial data. Future in-depth investigations can be performed once sufficient reaction data under diverse operating conditions are acquired in follow-up studies.
4. Conclusions
This study presents a multi-objective optimization design approach for microchannel reactors based on the integration of CFD, GENN and NSGA-II. It investigates the reactor performance of FTS microchannel reactors under different geometric parameters. Specifically, sensitivity analysis reveals that all four-dimensional design variables exert significant impacts on reaction outcomes, each with an optimal range that requires balancing during optimization. The developed GENN surrogate model exhibits excellent predictive accuracy and generalization capability, maintaining simulation precision while significantly reducing CFD computational load. Notably, the NSGA-II algorithm effectively obtained the Pareto optimal solution set, achieving the dual-objective optimization of maximizing YC5+ while controlling ΔTmax. Ultimately, the selected optimal scheme reduces ΔTmax by 7.20 °C and increases YC5+ by 1.86-fold. This optimized design exhibits substantial potential for engineering applications, providing technical support for the practical deployment of microchannel reactors in FTS.It should be noted that the present optimization focused exclusively on YC5+ maximization and ΔTmax minimization. Manufacturing cost, reactor volume, catalyst deactivation and pressure drop were reserved for future investigation because the multi-tube microchannel reactor examined in this study remains at the laboratory scale and reliable surrogate modeling of economic or durability metrics requires extensive pilot or industrial data. Comprehensive multi-objective studies that incorporate these additional criteria will be pursued once the requisite operational datasets are generated during the subsequent pilot stage.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the file Python_Code.txt contains the Python code for constructing surrogate models and implementing the multi-objective optimization process. The file data to plot.xlsx includes the data for some figures presented in the paper. See DOI: https://doi.org/10.1039/d5ra09551d.Acknowledgements
We thank Professor Wang Yuanyang for his invaluable guidance and support throughout this research. We are grateful to Wang Yanqian for their assistance with the experimental work. We also thank the anonymous reviewers for their constructive comments and suggestions that helped improve the manuscript.References
- J. E. Apolinar-Hernandez, S. L. Bertoli, H. G. Riella, C. Soares and N. Padoin, Energy Fuels, 2023, 38, 1–28 CrossRef
.
- Z. Teimouri, V. B. Borugadda, A. K. Dalai and N. Abatzoglou, Renewable Sustainable Energy Rev., 2022, 160, 112287 CrossRef CAS
.
- H. Cao, R. Xu, X. Tang, T. Yang, S. Hou and C. Hou, Chin. J. Chem. Eng., 2023, 64, 224–240 CrossRef CAS
.
- K. Lee and J. M. Lee, Comput. Chem. Eng., 2024, 185, 108658 Search PubMed
.
- Z. Teimouri, N. Abatzoglou and A. K. Dalai, Energy Convers. Manage., 2023, 296, 117659 Search PubMed
.
- J. Na, K. S. Kshetrimayum, U. Lee and C. Han, Chem. Eng. J., 2016, 1521–1534 Search PubMed
.
- J. Kong, J. P. Eason, X. Chen and L. T. Biegler, Ind. Eng. Chem. Res., 2020, 59, 9165–9179 CrossRef CAS
.
- P. Mishra and A. Yadav, Int. J. Hydrogen Energy, 2025, 164, 150726 CrossRef CAS
.
- Y. Qiu and P. Liu, Case Stud. Therm. Eng., 2025, 70, 106093 CrossRef
.
- I. Jung, J. Na, S. Park, J. Jeon, Y.-G. Mo, J.-Y. Yi, J.-T. Chung and C. Han, Fuel Process. Technol., 2017, 159, 448–459 CrossRef CAS
.
- The Ansys Product Release and Updates Online, 2024, https://www.ansys.com/products/release-high-lights, accessed December 2024 Search PubMed.
- T. Chen, R. Li, X. Hu, B. Zhang, Y. Liu, L. Wang and N. Gao, Build. Environ., 2025, 285, 113667 CrossRef
.
- Y.-T. Liu, C.-Y. Wu, T. Chen and Y. Yao, in Computer Aided Chemical Engineering, ed. A. C. Kokossis, M. C. Georgiadis and E. Pistikopoulos, Elsevier, 2023, vol. 52, pp. 57–63 Search PubMed
.
- Z. Jiang, J. Chen, S. Xie, X. Li, H. Liu, L. Wang, C. Hong, G. Li, H. Li and K. Chen, Chem. Eng. Sci., 2025, 311, 121614 CrossRef CAS
.
- L. Zhang, L. Chen, S. Xia, Y. Ge, C. Wang and H. Feng, Int. J. Heat Mass Transfer, 2020, 148, 119025 CrossRef CAS
.
- S. Ren and Y. Wang, RSC Adv., 2025, 15, 13137–13151 RSC
.
- Y. Wang, Research on synthesis of low carbon hydrocarbons by intedrated Fischer-Tropsch reaction of microreactor and Fe based catalyst, Master's thesis, Taiyuan University of Science and Technology, 2022, DOI:10.27721/d.cnki.gyzjc.2022.000362
.
- Z. Yu, Z. Wang, H. Zhong and K. Cheng, RSC Adv., 2024, 14, 28724–28739 RSC
.
- P. Saves, R. Lafage, N. Bartoli, Y. Diouane, J. Bussemaker, T. Lefebvre, J. T. Hwang, J. Morlier and J. R. R. A. Martins, Adv. Eng. Software, 2024, 188, 103571 Search PubMed
.
- J. Blank and K. Deb, IEEE Access, 2020, 8, 89497–89509 Search PubMed
.
- J. Sacks, S. B. Schiller and W. J. Welch, Technometrics, 1989, 31, 41–47 Search PubMed
.
- S. H. Berguin, arXiv, 2024, preprint, arXiv:2406.09132, DOI:10.48550/arXiv.2406.09132.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS
.
- J. S. Park, D. E. Kim, Y. J. Lee, G. Kwak and M. J. Park, Ind. Eng. Chem. Res., 2016, 55, 9416–9425 CrossRef CAS
.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef
.
| This journal is © The Royal Society of Chemistry 2026 |










