Molecular insights into the oil-in-water emulsification and demulsification of guanidino-based CO₂/N₂ switchable surfactants

Abstract

CO₂ switchable surfactants show broad application prospects in the treatment of oil-based drilling cuttings due to their reversible ‘active–inactive’ state switching characteristics. This study focuses on the typical guanidinium-based CO₂-responsive surfactant dodecyl tetramethyl guanidine (DTMG) and its protonated form (DTMGH), using a full-atom molecular dynamics simulation system to investigate their interfacial behavior and emulsification/demulsification mechanisms. DTMGH was easier to reach saturation at the interface due to the head-based positive charge repulsion. In terms of emulsification, DTMGH distributed more evenly, effectively encapsulating oil droplets to form stable oil-in-water emulsions. In contrast, DTMG cannot effectively maintain the dispersion of oil droplets, ultimately leading to demulsification. DTMGH exhibited stronger interfacial tension-reducing capabilities than DTMG. The DTMGH system formed a thicker interfacial adsorption layer due to the electrostatic repulsion of protonated head groups and hydrophilicity. Protonation transformed N1 from a hydrogen bond acceptor to a donor, weakening N2's hydration capacity, ultimately altering interfacial hydrophilicity and molecular arrangement. Additionally, the intensity of electrostatic repulsion was a key factor regulating surfactant molecule behavior during emulsification and demulsification. Solvent-accessible surface area revealed that the DTMGH system maintains higher surfactant and oil phase dispersion, directly related to emulsion formation. Our study elucidated the mechanism of action of guanidino-based CO₂-responsive surfactants at the molecular level, providing a theoretical foundation for the development of more efficient CO₂-responsive surfactant systems.

---

1 Introduction

With the ongoing development of shale gas (oil), a large amount of oil-based drill cuttings has been generated.¹ This type of solid waste is mainly formed by the mixture of drilling fluid and rock debris from the wellbore, with a complex composition that includes white oil/diesel and various drilling additives.^2–4 It poses significant hazards to the ecological environment and human health.^5,6 Currently, many countries have developed relatively mature oil-based drill cutting treatment methods, mainly including microbial degradation, pyrolysis, solvent extraction, and chemical cleaning.^7–10 As an amphiphilic molecule containing a hydrophilic head group and a hydrophobic tail chain, surfactants are widely used in the oil washing industry. However, traditional surfactants have certain limitations in oil removal applications, primarily including unstable treatment efficiency, difficulty in controlling emulsion systems, challenges in recovery and recycling, and risks of secondary pollution.^11–16 Therefore, it is necessary to study more effective, environmentally friendly, and cost-efficient surfactant systems. In this context, switchable surfactants as a special class of surfactants have received more and more attention and research. Switchable surfactants are a class of surfactants that induce structural changes in surfactant molecules through specific triggering mechanisms, thereby achieving controllable and reversible changes in their macroscopic physicochemical properties, and enabling reversible conversion between ‘surfactant’ and ‘non-surfactant’ states.¹⁷ Currently, there are various types of stimulus-induced transformation conditions for switchable surfactants, such as CO₂/N₂, pH, light, magnetic fields, redox reactions, and temperature.^18–23 Among these transformation conditions, CO₂/N₂ is a current research hotspot due to its advantages of widespread availability, low cost, mild conditions, and ease of separation from the system.

CO₂/N₂ responsive surfactants mainly contain groups such as amine, amidine and guanidine.^24–26 Significant progress has been made in the research of CO₂-responsive surfactants. In 2006, Liu et al.²⁷ first reported a CO₂/N₂ switchable surfactant. The study showed that the alkyl amidine group reacted with CO₂ to form a bicarbonate cationic surfactant, which had surface activity in this state, and the surfactant was introduced into N₂/Ar and heated at 65 °C. Under the condition, it is decomposed into alkyl amidines that do not have surface activity, thereby achieving reversible conversion. Hou et al.²⁸ systematically studied the effect of hydrophobic chain length on the protonation behavior of N′-alkyl-N,N-dimethylacetylamidine. It was found that short chains are more easily protonated but difficult to deprotonate, while long chains can form more stable oil–water emulsions. Ma et al.²⁹ found that inorganic salts can induce the protonation of N′-dodecyl-N,N-dimethylacetylamidine surfactants. Their research enhances the understanding of switchability and the efficient use of amidinate surfactants in salt-containing systems. Wang et al.³⁰ demonstrated that dialkyl acetylamidine bicarbonate has lower critical micelle concentration (CMC) and stronger interfacial activity than monoalkyl analogues. However, their research mainly focuses on the influence on macro performance, while the micro mechanism is not clear.

Molecular dynamics (MD) simulations have provided new insights into the microscopic mechanisms of switchable surfactants. Zhang et al.³¹ studied the behavior of CO₂/N₂ switchable surfactant dodecyl dimethyl amidine at the brine–oil interface by MD simulation. The results show that the protonated system can broaden the interface thickness and reduce the interfacial tension more significantly. It was found that the Coulomb interaction is crucial for the reversible emulsification/demulsification process. However, their research only focused on the interface effect and did not reflect the process of emulsification and demulsification. On this basis, Liu et al.³² used MD simulation to study the formation and demulsification process of n-hexadecane/water emulsion by CO₂/N₂ switchable surfactant dodecyl-N,N-dimethyl acetamidine bicarbonate. It is found that the reversible conversion of hydrophilicity is the key to the simultaneous use of switchable surfactants as emulsifiers and demulsifiers. Ahmadi et al.^33,34 used MD simulation to reveal the switchability of sodium dodecyl sulfate and sodium C18 naphthalene sulfonate with CO₂-switchable acetamidine surfactant N′-dodecyl-N,N-dimethyl acetamidine in the process of emulsification and demulsification. In addition, they further studied the effects of surfactant structure, concentration and salt content on the switchable emulsification process. The results show that the low concentration of surfactant will lead to the formation of some emulsions, and the presence of salt will destroy the hydration of surfactant and weaken the emulsifying properties. Zhang et al.³⁵ revealed through MD simulations that the protonation state transition of CO₂-responsive lauric acid can precisely regulate the stability of n-heptane/water emulsions: the deprotonated system stabilizes the emulsion through electrostatic repulsion, while the CO₂-triggered protonated system induces droplet coalescence through reduced hydrophilicity and charge neutralization. Additionally, Stavert et al.³⁶ investigated the self-assembly and phase behavior of alkylamine surfactant dodecylamine through multi-scale computational modeling, revealing that the degree of charge on the surfactants is key to regulating their hydrophilic–hydrophobic balance. This balance directly influences the surfactants' self-assembly behavior and solubility.

In practical applications, surfactants need to maintain sufficient stability in the aqueous phase to effectively exert emulsification. Due to low pK_a value of traditional amino and amidine surfactants, the formed bicarbonate is prone to deprotonation under neutral or weakly alkaline conditions, which remarkably affects its emulsifying properties. In contrast, guanidine-based surfactants exhibit better stability due to their unique molecular structure: a conjugated system formed by three nitrogen atoms and a central carbon atom enables the guanidine group to bind more stably to protons to form positively charged ions. This characteristic makes guanidinium bicarbonate have better chemical stability, which provides a new idea for solving the problem of easy decomposition of amino and amidine surfactants. It is worth noting that the current molecular dynamics simulation studies on guanidine-based CO₂-responsive surfactants are still very limited. Therefore, this study selected the typical guanidine-based CO₂-responsive surfactant dodecyl tetra methyl guanidine (DTMG) and its protonated state (DTMGH) as the research objects, and systematically investigated their interfacial behavior and emulsification/demulsification behavior using all-atom molecular dynamics simulation methods. Firstly, an oil–water interface model was established to analyze the changes of interfacial morphology and properties before and after CO₂ stimulation by regulating the protonation state of surfactant molecules at the interface. Then, an oil-in-water emulsion model was established to explore the microscopic mechanism of reversible emulsification/demulsification process. Through the synergistic study of these two models, we revealed the mechanism of guanidine-based CO₂-responsive surfactants at the molecular level, and may provide a theoretical foundation for subsequent development of more efficient CO₂-responsive surfactant systems.

2 Molecular simulation method

2.1 Model construction

To investigate the effect of DTMG on the morphology and properties of the interface before and after CO₂ triggering, an oil–water interface model was first adopted. The initial simulation box size was 5 nm × 5 nm × 20 nm. This box consisted of two oil phases with a water phase in between, and the surfactants were distributed between the oil and water phases. During the simulation, periodic boundary conditions (PBC) were used in three dimensions to eliminate any differences that might arise from the boundary conditions. The oil phase was represented by n-decane, because n-decane has been widely used to simulate the oil phase in oil–water interface systems.^37–39 The OPC water molecule model was selected for water molecule,⁴⁰ as it effectively reproduces surface tension and shows one of the best performances in modeling the general properties of water.^41,42 In the initial model, there were 350 n-decane molecules in the oil phase and 5000 water molecules in the water phase. Five different concentrations of surfactants were selected. The number of surfactant molecules on one side were 10, 20, 30, 40, 50 and the corresponding interface concentrations were 0.67, 1.33, 2.00, 2.67, 3.33 µmol m⁻², respectively. The hydrophilic groups of the surfactants were close to the aqueous phase, while the hydrophobic tails were close to the oil phase, enabling the system to reach equilibrium more quickly. To simulate the emulsification and demulsification process, emulsification models were constructed for DTMG and DTMGH, respectively. For each system, 26 000 water molecules, 100 surfactants and 300 n-decane molecules were randomly placed in a 10 nm-long cube box. For the protonated system (DTMGH), an appropriate amount of bicarbonate ions were added to the box to maintain electrical neutrality. The Packmol software package was used to assemble all molecules and ions in the simulation box.⁴³ Specific information about the simulation system is shown in Table 1. The molecular models used for simulation were constructed using the Materials Studio software package (2017 edition). All molecular structures and the initial configuration of the simulation systems are shown in Fig. 1.

Table 1 Detailed information on the simulation system^a

System	Decane	DTMG	DTMGH	H2O	HCO3^−
a Note: system 1–11 are the oil–water interface model, system 12 and 13 are emulsification models.
1	700	0	0	5000	0
2	700	20	0	5000	0
3	700	40	0	5000	0
4	700	60	0	5000	0
5	700	80	0	5000	0
6	700	100	0	5000	0
7	700	0	20	5000	20
8	700	0	40	5000	40
9	700	0	60	5000	60
10	700	0	80	5000	80
11	700	0	100	5000	100
12	300	100	0	26 000
13	300	0	100	26 000	100

---

Fig. 1 (a)–(e) Structures of DTMG, DTMGH, n-decane, water, and bicarbonate ion. (f) Initial configuration of the surfactant oil–water interface model, (g) initial configuration of the surfactant emulsification model. Grey represents carbon atoms, white represents hydrogen atoms, red represents oxygen atoms, and blue represents nitrogen atoms.

2.2 Simulation details

All molecular dynamics simulations in this study were performed using the Lammps-2Aug2023 software package.⁴⁴ The OPLS-AA force field was used to simulate the bonding and non-bonding interactions between n-decane and surfactant molecules,⁴⁵ The mode of action is shown in eqn (1):where r_ij is the distance between atoms i and j, ε_ij and σ_ij are the Lennard-Jones radius and well depth of the atom pair (i, j), respectively. q_i and q_j denote the charge of atoms i and j, respectively, e denotes the basic charge. For different kinds of atoms, their van der Waals potential energy parameters are calculated using the geometric mean mixing rule, as shown in eqn (2):

The charge calculation method adopts the 1.2 * CM5 method. The charge calculation method combined with the OPLS-AA force field has been proved to accurately describe the thermodynamic properties of various organic compounds and the oil–water interface properties of surfactants.^46,47 The simulation temperature and pressure were set to 298.15 K and 1 atm, respectively. Nosé–Hoover thermostat and Nosé–Hoover barostat were used to control the temperature and pressure, with relaxation times of 0.1 ps and 1.0 ps, respectively.^48–50 For interface model, the pressure coupling employed was anisotropic, with pressure controlled along the z-direction. For the emulsion model, isotropic pressure coupling was adopted. In the MD simulation, the simulation step size was set to 1 fs, with trajectory information recorded every 10 ps for subsequent structural analysis. A cutoff radius of 12 Å was used to calculate short-range interactions, and the particle–particle particle-mesh (PPPM) method was used to calculate long-range electrostatic interactions, with an accuracy setting of 10⁻⁵.⁵¹ The shake algorithm was used to constrain the bond lengths and bond angles of water molecules.⁵² The steepest descent method was used for energy minimization in all simulation systems. For the oil–water interface model, 500 ps was simulated under the NVT and NPT ensembles to make the system reach the equilibrium state, and finally 10 ns was simulated under the NVT ensemble to extract the data for further analysis. For the emulsification model, 2 ns was simulated under the NPT ensemble to make the system reach the equilibrium state, and then 20 ns was simulated under the NVT ensemble. The VMD package is used to visualize all MD trajectories.⁵³

3 Result and discussion

3.1 Interface morphology in oil–water interface models

To study the interface morphology of guanidino CO₂-switchable surfactants under different conditions, five groups of simulation experiments with different concentrations were carried out on DTMG and DTMGH systems. The interfacial morphology at different interfacial concentrations is shown in Fig. 2. Compared with the initial structure diagram, it was found that after 10 ns simulation, the surfactants in both states can form a single-molecule membrane structure at the oil–water interface, with the hydrophilic head groups oriented toward the aqueous phase and the hydrophobic tail chains penetrating into the oil phase. In addition, at low interface concentrations, a relatively flat interface was found in both DTMG and DTMGH systems, and the surfactants were distributed at the interface. As the interface concentration gradually increased, the interface of the DTMG system was still flat, indicating that it was less affected by the concentration, while the interface of the DTMGH system gradually becomes unstable, and when the interface concentration exceeds 2.00 µmol m⁻², the surfactant molecules at the interface reached saturation, and some surfactant molecules entered the aqueous phase, and as the concentration increased, the surfactant molecules in the aqueous phase gradually increased. Interestingly, when the interfacial concentration reaches 3.33 µmol m⁻², DTMGH molecules in the aqueous phase aggregated into a cluster, and the hydrophobic tail chain was concentrated inside the cluster, while the hydrophilic head group was surrounded by the cluster, indicating that DTMGH molecules formed micelles in the aqueous phase.

Fig. 2 The final configurations of DTMGH (a–e) and DTMG (f–j) systems at interface concentrations of 0.67, 1.33, 2.00, 2.67, 3.33 µmol m⁻², respectively. Among them, yellow represents oil phase, red represents water phase, green represents bicarbonate ion, carbon atom, nitrogen atom and hydrogen atom in surfactant are gray, blue and white respectively.

To more clearly understand the distribution of each component in the surfactant system in the two states, we calculated the density distribution of surfactant, n-decane, water, and HCO₃⁻ along the z-axis direction at the end of the simulation. As shown in Fig. 3, the phase density of water and n-decane in DTMG and DTMGH systems tended to be stable. The surfactants were mainly distributed in the transition region between the water phase and the oil phase. In the DTMGH system, HCO₃⁻ was concentrated in the vicinity of the head group of the surfactant, which was due to the electrostatic interaction between HCO₃⁻ and the positively charged head group. The molecular density peak of DTMGH gradually increased with the increase of concentration, but when the concentration reached 2.00 µmol m⁻² and above, the peak remained basically unchanged, while the molecular density peak of DTMG gradually increased with the increase of concentration. When the concentration reached about 2.00 µmol m⁻², the DTMGH molecules reached saturation at the interface. The main reason for this difference was that the DTMGH head group was positively charged, and the repulsion between the positive charges caused the interface to be less closely arranged than the DTMG system, which was easier to reach the interface saturation state.

Fig. 3 Density distribution of each component along the z-axis in the DTMGH (a, c, e, g, i) and DTMG (b, d, f, h, j) systems at interface concentrations of 0.67, 1.33, 2.00, 2.67, 3.33 µmol m⁻².

3.2 Interfacial tension and interfacial thickness in oil–water interface model

As an important parameter to describe the properties of oil–water interface, interfacial tension is widely used to verify the accuracy of oil–water interface properties under different force fields,^54–56 The method of calculating interfacial tension from MD simulation is based on the normal pressure (Pn) and tangential pressure (Pt) at the interface as shown in eqn 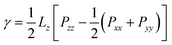(3):

P_zz is the pressure component perpendicular to the interface direction, P_xx and P_yy are the pressure component parallel to the interface direction, and L_z is the length of the box in the z direction. Ghoufi et al.'s research shows that the long-range dispersion correction has a strong effect on the interfacial tension.⁵⁷ The interfacial tension in this work was calculated using the long-range dispersion correction. The interfacial tension of pure water-n-decane system was calculated to be 53.26 mN m⁻¹, which is close to 52.50 mN m⁻¹ at 25 °C and 1 atm.⁵⁸ Therefore, from the results of interfacial tension, it was reasonable to use the OPLS-AA force field and the OPC water molecule model to describe the micro-scale oil–water interface interaction. Interfacial thickness refers to the thickness of the interface between two different phases in space, and is one of the important indicators for evaluating the ability of surfactants to separate water phases and oil phases. The interface thickness was calculated using the ‘90–90%’ criterion, which refers to the distance from 90% of the oil phase density to 90% of the water phase density and has been widely used in MD simulations, particularly in simulations of oil–water interface systems.^59–61 As shown in Fig. 4, when the surfactant interfacial concentration was 0.67 µmol m⁻², the interfacial tensions of both systems were relatively high, exceeding 40 mN m⁻¹, and the difference in interfacial tension between the two systems was small, only 5.3 mN m⁻¹. As the surfactant concentration increased, the interfacial tensions of both systems showed a downward trend, and the interfacial tension of the protonated system decreased more rapidly with increasing concentration. When the interfacial concentration reached 2.67 µmol m⁻², the interfacial tension of the DTMGH system was 3.2 mN m⁻¹, while that of the DTMG system was 27.8 mN m⁻¹. The difference in interfacial tension between the two systems became even greater, reaching 24.6 mN m⁻¹. In general, the protonated system was more effective at reducing interfacial tension, especially when the interfacial concentration was high. The interfacial tension of the two systems before and after protonation was significantly different. The difference in interfacial tension explained why emulsification and demulsification can be achieved by switching between DTMGH and DTMG. In addition, when the surfactant interface concentration was 3.33 µmol m⁻², the interfacial tension of the DTMGH system was calculated to be negative. The aggregation morphology of the surfactant at the oil–water interface gradually changed from a monolayer film structure to a microemulsion during the simulation process, and micelles were formed in the aqueous phase, rendering the formula for calculating interfacial tension inapplicable. As the interfacial concentration of surfactants increased, the interfacial thickness in both states gradually enhanced. Combined with the interface distribution in Fig. 2, it can be observed that the surfactant formed an obvious adsorption layer at the oil–water interface, and the layer structure was more dense with the increase of the interface concentration. It is worth noting that under the same interfacial concentration conditions, the DTMGH system exhibited a larger interfacial thickness, which was attributed to its protonated head group having stronger hydrophilicity, resulting in a wider overlap between the hydrophilic head group of the surfactant and the aqueous phase. In addition, since the hydrophilic head group of DTMGH was positively charged, the charge repulsion led to its less tightly pack than that of DTMG, which also promoted the entry of more water molecules into the vicinity of the hydrophilic head group. These two factors together contributed to the protonated system with a thicker external hydrophilic layer at the oil–water interface, resulting in a larger interface thickness.

Fig. 4 Interfacial tension and interfacial thickness of different concentration simulation systems in two states, where bar chart represents interfacial tension and dotted line graph represents interfacial thickness.

3.3 RDF of oil–water interface model

To further investigate the differences in interface properties before and after protonation, we also calculated the radial distribution functions between two different types of nitrogen atoms in the hydrophilic groups and hydrogen atoms in water, as well as between protonated hydrogen atoms and oxygen atoms in water. According to the difference in the chemical environment of the nitrogen atom, we define the protonable nitrogen atom as N1 and the nitrogen atom connected to the dimethyl as N2. As shown in Fig. 5, RDF analysis shows that the protonation state significantly changes the hydration behavior of N1 atoms. In the unprotonated DTMG system, N1 and water hydrogen atoms showed a strong characteristic peak at 2.01 Å, and the distance and peak intensity were typical corresponding to the formation of N1⋯H–O hydrogen bonds. In the protonated DTMGH system, the hydration peak shifted to 3.45 Å and the intensity decreased significantly due to the electrostatic interaction of N1–H, indicating that protonation led to nitrogen atom's loss of lone pair of electrons and breakdown of the original hydrogen bond network. It is worth noting that the protonated hydrogen atom in DTMGH and the oxygen atom in water had a stronger characteristic peak at 1.95 Å, which revealed that a new O⋯H–N1 hydrogen bond was formed after protonation. This hydrogen bond recombination was a key factor in the change of interface properties. For N2 atoms, the hydration patterns before and after protonation also showed significant differences: before protonation, there were multi-level hydration shells at 2.19 Å, 3.33 Å, and 4.71 Å, with the peak at 2.19 Å indicating that part of N2 may participate in hydration through weak hydrogen bonds. While after protonation, only the peak at 4.71 Å remained, indicating that the lone pair electrons of N2 were influenced by the inductive effect of the neighboring protonated N1, resulting in a significant reduction in its hydration capacity. Furthermore, to more clearly quantify the overall changes in the hydration behavior of protonated hydrogen and nitrogen atoms, we calculated the coordination numbers corresponding to the characteristic peak (around 2.0 Å) associated with the hydrogen bond distance. The results are shown in Table 2. In unprotonated DTMG, the hydrogen bond coordination numbers for N1 and N2 were approximately 1.51 and 0.53, respectively, indicating that N1 was the primary hydrogen bond acceptor site. After protonation (DTMGH), sites N1 and N2 no longer bound water as acceptors. Instead, their protonated hydrogen atoms (N1–H) acted as hydrogen bond donors, forming stable hydrogen bonds with the oxygen atom of water molecules with a coordination number of approximately 1.80. These RDF features collectively revealed that protonation weakened the hydration ability of N2 by transforming N1 from a hydrogen bond acceptor to a donor, which led to the reconstruction of the hydrogen bond network as well as a significant change in the hydrophilicity of the interface and the arrangement of molecules.

Fig. 5 RDF between some atoms before and after protonation, where (a, c and e) represent the RDF of N1 and N2 in DTMGH with hydrogen atoms in water, and the RDF of protonated hydrogen atoms with oxygen atoms in water, respectively; (b and d) denotes the RDF of N1 and N2 atoms in DTMG with hydrogen atoms in water molecules, respectively.

Table 2 Coordination numbers of varied atoms with water molecules

Interface concentration	N1DTMG	N2DTMG	HDTMGH
0.67 µmol m^−2	1.51	0.51	1.86
1.33 µmol m^−2	1.51	0.53	1.88
2.00 µmol m^−2	1.52	0.53	1.78
2.67 µmol m^−2	1.52	0.51	1.72
3.33 µmol m^−2	1.52	0.55	1.84

---

3.4 Emulsification and demulsification morphology in emulsification model

To study the emulsification and demulsification behavior of guanidino CO₂ switchable surfactants in different states, MD simulations of DTMG and DTMGH systems were carried out by emulsification model. Firstly, we calculated the system's total energy as a function of simulation time to verify thermal equilibrium. As shown in Fig. 6, the total energy exhibited random fluctuations around a stable average value after 20 ns, with no discernible upward or downward trend. This indicated that the system reached thermal equilibrium as early as 20 ns.

Fig. 6 The total energy of the system changes with the simulation time.

After 40 ns simulation, the two systems showed significantly different morphologies. As shown in Fig. 7 and S1, in the DTMGH system, multiple small oil droplets were formed, and the DTMGH molecules were distributed on the surface of the oil droplets. The hydrophilic head group was close to the water phase, and the hydrophobic tail chain was close to the oil phase, showing typical emulsion stability characteristics.

Fig. 7 Final configurations of the DTMGH and DTMG systems in the emulsion model, where (a and b) represent the three-dimensional views of the DTMGH and DTMG systems. Yellow represents the oil phase, green represents the carbonate ion, and the carbon, nitrogen, and hydrogen atoms in the surfactant are grey, blue, and white, respectively. Water molecules are hidden.

This result was consistent with the density distribution (Fig. 8): the oil molecules showed a bimodal distribution in the z-axis direction, indicating that the oil phase was dispersed by droplets. The density peak of DTMGH was highly coincident with the density peak of oil molecules, as surfactant molecules adsorbed on the surface of oil droplets. Notably, HCO₃⁻ partially aggregated near the hydrophilic head groups of DTMGH while another portion distributed within the aqueous phase farther from the head groups. Multiple oil droplets formed within the emulsion model, leading to relatively dispersed DTMGH distribution. Given the larger spatial volume of the entire system, HCO₃⁻ distribution in water was less influenced by DTMGH. In addition, the density distribution curve of HCO₃⁻ in the z direction showed a relatively flat feature. The density distribution calculation was based on statistics along the z-axis. Since multiple oil droplets were distributed along the z-axis, their distributions along this direction created a superposition effect, resulting in a statistically flat density distribution curve. Additionally, we calculated the RDF between the DTMGH head group and HCO₃⁻ in the emulsion model to validate our findings.

Fig. 8 The density distribution of some components in the DTMGH and DTMG systems along the z-axis.

As shown in Fig. 9, a peak at 1.9 Å indicated the electrostatic attraction between the DTMGH head group and HCO₃⁻, while the peak at 7.2 Å suggested that a portion of HCO₃⁻ were distributed in the aqueous phase farther from the hydrophilic head group. In contrast, the DTMG system eventually formed a larger oil droplet. The density distribution showed that n-decane only formed a large density peak, indicating that oil molecules tended to aggregate, and the density curve of DTMG was included in the density peak range of n-decane. The curve was relatively flat and no peak is formed, indicating that DTMG molecules were evenly distributed on the surface of oil droplets, but it failed to effectively prevent oil droplets from coalescing and eventually leads to demulsification.

Fig. 9 RDF between DTMGH head group and HCO₃⁻.

The total atomic radial density of oil droplets before and after protonation was calculated, as shown in Fig. 10. This distribution clearly characterizes the complete transition from the interior of the oil phase through the interfacial layer to the external aqueous phase. For the protonated DTMGH system, the density curve rose from approximately 0.7 to 1.0 within a narrow range of about 0.55 nm (radial distance 1.95 nm to 2.5 nm). This steep increase indicated that DTMGH molecules assemble into an ordered, oriented monolayer on the oil droplet surface through strong hydrophilic interactions and electrostatic repulsion, effectively separating the oil and water phases and stabilizing the droplet. In contrast, the deprotonated DTMG system exhibited a broad transition zone extending over 1.05 nm (2.50 nm to 3.55 nm). This extensive and gradual density change reflected a loose interfacial structure, indicating that DTMG molecules failed to form a tightly packed barrier. Oil, water, and surfactant molecules intermix and permeate within this region, ultimately leading to demulsification.

Fig. 10 Oil droplet radial density distribution under different protonation states, where (a) is DTMGH and (b) is DTMG.

3.5 Interaction energy in emulsification model

Interaction energy refers to the non-bond interaction energy between two or more molecules/groups, which can reflect the interaction strength between them. In MD simulation, non-bond interaction mainly includes van der Waals interaction and electrostatic interaction. The interaction energy is generally calculated by eqn (4):where E_total represents the total energy of the system composed of interacting molecules/groups, and E_componenti represents the energy of the i-th component in the same environment but in an isolated state. A negative interaction energy indicates an attractive force, while a positive interaction energy indicates a repulsive force. To further explore the intrinsic reasons for the emulsification and demulsification behavior of DTMG and DTMGH systems, we quantitatively analyzed the interaction energy of DTMGH and DTMG with water, decane, and each other in the last 2 ns of the simulation. As shown in Fig. 11, the interaction energy remained stable during this period, indicating that the system had reached a stable state and the calculation results were reliable. It is worth noting that the interaction energies between DTMGH and DTMG with water molecules were −4102.69 kcal mol⁻¹ and −3835.01 kcal mol⁻¹, respectively, indicating that there was a considerable attractive interaction between the surfactant molecules and water molecules before and after protonation. Furthermore, the interaction between DTMGH and water molecules was stronger, which was attributed to its enhanced hydrophilicity after protonation. The interaction energies of DTMGH and DTMG with n-decane were −1505.59 kcal mol⁻¹ and −1462.11 kcal mol⁻¹, respectively, indicating that there was also an attractive interaction between the surfactant molecules and n-decane molecules before and after protonation. Protonation had little effect on the interaction between surfactant molecules and oil molecules. DTMGH–DTMGH exhibited a strong repulsive interaction of 12 697.80 kcal mol⁻¹, while DTMG-DTMG exhibited a repulsive interaction of 10 801.08 kcal mol⁻¹. Although both were repulsive interactions, the stronger repulsive interaction between DTMGH molecules exerted a decisive influence on the behavior of the system.

Fig. 11 The interaction energy between DMTGH, DTMG and other components in the last 2 ns.

We also analyzed the contribution of van der Waals force and Coulomb force in the interaction energy of (DTMGH–DTMGH, DTMG–DTMG). As shown in Fig. 12, the van der Waals effect of the two systems was small, but the Coulomb effect was significantly different. The results showed that the intensity difference of electrostatic repulsion was the key factor to control the emulsification of surfactant molecules. Strong electrostatic repulsion makes DTMGH molecules evenly distributed at the interface formed a stable monolayer, which effectively separated oil droplets to achieve emulsification. The relatively weak electrostatic repulsion was not enough to prevent the attraction between oil droplets, resulting in oil droplets gathering and demulsification.

Fig. 12 The average interaction energy between DMTGH and DTMG itself in the last 2 ns, as well as the contributions of van der Waals forces and coulomb forces to the total interaction energy.

3.6 Solvent accessible surface area

Solvent accessible surface area (SASA) is a key parameter in molecular dynamics to characterize the contact area between molecules or aggregates and solvents. The calculation method was to use a spherical probe with a radius equivalent to the solvent molecule to move back and forth on the outer contour of the molecule or aggregate. The surface area surrounded by the center of the spherical probe was SASA. This parameter can effectively reflect the exposure degree and aggregation state of molecules in solution. In this study, we used a probe with a radius of 1.4 Å to systematically investigate the SASA changes of surfactant molecules and n-decane (C10) in the DTMGH and DTMG systems. As shown in Fig. 13, at the beginning of the simulation, all components showed high SASA values, which reflected the initial random distribution of molecules in the simulation system. With the extension of simulation time, the SASA values of each system showed a significant attenuation trend and gradually reached a stable state. It is worth noting that when the simulation was completed, the surfactant molecules and C10 molecules in the DTMGH system showed higher SASA values than the DTMG system. The difference in SASA between DTMGH and DTMG revealed that protonated DTMGH molecules remain more dispersed in solution, while DTMG molecules were less dispersed than DTMGH molecules. The SASA changes of C10 molecules were highly consistent with the behavior of surfactants. Although constrained by the scale of the simulated system, the emulsification system studied was small and the number of droplets was limited, resulting in minimal differences in SASA values of C10 between emulsified and demulsified states. We also observed consistent trends: the higher SASA values of C10 in the DTMGH system corresponds to the stable existence of multiple small oil droplets, while the lower SASA values of C10 in the DTMG system reflects the process of oil droplet aggregation. These quantitative results were consistent with the visualization results of the system, providing a new characterization method for the optimization design of CO₂-responsive emulsification system.

Fig. 13 The change of SASA of DTMGH, DTMG and C10 with simulation time in two states.

We also calculated the SASA of the hydrophilic head group and the hydrophobic tail chain of DTMGH and DTMG. The results are shown in Fig. 14. It can be found that the difference in SASA of the hydrophobic tail chain of the surfactant before and after protonation was relatively small, while the difference in SASA of the hydrophilic head group was large. This indicated that the tightness of the DTMGH head group arrangement decreased, and the head group spacing increased, which was more exposed to the solvent environment, leading to stronger interactions with the aqueous phase.

Fig. 14 DTMGH, DTMG hydrophilic head groups, and hydrophobic tail chains' SASA.

4 Conclusion

In this study, all-atom molecular dynamics simulations were used to explore not only the interfacial behavior differences of guanidine-based CO₂ switchable surfactant DTMG and its protonated form DTMGH in n-decane/water system, but also the microscopic mechanism of emulsification/demulsification through oil–water interface model and emulsification model. The main conclusions are as follows:

(1) Due to the strong electrostatic repulsion between the positive charges of the head groups, DTMGH exhibited interfacial saturation at an interfacial concentration of 2.00 µmol m⁻², with excess molecules entering the aqueous phase to form micelle structures; in contrast, DTMG maintained a stable adsorption state at the interface. In terms of emulsification performance, DTMGH was more evenly distributed and can effectively encapsulate oil droplets to form stable oil-in-water emulsions. In contrast, DTMG molecules failed to effectively prevent oil droplet aggregation, ultimately leading to emulsion breakdown.

(2) DTMGH exhibited stronger interfacial activity, and its ability to reduce interfacial tension increased significantly with increasing concentration. The analysis of interface thickness showed that both the charge repulsion of the protonated head group and the enhanced hydrophilicity promote DTMGH to form a thicker interface adsorption layer. The RDF study further revealed that protonation was caused the reconstruction of the hydrogen bond network by transforming N1 from a hydrogen bond acceptor to a donor and weakening the hydration ability of N2. This eventually led to a significant change in the hydrophilicity of the interface and the arrangement of molecules.

(3) Electrostatic repulsion strength played as a key factor in regulating the emulsification behavior of surfactants. The strong electrostatic repulsion makes the DTMGH molecules evenly distributed at the interface to form a monolayer, which effectively separated the oil droplets to achieve emulsification. The relatively weak electrostatic repulsion cannot prevent the attraction between oil droplets, resulting in oil droplets gathering and demulsification.

(4) The DTMGH system showed a higher SASA value, indicating that protonation promoted the surfactant molecules to maintain a more dispersed interface arrangement. The higher SASA of C10 value in the DTMGH system reflected its ability to maintain oil droplet dispersion, while the lower SASA of C10 value in the DTMG system corresponded to the oil droplet aggregation process.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5ra08773b.

Acknowledgements

This work is supported by the China National Petroleum Corporation Group (2023ZZ1303). The numerical calculations in this paper have been done on the supercomputing system in the High Performance Computing Center of Southwest Petroleum University.

References

1. Q. Lv, L. a. Wang, J. Jiang, S. Ma, L. Liu, Z. Zhou, L. Liu, X. Wang and J. Bai, Process Saf. Environ. Prot., 2022, 159, 354–361.
2. X. Duan, H. Yu, X. Wu, Y. Li, H. Chen, Y. Sun, H. Zheng and B. Wu, J. Environ. Chem. Eng., 2024, 12, 112846.
3. H. Yang, H. Diao, Y. Zhang and S. Xia, J. Environ. Manage., 2022, 317, 115462.
4. M. P. J. A. Annevelink, J. A. J. Meesters and A. J. Hendriks, Sci. Total Environ., 2016, 550, 431–438.
5. M. Aboutabikh, A. M. Soliman and M. H. El Naggar, Constr. Build. Mater., 2016, 111, 751–757.
6. Y. Deng, H. Yin, Z. Chen, Y. Chen, D. He, H. Gong, Z. Jiao, S. Yao and P. Tu, Geofluids, 2022, 2022, 8208912.
7. Y. Hou, S. Qi, H. You, Z. Huang and Q. Niu, J. Environ. Manage., 2018, 228, 312–318.
8. A. B. Guerra, J. S. Oliveira, R. C. B. Silva-Portela, W. Araújo, A. C. Carlos, A. T. R. Vasconcelos, A. T. Freitas, Y. S. Domingos, M. F. de Farias, G. J. T. Fernandes and L. F. Agnez-Lima, Environ. Pollut., 2018, 235, 869–880.
9. J. Hu, J. Gan, J. Li, Y. Luo, G. Wang, L. Wu and Y. Gong, Fuel, 2017, 188, 166–172.
10. Q. Hong, M. Jinan, W. Qing, L. Jianpo, C. Mingshu, Z. Lidong and L. Hongpeng, Chin. J. Environ. Eng., 2016, 10, 851–857.
11. H. W. Hernandez, W. Ehlert and S. Trabelsi, Fuel, 2019, 237, 398–404.
12. Y. Xu, Y. Zhang, X. Liu, H. Chen and Y. Fang, ACS Sustain. Chem. Eng., 2018, 6, 4981–4986.
13. E. Ceschia, J. R. Harjani, C. Liang, Z. Ghoshouni, T. Andrea, R. S. Brown and P. G. Jessop, RSC Adv., 2014, 4, 4638–4645.
14. J. M. Rosas, F. Vicente, A. Santos and A. Romero, Chem. Eng. J., 2013, 220, 125–132.
15. J. Gómez, M. T. Alcántara, M. Pazos and M. A. Sanromán, J. Hazard. Mater., 2010, 173, 794–798.
16. Y. Yang, D. Zhen, Z. Guofeng, Z. Huaqi, Z. Yongbin, H. Xue and Z. Ye, J. Dispersion Sci. Technol., 2024, 2422896, 1–6.
17. Y. Lu, D. Sun, J. Ralston, Q. Liu and Z. Xu, J. Colloid Interface Sci., 2019, 557, 185–195.
18. Y. Zhang, L. Liu, X. Liu and Y. Fang, Langmuir, 2018, 34, 2302–2311.
19. K. Liu, J. Jiang, Z. Cui and B. P. Binks, Langmuir, 2017, 33, 2296–2305.
20. Y. Chen, Z. Li, H. Wang, Y. Pei, Y. Shi and J. Wang, Langmuir, 2018, 34, 2784–2790.
21. F. Shehzad, S. M. S. Hussain, A. A. Adewunmi, A. Mahboob, M. Murtaza and M. S. Kamal, Adv. Colloid Interface Sci., 2021, 293, 102441.
22. H. Liu, L. Wang, X. Wang, Y. Hu, L. Feng, S. Dong and J. Hao, J. Colloid Interface Sci., 2019, 549, 89–97.
23. C. Han, Y. Guo, X. Chen, M. Yao, Y. Zhang, Q. Zhang and X. Wei, Soft Matter, 2017, 13, 1171–1181.
24. Y. Qin, H. Yang, J. Ji, S. Yao, Y. Kong and Y. Wang, Tenside, Surfactants, Deterg., 2009, 46, 294–297.
25. M. Zhou, G. Wang, Y. Xu, Z. Zhang, S. Li, B. Hu and Y. Zhao, J. Surfactants Deterg., 2017, 20, 1483–1489.
26. L. M. Scott, T. Robert, J. R. Harjani and P. G. Jessop, RSC Adv., 2012, 2, 4925–4931.
27. Y. Liu, P. G. Jessop, M. Cunningham, C. A. Eckert and C. L. Liotta, Science, 2006, 313, 958–960.
28. Q. Hou, Q. Wu, Y. Xu, X. Zheng, Y. Zhao, Y. Wang, D. Guo and X. Xu, Roles of the Hydrophobic Tail Groups on the Properties of CO-Switchable Surfactants, 2019.
29. S. Ma, Y. Wang, J. Sun, X. Yi, Z. Chang and Q. Hou, J. Phys.: Conf. Ser., 2023, 2587, 012010.
30. Y. Wang and Z. Ye, J. Dispersion Sci. Technol., 2019, 40, 355–360.
31. L. Zhang, X. Lu, X. Liu, Q. Li, Y. Cheng and Q. Hou, Phys. Chem. Chem. Phys., 2020, 22, 23574–23585.
32. X. Liu, Y. Li, S. Tian and H. Yan, J. Phys. Chem. C, 2019, 123, 25246–25254.
33. M. Ahmadi, Q. Hou, Y. Wang, X. Lei, B. Liu and Z. Chen, Energy, 2023, 279, 128100.
34. M. Ahmadi, Q. Hou, Y. Wang and Z. Chen, Chem. Eng. Res. Des., 2024, 210, 513–530.
35. M. Zhang, Y. Nan, Y. Lu, Q. You and Z. Jin, Fuel, 2023, 331, 125773.
36. T. Stavert and M. Jorge, J. Mol. Liq., 2025, 431, 127656.
37. W. Zhou, L. Jiang, X. Liu, Y. Hu and Y. Yan, Colloids Surf., A, 2022, 637, 128259.
38. M. Liu, H. Xiao, R. Pan, J. Ren, L. Zhang and L. Zhang, Langmuir, 2024, 40, 6898–6908.
39. W. Zhou, X. Tang, X. Liu, Y. Yan and C. Chen, J. Phys. Chem. B, 2024, 128, 2985–2994.
40. S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871.
41. S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. G. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves, T. C. Le, Q. A. Besford and A. J. Christofferson, J. Chem. Inf. Model., 2021, 61, 4521–4536.
42. J. Zhou and P. G. Ranjith, J. Mol. Liq., 2022, 346, 117865.
43. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
44. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
45. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
46. L. S. Dodda, J. Z. Vilseck, K. J. Cutrona and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 4273–4282.
47. G. D. Barbosa, C. L. Manske, F. W. Tavares and C. H. Turner, Fluid Phase Equilib., 2023, 575, 113925.
48. S. Nosé, Mol. Phys., 1984, 52, 255–268.
49. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
50. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 34, 2499–2500.
51. O. Buneman, SIAM Rev., 1983, 25, 425–426.
52. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
53. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
54. S. Gao, X. Bao, L. Yu, H. Wang, J. Li and X. Chen, Colloids Surf., A, 2022, 634, 127899.
55. X. Lei, B. Liu, Q. Hou, Y. Wang, M. Ahmadi, Z. Liu and Z. Chen, J. Mol. Liq., 2024, 405, 125051.
56. S. Li, Y. Liu, L. Xue and D. Zhu, J. Pet. Sci. Eng., 2022, 212, 110259.
57. A. Ghoufi, P. Malfreyt and D. J. Tildesley, Chem. Soc. Rev., 2016, 45, 1387–1409.
58. D. M. Mitrinović, A. M. Tikhonov, M. Li, Z. Huang and M. L. Schlossman, Phys. Rev. Lett., 2000, 85, 582–585.
59. J. Jia, J. Li, Y. Liang and B. Peng, Fuel, 2022, 308, 122013.
60. P. Shi, H. Luo, X. Tan, Y. Lu, H. Zhang and X. Yang, RSC Adv., 2022, 12, 27330–27343.
61. S. S. Jang, S.-T. Lin, P. K. Maiti, M. Blanco, W. A. Goddard, P. Shuler and Y. Tang, J. Phys. Chem. B, 2004, 108, 12130–12140.

---

Footnote

† These authors contributed equally to this work.

---