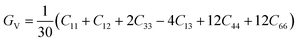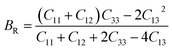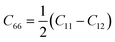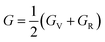Strain engineering of optoelectronic and ferroelectric properties in R3-phase Zn₃TeO₆: a first-principles study

Abstract

A systematic evaluation of the optoelectronic properties of ferroelectric ternary oxides under strain is essential for their integration into functional devices. In this study, the R3-phase ternary oxide Zn₃TeO₆ was investigated using density functional theory to examine its stability, electronic structure, optical properties, ferroelectric behavior, and carrier mobility under both compressive and tensile strain. Calculations of elastic constants, molecular dynamics simulations, and phonon spectra confirm the stability of Zn₃TeO₆ within a modest strain range. Compressive strain increases phonon frequencies, elastic constants, and bandgap, while enhancing ferroelectric polarization. In contrast, tensile strain decreases the bandgap and promotes visible-light absorption. Carrier transport analysis reveals pronounced n-type conduction, with electron mobility reaching ∼150 cm² V⁻¹ s⁻¹, further enhanced under compressive strain due to the suppression of polar optical phonon and piezoelectric scattering. These findings demonstrate that strain engineering offers an effective approach to tuning the multifunctional properties of R3-Zn₃TeO₆, highlighting its potential for ferroelectric and photovoltaic applications.

---

1. Introduction

X₃TeO₆ compounds (where X is a 3d transition metal) have attracted considerable attention due to their unique magnetic, electric, and dielectric properties.^1–5 Their complex magnetic behaviors and field-induced polarization effects, particularly the antiferromagnetic transitions and colossal magnetoelectric coupling observed in several members, highlight their great potential for multifunctional device applications.^1,3,5 Zn₃TeO₆ crystallizes in an isostructural β-Li₃VF₆-type structure, similar to X₃TeO₆, and contains five distinct Zn²⁺ coordination environments, including distorted octahedral, tetrahedral, and square-pyramidal sites.^6–8 While the C2/c phases of Co₃TeO₆ and Zn₃TeO₆ are enthalpically favored below 10 GPa, the R3 phase becomes energetically more stable above this pressure, resulting in a C2/c → R3 structural transition.⁹ While the R3 phase is a high-pressure phase in bulk materials, substrate-induced strain in epitaxial thin films can plausibly stabilize its polar structure as the energetic ground state, similar to the stabilization of polar R3c MgSnO₃ films grown epitaxially or by pulsed laser deposition.^10,11 Fernández-Catalá et al. successfully synthesized nanoscale Ni₃TeO₆ (R3) and Cu₃TeO₆ (Ia3̄) via an NaOH-assisted hydrothermal method, finding both materials exhibit semiconducting behavior (with respective band gaps of 2.44 eV and 2.56 eV) and pronounced photoconductivity.¹² A high-pressure phase, Mg₃TeO₆ (space group R3), was obtained under 12.5 GPa and 1570 K, with an experimental band gap of 3.5 eV, confirming its wide-bandgap semiconducting nature.¹³ Furthermore, crystallographic and optical investigations of Co_3−xZn_xTeO₆ revealed that Zn dopants preferentially occupy tetrahedral sites, enhancing local distortion, while the strong covalent character of Co–O bonds significantly affect the optical response.¹⁴ Magnetic studies by Sarkar et al. demonstrated that Zn substitution shortens the Co²⁺–O bond length and markedly suppresses the magnetic interactions in Co₃TeO₆.¹⁵ X₃TeO₆ compounds with the R3 structure not only have potential applications in magnetism, photoconductivity, and as semiconductors, but this polar R3 structure also suggests potential ferroelectric behavior, implying potential ferroelectric photovoltaic properties.^16–18

By applying tensile strain, the structural stability, bandgap characteristics, and optical responses of various emerging two-dimensional materials (such as Si₂C, C₃B, and h-BC₂N) can be effectively tuned, enabling bandgap modulation and enhanced optical absorption, which highlights the crucial role of strain engineering in optimizing their optoelectronic performance.^19–21 Likewise, for three-dimensional ferroelectric materials, strain engineering has also become an indispensable strategy for tailoring their intrinsic properties. Compared with chemical doping or external fields, strain offers advantages such as reversibility, continuity, and high precision, enabling the modulation of structural stability as well as electronic, magnetic, and optical properties without introducing chemical complexity.^22–24 Epitaxial strain, for instance, can reconstruct band structures, leading to bandgap enlargement and corresponding modifications of the optical response in materials such as R3c-BiFeO₃.²⁵ Strain effects during synthesis are also critically important, as research has shown that the lattice strain introduced by reducing the heating rate during calcination can enhance the oxygen evolution reaction (OER) activity and stability of Ni₃TeO₆ electrocatalysts.²⁶ It is reported in the literature that epitaxial strain can enhance ferroelectric properties while also favorably modifying the optical response of thin films, supporting their viability for optoelectronic device applications.²⁷

Despite substantial advances in elucidating the magnetic properties of the X₃TeO₆ system, its optoelectronic behavior—particularly the evolution of electronic structure and carrier dynamics of Zn₃TeO₆ under different strain conditions—remains insufficiently explored. In this work, first-principles calculations combined with strain engineering are employed to investigate the structural stability, band modulation, carrier transport, and polarization response of R3-Zn₃TeO₆ under both compressive and tensile strains. The aim is to uncover the mechanisms by which strain regulates its thermodynamic and mechanical stability as well as its coupled optoelectronic–ferroelectric properties, thereby providing theoretical guidance for the design and device integration of multifunctional tellurates.

2. Calculation model and method

All calculations in this work are mainly completed by the Vienna Ab initio Simulation Package (VASP) software package for first-principles calculations.^28,29 The interaction between electrons and atomic nuclei in the computational system is described using the projection additive wave (PAW) pseudo potential,³⁰ and the exchange correlation functional between electrons is processed using the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE).³¹ The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional is used to calculate the bandgap values and optical properties, as it is usually closer to the experimental values.^32,33 A plane-wave cutoff energy of 520 eV was employed, and the Brillouin zone was sampled using a 7 × 7 × 3 gamma-centered k-point mesh. The electronic configurations of pseudo potential for Zn, Te, and O atoms are chosen as d¹⁰p², s²p⁴, and s²p⁴, respectively. The iterative convergence accuracy of the energy is set to 10⁻⁶ eV, and the Hellman–Feynman forces are less than 0.01 eV Å⁻¹. The structural model of R3-Zn₃TeO₆ is shown in Fig. 1, which contains 30 atoms.

Fig. 1 The structure of R3-Zn₃TeO₆.

The calculated lattice parameters are shown in Table 1. The calculated lattice parameters a and c of R3-Zn₃TeO₆ by PBE method are 5.27 Å and 14.02 Å. As shown in Fig. 1, introducing a 3% compressive strain in the ab plane of R3-Zn₃TeO₆ reduces the lattice parameter a from 5.27 Å to 5.11 Å. At the same time, the lattice parameter c of R3-Zn₃TeO₆ under compression strain in the ab direction is changed to 14.38 Å, which is larger than the intrinsic R3-Zn₃TeO₆. When a similar tensile strain is introduced in the R3-Zn₃TeO₆ along ab plane, the lattice parameters a and c of R3-Zn₃TeO₆ are changed to 5.43 Å and 13.70 Å, respectively. When the compressive and tensile strains increase to 6%, the variation trends of the lattice parameters a and c remain essentially consistent with those observed under 3% strain. In all tables and pictures, c-Zn₃TeO₆ and t-Zn₃TeO₆ have been used to express as Zn₃TeO₆ under compressive strain and tensile strain, respectively. The lattice a/c ratios of Zn₃TeO₆ approach 0.37, closely matching those of Co₃TeO₆,⁹ Ni₃TeO₆ (ref. 12) and Mg₃TeO₆,¹³ indicating a highly similar crystal structure. The stability and photoelectric properties of R3-Zn₃TeO₆ under compressive and tensile strain have been analyzed by elastic properties, phonon spectrum and electronic structure.

Table 1 The calculated lattice parameters by PBE method

R3	a (Å)	c (Å)
c-Zn3TeO6 (−6%)	4.96	14.78
c-Zn3TeO6 (−3%)	5.11	14.38
Zn3TeO6	5.27	14.02
t-Zn3TeO6 (3%)	5.43	13.70
t-Zn3TeO6 (6%)	5.59	13.45
Co3TeO6 (ref. 9)	5.19	13.80
Ni3TeO6 (ref. 10)	5.11	13.75
Mg3TeO6 (ref. 11)	5.14	13.81

---

3. Results and discussion

3.1 Stability and mechanical properties

Ab initio molecular dynamics (AIMD) simulations were performed at 300 K within the NVT ensemble using the Nosé–Hoover thermostat, with a time step of 2 fs and a total simulation duration of 10 ps. Fig. 2 presents the evolution of the total energy of Zn₃TeO₆ under various strain conditions. As shown in Fig. 2, the compressive (−3%), unstrained, and tensile (+3%) configurations exhibit only minor fluctuations in total energy throughout the simulation, with no abrupt changes or indications of structural collapse. The atomic configurations after the AIMD run remain essentially identical to their initial structures, with no bond breaking or noticeable lattice distortion observed. These results confirm that R3-Zn₃TeO₆ retains good thermal and dynamic stability within the investigated strain range. In addition to the ±3% strain discussed in the main text, AIMD simulations under larger biaxial strains of −6% and +6% were included in the SI to provide a more comprehensive assessment of the strain-dependent thermal stability of R3-Zn₃TeO₆. As shown in Fig. S1 (SI), the system under −6% compressive strain exhibits an upward trend in total energy during the 300 K, 10 ps simulation, suggesting potential instability despite the absence of structural collapse or bond breaking. In contrast, the +6% tensile configuration shows relatively stable energy fluctuations and remains structurally intact, indicating that it still maintains dynamic stability. Overall, the stability of Zn₃TeO₆ deteriorates under such large strain conditions.

Fig. 2 AIMD energy evolution of Zn₃TeO₆ under (a) −3% compressive strain, (b) the unstrained structure, and (c) +3% tensile strain.

The phonon spectra of R3-Zn₃TeO₆ under compressive and tensile strain were calculated using the VASP + PHONOPY package.³⁴ As displayed in Fig. 3, all phonon frequencies are positive with no imaginary modes, demonstrating that the material satisfies the dynamic stability criteria within this strain range. Furthermore, compressive strain increases phonon frequencies, whereas tensile strain reduces them, indicating that compressive strain enhances the dynamic stability of R3-Zn₃TeO₆ while tensile strain slightly weakens it. Phonon calculations under larger biaxial strains of −6% and +6% were also provided in the SI. As shown in Fig. S2 (SI, imaginary phonon modes appear under both strain conditions, confirming that the dynamic stability of Zn₃TeO₆ deteriorates significantly when subjected to such large strains.

Fig. 3 The calculated phonon frequency of (a) c-Zn₃TeO₆, (b) Zn₃TeO₆ and (c) t-Zn₃TeO₆.

To assess the mechanical stability of R3-Zn₃TeO₆ under compressive and tensile strain, the elastic constants were calculated using the VASP package, as summarized in Table 2. Owing to the symmetry of the trigonal/rhombohedral system (R3 space group), seven independent elastic constants were obtained. According to the stability criteria proposed by Mouhat and Coudert,³⁵ R3-Zn₃TeO₆ is mechanically stable when the following inequalities are satisfied:

(i) C₁₁ > |C₁₂|

(ii) C₁₃² < 0.5 × C₃₃ × (C₁₁ + C₁₂)

(iii) C₁₄² + C₁₅² < 0.5C₄₄ × (C₁₁ − C₁₂)

(iv) C₄₄ > 0

Table 2 The calculated elastic constants and the unit is given in GPa

R3	C11	C12	C13	C14	C15	C33	C44
c-Zn3TeO6 (−6%)	290.948	177.480	127.568	14.680	1.569	285.218	32.349
c-Zn3TeO6 (−3%)	270.858	151.487	104.092	16.212	2.533	244.507	34.758
Zn3TeO6	238.136	130.239	79.997	17.669	8.430	202.499	26.784
t-Zn3TeO6 (3%)	207.301	121.390	62.335	19.075	14.730	174.200	19.133
t-Zn3TeO6 (6%)	141.795	114.394	34.617	20.679	19.190	139.421	16.947

---

Our results show that under +6% tensile strain, the elastic constants fail to satisfy these inequalities, indicating mechanical instability. In contrast, the unstrained configuration and all other strain states meet the criteria and thus remain mechanically stable. Notably, compressive strain increases the elastic constants, implying enhanced mechanical strength, whereas tensile strain reduces them, leading to weakened stability. This trend is consistent with our previous findings.³⁶ We further evaluated the bulk modulus B, shear modulus G, and Young's modulus E using the Voigt–Reuss–Hill (VRH) approximation.³⁷ The explicit formulas are:

As summarized in Table 3, compressive strain leads to an increase in Young's modulus, whereas tensile strain reduces it, consistent with trends reported in previous literature.³⁶ Integrating the results from molecular dynamics, phonon spectra, and elasticity-based stability analyses, we conclude that R3-Zn₃TeO₆ remains stable under small strains (±3%), while larger strains (±6%) are prone to inducing instability. This is in agreement with experimental observations: during the fabrication of three-dimensional polar films via pulsed laser deposition (PLD) or molecular beam epitaxy (MBE), substrates with closely matched lattice parameters are typically required.^10,11 Therefore, in the following discussions on electronic structure, band dispersion, optical properties, ferroelectric polarization, and carrier transport behavior, we primarily focus on configurations under small strain (±3%).

Table 3 The calculated Bulk modulus B, Shear modulus G and Young's modulus E

R3	B (GPa)	G (GPa)	E (GPa)
c-Zn3TeO6 (−6%)	192.957	52.858	145.307
c-Zn3TeO6 (−3%)	166.064	48.519	132.638
Zn3TeO6	138.108	38.794	106.417
t-Zn3TeO6 (3%)	117.896	24.267	68.126
t-Zn3TeO6 (6%)	93.096	14.764	46.763

---

3.2 Optoelectronic property

The energy band structure and densities of states (DOS) for R3-Zn₃TeO₆ under unstrained, compressive, and tensile conditions were calculated using the HSE06 hybrid functional. As shown in Fig. 4, the unstrained R3-Zn₃TeO₆ exhibits a calculated band gap of 2.60 eV. This value modulates under applied strain, widening to 2.72 eV under compressive strain (c-Zn₃TeO₆) and narrowing to 2.36 eV under tensile strain (t-Zn₃TeO₆). These calculated band gaps are considerably smaller than that of HP-Mg₃TeO₆ (3.5 eV), suggesting potential for absorption over a broader portion of the visible spectrum and potentially enhanced photoelectric conversion efficiency.¹³ Specifically, the band gap narrowing under tensile strain suggests enhanced visible light absorption, whereas the band gap widening under compression is expected to shift the absorption onset toward the ultraviolet region, reducing responsiveness to visible light. Analysis of the projected densities of states (PDOS) in Fig. 4 indicates that considerable hybridization between O 2p and Zn 3d orbitals occurs within the valence band (ca. −3.5 to −2.0 eV). This hybridization likely plays a significant role in determining the material's primary electronic properties. The states near the valence band maximum (VBM) are predominantly composed of hybridized O–Zn orbitals, while the states near the conduction band minimum (CBM) are mainly derived from O–Te hybrid orbitals. For both the VBM and CBM, O 2p states provide the most significant contribution. Compared to the unstrained structure, c-Zn₃TeO₆ exhibits a lower density of O-derived states at the VBM, whereas t-Zn₃TeO₆ shows a higher density. Simultaneously, the CBM energy level shifts upward for c-Zn₃TeO₆ and downward for t-Zn₃TeO₆ relative to the unstrained case. The mechanism for this band gap widening under compression is consistent with the findings of Liu H. L. et al.²³ and can be attributed to the shortening of O–Zn and O–Te bond lengths Table 4, which enhances orbital overlap. The band structures of Zn₃TeO₆ under ±6% compressive and tensile strain were also calculated, and the results are provided in the SI (Fig. S3). The bandgaps obtained under 6% compressive and 6% tensile strain are 2.68 eV and 2.03 eV, respectively. Relative to the unstrained state, the compressive strain results in an increased bandgap, whereas the tensile strain leads to a reduced bandgap.

Fig. 4 The calculated band structure and density of states of (a) c-Zn₃TeO₆, (b) Zn₃TeO₆ and (c) t-Zn₃TeO₆.

Table 4 The calculated bond length of Zn–O and Te–O. The unit is given in Å

	Zn1–O1	Zn1–O2	Zn2–O1	Zn2–O2	Zn3–O1	Zn3–O2	Te–O1	Te–O2
c-Zn3TeO6 (−6%)	2.25	2.00	2.00	2.18	1.95	2.18	1.96	1.92
c-Zn3TeO6 (−3%)	2.30	2.02	1.99	2.23	2.02	2.23	1.97	1.94
Zn3TeO6	2.33	2.04	2.03	2.27	2.05	2.29	1.98	1.95
t-Zn3TeO6 (3%)	2.36	2.07	2.08	2.32	2.08	2.35	2.00	1.97
t-Zn3TeO6 (6%)	2.37	2.10	2.09	2.45	2.14	2.30	2.01	1.98

---

The absorption coefficient α(ω) can be obtained from the real part ε₁(ω) and imaginary part ε₂(ω) of the dielectric function via the formula . As shown in Fig. 5, pristine Zn₃TeO₆ and its strained counterparts exhibit consistent optical-response trends in both ε₂(ω) and α(ω): negligible absorption is found in the low-energy region (<∼2.2 eV), indicating weak intrinsic absorption in the visible range, whereas a sharp rise emerges near the band edge, giving rise to pronounced peaks. Consequently, all three structures show strong ultraviolet absorption above ∼3 eV, with maximum absorption coefficients on the order of 10⁴ cm⁻¹. A clear divergence appears under tensile versus compressive strain. The 3% tensile strain narrows the band gap, causing a red shift of the absorption edge for t-Zn₃TeO₆ to ∼2.8 eV and producing a stronger main peak around 3.1–3.3 eV (maximum ε₂ ≈ 0.55 with a corresponding absorption peak of ∼8 × 10⁴ cm⁻¹), thereby enabling enhanced near-UV and lower-energy photon absorption. In contrast, −3% compressive strain widens the band gap, shifting the absorption edge of c-Zn₃TeO₆ to higher energy (∼3.1 eV) and slightly moving the main peak toward ∼3.7–3.8 eV with reduced intensity, confining its dominant response to the ultraviolet region. These results confirm that strain engineering is an effective approach for tuning band-edge optical transitions and optimizing the electronic and optical properties of R3-Zn₃TeO₆.

Fig. 5 (a) Imaginary component of the dielectric function (ε₂) and (b) optical absorption coefficient (α) of Zn₃TeO₆.

3.3 Ferroelectric property

The ferroelectric polarization of unstrained, compressively strained, and tensile-strained R3-Zn₃TeO₆ was calculated using the Berry-phase method.^38,39 Following this approach, a centrosymmetric R3 reference structure was constructed, and the energy and polarization were obtained through linear interpolation between the polar R3 phase (λ = 1) and the centrosymmetric phase (λ = 0). As shown in Fig. 6(a), the structural distortion energy curves of R3-Zn₃TeO₆ under all strain conditions exhibit a double-well potential, indicating robust ferroelectricity. The ferroelectric well depths are 0.86 eV (unstrained), 1.52 eV (compressive strain), and 0.53 eV (tensile strain). Because the calculations correspond to three formula units, the averaged well depths per Zn₃TeO₆ formula unit are 0.29 eV, 0.51 eV, and 0.18 eV, respectively. Under compressive strain, the well depth (0.51 eV f.u⁻¹) becomes comparable to that of the classical ferroelectric BiFeO₃ (0.43 eV f.u⁻¹),⁴⁰ demonstrating that compressive strain enhances the stability of the ferroelectric phase. The calculated spontaneous polarization of R3-Zn₃TeO₆ increases from 59.07 µC cm⁻² (unstrained) to 63.00 µC cm⁻² under compressive strain, approaching the reported value of 72 µC cm⁻² for Ni₃TeO₆.⁹ This enhancement originates from the reduced interatomic distances and strengthened polar phonon instability induced by compressive strain. Under 3% tensile strain, the polarization decreases to 55.90 µC cm⁻², which is consistent with the behavior observed in R3c-BiFeO₃.⁴¹ Fig. 6(b–d) show that at the polarization endpoints (λ = ±1), compressive strain significantly increases the slope of the polarization curve, indicating a stronger and faster lattice-distortion-induced polarization response. In contrast, tensile strain reduces both polarization and potential-well depth, thereby weakening ferroelectric stability. As shown in Fig. S4, the potential-energy curves under 0%, ±3%, and ±6% strain confirm these trends. Tensile strain gradually shallows the double-well potential and reduces the energy difference between the ferroelectric and paraelectric phases. At 6% tensile strain, the two wells nearly merge, and the interpolation-based Berry-phase method fails to converge. Conversely, 6% compressive strain deepens the ferroelectric–paraelectric potential well and increases the spontaneous polarization to 67.94 µC cm⁻².

Fig. 6 (a) Potential energy curves and ferroelectric polarization as a function of structural distortion for (b) −3% compressive strain, (c) the unstrained structure, and (d) +3% tensile strain.

3.4 Mobility

The carrier mobility of semiconductors governs the electrical conductivity and switching performance of devices and is therefore critical for many applications. Fig. 7 presents the electron and hole mobilities of the three structures as a function of n-type and p-type carrier concentrations, calculated using the AMSET code within the momentum relaxation time approximation (MRTA) framework.⁴² In these calculations, four dominant scattering mechanisms are explicitly considered: acoustic deformation potential (ADP) scattering, piezoelectric (PIE) scattering, polar optical phonon (POP) scattering, and ionized impurity (IMP) scattering. The total mobility is obtained by combining the contributions from these scattering processes, and all relevant parameters are derived from first-principles calculations. For ADP scattering, small uniaxial (or isotropic) strains are applied to the crystal, and the band structures are recalculated for each strain value. The deformation potential constant E₁ is then obtained by linearly fitting the variation of the conduction-band minimum (CBM) or valence-band maximum (VBM) energy with respect to strain, as summarized in Table 5, while the corresponding elastic constants are taken from Table 2. For PIE scattering, the piezoelectric tensor is evaluated using density functional perturbation theory (DFPT) under small strains by computing the change in polarization and is subsequently combined with the elastic constants and piezoelectric tensor for transport calculations Tables 2 and 6. For POP scattering, the longitudinal optical (LO) phonon frequency at the Γ point, together with the static and high-frequency dielectric constants (ε₀ and ε_∞), is obtained from DFPT Table 7, and these quantities are used to construct a Fröhlich-type electron–LO phonon coupling model. For IMP scattering, all dopants are assumed to be fully ionized, and the ionized impurity concentration is set equal to the carrier concentration specified in the transport calculations. The impurity charge number Z is chosen according to the assumed dopant valence, while the dielectric constant obtained from first-principles calculations is used to describe the screening of the coulomb interaction.

Fig. 7 The (a) electron and (b) hole mobility as a function of concentration for semiconductor Zn₃TeO₆ by AMSET code.

Table 5 The calculated the deformation potential calculations (eV)

		VBM			CBM
		DXX	DYY	DZZ	DXX	DYY	DZZ
c-Zn3TeO6 (−3%)	DXX	0.20	0.92	0.11	5.56	0.18	0.03
	DYY	0.92	0.22	0.03	0.18	5.57	0.08
	DZZ	0.11	0.03	2.32	0.03	0.08	7.87
Zn3TeO6	DXX	0.72	0.56	0.22	5.64	0.05	0.12
	DYY	0.56	0.71	0.21	0.05	5.64	0.11
	DZZ	0.22	0.21	1.83	0.12	0.11	5.83
t-Zn3TeO6 (3%)	DXX	1.61	0.22	0.31	5.67	0.09	0.1
	DYY	0.22	1.62	0.32	0.09	5.66	0.1
	DZZ	0.31	0.32	0.95	0.1	0.1	4.16

---

Table 6 The calculated piezoelectric tensor (C/m⁻²)

		XX	YY	ZZ	XY	YZ	ZX
c-Zn3TeO6	X	0.30	−0.30	0.00	0.12	0.00	−0.06
	Y	0.12	−0.12	0.00	−0.30	−0.06	0.00
	Z	−0.08	−0.08	−0.63	−0.01	0.00	0.00
Zn3TeO6	X	0.34	−0.34	0.00	0.25	0.05	−0.07
	Y	0.25	−0.25	0.00	−0.34	−0.06	−0.05
	Z	−0.56	−0.56	−1.10	−0.01	0.00	0.00
t-Zn3TeO6	X	0.45	−0.45	0.00	0.37	0.05	−0.15
	Y	0.37	−0.37	0.00	−0.45	−0.14	−0.05
	Z	−0.66	−0.66	−1.47	0.00	0.00	0.00

---

Table 7 Parameters and results of mobility calculation. ω₀ is polar-optical phonon frequency (THz), ε₀ and ε_∞ are static dielectric constant and high-frequency dielectric constant and m* is effective mass (m_e). S is the scattering rate of the material at a doping concentration of 10⁻¹⁸ cm⁻³ (10¹² S⁻¹)

		ω0	ε0	ε∞	m*	S
						ADP	IMP	PIE	POP
c-Zn3TeO6	Electron	10.82	14.82	4.72	0.23	6.6	13.9	19.5	252
	Hole				6.88	6.6	12.7	19.5	252
Zn3TeO6	Electron	10.04	17.3	4.85	0.21	9.1	15.9	58.5	271
	Hole				8.01	9.1	14.4	58.5	271
t-Zn3TeO6	Electron	9.23	21.09	5.09	0.18	20.8	14.4	195	295
	Hole				8.46	20.8	12.9	195	295

---

Within AMSET, the carrier mobility at different n-type and p-type doping levels is computed consistently under the MRTA framework. In this approach, doping is not modeled by explicit atomic substitution; instead, the target carrier concentration is provided as an input parameter. For a given electron or hole concentration, AMSET self-consistently determines the corresponding Fermi level and evaluates the scattering rates arising from ADP, POP, IMP, and other relevant mechanisms, and then solves the Boltzmann transport equation to obtain mobility. In this way, the dependence of electron and hole mobilities on n-type and p-type carrier concentrations is systematically established without modifying the underlying crystal structure.

The results show that at a moderate doping concentration of 10¹⁸ cm⁻³, the electron mobility for all three structures exceeds 150 cm² V⁻¹ s⁻¹, approaching that of conventional semiconductor ZnO.⁴³ The hole mobility is two orders of magnitude lower than the electron mobility, indicating that Zn₃TeO₆ is characterized by strong n-type behavior. From the input parameters Table 7, the hole effective mass is significantly larger than the electron effective mass, consistent with the relatively flat band structure near the VBM. This results in substantially lower hole transport capability compared to electrons. Among the scattering mechanisms, POP scattering dominates, reaching an order of magnitude of approximately 10¹⁴ s⁻¹, which critically determines the carrier relaxation time.

Notably, among the three structures c-Zn₃TeO₆ exhibits the highest electron mobility value. Although compressive strain slightly increases the effective mass of Zn₃TeO₆, it concurrently elevates the characteristic frequency ω₀ of the polar optical phonons. As evident in the phonon dispersion spectra Fig. 3, c-Zn₃TeO₆ possesses higher optical phonon frequencies. A higher ω₀ implies that greater energy is required for electrons to exchange energy with optical phonons, thereby significantly reducing POP scattering intensity. Furthermore, as strain transitions from tensile to compressive, the high-frequency dielectric constant ε_∞ and the static dielectric constant ε₀ decrease slightly. Since the polar coupling strength is proportional to , which equals 0.149, 0.148, and 0.144 for the t-Zn₃TeO₆, Zn₃TeO₆, and c-Zn₃TeO₆ structures respectively, compressive strain weakens polar coupling, further suppressing POP scattering. For PIE scattering, under tensile strain, the scattering rate can reach the order of 10¹⁴ s⁻¹, highlighting its significant contribution to carrier scattering. However, as shown in Table 6, under compressive strain, the tensor components of the piezoelectric coefficients are notably reduced due to decreased lattice dimensions and restricted atomic displacements. This reduction stems from the smaller lattice dimensions and constrained atomic displacements within the unit cell, leading to diminished piezoelectric response and consequently reduced PIE scattering intensity. Overall, the analysis shows that compressive strain helps suppress the dominant scattering mechanisms POP and PIE, thereby enhancing the electron mobility in Zn₃TeO₆.

4. Conclusion

Using density functional theory, the elastic constants, phonon spectra, and molecular dynamics of R3-Zn₃TeO₆ under compressive and tensile strain were systematically investigated to assess its structural stability. Electronic structure analyses reveal that the valence band is predominantly determined by Zn–O interactions, while the conduction band mainly arises from Te–O hybridization. Under compressive strain, the O orbital contribution near the valence band maximum decreases and the conduction band minimum shifts upward, resulting in a bandgap widening from 2.60 eV to 2.72 eV. Conversely, tensile strain enhances the O orbital contribution and lowers the conduction band minimum, narrowing the bandgap to 2.36 eV—favorable for visible-light absorption. Compressive strain significantly enhances the ferroelectric polarization of Zn₃TeO₆, conferring excellent ferroelectric performance and structural robustness. In terms of charge transport, Zn₃TeO₆ exhibits high electron mobility (>150 cm² V⁻¹ s⁻¹) and hole mobility two orders of magnitude lower, indicative of a strong n-type character. Notably, compressive strain further promotes electron mobility through increased optical phonon frequencies and reduced piezoelectric coefficients, effectively suppressing carrier scattering. These results provide theoretical insight into the potential of R3-Zn₃TeO₆ for stable, high-performance ferroelectric and optoelectronic applications.

Conflicts of interest

The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5ra08570e.

Acknowledgements

This work was supported by the Maoming Municipal Science and Technology Program (No 2023023), the Guangdong University of Petrochemical Technology 2022 University-level Educational and Teaching Reform Research Project (No. JY202245), Guangdong Provincial Key Areas Special Project for Regular Higher Education Institutions (Grant No. 2023ZDZX3014).

References

1. M. Hudl, R. Mathieu and S. A. Ivanov, et al., Complex magnetism and magnetic-field-driven electrical polarization of Co₃TeO₆, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 180404.
2. S. A. Ivanov, R. Tellgren and C. Ritter, et al., Temperature-dependent multi-k magnetic structure in multiferroic Co₃TeO₆, Mater. Res. Bull., 2012, 47, 63–72.
3. J. W. Kim, S. Artyukhin and E. D. Mun, et al., Successive magnetic-field-induced transitions and colossal magnetoelectric effect in Ni₃TeO₆, Phys. Rev. Lett., 2015, 115, 137201.
4. X. Zhu, Z. Wang and X. Su, et al., New Cu₃TeO₆ ceramics: phase formation and dielectric properties, ACS Appl. Mater. Interfaces, 2014, 6, 11326–11332.
5. S. A. Ivanov, P. Nordblad and R. Mathieu, et al., New type of incommensurate magnetic ordering in Mn₃TeO₆, Mater. Res. Bull., 2011, 46, 1870–1877.
6. M. Weil, Zn₃TeO₆, Struct. Rep., 2006, 62, i246–i247.
7. W. Massa, Die Kristallstruktur von β-Li₃VF₆, Z. Kristallogr.–Cryst. Mater., 1980, 153, 201–210.
8. R. Becker, M. Johnsson and H. Berger, A new synthetic cobalt tellurate: Co₃TeO₆, Cryst. Struct. Commun., 2006, 62, i67–i69.
9. Y. Han, M. Wu and C. Gui, et al., Data-driven computational prediction and experimental realization of exotic perovskite-related polar magnets, NPJ Quantum Mater., 2020, 5, 92.
10. K. Fujiwara, et al., Thin-film stabilization of LiNbO₃-type ZnSnO₃ and MgSnO₃ by molecular-beam epitaxy, APL Mater., 2019, 7, 022505.
11. X. Han, et al., MgSnO₃ epitaxial thin films for solar-blind photodetection: Fabrication and properties, Vacuum, 2024, 226, 113340.
12. J. Fernández-Catalá, H. Singh and S. Wang, et al., Hydrothermal synthesis of Ni₃TeO₆ and Cu₃TeO₆ nanostructures for magnetic and photoconductivity applications, ACS Appl. Nano Mater., 2023, 6, 4887–4897.
13. E. Selb, L. Declara and L. Bayarjargal, et al., Crystal Structure and Properties of a UV-Transparent High-Pressure Polymorph of Mg₃TeO₆ with Second Harmonic Generation Response, Eur. J. Inorg. Chem., 2019, 4668–4676.
14. D. Reichartzeder, M. Wildner and M. Weil, et al., Crystal Chemistry, Optical Spectroscopy and Crystal Field Calculations of Co₃TeO₆ and Solid Solutions Co₃–xZnxTeO₆, Eur. J. Inorg. Chem., 2018, 4221–4233.
15. T. Sarkar, S. A. Ivanov and M. Weil, et al., Compositional dependence of the magnetic state of Co₃− xZnxTeO₆ solid solutions, J. Alloys Compd., 2021, 884, 161111.
16. G. Song and W. Zhang, Comparative studies on the room-temperature ferrielectric and ferrimagnetic Ni₃TeO₆-type A₂FeMoO₆ compounds (A = Sc, Lu), Sci. Rep., 2016, 6, 20133.
17. A. F. Lima, Electronic and optical properties of the R3 Ni₃TeO₆ compound described by the modified Becke-Johnson exchange potential, Opt. Mater., 2023, 136, 113419.
18. M. Ye and D. Vanderbilt, Ferroelectricity in corundum derivatives, Phys. Rev. B, 2016, 93, 134303.
19. H. Shu and J. Guo, Enhanced stability and tunable optoelectronic properties of silicon–carbon monolayers by strain and surface functionalization, J. Mater. Chem. C, 2024, 12(16), 5916–5925.
20. H. Shu, Assessing stability and optoelectronic properties of 2D carbon-boron compounds under elastic strains, Surf. Interfaces, 2025, 106702.
21. H. Shu and H. Xu, Effects of strain on the stability, electronic, and optical properties of new h-BC 2 N: a many-body study, Phys. Chem. Chem. Phys., 2025, 27(32), 16972–16979.
22. D. G. Schlom, L. Q. Chen and X. Pan, et al., A thin film approach to engineering functionality into oxides, J. Am. Ceram. Soc., 2008, 91, 2429–2454.
23. J. Li, Y. Lee and Y. Choi, et al., The classical-to-quantum crossover in the strain-induced ferroelectric transition in SrTiO₃ membranes, Nat. Commun., 2025, 16, 4445.
24. Y. Hu, J. Yang and S. Liu, Giant piezoelectric effects of topological structures in stretched ferroelectric membranes, Phys. Rev. Lett., 2024, 133, 046802.
25. H. L. Liu, M. K. Lin and Y. R. Cai, et al., Strain modulated optical properties in BiFeO₃ thin films, Appl. Phys. Lett., 2013, 103, 181907.
26. M. Sharma, et al., Lattice strain engineering in Ni₃TeO₆ nanostructure for enhanced oxygen evolution reaction in alkaline medium, Int. J. Hydrogen Energy, 2025, 132, 116–129.
27. D. Sando, Y. Yang and C. Paillard, et al., Epitaxial ferroelectric oxide thin films for optical applications, Appl. Phys. Rev., 2018, 5, 041108.
28. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
29. G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B, 1993, 48, 13115–13118.
30. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59, 1758–1775.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
33. O. A. Vydrov and G. E. Scuseria, Assessment of a long-range corrected hybrid functional, J. Chem. Phys., 2006, 125, 234109.
34. A. Togo, First-principles phonon calculations with phonopy and phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001.
35. F. Mouhat and F. X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B, 2014, 90, 224104.
36. X. F. Xu, X. L. Cai and K. R. Su, et al., Tuning mechanical properties, ferroelectric properties and electronic structure in R3c-MgSnO₃ by compressive strain: A first-principle study, Phys. B, 2021, 618, 413143.
37. R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc. A., 1952, 65(5), 349.
38. R. Resta, Macroscopic polarization in crystalline dielectrics: the geometric phase approach, Rev. Mod. Phys., 1994, 66, 899–915.
39. R. D. King-Smith and D. Vanderbilt, Theory of polarization of crystalline solids, Phys. Rev. B, 1993, 47, 1651–1654.
40. S. Song, H. M. Jang and N. S. Lee, et al., Ferroelectric polarization switching with a remarkably high activation energy in orthorhombic GaFeO₃ thin films, NPG Asia Mater., 2016, 8, e242.
41. C. Ederer and N. A. Spaldin, Effect of epitaxial strain on the spontaneous polarization of thin film ferroelectrics, Phys. Rev. Lett., 2005, 95, 257601.
42. A. M. Ganose, J. Park and A. Faghaninia, et al., Efficient calculation of carrier scattering rates from first principles, Nat. Commun., 2021, 12, 2222.
43. E. M. Likovich, K. J. Russell and E. W. Petersen, et al., Weak localization and mobility in ZnO nanostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245318.

---