 Open Access Article
Open Access ArticleElectronic and magnetic properties of defective and Fe-doped InS monolayers adjusted by hole doping as a second functionalization step: a first-principles study
Nguyen Thanh Tien a,
Nguyen Thanh Sonb,
Truong Tuan Vuacd,
R. Ponce-Péreze,
J. Guerrero-Sancheze and
D. M. Hoat
a,
Nguyen Thanh Sonb,
Truong Tuan Vuacd,
R. Ponce-Péreze,
J. Guerrero-Sancheze and
D. M. Hoat *cd
*cd
aCollege of Natural Sciences, Can Tho University, 3-2 Road, Can Tho City 900000, Vietnam
bCenter of Scientific Research and Application, Lac Hong University, No. 10 Huynh Van Nghe Str, Tran Bien Ward, Dong Nai Province, Vietnam
cInstitute of Theoretical and Applied Research, Duy Tan University, Ha Noi 100000, Vietnam. E-mail: dominhhoat@duytan.edu.vn
dSchool of Engineering and Technology, Duy Tan University, Da Nang 550000, Vietnam
eUniversidad Nacional Autónoma de México, Centro de Nanociencias y Nanotecnología, Apartado Postal 14, Ensenada, Baja California Código Postal 22800, Mexico
First published on 16th January 2026
Abstract
In this work, hole doping is proposed as a second functionalization step to modify the electronic and magnetic properties of defective and Fe-doped InS monolayers. The pristine monolayer is confirmed to be a two-dimensional (2D) material with an indirect gap of 1.65 eV, whose In–S chemical bonds exhibit both covalent and ionic characters. The creation of a single In vacancy (1VaIn) or a pair of In vacancies (2VaIn) induces half-metallicity in the InS monolayer. In these cases, total magnetic moments of 1.00 and 2.00µB, respectively, are obtained, where S atoms closest to defect sites produce primarily the system magnetic moments. Meanwhile a single S vacancy (1VaS) induces no magnetism, however this defect causes a band gap reduction of the order of 28.48%. Significant magnetism is also obtained by Fe doping (FeIn) with an overall moment of 5.00µB, originating primarily from the transition metal impurity. Moreover, a magnetic semiconductor nature is also developed in the InS monolayer through doping with an Fe atom. The in-plane magnetic anisotropy (IMA) is confirmed for the magnetic 1VaIn@mo, 2VaIn@mo, and FeIn@mo systems. Further, the pristine InS monolayer is magnetized with a hole concentration of 1.5 holes per supercell. Both the magnetization and IMA of the 1VaIn@mo system can be significantly enhanced by hole doping, while the magnetism in the 2VaIn@mo system disappears upon adding a hole in its lattice. The nonmagnetic 1VaS@mo system becomes magnetic when it has been hole-doped with total magnetic moment up to 0.89µB. It is found that hole doping enhances the IMA of the FeIn@mo system, despite its magnetic moment reducing. In addition, the electronic structures of the considered InS systems can be effectively controlled by hole doping, where the hole level plays a key role. Our findings pave a solid way to functionalize the InS monolayer towards diverse spintronic and optoelectronic applications.
1. Introduction
Since the successful isolation of graphene,1 two-dimensional (2D) crystalline structures have been attracting enormous research attention from the scientific community. Intriguing properties such as high carrier mobility derived from its Dirac cone with linear energy dispersion, high mechanical strength, and large surface area, etc. have been found for graphene,2,3 making it the most studied 2D material. However, graphene is intrinsically a semimetal, not a semiconductor with an intrinsic band gap, such that its use in electronic nanodevices is considerably hindered. To overcome this limitation, different band gap opening strategies have been proposed through chemical modification4,5 or edge controlling.6,7 Simultaneously, researchers have also devoted extensive efforts to the continuous discovery of new 2D alternative materials. Consequently, a large variety of 2D families have been explored experimentally and theoretically, including transition metal dichalcogenides (TMDs)8,9 and nitrides/carbides (MXenes),10,11 pnictogens,12,13 and II–VI group14,15 and III–VI group materials,16,17 etc. Exceptional physical and chemical properties endow the 2D materials with promise for diverse applications in catalysis,18,19 optoelectronics, electronics, and photonics,20,21 photovoltaics,22,23 energy storage,24,25 and spintronics,26,27 etc.In the past years, atomically thin III-group monochalcogenides (III–X; III = Al, Ga, and In; X = S, Se, and Te) have been prepared successfully in experiments using either top-down exfoliation from their bulk counterpart28,29 or bottom-up chemical vapor deposition (CVD),30,31 providing opportunity to study their properties. These 2D III–X members are semiconductors with relatively large band gaps, exhibiting strong absorption in the UV-vis regime and promising photodetection performance.16,32 Particularly, the first successful synthesis of large-area indium sulfide (InS) atomic layers was reported by Tu et al.33 using the CVD method. The fabricated InS field-effect transistors (FETs) exhibit n-type transport behavior and have an on/off current ratio exceeding 103. Using first-principles calculations, several groups have investigated the electronic modification of the InS monolayer through strain engineering34,35 and the formation of heterostructures.36,37 Moreover, the adsorption and doping with transition metals have been predicted to induce significant magnetism in the InS monolayer, making it suitable for spintronic applications.38,39
On the other hand, the majority of the discovered 2D materials have no intrinsic magnetism, raising a great challenge to induce and control the magnetism in 2D materials towards opening new functionalities. In this regard, vacancy defects have been widely explored to create magnetic moment and alter the electronic structure of 2D materials. For example, the theoretical study of Ao et al.40 has asserted that Ga vacancies in the GaSe monolayer gives a total magnetic moment of between 1.00 and 4.00µB, while the band gap narrowing is achieved by a single Se vacancy. Similar effects of native vacancy defects have been found for the GaS monolayer.41 In addition, carrier doping has been also explored as an effective way to modify the 2D materials’ electronic and magnetic properties. For example, Meng et al.42 have demonstrated the emergence of half-metal behavior in nonmagnetic metal oxide monolayers MO (M = Ga and In) induced by hole doping. Similarly, a magnetic moment up to 1.00µB with the half-metal state can be achieved for the GaSe monolayer, depending on the hole level.43
To the best of our knowledge, the effects of vacancy defects, Fe doping and hole doping, as well as their coeffects on the InS monolayer’s electronic and magnetic properties have not been investigated well, so far. In this work, our main aim is to report new results to rectify this gap in the research. To achieve this goal, a 4 × 4 × 1 supercell of the InS monolayer is generated to model a single In vacancy, a pair of In vacancies, a single S vacancy, and Fe doping. Moreover, different hole levels of 0.5, 1.0, and 1.5 holes per supercell are considered for all the perfect, defective, and doped systems. Our results demonstrate the effectiveness of using defects, doping and hole doping to alter and control the electronic and magnetic properties of the InS monolayer, which can be useful theoretical guidance for the field of 2D materials.
2. Computational details
Within the framework of density functional theory (DFT),44 spin-polarized calculations are performed using the projector augmented wave (PAW) method and Perdew–Burke–Ernzerhof-parameterised generalized gradient approximation (GGA-PBE) as implemented in Vienna ab initio simulation package (VASP).45–47 Despite the well-known band gap underestimation, the PBE functional can describe very well the variation trends of the band gap and magnetic moment of the perfect and defective InS monolayer upon hole doping. In addition, the DFT+U method with an effective Hubbard parameter of 5.40 eV (ref. 48 and 49) is also adopted to treat properly the high-correlation effects of Fe-3d electrons. For the plane-wave expansion of the electronic wave function, the cutoff energy is set to 500 eV. k-Point grids of 20 × 20 × 1 and 4 × 4 × 1 are generated using the Monkhorst–Pack method50 to sample the Brillouin zone of the InS unit cell and supercell, respectively. The relaxation of geometry structures is realized until the force acting on each In and S atom is less than 1 × 10−2 eV Å−1. The convergence criterion of self-consistency for energy is set to 1 × 10−6 eV. In all cases, a vacuum space with width more than 19 Å is placed along the z-axis to eliminate the interaction between periodic monolayer images along the perpendicular direction, where the monolayer systems are expanded in the xy-plane. It is important to mention that the spurious Coulombic interactions can be corrected by using a uniformly scaled supercell with equal lateral sizes (Lxx = Lyy = Lzz), which is a proven method from previous studies.51–55 However, for the 4 × 4 × 1 supercell, the correction can be achieved with a special vacuum Lsz of about 16 Å.56 Therefore, it can be expected that the vacuum gap inserted in our structural models is reasonable and produces reliable results.The formation energy Ef values of the defective and doped InS systems are calculated using the following expression:
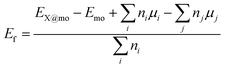 | (1) |
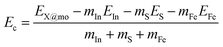 | (2) |
The magnetic anisotropy of the magnetic InS-based systems is studied by calculating the magnetic anisotropy energy (MAE) as follows:
| MAE = E[100] − E[001] | (3) |
3. Results and discussion
3.1. Stability and electronic properties of InS monolayer
A 4 × 4 × 1 supercell of the InS monolayer at equilibrium is visualized in Fig. 1a. Note that the atomic structure is composed by S–In–In–S atomic sublayer stacking, in which two In sublayers are vertically bound and aligned. The vertical alignment is also observed for two S sublayers. From the top-view, In and S atoms are situated in a graphene-like honeycomb configuration. After the structural relaxation, the following parameters for the InS monolayer unit cell are obtained: (1) lattice constant a = 3.94 Å; (2) chemical bond lengths dIn–S = 2.57 Å and dIn–In = 2.82 Å, which are in good agreement with previous studies;57 (3) total structural buckling height Δt = 2 × ΔIn–S + ΔIn–In = 2 × 1.19 + 2.82 = 5.20 Å; and (4) interatomic angles ∠SInS = 100.29° and ∠SInIn = 117.57°. In the following, the stability of the InS monolayer is analyzed. | ||
| Fig. 1 Atomic structure in a 4 × 4 × 1 supercell of the InS monolayer (a) before (optimized) and (b) after AIMD simulations. | ||
• Adopting the finite displacement method, we calculate the phonon dispersion curves of the InS monolayer with the help of the PHONOPY code.58 Results given in Fig. 2a confirm good dynamical stability for the studied InS monolayer, considering the absence of nonphysical imaginary frequencies in its phonon spectra.
 | ||
| Fig. 2 (a) Phonon dispersion curves and (b) AIMD simulations at 300 K (fluctuation of E – energy and T – temperature) of the InS monolayer. | ||
• Ab initio molecular dynamics (AIMD) simulations are carried out to examine the InS monolayer thermal stability, using a canonical ensemble and Nosé–Hoover thermostat.59,60 Output is recorded for total time of 5 ps with time steps of 2 fs. From Fig. 1b, we can see that after 5 ps of AIMD simulations, constituent In and S atoms displace slightly from their equilibrium. Importantly, no structural reconstruction is produced, such that the initial atomic configuration is well preserved. In addition, the energy and temperature parameters exhibit stable fluctuation within a small range during AIMD simulations as observed in Fig. 2b. These results confirm that the InS monolayer is thermally stable.
• To verify the mechanical stability, we calculate the elastic constants C11 and C12 of the InS monolayer, which can describe the elasticity because of the 2D hexagonal symmetry. According to our simulations, these constants are calculated to be 57.26 and 16.64 N m−1, respectively. Importantly, these values satisfy that C11 > 0 and C11 > |C12|, which have been proposed to determine the mechanical stability.61 These results confirm that the InS monolayer is mechanically stable.
Using the optimized unit cell, we calculate the InS monolayer electronic band structure. Results are plotted in Fig. 3a with the orbital-decomposed contribution of each atom. The Mexican-hat-like energy dispersion around the Fermi level can be observed, giving the indirect gap of this 2D material. Our calculations provide an energy gap of 1.65 eV for the InS monolayer, which agrees well with previous studies.16 Note that this gap is determined by the upper valence band originated from In-pz/S-pz states and the lower conduction band formed mainly by the In-s state. Moreover, the In-s and S-px,y,z states also make contributions to the lower part of the valence band, meanwhile the In-px,y,z states build mainly the upper part of the conduction band. In order to get a more accurate band gap for the InS monolayer, the hybrid functional HSE06 with a 25% fraction of the exact Hartree exchange potential is adopted.62 Our HSE06-based calculations provide a band gap of 2.49 eV that is larger than that obtained using the PBE functional, however both functionals produce quite similar band structure profiles with indirect-gap semiconductor character (see Fig. S1 in the SI file). The band structure profiles also assert the hybridization of In-belonging and S-belonging electronic states, suggesting a covalent In–S bond. This feature is also confirmed by the charge accumulation between In and S atoms as observed in the electron localization function visualized in Fig. 3b. Similarly, the interaction between In–In atoms is predominantly covalent as confirmed by the large charge accumulations between them. However, it is flawed to not consider the ionic character of the In–S chemical bond since the chemical bonds in 2D compounds are not purely covalent because of the difference in electronegativity. To quantitatively study this interaction, the Bader charges of the In and S atoms are analyzed. It is found that each S atom attracts a charge quantity of 0.74e from In atoms. These results confirm the mix of covalent and ionic characters in the In–S bond in the InS monolayer.
 | ||
| Fig. 3 (a) Projected band structure (the Fermi level is set to 0 eV) and (b) electron localization function (iso-surface level: 0.6 e Å−3) of the InS monolayer. | ||
3.2. Effects of vacancy defects
In this part, the effects of a single In vacancy, a pair of In vacancies, and a single S vacancy on the InS monolayer’s electronic and magnetic properties are studied. The defective systems are denoted by 1VaIn@mo, 2VaIn@mo, and 1VaS@mo, respectively. The formation energies of these systems are calculated to be 3.64, 3.57, and 2.20 eV per atom, respectively. Note that the creation of the S vacancy requires less energy than In vacancies. In addition, the structural–chemical stability of defective InS monolayers is confirmed by the negative Ec values of −3.39, −3.40, and −3.35 eV per atom, respectively.Our spin-polarized calculations provide overall magnetic moments of 1.00 and 2.00µB for the 1VaIn@mo and 2VaIn@mo systems, respectively. These results assert the magnetization of the InS monolayer induced by creating In vacancies. To further study the magnetism origin, the spin density is illustrated in Fig. 4. This parameter measures the difference in charge density distributed in spin channels that originates the magnetism. From the figure, it can be seen that the magnetic properties of the 1VaIn@mo and 2VaIn@mo systems are produced mainly by S atoms around vacancy sites, considering the spin iso-surface centered at their sites. Moreover, negative MAE values of −9.89 and −42.99 µeV are obtained for these magnetic systems, respectively, indicating their in-plane magnetic anisotropy (IMA). The more negative MAE value demonstrates that the pair of In vacancies induces stronger IMA than the single In vacancy. In contrast, the single S vacancy preserves the InS monolayer nonmagnetic nature as confirmed by the zero magnetic moment of the 1VaS@mo system. Fig. 5 shows the spin-resolved band structure of the defective InS monolayers. The spin polarization around the Fermi level for the 1VaIn@mo and 2VaIn@mo systems can be noted . One of their spin states exhibits semiconductor character with energy gaps of 1.44 and 0.19 eV, respectively. Meanwhile, metallic character is obtained in the other spin state. These results confirm that half-metallicity in the InS monolayer is induced by creating In vacancies. Along with the confirmed IMA, the magnetic 1VaIn@mo and 2VaIn@mo systems may hold promise for magnetic field sensing applications. In contrast, the nonmagnetic nature of the 1VaS@mo system is also reflected in its spin-symmetric band structure profile. In this case, the mid-gap flat subbands cause the band gap reduction to 1.18 eV that corresponds to a reduction of 28.48%. Therefore, it can be concluded that the creation of a single S vacancy may widen the light absorption range of the InS monolayer, making it more suitable for optoelectronic applications.
 | ||
| Fig. 4 Spin density in the InS monolayer with (a) a single In vacancy and (b) a pair of In vacancies (vacancies are marked with black color; iso-surface value: 0.002 e Å−3). | ||
 | ||
| Fig. 5 Spin-resolved band structure of the InS monolayer with (a) a single In vacancy, (b) a pair of In vacancies, and (c) a single S vacancy (the Fermi level is set to 0 eV). | ||
To get more insights into the atom contributions, the projected density of states (PDOS) spectra of the defective InS monolayers are given in Fig. 6. Note that the magnetism and half-metallicity of the magnetic 1VaIn@mo and 2VaIn@mo systems are determined primarily by S-px,y,z and In-pz states since they build mainly the strongly spin-polarized subband structure around the Fermi level. In the case of the 1VaS@mo system, the flat subband below the Fermi level is originated mainly from S-pz and In-pz states, while the lower conduction band part is formed mainly by the In-s state. These mentioned electronic states are responsible for the band gap reduction as analyzed above.
 | ||
| Fig. 6 Spin-resolved projected density of states of the InS monolayer with (a) a single In vacancy, (b) a pair of In vacancies, and (c) a single S vacancy (the Fermi level is set to 0 eV). | ||
3.3. Effects of Fe doping
The effects of Fe doping on the InS monolayer’s electronic and magnetic properties are investigated herein. The Fe-doped InS system is denoted by FeIn@mo. From the calculation of formation energy, it is found that an energy quantity of 0.80 eV per atom is required to realize the Fe doping in the InS monolayer. Moreover, the FeIn@mo system has a negative cohesive energy of −3.44 eV per atom that suggests its good structural–chemical stability.The interaction between the Fe impurity and the host InS monolayer is studied through charge density difference Δρ as follows: Δρ = ρ(FeIn@mo) − ρ(mo) − ρ(Fe), where the terms in the right-hand side refer to the charge density of the doped system, InS monolayer system, and single Fe atom, respectively. From the illustration in Fig. 7a, it can be seen that charge is depleted from the Fe impurity as represented by green iso-surfaces, meanwhile its nearest neighboring S atoms exhibit charge enrichment as indicated by orange iso-surfaces. The Δρ profile suggests charge transfer from the Fe impurity to the host InS monolayer. To quantify the process, Bader charge analysis is performed, which asserts that the host InS monolayer attracts a charge quantity of 0.87e from the Fe impurity. These results satisfy the rule of electronegativity since the Fe atom is surrounded by the more electronegative S atoms. In addition, an overall magnetic moment of 5.0µB is obtained for the FeIn@mo system, confirming the magnetization of the InS monolayer upon doping with the Fe impurity. The spin density visualized in Fig. 7b shows the main contribution to the system magnetic moment is from the Fe atom since a large spin iso-surface is centered at its site. The local magnetic moment of the Fe impurity is calculated to be 3.72µB. Moreover, IMA in the InS monolayer induced by the Fe doping is found considering the negative MAE value of −176.24 µeV of the FeIn@mo system, which is much stronger than the IMA in the defective systems analyzed above. Such that Fe doping may functionalize the InS monolayer towards magnetic field sensing applications.
Fig. 8 shows the spin-resolved band structure of the FeIn@mo system, and the PDOS spectra of the Fe impurity and its nearest neighboring S and In atoms are also given to analyze the origin of the mid-gap subbands. From panels a-1 and b-1, diverse flat energy curves either below (in the spin-up channel) or above (in the spin-down channel) the Fermi level can be observed. Importantly, Fe doping induces the magnetic semiconductor nature in the InS monolayer with spin-up and spin-down gaps of 1.01 and 1.34 eV, respectively. The flat mid-gap energy curves are originated mainly from the Fe-dz2 state, where small contributions from the S-pz, In-s, and In-pz states are also observed. Moreover, Fe-dxy–dyz–dxz–dx2−y2 states also participate in the formation of the spin-down conduction band of the FeIn@mo system.
3.4. Effects of hole doping
Now, effects of hole doping on the electronic and magnetic properties of the pristine, defective, and doped InS systems are studied. In a 4 × 4 × 1 supercell, hole concentrations of 0.5, 1.0, and 1.5 (hole) are added. Then, the variations in the magnetic moment, magnetic anisotropy, and electronic band structure are analyzed. The obtained results are summarized in Table 1.| Hole concentration | ||||
|---|---|---|---|---|
| 0.0 | 0.5 | 1.0 | 1.5 | |
| pris@mo | ||||
| Mt | 0.00 | 0.00 | 0.00 | 0.66 |
| MAE | −8.26 | |||
| Eg | 1.65/1.65 | 1.66/1.66 | 1.67/1.67 | 1.68/M |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 1VaIn@mo | ||||
| Mt | 1.00 | 1.50 | 1.98 | 2.42 |
| MAE | −9.89 | −38.99 | −84.82 | −127.76 |
| Eg | 1.44/M | 1.50/M | 1.52/M | 1.54/M |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 2VaIn@mo | ||||
| Mt | 2.00 | 0.96 | 0.00 | 0.00 |
| MAE | −42.99 | −8.77 | ||
| Eg | M/0.19 | M/M | M/M | M/M |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 1VaS@mo | ||||
| Mt | 0.00 | 0.46 | 0.89 | 0.68 |
| MAE | −14.42 | −37.42 | −8.85 | |
| Eg | 1.18/1.18 | 1.23/M | 1.24/M | M/M |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| FeIn@mo | ||||
| Mt | 5.00 | 4.50 | 4.00 | 3.86 |
| MAE | −176.24 | −171.80 | −205.78 | −215.43 |
| Eg | 1.01/1.34 | M/1.01 | 0.23/0.69 | 0.74/0.27 |
Fig. 9 shows the variation in total magnetic moment as a function of hole concentration. It can be seen that the pristine InS monolayer is magnetized only with 1.5 holes per supercell, for which a value of 0.66µB is obtained. Our calculations also assert the IMA of the hole-doped InS monolayer with a negative MAE value of −8.26 µeV. The magnetism of the 1VaIn@mo system can be significantly enhanced by hole doping since its magnetic moment is increased and the IMA becomes stronger (with a MAE value up to −127.76 µeV obtained with 1.5 holes per supercell) with increasing the hole level. In contrast, the magnetization induced by a pair of In vacancies is made weaker with hole doping since the total magnetic moment decreases from 2.00 to 0.96µB, and the magnetism disappears when the hole level is 1.0 hole per supercell. Moreover, the IMA of the 2VaIn@mo system becomes weaker considering the less negative MAE value up to 0.5 holes per supercell. As analyzed above, a single S vacancy induces no magnetism in the InS monolayer, however further adding holes in the 1VaS@mo system can lead to the appearance of magnetism. Specifically, total magnetic moments between 0.46 and 0.89µB can be obtained with the IMA confirmed by negative MAE values between −37.42 and −8.85 µeV. Interestingly, opposite trends are noted for the magnetic moment and IMA of the FeIn@mo system. Specifically, the magnetic moment decreases upon increasing the hole concentration, meanwhile the IMA can be enhanced significantly since the MAE value becomes much more negative with hole concentrations up to 1.5 holes per supercell. Such that hole doping may be an efficient method to consolidate the application of the FeIn@mo system in magnetic field sensing.
 | ||
| Fig. 9 Total magnetic moment of the pristine, defective, and Fe-doped InS monolayers at various hole concentrations. | ||
From Table 1, it can be seen that the pristine InS monolayer preserves its nonmagnetic semiconductor nature with hole doping, however it becomes a half-metallic 2D system at a hole concentration of 1.5 holes per supercell. In the case of 1VaIn@mo, half-metallicity is obtained regardless of hole concentration level. Meanwhile, the hole doping is found to metallize the 2VaIn@mo system, since both of its spin states exhibit metallic character. Upon hole doping, the feature-rich half-metallicity is induced in the 1VaS system, however metallization of the system takes place at a high hole concentration of 1.5 holes per supercell. When adding holes into the FeIn@mo system, the magnetic semiconductor to half-metallic nature transition, and vice versa, can be controlled by hole level. Our findings show that the electronic and magnetic properties of the pristine, defective, and Fe-doped InS monolayers can be effectively modified through hole doping, where the hole level may be a key role in obtaining the desirable features.
4. Conclusions
In summary, first-principles calculations have been performed to investigate systematically the effects of vacancy defects and Fe doping, as well as further hole doping, on the InS monolayer’s electronic and magnetic properties. The calculated phonon dispersion relations, AIMD simulations, and elastic constants confirm good stability for the InS monolayer. The band structure of the pristine monolayer is formed mainly by In-s–px,y,z and S-px,y,z states, which show significant hybridization to form covalent bonds. Moreover, the ionic character is also demonstrated for the In–S chemical bonds since the S atoms attract charge from the In atoms. The In–In bond is purely covalent. Significant monolayer magnetization is induced by creating In vacancies and doping with Fe atoms. In defective systems, S atoms around the doping site mainly produce the magnetic moment. Meanwhile the Fe impurity determines the magnetic properties of the Fe-doped InS monolayer. In these cases, feature-rich magnetic semiconductor and half-metallic natures are obtained, along with the in-plane magnetic anisotropy. Further hole doping can enhance significantly the magnetic properties of the 1VaIn@mo system, but causes the disappearance of magnetism in the 2VaIn@mo system. Interestingly, the nonmagnetic pristine InS and 1Va2@mo systems are magnetized with hole concentrations from 0.5 and 1.5 holes per supercell, respectively, giving place to the IMA. Importantly, hole doping is predicted to strengthen the IMA of the Fe-doped InS monolayer, however the total magnetic moment decreases increasing the hole level. Except for the 2VaIn@mo system, the magnetic semiconducting to half-metallicity transition, and vice versa, can take place by properly controlling the hole concentration. Our results may suggest functionalization methods to make the InS monolayer a promising 2D platform for magnetic field sensing applications, where electronic and magnetic properties can be effectively controlled by hole doping.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
Data related to this study are available upon reasonable request.Supplementary information: Electronic band structure of InS monolayer calculated with stadard PBE and hybrid HSE06 functionals. See DOI: https://doi.org/10.1039/d5ra07951a.
Acknowledgements
Calculations were performed in the DGTIC-UNAM Supercomputing Center projects LANCAD-UNAM-DGTIC-422 and LANCAD-UNAM-DGTIC-368.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-E. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306(5696), 666–669 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, The rise of graphene, Nat. Mater., 2007, 6(3), 183–191 CrossRef CAS.
- C. Soldano, A. Mahmood and E. Dujardin, Production, properties and potential of graphene, Carbon, 2010, 48(8), 2127–2150 CrossRef CAS.
- X. Fan, Z. Shen, A. Liu and J.-L. Kuo, Band gap opening of graphene by doping small boron nitride domains, Nanoscale, 2012, 4(6), 2157–2165 RSC.
- J. E. Johns and M. C. Hersam, Atomic covalent functionalization of graphene, Acc. Chem. Res., 2013, 46(1), 77–86 CrossRef CAS PubMed.
- M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Energy band-gap engineering of graphene nanoribbons, Phys. Rev. Lett., 2007, 98(20), 206805 CrossRef PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Energy gaps in graphene nanoribbons, Phys. Rev. Lett., 2006, 97(21), 216803 CrossRef PubMed.
- M. Chhowalla, Z. Liu and H. Zhang, Two-dimensional transition metal dichalcogenide (TMD) nanosheets, Chem. Soc. Rev., 2015, 44(9), 2584–2586 RSC.
- B. Zhao, D. Shen, Z. Zhang, P. Lu, M. Hossain, J. Li, B. Li and X. Duan, 2D metallic transition-metal dichalcogenides: structures, synthesis, properties, and applications, Adv. Funct. Mater., 2021, 31(48), 2105132 CrossRef CAS.
- A. VahidMohammadi, J. Rosen and Y. Gogotsi, The world of two-dimensional carbides and nitrides (MXenes), Science, 2021, 372(6547), eabf1581 Search PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, 25th anniversary article: MXenes: a new family of two-dimensional materials, Adv. Mater., 2014, 26(7), 992–1005 CrossRef CAS PubMed.
- A. Carvalho, M. Wang, X. Zhu, A. S. Rodin, H. Su and A. H. Castro Neto, Phosphorene: from theory to applications, Nat. Rev. Mater., 2016, 1(11), 16061 CrossRef CAS.
- M. Pumera and Z. Sofer, 2D monoelemental arsenene, antimonene, and bismuthene: beyond black phosphorus, Adv. Mater., 2017, 29(21), 1605299 CrossRef.
- H. Zheng, X.-B. Li, N.-K. Chen, S.-Y. Xie, W. Q. Tian, Y. Chen, H. Xia, S. Zhang and H.-B. Sun, Monolayer II-VI semiconductors: A first-principles prediction, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92(11), 115307 CrossRef.
- Y. Yang, Y. Yan, M. Sun, Y. Ma, Q. Chen and J. Z. Liu, Structural landscape of two-dimensional phases in group II–VI semiconductors, Appl. Phys. Lett., 2025, 127(14), 142106 CrossRef CAS.
- S. Demirci, N. Avazlı, E. Durgun and S. Cahangirov, Structural and electronic properties of monolayer group III monochalcogenides, Phys. Rev. B:Condens. Matter Mater. Phys., 2017, 95(11), 115409 CrossRef.
- Z. Yang and J. Hao, Recent progress in 2D layered III–VI semiconductors and their heterostructures for optoelectronic device applications, Adv. Mater. Technol., 2019, 4(8), 1900108 CrossRef CAS.
- L. Zhao, B. Wang and R. Wang, A critical review on new and efficient 2D materials for catalysis, Adv. Mater. Interfaces, 2022, 9(29), 2200771 CrossRef.
- D. Deng, K. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Catalysis with two-dimensional materials and their heterostructures, Nat. Nanotechnol., 2016, 11(3), 218–230 CrossRef CAS.
- J. S. Ponraj, Z.-Q. Xu, S. C. Dhanabalan, H. Mu, Y. Wang, J. Yuan, P. Li, S. Thakur, M. Ashrafi and K. Mccoubrey, et al., Photonics and optoelectronics of two-dimensional materials beyond graphene, Nanotechnology, 2016, 27(46), 462001 CrossRef.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Electronics and optoelectronics of two-dimensional transition metal dichalcogenides, Nat. Nanotechnol., 2012, 7(11), 699–712 CrossRef CAS.
- L. Wang, L. Huang, W. C. Tan, X. Feng, L. Chen, X. Huang and K.-W. Ang, 2D photovoltaic devices: progress and prospects, Small Methods, 2018, 2(3), 1700294 CrossRef.
- S. Das, D. Pandey, J. Thomas and T. Roy, The role of graphene and other 2D materials in solar photovoltaics, Adv. Mater., 2019, 31(1), 1802722 CrossRef.
- Y. Xue, Q. Zhang, W. Wang, H. Cao, Q. Yang and L. Fu, Opening two-dimensional materials for energy conversion and storage: a concept, Adv. Energy Mater., 2017, 7(19), 1602684 CrossRef.
- X. Zhang, L. Hou, A. Ciesielski and P. Samorì, 2D materials beyond graphene for high-performance energy storage applications, Adv. Energy Mater., 2016, 6(23), 1600671 Search PubMed.
- Y. Liu, C. Zeng, J. Zhong, J. Ding, Z. M. Wang and Z. Liu, Spintronics in two-dimensional materials, Nano-Micro Lett., 2020, 12(1), 93 Search PubMed.
- I. Choudhuri, P. Bhauriyal and B. Pathak, Recent advances in graphene-like 2D materials for spintronics applications, Chem. Mater., 2019, 31(20), 8260–8285 Search PubMed.
- G. W. Mudd, S. A. Svatek, T. Ren, A. Patanè, O. Makarovsky, L. Eaves, P. H. Beton, Z. D. Kovalyuk, G. V. Lashkarev and Z. R. Kudrynskyi, et al., Tuning the bandgap of exfoliated InSe nanosheets by quantum confinement, Adv. Mater., 2013, 25(40), 5714 Search PubMed.
- D. Hlushchenko, A. Siudzinska, J. Cybinska, M. Guzik, A. Bachmatiuk and R. Kudrawiec, Stability of mechanically exfoliated layered monochalcogenides under ambient conditions, Sci. Rep., 2023, 13(1), 19114 Search PubMed.
- H.-C. Chang, C.-L. Tu, K.-I. Lin, J. Pu, T. Takenobu, C.-N. Hsiao and C.-H. Chen, Synthesis of large-area InSe monolayers by chemical vapor deposition, Small, 2018, 14(39), 1802351 CrossRef.
- T. Afaneh, A. Fryer, Y. Xin, R. H. Hyde, N. Kapuruge and H. R. Gutierrez, Large-area growth and stability of monolayer gallium monochalcogenides for optoelectronic devices, ACS Appl. Nano Mater., 2020, 3(8), 7879–7887 Search PubMed.
- H. Wang, G. Qin, J. Yang, Z. Qin, Y. Yao, Q. Wang and M. Hu, First-principles study of electronic, optical and thermal transport properties of group III–VI monolayer MX (M = Ga, In; X = S, Se), J. Appl. Phys., 2019, 125(24), 245104 CrossRef.
- C.-L. Tu, K.-I. Lin, J. Pu, T.-F. Chung, C.-N. Hsiao, A.-C. Huang, J.-R. Yang, T. Takenobu and C.-H. Chen, CVD growth of large-area InS atomic layers and device applications, Nanoscale, 2020, 12(17), 9366–9374 Search PubMed.
- J. Jalilian and M. Safari, Electronicand optical properties of α-InX (X = S, Se and Te) monolayer: Under strain conditions, Phys. Lett. A, 2017, 381(15), 1313–1320 CrossRef CAS.
- H. Jin, J. Li, Y. Dai and Y. Wei, Engineering the electronic and optoelectronic properties of InX (X = S, Se, Te) monolayers via strain, Phys. Chem. Chem. Phys., 2017, 19(6), 4855–4860 RSC.
- H. Jin, J. Li, B. Wang, Y. Yu, L. Wan, F. Xu, Y. Dai, Y. Wei and H. Guo, Electronics and optoelectronics of lateral heterostructures within monolayer indium monochalcogenides, J. Mater. Chem. C, 2016, 4(47), 11253–11260 RSC.
- A. Rawat, R. Ahammed, Dimple, N. Jena, M. K. Mohanta and A. De Sarkar, Solar energy harvesting in type II van der Waals heterostructures of semiconducting group III monochalcogenide monolayers, J. Phys. Chem. C., 2019, 123(20), 12666–12675 Search PubMed.
- R. Xue, R. Han, X. Lin and P. Wu, First-principles investigate on the electronic structure and magnetic properties of 3d transition metal doped honeycomb InS monolayer, Appl. Surf. Sci., 2023, 608, 155240 CrossRef CAS.
- B. Xu, L. Zuo, W. Zhao, Q. Yang, Y. Wang, M. Zhang and L. Yi, et al., Prediction of magnetic properties of 3d transition-metal adsorbed InS monolayers, J. Magn. Magn. Mater., 2024, 603, 172241 CrossRef CAS.
- L. Ao, H. Xiao, X. Xiang, S. Li, K. Liu, H. Huang and X. Zu, Functionalization of a GaSe monolayer by vacancy and chemical element doping, Phys. Chem. Chem. Phys., 2015, 17(16), 10737–10748 RSC.
- D. Hoat, N. T. Tien, D. K. Nguyen and J. Guerrero-Sanchez, Antiferromagnetism in gas monolayer doped with TM–TM atom pairs (TM = V, Cr, Mn, and Fe), Phys. Chem. Chem. Phys., 2024, 26(27), 18657–18666 Search PubMed.
- R. Meng, M. Houssa, K. Iordanidou, G. Pourtois, V. Afanasiev and A. Stesmans, Ferromagnetism and half-metallicity in two-dimensional MO (M = Ga, In) monolayers induced by hole doping, Phys. Rev. Mater., 2020, 4(7), 074001 CrossRef CAS.
- T. Cao, Z. Li and S. G. Louie, Tunable magnetism and half-metallicity in hole-doped monolayer GaSe, Phys. Rev. Lett., 2015, 114(23), 236602 Search PubMed.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140(4A), A1133, DOI:10.1103/PhysRev.140.A1133.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54(16), 11169, DOI:10.1103/PhysRevB.54.11169.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865, DOI:10.1103/PhysRevLett.77.3865.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B:Condens. Matter Mater. Phys., 1998, 57(3), 1505 Search PubMed.
- Y. Wang, S. Li and J. Yi, Transition metal-doped tin monoxide monolayer: a first-principles study, J. Phys. Chem. C., 2018, 122(8), 4651–4661 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188, DOI:10.1103/PhysRevB.13.5188.
- A. Singh and A. K. Singh, Origin of n-type conductivity of monolayer MoS2, Phys. Rev. B, 2019, 99(12), 121201 CrossRef CAS.
- J. Zhang, Y. Liu, C. Yang, Y. Qu, A. Zhang, Z. Feng, W. Wang and P. Ou, Design of bifunctional oxygen evolution/reduction electrocatalysts on g-C3N3 monolayer by a defect physics method, J. Catal., 2025, 447, 116135 CrossRef CAS.
- C. Yang, C. Yang, Y. Liang, H. Yan, A. Zhang, G. Ge, W. Wang and P. Ou, Machine-learning enables nitrogen reduction reaction on transition metal doped C3B by controlling the charge states, Mater. Chem. Front., 2025, 9(11), 1681–1689 Search PubMed.
- S. Yue, D. Li, A. Zhang, Y. Yan, H. Yan, Z. Feng and W. Wang, Rational design of single transition-metal atoms anchored on a PtSe2 monolayer as bifunctional OER/ORR electrocatalysts: a defect chemistry and machine learning study, J. Mater. Chem. A, 2024, 12(9), 5451–5463 RSC.
- W. Wentao, Y. Qu, D. Li, A. Zhang, H. Yan, Z. Feng and W. Yao, The defect chemistry and machine learning study 5d transition metal doped on graphitic carbon nitride for bifunctional oxygen electrocatalyst with low overpotential, Int. J. Hydrogen Energy, 2024, 79, 702–714 CrossRef.
- H.-P. Komsa, N. Berseneva, A. V. Krasheninnikov and R. M. Nieminen, Charged point defects in the flatland: Accurate formation energy calculations in two-dimensional materials, Phys. Rev. X, 2014, 4(3), 031044 CAS.
- A. S. Nissimagoudar, Z. Rashid, J. Ma and W. Li, Lattice thermal transport in monolayer group 13 monochalcogenides MX (M = Ga, In; X = S, Se, Te): Interplay of atomic mass, harmonicity, and lone-pair-induced anharmonicity, Inorg. Chem., 2020, 59(20), 14899–14909 CrossRef CAS PubMed.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys. Condens. Matter, 2023, 35(35), 353001, DOI:10.1088/1361-648X/acd831.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev., 1985, 31(3), 1695 Search PubMed.
- F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |


