Understanding phonon polaritons and epsilon-near-zero modes in sapphire nanocones across the broad Reststrahlen band (385–1050 cm⁻¹)

Abstract

Tailoring light–matter interactions is crucial for advancing nanophotonics. Surface phonon polaritons are promising candidates for enhanced light–matter interactions due to their efficient, low-loss light confinement. In this work, we experimentally investigate the Reststrahlen bands in sapphire across the infrared spectrum, spanning ω = 385–1050 cm⁻¹. We extended this investigation to nanocone-patterned sapphire resonators, with specific attention to its in-plane and out-of-plane permittivity components. Infrared spectroscopy and full-wave simulations revealed a range of optical excitations, including three surface phonon polaritons with quality factors as high as 40 ± 1, two hyperbolic volume phonon polaritons with quality factors as high as 83 ± 4, and one epsilon-near-zero mode with a quality factor of 122 ± 8 across the various Reststrahlen bands. Furthermore, confocal Raman scattering measurements showed enhanced Raman signals with maximum enhancement factors of 7.0 ± 0.6 on the nanostructured surface, indicating coupling between phonons and phonon–polaritons. Finally, finite element modeling of polarizability demonstrates good quantitative agreement with the measured results. This study is the first exploration of sapphire nanostructures and gives an in-depth understanding of phonon polaritons and epsilon-near-zero modes from nanocone-structured sapphire. The reported Raman enhancement attributed to coupling of phonon and phonon polariton modes holds promise for sensing through surface-enhanced Raman spectroscopy.

---

1 Introduction

Phonon polaritons (PhPs) are collective electromagnetic modes that arise from the coupling of photons with lattice vibrations in ionic crystals.^1,2 Nanoscale structures which generate PhPs have attracted considerable attention due to their ability to manipulate light at sub-wavelength scales in the infrared (IR) range, within Reststrahlen bands (RBs) where the material exhibits negative permittivity.¹ Additionally, since phonons possess significantly longer scattering lifetimes than electrons, surface phonon polaritons (SPhPs) experience lower loss compared to surface plasmons.¹ Extensive research has been conducted on SPhPs in nanostructures fabricated from isotropic polar dielectrics, such as silicon carbide (SiC). These include localized SPhPs from SiC nanopillar antenna arrays,³ high-order, multipolar SPhPs from SiC rectangular pillars,⁴ and collective SPhPs in complex unit cells comprising SiC nanopillar subarrays.⁵ The ability to harness enhanced light–matter interactions from SPhPs enables a range of applications, including sensing,⁴ surface-enhanced spectroscopy,^6,7 and heat dissipation.⁸

In parallel, natural hyperbolic materials (HMs) have drawn significant attention because of their unique optical properties. These anisotropic materials exhibit both metallic-like (Re[ε] < 0) and dielectric-like (Re[ε] > 0) behavior along different orthogonal axes within hyperbolic RBs, facilitating access to high optical density of states and offering control over optical modes with hyperbolic dispersion properties.⁹ Unlike SPhP modes, HMs support hyperbolic volume phonon polariton (HVPhP) modes, which lead to a large density of states and strong field localization. HVPhP modes have been studied in hexagonal boron nitride (hBN) nanocones,^10,11 hBN cuboid nanoantennas,¹² molybdenum trioxide (α-MoO₃) nanoribbons,^13,14 and calcite (Ca₂CO₃) nanopillars.¹⁵ The highly directional nature of HVPhP excitations holds promise for potential applications in areas such as super-resolution imaging¹⁶ and nanolithography.¹⁷

While isotropic phonon polariton materials and HMs have many differences, the aforementioned materials have relatively narrow RBs, hindering their use in certain applications. To overcome the spectral narrowness of phonon bands and enable long-wavelength IR nanophotonics, tunable SPhPs have been demonstrated in lanthanum aluminate (LaAlO₃)/strontium titanate (SrTiO₃) heterostructures.¹⁸ Additionally, sub-wavelength IR confinements have been studied through excitations of epsilon-near-zero (ENZ) and SPhP modes in SrTiO₃ membranes.¹⁹ Furthermore, broadband IR response has been reported in hBN/α-MoO₃ integrated heterostructures.²⁰

Another broadband alternative is sapphire (α-Al₂O₃), a complex naturally occurring HM that exhibits multiple RBs within the IR spectrum. These RBs feature spectral regions that exhibit both metallic and hyperbolic optical properties, driven by the material's anisotropic permittivity. As shown in this work, the rich response of metallic-like and hyperbolic RBs provides a diverse playground in which SPhPs, HVPhPs and ENZ modes can be explored simultaneously on the same material. Although the real and imaginary part of the dielectric function in sapphire have been determined from visible to the IR regime,^21,22 a detailed study of its various RBs is needed to fully understand the optical response of sapphire-based systems and heterostructures.^23,24 Furthermore, sapphire nanostructures capable of supporting sub-wavelength confinement across a broadband IR spectral range, without the need for integrating multiple materials or complex heterostructures, are still lacking.

In this work, the PhP modes in sapphire nanocones (NCs) were investigated. This study constitutes the first exploration of PhP modes in nanostructured Al₂O₃. The work experimentally identifies several RBs of Al₂O₃, highlighting its distinct metallic and hyperbolic regions across the IR spectrum from ω = 385–1050 cm⁻¹. A nanocone array (NCA) structure was investigated incorporating the material's in-plane and out-of-plane permittivity components. IR spectroscopy measurements and full-wave simulations revealed a diverse range of optical excitations, including three SPhP resonances, two HVPhP modes, and an ENZ mode across multiple RBs. Additionally, confocal Raman scattering (RS) measurements showed spatial variations in the RS signals across the NC surface, suggesting phonon–PhP coupling. Finite element modeling of the electromagnetic fields was also performed, yielding good quantitative agreement with the observed RS results.

This study shows an in-depth understanding of PhPs and ENZ modes in Al₂O₃ nanostructures that was lacking at this time. Additionally, understanding several RBs in sapphire should provide valuable insights into the physics of the infrared optical response of GaN/AlGaN heterostructures grown on Al₂O₃ (ref. 23) and the physics of emerging phononic-induced magnetization switching systems, leveraging phononic properties of sapphire.²⁴ A recent breakthrough experiment showed remotely steering magnetization of a magnetic layer mounted atop sapphire substrate through circularly polarized phonons of sapphire with special attention to its ENZ regions.²⁴

2 Optical properties of c-plane bulk Al₂O₃

Fig. 1(a) shows the crystallographic unit cell of α-Al₂O₃ aligned with the laboratory coordinates. The crystal exhibits an identical atomic structure perpendicular to the c axis in both the x and the y directions (Fig. 1(a), top right panel), while the atomic arrangement differs along the z direction, parallel to the c axis (Fig. 1(a), bottom right panel), resulting in anisotropic optical properties of the crystal. This anisotropy is demonstrated in Fig. 1(b and c), which present IR reflection spectroscopy (see Experimental) for both s- and p-polarized light at various angles of incidence (see SI Fig. S1). Significant variations in reflectivity were observed for both polarizations, particularly at the high-energy edges of the reflection bands, as the angle of incidence changed. This is primarily attributed to the critical condition for the material's total reflection (further details are provided in SI Section 1).²¹

Fig. 1 (a) Schematic of the crystallographic unit cells for α-Al₂O₃. The left panel shows the 3D atomic structure, while the right panels show xy and xz orientations. The blue and red circles indicate aluminum and oxygen atoms, respectively. (b) Angle-dependent reflectance measurements for s-polarized excitation (polarization is perpendicular to the optic axis) and (c) for p-polarized excitation (polarization is parallel to the optic axis) for the bulk material. (d) Reflectance measurements for s- and p-polarized excitations for the bulk material with θ = 45°. (e) The real part of permittivity components for (001) sapphire ranging from 385–1050 cm⁻¹. The blue curve shows permittivity in x and y directions (perpendicular to the optic axis), and the red curve indicates the permittivity along z direction (parallel to the optic axis).²¹ Color coding indicates various RBs of the material which are metallic (cyan), hyperbolic type I (magenta), and type II (green).

Group theory predicts five pairs of IR-active optical phonons within the studied spectral range: three with E_u symmetry, which are characterized by dipole oscillations perpendicular to the optic axis (E ⊥ c), and two with A_2u symmetry, where dipole oscillations occur parallel to the optic axis (E ‖ c).^21,22 The three reflection bands observed in the s-polarized reflectivity (Fig. 1(b)) are each bounded by E_u symmetry transverse optic (TO_Eu) and longitudinal optic (LO_Eu) phonons. In contrast, the p-polarized reflectivity comprises five reflection bands arising from the combination of three E_u and two A_2u phonon pairs, as shown in Fig. 1(c).²¹

In contrast to many polar dielectric systems which have been studied in the IR spectrum, such as SiC with a metallic RB^3–5 and hBN,^10,11 which exhibits two hyperbolic RBs (i.e., spectral regions where Re[ε_xx,yy]·Re[ε_zz] < 0), Al₂O₃ is a naturally hyperbolic material featuring both metallic and hyperbolic windows within its RBs. This unique characteristic allows for the excitations of both SPhP and HVPhP within the IR spectrum.

The color coding in Fig. 1(d) and (e) highlights distinct spectral regions of the material, based on the sign of the real parts of the dielectric function for both axes, as shown in Fig. 1(e).²¹ Each color corresponds to a specific spectral range based on the sign of the in-plane (ε_xx,yy) and out-of-plane (ε_zz) permittivity components, resulting in intervals with distinct optical behaviors, including metallic, dielectric, and hyperbolic properties. As shown in Fig. 1(e), the magenta regions correspond to type I hyperbolicity (HT I), where the material exhibits metallic-like behavior along the z direction with negative Re[ε_zz], and dielectric-like behavior along other directions with positive Re[ε_xx,yy]. Conversely, the green-colored regions, corresponding to type II hyperbolicity (HT II) show the opposite behavior: metallic-like properties are displayed in-plane and dielectric-like properties along the z-direction.

Additionally, the cyan regions correspond to metallic behavior, where all permittivity components are negative resulting in total reflection bands, as seen in Fig. 1(d). In contrast, the orange regions indicate the material behaves as an anisotropic dielectric, with positive permittivity components in all directions (the exact ranges of various spectral regions are presented in SI Table S1). Understanding the various bands of Al₂O₃ is crucial for advancing research on heterostructures incorporating sapphire, including novel phonon-induced magnetization switching systems²⁴ and the infrared response of GaN/AlGaN heterostructures grown on Al₂O₃.²³

3 Light-matter interactions from nanostructured Al₂O₃

PhPs are quasiparticles with high momentum and therefore cannot be directly excited in the bulk of a material.¹ Given that surface structuring can overcome this momentum mismatch, we investigated an array of nanoconical resonators on sapphire. Fig. 2(a) and (b) show both experimentally measured and numerically calculated reflectivity for the sapphire NCA, along with the experimental reflectivity of the bulk material, for both s- and p-polarized excitations with oblique incidence of θ = 45°. As shown by annotation arrows, in both experimental spectra, we observed regions of significantly reduced reflection, attributed to the excitation of various modes. A comprehensive study of the NCA optical response, including measurements of the IR reflectivity at various polarizations and oblique angles of incidence has also been conducted, verifying the robust presence of the observed reflection dips (see SI, Fig. S4). To gain a deeper understanding of light–matter interactions, full-wave simulations were conducted for the sapphire NCA using COMSOL Multiphysics. The calculated reflectivity plots are shown as dashed lines in Fig. 2(a, b), and (d) (see SI, Fig. S3).

Fig. 2 Optical properties of nanocone-structured sapphire (a) reflection spectra for the bulk and nanocone-structured material for the oblique s-polarized and (b) p-polarized incidence with angle of θ = 45°. The solid curves show reflection measurements for the bulk and nanostructured samples, and the dashed curves represent the simulation results obtained from modeling of the NCAs using COMSOL Multiphysics. (c) The SEM images indicate the side view (left panel) and the top view (right panel) of the NC-structured sample. The nanostructure dimensions and the periodic rectangular unit cell used in the simulation shown on the images. The 3 µm scale bars indicate the size of the structure. (d) Reflection spectra for the bulk and nanostructured samples for p-polarized incidence with angles of θ = 45° and θ = 70° within the spectral range of 482–511 cm⁻¹ where the material exhibits hyperbolic type I behavior. The solid curves represent reflection measurements for the bulk and nanostructured samples, and the dashed curves indicate simulation results.

To model the optical response, the NCA structure was characterized by Scanning Electron Microscopy (SEM) (see Experimental). Fig. 2(c) shows an SEM image with the left panel showing the side view and the right panel showing the top view of the NCA structure. The SEM image shows a hexagonal periodic pattern which the NCA takes, with a periodicity of p = 3.2 ± 0.1 µm, a height of h = 1.96 ± 0.05 µm, and a basal diameter of d = 2.93 ± 0.07 µm, as determined from histograms of measurements over 30 nanocones (see SI Section 3 and Fig. S11). The green rectangles with height of 3.2 ± 0.1 µm and length of 5.6 ± 0.2 µm in the right panel indicate unit cells and periodic boundary conditions used in the modeling. Additionally, to ensure convergence of the simulation results, free tetrahedral meshes with element sizes ranging from 0.026 µm to 1.8 µm were employed. Furthermore, the refractive index of sapphire was taken from Schubert et al.²¹

As evident from the reflection spectra in Fig. 2(a) and (b), three SPhP modes are excited by the NCA structure, indicated by reflection dips superimposed on the metallic RBs (Fig. 1(d)).^1,21 For the s-polarized light, the experimental data (solid lines) reveal two SPhP modes, denoted I and II, at wavenumbers ω = 734.32 ± 0.06 cm⁻¹ and ω = 790.40 ± 0.05 cm⁻¹ (wavelengths λ = 13.618 ± 0.001 µm and λ = 12.652 ± 0.001 µm, respectively) with quality factors (Qs) of 32.5 ± 0.3 and 40 ± 1, respectively (see SI, Fig. S9 and Table S2). For p-polarized excitation, a broad SPhP resonance, labeled III, is observed at ω = 779.24 ± 0.28 cm⁻¹ (wavelength λ = 12.833 ± 0.004 µm) with a linewidth of 148 ± 8 cm⁻¹ and Q = 5.3 ± 0.3 (further details on mode III are provided in SI, Fig. S9 and Table S2).

The measured and calculated data exhibit good agreement in peak position and modal quality (see SI, Fig. S10), especially for the ENZ and HVPhP modes. Larger discrepancies are observed for the SPhP modes. These discrepancies might arise from minor differences of the actual NC compared to the idealized NC employed in the modeling (see SI Fig. S7).¹⁰ For example, rounding of the apex and/or trough of the order of 10 nm (smaller than the error bars determined from SEM) can have significant effects on the position of the modes. This is of particular importance for metallic modes such as SPhPs, as the concentration of the electrical fields is highly dependent on the sharpness of these edges.

Additionally, three resonances are observed in the calculated reflectivity at spectral positions ω = 463.15 ± 0.23 cm⁻¹, ω = 702.07 ± 0.0.46 cm⁻¹, and ω = 724.77 ± 1.75 cm⁻¹, as indicated by asterisks in Fig. 2(b). These resonances are absent in the measured reflectance spectrum. However, given their weaker amplitudes compared to the other measured modes, it is probable that these resonances are below the detection threshold of our measurement systems⁴ (refer to SI, Fig. S6(g–i) for the E-field profiles corresponding to these resonances).

The corresponding E-field spatial distributions in ZY plane for each mode is shown in color plots in Fig. 3. Numerical calculations of E_y-field spatial distribution at normal incidence reveal that mode I is a localized surface confinement along the face of the NC (Fig. 3(d)). Mode II is a transverse dipole with optical fields concentrated at the apex and troughs of the NC (Fig. 3(e)). Since s – polarized light is perpendicular to the plane of incidence (see SI, Fig. S1), it primarily excites transverse surface modes along the NC. Fig. 3(f) shows the calculated E_z-field spatial distribution for mode III at normal incidence, where it is clear that p – polarized light enhances the vertical confinement in the tip, sides, and troughs of the NC. In contrast, p – polarized light with its E_z component primarily excites vertical modes in the nanostructure. The relatively broad linewidth of 148 ± 8 cm⁻¹ in mode III may be attributed to the tapered shape of the NC along the z direction (see SI, Fig. S5).^25,26

Fig. 3 E-field spatial distribution in NCA sapphire system. E_z simulated cross-sectional plots for HVPhP at (a) 497 cm⁻¹, and (b) 502 cm⁻¹ with near grazing incidence of θ = 70°. The normal incidence E_y simulated cross-sectional plots for (c) ENZ mode at 563 cm⁻¹, and for s-polarized SPhP resonances at (d) 763 cm⁻¹, and (e) 800 cm⁻¹. Normal incidence E_z surface plot for p-polarized SPhP at (f) 795 cm⁻¹. The 1 µm scale bar in each panel indicates the size of the structure.

In addition to SPhPs, HVPhPs are excited in the studied NCA platform under p – polarized excitation within the HT I spectral region from ω = 481.68 ± 0.05 cm⁻¹ to ω = 510.87 ± 0.02 cm⁻¹.²¹ As demonstrated by arrows in Fig. 2(d), the dominant HVPhPs manifest as reflection peaks at ω = 497.87 ± 0.04 cm⁻¹ and ω = 506.86 ± 3.37 cm⁻¹ (wavelengths λ = 20.085 ± 0.0001 µm and λ = 19.730 ± 0.131 µm, respectively) with Q = 83 ± 4 and Q = 40 ± 39, respectively. Measurements taken at off-normal incidence (θ = 45°) and near-grazing incidence (θ = 70°), reveal that the strength of the HVPhPs depends on the incident angle. As the incident angle increases, the electric field along the material's metallic direction (E_z) intensifies, resulting in stronger resonances in the solid magenta plot compared to the green reflectivity plot. Fig. 3(a and b) illustrate calculated E_z-field distribution and provide further insight into the nature of the HVPhPs. The cross-hatch E – field profile is attributed to the propagation direction of the HVPhPs which is restricted to the angle between the field crossing lines and the optical axis (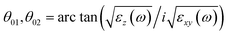 in Fig. 3(a and b)).¹⁰

Given that the NC platform features a spheroid-like geometry with its symmetrical axis aligned parallel to the c axis, the HVPhP eigenmodes are denoted as TM_ml, where TM (transverse magnetic) indicates that the magnetic field is perpendicular to the z axis.¹⁰ The parameter m represents the angular momentum along the z axis, and l corresponds the orbital index.¹⁰ Since the HVPhPs are symmetric modes around the z axis, m = 0 for both observed modes.¹⁰ Additionally, l = 1 characterizes the first-order mode with a single node in the E – field profile, while l = 2 denotes the second-order mode, which features two nodes in the E – field profile, as illustrated in Fig. 3(a) and (b), respectively. The directional HVPhPs supported by the sapphire NCA platform make it a promising candidate for potential applications such as super-resolution imaging and nanolithography.^16,17

Furthermore, outside the HT II spectral region (from 569.00 ± 0.04–582.41 ± 0.06 cm⁻¹),²¹ near the transverse optical phonon a strong resonance observed at ω = 565.47 ± 0.05 cm⁻¹ (λ = 17.684 ± 0.001 µm) in both s and p – polarized reflection spectra, connected by a dashed line in Fig. 2(a) and (b). This ENZ state owes its existence to the strong dispersion of the material's in-plane permittivity (Re[ε_x,y]) close to the hyperbolic transition point, enabling enhanced light confinement with Q = 122 ± 8 inside the NC structures as depicted in Fig. 3(c).²⁷ (refer to SI Fig. S6 for the E-field profiles of the observed modes for the oblique incidence of θ = 45°)

4 Raman enhancement from nanostructured Al₂O₃

Since, sapphire is a centrosymmetric material, all IR allowed vibrations discussed in Section 3 are Raman forbidden, and vice versa.²⁸ The Raman-active phonons in sapphire have been extensively studied. Within the investigated range, six Raman modes have been reported for the material: two classified as A_1g and four as E_g modes.^28–33 To explore the spatial variation of the vibrational modes, confocal RS measurements were performed at various points on the sapphire NC sample: the apex, the trough, and 2 µm deep into the substrate (see Experimental). The results indicated by the red, blue, and green plots in Fig. 4(a) correspond to the scan points A, B, and C, respectively. The distinct spectral responses highlight the significant spatial dependency of RS on the NC geometry.

Fig. 4 Mapping PhPs in Al₂O₃ NCA. (a) Measured Raman spectra at three different points (as shown in the inset) across the NCA indicating the spatial dependence of Raman modes. The inset with red frame indicates the Raman enhancement signal at various points on the NC at ω ≈ 645 cm⁻¹. ZY cross sectional view of Raman intensity obtained from experimental measurements for (b) A_1g phonon mode at ω = 418 cm⁻¹, and (c) E_g phonon mode at ω = 751 cm⁻¹ for three adjacent NCs. Theoretically simulated Raman intensity shown in ZY cut plane for (d) A_1g and (e) E_g phonon modes. The dashed green lines indicate the NCs-air interface. The 3 µm scale bar in each panel indicates the size of the structure.

Additionally, enhanced Raman signals of the A_1g Raman mode at ω = 645.85 ± 0.08 cm⁻¹ was measured for the NCA structure, with a maximum enhancement factor of 7.0 ± 0.6 at the trough (point B) and 1.8 ± 0.5 at the apex (point A), as shown in the inset of Fig. 4(a) (see SI Fig. S12 for more information on the enhancement factor on the NC). The A_1g Raman mode appears only in the diagonal components of the Raman tensor, particularly in the z direction. As a result this mode is weak in the c-cut sapphire when RS measurement is conducted using z(y,−)z̄ geometry.^28,29 However, the same mode has been observed in a-cut sapphire under similar measurement configuration.³² This Raman enhancement may be attributed to the relaxation of Raman selection rules in nanostructured system leading to the activation of forbidden vibrational mode in perfect crystal.^34,35

Furthermore, two-dimensional (2D) Raman spatial mapping was performed by scanning three adjacent NCs in the ZY plane (the right panel in Fig. 2(c) shows the top view of the 2D scanned plane). As depicted in Fig. 4(b) and (c), the Raman mapping extended from 2 µm above the NC apex to 6 µm deep into the substrate. These Raman images visualize coupling between bulk phonons and PhP, including SPhP and HVPhP^33,36 (see SI, Fig. S8). The Raman image in Fig. 4(b) shows that the A_1g mode exhibits strong intensity at the apex, troughs, and within the volume of the NC, analogous to SPhP mode II and HVPhP modes. In contrast, Fig. 4(c) demonstrates that the E_g mode intensity is stronger at the NC troughs, like the SPhP mode I. This variation in coupling is driven by changes in local polarizability, described by Raman selection rules.³⁶

To further support our experimental data, the Raman selection rules for both A_1g and E_g modes were employed to reconstruct the field intensity within the NCAs. Raman intensity corresponding to these phonon scattering modes was theoretically simulated with COMSOL Multiphysics, with the results shown in Fig. 4(d) and (e). To model the Raman intensity, the eigenmodes obtained from IR reflection spectra were subjected to the Raman selection rules for A_1g and E_g symmetries. Finally, the Raman scattering intensity was reconstructed by averaging the combined polarization intensities of the selected PhP eigenmodes. The calculated Raman data shows good agreement with the experimental findings (see SI Fig. S10), visualizing the coupling between phonons and PhPs in NC structure.³⁶

5 Conclusions

In conclusion, our study provides a thorough analysis of the optical properties of Al₂O₃ within the IR spectral range from ω = 385 – 1050 cm⁻¹. We demonstrated that sapphire is a complex polar dielectric material featuring both hyperbolic and metallic RBs. Through experimental analysis and full-wave simulation, we demonstrated strong light confinement below the diffraction limit within the sapphire NC structure, arising from excitation of PhPs and ENZ modes. Specifically, three SPhPs, two HVPhPs and one ENZ modes observed in the studied nanostructure. Furthermore, confocal RS revealed enhanced Raman signals on the nanostructured surface and demonstrated phonon–PhP coupling through spatial mapping. This study confirms that the sapphire NCA structure can serve as a promising platform for advanced IR nanophotonic and surface enhanced Raman scattering (SERS) applications and provides valuable insights into the physics of the novel remote phonon-induced magnetization switching systems and heterostructures, leveraging phononic properties of sapphire.

6 Experimental

6.1 Scanning electron microscopy (SEM)

The 2-inch patterned sapphire substrates were purchased from Crystal Optoelectronics Company in Zhejiang, China. The preparation process of the 2-inch patterned sapphire substrate starts from spin-coating a layer of photoresist on the surface of a 2-inch sapphire substrate. Through the steps of pre-backing, alignment, ultraviolet light exposure, baking, development, etc., the pattern on the mask is replicated onto the photoresist. Then, using the patterned photoresist film as a mask, an etching process was performed to obtain a patterned sapphire substrate. The patterned sapphire substrate morphology was measured using the field-emission scanning electron microscope (SEM, Hitachi S-4800).

6.2 Far-field measurement using FTIR spectroscopy

Reflectance measurements for bulk and NC sapphire samples (Fig. 1(b–d) and 2(a, b), and (d) in the main text and Fig. S3 and S4 in the SI) were carried out using a Bruker Invenio FTIR spectrometer. The spectrometer was equipped with a KBr beam splitter covering the spectral range of ∼400–40000 cm⁻¹ (0.25–25 µm), a broad spectral range DLaTGS detector, and a PIKE Technologies VeeMAX III specular reflectance accessory enables the samples to be analyzed over a range of incident angles from 30° to 80°. A Thorlabs' holographic wire grid polarizer on KRS5, which operates in the spectral range of ∼ 333–5000 cm⁻¹ (2–30 µm), was used to select the s and p polarizations. All measurements were carried out under room temperature and ambient pressure conditions, with a controlled nitrogen gas purging atmosphere to remove moisture interference. 60 scans with a spectral resolution of 4 cm⁻¹ were averaged to produce the reflection spectra extending the wavenumber range of 385–1050 cm⁻¹ (corresponding to a wavelength range of 9–26 µm).

6.3 Confocal Raman spectroscopy

Several Raman spectra were acquired and averaged using a WITec Alpha 300R confocal Raman microscope equipped with a 100× Zeiss EC Epiplan-Neofluar objective (0.95 NA), yielding a laser spot size of 0.720 ± 0.005 µm at the sample plane, an ultra-high throughput spectrometer WITec UHTS 300, a charged-coupled device (CCD) detector, and a λ/2 calcite waveplate. All Raman scattering measurements were performed using z(y,−)z̄ geometry with a green laser centered at λ = 532 nm with power of P = 46.60 ± 0.05 mW, where the y-polarized incident and unpolarized scattered light propagated along the z axis. The Raman scattering measurements at various spatial points on the nanostructure and the bulk material (Fig. 4(a) in the main text) were collected at room temperature and under ambient pressure condition with accumulation and an integration time of 80 and 80 seconds, respectively.

Additionally, a similar setup was used to measure the ZY cross-sectional spatial Raman intensity for the nanostructure (Fig. 4b and c in the main text and Fig. S8g and h in the SI). To measure the spatial Raman intensity shown in Fig. 4b and c in the main text, a Raman depth scan was performed on three adjacent NCs across the ZY plane (a green line in Fig. 2(c) shows the top view of scanned area). The scan resolution was 0.50 ± 0.01 µm, i.e., Raman intensity was measured at every ∼0.5 µm interval in both the z and y directions across the selected plane. Each point was scanned with an accumulation of 30 and an integration time of 25 seconds, respectively allowing for precise mapping of the spatial variations in both dimensions.

Author contributions

M. N. performed numerical simulations and wrote the manuscript with K. E. A., M. N. and V. R. W. performed confocal Raman spectroscopy. M. N. and K. E. A. performed FTIR spectroscopy. J. M. provides the samples and conducted SEM scan on NCA. All authors contributed to analyzing results and discussion. J. G. T. and B. W. supervised the project.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: provides further details on spectral ranges of the material's various RBs, and represents additional experimental and numerical data, including reflection spectra, sub-diffraction mode profiles in nanocone-structured sapphire, and data quantification. See DOI: https://doi.org/10.1039/d5ra06643c.

Acknowledgements

Authors acknowledge partial supports by the U.S. National Science Foundation (NSF) Partnership for International Research and Education (PIRE) program under the Grant No. OISE-2230706. J. G. T. acknowledges a partial support by Oklahoma Center for the Advancement of Science and Technology’s Research Grant No. AR21-032. B. W. acknowledges a partial support by U.S. NSF CAREER Award under Grant No. 2340060. J. M. acknowledges partial supports by the National Natural Science Foundation of China under Grant No. 12474164, and the Science Technology Program of Jilin Province under Grant No. YDZJ202502CXJD081. M. N. acknowledges Mathias Schubert and Megan Stocky for providing sapphire refractive index data used in the modeling for both bulk and nanostructured material.

Notes and references

1. J. D. Caldwell, L. Lindsay, V. Giannini, I. Vurgaftman, T. L. Reinecke, S. A. Maier and O. J. Glembocki, Nanophotonics, 2015, 4, 44–68.
2. C. R. Gubbin and S. De Liberato, Nanophotonics, 2023, 12, 2849–2864.
3. J. D. Caldwell, O. J. Glembocki, Y. Francescato, N. Sharac, V. Giannini, F. J. Bezares, J. P. Long, J. C. Owrutsky, I. Vurgaftman and J. G. Tischler, et al., Nano Lett., 2013, 13, 3690–3697.
4. C. T. Ellis, J. G. Tischler, O. J. Glembocki, F. J. Bezares, A. J. Giles, R. Kasica, L. Shirey, J. C. Owrutsky, D. N. Chigrin and J. D. Caldwell, Sci. Rep., 2016, 6, 32959.
5. G. Lu, C. R. Gubbin, J. R. Nolen, T. G. Folland, K. Diaz-Granados, I. I. Kravchenko, J. A. Spencer, M. J. Tadjer, O. J. Glembocki and S. De Liberato, et al., ACS Nano, 2021, 16, 963–973.
6. B. Neuner III, D. Korobkin, C. Fietz, D. Carole, G. Ferro and G. Shvets, J. Phys. Chem. C, 2010, 114, 7489–7491.
7. M. L. Tseng, Y. Jahani, A. Leitis and H. Altug, ACS Photonics, 2020, 8, 47–60.
8. M. Ghashami, H. Geng, T. Kim, N. Iacopino, S. K. Cho and K. Park, Phys. Rev. Lett., 2018, 120, 175901.
9. S. Mukhopadhyay, C. T. Ellis, D. C. Ratchford, E. M. Jackson, J. G. Tischler, T. L. Reinecke and M. D. Johannes, J. Appl. Phys., 2021, 130, 143101.
10. J. D. Caldwell, A. V. Kretinin, Y. Chen, V. Giannini, M. M. Fogler, Y. Francescato, C. T. Ellis, J. G. Tischler, C. R. Woods and A. J. Giles, et al., Nat. Commun., 2014, 5, 5221.
11. A. J. Giles, S. Dai, O. J. Glembocki, A. V. Kretinin, Z. Sun, C. T. Ellis, J. G. Tischler, T. Taniguchi, K. Watanabe and M. M. Fogler, et al., Nano Lett., 2016, 16, 3858–3865.
12. V. E. Babicheva, Nanomaterials, 2024, 14, 1539.
13. W. Huang, T. G. Folland, F. Sun, Z. Zheng, N. Xu, Q. Xing, J. Jiang, H. Chen, J. D. Caldwell and H. Yan, et al., Nat. Commun., 2023, 14, 2716.
14. S.-J. Yu, Y. Jiang, J. A. Roberts, M. A. Huber, H. Yao, X. Shi, H. A. Bechtel, S. N. Gilbert Corder, T. F. Heinz and X. Zheng, et al., ACS Nano, 2022, 16, 3027–3035.
15. V. M. Breslin, D. C. Ratchford, A. J. Giles, A. D. Dunkelberger and J. C. Owrutsky, Opt. Express, 2021, 29, 11760–11772.
16. Z. Liu, H. Lee, Y. Xiong, C. Sun and X. Zhang, science, 2007, 315, 1686.
17. Y. Xiong, Z. Liu and X. Zhang, Appl. Phys. Lett., 2009, 94, year.
18. Y. Zhou, A. Waelchli, M. Boselli, I. Crassee, A. Bercher, W. Luo, J. Duan, J. Van Mechelen, D. van der Marel and J. Teyssier, et al., Nat. Commun., 2023, 14, 7686.
19. R. Xu, I. Crassee, H. A. Bechtel, Y. Zhou, A. Bercher, L. Korosec, C. W. Rischau, J. Teyssier, K. J. Crust and Y. Lee, et al., Nat. Commun., 2024, 15, 4743.
20. T. Qin, W. Ma, T. Wang and P. Li, Nanoscale, 2023, 15, 12000–12007.
21. M. Schubert, T. Tiwald and C. Herzinger, Phys. Rev. B, 2000, 61, 8187.
22. M. Stokey, R. Korlacki, M. Hilfiker, S. Knight, S. Richter, V. Darakchieva, R. Jinno, Y. Cho, H. G. Xing and D. Jena, et al., Phys. Rev. Mater., 2022, 6, 014601.
23. A. Bile, M. Centini, D. Ceneda, C. Sibilia, A. Passaseo, V. Tasco and M. Larciprete, Opt. Mater., 2024, 147, 114708.
24. C. Davies, F. Fennema, A. Tsukamoto, I. Razdolski, A. Kimel and A. Kirilyuk, Nature, 2024, 628, 540–544.
25. Y. Cui, K. H. Fung, J. Xu, H. Ma, Y. Jin, S. He and N. X. Fang, Nano Lett., 2012, 12, 1443–1447.
26. J. Yang, Z. Zhu, J. Zhang, C. Guo, W. Xu, K. Liu, X. Yuan and S. Qin, Sci. Rep., 2018, 8, 3239.
27. D. Fomra, A. Ball, S. Saha, J. Wu, M. Sojib, A. Agrawal, H. J. Lezec and N. Kinsey, Applied Physics Reviews, 2024, 11, year.
28. G. Watson Jr, W. Daniels and C. Wang, J. Appl. Phys., 1981, 52, 956–958.
29. T. Wermelinger, C. Borgia, C. Solenthaler and R. Spolenak, Acta Mater., 2007, 55, 4657–4665.
30. W. Zhu and G. Pezzotti, J. Appl. Phys., 2011, 109(7), 073502.
31. D. N. Talwar, H.-H. Lin and Z. C. Feng, Mater. Sci. Eng., B, 2020, 260, 114615.
32. Z. Tao, Y. Song and Z. Xu, Ceram. Int., 2023, 49, 33175–33187.
33. A. Bergeron, C. Gradziel, R. Leonelli and S. Francoeur, Nat. Commun., 2023, 14, 4098.
34. L. Sirleto, A. Vergara and M. A. Ferrara, Adv. Opt. Photonics, 2017, 9, 169–217.
35. P.-H. Tan and L. Tan, Raman Spectroscopy of Two-Dimensional Materials, Springer, 2019, vol. 276.
36. K. E. Arledge, C. T. Ellis, N. R. Sarabi, V. R. Whiteside, C. S. Kim, M. Kim, D. C. Ratchford, M. A. Meeker, B. Weng and J. G. Tischler, arXiv arXiv:2404.13759, 2024.

---