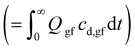Open Access Article
Open Access ArticleEnhancing the bioavailability of sparingly-soluble drugs by expandable, solid-solution fibrous dosage forms
Aron H.
Blaesi
 *ab,
Henning
Richter
*ab,
Henning
Richter
 c and
Nannaji
Saka
d
c and
Nannaji
Saka
d
aEnzian Pharmaceutics Blaesi AG, CH-7078 Lenzerheide, Switzerland
bEnzian Pharmaceutics, Inc., Cambridge, MA 02139, USA. E-mail: ablaesi@enzianpharma.com
cDiagnostic Imaging Research Unit (DIRU), Department of Clinical Diagnostics and Services, Vetsuisse Faculty, University of Zurich, CH-8057 Zurich, Switzerland
dDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 23rd December 2025
Abstract
Many kinds of drug are sparingly soluble in the acidic gastric fluid, and are practically insoluble in the pH-neutral intestinal fluid. The efficacy of oral therapies employing such drugs is often limited by the amount of drug that can be delivered into the blood stream. For enhancing the amount delivered, in the present work an expandable, solid-solution fibrous dosage form is presented. The dosage form investigated was a cross-ply structure of fibers comprising 200 mg of the sparingly-soluble drug nilotinib molecularly dispersed in hydroxypropyl methylcellulose (HPMC)-based excipient. Upon administering to a dog, it expanded to a normalized radial expansion of 0.5 within an hour and resided in the stomach for about five hours. The drug concentration in blood rose to a maximum of 1.82 µg ml−1 by 4 hours, and decayed exponentially thereafter. The bioavailability (area under the drug concentration in blood versus time curve) was 10.81 µg h ml−1. For comparison, the maximum drug concentration of an immediate-release capsule filled with 200 mg crystalline nilotinib particles was 0.68 µg ml−1 by 2.5 hours. The bioavailability was 2.94 µg h ml−1, a third of that of the fibrous form. Models suggest that the greater bioavailability of the fibrous dosage form is due to increased gastric residence time and supersaturation of the gastric fluid with the drug.
1. Introduction
At present, many kinds of drug are sparingly soluble in the acidic gastric fluid, and are virtually insoluble in pH-neutral intestinal fluid.1–5 The efficacy of oral therapies employing such drugs is often limited by the drug's bioavailability, A, defined here as: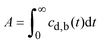 | (1) |
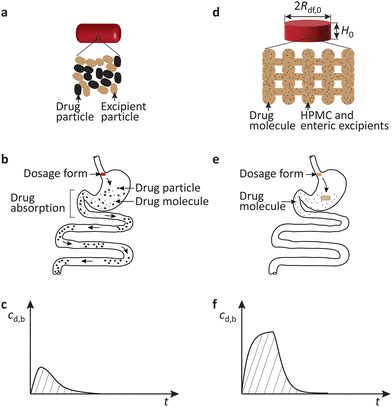
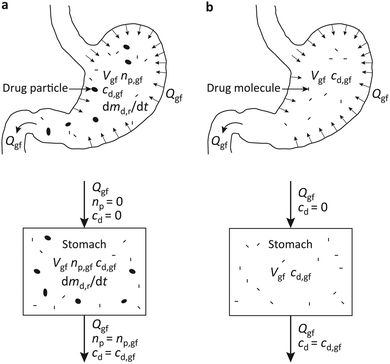
More specifically, as shown schematically in Fig. 1a, the most prevalent oral dosage forms at present are loose or lightly compacted mixtures of crystalline drug and excipient particles.5–7 Upon ingestion, they disintegrate into their constituents in the stomach, Fig. 1b. The drug particles then release drug molecules which pass into the intestine and are absorbed by the blood stream. As a result, the drug concentration in blood increases, Fig. 1c.
However, because the drug solubility in the gastric fluid is low, the drug particle dissolution rate is slow, and the drug concentration in blood increases slowly. Moreover, the small drug particles readily pass from the stomach into the intestine with the flowing gastric fluid. In the intestine they will not dissolve any further, Fig. 1b, and drug absorption stops. Thus, the drug concentration in blood peaks at a low value, the bioavailability is low, and the drug therapy may not be effective, Fig. 1c.
Over the years, therefore, numerous techniques have been developed to alter the physical state of sparingly-soluble drug particles. Such techniques include, for example, salt or co-crystal formation,8,9 crystalline-to-amorphous phase transformation,10–12 polymorphic change,13,14 and formation of solid solutions.15–20 While enhanced dissolution rates were achieved, the small drug particles still pass into the intestine prematurely.
Such limitations could be mitigated by the expandable fibrous dosage forms introduced recently.21–28 As shown schematically in Fig. 1d, the fibrous dosage form considered here is a cross-ply structure of solid-solution fibers comprising dissolved drug molecules in a water-absorbing excipient matrix. Upon ingestion, the dosage form expands in the gastric fluid and releases drug molecules at a high rate. The expanded dosage form will not pass into the intestine instantly, and a high absorption rate can be maintained for prolonged time, Fig. 1e. This enhances the drug concentration in blood, bioavailability, and the efficacy of the drug therapy, Fig. 1f.
The specific solid-solution fibrous dosage forms investigated in the present work comprise 200 mg of the sparingly-soluble drug nilotinib dispersed in a matrix of hydroxypropyl methylcellulose (HPMC) and methacrylic acid–ethyl acrylate excipients. Dosage form expansion, drug release rate, gastric residence time, drug concentration in gastric fluid, drug concentration in blood, and bioavailability are determined by experiments and theoretical models. The dog is used as an animal model for in vivo studies.
The results are compared with those of a previously presented immediate-release capsule containing 200 mg crystalline nilotinib particles.25–28 Details of the preparation, theoretical models, and properties of the particulate dosage forms are given in Appendix A.
2. Materials and methods
2.1. Materials of solid-solution fibrous dosage forms
The materials used for preparing the fibrous dosage forms were as follows.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), with a molecular weight of about 250 kg mol−1 (trade name: Eudragit L100-55), received from Evonik, Essen, Germany.
1), with a molecular weight of about 250 kg mol−1 (trade name: Eudragit L100-55), received from Evonik, Essen, Germany.
2.2. Preparation of solid-solution fibrous dosage forms
First, solid particles of nilotinib, HPMC, Eudragit L100-55, and BaSO4 were mixed with liquid DMSO to form a uniform suspension. The concentrations of nilotinib, HPMC, Eudragit L100-55, and BaSO4 were 105.2, 161.3, 53.8, and 137.3 mg ml−1 DMSO, respectively.Then the suspension was extruded through a laboratory extruder to form a uniform viscous paste. The viscous paste was put in a syringe equipped with a hypodermic needle of inner radius, Rn = 205 μm. The paste was extruded through the needle to form wet fiber that was patterned layer-by-layer as a fibrous dosage form with cross-ply structure.21–30 The nominal inter-fiber spacing, λn, in the patterned structure was 820 μm.
After patterning, to evaporate the solvent and solidify the structure the dosage forms were put in a vacuum chamber maintained at a pressure of 200 Pa and a temperature of about 35 °C for a day. The solid dosage forms then consisted of 23 wt% nilotinib, 35.25 wt% HPMC, 11.75 wt% Eudragit L100-55, and 30 wt% BaSO4. They were 6.5 mm thick, and were trimmed to circular disks with nominal diameter 14 mm. The weight of the final, circular dosage forms was about 870 mg, and the weight of nilotinib in the dosage form was 200 mg, Table 1.
| Symbol | Description | Value |
|---|---|---|
| a From the scanning electron micrographs shown in Fig. 2. b From eqn (2) and (3). | ||
| H 0 | Thickness of solid dosage form | 6.5 mm |
| M d,0 | Mass of drug in dosage form | 200 mg |
| M df | Mass of the “final” dosage form | 870 mg |
| n l | Number of fiber layers in dosage form | 32 |
| R df,0 | Radius of dosage form | 7 mm |
| R f,0 | Fiber radius | 149 ± 7 µma |
| w BaSO4 | Weight fraction of BaSO4 in fibers | 0.3 |
| w d | Weight fraction of drug in fibers | 0.23 |
| w ee | Weight fraction of enteric excipient (Eudragit L100-55) in fibers | 0.1175 |
| w HPMC | Weight fraction of HPMC in fibers | 0.3525 |
| λ 0 | Inter-fiber distance | 601 ± 12 µma |
| φ f | Volume fraction of fibers in dosage form | 0.57b |
2.3. Imaging the microstructures of the fibrous dosage forms
The microstructures of the fibrous dosage forms were imaged by a Zeiss Merlin High Resolution SEM with a GEMINI column. Top surfaces were imaged after coating with a 10 nm thick layer of gold. Longitudinal sections were imaged after cutting the dosage form with a thin blade (MX35 Ultra, Thermo Scientific, Waltham, MA) and coating with gold as above. All specimens were imaged with an in-lens secondary electron detector. The accelerating voltage was 5 kV, and the probe current 95 pA.2.4. Differential scanning calorimetry (DSC)
DSC experiments were conducted on fibers of a fibrous dosage form after one year of storage at room temperature, and on the solid particles of nilotinib hydrochloride monohydrate used to prepare them. A sample of about 10 mg was placed in an aluminum pan, and the specific heat flow to increase the temperature from 30 to 300 °C was measured with a NETZSCH DSC 204F1 Phoenix. The rate of temperature rise was 10 °C per minute.2.5. In vitro expansion of the fibrous dosage forms
The dosage forms were immersed in a beaker filled with 400 ml dissolution fluid (0.03 M HCl in DI water, pH = 1.5, at 37 °C). The fluid was stirred with a paddle rotating at 70 rpm. The immersed samples were then imaged periodically by a Nikon DX camera.2.6. In vitro drug release by the dosage forms
Drug release by the dosage forms was determined by a USP dissolution apparatus II (Sotax AG, Aesch, Switzerland). The dissolution bath was filled with 1200 ml dissolution fluid (0.03 M HCl in DI water, pH = 1.5, at 37 °C). The fluid was stirred with a paddle rotating at 70 rpm. The dosage forms were immersed in the fluid, and the concentration of dissolved drug versus time was measured by UV absorption using a fiber optic probe connected to a Cary 60 UV-vis spectrophotometer (Agilent Technologies, Santa Clara, CA). Drug concentrations were determined by subtracting the UV absorbance at 310 nm wavelength from the absorbance at 300 nm.2.7. In vivo gastric residence time of the dosage forms in dogs
For determining the gastric residence time of the fibrous dosage forms, two healthy beagle dogs (12.2 and 15.2 kg) were assigned an experiment each. The dogs fasted for 18 hours prior to the experiment.The dosage forms were administered to an awake dog with 20 ml water as described previously.23,28 Thereafter the dog was periodically placed in an X-ray permeable box, and the position of the dosage form in the gastrointestinal tract was monitored by biplanar fluoroscopy (using a Philips Allura Clarity fluoroscopy system). Between imaging, the dogs were allowed to roam about freely with access to water.
Five hours after administration, 180 grams of basic dry food was given (Grainfree 25/17, Petzeba AG, Alberswil, Switzerland). No sedatives, anesthesia, or other supplements were administered before, during, or after the experiment.
The study was conducted in compliance with the Swiss Animal Welfare Act (TSchG, 2005) and the Swiss Animal Welfare Ordinance (TSchV, 2008). It was approved by the Swiss Federal Veterinary Office Zurich; the animal license number was ZH072/2021.
2.8. Monitoring in vivo drug concentration in the blood of dogs
In addition to monitoring gastric residence, blood samples were periodically collected using a central venous catheter that was surgically inserted into the jugular vein of the dog at least 48 hours before the experiment. After collecting a sample, blood plasma was extracted. The nilotinib concentration in the plasma was measured by liquid chromatography coupled to tandem mass spectrometry (LC-MS/MS) as described previously.283. Results and discussion
3.1. Microstructures of solid-solution fibrous dosage forms
Fig. 2a and b are the top and sectional views of the fibrous dosage form. The fiber radius, Rf,0 = 149 μm, and the inter-fiber spacing, λ0 = 601 μm, Table 1. | ||
| Fig. 2 Scanning electron micrographs of solid-solution fibrous dosage forms: (a) top view and (b) longitudinal section. | ||
The volume fraction of fibers in the dosage form may be obtained by:21–30
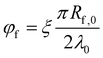 | (2) |
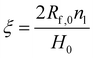 | (3) |
3.2. Differential scanning calorimetry (DSC)
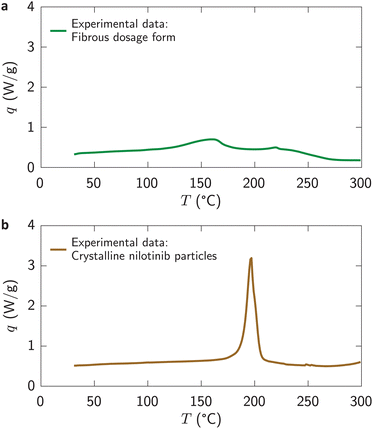
Fig. 3a presents the specific heat flow, q, into the fibers of the fibrous dosage form versus temperature, T. The heat flow was slightly greater than the baseline between 100 and 250 °C, and exhibited a broad peak at roughly 160 °C. However, no evidence of the presence of a crystalline nilotinib phase (i.e., a sharp peak at ∼200 °C, Fig. 3b) was found. Thus, the drug was molecularly dispersed in the excipient forming a solid solution.3.3. In vitro expansion of fibrous dosage forms
Fig. 4 presents a sequence of top-view images of the fibrous dosage form after immersing in a stirred dissolution fluid. Fig. 5 in turn plots the normalized radial expansion, ΔRdf/Rdf,0, versus time, t. Initially, ΔRdf/Rdf,0 increased steeply, to 0.55 by 50 minutes. Thereafter it remained roughly constant. | ||
| Fig. 4 Top-view images of a fibrous dosage form at various times after immersing in a dissolution fluid. | ||
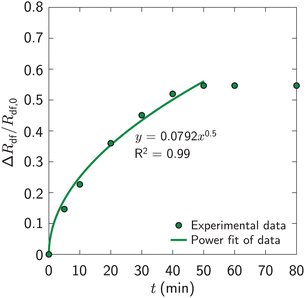 | ||
| Fig. 5 Normalized radial expansion, ΔRdf/Rdf,0, of fibrous dosage form versus time, t, after immersing in the dissolution fluid. The data represent the sample shown in Fig. 4. | ||
As detailed in prior work,21–23 the dosage forms expand due to the diffusion of water into the fibers. If the normalized radial expansion of the dosage form is assumed the same as the normalized radial expansion of a single fiber, an engineering approximation for ΔRdf/Rdf,0 may be written as:21–23
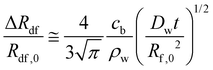 | (4) |
As shown in Fig. 5, up to 50 minutes the experimental data follow the curve ΔRdf/Rdf,0 = 0.0792t1/2. Substituting this result in eqn (4), and using cb/ρw = 1 (Appendix B) and Rf,0 = 149 μm, the diffusivity, Dw = 4.1 × 10−12 m2 s−1. This is of the order of the previously reported Dw ∼ 1 × 10−11 m2 s−1.22,23 Thus, the expansion mechanism of the present fibrous dosage forms is comparable to that of previously reported fibrous forms, and eqn (4) is reasonable.
3.4. In vitro drug release
Fig. 6 plots the fraction of drug released, md,r/Md,0, by the fibrous dosage forms into the in vitro dissolution fluid versus time, t. The dosage forms released 20, 40, 60, and 80 percent of the drug by 0.7, 1.8, 4.4, and 10.8 hours.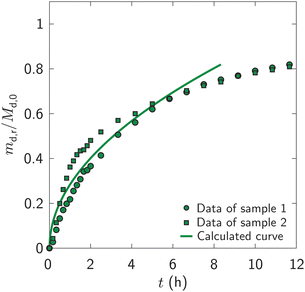 | ||
| Fig. 6 Measured and calculated fraction of drug released, md,r/Md,0, versus time, t, after immersing fibrous dosage forms in the dissolution fluid. The calculated curve is from eqn (8) using the parameter values of Appendix B. The data represent two samples. | ||
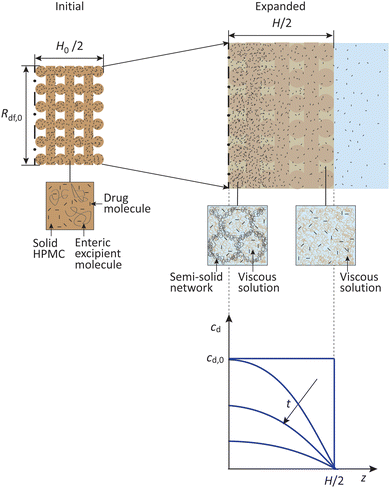
As shown schematically in Fig. 7, because the fibers of the dosage forms considered here are fairly tightly packed (Rf,0/λ0 = 0.25 and φf = 0.57, Table 1), fluid flow through the inter-fiber space may be assumed small. Moreover, the expansion time, te ∼ 1 h, is much smaller than the drug release time, tdr ∼ 10 h. Within the expansion time, however, the drug molecules readily diffuse out of the thin, water-penetrated fibers. Thus, for modeling drug release the “initial” dosage form may be considered an expanded composite slab with uniform drug concentration.
The drug molecules then diffuse out of the slab, and the drug concentration decreases from the center of the slab to the surface. Assuming that the molecules do not precipitate and the geometry of the expanded dosage form is constant, for one-dimensional drug transport across the thickness, H, the diffusion equation may be written as:31
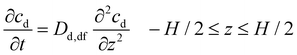 | (5a) |
The initial and boundary conditions are:
| cd = cd,0 t = 0, −H/2 < z < H/2 | (5b) |
| cd = 0 t ≥ 0, z = H/2 | (5c) |
| cd = 0 t ≥ 0, z = −H/2 | (5d) |
The solution to eqn (5) may then be written as:31
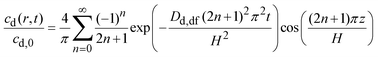 | (6) |
By integrating eqn (6) over the volume of the dosage form and rearranging, the fraction of drug released may be obtained as:31
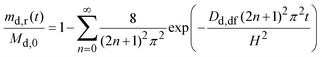 | (7) |
For short times, eqn (7) may be approximated as:31
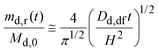 | (8) |
Fig. 6 also plots the calculated fraction of drug released by eqn (8) using Dd,df = 4.22 × 10−10 m2 s−1 and H = 9.8 mm (Appendix B). Up to seven hours (md,r/Md,0 ∼ 0.75), the calculated fraction is comparable to the measured values. Thus, eqn (8) is reasonable; the drug is released in proportion to the square-root of time.
3.5. Gastric residence time
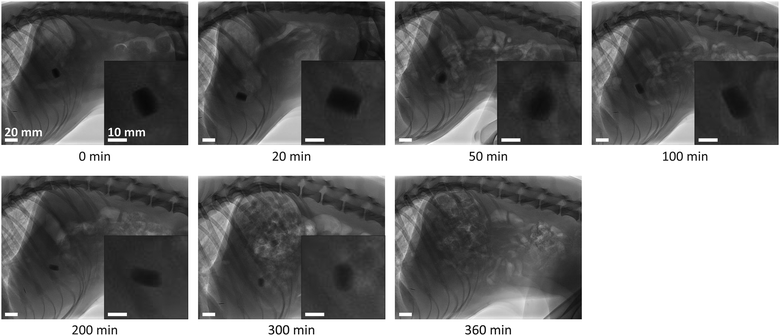
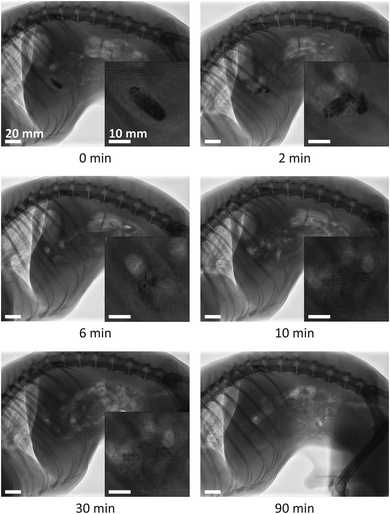
Fig. 8 presents fluoroscopic images of the position, shape, and size of a fibrous dosage form at various times after administering to a dog. The dosage form reached the stomach almost immediately, expanded, and formed a semi-solid mass. Initially, the normalized radial expansion, ΔRdf/Rdf,0, increased steadily with time, to 0.45 by 50 minutes. Thereafter, the dosage form was rounded off at the edges and ΔRdf/Rdf,0 decreased. By 330 minutes the remainder of the dosage form passed into the intestine and dissolved.The average gastric residence time, tr,f, of the two fibrous dosage forms tested was 5.5 h, Table 2. This value will be used in the models that follow.
| Quantity | Symbol and unit | Fibrous dosage forms | Particulate dosage forms | ||
|---|---|---|---|---|---|
| Measured | Calculated | Measured | Calculated | ||
| a The measured in vitro properties of ΔRdf/Rdf,0, te, and ΔRdf/Rdf,0|t=te are from Fig. 4 and 5. The unit of the time, t, is hours. b The measured t0.8 of the fibrous dosage forms represents the average of two samples. The t0.8 times of the individual samples were 10.5 and 11.1 hours, respectively, Fig. 6. The calculated t0.8 is from eqn (8) using the parameter values of Appendix B. c The in vivo values represent averages of two fibrous and four particulate dosage forms. The mass of drug in all dosage forms was 200 mg. The masses of the dogs were 12.2 and 15.2 kg (fibrous dosage forms) and between 12.6 and 16.1 kg (particulate dosage forms). d Measured in vivo properties of te and ΔRdf/Rdf,0|t=te are from fluoroscopic images as shown in Fig. 8. e The gastric residence time of the individual fibrous dosage forms, tr,f = 6 and 5 h, respectively. The measured and calculated gastric residence times of the particulate forms, tr,p, are from ref. 27 and 28 and recited in section A.3 of Appendix A. f The measured values of tmax, cmax, and A of the individual fibrous dosage forms were tmax = 4 h, cmax = 2.24 μg ml−1, and A = 14.95 μg h ml−1 (sample 1), and tmax = 4 h, cmax = 1.41 μg ml−1, and A = 6.68 μg h ml−1 (sample 2). The calculated values of tmax, cmax, and A of the fibrous dosage forms are from eqn (19), (21), and (22) using the parameter values of Appendix B. The measured and calculated values of tmax and cmax of the particulate dosage forms are from section A.5 of Appendix A.27,28 The bioavailability, A, is from eqn (22) using the results and equations of section A.5 with the parameter values of Appendix B. | |||||
| In vitro | |||||
| Normalized radial expansiona | ΔRdf/Rdf,0 (—) | 0.614t1/2 | — | — | — |
| Time to reach “terminal” expansiona | t e (h) | 0.83 | — | — | — |
| “Terminal” normalized expansiona |
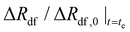 (—) (—) |
0.55 | — | — | — |
| Time to release eighty percent of drugb | t 0.8 (h) | 10.8 | 7.9 | — | — |
| In vivo | |||||
| Time to reach “terminal” expansiond | t e (h) | 0.83 | — | — | — |
| “Terminal” normalized expansiond |
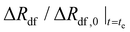 (—) (—) |
0.45 | — | — | — |
| Gastric residence timee | t r,f and tr,p (h) | 5.5 | — | 1–1.5 | 1.43 |
| Time at which drug concentration in blood is maximalf | t max (h) | 4.0 | 4.3 | 2.5 | 2.2 |
| Maximum drug concentration in bloodf | c max (μg ml−1) | 1.82 | 1.2 | 0.68 | 0.59 |
| Bioavailabilityf | A (μg h ml−1) | 10.81 | 8.43 | 2.96 | 2.83 |
3.6. Drug concentration in gastric fluid
As will be shown later, the drug concentration in blood is directly dependent on the drug concentration in gastric fluid. Repeated collection of gastric fluid samples, however, is complex and beyond the scope of this work. Accordingly, the drug concentration in gastric fluid is estimated by mathematical models.As shown schematically in Fig. 9, unlike the closed in vitro dissolution vessel, the stomach is an open system which is continuously filled by fresh gastric fluid (i.e., fluid without any drug) and emptied by drug-containing fluid. The volume of the fasted stomach is small, and the mass of drug in the dosage form per unit volume of gastric fluid, Md,0/Vgf ≫ cs,gf, the drug solubility (in this work, Md,0/Vgf = 10 mg ml−1 and cs,gf = 1 mg ml−1, Appendix B).
 | ||
| Fig. 9 Drug release in the stomach and drug transport from the stomach into the duodenum: (a) 0 ≤ t ≤ tr,f and (b) t > tr,f. | ||
Assuming that: (a) the drug concentration in gastric fluid is uniform, (b) the drug does not precipitate in the gastric fluid, and (c) the flow rate of gastric fluid into the stomach is the same as the flow rate out, by mass balance the drug concentration in the gastric fluid may be written as:27
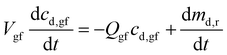 | (9) |
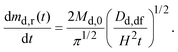 | (10) |
For the parameter values listed in Appendix B, Md,0 = 200 mg, Dd,df = 4.22 × 10−10 m2 s−1, and H = 9.8 mm, by eqn (9) dmd,r/dt = 50, 30, and 14 mg h−1 after 1, 3, and 5 hours, respectively. Thus, up to 5 hours the drug release rate from the dosage form is greater than the flow rate of drug out of the stomach at solubility, Qgfcs,gf = 14 mg h−1, Appendix B. Consequently, the gastric fluid may supersaturate with the drug.
Substituting eqn (10) in eqn (9) and rearranging gives:
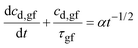 | (11a) |
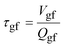 | (11b) |
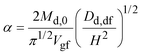 | (11c) |
Eqn (11a) is a first-order heterogeneous linear differential equation with positive and constant coefficients, and a source term that is a function of t−1/2. To our knowledge, such a differential equation cannot be solved analytically. Thus, an approximate of eqn (11a) is written as a finite difference equation with time points, ti, and time increment, Δt:
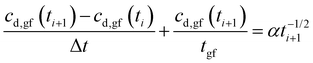 | (12a) |
 | (12b) |
Rearranging eqn (11a), the drug concentration in gastric fluid at time ti+1 may be written as:
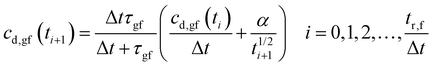 | (13) |
Fig. 10a plots eqn (13) for the condition, cd,gf = 0 at t = 0, and the relevant parameter values listed in Appendix B. The drug concentration in gastric fluid rises rapidly to a maximum, cmax = 1.57 mg ml−1 (1.57 times the solubility) by tmax = 1.6 hours. Then it drops slowly to 1.03 mg ml−1 by the gastric residence time, tr,f = 5.5 hours.
 | ||
| Fig. 10 (a) Calculated drug concentration in gastric fluid versus time after administering solid-solution fibrous and particulate dosage forms. The curve of the fibrous dosage form is from eqn (13) and (16) using the parameter values of Appendix B. The curve of the particulate form is from eqn (A3) and (A4) of Appendix A using the parameter values of Appendix B. (b) Measured and calculated drug concentrations in blood versus time. The measured values of the fibrous dosage forms represent the average drug concentration in blood plasma of two samples. Data of the individual samples are shown in Appendix C. Calculated values are from eqn (19) and (21) using the parameter values of Appendix B. Measured and calculated values of particulate dosage forms are reused from ref. 27 and 28 and recited in section A.5 of Appendix A. | ||
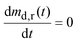 | (14) |
Substituting eqn (14) in eqn (9) and rearranging gives:
 | (15) |
Solving eqn (15) gives:
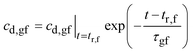 | (16) |
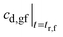 may be obtained from eqn (13).
may be obtained from eqn (13).
Fig. 10a also plots eqn (16) for the relevant parameter values listed in Appendix B. After the residence time of the fibrous dosage form (at 5.5 hours) the drug concentration in gastric fluid drops exponentially at the time constant, τgf = 1.43 hours.
For comparison, as shown in Appendix A and plotted in Fig. 10a, after administering the crystalline particle-filled immediate-release capsule with the same drug content the drug concentration in gastric fluid drops already after about 1.5 hours and does not supersaturate. The calculated mass of drug dissolved in the gastric fluid
3.7. Drug concentration in blood of dogs versus time
Fig. 10b plots the measured drug concentration in blood plasma versus time after administering the fibrous dosage forms. Initially, the concentration remained small for about an hour, but then it increased at a high rate to a maximum of 1.82 µg ml−1 by 4 hours. Past the maximum it decreased to 1.2 μg ml−1 by 6 hours, 0.21 μg ml−1 by 12 hours, and essentially zero by 18 hours.The course of the drug after administering a fibrous dosage form is shown schematically in Fig. 11. It is assumed that (a) all drug molecules that are released into the stomach pass into the duodenum and are absorbed by the blood stream, (b) drug distribution through the blood and tissues is fast, and (c) the drug is eliminated from the blood at a rate proportional to the drug concentration in blood.
 | ||
| Fig. 11 Block diagram of drug release, absorption by the blood, interdiffusion with tissues, and elimination. The absorption rate, dma/dt = Qgfcd,gf, and the elimination rate, dmel/dt = (Vb + Kp,tVt)cd,b/τel.27 | ||
By mass balance the drug concentration in blood may then be written as:27
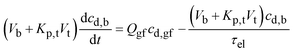 | (17) |
Eqn (17) shows that the drug concentration in blood is a function of the drug concentration in gastric fluid, cd,gf, which in turn depends on the gastric residence time of the dosage form, tr,f.
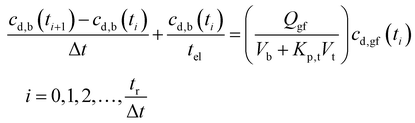 | (18) |
Further rearranging:
 | (19) |
Eqn (19) provides a model for estimating the drug concentration in the whole blood comprising both blood cells and plasma. If it is assumed that the partition coefficient between blood cells and plasma is unity, the drug concentrations in the blood (as modeled) and in the plasma (as measured) are the same.
Fig. 10b plots eqn (19) for the condition, cd,b = 0 at t = 0, and the parameter values listed in Appendix B. The calculated drug concentration rises to a maximum, cmax = 1.2 μg ml−1 by tmax = 4.3 h, Table 2, and then drops. The calculated cmax is about 34 percent smaller than the measured value, and the calculated tmax is about the same.
The measured cmax may be greater because in the experiments the dosage form was rounded off in the stomach, and thus drug was released faster than predicted by eqn (8). Nonetheless, the agreement between model and data is fair.
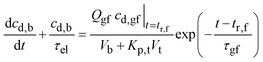 | (20) |
Solving gives:
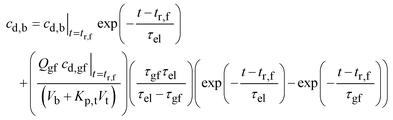 | (21) |
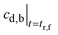 may be obtained from eqn (19).
may be obtained from eqn (19).
Eqn (21) is plotted in Fig. 10b for the parameter values listed in Appendix B. The calculated curve decays at about the same rate as the measured values.
For comparison, the measured and calculated drug concentrations in blood after administering the immediate-release capsules containing 200 mg crystalline nilotinib particles are also plotted in Fig. 10b. The measured and calculated cmax were 0.68 µg ml−1 by 2.5 hours and 0.59 µg ml−1 by 2.2 hours, respectively, Table 2.
Thus, as detailed in Appendix A, because the crystalline drug particles do not supersaturate the gastric fluid and the gastric residence time of the small particles is short, the drug concentration in blood increases at a lower rate and for a shorter time.
3.8. Bioavailability
Finally, by numerically integrating the integral in eqn (1), the bioavailability may be written as: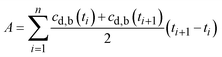 | (22) |
Substituting the measured and calculated drug concentrations in the blood after administering the fibrous dosage forms, the measured and calculated bioavailabilities, 10.81 and 8.43 µg h ml−1, respectively, Table 2.
For comparison, the measured and calculated bioavailabilities of the particulate dosage forms with crystalline drug particles are only 2.96 and 2.83 μg h ml−1.
Thus, the solid-solution fibrous dosage forms enable enhanced bioavailablity compared with that of particulate dosage forms—in the present work by a factor three.
4. Conclusions
In this work, bioavailability of expandable, solid-solution fibrous dosage forms was investigated. The fibrous dosage forms were a cross-ply arrangement of fibers comprising 200 mg nilotinib molecularly dispersed in HPMC and methacrylic acid–ethyl acrylate excipients.(a)In vitro expansion of fibrous dosage forms.
Upon immersing in a dissolution fluid, the fibrous dosage form expanded to 1.5 times the initial radius in 50 minutes. Models suggest that the normalized radial expansion of the dosage form initially scales as (Dwt)1/2/Rf,0. Thus, the expansion was fast because the fibers were thin.(b)In vitro drug release.
In the experiments, the dosage form released 20, 40, 60, and 80 percent of the drug by 0.7, 1.8, 4.4, and 10.8 hours. The modeled fraction of drug released scales as (Dd,dft)1/2/H. Thus, because the expanded dosage form was thick, drug was released over prolonged time.(c) Gastric residence time.
Upon administering to a dog, the fibrous dosage forms remained in the stomach for about 5.5 hours, and then passed into the intestine and dissolved.(d) Drug concentration in gastric fluid.
Models suggest that during gastric residence the drug release rate by the fibrous dosage form into the gastric fluid, dmd,r/dt > Qgfcs,gf, the mass flow rate of drug out of the stomach at solubility. Thus, the gastric fluid may supersaturate with the drug. After the gastric residence time, the drug concentration in gastric fluid falls exponentially.(e) Drug concentration in the blood of dogs and bioavailability.
In the experiments, the drug concentration in blood rose to a maximum of 1.82 μg ml−1 by 4 hours and then decreased. The bioavailability (area under the drug concentration-time curve) was 10.81 μg h ml−1. The data were reasonably close to the calculated values.(f) Gastric residence time and drug concentration in gastric fluid of immediate-release particulate dosage forms.
By comparison, the modeled “gastric residence time” of small, sparingly soluble drug particles, tr,p = Vgf/Qgf = 1.43 hours, much shorter than that of the fibrous forms. Moreover, the drug release rate by crystalline drug particles, dmd,r/dt ∼ (cs,gf − cd,gf). Thus, the gastric fluid does not supersaturate. Due to both limitations the calculated mass of nilotinib dissolved in the gastric fluid is 3 times smaller than that of the fibrous dosage forms.(g) Drug concentration in blood and bioavailability of particulate dosage forms.
Not surprisingly, therefore, after administering an immediate-release capsule filled with 200 mg crystalline nilotinib particles the maximum drug concentration was just 0.68 µg ml−1 by 2.5 hours. The bioavailability was only 2.96 μg h ml−1.It may be concluded, therefore, that due to the longer gastric residence time and supersaturation of the gastric fluid, the solid-solution fibrous dosage forms enhance the bioavailability of sparingly-soluble drugs. In the present work, the bioavailabiliy was enhanced by a factor of three.
Author contributions
Aron H. Blaesi: Development of dosage forms (conceptualization); production of dosage forms (resources); design and execution of in vitro experiments (methodology and investigation); design and assistance with in vivo experiments (methodology and investigation); data analysis (formal analysis); development of theory (methodology and investigation); writing (draft and editing). Henning Richter: Design and execution of in vivo experiments (methodology and investigation). Nannaji Saka: Data analysis (formal analysis); development of theory (methodology and investigation); writing (editing). All authors accepted the final manuscript for publication.Conflicts of interest
AHB owns shares of Enzian Pharmaceutics. AHB and NS have filed for patents related to the technology presented in this manuscript. HR declares no competing interests.Abbreviations
| A | Bioavailability (area under drug concentration-time curve in units μg h ml−1) |
| c b | Concentration of water at fiber–fluid interface |
| c d | Drug concentration |
| c d,0 | “Initial” drug concentration in expanded dosage form |
| c d,b | Drug concentration in blood or blood plasma |
| c d,gf | Drug concentration in gastric fluid |
| c max | Maximum drug concentration in blood |
| c s,gf | Drug solubility in gastric or dissolution fluid |
| D d,df | Diffusivity of drug through dosage form |
| D d,fl | Diffusivity of drug in dissolution fluid |
| D w | Diffusivity of water in fiber |
| H | Thickness of expanded dosage form |
| H 0 | Thickness of solid dosage form |
| i | Integer index |
| K p,t | Tissue-blood partition coefficient of drug |
| M d,0 | Mass of drug in dosage form |
| m d,r | Mass of drug released |
| m d,r/Md,0 | Fraction of drug released |
| dmd,r/dt | Drug release rate |
| n | Number of time points |
| n l | Number of stacked layers in dosage form |
| n p,0 | Number of drug particles in capsule |
| n p,gf | Number of drug particles in gastric fluid |
| Q gf | Flow rate of gastric fluid into the duodenum |
| q | Heat flow |
| R df | Radius of expanding/expanded dosage form |
| R df,0 | Radius of solid dosage form |
| R f,0 | Radius of solid fiber |
| T | Temperature |
| t | Time |
| t i | Time at index i |
| t max | Time to reach maximum drug concentration in blood |
| t r,f, tr,p | Gastric residence time of fibrous and particulate dosage forms |
| t 0.8 | Time to release 80 percent of drug content in a large-volume dissolution fluid |
| Δt | Time increment between integer indexes |
| V b | Volume of blood |
| V gf | Volume of gastric fluid |
| V t | Volume of organs and tissues |
| x, y, z | Cartesian coordinates |
| α | Dimensional constant |
| β | Dimensional constant |
| λ 0 | Inter-fiber distance in solid dosage form |
| ξ | Dimensionless constant |
| ρ w | Density of dissolution fluid (acidic water) |
| τ el, τgf | Time constants |
| φ f | Volume fraction of fibers in dosage form |
Data availability
The data that support the findings of this study are presented in the manuscript.Appendix
A: Preparation and properties of particulate dosage forms
In this appendix, the previous studies on immediate-release particulate dosage forms26,28 are reviewed and augmented by differential scanning calorigrams.Fig. 12 is a scanning electron micrograph of drug and excipient particles of the dosage form prior to mixing with the contrast agent.26,28 The average particle radius was about 18.5 μm.
 | ||
| Fig. 12 Scanning electron micrograph of drug and excipient particles of the previously presented particulate dosage form. The image is reused from ref. 26. | ||
Fig. 13 plots the specific heat flow, q, into the drug and excipient particles versus temperature. The heat flow exhibited narrow peaks at 147, 169, and 204 °C. Fig. 3b and prior work32 suggest that the peak at 204 °C represents phase transformation of nilotinib from crystalline to a melt. Thus, the drug particles in the particulate dosage forms were in crystalline form.
 | ||
| Fig. 14 Position and shape of a particulate dosage form administered to a fasted dog. The images were obtained by biplanar fluoroscopy. They show the abdomen in lateral projection (cranial left, caudal right). The images are reused from ref. 28. | ||
As detailed in prior work27,28 and Fig. 15, upon entering the stomach the particle-filled capsule disintegrates, and releases drug, excipient, and contrast agent particles into the gastric fluid. The drug particles then dissolve. But because the mass of drug in the dosage form per unit volume of gastric fluid, Md,0/Vgf ≫ cs,gf, the drug particles do not dissolve entirely, and are carried out of the stomach with the gastric fluid flow.
 | ||
| Fig. 15 Schematic of mass flow rates into and out of the stomach after administering particulate dosage forms: (a) t < tr,p and (b) t ≫ tr,p. Here tr,p is the residence time of drug particles in the stomach. The schematic is reproduced from ref. 27. | ||
Assuming that (a) the volumetric inflow and outflow rates of gastric fluid, Qgf, are the same and time-invariant, (b) the particles in the stomach are perfectly mixed with the gastric fluid, and (c) no drug particle will dissolve completely so that the number of drug particles is conserved, the time to reduce the number of particles to 37 percent of the initial value may be written as:27
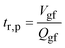 | (A1) |
In the fasted stomach of a dog, the gastric fluid volume, Vgf = 20 ml, and the volumetric flow rate of gastric fluid into and out of the stomach, Qgf = 14 ml h−1, Appendix B. Thus, by eqn (A1) the calculated “gastric residence time” of drug particles, tr,p = 1.43 h. This is about the same as the measured residence time of the (comparable) contrast agent particles, 1–1.5 h.
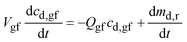 | (A2) |
From prior work, dmd,r/dt ∼ Md,0(cs,gf − cd,gf)/R5/3p,0 where Md,0 is the mass of drug in the dosage form, cs,gf the drug solubility in the gastric fluid, and Rp,0 the radius of the drug particles. Because the particles are small and the mass of drug in the dosage form per unit volume of gastric fluid, Md,0/Vgf ≫ cs,gf, cd,gf reaches cs,gf rapidly.
Further assuming that the drug particles remain in the stomach up to t = tr,p, and then are flushed out immediately,27 the drug concentration in gastric fluid may be written as:
(a) 0 ≤ t ≤ tr,p. Up to t = tr,p,27
| cd,gf = cs,gf | (A3) |
(b) t > tr,p. After the “residence time” of the drug particles, analogous to eqn (16),27
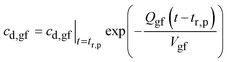 | (A4) |
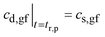 , eqn (A3).
, eqn (A3).
Fig. 16a plots eqn (A3) and (A4) for the relevant parameters. Up to the “residence time” of the drug particles the concentration of drug molecules in the gastric fluid is at solubility. After the “residence time” the concentration drops exponentially at the time constant, τgf = Vgf/Qgf = 1.43 h.
 | ||
| Fig. 16 (a) Molecular concentration of drug in the gastric fluid, cd,gf, versus time after administering a particulate dosage form. The drug concentration is calculated by eqn (A3) and (A4) using the parameter values of Appendix B. The graph is reproduced from ref. 27. (b) Measured and calculated drug concentrations in blood versus time after administering particulate dosage forms. The measured values represent the average drug concentration in blood plasma of four particulate dosage forms. The calculated values are drug concentrations in blood from eqn (A5) and (A6) using the parameter values of Appendix B. The graph is reproduced from ref. 28. | ||
In prior work, under the highly approximate assumptions that (a) all drug molecules that are released into the stomach pass into the duodenum and are absorbed by the blood stream, (b) drug distribution through the blood and tissues is fast, and (c) the drug is eliminated from the blood at a rate proportional to the drug concentration in blood, the following equations were derived for the drug concentration blood.27
(a) 0 ≤ t ≤ tr,p. Up to tr,p, for cd,b = 0 at t = 0,27
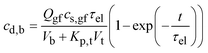 | (A5) |
Eqn (A5) is also plotted in Fig. 16b for the relevant parameter values listed in Appendix B (Qgf = 14 ml h−1, cs,gf = 1 mg ml−1, τel = 1.96 h, Vb = 1.1 l, Kp,t = 2.08, and Vt = 12.8 l). The agreement between data and model is fairly good.
(b) t > tr,p. After the “residence time” of the particles,27
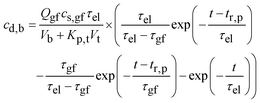 | (A6) |
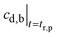 may be obtained from eqn (A5).
may be obtained from eqn (A5).
Fig. 16b further plots eqn (A6) for Qgf = 14 ml h−1, cs,gf = 1 mg ml−1, τel = 1.96 h, Vb = 1.1 l, Kp,t = 2.08, Vt = 12.8 l, and τgf = tr,p = 1.43 h. Because τel > τgf, the drug concentration in blood drops exponentially at the time constant, τel = 1.96 h. Again, the model and data agree.
B: Parameters and properties
| Symbol | Description | Value | Ref. |
|---|---|---|---|
| a Assumed to be the same as the density of water, ρw. b Assumed to be the same as the diffusivity of drug in the dissolution fluid. In ref. 25 the diffusivity of drug molecules in the dissolution fluid (acidic water), Dd,fl, was estimated by an adapted form of the Stokes–Einstein equation: Dd,fl = kbT/6πrdμfl, where kb is Boltzmann's constant, T the temperature, rd the radius of a drug molecule, and μfl the viscosity of the dissolution fluid. The radius of a drug molecule was approximated as rd = (3Mw,d/4πNAρd)1/3 where Mw,d is the molecular weight of the drug, NA Avogadro's number, and ρd the density of the solid drug. For the parameters of this work, Mw,d = 0.53 kg mol−1, ρd = 1360 kg m−3, T = 310 K, and μfl = 0.001 Pa s, the diffusivity, Dd,fl = 4.22 × 10−10 m2 s−1. c In agreement with the results shown in Fig. 5, the dimensions of the expanded dosage form are about 1.5 times the dimensions of the solid dosage form. Thus, H = 1.5 × H0, where H0 = 6.5 mm. d From prior work,28 reasonable estimates of the volume of blood and tissue of beagle dogs of size and weight used in this study are 1.1 and 12.8 l, respectively. e From prior work,27,28 if the drug is eliminated in the liver by Fickian diffusion from the sinusoidal blood capillaries across the hepatic plates into the bile, τel = (Vb + Kp,tVt)ln(Ro/Ri)Qb,s/2πKp,hpDd,hpLsQb,l, where Ro is the outer radius of the annulus of hepatic plate surrounding a sinusoid, Ri the radius of a sinusoidal capillary, Qb,s the flow rate of blood through a sinusoid, Kp,hp the partition coefficient of drug between a sinusoidal capillary and hepatic plates, Dd,hp the drug diffusivity through hepatic plates, Ls the length of a sinusoid, and Qb,l the flow rate of blood through the portal vein into the liver. From prior work, Ro = 15 μm, Ri = 5 μm, Kp,hp = 2.08, Dd,hp = 5.24 × 10−12 m2 s−1, Ls = 275 μm, and Qb,l = 9 ml s−1. | |||
| c b | Concentration of water at fiber–fluid interface | 1000 kg m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
— |
| D d,df | Drug diffusivity through expanded dosage form | 4.22 × 10−10 m2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
25 |
| D w | Diffusivity of water or gastric fluid in fiber | 4.1 × 10−12 m2 s−1 | From section 3.3 |
| H | Thickness of expanded fibrous dosage form | 9.8 mmc | — |
| H 0 | Thickness of solid fibrous dosage form | 6.5 mm | From Table 1 |
| K p,t | Tissue-blood partition coefficient | 2.08 | 28 |
| M d,0 | Drug mass in solid dosage forms | 200 mg | — |
| Q gf | Flow of gastric fluid into the intestines | 14 ml h−1 | 28 |
| R f,0 | Radius of solid fibers | 149 µm | From Table 1 |
| Δt | Time increment between integer indexes in numerical calculations | 0.1 h | — |
| V b | Volume of blood | 1.1 ld | 28 |
| V gf | Volume of gastric fluid in fasted stomach | 20 ml | 28 |
| V t | Volume of organs and tissues | 12.8 ld | 28 |
| λ 0 | Inter-fiber spacing in solid fibrous dosage form | 601 μm | From Table 1 |
| ρ w | Density of water | 1000 kg m−3 | — |
| τ el | Time constant of the process by which drug is eliminated from the blood | 1.96 he | 28 |
| φ f | Volume fraction of fibers in solid fibrous dosage form | 0.57 | From Table 1 |
C: Data of drug concentration in blood plasma after administering the fibrous dosage forms to the dogs
| Experiment 1 (dog 1) | Experiment 2 (dog 2) | ||
|---|---|---|---|
| t (h) | c d,b (μg ml−1) | t (h) | c d,b (μg ml−1) |
| 0 | 0 | 0 | 0 |
| 0.5 | 0.05 | 0.5 | 0.05 |
| 1 | 0.086 | 1 | 0.168 |
| 1.5 | 0.419 | 1.5 | 0.618 |
| 2 | 1.241 | 2 | 0.934 |
| 2.5 | 1.699 | 2.5 | 1.26 |
| 3 | 2.09 | 3 | 1.296 |
| 4 | 2.242 | 4 | 1.406 |
| 4.5 | 2.227 | 4.5 | 1.147 |
| 5 | 2.034 | 5 | 1.037 |
| 6 | 1.782 | 6 | 0.612 |
| 6.5 | 1.346 | 6.5 | 0.567 |
| 7 | 1.302 | 7 | 0.452 |
| 7.5 | 0.984 | 7.5 | 0.38 |
| 8 | 0.945 | 8 | 0.317 |
| 8.5 | 0.86 | 8.5 | 0.269 |
| 9 | 0.705 | 9 | 0.168 |
| 9.5 | 0.671 | 9.5 | 0.154 |
| 10 | 0.612 | 10 | 0.111 |
| 10.5 | 0.616 | 10.5 | 0.081 |
| 11 | 0.521 | 11 | 0.057 |
| 11.5 | 0.448 | 11.5 | 0.05 |
| 12 | 0.423 | 12 | 0 |
| 13 | 0.3 | 13 | 0 |
| 14 | 0.257 | 14 | 0 |
| 15 | 0.199 | 15 | 0 |
| 16 | 0.174 | 16 | 0 |
| 17 | 0.128 | 17 | 0 |
| 18 | 0.095 | 18 | 0 |
Acknowledgements
Prof. Giovanni Terrasi, Mr Silvain Michel and Mr Cyrill Schmid of Empa Dübendorf, Switzerland, are acknowledged for providing access to the DSC testing facilities at Empa Dübendorf. Dr Thomas Echtermann and Dr Nadja Aeberhard of the Vetsuisse Faculty, University of Zurich, are acknowledged for assistance with in vivo studies. Mr Fabian Weber of Polarwind AG in Zurich, Switzerland, is acknowledged for photographing the dosage forms shown on the cover image. This project received financial support from Enzian Pharmaceutics and the innovation agency of the government of Switzerland (Innosuisse).References
- G. L. Amidon, H. Lennernäs, V. P. Shah and J. R. Crison, A theoretical basis for a biopharmaceutic drug classification: The correlation of in vitro drug product dissolution and in vivo bioavailability, Pharm. Res., 1995, 12, 413–420 CrossRef CAS.
- C. A. Lipinski, Drug-like properties and the causes of poor solubility and poor permeability, J. Pharmacol. Toxicol. Methods, 2000, 44, 235–249 CrossRef CAS.
- I. L. O. Buxton and L. Z. Benet, in Goodman & Gilman's the pharmacological basis of therapeutics, ed. L. L. Brunton, B. Chabner and B. C. Knollmann, McGraw Hill, New York, NY, 12th edn, 2011, ch. 2, pp. 17–39 Search PubMed.
- N. R. Budha, A. Frymoyer, G. S. Smelick, J. Y. Jin, M. R. Yago, M. J. Dresser, S. N. Holden, L. Z. Benet and J. A. Ware, Drug Absorption Interactions Between Oral Targeted Anticancer Agents and PPIs: Is pH-Dependent Solubility the Achilles Heel of Targeted Therapy?, Clin. Pharmacol. Ther., 2012, 92, 203–213 CrossRef CAS PubMed.
- M. Ashford, in Aulton's Pharmaceutics: The design and manufacture of medicines, ed. M. E. Aulton and K. M. G. Taylor, Elsevier, London, UK, 5th edn, 2018, Part 4, ch. 20, pp. 319–338 Search PubMed.
- J. Siepmann and F. Siepmann, Mathematical modeling of drug dissolution, Int. J. Pharm., 2013, 453, 12–24 CrossRef CAS.
- S. Yassin, D. J. Goodwin, A. Anderson, J. Sibik, D. I. Wilson, L. F. Gladden and J. A. Zeitler, The disintegration process in microcrystalline cellulose based tablets, part 1: influence of temperature, porosity and superdisintegrants, J. Pharm. Sci., 2015, 104, 3440–3450 CrossRef CAS PubMed.
- A. T. M. Serajuddin, Salt formation to improve drug solubility, Adv. Drug Delivery Rev., 2007, 59, 603–616 CrossRef CAS PubMed.
- S. Sarkar, A. P. Roy, S. Mitra, G. Nandi, R. Sahu, T. K. Dua and P. Paul, Preparation and characterization of efavirenz cocrystal-encapsulated pronanoliposomes for antiretroviral therapy with improved bioavailability, RSC Pharm., 2025, 2, 342–352 RSC.
- B. C. Hancock and G. Zografi, Characteristics and significance of the amorphous state in pharmaceutical systems, J. Pharm. Sci., 1997, 86, 1–12 Search PubMed.
- B. C. Hancock and M. Parks, What is the true solubility advantage for amorphous pharmaceuticals?, Pharm. Res., 2000, 17, 397–404 Search PubMed.
- B. C. Hancock, Disordered drug delivery: destiny, dynamics and the Deborah number, J. Pharm. Pharmacol., 2002, 54, 737–746 CrossRef CAS PubMed.
- M. Pudipeddi and A. T. M. Serajuddin, Trends in solubility of polymorphs, J. Pharm. Sci., 2005, 94, 929–939 Search PubMed.
- A. Parkes, E. Spoletti, J. O'Reilly, M. Lusi, A. Ziaee and E. O'Reilly, Controlled isolation of a novel polymorphic form of chlorothiazide by spray drying, RSC Pharm., 2025, 2, 398–412 Search PubMed.
- W. L. Ciou and S. Riegelman, Pharmaceutical applications of solid dispersion systems, J. Pharm. Sci., 1971, 60, 1281–1302 Search PubMed.
- A. T. M. Serajuddin, Solid dispersion of poorly water-soluble drugs: early promises, subsequent problems, and recent breakthroughs, J. Pharm. Sci., 1999, 88, 1058–1066 CrossRef CAS.
- H. Joshi, R. Tejwani, M. Davidovich, V. P. Sahasrabudhe, M. Jemal, M. S. Bathala, S. A. Varia and A. T. M. Serajuddin, Bioavailability enhancement of a poorly water-soluble drug by solid dispersion in polyethylene glycol-polysorbate 80 mixture, Int. J. Pharm., 2004, 269, 251–258 CrossRef CAS PubMed.
- D. E. Alonzo, G. G. Z. Zhang, D. Zhou, Y. Gao and L. S. Taylor, Understanding the behavior of amorphous pharmaceutical systems during dissolution, Pharm. Res., 2010, 27, 608–618 CrossRef CAS.
- G. A. Ilevbare, H. Liu, K. J. Edgar and L. S. Taylor, Understanding polymer properties important for crystal growth inhibition-impact of chemically diverse polymers on solution crystal growth of ritonavir, Cryst. Growth Des., 2012, 12, 3133–3143 Search PubMed.
- B. R. de Alvarenga Jr. and L. S. Taylor, Release performance and crystallization of racemic and enantiopure praziquantel amorphous solid dispersion in various media, RSC Pharm., 2025, 2, 1125–1138 RSC.
- A. H. Blaesi and N. Saka, Expandable fibrous dosage forms for prolonged drug delivery, Mater. Sci. Eng., C, 2021, 120, 110144 Search PubMed.
- A. H. Blaesi and N. Saka, Expandable, dual-excipient fibrous dosage forms for prolonged delivery of sparingly soluble drugs, Int. J. Pharm., 2022, 615, 120396 Search PubMed.
- A. H. Blaesi, D. Kümmerlen, H. Richter and N. Saka, Mechanical strength and gastric residence time of expandable fibrous dosage forms, Int. J. Pharm., 2022, 613, 120792 Search PubMed.
- A. H. Blaesi, T. Echtermann, H. Richter and N. Saka, The effect of a semi-permeable, strengthening fiber coating on the expansion, mechanical properties, and residence time of gastroretentive fibrous dosage forms, Int. J. Pharm., 2023, 642, 122378 Search PubMed.
- A. H. Blaesi and N. Saka, Gastroretentive fibrous dosage forms for prolonged delivery of sparingly-soluble tyrosine kinase inhibitors. Part 1: Dosage form design, and theoretical models of expansion, mechanical strength, and drug release, Int. J. Pharm., 2025, 674, 124360 Search PubMed.
- A. H. Blaesi and N. Saka, Gastroretentive fibrous dosage forms for prolonged delivery of sparingly-soluble tyrosine kinase inhibitors. Part 2: Experimental validation of the models of expansion, mechanical strength, and drug release, Int. J. Pharm., 2025, 674, 124361 CrossRef CAS PubMed.
- A. H. Blaesi and N. Saka, Gastroretentive fibrous dosage forms for prolonged delivery of sparingly-soluble tyrosine kinase inhibitors. Part 3: Theoretical models of drug concentration in blood, Int. J. Pharm., 2025, 674, 124362 CrossRef CAS PubMed.
- A. H. Blaesi, H. Richter and N. Saka, Gastroretentive fibrous dosage forms for prolonged delivery of sparingly-soluble tyrosine kinase inhibitors. Part 4: Experimental validation of the models of drug concentration in blood, Int. J. Pharm., 2025, 674, 124363 CrossRef CAS.
- A. H. Blaesi and N. Saka, 3D-micro-patterned fibrous dosage forms for immediate drug release, Mater. Sci. Eng., C, 2018, 84, 218–229 CrossRef CAS.
- A. H. Blaesi and N. Saka, Fibrous dosage forms by wet 3D-micro-patterning: Process design, manufacture, and drug release rate, Eur. J. Pharm. Biopharm., 2018, 130, 345–358 Search PubMed.
- J. Crank, The Mathematics of Diffusion, Oxford University Press, Oxford, UK, 2nd edn, 1975, pp. 47–49 Search PubMed.
- M. Herbrink, H. Vromans, J. Schellens, J. Beijnen and B. Nuijen, Thermal stability study of crystalline and novel spray-dried amorphous nilotinib hydrochloride, J. Pharm. Biomed. Anal., 2018, 148, 182–188 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |