Engineering high-capacity hydrogen storage in pristine Ca₁₂O₁₂ nanocages via cooperative adsorption

Abstract

A comprehensive in silico investigation of pristine Ca₁₂O₁₂ nanocages as potential hydrogen storage materials is presented. Our study focuses on assessing the structural, electronic, and adsorption properties of Ca₁₂O₁₂ relative to its Be₁₂O₁₂ and Mg₁₂O₁₂ analogs. The larger internal cavity, resulting from increased interatomic distances in Ca₁₂O₁₂, not only supports stable endohedral adsorption—a capability not observed in Be₁₂O₁₂ or Mg₁₂O₁₂—but also facilitates a greater number of exohedral H₂ adsorption events compared to the more compact nanocages. Notably, our results reveal a clear preference for end-on coordination in Ca₁₂O₁₂, in contrast to the side-on adsorption observed for the smaller cages. Although the overall adsorption process remains exothermic across a broad range of hydrogen loadings, the most favorable cooperative effects occur at moderate coverages, with the lowest normalized adsorption enthalpy observed at 13H₂ molecules and favorable interactions maintained up to 32. Additionally, mixed adsorption configurations incorporating one endohedral H₂ alongside multiple exohedral H₂ molecules yield a maximum hydrogen uptake of 9.24 wt%, exceeding the U.S. DOE target of 5.5 wt%. These findings highlight the potential of pristine Ca₁₂O₁₂ nanocages as effective hydrogen storage media and offer strategic guidance for the development of high-performance storage systems.

---

1 Introduction

The rapid and continuous growth of the global population, coupled with ongoing deforestation and heavy reliance on fossil fuels, has intensified environmental concerns and raised fears of future energy shortages. To mitigate these challenges, considerable efforts from diverse research groups worldwide have been directed toward developing alternative energy sources that are both sustainable and eco-friendly. Among these, hydrogen gas has emerged as a promising, safe, and versatile energy carrier that can be efficiently converted into usable power without generating harmful emissions. Its combustion yields only water as a byproduct, positioning it as an environmentally sustainable alternative for addressing global energy demands.^1–5

Despite its promise, the primary obstacle in hydrogen technology remains the development of compact, safe, and cost-effective storage systems. An ideal hydrogen storage material should achieve high gravimetric and volumetric densities under ambient conditions.⁶ Solid-state hydrogen storage has emerged as a compelling strategy in this regard, as it enables storage in molecular or atomic forms while ensuring fast kinetics and enhanced safety.^7–9 However, weak physisorption interactions typically lead to desorption at low temperatures, and chemisorption can sometimes be too strong or irreversible, highlighting the need for adsorption energies in the intermediate range of 0.01–0.5 eV per hydrogen atom.¹⁰ Progress has been made through research on various nanomaterials,^11–17 but from a practical standpoint, no single medium has yet met the U.S. Department of Energy (DOE)'s 2025 target of 5.5 wt%.¹⁸

The discovery of buckminsterfullerene C₆₀ in 1985¹⁹ catalyzed an intensive exploration of fullerene-like architectures, encompassing both homoatomic (A_n) and heteroatomic, binary (AB)_n nanocages. These hollow clusters offer unique potential as molecular containers, a feature extensively studied for fullerenes.^20–27 Beyond carbon-based systems, homoatomic nanocages such as those formed by gold (Au_n) and boron (B_n) have sparked significant interest, particularly for their encapsulation capabilities.^28–31 For instance, Au_n nanocages have demonstrated applications in catalysis and photochemistry,³⁰ as well as in biological fields including sensing, imaging, diagnosis, and treatment.^32–34 Similarly, B_n nanocages are attractive for biomedical imaging,³⁵ anti-cancer drug delivery,³⁶ and sensing applications.³⁷ Notable milestones include the first all-boron fullerene (B₄₀⁻) reported by Wang and co-workers³⁸ and the recent discovery of the fullerene-like 80-atom boron cluster (B₈₀⁻), whose electronic structure and bonding closely resemble C₆₀.³⁹

While homoatomic nanocages have been extensively studied, heteroatomic nanocages, particularly those composed of main group elements, have emerged as a focal point for research due to their chemical diversity and potential applications. Examples include systems such as CSi,^40,41 BN,^40,42–47 BP,^46–48 AlN,^{40,46,47,49,50} AlP,^40,46,47 BeO,^{10,40,51–54} MgO,^40,50,51,55 CaO,^{50,54,56–58} ZnO,^56,59 and LiF.^60,61 Particular attention has been devoted to (AB)₁₂ nanocages, as sodalite-type structures featuring this stoichiometry are recognized for their exceptional stability,⁴² even though they are not always the global minimum.^62,63 This inherent stability has spurred extensive analysis of (AB)₁₂ nanocages as potential materials for diverse applications, including hydrogen storage.

Among the sodalite-type nanocages, a notable example is Ca₁₂O₁₂, which has a radius (3.55 Å) comparable to that of C₆₀.⁵⁶ This structural similarity enables Ca₁₂O₁₂ to encapsulate small molecules and toxic gases, such as phosgene (Cl₂CO), H₂S, CO₂, SO₂, and NO₂,^50,57,64 highlighting its potential as a nanosensor or molecular trap. Furthermore, its applicability as a nanocarrier for drug delivery has been demonstrated with compounds like 5-fluorouracil and thymine derivatives,^54,65 and adsorption studies have further emphasized its capability for storing molecules such as sulforaphane.⁶⁶ In the context of hydrogen storage, Louis and co-workers computationally investigated pristine and transition-metal-decorated Ca₁₂O₁₂ (M−Ca₁₂O₁₂), reporting the favorable adsorption of up to ten H₂ molecules.⁵⁸ Their analysis, however, was limited to low-coverage adsorption and did not explore cooperative effects, multi-molecule occupation of individual sites, or the interplay between exohedral and endohedral adsorption modes—factors that can critically influence hydrogen uptake.

Herein, we extend that investigation by examining pristine Ca₁₂O₁₂ for both endohedral and exohedral hydrogen adsorption, considering a broader range of adsorption scenarios. In addition, we present a comparative analysis with Be₁₂O₁₂ and Mg₁₂O₁₂ to assess how cage size and metal character affect hydrogen accommodation. This study employs dispersion-corrected and range-separated density functional theory (DFT), together with complementary wave-function-based benchmarks, to evaluate the structural, energetic, and electronic features that govern hydrogen adsorption on these nanocages. Our findings refine the understanding of Ca₁₂O₁₂ as a hydrogen host and contribute to the broader search for high-performance materials for reversible hydrogen storage.

2 Computational details

Full geometry optimizations were carried out using dispersion-corrected DFT with the Gaussian 16, Revision C.01 software package.⁶⁷ The B3LYP hybrid functional,^68–71 combined with Grimme's zero-damping D3 dispersion correction⁷² (with the default Axilrod–Teller–Muto three-body dispersion term) and the 6-31G(d,p) basis set, was employed. This combination was chosen based on preliminary benchmark results, which demonstrated comparable structural accuracy to the range-separated ωB97X-D functional⁷³ but with significantly lower computational costs. To obtain more reliable electronic energies, we performed single-point calculations on the optimized geometries using a range of DFT functionals, including B3LYP-D3, BP86-D3,^74,75 M06-D3,⁷⁶ PBE0-D3,^77,78 and ωB97X-D, all with the 6-311++G(d,p) basis set. These values were benchmarked against high-level DLPNO-CCSD(T)/6-311++G(d,p) calculations⁷⁹ performed with Orca 5.0.3,⁸⁰ employing the NormalPNO threshold settings. Among the functionals tested, ωB97X-D provided the closest agreement with the DLPNO-CCSD(T) reference. Indeed, previous studies on hydrogen storage materials have also highlighted the superior performance of ωB97X-D for accurately capturing long-range noncovalent interactions.^81,82 Based on these findings, we have adopted the ωB97X-D/6-311++G(d,p)//B3LYP-D3/6-31G(d,p) level of theory for all subsequent calculations in this work. More details about the benchmark calculations done can be found in Section S1 of the SI.

Harmonic vibrational frequency calculations were conducted on all optimized geometries to confirm their characterization as local minima on the potential energy surface and to compute thermochemical corrections. Key features of the electronic structure were elucidated through the analysis of frontier molecular orbitals (FMOs). Additionally, adsorption energy (ΔE_ads), adsorption enthalpy (ΔH_ads), and HOMO–LUMO energy gap (E_g) calculations were performed to evaluate the thermodynamic and electronic properties associated with hydrogen adsorption.

The adsorption energy (ΔE_ads) for the adsorption of n hydrogen molecules on the Ca₁₂O₁₂ nanocage was calculated as:

ΔE_ads[n] = E[Ca₁₂O₁₂·nH₂] − {E[Ca₁₂O₁₂] + n × E[H₂]} (1)

where E[Ca₁₂O₁₂·nH₂] is the total energy of the nanocage with n adsorbed H₂ molecules, E[Ca₁₂O₁₂] is the energy of the pristine nanocage, and E[H₂] is the energy of an isolated H₂ molecule. Each energy value includes its corresponding zero-point energy (ZPE) correction. A more negative ΔE_ads value indicates stronger binding and greater stability of the interacting complex.

The adsorption enthalpy (ΔH_ads) was calculated using:

ΔH_ads[n] = H[Ca₁₂O₁₂·nH₂] − {H[Ca₁₂O₁₂] + n × H[H₂]} (2)

where each H term includes the electronic energy, ZPE correction, and thermal correction to enthalpy, herein obtained at 298 K. A negative ΔH_ads value denotes an exothermic and enthalpically favorable adsorption process.

To evaluate the enthalpic cooperativity in the adsorption of multiple hydrogen molecules, we define a normalized adsorption enthalpy:

ΔH^norm_ads[n] = ΔH_ads[n] − nΔH_ads[1] (3)

This expression compares the total enthalpy change upon adsorbing nH₂ molecules, ΔH_ads[n], to the sum of n single-molecule adsorption enthalpies, nΔH_ads[1]. Here, ΔH_ads[1] refers to the adsorption enthalpy for the most favorable exohedral adsorption mode of H₂ on Ca₁₂O₁₂ (mode O), as described later. If ΔH^norm_ads[n] is negative, adsorbing n molecules is more exothermic than simply adding up the enthalpies for n separate single-molecule adsorptions, indicating a favorable cooperative effect. Conversely, a positive ΔH^norm_ads[n] implies that the multi-molecule adsorption is less exothermic than expected from single adsorptions alone, suggesting reduced favorability or an antagonistic effect. In this way, the quantity is used to assess whether the adsorption of additional hydrogen molecules becomes more or less enthalpically advantageous as coverage increases.

The energy gap (E_g) was calculated as the energy difference between the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO), determined at the ωB97X-D/6-311++G(d,p)//B3LYP-D3/6-31G(d,p) level of theory:

The weight percentage (wt%) of hydrogen adsorption was calculated using the following expression:

where n is the number of adsorbed H₂ molecules, M_H2 is the molar mass of a hydrogen molecule, and M_nanocage is the molar mass of the Ca₁₂O₁₂ nanocage. This formula provides a quantitative measure of the hydrogen content relative to the total mass of the loaded system, allowing for direct comparison with established gravimetric hydrogen storage targets.

Building upon the adsorption energy, enthalpy, and electronic gap evaluations detailed above, it is essential to acknowledge that the focus on enthalpic and electronic properties represents only one facet of the overall thermodynamic behavior of hydrogen adsorption. Recent findings by Wang and Chen⁸³ highlight that low-frequency vibrational modes can yield significant entropy contributions during hydrogen adsorption, potentially compensating for relatively modest enthalpy values. While these observations emphasize the importance of anharmonic vibrational effects for accurate free-energy estimates, many computational studies (including the present one) primarily concentrate on adsorption enthalpies. This focus is largely due to the increased complexity and computational cost associated with capturing entropic contributions beyond the harmonic approximation. Moreover, when screening a wide array of potential materials, harmonic-based enthalpy calculations are often sufficient to identify promising candidates. Therefore, although a complete thermodynamic analysis (i.e., obtaining ΔG_ads) would involve evaluating both ΔH_ads and ΔS_ads at an anharmonic level, our study is limited to the enthalpy term in line with standard practices for initial screening.

3 Results and discussion

3.1 Structural, electronic, and adsorptive properties of pristine M₁₂O₁₂ (M = Be, Mg, Ca) nanocages

Fig. 1a displays the optimized structures of the M₁₂O₁₂ nanocages (Be₁₂O₁₂, Mg₁₂O₁₂, and Ca₁₂O₁₂). Although these clusters have been examined previously (vide supra), a systematic comparison at a uniform computational level enables a rigorous evaluation of their relative stabilities, electronic properties, and potential as hydrogen-storage hosts. This subsection outlines the key structural and electronic characteristics of the nanocages, with a focus on the attributes that render Ca₁₂O₁₂ especially suitable for H₂ adsorption. Comprehensive electronic structure and thermochemical data are summarized in Table 1.

Fig. 1 (a) Optimized structures of the M₁₂O₁₂ (M = Be, Mg, and Ca) nanocages obtained at the B3LYP-D3/6-31G(d,p) level. The distance labels d_hh and d_hs denote the bond lengths between hexagonal–hexagonal and hexagonal–square faces, respectively. (b) Frontier molecular orbitals (FMOs) of the pristine M₁₂O₁₂ nanocages, calculated from ωB97X-D/6-311++G(d,p) single-point calculations at geometries optimized at the B3LYP-D3/6-31G(d,p) level of theory. The boxed numbers indicate the corresponding E_g values. (c) Distinct adsorption patterns for a single H₂ molecule on the M₁₂O₁₂ systems; the annotated numerical values represent the adsorption energies (ΔE_ads) and adsorption enthalpies (ΔH_ads), with the latter provided in square brackets. Energies are obtained at the ωB97X-D/6-311++G(d,p)//B3LYP-D3/6-31G(d,p) level of theory. For cluster labels, see the text.

Table 1 Summary of the key structural and energetic properties of the primary systems investigated. n: total number of H₂ molecules; ΔE_ads: adsorption energy (kJ mol⁻¹); ΔH_ads: adsorption enthalpy (kJ mol⁻¹); ΔH^norm_ads: normalized adsorption enthalpy (kJ mol⁻¹); wt%: hydrogen weight percentage. See the ESI for a full version of this table. Energies are obtained at the ωB97X-D/6-311++G(d,p)//B3LYP-D3/6-31G(d,p) level of theory. For cluster labels, see the text

Structure	n	ΔEads (ΔHads)	ΔH^normads	wt%
Be12O12	0	—	—	0.00
Mg12O12	0	—	—	0.00
Ca12O12	0	—	—	0.00
Be12O12·H2	1	−4.4 (−5.3)	—	0.67
Mg12O12·H2 (M)	1	−6.8 (−7.3)	—	0.42
Mg12O12·H2 (O)	1	−1.5 (−3.6)	—	0.42
Ca12O12·H2 (M)	1	−0.9 (−0.5)	—	0.30
Ca12O12·H2 (O)	1	−1.8 (−4.3)	0.0	0.30
(H2@Ca12O12)	1	−9.0 (−9.2)	−4.8	0.30
Ca12O12·2H2	2	−4.1 (−9.9)	−1.3	0.60
(2H2@Ca12O12)	2	57.3 (49.2)	57.8	0.60
Ca12O12·3H2	3	−6.5 (−14.9)	−1.9	0.89
Ca12O12·4H2	4	−9.0 (−20.5)	−3.2	1.18
Ca12O12·5H2	5	−10.9 (−25.3)	−3.7	1.48
Ca12O12·6H2	6	−13.9 (−31.2)	−5.3	1.77
Ca12O12·7H2	7	−16.2 (−36.5)	−6.2	2.05
Ca12O12·8H2	8	−19.5 (−42.7)	−8.2	2.34
Ca12O12·9H2	9	−21.8 (−47.8)	−8.9	2.63
Ca12O12·10H2	10	−25.5 (−54.8)	−11.6	2.91
Ca12O12·11H2	11	−26.9 (−59.3)	−11.7	3.19
Ca12O12·12H2	12	−29.2 (−64.9)	−13.0	3.47
(H2@Ca12O12)·12H2	13	−40.0 (−75.8)	−19.6	3.75
Ca12O12·13H2	13	−30.9 (−69.3)	−13.1	3.75
(H2@Ca12O12)·13H2	14	−40.8 (−83.4)	−22.9	4.03
Ca12O12·14H2	14	−32.4 (−73.3)	−12.7	4.03
Ca12O12·15H2	15	−33.9 (−77.7)	−12.8	4.30
Ca12O12·16H2	16	−33.9 (−80.5)	−11.4	4.57
Ca12O12·17H2	17	−34.7 (−84.3)	−10.8	4.85
Ca12O12·18H2	18	−35.9 (−87.7)	−9.9	5.12
Ca12O12·19H2	19	−36.6 (−91.3)	−9.2	5.39
Ca12O12·20H2	20	−35.8 (−94.5)	−8.0	5.65
Ca12O12·21H2	21	−36.7 (−98.2)	−7.4	5.92
Ca12O12·22H2	22	−37.9 (−102.1)	−7.0	6.18
Ca12O12·23H2	23	−37.4 (−104.8)	−5.4	6.45
Ca12O12·24H2	24	−41.8 (−110.6)	−6.9	6.71
(H2@Ca12O12)·24H2	25	−50.6 (−120.3)	−12.2	6.97
Ca12O12·25H2	25	−42.7 (−113.5)	−5.4	6.97
Ca12O12·26H2	26	−43.7 (−115.6)	−3.2	7.23
Ca12O12·27H2	27	−44.6 (−123.4)	−6.7	7.48
Ca12O12·28H2	28	−45.8 (−126.4)	−5.4	7.74
Ca12O12·29H2	29	−42.3 (−126.7)	−1.3	7.99
Ca12O12·30H2	30	−47.7 (−133.6)	−3.9	8.25
Ca12O12·31H2	31	−47.0 (−131.6)	2.4	8.50
Ca12O12·32H2	32	−52.9 (−140.7)	−2.3	8.75
(H2@Ca12O12)·32H2	33	−60.7 (−144.0)	−1.4	9.00
Ca12O12·33H2	33	−44.7 (−138.8)	3.8	9.00
(H2@Ca12O12)·33H2	34	−53.5 (−148.7)	−1.7	9.24
Ca12O12·34H2	34	−51.2 (−140.1)	6.9	9.24
(H2@Ca12O12)·34H2	35	−51.1 (−150.9)	0.4	9.49
Ca12O12·35H2	35	−51.6 (−146.7)	4.6	9.49

---

Each M₁₂O₁₂ nanocage adopts a framework reminiscent of a sodalite unit, featuring eight 6-membered rings and six 4-membered rings arranged in a near-spherical geometry with T_h symmetry. Inspection of Fig. 1a reveals two distinct types of M–O bonds: d_hh, connecting two hexagonal faces, and d_hs, bridging a hexagonal and a square face. The d_hh bond length in Be₁₂O₁₂ is approximately 1.521 Å, increasing to 1.891 Å in Mg₁₂O₁₂ and reaching 2.220 Å in Ca₁₂O₁₂. A similar upward trend is observed for the d_hs bond, which measures 1.579 Å in Be₁₂O₁₂, 1.946 Å in Mg₁₂O₁₂, and 2.264 Å in Ca₁₂O₁₂.

These increases in bond lengths reflect the larger ionic radii of the heavier Group 2 metals relative to beryllium, consistent with periodic trends. The corresponding expansion of the cage volume indicates that the internal cavity of Ca₁₂O₁₂ is substantially more spacious, a feature that not only benefits endohedral adsorption but also enhances the adsorption characteristics of exohedral H₂ molecules. In the larger Ca₁₂O₁₂ framework, the cluster atoms are positioned further apart, which leads to greater separation between adjacent exohedral adsorption sites and, consequently, reduced repulsive interactions among adsorbed H₂ molecules. In addition, the difference between d_hh and d_hs highlights variations in the local bonding environments, which may influence site-specific adsorption geometries. Overall, the structural analysis confirms that Be₁₂O₁₂ possesses the most compact framework, while Ca₁₂O₁₂ exhibits the most open structure.

Fig. 1b presents the frontier molecular orbitals (FMOs) of the pristine nanocages, and Table 1 provides the numerical values of the HOMO–LUMO gaps (E_g). In particular, Be₁₂O₁₂ exhibits the largest gap (11.32 eV), indicative of a highly insulating character. In contrast, Mg₁₂O₁₂ has a gap of 8.71 eV, and Ca₁₂O₁₂ the smallest at 7.48 eV. A narrower gap is generally associated with increased polarizability and, in some instances, enhanced chemical reactivity—factors that are significant for molecular adsorption and charge-transfer processes.

Further examination of the LUMOs in the M₁₂O₁₂ nanocages shows that they are predominantly localized within the interior of the cages. This observation suggests that these clusters can serve as internal electron reservoirs, analogous to perfluorinated fullerenes known for endohedral electron trapping.⁸⁴ Such an orbital configuration may also facilitate the stabilization of small molecules inside the cage. Among the systems examined, Ca₁₂O₁₂ is particularly notable due to its narrower E_g value and larger interior volume, attributes that could promote effective H₂ adsorption. Although calcium is heavier than beryllium or magnesium, its enhanced capacity to accommodate multiple adsorbates may compensate for the increased mass, making Ca₁₂O₁₂ a promising scaffold for hydrogen storage applications.

A natural follow-up question is whether moving further down Group 2, to hypothetical Sr₁₂O₁₂ or Ba₁₂O₁₂ sodalite-type cages, would provide an additional benefit. While larger metals would be expected to further expand the cage cavity and ease steric crowding between neighboring exohedral adsorption sites, two considerations suggest that calcium already represents an effective balance. First, continued bond elongation in heavier alkaline earth oxides could compromise the mechanical rigidity of the M₁₂O₁₂ framework, whose stability is well established for calcium but remains uncertain for strontium- and barium-based analogs. Second, the much higher atomic mass of Sr and Ba would directly penalize the gravimetric hydrogen capacity, even if a comparable absolute number of H₂ molecules could in principle be accommodated. Taken together, these factors indicate that Ca₁₂O₁₂ offers a favorable compromise between cavity size, structural stability, and mass efficiency, whereas heavier congeners may deliver diminishing returns—an aspect that warrants future computational assessment.

Fig. 1c illustrates the adsorption preferences of a single H₂ molecule on the Be₁₂O₁₂, Mg₁₂O₁₂, and Ca₁₂O₁₂ nanocages. For Be₁₂O₁₂, only a single adsorption mode was found in which the H₂ molecule binds in a side-on configuration with a Be atom; the absence of any endohedral adsorption minima indicates that the small cavity is unsuitable for internal adsorption. In contrast, Mg₁₂O₁₂ exhibits two exohedral modes. In the more favorable configuration, denoted as Mg₁₂O₁₂·H₂ (M), the H₂ molecule adopts a side-on orientation similar to that of Be₁₂O₁₂, whereas a less stable mode, Mg₁₂O₁₂·H₂ (O), features an end-on coordination where one hydrogen atom interacts with an oxygen atom. This end-on configuration shows less negative adsorption energy and enthalpy values (−1.5 and −3.6 kJ mol⁻¹, respectively) compared to −6.8 and −7.3 kJ mol⁻¹ for the side-on mode. Notably, no stable endohedral adsorption was observed for Mg₁₂O₁₂.

For Ca₁₂O₁₂, three adsorption modes were identified: two exohedral modes analogous to those in Mg₁₂O₁₂ and an additional endohedral mode. Among these, the configuration corresponding to endohedral adsorption exhibits the most negative adsorption energy and enthalpy (−9.0 and −9.2 kJ mol⁻¹, respectively), followed by the exohedral end-on mode, Ca₁₂O₁₂·H₂ (O), with values of −1.8 and −4.3 kJ mol⁻¹. The exohedral side-on mode, Ca₁₂O₁₂·H₂ (M), shows the least favorable binding (−0.9 and −0.5 kJ mol⁻¹). These results indicate that the energetic preference for an end-on adsorption configuration increases from Be₁₂O₁₂ (where it is absent) to Mg₁₂O₁₂ (where it is less stable) and is most pronounced in Ca₁₂O₁₂. Consequently, the exohedral end-on mode in Ca₁₂O₁₂ is adopted as the reference state for the ΔH^norm_ads calculations discussed in subsequent sections.

An additional observation pertains to the impact of H₂ adsorption on the E_g values. As summarized in Table 1, the adsorption of a single H₂ molecule induces subtle but distinct changes in E_g across the different nanocages. For Be₁₂O₁₂, E_g decreases by 0.014 eV (from 11.319 to 11.305 eV) upon adsorption. In contrast, for Mg₁₂O₁₂ the gap increases by 0.013 eV in the side-on mode and by 0.026 eV in the end-on mode, while for Ca₁₂O₁₂ the increases are 0.001 eV for the side-on, 0.025 eV for the end-on, and 0.022 eV for the endohedral adsorption modes. These variations underscore the sensitivity of the electronic structure to the adsorption geometry and the nature of the metal center.

Finally, it is also important to highlight the limits of endohedral adsorption in Ca₁₂O₁₂. Although a single H₂ molecule can be favorably adsorbed within the cavity, the introduction of a second H₂ molecule results in a positive adsorption enthalpy of 49.2 kJ mol⁻¹. This unfavorable energy change clearly indicates that the accommodation of more than one H₂ molecule within the Ca₁₂O₁₂ cage is not energetically viable.

As discussed in subsequent sections, these structural and electronic distinctions result in Ca₁₂O₁₂ offering both endohedral and exohedral sites for H₂ adsorption. This balanced geometry suggests that multiple H₂ molecules can be accommodated simultaneously, potentially achieving the density targets necessary for practical fuel-cell applications.

3.2 Multiple H₂ adsorption on Ca₁₂O₁₂: exohedral adsorption

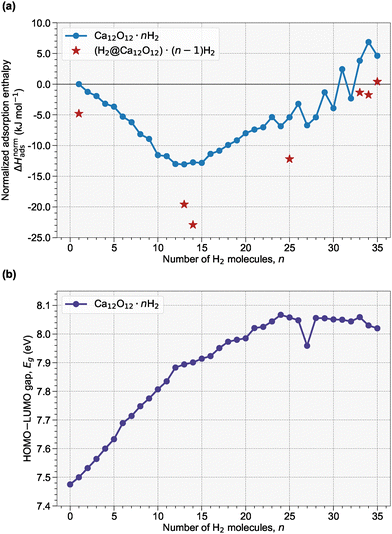
Next, we turn our attention to the multiple adsorption of H₂ molecules on the Ca₁₂O₁₂ nanocage, focusing exclusively on exohedral adsorption. The exohedral adsorption process was systematically investigated for configurations containing up to 48H₂ molecules. Key adsorption properties for the first 35 adsorption events are summarized in Table 1, with complete data for all 48 adsorptions provided in Table S2 of the SI.

As highlighted in Section 3.1, our preliminary single-molecule studies identified the oxygen sites as the most active centers for H₂ uptake. Each oxygen site can formally accommodate up to three H₂ molecules via favorable interactions—a capacity enabled by the larger cavity of the Ca₁₂O₁₂ nanocage, which is not observed in the analogous Be₁₂O₁₂ and Mg₁₂O₁₂ systems. In combination with one H₂ molecule adsorbed on each calcium site, the theoretical maximum capacity of the nanocage is 48H₂ molecules. To properly assess the cooperative effects during sequential adsorption, we evaluated both the overall adsorption enthalpy, ΔH_ads, and the normalized adsorption enthalpy, ΔH^norm_ads, defined as the deviation from the sum of n independent single-molecule adsorption events (see Section 2 for further details).

Our analysis reveals that ΔH_ads remains negative throughout the entire adsorption interval, confirming that the overall exohedral adsorption process is exothermic. However, the cooperative behavior, as captured by ΔH^norm_ads, exhibits more nuanced trends (see Fig. 2a). For exohedral adsorption, negative ΔH^norm_ads values are observed up to n = 32, indicating that each additional H₂ molecule is adsorbed more favorably than predicted by an independent adsorption model. The most pronounced cooperative effect is observed at n = 13, where ΔH^norm_ads = −13.1 kJ mol⁻¹ and the cumulative adsorption energy reaches −69.3 kJ mol⁻¹. For n = 31 and for all systems beyond n = 32, ΔH^norm_ads becomes positive, signaling that further H₂ adsorption is less exothermic than anticipated, likely due to increased steric hindrance and repulsive interactions among the adsorbed molecules.

Fig. 2 (a) Normalized adsorption enthalpy, ΔH^norm_ads, plotted as a function of the total number of H₂ molecules (n). Red star symbols denote systems containing one endohedral H₂ molecule. (b) Evolution of the HOMO–LUMO gap, E_g, as a function of n. All calculations were performed at the ωB97X-D/6-311++G(d,p)//B3LYP-D3/6-31G(d,p) level of theory.

In parallel, the E_g values (Fig. 2b) exhibit an increasing trend with successive H₂ adsorption, reflecting a gradual shift toward more insulating behavior. Notably, this increase in E_g plateaus after the adsorption of 24H₂ molecules, suggesting that the electronic structure of the nanocage reaches a saturation point with respect to further H₂ loading.

Furthermore, hydrogen uptake was quantified in terms of weight percentage (wt%). As shown in Table 1, all structures with n > 19H₂ molecules exceed the U.S. DOE's target of 5.5 wt%, with many of these configurations still featuring negative ΔH^norm_ads values. Collectively, these findings illustrate that while the Ca₁₂O₁₂ nanocage is theoretically predicted to be an effective host for exohedral H₂ adsorption—exhibiting favorable cooperative interactions at moderate loadings—the breakdown of cooperativity (as indicated by positive ΔH^norm_ads values) at higher coverages defines a distinct limit for additional adsorption. It is noteworthy that the per-molecule adsorption enthalpies at moderate coverages lie in the few-kJ mol⁻¹ range, which is generally regarded as favorable for reversible physisorption-based hydrogen storage: sufficiently attractive to retain H₂ on the scaffold, but not so strong as to require harsh conditions for desorption.

From an electronic perspective, the adsorbed H₂ molecules considered above remain intact, with H−H bond lengths close to that of free H₂ and no evidence of dissociative chemisorption, even at high coverage. The preferred end-on orientation at oxygen sites in Ca₁₂O₁₂ can be rationalized by attractive electrostatic and induction interactions between the partially negative O centers and the quadrupole of H₂, whereas side-on approaches to the metal sites are generally less stabilizing. In Ca₁₂O₁₂, the relatively narrow HOMO–LUMO gap and higher metal polarizability enhance these induced-dipole interactions. This behavior is consistent with the notion that heavier alkaline earth elements, including Ca, can access low-lying d-like acceptor character,⁸⁵ enabling stronger yet still non-dissociative interactions with H₂. These features help explain why Ca₁₂O₁₂ supports both high-density exohedral loading and distinct endohedral stabilization, outperforming Be₁₂O₁₂ and Mg₁₂O₁₂.

From an application standpoint, the magnitudes of the adsorption enthalpies reported here (on the order of a few kJ mol⁻¹ per H₂, and up to ∼10 kJ mol⁻¹ for the most favorable individual events) are consistent with weak, largely physisorptive binding rather than dissociative chemisorption. Such interaction strengths are generally considered attractive for reversible hydrogen storage, insofar as they are strong enough to stabilize molecular H₂ on the scaffold but not so strong as to make desorption prohibitively energy-intensive. We emphasize, however, that the present analysis is based on enthalpic trends at 298 K and does not explicitly include entropic contributions or kinetic barriers. As a result, assigning a precise working temperature or pressure window for hydrogen uptake and release lies beyond the scope of this study and will require future free-energy and finite-temperature simulations.

3.3 Multiple H₂ adsorption on Ca₁₂O₁₂: mixed exohedral-endohedral adsorption

In the previous section, we determined that systems with purely exohedral adsorption maintained favorable cooperative interactions, evidenced by negative ΔH^norm_ads values, up to 32H₂ molecules. However, as noted in Section 3.1, the Ca₁₂O₁₂ nanocage can also accommodate an additional H₂ molecule in an endohedral position, a feature that is absent in the Be₁₂O₁₂ and Mg₁₂O₁₂ cases. This observation motivated an investigation into how the adsorption energetics are affected when both exohedral and endohedral H₂ adsorption modes are combined.

The mixed adsorption configurations are denoted as (H₂@Ca₁₂O₁₂)·nH₂, with n representing the number of exohedrally adsorbed H₂ molecules. Specifically, we examined structures with 12, 13, 24, 32, 33, and 34 exohedral H₂ molecules, each accompanied by one endohedral H₂ (see Fig. 3 for their optimized structures). The results reveal that the highly negative adsorption energy associated with the first endohedral H₂ substantially enhances the overall adsorption process. In fact, this favorable endohedral contribution promotes the adsorption of additional exohedral H₂ molecules, leading to a maximum configuration with 33 exohedral and one endohedral H₂ (i.e., a total of 34H₂ molecules). This configuration exhibits an adsorption energy of −148.7 kJ mol⁻¹ and a normalized adsorption enthalpy of −1.7 kJ mol⁻¹, thereby favorably achieving a hydrogen uptake of 9.24 wt%.

Fig. 3 Three-dimensional representations of the optimized structures of Ca₁₂O₁₂ nanocages with one endohedral H₂ molecule and (n − 1) exohedral H₂ molecules adsorbed. These systems are denoted as (H₂@Ca₁₂O₁₂)·(n − 1)H₂, where n (the total number of H₂ molecules) is 13, 14, 25, 33, 34, or 35 (from top left to bottom right).

In turn, when a 34th exohedral H₂ molecule is added, yielding the system (H₂@Ca₁₂O₁₂)·34H₂ (total of 35H₂ molecules), the normalized adsorption enthalpy sharply increases to a positive value of 6.9 kJ mol⁻¹. This positive shift indicates that the cooperative benefits are lost and that further H₂ adsorption becomes energetically unfavorable, likely due to enhanced steric hindrance and repulsive interactions. Additionally, the most negative normalized adsorption enthalpy was observed for a configuration with 14 adsorbed molecules (corresponding to a hydrogen uptake of 4.03 wt%), with a value of −22.9 kJ mol⁻¹, highlighting the strong cooperative interactions at intermediate loadings. The mixed exohedral–endohedral adsorption strategy on Ca₁₂O₁₂, therefore, enhances the overall adsorption capacity by leveraging the favorable energetics of endohedral H₂ adsorption. However, these cooperative interactions break down beyond a critical coverage level, delineating an energetic limit for further H₂ uptake.

This enhancement arises from two contributions. First, the initial endohedral H₂ is strongly stabilized by the electrostatic potential within the cage cavity, contributing an enthalpically favorable term (ΔH_ads ≈ −9 kJ mol⁻¹) that lowers the overall adsorption enthalpy of the mixed systems. Second, filling the interior slightly redistributes electron density toward the cage center, which mitigates intermolecular repulsion between neighboring exohedral H₂ molecules at high surface coverage. As a result, introducing one endohedral H₂ effectively promotes one additional shell of exohedral adsorption before steric and repulsive penalties dominate.

4 Conclusions

In summary, we performed a comprehensive in silico investigation of pristine Ca₁₂O₁₂ nanocages as potential hydrogen storage materials, utilizing dispersion-corrected and range-separated DFT methods, benchmarked against coupled-cluster calculations. The structural, electronic, and adsorptive properties of Ca₁₂O₁₂ were systematically compared with those of its Be₁₂O₁₂ and Mg₁₂O₁₂ analogs, revealing that the larger framework of Ca₁₂O₁₂ is particularly advantageous for hydrogen uptake. Single H₂ adsorption studies demonstrated that Ca₁₂O₁₂ exhibits distinct exohedral adsorption modes, with oxygen sites providing the most favorable interactions and even enabling stable endohedral adsorption—a feature not observed in the smaller Be₁₂O₁₂ and Mg₁₂O₁₂ nanocages. In multiple H₂ adsorption analyses, the overall adsorption enthalpy, ΔH_ads, remains negative across the entire loading range, confirming an exothermic process. However, examination of the normalized adsorption enthalpy, ΔH^norm_ads, reveals that while cooperative adsorption is favorable (i.e., ΔH^norm_ads is negative) up to 32H₂ molecules, this benefit diminishes at higher coverages—with positive ΔH^norm_ads values observed for configurations beyond n = 32. Notably, the most pronounced cooperative effect is observed at n = 13, where ΔH^norm_ads reaches −13.1 kJ mol⁻¹ and the cumulative adsorption energy attains −69.3 kJ mol⁻¹. Furthermore, mixed adsorption configurations combining exohedral and endohedral H₂ molecules were explored. The incorporation of a single endohedral H₂ molecule significantly enhances the overall adsorption energetics, yielding an optimal configuration with 33 exohedral plus one endohedral H₂ (a total of 34H₂ molecules) that exhibits ΔH_ads = −148.7 kJ mol⁻¹ and ΔH^norm_ads = −1.7 kJ mol⁻¹. This configuration corresponds to a hydrogen uptake of 9.24 wt%, which comfortably exceeds the U.S. DOE target of 5.5 wt%. Importantly, the calculated adsorption enthalpies fall in the regime typically considered optimal for reversible storage media, supporting the practical relevance of Ca₁₂O₁₂ as a physisorptive hydrogen host. The evolution of the E_g gap with increasing H₂ coverage further suggests that the electronic structure of the nanocage gradually shifts toward a more insulating character, although this effect plateaus beyond moderate adsorption levels. Collectively, these findings establish Ca₁₂O₁₂ as a promising candidate for hydrogen storage due to its capacity to support both exohedral and endohedral H₂ adsorption, its favorable cooperative adsorption behavior at moderate loadings, and its potential to achieve high gravimetric hydrogen densities. While this study provides key information on the thermodynamic and electronic characteristics of hydrogen adsorption on Ca₁₂O₁₂, it is based primarily on adsorption enthalpies and does not yet incorporate full finite-temperature free-energy profiles or desorption kinetics. Future work should therefore address anharmonic vibrational effects, entropic contributions under realistic pressures, finite-temperature molecular dynamics, and explicit many-body dispersion contributions, in order to evaluate stability and reversibility under working conditions and to establish practical operating windows (temperature and pressure ranges) for reversible hydrogen uptake and release. Overall, the present work contributes to the growing body of research on nanostructured hydrogen storage materials and offers a robust computational framework for the design and evaluation of advanced storage systems.

Author contributions

Saeedeh Kamalinahad: conceptualization (equal); methodology (equal); formal analysis (equal); investigation (equal); data curation (equal); writing − original draft (equal); writing − review & editing (equal). Aritra Roy: methodology (equal); formal analysis (equal); investigation (equal); data curation (equal); writing − original draft (equal); writing − review & editing (equal). Pablo Gamallo: conceptualization (equal); methodology (equal); resources (equal); writing − review & editing (equal); supervision (equal); project administration (equal); funding acquisition (equal). Felipe Fantuzzi: conceptualization (equal); methodology (equal); validation (lead); resources (equal); writing − original draft (equal); writing − review & editing (equal); visualization (lead); supervision (equal); project administration (equal); funding acquisition (equal).

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available within the article and its supplementary information (SI). Additional data are available from the corresponding authors upon reasonable request. Supplementary information: Benchmarking; summary of key structural, energetic, and electronic properties of all the investigated systems; cartesian coordinates. See DOI: https://doi.org/10.1039/d5nj04215a.

Acknowledgements

S. K. thanks Dr Motahareh Noormohammadbeigi and Dr Masoud Haratian for insightful scientific discussions. P. G. acknowledges support from the Spanish Ministry of Science and Innovation (MICIN) through the project PID2022-138180OB-I00 funded by MCIN/AEI/10.13039/501100011033 and by the European Union through ERDF A way of making Europe. Additional support has been provided by the CEX2021-001202-M María de Maeztu Unit of Excellence and by the Generalitat de Catalunya (project 2021SGR00079 and P. G. Serra Hunter Associate Professorship). F. F. gratefully acknowledges the University of Kent and Julius-Maximilians-Universität Würzburg for providing complementary computational resources whereas P. G. and S. K. also acknowledges the computational resources provided by Red Española de Supercomputación (RES) and by Consorci de Serveis Universitaris de Catalunya (CSUC).

Notes and references

1. S. Studer, S. Stucki and J. D. Speight, Hydrogen as a Future Energy Carrier, John Wiley & Sons, Ltd, 2008, pp. 23–69.
2. Energy White Paper: Our Energy Future: Creating a Low Carbon Economy, 2024, https://assets.publishing.service.gov.uk/media/5a7c1f5940f0b645ba3c6d4f/5761.pdf.
3. R. B. Gupta, Hydrogen Fuel: Production, Transport, and Storage, CRC Press, 2008.
4. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
5. N. Ma, W. Zhao, W. Wang, X. Li and H. Zhou, Int. J. Hydrogen Energy, 2024, 50, 379–396.
6. R. A. Varin, T. Czujko and Z. S. Wronski, Nanomaterials for Solid State Hydrogen Storage, Springer Science & Business Media, 2009.
7. F. Birol, International Energy Agency, The Future of Hydrogen, IEA technical report, 2019.
8. I. Hassan, H. S. Ramadan, M. A. Saleh and D. Hissel, Renewable Sustainable Energy Rev., 2021, 149, 111311.
9. E. Harrak Abdechafik, H. Ait Ousaleh, S. Mehmood, Y. Filali Baba, I. Bürger, M. Linder and A. Faik, Int. J. Hydrogen Energy, 2024, 52, 1182–1193.
10. J. Beheshtian and I. Ravaei, Appl. Surf. Sci., 2016, 368, 76–81.
11. Q. Wang and J. K. Johnson, J. Phys. Chem. B, 1999, 103, 277–281.
12. C. Liu, Y. Fan, M. Liu, H. Cong, H. Cheng and M. S. Dresselhaus, Science, 1999, 286, 1127–1129.
13. E. Beheshti, A. Nojeh and P. Servati, Carbon, 2011, 49, 1561–1567.
14. M. F. Fellah, Appl. Surf. Sci., 2017, 394, 9–15.
15. A. Blomqvist, C. M. Araújo, P. Srepusharawoot and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20173–20176.
16. P. Weis, P. R. Kemper and M. T. Bowers, J. Phys. Chem. A, 1997, 101, 2809–2816.
17. M. D. Ganji, S. Hosseini-Khah and Z. Amini-Tabar, Phys. Chem. Chem. Phys., 2015, 17, 2504–2511.
18. U.S. Department of Energy, Target Explanation Document: Onboard Hydrogen Storage for Light-Duty Fuel Cell Vehicles, U.S. Department of Energy technical report, 2017.
19. H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
20. Y. Rubin, T. Jarrosson, G.-W. Wang, M. D. Bartberger, K. Houk, G. Schick, M. Saunders and R. J. Cross, Angew. Chem., Int. Ed., 2001, 40, 1543–1546.
21. K. Komatsu, M. Murata and Y. Murata, Science, 2005, 307, 238–240.
22. T. B. Lee and M. L. McKee, J. Am. Chem. Soc., 2008, 130, 17610–17619.
23. O. V. Pupysheva, A. A. Farajian and B. I. Yakobson, Nano Lett., 2008, 8, 767–774.
24. K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616.
25. A. Kaiser, C. Leidlmair, P. Bartl, S. Zöttl, S. Denifl, A. Mauracher, M. Probst, P. Scheier and O. Echt, J. Chem. Phys., 2013, 138, 074311.
26. A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
27. X. Chang, Y. Xu and M. von Delius, Chem. Soc. Rev., 2024, 53, 47–83.
28. M. P. Johansson, D. Sundholm and J. Vaara, Angew. Chem., Int. Ed., 2004, 43, 2678–2681.
29. Y. Gao and X. C. Zeng, J. Am. Chem. Soc., 2005, 127, 3698–3699.
30. B. Yin and Z. Luo, Coord. Chem. Rev., 2021, 429, 213643.
31. T. N. Gribanova, R. M. Minyaev, V. I. Minkin and A. I. Boldyrev, Struct. Chem., 2020, 31, 2105–2128.
32. S. E. Skrabalak, J. Chen, Y. Sun, X. Lu, L. Au, C. M. Cobley and Y. Xia, Acc. Chem. Res., 2008, 41, 1587–1595.
33. Y. Xia, W. Li, C. M. Cobley, J. Chen, X. Xia, Q. Zhang, M. Yang, E. C. Cho and P. K. Brown, Acc. Chem. Res., 2011, 44, 914–924.
34. V. Alimardani, G. Farahavar, S. Salehi, S. Taghizadeh, M. R. Ghiasi and S. S. Abolmaali, Front. Mater. Sci., 2021, 15, 494–511.
35. E. Shakerzadeh, E. Tahmasebi, L. Van Duong and M. Tho Nguyen, Charact. Appl. Boron, IntechOpen, 2022, ch. 6, pp. 1–31.
36. L. Zhang, Y.-L. Ye, X.-H. Li, J.-H. Chen and W.-M. Sun, J. Mol. Liq., 2021, 342, 117533.
37. H. Kaur, J. Kaur and R. Kumar, Mater. Today Proc., 2022, 48, 1095–1102.
38. H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu, Y.-B. Wu, Y.-W. Mu, G.-F. Wei, Z.-P. Liu, J. Li, S.-D. Li and L.-S. Wang, Nat. Chem., 2014, 6, 727–731.
39. H. W. Choi, Y.-Y. Zhang, D. Kahraman, C.-Q. Xu, J. Li and L.-S. Wang, Boron Buckminsterfullerene, 2024, https://chemrxiv.org/engage/chemrxiv/article-details/676da75efa469535b9e4a03b.
40. H. Jouypazadeh and H. Farrokhpour, J. Mol. Struct., 2018, 1164, 227–238.
41. H. O. Edet, H. Louis, I. Benjamin, M. Gideon, T. O. Unimuke, S. A. Adalikwu, A. D. Nwagu and A. S. Adeyinka, Chem. Phys. Impact, 2022, 5, 100107.
42. D. L. Strout, J. Phys. Chem. A, 2000, 104, 3364–3366.
43. Q. Sun, Q. Wang and P. Jena, Nano Lett., 2005, 5, 1273–1277.
44. N. S. Venkataramanan, R. V. Belosludov, R. Note, R. Sahara, H. Mizuseki and Y. Kawazoe, Chem. Phys., 2010, 377, 54–59.
45. S. Giri, A. Chakraborty and P. Chattaraj, Nano Rev., 2011, 2, 5767.
46. K. Ayub, J. Mater. Chem. C, 2016, 4, 10919–10934.
47. A. S. Rad and K. Ayub, J. Mol. Liq., 2017, 238, 303–309.
48. R. Baloach, K. Ayub, T. Mahmood, A. Asif, S. Tabassum and M. A. Gilani, J. Inorg. Organomet. Polym. Mater., 2021, 31, 3062–3076.
49. Y. Zhang, X. Zheng, S. Zhang, S. Huang, P. Wang and H. Tian, Int. J. Hydrogen Energy, 2012, 37, 12411–12419.
50. H. Louis, I. O. Amodu, T. O. Unimuke, T. E. Gber, B. B. Isang and A. S. Adeyinka, Mater. Today Commun., 2022, 32, 103946.
51. N. Kosar, S. Gul, K. Ayub, A. Bahader, M. A. Gilani, M. Arshad and T. Mahmood, Mater. Chem. Phys., 2020, 242, 122507.
52. M. Rezaei-Sameti and S. Abdoli, J. Mol. Struct., 2020, 1205, 127593.
53. S. Gul, Kainat, Q. Ali, M. Khan, M. Ur Rehman, A. F. AlAsmari, F. Alasmari and M. Alharbi, Sci. Rep., 2023, 13, 18481.
54. J. S. Al-Otaibi, Y. S. Mary, Y. S. Mary, A. Mondal, N. Acharjee and D. S. Rajendran Nair, Spectrochim. Acta, Part A, 2024, 308, 123728.
55. Y. Zhang and H. Chen, Int. J. Hydrogen Energy, 2018, 43, 16609–16616.
56. O. V. de Oliveira, J. M. Pires, A. C. Neto and J. D. dos Santos, Chem. Phys. Lett., 2015, 634, 25–28.
57. A. S. Rad, S. M. Aghaei, H. Pazoki, E. Binaeian and M. Mirzaei, Surf. Interface Anal., 2018, 50, 411–419.
58. M. D. Mohammadi, H. Louis, O. J. Ikenyirimba, G. E. Mathias, T. O. Unimuke and M. E. Rasaki, Int. J. Hydrogen Energy, 2023, 48, 29446–29460.
59. M. Kazemi and A. S. Rad, Superlattices Microstruct., 2017, 106, 122–128.
60. Y. Zhang and X. Cheng, Chem. Phys. Lett., 2017, 672, 105–111.
61. F. Fantuzzi, R. R. Oliveira, A. V. Henkes, J. Rubayo-Soneira and M. A. C. Nascimento, Chem. – Eur. J., 2019, 25, 5269–5279.
62. M. R. Farrow, Y. Chow and S. M. Woodley, Phys. Chem. Chem. Phys., 2014, 16, 21119–21134.
63. R. R. Oliveira, F. Fantuzzi and M. A. C. Nascimento, J. Appl. Phys., 2021, 129, 205102.
64. H. Louis, T. C. Egemonye, T. O. Unimuke, B. E. Inah, H. O. Edet, E. A. Eno, S. A. Adalikwu and A. S. Adeyinka, ACS Omega, 2022, 7, 34929–34943.
65. G. J. Ogunwale, H. Louis, T. O. Unimuke, G. E. Mathias, A. E. Owen, H. O. Edet, O. C. Enudi, E. O. Oluwasanmi, A. S. Adeyinka and M. Doust Mohammadi, ACS Omega, 2023, 8, 13551–13568.
66. S. Wu, L. Li, Q. Liang, H. Gao, T. Tang and Y. Tang, Mater. Today Commun., 2024, 38, 107687.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016.
68. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
69. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
70. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
71. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
72. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
73. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
74. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
75. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
76. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
77. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
78. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
79. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, J. Chem. Phys., 2018, 148, 011101.
80. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606.
81. Y.-J. Wang, L. Xu, L.-H. Qiao, J. Ren, X.-R. Hou and C.-Q. Miao, Int. J. Hydrogen Energy, 2020, 45, 12932–12939.
82. H.-R. Li, C. Zhang, W.-B. Ren, Y.-J. Wang and T. Han, Int. J. Hydrogen Energy, 2023, 48, 25821–25829.
83. X. Wang and H. Chen, Appl. Phys. Lett., 2018, 112, 093903.
84. Y. Wang, Z. Li, D. Wu, C. Sun and F. Gu, J. Comput. Chem., 2010, 31, 195–203.
85. M. Zhou and G. Frenking, Acc. Chem. Res., 2021, 54, 3071–3082.

---

Footnotes

† Present address: Department of Chemistry Education, Farhangian University, P.O. Box 14665-889, Tehran, Iran.

‡ These authors contributed equally to this work.

---