Interfacial charge transfer-mediated Fermi level pinning in MBE-grown 2D 2H-MoSe₂/2H-MoTe₂ heterostructures

Abstract

MoSe₂ and MoTe₂ based heterostructures, owing to their remarkable photoresponsivity and tunable electrical characteristics, have emerged as promising candidates for field-effect transistors (FETs) and near-infrared (NIR) optoelectronic applications. However, the contributions of different interfacial processes impose limitations on the band tunability and carrier dynamics of the heterostructure, posing challenges in their device engineering. In this work, we present the scalable, layer-by-layer growth of a trilayer MoSe₂/MoTe₂ heterostructure over a SiO₂ substrate via molecular beam epitaxy (MBE). By leveraging the tunable probing depth of AR-XPS, we successfully resolve the interfacial bonding modifications, such as Te migration across the interface and localized Mo–Se–Te bonding. Our investigations show that these site-specific processes at the interface induce asymmetric energy level shifts, Fermi level pinning, and modulation of the valence band edge. Consequently, deviations from predicted band alignment are observed, with the Fermi level pinned around 0.58 eV above the valence band edge on the MoTe₂ side and the anomalous upshift of the valence band maximum of MoSe₂ in the heterostructure. These interfacial effects also result in a reduced barrier for hole injection, which can improve bidirectional carrier transport and gate-tunable hole conduction in such heterostructure-based devices. The findings highlight the critical role of interfacial interactions in governing band alignment of the ultrathin transition metal dichalcogenide (TMDC) heterostructures, providing key insights for advancing nanoelectronic and optoelectronic devices through heterostructure band engineering.

---

New concepts

This work introduces the concept that localized interfacial charge transfer, beyond conventional interlayer charge transfer, plays a dominant role in redefining band alignment and electronic structure in TMDC van der Waals heterostructures. Unlike previous studies that predominantly focus on band offsets based on interlayer charge redistribution, our findings reveal that site-specific processes at the interface, such as Te migration and localized Mo–Se–Te bonding, can induce asymmetric energy level shifts, Fermi level pinning, and modulation of valence band edge. These effects challenge simplified band alignment models, highlighting the importance of interfacial stoichiometry and site-specific bonding in determining device properties. In addition to the material-level insights, this work also presents a novel, non-destructive approach for probing buried interface physics using angle-resolved X-ray photoelectron spectroscopy (AR-XPS). By leveraging the tunable probing depth of AR-XPS, we successfully deconvolute interfacial contributions from bulk signals. This is traditionally achievable only via cross-sectional TEM or XPS depth-profiling; however, the former is highly localized and involves complex, potentially damaging sample preparation, while the latter results in selective etching of chalcogen atoms in TMDCs. This combination of scalable heterostructure growth with interface-specific probing offers a platform for studying buried interfaces and opens new possibilities in nanoscale device engineering.

1. Introduction

The exploration of advanced heterostructures based on two-dimensional (2D) transition metal dichalcogenides (TMDCs) has emerged as an important area of research to leverage the distinct characteristics of individual TMDC materials for achieving novel functionalities.^1–4 These exciting heterostructure properties extend beyond conventional optical and electrical characteristics, including novel quantum phenomena such as emergent quantum states and excitonic dynamics, which are essential for innovative applications in quantum computing and the development of high-efficiency optoelectronic devices.^5–7 MoSe₂/MoTe₂ heterostructures show great promise in flexible field-effect transistor (FET) devices and near-infrared (NIR) applications owing to their remarkable photoresponsivity and tunable electrical properties, while also laying the groundwork for advancements in quantum technologies.^8–16 Both MoSe₂ and MoTe₂ exhibit band absorption in the NIR-to-visible range.^17,18 While MoSe₂ exhibits strong excitonic effects with a higher bandgap and better environmental stability, MoTe₂ is characterized by strong spin–orbit coupling and higher electron mobility.^19–23 In addition, MoTe₂ possesses the advantage of an electrically ambipolar nature, enabling broad tunability of its Fermi level across the bandgap for optimizing the heterostructure's properties.^24,25 Together, these materials can enable a heterostructure with type-II band alignment, which facilitates efficient spatial separation and transport of carriers, essential for high-performance optoelectronic devices.

The interface in such layered heterostructures plays an important role in determining the overall heterostructure properties, as it facilitates crucial interfacial charge transfer processes that can drastically affect the device performance.²⁶ Despite the promise of TMDC heterostructures for high-performance FETs and NIR optoelectronics, a major challenge lies in understanding and controlling the role of these interfacial interactions in determining their electronic band alignment. As a result, experimentally observed band alignments and carrier dynamics often deviate from conventional interlayer charge transfer (ILCT) models. These discrepancies arise from atomically localized interfacial processes, such as interfacial charge redistribution, electronic hybridization from localized bonding modifications, vacancy defect formation and twist-angle-dependent interlayer coupling, which critically alter the local electronic structure.^27–31 Such interfacial interactions introduce complexities in heterostructure band tunability, affecting carrier dynamics and recombination kinetics.³² Previous studies have demonstrated electric-field-induced band alignment transitions in MoSe₂/WS₂ using a photoluminescence (PL) study³³ and ultrafast charge transfer in WS₂/MoSe₂ heterostructures through pump–probe spectroscopy.³⁴ However, the techniques are limited in resolving atomic-scale interfacial bonding changes and lack sufficient depth sensitivity to probe buried interfaces. The lack of understanding of interfacial processes leads to ambiguities in controlling heterostructure characteristics through band engineering, thereby limiting their potential for advanced device applications.

The present study aims to address this gap by providing insights into the interfacial interactions and band modifications in TMDC heterostructures by providing quantitative band alignment determination coupled with depth-resolved bonding analysis. Our investigation on MoSe₂/MoTe₂ heterostructures reveals how atomic-scale interfacial interactions and bonding modifications, coupled with interlayer charge transfer, govern band alignment and carrier injection barriers in these 2D heterostructures.

To achieve this, we employ scalable, layer-by-layer growth of the MoSe₂/MoTe₂ heterostructure with controlled trilayer thicknesses on SiO₂ substrates using MBE, combined with scanning Kelvin probe force microscopy, ultraviolet photoelectron spectroscopy, and X-ray photoelectron spectroscopy. By leveraging the tunable probing depth of AR-XPS, we successfully resolve the interfacial bonding modifications and observe that Te migration and localized Mo–Se–Te bonding near the interface induce asymmetric energy level shifts, Fermi level pinning, and valence band edge modulation. This results in an experimental heterostructure band alignment that deviates substantially from predictions based on interlayer charge transfer (ILCT) models, with a reduced valence band offset (VBO) in the heterostructure, which can be favorable for enhanced hole injection.

2. Experimental section

2.1. Thin film growth

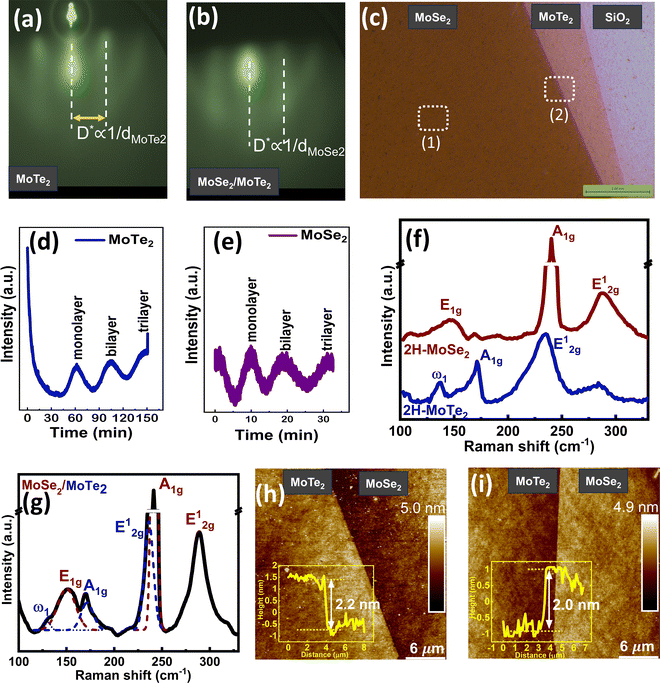
The two-dimensional MoSe₂ and MoTe₂ thin films were grown on SiO₂/Si substrates using the molecular beam epitaxy technique with a 2D MBE system from Vinci Technology, France, equipped with an in situ reflection high-energy electron diffraction (RHEED) characterization facility. The detailed description of the system and pre-growth calibration have been reported elsewhere previously.³⁵ Before loading the substrate into the MBE chambers, it was ultrasonicated in acetone, IPA and DI water. The substrate was pre-annealed before growth for one hour at 700 °C in a separate UHV chamber to desorb surface impurities. To avoid the cross-contamination of Se and Te, the sample puck was transferred from the growth chamber to the storage chamber after the first material of the heterostructure had been grown and the growth chamber was degassed thoroughly. A small piece of sapphire substrate was clipped on top of the first deposited material as a mask to create a lateral heterojunction for measuring film thickness. The growth temperatures were chosen as 450 °C and 350 °C for MoTe₂ and MoSe₂ film growth, respectively. The beam equivalent pressures (BEP), a measure of the evaporating elemental flux, for Te and Se were 4.2 × 10⁻⁷ mbar and 2.3 × 10⁻⁷ mbar, respectively. Since the growth rate is solely determined by the metal flux in TMDCs, the Mo flux was varied to achieve the desired growth rates. The growth rates of ∼40 min/layer and ∼12 min/layer were obtained at the e-beam emission current of 68 mA and 75 mA for MoTe₂ and MoSe₂, respectively. These lower growth rates are essential to achieve low roughnesses of surface and interfaces, as the slower rates provide sufficient time for Mo adatoms to coalesce properly in the lateral directions. The growth temperature at these particular flux rates was optimized to achieve the layer-by-layer growth modes, which is critical to realize sharp interface heterostructures by surpassing island formation during the growth. For MoSe₂, the layer-by-layer growth was achieved comparatively easily over a wider range of growth temperatures, while for MoTe₂, it was achieved for the growth temperature ranging from 380 °C to 480 °C only. Outside this temperature regime, the RHEED oscillations could not be obtained for MoTe₂. The thickness of each material was specifically chosen to be three unit layers because (1) only bilayer or thicker heterostructures demonstrate band quantization phenomena in 2D materials which are absent in monolayers, (2) the unique 2D characteristics of TMDCs are distinctive only below 4–5 layers and tend towards bulk behavior exceeding this thickness, and (3) the inversion symmetry is broken in the odd number of layers of TMDCs in their 2H phase which is crucial for spin-valley coupled effects³⁶ and non-linear optical effects such as single harmonic generation.³⁷

2.2. Material characterization

The grown films were characterized during the growth using RHEED (Staib Instruments) to investigate the crystalline quality and layer numbers by observing RHEED diffraction patterns and intensity oscillations. The large area homogeneity was confirmed by taking images of the grown films and heterostructure using the LEICA M125 C microscope at different magnifications. The high-resolution height-sensor images were taken using Atomic Force Microscopy (Bruker Dimension Icon XR) in tapping mode using a TESPA-V2 probe (tip radius ∼7 nm). Raman spectroscopy was performed using a Renishaw inVia Raman spectrometer in backscattering geometry with a 532 nm laser operated at 10 mW power. Raman mapping was performed over a 20 × 20 μm² area across the lateral edge of the MoSe₂/MoTe₂ heterostructure, but with a lower power of 5 mW to avoid film damage due to longer laser exposures.

2.3. Charge-transfer-study experiments

The scanning Kelvin probe force microscopy (SKPFM) measurements were performed with the same AFM instrument in the amplitude modulation mode using a conductive platinum–iridium coated probe (tip radius ∼5 nm). The work function calibration of the tip was done using a freshly exfoliated HOPG substrate. X-ray photoelectron spectroscopy was performed using an Axis-Supra from Kratos Analytical, equipped with a monochromatic Al Kα (1486.6 eV) source, using a step size of 0.05 eV and a pass energy of 20 eV for acquiring the core level spectra. A conducting path was established from the film surface to the sample stage using conductive carbon tape to avoid a charging effect at the film surface. To investigate the interfacial interactions, angle-resolved XPS (AR-XPS) measurements were performed, in which the angle between the source and the analyzer remained fixed while the stage was rotated in the source–sample–analyzer plane to change the emission angle. The acquired data were fitted and analyzed using the CasaXPS software.³⁸ The binding energy scale was calibrated with the Fermi edge position of gold. To ensure the physical significance of the fitting and avoid the false assignment of components, the peak-area ratio of the two spin–orbit components was kept nearly fixed (e.g., 3d_5/2 : 3d_3/2 = 3 : 2). The film stoichiometry was determined using the relative sensitivity factor (RSF)-corrected peak areas of different components. The RSF values were imported from the Kratos library as 3.32, 9.51 and 0.85 for Mo 3d, Te 3d and Se 3d, respectively. Ultraviolet photoelectron spectroscopy (UPS) measurements were performed with the same XPS system for acquiring valence band spectra using a He I source (with an energy of 21.22 eV), as the technique provides a greater photoionization cross-section for valence band states with its low photon energy and a much better energy resolution.³⁹ The measurements have been performed with a collimation setting of 27 μm aperture size and a pass energy of 5 eV, with a step size of 0.05 eV, while the sweep times were chosen to achieve the count rates of <15 kcps around the valence band edge. The precise value of the valence band edge was calculated by fitting the VB edge using the Edge Down function in the CasaXPS software.

2.4. Theoretical calculations

First-principles calculations based on density functional theory (DFT) were performed using the codes of the Vienna ab initio simulation package (VASP). The projector augmented wave (PAW) approach was used to describe the interaction of core valence electrons.⁴⁰ The exchange and correlation energies were considered in the generalized gradient approximation following the Perdew–Burke–Ernzerhof (PBE) scheme.⁴¹ The energy cut-off was set to 500 eV with the Γ-centered k-point mesh of 8 × 8 × 1. Spin–orbit coupling (SOC) effects were considered to capture the electronic structure accurately. All atomic positions were relaxed until forces were below 0.01 eV Å⁻¹, with the electronic self-consistency criterion set to 10⁻⁶ eV. The density of states (DOS) calculations were computed using the tetrahedron method to analyze the electronic structure modifications induced by vacancy defects. A 3 × 3 × 3 supercell was employed to model the atomic environment and to avoid interactions between periodic images in the out-of-plane (z) direction, and a vacuum layer of 20 Å was introduced in the simulation cell. The crystal structures of MoSe₂ and MoTe₂ were obtained from the Crystallography Open Database (COD).^42,43

3. Results and discussion

3.1. Layer-by-layer growth of vertical heterostructures (trilayer MoSe₂/MoTe₂)

The growth of thin films was carried out using the molecular beam epitaxy technique to achieve a high-quality film with precise control over the layer thickness and film stoichiometry. Since controlling the growth mode is crucial for fabricating sharply interfaced vertical heterostructures, the individual growth temperatures and metal fluxes were optimized for both materials (given in the Experimental section) to achieve a layer-by-layer growth mode, as evident from the observation of oscillations in the RHEED intensity (Fig. 1d and e). Each maximum in the intensity oscillations represents the completion of a single-layer growth, thus confirming a precise thickness-controlled growth.⁴⁴ We have observed that achieving the layer-by-layer growth mode for MoTe₂ is much more challenging than for MoSe₂. The Mo flux can be adjusted over a wide range to achieve the required growth rate (from 3 minutes per layer to 45 minutes per layer); however, there lies only a narrow window of the growth temperature within which layered growth of the 2H phase of MoTe₂ is achieved (refer to the Experimental section).

Fig. 1 (a) RHEED patterns showing a streaky diffraction pattern corresponding to the grown MoTe₂ and (b) MoSe₂/MoTe₂, where the streak spacing D* is inversely proportional to the lattice spacing d, of MoTe₂ and MoSe₂, respectively, (c) the optical image taken on the edge of the uniformly grown vertical heterostructure (the two squared locations represent the two different positions where SKPFM measurements are performed (discussed later)), (d) appearance of the RHEED intensity oscillations confirming layer-by-layer growth of MoTe₂ and (e) MoSe₂ on MoTe₂, (f) Raman spectra of individual MoTe₂ and MoSe₂ and (g) the MoSe₂/MoTe₂ heterostructure with different vibration modes corresponding to their 2H phases, (h) AFM height image of MoSe₂/MoTe₂ and (i) reverse stacked MoTe₂/MoSe₂ with height profiles drawn at the step-edge confirming the thicknesses of grown films.

The streaky RHEED pattern in Fig. 1a and b indicates a crystalline growth with a flat surface for both MoTe₂ and MoSe₂. Since the in-plane lattice constants for the 2H phase of MoSe₂ and MoTe₂ have nearly the same values (a_MoTe2 = 0.352 nm and a_MoSe2 = 0.332 nm)^45,46 within the FWHM limits of the observed RHEED streaks (∼0.092 nm), we obtain similar streak spacing (D*) for the new set of streaks after the heterostructure formation. Also, the diffraction pattern remains the same for all azimuthal angles, corresponding to the random in-plane orientations of the grown crystalline domains. Fig. 1c shows the optical image taken at the hetero-edge of the uniformly grown MoSe₂/MoTe₂ heterostructure on SiO₂. It is also challenging to achieve a single phase for MoTe₂ due to a small energy difference between its two phases (∼40 meV); consequently, it often results in a mixed 2H-1T′ phase.^47,48 The Raman spectra of the individual materials and heterostructure further confirm the crystallographic phase purity of the two materials (Fig. 1f and g). The phonon modes around 136 cm⁻¹ (ω₁), 171 cm⁻¹ (A¹_g) and 234 cm⁻¹ (E¹_2g) correspond to the 2H phase of MoTe₂, while those around 151 cm⁻¹ (E¹_g), 241 cm⁻¹ (A¹_g) and 288 cm⁻¹ (E¹_2g) correspond to the 2H phase of MoSe₂.^49,50 Furthermore, Raman mapping is performed across the lateral hetero-edge of the MoSe₂/MoTe₂ heterostructure, and multipoint Raman spectra are acquired from multiple locations across the heterostructure, which confirm the large-area phase uniformity of the grown heterostructure (SI S1). The film thicknesses in the heterostructures are reconfirmed ex situ using AFM by drawing height profiles at the sharp hetero step-edge (Fig. 1h and i). The AFM images, as shown in SI Fig. S2, further confirm the smooth surfaces of the grown films in the heterostructure with the rms roughness of 0.28 nm and 0.33 nm for MoTe₂ and MoSe₂, respectively. The obtained results from our MBE-grown heterostructures, characterized by large-area uniformity, layer-by-layer growth with precise trilayer thickness control, low surface roughness and consistent phase purity in the 2H phase, address the common challenges reported for CVD-grown TMDC films and heterostructures, including higher surface roughnesses (0.6–1.7 nm),^51,52 the coexistence of multiple phases in MoTe₂,⁵³ partial film coverage and spatial non uniformity.^54–56 Also, our MBE growth at significantly lower growth temperatures (350–450 °C) under UHV conditions, compared to high-temperature CVD processes (>650 °C),⁵¹ ensures reduced thermal stress and provides better control over phase formation.

3.2. Inter-layer charge transfer study: SKPFM and valence band spectra

The scanning Kelvin probe force microscopy (SKPFM) measurements were performed to calculate the work functions of the individual materials (Fig. 2a and b) and heterostructures (Fig. 2c and d). SKPFM maps the surface potential by measuring the contact potential difference (V_CPD) between the tip and the sample locally, which is then used to calculate the work function of the material with the following equation:

ϕ_sample = ϕ_tip − eV_CPD,

where ϕ_tip is the work function of the probing tip (∼4.60 eV for the Pt–Ir tip). A work function of 4.99 ± 0.01 eV is obtained for MBE-grown trilayer MoSe₂ and 4.73 ± 0.01 eV for trilayer MoTe₂ (Fig. 2a and b). The individual band diagrams for the two materials (as shown in Fig. 3a) are experimentally obtained based on these work function values and the valence band maxima (VBM) positions from the valence band spectra (shown later in Fig. 4a). The band offsets (CBO and VBO) at the heterojunction are calculated taking the vacuum level as a reference:

VBO = ϕ(MoSe₂) + VBM(MoSe₂) − ϕ(MoTe₂) − VBM(MoTe₂)

CBO = ϕ(MoSe₂) + VBM(MoSe₂) − E_g(MoSe₂) − [ϕ(MoTe₂) + VBM(MoTe₂) − E_g(MoTe₂)]

Fig. 2 SKPFM images show surface potential mapping with attached histogram profile for individual materials: (a) MoSe₂ and (b) MoTe₂ and for vertical heterostructures (c) MoSe₂/MoTe₂ and (d) MoTe₂/MoSe₂. (e) The plot shows surface potential and the corresponding work function values for individual materials and heterostructures. The 3D SKPFM image taken over a 30 × 30 μm² area at the heterojunction step-edge of (f) MoSe₂/MoTe₂ and (g) MoTe₂/MoSe₂ heterostructures (the insets show the corresponding 3D AFM height images at the same hetero step-edge).

Fig. 3 (a) Band diagrams of individual MoSe₂ and MoTe₂ before heterostructure formation, depicting a possible pathway for interlayer charge transfer (ILCT), based on the relative positions of different energy levels, (b) MoSe₂/MoTe₂ heterostructure band alignment, which is predicted based on conventional ILCT between the individual layers (the upward/downward arrows show the predicted change in the energy difference between different energy levels due to the ILCT process after the heterostructure formation).

Fig. 4 The high-resolution UPS spectra of MoTe₂ and MoSe₂ taken around the valence band edge for (a) individual materials and (b) heterostructures, where the arrows are used to represent the band edge positions, which are determined using the Edge Down function fitting shown in SI Fig. S3.

The heterostructure band alignment is proposed based on the conventional interlayer charge transfer (ILCT) theory, as shown in Fig. 3b, in which the electronic charge is transferred in the heterostructure from MoTe₂ (with a lower work function) to MoSe₂ (with a higher work function). The heterostructure possesses a type-II band alignment with a valence band offset (VBO) of 0.64 eV and a conduction band offset (CBO) of 0.24 eV. Due to this interlayer charge transfer across the interface, the MoTe₂ side of the interface becomes partially positive while the MoSe₂ side becomes negative, which leads to interface dipole formation. The interface dipole in such heterostructures creates a local potential gradient across the interface (Δϕ) from the MoTe₂ to the MoSe₂ side, lowering the vacuum level of MoTe₂ relative to MoSe₂. The work function of the heterostructure that we obtain using SKPFM will be a combined effect of the intrinsic material and the interface dipole. These ILCT-driven changes in different energy levels are indicated qualitatively in Fig. 3b, where Δϕ₁ and Δϕ₂ are the interfacial dipole-induced shifts in different energy levels of MoSe₂ and MoTe₂, respectively.

The SKPFM measurements were carried out around two positions in the heterostructures: (1) away from the hetero step-edge and (2) on and near the hetero step-edge (refer to Fig. 1c). The SKPFM measurements on the vertical heterostructure (Fig. 2c and d), which were performed far from the hetero-edge, show that the interface dipole effectively changes the work function of MoSe₂ to 4.84 ± 0.01 eV from 4.99 ± 0.01 eV for pristine MoSe₂ (Fig. 2e). To investigate the ILCT effect on MoTe₂, we performed SKPFM measurement on the reverse order-stacked MoTe₂/MoSe₂ heterostructure (Fig. 2d). The work function of MoTe₂ after the heterostructure formation remains nearly unchanged (4.72 ± 0.01 eV), which contradicts ILCT predictions according to which the transferred electronic charge from MoTe₂ should lead to an increase in its work function (as shown in Fig. 3b). This indicates that the Fermi level is pinned on the MoTe₂ side in the heterostructure.

Furthermore, the measurements were performed on the hetero step-edge of the MoSe₂/MoTe₂ heterostructure over a 30 × 30 μm² area to observe the lateral charge transfer effects in the heterostructure (Fig. 2f). Interestingly, the work function of MoTe₂ near the lateral hetero-edge increases to 4.76 ± 0.01 eV with a decrease in MoSe₂'s work function to 4.80 ± 0.01 eV. The same is observed in the reverse-stacked MoTe₂/MoSe₂ heterostructure with work functions of MoSe₂ and MoTe₂ being 4.91 ± 0.01 eV and 4.77 ± 0.01 eV, respectively (Fig. 2g). This significant change in the work function of MoTe₂ demonstrates that the previously observed Fermi level pinning is not an intrinsic property of the grown MoTe₂ film itself, but rather results from some other charge distribution processes in the vertical heterostructure, which makes it insensitive to the direct ILCT effects. Furthermore, as we move away from the step-edge on both sides for the measurements, these surface potential and work function values gradually approach those obtained in Fig. 2a–d for pristine materials and vertical heterostructures.

To further investigate the charge transfer process in the MoSe₂/MoTe₂ heterostructure, the valence band spectra were recorded using UPS. Fig. 4 shows the high-resolution UPS spectra acquired around the valence band edge for the individual materials (Fig. 4a) and for the heterostructure materials (Fig. 4b). The VBM values were measured precisely by fitting the valence band edge using the Edge Down function (SI S3). The valence band edge lies at 0.58 ± 0.05 eV for MoTe₂ and at 0.96 ± 0.05 eV for MoSe₂ with respect to the Fermi level. In the heterostructure, the valence band edge of MoTe₂ does not show any significant shift and lies at 0.56 ± 0.05 eV, which follows its work function change, as previously measured using SKPFM and further confirms that the Fermi level of MoTe₂ remains pinned. In the case of MoSe₂, the VBM value decreases to 0.88 ± 0.05 eV in the heterostructure. It may be mentioned here that the ILCT process decreases the work function of MoSe₂ in the heterostructure (Fig. 2e), which means the Fermi level moves away from the valence band and other core levels. However, this decrement in the energy difference between the VBM and the Fermi level is anomalous, as it contradicts the KPFM results. This reduction in the energy difference may be due to the upshift of the VBM itself.

In the following sections, we investigate the underlying charge redistribution mechanisms for (a) the pinning of the Fermi level of MoTe₂ and (b) the abnormal upward shift of the VBM of MoSe₂ in the MoSe₂/MoTe₂ vertical heterostructure.

3.3. Origin of different charge transfer processes: XPS core level spectra and energy shifts

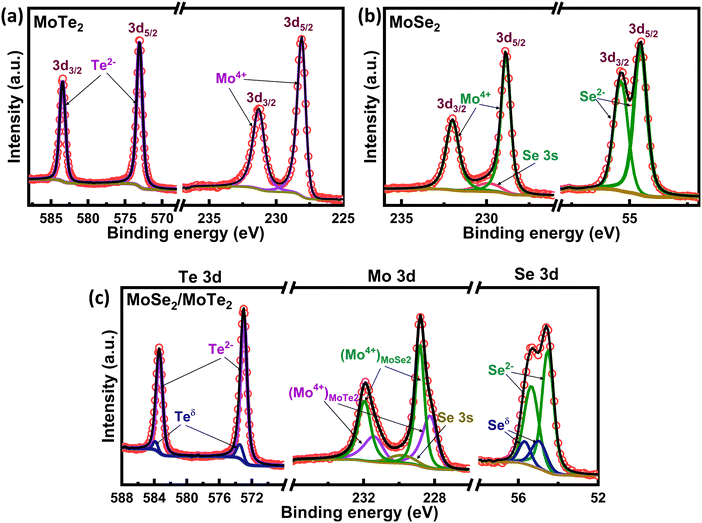
To understand these charge transfer processes in the heterostructure, which lead to the anomaly in the different energy levels, we studied XPS core level spectra of the constituent elements in the pristine materials and the heterostructure under surface normal emission mode (Fig. 5). It is emphasized that it is the energy of a core level from the valence band edge, not the one measured from the Fermi level, that remains constant in the absence of any change in the chemical environment of the element. However, in XPS, the binding energy of a core-level electron is measured from the Fermi level. So, any change in the Fermi level position, as represented by its work function, should also be reflected in the core level binding energy shift. The Mo 3d, Te 3d and Se 3d core levels are taken as the representative core levels in MoTe₂ and MoSe₂. The spectra are deconvoluted to obtain the contribution of different bonding states of an element in the material (Fig. 5). SI Table S2 includes the binding energy peak position and various fitting parameters corresponding to a particular bonding state.

Fig. 5 Deconvoluted XPS core level spectra of (a) Mo 3d, Te 3d in MoTe₂, (b) Mo 3d, Se 3d in MoSe₂ and (c) for these three core levels in the MoSe₂/MoTe₂ heterostructure, all taken at the normal emission angle. The experimentally observed spectra (represented by circles) are well fitted using the peak sum (solid black line) of different components corresponding to different bonding states (represented by colored solid lines).

In MoTe₂, Mo gets bonded in its 4+ oxidation state while Te is in its 2− oxidation state.⁵⁷ The Mo 3d core level (Fig. 5a) shows two spin–orbit-splitted peaks corresponding to the Mo–Te bond at 228.32 ± 0.05 eV (Mo 3d_5/2) and 231.51 ± 0.05 eV (Mo 3d_3/2). Similarly, the Te 3d spectrum contains two peaks at 573.15 ± 0.05 eV (Te 3d_5/2) and 583.43 ± 0.05 eV (Te 3d_3/2) corresponding to the Mo–Te bond in MoTe₂. In MoSe₂ (Fig. 5b), the Mo 3d core level overlaps with the Se 3s core level. The spectrum shows the peaks corresponding to the Mo–Se bond at 228.87 ± 0.05 eV and 232.07 ± 0.05 eV, which are at slightly higher binding energies than those for Mo–Te. This reflects a stronger interatomic bonding in MoSe₂ than in MoTe₂. The additional component around 229.85 ± 0.05 eV is contributed from Se 3s core level electrons. The Se 3d spectrum shows 3d_5/2 and 3d_3/2 components corresponding to the Mo–Se bond at 54.52 ± 0.05 eV and 55.34 ± 0.05 eV, respectively.

The changes in the binding energies and relative contribution of these different bonding states in the heterostructure strongly depend on the competition between the different charge transfer processes between the two materials (Fig. 5c). The peak corresponding to the Mo–Te bonding state in the Mo 3d spectrum of the heterostructure shows a shift of 0.05 eV towards the lower binding energy (refer to SI Table S2). Although the shift can be considered insignificant within the measurement uncertainty limits, the small reduction in the oxidation state of Mo may also arise from the change in Te interactions around Mo atoms, which is discussed in a later section. For Te 3d, no significant shift is observed in the Mo–Te peak, which aligns well with its VBM changes; however, an additional pair of bonding states (Te^δ) is observed at a higher binding energy (573.46 eV), leading to an asymmetric peak shape. Since the additional contribution appears at much lower energy than the 4+ oxidation state of Te in TeO₂ (which usually occurs at ∼576.60 eV⁵⁸), this cannot be assigned to the oxide contribution of tellurium. Therefore, this contribution suggests the presence of another type of bonding of Te with an oxidation state (4+) > δ > (2−).

The peak corresponding to the Mo–Se bond in both Mo 3d and Se 3d spectra shows a shift (∼0.12 eV) towards higher binding energy, which aligns well with its decreased work function. Additionally, the Se 3d spectrum shows a slightly different convoluted peak shape in the heterostructure, which can be fitted if the additional pair of components is introduced at a higher binding energy. These energy shifts in the core level and the work function both confirm that the ILCT process is dominant in the heterostructure, making MoSe₂ more n-type. However, the energy difference between the Mo 3d core level and the VBM increases from 228.10 eV in MoSe₂ (Fig. 3a) to 228.30 eV in the heterostructure (Fig. 6d). This further confirms the upward shift in the VBM of MoSe₂ towards the Fermi level. This shift can possibly arise due to the redistribution of the states near the valence band edge of MoSe₂. Since the additional bonding state contributions are observed in both Se and Te core levels, there is a possibility of bonding between Se and Te due to a site-to-site charge transfer leading to this modification in the valence band edge states, which is further investigated in the following section.

Fig. 6 (a) Schematic representation of the AR-XPS measurement geometry, showing variation in effective probing depth at two different emission angles, which enables extraction of interfacial contributions, (b) AR-XPS core level spectra of Te 3d, Mo 3d and Se 3d, taken at 30° emission angle and fitted using different bonding states to quantify individual contributions of these states, (c) relative changes in the ratio of different bonding state components taken at normal (90°) emission and 30° emission, calculated using RSF-corrected areas of different peaks, and (d) experimentally observed band alignment for the MoSe₂/MoTe₂ heterostructure based on the obtained work function and VBM values for the heterostructure, which shows a decreased value of the valence band offset of ∼0.43 eV arising from Fermi level pinning of MoTe₂ and VBM upshift of MoSe₂ (the upward/downward arrows indicate the increase/decrease in the particular energy after heterostructure formation, while the green/red color of the arrowhead represents that the experimentally obtained shifts do/do not follow the ILCT predictions).

3.4. The mechanism behind the unconventional energy shifts: angle-resolved XPS

To investigate the underlying mechanism behind the charge redistribution in the MoSe₂/MoTe₂ heterostructure, we performed angle-resolved XPS at photoemission angles other than surface normal (90°) (Fig. 6a). The effective photoemission depth is related to the photoemission angle (θ), the angle between the analyzer and the film surface, as follows:

d_eff ∝ λ_EAL × sin θ, (1)

where λ_EAL is the effective attenuation length of electrons in a material, a characteristic depth from which an electron with a particular kinetic energy can escape effectively to the material's surface.⁵⁹ The effective attenuation length accounts for inelastic as well as elastic scattering of electrons and is preferred over the inelastic mean free path (IMFP), which considers the inelastic scattering effects only.⁶⁰

In normal emission mode, the intensity of the photoelectrons reaching the surface, which were produced at a depth greater than d, is given by

I = I₀ exp(−d/λ_EAL) (2)

where I₀ is the initial intensity of the photoelectrons at the depth d.⁶¹

According to eqn (2), the majority of the detected signal originates from the top few nanometers of the film. About 80% of the total measured signal is contributed from a depth d_eff ≤ 1.6(λ_EAL) while about 90% of the total signal is from d_eff ≤ 2.4(λ_EAL). If we consider the values of λ_EAL for MoSe₂ (∼2.0 nm) and MoTe₂ (∼2.2 nm) from the NIST database,⁶² the effective photoemission depths at normal emission (sin θ = 1) can be approximated as (d_eff)_80% ≈ 3.2 nm and (d_eff)_90% ≈ 4.8 nm.

At 60° emission, the relative contribution of different binding states remains nearly unchanged (see SI Fig. S4a), as the effective photoemission depth only decreases by a factor of 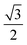(from eqn (1)), resulting in a combined contribution from the entire MoSe₂/MoTe₂ stacked structure. However, at 30° emission, the effective photoelectron depth is halved compared to normal emission, and we observe significant changes in the spectra (Fig. 6b). As summarized in Fig. 6c, the relative contribution of the higher binding energy peak (Te^δ) in the Te 3d spectrum increases from 8.5% to 16.9%. This indicates that this feature is not uniformly present in the MoTe₂ film but is predominantly localized towards the upper layer, i.e., near the MoSe₂/MoTe₂ interface. Similarly, in the Se 3d spectrum, the higher binding energy component (Se^δ) decreases from 26.9% to 10.4% at 30° emission, suggesting that this contribution is not prominent in the upper side of MoSe₂, which again shows its confined presence near the heterostructure interface. For further lower-angle emission at 20° (SI Fig. S4b), the signal-to-noise ratio is insufficient to ensure a reliable spectral fitting. Collectively, these observations confirm that the higher binding energy components in both Se 3d and Te 3d spectra originate from a region near the heterostructure interface.

Furthermore, the variation in the film stoichiometry was investigated using the RSF-corrected areas of the individual peaks (SI S8). The Mo : Te ratio changes from 1 : 1.90 at normal emission to 1 : 1.60 at 30° emission (Fig. 6c), indicating that some of the Te atoms near the interface migrate from the MoTe₂ lattice, leaving Te vacancies there. This Te vacancy creation in MoTe₂ is relatively easier owing to the weaker Mo–Te bonding compared to the Mo–Se bonding. The DFT calculations (SI Table S1) reveal that the formation energy of the Te vacancy (2.64 eV) is significantly lower than that of the Mo (2.89 eV) and Se (3.10 eV) vacancies in MoTe₂ and MoSe₂, respectively. This shows that Te vacancies are the favorable intrinsic defect in the heterostructure. Moreover, there is a high electronegativity difference (∼0.45) between Se (2.55) and Te (2.10), which is even more than that (∼0.06) between Mo (2.16) and Te according to the Pauling scale.⁶³ Therefore, it can preferably lead to the migration of Te near the heterostructure interface, leaving vacancies on the MoTe₂ side and forming the Mo–Se–Te/Se–Te bonding on the MoSe₂ side. This is experimentally observed in both the Se 3d and Te 3d core levels, as indicated by the Se^δ and Te^δ contributions in Fig. 5c and Fig. 6b. Due to the higher electronegativity of Se, the electronic charge transfer takes place from Te to Se, giving a slightly positive oxidation state to Te (δ+) and a negative oxidation state to Se (δ−). Since the above charge transfer is localized, affecting the Se and Te atoms near the interface more dominantly, the binding energy of the Mo–Se component remains nearly unaffected by this charge transfer.

The experimentally observed Fermi level pinning in MoTe₂ (Fig. 2e) can be explained by the interplay of interlayer charge transfer and intrinsic doping induced by these Te-vacancies. In principle, interlayer charge transfer across the heterostructure interface should shift the Fermi level of MoTe₂ downward, as electrons redistribute from MoTe₂ toward MoSe₂ (as indicated in ILCT predicted band-alignment in Fig. 3b). However, our DFT density of states calculations for MoTe₂ with Te vacancies reveal that the presence of Te vacancies in MoTe₂ modifies its electronic band structure by contributing to localized states just below the conduction band (SI Fig. S5). Since these donor-like states intrinsically drive MoTe₂ toward n-type doping, they counteract the ILCT-driven downward shift by pulling the Fermi level upward. The combined effect of these two competing mechanisms results in the apparent pinning of the Fermi level near its experimentally observed position (0.58 ± 0.05 eV above the VBM).

Based on these obtained values of work function and different energy levels, we present the experimentally observed band alignment for the MoSe₂/MoTe₂ heterostructure (Fig. 6d), in which the energy level shift differs from that in the ILCT-driven band alignment with modified interfacial band bending. The effective VBO decreases to 0.45 eV, which indicates a reduced barrier for hole injection. The enhanced hole injection in such heterostructure-based devices can improve bidirectional carrier transport and gate-tunable hole conduction. A comparative summary is included in Table 1, which compares our findings with reported interfacial band alignments and charge redistribution mechanisms for closely related TMDC heterostructures. It is also important to mention that our study highlights the role of interfacial charge redistribution and bonding modifications, while the twist angle between TMDC layers can also influence interfacial electronic properties. Since the grown films are limited by the multiple in-plane orientations of the grains, further investigations on twist-controlled single-crystalline heterostructures will be essential to understand the contributions of twist angle to the band alignment and carrier dynamics of such heterostructures.

Table 1 Comparison of band alignments and charge redistribution mechanisms in TMDC heterostructures

Heterostructure	Methods	Band alignment	Reported interfacial mechanisms	Key findings	Ref.
MoSe2/MoTe2 trilayer	AR-XPS, UPS, SKPFM	Modified, Type II, reduced VBO ≈ 0.43 eV	ILCT, Te migration and localized Mo–Se–Te bonding	MoTe2 Fermi level pinning and upshift in the MoSe2 VBM	This work
Individual bulk MoSe2 and MoTe2	SXPS, HAXPES	Type II, VBO ≈ 0.40 eV	Conventional ILCT (calculated based on their ionization potentials)	IP: 5.40 eV (MoSe2), 5.00 eV (MoTe2)	67
MoTe2(1L)/MoS2	STS, UPS	Type II, VBO ≈ 0.53 eV	ILCT, interfacial screening	Fermi level pinning due to gap states	64
MoTe2/MoS2	DFT	Type I and Type II	ILCT	Biaxial strain and electric field-induced Type II–Type I conversion	65
MoSe2/WS2 bilayers	Electrical gating and PL	Type I and Type II	ILCT, trapping of interfacial carriers by the interlayer exciton	Field-tuned band re-ordering	66

---

3.5. Modification of band-edge states in MoSe₂: DFT calculations

The valence band edge in most of the TMDC materials is predominantly defined by metal-derived electronic states, so any modifications in the chalcogen bonding do not have a significant impact on the valence band edge; however, in some TMDCs, the chalcogen atoms can also contribute to these band-edge states.⁶⁷ To investigate this for MoSe₂, density functional theory (DFT) calculations were performed, mapping the individual contributions of Mo and Se to the total density of states (DOS) in MoSe₂ (Fig. 7). The DOS spectra reveal that the states around the VBM in MoSe₂ have significant contributions from 4p orbitals of Se in conjunction with Mo 4d orbitals. Consequently, any change in the chemical bonding of Se atoms can significantly influence the position of the band edge. This makes the valence band edge of MoSe₂ sensitive to the chemical environment of Se, particularly at surfaces or interfaces where it is Se-terminated. In the grown MoSe₂/MoTe₂ heterostructure, the additional features observed in the Se and Te core-level spectra (Fig. 5c and 6b) confirm that the bonding of interfacial Se atoms is modified, with the formation of Mo–Se–Te/Se–Te near the interface. Therefore, these bonding modifications can be responsible for the experimentally obtained upshift of the valence band edge of MoSe₂.

Fig. 7 DFT calculations mapping the partial density of states of (a) Se and (b) Mo in MoSe₂, showing major contributions from Se 4p orbitals and Mo 4d orbitals to the valence band edge states, (c) total density of states of MoSe₂ with the individual contribution of Se (red) and Mo (black), and (d) DFT-calculated band-structure of MoSe₂ with its VBM appearing around the Γ-point.

4. Conclusion

In conclusion, we have successfully achieved the scalable layer-by-layer growth of a trilayer MoSe₂/MoTe₂ heterostructure uniformly over SiO₂ using MBE and observed abnormal shifts in the energy levels of the heterostructure. Our investigation based on SKPFM, XPS and AR-XPS reveals that this anomaly in the energy levels arises from the complex interfacial charge transfer processes occurring around the heterostructure interface. The migration of Te atoms induces n-type doping in MoTe₂, which compensates for the effect of inter-layer charge transfer, thus pinning its Fermi level. The modified bonding in MoSe₂ near the interface affects the electronic states near its valence band edge, resulting in the upshift of its VBM. Such interfacial effects not only lead to deviations from ILCT-driven band alignment but also introduce an asymmetric band profile with reduced valence band offset.

The experimentally established band alignment of the MoSe₂/MoTe₂ heterostructure in the present study overcomes the ILCT-based ambiguity, which is critical for precise heterostructure band-engineering of future devices. The reduced VBO corresponds to a lower energy barrier for hole transport across the interface, which is favorable for efficient hole injection and extraction in both directions. In photodetectors, such improved hole extraction can result in enhanced carrier collection and responsivity, while the enhanced bidirectional transport can be crucial for ambipolar FETs, where a small VBO supports balanced and symmetric switching between electron and hole conduction. Combined with the demonstrated large area thickness-controlled growth of the ultrathin heterostructure, the findings provide key insights into the intricate charge transfer in TMDC heterostructures and the impact on the band alignment, which is crucial for advancing their nanoelectronic and optoelectronic device applications.

Author contributions

Kamlesh Bhatt: conceptualization, methodology, writing – original draft, formal analysis, writing – review & editing, data curation, and visualization. Santanu Kandar: methodology and investigation. Lipika: formal analysis and investigation. Ashok Kapoor: validation, formal analysis, and writing – review & editing. Rajendra Singh: supervision, conceptualization, writing – review & editing, resources, and funding acquisition.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data that support the findings of this study can be made available from the corresponding author upon reasonable request.

Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5nh00663e.

Acknowledgements

K. Bhatt would like to acknowledge the University Grant Commission (UGC), India, for providing a fellowship. The authors acknowledge the “Grand Challenge Project on MBE Growth of 2D Materials” sponsored by the Ministry of Human Resource Development (MHRD), India and the Indian Institute of Technology Delhi for providing financial support for this work. The authors also acknowledge the partial funding support from the Department of Science and Technology (DST-Nano Mission) under the project scheme “Consortium for Collective and Engineered Phenomena in Topology (CONCEPT).” The authors also thank Dr B.G. Ganga and Dr Atul Kumar Singh for their kind support with detailed AR-XPS and UPS measurements. The authors also want to acknowledge the Central Research Facility (CRF) and Department of Physics, Indian Institute of Technology Delhi, New Delhi, for the characterization facilities.

References

1. J. M. Shainline, Appl. Phys. Lett., 2021, 118, 160501.
2. L. H. Fowler-Gerace, Z. Zhou, E. A. Szwed, D. J. Choksy and L. V. Butov, Nat. Photonics, 2024, 18, 823–828.
3. P. V. Pham, S. C. Bodepudi, K. Shehzad, Y. Liu, Y. Xu, B. Yu and X. Duan, Chem. Rev., 2022, 122, 6514–6613.
4. L. Yin, F. Wang, R. Cheng, Z. Wang, J. Chu, Y. Wen and J. He, Adv. Funct. Mater., 2019, 29, 1804897.
5. M. Rahaman, G. Kim, K. Y. Ma, S. Song, H. S. Shin and D. Jariwala, npj 2D Mater. Appl., 2023, 7, 66.
6. Y. Wang, L. Yin, W. Huang, Y. Li, S. Huang, Y. Zhu, D. Yang and X. Pi, Adv. Intell. Syst., 2021, 3, 2000099.
7. B. Zhao, Z. Wan, Y. Liu, J. Xu, X. Yang, D. Shen, Z. Zhang, C. Guo, Q. Qian, J. Li, R. Wu, Z. Lin, X. Yan, B. Li, Z. Zhang, H. Ma, B. Li, X. Chen, Y. Qiao, I. Shakir, Z. Almutairi, F. Wei, Y. Zhang, X. Pan, Y. Huang, Y. Ping, X. Duan and X. Duan, Nature, 2021, 591, 385–390.
8. Y.-C. Lin, R. K. Ghosh, R. Addou, N. Lu, S. M. Eichfeld, H. Zhu, M.-Y. Li, X. Peng, M. J. Kim, L.-J. Li, R. M. Wallace, S. Datta and J. A. Robinson, Nat. Commun., 2015, 6, 7311.
9. X. Zhang, Z. Kang, L. Gao, B. Liu, H. Yu, Q. Liao, Z. Zhang and Y. Zhang, Adv. Mater., 2021, 33, 2104935.
10. H. Son, H. Choi, J. Jeon, Y. J. Kim, S. Choi, J. H. Cho and S. Lee, ACS Appl. Mater. Interfaces, 2021, 13, 8692–8699.
11. W. Choi, J. Ahn, K. Kim, H. Jin, S. Hong, D. K. Hwang and S. Im, Adv. Mater., 2021, 33, 2103079.
12. Y.-C. Lin, R. K. Ghosh, R. Addou, N. Lu, S. M. Eichfeld, H. Zhu, M.-Y. Li, X. Peng, M. J. Kim, L.-J. Li, R. M. Wallace, S. Datta and J. A. Robinson, Nat. Commun., 2015, 6, 7311.
13. X. Zhou, Z. Tian, H. J. Kim, Y. Wang, B. Xu, R. Pan, Y. J. Chang, Z. Di, P. Zhou and Y. Mei, Small, 2019, 15, 1902528.
14. B. Zhao, Z. Wan, Y. Liu, J. Xu, X. Yang, D. Shen, Z. Zhang, C. Guo, Q. Qian, J. Li, R. Wu, Z. Lin, X. Yan, B. Li, Z. Zhang, H. Ma, B. Li, X. Chen, Y. Qiao, I. Shakir, Z. Almutairi, F. Wei, Y. Zhang, X. Pan, Y. Huang, Y. Ping, X. Duan and X. Duan, Nature, 2021, 591, 385–390.
15. S. Kandar, K. Bhatt, N. Kumar, A. K. Kapoor and R. Singh, ACS Appl. Nano Mater., 2024, 7, 8212–8220.
16. X. Li, M.-W. Lin, J. Lin, B. Huang, A. A. Puretzky, C. Ma, K. Wang, W. Zhou, S. T. Pantelides, M. Chi, I. Kravchenko, J. Fowlkes, C. M. Rouleau, D. B. Geohegan and K. Xiao, Sci. Adv., 2016, 2, 1501882.
17. C. Ruppert, B. Aslan and T. F. Heinz, Nano Lett., 2014, 14, 6231–6236.
18. H. Lee, J. Ahn, S. Im, J. Kim and W. Choi, Sci. Rep., 2018, 8, 11545.
19. K. L. Seyler, P. Rivera, H. Yu, N. P. Wilson, E. L. Ray, D. G. Mandrus, J. Yan, W. Yao and X. Xu, Nature, 2019, 567, 66–70.
20. B. Han, C. Robert, E. Courtade, M. Manca, S. Shree, T. Amand, P. Renucci, T. Taniguchi, K. Watanabe, X. Marie, L. E. Golub, M. M. Glazov and B. Urbaszek, Phys. Rev. X, 2018, 8, 031073.
21. A. Arora, K. Nogajewski, M. Molas, M. Koperski and M. Potemski, Nanoscale, 2015, 7, 20769–20775.
22. C. Jiang, F. Liu, J. Cuadra, Z. Huang, K. Li, A. Rasmita, A. Srivastava, Z. Liu and W.-B. Gao, Nat. Commun., 2017, 8, 802.
23. A. M. Shafi, M. G. Uddin, X. Cui, F. Ali, F. Ahmed, M. Radwan, S. Das, N. Mehmood, Z. Sun and H. Lipsanen, Adv. Sci., 2023, 10, 2303437.
24. Y. Lin, Y. Xu, S. Wang, S. Li, M. Yamamoto, A. Aparecido-Ferreira, W. Li, H. Sun, S. Nakaharai, W. Jian, K. Ueno and K. Tsukagoshi, Adv. Mater., 2014, 26, 3263–3269.
25. M. A. Khan, M. F. Khan, S. Rehman, H. Patil, G. Dastgeer, B. M. Ko and J. Eom, Sci. Rep., 2022, 12, 12085.
26. X. Jiang, T. Yilmaz, E. Vescovo and D. Lu, Phys. Rev. B, 2024, 109, 115112.
27. N. Gasparini, F. V. A. Camargo, S. Frühwald, T. Nagahara, A. Classen, S. Roland, A. Wadsworth, V. G. Gregoriou, C. L. Chochos, D. Neher, M. Salvador, D. Baran, I. McCulloch, A. Görling, L. Lüer, G. Cerullo and C. J. Brabec, Nat. Commun., 2021, 12, 1772.
28. G. Wen, S. Fu, M. Bonn and H. I. Wang, J. Chem. Phys., 2024, 161, 054714.
29. F. H. Davies, C. J. Price, N. T. Taylor, S. G. Davies and S. P. Hepplestone, Phys. Rev. B, 2021, 103, 045417.
30. Y. Jiang, S. Chen, W. Zheng, B. Zheng and A. Pan, Light: Sci. Appl., 2021, 10, 72.
31. T. Naimer, K. Zollner, M. Gmitra and J. Fabian, Phys. Rev. B, 2021, 104, 195156.
32. R. Rosati, I. Paradisanos, L. Huang, Z. Gan, A. George, K. Watanabe, T. Taniguchi, L. Lombez, P. Renucci, A. Turchanin, B. Urbaszek and E. Malic, Nat. Commun., 2023, 14, 2438.
33. J. Kistner-Morris, A. Shi, E. Liu, T. Arp, F. Farahmand, T. Taniguchi, K. Watanabe, V. Aji, C. H. Lui and N. Gabor, Nat. Commun., 2024, 15, 4075.
34. A. Bian, S. Fu, P. Wang, K. Zhao, J. He, X. Zhang, D. He, Y. Wang and H. Zhao, J. Mater. Chem. C, 2022, 10, 5328–5335.
35. K. Bhatt, S. Kandar, N. Kumar, A. Kapoor and R. Singh, Nanoscale, 2024, 16, 15381–15395.
36. J. Xia, J. Yan and Z. X. Shen, FlatChem, 2017, 4, 1–19.
37. H. Jiang, L. Zheng, J. Wang, M. Xu, X. Gan, X. Wang and W. Huang, Nanoscale, 2021, 13, 18103–18111.
38. N. Fairley, V. Fernandez, M. Richard-Plouet, C. Guillot-Deudon, J. Walton, E. Smith, D. Flahaut, M. Greiner, M. Biesinger, S. Tougaard, D. Morgan and J. Baltrusaitis, Appl. Surf. Sci. Adv., 2021, 5, 100112.
39. J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. P. B. James and M. T. Lavik, Acta Crystallogr., 1963, 16, 1183.
43. D. Puotinen and R. E. Newnham, Acta Crystallogr., 1961, 14, 691–692.
44. S. Hasegawa, in Characterization of Materials, ed. E. N. Kaufmann, Wiley, 2012, pp. 1–14.
45. D. Puotinen and R. E. Newnham, Acta Crystallogr., 1961, 14, 691–692.
46. P. B. James and M. T. Lavik, Acta Crystallogr., 1963, 16, 1183.
47. F. Zhang, H. Zhang, S. Krylyuk, C. A. Milligan, Y. Zhu, D. Y. Zemlyanov, L. A. Bendersky, B. P. Burton, A. V. Davydov and J. Appenzeller, Nat. Mater., 2019, 18, 55–61.
48. K.-A. N. Duerloo, Y. Li and E. J. Reed, Nat. Commun., 2014, 5, 4214.
49. S. Kandar, K. Bhatt, N. Kumar, A. Kapoor and R. Singh, Nanoscale, 2024, 16, 18609–18619.
50. N. Kumar, K. Bhatt, S. Kandar, G. Rana, C. Bera, A. K. Kapoor and R. Singh, ACS Appl. Nano Mater., 2024, 7, 23834–23841.
51. J. P. Fraser, L. Masaityte, J. Zhang, S. Laing, J. C. Moreno-López, A. F. McKenzie, J. C. McGlynn, V. Panchal, D. Graham, O. Kazakova, T. Pichler, D. A. MacLaren, D. A. J. Moran and A. Y. Ganin, Commun. Mater., 2020, 1, 48.
52. M. G. Choi, A. Belianinov, A. Pawlicki, S. Park, H. Lee, O. S. Ovchinnikova and S. Kim, Surf. Interfaces, 2021, 26, 101437.
53. V. O. Khaustov, D. Convertino, J. Köster, A. A. Zakharov, M. J. Mohn, Z. M. Gebeyehu, L. Martini, S. Pace, G. Marini, M. Calandra, U. Kaiser, S. Forti and C. Coletti, ACS Appl. Nano Mater., 2024, 7, 18094–18105.
54. L. Tang, J. Tan, H. Nong, B. Liu and H.-M. Cheng, Acc. Mater. Res., 2021, 2, 36–47.
55. Y. Gong, S. Lei, G. Ye, B. Li, Y. He, K. Keyshar, X. Zhang, Q. Wang, J. Lou, Z. Liu, R. Vajtai, W. Zhou and P. M. Ajayan, Nano Lett., 2015, 15, 6135–6141.
56. Y. Ding, N. Zhou, L. Gan, X. Yan, R. Wu, I. H. Abidi, A. Waleed, J. Pan, X. Ou, Q. Zhang, M. Zhuang, P. Wang, X. Pan, Z. Fan, T. Zhai and Z. Luo, Nano Energy, 2018, 49, 200–208.
57. Y. Yoo, Z. P. DeGregorio, Y. Su, S. J. Koester and J. E. Johns, Adv. Mater., 2017, 29, 1605461.
58. K. Bhatt, S. Kandar, N. Kumar, A. Kapoor and R. Singh, Appl. Surf. Sci., 2024, 659, 159832.
59. A. Jablonski and C. J. Powell, J. Phys. Chem. Ref. Data, 2020, 49, 033102.
60. F. A. Stevie and C. L. Donley, J. Vac. Sci. Technol., A, 2020, 38, 063204.
61. A. Jablonski and C. J. Powell, J. Electron Spectrosc. Relat. Phenom., 2017, 218, 1–12.
62. C. J. Powell and A. Jablonski, NIST Electron Effective-Attenuation-Length Database, National Institute of Standards and Technology, Gaithersburg, MD, 2011.
63. J. F. Ogilvie, in Conceptual Trends in Quantum Chemistry, Springer, Netherlands, Dordrecht, 1994, pp. 171–198.
64. H. C. Diaz, Y. Ma, R. Chaghi and M. Batzill, Appl. Phys. Lett., 2016, 108, 191606.
65. S. T. Nguyen, N. V. Hieu, H. Le-Quoc, K. Nguyen-Ba, C. V. Nguyen, H. V. Phuc and C. Q. Nguyen, Nanoscale Adv., 2024, 6, 3624–3631.
66. J. Kistner-Morris, A. Shi, E. Liu, T. Arp, F. Farahmand, T. Taniguchi, K. Watanabe, V. Aji, C. H. Lui and N. Gabor, Nat. Commun., 2024, 15, 4075.
67. L. A. H. Jones, Z. Xing, J. E. N. Swallow, H. Shiel, T. J. Featherstone, M. J. Smiles, N. Fleck, P. K. Thakur, T.-L. Lee, L. J. Hardwick, D. O. Scanlon, A. Regoutz, T. D. Veal and V. R. Dhanak, J. Phys. Chem. C, 2022, 126, 21022–21033.

---