Physics-based compact model for 2D TMD FETs with full-range validation from single device to circuit
Dokyoung
Lee
 ab,
Jeongyun
Jang
a,
Jimin
Han
a,
Sae Rim
Kim
a,
Jiwon
Baik
a,
Hayoung
Roh
a and
Sungho
Kim
ab,
Jeongyun
Jang
a,
Jimin
Han
a,
Sae Rim
Kim
a,
Jiwon
Baik
a,
Hayoung
Roh
a and
Sungho
Kim
 *ab
*ab
aDivision of Electronic and Semiconductor Engineering, Ewha Womans University, Seoul 03670, Republic of Korea. E-mail: sunghok@ewha.ac.kr
bInstitute of Multiscale Matter and Systems (IMMS), Ewha Womans University, Seoul 03760, Republic of Korea
First published on 5th November 2025
Abstract
Two-dimensional (2D) semiconductors, particularly transition-metal dichalcogenides (TMDs), offer transformative potential for next-generation electronics because of their ultrathin atomic structures and superior electrostatic gate control. However, the practical realization of complex integrated circuits based on 2D TMD-based field-effect transistors (2D FETs) is critically constrained by the absence of robust, accurate, compact, and computationally efficient models suitable for SPICE (simulation program with integrated circuit emphasis)-based circuit simulations. This study demonstrated a physics-based, fully analytical, and SPICE-compatible compact model for 2D FETs. The model introduces a continuous, closed-form analytical framework that incorporates key physical mechanisms, such as interface trap states and gate-bias-dependent mobility degradation, through an efficient approximation of the Lambert W function. By avoiding iterative solvers and artificial segmentation, the model ensures compatibility with circuit simulators while maintaining high fidelity. Extensive validation against experimental data demonstrated quantitative agreement between the model and either single-device characteristics or the dynamic behavior of various circuits, including inverters, SRAM cells, NAND gates, and ring oscillators. Overall, the study established a robust and scalable modeling approach that effectively bridges device-level physics and system-level circuit designs for 2D semiconductors.
New conceptsThis study introduces a fully analytical, SPICE-compatible compact model for two-dimensional (2D) TMD-based field-effect transistors (FETs), which accurately captures both single-device and circuit-level behaviors without relying on iterative solvers or artificial bias segmentation. The key innovation lies in the incorporation of an approximated Lambert W function, which enables a closed-form drain current expression compatible with standard circuit simulators. Unlike previous models, our formulation explicitly accounts for interface trap dynamics and vertical-field-induced mobility degradation within a unified analytical framework. The model was rigorously validated using experimental data from fabricated MoS2 FETs and MoS2-based logic circuits, including inverters, SRAMs, NAND gates, and ring oscillators. This work bridges the gap between device-level physics and system-level simulation in 2D electronics, offering a predictive tool for integrated circuit design based on emerging atomically thin semiconductors. The approach provides new physical insights into the role of nonidealities in 2D FET operation and lays the foundation for scalable modeling of next-generation energy-efficient electronics. |
1. Introduction
Two-dimensional (2D) semiconductor materials, particularly transition-metal dichalcogenides (TMDs) such as MoS2, MoSe2, WS2, and WSe2, have emerged as promising candidates to overcome the limitations of conventional silicon-based complementary metal–oxide–semiconductor (CMOS) technology.1,2 The intrinsic atomic-scale thickness of TMDs provides superior electrostatic gate control, enabling extreme downscaling of the channel dimensions to subnanometer thicknesses beyond the reach of traditional bulk semiconductors.3 This aggressive scaling not only suppresses short-channel effects but also markedly reduces power consumption, supplementary ultralow power and energy-efficient transistor operation at the limits of miniaturization. Additionally, the inherently clean, dangling-bond-free surfaces of TMDs, along with their mechanical flexibility and compatibility with a wide range of substrates, have opened new possibilities in emerging fields such as flexible electronics4,5 and ultrasensitive sensors.6,7 As a result, TMD-based field-effect transistors (2D FETs) are increasingly regarded as essential building blocks for next-generation transistor architectures and system-on-chip (SoC) platforms, addressing key limitations of traditional silicon-based technologies.8Despite significant progress in the fabrication and characterization of individual 2D FETs, the development of fully functional electronic systems critically depends on the availability of accurate, robust, computationally efficient, and compact device models. These models are vital for translating the complex physical behaviors of individual devices into forms suitable for system-level circuit simulation.9,10 However, accurately capturing the distinct physical phenomena governing 2D FET operation, such as quantum confinement, atomically thin channels, and 2D density of states (DOS2D), remains a substantial challenge. Although numerous compact models have been proposed, many suffer from critical shortcomings. For example, some models fundamentally misinterpret device physics by incorrectly treating the surface potential as a quasi-Fermi level,11,12 leading to significant errors in electrostatic modeling and reduced predictive accuracy. Others rely on overly idealized assumptions, neglecting key nonidealities such as interface trap states and field-dependent mobility degradation due to carrier scattering,13,14 which compromises reliability under realistic operating conditions. Moreover, many physics-based compact models depend on iterative numerical methods (e.g., Newton–Raphson or Halley's methods),15,16 which hinders their integration into SPICE (simulation program with integrated circuit emphasis)-compatible simulation environments essential for large-scale integrated circuit (IC) design. Although some piecewise analytical models offer improved computational efficiency,17 they often introduce artificial discontinuities and depend on empirically selected smoothing parameters, limiting their accuracy and applicability across diverse operating regimes.
Most importantly, a significant gap remains in the experimental validation of compact models at the circuit level. Although prior studies have used such models to simulate basic circuit elements, such as inverters and ring oscillators, they have not rigorously evaluated whether the simulated results accurately reflect the performance of experimentally fabricated circuits.12,13,16,17 Consequently, the validity of circuit-level simulation results remains uncertain.18–20 The lack of comprehensive benchmarking against measured performance in integrated circuits undermines the reliability, generalizability, and practical applicability of existing models. Without addressing this validation gap, the transition of 2D FETs from device-level demonstrations to scalable real-world electronic systems remains severely constrained.
In this study, we present a compact, SPICE-compatible model for 2D FETs that employs a continuous, closed-form analytical framework valid across all device operating regimes. By leveraging an approximation of the Lambert W function, the model eliminates the need for iterative numerical solvers and avoids artificial segmentation of bias regions. Critically, it incorporates key physical phenomena (such as interface trap states and gate-bias-dependent mobility degradation) within a fully analytical formulation, achieving high predictive accuracy without empirical parameter fitting. Extensive experimental validation confirms the robustness of the model, showing excellent agreement with the DC characteristics of individual MoS2 FETs and the circuit-level performance of integrated elements, including inverters, static random-access memory (SRAM) cells, NAND gates, and ring oscillators based on MoS2 FETs. This study thus presents a rigorously validated compact model for 2D FETs that bridges single-device physics and system-level circuit behavior, providing a predictive and reliable modeling framework essential for the advancement of next-generation 2D semiconductor technologies.
2. Model description
2.1 Core drain current model
In 2D FETs, the atomically thin nature of the channel, typically comprising only a few monolayers, permits the assumption that the electrostatic potential in the channel ϕ(x, y) can be considered uniform across the vertical direction. Therefore, ϕ(x, y) reduces to a one-dimensional surface potential ϕ(x). Furthermore, in the long-channel device, the lateral electric field was considerably weaker than the vertical gate-induced field, thereby validating the application of the gradual channel approximation. Based on these assumptions, Gauss's law applied to an infinitesimal segment of the channel (Fig. 1a) yields the following electrostatic equilibrium conditions:| (εtoxEtoxΔx) + (εboxEboxΔx) = q(n2D − Nimp)Δx | (1) |
Here, εtox and εbox denote the dielectric permittivities of the top and bottom gate oxides, respectively. Nimp represents the areal density of fixed charged impurities, which are commonly attributed to intrinsic defects, such as sulfur vacancies in MoS2.21n2D refers to the mobile electron density in the 2D channel, assuming n-type conduction. The vertical electric fields across the top and bottom gate oxides (Etox and Ebox) are given by:
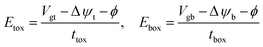 | (2) |
| Ctox(Vgt − Δψt − ϕ) + Cbox(Vgb − Δψb − ϕ) = q(n2D − Nimp) | (3) |
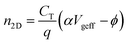 | (4) |
 | (5) |
Notably, n2D is intrinsically governed by the conduction-band structure of the TMD material. In most TMDs, the conduction band comprises multiple energy valleys, with the most prominent minima located at the K and Q points of the Brillouin zone (Fig. S1).22 The energy separation between two valleys (ΔEK–Q) significantly influences the thermal occupation of higher-energy states and thus plays a critical role in determining the total mobile electron density in the channel. To account for this multivalley nature, DOS2D was modeled as the weighted sum of the individual contributions from each valley:
 | (6) |
Here, gs denotes the spin degeneracy, gK and gQ represent the valley degeneracies associated with the K and Q valleys, respectively,  and
and  are the corresponding in-plane effective masses of the conduction band minima in each valley. The exponential term accounts for the thermally activated occupation in the higher-energy Q valley. This formulation assumes a step-like constant density of states within each valley, consistent with the parabolic band approximation, which is widely employed for 2D TMDs owing to its relatively simple and isotropic conduction-band curvature.22 Consequently, n2D can be obtained by integrating DOS2D over the energy weighted by the Fermi–Dirac distribution.
are the corresponding in-plane effective masses of the conduction band minima in each valley. The exponential term accounts for the thermally activated occupation in the higher-energy Q valley. This formulation assumes a step-like constant density of states within each valley, consistent with the parabolic band approximation, which is widely employed for 2D TMDs owing to its relatively simple and isotropic conduction-band curvature.22 Consequently, n2D can be obtained by integrating DOS2D over the energy weighted by the Fermi–Dirac distribution.
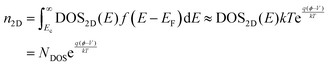 | (7) |
In this formulation, the Fermi–Dirac distribution function f(E − EF) is approximated by the Boltzmann distribution under the assumption of nondegenerated carrier statistics. The conduction band edge is defined as Ec = −qϕ, whereas the electron quasi-Fermi level is given by EF = −qV, with V representing the electrochemical potential. Note that some previously reported compact models incorrectly assume that the surface potential is equivalent to the quasi-Fermi level (i.e., EF = −qϕ),11,12 which leads to fundamental errors in the electrostatic formulation and significantly compromises the model's predictive accuracy.
This analytical formulation of n2D as a function of ϕ serves as the foundation for the subsequent derivation of the drain current model. By combining eqn (4) and (7), V can be expressed in terms of ϕ:
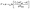 | (8) |
 | (9) |
Here, W is the channel width. μeff denotes the effective electron mobility, which is initially assumed to be constant at μ0 for analytical tractability. Field-dependent correction is introduced in a later section. Under steady-state conditions, the drain current is spatially invariant along the channel, and eqn (9) can therefore be integrated to yield
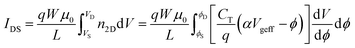 | (10) |
 | (11) |
This expression provides a continuous and physically consistent description of the drain current across all operating regimes of the 2D FET, from subthreshold to strong inversion, without requiring artificial segmentation of the bias regions. Although the analytical structure of this core model has been introduced in the literature,15,16 the following sections detail the additional physical mechanisms and the original contributions of our model.
2.2 Lambert W function for SPICE-compatible model
To evaluate the drain current using the core model, ϕS and ϕD should be determined by solving eqn (8) with V = VS and VD, respectively. However, because ϕ appears implicitly in this equation, previous studies have relied on iterative numerical approaches such as the Newton–Raphson or Halley's methods.15,16 These iterative procedures are unsuitable for SPICE-based circuit simulations, which require computationally efficient and robust analytical formulations. To address this limitation, we employed the Lambert W function, defined by the relation W(x)eW(x) = x. This function enables the explicit inversion of transcendental equations where a variable appears inside and outside the exponential term. By leveraging this property, a closed-form analytical expression for the surface potential ϕ is derived (detailed derivations are provided in SI Note S1):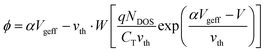 | (12) |
However, the standard SPICE simulators do not support the Lambert W function. Moreover, although the Lambert W function provides a compact analytical solution, its steep derivative and near-singular logarithmic behavior around ϕ = 0 can lead to numerical instability and convergence issues in circuit simulations, where continuity and smoothness of derivatives are critical.
A piecewise analytical approximation of the Lambert W function was introduced to ensure a robust numerical performance across the entire bias range. For small values of ϕ near zero, a Taylor series expansion is employed to approximate the Lambert W function, thereby stabilizing its derivatives, mitigating numerical sensitivity in this region. This approximation is particularly effective in the subthreshold regime, where the argument of the Lambert W function reduces, and the carrier density decays exponentially. For moderate to high values of ϕ, the model transitions seamlessly to a nested-logarithmic approximation of the Lambert W function, which retains high accuracy. The maximum relative error of this approximation is only 0.914% compared with the exact Lambert W function.23 Accordingly, two piecewise-defined functions, W+(x) and W−(x), are introduced to approximate the principal branch of the Lambert W function over the domains x ≥ 0.1 and x < 0.1, respectively:
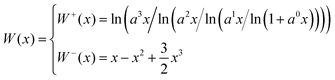 | (13) |
In this approximation, the coefficients are defined as a3 = 50/47, a2 = 6/5a3 = 60/47, a1 = 2a2 = 120/47, and a0 = a1 = 120/47.23 Through this smooth piecewise analytical approximation of the Lambert W function, our model achieved numerical stability while maintaining full compatibility with SPICE-based circuit simulation environments.
2.3 Interface trap model
Interface traps constitute a critical nonideal factor that significantly influences the electrical characteristics of 2D FETs. Although TMDs exhibit intrinsically dangling-bond-free surfaces, finite densities of interface traps inevitably arise at the gate oxide/TMD interfaces. For example, sulfur vacancies in MoS2 introduce defect-induced trap states within the bandgap.24 Additionally, gate oxides, particularly high-k dielectric materials, typically contain oxygen vacancies that further contribute to the interface trap states. As a result, interface trap densities (Dit) at oxide/TMD interfaces reported in previous literature broadly range from 1011 to 1013 cm−2 eV−1.24 In n-type devices, these interface traps become negatively charged upon electron occupation, introducing additional fixed charges that perturb channel electrostatics. This phenomenon leads to the degradation of the subthreshold swing and induces threshold voltage shifts, which cannot be captured by intrinsic electrostatic models alone. Therefore, incorporating the effects of interface traps into a compact drain-current model is essential for accurately reproducing the experimentally observed characteristics of 2D FETs.The density of electrons occupying the interface trap states (Nit) was modeled as a summation over multiple discrete energy levels, each weighted by the Fermi–Dirac distribution (Fig. S2),15,16 expressed as
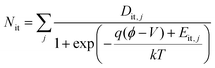 | (14) |
Here, Dit,j denotes the trap density and Eit,j represents the energy level of j-th trap state relative to the conduction band minimum. This multilevel formulation effectively captures the energetic distribution of interface traps, enabling accurate modeling of their cumulative impact on the device's behavior. To incorporate the electrostatic influence of interface traps, Nimp in eqn (1), (3) and (5) should be modified to Nimp − Nit. However, because Nit depends on ϕ and V, it exhibits spatial variation along the channel. Such spatial dependence prevents obtaining a closed-form analytical expression for the drain current via the direct integration of eqn (10). Consequently, previous studies have inevitably relied on numerical methods to account for interface trap effects13–16 or simply neglected them.11,17,25,26
To preserve the closed-form analytical formulation, our model introduces a quasi-static approximation where the spatially varying V is replaced by an effective fixed value. Specifically, the trap occupancy is evaluated at a representative potential V ≈ VD/2, under the assumption that VD is sufficiently small to maintain near-uniform V. Substituting V ≈ VD/2 into eqn (8) yields a constant representative surface potential ϕit, from which Nit can be approximated as spatially invariant:
 | (15) |
With Nit approximated as a constant, the need for position-dependent integration in eqn (10) is circumvented, enabling a fully closed-form drain current expression. By incorporating this approximation, the modified drain current model with interface trap effects is given by:
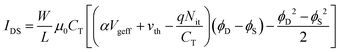 | (16) |
The correction term qNit/CT explicitly accounts for the shift in the channel electrostatics caused by trapped charges. This formulation preserves the analytical integrity of the model without requiring numerical integration, thereby enhancing its suitability for SPICE-compatible circuit simulations.
2.4 Field-dependent mobility model
Incorporating field-dependent mobility degradation is essential for enhancing the predictive accuracy of the model across realistic operating conditions of 2D FETs. For long-channel devices, the lateral electric field typically remains below the critical threshold for velocity saturation in TMDs (approximately 105 V cm−1); thus, the mobility degradation arising from the lateral-field-induced velocity saturation is negligible. However, atomically thin 2D TMDs strongly confine carriers near the gate-oxide interface, which significantly increases their susceptibility to scattering mechanisms driven by vertical electric fields. These vertical fields became particularly pronounced at high gate biases, substantially reducing the effective carrier mobility. To account for such vertical-field-induced mobility degradation, the effective carrier mobility μeff is empirically modeled as:27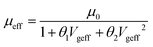 | (17) |
Here, θ1 and θ2 are empirical fitting parameters capturing the first- and second-order dependencies of mobility degradation on the vertical electric field, respectively. Replacing μ0 with the field-dependent μeff in the drain current expression allows the model to accurately represent experimentally observed device behavior, as demonstrated in the subsequent section. This modification preserves the closed-form analytical structure of the model, ensuring compatibility with SPICE-based circuit simulations and enabling reliable system-level modeling of circuits employing 2D FETs.
2.5 The limitation of the model
The present compact model is developed within the drift–diffusion framework, where carrier scattering predominates over ballistic transport. This approximation remains valid for devices whose channel length greatly exceeds the electron mean free path in TMDs (typically 5–20 nm at room temperature), ensuring that carrier transport occurs in the diffusive regime. However, as the channel length is reduced below approximately 50 nm, quasi-ballistic or fully ballistic effects may become non-negligible. In such cases, the analytical framework should be extended to include a ballistic correction term or reformulated using a Landauer-based formalism.Furthermore, the model assumes ideal ohmic contacts between the metal electrodes and the 2D TMD channel, thereby neglecting parasitic series resistance and Schottky barrier effects at the metal–semiconductor interface. This assumption facilitates SPICE compatibility and enhances numerical stability but limits the model's predictive accuracy under contact-limited conditions. Specifically, the absence of thermionic emission and Fowler–Nordheim tunneling mechanisms associated with Schottky barriers may cause the drain current to be slightly overestimated in the low-bias regime and underestimated in the high-bias regime.
3. Results and discussion
3.1 Model verification
To validate the proposed compact model for 2D FETs, we fabricated a reference MoS2 FET as shown in Fig. 1b (the detailed fabrication procedure is described in the Methods section). A heavily n-doped silicon substrate and 300-nm-thick thermally grown SiO2 layer served as the bottom gate electrode and bottom gate oxide, respectively. The top-gate stack consisted of an Au top-gate electrode and a 15-nm-thick Al2O3 dielectric layer. The thicknesses of the MoS2 channel and Al2O3 top-gate oxide were confirmed by atomic force microscopy (AFM), as shown in Fig. 1b. During the electrical measurements, the bottom gate and source terminals were grounded, and voltage biases were applied to the top gate and drain terminals. This measurement configuration was chosen because the influence of the bottom-gate bias on the channel was negligible owing to the large thickness of the bottom-gate oxide. Nevertheless, our compact model explicitly supports independent electrostatic modulation from top and bottom gates. The gate bias terms Vgt and Vgb were treated as independent variables in the model formulation, allowing for accurate simulation under dual-gate configurations.Fig. 2a presents a comparison of the measured and simulated transfer characteristics. The compact model accurately captured the device transfer behavior across the entire range of operations, from subthreshold to strong inversion. To achieve optimal agreement with the experimental data, three discrete interface trap states were introduced (j = 3 in eqn (14)). The parameters used in the simulation are listed in Table 1. Notably, the fitting parameter set {Nimp, Dit,j, Eit,j, μ0, θ1, θ2} was extracted using a particle swarm optimization (PSO) algorithm, which is a global optimization technique particularly well-suited for solving complex combinatorial problems (see Note S2 for details). By employing such an optimization algorithm, the key model parameters required for an accurate simulation can be efficiently extracted without relying on elaborate or time-consuming physical characterization techniques. Particularly, when multiple interdependent physical parameters jointly affect the device behavior, global optimization approaches, such as PSO, offer a practical and robust alternative to conventional experimental parameter extraction. This strategy enables accurate parameter extraction using only a limited set of electrical measurements from fabricated devices, thereby significantly streamlining the characterization process and broadening the applicability of the model to circuit-level designs and system-level integration.
Fig. 2b illustrates the individual and combined effects of the interface traps and mobility degradation on the accuracy of the compact model. When only the interface trap effect (Nit) is included (red curve), the model closely follows the measured data in the subthreshold regime but significantly deviates in the strong inversion region. Conversely, when only field-dependent mobility degradation (μeff) is considered (green curve), the model agrees well with the measured data in the strong inversion regime but fails to capture the subthreshold behavior accurately. These observations highlight that both nonidealities play distinct and complementary roles in different bias regimes. Therefore, the simultaneous incorporation of interface traps and mobility degradation (blue curve) is essential to achieve quantitative agreement with the experimental data across the full operating range of the device.
3.2 Validation with circuit-level simulation
Although reproducing single-device characteristics is necessary for compact model validation, it is insufficient to establish practicality in a circuit-level design. A truly predictive and SPICE-compatible compact model should demonstrate the ability to simulate the circuit-level behavior of 2D FETs. Although several prior studies have attempted to evaluate the performance of basic circuits such as inverters using their proposed compact models,12,13,16 the simulation results were not directly benchmarked against the experimental measurements from the fabricated circuits. Therefore, the validity of the previously proposed models remains only partially verified, and their practical reliability for circuit-level simulations is yet to be conclusively established.To address this limitation, we further validated the predictive capability of our compact model by simulating the operation of experimentally fabricated MoS2 FET-based circuits, including an inverter, a SRAM cell, a NAND gate, and a ring oscillator, as previously reported.28 In that study, depletion-load NMOS logic circuits were demonstrated exclusively using n-type MoS2 FETs. To enable complementary logic functionality, two distinct types of MoS2 FETs were deliberately fabricated: depletion-mode (D-mode) and enhancement-mode (E-mode) devices, realized by employing Al and Pd as the top-gate metals, respectively. Fig. 3 shows the transfer characteristics of the two types of devices. The Al-gated D-mode FET exhibited a substantial negative threshold voltage shift relative to the Pd-gated E-mode FET, which is consistent with the work function difference between Al and Pd. This dual-mode implementation enabled complementary logic behavior using only n-type MoS2 FETs, thereby providing a practical platform for validating the circuit-level applicability of 2D FETs.
 | ||
| Fig. 3 Transfer characteristics of MoS2 FETs with different gate materials. Simulated and measured transfer characteristics of enhancement-mode (E-mode, Al-gated) and depletion-mode (D-mode, Pd-gated) MoS2 FETs as reported in ref. 28. The model accurately captures the threshold voltage shift induced by the work function difference between Al and Pd, demonstrating its adaptability to different material configurations. | ||
Notably, as shown in Fig. 3, our compact model accurately reproduced the transfer characteristics of the D-mode and E-mode FETs, exhibiting excellent agreement across the entire bias range. Table S1 lists the simulation parameters used for these devices and highlights their key differences from those used in our devices. These results confirm the versatility and predictive capability of our compact model. Despite variations in material composition (e.g., gate metal, gate dielectric, or 2D channel material), structural configuration (e.g., layer thicknesses), and biasing scheme (e.g., single-gate versus dual-gate operation), the model consistently achieved high-fidelity agreement with experimental observations. This level of generalizability is critical for extending the compact modeling frameworks to a broad class of 2D FET architectures.
Fig. 4a–d compare the simulation results using our compact model with the experimental measurements from various MoS2 FET-based logic circuits.28Fig. 4a shows the voltage transfer characteristics (VTC) of an inverter composed of D-mode and E-mode FETs. The simulation closely reproduced the experimental VTC and accurately captured the switching threshold and output voltage swing. This confirms the ability of the model to predict logic-level transitions in complementary-like configurations. Fig. 4b shows the operation of a static random-access memory (SRAM) cell implemented using cross-coupled inverters. When the input Vin is set to a logic high (2 V) or low (0 V), the output Vout switches to the opposite logic state. Notably, the output state remains stable even after the input is disconnected (floating), as expected from the bistable behavior of the latch circuit. This memory-holding capability was accurately captured by simulation, validating the model's ability to reproduce feedback-dependent multistable circuit operations. Fig. 4c illustrates the functionality of the NAND gate constructed with MoS2 FETs. Because the input combinations vary over time, the simulated output precisely follows the NAND logic truth table. The close agreement between the measured and simulated waveforms confirms the robustness of the model in capturing the dynamic logic behavior under time-varying input conditions. Finally, Fig. 4d presents the output of the ring oscillator composed of five inverter stages connected by a feedback loop. In this configuration, the oscillation frequency is determined not only by the DC transfer characteristics of the individual MoS2 FETs but also by the parasitic capacitance at each inverter stage. Because our compact model does not explicitly incorporate a capacitance model (e.g., gate-to-source or gate-to-drain capacitances), we incorporated a representative node capacitance of approximately 0.37 pF per stage, based on values reported in prior analysis.28 With this addition, the simulated oscillation waveform exhibits excellent agreement with the experimental results, accurately reproducing the frequency and waveform shape. Collectively, these circuit-level validations confirm the generalizability and predictive accuracy of the proposed compact model, demonstrating its applicability at the single-device level and in the simulation of complex 2D FET-based circuits.
3.3 Discussion
To clarify the novelty and positioning of the present model, Table S2 summarizes representative compact models and specifies whether each includes interface-trap effects, quantum capacitance, and whether its simulation data were directly obtained from SPICE. As shown, most earlier models incorporate interface-trap effects, whereas quantum capacitance was generally neglected and has been considered only in a few recent studies.The current formulation of our model does not explicitly include quantum capacitance. However, because the analytical framework already contains an explicit density-of-states expression, incorporating quantum capacitance is straightforward. Its omission reflects only the absence of suitable experimental validation rather than any intrinsic limitation of the model.
The defining distinction of our work lies in its complete SPICE compatibility. Although several prior studies claimed SPICE readiness, most of their simulation data were not actually generated in SPICE environments, as ensuring convergence in SPICE requires a higher degree of analytical compactness than those models provided. Ref. 12, 13 and 16 presented some SPICE-based simulations, but these were limited to simple inverter or oscillator demonstrations, and most of their results were not produced in SPICE. In contrast, all simulations in this study were performed directly using SPICE, confirming full numerical stability and predictive accuracy from single-device characteristics to circuit-level operation.
It is also important to address the intrinsic variability of 2D FETs. The proposed compact model can accurately reproduce the I–V characteristics of various TMD-based devices by adjusting key fitting parameters. However, device-to-device variability may arise from factors not included in the current formulation, such as gate-length fluctuations or fabrication-induced defect variations. In such cases, fitting remains possible, but the extracted parameters may not correspond directly to their physical counterparts. Thus, while parameter tuning enables faithful reproduction of measured data, it cannot explain the physical origin of variability. Building a variability-aware model will require identifying the dominant sources of variation and incorporating statistical data from a sufficiently large number of devices. Future work will focus on extending the present model with such statistical datasets to more comprehensively capture variability effects.
4. Conclusions
In this study, we developed and experimentally validated a compact, SPICE-compatible model for 2D semiconductor transistors, enabling accurate and efficient simulation of device and circuit behavior across all operational regimes. The model uniquely integrates a closed-form analytical solution using an approximated Lambert W function and incorporates key physical phenomena, including interface trap dynamics and vertical-field-induced mobility degradation, within a continuous framework. These features eliminate the need for iterative numerical solvers and empirical parameter tuning, ensuring physical rigor and computational efficiency.Importantly, our model shows excellent agreement with experimental measurements not only at the single-device level but also across a suite of functional logic circuits fabricated with MoS2 FETs. These circuits include inverter chains, SRAM cells, NAND gates, and ring oscillators, all of which were accurately reproduced without compromising the analytical nature of the model. This comprehensive validation highlights the model's generalizability and predictive power, representing a significant advance in the circuit-level design with 2D semiconductors.
Future work should explore extending this modeling framework to additional 2D materials, scaling-induced effects, thickness-dependent electrostatics, and temperature-dependent behavior. Incorporating parasitic capacitance modeling and dynamic switching characteristics would further improve its applicability in high-speed and energy-efficient electronic designs. The proposed model, therefore, provides a foundation for a unified predictive toolset essential for the development of next-generation 2D-material-based integrated circuits.
5. Methods
5.1 Device fabrication
The MoS2 FET was fabricated on a heavily n-doped Si wafer (resistivity <0.005 Ω cm), which served as the back gate electrode. A 300 nm-thick silicon dioxide (SiO2) layer was grown on the wafer by thermal oxidation. Thin MoS2 flakes were mechanically exfoliated from bulk MoS2 (HQ graphene) using the Scotch tape method and transferred onto the Si/SiO2 substrate using a dry transfer technique with a polydimethylsiloxane (PDMS) stamp. Source and drain electrodes were patterned via electron-beam lithography, followed by deposition of Cr/Au (10 nm/50 nm) by thermal evaporation. Lift-off was performed by immersing the devices in acetone and methanol (CH3OH) for 3–4 h to remove the resist and complete the patterning. A 15-nm-thick aluminum oxide (Al2O3) gate dielectric was then deposited by atomic layer deposition (Nano-ALD2000, IPS) at 350 °C. Electron-beam lithography was used again to define the top-gate electrode region on the Al2O3 layer, followed by Cr/Au (10 nm/100 nm) deposition via thermal evaporation. A second lift-off process finalized the top-gate electrode patterning.5.2 Simulation
All circuit simulations were performed using LTspice, a freely available circuit simulation software package (see Note S3 for details).Conflicts of interest
The authors declare no competing interests.Data availability
The compact model described in this article was implemented and simulated using LTspice. The associated simulation code and model parameters, including PSO-optimized fitting sets, have been provided as part of the supplementary information (SI). The supplementary information includes detailed formulations of the model (closed-form surface-potential solution using the Lambert W function), the parameter-extraction procedure and pseudocode based on Particle Swarm Optimization, the SPICE-compatible compact-model pseudocode, and supplementary figures and tables supporting the main text. See DOI: https://doi.org/10.1039/d5nh00341e.Acknowledgements
This work was supported by a grant from the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT and MOE) (RS-2024-00334953, RS-2025-16063688).References
- J. A. Robinson, APL Mater., 2018, 6, 58202 CrossRef.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS.
- A. Nourbakhsh, A. Zubair, R. N. Sajjad, T. K. G. Amir, W. Chen, S. Fang, X. Ling, J. Kong, M. S. Dresselhaus, E. Kaxiras, K. K. Berggren, D. Antoniadis and T. Palacios, Nano Lett., 2016, 16, 7798–7806 CrossRef CAS PubMed.
- D. Jiang, Z. Liu, Z. Xiao, Z. Qian, Y. Sun, Z. Zeng and R. Wang, J. Mater. Chem. A, 2022, 10, 89–121 RSC.
- E. Singh, P. Singh, K. S. Kim, G. Y. Yeom and H. S. Nalwa, ACS Appl. Mater. Interfaces, 2019, 11, 11061–11105 CrossRef CAS.
- S. Rehman, M. F. Khan, H. D. Kim and S. Kim, Nat. Commun., 2022, 13, 2804 CrossRef CAS PubMed.
- D. Sarkar, W. Liu, X. Xie, A. C. Anselmo, S. Mitragotri and K. Banerjee, ACS Nano, 2014, 8, 3992–4003 CrossRef CAS PubMed.
- S. Zeng, C. Liu and P. Zhou, Nat. Rev. Electr. Eng., 2024, 1, 335–348 CrossRef.
- I. J. Umoh, T. J. Kazmierski and B. M. Al-Hashimi, IEEE Trans. Nanotechnol., 2013, 12, 427–435 CAS.
- S. Fregonese, M. Magallo, C. Maneux, H. Happy and T. Zimmer, IEEE Trans. Nanotechnol., 2013, 12, 539–546 CAS.
- D. Jiménez, Appl. Phys. Lett., 2012, 101, 243501 CrossRef.
- S. V. Suryavanshi and E. Pop, J. Appl. Phys., 2016, 120, 224503 CrossRef.
- S. A. Ahsan, S. K. Singh, C. Yadav, E. G. Marin, A. Kloes and M. Schwarz, IEEE Trans. Electron Devices, 2020, 67, 5188–5195 CAS.
- E. Yarmoghaddam, N. Haratipour, S. J. Koester and S. Rakheja, IEEE Trans. Electron Devices, 2020, 67, 389–396 CAS.
- W. Cao, J. Kang, W. Liu and K. Banerjee, IEEE Trans. Electron Devices, 2014, 61, 4282–4290 Search PubMed.
- C. Yadav, A. Agarwal and Y. S. Chauhan, IEEE Trans. Electron Devices, 2017, 64, 1261–1268 Search PubMed.
- H. Omdeh Ghiasi, A. Safarian and M. Pourfath, IEEE Trans. Electron Devices, 2019, 66, 5011–5018 Search PubMed.
- Z. Y. Yan, Z. Hou, F. Wu, R. Zhao, J. Yan, A. Yan, Z. Wang, K. H. Xue, H. Liu, H. Tian, Y. Yang and T. L. Ren, 2D Mater., 2023, 10, 045026 CrossRef CAS.
- A. Mounir, B. Iñiguez, F. Lime, A. Kloes, T. Knobloch and T. Grasser, Solid-State Electron., 2023, 207, 108702 CrossRef CAS.
- A. M. de Souza, D. R. Celino, R. Ragi and M. A. Romero, IEEE Access, 2025, 13, 138112–138124 Search PubMed.
- H. P. Komsa, S. Kurasch, O. Lehtinen, U. Kaiser and A. V. Krasheninnikov, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 035301 CrossRef.
- A. Kormányos, G. Burkard, M. Gmitra, J. Fabian, V. Zólyomi, N. D. Drummond and V. Fal’ko, 2D Mater., 2015, 2, 022001 CrossRef.
- D. A. Barry, J. Y. Parlange, L. Li, H. Prommer, C. J. Cunningham and F. Stagnitti, Math. Comput. Simul., 2000, 53, 95–103 CrossRef.
- P. Xia, X. Feng, R. J. Ng, S. Wang, D. Chi, C. Li, Z. He, X. Liu and K. W. Ang, Sci. Rep., 2017, 7, 1–9 CrossRef.
- E. G. Marin, S. J. Bader and D. Jena, IEEE Trans. Electron Devices, 2018, 65, 1239–1245 CAS.
- S. A. Ahsan, S. K. Singh, M. A. Mir, M. Perucchini, D. K. Polyushkin, T. Mueller, G. Fiori and E. G. Marin, IEEE Trans. Electron Devices, 2021, 68, 3096–3103 CAS.
- P. K. McLarty, S. Cristoloveanu, O. Faynot, V. Misra, J. R. Hauser and J. J. Wortman, Solid-State Electron., 1995, 38, 1175–1177 CrossRef CAS.
- H. Wang, L. Yu, Y. H. Lee, Y. Shi, A. Hsu, M. L. Chin, L. J. Li, M. Dubey, J. Kong and T. Palacios, Nano Lett., 2012, 12, 4674–4680 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2026 |