 Open Access Article
Open Access ArticleThe effects of aspect ratio and orientation on the mechanical properties of nanocomposites reinforced with carbon nanotubes
Robert J
Young
 *a,
Mufeng
Liu
*a,
Mufeng
Liu
 a,
Wei
Yang
a,
Wei
Yang
 *b and
Junhong
Pu
*b and
Junhong
Pu
 *c
*c
aNational Graphene Institute and Department of Materials, University of Manchester, Manchester M13 9PL, UK. E-mail: robert.young@manchester.ac.uk
bCollege of Polymer Science and Engineering, National Key Laboratory of Advanced Polymer Materials, Sichuan University, Chengdu 610065, China. E-mail: weiyang@scu.edu.cn
cResearch Institute for Intelligent Wearable Systems, School of Fashion and Textiles, The Hong Kong Polytechnic University, Kowloon, Hong Kong, China. E-mail: Junhong.pu@polyu.edu.hk
First published on 22nd October 2025
Abstract
Many studies have been carried out on the effect of the addition of carbon nanotubes on the mechanical properties of polymer-based nanocomposites. A fundamental understanding of the mechanisms of reinforcement and the factors that control mechanical properties has been hampered by the lack of measurements on specimens with well-characterised nanotube microstructures. In the present study we have used a series of multi-walled carbon nanotubes (MWCNTs) with different aspect ratios (length/diameter) to prepare nanocomposites and determine their mechanical properties as a function of nanotube volume fraction. In addition a similar investigation has been carried out on the effect of MWCNT alignment for one type of nanotube, with nanotube orientation being determined from the quantitative analysis of transmission electron micrographs of microtomed sections of the nanocomposites. The findings have been analysed using a new theory that combines the rule of mixtures with shear lag theory. Overall it is predicted that the stiffness of the nanocomposites depends only upon the aspect ratio, orientation and volume fraction of the MWCNTs and is independent of their Young's modulus. Good agreement is found between the experimental data and theoretical analysis. This is of profound importance for our understanding of the mechanisms of reinforcement of CNT/polymer nanocomposites and points to how the properties of polymer-based nanocomposite systems may be optimised in the future.
New conceptsA simple theory has been developed and employed to explain the dependence of the stiffness of polymer-based nanocomposites reinforced with carbon nanotubes. The theory predicts that the stiffness depends only upon the aspect ratio, orientation and volume fraction of the nanotubes and is independent of their Young's modulus. A new approach has been developed to quantify the orientation of the MWCNTs from the analysis of microtomed sections imaged using a transmission electron microscope. The theory has been tested upon a series of nanocomposites reinforced with a set of MWCNTs with known nanotube aspect ratios, orientations and volume fractions. Good agreement is found between the experimental results and theoretical analysis. It is proposed that the findings will be of major importance to our understanding of the mechanical properties of nanocomposites in general. |
Introduction
Carbon nanotubes (CNTs) are known to have high levels of intrinsic stiffness and strength,1 with Young's moduli in the order of 1 TPa and strengths in the range 50–100 GPa. They have therefore long been thought of as ideal fillers for nanocomposites2–7 but their performance often falls short of expectations.8 Two issues that have arisen are the expected levels of intrinsic reinforcement from a high-modulus 1D nanofiller and the effect of CNT alignment on the mechanical properties of polymer–nanotube composites.8 A major step forward in our understanding was the study of Blighe et al.9 who employed Raman spectroscopy10 to separate intrinsic reinforcement from orientation effects for coagulation-spun polymer–nanotube composite fibres. They showed that single-walled carbon nanotubes (SWCNTs) had an effective modulus in nanocomposite fibres of around 480 GPa and that the stiffness of the fibres depended upon the orientation of the SWCNTs. Moreover, they demonstrated that continuum mechanics theory is still applicable at the near-molecular level.The present study brings together state-of-the art characterisation of the microstructure of CNT–polymer nanocomposites using transmission electron microscopy11,12 and its effect on mechanical properties along with a recent new understanding of the mechanisms of reinforcement.13 This has been carried out by producing polymer-based nanotubes using a set of nanocomposites with randomly oriented multi-walled carbon nanotubes with three different aspect ratios and samples of one type of nanotube with different degrees of alignment. Image analysis has been employed to quantify the orientation of the MWCNTs in the specimens and the mechanical properties have been analysed in terms of a theoretical approach13 that combines shear-lag theory with the rule of mixtures.
Experimental
Materials
An ethylene-α-octene block copolymer (OBC) (Infuse 9807), with a density of 0.866 g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−3 and a melt flow rate of 15 g/10 min, was obtained from Dow Chemical Co. (Midland, MI, USA). MWCNTs with the same diameter of 10–20 nm but different lengths were employed. Nanotubes XFM13 and XFM16 with lengths of 10–30 μm and 0.5–2 μm, respectively, were purchased from XFNANO Inc. (Nanjing, China), and TNIM-3 MWCNTs with a length of 20–100 μm were purchased from Chengdu Institute of Organic Chemistry, Chinese Academy of Sciences (Chengdu, China). The density of MWCNTs is 2.1 g
cm−3 and a melt flow rate of 15 g/10 min, was obtained from Dow Chemical Co. (Midland, MI, USA). MWCNTs with the same diameter of 10–20 nm but different lengths were employed. Nanotubes XFM13 and XFM16 with lengths of 10–30 μm and 0.5–2 μm, respectively, were purchased from XFNANO Inc. (Nanjing, China), and TNIM-3 MWCNTs with a length of 20–100 μm were purchased from Chengdu Institute of Organic Chemistry, Chinese Academy of Sciences (Chengdu, China). The density of MWCNTs is 2.1 g![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cm−3. The aspect ratio of the nanotubes was calculated from the mean values of the length and diameter giving a set of three types of nanotubes with aspect ratios, s, of 4000 (SD-4000), 1300 (SD-1300) and 80 (SD-80).12 The surface chemistry of all MWCNTs is similar and the MWCNTs were used without further treatment. SD-1300 nanotubes were also employed for the analysis of the effect of the nanotube aspect ratio and nanotube alignment on mechanical properties.
cm−3. The aspect ratio of the nanotubes was calculated from the mean values of the length and diameter giving a set of three types of nanotubes with aspect ratios, s, of 4000 (SD-4000), 1300 (SD-1300) and 80 (SD-80).12 The surface chemistry of all MWCNTs is similar and the MWCNTs were used without further treatment. SD-1300 nanotubes were also employed for the analysis of the effect of the nanotube aspect ratio and nanotube alignment on mechanical properties.
Sample preparation
The OBC polymer and MWCNTs were melt compounded in an internal mixer (XSS-300, Shanghai Kechuang Rubber Plastics Machinery Set Ltd., China) with a rotor speed of 50 rpm at 150 °C for 8 min.To determine the effect of the CNT aspect ratio, after compounding the OBC nanocomposites were compression moulded into sheets, at 150 °C for 10 min under a pressure of 10 MPa. All the preparation processes were the same except for the type and content of MWCNTs, as it is known12 that processing can influence the morphology and distribution of MWCNTs.
To determine the effect to CNT alignment, the OBC copolymer was added into the mixer first, and after 30 s, MWCNTs were added and melt compounding continued for another 8 min, after which the mixture was taken out and cut up. The MWCNTs were then aligned using a BOY 2CXS auxiliary injection unit with an injection speed of 38.4 ccm s−1 at a set temperature of 180 °C for the plasticizing section and 170 °C for the nozzle (diameter ∼1 mm). The injected samples were cooled down quickly using cold water and cut into strips. Samples with randomly oriented MWCNTs were compression-moulded at 180 °C for 10 min under a pressure of 10 MPa. They were produced in the form of sheets with a thickness of about 1.0 mm that were cut into strips of the same length.
Dispersion of MWCNTs
The dispersion of MWCNTs in the OBC nanocomposites was characterized using a transmission electron microscope (TEM, Philips CM120) equipped with a field emission gun (FEG) operating at 200 kV. For TEM characterization, ultrathin sample sections with a thickness of 50–100 nm were cut using a Leica EM UC6 ultramicrotome (Leica Microsystems, Wetzlar, Germany) at −120 °C from the cross-section of compression molded plates. Sections were also cut parallel to the injection direction from the injection-shaped specimens.The orientation distributions of the MWCNTs in the micrographs were analysed using the OrientationJ plug-in of the ImageJ open-source software. This is an image processing program developed for biomedical image analysis at the US National Institutes of Health and the Laboratory for Optical and Computational Instrumentation (LOCI, University of Wisconsin). The images were analysed in the form of JPEG grayscale TEM micrographs. ImageJ digitises the images and can be used to calculate the area and pixel value statistics of user-defined intensity-thresholded objects and measure distances and angles. The orientation is evaluated for every pixel of the image based upon the structure tensor as explained by Rezakhaniha et al.14
Tensile tests
Tensile tests were conducted using a universal tensile instrument (Model 5967, Instron Instrument, USA) at a crosshead speed of 100 mm min−1 at room temperature with a gauge length of 10 mm. The filaments with a length of 25 mm and dumb-bell samples with the dimensions of 25 mm × 2 mm × 1 mm cut from pressed plates were used. The stiffness of the elastomeric materials was determined from the stress at a high strain, rather than the initial slope of the stress–strain curve. The strain was determined from the crosshead displacement. At least five samples were tested and the average results were reported.Theoretical analysis
It has been shown15 that the combination of the rule of mixtures and shear-lag analysis can be used successfully for the analysis of the reinforcement of polymers with graphene nanoplatelets (GNPs). The well-established rule of mixtures16 predicts that the modulus of a nanocomposite, Ec, is given by| Ec = EfVf + Em(1 − Vf) | (1) |
Young et al.15 evaluated the reinforcing efficiency of graphene-based nanofillers in a number of polymers of different stiffnesses ranging from soft (e.g. elastomers) to rigid (e.g. epoxy resins). They showed that the stiffness of the nanocomposites, Ec, generally increased monotonically with a filler volume fraction, Vf, following the simple rule-of-mixtures (eqn (1)). The actual filler modulus depends upon a number of factors including the dimensions of the reinforcing particles as well as their inherent stiffness. Assuming that a similar relationship can be applied to CNTs, eqn (1) can be modified to take these factors into account15 by replacing Ef with Eeffηoηl to give
| Ec = Eeffηoη1Vf + Em(1 − Vf) | (2) |
It is shown in the SI that as long as Eeff ≫ Em, the value of Ec for the nanocomposite is found to be independent of Eeff. Further analysis in the SI shows that taking into account the packing of the CNTs in the polymer and the rule of mixtures leads to a simple equation for Young's modulus of the nanocomposites, Ec of the form
 | (3) |
Results
Effect of the CNT aspect ratio on the mechanical properties of the nanocomposites
The dispersion of the three different types of MWCNTs in the nanocomposites is shown in the TEM micrographs in Fig. 1 for a volume fraction of 0.020. It can be seen that the nanotubes are relatively well dispersed and show little preferred alignment. | ||
| Fig. 1 TEM micrographs of the MWCNT–polymer nanocomposites with volume fractions of 0.020 of the 3 types of CNTs with different aspect ratios, s. | ||
The dependence of the mechanical properties of the nanocomposites with MWCNTs on three different aspect ratios was determined as a function of volume fraction as reported in our earlier publication.12 Since the polymers are essentially elastomers, the stiffness can be determined from the stress at 300% strain. The stiffness values of the nanocomposites are summarised in Table S1 in the SI. Fig. 2 shows the dependence of the stress at 300% strain (divided by the value for the pure polymer) upon CNT volume fraction. It can be seen that the stiffness increases with volume fraction and moreover, for a given volume fraction, the level of stiffness increases with the CNT aspect ratio. The data in Fig. 2 were fitted to the relationship in eqn (3) for appropriate values of aspect ratio s and it can be seen that the data fall close to the theoretical curves. A value of Krenchel orientation factor ηo of 0.2, assuming a random orientation of the CNTs,9 was used in each case (Fig. 1).
 | ||
| Fig. 2 Stiffness of the nanocomposites as a function of MWCNT volume fraction for the CNTs with different aspect ratios. The data were fitted to eqn (3) using appropriate values of seff. | ||
Although the experimental data fall close to the theoretical lines the values of aspect ratio predicted from the theory are significantly lower than the nominal values determined for the CNTs.12 Hence values of effective aspect ratio, seff, used to fit the theoretical curves to the experimental data are cited rather than the nominal values. In the case of SD-80 CNTs the data are fitted by an seff value of 25, which is around 1/3 of the nominal value of 80. In contrast, the data for SD-4000 CNTs are fitted by a value of seff of 40, i.e. only 1/100 of the starting value.
This behaviour can be explained through a number of factors. Firstly, the theory assumes that the CNTs remain perfectly straight in nanocomposites. Fig. 1, which presents 50–100 nm thick sections through the nanotubes, shows that lengths of the CNTs are wavy and looped. Secondly, the dimensions of the nanotubes were determined before they were incorporated into the polymer and they can be shortened by attrition during processing.12,20 These observations are significant in that they show that by using nanotubes that are initially 50× longer only give a level of stiffening less than a factor of 2 higher. Guo et al.20 made a similar observation for a MWCNT/polycarbonate nanocomposite pointing out that regardless of the original aspect ratio of the nanotubes, they tend to have similar effective values after processing. Another factor is that the higher aspect ratio and longer CNTs will be more prone to folding and looping than shorter ones, again reducing their effective aspect ratio.
Effect of CNT orientation on the mechanical properties of the nanocomposites
The dependence of the mechanical properties of the nanocomposites was determined as a function of orientation for different volume fractions of SD-1300 MWCNTs. Different levels of alignment were obtained by preparing specimens of the same formulations using different processing techniques.11 As explained earlier, the specimens with randomly oriented CNTs were prepared by compression moulding whereas those with aligned CNTs were produced using injection shaping.Fig. 3 shows TEM micrographs of the nanocomposites with randomly-oriented and aligned MWCNTs for a volume fraction of 0.0896. Polar plots of the orientation of the CNTs determined using the OrientationJ plug-in of ImageJ are also presented for each micrograph. It is possible to determine the orientation distribution function (ODF)21 from the polar plots in Fig. 3 using the approach proposed by Liu and Kumar22 for the quantitative characterisation of CNT orientation distributions using polarized Raman spectroscopy. In this case, the intensity of the scattering as a function of the angle of rotation of the specimen, Φ is given by an equation of the form21,22
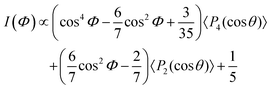 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 are second- and fourth-order orientation parameters22 that are analogous to similar parameters used in the analysis of molecular orientation in polymers.23 An equation of this form can be employed to analyse the data in the polar plots in Fig. 3 and determine 〈P2(cos
θ)〉 are second- and fourth-order orientation parameters22 that are analogous to similar parameters used in the analysis of molecular orientation in polymers.23 An equation of this form can be employed to analyse the data in the polar plots in Fig. 3 and determine 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 from the micrographs. The solid lines in Fig. 3(b) and (d) are fits of the experimental intensity data to eqn (4) obtained using Origin 19 graph-plotting software (OriginLab Corporation, Northampton, Ma, USA), with 〈P2(cos
θ)〉 from the micrographs. The solid lines in Fig. 3(b) and (d) are fits of the experimental intensity data to eqn (4) obtained using Origin 19 graph-plotting software (OriginLab Corporation, Northampton, Ma, USA), with 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 as the fitting parameters. The individual values are indicated in the figures. A similar analysis for a specimen of the same nanocomposite system with a volume fraction of 0.0546 is given in Fig. S2 of the SI.
θ)〉 as the fitting parameters. The individual values are indicated in the figures. A similar analysis for a specimen of the same nanocomposite system with a volume fraction of 0.0546 is given in Fig. S2 of the SI.
The measurements reported in Fig. 3 and Fig. S2 for the TEM micrographs are for relatively small regions of the specimens of 2 μm × 2 μm size (i.e. 4 μm2). Similar measurements were therefore carried out on a number of other sections for both randomly oriented and aligned specimens, with volume fractions of 0.0546 and 0.0896. The values of 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 determined from all these findings are summarised in Table 1 for Vf = 0.0546 and Table 2 for Vf = 0.0896.
θ)〉 determined from all these findings are summarised in Table 1 for Vf = 0.0546 and Table 2 for Vf = 0.0896.
〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 θ)〉 |
〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 θ)〉 |
η o | |
|---|---|---|---|
| Random 1 | 0.103 | 0.134 | 0.289 |
| Random 2 | 0.029 | −0.126 | 0.188 |
| Random 3 | 0.297 | 0.054 | 0.382 |
| Random 4 | 0.167 | 0.015 | 0.299 |
| Mean ηo | 0.290 ± 0.080 | ||
| Aligned 1 | 0.384 | 0.381 | 0.507 |
| Aligned 2 | 0.357 | 0.440 | 0.505 |
| Aligned 3 | 0.281 | 0.269 | 0.422 |
| Aligned 4 | 0.307 | 0.352 | 0.456 |
| Mean ηo | 0.472 ± 0.041 | ||
〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 θ)〉 |
〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 θ)〉 |
η o | |
|---|---|---|---|
| Random 1 | 0.102 | 0.088 | 0.278 |
| Random 2 | 0.100 | 0.054 | 0.269 |
| Random 3 | 0.066 | −0.008 | 0.236 |
| Mean ηo | 0.261 ± 0.022 | ||
| Aligned 1 | 0.508 | 0.552 | 0.616 |
| Aligned 2 | 0.575 | 0.916 | 0.738 |
| Aligned 3 | 0.286 | 0.166 | 0.401 |
| Aligned 4 | 0.344 | 0.432 | 0.495 |
| Mean ηo | 0.563 ± 0.146 | ||
The value of the Krenchel orientation parameter can be determined directly from the values of 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 determined from the TEM micrographs using the following relationship21
θ)〉 determined from the TEM micrographs using the following relationship21
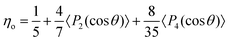 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 are both equal to 0, the value of η0 is 1/5. The values of ηo for each TEM micrograph analysed are given in Tables 1 and 2 along with the mean and standard deviation for each set. It can be seen for both volume fractions investigated that the mean values of ηo for the randomly oriented specimens are slightly higher than 0.2. This indicates that the CNTs in the specimens have some in-plane alignment, presumably as a result of the compression moulding process. In contrast for the specimens with aligned CNTs the ηo values are of the order of 0.5 showing the presence of preferred CNT alignment. The level of alignment is, however, far from perfect for which in this case ηo = 1 since 〈P2(cos
θ)〉 are both equal to 0, the value of η0 is 1/5. The values of ηo for each TEM micrograph analysed are given in Tables 1 and 2 along with the mean and standard deviation for each set. It can be seen for both volume fractions investigated that the mean values of ηo for the randomly oriented specimens are slightly higher than 0.2. This indicates that the CNTs in the specimens have some in-plane alignment, presumably as a result of the compression moulding process. In contrast for the specimens with aligned CNTs the ηo values are of the order of 0.5 showing the presence of preferred CNT alignment. The level of alignment is, however, far from perfect for which in this case ηo = 1 since 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 and 〈P4(cos
θ)〉 and 〈P4(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉 are then both equal to unity.21
θ)〉 are then both equal to unity.21
The dependence of the mechanical properties of the nanocomposites with MWCNTs either randomly oriented or aligned was determined as a function of volume fraction as reported in our earlier publication.11 The stiffness values of the nanocomposites are summarised in Table S2 in the SI. Since the polymers are essentially elastomers, the stiffness can best be determined from the stress at a high strain, such as the UTS (i.e. ∼200% strain). Fig. 4 shows the dependence of the stress at the UTS (divided by the value for the pure polymer, UTS0) upon CNT volume fraction, for both randomly oriented or aligned CNTs.
 | ||
| Fig. 4 UTS of the nanocomposites as a function of MWCNT volume fraction for randomly-oriented or aligned SD-1300 CNTs compared with the UTS of the matrix. The data were fitted to eqn (3) using an seff value of 22. | ||
Eqn (3) was first fitted to the data for the randomly aligned MWCNTs using a value of η0 = 0.27 (for the randomly aligned CNTs, Tables 1 and 2). This generated a value of seff ∼22, which was then used to determine an ηo value to fit the data for the aligned specimen using the same type of CNT. This generated a value of ηo = 0.53. It should be noted that the seff value of 35 was determined for the same SD-1300 MWCNTs in Fig. 2. The lower level of seff for the same nanotubes in Fig. 4 is the result of the nanocomposites in this case being processed by an additional injection shaping step, leading to a further reduction in effective MWCNT aspect ratio, due most likely to CNT attrition.
It is interesting to compare the ηo value generated for the aligned specimen from the mechanical property data in Fig. 4 with that determined from the analysis of the TEM micrographs listed in Tables 1 and 2. A mean ηo value of 0.472 ± 0.041 is found for the oriented specimens with Vf = 0.0546 and ηo = 0.563 ± 0.146 for the specimen with Vf = 0.0896. Overall this demonstrates good agreement between the theory and experimental data.
Discussion
It is clear that we have confirmed that the mechanical properties of nanocomposites reinforced with carbon nanotubes can be analysed through the use of continuum mechanics. In particular, combining the rule of mixtures with shear lag theory enables studying the effect of CNT aspect ratios and orientations on the stiffness of the nanocomposites to be modelled. One important finding is that nanocomposite stiffness is independent of the Young's modulus of the CNTs as long as the nanotubes are very much stiffer than the polymer matrix.It has been demonstrated that it is possible to quantify the orientation of the CNTs in a nanocomposite from the analysis of TEM images. Although each image is from a region of only around 4 μm2 of the nanocomposite, average levels of orientation can be determined using a number of images. It has also been shown that the Krenchel orientation factor, ηo, can be determined directly from the results of the image analysis. There may also be scope to use the image analysis method to determine CNT waviness as well as orientation as has been demonstrated for collagen fibres.14 In the case of CNTs, however, this may be of limited use as the TEM sections are normally only from small lengths of the nanotubes. The level of CNT dispersion and cluster size are other factors of interest and it may be possible in the future to analyse them as well.
It is interesting to compare the results of the TEM image analysis with other approaches such as from fast Fourier transform of scanning electron micrographs (SEM)24 or polarised Raman spectroscopy.10,22 Brandley et al.24 showed that it was possible to determine the Hermans orientation parameter (related to 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉) from SEM images of CNT veils, rather than for CNTs in a nanocomposite. Polarised Raman spectroscopy10,22 enables a full analysis of the orientation distribution of CNTs in a nanocomposite and eqn (4) was developed originally for the Raman method. The technique does, however, have some drawbacks in that the Raman laser spot samples have only a small area (∼1 μm2) and measurements are taken on the surface of the specimen rather than from the bulk. It will also be of interest to correlate the findings of these microscopic methods of orientation analysis with bulk techniques such as wide- or small-angle X-ray diffraction.
θ)〉) from SEM images of CNT veils, rather than for CNTs in a nanocomposite. Polarised Raman spectroscopy10,22 enables a full analysis of the orientation distribution of CNTs in a nanocomposite and eqn (4) was developed originally for the Raman method. The technique does, however, have some drawbacks in that the Raman laser spot samples have only a small area (∼1 μm2) and measurements are taken on the surface of the specimen rather than from the bulk. It will also be of interest to correlate the findings of these microscopic methods of orientation analysis with bulk techniques such as wide- or small-angle X-ray diffraction.
A major finding of this study is that there is no great advantage of employing CNTs with very high aspect ratios. They may make processing of the nanocomposite more difficult and the effective aspect ratio within the nanocomposite is invariably less than the starting value. The effective aspect ratio will be reduced by a number of factors such as nanotube attrition, waviness, folding and looping, all of which are difficult to characterise directly. Our approach enables the effects of such processes on mechanical properties to be studied without having to identify the individual mechanisms.
Conclusions
We have demonstrated that the mechanics of reinforcement of MWCNT/polymer nanocomposites can be fundamentally understood using a set of well-characterised specimens with nanotubes of controlled aspect ratios and orientations. The behaviour has been interpreted using a continuum mechanics approach that combines the rule of mixtures with shear lag theory. The microstructures of the nanocomposites have been characterised using transmission electron microscopy and the orientation of the MWCNTs has been quantified using biomedical image analysis software. It has been shown that the level of reinforcement improves with increasing aspect ratio (length/diameter), volume fraction and orientation of the nanotubes. A major conclusion is that there is no advantage of starting with nanotubes of very high aspect ratios since their effective aspect ratio in the nanocomposite is reduced as a result of waviness, folding and looping, and through attrition during processing. Additionally, there is no advantage of employing nanotubes with very high levels of Young's modulus as long as they are very much stiffer than the matrix polymer. Overall, we expect that these findings will be of significant importance to our understanding of the mechanical properties of nanocomposites in general.Conflicts of interest
There are no conflicts to declare.Data availability
All of the data analysed are presented within the main paper or supplementary information (SI). Supplementary information includes a full derivation of eqn (3), tables of data for Fig. 2 and 4, and the analysis of TEM micrographs of nanocomposites with randomly-oriented and aligned MWCNTs for a volume fraction of 0.0546. See DOI: https://doi.org/10.1039/d5nh00638d.Acknowledgements
Our original study was supported by both the National Natural Science Foundation of China (NNSFC Grants 51422305 & 51721091) and the Sichuan Provincial Science Fund for Distinguished Young Scholars (2015JQO003).References
- D. G. Papageorgiou, Z. Li, M. Liu, I. A. Kinloch and R. J. Young, Nanoscale, 2020, 12, 2228–2267 RSC
.
- E. T. Thostenson, Z. Ren and T.-W. Chou, Compos. Sci. Technol., 2001, 61, 1899–1912 CrossRef CAS
.
- P. Kannan, S. J. Eichhorn and R. J. Young, Nanotechnology, 2007, 18, 235707 CrossRef
.
- S. Cui, I. A. Kinloch, R. J. Young, L. Noé and M. Monthioux, Adv. Mater., 2009, 21, 3591–3595 CrossRef CAS
.
- T.-W. Chou, L. Gao, E. T. Thostenson, Z. Zhang and J.-H. Byun, Compos. Sci. Technol., 2010, 70, 1–19 CrossRef CAS
.
- A. de la Vega, I. A. Kinloch, R. J. Young, W. Bauhofer and K. Schulte, Compos. Sci. Technol., 2011, 71, 160–166 CrossRef CAS
.
- Y. Martinez-Rubi, B. Ashrafi, J. Guan, C. Kingston, A. Johnston, B. Simard, V. Mirjalili, P. Hubert, L. Deng and R. J. Young, ACS Appl. Mater. Interfaces, 2011, 3, 2309–2317 CrossRef CAS
.
- I. A. Kinloch, J. Suhr, J. Lou, R. J. Young and P. M. Ajayan, Science, 2018, 362, 547–553 CrossRef CAS
.
- F. M. Blighe, K. Young, J. J. Vilatela, A. H. Windle, I. A. Kinloch, L. Deng, R. J. Young and J. N. Coleman, Adv. Funct. Mater., 2011, 21, 364–371 CrossRef CAS
.
- Z. Li, L. Deng, I. A. Kinloch and R. J. Young, Prog. Mater. Sci., 2023, 135, 101089 CrossRef CAS
.
- J. H. Pu, X. J. Zha, M. Zhao, S. Li, R. Y. Bao, Z. Y. Liu, B. H. Xie, M. B. Yang, Z. Guo and W. Yang, Nanoscale, 2018, 10, 2191–2198 RSC
.
- J. Qian, J.-H. Pu, X.-J. Zha, R.-Y. Bao, Z.-Y. Liu, M.-B. Yang and W. Yang, J. Polym. Res., 2019, 26, 275 CrossRef CAS
.
- Z. Li, M. Liu and R. J. Young, Nano Mater. Sci., 2024 DOI:10.1016/j.nanoms.2024.04.014
.
- R. Rezakhaniha, A. Agianniotis, J. T. C. Schrauwen, A. Griffa, D. Sage, C. V. C. Bouten, F. N. van de Vosse, M. Unser and N. Stergiopulos, Biomech. Model. Mechanobiol., 2012, 11, 461–473 CrossRef CAS
.
- R. J. Young, M. Liu, I. A. Kinloch, S. Li, X. Zhao, C. Vallés and D. G. Papageorgiou, Compos. Sci. Technol., 2018, 154, 110–116 CrossRef CAS
.
-
R. J. Young and P. A. Lovell, Introduction to Polymers, CRC Press, Boca Raton, 2011 Search PubMed
.
- R. J. Young, L. Deng, T. Z. Wafy and I. A. Kinloch, J. Mater. Sci., 2016, 51, 344–352 CrossRef CAS
.
- H. Liu and L. C. Brinson, Compos. Sci. Technol., 2008, 68, 1502–1512 CrossRef CAS
.
-
H. Krenchel, Fibre Reinforcement, Akademisk Forlag, Copenhagen, 1964 Search PubMed
.
- J. Guo, Y. Liu, R. Prada-Silvy, Y. Tan, S. Azad, B. Krause, P. Pötschke and B. P. Grady, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 73–83 CrossRef CAS
.
- J. Li, T. Guan, Z. Zhang, Y.-T. Fu, F.-L. Guo, P. Huang, Z. Li, Y.-Q. Li and S.-Y. Fu, Prog. Mater. Sci., 2025, 148, 101360 CrossRef CAS
.
- T. Liu and S. Kumar, Chem. Phys. Lett., 2003, 378, 257–262 CrossRef CAS
.
- M. Tanaka and R. J. Young, J. Mater. Sci., 2006, 41, 963–991 CrossRef CAS
.
- E. Brandley, E. S. Greenhalgh, M. S. P. Shaffer and Q. Li, Carbon, 2018, 137, 78–87 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2026 |

