 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio force prediction for single molecule force spectroscopy made simple
Pooja Bhat†
 ab,
Wafa Maftuhin†
ab,
Wafa Maftuhin† ac and
Michael Walter†
ac and
Michael Walter† *abd
*abd
aFIT Freiburg Centre for Interactive Materials and Bioinspired Technologies, University of Freiburg, Freiburg, Germany. E-mail: Michael.Walter@fmf.uni-freiburg.de
bCluster of Excellence LivMatS @ FIT, Freiburg, Germany
cUniversitas Negeri Surabaya, Surabaya, Indonesia
dFraunhofer IWM, MikroTribologie Centrum µTC, Freiburg, Germany
First published on 7th January 2026
Abstract
Bond rupture under the action of external forces is induced by temperature fluctuations. We show that measured forces from single molecule force spectroscopy experiments can be predicted from two quantities describing the bond that are the barrier to break the bond in absence of force as well as the maximal force the bond can withstand. The former can be obtained by a force-free transition state calculation and the latter is determined by a simple constrained geometry simulates forces (COGEF) calculation. Considering experimental temperature and force loading rate allows the prediction of measured bond rupture forces from a closed expression with very good accuracy.
Introduction
Mechanochemistry is the change or modification of chemical bonds through the action of mechanical forces. It allows for modification of materials via the application of external forces which are usually acting in the form of external stress. External forces offer the possibility to enable reactions that are improbable or not possible by other means, such as thermal or optical activation alone.1,2 Examples are the force induced change of ceiling temperature in a polymer3 or enabling reactions not thermally allowed by Woodward–Hoffmann rules.4–6Mechanochemistry acts on the molecular level, where bonds are broken or reformed, but mechanical forces are often applied to materials in rather unspecific methods like ball milling or ultra-sonification, where the force acting on specific bonds within the material is hard to control. Also the modification of molecular bonds by stretching of polymeric material7 and the application of rheological methods8 is complex due to the not well understood force distribution in complex materials, despite recent advances in this direction.9–11
The cleanest experimental observation of mechanochemical effects is given by measuring molecular forces in single molecule force spectroscopy (SMFS) experiments.4,6,12–17 Here, single polymer chains are stretched and force plateaus are observed when multiple bonds in monomers are broken.6 It is well understood that these plateaus reflect properties of the monomers experiencing the bond break.18 The force at bond break can also be determined from a sudden drop in the force extension curve.19–21 The numerical determination of force dependent barriers has been successfully employed by several groups22–26 and it was shown that experimental force–extension curves can be reproduced based on properties determined from ab initio calculations.18,27 Interestingly, often the properties of the monomer are sufficient to characterize the measured rupture forces.18
The most straightforward computational strategy to describe the effect of forces within calculations is probably the constrained geometry simulates forces (COGEF) method developed by Beyer.28,29 It is therefore applied in many mechanochemical investigations.30–32 The prediction of measured forces directly from COGEF has not been successful,32 as the forces obtained are up to an order of magnitude larger than the measured ones.33 The underlying reason is the lack of consideration of temperature8,12,34,35 as it is the temperature fluctuations that allow to overcome the barriers for bond breaking.36 Due to the stochastic nature of these fluctuations, only the most probable forces for bond rupture can be given. Recent investigations37,38 use empirical correlations between the force-free bond strength and force vs. length correlations to fit a linear model to existing experimental data in order to obtain some predictive power.
The determination of most probable forces has a long history and several expressions were derived mainly to analyse bond rupture or friction experiments.39–44 Expressions for most probable forces were given by Garg39 in a very general form. These were then used by Hummer, Dudko and co-workers.41 Rebinding effects occurring at low applied forces and slow pulling speed were considered also.43,45
Here we address the question of how the most probable force measured in experiment can be predicted from ab initio calculations without the need to fit to experimental data. We show that the experimentally measured force is mainly determined by two quantities describing the bond: its dissociation energy and the maximal force the bond can withstand. These two quantities can be obtained from ab initio calculations of the monomer.
The manuscript is organized as follows. We first formulate the theory and assumptions underlying our description of the bond rupture processes, where we detail the properties of the force dependent probability functions determining the most probable force. The effects of the speed of force increase (the loading rate) and the temperature are discussed. We then apply our description to published SMFS data. The paper ends with conclusions.
Results and discussion
Theory
We first consider an isolated bond of length d to develop our description. We treat bond breaking in a probabilistic picture in the spirit of Kauzman, Eyring, Evans and Ritchie46,47 where the bond potential U(d) is modified by the external force as illustrated in Fig. 1, where d denotes the bond length. The force F is aligned to the direction of the bond (the bond can rotate freely).48 Subtracting the work performed on the molecule by the force F leads to the enthalpy36| H(F;d) = U(d) − Fd | (1) |
 | ||
| Fig. 1 Force dependent potentials according to eqn (1) of the AuAg2 model sketched in Fig. 2. The barriers for bond rupture without force ΔU‡ = ΔH‡(0) and with force ΔH‡(F) are indicated. | ||
Apart from the bond-strength ΔU‡ often considered, there is another fundamental property of the bond, Fmax. This is the maximal force it can withstand, i.e. the maximal spatial derivative of U(d). It turns out, that the force dependence of the barrier ΔH‡(F) for many potentials can be expressed to good approximation in the form35,36
| ΔH‡(f) = ΔU‡(1 − f)2, | (2) |
| ΔH‡(F) = ΔU‡ − Fx‡ | (3) |
We now use the approximate form of the barrier in eqn (2) to derive the most probable force for bond rupture measured in the experiment under the assumption of a constant loading rate (rate of force increase). In order to illustrate the steps taken, we consider a simple linear AuAg2 toy molecule (depicted in Fig. 2) described by its potential energy obtained from effective medium theory as implemented in the atomic simulation environment (ASE).51 The potential in Fig. 1 is that of this model molecule where d is the length of the weaker Ag–Ag bond and the force F is considered to be applied to the two silver atoms directly.
 | ||
| Fig. 2 Barriers for breaking of the Ag–Ag bond under the constraint of a given external force F applied to the outer Au and Ag atoms. The numerical barrier (determined by an explicit inclusion of the external force) is compared to the analytical expression of eqn (2). The setup of the AuAg2 model is sketched. | ||
It is practically impossible to apply an external force directly on two bound atoms in reality. There are always other atoms and bonds mediating the external force to the bond that ruptures. We mimic this fact in a very simplistic picture by the additional Au atom representing the environment through which the force is transferred. When a force acts on the outer atoms, the atoms respond by arranging into a new minimum energy configuration. This situation can be simulated by displacing the outer atoms using the COGEF strategy and relaxing all other degrees of freedom. This in turn gives the corresponding force needed to stabilize the given outer length. Increasing the outer distance eventually leads to rupture of the Ag–Ag bond for ΔU‡ = 1.80 eV in our example. The maximal outer force appearing in this process is Fmax = 2.38 nN. These values completely define the form of the barrier according to eqn (2).
Alternatively, we may also determine the force dependent barrier using the external force is explicitly included (EFEI) strategy,48,52 where the potential at a fixed external force as in Fig. 1 is analyzed. This strategy leads to a barrier that interpolates between ΔH‡(F = 0) = ΔU‡ and ΔH‡(Fmax) = 0. Its form is closely resembled by the quadratic barrier from eqn (2).
The analytic expression from eqn (2) may therefore be used to derive additional analytic results to predict bond rupture at nonzero temperature. Bond breaking induced by thermal fluctuations is a probabilistic process. Denoting the probability that the bond is intact as P and assuming first order transitions,41 P follows
 | (4) |
Further simplifications can be achieved by considering a constant loading rate α35,39 such that the external force at a given time t satisfies F = αt. This assumption differs from that of a constant velocity of the surrounding of the bond sometimes used,53 but should be similar if the connected cantilever and polymer spring constant kc is much smaller than the spring constant of the bond k. This is practically always the case for the strong chemical bonds considered here as the spring constant of the environment kc typically involves thousands of co-monomers including the atomic force microscopy cantilever. This results in a very small total effective spring constant ktotal, for which the loading rate is proportional to velocity v as α = ktotalv, where ktotal ≈ kc (for kc ≪ k) is spring constant of system. The constant loading rate then defines the time required to reach the maximal force as tmax = Fmax/α.
With the force given by F = αt at all times and setting kr = 0, we may replace t = ftmax by f = F/Fmax and write eqn (4) as35
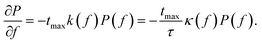 | (5) |
Here we have defined the relative rate
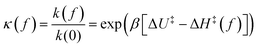 | (6) |
Eqn (5) can be formally integrated to lead to
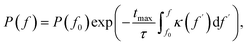 | (7) |
The distribution ∂P/∂f determines the most probable relative force f* measured in the experiment via7,55,56
 | (8) |
This function is usually highly peaked,35,57 such that within the peaking approximation the most probable force f* will be that at the maximum, i.e. f where
| ∂2P(f)/∂f2 = 0 | (9) |
(note that  ). Eqn (9) can be analytically solved for the Bell barrier from eqn (3), and we get36,47
). Eqn (9) can be analytically solved for the Bell barrier from eqn (3), and we get36,47
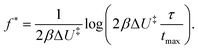 | (10) |
Analytic integration is also possible the quadratic form of the barrier from eqn (2) as detailed in Eqs. (S10–S18) resulting in
 | (11) |
In order to get a feeling about the validity of the peaking approximation, the distributions ∂P/∂F=F−1max∂P/∂f are shown in Fig. 3 for different loading rates and temperatures. We have used the analytic quadratic barrier eqn (2) using ΔU‡ and Fmax from AuAg2. Similar distributions appear for the decay in Josephson junctions,57 where an increasing external flux represents the increasing force as was noted already by Garg.39 These distributions are peaked in all cases and the peak position is always at forces smaller than Fmax. Increasing the loading rate (pulling speed) increases the mean force corresponding to the peak as there is less time to overcome the barrier at higher α. The distribution gets significantly broader with increasing α as the potential flattens with increasing force.
 | ||
| Fig. 3 ∂P/∂F of the AuAg2 molecule for (a) various loading rates at T = 300 K and (b) different temperatures at α = 100 nN s−1. The broken line indicates Fmax. | ||
The dependence on temperature is opposite to that on α. Increasing the temperature allows to overcome higher barriers which leads to peak positions at lower force. Increasing T also leads to a broadening of the distribution, such that the distributions get broader for smaller most probable forces in contrast to the effect of increasing α.
It could be estimated from Fig. 3 that the peak position can also appear at negative values of f if α gets very small [c.f. Fig. 4a] or if the temperature gets very large. This is indeed the case for
 | (12) |
 | ||
| Fig. 4 (a) Most probable force from eqn (8) (Numeric), from eqn (9) (Quadratic), and from max (∂P/∂f) depending on loading rate at T = 500 K. (b) The probability derivative distribution scaled by the loading rate α when the peak position goes towards negative values. | ||
Fig. 4b depicts the distribution of ∂P/∂F with decreasing loading rate α values. The distribution is no longer peaked in the positive force direction and thus the estimation of f* from eqn (9) breaks down as it ultimately leads to negative values. However, the most probable force from eqn (8) is strictly positive even at lower forces.
Fig. 5 shows the most probable force for a large range of loading rates (keeping temperature, T = 300 K constant) and temperatures (keeping loading rate, α = 10 nN s−1 constant). The errorbars for numerical values are determined by the full width at half measurement (FWHM) of the dP/dF distribution. The shaded region indicating the error of the Bell prediction is obtained from eqn (S31). The analytic prediction based on the quadratic barrier closely follows the numeric integration except of the region where negative values appear (for very low forces). The Bell model is accurate only for low loading rates40 and high temperatures. Hence it is useful for approximations at low forces only. Additionally, the Bell uncertainty can only describe the increase of the width for large temperatures, but the dependence on the loading rate is not covered as is explicit from eqn (S31). Most probable force and error estimates from the literature39,42,43,49,58,59 are discussed in detail using a simple example in SI.
 | ||
| Fig. 5 Most probable force for AuAg2 molecule at various loading rates (left, for T = 300 K) and temperatures (right, for α = 10 nN s−1). Eqn (8) (Numeric), eqn (10) (Bell) and eqn (11) (Quadratic) are compared. | ||
Comparison to single molecule force spectroscopy experiments
We have shown above that the dissociation energy ΔU‡ and the maximal force that the bond can withstand Fmax determine the most probable force measured in the experiment through eqn (11). The similarity of force dependent barriers with the quadratic form seen in our toy model above and in other cases8,35,36 suggests that these two quantities are most important and may be sufficient for an accurate estimate of rupture forces measured in SMFS experiments.We test this assumption for available experimental data from the literature for force opening reactions of cyclopropanes13,15,16,60,61 and benzocyclobutenes.6,16 These types of monomers were investigated in the literature within SMFS experiments in many variants and represent non-trivial reactions involving the re-arrangements of multiple bonds. The force induced reactions are illustrated in Fig. 6, where the triangular cyclopropane is re-arranged to form a double and a single bond via movement of one of the halogens, while the benzocyclobutenes open the cyclobutene square to form two double bonds when forces are applied. The observed rupture forces are influenced by side groups as well as by variation of the halogens in cyclopropanes. Detailed schematics of all the reactions considered can be found in SI. An extensive investigation of these compounds using COGEF considering step size of 0.075 Å did see some correlations, but was unable to get forces similar to the experimental measurements.32
The basic ingredients we need are ΔU‡ and Fmax, which we calculate within density functional theory (DFT) as implemented in the GPAW package.62–64 GPAW applies the projector augmented wave (PAW) method,65 where the smooth wave functions are represented on real space grids with grid spacing of 0.2 Å, while we used grid spacing of 0.1 Å for the smooth electron density. The exchange–correlation functional is approximated as devised by Perdew, Burke and Ernzerhof (PBE).66
The question arises about the best method to evaluate ΔU‡ and Fmax. The first idea may be to use a COGEF calculation32 via the maximal energy and the maximal force observed. While this approach gives good estimates for Fmax, it generally leads to an overestimation of the dissociation energy. The overestimation is larger for a softer elastic environment coupled to the bond, as soft elastic environments are able to absorb large amounts of energy via the applied force.36 This environment consists of the rest of the monomer-molecule surrounding the bond that breaks as well as co-monomers considered in the calculation. A larger model (which is would appear superior at first sight) therefore worsens the effect. In order to avoid these extra contributions, we determine the barrier in absence of force ΔU‡ = ΔH‡(F = 0) via nudged elastic band calculations.51,67
We have considered the medium sized monomers (i.e. ring molecule and a two carbon atom chain on either side) for each molecule, as we did not observe major changes by increasing the monomer size further (detailed analysis is given in SI). The stress induced pericyclic ring opening in molecules is suspected to steer the reaction in a direction away from thermally induced lower barrier reaction pathway.68 These thermally activated reactions are in accordance with conservation of orbital symmetry as explained by Woodward–Hoffmann (WH)69 and Woodward–Hoffmann–DePuy (WHD)70 rules. It was shown computationally for benzocyclobutenes22,71 and cyclopropanes5,26 and also proved experimentally4–6 that the force induced activation may not always agree with these rules. In cases where forbidden reactions occur in COGEF, the expected product state in accordance with the WH/WHD rules was considered to calculate ΔU‡. This ensures the use of the correct thermal activation barrier (see SI for details).
Using the monomer properties ΔU‡ and Fmax, the missing ingredients to predict the most probable rupture force F* are the loading rate and the temperature at which the SMFS experiment is performed. Room temperature was assumed throughout. The experimental loading rate specified in the references is directly chosen.13 In cases where the values are not specified, we estimate it using the product of spring constant and experimental velocity (as α = ktotalv). The total spring constant of the experimental setup ktotal is obtained from a linear fit of the experimental SMFS force vs. elongation. If this calculated value results in a value larger than the given cantilever spring constant, we consider the latter for the calculation of loading rate (see Tabs. S1 and S3 in SI for details).
Using these values, we compare our predictions using eqn (11) to the measured rupture forces4,6,13–16 in Fig. 7. The horizontal error bars correspond to the experimental error range and the vertical error bars correspond to the prediction errors (Eq. (S67) in SI), which is close to the width of the probability density distribution. We obtain very good agreement between our model and the experiment over a large force range. The prediction is quantitative and much better than the usage of Fmax32 as seen explicitly in Fig. S9 of SI. Our description is thus able to predict experimentally observed rupture forces directly from this minimal set of parameters, where only ΔU‡ and Fmax obtained from DFT enter.
We have also incorporated diarylethene (DAE) mechanophores that were investigated in a recent study72 into the estimation of the most probable forces from our model. The DAEs were reported to undergo mechanically driven noncovalent transformations showing pronounced lever arm effects. We have used the COGEF Fmax and the thermal barriers ΔU‡ for rotation for these molecules as given in this study. The loading rate is estimated (0.9 nN s−1 for a velocity of 3000 Å s−1) using the cantilever spring constant from the force–extension curve similar to other molecules discussed in SI. Inclusion of these additional molecules expands the diversity as comparably low forces were detected (Fig. 7). We also get very good agreement in our prediction of the most probable force with the measured one for this noncovalent, but still barrier-controlled force-induced transition.
Conclusions
In conclusion, we have derived a closed form for the prediction of most probable bond-rupture forces as measured in single molecule force spectroscopy experiments. The nature of the bond exposed to external forces can be conveniently described by two key parameters which are the bond energy in absence of force and the maximal force that the bond can withstand. These two quantities are usually sufficient to characterize the force-dependent barrier until a bond breaks to good accuracy. The approximative quadratic form assumed naturally leads to the famous Bell model for small forces. These necessary properties of the bond can be obtained via density functional theory calculations using force-free transition state modeling and a COGEF calculation.Assuming a constant force increase, the rest is statistics as the bond is broken by thermal fluctuations. The experimentally observed most probable breaking force is governed by the time scales of the force increase and the attempt frequency to break the bond. This leads to a closed and simple form for the prediction of the forces measured in experiment in eqn (11) without the involvement of any empirical parameter.
The effectiveness and accuracy of this description is tested on rupture forces from ring opening reactions of cyclopropanes and benzocyclobutenes as well as for diarylethene noncovalent rearrangements reported in the literature. We find very good agreement of our predicted forces and the experimentally observed ones in all cases with a coefficient of determination of R2 = 90.1%.
We expect that the approximations adopted are widely applicable also to other types of bond openings or bond formations under external stimuli. A similar description may also be valid for pressure or shear induced reactions, where the external force is replaced by external pressure p, or more generally the stress tensor σ. Usually, a linear approximation defining an activation volume V‡73 similar to the Bell length x‡ is applied, but also descriptions going beyond that exist.74 Very similar expressions as eqn (11) for the most probable pressure should appear under a constant pressure increase defining the loading rate and it is an interesting question whether V‡ can also be related to ΔU‡ at p = 0 and the maximal pmax where the reaction occurs without barrier. This may help us understand the puzzling large variation of activation volumes observed.75 The general form of the deformation tensor σ will require modifications and the approximation may also break down for very complicated barriers that can not be described by the simple quadratic form of ΔH‡(F), like retro-Diels–Alder bond openings, however.8
Conflicts of interest
There are no conflicts of interest to declare.Data availability
The software used is open source and can be installed cross platform using pip (for Python): the atomic simulation environment ASE (https://www.ase-lib.org/ase/atoms.html), GPAW (https://www.gpaw.readthedocs.io) and cogef (https://www.cogef.gitlab.io/cogef/index.html). The relaxed structures of the molecules, their force free transition states and COGEF trajectories will be openly published in a gitlab repository (https://www.gitlab.com/ag_walter).Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5mr00129c.
Acknowledgements
M. W. thanks L. Mayrhofer for discussions about activation volumes. The authors are grateful for funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy-EXC-2193/1-390951807 and WA 1687/11-1. The authors acknowledge computational resources by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 39/963-1 FUGG (bwForCluster NEMO) and INST 40/575-1 FUGG (bwForCluster JUSTUS2).References
- L. Yang, Z. Chen, C. A. Goult, T. Schlatzer, R. S. Paton and V. Gouverneur, Nature, 2025, 1–7 Search PubMed.
- J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3, 13 CrossRef CAS PubMed.
- T.-G. Hsu, S. Liu, X. Guan, S. Yoon, J. Zhou, W.-Y. Chen, S. Gaire, J. Seylar, H. Chen, Z. Wang, J. Rivera, L. Wu, C. J. Ziegler, R. McKenzie and J. Wang, Nat. Commun., 2023, 14, 225 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. S. Kean, L. Fan, B. D. Mar, T. J. Martínez and S. L. Craig, J. Am. Chem. Soc., 2014, 136, 15162 CrossRef CAS PubMed.
- J. M. Lenhardt, M. T. Ong, R. Choe, C. R. Evenhuis, T. J. Martinez and S. L. Craig, Science, 2010, 329, 1057 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. Niu, A. L. Rheingold and S. L. Craig, J. Org. Chem., 2015, 80, 11895 CrossRef CAS PubMed.
- F. Kempe, O. Brügner, H. Buchheit, S. N. Momm, F. Riehle, S. Hameury, M. Walter and M. Sommer, Angew. Chem., Int. Ed., 2018, 57, 997 CrossRef CAS PubMed.
- M. Walter, D. Linsler, T. König, C. Gäbert, S. Reinicke, M. Moseler and L. Mayrhofer, J. Phys. Chem. Lett., 2023, 14, 1445 CrossRef CAS PubMed.
- R. Hertel, M. Raisch, M. Walter, G. Reiter and M. Sommer, Angew. Chem., Int. Ed., 2024, e202409369 CAS.
- H. Traeger, D. Kiebala, C. Calvino, Y. Sagara, S. Schrettl, C. Weder and J. M. Clough, Mater. Horiz., 2023, 10, 3467 RSC.
- M. Raisch, G. Reiter and M. Sommer, ACS Macro Lett., 2022, 11, 760 CrossRef CAS PubMed.
- M. Grandbois, M. Beyer, M. Rief, H. Clausen-Schaumann and H. E. Gaub, Science, 1999, 283, 1727 CrossRef CAS PubMed.
- H. M. Klukovich, T. B. Kouznetsova, Z. S. Kean, J. M. Lenhardt and S. L. Craig, Nat. Chem., 2013, 5, 110 CrossRef CAS PubMed.
- O. N. Faza, C. S. López, R. Álvarez and A. R. de Lera, J. Org. Chem., 2004, 69, 9002 CrossRef PubMed.
- J. Wang, T. B. Kouznetsova, Z. S. Kean, L. Fan, B. D. Mar, T. J. Martínez and S. L. Craig, J. Am. Chem. Soc., 2014, 136, 15162 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, Z. Niu, M. T. Ong, H. M. Klukovich, A. L. Rheingold, T. J. Martinez and S. L. Craig, Nat. Chem., 2015, 7, 323 CrossRef CAS PubMed.
- W. Cai, J. T. Bullerjahn, M. Lallemang, K. Kroy, B. N. Balzer and T. Hugel, Chem. Sci., 2022, 13, 5734 RSC.
- S. Akbulatov, Y. Tian and R. Boulatov, J. Am. Chem. Soc., 2012, 134, 7620 CrossRef CAS PubMed.
- S. W. Schmidt, M. K. Beyer and H. Clausen-Schaumann, J. Am. Chem. Soc., 2008, 130, 3664 CrossRef CAS PubMed.
- S. W. Schmidt, A. Kersch, M. K. Beyer and H. Clausen-Schaumann, Phys. Chem. Chem. Phys., 2011, 13, 5994 RSC.
- S. W. Schmidt, M. F. Pill, A. Kersch, H. Clausen-Schaumann and M. K. Beyer, Faraday Discuss., 2014, 170, 357 RSC.
- M. T. Ong, J. Leiding, H. Tao, A. M. Virshup and T. J. Martínez, J. Am. Chem. Soc., 2009, 131, 6377 CrossRef CAS PubMed.
- P. Dopieralski, P. Anjukandi, M. Rückert, M. Shiga, J. Ribas-Arino and D. Marx, J. Mater. Chem., 2011, 21, 8309 RSC.
- P. Dopieralski, J. Ribas-Arino and D. Marx, Angew. Chem., Int. Ed., 2011, 50, 7105 CrossRef CAS PubMed.
- M. Wollenhaupt, M. Krupička and D. Marx, ChemPhysChem, 2015, 16, 1593 CrossRef CAS PubMed.
- M. Wollenhaupt, C. Schran, M. Krupička and D. Marx, ChemPhysChem, 2018, 19, 837 CrossRef CAS PubMed.
- J. Wang, T. B. Kouznetsova, R. Boulatov and S. L. Craig, Nat. Commun., 2016, 7, 1 Search PubMed.
- M. K. Beyer, J. Chem. Phys., 2000, 112, 7307 CrossRef CAS.
- J. Ribas-Arino and D. Marx, Chem. Rev., 2012, 112, 5412 CrossRef CAS PubMed.
- J. R. Hemmer, C. Rader, B. D. Wilts, C. Weder and J. A. Berrocal, J. Am. Chem. Soc., 2021, 143, 18859 CrossRef CAS PubMed.
- J. R. Hemmer, V. Bauernfeind, C. Rader, M. Petroselli, C. Weder and J. A. Berrocal, Macromolecules, 2023, 56, 8614 CrossRef CAS.
- I. M. Klein, C. C. Husic, D. P. Kovács, N. J. Choquette and M. J. Robb, J. Am. Chem. Soc., 2020, 142, 16364 CrossRef CAS PubMed.
- C. R. Wick, E. Topraksal, D. M. Smith and A.-S. Smith, Forces Mech., 2022, 9, 100143 CrossRef.
- I. V. Pobelov, K. P. Lauritzen, K. Yoshida, A. Jensen, G. Meszaros, K. W. Jacobsen, M. Strange, T. Wandlowski and G. C. Solomon, Nat. Commun., 2017, 8, 1 CrossRef PubMed.
- F. Hanke and H. J. Kreuzer, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2006, 74, 1 CrossRef PubMed.
- S. Khodayeki, W. Maftuhin and M. Walter, ChemPhysChem, 2022, e202200237 CrossRef CAS PubMed.
- Y. Sun, I. Kevlishvili, T. B. Kouznetsova, Z. P. Burke, S. L. Craig, H. J. Kulik and J. S. Moore, Chem, 2024, 10, 3055 CAS.
- Y. Sun, F. Xie and J. S. Moore, J. Am. Chem. Soc., 2024, 146, 31702 CrossRef CAS PubMed.
- A. Garg, Phys. Rev. B, 1995, 51, 15592 CrossRef CAS PubMed.
- G. Hummer and A. Szabo, Biophys. J., 2003, 85, 1 CrossRef PubMed.
- O. K. Dudko, G. Hummer and A. Szabo, Phys. Rev. Lett., 2006, 96, 108101 CrossRef PubMed.
- J. T. Bullerjahn, S. Sturm and K. Kroy, Nat. Commun., 2014, 5, 4463 CrossRef CAS PubMed.
- R. W. Friddle, A. Noy and J. J. De Yoreo, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 13573 CrossRef CAS PubMed.
- W. Cai, M. Jäger, J. T. Bullerjahn, T. Hugel, S. Wolf and B. N. Balzer, Nano Lett., 2023, 23, 4111 CrossRef CAS PubMed.
- J. T. Bullerjahn and G. Hummer, Phys. Rev. Res., 2022, 4, 033097 CrossRef CAS.
- W. Kauzman and H. Eyring, J. Am. Chem. Soc., 1940, 62, 3113 CrossRef.
- E. Evans and K. Ritchie, Biophys. J., 1997, 72, 1541 CrossRef CAS PubMed.
- T. Stauch and A. Dreuw, Chem. Rev., 2016, 116, 14137 CrossRef CAS PubMed.
- G. I. Bell, Science, 1978, 200, 618 CrossRef CAS PubMed.
- S. M. Avdoshenko and D. E. Makarov, J. Chem. Phys., 2015, 142, 174106 CrossRef PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190 CrossRef CAS PubMed.
- O. K. Dudko, A. E. Filippov, J. Klafter and M. Urbakh, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11378 CrossRef CAS PubMed.
- F. Rico, A. Russek, L. González, H. Grubmüller and S. Scheuring, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6594 CrossRef CAS PubMed.
- P. M. Williams, Anal. Chim. Acta, 2003, 479, 107 CrossRef CAS.
- O. Brügner and M. Walter, Phys. Rev. Mater., 2018, 2, 1 Search PubMed.
- J. Kurkijärvi, Phys. Rev. B, 1972, 6, 832 CrossRef.
- O. K. Dudko, J. Mathé, A. Szabo, A. Meller and G. Hummer, Biophys. J., 2007, 92, 4188 CrossRef CAS PubMed.
- R. W. Friddle, Phys. Rev. Lett., 2008, 100, 138302 CrossRef PubMed.
- J. Wang, T. B. Kouznetsova and S. L. Craig, J. Am. Chem. Soc., 2014, 137, 11554 CrossRef PubMed.
- D. Wu, J. M. Lenhardt, A. L. Black, B. B. Akhremitchev and S. L. Craig, J. Am. Chem. Soc., 2010, 132, 15936 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B, 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys. Condens. Matter., 2010, 22, 253202 CrossRef CAS PubMed.
- J. J. Mortensen, A. H. Larsen, M. Kuisma, A. V. Ivanov, A. Taghizadeh, A. Peterson, A. Haldar, A. O. Dohn, C. SchÄfer, E. Ö. Jonsson, E. D. Hermes, F. A. Nilsson, G. Kastlunger, G. Levi, H. Jonsson, H. Häkkinen, J. Fojt, J. Kangsabanik, J. Sødequist, J. Lehtomäki, J. Heske, J. Enkovaara, K. T. Winther, M. Dulak, M. M. Melander, M. Ovesen, M. Louhivuori, M. Walter, M. Gjerding, O. Lopez-Acevedo, P. Erhart, R. Warmbier, R. Würdemann, S. Kaappa, S. Latini, T. M. Boland, T. Bligaard, T. Skovhus, T. Susi, T. Maxson, T. Rossi, X. Chen, Y. L. A. Schmerwitz, J. Schiøtz, T. Olsen, K. W. Jacobsen and K. S. Thygesen, J. Chem. Phys., 2024, 160, 092503 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- G. Henkelman, G. Jóhannesson and H. Jónsson, in Methods for Finding Saddle Points and Minimum Energy Paths, ed. S. D. Schwartz, Theoretical Methods in Condensed Phase Chemistry, Progress in Theoretical Chemistry and Physics, Springer Netherlands, Dordrecht 2002, pp. 269–302 Search PubMed.
- R. B. Woodward and R. Hoffmann, Angew Chem. Int. Ed. Engl., 1969, 8, 781 CrossRef CAS.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395 CrossRef CAS.
- C. H. DePuy, Acc. Chem. Res., 1968, 33–41 CrossRef CAS.
- C. R. Hickenboth, J. S. Moore, S. R. White, N. R. Sottos, J. Baudry and S. R. Wilson, Nature, 2007, 446, 423 CrossRef CAS PubMed.
- C. Zhang, T. B. Kouznetsova, B. Zhu, L. Sweeney, M. Lancer, I. Gitsov, S. L. Craig and X. Hu, J. Am. Chem. Soc., 2025, 147, 2502 CrossRef CAS PubMed.
- A. Martini and S. H. Kim, Tribol. Lett., 2021, 69, 150 CrossRef.
- N. Hopper, F. Sidoroff, J. Cayer-Barrioz, D. Mazuyer, B. Chen and W. T. Tysoe, RSC Mechanochem., 2024, 1, 402 RSC.
- Z. Li and I. Szlufarska, Phys. Rev. Lett., 2021, 126, 076001 CrossRef CAS PubMed.
Footnotes |
| † These authors contributed equally. |
| ‡ This assumption breaks down for very soft bonds as occurring in biological systems.54 |
| This journal is © The Royal Society of Chemistry 2026 |


