Smart mechanochemistry: optimizing amino acid acylation with one factor at a time, design of experiments and machine learning methods

Abstract

The formation of amide bonds is of major interest in organic chemistry. Several methodologies have emerged in mechanochemistry to promote this reaction by using coupling agents. Herein, the acylation of unprotected amino acids using an acyl chloride in a ball-mill is described with different optimization processes. Indeed, the optimization of reaction conditions is part of every development of a new synthetic pathway. However, depending on the method which is used, the number of experiments to carry out can increase exponentially. Three different optimization methods were compared in the acylation of amino acids: One Factor at a Time (OFAT), Design of Experiments (DoE) and Bayesian Optimization (BO). The strengths and limitations of each methodology are highlighted providing new insights and an optimized practical amidation method taking into account the sustainability of this chemistry.

---

Introduction

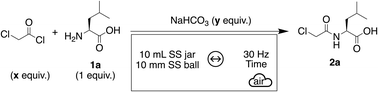
Amino acids and their derivatives are widely used in different fields of application. Of course, their importance in peptide synthesis is not to be proven anymore,^1–4 but they can also be functionalized by reacting either the amine or the carboxylic acid to form an amide bond that is particularly relevant in medicinal chemistry.⁵ Such couplings are greatly facilitated by the use of coupling agents to activate the acid.^5–7 Another possibility is to use an activated carboxylic acid derivative such as an acyl chloride. Indeed, the easy acylation of amino acids by reaction with an acyl chloride offers a broad panel of intermediates that can be further transformed to find applications in medicinal chemistry^8,9 or polymer chemistry^10–13 for instance. Since our pioneering studies in amidation¹⁴ and peptide synthesis,² these approaches, combined with mechanochemistry, have found many developments to identify more sustainable ways to form amide bonds. Noteworthily, a large excess of either the carboxylic acid or the amine is often used in such amidation reactions, requiring a thorough optimization of reaction parameters to satisfy as much as possible the twelve principles of green chemistry.¹⁵ Different optimization methods are nowadays available. We herein focused our attention on three of them, beginning with the most commonly used in mechanochemistry and broader chemistry – One Factor at a Time (OFAT) – and concluding with a novel approach that is steadily gaining interest – Bayesian-based machine learning (BO). While OFAT experimentation can be effective, it is time-consuming and inefficient when multiple factors are involved, often missing optimal conditions due to unaccounted variable interactions. To address these limitations, Design of Experiments (DoE) has become a widely used statistical method that allows the variation of multiple parameters, significantly reducing the number of experiments needed.^16,17 Despite its advantages, DoE requires predefined experimental points and often multiple iterations to refine conditions, limiting flexibility in exploring promising areas. More recently, BO has emerged as a powerful alternative, offering faster optimization by balancing exploration and exploitation.^18–22

Our group decided to combine these statistical approaches with solvent-free methodologies (ball-milling, twin-screw extrusion…) as a support to design a more sustainable chemistry. Indeed, as said earlier, DoE or BO can determine an optimum with only a few experiments, meaning that less reagents are used in this process, as well as time or energy. To find out which method best reduces the number of experiments needed to optimize a reaction, OFAT, DoE and BO were performed in the acylation of amino acids by mechanochemistry.

Results and discussion

One factor at a time (OFAT)

OFAT works by varying one experimental factor while keeping all others constant to assess its individual effect on the outcome. Several articles in the literature have reported the acylation of amino acids by an acyl chloride.^23–27 These methodologies involve the use of problematic organic solvents such as diethyl ether or tetrahydrofuran and sometimes organic bases like triethylamine. A mechanochemical alternative is herein described. As part of an ongoing project that includes the preparation of heterocyclic structures for the synthesis of polymers,^10–12 L-leucine 1a, used as a model substrate, was reacted with chloroacetyl chloride and a base to give the corresponding N-(2-chloroacetyl)-L-leucine 2a according to an OFAT approach with a 10 mL stainless-steel (SS) jar, containing a 10 mm SS ball, in a vibratory ball-mill agitated at a frequency of 30 Hz. Although chloroacetyl chloride is highly corrosive, stainless steel was nonetheless selected, mainly for its chemical resistance, cost-effectiveness and facilitated scalability. Regarding the other mechanochemical parameters (size of the jar, number and size of balls, milling frequency), we decided to keep them constant, following conventional practices, like working at the maximum frequency allowed by the instrument. Since this study marks our first steps into DoE and BO, including these variables would have significantly increased the complexity and risked diluting the core findings. Future investigations could benefit from including these parameters, thereby extending and complementing the contributions made by Stolle and Mack.^28–31 Additionally, given the potential of mechanochemistry to enhance the sustainability of chemical processes – through solvent elimination and the use of safer inorganic reagents to replace hazardous substances usually employed in solution – we began by exploring various inorganic bases for the acylation of 1a.³² Preliminary tests showed that due to the high reactivity of chloroacetyl chloride, a violent exothermic reaction occurred upon direct contact with either NaOH, K₂CO₃ or Cs₂CO₃. In contrast, the formation of product 2a was confirmed by ¹H NMR when Na₂CO₃, NaHCO₃ and K₃PO₄ were employed as bases. In the case of L-leucine 1a, evaluating the conversion by HPLC was not possible since 1a is not detected at a routine wavelength of 214 nm. All the experiments were subjected to a classical workup by liquid–liquid extraction and ¹H NMR analysis of the crude solid (mixture of 2a and chloroacetic acid) allowed to calculate an NMR adjusted yield of 2a (see the SI for details). When stoichiometric amounts of L-leucine, chloroacetyl chloride and Na₂CO₃ or K₃PO₄ were milled for 1 hour at 30 Hz, the product was obtained in a 57 ± 6% NMR adjusted yield. Under identical conditions, the use of NaHCO₃ resulted in a yield of 59 ± 11%. In order to differentiate the two carbonates, complementary experiments were conducted over 5 min using 1.3 equiv. of acyl chloride and either 1.3 or 1.5 equiv. of Na₂CO₃ or NaHCO₃. In both scenarios, NaHCO₃ proved superior, yielding the desired product in a 70% NMR adjusted yield in the first case (versus 59% with Na₂CO₃) and 68% in the second (versus 43% with Na₂CO₃). The optimization of the amount of chloroacetyl chloride was first studied. Using a single equivalent of acyl chloride gave a 55% NMR adjusted yield of 2a (Table 1, Entry 1). This results from the hydrolysis of chloroacetyl chloride into chloroacetic acid by the water released during the decomposition of carbonic acid H₂CO₃, which is formed through the protonation of the base. Increasing the amount of acyl chloride improved the reaction outcome (Table 1, Entries 2–6), reaching an optimum of 82% NMR adjusted yield at 1.6 equiv. (Table 1, Entry 5). The results obtained with 1.5 and 1.6 equiv. were very similar. However, since chloroacetyl chloride is a potentially hazardous reagent, the decision was made to proceed with 1.5 equiv. for the rest of the study.

Table 1 One factor at a time optimization for the synthesis of 2a^a

Entry	x (equiv.)	y (equiv.)	Time (min)	Liquid additive	NMR adjusted yield^b^,^c (%)
a The reaction was performed in a Retsch Mixer Mill 400 on 1 mmol scale.b See SI section for more details.c Values represent the 95% confidence interval, expressed as: mean values of several experiments ± 1.96 * standard error.
1	1	1.5	60	—	55
2	1.2	1.5	60	—	64
3	1.3	1.5	60	—	74
4	1.5	1.5	60	—	79 ± 9
5	1.6	1.5	60	—	82 ± 8
6	2	1.5	60	—	76 ± 2
7	1.5	1.5	30	—	76
8	1.5	1.5	15	—	79
9	1.5	1.5	10	—	68
10	1.5	1.5	5	—	80 ± 8
11	1.5	1.4	15	—	87 ± 17
12	1.5	1.3	15	—	71 ± 5
13	1.5	1.2	15	—	72 ± 17
14	1.5	1	15	—	79
15	1.5	1.4	15	Ethyl acetate	82 ± 12
16	1.5	1.4	15	Acetone	65 ± 3
17	1.5	1.4	15	2-Methyl tetrahydrofuran	65 ± 4
18	1.5	1.4	15	Acetonitrile	64 ± 19
19	1.5	1.4	15	Nitromethane	88 ± 7
20	1.5	1.4	15	Dimethyl carbonate	80 ± 12

---

As the amidation reaction is performed with an activated acid, we expected that it could be complete in a reaction time shorter than 1 h. Therefore, 4 additional experiments were carried out at different milling times. To our delight, it appeared that milling the reaction media only 15 min provides a very good NMR adjusted yield (Table 1, Entry 8), not improved by prolonged milling time. Then, the optimization process focused on the amount of base. Since several acidic species are released during the reaction, it came as no surprise that adjusting the amount of base can influence the outcome. The best result was obtained with 1.4 equiv. of NaHCO₃ (Table 1, Entry 11). Above this quantity, no improvement was observed. Finally, noting the high standard deviation in entry 11, attributed to an unfavourable rheology, the addition of a liquid additive was studied to improve the mixing and overcome this issue. While ethyl acetate and dimethyl carbonate (Table 1, Entry 15 and 20) did not alter the outcome of the reaction, the addition of acetone (Table 1, Entry 16), 2-methyl tetrahydrofuran (Table 1, Entry 17) or acetonitrile (Table 1, Entry 18) decreased the NMR adjusted yield by 20%. Only nitromethane improved the result, reaching 88% (Table 1, Entry 19), with a standard error reduced by a factor 2.5. Increasing the quantity of nitromethane in the reaction medium did not lead to any significant improvement in the outcome. Thus, according to the OFAT approach, product 2a was obtained with a very good NMR adjusted yield (88%) by milling for 15 min a mixture of 1 mmol of L-leucine 1a (1 equiv.), chloroacetyl chloride (1.5 equiv.), NaHCO₃ (1.4 equiv.) and nitromethane as a liquid additive (η = 0.3 µL mg⁻¹). However, even if the use of this additive proved to be efficient, its hazardous nature cannot be denied. In 2016, it has been classified as “Highly Hazardous” in the CHEM21 solvent guide.³³ Therefore, since chloroacetyl chloride is a liquid reagent, it was interesting to investigate whether the reaction conditions could be improved without the use of a liquid additive. Such an approach would provide a safer and easier way to prepare acylated amino acid 2a.

OFAT is the most used method to optimize steps in organic chemistry. However, even if this method showed its relevance, it is time-consuming and the number of experiments required increases exponentially with the number of parameters studied. Furthermore, it is not guaranteed that the “real” optimum would be found, often because of unconsidered synergetic effects. Moreover, the optimum is generally found for one substrate, and changing the reagents might not directly lead to the corresponding optimum. To determine whether the global optimum was reached, we turned our attention to a more efficient and informative methodology: design of experiments.

Design of experiments (DoE)

Design of experiments was developed as an alternative to OFAT for significantly improving the optimization process. DoE, applied to chemistry, is a statistical strategy for optimizing reactions by varying multiple parameters at once, enabling efficient exploration of the reaction space for a specific process. Thanks to this method, and depending on the experimental design chosen, a large number of parameters can be evaluated with a relatively small number of reactions. However, several DoEs are often required to determine precise conditions and the experiments are selected in advance, making no room for the exploitation of a promising area of the reaction space. In 2016, Murray et al. showed that DoE could be applied to go deeper into the optimization of a reaction by determining the best choice of solvent.³⁴ In other words, either continuous and discrete variables can be studied, unlocking a wide range of possibilities for synthetic chemists. Unfortunately, even if the DoE is widely used in industries as a tool for process optimization,³⁵ this is still not the case in academia, with only a small number of studies and related articles using this methodology in organic chemistry and even less in mechanochemistry.^{17,29,36–38}

The determination of the experimental space was made following the first intuition of the chemist. Setting suitable ranges in a DoE study is crucial as poor decisions can significantly reduce the study's effectiveness. In the case of too narrow ranges, the relevant trends may be missed but too large ones may compromise precision. Actually, such a difficulty was faced when we initially chose to adopt the same parameter variation ranges as those used in the OFAT section. It ended up with a surface response showing the optimum value on one of the corners of the experimental space (see the SI). An extension of the reaction space was necessary to assess whether the previously obtained value was near the optimum or if the global optimum resided in a different region of the experimental domain. Hence, it is important to define sufficiently broad ranges for each factor to ensure the design can explore a wide portion of the reaction space. In our case, we chose to keep the amount of 1a constant to 1 mmol (1 equiv.) and all the mechanochemical parameters (size/material of both jar and ball, milling frequency) identical to the ones in the OFAT optimization. The use of a liquid additive was discarded in this section. The screening study included three factors: amount of chloroacetyl chloride, amount of NaHCO₃ and reaction time. A central composite face-centered design (CCF) was constructed in which each parameter has three levels whose values are described in Table 2.

Table 2 Range of variation of the studied factors

Factors	Levels
	−1	0	+1
Amount of chloroacetyl chloride (equiv.)	1	1.5	2
Amount of NaHCO3 (equiv.)	1	2	4
Reaction time (min)	5	30	60

---

A CCF design offers a practical and efficient balance between model accuracy and feasibility. Such a design consists of 14 experiments and 3 centre points. The centre points consist of three reactions conducted under identical conditions at the midpoint of the design space – average of all factor ranges. These points help assess the reproducibility of the reaction. Ideally, identical conditions should yield consistent results. However, minor inevitable errors in experimental or analytical procedures can introduce some variation of the yields. The model imposes a minimum number of center points, while no upper limit is defined. Thus, 5 experiments were run as center points and other experiments were run in duplicate. To simplify the construction and the analysis of the DoE, Ellistat Software (version 7.8.7) was used. The 15 different experiments' dataset is displayed in Table 3. Noteworthily, the five center points (Table 3, Entry 9) yielded fairly consistent results suggesting a good reproducibility.

Table 3 Experiments suggested by the DoE

Entry	x (equiv.)	y (equiv.)	Reaction time (min)	NMR adjusted yield^b (%)
a Values calculated on the basis of 5 experiments.b Values represent the 95% confidence interval, expressed as: mean values of several experiments ± 1.96 * standard error.
1	1	1	5	52 ± 7
2	1	1	60	59 ± 11
3	1	4	5	53 ± 6
4	1	4	60	61 ± 1
5	2	1	5	62
6	2	1	60	66
7	2	4	5	78 ± 35
8	2	4	60	83 ± 1
9^a	1.5	2	30	91 ± 4
10	1	2	30	56 ± 0
11	2	2	30	87 ± 6
12	1.5	1	30	68
13	1.5	4	30	93 ± 19
14	1.5	2	5	90 ± 8
15	1.5	2	60	83 ± 4

---

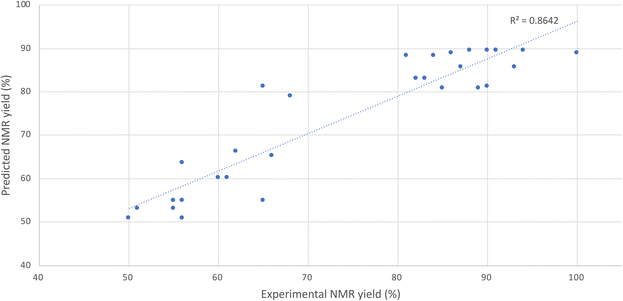
As shown in Fig. 1, which represents the comparison between the calculated NMR adjusted yield by DoE and the experimental value, the statistical model is reliable enough to predict accurately the best conditions for the transformation of 1a into 2a. Despite the remaining substantial variability in the response (R² = 0.86), DoE proves to be a powerful tool for conduction of fast and trustworthy optimization studies. Noteworthily, the model is more reliable with high values of NMR adjusted yield. More statistical information is available in the SI.

Fig. 1 Comparison between calculated and experimental NMR adjusted yield.

Finally, the suggested best conditions for the acylation of L-leucine 1a required 1.66 equiv. of chloroacetyl chloride, 3.07 equiv. of NaHCO₃ and 40 min milling time. The predicted NMR adjusted yield under these conditions is about 95% (Fig. 2). The experiment was run as a duplicate under these conditions and provided an NMR adjusted yield of 89 ± 1%. Notably, entry 13 in Table 3 shows a better result than the conditions suggested by the DoE model. Regarding the high standard error, the observed improvement may be due to random variation rather than a systematic effect.

Fig. 2 Correlation between the amount of chloroacetyl chloride, amount of NaHCO₃ and NMR adjusted yield with reaction time fixed at 30 min.

Moreover, since 49 experiments (113 if replicates are considered) were performed in the first part of the optimization (OFAT), we decided to include all these results in the DoE to strengthen our DoE model. The implementation of this non-classical approach was made possible by the prior availability of a comprehensive library of experimental data. It appeared that a little improvement could be obtained thanks to this approach. It suggested that a 94% NMR adjusted yield could be reached if 1 equiv. of 1a was milled for 30 min with 1.9 equiv. of chloroacetyl chloride and 3.4 equiv. of NaHCO₃ (see the SI). This result is really close to the one determined when running the DoE model, suggesting the high suitability of the model established with only 19 experiments required through the DoE (32 experiments effectively performed when including the replicates). By running the reaction under the last conditions, the product of acylation 2a could be obtained with a 93% experimental NMR adjusted yield proving the effectiveness of the model. Analysis of the results provides an insight on the weight of each parameter on the formation of the product. The amounts of chloroacetyl chloride and NaHCO₃ seem to be significant parameters while the reaction time is less influent. DoE enabled the identification of optimal conditions for converting 1a into 2a more efficiently than the OFAT approach, without requiring the use of any liquid additive.

DoE can easily be implemented to mechanochemical systems, helping to optimize experimental conditions in a straightforward manner and providing very accurate results. As a comparison point and to confirm the last conditions or even improve them without running again tens of additional experiments, we ultimately transitioned to a brand-new optimization method in mechanochemistry: Bayesian optimization (BO).

Bayesian optimization (BO)

BO has emerged recently as a new way to carry out optimization studies. It offers the possibility to perform faster optimizations and provides a good balance between exploration (testing new areas) and exploitation (refining promising areas). BO has already been adapted by several groups in solution for C–N bond formation,¹⁸ nucleophilic aromatic substitution,²⁰ automated flow cycloaddition^19,21 or automated flow photocatalyzed reactions.²² Recently, our group reported the very first example of the application of BO to mechanochemistry by optimizing thermal amidation by reactive extrusion.³⁹ To date,⁴⁰ there is no example of BO applied to reactions performed in ball-mills.

In the case of acylation of 1a into 2a, and following the initial five reactions, which were developed using a straightforward DoE approach (centered factorial design), the NMR adjusted yield data were sufficient for the BO algorithm to construct a preliminary surrogate model. For each iteration, the BO algorithm provided a series of 5 suggested experiments. The two showing the highest expected improvement (EI) were selected for running (see the SI). High yield values were easily reached, with two sets of conditions providing product 2a in 93% NMR-adjusted yield (Fig. 3, Entries 8 and 15). The conditions related to each iteration are described in the SI.

Fig. 3 NMR adjusted yield results for the BO of the acylation of L-leucine 1a.

In summary, the optimal conditions for the acylation of L-leucine 1a are presented in Scheme 1. In both optimized cases, the amount of acyl chloride exceeds that of the base. Using approximately three equivalents of chloroacetyl chloride, a liquid reagent, appears to improve the rheology of the system, resulting in a more fluid reaction medium and enhances compound formation. However, increasing the amount of acyl chloride beyond this level, while maintaining a similar base proportion, does not further improve the outcome and instead reduces the yield to 88% (Fig. 3, iterations 14 and 16). Conditions (i), shown in the upper part of Scheme 1, were finally performed as a triplicate and the three experiments delivered consistent results, with an NMR adjusted yield of 92 ± 2%, showing the robustness of the methodology.

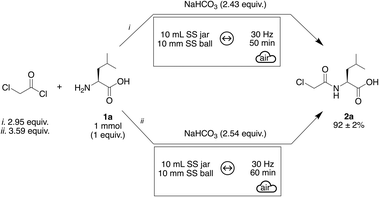Scheme 1 Best conditions provided by BO for the synthesis of 2a. (i) refers to Fig. 3, iteration 8. (ii) refers to Fig. 3, iteration 15.

Thanks to BO, the optimal conditions providing product 2a in a very good yield could be determined. This result has been obtained, after the initialization phase, after only 3 experiments in the iteration phase, proving the efficiency of such an approach in optimization studies. To confirm that the maximum was reached, 8 additional iterations were then performed without finding a better optimum.

Combination of OFAT/DoE with BO

Considering the great results obtained with BO and having a broad panel of experimental data, we turned our attention to the combination of the three optimization methodologies. The model was initiated with the results from OFAT and DoE. The studied parameters were still the same, to which a final one was added: the milling load. It plays a pivotal role in mechanochemistry, as it directly influences the energy transfer efficiency and reaction kinetics, making it a critical parameter to consider in the optimization of reaction conditions. Indeed, in the comparison studies, the reactions were set on a 1 mmol scale of L-leucine 1a, the milling load was therefore changing with the number of equivalents of both acyl chloride and base. Thus, as it is a crucial variable in mechanochemical reactions as well as regarding scaling up considerations, it seems relevant to evaluate its role in the outcome of the reaction. We were then able to run a series of 10 more experiments. As shown in Fig. 4, the BO confirmed the conditions determined by DoE without finding a better optimum. However, as our objective is to develop a sustainable approach, the reaction Process Mass Intensity (PMI), a green metrics defined as ratio between the mass of reactants and the mass of product, described in eqn (1), was also included in the target jointly to the NMR adjusted yield, effectively converting the problem of finding the highest sustainable yield to a global optimization. It must be noted that PMI and yield are not independent parameters.

Fig. 4 Values of NMR adjusted yield and PMI for each iteration of the BO in the case of acylation of L-leucine 1a.

This study revealed a powerful aspect of BO as it determines the conditions for the Pareto efficiency between PMI and NMR adjusted yield: it finds conditions where no objective can be improved without worsening the other objective. The acylation of 1a into 2a can be performed in an eco-friendlier way removing a third of the waste production (lowest PMI = 2.6) if a little decrease of the NMR adjusted yield to 88% is accepted (iteration 8 in Fig. 3). The conditions related to each iteration are described in the SI.

Since the BO method facilitates the extrapolation and optimization on other substrates, the acylation of L-phenylalanine 1b was studied. With 1b bearing an aromatic ring, the conversion could easily be measured by HPLC at 214 nm. Noteworthily, the consistency of the analytical method was assessed in duplicates by comparing the values of conversion obtained by HPLC and NMR. In the case of the NMR evaluation, the same treatment (liquid–liquid extraction) as for L-leucine 1a was applied to l-phenylalanine 1b. HPLC conversion and NMR-adjusted yield values were found to be very similar, highlighting the robustness of both analytical methods. When starting a new optimization, it is recommended to explore 2n + 1 experiments, where n is the number of dimensions (in our case, n = 4) to initiate the algorithm. However, another possibility is to use prior results and consider them as low fidelity data to stabilize the model in a rapid manner (see the SI) and therefore reducing the number of additional experimental points to run at the beginning of the optimization. Our initialization strategy combined proven-effective conditions from L-leucine 1a with a diverse set of exploratory experiments, providing a solid foundation for the Bayesian model. A weighting factor of 1/1000 was applied, where a weight of 1 was assigned to the values from 1a and a weight of 1000 to the experimental data from 1b. Remarkably, after only six conditions, the model exhibited sufficient stability to transition into the iterative optimization phase. Once the model stabilized, the surrogate function thus created was queried to systematically identify the most informative experimental conditions (see the SI). This approach aimed to maximize the efficiency of model refinement while simultaneously steering the optimization process toward the most favourable experimental outcomes. For implementation considerations, as the experiments were carried out on a Retsch Mixer Mill 400 requiring to load 2 milling jars, two experiments were suggested at each iteration. These were selected to maximize informational gain by minimizing overlap between the explored conditions (see the SI). Thanks to this strategy a sufficiently trained and stable model was achieved after just eight cycles of two experiments each. Finally, the model was asked to provide conditions either maximizing the HPLC conversion, or minimizing the PMI value or establishing a compromise between both responses. Gratifyingly, several sets of conditions were identified yielding results with high reproducibility and Pareto efficiency (Fig. 4).

The Pareto front represents the set of best trade-offs between the conflicting objectives. Once again, two sets of conditions were established: one maximizing the HPLC conversion and another minimizing the PMI, both representing the endpoints of the Pareto front (Fig. 5). Additionally, the final surrogate model can give insights into the impact of the milling load, a critical parameter in mechanochemistry. Since the milling load may influence the level of completion of a reaction, its role was specifically examined in the context of this transformation (Fig. 6). Two distinct trends emerge. The first and most prominent is the decline in conversion at higher milling loads, likely due to a fixed energy input (i.e., constant milling frequency, ball mass, and ball number), while the amount of substrate increases, diluting the energy delivered per unit of material. Additionally, at these milling loads, snowball effects were occasionally observed, which may also account for the decrease in HPLC conversion.^41,42 On the other hand, the loss of conversion observed at the lowest milling loads may be attributed to the rheology of the “soft solid” reaction mixture. In this regime, the formation of preferred pathways for the milling ball may occur, resulting in poor mixing efficiency. This, in turn, can lead to lower conversions and reduced reproducibility. Although poor mixing can lead to erroneous data, these experimental points should not be discarded from the study. In such cases, the response would always be lower than the expected one. However, BO (and the broader DoE) is able to consider several experimental points for one set of conditions, thus enriching the information available and adding variance to the model. Such an approach would prioritize areas providing high expected values and good reproducibility. Overall, the optimal conversion appears to be achieved at a milling load of approximately 30 mg mL⁻¹. The influence of this parameter should not be underestimated, as a mere 10% variation in milling load can lead to a significant difference in outcome, especially when considering potential scale-up.

Fig. 5 Pareto front corresponding to the BO for the acylation of L-phenylalanine 1b.

Fig. 6 Influence of the milling load (decorrelated from the other variables) in the acylation of L-phenylalanine 1b by chloroacetyl chloride.

Finally, BO also allows the identification of parameter weights. As shown previously, it has been confirmed that the milling time has a lower order of magnitude on the reaction while the amount of both chloroacetyl chloride and base will have a high one. The quantities of these reactants will determine the outcome of the reaction. The milling load, on its side, was easily implemented into the study and showed an average impact on conversion and reproducibility, the importance of this parameter might differ when scale-up is envisioned for the studied transformation.

Comparison of methods

The optimization of the experimental conditions for the acylation of L-leucine 1a has been carried out through 3 different methods (Table 4). The OFAT approach required to run 49 experiments (113 if replicates are considered), including the ones presented in Table 1, as well as preliminary tests related to the nature of the base, repeated trials for consistency, and additional investigations into the amount of liquid additive as discussed at the end of the corresponding section. It is an easy method to implement, useful for preliminary studies and it provided experimental conditions that would allow the synthesis of the desired product with a very good yield. However, as demonstrated before, the conditions were related to a local optimum and the results could be further optimized. DoE allowed us to explore a broader reaction space than in the OFAT part with the 19 experiments built with the DoE (32 experiments if replicates are considered) and thus provided a reliable estimation of the optimal conditions. By applying BO to the acylation of 1a, a slight improvement in terms of NMR adjusted yield could be achieved – from 88% to 92% – along with a reduction in standard deviation, all within just 16 experiments, including those used to initialize the algorithm. Noteworthily, the best conditions were obtained at the second iteration after the 5 experiments of the initialization phase, meaning that only 8 experiments in total have been necessary to reach the optimal value. Although the number of experiments to be conducted is easier to estimate with OFAT and DoE, it remains more difficult to predict for BO, as it evolves with each new set of data provided to the algorithm. However, BO-based optimizations are generally faster. BO, requiring less experiments in the optimization process, is well-adapted for application to technologies such as ball-milling which have not yet been developed in a high-throughput approach. Furthermore, BO facilitated the integration of the milling load as a parameter and PMI as an optimization target, thereby enabling a more sophisticated experimental design and a greener outcome – an approach that would have been considerably more challenging to implement using one of the two other methods. Of note, unlike DoE, which requires completing all planned experiments, BO allows the process to be stopped as soon as the model is sufficiently trained, making it more flexible and resource-efficient. In addition, BO enlightened the fact that conditions could be easily modified in order to optimize one target value or another (maximization of the conversion vs. minimization of the PMI) and showed in the case of L-phenylalanine 1b that experimental conditions can be adapted in a straightforward manner to another amino acid, hence to any amino acid. Indeed, rapid extrapolation of the BO method to various substrates, in the same transformation, is a strong advantage compared to OFAT or DoE approaches.

Table 4 Summary table for the three optimization methods

Method	Number of experiments required by the method	Number of experiments actually performed	Best conditions	NMR adjusted yield^a (%)	Comment
a Values represent the 95% confidence interval, expressed as: mean values of several experiments ± 1.96 * standard error.b Including preliminary tests for the nature of the base, repeated trials for consistency and further investigations into the amount of liquid additives.c Adding nitromethane as a liquid additive, η = 0.3 µL mg^−1.d Including replicates.
OFAT	49	113^b	x = 1.5	87 ± 17%	Easiest implementation
			y = 1.4	88 ± 7%^c	Suitable for preliminary studies
			Time = 15 min
DoE	19 (14 + 5 centre points)	32^d	x = 1.66	89 ± 1%	Reliable estimation of the optimum value
			y = 3.07		A second DoE should be necessary in a narrower space around the given value to be more precise
			Time = 40 min
BO	8 (initialization: 5 + iteration: 3)	16	x = 2.95	92 ± 2%	Faster optimization
			y = 2.43		Inherently optimizes high yield and reproducibility
			Time = 50 min		Easier implementation of additional parameters or targets
					Facilitated exemplification

---

Scope of the reaction

Classically, in organic chemistry, once the conditions are optimized on a model substrate, they are applied to a selection of chosen molecules to demonstrate the suitability and versatility of the method. However, BO builds on previous results, and thus offers the great opportunity to specifically optimize, with a few additionnal experiments, the reaction conditions for each substrate included in the scope of the study. This results in drastically reducing the waste generated when unsuitable conditions are employed. Successively, a series of six additional amino acids, besides L-leucine, were subjected to BO for their acylation by chloroacetyl chloride (Scheme 2).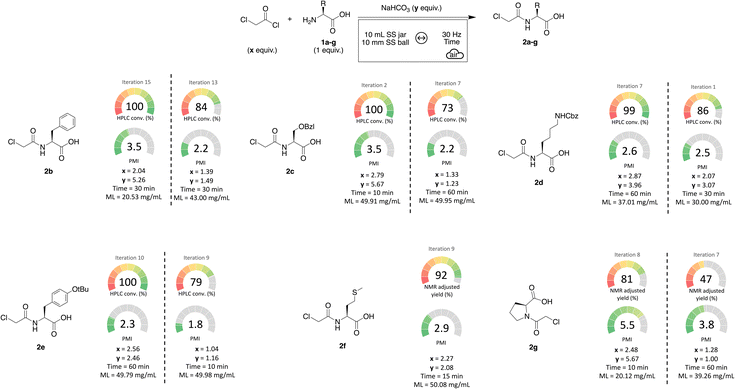

Scheme 2 Exemplification of BO describing the conditions maximizing the conversion (left) or minimizing the PMI (right). ML = milling load.

For the ones bearing an aromatic ring, the conversion could easily be followed by HPLC at 214 nm. The others were subjected to the same treatment as L-leucine 1a. Complete conversions were obtained in a fast and straightforward manner. Moreover, two sets of Pareto efficient conditions may be proposed: one that maximizes conversion (reaching or nearing 100%) but results in a higher PMI due to the excess reactants, and another that reduces the waste generation while maintaining high conversions.

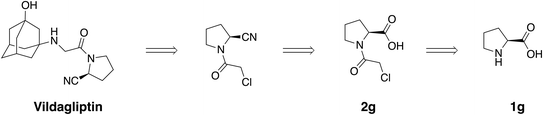
After exploring a selection of primary amines, we turned our attention to a more challenging hindered substrate: L-proline 1g. The corresponding acylation product 2g is of high interest since it appears as a key intermediate in the synthesis of vildagliptin, an antidiabetic drug used for the treatment of type II diabetes which was approved by the European Medical Agency in 2007 (Scheme 3).⁹

Scheme 3 Retrosynthesis of vildagliptin.

Under mechanochemical conditions, the secondary amine of L-proline 1g could be acylated with an 81% NMR adjusted yield. Although the isolated yield was modest (52%) due to the strong hydrophilicity of the molecule, intermediate 2g was successfully obtained via a solvent-free method, paving the way for a more sustainable synthesis of vildagliptin.

Conclusions

The solventless acylation of various unprotected amino acids using an acyl chloride under mechanochemical conditions in a ball-mill was optimized herein through three methodologies: One Factor at a Time, Design of Experiments and Bayesian-based machine learning. The results clearly demonstrate that mathematical and statistical tools can significantly enhance the optimization of chemical processes. The integration of BO as a continuation of the classical OFAT and DoE frameworks presents a highly promising approach for reaction development. OFAT effectively mirrors the intuitive strategies often employed by experimental chemists, and its partial success – requiring at least 49 experiments to achieve an 88% NMR adjusted yield for acylation product 2a – can be both motivating and informative. Since OFAT does not consider interactions between factors, the improvements observed with DoE are particularly compelling (89% after 19 experiments, 32 if replicates are considered), suggesting that chemists should look beyond the conventional OFAT approach. BO was able to further optimize the process by reducing the number of experiments to 16, the best result being obtained after 8 experiments (5 for the initialization phase and 3 for the iteration phase), while increasing the yield to 92%. Beyond drastically reducing the number of experiments required to identify optimal conditions – thereby saving reagents, time and operational resources – DoE, and even more BO, enable faster and more effective optimization. This facilitates the fine-tuning of reaction conditions for each substrate, minimizing waste associated with suboptimal parameters. Additional parameters (i.e., milling load) as well as targets (i.e., PMI) can be easily introduced in BO models to better understand complex systems and the optimization can be tailored to the outcome. Future work will be devoted to include mechanochemical parameters such as nature and size of both jar and balls, milling frequency or even type of milling device (vibratory or planetary ball-mill) in reaction optimizations. Following our pioneering work on BO for thermal amidation via reactive extrusion,³⁹ this work represents the first application of this approach for reactions performed in a ball-mill and highlights that mathematical approaches can considerably improve the optimization processes in mechanochemistry. The combination of Bayesian Optimization, which reduces the number of experiments and therefore the consumption of chemicals in process development, and solvent-free mechanochemistry provides an optimal strategy for implementing more sustainable chemistry.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5mr00096c.

Acknowledgements

The Centre National de la Recherche Scientifique (CNRS), University of Montpellier and the French National Research Agency (ANR-22-CE19-0036) are gratefully acknowledged for the financial support. Analyses were carried out at ‘PAC Chimie Balard’, analytical facilities of Univ Montpellier, CNRS, ENSCM. Marcelin Lamaty is recognized for his contribution to the design of the graphical artwork.

References

1. J. Bonnamour, T.-X. Métro, J. Martinez and F. Lamaty, Green Chem., 2013, 15, 1116–1120.
2. V. Declerck, P. Nun, J. Martinez and F. Lamaty, Angew. Chem., Int. Ed., 2009, 48, 9318–9321.
3. S.-Y. Han and Y.-A. Kim, Tetrahedron, 2004, 60, 2447–2467.
4. J. M. Humphrey and A. R. Chamberlin, Chem. Rev., 1997, 97, 2243–2266.
5. P. Acosta-Guzmán, A. Ojeda-Porras and D. Gamba-Sánchez, Adv. Synth. Catal., 2023, 365, 4359–4391.
6. C. A. G. N. Montalbetti and V. Falque, Tetrahedron, 2005, 61, 10827–10852.
7. E. Valeur and M. Bradley, Chem. Soc. Rev., 2009, 38, 606–631.
8. S. K. Singh, N. Manne and M. Pal, Beilstein J. Org. Chem., 2008, 4, 20.
9. D. Yu, W. Anmin, T. Zhu, C. Yingjie, P. Xinmei and H. Xiangnan, Lett. Org. Chem., 2014, 11, 780–784.
10. T. F. Burton, Z. Garisoain, C. Chaix, J. Aassine, E. Virapin, A. Voronova, J. Pinaud and O. Giani, ACS Omega, 2024, 9, 28583–28593.
11. T. F. Burton, J. Pinaud and O. Giani, Macromolecules, 2020, 53, 6598–6607.
12. T. F. Burton, J. Pinaud, N. Pétry, F. Lamaty and O. Giani, ACS Macro Lett., 2021, 10, 1454–1459.
13. N. E. Göppert, M. Dirauf, P. Liebing, C. Weber and U. S. Schubert, Macromol. Rapid Commun., 2023, 44, 2200651.
14. T.-X. Métro, J. Bonnamour, T. Reidon, J. Sarpoulet, J. Martinez and F. Lamaty, Chem. Commun., 2012, 48, 11781–11783.
15. P. T. Anastas and J. C. Warner, Green Chemistry: Theory and Practice, Oxford University Press, 2000.
16. S. M. Asaad, A. Inayat, F. Jamil, C. Ghenai and A. Shanableh, Energies, 2023, 16.
17. K. Brugemann, M. Pereira, P. Steinsoultz, C. Peter, S. Hammoud, M. Schmitt, G. Blond and F. Bihel, ACS Sustainable Chem. Eng., 2025, 13, 12232–12241.
18. E. Braconi and E. Godineau, ACS Sustainable Chem. Eng., 2023, 11, 10545–10554.
19. N. El Sabbagh, M. Bazzoni, Y. Horbenko, A. Bernard, D. Cortés-Borda, P. Giraudeau, F.-X. Felpin and J.-N. Dumez, React. Chem. Eng., 2024, 9, 2599–2609.
20. K. C. Felton, J. G. Rittig and A. A. Lapkin, Chem.:Methods, 2021, 1, 116–122.
21. A. Senthil Vel, K. E. Konan, D. Cortés-Borda and F.-X. Felpin, Org. Process Res. Dev., 2024, 28, 1597–1606.
22. A. Slattery, Z. Wen, P. Tenblad, J. Sanjosé-Orduna, D. Pintossi, T. den Hartog and T. Noël, Science, 2024, 383, eadj1817.
23. F. Wojciechowski, M. Suchy, A. X. Li, H. A. Azab, R. Bartha and R. H. E. Hudson, Bioconjugate Chem., 2007, 18, 1625–1636.
24. T. P. Singh and R. Shunmugam, New J. Chem., 2016, 40, 3024–3027.
25. L. K. Beagle, F. K. Hansen, J.-C. M. Monbaliu, M. P. DesRosiers, A. M. Phillips, C. V. Stevens and A. R. Katritzky, Synlett, 2012, 23, 2337–2340.
26. P. Lloyd-Williams, A. Sánchez, N. Carulla, T. Ochoa and E. Giralt, Tetrahedron, 1997, 53, 3369–3382.
27. S. Vizcaíno Páez, D. Durango, C. J. Müller, M. Breuning and W. Q. Fletcher, RSC Adv., 2024, 14, 3790–3797.
28. A. Stolle, in Ball Milling towards Green Synthesis: Applications, Projects, Challenges, ed. B. Ranu and A. Stolle, The Royal Society of Chemistry, 2014, p. 241,  10.1039/9781782621980-00241.
29. A. Stolle, T. Szuppa, S. E. S. Leonhardt and B. Ondruschka, Chem. Soc. Rev., 2011, 40, 2317–2329.
30. T. Szuppa, A. Stolle, B. Ondruschka and W. Hopfe, ChemSusChem, 2010, 3, 1181–1191.
31. J. M. Andersen and J. Mack, Chem. Sci., 2017, 8, 5447–5453.
32. A. Gallego, N. Pétry, J. Pinaud, O. Giani and F. Lamaty, ChemistryEurope, 2025, e202500232.
33. D. Prat, A. Wells, J. Hayler, H. Sneddon, C. R. McElroy, S. Abou-Shehada and P. J. Dunn, Green Chem., 2016, 18, 288–296.
34. P. M. Murray, F. Bellany, L. Benhamou, D.-K. Bučar, A. B. Tabor and T. D. Sheppard, Org. Biomol. Chem., 2016, 14, 2373–2384.
35. S. A. Weissman and N. G. Anderson, Org. Process Res. Dev., 2015, 19, 1605–1633.
36. D. Zanolla, B. Perissutti, P. C. Vioglio, M. R. Chierotti, L. Gigli, N. Demitri, N. Passerini, B. Albertini, E. Franceschinis, J. Keiser and D. Voinovich, Eur. J. Pharm. Sci., 2019, 140, 105084.
37. O. M. Lemine, M. A. Louly and A. M. Al-Ahmari, Int. J. Phys. Sci., 2010, 5, 2721–2729.
38. E. Suut-Tuule, T. Jarg, P. Tikker, K.-M. Lootus, J. Martõnova, R. Reitalu, L. Ustrnul, J. S. Ward, V. Rjabovs, K. Shubin, J. V. Nallaparaju, M. Vendelin, S. Preis, M. Öeren, K. Rissanen, D. Kananovich and R. Aav, Cell Rep. Phys. Sci., 2024, 5, 102161.
39. M. Lavayssiere, X. Bantreil and F. Lamaty, Optimizing Reactions in Reactive Extrusion by a Bayesian Approach: the Case of Thermal Amidation, ChemRxiv, 2025 DOI:10.26434/chemrxiv-2025-zgpnz.
40. For a recent preliminary report: F. Mele, A. M. Constantin, M. Barezzi, L. Rossi, A. Ergasti, T. Fontanini, S. Civardi, R. M. Sundermann, P. P. Mazzeo and R. Maggi, Machine Learning–Assisted Development of a Fast Mechanochemical Johnson–Corey–Chaykovsky Reaction, ChemRxiv, 2025 DOI:10.26434/chemrxiv-2025-xwgpn.
41. M. Carta, S. L. James and F. Delogu, Molecules, 2019, 24, 3600.
42. V. K. Smolyakov, O. V. Lapshin, V. V. Boldyrev and E. V. Boldyreva, Russ. J. Phys. Chem., 2018, 92, 2542–2547.

---