Machine learning-enabled discovery of ionic liquid–solvent electrolytes exhibiting high ionic conductivity

Abstract

Ionic liquids (ILs), which are a class of materials with versatile nature and growing popularity, are facing impediments toward widespread usage as electrolytes due to various factors such as low ionic conductivity, high viscosity, high market price etc. One of the ways these limitations can be addressed is by mixing ILs with a molecular solvent. In a combinatorial sense, there exists an immense number of specific IL–solvent combinations. An exhaustive experimental or even simulation-based investigation of the chemical space spanned by such combinations can be extremely time-consuming, expensive, and nearly impossible. An alternative approach is to employ machine learning-based models developed from available databases. Although there exists prior literature that integrates machine learning to investigate mixtures of specific solvents with ILs, these models lack generalization necessitating development of a large number of ML models to handle various solvents. To remedy this shortcoming, as a part of designing green electrolytes with high ionic conductivity that can have potential applications in next-generation batteries and solar cells, this work aims to develop a unified machine learning model to predict ionic conductivity of any IL–solvent mixture system. In this regard, three models, namely, Random Forest, extreme gradient boosting (XGBoost), and artificial neural network (ANN) were formulated using the NIST ILThermo database. The dataset contained 549 unique ionic liquids from 16 cation families and 81 unique solvents, representing a total of 23 712 datapoints. SHAPLEY additive explanation (SHAP) method was used to assess the impact of various features on model prediction and their significance was compared with literature to gain physical insight about the model behavior. Finally, using the developed models, approximately 2.5 million IL–solvent mixtures at five different compositions were screened at room temperature. The high-throughput screening yielded nearly 19 000 IL–solvent mixtures for which ionic conductivity was found to exceed the ionic conductivity of conventional Li-ion battery electrolyte.

---

Design, System, Application

The article focuses on the design of ionic liquid (IL)–solvent mixtures with high ionic conductivity. To realize the objective, the approach adopted here involves developing a machine learning model that correlates the experimental ionic conductivity data for a large number of IL–solvent mixtures extracted from NIST ILThermo database. We considered ∼23 000 data points covering 549 ILs represented by 308 cations, 96 unique anions and approximately 80 solvents. After testing the accuracy of the model on the test data set, we leveraged the machine learning approach to predict ionic conductivity of unique combinations of cation, anion, and solvent mixtures as a function of IL mole fractions. The approach resulted into roughly 2.5 million unique IL–solvent systems and 12.5 million data points at room temperature. Out of these data points, close to ∼19 000 IL–solvent mixtures were found to exhibit ionic conductivity greater than 2.0 S m⁻¹ (threshold based on the ionic conductivity for current electrolytes containing LiPF6 as the salt in 1 : 1 mixture of ethylene carbonate and dimethyl carbonate) in comparison to only 88 IL–solvent mixtures showcasing ionic conductivity greater than 2.0 S m⁻¹, considerably expanding the design space as potential electrolytes for the next-generation Li-ion batteries and energy storage devices.

Introduction

The development of novel molecules and materials is critical for scientific, technological, and societal growth. Ionic liquids (ILs) are a specific type of material that are comprised entirely of cations and anions and can be designed to exist in a liquid state below 100 °C.¹ A large number of ILs exhibit favorable characteristics such as high thermal and electrochemical stability, negligible volatility, low melting point, etc. which are appealing for their usage as green solvents in applications such as battery electrolytes, atmospheric carbon dioxide absorption, chemical separation, catalysis etc.^2–4 Additionally, the ability of tuning their structures by changing the cation and/or anion type, and functional groups on cation and anion to tailor properties for a desired application imply that the ILs are designer solvents.

However, despite these attractive properties, the industry-wide adoption of IL is still lagging behind. One of the key challenges is that a large number of ILs tend to be highly viscous due to strong electrostatic and hydrogen bonding interactions.⁵ The high viscosity is a hindrance for the charge transport resulting into low ionic conductivity.⁶ Additional impediments toward the widespread industrial usage of ILs are their limited biodegradability,⁷ high cytotoxicity, and relatively high market price.³

One of the viable ways some of these limitations can be addressed is by formulating IL–IL mixtures, which significantly expands the available chemical space for the discovery of new ILs. Over the last few years, several researchers have shown that the interaction such as hydrogen bonding dynamics,⁸ structure,^9–11 transport properties,¹² and phase-equilibria^13,14 can be tuned by adopting such a strategy. Our research group has previously leveraged ionic conductivity of pure ILs and linear combination of molecular descriptors to estimate the ionic conductivity of IL–IL mixtures.^15,16 Experimental data for IL–IL mixtures is still scarce, making it challenging to perform and evaluate data-driven discoveries. A possible alternative is to add organic solvents which can potentially break the hydrogen bonding network and reduce electrostatic interaction in ILs, facilitating an enhancement in transport properties.⁵ In almost all instances, there is a significant decrease in viscosity while a maximum in ionic conductivity can be obtained using an appropriate concentration of an IL and organic solvent such as ethylene glycol.¹⁷ acetonitrile,¹⁸ and ethanol.¹⁹ Additionally, there exist a large amount of data for properties of IL–solvent mixtures in the literature enabling us to perform a data-driven study by creating machine learning models. Furthermore, such mixtures open up a new dimension for tuning additional properties, resulting in a larger chemical space to explore.

To discover particular IL–solvent systems for specific use cases, it is necessary to understand the interaction between various ILs and solvents. Also, in industrial applications, ILs are often accompanied by a molecular solvent and the property of those mixtures are significantly different than pure IL or pure solvent.⁶ Therefore the necessity of a study dedicated to predicting and understanding the properties of IL–solvent mixture is substantial. However, so far the studies in this field have been limited to specific IL–solvent combinations,^6,20–22 resulting in the vast potential of IL–solvent mixtures relatively underdeveloped. Experimentally exploring this large combination space is nearly impossible. Physics-based computations such as molecular dynamics simulation and density functional theory calculations have good accuracy, but their high computational cost is prohibitive for large scale screening tasks. Thermodynamic models such as statistical associating fluid theory (SAFT) and conductor-like screening model for real solvents (COSMO-RS) can be leveraged to study complex fluids like ionic liquids and their mixtures. However, they require a separate transport model (such as Nernst Einstein or Einstein model) to calculate ionic conductivity, and these models are dependent on ion-specific parameter tuning.²³ Hence, the developed model will be relevant to certain ion families, but may lack generalizability. An alternative approach is to exploit machine learning, which has wide application as a screening tool across various fields of science and engineering.²⁴ Machine learning models rely on the data to detect complex patterns associated between property output and structural information encoded as inputs. Once a model is developed, predictions of properties of novel combinations are several orders of magnitude faster than experiments or computational approaches, as long as the structural space is, at least partly, learned when the model is trained. The performance of machine learning models may depend on various factors, i.e. algorithm type (parametric or non-parametric, tree-based or kernel based or neutral network based etc.), featurization type (group-contribution based, descriptor-based, sigma-profile based, fingerprint-based, graph-based etc.), and last but not least the size and diversity of the dataset.²⁵

Many works in the literature have employed machine learning to predict properties of pure ILs.^15,16,26 Datta et al. created an artificial neural network (ANN) using RDKit descriptors as features to predict the ionic conductivity of pure ILs.²⁶ Their dataset was obtained from the NIST ILThermo Database and was comprised of 406 unique ILs and a total of 4259 datapoints. They also compared two types of splitting methods namely, random split and IL-split and showed how conventionally used random split can overestimate the results. Venkatraman et al. created a virtual library of over 8 million synthetically feasible ILs with 12 predicted properties.²⁷ Abdullah et al. presented the effect of featurization toward prediction of ionic conductivity by comparing graph convolution and RDKit descriptors.²⁸ They showed that graph convolution outperformed RDKit features, but it was only by a small margin. Dhakal et al. developed support vector machine (SVM) and ANN models to predict the ionic conductivity of imidazolium-based ILs,¹⁵ and showed how learning from pure ILs could be translated to generate a large number of IL–IL mixtures exhibiting non-ideal behavior; mixtures for which the ionic conductivity was enhanced (suppressed) relative to those for the pure counterparts. In their subsequent paper, they developed a generalized model with 10 different cation families using multiple linear regression, Random Forest, and extreme gradient boosting (XGBoost) algorithms.¹⁶ In both of these papers they employed RDKit descriptors as featurization technique and random split as their splitting technique. Chen et al. generated COSMO-RS driven quantitative structure property relationship (QSPR) models to predict conductivity and then leveraged Random Forest and XGBoost models to correlate QSPR prediction to actual conductivity.²⁹ This two-step methodology significantly improved their initial QSPR results. Recently, Mohan et al. optimized four machine learning models (polynomial regression, support vector regression, feed-forward neural network and categorical boosting) to predict the viscosity of pure ILs.³⁰ They used a combination of COSMO-RS and RDkit-derived features and showed an improvement in the prediction capability over the models trained only on RDkit features.

Although an impressive amount of work has been carried out with respect to developing machine learning models for predicting the ionic conductivity of pure ILs, a research gap and the necessity of machine learning models capable of predicting properties of IL–solvent mixtures still remain. As many ILs are hygroscopic in nature, absorption of water will modify their properties, which the models developed on pure IL properties would not be able to capture. Furthermore, due to the relatively high cost of ILs compared to conventional molecular solvents, it is likely that ILs will be deployed as mixtures. Unfortunately, studies involving IL mixtures are limited in comparison to those that focus on pure ILs. In fact, among the very few studies that report properties of IL mixtures, most of them are limited to one or two common molecular solvents.^31–34 Hezave et al. used ANN to predict the electrical conductivity of the ternary mixtures involving IL, water and another organic solvent.³¹ Their dataset only had 104 datapoints with single IL and two solvents, making it difficult to generalize for other solvents of ILs. Lashkarblooki et al. developed ANN model to predict the viscosity of ternary mixtures comprised of IL, water and an organic solvent.³² Similar to the work by Hezave et al.,³¹ the model development relied on rather a small dataset containing only 729 datapoints for five ILs. Chen et al. developed ANN using group contribution method as features to predict the viscosity of IL and water mixtures.³⁴ Duong et al. used variants of multiple linear regression and ANN to predict the ionic conductivity of protic ILs that can account for water content upto 5 wt%.³³ Among the very few studies that aimed at developing generalized models to predict the properties of IL–solvent mixtures, Liu et al. focused on heat capacity and density³⁵ while Lei et al. studied surface tension and viscosity.^35,36 In both of the works, three machine learning models (ANN, XGBoost and light gradient boosting) with group contribution methods were employed.

To address the gaps identified above in the literature, our objective in this work was to develop a generalized machine learning model capable of predicting the ionic conductivity of any IL–solvent mixture. To achieve this target, we formulated a diverse dataset of 549 unique ILs from 16 cation families, 81 unique molecular solvents and 7123 unique IL–solvent mixtures resulting in a total of 23 712 datapoints. Using this dataset, three machine learning models, namely Random Forest, XGBoost and ANN were trained. A schematic of our workflow is presented in Fig. 1. We used RDKit descriptors as our featurization technique. We used two splitting techniques, stratified-IL split and random split, the detail behind these selections is presented in the Methods section. To the best of our knowledge as of writing this paper, this is the first study that addresses the development of a generalized data-driven model for the prediction of ionic conductivity of IL–solvent mixtures. Based on this work, a web tool was developed that can be found in https://ionicliquid.streamlit.app.

Fig. 1 General workflow of our work.

Method

Parsing, cleaning and formulating an ionic conductivity dataset

The dataset was created by downloading the ionic conductivity data from the NIST ILThermo database^37,38 using a modified version of the pyILT2 library.³⁹ A schematic of data collection, cleaning and dataset formulation process can be found in Fig. 2. The downloaded data for IL–solvent mixture was from a total of 1079 publications. Then we acquired the simplified molecular input line entry system (SMILES) strings⁴⁰ for ILs and solvents using two python wrappers: PubChemPy⁴¹ and CIRpy.⁴² PubChemPy uses the Pubchem database,⁴³ and CIRpy uses the Chemical Identifier Resolver (CIR)⁴⁴ web service provided by the NCI/CADD group at the National Institute of Health. We only retained datapoints for which the SMILES of the components could be found in the either of the two databases. Following this step, all the SMILES were canonicalized using the RDkit to ensure uniformity. We observed that the ionic conductivity was reported either in terms of either electrical conductivity or molar conductivity. Similarly, the concentration was expressed in a number of ways: mole fraction, weight fraction, volume fraction, molar ratio, mass ratio, molarity, and molality of either the IL or the solvent. We found that the mixtures included not only IL–solvent but also IL–IL, IL–salt, and IL–gas mixtures. In the NIST ILThermo database, ionic conductivities collected from various papers are termed as electrical conductivity. It is not apparent to us the reasoning why the developers of the NIST ILThermo Database preferred to use electrical conductivity; however, we ensured that the original publications list these conductivities as ionic conductivity. In our dataset, we elected to use ionic conductivity (reported as electrical conductivity (S m⁻¹) in the NIST ILThermo database) for IL–solvent mixtures excluding those in which the composition was provided either in terms of molarity or volume fraction due to the absence of density or molar volume data for IL–solvent mixtures. For the same reason, we removed datapoints for which molar conductivity was reported instead of ionic conductivity. We further enhanced the diversity of our dataset by adding the ionic conductivity data for pure ILs reported in the NIST ILThermo database. We represented pure ILs as “mixtures” by pairing each IL with two randomly selected solvents. For these mixtures, the mole fraction of the IL was set to unity. This was adopted to make our models agnostic of solvent identity while predicting ionic conductivity for pure ILs. This procedure of augmenting the dataset resulted in a significant increase in the number of datapoints (from 17 535 to 27 910) and in the number of unique cation families (from 10 to 16). For multiple data entries for a given IL or IL–solvent mixtures, we retained the datapoint with the smallest uncertainty, which is reported as the δ parameter in the NIST database. We also eliminated datapoints for which the δ parameter was higher than 0.5. As our primary objective was to identify IL–solvent mixtures exhibiting high ionic conductivity, we set the lower bound for ionic conductivity to 0.001 S m⁻¹. The final dataset contained a total of 23 712 datapoints that represented 16 cation families, 549 unique ILs, 308 unique cations, 96 unique anions and 81 unique solvents. The temperature ranged from 233 K to 528.55 K. The distributions of ionic conductivity and temperature of the dataset is presented in Fig. S1 and S2.

Fig. 2 A brief illustration of the dataset formulation pipeline.

Featurization

After creating the dataset, we calculated RDkit descriptors⁴⁵ separately for cations, anions, and solvents using their SMILES strings. These descriptors include physical properties such as molecular weight, topological properties (e.g., Kappa, VSA_Estate, Balabanj), molecular fingerprints densities (FpDensityMorgan), presence of fragment groups and specific structures (fr_AL_OH, fr_imidazole, NumAromaticRings) etc. Initially, we obtained 209 descriptors for each of the cations, anions and solvents for a total of 627 features. As a large number of features can result in over-fitting and degrade predictive capability of the model, we trimmed the number of features using a number of techniques. Any feature containing less than five unique values was removed. Additionally, we kept only one of the two features that showed high correlation for which we set the correlation coefficient threshold to 0.8. These strategies led to a considerable decrease in the number of features for each of the species: 46 features for cations, 43 features for anions, and 53 features for solvents. As we used temperature and mole fraction as additional features, there were a total of 144 features for the machine learning model development.

Scaling

The ionic conductivity values in the dataset spanned six orders of magnitude ranging from 0.001 S m⁻¹ to 140.6 S m⁻¹ (Fig. S1). Such a wide range of ionic conductivity values necessitated that the prediction range be narrowed for which we log-transformed the values using base 10. For improved training accuracy, we applied standard scaling to each feature while developing neural network-based model. However, tree based models are non-parametric which operate by simple if-else logic and do not require any weight matrix. For those models, scaling is not necessary, and hence we did not perform any feature scaling for Random Forest and XGBoost models.

Splitting

For data splitting, we used random split and a modified version of the stratified split. For both split types, 10% of the original data (IL–solvent mixtures without augmentation) was set aside for final testing while the remaining data was used for training and validation. Random split is most commonly seen in literature, but it carries a significant caveat. As this type of split is carried out without regard to the identity of IL (or chemical structures), it is possible that the split results into the same IL structure being present in both training and test datasets, for example, at a different temperature(s) or mole fraction(s). This may result in a model primarily learning to capture the temperature and/or composition dependence rather than the impact of inherent structural diversity on the target property. Therefore, the accuracy of the predictions for the test dataset may be overly optimistic. A possible remedy is to split the dataset ensuring that a given IL structure is present exclusively either in the train or the test dataset; the split is referred as IL-split in the literature.²⁶ A key feature of this type of splitting method is that it evaluates the ability of the model to capture the structural dependence as well as the system variable (temperature and pressure) dependence.

Our modification of the IL-split stems from diversity of the dataset, which contains 16 cation families and a significant imbalance in the number of datapoints for each family (Fig. 3). An exact stratified split would have ensured the retainment of the 90–10 split in specific cation families as well (for example, 90% of imidazolium in training set, 10% of imidazolium in the test set, 90% of ammonium in the train set, 10% of ammonium in the test set and so forth). However, the stratified-IL split that we used in this work combines both IL-split and stratified split. As different ILs in each cation family have unequal number of datapoints, an exact 90–10 split for all the cation families was not possible. For that reason, cation families (piperidinium, triazolium, guanidium, pyrazolium, thiophenium) that have only a few datapoints are not included in the test dataset. By performing a startified-IL split, we guarantee that both the train and the test set correctly represents the distribution of the overall dataset (Fig. 3) and a specific cation is present in either train or test set. A similar imbalance in the anions and solvents can be seen (Fig. 4). However, there are a large number of structurally unique anions compared to cation families. Therefore, the stratified-IL split was carried out based solely on the cation family.

Fig. 3 Percentage of cation families present in the train and test set after stratified-IL split. Cations that have small presence in the dataset (<2%) are not included in the test set. Stratified-IL split ensures that the train and test sets maintain almost similar distribution of families and they do not possess the same cation.

Fig. 4 Diversity of (a) cation families, (b) anions and (c) solvents in the dataset.

Model development

We developed two separate sets of three models (Random Forest, XGBoost and ANN) for the two different splitting types. For the Random Forest and XGBoost models optimization of the hyperparameters was carried out using a grid-search method and five-fold cross validation. The final sets of hyperparameters for the models are reported in SI. ANN was manually tuned to determine the optimum number of hidden layers and number of nodes in each of the hidden layers. The procedure led to six hidden layers for each of the models developed using the random and stratified-IL splits. However, the number of nodes in each of the hidden layers differed for the two splits such that 1000 units were required for the random split while only 100 units were necessary to correlate the data using stratified-IL split. Ridge regression (L2) and dropout of 0.2 was used as regularization parameters. Detailed architecture along with improvement of train and validation scores with respect to epochs can be seen in SI. After that, the performances of the models were evaluated in 10 random validation sets. Finally the models were evaluated on the held out test sets. The learning and predicting capability of the three models were tested using two performance metrics: correlation coefficient (R²) and mean absolute error (MAE).

Results and discussion

Dataset diversity

The dataset that we gathered consisted of 308 unique cations from 16 cation families, 96 unique anions and 81 solvents. Fig. 4 depicts the diversity of cations, anions, and solvents present in the dataset. It is evident that, from the 16 cation families, imidazolium was the most studied cation type in the NIST ILThermo Database, which accounted for almost half of the datapoints. Ammonium, pyridinium, aminium, pyrrolidinium, phosphonium, and piperidinium families represented 15.3%, 11.2%, 8.8%, 5.3%, 4.4% and 1.3% datapoints, respectively. Several other types of cations such as guanidinium, triazolium, morpholinium, pyrazolium, thiophenium, piperazinium, pyrrolidone and amidium were present in significantly smaller numbers and together formed only 2.7% of the entire dataset. For anions, the distribution was comparatively less skewed such that bis(trifluoromethanesulfonyl)imide ([NTf₂]⁻ also commonly referred to as TFSI), Br⁻ and tetrafluoroborate [BF₄]⁻ accounted for 17.8%, 13.7% and 13.6%, respectively. We observed a gradual decline in the distribution starting from Cl⁻ (5.5%) to [ClO₄]⁻ which was present only at 4 × 10⁻⁴%. To characterize the diversity of solvents, we separated the solvents into various families based on their structure and functional groups (Fig. 4(c)).^46,47 For structures containing multiple functional groups, we used the priority list for IUPAC naming of compounds.⁴⁸ For example, a solvent containing both an amine group together with an alcohol moiety would be classified as aminoalcohol. We observe that approximately one third of the datapoints involved water as a solvent. The remaining datapoints were for organic solvents with alcohols, acids, and esters leading the list. A gradual decrease in the fraction of datapoints containing amide to ether can be seen. About 4% of the datapoints were for solvents such as nitro compounds, diketones, amines, organosulfurs and diazoles.

Additionally, we performed Tanimoto similarity analysis to gauge the extent of structural diversity of the chemical constituents in our dataset.⁴⁹ A Tanimoto similarity score of 1 denotes perfect similarity and 0 implies lowest similarity.⁵⁰ Among a wide range of similarity fingerprints available, extended connectivity fingerprints with diameter 4 and 6 (ECFP4, ECFP6) are the best performing fingerprints for ranking diverse structures.⁵¹ In this work, we calculated the Tanimoto similarity score of all possible pairs of cations, anions, ionic liquids, and solvents using Morgan Fingerprint with diameter 6 (radius = 3), which is an RDKit implementation of ECFP6.⁵² As an example, for 81 solvents, we calculated the Tanimoto similarity index for each pair of solvents, resulting in an 81 × 81 matrix. As such a matrix is symmetric, we removed the entries in the diagonal (self–self), and only retained the upper triangle of the matrix. Results from such a computation are presented for the cation, anion, ILs, and solvents as a violin plot in Fig. 5. It can be seen that the Tanimoto similarity index spans the entire range from 0 to 1. However, a large fraction of the similarity indexes fall within 0 to 0.2 as evidenced by a width of the violin plots in this range, suggesting structural diversity in cations, anions, ILs, and solvents. For a given violin plot, the probability of the Tanimoto similarity index exceeding 0.5 is significantly diminished as indicated by a very narrow region above this value. Also, anions and solvents exhibit even greater dissimilarity with more than 25% of the pairs showing similarity close to zero. Overall, a broad chemical diversity of the dataset is apparent from our analyses.

Fig. 5 Tanimoto score distribution of cation, anions, ILs, and solvents in the dataset; the three dotted lines inside each of the violins represents quartiles.

Model performance

We evaluated the performance of the three models developed in this work along with the influence of the type of data splitting in terms of correlation coefficient (R²) and the mean absolute error (MAE) computed in terms of predictions expressed in log values on a base-10 scale. The values for the two metrics for a given model and the way data was split in the training and test datasets are summarized in Table 1. Comparing three models, we notice that the tree-based models (Random Forest and XGBoost) yielded almost similar performance. The R² values and MAE obtained in this work are in line with those obtained in our previous work on correlating ionic conductivity for pure ionic liquids using Random Forest and XGBoost methods.¹⁶ The accuracy of the ANN model developed here is somewhat lower than that of the tree-based models, which is consistent with literature reports on IL property predictions comparing the two models.^30,36 Although both the tree-based and ANN models attempt to capture nonlinear structure–property relationship, neural network-based models tend to outperform other models when a large amount of data is used so that the model can discover complex relationships between features and target variables. On the other hand, the if-then-else logic-based tree models can be used with significantly less amount of data. Despite the fact that our dataset is large and structurally diverse compared to other works in the literature, it shows limitation for the ANN model, but it appears adequate for the tree-based models.

Table 1 Performances of the three models in train, validation and test set according to the two split types. Here, train and validation incorporate average scores and standard deviations of that score after ten shuffles of train-validation (90 : 10) splits. There was only one test set, which was held out from the beginning. Hence there is no standard deviation of test scores. The evaluation metrics used here are correlation coefficient (R²) and mean absolute error (MAE)

Model	Dataset	Random split		IL stratified split
		R^2	MAE	R^2	MAE
Random forest	Train	0.996 ± 0.0004	0.028 ± 0.00	0.995 ± 0.0004	0.028 ± 0.001
	Validation	0.971 ± 0.004	0.073 ± 0.002	0.674 ± 0.137	0.295 ± 0.049
	Test	0.98	0.051	0.857	0.259
XGBoost	Train	0.991 ± 0.0003	0.053 ± 0.0006	0.992 ± 0.0006	0.049 ± 0.001
	Validation	0.972 ± 0.003	0.079 ± 0.002	0.79 ± 0.055	0.273 ± 0.037
	Test	0.98	0.067	0.875	0.252
ANN	Train	0.889 ± 0.015	0.150 ± 0.01	0.78 ± 0.042	0.212 ± 0.016
	Validation	0.89 ± 0.017	0.150 ± 0.011	0.196 ± 0.222	0.588 ± 0.259
	Test	0.857	0.297	0.613	0.481

---

For Random Forest and XGBoost models, the training accuracy is similar for both the random split and stratified-IL split approaches, while the training accuracy degrades when stratified-IL split is employed in developing the ANN model. On the other hand, the accuracy in predictions for all the models is considerably lower for the test dataset in the case of stratified-IL split. In terms of random split, it was found that all the ILs (175 in total) present in the test set were also included in the train set. Therefore, the models developed using such a split have already learned IL structures, so rather than capturing structural diversity, the models tend to express the dependence of temperature, mole fraction or pressure on ionic conductivity. This was the primary reason underlining the high predictive capabilities of the models when random split was used. Whereas in stratified-IL split, structures included in the test dataset were unseen in the model development. This feature enabled the models to take into account structural dependence along with system variable dependence, which is primarily the intent of developing machine learning models for IL property predictions. This variation in results for two different type of splits agrees with the work of Datta et al. and Bilodeau et al.^26,53

Due to their higher prediction capability, hereafter, we will discuss only the Random Forest and XGBoost models. For better generalization capability, we will consider only the stratified-IL split. The performances of Random Forest and XGBoost models on stratified-IL split is visually presented in Fig. 6 in logarithmic scale. Results in actual scale can be found in Fig. S3. In Fig. 6a and c, we observe that the models predict reasonably well the experimental data on the training set. In addition, both the models satisfactorily generalize on test sets with greater accuracy in the high-conductivity region as compared to that for low conductivity. Given that our interest is in discovering high ionic conductivity IL–solvent mixtures, both models can be used with good accuracy. Fig. 6e depicts the average error in the ionic conductivity predictions on the test set for different cation families while Fig. 6f presents the average error as a function of solvent families. We observe that the contribution of imidazolium-based ILs to the overall error is the largest across all the IL families. This can be due to the fact that the quantity and diversity of imidazolium cations were much broader compared to other cation families. In terms of solvents, mixtures containing water are the primary contributors to the overall error, which can be attributed to the fact that water is the only inorganic solvent in the dataset while the rest are organic in nature. Therefore, it is possible that significant structural disparity between water and organic solvents gives rise to the high average errors for water. As a significant fraction of the dataset is due to imidazolium–water mixtures, developing specific models instead of generalized models encompassing all the ionic liquid families and solvent types could improve the accuracy of predictions. Additionally, it can be seen that different models can favor different solvents. For example, average errors of diketone and nitro compounds are much lower for XGBoost model compared to those of the Random Forest model, whereas for nitriles and amines exhibit an opposite (Fig. 6f) Hence, for future work, multiple models could be combined so that their strengths for accurately predicting ionic conductivities for different solvents can be leveraged to develop an overall model that performs much better than a single model. Furthermore, we observed that data augmentation did not have any beneficial effect in the model performance (Fig. S4). This can be due to the fact that model did not properly learn pure IL systems which is evident by the large prediction spread observed for same IL coupled with different solvents at mole fraction of IL set to unity (Fig. S5). However, data augmentation improved the overall diversity of the dataset, providing more cation families for the high-throughput screening.

Fig. 6 Performance analysis on stratified-IL split: (a) random Forest, training dataset; (b) Random Forest, test dataset; (c) and (d) XGboost on training and test datasets, respectively. Figures (a)–(d) also include the information on the MAE for each of the quartiles. (e) and (f) depict MAE calculated for representative cation and solvent families, respectively.

Model interpretation

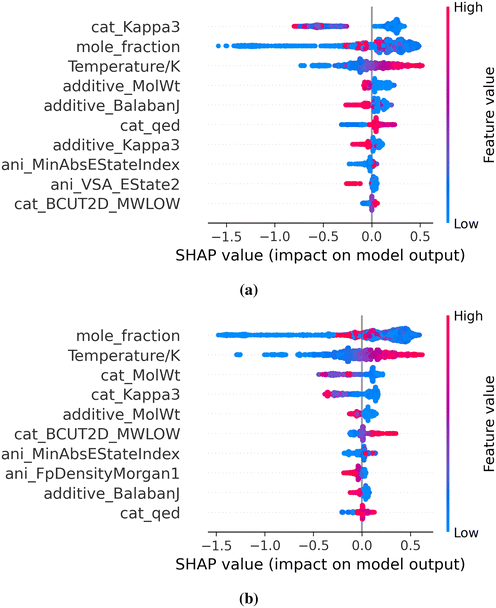
To interpret the effect of features and determine the important features influencing model performance, we carried out Shapley additive explanations (SHAP) analysis of the Random Forest and XGBoost models. Fig. 7 displays the SHAP feature importance for the two models. For each feature, a positive SHAP value indicates that the contribution of the feature for the given datapoint to ionic conductivity prediction is positive while negative SHAP value indicates otherwise. The spread of the SHAP values for a given feature also points to the extent to which a given feature affects the prediction over the mean prediction. Additional insight into the directionality of the effect of a feature can be gleaned based on the color of the scale. In the present case, blue denotes low values while red color is indicative of the high value of the features. We see that temperature is one of the most important features for both of these models. Temperature is also predicted to be positively correlated with ionic conductivity, which captures the well-known trend that the ionic conductivity increases with an increase in the temperature. The SHAP values of temperature vary over a wide range, which implies strong influence of temperature on the ionic conductivity prediction. The mole fraction of ILs is ranked very high in terms of feature importance (second in the Random Forest model and the first in the XGBoost model). Unlike other features that are either positively or negatively correlated with ionic conductivities, the influence of mole fraction is rather unique. For example, high values of mole fractions result into decreasing ionic conductivity trends, which can be understood from the observation that these mixtures correspond to nearly pure ILs for which ionic conductivities are low. On the other hand, intermediate mole fractions are positively correlated while the low values lead to a decreasing trend of ionic conductivities. A decreasing trend in the ionic conductivity when the ionic liquid mole fraction is low can be attributed to low concentrations of ions available in the system. This behavior suggests that the ionic conductivity passes through a maximum which agrees well with the findings of Chauhan et al.¹⁷ The features Kappa3, Balabanj and Ipc provide a measure of branching and structural complexity of molecules.^54–56 As branching tends to increase viscosity, these three features are inversely correlated to ionic conductivity, which is evident in Fig. 7. Similarly increasing molecular weight increases the bulkiness of the molecule and decreases conductivity. Quantitative estimation of drug likeness (QED) gives a measure of hydrophobicity and non-polar nature.⁵⁷ We see that low values of cation QED negatively affect ionic conductivity, meaning highly polar cations yield low ionic conductivity. VSA_Estates are the sum of electrotopological state indices in specific van der Waals surface domains.^16,58 Anion VSA_Estate2 shows positive correlation but estate 3 shows negative correlation to model prediction. MaxAbsEstateIndex and MinAbsEstateIndex are maximum and minimum absolute estate index in the molecule and they show positive and negative correlation respectively. The correlation that we observed for XGBoost model agrees well with Dhakal et al.¹⁶ However, the priority of features changed due to the inclusion of solvent features. For example, mole fraction of IL is the most important feature in our model instead of temperature. Some features such as cation Ipc, Chi0, BertzCT, anion MaxAbsPartialCharge have too low of an impact in our model and cannot be seen in the list of top 10 important features in the SHAP plot. Another thing to observe from the SHAP plot is that the composition of solvent is a much more important feature compared to the type of solvent used or, more specifically, the structure of solvent. This phenomenon for mixture systems agrees with the findings of Seddon et al.⁵⁹ that the physicochemical properties of ionic liquids are influenced greatly by the amount of a solvent rather than its type.

Fig. 7 SHAP feature importance for (a) Random Forest and (b) XGBoost model.

Screening

In an effort to expand into the unexplored chemical space and discover novel IL–solvent mixtures for their applications as electrolytes, we performed a high-throughput screening using hyper parameters of the XGBoost model developed in this work refitted with all the available datapoints. The selection of XGBoost was motivated by the fact that the model yielded the best performance on both validation and test sets among the three models. First, we created a screening dataset from all the possible combinations of unique cations, anions, and solvents. Five intermediate mole fractions [0.1, 0.3, 0.5, 0.7 and 0.9] were sampled for a given IL–solvent combination, which resulted into approximately 2.5 M unique IL–solvent systems and 12.5 M data points; the temperature for the screening was set to 298 K.

For an IL–solvent mixture to be considered as a potential electrolyte, it has to exceed or at least match the ionic conductivity of the conventional electrolyte used in practice. The current conventional electrolyte in Li-ion batteries is LP30, which is a mixture of 1 M LiPF6 in a 1 : 1 ethylene carbonate and dimethylcarbonate.^60,61 At room temperature (298 K), LP30 has an ionic conductivity of 1.26 S m⁻¹. Therefore, for an IL–solvent system to be a potential for replacement of LP30, it should exhibit ionic conductivity ∼2 S m⁻¹, as the addition of of Li salt is expected to reduce the conductivity by 30–50%.¹⁶ The original dataset used to develop ML models contained only 88 unique IL–solvent mixtures exceeding 2.0 S m⁻¹ ionic conductivity at room temperature. After carrying out the high-throughput screening with our XGBoost model, the number of such IL–solvent mixtures increased dramatically to ∼19 000. Fig. 8 depicts two heatmaps: one generated from the original dataset (Fig. 8a) and the other obtained from the high-throughput screening (Fig. 8b). Both the heatmaps show cation and solvent families of IL–solvent mixtures exhibiting ionic conductivities higher than 2.0 S m⁻¹. For each pair of cation family–solvent family, the maximum conductivity found is reported in the corresponding heatmaps. All the combinations presented in Fig. 8b are listed in the SI. We observe that the screening leads to a considerable expansion in the number of potential cation and solvent families that can be combined to produce electrolytes with desired ionic conductivities. In fact, the model predictions for some of the cation–solvent families are almost an order of magnitude higher than 2.0 S m⁻¹ suggesting exciting opportunities for further investigation.

Fig. 8 Heatmap of IL–solvent mixtures with ionic conductivity higher than 2.0 S m⁻¹, from (a) original dataset, (b) high-throughput screening of all possible combinations of cations, anion, solvents. Five mole fractions 0.1, 0.3, 0.5, 0.7, and 0.9 were used to represent IL–solvent mixtures.

We, however, note that the screening is only based on predicted ionic conductivities of ionic liquid–solvent mixtures at 298 K and does not necessarily represent the capability of any of those mixtures to be used as a battery electrolyte. Apart from ionic conductivity, the actual application as battery electrolyte will depend on various factors such as battery type, viscosity, electrochemical stability, reactivity, melting point etc. For example, mixtures that contain water as molecular solvent may cause stability issues in Li-ion batteries despite their large ionic conductivities. Also, all the mixture systems presented in Fig. 8 may not be liquid at the operating conditions of the battery. For instance, the performance of a particular combination needs to be tested over a range of temperatures in which batteries are likely to be operated. Therefore, to fully exploit the applicability of a mixture as electrolytes, a multi-objective optimization approach or multiple machine learning models targeting desired properties (e.g., viscosity, melting point, etc.) is required. As our primarily objective in this work concerns only the ionic conductivity, this is beyond the scope of this paper. Interested readers are suggested to refer to the work of Chen et al. where pure ionic liquids were screened with consideration for multiple constraints such as melting point, viscosity, thermal decomposition temperature, toxicity and heat capacity.⁶²

Conclusion

This work aimed to address the lack of an all encompassing general model to predict ionic conductivities of IL–solvent mixtures. To address the research gap, a diverse dataset of IL–solvent mixtures was developed based on the data extracted from the NIST ILThermo Database. Pure ionic liquids were represented as “mixtures” with solvents with mole fraction of the IL set to unity. Three machine learning models, viz. Random Forest, XGBoost and ANN were developed based on random split of the data and novel stratified-IL split that partitioned a given ionic liquid exclusively into the training dataset or test data set to handle imbalanced data and improve generalization. The results showed that the evaluation metrics for the random split were significantly higher than those for the stratified-IL split, which was attributed to the models capturing trends of temperature and mole fraction rather than structural diversity. Out of the three models, Random Forest and XGBoost outperformed the ANN model, which could be due to the limited amount of data. Feature importance gleaned from the SHAP analysis revealed that the models were capable of capturing complex non-monotonic dependence of ionic conductivity on IL–solvent mole fractions. The SHAP analysis also correctly identified a positive correlation between temperature and ionic conductivity.

In order to identify potential IL–solvent electrolytes exceeding the ionic conductivity of the conventional electrolyte LP30 for Li-ion batteries, a high-throughput screening of all the possible combinations of cations, anions, and solvents at various mole fractions was carried out. The approach yielded approximately 19 000 unique IL–solvent candidates with some showing ionic conductivity as high as 70 S m⁻¹ at 298 K. Although promising and exciting, one limitation of our work is the exclusive focus on ionic conductivity. For an IL–solvent mixture to be considered as potential battery electrolyte, various properties such as electrochemical stability, melting point, chemical reactivity, etc. should also be considered in addition to ionic conductivity. In future work, we plan to develop additional models that can predict relevant properties for electrochemical applications, providing multiple constraints to the high-throughput screening, which will result in a narrower list of potential candidates. These candidates can then be subjected to experimentation.

As the primary objective of the present work was to obtain a generalized machine learning model encompassing all available solvents. Therefore, water, as the only inorganic solvent, was included; however, these mixtures contribute significantly to the overall error, which would suggest model development without the inclusion of water. Although this may reduce the overall error in the ionic conductivity prediction, such an approach would also eliminate a large number of data points. Additionally, the high-throughput screening shows that a large number of IL–water systems with high ionic conductivity can be envisioned, potentially reducing the cost of battery electrolytes. There is also an evidence that IL-based electrolytes can tolerate large amounts of water without showing stability issues.⁶³ So, inclusion or exclusion of water will require a thorough inspection, which will be a subject for a future study.

Conflicts of interest

There are no conflicts to declare.

Data availability

It is our intention to provide access to the models developed and data employed in this work via GitHub. https://github.com/ShahResearchGroup/IL-Solvent_Mixtures. Supplementary information (SI): SI contains distribution of ionic conductivity data, temperature distribution, performance of XGBoost and Random Forest models, hyperparameters for developed models, model training for ANN, and a list of high ionic conductivity ionic liquid–solvent mixtures, corresponding cation, anion, and solvent along with the ionic liquid mole fraction and the value of ionic conductivity. See DOI: https://doi.org/10.1039/d5me00146c.

Acknowledgements

This material is based upon the work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences Separation Science program under the Award Number SC-0022321. The computing for this project was performed at the OSU High Performance Computing Center at Oklahoma State University, which was supported, in part, by the National Science Foundation (Grant No. OAC-1531128). Authors also acknowledge partial funding from Oklahoma State University in support of this work.

References

1. T. Welton, Ionic Liquids: A Brief History, Biophys. Rev., 2018, 10, 691–706.
2. P. Wasserscheid and T. Welton, Ionic Liquids in Synthesis, Wiley Online Library, 2008, vol. 1.
3. N. V. Plechkova and K. R. Seddon, Applications of ionic liquids in the chemical industry, Chem. Soc. Rev., 2008, 37, 123–150.
4. E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis, CO2 Capture by a Task-Specific Ionic Liquid, J. Am. Chem. Soc., 2002, 124, 926–927 , PMID: 11829599.
5. Q. Yang, H. Xing, B. Su, K. Yu, Z. Bao, Y. Yang and Q. Ren, Improved separation efficiency using ionic liquid–cosolvent mixtures as the extractant in liquid–liquid extraction: a multiple adjustment and synergistic effect, Chem. Eng. J., 2012, 181–182, 334–342.
6. Q. Yang, K. Yu, H. Xing, B. Su, Z. Bao, Y. Yang and Q. Ren, The effect of molecular solvents on the viscosity, conductivity and ionicity of mixtures containing chloride anion-based ionic liquid, J. Ind. Eng. Chem., 2013, 19, 1708–1714.
7. S. K. Das and J. K. Shah, Exploring Binding Affinity of 1-n-Alkyl-3-Methylimidazolium Chloride with Iron Porphyrin and Electron Uptake Ability of the Ionic Liquid-FeP Complex, J. Ion. Liq., 2024, 100078.
8. P. Dhakal, S. K. Das and J. K. Shah, Revealing hydrogen bond dynamics between ion pairs in binary and reciprocal ionic liquid mixtures, J. Mol. Liq., 2022, 368, 120515.
9. U. Kapoor and J. K. Shah, Macroscopic Differentiators for Microscopic Structural Nonideality in Binary Ionic Liquid Mixtures, J. Phys. Chem. B, 2020, 124, 7849–7856.
10. U. Kapoor and J. K. Shah, Preferential Ionic Interactions and Microscopic Structural Changes Drive Nonideality in the Binary Ionic Liquid Mixtures as Revealed from Molecular Simulations, Ind. Eng. Chem. Res., 2016, 55, 13132–13146.
11. R. P. Matthews, I. J. Villar-Garcia, C. C. Weber, J. Griffith, F. Cameron, J. P. Hallett, P. A. Hunt and T. Welton, A structural investigation of ionic liquid mixtures, Phys. Chem. Chem. Phys., 2016, 18, 8608–8624.
12. U. Kapoor and J. K. Shah, Thermophysical Properties of Imidazolium-Based Binary Ionic Liquid Mixtures Using Molecular Dynamics Simulations, J. Chem. Eng. Data, 2018, 63, 2512–2521.
13. U. Kapoor and J. K. Shah, Monte Carlo Simulations of Pure and Mixed Gas Solubilities of CO₂ and CH₄ in NonIdeal Ionic Liquid-Ionic Liquid Mixtures, Ind. Eng. Chem. Res., 2019, 58, 22569–22578.
14. U. Kapoor and J. K. Shah, Molecular Origins of the Apparent Ideal CO2 Solubilities in Binary Ionic Liquid Mixtures, J. Phys. Chem. B, 2018, 122, 9763–9774.
15. P. Dhakal and J. K. Shah, Developing machine learning models for ionic conductivity of imidazolium-based ionic liquids, Fluid Phase Equilib., 2021, 549, 113208.
16. P. Dhakal and J. K. Shah, A generalized machine learning model for predicting ionic conductivity of ionic liquids, Mol. Syst. Des. Eng., 2022, 7, 1344–1353.
17. R. Chauhan, R. Sartape, A. Thorat, J. K. Shah and M. R. Singh, Theory-Enabled High-Throughput Screening of Ion Dissociation Explains Conductivity Enhancements in Diluted Ionic Liquid Mixtures, ACS Sustainable Chem. Eng., 2023, 11, 14932–14946.
18. M. Bester-Rogac, A. Stoppa and R. Buchner, Ion association of imidazolium ionic liquids in acetonitrile, J. Phys. Chem. B, 2014, 118, 1426–1435.
19. E. Rilo, J. Vila, M. Garcia, L. M. Varela and O. Cabeza, Viscosity and electrical conductivity of binary mixtures of C n MIM-BF4 with ethanol at 288 K, 298 K, 308 K, and 318 K, J. Chem. Eng. Data, 2010, 55, 5156–5163.
20. N. Zec, M. Bešter-Rogač, M. Vraneš and S. Gadžurić, Physicochemical properties of (1-butyl-1-methylpyrrolydinium dicyanamide+-butyrolactone) binary mixtures, J. Chem. Thermodyn., 2015, 91, 327–335.
21. Q. Zhang, Q. Li, D. Liu, X. Zhang and X. Lang, Density, dynamic viscosity, electrical conductivity, electrochemical potential window, and excess properties of ionic liquid N-butylpyridinium dicyanamide and binary system with propylene carbonate, J. Mol. Liq., 2018, 249, 1097–1106.
22. M. Bešter-Rogač, J. Hunger, A. Stoppa and R. Buchner, 1-Ethyl-3-Methylimidazolium Ethylsulfate in Water, Acetonitrile, and Dichloromethane: Molar Conductivities and Association Constants, J. Chem. Eng. Data, 2011, 56, 1261–1267.
23. A. K. Verma, A. S. Thorat and J. K. Shah, Estimating ionic conductivity of ionic liquids: nernst–einstein and einstein formalisms, Journal of Ionic Liquids, 2024, 4, 100089.
24. Y.-C. Lo, S. E. Rensi, W. Torng and R. B. Altman, Machine Learning in Chemoinformatics And Drug Discovery, Drug Discovery Today, 2018, 23, 1538–1546 , Cited by: 611; All Open Access, Green Open Access, Hybrid Gold Open Access.
25. S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, A review on machine learning algorithms for the ionic liquid chemical space, Chem. Sci., 2021, 12, 6820–6843.
26. R. Datta, R. Ramprasad and S. Venkatram, Conductivity prediction model for ionic liquids using machine learning, J. Chem. Phys., 2022, 156, 214505.
27. V. Venkatraman, S. Evjen and K. Chellappan Lethesh, The ionic liquid property explorer: an extensive library of task-specific solvents, Data, 2019, 4, 88.
28. M. Abdullah, K. Chellappan Lethesh, A. A. Baloch and M. O. Bamgbopa, Comparison of molecular and structural features towards prediction of ionic liquid ionic conductivity for electrochemical applications, J. Mol. Liq., 2022, 368, 120620.
29. Z. Chen, J. Chen, Y. Qiu, J. Cheng, L. Chen, Z. Qi and Z. Song, Prediction of Electrical Conductivity of Ionic Liquids: From COSMO-RS Derived QSPR Evaluation to Boosting Machine Learning, ACS Sustainable Chem. Eng., 2024, 4c00307.
30. M. Mohan, K. D. Jetti, S. Guggilam, M. D. Smith, M. K. Kidder and J. C. Smith, High-Throughut Screening and Accurate Prediction of Ionic Liquid Viscosities Using Interpretable Machine Learning, ACS Sustainable Chem. Eng., 2024, 4c00631.
31. A. Z. Hezave, M. Lashkarbolooki and S. Raeissi, Using artificial neural network to predict the ternary electrical conductivity of ionic liquid systems, Fluid Phase Equilib., 2012, 314, 128–133.
32. M. Lashkarblooki, A. Z. Hezave, A. M. Al-Ajmi and S. Ayatollahi, Viscosity prediction of ternary mixtures containing ILs using multi-layer perceptron artificial neural network, Fluid Phase Equilib., 2012, 326, 15–20.
33. D. V. Duong, H.-V. Tran, S. K. Pathirannahalage, S. J. Brown, M. Hassett, D. Yalcin, N. Meftahi, A. J. Christofferson, T. L. Greaves and T. C. Le, Machine learning investigation of viscosity and ionic conductivity of protic ionic liquids in water mixtures, J. Chem. Phys., 2022, 156, 154503.
34. Y. Chen, B. Peng, G. M. Kontogeorgis and X. Liang, Machine learning for the prediction of viscosity of ionic liquid–water mixtures, J. Mol. Liq., 2022, 350, 118546.
35. X. Liu, J. Gao, Y. Chen, Y. Fu and Y. Lei, Machine learning-assisted modeling study on the density and heat capacity of ionic liquid-organic solvent binary systems, J. Mol. Liq., 2023, 390, 122972.
36. Y. Lei, Y. Shu, X. Liu, X. Liu, X. Wu and Y. Chen, Predictive modeling on the surface tension and viscosity of ionic liquid-organic solvent mixtures via machine learning, J. Taiwan Inst. Chem. Eng., 2023, 151, 105140.
37. Q. Dong, C. Muzny, A. Kazakov, V. Diky, J. Magee, J. Widegren, R. Chirico, K. Marsh and M. Frenkel, ILThermo: A Free-AccessWeb Database for Thermodynamic Properties of Ionic Liquids, 2007.
38. A. Kazakov, J. Magee, R. Chirico, V. Diky, K. Kroenlein, C. Muzny and M. Frenkel, Ionic Liquids Database – ILThermo (v2.0), 2013.
39. https://github.com/KanHatakeyama/pyilt2.
40. D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
41. PubChemPy, 2024, https://pypi.org/project/PubChemPy, [Online; accessed 3, Jul 2024].
42. CIRpy – CIRpy 1.0.2 documentation, 2021, https://cirpy.readthedocs.io/en/latest, [Online; accessed 3, Jul 2024].
43. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, PubChem 2023 update, Nucleic Acids Res., 2023, 51, D1373–D1380.
44. Ncicadd Group, N. C. I. NCI/CADD Chemical Identifier Resolver, 2024, https://cactus.nci.nih.gov/chemical/structure, [Online; accessed 3, Jul 2024].
45. G. Landrum, et al., rdkit/rdkit: 2023_03_1 (Q1 2023) Release, 2023, https://doi.org/10.5281/zenodo.7880616.
46. J. D. Roberts and M. C. Caserio, Basic Principles of Organic Chemistry, W. A. Benjamin Inc., 2nd edn, 2023, ch. 2.
47. B. Averill and P. Eldredge, Chemistry: Principles, Patterns, and Applications, Pearson Benjamin Cummings, 2007, ch. 23.
48. X. Liu, Organic Chemistry I; Open textbook library, Kwantlen Polytechnic University, 2021, ch. 2.
49. P. Willett, Similarity-based virtual screening using 2D fingerprints, Drug Discovery Today, 2006, 11, 1046–1053.
50. D. Bajusz, A. Racz and K. Heberger, Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations?, Aust. J. Chem., 2015, 7, 1–13.
51. N. M. O'Boyle and R. A. Sayle, Comparing structural fingerprints using a literature-based similarity benchmark, Aust. J. Chem., 2016, 8, 1–14.
52. Getting Started with the RDKit in Python – The RDKit 2024.03.4 documentation, 2024, https://www.rdkit.org/docs/GettingStartedInPython.html#morgan-fingerprints-circular-fingerprints, [Online; accessed 6, Jul 2024].
53. C. Bilodeau, A. Kazakov, S. Mukhopadhyay, J. Emerson, T. Kalantar, C. Muzny and K. Jensen, Machine learning for predicting the viscosity of binary liquid mixtures, Chem. Eng. J., 2023, 464, 142454.
54. Q.-N. Hu, Y.-Z. Liang, H. Yin, X.-L. Peng and K.-T. Fang, Structural Interpretation of the Topological Index. 2. The Molecular Connectivity Index, the Kappa Index, and the Atom-type E-State Index, J. Chem. Inf. Comput. Sci., 2004, 44, 1193–1201 , PMID: 15272826.
55. A. T. Balaban, Highly discriminating distance-based topological index, Chem. Phys. Lett., 1982, 89, 399–404.
56. D. Bonchev and N. Trinajstić, Information theory, distance matrix, and molecular branching, J. Chem. Phys., 1977, 67, 4517–4533.
57. G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Quantifying the chemical beauty of drugs, Nat. Chem., 2012, 4, 90–98.
58. L. H. Hall and L. B. Kier, Electrotopological State Indices for Atom Types: A Novel Combination of Electronic, Topological, and Valence State Information, J. Chem. Inf. Comput. Sci., 1995, 35, 1039–1045.
59. K. R. Seddon, A. Stark and M.-J. Torres, Influence of chloride, water, and organic solvents on the physical properties of ionic liquids, Pure Appl. Chem., 2000, 72, 2275–2287.
60. J. Tarascon and D. Guyomard, New electrolyte compositions stable over the 0 to 5 V voltage range and compatible with the Li1+xMn2O4/carbon Li-ion cells, Solid State Ionics, 1994, 69, 293–305.
61. A. Tsurumaki, M. Agostini, R. Poiana, L. Lombardo, E. Lufrano, C. Simari, A. Matic, I. Nicotera, S. Panero and M. A. Navarra, Enhanced safety and galvanostatic performance of high voltage lithium batteries by using ionic liquids, Electrochim. Acta, 2019, 316, 1–7.
62. G. Chen, Z. Song, Z. Qi and K. Sundmacher, Generalizing property prediction of ionic liquids from limited labeled data: a one-stop framework empowered by transfer learning, Digital Discovery, 2023, 2, 591–601.
63. Q. Liu, W. Jiang, Z. Yang and Z. Zhang, An Environmentally Benign Electrolyte for High Energy Lithium Metal Batteries, ACS Appl. Mater. Interfaces, 2021, 13, 58229–58237.

---