Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancing generative molecular design via uncertainty-guided fine-tuning of variational autoencoders
A. N. M. Nafiz
Abeer
 a,
Sanket
Jantre
b,
Nathan M.
Urban
b and
Byung-Jun
Yoon
a,
Sanket
Jantre
b,
Nathan M.
Urban
b and
Byung-Jun
Yoon
 *ab
*ab
aDepartment of Electrical and Computer Engineering, Texas A&M University, College Station, TX, USA. E-mail: bjyoon@tamu.edu
bApplied Mathematics Department, Computing and Data Sciences, Brookhaven National Laboratory, Upton, NY, USA
First published on 17th October 2025
Abstract
In recent years, deep generative models have been successfully applied to various molecular design tasks, particularly in the life and materials sciences. One critical challenge for pre-trained generative molecular design (GMD) models is to fine-tune them to be better suited for downstream design tasks that aim at optimizing specific molecular properties. However, redesigning and training an existing effective generative model from scratch for each new design task are impractical. Furthermore, the black-box nature of typical downstream tasks that involve property prediction makes it nontrivial to optimize the generative model in a task-specific manner. In this work, we propose an uncertainty-guided fine-tuning strategy that can effectively enhance a pre-trained variational autoencoder (VAE) for GMD through performance feedback in an active learning setting. The strategy begins by quantifying the model uncertainty of the generative model using an efficient active subspace-based UQ (uncertainty quantification) scheme. Next, the decoder diversity within the characterized model uncertainty class is explored to expand the viable space of molecular generation. The low-dimensionality of the active subspace makes this exploration tractable using a black-box optimization scheme, which in turn enables us to identify and leverage a diverse set of high-performing models to generate enhanced molecules. Empirical results across six target molecular properties using multiple VAE-based generative models demonstrate that our uncertainty-guided fine-tuning strategy consistently leads to improved models that outperform the original pre-trained models.
Design, System, ApplicationVariational autoencoders (VAEs), a particular class of generative models widely applied in diverse molecular design tasks, learn a continuous latent representation of their input (molecules in this case) that is leveraged in the search for molecules with optimized properties. This work proposed a black-box optimization strategy for finding VAE model parameters that can outperform the pre-trained VAE parameters in constructing molecules with better properties from a set of latent points. Specifically, our strategy takes the latent points found by any latent space optimization approach and explores the uncertainty classes of VAEs through their low-dimensional active subspace to find the diverse models that improve the properties of the molecules corresponding to those latent points. Due to the model-agnostic nature, our approach can be applied in complement to any latent space optimization algorithm with VAEs to go beyond the pre-trained model's performance. This can assist computational designers to retain most of the pre-trained model's capability before adopting a new generative model for the application of interest. |
1 Introduction
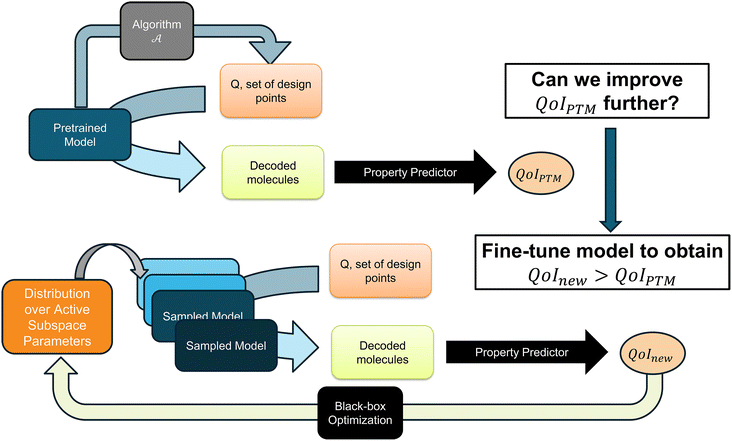
Machine learning has evolved significantly in the field of drug discovery, with an early focus on quantitative structure–activity relationships (QSARs)1 for high-throughput screening (HTS),2,3 and is now attracting research interest in de novo molecule design, driven by the rise of deep generative models. Such models4–7 allow exploration of molecular space using optimization algorithms in a low-dimensional latent space derived from high-dimensional chemical data. However, the effectiveness of these generative models in creating target molecules is constrained by their training datasets, as is the case with any data-driven approach. Depending on downstream tasks–such as generating valid molecules with optimum properties using specific reactants–research efforts have focused on either the optimization algorithm8–11 with minimal model changes or complete redesign of the generative model.12–17 Improving performance for new downstream tasks often requires rethinking generative model design. However, finding a universally effective design remains challenging, as evidenced by the aforementioned studies. By building upon existing pre-trained models, we aim to leverage insights embedded within those models from the collective experience of the research community to enhance their performance in various downstream design tasks of interest.Fine-tuning a generative model for a quantity of interest in a molecular design task can be challenging, especially with limited data.18 We address this challenge by efficiently quantifying the model uncertainty by employing active subspace reduction of a generative model,19 which constructs a low-dimensional subspace of the generative model parameters capturing most of the variability in the model's output. Incorporating model uncertainty leads to diversity in VAE model parameters (specifically the decoder in our problem setting), which expands the space of viable molecules compared to the pre-trained model. First, we assume that optimization over the latent space of a pre-trained variational autoencoder (VAE) model yields a list of candidate designs. These candidates, which can result from multiple runs of some optimization procedure with different hyperparameters, are decoded to generate molecules that determine the model's downstream performance. For these candidates within latent space, we adapt the generative model in its low-dimensional active subspace to enhance its performance beyond that of the pre-trained model, i.e. to learn a better decoding strategy than the pre-trained model to obtain decoded molecules with better properties from the candidates. We achieve this through black-box optimization, guided by performance feedback from downstream tasks. This optimization tunes the distribution of active subspace parameters to generate diverse models that outperform the pre-trained model for those candidate latent points. The black-box nature of our optimization for improving model performance in downstream molecular design tasks simplifies its integration with existing optimization methods in latent space of VAE-based generative models.
To this end, our contributions are as follows:
• We explore the model uncertainty class of VAE-based generative models, effectively represented by their low-dimensional active subspace parameters, using black-box optimization algorithms: Bayesian optimization (BO) and REINFORCE. The proposed fine-tuning approach yields diverse high-performing models which improve the generative model's performance in downstream design tasks of interest.
• We demonstrate the effectiveness of our uncertainty-guided fine-tuning approach in leveraging model uncertainty to enhance downstream performance across six target molecular properties. Our method consistently improves design performance of multiple pre-trained VAE-based models through the proposed closed-loop optimization scheme.
• We empirically analyze the impact of the active subspace parameter-based optimization of the acquisition function in latent space Bayesian optimization for three high-dimensional optimization problems.
2 Background
2.1 VAE-based generative models for molecular design
Across VAE-based generative models for molecular design tasks,20 the encoder embeds molecular representations into a low-dimensional continuous latent space, while the decoder converts the latent space embeddings back to the chemical space. For inverse molecular design, various optimization approaches can be applied on the learned latent space of a trained VAE. For example, Gómez-Bombarelli et al.4 trained a VAE jointly with a property predictor network using SMILES representation of molecules. Subsequently, a Gaussian process (GP) was trained to predict target properties from the latent representation, leading to some latent points corresponding to high-scoring molecules. Similarly, Jin et al.6 used Bayesian optimization on the latent space of their junction tree VAE (JT-VAE) model to generate molecules with optimized properties.2.2 Optimization over latent space of VAEs
Given a trained VAE model with parameters θ0,encoder and θ0,decoder, the optimization over the latent space of the model solves the problem in eqn (1) by reformulating it as in eqn (2):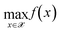 | (1) |
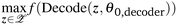 | (2) |
![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) is the input space for which the latent space of the VAE is learned. f(·) represents a black-box function which quantifies the quantity of interest for sample x. Instead of the high-dimensional discrete input space, this reformulation searches the continuous latent space
is the input space for which the latent space of the VAE is learned. f(·) represents a black-box function which quantifies the quantity of interest for sample x. Instead of the high-dimensional discrete input space, this reformulation searches the continuous latent space 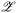 learned by the VAE model. Decode(z, θ0,decoder) uses the learned parameter θ0,decoder to reconstruct a sample in
learned by the VAE model. Decode(z, θ0,decoder) uses the learned parameter θ0,decoder to reconstruct a sample in ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) from its corresponding latent point z. Different optimization strategies can find the optimum latent point z. Under the Bayesian optimization framework, the process is as follows.
from its corresponding latent point z. Different optimization strategies can find the optimum latent point z. Under the Bayesian optimization framework, the process is as follows.
Starting from a collection of observations, i.e. {x(i), f(x(i))}ni=1, a surrogate model (e.g. Gaussian process) fsurrogate: 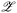 →
→ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) is learned to predict the objective value from the latent space representation. In this step, each sample x(i) is embedded to the corresponding latent point z(i) through the encoder with θ0,encoder. At each BO iteration, a new candidate z(n+1) ∈
is learned to predict the objective value from the latent space representation. In this step, each sample x(i) is embedded to the corresponding latent point z(i) through the encoder with θ0,encoder. At each BO iteration, a new candidate z(n+1) ∈ 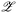 is selected to query its objective value given by f(·). This selection is done by optimizing the acquisition function (e.g. expected improvement,21 upper confidence bound,22etc.), which is a function on z through the surrogate model fsurrogate.
is selected to query its objective value given by f(·). This selection is done by optimizing the acquisition function (e.g. expected improvement,21 upper confidence bound,22etc.), which is a function on z through the surrogate model fsurrogate.
 | (3) |
2.3 Focus of our work
The efficiency of the optimization strategy over latent space strongly depends on the VAE model's latent space through its learned parameters: θ0,encoder and θ0,decoder. To improve the sample efficiency of the optimization process, different strategies23–25 are proposed to update the VAE model parameters utilizing the samples suggested by the latent space optimization process. In this work, we investigated whether better samples (e.g. molecules with better properties) could be found if the decoder was tuned to transform the latent point z (found by the optimization process) into a better reconstructed sample x.The objective in eqn (2) consists of two functions, i.e. the black-box function f and the decoder process parameterized with θdecoder. Existing studies on latent space optimization only optimize for the latent point using a fixed decoder, i.e. the pre-trained VAE model's decoder. In this work, we asked whether this optimization could benefit from performing optimization on the decoder parameters. Specifically, we looked at two directions:
• (RQ1) can we improve the decoding process of the pre-trained VAE to obtain better samples from the set of latent points found by any latent space optimization algorithm? Note that the latent points are obtained by solving eqn (2) with pre-trained model parameters. Hence, the goal here is to see whether we can do better than the pre-trained model by tuning its decoding process, i.e. optimizing the decoder parameters.
• (RQ2) can we find a better solution for eqn (1) by optimizing both the latent point z and decoder parameter θdecoder in f(Decode(z, θdecoder))? This direction focuses on incorporating the optimization of decoder parameters inside the latent space optimization iteration.
For the first direction, we focus on VAE-based generative models for molecular design with an arbitrary latent space optimization algorithm. Here, the decoding process is optimized after the completion of latent space optimization. For joint optimization of the latent point and decoder (RQ2), we consider optimizing the decoder within the latent space Bayesian optimization that is adopted to suggest new samples in each weighted retraining iteration (PG-LBO,24 a recently proposed variant of Tripp et al.23). Sections 4.1 and 4.2 provides a formal description of these two directions.
3 Related work
Different application areas in materials and chemical engineering have adopted VAEs as one of the generative models26 to explore the design space. The architecture of VAEs in these applications varies depending on the specific design choices and problem settings. Specifically, specialized data and design settings often necessitate custom VAE (or other generative model) architectures that are suitable for the specific goal at hand. For example, Yao et al.27 developed a supramolecular variational autoencoder (SmVAE) for metal–organic framework (MOF) structures for the inverse design of novel MOF structures with improved CO2 gas separation capacity. For the design space of porous organic cages (POCs), the Cage-VAE28 is introduced for representing the cages constrained to a specific topology, which learns a latent space from the building blocks, i.e., molecules and the reaction type. The authors also performed latent space optimization to generate shape-persistent POCs utilizing the shape persistence predictor, trained jointly with the VAE, as the objective function. Vogel and Weber29 adopted a graph-to-string VAE, where a graph neural network (GNN) encodes the polymer graph to a latent embedding, which can be decoded by a transformer-based decoder to a polymer string consisting of the monomers' SMILES, stoichiometry, and connectivity (between monomers) information. The learned latent space is later used to design polymer photocatalysts in photocatalytic water splitting for hydrogen production.In some cases, it is not necessary to design a specific VAE architecture specifically designed for the problem. For example, Lopez et al.30 utilized the attention VAE model from Dollar et al.31 to generate SMILES strings of corrosion inhibitor candidates. Nevertheless, given the substantial effort and expertise required to design and train such models, we believe it is essential to maximize the utility of existing pre-trained architectures. Our work is complementary to other approaches, e.g., Paddy,32 which focus on improving optimization strategies in the latent space of these pre-trained models, enabling more effective downstream performance without the need for designing new architectures from scratch.
MacKay33 introduced the concept of data-dependent effective dimensionality of neural network parameter space in the Bayesian framework. The experiments of Maddox et al.34 demonstrated the existence of many directions within the neighborhood of trained neural network weights where predictions remain unchanged. Several studies35–40 utilized this concept to compress over-parameterized neural networks by pruning. Furthermore, this low dimensionality in parameter space enables scalable uncertainty quantification through various subspace inference techniques.41,42 In our work, we chose the active subspace approach42 over other methods since it allows learning the subspace without retraining or modifying the architecture of the pre-trained model.
Previous efforts to fine-tune GMD models have been limited to using small, select molecule sets that fit specific design criteria. For example, Blaschke and Bajorath18 fine-tuned the REINVENT model43 to improve its ability to recognize molecules with multi-target attributes via transfer learning, i.e. retraining the pre-trained model with a pool of multi-target molecules. In contrast, our approach adapts the generative model based on downstream task performance. This problem is conceptually similar to the work by Krupnik et al.,44 who updated the pre-trained generative model parameters to generate samples matching the observed data from a robotics task simulator.
4 Problem setting
4.1 Downstream performance improvement of pre-trained models (RQ1)
Given a pre-trained VAE model, we want to use it for a downstream task of generating molecules with desired properties. Let's denote the pre-trained model by![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0 where θ0 is the pre-trained model parameter. For the downstream task of interest –
θ0 where θ0 is the pre-trained model parameter. For the downstream task of interest – ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , algorithm
, algorithm ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (e.g. Bayesian optimization in the work of Gómez-Bombarelli et al.4 and Jin et al.6) is applied in conjunction with the pre-trained model
(e.g. Bayesian optimization in the work of Gómez-Bombarelli et al.4 and Jin et al.6) is applied in conjunction with the pre-trained model ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0 to look for candidate points within the latent space of
θ0 to look for candidate points within the latent space of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0 so that properties of the molecules corresponding to those candidates are optimized. Specifically, for a given pre-trained model (PTM), the algorithm
θ0 so that properties of the molecules corresponding to those candidates are optimized. Specifically, for a given pre-trained model (PTM), the algorithm ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) finds a set of candidate design points, Q = {z(i)}, which
finds a set of candidate design points, Q = {z(i)}, which ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0 decodes to generate corresponding molecules {x(i)}. The properties of these molecules define the quantity of interest (QoI) of the pre-trained model QoIPTM, e.g. average property value of top 10% molecules out of {x(i)}. For design goals involving a specific target value, QoI can be defined as the top 10% of the differences between a target property value and the properties of the molecules {x(i)}.
θ0 decodes to generate corresponding molecules {x(i)}. The properties of these molecules define the quantity of interest (QoI) of the pre-trained model QoIPTM, e.g. average property value of top 10% molecules out of {x(i)}. For design goals involving a specific target value, QoI can be defined as the top 10% of the differences between a target property value and the properties of the molecules {x(i)}.
Our contention is that while the set Q may achieve the best QoI for the pre-trained model, the algorithm ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) can perform better if the VAE model is fine-tuned for task –
can perform better if the VAE model is fine-tuned for task – ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . However, fine-tuned models are not always available for the task at hand. In this work, we investigate whether we can tune a given pre-trained model so that the molecules generated from the set Q (found by
. However, fine-tuned models are not always available for the task at hand. In this work, we investigate whether we can tune a given pre-trained model so that the molecules generated from the set Q (found by ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) using
using ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0) achieve a QoI better than QoIPTM. Here, the set Q contains the candidate latent points found by some optimization procedure in the latent space of the pre-trained VAE, and QoIPTM is some target property statistics over the associated molecules. Our goal is to bias the pre-trained model to produce molecules with better QoI for the same design points in Q.
θ0) achieve a QoI better than QoIPTM. Here, the set Q contains the candidate latent points found by some optimization procedure in the latent space of the pre-trained VAE, and QoIPTM is some target property statistics over the associated molecules. Our goal is to bias the pre-trained model to produce molecules with better QoI for the same design points in Q.
To summarize our objective, as illustrated in Fig. 1, we assume a set of design points – Q has been found using a latent space optimization algorithm ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) applied to the pre-trained VAE model. These design points can be decoded by the model to reconstruct molecules. We aim to further optimize the model parameters to generate better molecules from Q than the pre-trained model does. Denoting the QoI of the pre-trained model as QoIPTM = ϕ(
applied to the pre-trained VAE model. These design points can be decoded by the model to reconstruct molecules. We aim to further optimize the model parameters to generate better molecules from Q than the pre-trained model does. Denoting the QoI of the pre-trained model as QoIPTM = ϕ(![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0,Q), our goal is
θ0,Q), our goal is
 | (4) |
4.2 Integrating active subspace-based VAE decoder optimization in latent space Bayesian optimization (RQ2)
The goal of this direction is to solve the black-box optimization in eqn (1) by optimizing both the latent point z and decoder parameter θdecoder. Specifically, we extend the Bayesian optimization in section 2.2 to incorporate the decoder parameter optimization into the latent space optimization. | (5) |
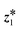 for a simpler presentation of the next stage. Next, we attempt to find whether a better solution is available by optimizing the decoder parameters. The intuition is that the optimized decoder may decode
for a simpler presentation of the next stage. Next, we attempt to find whether a better solution is available by optimizing the decoder parameters. The intuition is that the optimized decoder may decode  to a sample whose encoded latent point
to a sample whose encoded latent point 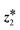 shows a better acquisition score. Finally, the candidate latent point (eqn (9)) for query is selected from
shows a better acquisition score. Finally, the candidate latent point (eqn (9)) for query is selected from  and
and  based on their acquisition scores. Like in section 4.1, we also use the concept of active subspace to facilitate a black-box optimization for eqn (7).
based on their acquisition scores. Like in section 4.1, we also use the concept of active subspace to facilitate a black-box optimization for eqn (7).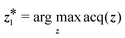 | (6) |
 | (7) |
 | (8) |
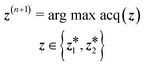 | (9) |
5 Methods
5.1 Active subspace of neural network parameters
The active subspace (AS) of deep neural networks, as described by Jantre et al.,42 aims to identify a low-dimensional subspace in the high-dimensional neural network parameter space that has the most influence on the network's output. Given a neural network fθ(x) with input – x and stochastic network parameters – θ ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) D following probability distribution p(θ), we can construct an uncentered covariance matrix of the gradients:
D following probability distribution p(θ), we can construct an uncentered covariance matrix of the gradients: ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) =
= ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) θ[(∇θfθ(x))(∇θfθ(x))T]. If
θ[(∇θfθ(x))(∇θfθ(x))T]. If ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) admits the eigendecomposition:
admits the eigendecomposition: ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = VΛVT where V includes the eigenvectors and Λ = diag(λ1, …, λD) are the eigenvalues with λ1 ≥…λD ≥ 0. We then can extract k dimensional active subspace by partitioning V into [V1, V2] where V1 ∈
= VΛVT where V includes the eigenvectors and Λ = diag(λ1, …, λD) are the eigenvalues with λ1 ≥…λD ≥ 0. We then can extract k dimensional active subspace by partitioning V into [V1, V2] where V1 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) D×k and V2 ∈
D×k and V2 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) D×k with k ≤ n ≪ D where n is the number of gradient samples to estimate the covariant matrix
D×k with k ≤ n ≪ D where n is the number of gradient samples to estimate the covariant matrix ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . Accordingly, the active subspace is spanned by V1 corresponding to the largest k eigenvalues.
. Accordingly, the active subspace is spanned by V1 corresponding to the largest k eigenvalues.
5.2 Optimization over active subspace
Similar to Abeer et al.,19 we have considered two disjoint partitions of the parameter space Θ: ΘS – containing a set of stochastic parameters, θS, and ΘD – containing the rest of the deterministic parameters, θD. In section 5.2.3, we discuss how we can intuitively distribute the generative model's components into these two partitions for solving the optimization problem in eqn (4) and (7). Instead of directly approximating the epistemic uncertainty of the stochastic parameters θS, we construct the active subspace Ω within ΘS while keeping the parameters in ΘD fixed at their pre-trained values, i.e.θD = θD0. Specifically, we learn the projection matrix, P, which maps the active subspace parameters, ω ∈ Ω, to their corresponding parameter space, ΘS, as follows| θS = θS0 + Pω | (10) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θ0. In this work, we considered the combination of the reconstruction loss and the KL divergence loss of the VAE models as the fθ(x) mentioned in section 5.1 while freezing the parameters in ΘD to θD0. Next, we apply the variational inference method45 to approximate the posterior distribution of ω, i.e. p(ω|
θ0. In this work, we considered the combination of the reconstruction loss and the KL divergence loss of the VAE models as the fθ(x) mentioned in section 5.1 while freezing the parameters in ΘD to θD0. Next, we apply the variational inference method45 to approximate the posterior distribution of ω, i.e. p(ω|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ) using the training dataset of the pre-trained model. Specifically, we learn the active subspace posterior distribution parameters by minimizing the sum of the training loss of the VAE model and the KL divergence loss between the approximated posterior distribution and the prior distribution over the active subspace parameters. Details of constructing the active subspace and posterior approximation are given in section 6.2.
) using the training dataset of the pre-trained model. Specifically, we learn the active subspace posterior distribution parameters by minimizing the sum of the training loss of the VAE model and the KL divergence loss between the approximated posterior distribution and the prior distribution over the active subspace parameters. Details of constructing the active subspace and posterior approximation are given in section 6.2.
During the inference stage, we draw M samples {ωi}Mi=1 independently from approximated p(ω|![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) ), and using eqn (10) we have an M number of model instances in parameter space Θ. Hence for the downstream task, we now have a diverse pool of models instead of a single pre-trained model. To quantify the uncertainty of the model's output, we can perform the Bayesian model averaging with this collection of models as in Abeer et al.19 Next, we use the distribution over active subspace parameters ω as the design space for finding a collection of models suitable for producing molecules with better QoI over set Q (RQ1) and finding a latent point with a better acquisition value (RQ2).
), and using eqn (10) we have an M number of model instances in parameter space Θ. Hence for the downstream task, we now have a diverse pool of models instead of a single pre-trained model. To quantify the uncertainty of the model's output, we can perform the Bayesian model averaging with this collection of models as in Abeer et al.19 Next, we use the distribution over active subspace parameters ω as the design space for finding a collection of models suitable for producing molecules with better QoI over set Q (RQ1) and finding a latent point with a better acquisition value (RQ2).
 | (11) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) θi}Mi=1, using eqn (10). The design points in Q are uniformly distributed among these M models for decoding. The property of interest is predicted for the reconstructed molecules and the predicted values are summarized, e.g. the average property value as QoI for the given distribution parameters.
θi}Mi=1, using eqn (10). The design points in Q are uniformly distributed among these M models for decoding. The property of interest is predicted for the reconstructed molecules and the predicted values are summarized, e.g. the average property value as QoI for the given distribution parameters.
 (found by optimizing the acquisition function over the latent space) to a corresponding molecule. These decoded M molecules are further encoded using the pre-trained encoder network of the VAE, and their acquisition scores are computed. We select the maximum acquisition scores out of M encoded latent points and their acquisition score is the optimization objective, i.e. acq(Encode(Decode(
(found by optimizing the acquisition function over the latent space) to a corresponding molecule. These decoded M molecules are further encoded using the pre-trained encoder network of the VAE, and their acquisition scores are computed. We select the maximum acquisition scores out of M encoded latent points and their acquisition score is the optimization objective, i.e. acq(Encode(Decode( , θdecoder), θ0,encoder)).
, θdecoder), θ0,encoder)). | (12) |
 , we have
, we have | (13) |
In our work (RQ1), we consider VAE-based generative models for molecular design, including the JT-VAE,6 SELFIES-VAE,20 and SMILES-VAE.4 Given the design points Q in the latent space of the pre-trained VAE model suggested by some generic optimization algorithm ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , decoders of the VAE models transform them into molecules. To obtain molecules with better properties for the same design points Q than the pre-trained model, we learn the active subspace of the decoders of the SELFIES-VAE and SMILES-VAE. For the JT-VAE, reconstruction of molecules involves two types of decoders. First, the tree decoder predicts a junction tree from a latent point. Conditioned on this predicted junction tree, the graph decoder constructs the molecular graph by selecting the best arrangement in each node of the junction tree. Out of these two components, the tree decoder plays the pivotal role in deciding the molecular structure as the junction tree contains all coarse information, i.e. which molecular units will be present in the constructed molecule. The graph decoder tracks the fine details of the interconnection between the nodes of the junction tree. Consequently, the tree decoder has broad control over the decision rules for constructing molecules from latent space. Therefore, we construct the active subspace over the JT-VAE's tree decoder, effectively allowing us to control the decision rules for constructing the junction tree from a latent point. Our optimization process attempts to change those rules, i.e. by changing decoder weights so that a latent point is decoded to a different junction tree yielding a better molecular graph than the pre-trained JT-VAE model.
, decoders of the VAE models transform them into molecules. To obtain molecules with better properties for the same design points Q than the pre-trained model, we learn the active subspace of the decoders of the SELFIES-VAE and SMILES-VAE. For the JT-VAE, reconstruction of molecules involves two types of decoders. First, the tree decoder predicts a junction tree from a latent point. Conditioned on this predicted junction tree, the graph decoder constructs the molecular graph by selecting the best arrangement in each node of the junction tree. Out of these two components, the tree decoder plays the pivotal role in deciding the molecular structure as the junction tree contains all coarse information, i.e. which molecular units will be present in the constructed molecule. The graph decoder tracks the fine details of the interconnection between the nodes of the junction tree. Consequently, the tree decoder has broad control over the decision rules for constructing molecules from latent space. Therefore, we construct the active subspace over the JT-VAE's tree decoder, effectively allowing us to control the decision rules for constructing the junction tree from a latent point. Our optimization process attempts to change those rules, i.e. by changing decoder weights so that a latent point is decoded to a different junction tree yielding a better molecular graph than the pre-trained JT-VAE model.
In experiments for RQ2, we consider three high-dimensional optimization tasks where latent space Bayesian optimization is used with a weighted retraining framework. We take the active subspace of the decoders of the corresponding VAEs for all tasks except for Molecule where we consider the JT-VAE tree decoder.
| μpost − 3σpost ≤ μf ≤ μpost + 3σpost | (14) |
| 0.75σpost ≤ σf ≤ 1.25σpost | (15) |
We chose the 3σpost half-width around the posterior mean, μpost, to enable the fine-tuned distribution to navigate within the subspace region aligned with the posterior. The bounds for σf are set to avoid significant variance changes, as this could introduce excess noise in objective query evaluation, potentially hindering the optimization algorithm's performance.
With the above uncertainty guided design space, we impose the constraint in eqn (16) based on the KL divergence between the fine-tuned and posterior distributions. By setting threshold – δKL, we control how far from the inferred posterior we search for a better pool of models. If the design space is already very narrow, this constraint can be dropped for optimization.
| KL(p(ω; μf, σf)‖p(ω; μpost, σpost)) ≤ δKL | (16) |
5.3 Optimization procedure
We employ two black-box optimization approaches – Bayesian optimization and REINFORCE46 – to fine-tune distribution parameters for the optimization problem in eqn (4). In the following sections, we discuss how these approaches (details in the SI) improve the pre-trained model's QoI (RQ1). The description also applies for finding a better latent point (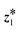 vs.
vs. in eqn (13)) by the acquisition score (RQ2), where the optimization goal is ϕacq (eqn (13)) instead of ϕ (eqn (11)).
in eqn (13)) by the acquisition score (RQ2), where the optimization goal is ϕacq (eqn (13)) instead of ϕ (eqn (11)).
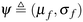 are first initialized to the active subspace posterior distribution parameters, i.e.μpost and σpost, respectively. At each iteration of REINFORCE, we draw M samples from the current policy network p(ω; μf, σf) and compute the corresponding QoI, i.e. ϕ(μf, σf, Q) following the steps mentioned in section 6.1. Then we use the Adam optimizer49 with a learning rate α = 0.005 to update the policy parameters according to the following update rule:
are first initialized to the active subspace posterior distribution parameters, i.e.μpost and σpost, respectively. At each iteration of REINFORCE, we draw M samples from the current policy network p(ω; μf, σf) and compute the corresponding QoI, i.e. ϕ(μf, σf, Q) following the steps mentioned in section 6.1. Then we use the Adam optimizer49 with a learning rate α = 0.005 to update the policy parameters according to the following update rule: | (17) |
6 Results
In this section, we demonstrate the performance of our approach (summarized in Algorithm 2) in improving QoI (RQ1) using three VAE models – JT-VAE, SELFIES-VAE, and SMILES-VAE with two optimization methods – Bayesian optimization (BO) and REINFORCE. First, we detail downstream design tasks in section 6.1 and describe the procedure to construct active subspace in section 6.2, and then present results in section 6.3 on improved molecular properties using our uncertainty-guided fine-tuning approach over pre-trained models. Section 6.4 offers further insights into the active subspaces constructed for each VAE model. Finally, we demonstrate the impact of active subspace-based optimization in latent-space BO (RQ2) in section 6.5.6.1 Simulation of downstream tasks
To demonstrate our approach for any set of design points Q, we use a random selection strategy as the algorithm![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) drawing 1000 points in the pre-trained VAE's latent space according to
drawing 1000 points in the pre-trained VAE's latent space according to ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (0, I). To simulate QoIPTM, we convert this random collection Q to corresponding molecules using the pre-trained model and predict the property of interest for all unique molecules. QoIPTM is defined as the average property value of the top 10% samples among those unique molecules. For properties that need to be minimized, the top 10% samples are those with the lowest property values, and the sign of their average is altered to maximize the QoI.
(0, I). To simulate QoIPTM, we convert this random collection Q to corresponding molecules using the pre-trained model and predict the property of interest for all unique molecules. QoIPTM is defined as the average property value of the top 10% samples among those unique molecules. For properties that need to be minimized, the top 10% samples are those with the lowest property values, and the sign of their average is altered to maximize the QoI.
For the posterior and fine-tuned distributions over AS parameters, we independently sample 10 models using the AS parameter distribution and divide the 1000 latent points of Q equally among them, giving each model 100 design points to decode. This ensures up to 1000 unique molecules for a fair comparison with the pre-trained model. We then use the same property predictor on unique molecules that we used for the pre-trained model and define the QoI as the average of the top 10% properties for the given distribution parameters. If the pre-trained model or any of the sampled models cannot decode a latent point into a valid molecule, we discard it in the QoI estimation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), synthetic accessibility score (SAS), natural product-likeness score (NP score),50 and inhibition probability against dopamine receptor D2 (DRD2),51 c-Jun N-terminal kinase-3 (JNK3) and glycogen synthase kinase-3 beta (GSK3β).13 We aim to maximize all properties except SAS, where lower values indicate easier synthesizability. Details of predictors for these six properties are provided in the SI along with the computed cost for evaluating QoI for 1000 latent points.
P), synthetic accessibility score (SAS), natural product-likeness score (NP score),50 and inhibition probability against dopamine receptor D2 (DRD2),51 c-Jun N-terminal kinase-3 (JNK3) and glycogen synthase kinase-3 beta (GSK3β).13 We aim to maximize all properties except SAS, where lower values indicate easier synthesizability. Details of predictors for these six properties are provided in the SI along with the computed cost for evaluating QoI for 1000 latent points.
6.2 Learning active subspace
We randomly sampled 100 molecules from the training dataset of each VAE model considered. For each sample – consisting of one input molecule and a set of perturbed model parameters – we followed Algorithm 1 to compute the gradient of the training loss. These gradients were then used to construct the active subspace over the stochastic parameters: the tree decoder in the JT-VAE, and the decoders in the SELFIES-VAE and SMILES-VAE. During each forward pass, we only perturbed the stochastic parameters and left all others fixed. We constructed a 20-dimensional active subspace using perturbation standard deviation σ0 = 0.1 for the JT-VAE tree decoder (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756
756![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 parameters) and σ0 = 0.01 for the SELFIES-VAE (4
131 parameters) and σ0 = 0.01 for the SELFIES-VAE (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419
419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177 parameters) and SMILES-VAE (4
177 parameters) and SMILES-VAE (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281
281![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 894 parameters) decoders. Although the JT-VAE subspace showed a lower rank (see Fig. 3), its smallest singular value remained sufficiently large, so we retained 20 dimensions for our main experiments. Additional results with a 5-dimensional active subspace are provided in the SI.
894 parameters) decoders. Although the JT-VAE subspace showed a lower rank (see Fig. 3), its smallest singular value remained sufficiently large, so we retained 20 dimensions for our main experiments. Additional results with a 5-dimensional active subspace are provided in the SI.
We use the training dataset of the VAE model to perform variational inference to approximate the posterior distribution over active subspace parameters. We applied the Adam optimizer49 with a learning rate of 0.001 to find the approximate mean and standard deviation over 20-dimensional AS parameters by minimizing the combined loss of the VAE training loss (which includes the reconstruction loss and KL divergence of the VAE) with the KL divergence loss between approximated posterior distribution and prior distribution over AS. We use a multivariate normal distribution with a zero mean and 5 standard deviations as a prior distribution over AS parameters.
6.3 Optimization over active subspace improves QoI (RQ1)
For each of the six properties, we applied Bayesian optimization (BO) and REINFORCE separately to fine-tune distribution parameters over the active subspaces of the JT-VAE tree decoder, SELFIES-VAE decoder, and SMILES-VAE decoder. For BO, we initialized the GP surrogate with 5 sample candidates from the design space described in section 5.2.4 and used the expected improvement (EI) acquisition function to optimize the QoI function ϕ over 25 BO iterations. For REINFORCE, the policy network was initialized with the posterior distribution parameterized by μpost and σpost and updated over 30 iterations. Both optimization strategies used the same budget of 30 QoI evaluations per property. In BO, the QoI evaluations for 5 initial candidates and 25 BO-suggested candidates constitute a total of 30 QoI evaluations.For each property, we ran 3 trials of BO and REINFORCE on 10 independently generated Q sets of design points (30 runs in total). Each boxplot in Fig. 2 shows QoI improvement over the pre-trained JT-VAE model. The results indicate that BO consistently outperforms the reward-based approach – REINFORCE in achieving larger QoI improvements across all six properties. Fig. S1 and S2 in the SI present analogous results for the SELFIES-VAE and SMILES-VAE, where REINFORCE matches BO. For a quantitative comparison, Table 1 reports the QoI values for both the pre-trained model and the fine-tuned distributions obtained by our approach, confirming our method's consistent gains over the pre-trained model in generating molecules with better properties. We have also performed the Wilcoxon signed-rank test52 with the alternative hypothesis that QoI values obtained by our approach of optimization over the active subspace distribution parameters are better than those of the pre-trained model (PTM). Specifically, we considered the paired QoI data, i.e. QoI for the pre-trained and finetuned models in the Wilcoxon signed-rank test. As shown in Table S2 of the SI, all cases showed statistically significant improvement over the pre-trained model, with the exception of SAS optimization using the JT-VAE model with the REINFORCE strategy.
| Models | Pre-trained/fine-tuned | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P (↑) P (↑) |
SAS (↓) | NP score (↑) | DRD2 (↑) | JNK3 (↑) | GSK3β (↑) |
|---|---|---|---|---|---|---|---|
| JT-VAE | PTM | 4.263 (0.084) | 2.034 (0.027) | 0.039 (0.037) | 0.039 (0.008) | 0.061 (0.004) | 0.135 (0.009) |
| PTM + BO | 4.367 (0.078) | 2.017 (0.029) | 0.076 (0.039) | 0.047 (0.009) | 0.065 (0.005) | 0.140 (0.008) | |
| PTM + R | 4.332 (0.093) | 2.031 (0.034) | 0.062 (0.042) | 0.042 (0.010) | 0.062 (0.004) | 0.138 (0.009) | |
| SELFIES-VAE | PTM | 4.741 (0.083) | 2.086 (0.043) | 0.722 (0.035) | 0.039 (0.008) | 0.065 (0.006) | 0.126 (0.007) |
| PTM + BO | 5.059 (0.043) | 2.010 (0.017) | 0.798 (0.028) | 0.064 (0.005) | 0.076 (0.002) | 0.146 (0.004) | |
| PTM + R | 5.044 (0.039) | 2.001 (0.018) | 0.801 (0.021) | 0.069 (0.009) | 0.076 (0.002) | 0.147 (0.004) | |
| SMILES-VAE | PTM | 4.869 (0.050) | 1.952 (0.024) | 0.194 (0.050) | 0.036 (0.009) | 0.067 (0.005) | 0.117 (0.011) |
| PTM + BO | 5.050 (0.042) | 1.903 (0.008) | 0.284 (0.022) | 0.059 (0.006) | 0.080 (0.004) | 0.137 (0.006) | |
| PTM + R | 5.069 (0.055) | 1.900 (0.010) | 0.289 (0.027) | 0.063 (0.004) | 0.081 (0.003) | 0.140 (0.005) |
Since BO outperforms REINFORCE in the JT-VAE model, we ran additional JT-VAE experiments to assess the effect of a noisy EI acquisition function, δKL sensitivity, the effect of active-subspace dimension k in BO, and the generalizability of the fine-tuned distribution's impact on the JT-VAE latent space (see SI section S7).
6.4 Does active subspace have an intrinsic bias?
We construct the active subspace from n = 100 gradient samples (see Algorithm 1), with each gradient sample derived from the loss for a single molecule. It is natural to question whether these gradient samples lead to a learned active subspace similar to a random subspace. To investigate this, we compare the subspace similarity between two active subspaces constructed using two random seeds. We use the Grassmann distance-based normalized subspace similarity measure from Hu et al.53 For two subspaces with projection matrices P1 and P2, the subspace similarity is defined as: | (18) |
 | ||
| Fig. 3 Comparison of subspace similarity between random subspaces and active subspaces for the JT-VAE tree decoder, SELFIES-VAE decoder, and SMILES-VAE decoder. Each entry of the normalized similarity is computed viaeqn (18) between subspaces generated using two different random seeds. For each VAE model, we constructed two (corresponding to two random seeds) 20-dimensional active subspaces – each using 100 gradient samples corresponding to randomly selected 100 molecules from the training dataset. Across the two seeds, we obtained two projection matrices P1 and P2 with Algorithm 1, starting from the pre-trained model weights. | ||
Since random subspaces are independently generated, there is no similarity between them (the subspace similarity measure is near 0). Active subspaces are also generated independently across two random seeds, but the learned projection matrices share a certain degree of intrinsic structure for the JT-VAE tree decoder and SELFIES-VAE decoder, where the first few projection vectors show significant similarity (values closer to 1). This indicates that the learned active subspace focuses on a specific model parameter space, even though it is created through random perturbation (Algorithm 1) around the pre-trained model parameters. Since we construct the active subspace by taking gradients around the pre-trained model parameters, this pattern of subspace similarity implies that the pre-trained model is located in such a loss landscape, where moving along certain directions can significantly impact the loss function. Such subspace similarity also means that our proposed active subspace optimization approach explores the model parameter space in 20 directions that are highly relevant to the molecular optimization task, rather than just randomly selected directions. In the JT-VAE's case, this similarity is particularly pronounced which may contribute to its higher QoI improvements using Bayesian optimization over REINFORCE. This intrinsic bias might be introduced due to the way the JT-VAE tree decoder reconstructs a molecule from its latent space. In contrast, the SMILES-VAE decoder's active subspaces show negligible similarity, despite the similar architecture to the SELFIES-VAE, except for different molecular representations. This difference suggests that the SMILES-VAE's pre-trained weights may reside in a very sharp loss surface. Perturbing the weights (for active subspace construction) in any direction can cause large loss changes, yielding subspaces akin to random ones. These observations highlight the need for robust input representations, as in the JT-VAE and SELFIES-VAE, to learn meaningful low-dimensional active subspaces. Furthermore, it may be possible to construct subspaces that favor QoI-optimal regions, offering a promising future direction.
6.5 Active subspace-based optimization of the acquisition function in latent space Bayesian optimization can enhance query efficiency (RQ2)
We consider three commonly used high-dimensional optimization tasks,23–25i.e., generating molecules with a maximum penalized water–octanol partition coefficient (penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P), fitting an arithmetic expression to a target expression, and producing a binary image with maximum similarity to a target topology. We have provided a brief description of these standard optimization tasks in the SI. For each of these three tasks (denoted as Molecule, Expression and Topology, respectively), we apply the PG-LBO weighted-retraining framework,24 performing 10 weighted retraining iterations and using latent-space Bayesian optimization to suggest 50 diverse samples at the end of each iteration.
P), fitting an arithmetic expression to a target expression, and producing a binary image with maximum similarity to a target topology. We have provided a brief description of these standard optimization tasks in the SI. For each of these three tasks (denoted as Molecule, Expression and Topology, respectively), we apply the PG-LBO weighted-retraining framework,24 performing 10 weighted retraining iterations and using latent-space Bayesian optimization to suggest 50 diverse samples at the end of each iteration.
We introduced our active subspace-based optimization (RQ2) within each BO iteration, keeping all other components of weighted retraining the same as in PG-LBO. Fig. 4 shows the top-1 sample's objective score and total unique queries out of 500 suggested samples over 10 weighted retraining iterations for 5 trials across three tasks, both with (‘w AS’) and without (‘w/o AS’) active subspace-based optimization of the acquisition function. In Fig. 4, each best objective score was found by the optimization procedure, i.e., 10 iterations of weighted retraining, and the number of unique queries represents the number of unique samples we needed to evaluate for the Bayesian optimization. Note that each weighted retraining iteration involves performing Bayesian optimization (with or without our active subspace) to generate 50 samples and retraining the VAE model with the weighted dataset of existing training samples updated with the suggested 50 samples. As detailed in section 4.2, under the active subspace-based optimization of the acquisition function, we accept the latent point  suggested by this decoder optimization only if its acquisition score exceeds that of
suggested by this decoder optimization only if its acquisition score exceeds that of 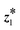 found by optimizing the acquisition function over the latent space. This potentially skips the samples suggested by regular BO (‘w/o AS’). For Molecule and Expression, this reduces unique queries without largely affecting the top-1 score. This boosts query efficiency, i.e., it limits the number of unique samples to be evaluated for their objective score, which can be crucial for expensive black-box objective functions. In the Topology task, weighted retraining using vanilla BO (without active subspace) and BO with active subspace ended up generating all 500 unique samples, resulting in a constant number of unique queries for all trials. This task involves generating a 40 × 40 binary image where two generated samples are identical when they match exactly in all pixels, and this has a very low probability of occurrence (21600 possible binary images). Hence, having a duplicate image from the weighted retraining process is a very rare event and this potentially explains the constant number of unique queries. This result highlights that BO with active subspace (RQ2) can improve the query efficiency (in terms of unique samples) in the weighted retraining framework, but the performance depends on the data space encoded by the VAE.
found by optimizing the acquisition function over the latent space. This potentially skips the samples suggested by regular BO (‘w/o AS’). For Molecule and Expression, this reduces unique queries without largely affecting the top-1 score. This boosts query efficiency, i.e., it limits the number of unique samples to be evaluated for their objective score, which can be crucial for expensive black-box objective functions. In the Topology task, weighted retraining using vanilla BO (without active subspace) and BO with active subspace ended up generating all 500 unique samples, resulting in a constant number of unique queries for all trials. This task involves generating a 40 × 40 binary image where two generated samples are identical when they match exactly in all pixels, and this has a very low probability of occurrence (21600 possible binary images). Hence, having a duplicate image from the weighted retraining process is a very rare event and this potentially explains the constant number of unique queries. This result highlights that BO with active subspace (RQ2) can improve the query efficiency (in terms of unique samples) in the weighted retraining framework, but the performance depends on the data space encoded by the VAE.
7 Conclusion and discussion
We introduced an uncertainty-guided fine-tuning approach that leverages a pre-trained VAE-based generative model's low-dimensional active subspace to quantify and exploit model uncertainty for performance enhancement in downstream molecular design tasks. Our method showed significant improvements over pre-trained models in optimization tasks for six molecular properties across three VAE variants: JT-VAE, SELFIES-VAE, and SMILES-VAE. By using black-box optimization, our approach fine-tunes the generative model to improve predicted properties using any property predictor, either ML or mechanistic. Our Bayesian optimization framework can also extend to multi-objective optimization when multiple molecular properties are of interest simultaneously. For instance, one can quantify QoI(i) for each ith property in multiple property optimization, where the molecules are ranked in terms of their ith property values. Subsequently, these multiple QoI(i)s can be used in multi-objective Bayesian optimization where the design space remains the same (i.e., the active subspace distribution parameters). However, considering each property separately for ranking the molecules may not be ideal when there are trade-offs due to conflicting properties. In such a case, the Pareto optimality-based ranking54 may be used for ranking the molecules based on multiple properties. Our results highlight varied impacts of the models derived from the active subspace distribution across different molecular properties, motivating objective-guided active subspace development. Finally, active subspace inference enables formal uncertainty quantification of generative models and property predictors in a computationally efficient manner, which may offer insights into data-driven generative molecular discovery.In our work, we have used the top 10% average as the reward (QoI), which can be a bottleneck for expensive oracles, e.g. wet-lab experiments, physics-based simulation, etc. Specifically, such a rank-based objective requires evaluation of all molecules in the current batch before taking the top 10% average of their properties, and this complexity increases with the size of the batch. However, one can utilize property predictors as a proxy for the expensive oracles to estimate the top 10% reward that can be used as the objective in our proposed active subspace-based optimization. For example, rank-based acquisition functions, e.g. qPO (multiple point probability of optimality) proposed by Fromer et al.,55 can be potentially applied to suggest the optimal batch (top 10%) for evaluation under resource-constrained scenarios.
It is important to note that the success of our proposed fine-tuning approach hinges on the quality of the pre-trained generative model, as we learn the active subspace posterior distribution parameters over which the design space is defined, by perturbing the pre-trained weights. If the pre-trained model fails to capture the underlying molecular generation rules, our active subspace-based method is unlikely to improve the design. In this direction, we explored (in RQ2) the potential of integrating our approach with iterative refinement methods23,24,54,56 to enhance the generative model's sampling efficiency. If surrogate models used for QoI feedback misrepresent the ground truth, this may misguide the fine-tuning method.57 To mitigate this, one can also leverage our black-box treatment to adopt a systematic, formal risk-aware optimization approach for robust fine-tuning under uncertainty.
Conflicts of interest
The authors do not have any conflicts of interest to declare.Data availability
The pre-trained model parameters of JT-VAE and the corresponding training dataset were collected from https://github.com/cambridge-mlg/weighted-retraining. For SELFIES-VAE and SMILES-VAE models, we used the data available at https://github.com/wenhao-gao/mol_opt. The PG-LBO framework considered is the same as the one described in https://github.com/TaicaiChen/PG-LBO.Supplementary information is available. See DOI: https://doi.org/10.1039/d5me00081e.
Acknowledgements
This research was supported by funding from the Advanced Scientific Computing Research program of the United States Department of Energy's Office of Science under grant 0000269227 and projects B&R# KJ0402010 and FWP# CC125. We would like to thank the anonymous reviewers who provided significant feedback that helped to design our study. Specifically, optimization of the acquisition function with active subspace parameters of VAE decoders (section 4.2) was developed by exploring one such suggestion.Notes and references
- E. N. Muratov, J. Bajorath, R. P. Sheridan and I. V. Tetko, et al. , Chem. Soc. Rev., 2020, 49, 3525–3564 RSC.
- A. Clyde, S. Galanie, D. W. Kneller and H. Ma, et al. , J. Chem. Inf. Model., 2021, 62, 116–128 CrossRef.
- H.-M. Woo, X. Qian, L. Tan, S. Jha, F. J. Alexander, E. R. Dougherty and B.-J. Yoon, Patterns, 2023, 4(11), 100875 CrossRef.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud and J. M. Hernández-Lobato, et al. , ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- R. Winter, F. Montanari, A. Steffen, H. Briem, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 8016–8024 RSC.
- W. Jin, R. Barzilay and T. Jaakkola, International Conference on Machine Learning, 2018 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, International Conference on Machine Learning, 2020 Search PubMed.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminformatics, 2017, 9, 48 CrossRef.
- R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586 RSC.
- X. Liu, Q. Liu, S. Song and J. Peng, International Conference on Machine Learning, 2020 Search PubMed.
- P. Notin, J. M. Hernández-Lobato and Y. Gal, Advances in Neural Information Processing Systems, 2021 Search PubMed.
- B. Sanchez-Lengeling, C. Outeiral, G. Guimaraes and A. Aspuru-Guzik, ChemRxiv, 2017, preprint, ChemRrXiv:5309668, DOI:10.26434/chemrxiv.5309668.v3.
- Y. Li, L. Zhang and Z. Liu, J. Cheminf., 2018, 10, 1–24 Search PubMed.
- S. Kang and K. Cho, J. Chem. Inf. Model., 2019, 59, 43–52 CrossRef CAS.
- W. Jin, R. Barzilay and T. Jaakkola, International Conference on Machine Learning, 2020 Search PubMed.
- Y. Xie, C. Shi, H. Zhou, Y. Yang, W. Zhang, Y. Yu and L. Li, International Conference on Learning Representations, 2021 Search PubMed.
- W. Gao, R. Mercado and C. W. Coley, International Conference on Learning Representations, 2022 Search PubMed.
- T. Blaschke and J. Bajorath, J. Comput.-Aided Mol. Des., 2022, 36, 363–371 CrossRef CAS.
- A. N. Abeer, S. Jantre, N. M. Urban and B.-J. Yoon, The 34th International Workshop on Machine Learning for Signal Processing (MLSP), London, UK, 2024 Search PubMed.
- W. Gao, T. Fu, J. Sun and C. Coley, Advances in neural information processing systems, 2022 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- N. Srinivas, A. Krause, S. M. Kakade and M. Seeger, arXiv, 2009, preprint, arXiv:0912.3995, DOI:10.48550/arXiv.0912.3995.
- A. Tripp, E. Daxberger and J. M. Hernández-Lobato, Adv. Neural Inf. Process. Syst., 2020, 33, 11259–11272 Search PubMed.
- T. Chen, Y. Duan, D. Li, L. Qi, Y. Shi and Y. Gao, Proceedings of the AAAI Conference on Artificial Intelligence, 2024, pp. 11381–11389 Search PubMed.
- N. Maus, H. Jones, J. Moore, M. J. Kusner, J. Bradshaw and J. Gardner, Adv. Neural Inf. Process. Syst., 2022, 35, 34505–34518 Search PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha and R. Q. Snurr, et al. , Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- J. Zhou, A. Mroz and K. E. Jelfs, Digital Discovery, 2023, 2, 1925–1936 RSC.
- G. Vogel and J. M. Weber, Chem. Sci., 2025, 16, 1161–1178 RSC.
- L. M. Lopez, Q. Zhang, O. Dollar, J. Pfaendtner, B. H. Shanks and L. J. Broadbelt, Mol. Syst. Des. Eng., 2024, 9, 352–371 RSC.
- O. Dollar, N. Joshi, D. A. Beck and J. Pfaendtner, Chem. Sci., 2021, 12, 8362–8372 RSC.
- A. G. Beck, S. Iyer, J. Fine and G. Chopra, Digital Discovery, 2025, 4, 1352–1371 RSC.
- D. MacKay, Advances in Neural Information Processing Systems, 1991 Search PubMed.
- W. J. Maddox, G. Benton and A. G. Wilson, arXiv, 2020, preprint, arXiv:2003.02139, DOI:10.48550/arXiv.2003.02139.
- J. Frankle and M. Carbin, International Conference on Learning Representations, 2019 Search PubMed.
- C. Blundell, J. Cornebise, K. Kavukcuoglu and D. Wierstra, International Conference on Machine Learning, 2015 Search PubMed.
- C. Louizos, K. Ullrich and M. Welling, Advances in Neural Information Processing Systems, 2017 Search PubMed.
- S. Jantre, S. Bhattacharya and T. Maiti, Neural Netw., 2023, 167, 309–330 CrossRef.
- S. Jantre, S. Bhattacharya and T. Maiti, IEEE Trans. Neural Netw. Learn. Syst., 2024, 36, 11176–11188 Search PubMed.
- S. Jantre, S. Bhattacharya, N. M. Urban, B.-J. Yoon, T. Maiti, P. Balaprakash and S. Madireddy, arXiv, 2022, preprint, arXiv:2206.00794, DOI:10.48550/arXiv.2206.00794.
- P. Izmailov, W. J. Maddox, P. Kirichenko, T. Garipov, D. Vetrov and A. G. Wilson, Uncertainty in Artificial Intelligence, 2020 Search PubMed.
- S. Jantre, N. M. Urban, X. Qian and B.-J. Yoon, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2024 Search PubMed.
- T. Blaschke, J. Arús-Pous, H. Chen, C. Margreitter, C. Tyrchan, O. Engkvist, K. Papadopoulos and A. Patronov, J. Chem. Inf. Model., 2020, 60, 5918–5922 CrossRef CAS.
- O. Krupnik, E. Shafer, T. Jurgenson and A. Tamar, Conference on Robot Learning, 2023 Search PubMed.
- D. Blei, A. Kucukelbir and J. McAuliffe, J. Am. Stat. Assoc., 2017, 112, 859–877 CrossRef CAS.
- R. J. Williams, Mach. Learn., 1992, 8, 229–256 Search PubMed.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT press Cambridge, MA, 2006 Search PubMed.
- I. Sobol', Comput. Math. Math. Phys., 1967, 7, 86–112 Search PubMed.
- D. P. Kingma and J. Ba, arXiv, 2014, preprint, arXiv:1412.6980, DOI:10.48550/arXiv.1412.6980.
- A. Harvey, Drug Discovery Today, 2008, 13, 894–901 CrossRef CAS PubMed.
- S. Wang, T. Che, A. Levit, B. K. Shoichet, D. Wacker and B. L. Roth, Nature, 2018, 555, 269–273 CrossRef CAS.
- F. Wilcoxon, Breakthroughs in statistics: Methodology and distribution, Springer, 1992, pp. 196–202 Search PubMed.
- E. J. Hu, Y. Shen, P. Wallis, Z. Allen-Zhu, Y. Li, S. Wang, L. Wang and W. Chen, arXiv, 2021, preprint, arXiv:2106.09685, DOI:10.48550/arXiv.2106.09685.
- A. N. Abeer, N. M. Urban, M. R. Weil, F. J. Alexander and B.-J. Yoon, Patterns, 2024, 5(10), 101042 CrossRef.
- J. Fromer, R. Wang, M. Manjrekar, A. Tripp, J. M. Hernández-Lobato and C. W. Coley, J. Chem. Inf. Model., 2025, 65, 4808–4817 CrossRef CAS.
- K. Yang, W. Jin, K. Swanson, R. Barzilay and T. Jaakkola, International Conference on Machine Learning, 2020 Search PubMed.
- J. Martinelli, Y. Nahal, D. Lê, O. Engkvist and S. Kaski, NeurIPS 2023 Workshop on New Frontiers of AI for Drug Discovery and Development, 2023 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |