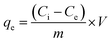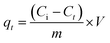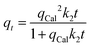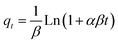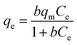Eco-inspired synthesis of a melamine formaldehyde-reinforced onion peel biochar/alginate composite for efficient lead ion removal from wastewater

Abstract

The present study focuses on the fabrication of a highly efficient, eco-friendly solid adsorbent, namely melamine formaldehyde-reinforced onion peel biochar/alginate composite (MCAg), along with onion peel-based biochar (C) and biochar/alginate composite beads (CAg). The synthesized adsorbents were characterized using various instrumental techniques. MCAg exhibited a surface area of 309.4 m² g⁻¹, a point of zero charge at pH 6.6, and the presence of multiple surface chemical functional groups as identified by FTIR analysis. The fabricated adsorbents were applied for the batch adsorption of Pb²⁺ ions under different operating conditions, in addition to desorption, reusability, and real-sample studies. MCAg showed the highest Langmuir adsorption capacity (348.9 mg g⁻¹) at pH 6, a solid dosage of 2.5 g L⁻¹, 20 °C, and 50 min of shaking time. The presence of coexisting ions in real polluted samples reduced the adsorption capacity for Pb²⁺ ions by an average of approximately 30%. Ethylenediaminetetraacetic acid was found to be the most effective desorbing agent for Pb²⁺ ions from the adsorbent surfaces. Kinetic and thermodynamic studies confirmed the applicability of the pseudo-first order and van’t Hoff models, indicating a physisorption mechanism and a spontaneous adsorption process. Column adsorption of Pb²⁺ ions was evaluated at three different bed heights (2, 3, and 4 cm) using an initial concentration of 80 mg L⁻¹ and a flow rate of 15 mL min⁻¹, achieving a maximum adsorption capacity of 232.7 mg g⁻¹ at a 4 cm bed height, with the experimental data fitting well with the Yoon–Nelson and Thomas models. The effective adsorption of Pb²⁺ by MCAg is mainly related to the synergistic action of surface functional groups enabling ion exchange, electrostatic attraction, and complexation with Pb²⁺ ions, highlighting the composite's strong potential for polluted water treatment.

---

1. Introduction

Environmental pollution caused by heavy metals has become a serious concern due to its impact on ecosystem sanitation and human health. Lead ions (Pb²⁺), the second most toxic metal contaminant in water after arsenic, severely affect aquatic bodies.^1,2 Lead ions have no beneficial biological function but are neurotoxic and damage multiple organ systems in animals. Lead causes nervous system diseases and developmental disorders in children, and damages bones, liver, kidneys, brain, and heart. The World Health Organization (WHO) has set permissible Pb²⁺ levels in drinking water at 10 µg L⁻¹.³ Lead pollution is problematic because lead is non-degradable and undergoes bioaccumulation through food webs, which amplifies its toxic effects across trophic levels. Sources of Pb²⁺ pollution include mining, metallurgy, battery production, electroplating, and fossil fuel combustion.⁴ Adsorption is considered favorable due to its low cost, high efficiency, and ease of use with possible regeneration, but commercial implementation awaits. Widespread adoption depends on creating efficient, low-cost, sustainable adsorbents that meet regulatory requirements.^5–7

The materials employed in this study combine aspects of sustainable biomass utilization for eco-inspired composite engineering, with each having unique advantages and disadvantages.¹ Onion peel biochar valorizes agricultural waste and offers several adsorption benefits. Its advantages include high carbon content (typically 60–80%), porous structure with surface area between 200 and 800 m² g⁻¹, and oxygen-containing functional groups (e.g., carboxyl, hydroxyl, and phenolic), which promote metal ion binding.⁵ Onion peel biochar is cost-efficient, sustainable, and chemically stable across varying pH values. The hydrophobic nature of biochar may reduce water dispersibility and active site accessibility for ion adsorption.^8,9 Sodium alginate is a naturally occurring biopolymer from brown seaweed with features relevant to environmental applications. Biopolymer compatibility and biodegradability raise disposal concerns, while its gel-forming ability enables separation from treated water. Sodium alginate contains various chemical functional groups such as carboxyl and hydroxyl that show high affinity for metal ions through ionic interactions. However, limitations include poor mechanical stability in aqueous environments, which leads to swelling; sensitivity to pH, restricting its use to near-neutral conditions; and a lower surface area compared to carbon-based materials, thereby limiting its adsorption applications.^10–12 Melamine-formaldehyde is a key matrix-forming component that provides properties essential for composite stability. Formaldehyde leaching can introduce harmful organic pollutants into water bodies, which can be dangerous even at low concentrations due to their cytotoxic and genotoxic properties. Such leakage may harm aquatic species, disturb vital microbial ecosystems in wastewater treatment systems, and perhaps endanger human health if contaminated water is reused. In our situation, formaldehyde is not employed as a freestanding solid adsorbent; rather, it is integrated into a highly stable composite matrix, considerably reducing the possibility of its release. Nonetheless, monitoring and minimizing potential formaldehyde leaching is critical to ensuring the environmental safety of the developed material. The composite system combines three components that reinforce mutual weaknesses and enhance advantages. Biochar's surface area and functional groups, sodium alginate's gelation and metal-binding abilities, and melamine's mechanical reinforcement create a composite with enhanced properties and operational stability.^13,14 Several diverse adsorbents have been developed for Pb²⁺ ion removal, with different methodologies showing positive results. Recent studies demonstrate materials with high potential for Pb²⁺ ion removal applications. Gao et al. produced an alginate/melamine/chitosan gel composite achieving a Pb²⁺ ion uptake of 1331.6 mg g⁻¹. The composite showed excellent Pb²⁺ ion selectivity and retained 60% capacity after eight sorption–desorption cycles.¹⁵ A sepiolite-polyethylenimine/sodium alginate composite demonstrated a Pb²⁺ ion adsorption capacity of 1094.9 mg g⁻¹, following the Langmuir isotherm model. The adsorption mechanism was governed by ion exchange and electrostatic interactions, following pseudo-second order kinetics.¹⁶ He et al. prepared a molybdenum disulfide biochar/calcium carbonate/alginate composite with an adsorption capacity of 909.1 mg g⁻¹, combining biochar's surface area with alginate's metal-binding properties.¹⁷ Liu et al. developed a sodium alginate melamine@zeolitic imidazolate framework-67 composite with a Pb²⁺ ion adsorption capacity of 635.0 mg g⁻¹, removing lead through electrostatic interactions and complexation.¹⁸ Wang et al. created a calcium alginate/biochar composite achieving a Pb²⁺ ion removal of 664.6 mg g⁻¹, demonstrating synergy between biopolymers and biomaterials.¹⁹ Blending biochar, biopolymers, and synthetic reinforcing agents offers a promising pathway for next-generation materials, overcoming individual performance limitations with good cost-effectiveness and environmental sustainability. Although MF-based composites have been described, this work is unique in combining melamine-formaldehyde with alginate and onion-peel-derived biochar, with the last component being an eco-friendly, heteroatom-rich feedstock that has not been employed before in such ternary systems. Our easy and ecologically friendly synthesis method produces a composite with increased mechanical strength, numerous active sites, and high reusability. This technique improves conventional MF-based adsorbents by including sustainable materials, simplifying manufacture, and improving performance for effective Pb²⁺ removal. Synergistic integration would yield superior adsorption capacity, mechanical stability, and regeneration efficiency.

This study addresses Pb²⁺ ion contamination by developing low-cost adsorbents from agricultural waste, supporting environmental protection, public health, and circular economy goals through sustainable water treatment solutions. The methodology involves eco-inspired synthesis, characterization, and performance testing through pyrolytic conversion of onion peel waste to biochar, melamine-formaldehyde resin preparation, and composite formulation in an alginate matrix. Physicochemical techniques were utilized for comprehensive characterization of thermal, chemical, and textural properties. The adsorption of Pb²⁺ ions was investigated under varied conditions such as adsorbent dosage, initial solution pH, contact time, temperature, and initial pollutant concentration, using batch (static) adsorption experiments. Real water samples were also tested. Additionally, dynamic fixed-bed adsorption experiments were conducted using the most efficient adsorbent material.

2. Materials and methods

2.1. Materials

Sodium alginate (>99.5%), melamine (99%), ethylenediaminetetraacetic acid (99.5%), cysteine (>98%), and lead nitrate (≥99.5%) were obtained from Sigma Aldrich, Czechia. Sodium hydroxide (≥98%), hydrochloric acid (37%), nitric acid (70%), and potassium carbonate (96%) were purchased from El-Nasr for pharmaceutical and chemical industries Co., Egypt. Formaldehyde (%), methanol (≥99.5%), anhydrous calcium chloride (97%), and sodium chloride (>99%) were obtained from Loba Chemie, Mumbai, India.

2.2. Solid adsorbent preparation

2.2.1. Preparation of onion peel biochar (C). Onion peels were collected from a specialized kitchen, washed several times with distilled water, dried at 90 °C for 10 h, and ground using a 650-watt DSP powerful coffee seasoning mill. The resulting powder was stored in a clean, dry bottle. Next, 20 g of onion peel powder was carbonized in a tubular muffle furnace for 3 h at 500 °C under a nitrogen flow rate of 10 mL min⁻¹. After cooling, the produced biochar was subjected to ultrasonic grinding using a Sonics VCX 750 digital ultrasonic homogenizer (USA) for 30 min. Ice baths were used to prevent sample degradation and solvent evaporation. The resulting biochar particles were separated from the mother liquor via centrifugation, gently washed with distilled water, and dried at 120 °C for 6 h.

2.2.2. Preparation of melamine formaldehyde resin (MF). The synthesis of melamine formaldehyde resin was carried out following a modified procedure based on Hassan et al.¹³ Initially, 1.66 g of melamine was dissolved in 20 mL of methanol in a round-bottom flask and stirred at 70 °C for 20 min. Subsequently, 10 mL of 37% formaldehyde solution was introduced to enable the formation of hexamethyl melamine. The mixture's pH was adjusted to nearly 8.5 using potassium carbonate, and the reaction was allowed to proceed under continuous stirring for 3 h to promote polymerization. The resulting resin was then separated via centrifugation, washed with a methanol/distilled water mixture, and dried at 110 °C. The dried resin was pulverized using a 650-watt DSP coffee seasoning mill and further processed via ultrasonic grinding (Sonics VCX 750 homogenizer, USA) for 30 min under ice-cooled conditions to prevent overheating. Finally, the product was dried at 120 °C.

2.2.3. Preparation of biochar/alginate composite beads (CAg). Sodium alginate (1.0 g) was dissolved in a 250 mL beaker containing 100 mL of distilled water at 60 °C under continuous magnetic stirring for 15 min. Then, 0.5 g of the produced biochar was mixed into the sodium alginate solution, and magnetic stirring was continued for another 30 min until a completely homogeneous mixture was obtained. The resulting mixture was dropped using a 50 mL microsyringe into 100 mL of 2% (w/v) calcium chloride solution. The formed beads were collected, filtered, washed with distilled water, and dried at 110 °C overnight. The dried material was then ground using a 650-watt DSP coffee seasoning mill and further processed via ultrasonic grinding (Sonics VCX 750 homogenizer, USA) for 30 min under ice-bath cooling to prevent overheating. Finally, the material was dried at 120 °C for 10 h.

2.2.4. Preparation of the melamine formaldehyde/biochar/alginate composite (MCAg). Melamine formaldehyde/biochar/alginate composite beads were prepared using the same procedure as that for the biochar/alginate composite beads, except that 0.25 g of biochar and 0.25 g of melamine formaldehyde (MF) powders were mixed with 1.0 g of sodium alginate solution (see Scheme S1). The ratio of melamine formaldehyde, biochar, and alginate was selected based on preliminary experiments, with the chosen ratio optimized to achieve maximum adsorption capacity.

2.3. Characterization of the prepared solid adsorbents

Thermal, chemical, and textural characterization is essential for the investigation of solid adsorbent materials. The textural properties of the synthesized materials (C, CAg, and MCAg) were characterized using N₂ gas adsorption–desorption analysis performed on a NOVA 3200e gas sorption analyzer (Quantachrome Corp., USA). Prior to measurements, all solid samples were degassed under vacuum (10⁻⁴ Torr) at 120 °C for 15 h to remove adsorbed contaminants. The analysis aimed to determine key structural parameters, including specific surface area (S_BET, m² g⁻¹), total pore volume (V_p, cm³ g⁻¹), and average pore diameter (nm).

X-ray diffraction analysis was conducted to determine the crystalline composition of samples C, CAg, and MCAg using a D8 Advance diffractometer (Bruker, Germany). The instrument operated with Cu-Kα radiation (λ = 1.5406 Å) at 40 kV and 40 mA. Scans were performed over a 2θ range of 10° to 50° with a scanning rate of 1° min⁻¹.

Thermogravimetric analysis (TGA) was performed on the solid adsorbents (C, CAg, and MCAg) using an SDT Q600 thermoanalyzer (TA Instruments, V20.9 Build 20) under a nitrogen atmosphere (20 mL min⁻¹ flow rate). The samples were heated from ambient temperature to 900 °C to evaluate their thermal stability and decomposition behavior.

The surface chemical functional groups of C, CAg, and MCAg were detected using attenuated total reflectance Fourier transform infrared spectroscopy (ATR-FTIR) utilizing a ZnSe crystal on a Nicolet Impact 400 D spectrometer, operating at a resolution of 5 cm⁻¹ and a scan range of 4000–400 cm⁻¹.

The pH_PZC values of C, CAg, and MCAg as solid adsorbents were evaluated using the salt addition method. For each sample, 0.2 g of dried material was dispersed in 50 mL of 0.1 M NaCl solution (prepared with deoxygenated distilled water) in sealed containers. The initial pH (pH_initial) was systematically adjusted from 2 to 12 using 0.05 mol L⁻¹ HCl or NaOH solutions. Following 4 h of agitation, the equilibrium pH (pH_final) was measured using a calibrated HI 2020 pH meter (Hanna Instruments). pH_PZC was identified as the pH value where ΔpH (pH_final − pH_initial) = 0.

The surface morphology of C, CAg, and MCAg particles was investigated by scanning electron microscopy (SEM). Prior to imaging, sample fragments were sputter-coated with a 10 nm gold layer to enhance conductivity. High-resolution micrographs were obtained using a JEOL JSM-6510LV analytical SEM (Japan) operating at an acceleration voltage of 10 kV.

The nanostructure features of all materials were characterized using a JEOL JEM-2100 transmission electron microscope (Japan). For sample preparation, the solids were first dispersed in ethanol via 20-min ultrasonication, and then deposited onto carbon-coated copper TEM grids. This preparation protocol ensured optimal particle distribution for high-resolution imaging.

2.4. Adsorption procedures of Pb²⁺ ions

2.4.1. Batch adsorption of Pb²⁺ ions. The batch adsorption of Pb²⁺ ions onto C, CAg, and MCAg was carried out using a static method. In this procedure, 0.125 g of each adsorbent was added to 50 mL of 800 mg L⁻¹ Pb²⁺ solution at pH 6 and maintained at 20 °C with constant shaking at 120 rpm for 80 min. At pH 6, Pb²⁺ is the dominating species, followed by PbOH⁺ (based on Pb²⁺ hydrolysis behaviour). At the studied pH and concentrations, no precipitation of Pb(OH)_2(s) occurs, indicating that Pb²⁺ is removed through adsorption rather than precipitation. After the adsorption period, the solid adsorbent was separated by centrifugation. The remaining Pb²⁺ concentration in the filtrate (C_e, mg L⁻¹) was measured using an atomic absorption spectrometer (HG-AAS; Agilent AA240 with VGA-77, Australia). All measurements were performed in triplicate to ensure accuracy. The percentage of Pb²⁺ removal (R%) and equilibrium adsorption capacity (q_e, mg g⁻¹) were calculated using eqn (1) and (2) (see Table 1). To determine the optimal adsorption conditions, several parameters were varied, including adsorbent dosage (0.5–3.0 g L⁻¹), solution pH (2–8) with the help of 0.05 mol L⁻¹ HCl or NaOH solutions, contact time (2.5–80.0 min), initial Pb²⁺ concentration (50–800 mg L⁻¹), and temperature (20–45 °C).

Table 1 Adsorption models employed to characterize both static and dynamic adsorption behaviors

Name of models	Applied models	Symbols	No.
Removal percentage		R% (removal% of Pb^2+ ions)	1
Equilibrium adsorption capacity		qe (adsorption capacity at equilibrium, mg g^−1); V (volume of Pb^2+ solution, L); m (mass of solid adsorbent, g); Ci (initial conc. of Pb^2+, mg L^−1); Ce (equilibrium conc. of Pb^2+, mg L^−1)	2
Pseudo-first order	qt = qCal(1 − e^−k1t)	k1 (PFO rate constant, min^−1); qCal (adsorption capacity, mg g^−1 with the kinetic model)	3
Adsorption capacity at certain time		qt (adsorption capacity at time t (min), mg g^−1)	4
Pseudo-second order		k2 (PSO rate constant, g mg^−1 min^−1)	5
Elovich		α (initial rate of Pb^2+ adsorption, mg g^−1 min^−1); β (extent of surface coverage, g mg^−1)	6
Weber and Morris intraparticle diffusion		Kdiff (rate constant of intra-particle diffusion, mg g^−1 min^−1/2); C (thickness of the boundary layer, mg g^−1)	7
Langmuir		b (Langmuir constant, L mg^−1); qm (maximum Langmuir adsorption capacity, mg g^−1)	8
Dimensionless separation factor		RL (dimensionless separation factor)	9
Freundlich		n (Freundlich constant related to the adsorption intensity); KF (Freundlich constant related to the extent of adsorption, L^1/n mg^1–1/n g^−1)	10
Temkin		R (universal gas constant, 8.314 J mol^−1 K^−1); T (absolute adsorption temperature, K); KT (equilibrium binding constant, L g^−1); bT (Temkin constant, J mol^−1)	11
Dubinin-Radushkevich		qDR (DR adsorption capacity, mg g^−1); KDR (DR constant, mol^2 kJ^−2)	12
Mean adsorption-free energy		EDR (mean adsorption-free energy, kJ mol^−1)	13
Distribution constant		Cs (surface adsorbed Pb^2+, mg g^−1)	14
Van’t Hoff model		ΔS° (entropy change, kJ mol^−1 K^−1); ΔH° (heat change, kJ mol^−1)	15
Gibbs free energy	ΔG° = ΔH° − TΔS°	ΔG° (free energy change, kJ mol^−1)	16
Desorption efficiency		Cd (Pb^2+ concentration after desorption, mg L^−1); V (desorbing agent volume, L)	17
The entire amount of adsorbed Pb^2+		qtotal (total amount of adsorbed Pb^2+, mg); µ (solution flow rate, mL min^−1)	18
Maximum column adsorption capacity (mg g^−1)		m (mass of solid adsorbent, g)	19
Yoon-Nelson model		τ (the time at which Ct/Ci = 0.5 in min); KYN (Yoon-Nelson rate constant in min^−1)	20
Thomas model		Veff (solution volume of Pb^2+ in L); KTh (Thomas rate constant in L mg^−1 min^−1); qTh (maximal adsorption column capacity in mg g^−1)	21

---

Different nonlinear kinetic and equilibrium adsorption models were applied to evaluate key adsorption parameters. The kinetics of Pb²⁺ adsorption onto C, CAg, and MCAg were analyzed using nonlinear formulations of the pseudo-first order (eqn (3)), pseudo-second order (eqn (5)), Elovich (eqn (6)), and Weber–Morris intraparticle diffusion models (eqn (7)). The amount of Pb²⁺ adsorbed at a specific time (q_t, mg g⁻¹) was calculated using eqn (4). In addition, the equilibrium adsorption data (as summarized in Table 1) were interpreted using several nonlinear isotherm models, including Langmuir (eqn (8)), Freundlich (eqn (10)), Temkin (eqn (11)), and Dubinin–Radushkevich (eqn (12)). The dimensionless separation factor (R_L), which indicates the favorability of adsorption, was calculated using eqn (9). Furthermore, eqn (13) was employed to estimate the mean free energy of adsorption.

The effect of temperature on the batch adsorption of Pb²⁺ ions was examined by conducting experiments with 0.125 g of the adsorbent in 50 mL of 800 mg L⁻¹ Pb²⁺ solution at pH 6, under shaking for 50 min and 120 rpm. The experiments were performed at varying temperatures (20, 30, 40, and 45 °C). Thermodynamic parameters, including the changes in enthalpy (ΔH°, kJ mol⁻¹), entropy (ΔS°, kJ mol⁻¹ K⁻¹), and Gibbs free energy (ΔG°, kJ mol⁻¹), were calculated using eqn (14)–(16) as presented in Table 1.

2.4.2. Simulated wastewater system experiment. A real wastewater sample was collected from the inorganic laboratory of the Chemistry Department, Faculty of Science, Umm Al-Qura University, Saudi Arabia, prior to treatment processes. The sample contained a mixture of various inorganic and organic ions (supplementary materials S1) and was analyzed for its Pb²⁺ content, which was found to be 45 mg L⁻¹. To simulate high contamination levels, the Pb²⁺ concentration in the sample was increased to 800 mg L⁻¹ by dissolving additional Pb²⁺ ions. The Pb²⁺ concentration utilized in the ‘real wastewater’ experiment is that of a simulated high-strength wastewater, as the original sample only had 45 mg L⁻¹ of Pb²⁺, which was totally removed by all materials. This adjustment was required to make a valid comparison between C, CAg, and MCAg. To account for interference effects, the original wastewater's realistic ion matrix was left intact. The nonlinear Langmuir isotherm model was applied to determine the maximum adsorption capacity (q_m, mg g⁻¹).

2.4.3. Evaluation of adsorbent regeneration and reuse potential. Desorption studies of Pb²⁺ ions were conducted by mixing 0.2 g of the tested adsorbent with 50 mL of 1000 mg L⁻¹ Pb²⁺ solution at pH 6, followed by stirring for 50 min at 20 °C. After the adsorption step, the solid adsorbent was separated via centrifugation, thoroughly washed with distilled water, and then treated with 100 mL of 0.1 mol L⁻¹ solutions of HCl, HNO₃, EDTA, and cysteine for 30 min to facilitate desorption. The concentration of Pb²⁺ ions released into the solution was quantified using atomic absorption spectroscopy. The desorption efficiency (Des.%) was calculated using eqn (17) to assess the potential of the adsorbents for reuse in successive adsorption cycles.²⁰

To evaluate the reusability of the solid adsorbent, ten successive adsorption/desorption cycles were performed under fixed conditions: an adsorbent dosage of 2.5 g L⁻¹, an initial Pb²⁺ concentration of 800 mg L⁻¹, a contact time of 50 min, pH 6, and a temperature of 20 °C. After each cycle, the adsorbent was separated by centrifugation, thoroughly washed multiple times with 50 mL of 0.1 mol L⁻¹ EDTA solution to remove any residual Pb²⁺ and then dried at 100 °C before reuse in the next cycle.

2.4.4. Column adsorption of Pb²⁺ ions. The melamine formaldehyde/biochar/alginate composite (MCAg) was selected for dynamic (column) adsorption studies of Pb²⁺ ions due to its superior static adsorption performance. Column experiments were conducted using a glass burette (1.5 cm inner diameter, 50.0 cm in length). MCAg was packed into the column at varying bed heights (2.0, 3.0, and 4.0 cm) to investigate the effect of bed depth. To support the adsorbent, fill the glass column with Milli-Q water and deposit a 1 cm coating of clean glass powder on the sintered glass disc. MCAg particles (0.5 mm) were pre-wetted in water overnight to achieve appropriate hydration. The wetted adsorbent was then carefully placed into the column in small pieces, with the column gently tapped to remove air pockets and establish a consistent bed. To prevent adsorbent floating, 1 cm of glass powder was added on top of the MCAg layer. After packing, the column was flushed with Milli-Q water for 5 min to remove contaminants and condition it before adding the Pb⁺ solution. The adsorption process was carried out under the following conditions: an initial Pb²⁺ concentration of 80 mg L⁻¹, a pH of 6, a flow rate of 15 mL min⁻¹, and a temperature of 20 °C. Effluent samples were collected at regular intervals to determine Pb²⁺ concentrations. The exhaustion time (t_e, min) was defined as the point when the effluent concentration reached approximately 95% of the influent Pb²⁺ concentration (C_t/C_i = 0.95), while the breakthrough time (t_b, min) corresponded to the point when the effluent concentration reached 5% of the initial value (C_t/C_i = 0.05). The total amount of Pb²⁺ adsorbed (q_total, mg) was determined using eqn (18) (Table 1) by integrating the area above the breakthrough curve. Adsorption capacity was calculated at C_t/C_i = 0.85 to minimize curve distortion.¹³ The maximum adsorption capacity (q_o, mg g⁻¹) was calculated using eqn (19) (Table 1). Experimental data were further analyzed using the nonlinear forms of the Yoon–Nelson and Thomas models (eqn (20) and (21)) to describe the column adsorption behaviour of Pb²⁺ on MCAg.

3. Results and discussion

3.1. Solid adsorbent characterization

The textural characterization of the synthesized adsorbents, namely C, CAg and MCAg, was determined by displaying their nitrogen adsorption/desorption isotherms as shown in Fig. 1a. According to the IUPAC classification, all synthesized adsorbents exhibit type IV adsorption isotherms, confirming that they are mesoporous materials.²¹ Moreover, the isotherms of all the adsorbents show distinct hysteresis loops of H3-type, starting at 0.4 P/P°, associated with the capillary condensation phenomenon occurring within the pores. These hysteresis loops indicate the presence of slit-like pores of adsorbents.^22,23 The specific surface area, the total pore volume, and the average pore diameter of all adsorbents were analyzed based on the Brunauer–Emmett–Teller (BET) theory, as shown in Table 2. The C, CAg, and MCAg adsorbents exhibit specific surface areas of 466.3, 134.6, and 309.4 m² g⁻¹, respectively, with total pore volumes of 0.8153, 0.2749, and 0.3908 cm³ g⁻¹, showing a consistent pattern following the order of C > MCAg > CAg. The MCAg adsorbent exhibits a greater specific surface area and total pore volume than CAg by 2.29 and 1.42 times, respectively, demonstrating the successful combination of melamine formaldehyde with the CAg adsorbent. Furthermore, the average pore diameters of C, CAg and MCAg are 6.98, 8.16, and 5.06 nm, respectively. Barrett–Joyner–Halenda (BJH) pore size distribution analysis, as presented in Fig. S1a, revealed distinct maxima for samples C, CAg, and MCAg at 6.98 nm, 8.16 nm, and 5.06 nm, respectively, indicating their mesoporous structures and differences in pore development among the synthesized adsorbents.²⁴ The pore size distribution of the MCAg composite predominantly falls within the mesoporous range, according to IUPAC classification, serving as efficient transport pathways for pollutants. The enhancement of the surface area, total pore volume and average pore diameter of the MCAg composite provides more active sites for adsorption with effective performance, making it a potential candidate for lead ion adsorption.

Fig. 1 Nitrogen adsorption (a), TGA (b), ATR-FTIR (c), and pH at point of zero charge (d) for C, CAg, and MCAg.

Table 2 Characterization of the synthesized solid-phase materials

Properties	C	CAg	MCAg
SBET (m^2 g^−1)	466.3	134.6	309.4
VP (cm^3 g^−1)	0.8153	0.2749	0.3908
Average pore diameter (nm)	6.98	8.16	5.06
pHPZC	6.1	6.4	6.6

---

The thermal stability of the prepared adsorbents was assessed using thermogravimetric analysis, and the results are presented in Fig. 1b. All the prepared adsorbents are thermally stable up to 300 °C before undergoing decomposition. At 175 °C, the C, CAg, and MCAg adsorbents show mass reductions of 1.5, 7.2 and 7.7%, respectively, due to the evaporation of adsorbed water from their surfaces.²⁵ The C adsorbent exhibits a lower mass loss compared to CAg and MCAg adsorbents, due to its higher carbon content resulting from pyrolysis at 500 °C. Also, biochar exhibited fewer active functional sites compared to CAg and MCAg adsorbents. Between 250 and 400 °C, all three adsorbents started to decompose significantly. The biochar adsorbent (C) undergoes a notable mass loss of 11.9% at 350 °C, indicating the decomposition of the residual volatile components, whereas the beads of CAg and MCAg composites lose considerable masses of 31.1 and 24.4%, respectively, which is related to the thermal degradation of polysaccharide chains and destruction of melamine formaldehyde resin. At 900 °C, the residual mass percentages of C, CAg and MCAg are 73.7, 37.4, and 44.4%, respectively. Such high residual masses of all the prepared adsorbents are owing to the substantial carbon content of the biochar component. The order of thermal stability of all the prepared adsorbents is C > MCAg > CAg. The MCAg composite shows good thermal stability, indicating a successful combination of biochar with adsorbents derived from alginate and melamine formaldehyde.

The XRD patterns shown in Fig. S1b give information on the structural properties of the synthesized materials. The biochar sample (C) shows a broad diffraction peak between approximately 12.9° and 26.3° (2θ), reflecting its largely amorphous structure with minimal graphitic order, which is typical of carbon-based materials produced from biomass.²⁶ The sharper and more intense peak at 27.4° observed in the CAg composite (biochar–alginate) suggests greater structural order, likely arising from the interactions between biochar and alginate, as well as the incorporation of silver species. This reflects a noticeable improvement in the crystallinity compared to pure biochar. The XRD pattern of the MCAg composite (melamine-formaldehyde/biochar/alginate) shows peaks at 12.9° and 23.8°, as well as larger characteristics that indicate a more heterogeneous and semi-crystalline structure. The peak at 23.8° is most likely connected with the presence of melamine-formaldehyde resin,²⁷ indicating that it was successfully incorporated into the biochar-alginate matrix. These structural changes are significant because they can impact the physicochemical characteristics of the material and perhaps improve its adsorption effectiveness.

The ATR-FTIR spectral data of C, CAg, and MCAg adsorbents are depicted in Fig. 1c. Different characteristic peaks appear in the FTIR spectra of the biochar adsorbent; the broad peak at 3333.1 cm⁻¹ confirms the intermolecular and intramolecular stretching vibrations of –OH groups. The characteristic peak at 1592.1 cm⁻¹ is caused by stretching vibrations of C=O groups. A strong peak appears at 1024.7 cm⁻¹ due to the C–O stretching vibrations of different functional groups, including alcohols, phenols and carboxylic acids, on the surface of the biochar adsorbent. A weak peak at 2093.8 cm⁻¹ was noted, which is typically related to C≡C or C≡N stretching vibrations; such groups can appear in small magnitudes during the pyrolysis of lignocellulosic biomass. The C–H group causes multiple peaks, including one in the 2800–2900 cm⁻¹ range, caused by stretching vibrations. Additionally, peaks at 1430.2, 1324.3, 883.1, and 815.9 cm⁻¹ are attributed to bending vibrations of the aliphatic and aromatic C–H group. The IR spectrum of the CAg adsorbent has nearly the same characteristic peaks as adsorbent C, indicating the presence of similar functional groups in both adsorbents, with slight variations. For example, the peak of the –OH group slightly broadens and shifts to 3364.7 cm⁻¹ because of the overlapping of –OH peaks from both C and CAg adsorbents, as well as hydrogen bond formation between both adsorbents. In addition, the noticeable peaks of alginate (CAg) are observed at 1592.1 and 1412.4 cm⁻¹, which correspond to symmetric and asymmetric stretching vibrations of the C=O group.¹⁸ When combining melamine formaldehyde with biochar and alginate to form the MCAg composite, a roughly similar pattern to that of C and CAg adsorbents appears, with some variations in peaks, including their shapes, intensities and positions.¹³ The lower intensity peak appears at 3388.6 cm⁻¹, which could result from the overlapping signals of –OH and –NH derived from the different prepared adsorbents. A sharp peak with a slight widening is seen at 1575.1 cm⁻¹, which could be related to the interactions between vibrations of functional groups of all three adsorbents (asymmetric stretching of C–O derived from CAg and C=N vibrations). Moreover, a low intensity peak disappears and a noticeably wider peak with a small shoulder appears at 1162.3 and 1059.5 cm⁻¹, indicating the overlapping absorption peaks of different functional groups (stretching vibrations of C–O and C–N groups, the former arising from C and Ag adsorbents, and the latter arising from the MF adsorbent). Overall, all observations support the successful integration of the three adsorbents.

The zeta potential of the adsorbent has a significant impact on the ion adsorption process. The pH_PZC of C, CAg and MCAg adsorbents was determined and is displayed in Fig. 1d and Table 2. The graph shows a sharp decline in the zeta potentials of all prepared adsorbents as the pH values increase, with the pH_PZC values being 6.1, 6.4, and 6.6, respectively. As the pH rises, the protonation of functional groups on the surface of adsorbents reduces until the pH value exceeds pH_PZC, at which point the adsorbent surface becomes entirely negatively charged. Oppositely, when the pH level decreases below pHpzc, the protonation of the functional groups on the adsorbent surface increases, resulting in an entirely positively charged surface.²⁸ Furthermore, it can be seen from the pH_PZC results that the higher zeta potential value of the MCAg composite indicates that it has a greater number of functional groups than C and CAg adsorbents.

Scanning electron microscopy (SEM) is used to determine the surface properties and morphology of the C, CAg and MCAg adsorbents as shown in Fig. 2a–c, respectively. The surface of the C adsorbent features rectangular, plate-like structures arranged vertically with a rough texture. In addition, large, darker regions corresponding to pore holes are observed, proving the highly intrinsic nature of biochar. The SEM of the CAg adsorbent shows large, rectangular, stacked, sheet-like structures. The surfaces of these particles are granular with characteristic brighter edges, confirming the variability of adsorbents’ surface composition. Lower pore holes compared to the C adsorbent are also observed. The SEM image of the MCAg composite shows features like both C and CAg adsorbents, with agglomerations of granular particles being densely packed; however, it reveals some different features. Firstly, granules are packed loosely, creating narrow channels between them. In addition, the surface of the MCAg composite presents clear, distinct, and well-defined grooves and ridges with varying sizes. Such specific features of the MCAg composite result from the interactions of functional groups of all three adsorbents, which contribute effectively to enhancing surface porosity and prove the successful combination of MF with C and Ag adsorbents.

Fig. 2 SEM (a)–(c) and TEM (d)–(f) images for C, CAg, and MCAg.

Transmission electron microscopy (TEM) is also used to examine the internal structures of the C, CAg and MCAg adsorbents at the nanoscale, giving 2D images as shown in Fig. 2c–e, respectively. The C adsorbent shows a folded structure of stacked tube-like particles with dense masses that resemble clouds, confirming the intrinsic behaviour of carbon-based biochar adsorbents. Open-structure clusters, including small spherical particles and large cloud-like structures with large voids, are observed in the TEM of the CAg adsorbent. The appearance of these two features indicates the successful insertion of alginate into biochar, as small spherical particles correspond to alginate, while cloud-like structures are attributed to biochar. The TEM image of the MCAg composite shows clusters composed of multiple chains of small, monodisperse spherical particles, characterised by a combination of transparent and darker spots, penetrated by multiple voids that are homogeneously distributed. Such homogeneity of particles and voids indicates the well-controlled synthesis of the MCAg composite. The dark and transparent regions are evidence of variation in composition, confirming the effective integration of the three prepared adsorbents. The larger number of spherical particles could be linked to the increased number of functional groups present in the MF adsorbent.²⁹

3.2. Batch adsorption of Pb²⁺ ions

3.2.1. Effect of adsorbent dosage. The efficacy of Pb²⁺ removal at different adsorbent doses was examined in a solution with an initial Pb²⁺ concentration of 800 mg L⁻¹ for the three distinct adsorbents, as shown in Fig. 3a. The development in the removal of Pb²⁺ was more or less positively related to the solid adsorbent dosage, which was the same for the three adsorbents. Over the examined range of dosages, MCAg showed superior ability to remove Pb²⁺ ions. Considering the lowest adsorbent dosage (0.5 mg L⁻¹), the removal efficiencies of MCAg, CAg, and C for Pb²⁺ ions were 20.0, 13.7, and 10.0%, respectively. The removal efficiencies of C, CAg, and MCAg increased significantly to 38%, 49%, and 58%, respectively, when the adsorbent dose was increased to 1.5 g L⁻¹. This enhancement is ascribed to the increased availability of surface-active adsorption sites.³⁰ The removal efficiency increased with adsorbent dose up to 2.5 g L⁻¹, albeit gradually, reaching 50.0%, 68.8%, and 98.5% for C, CAg, and MCAg. As a result, the best adsorbent dose for subsequent studies was determined to be 2.5 g L⁻¹. An increase in adsorbent dose over 2.5 g L⁻¹ resulted in no significant improvement in removal efficiency for all three adsorbents.³¹ This is due to a lower ratio of Pb²⁺ ions to accessible active sites.

Fig. 3 The impact of solid adsorbent dosage (a) and pH (b) on the adsorption of Pb²⁺ ions onto C, CAg, and MCAg (C_i = 800 mg L⁻¹, t = 80 min, T = 20 °C, adsorbent dosage = 0.5–3.0 g L⁻¹, pH = 2–8).

3.2.2. Effect of solution pH. The influence of initial solution pH on Pb²⁺ adsorption by C, CAg, and MCAg solid adsorbents is displayed in Fig. 3b. For all three compounds, the removal efficiency considerably increased as the pH increased from 2 to 6. Adsorption was reduced at lower pH values (2–3) due to large concentrations of H⁺ ions competing with Pb²⁺ for active sites.³² Removal efficiencies for C, CAg, and MCAg were 24.0%, 28.9%, and 54.7%, respectively. The development in removal with increasing pH is accredited to the reduction in electrostatic repulsion and the increased deprotonation of surface functional groups, which enables stronger interactions with Pb²⁺ ions.³³ At pH 6, the maximum removal rates were 50.1% for C, 68.4% for CAg, and 99.1% for MCAg. These ideal adsorption conditions are closely related to the materials' pHpzc values, which were found to be 6.1, 6.4, and 6.6 for C, CAg, and MCAg, respectively. The adsorbent surfaces become more negatively charged at pH values close to or slightly below pHpzc, which promotes the attraction of positively charged Pb²⁺ ions. A slight reduction in removal for C and CAg was noted at pHpzc, especially above pH 6. This might be caused by the production of lead hydroxide precipitates or active site saturation. The drop in Pb²⁺ removal efficiency under alkaline conditions can be ascribed to electrostatic repulsion between the negatively charged surface of the adsorbent (at pH values above its pH_pzc) and the negatively charged PbO₂²⁻ ions created in the solution.^34,35 In contrast, MCAg preserved a high removal efficiency (87.3%) even at pH 8, suggesting superior surface characters, greater functional group availability, and better performance across a broader pH range. This performance emphasizes MCAg as the most effective adsorbent among the three for Pb²⁺ removal under varying pH conditions.

3.2.3. Adsorption time and kinetics analysis. Adsorption kinetics analysis is a significant factor in evaluating the adsorbents’ performance by understanding the adsorption mechanism and measuring their ability to remove pollutants from the medium. Pb²⁺ adsorption using the prepared adsorbents C, CAg and MCAg was studied for various agitation periods from 2.5 to 80.0 min at a pH of 6, an adsorbent dose of 2.5 g L⁻¹, a temperature of 20 °C and an initial Pb²⁺ concentration of 800 mg L⁻¹. It can be seen from the dot plots of Fig. 4 that the rate of initial adsorption of Pb²⁺ increased rapidly up to 30 min mainly due to the abundance of available active sites on the adsorbent's surface, in addition to the high concentration of Pb²⁺. Then, the adsorption rate decreased sharply due to the substantial diminution of active sites and attempts of Pb²⁺ ions to enter pores and bind with them as the adsorption approached the equilibrium stage.³⁶ For a more profound understanding of the Pb²⁺ adsorption mechanism, four nonlinear models were applied: pseudo-first order (PFO), pseudo-second order (PSO), Elovich, and Weber and Morris models, as shown in Fig. 4a–d, respectively, and the related adsorption parameters were calculated and displayed in Table 3.

Fig. 4 PFO (a), PSO (b), Elovich (c), and Weber and Morris nonlinear plot for the adsorption of Pb²⁺ ions onto C, CAg, and MCAg (C_i = 800 mg L⁻¹, T = 20 °C, adsorbent dosage = 2.5 g L⁻¹, pH = 6, t = 2.5–80.0 min).

Table 3 Nonlinear kinetic adsorption parameters for Pb²⁺ adsorption on all solid adsorbents (T = 20 °C, C_i = 800 mg L⁻¹, dosage 2.5 g L⁻¹, pH= 6, t = 2.5–80.0 min)

Models	Parameters	C	CAg	MCAg
PFO	qcal (mg g^−1)	166.3	221.8	333.8
	k1 (min^−1)	0.0451	0.0631	0.0800
	R^2	0.9913	0.9777	0.9914
	χ^2	0.1184	0.4716	0.3265
PSO	qcal (mg g^−1)	221.44	275.56	375.95
	k2 (g mg^−1 min^−1) × 10^−4	1.7702	2.3103	2.3388
	R^2	0.9797	0.9674	0.9825
	χ^2	0.2754	0.6878	0.4849
Elovich	α (mg g^−1 min^−1)	10.3726	24.4715	52.0193
	β (g mg^−1)	0.0149	0.0139	0.0112
	R^2	0.9639	0.9468	0.9706
	χ^2	0.4899	1.1234	1.1130
Weber and Morris intraparticle diffusion	kdiff (mg g^−1 min^−1/2)	21.7535	26.8936	35.9692
	C	1.7820	14.5918	46.6761
	R^2	0.9263	0.8877	0.8922
	χ^2	0.9998	2.3707	4.0850

---

The findings clarify that all models well demonstrated Pb²⁺ adsorption by C, CAg, and MCAg supported by the high values of regression coefficients (R²), ranging from 0.8877 to 0.9914, in addition to declining values of the reduced chi-square (χ²), ranging from 0.1184 to 4.0850. The PFO model is a more optimal model, with a better fit of the Pb²⁺ adsorption data by C, CAg, and MCAg compared to the PSO model, supported by higher R² (0.9913, 0.9777, and 0.9914 by C, CAg, and MCAg, respectively), accompanied by lower χ² (0.1184, 0.4716, and 0.3265, respectively). The adsorption capacities (q_cal, mg g⁻¹) obtained with PFO (166.25, 221.75, and 333.82 mg g⁻¹) are much closer to those relative to the Langmuir model with a reduced average deviation of 6.1%. The PFO model exhibits a range of root means square error (RMSE) values from 0.3441 to 0.5714. The highest rate constant value (k₁, 0.0800 min⁻¹) was achieved by the MCAg composite, demonstrating the highest rate of Pb²⁺ adsorption due to its high surface area with a variety of functional groups on its surface. The PFO model is more suitable for describing the adsorption of Pb²⁺ ions onto all the synthesized adsorbents (C, CAg, and MCAg) than the PSO model. This conclusion is supported by the higher R² values, lower χ² values, and smaller deviations between the experimental and calculated adsorption capacities observed for the PFO model compared to those of the PSO model. In the Elovich model, the β values follow the order C (0.0149) > CAg (0.0139) > MCAg (0.0112), suggesting the quickest surface coverage of MCAg by Pb²⁺ ions. The most outstanding α value (52.0193 mg g⁻¹ min^1/2) has been obtained with MCAg, indicating the fastest initial rate of Pb²⁺ adsorption onto its surface among other prepared adsorbents. The superior C value of 46.6761 calculated by the Weber and Morris model has been reached by the MCAg adsorbent, confirming that the interactions of Pb²⁺ ions with the outer surface of pores, besides their diffusion into pores, significantly affect the Pb²⁺ adsorption rate. Moreover, MCAg with the highest intraparticle diffusion rate constant (k_diff, 35.9692 mg g⁻¹ min^1/2) suggests the enhanced diffusion of Pb²⁺ particles into internal pores of such adsorbent, resulting in quicker adsorption.²⁰

3.2.4. Adsorption isotherm investigation. The investigation of adsorption isotherms plays a significant role in evaluating the adsorption performance, understanding the adsorption mechanism and determining the adsorbent's capacity by deriving the isothermal parameters using suitable isothermal models. The static adsorption of different Pb²⁺ concentrations (50–800 g L⁻¹) was investigated using a dose of 2.5 g L⁻¹, under agitation for 50 min at 20 °C and a pH of 6. The equilibrium adsorption isotherm points of Pb²⁺ were determined by fitting a spectrum of non-linear adsorption isotherm models, including Langmuir, Freundlich, Temkin and Dubinin-Radushkevich, as shown in Fig. 5a–d, respectively, and the related parameters of each model were computed as displayed in Table 4.

Fig. 5 Langmuir (a), Freundlich (b), Temkin (c), and Dubinin–Radushkevich (d) nonlinear plot for the adsorption of Pb²⁺ ions onto C, CAg, and MCAg (T = 20 °C, adsorbent dosage = 2.5 g L⁻¹, pH = 6, t = 50 min, C_i = 50–800 mg L⁻¹).

Table 4 Nonlinear adsorption isotherm models for the adsorption of Pb²⁺ on solid adsorbents (T = 20 °C, dosage 2.5 g L⁻¹, pH = 6, t = 50 min, C_i = 50–800 mg L⁻¹)

Models	Parameters	C	CAg	MCAg
Langmuir	qm (mg g^−1)	184.5	236.4	348.9
	b (L mg^−1)	0.0881	0.1606	0.1860
	KL	0.0409	0.0148	0.0080
	R^2	0.9760	0.9873	0.9462
	χ^2	0.2193	0.1734	2.5603
Freundlich	1/n	0.3385	0.2786	0.2938
	KF(L^1/n mg^1−1/n g^−1)	38.2563	69.6008	103.2916
	R^2	0.8534	0.9285	0.7894
	χ^2	1.3419	0.9757	7.3066
Temkin	bT (J mol^−1)	61.3284	54.3202	35.1652
	KT (L g^−1)	1.0271	2.1388	2.2000
	R^2	0.9568	0.9761	0.9436
	χ^2	0.3950	0.3257	2.0380
Dubinin–Radushkevich	qDR (mg g^−1)	158.2	209.5	304.4
	EDR (kJ mol^−1)	0.2382	0.5127	0.5466
	R^2	0.9599	0.9166	0.9287
	χ^2	0.3669	1.9580	2.5549

---

All isotherm models show a notable increase in adsorption capacity (q_e, mg g⁻¹) at lower equilibrium concentrations (C_e < 30 mg L⁻¹) of Pb²⁺, resulting from the availability of more accessible binding sites on the surfaces of the C, CAg, and MCAg adsorbents. As the Pb²⁺ concentration increases, q_e also increases due to the occupation of additional binding sites until the adsorbent surfaces become saturated. Consequently, the rate of increase of q_e becomes nearly constant, even at higher concentrations (C_e > 45 mg L⁻¹) of Pb²⁺, due to the progressive depletion of available binding sites for adsorption.³⁷

The Langmuir isotherm provided the best match for C and CAg, with high correlation coefficients (R² = 0.9760 and 0.9873, respectively) and low reduced chi-square (χ²) values (0.2193 and 0.1734, respectively). This shows that the adsorption of Pb⁺ ions on these two materials happens mostly as monolayer coverage on a homogeneous surface. The predicted maximum adsorption capacities (q_m, mg g⁻¹) demonstrate the effectiveness of these materials, increasing from 184.5 mg g⁻¹ (C) to 236.4 mg g⁻¹ (CAg). The CAg composite has a lesser surface area (134.6 m² g⁻¹) than C (466.3 m² g⁻¹), but the composite performs better due to greater affinity from alginate functional groups. The MCAg composite, constructed from melamine formaldehyde, onion peel biochar, and alginate, had the greatest Langmuir q_m value (348.9 mg g⁻¹). However, its R² value (0.9462) was somewhat lower than that for C and CAg. This finding can be explained by the extensive surface heterogeneity and different functional groups seen in MCAg, as indicated by ATR-FTIR studies. These functional groups improve Pb²⁺ binding efficiency through various interactions (e.g., electrostatic, coordination). However, the larger χ² value (2.5603) indicates a weaker Langmuir model fit, potentially due to departure from idealized monolayer behaviour.³⁸ MCAg demonstrates the highest adsorption rate and the most favorable affinity toward Pb²⁺ ions, as evidenced by its Langmuir constant (b = 0.1860 L mg⁻¹), indicating stronger interactions with the target metal ions.³⁹ The separation factor (K_L) values for Pb²⁺ adsorption onto C, CAg, and MCAg (0.0409, 0.0148, and 0.0080, respectively) all lie between 0 and 1, confirming that the adsorption process is favorable for all three adsorbents, with MCAg showing superior performance.⁴⁰ Additionally, the 1/n values obtained from the Freundlich model for C (0.3385), CAg (0.2786), and MCAg (0.2938) also fall within the range of 0 to 1, reinforcing the favorable nature of Pb²⁺ adsorption.⁴¹ These findings agree with the corresponding K_L values, further validating the efficiency of the prepared adsorbents.

Adsorption on heterogeneous surfaces is considered using the Freundlich model, which demonstrated a moderate correlation for CAg (R² = 0.9285) but a rather poor match for MCAg (R² = 0.7894) and C (R² = 0.8534). Furthermore, this model's higher χ² values, especially for MCAg (7.3066), suggest that it falls short in describing the adsorption process for these substances. However, the Freundlich constant (K_F) gradually increased from C (38.26) to MCAg (103.29), indicating that greater material complexity is associated with a higher adsorption capacity and surface affinity.

The Temkin model further confirmed that all materials exhibited favorable adsorption behaviour, with decreasing b_T values (heat of adsorption) from C (61.33 J mol⁻¹) to MCAg (35.17 J mol⁻¹) and R² values ranging from 0.9436 to 0.9761. Because of either a wider spread of binding sites on the modified surface or the saturation of high-energy sites, the lower b_T for MCAg suggests that Pb²⁺ adsorption entails less strong interactions.

The Dubinin–Radushkevich (D–R) model offered new information on the adsorption process. The calculated average adsorption energy (E_DR) values for all materials were less than 1 kJ mol⁻¹, indicating that physisorption is the primary process. MCAg had the greatest E_DR value (0.5466 kJ mol⁻¹) and q_DR (304.4 mg g⁻¹), showing improved adsorption performance driven by both surface textural aspects and the presence of active functional groups.³⁸ Despite having a modest surface area (309.4 m² g⁻¹), MCAg outperformed C and CAg in terms of Pb²⁺ removal capability. The plentiful and diverse surface functional groups on MCAg, as revealed by ATR-FTIR analysis, played an important role in improving its adsorption behaviour.

Overall, the isothermal results show that surface chemistry and functionalization, especially in MCAg, are important factors that determine adsorption capacity, even if surface area is a major factor. The difference in model fitting further shows that because of its structural complexity, Pb²⁺ adsorption onto MCAg could not precisely adhere to ideal monolayer or homogeneous site assumptions.

The adsorption of Pb²⁺ onto the created MCAg composite as a solid adsorbent sample is regulated by a succession of physicochemical interactions arising from its heterogeneous surface chemistry. The melamine-formaldehyde resin, alginate matrix, and biochar have oxygen- and nitrogen-bearing functional groups (e.g., –OH, –COOH, –NH, and C=O) that promote significant electrostatic attraction and surface complexation with Pb²⁺ ions. Additionally, Pb²⁺ in solution undergoes ion-exchange reactions with exchangeable cations on alginate and charcoal surfaces. MCAg's porous structure improves Pb⁺ absorption by facilitating adsorption and intraparticle diffusion. Electrostatic attraction, ion exchange, and inner-sphere complexation work together contributing to MCAg's high affinity for Pb²⁺.

3.2.5. Adsorption of Pb²⁺ ions from the simulated wastewater system. The effect of coexisting ions and the real wastewater matrix on the adsorption efficiency of Pb²⁺ ions onto the prepared solid adsorbents was investigated, and the nonlinear Langmuir fitting results are presented in Fig. 6a. Data from pure Pb²⁺ solutions and actual wastewater samples with a combination of inorganic and organic co-contaminants were directly compared in order to assess the adsorption performance of the produced adsorbents C, CAg, and MCAg using the Langmuir model. When compared to clean systems, the adsorption capacity (q_m, mg g⁻¹) and affinity constant (b, L mg⁻¹) were consistently lower in the real wastewater samples, demonstrating the detrimental impact of competing ions and interfering contaminants on Pb²⁺ absorption. The maximum adsorption capabilities (q_m, mg g⁻¹) were clearly reduced when complex wastewater elements were present: MCAg showed a reduction from 348.9 to 244.2 mg g⁻¹, CAg from 236.4 to 158.7 mg g⁻¹, and C from 184.5 to 109.7 mg g⁻¹. This decrease suggests that coexisting ions and organic materials are interfering with Pb²⁺ absorption through competing adsorption and site blockage effects. The Langmuir constant (b, L mg⁻¹), which represents the affinity between Pb²⁺ and the adsorbents, reduced significantly across all samples in actual wastewater (e.g., for MCAg, b dropped from 0.1860 L mg⁻¹ to 0.0553 L mg⁻¹). The higher correlation values (R² > 0.9730) for all solid adsorbents confirm that the Langmuir model well describes equilibrium adsorption behaviour, even in complicated polluted samples. These findings demonstrate the model's stability under real-world wastewater circumstances, despite the lower adsorption capability induced by competing ions and organic contaminants.

Fig. 6 Nonlinear Langmuir plot for the adsorption of Pb²⁺ ions onto all solid samples from the real sample solution (a) (T = 20 °C, adsorbent dosage = 2.5 g L⁻¹, pH = 6, t = 50 min, C_i = 50–800 mg L⁻¹). Van’t Hoff plot (b) (adsorbent dosage = 2.5 g L⁻¹, pH = 6, t = 50 min, C_i = 800 mg L⁻¹, T = 20–45 °C). Desorption studies (c) and reusability of the solid adsorbent (d) for the adsorption of Pb²⁺ ions (T = 20 °C, adsorbent dosage = 2.5 g L⁻¹, pH = 6, t = 50 min, C_i = 800 mg L⁻¹).

3.2.6. Adsorption thermodynamic parameters. The thermodynamic analysis is essential to understand the adsorption behaviour and the energy variations. The thermodynamic parameters, including the enthalpy change (ΔH°), entropy (ΔS°), and Gibbs free energy (ΔG°), were provided by the Van’t Hoff model as illustrated in Fig. 6b and Table 5. The provided values of correlation coefficient (R²) of C, CAg, and MCAg (0.9843, 0.9725, and 0.9647, respectively) are high and close to 1, confirming the excellent fit of the Pb²⁺ adsorption data with this model. The negative ΔG° values of all prepared adsorbents confirm the spontaneous nature of Pb²⁺ to bind to the surface of the adsorbent without the need for external energy.⁴² The provided ΔH° values of C, CAg, and MCAg (12.73, 10.11, and 7.58 kJ mol⁻¹) are positive and less than 40 kJ mol⁻¹, indicating the endothermic and physisorption process.²⁶ MCAg has the lowest value of enthalpy, which could be due to the specific interactions of its surface functional groups with Pb²⁺ ions. The ΔS° values of all adsorbents are positive, indicating the increased randomness of Pb²⁺ ions at the solid–liquid interface and an enhanced adsorption process. This disorder, particularly near the adsorbent/adsorbate interface, may result from the release of water molecules surrounding the Pb²⁺ ions prior to their binding to the adsorbent surface.

Table 5 Thermodynamic parameters for Pb²⁺ adsorption on all solid samples at different temperatures (C_i = 800 mg L⁻¹, t = 50 min, dosage 2.5 g L⁻¹, pH = 6, T = 20–45 °C)

Samples	R^2	ΔH° (kJ mol^−1)	ΔS° (kJ mol^−1 K^−1)	−ΔG° at 25 °C (kJ mol^−1)
C	0.9843	12.73	80.49	11.25
CA	0.9725	10.11	75.60	12.42
MCAg	0.9647	7.58	71.13	13.61

---

3.2.7. Desorption and reusability studies. To enhance the productivity of adsorbents and evaluate their sustainability and cost-effectiveness, several desorption tests of Pb²⁺ ions in various eluents were conducted as presented in Fig. 6c. All eluents effectively desorbed Pb²⁺ ions with a high desorption percentage (Des.%), following the tendency of EDTA > HCL > HNO₃ > cysteine. The highest Des.% (100, 98, and 100 for C, CAg, and MCAg, respectively) is identified by EDTA, followed by HCl (92, 95, and 96, respectively). The mechanism of the desorption reaction proceeds through protonation of the adsorbent surface, causing Pb²⁺ ions to be removed from the surface. Acidic eluents are rich in H⁺ ions, allowing them to compete with Pb²⁺ ions to bind with the active site on the adsorbent surface, resulting in repulsion with Pb²⁺ ions and then forcing them to elute into the solution.⁴³ The most efficient desorbing agent for Pb²⁺ ions was found to be EDTA because of its capacity to combine with Pb²⁺ to form extremely stable and water-soluble complexes.⁴⁴ With a stability constant (log K_st) of around 18.0, the Pb²⁺–EDTA complex exhibits a strong chelation interaction that greatly increases the desorption efficiency from the adsorbent surface.⁴⁵ To prevent secondary contamination from the Pb-EDTA complex, post-treatment alternatives include chemical precipitation (Ca²⁺/Fe³⁺), advanced oxidation to break down EDTA, and membrane/ion-exchange separation for safe handling of the desorption effluent.

As shown in Fig. 6d, ten successive adsorption/desorption cycles were carried out to assess the produced adsorbents' durability and reusability. Following the tenth cycle, a little decrease in adsorption capacity was noted (19, 14, and 16 mg g⁻¹ for C, CAg, and MCAg, respectively); this was probably brought on by the slow loss or obstruction of active sites throughout the washing and filtration procedures.⁴⁶ All adsorbents, however, maintained a high level of performance, exhibiting outstanding regeneration capability and validating their appropriateness, effectiveness, and stability for recurring Pb²⁺ adsorption applications.

The MCAg sample retrieved after ten adsorption–desorption cycles was analyzed by SEM and ATR-FTIR to evaluate its structural stability (Fig. S2). SEM images showed no noticeable change in surface morphology, with only slight particle aggregation. The ATR-FTIR spectra displayed the same characteristic functional groups, with a minor decrease in peak transmittance, likely linked with the repeated adsorption–desorption cycles. These results prove that MCAg maintains its structural reliability and demonstrates exceptional reusability.

3.3. Column adsorption of Pb²⁺ ions

3.3.1. Bed height effect. Bed height within the column is a vital factor that determines the effectiveness of the adsorption process. The effect was examined using three different bed heights of the MCAg adsorbent: 2, 3, and 4 cm, while keeping a fixed intake Pb²⁺ ion concentration of 80 mg L⁻¹, a flow rate of 15 mL min⁻¹, a temperature of 20 °C, and a pH of 6, as depicted in Fig. 7a. Table 6 summarizes the associated parameters.

Fig. 7 Column adsorption of Pb²⁺ ions onto MCAg (a), Yoon-Nelson (b), and Thomas (c) nonlinear models for Pb²⁺ ion adsorption at different bed heights (C_i = 80 mg L⁻¹, µ = 15 mL min⁻¹, pH = 6, T = 20 °C, BH = 2, 3, and 4 cm).

Table 6 Parameters obtained from column adsorption experiments, including the nonlinear Thomas and Yoon-Nelson model fittings, for the removal of Pb²⁺ using MCAg (C_i = 80 mg L⁻¹, µ = 15 mL min⁻¹, pH = 6, T = 20 °C, BH = 2, 3, and 4 cm)

Parameters	BH (cm)
	2.0	3.0	4.0
te (min)	174	187	208
tb (min)	90	115	133
qo (mg g^−1)	360.5	285.9	232.7
Yoon-Nelson model
τexp (min)	147	165	178
τcal (min)	146	163	176
KYN (min^−1)	0.0864	0.0854	0.0842
R^2	0.9881	0.9902	0.9962
χ^2	0.0018	0.0013	0.0004
Thomas model
qTh (mg g^−1)	18.9	14.0	11.4
KTh (L mg^−1 min^−1) × 10^−3	1.0542	1.0412	1.0370
R^2	0.9881	0.9901	0.9962
χ^2	0.0018	0.0013	0.0004

---

The breakthrough times (t_b, min) were found to be 90, 115, and 133 min for the bed heights of 2.0, 3.0, and 4.0 cm, respectively, while the exhaust times (t_e, min) were 174, 187, and 208, respectively. It is noticed that t_b and t_e increased proportionally by 1.27 and 1.15, and by 1.07 and 1.11 with the increasing bed height of the column from 2.0 to 3.0, then to 4.0 cm, confirming the higher availability of active sites on the longer path of the adsorbent.⁴⁷ In addition, the values of column adsorption capacity of MCAg (q_o, mg g⁻¹) were enhanced by 1.54, as the height of the bed column decreased from 4 to 2 cm because of the limitation of adsorption sites caused by solid packing.⁴⁸

The empty bed residence time (EBRT) for the column adsorption equals (πr²/µ)BH, where r represents the inner column radius (cm), while the bed mass transfer zone (MTZ) equals BH(1−t_b/t_e). The EBRT values for the applied 2, 3, and 4 cm bed heights were computed as 0.236, 0.353, and 0.471 min, respectively, signifying that increasing the bed height spreads the contact time between Pb²⁺ and the MCAg active adsorption sites. This enhanced residence time endorses better diffusion and more efficient application of the adsorbent, consistent with fixed-bed adsorption principles where higher beds support enhanced metal uptake before breakthrough. Similarly, the MTZ values increased from 0.966 to 1.155 and 1.442 cm as the bed height increased, reflecting the development of a broader mass transfer region due to the accessibility of more active sites for adsorption. Despite the larger MTZ at higher beds, the decreasing MTZ-to-bed-height ratio indicates more effective bed utilization, amended adsorption kinetics, and enhanced interaction between Pb²⁺ and the MCAg surface in deeper beds. Collectively, these results prove that the 4 cm bed provides the most favorable working conditions for Pb²⁺ column removal under the applied flow rate.

3.3.2. Dynamic modelling of Pb²⁺ column adsorption onto MCAg. To assess the dynamic adsorption activity of Pb²⁺ on MCAg fixed inside the column, two nonlinear mathematical models, the Yoon–Nelson and Thomas models, were applied as shown in Fig. 7b and c, with related parameters of each model as stated in Table 6. The well-fitted Yoon–Nelson model for the Pb²⁺ adsorption data onto 2.0, 3.0, and 4.0 cm height of the MCAg adsorbent was supported by the elevated values of correlation coefficient (R²), varying from 0.9881 to 0.9962, as well as the accepted lower reduced chi-square values (χ² < 0.0018). In addition, the values of experimental time (τ_exp) are in good agreement with the estimated time (τ_cal) with a slight variance of 1.02% as average values. The values of τ_cal went up with the increase in the bed height of MCAg inside the column due to the greater mass of the MCAg adsorbent, more available active binding sites, and extended contact time between Pb²⁺ and the MCAg adsorbent. In contrast, the Yoon-Nelson rate constant (K_YN) declined from 0.0864 min⁻¹ to 0.0842 min⁻¹ with increasing bed height from 2.0 cm to 4.0 cm due to the slower breakthrough rate, resulting from a larger amount of MCAg particles and longer contact time between Pb²⁺ ions and the adsorbent.⁴⁹ The satisfactory representation of the breakthrough curve by the Thomas model is supported by its R² value exceeding 0.9962, with adequately lowered χ² values for all different heights of the column. The values of q_Th declined from 18.9 to 11.4 as expected when the bed height increased from 2.0 cm to 4.0 cm, as well as the Thomas rate constant (K_Th, L mg⁻¹ min⁻¹ × 10⁻³) slightly decreased from 1.0542 to 1.0370. The considerable decrease in q_TH (mg g⁻¹) anticipated by the Thomas model compared to the experimental q_o (mg g⁻¹) achieved from the column investigation can be attributed to the Thomas model's underlying assumptions and constraints. The Thomas model considers optimal plug flow conditions, zero axial dispersion, and no interactions such as external film resistance or intra-particle diffusion limits, which are seldom encountered in actual fixed-bed systems. This can lead to an underestimation of the true adsorption capacity, particularly in cases when non-equilibrium effects and mass transfer resistances are substantial. The Thomas model's accuracy is further constrained by its reliance on breakthrough curve data, which mostly depict the early phases of the adsorption process rather than the bed's full saturation capacity. On the other hand, the experimental data's q_o (mg g⁻¹) captures the complete amount of adsorption, including the slower diffusion-controlled uptake close to saturation, and accounts for the whole adsorption process until exhaustion.⁵⁰ As a result, the Thomas model's idealized circumstances underestimate the maximal adsorption capacity, resulting in a significantly lower q_TH (mg g⁻¹) value than the empirically obtained q_o (mg g⁻¹).

3.4. Comparison of MCAg capability with other materials

Table 7 shows the greatest adsorption capacity for batch and column adsorption when using the synthesized MCAg composite compared to other solid adsorbents.^51–56 Overall, MCAg appears to be a viable adsorbent for treating lead ion-contaminated wastewater.

Table 7 Comparative analysis of the maximum adsorption performance of MCAg and various other adsorbents

Adsorbents	Conditions	Adsorption capacity (mg g^−1)	Ref.
Batch adsorption
Polyaniline alginate nanofibers	pH = 5, t = 10 min, T = 25 °C	202.00	51
Araucaria gum/calcium alginate composite beads	pH = 5, t = 10 min, T = 25 °C	149.95	52
Cellulose nanoparticles/chitosan composite	pH = 6.5, t = 120 min, T = 25 °C	221.10	53
GO/Ch/FeOOH	pH = 5.5, t = 70 min, T = 40 °C	111.11	54
MCAg	pH = 6, t = 50 min, T = 20 °C	348.9	This study
Column adsorption
MgAl@AC	Ci = 36 mg L^−1, µ = 30 mL min^−1, pH = 5	37.5	55
Palm shell activated carbon	Ci = 50 mg L^−1, µ = 33.33 mL min^−1, pH = 5	92.6	56
CR11	Ci = 225 mg L^−1, µ = 10 mL min^−1, pH = 6.5	161.1	52
MCAg	Ci = 80 mg L^−1, µ = 15 mL min^−1, pH = 6	285.9	This study

---

4. Conclusion

Adsorption, as an efficient procedure for pollutant removal, requires a tailored solid adsorbent with specific characteristics such as sustainability, eco-friendliness, low cost, high adsorption capacity, and easy modifiability. Herein, a melamine formaldehyde-reinforced onion peel biochar/alginate composite (MCAg) was fabricated for the removal of Pb²⁺ ions from aqueous media. The fabricated solid adsorbent exhibited a considerable surface area (309.4 m² g⁻¹) and a neutral pH_PZC, and was rich in active chemical functional groups. Batch adsorption of Pb²⁺ ions reached 348.9 mg g⁻¹ at pH 6 after 50 min, while column adsorption reached 232.7 mg g⁻¹ at a bed height of 4 cm, an initial pollutant concentration of 80 mg L⁻¹, and a solution flow rate of 15 mL min⁻¹. The combination of biochar, melamine formaldehyde, and alginate produced a mechanically and thermally stable material with a higher surface area and mesoporosity, along with various channels that facilitate pollutant ion penetration and adsorption. Additionally, the diverse surface chemical functional groups originating from the material combination can readily attract pollutant ions. It is recommended that the developed material can serve as a solid adsorbent for various organic and inorganic pollutants. Furthermore, after modification with semiconductor catalysts, it could be employed for the degradation of organic pollutants. In conclusion, the authors state that the fabricated MCAg material is a promising candidate for environmental applications.

Author contributions

Sarah A. Felemban and Alaa O. Baryyan: conceptualization and methodology, Alaa O. Baryyan: formal analysis and investigation, Sarah A. Felemban and Alaa O. Baryyan: writing – original draft preparation, data handling, and analysis of data. Sarah A. Felemban: investigation and revision of the final article.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this work.

Data availability

The data supporting this article are provided in the supplementary information (SI) and are also presented in the tables and figures of the main manuscript. Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma01050k.

References

1. F. C. P. Tonelli and F. M. P. Tonelli, in Bioremediation and Biotechnology, Persistent and Recalcitrant Toxic Substances, ed. R. A. Bhat, K. R. Hakeem and N. B. Saud Al-Saud, Springer International Publishing, Cham, 2020, vol. 3, pp. 15–23.
2. T. A. Al-Sabbagh and S. Shreaz, Int. J. Environ. Res. Public Health, 2025, 22, 1–30.
3. World Health Organization, WHO Housing and health guidelines, 2018.
4. C. Filote, M. Roşca, R. M. Hlihor, P. Cozma, I. M. Simion, M. Apostol and M. Gavrilescu, Processes, 2021, 9, 1–38.
5. N. A. A. Qasem, R. H. Mohammed and D. U. Lawal, npj Clean Water, 2021, 4, 36.
6. C. Saka, Ö. Şahin and M. M. Küçük, Int. J. Environ. Sci. Technol., 2012, 9, 379–394.
7. A.-A. Ciobanu, I. Michalak and L. Bulgariu, in Bio-organic Amendments for Heavy Metal Remediation, ed. A. Husen, M. Iqbal, A. Ditta, S. Mehmood, M. Imtiaz and M. S. Tu, Elsevier, 2024, pp. 69–84.
8. P. Granados, S. Mireles, E. Pereira, C. L. Cheng and J. J. Kang, Appl. Sci., 2022, 12, 5040.
9. M. Prelac, I. Palčić, D. Cvitan, D. Anđelini, M. Repajić, J. Ćurko, T. K. Kovačević, S. Goreta Ban, Z. Užila, D. Ban and N. Major, Antioxidants, 2023, 12, 1697.
10. J. Kurowiak, A. Kaczmarek-Pawelska, A. G. Mackiewicz and R. Bedzinski, Processes, 2020, 8, 304.
11. B. Wang, Y. Wan, Y. Zheng, X. Lee, T. Liu, Z. Yu, J. Huang, Y. S. Ok, J. Chen and B. Gao, Crit. Rev. Environ. Sci. Technol., 2019, 49, 318–356.
12. A. Wierzbicka, M. Bartniak, J. Waśko, B. Kolesińska, J. Grabarczyk and D. Bociaga, Gels, 2024, 10, 491.
13. A. F. Hassan and M. A. Khoj, Environ. Sci. Pollut. Res., 2024, 31, 35233–35248.
14. M. X. Tan, Y. N. Sum, J. Y. Ying and Y. Zhang, Energy Environ. Sci., 2013, 6, 3254–3259.
15. C. Gao, X.-L. Wang, Q.-D. An, Z.-Y. Xiao and S.-R. Zhai, Carbohydr. Polym., 2021, 256, 117564.
16. X. Wu, Y. Song, P. Yin, Q. Xu, Z. Yang, Y. Xu, X. Liu, Y. Wang, W. Sun and H. Cai, Appl. Clay Sci., 2022, 228, 106647.
17. Y. He, X. Jia, S. Zhou, J. Chen, S. Zhang, X. Li, Y. Huang, T. Wågberg and G. Hu, Sep. Purif. Technol., 2022, 303, 122212.
18. X. Zhang, Z. Li, T. Zhang, J. Chen, W. Ji and Y. Wei, Environ. Sci. Pollut. Res., 2023, 30, 18364–18379.
19. L. Gao, Z. Li, W. Yi, L. Wang, N. Song, W. Zhang, G. Li, S. Wang, N. Li and A. Zhang, J. Environ. Chem. Eng., 2023, 11, 109074.
20. N. A. Alamrani, Int. J. Biol. Macromol., 2025, 318, 145023.
21. J. C. P. Broekhoff, in Preparation of Catalysts II, ed. B. Delmon, P. Grange, P. Jacobs and G. Poncelet, Elsevier, 1979, vol. 3, pp. 663–684.
22. J. Wang, H. Zhang, N. Wang, H. Mo, Z. Yang, Y. Dong, Q. Liu, X. Huang and B. Han, Polymers, 2025, 17, 826.
23. J. Zuo, W. Li, Z. Xia, T. Zhao, C. Tan, Y. Wang and J. Li, Coatings, 2023, 13, 1884.
24. A. F. Hassan, G. A. El-Naggar, G. Esmail and W. A. Shaltout, Appl. Surf. Sci. Adv., 2023, 13, 100388.
25. Y. Chun, K. R. Kim, H. R. Kim, S. K. Lee, J. H. Lee, J. H. Lee, C. Park, H. Y. Yoo and S. W. Kim, J. Polym. Environ., 2022, 30, 2037–2049.
26. M. M. M. Madkhali, R. Ghubayra, A.-N. M. A. Alaghaz, A. F. Hassan and A. G. Braish, Int. J. Biol. Macromol., 2024, 281, 136451.
27. M. Rashid, M. M. Islam, H. Minami, M. Aftabuzzaman, M. A. Rahman, M. M. Hossain, S. M. Hoque, M. A. Alam and H. Ahmad, Mater. Chem. Phys., 2020, 249, 122957.
28. M. Khajavian, S. Ismail and M. Afshari, Sep. Purif. Technol., 2025, 373, 133611.
29. M. A. Khoj, RSC Adv., 2024, 14, 24322–24334.
30. A. S. Eltaweil, H. A. Mohamed, E. M. Abd El-Monaem and G. M. El-Subruiti, J. Mol. Liq., 2024, 408, 125275.
31. V. Dhanya and N. Rajesh, Groundw. Sustain. Dev., 2024, 26, 101209.
32. C. Zhang, J. Sui, J. Li, Y. Tang and W. Cai, Chem. Eng. J., 2012, 210, 45–52.
33. J. Li, G. Lin, F. Tan, L. Fu, B. Zeng, S. Wang, T. Hu and L. Zhang, J. Colloid Interface Sci., 2023, 651, 659–668.
34. R. Ghubayra, I. Mousa, M. M. M. Madkhali, A. N. M. A. Alaghaz and A. F. Hassan, RSC Adv., 2024, 14, 37859–37870.
35. R. E. K. Billah, M. A. Islam, M. A. Khan, M. K. Nazal, L. Bahsis, M. Achak, A. E. D. Mahmoud, M. A. Aziz and B.-H. Jeon, Mater. Chem. Phys., 2025, 332, 130249.
36. D. Xiang, R. Zhu, Y. Chen, M. Zhu, S. Wang, Y. Wu, J. Luo and L. Fu, Chem. Eng. J., 2024, 492, 152292.
37. B. Moghtaderi-Esfahani, K. Ghanemi and Y. Nikpour, Desalin. Water Treat., 2025, 321, 100921.
38. W. A. Shaltout, A. F. Hassan, M. S. Elsayed and H. Hafez, Mater. Adv., 2025, 6, 4418–4437.
39. C. H. C. Tan, S. Sabar and M. H. Hussin, S. Afr. J. Chem. Eng., 2018, 26, 11–24.
40. R. Vinayagam, S. Ganga, G. Murugesan, G. Rangasamy, R. Bhole, L. C. Goveas, T. Varadavenkatesan, N. Dave, A. Samanth, V. Radhika Devi and R. Selvaraj, Chemosphere, 2023, 310, 136883.
41. S. Mustafa, H. N. Bhatti, M. Maqbool, A. Khan, A. M. Alraih and M. Iqbal, Sustainable Chem. Pharm., 2024, 39, 101577.
42. J. N. Naat, S. Suyanta and N. Nuryono, Mater. Adv., 2025, 6, 3220–3236.
43. R. S. El Shenawy, E. A. El Fadaly and A. F. Hassan, Environ. Sci. Pollut. Res., 2025, 32, 13982–14001.
44. M. B. Đolić, V. N. Rajaković-Ognjanović, J. P. Marković, L. J. Janković-Mandić, M. N. Mitrić, A. E. Onjia and L. V. Rajaković, Appl. Surf. Sci., 2015, 324, 221–231.
45. T. P. Nguyen, V. D. Nguyen, M. T. Trinh, P. L. Han, T. H. Nguyen, M. T. Nguyen and A.-T. Vu, J. Hazard. Mater. Adv., 2025, 19, 100770.
46. A. F. Hassan, A. Elhassanein, W. A. Shaltout and G. H. G. Ahmed, Int. J. Biol. Macromol., 2025, 294, 139465.
47. I. S. Aldabagh and K. K. Hummadi, Environ. Adv., 2025, 19, 100606.
48. A. Samanth, R. Vinayagam, T. Varadavenkatesan and R. Selvaraj, Environ. Res., 2024, 261, 119696.
49. A. H. Jawhari, H. Y. Otaif, N. Amri and Y. E. Mukhrish, Int. J. Biol. Macromol., 2025, 318, 145075.
50. W. A. Shaltout, H. Hafez, M. S. Elsayed and A. F. Hassan, RSC Adv., 2025, 15, 16901–16920.
51. N. Jiang, Y. Xu, Y. Dai, W. Luo and L. Dai, J. Hazard. Mater., 2012, 215–216, 17–24.
52. M. A. Khoj, A. F. Hassan, N. S. Awwad, H. A. Ibrahium and W. A. Shaltout, Int. J. Biol. Macromol., 2024, 255, 128234.
53. E. A. Matter, A. F. Hassan, N. M. Elfaramawy and G. Esmail, Biomass Convers. Biorefinery, 2025, 15, 10961–10976.
54. S. Sheshmani, M. Akhundi Nematzadeh, S. Shokrollahzadeh and A. Ashori, Int. J. Biol. Macromol., 2015, 80, 475–480.
55. A. K. A. Khalil, I. W. Almanassra, A. Chatla, I. Ihsanullah, T. Laoui and M. Ali Atieh, Chem. Eng. Sci., 2023, 281, 119192.
56. G. Issabayeva, M. K. Aroua and N. M. Sulaiman, J. Hazard. Mater., 2008, 155, 109–113.

---