 Open Access Article
Open Access ArticleRaman spectroscopy of electrochemically exfoliated graphene: defect evolution, doping effects, and interpretive frameworks
M. J.
Madito

Institute for Nanotechnology and Water Sustainability (iNanoWS), College of Science, Engineering and Technology, University of South Africa, Johannesburg 1710, South Africa. E-mail: maditmj@unisa.ac.za
First published on 19th January 2026
Abstract
Electrochemical exfoliation offers a scalable method for graphene production, but it introduces a complex interplay of structural defects, chemical functionalization, and electronic doping. These factors result in Raman signatures that differ significantly from those observed in mechanically exfoliated graphene and high-quality chemical vapor deposition (CVD) graphene. Consequently, conventional Raman metrics require careful and context-specific reinterpretation. Raman spectroscopy remains essential for graphene characterization due to its high sensitivity to disorder and charge-transfer effects. This review provides a critical assessment of the Raman characteristics of electrochemically exfoliated graphene (EEG), integrating established defect models with a systematic analysis of Raman datasets from the literature. Detailed examination of key spectral parameters, including the I(D)/I(G) and I(D′)/I(G) intensity ratios, G-band position and full width at half maximum, and 2D-band position, reveals the coexistence of basal-plane defects, edge-related contributions, and dopant-induced effects in EEG. These findings indicate that Raman responses in EEG deviate from pristine graphene benchmarks and challenge the direct application of standard interpretative frameworks. The influence of electrolyte chemistry and applied potential on defect landscapes and doping levels is further evaluated through direct comparison with mechanically exfoliated and CVD graphene. Finally, emerging approaches such as in situ Raman spectroscopy, multivariate analysis, and machine-learning-assisted interpretation are identified as promising strategies for achieving more reliable structure–property correlations in EEG.
Introduction
Electrochemical exfoliation is a promising method for large-scale graphene production. In contrast to chemical vapor deposition and mechanical exfoliation, the electrochemical approach provides a simple, scalable, and cost-effective means of converting bulk graphite into few-layer graphene.1,2 This method is attractive due to its high yield and adaptability to various electrolytes and reaction conditions. However, these benefits are accompanied by significant challenges. Electrochemical processes introduce structural defects, functional groups, and electronic doping, resulting in a highly heterogeneous material known as electrochemically exfoliated graphene (EEG).1,3,4The quality of the EEG varies widely depending on the electrolyte used, the applied potential, and the graphite source.5–7 As a result, robust characterization is essential not only for understanding the fundamental processes involved but also for tailoring the material to meet the needs of applications in energy storage, catalysis, sensing, and electronics. Among the available techniques, Raman spectroscopy has been established as the most powerful and versatile tool for rapid, non-destructive assessment of graphene produced through a wide variety of synthesis routes. These include micromechanical cleavage of graphite, chemical vapor deposition (CVD) on catalytic substrates, plasma-enhanced CVD (PECVD) on non-catalytic dielectric or semiconducting substrates, and chemical or electrochemical exfoliation of graphite.8–13 Its ability to probe crystallinity, layer number, defect density, doping, and strain makes it particularly valuable for the study of EEG, where conventional metrics must often be adapted to account for chemical complexity.14–18 This review provides a critical examination of the Raman characteristics of EEG. It synthesizes current knowledge regarding Raman defect models, doping-induced modifications in graphene, and the effects of electrochemical synthesis conditions on Raman signatures. In addition to evaluating established interpretative approaches, the review analyses a dataset of Raman measurements, including the intensity ratio of the D band to the G band (I(D)/I(G)), G-band position, G-band full width at half maximum (FWHM), 2D-band position, and the intensity ratio of the D′ band to the G band (I(D′)/I(G)), all extracted from previously published EEG Raman spectra recorded with a 532 nm excitation source, as detailed in the SI. Spectra were selected for the dataset based on criteria emphasizing data quality and completeness, ensuring a representative sample of the literature.
To establish consistent structure–property relationships, statistical correlation analysis was employed to identify and validate trends across the compiled dataset of Raman measurements from prior EEG studies. This comprehensive dataset enables the identification of subtle trends and patterns that have not been thoroughly explored in earlier research. The review's unique contribution lies in the identification of previously overlooked relationships and the demonstration of how specific electrochemical synthesis conditions affect Raman signatures, thereby advancing the understanding of EEG's structural and electronic complexities.
To further elucidate the EEG's distinctive characteristics, this analysis contrasts these trends with benchmark values from mechanically exfoliated graphene (obtained through micromechanical cleavage of graphite) and high-quality graphene grown by CVD.8–10 This comparison highlights EEG's unique position within the broader graphene landscape, emphasizing how electrochemical synthesis introduces specific structural and electronic signatures that differ significantly from those observed in alternative synthesis methods. For clarity and completeness, the SI provides schematic illustrations of the fundamental Raman scattering mechanisms in graphene, along with representative Raman spectra and corresponding Lorentzian peak fits for electrochemically exfoliated graphene (Fig. S1–S3).
Electrochemical synthesis of EEG: process parameters and Raman signatures
The Raman spectrum of EEG is strongly influenced by the conditions under which exfoliation occurs, as shown in Table S1. The electrolyte composition, applied potential, and the nature of the graphite source collectively determine the balance between intercalation, oxidation, and structural disruption, thereby shaping the defect landscape that Raman spectroscopy detects. Understanding these relationships is essential for interpreting spectra not merely as fingerprints of quality, but as mechanistic readouts of the underlying electrochemical processes.Electrochemical cell configuration and reaction mechanism
Electrochemically exfoliated graphene is typically synthesised using a parallel two-electrode electrochemical cell consisting of a metal cathode and a graphite-based anode, such as graphite foil, flakes, rods, powders, or highly oriented pyrolytic graphite (HOPG), immersed in a liquid electrolyte. In some configurations, graphite serves as both the anode and cathode.19 Upon application of a suitable potential, a sequence of electrochemical reactions is initiated, driving the exfoliation process. Initially, water reduction at the cathode generates reactive hydroxyl radicals (˙OH), which nucleophilically attack the edge sites and grain boundaries of graphite.5,20 This is followed by anodic oxidation reactions that expand and disrupt the graphite structure, enabling layer separation. Concurrently, intercalation of anions, particularly sulphate ions from electrolytes such as ammonium sulphate ((NH4)2SO4), facilitates gas evolution (e.g., SO2, CO, O2), further assisting exfoliation by increasing interlayer pressure (Fig. 1(a)). The primary electrochemical reactions involved include:| H2O → HO˙ + H+ + e− → O˙ + 2H+ + 2e− | (i) |
| SO42− + 2e− + 4H+ → SO2 + H2O | (ii) |
| 2H2O → O2 + 4H+ + 4e− | (iii) |
| 2H2O + 2e− → H2 + 2OH− | (iv) |
| Cx + 2H2O → Cx−1 + CO2 + 4H+ + 4e−. | (v) |
 | ||
| Fig. 1 Schematic illustrations of graphite electrochemical exfoliation mechanisms: (a) standard electrochemical exfoliation. Reproduced with permission from ref. 20, Copyright 2014, American Chemical Society. (b) Radical-assisted electrochemical exfoliation reproduced with permission from ref. 7, Copyright 201, American Chemical Society. | ||
The gases evolved during these reactions generate sufficient internal pressure to overcome van der Waals forces holding the graphene layers together, effectively driving exfoliation. Sulphate anions are particularly effective due to their moderate reduction potential (+0.20 V) and ability to produce SO2 gas, which enhances the exfoliation efficiency.20
The electrolyte composition plays a crucial role in defect generation. Sulphate- and nitrate-based electrolytes, for example, promote intercalation.
The effect is especially pronounced under neutral pH conditions.5,20,21 The resulting Raman spectra exhibit high-intensity D bands and broadened G band responses (Fig. 1(a)). Representative Raman spectrum of EEG, illustrating the characteristic bands discussed here, is provided in the SI (Fig. S3). To mitigate overoxidation, various additives have been introduced into the electrolyte.7 Examples include melamine, sodium borohydride, ascorbic acid, and 2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO). These additives serve as radical scavengers or reducing agents. In this mechanism (Fig. 1(b)), TEMPO radicals scavenge hydroxyl radicals to form a metastable TEMPO–OH intermediate, which subsequently converts into oxoammonium cations. These cations are electrochemically reduced at the cathode, regenerating TEMPO radicals and sustaining a redox cycle throughout the exfoliation process, suppressing structural damage. As a result, the EEG produced under these conditions typically consists of more than 80% few-layer flakes (1–3 layers) with low defect densities (high C/O ratio >20). Raman spectroscopy confirms this improved structural order through lower D-band intensity and a decreased G-band FWHM (Fig. 1(b)). These observations demonstrate that Raman features reflect the relative contributions of intercalation-driven exfoliation and oxidation-induced disorder during the electrochemical exfoliation process.
Electrochemical cell potential, exfoliation duration, and graphite anode type
The applied cell potential, direct current (DC) or alternating current (AC), determines whether anion intercalation results in exfoliation or whether oxidation processes generate defects. The selection of a specific potential dictates whether efficient layer separation or increased structural disorder predominates in the EEG. At lower potentials (e.g., 2–6 V), oxidation is the dominant process, as evidenced by a progressive increase in the I(D)/I(G) ratio, which is consistent with edge-site activation (Fig. 2(a)).22 This potential range often leads to increased structural disorder, which can be beneficial for applications requiring high edge reactivity, such as sensors and catalysts. At higher potentials (e.g., 8–10 V), the I(D)/I(G) ratio decreases while the 2D-band intensity increases.22 This trend suggests that higher exfoliation potentials facilitate more efficient layer separation and a reduction in the number of graphene layers, making this condition ideal for applications in electronic devices that require higher conductivity and fewer defects. Excessive potentials (>20 V) may drive the EEG toward amorphization, resulting in Raman signatures characteristic of highly disordered carbon, which could negatively impact material performance in devices by reducing conductivity and mechanical integrity.23 These observations demonstrate that the applied potential directly modulates the Raman response of EEG, controlling both structural disorder (as indicated by the D band) and layer number (as indicated by the 2D band). | ||
| Fig. 2 (a) Raman spectra of graphite and graphene prepared at different potentials. Reproduced with permission from ref. 22, Copyright 2015, The Royal Society of Chemistry. (b) Raman spectra of EEG exfoliated from graphite powder (3 min), graphite foil (15 and 60 min), and HOPG (60 min), compared to their respective unexfoliated materials. Reproduced with permission from ref. 24, Copyright 2015, Elsevier Ltd. | ||
Furthermore, Yang et al. developed an AC-driven approach utilizing ±10 V with tunable frequencies (0.01–20 Hz) applied to graphite foil electrodes in organic bisulphate aqueous electrolytes.25 This alternating polarity was proposed to enable in situ reduction reactions and limit anodic overoxidation, yielding graphene with lower defect densities. However, the production rate achieved by this method (≈20 g h−1) remains relatively low, and its scalability is limited when compared to optimized DC-based protocols.5
The choice of graphite anode has a significant impact on both the efficiency of electrochemical exfoliation and the structural quality of the resulting EEG. Highly ordered pyrolytic graphite (HOPG) and graphite foil display compact, well-aligned stacking of graphitic planes at their prismatic edges, a feature indicative of high crystallinity. In contrast, graphite powder or flakes are composed of smaller particles, typically 1–4 µm thick and 10–50 µm in lateral dimension, with irregular and rough edge surfaces. These structural differences directly affect electrochemical exfoliation behaviour. Comparative Raman analysis of EEG samples prepared from HOPG, graphite foil, graphite flakes, and graphite powder shows a progressive increase in structural order along this sequence, reflected in the systematic decrease in D-band intensity and corresponding rise in C/O ratio (Fig. 2(b)).24 In addition, the closely packed layers of HOPG restrict electrolyte penetration and intercalant diffusion. This limitation results in poor exfoliation yields and increased defect formation during oxidative breakdown.
In aqueous electrolytes, the electrochemical exfoliation time plays a critical role in determining the structural quality of EEG. Short exfoliation periods, typically on the order of a few minutes, tend to yield an EEG with fewer structural defects. This is evidenced by lower I(D)/I(G) ratios, narrower FWHM of the G band, and relatively high C/O ratios exceeding 15 (Fig. 2(b)).24 Conversely, prolonging the exfoliation process to an hour or several hours significantly increases basal-plane oxidation and defect formation. As a result, Raman spectra show higher I(D)/I(G) ratios, noticeable broadening of the G band, suppression of the 2D band, and reduced C/O ratios below 10. These trends are clearly observed in Fig. 2(b) for graphite foil exfoliated for 15 min and 60 min under comparable conditions.24 Generally, these parameters illustrate the mechanistic sensitivity of Raman spectroscopy to electrochemical conditions. Rather than serving only as markers of quality, Raman features can be understood as a dynamic record of how specific reaction pathways imprint themselves on the graphene lattice. By correlating electrolyte chemistry, cell potential, exfoliation duration, and graphite anode type with spectral evolution, Raman spectroscopy provides fundamental insight into the interplay between electrochemical processes and structural modification in EEG.
EEG samples are substrate-free and are typically deposited onto SiO2/Si substrates using spin-coating for Raman analysis. Although graphene generally conforms to underlying substrates owing to its facile out-of-plane deformation, experimental studies have shown that regions of graphene on SiO2 can exhibit quasi-freestanding behaviour.26 This is particularly relevant for EEG, where intrinsic corrugation and partial suspension over substrate roughness may locally reduce substrate coupling. The 300 nm SiO2 layer enhances optical contrast, enabling clear differentiation between single-layer and few-layer graphene. Additionally, this layer exhibits minimal intrinsic Raman features, resulting in an unobstructed spectral baseline. These characteristics establish SiO2/Si as a preferred and widely used platform for reproducible Raman characterization of graphene-based materials.
Raman scattering in graphene and its defect sensitivity
The Raman spectrum of graphene is dominated by three major features: the G, D, and 2D bands. The G band, located near 1580 cm−1, arises from the in-plane stretching of sp2 carbon atoms and is attributable to graphitic materials.27 The D band, appearing near 1350 cm−1, is defect-activated and requires a breakdown of translational symmetry to become Raman active.27,28 Its intensity is therefore a sensitive probe of disorder. According to the Raman selection rule of momentum conservation, only phonons near the Brillouin zone center (Γ point) can be Raman active in a first-order process, provided they are symmetry-allowed.29 The G band, arising from such a first-order process, is the only mode allowed at the Γ point and involves in-plane optical phonons with E2g symmetry (schematically illustrated in SI, Fig. S1 and S2).The 2D band, typically around 2700 cm−1, is the overtone of the D band but does not require defects for activation. Its shape and intensity provide information about the number of graphene layers and the stacking order.27,30 Building on this overview of Raman features, the underlying mechanisms further illustrate graphene's sensitivity to defects. The double-resonance mechanism underpins both the D and 2D bands, involving electronic transitions between valleys in the Brillouin zone (schematically illustrated in the SI, Fig. S2).9,29 This sensitivity to the electronic band structure makes the 2D band particularly responsive to doping and strain. These spectroscopic responses are further interpreted through diagnostic intensity ratios. Two intensity ratios serve as diagnostic tools: I(D)/I(G), which quantifies defect density,15,31 and I(2D)/I(G), commonly used to assess layer thickness.
In graphene-based materials, the D and 2D bands originate from double-resonance (DR) and triple-resonance (TR) processes, with the relevant phonon wavevector determined by the excitation laser energy (εL).32–34 Consequently, the positions of these Raman bands vary with laser energy (Fig. 3(a)–(c)). The 2D band, generated by a two-phonon TR process involving transverse optical (TO) phonons near the K point, exhibits a dispersion of approximately 100 cm−1 eV−1 (Fig. 3(a) and (b)), which is about twice the slope observed for the defect-activated D band (≈50 cm−1 eV−1).29 This difference reflects their distinct scattering mechanisms. At or below 1.16 eV excitation, the D band is more intense than the G band; however, it diminishes and nearly vanishes above 3.7 eV.34 This trend demonstrates the pronounced dispersion of the D band with εL. Therefore, in EEG studies where the I(D)/I(G) ratio is critical for electrochemical analysis, this dispersion necessitates careful consideration when comparing Raman datasets from different published EEG spectra.
 | ||
| Fig. 3 (a) Raman spectra of monolayer graphene (1LG) measured at multiple excitation energies, and (b) dispersion of the 2D peak position as a function of excitation energy. Reproduced with permission from ref. 29, Copyright 2018, The Royal Society of Chemistry. (c) Raman spectra of graphite recorded using various laser excitations. Reproduced with permission from ref. 34, Copyright 1998, Elsevier Science B.V. | ||
Defect models and Raman metrics in EEG
Interpretation of graphene Raman spectra frequently relies on disorder-based models that associate vibrational and electronic features with defect density and crystallite size. While these models are widely applicable to graphene-based materials, their application requires careful consideration when structural disorder coincides with chemical modifications, such as functionalization or doping. Electrochemically exfoliated graphene represents a significant material within this category, as it inherently incorporates multiple defect types introduced during synthesis. Assessing the applicability and limitations of conventional Raman interpretation frameworks in the context of EEG provides broader insights into the analysis of chemically and structurally complex graphene systems.The Tuinstra–Koenig relation originally linked the intensity ratio I(D)/I(G) to the in-plane crystallite size (La) of graphitic domains:
 | (1) |
This relationship is valid in the nanocrystalline regime, typically defined by La ≥ 2 nm (Fig. 4). In this regime, the D band originates primarily from edge scattering under low defect concentrations. In EEG, however, the situation is more complex. Basal-plane defects, vacancies, and oxygen-containing functional groups contribute to the activation of the D band and decrease crystallite size by disrupting extended sp2 domains. This reduction in the average crystallite size is observed in Raman spectroscopy as an increased intensity of the D band relative to the G band. Therefore, the intensity ratio I(D)/I(G) should not be interpreted as a direct or exclusive measure of crystallite size. Rather, it reflects an effective crystallite size of sp2 domains, determined by the combined effects of multiple defect types introduced during the electrochemical exfoliation process. However, published data on EEG often demonstrate an approximate inverse relationship between I(D)/I(G) and La, as shown in Fig. 4. This observation suggests that edge-related scattering is the primary contributor compared to other defect-related mechanisms in many EEG samples.4,5,20,21,25,36–42
 | ||
| Fig. 4 Variation of the I(D)/I(G) intensity ratio as a function of in-plane crystallite size (La). Reproduced with permission from ref. 36. Copyright 2000, The American Physical Society. The shaded region over the EEG data points indicates defect-related contributions. The EEG data points were extracted from Raman spectra provided in Table S1, as reported by various research groups. | ||
Comprehensive interpretative frameworks, such as the two-stage defect evolution model proposed by Eckmann et al. and the Ferrari–Robertson amorphization trajectory, elucidate the evolution of Raman features from graphene and crystalline graphite to amorphous carbon.15,27 In the two-stage model, the I(D)/I(G) ratio increases with the introduction of defects and subsequently decreases when disorder disrupts π-conjugation.15Fig. 5(a) illustrates the Ferrari–Robertson model as a conceptual framework, without presenting EEG-specific data. Because EEG is directly derived from graphite, its Raman features can be analysed within this trajectory. Reported EEG Raman data (Fig. 5(b) and (c) and cited literature) indicate that EEG typically occupies an intermediate region between crystalline graphite and more disordered carbon, reflecting the coexistence of ordered and disordered sp2 domains. Within the Ferrari–Robertson framework, EEG Raman signatures frequently overlap with those of nanocrystalline graphite, particularly regarding G-band position and I(D)/I(G) ratio. This overlap is consistent with the fragmentation of graphite into finite sp2 domains bounded by edges, basal-plane defects, and oxygen-containing functional groups.
 | ||
| Fig. 5 (a) Amorphization trajectory showing the schematic evolution of the G band position and I(D)/I(G) ratio as a function of increasing disorder, progressing from crystalline graphite to nanocrystalline graphite, amorphous carbon, and ultimately to tetrahedral amorphous carbon (ta-C), in accordance with the Ferrari–Robertson model. Reproduced with permission from ref. 36. Copyright 2000, The American Physical Society. (b) Correlation plot of G band position versus G band FWHM for nanocrystalline graphite (nc-G), and various hydrogenated and amorphous carbon materials. Reproduced with permission from ref. 43, MDPI, Creative Commons CC BY 4.0 license. (c) G band FWHM versus G band position for EEG. The EEG data points were extracted from Raman spectra provided in Table S1, as reported by various research groups. | ||
Additional structural insight is provided by analysing the relationship between G-band FWHM and position (Fig. 5(b)), which allows materials to be situated within the three-stage Ferrari–Robertson model.36 In this framework, nanocrystalline graphite demonstrates the lowest disorder, followed by hydrogenated amorphous carbons (a-C:H, a-C:D), while tetrahedral amorphous carbons (ta-C, ta-C:H) exhibit progressively greater disorder. For intrinsic, high-quality graphene with negligible D-band intensity, the G-band FWHM is approximately 16 cm−1, marginally higher than that of crystalline graphite. To provide more tangible insights, materials with an FWHM of around 16 cm−1 could be associated with an approximate sp2 cluster size of ≈30 nm. With increasing disorder toward nanocrystalline graphite, as shown by EEG (Fig. 5(c)), both G-band FWHM and position increase (exceeding an FWHM of 16 cm−1 and a position above 1580 cm−1), indicating a reduction in crystallite size.8 These findings support the interpretation of the EEG as moderately disordered graphene that maintains partial graphitic order.
Raman ratios provide additional diagnostic sensitivity. The I(D)/I(D′) ratio distinguishes between edge defects (I(D)/I(D′) ≈ 3.5), vacancies (I(D)/I(D′) ≈ 7), and sp3-related disruptions (I(D)/I(D′) ≈ 13), offering a finer classification of disorder in the EEG.44 Linewidths and peak shifts of the G and 2D bands also carry valuable information, encoding the interplay between strain, charge transfer, and phonon renormalization. Collectively, these models and metrics demonstrate that the Raman spectrum of EEG cannot be reduced to a single structural parameter. Rather, it reflects the combined effects of defects, chemical modifications, and doping on the vibrational and electronic properties of graphene. Application of defect evolution models to EEG requires careful consideration of both their predictive capabilities and inherent limitations. When appropriately contextualized, these frameworks enable Raman spectroscopy to probe the fundamental physics of disorder in electrochemically exfoliated graphene.
Layer number and stacking order in EEG
The Raman 2D band is a highly sensitive indicator of the electronic band structure in few-layer graphene, displaying significant changes in response to variations in layer number, interlayer coupling, and stacking order.9,29,45 In mechanically exfoliated and high-quality CVD-grown pristine monolayer graphene (1LG), the 2D band appears as a single, sharp, and symmetric peak with an FWHM of approximately 25 cm−1 (ref. 10). As additional layers are introduced, such as in Bernal (AB) stacked bilayer graphene (2LG), multilayer graphene (≥3LG), or well-ordered graphite, the 2D band broadens (FWHM ≈ 40–100 cm−1), becomes asymmetric, and splits into multiple components (typically four sub-bands in 2LG) due to the splitting of the π and π* electronic bands.9,10 In contrast, turbostratically stacked multilayer graphene exhibits a broadened (FWHM > 70 cm−1), single-component, and often a red-shifted 2D band, which indicates weakened interlayer coupling and rotational misalignment. The electronic structure in this case closely resembles that of pristine 1LG, with Dirac-like dispersion.9,10 Consequently, the 2D band profile serves to distinguish stacking configurations: Bernal, rhombohedral (ABC), and turbostratically stacked multilayers each produce distinct 2D-band signatures due to their unique symmetry conditions and interlayer interactions. In summary, the 2D band shape directly reflects stacking and interlayer interactions.These stacking-dependent Raman signatures are well established for both mechanically exfoliated and CVD-grown graphene. In contrast, the EEG does not display evidence of stabilized non-equilibrium stacking arrangements such as rhombohedral (ABC) order. The electrochemical exfoliation process, which involves rapid ion intercalation, layer expansion, and oxidative reactions, disrupts long-range stacking order. The ions wedge between layers, breaking registry and promoting rotational misalignment. Because the fast kinetics of ion intercalation lead to a loss of registry between layers, EEG typically demonstrates turbostratic restacking, as evidenced by a broadened, red-shifted, nearly single-component 2D band. This behaviour is in marked contrast to well-ordered graphite, which exhibits an asymmetric 2D band with a FWHM of approximately 40–100 cm−1 (Fig. 6(a) and Table S1).
 | ||
| Fig. 6 (a) Average Raman spectra of EEG samples prepared with various concentrated H2SO4:H3PO4 intercalant blends for an 800 s intercalation, compared with the spectrum of the pristine graphite. Reproduced with permission from ref. 46, Copyright 2025, Elsevier B.V. (b) Evolution of the D, D′, G, and 2D band intensities with increasing defect concentration in graphene. Reproduced with permission from ref. 15, Copyright 2013, American Physical Society. | ||
X-ray diffraction (XRD) data further corroborate this interpretation. EEG typically exhibits a broad (002) reflection near 25.7° (Table S1), corresponding to an expanded interlayer spacing of approximately 0.345 nm,47 which is larger than the ≈0.335 nm spacing observed in parent graphite. Well-ordered carbon materials exhibit additional peaks, such as the (100), (101), and (004) reflections, located near 44°, 46°, and 54°, respectively. In contrast, turbostratic carbons show only a broad (002) peak and lack these additional reflections, consistent with rotational disorder and poor three-dimensional order.48,49 Although the presence of small Bernal-like regions in the EEG cannot be entirely excluded, as some studies report their XRD patterns (e.g., ref. 50). The combined Raman and XRD data strongly support turbostratic reassembly rather than the preservation or emergence of rhombohedral stacking. Identification of such rare configurations would require high-resolution Raman mapping and multi-component line-shape analysis.
Although the I(2D)/I(G) ratio is commonly used to estimate layer number in mechanically exfoliated and high-quality CVD-grown graphene, its interpretation is complicated by factors such as doping, functionalization, and residual disorder. As shown by Casiraghi et al., the variation in I(2D)/I(G) observed in mechanically exfoliated pristine monolayer graphene is larger than the changes expected from increasing the layer number.8 This makes the ratio unreliable as a thickness indicator in non-pristine graphene samples. This observation aligns with the two-stage defect evolution model (Fig. 6(b)) proposed by Eckmann et al., where the D-band intensity initially increases and then decreases as disorder (doping or functionalization) progresses, while the 2D-band intensity steadily declines due to defect-induced modifications in phonon dispersion.15 The G band remains relatively stable because it arises from in-plane C–C stretching in sp2 carbon networks, making it a reliable reference. Given how the 2D band evolves relative to the D band across all forms of graphene, especially in disordered graphene, estimating the layer number of the EEG using Raman spectroscopy becomes highly uncertain. In such cases, high-resolution transmission electron microscopy (HRTEM) provides a more reliable method for determining layer thickness and assessing structural integrity.
Doping and functionalization effects
Beyond structural disorder, EEG invariably incorporates chemical dopants and oxygen-containing functional groups derived from the electrolyte and reaction environment. These modifications introduce charge transfer and electronic perturbations that strongly influence the Raman response. Interpreting EEG spectra, therefore, requires careful separation of structural contributions from those arising due to doping and functionalization.Doping, whether electrostatic or chemical, manifests most clearly in the G band. Hole doping typically upshifts the G band frequency and narrows its linewidth, while electron doping can cause either softening or stiffening, depending on the Fermi level shift.30,35 Such changes arise from the nonadiabatic coupling between charge carriers and phonons, making Raman spectroscopy uniquely sensitive to doping in graphene-based materials. Since electrochemical environments can dynamically modulate charge density, the G band often serves as a direct spectroscopic probe of charge transfer processes at the graphene–electrolyte interface. To quantitatively estimate doping levels, Raman-based metrics such as the G band position shift (Δω(G)) and the square root of the 2D-to-G area ratio (√A(2D)/A(G)) are commonly used.51 A linear relationship has been established between EF and Δω(G) for shifts greater than ≈0.1 eV, enabling semi-quantitative assessment of doping. Two frequently used empirical relationships include:
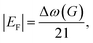 | (2) |
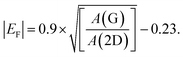 | (3) |
Eqn (3) is valid specifically for Raman spectra acquired with 514 nm excitation.51 Its parameters must be adjusted for other laser wavelengths. When eqn (3) is applied to EEG Raman data extracted from literature, typical |EF| values fall within the range of ≈0.1 to 0.5 eV, indicating significant levels of p-type or n-type doping depending on the exfoliation conditions.
Although eqn (2) and (3) offer a useful starting point for estimating doping levels, the G-band position is affected by several overlapping factors, including lattice defects, residual strain, differences in layer number, stacking order, and the presence of functional groups. As a result, single-spot Raman measurements may not reliably distinguish between p-type and n-type carriers. A more robust approach involves spatial Raman mapping over a large area, which can verify whether the G-band is uniformly red- or blue-shifted and thereby provide a more physically meaningful basis for interpreting doping and related spectral changes.
For instance, Kgwadibane et al. recently reported large-area spatial Raman mapping of EEG films over a 100 × 100 µm2 region, comprising 160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 spectra.46 Their results showed that intensity variations were mainly correlated with changes in the integrated D-peak intensity, indicating a non-uniform distribution of defects across the samples (Fig. 7(a)). In contrast, the G-band position remained consistent throughout the mapped regions, as reflected by the uniform distribution of Fermi-level shifts relative to the parent graphite material (Fig. 7(b)).46 These findings demonstrate that homogeneous spectral shifts, which are difficult to infer from single-point measurements, can be clearly resolved through large-area mapping. Overall, spatial Raman mapping provides a more physically grounded and reliable framework for assessing doping and other spectral shifts in graphene-based materials.
000 spectra.46 Their results showed that intensity variations were mainly correlated with changes in the integrated D-peak intensity, indicating a non-uniform distribution of defects across the samples (Fig. 7(a)). In contrast, the G-band position remained consistent throughout the mapped regions, as reflected by the uniform distribution of Fermi-level shifts relative to the parent graphite material (Fig. 7(b)).46 These findings demonstrate that homogeneous spectral shifts, which are difficult to infer from single-point measurements, can be clearly resolved through large-area mapping. Overall, spatial Raman mapping provides a more physically grounded and reliable framework for assessing doping and other spectral shifts in graphene-based materials.
 | ||
| Fig. 7 Large-area Raman mapping of EEG samples: (a) true-component Raman intensity distribution images with corresponding average Raman spectra for samples prepared using different H2SO4:H3PO4 intercalant blends during 800 s intercalation; (b) spatial maps showing the corresponding Fermi-level shifts. Reproduced with permission from ref. 46, Copyright 2025, Elsevier B.V. | ||
Furthermore, the 2D band provides a complementary window into electronic modification. Doping alters the resonance conditions governing the double-resonance process, leading to shifts in position, changes in intensity, and modifications in line shape.51–54 Suppression of the 2D band is frequently observed in heavily functionalized EEG, reflecting both disruption of electronic coherence and increased scattering. In this sense, the evolution of the 2D band traces the delicate balance between preserved π-conjugation and its disruption by dopants or oxygen functionalities. Furthermore, strain can also contribute to such shifts, making it necessary to disentangle the effects of both. To achieve this, correlation plots between the 2D and G band positions have been used, commonly known as Lee diagrams, as shown in Fig. 8.55 Originally developed for mechanically exfoliated, high-quality graphene, this method has also been applied qualitatively to few-layer and multilayer graphene materials.26,56–62 In these plots, a slope of approximately 0.75 (shown by the red solid line along the magenta dashed guideline in Fig. 8) indicates doping-induced shifts, stemming from non-adiabatic electron–phonon coupling that affects the G band. Conversely, a steeper slope of ≈2.2 (black dashed line in Fig. 8) corresponds to strain-induced shifts, where both the 2D and G bands shift in a nearly linear and correlated manner in response to uniaxial or biaxial strain.26,55 Data points falling between these reference slopes indicate a combination of both effects.
 | ||
| Fig. 8 Correlation plot of 2D versus G band positions used to distinguish strain and doping effects in few-layer and multilayer graphene. Reference strain and doping lines for freestanding graphene (reproduced with permission from ref. 26, Copyright 2012, Macmillan Publishers Limited) were originally measured at 514 nm excitation. The 2D-band positions have been adjusted for 532 nm excitation using a dispersion of ≈100 cm−1 eV−1, corresponding to an ≈8 cm−1 downward shift. Point O denotes charge-neutral, strain-free graphene. Solid red and blue lines indicate the evolution of Raman band positions under p-type and n-type electrical doping, respectively.26 The magenta dashed line corresponds to strain-free graphene with increasing p-type doping, while the black dashed line represents the strain vector for charge-neutral graphene. The EEG data points were extracted from Raman spectra provided in Table S1, as reported by various research groups. | ||
Although both the G and 2D bands respond to charge doping and strain, the ratio of their shifts, defined as the change in the 2D band position relative to that of the G band, differs markedly depending on the underlying mechanism. For biaxially strained graphene, experimental fractional variations typically lie between 2.45 and 2.8, while theoretical predictions suggest slightly lower values in the range of 2.25–2.48.26,55 Under uniaxial strain, the G and 2D bands split into G−/G+ and 2D−/2D+ components, depending on the orientation of the strain with respect to the crystallographic axes.26,55 When this splitting cannot be resolved experimentally, the resulting effective slope usually falls between 2.02 and 2.44.26,55 By comparison, hole doping produces a nearly linear slope of around 0.75, whereas electron doping (blue solid line in Fig. 8) shows increasingly nonlinear behaviour at higher charge densities.
Although originally developed for monolayer graphene, correlation plots of 2D versus G band positions can be qualitatively extended to multilayer graphene samples to distinguish regions where strain or doping dominates. In EEG, the G and 2D band positions tend to cluster above both the doping-related and strain-related reference lines (as seen in Fig. 8), suggesting a consistent spectral response influenced by multiple overlapping perturbations. A similar trend has been reported for defective few-layer graphene by Nikolaievskyi et al., where data points also cluster above both reference lines, pointing to a common Raman response across structurally perturbed graphene systems.55
Moreover, functionalization introduces additional complexity. Oxygen groups attached to basal-plane carbons or edges generate localized sp3 defects that enhance the D band while simultaneously perturbing the electronic background. The I(D)/I(D′) ratio, which varies systematically with defect type, becomes particularly useful in this context, as it distinguishes between sp3-type defects, vacancies, and edge contributions Fig. 9(a).29 The D and D′ band intensities scale linearly with defect concentration nd:44
| ID ∼ Adnd and ID′ ∼ Bdnd, | (4) |
 | ||
| Fig. 9 (a) Schematics of typical defect structures: (i) vacancies, (ii) grain boundaries, and (iii) sp3-type chemical defects. Reproduced with permission from ref. 29, Copyright 2018, The Royal Society of Chemistry. (b) I(D)/I(G) vs. I(D′)/I(G) plot; bottom panels: linear trend at low defect density, indicating different I(D)/I(D′) ratios for different defect types. Reproduced with permission from ref. 44, Copyright 2012, American Chemical Society. (c) I(D)/I(G) vs. I(D′)/I(G) plot of EEG data points. The EEG data points were extracted from Raman spectra provided in Table S1, as reported by various research groups. | ||
Thus, the ratio ID/ID′ ∼ Ad/Bd serves as a fingerprint of defect nature, as demonstrated by Eckmann et al. and illustrated in Fig. 9(b).44 This distinction arises because the D band is activated by intervalley scattering, while the D′ band originates from intravalley scattering, with each pathway responding differently to symmetry breaking. As shown in Fig. 9(c), EEG data exhibit an average I(D)/I(D′) ratio of approximately 3.5, indicative of edge (boundary-like) defects. The predominance of such edge disorder is consistent with structural fragmentation introduced during electrochemical exfoliation.
Collectively, Raman signatures of doping and functionalization extend the interpretation of EEG beyond purely structural considerations. They reveal how electronic interactions, chemical bonding, and lattice vibrations are intertwined in electrochemically derived graphene. In this way, Raman spectroscopy does not merely diagnose the presence of dopants or oxygen groups, but provides fundamental insight into how these modifications reshape the vibrational and electronic structure of the graphene lattice.
Conclusions and outlook
Raman spectroscopy is considered one of the most effective techniques for investigating the structural and electronic characteristics of graphene-based materials. In highly disordered graphene, such as EEG, interpreting Raman spectra is particularly complex because structural disorder, chemical functionalization, and doping simultaneously influence peak intensities, positions, and line shapes. For instance, the ID/IG ratio in such materials may range from 1.5 to 3, indicating significant levels of defects and disorder. Consequently, extracting meaningful information necessitates a careful and nuanced analysis.Recent advancements have enabled a deeper mechanistic understanding of graphene-based materials. Spatially resolved Raman mapping facilitates visualization of variations in strain, defect density, and doping across large sample areas, thereby providing a clearer assessment of material heterogeneity. Additionally, correlation plots between Raman features yield qualitative insights into the interactions among these factors. In situ and operando Raman spectroscopy further expand the technique's capabilities by enabling real-time monitoring of processes such as intercalation, oxidation, and layer separation. Tracking the time-dependent evolution of the G, D, D′, and 2D bands allows for the elucidation of exfoliation mechanisms and clarifies the balance between defect generation and structural preservation, which static spectra alone cannot achieve.
More recently, machine learning-based methods have emerged as powerful tools for spectroscopic materials characterisation. Instead of relying on predefined peak ratios or manual fitting procedures, data-driven models can capture complex correlations across the entire spectral range. When trained on well-characterized datasets, these approaches can distinguish between different defect types and doping states with greater sensitivity than conventional methods, while also uncovering subtle spectral–structural relationships that refine existing defect models.
Combining Raman spectroscopy with complementary techniques such as X-ray photoelectron spectroscopy, X-ray diffraction, high-resolution transmission electron microscopy, and atomic force microscopy further strengthens materials characterization by linking chemical and structural information across multiple length scales. Together, these integrated strategies help bridge the gap between idealized theoretical models and the complexity of real-world materials.
In summary, Raman spectroscopy of defective graphene has progressed beyond a purely descriptive technique to become a powerful mechanistic probe of synthesis and processing pathways. The integration of spatially resolved measurements, time-resolved experiments, and advanced computational analysis establishes Raman spectroscopy as a versatile diagnostic platform for tracking defect formation, doping, and structural evolution. Continued advances will depend on the parallel development of real-time experimental methods, sophisticated data-analysis tools, and theoretical models that account for the coupled effects of disorder, chemistry, and doping. Within this comprehensive framework, Raman spectroscopy will remain central to understanding the fundamental physics and chemistry of electrochemically exfoliated graphene.
Author contributions
M. J. Madito: conceptualization, investigation, validation, and writing – original draft preparation, funding acquisition, and resources.Conflicts of interest
There are no conflicts to declare.Data availability
Supplementary information (SI): Raman spectra of EEG reported in the literature. See DOI: https://doi.org/10.1039/d5ma01009h.No primary research results, software, or code have been included, and no new data were generated or analysed as part of this review.
Acknowledgements
This work is part of the research supported by the University of South Africa, Institute for Nanotechnology and Water Sustainability (iNanoWS). The author acknowledges the financial support from iNanoWS.References
- N. S. Mankge, M. J. Madito, N. W. Hlongwa and A. T. Kuvarega, Elsevier Ltd, 2022, preprint DOI:10.1016/j.est.2021.103527.
- D. Momodu, A. S. Zeraati, F. L. Pablos, U. Sundararaj and E. P. Roberts, Electrochim. Acta, 2021, 388, 138664 CrossRef CAS.
- D. Momodu, M. J. Madito, A. Singh, F. Sharif, K. Karan, M. Trifkovic, S. Bryant and E. P. L. Roberts, Carbon, 2021, 171, 130–141 Search PubMed.
- K. Parvez, R. Worsley, A. Alieva, A. Felten and C. Casiraghi, Carbon, 2019, 149, 213–221 CrossRef CAS.
- F. Sharif, A. S. Zeraati, P. Ganjeh-Anzabi, N. Yasri, M. Perez-Page, S. M. Holmes, U. Sundararaj, M. Trifkovic and E. P. L. Roberts, Carbon, 2020, 157, 681–692 CrossRef CAS.
- J. M. Munuera, J. I. Paredes, S. Villar-Rodil, M. Ayán-Varela, A. Martínez-Alonso and J. M. D. Tascón, Nanoscale, 2016, 8, 2982–2998 RSC.
- S. Yang, S. Brüller, Z. S. Wu, Z. Liu, K. Parvez, R. Dong, F. Richard, P. Samorì, X. Feng and K. Müllen, J. Am. Chem. Soc., 2015, 137, 13927–13932 Search PubMed.
- C. Casiraghi, S. Pisana, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Appl. Phys. Lett., 2007, 91, 233108 CrossRef.
- L. M. Malard, M. A. Pimenta, G. Dresselhaus and M. S. Dresselhaus, Phys. Rep., 2009, 473, 51–87 CrossRef CAS.
- A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314 CrossRef CAS PubMed.
- C. Yang, H. Bi, D. Wan, F. Huang, X. Xie and M. Jiang, J. Mater. Chem. A, 2013, 1, 770–775 RSC.
- A. Ciesielski and P. Samorì, Chem. Soc. Rev., 2014, 43, 381–398 RSC.
- A. Eckmann, A. Felten, I. Verzhbitskiy, R. Davey and C. Casiraghi, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 1–11 CrossRef.
- A. Ambrosi and M. Pumera, Chem. – Eur. J., 2016, 22, 153–159 CrossRef CAS PubMed.
- P. Tripathi, C. Ravi, P. Patel, A. Dixit, A. P. Singh, P. Kumar, M. A. Shaz, R. Srivastava, G. Gupta, S. K. Dhawan, B. Kumar Gupta and O. N. Srivastava, RSC Adv., 2015, 5, 19074 RSC.
- M. J. Madito, Elsevier B.V., 2025, preprint DOI:10.1016/j.vibspec.2025.103814.
- K. Chen, D. Xue and S. Komarneni, J. Colloid Interface Sci., 2017, 487, 156–161 CrossRef CAS PubMed.
- K. Parvez, W. ZS, R. Li, X. Liu, R. Graf, X. Feng and K. Müllen, J. Am. Chem. Soc., 2014, 136, 6083–6091 Search PubMed.
- J. M. Munuera, J. I. Paredes, M. Enterría, A. Pagán, S. Villar-Rodil, M. F. R. Pereira, J. I. Martins, J. L. Figueiredo, J. L. Cenis, A. Martínez-Alonso and J. M. D. Tascón, ACS Appl. Mater. Interfaces, 2017, 9, 24085–24099 CrossRef CAS PubMed.
- M. K. Punith Kumar, S. Shanthini and C. Srivastava, RSC Adv., 2015, 5, 53865–53869 Search PubMed.
- S. Roscher, R. Hoffmann, M. Prescher, P. Knittel and O. Ambacher, RSC Adv., 2019, 9, 29305–29311 Search PubMed.
- J. M. Munuera, J. I. Paredes, S. Villar-Rodil, M. Ayán-Varela, A. Pagán, S. D. Aznar-Cervantes, J. L. Cenis, A. Martínez-Alonso and J. M. D. Tascón, Carbon, 2015, 94, 729–739 Search PubMed.
- S. Yang, A. G. Ricciardulli, S. Liu, R. Dong, M. R. Lohe, A. Becker, M. A. Squillaci, P. Samorì, K. Müllen and X. Feng, Angew. Chem., Int. Ed., 2017, 56, 6669–6675 CrossRef CAS PubMed.
- J. E. Lee, G. Ahn, J. Shim, Y. S. Lee and S. Ryu, Nat. Commun., 2012, 3, 1024 CrossRef PubMed.
- A. C. Ferrari and J. Robertson, Phys. Rev. B:Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef CAS.
- A. C. Ferrari and D. M. Basko, 2013, preprint DOI:10.1038/nnano.2013.46.
- J. Bin Wu, M. L. Lin, X. Cong, H. N. Liu and P. H. Tan, Chem. Soc. Rev., 2018, 47, 1822–1873 RSC.
- D. M. Basko, S. Piscanec and A. C. Ferrari, Phys. Rev. B, 2009, 80, 165413 CrossRef.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126–1130 Search PubMed.
- C. Cong, T. Yu, R. Saito, G. F. Dresselhaus and M. S. Dresselhaus, ACS Nano, 2011, 5, 1600–1605 CrossRef CAS PubMed.
- S. Piscanec, M. Lazzeri, F. Mauri, A. C. Ferrari and J. Robertson, Phys. Rev. Lett., 2004, 93, 185503 Search PubMed.
- I. Pocsik, M. Hundhausen, M. Koos and L. Ley, Origin of the D peak in the Raman spectrum of microcrystalline graphite, 1998, vol. 227 Search PubMed.
- A. C. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef CAS.
- A. C. Ferrari and J. Robertson, Phys. Rev. B:Condens. Matter Mater. Phys., 2000, 61, 14095–14107 CrossRef CAS.
- M. Borah, A. Sikdar, S. Kapse, A. Majumdar and P. Dutta, Catal. Today, 2021, 370, 83–92 CrossRef CAS.
- M. J. Vujković, B. A. Vidoeski, S. P. Jovanović, D. V. Bajuk-Bogdanović, M. D. Budimir, Z. M. Marković, V. B. Pavlović, B. M. Todorović-Marković and I. D. Holclajtner-Antunović, Electrochim. Acta, 2016, 217, 34–46 CrossRef.
- A. M. Abdelkader, I. A. Kinloch and R. A. W. Dryfe, ACS Appl. Mater. Interfaces, 2014, 6, 1632–1639 CrossRef CAS.
- T. C. Achee, W. Sun, J. T. Hope, S. G. Quitzau, C. B. Sweeney, S. A. Shah, T. Habib and M. J. Green, Sci. Rep., 2018, 8, 1–8 Search PubMed.
- A. Mir and A. Shukla, Mater. Des., 2018, 156, 62–70 CrossRef CAS.
- T. N. J. I. Edison, R. Atchudan, N. Karthik, P. Chandrasekaran, S. Perumal, P. Arunachalam, P. B. Raja, M. G. Sethuraman and Y. R. Lee, Surf. Coat. Technol., 2021, 416, 127150 CrossRef CAS.
- A. Merlen, J. G. Buijnsters and C. Pardanaud, MDPI AG, 2017, preprint DOI:10.3390/coatings7100153.
- A. Eckmann, A. Felten, A. Mishchenko, L. Britnell, R. Krupke, K. S. Novoselov and C. Casiraghi, Nano Lett., 2012, 12, 3925–3930 CrossRef CAS PubMed.
- A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- T. Kgwadibane, R. Morad, D. Y. Momodu, N. W. Hlongwa, X. Fuku and M. J. Madito, Diamond Relat. Mater., 2025, 160, 113058 CrossRef CAS.
- C. H. Chen, S. W. Yang, M. C. Chuang, W. Y. Woon and C. Y. Su, Nanoscale, 2015, 7, 15362–15373 RSC.
- H. Fujimoto, Carbon, 2003, 41, 1585–1592 CrossRef CAS.
- P. Puech, M. Jeanningros, D. Neumeyer and M. Monthioux, Carbon Trends, 2023, 13, 100311 CrossRef CAS.
- N. Parveen, M. O. Ansari, S. A. Ansari and M. H. Cho, J. Mater. Chem. A, 2016, 4, 233–240 RSC.
- W. J. Zhao, P. H. Tan, J. Liu and A. C. Ferrari.
- A. Das, S. Pisana, B. Chakraborty, S. Piscanec, S. K. Saha, U. V. Waghmare, K. S. Novoselov, H. R. Krishnamurthy, A. K. Geim, A. C. Ferrari and A. K. Sood, Nat. Nanotechnol., 2008, 3, 210–215 CrossRef CAS PubMed.
- Y. Li, Probing the Response of Two-Dimensional Crystals by Optical Spectroscopy, 2016 Search PubMed.
- M. J. Madito, ACS Appl. Mater. Interfaces, 2021, 13, 37014–37026 CrossRef CAS PubMed.
- D. Nikolaievskyi, M. Torregrosa, A. Merlen, S. Clair, O. Chuzel, J. L. Parrain, T. Neisus, A. Campos, M. Cabie, C. Martin and C. Pardanaud, Carbon, 2023, 203, 650–660 CrossRef CAS.
- N. S. Mueller, S. Heeg, M. P. Alvarez, P. Kusch, S. Wasserroth, N. Clark, F. Schedin, J. Parthenios, K. Papagelis, C. Galiotis, M. Kalbáč, A. Vijayaraghavan, U. Huebner, R. Gorbachev, O. Frank and S. Reich, 2D Mater., 2018, 5, 015016 CrossRef.
- W. Lin and P. Zhuang, Appl. Surf. Sci., 2022, 595, 153517 CrossRef CAS.
- P. Zhuang, J. Liu, J. Huang, C. Dou, W. Cai and W. Lin, Carbon, 2022, 189, 21–26 Search PubMed.
- U. Lee, Y. Han, S. Lee, J. S. Kim, Y. H. Lee, U. J. Kim and H. Son, ACS Nano, 2020, 14, 919–926 Search PubMed.
- J. Amontree, A. Marchese, J. Pack, T. Chung, X. Yan, Y. Borisenkov, B. Yang, K. Davis, K. Watanabe, T. Taniguchi, C. Dean and J. Hone, American Chemical Society, 2025, preprint DOI:10.1021/acs.nanolett.5c03305.
- A. Armano, G. Buscarino, M. Cannas, F. M. Gelardi, F. Giannazzo, E. Schilirò and S. Agnello, Carbon, 2018, 127, 270–279 CrossRef CAS.
- Š. Meškinis, A. Vasiliauskas, A. Guobienė, M. Talaikis, G. Niaura and R. Gudaitis, RSC Adv., 2022, 12, 18759–18772 RSC.
| This journal is © The Royal Society of Chemistry 2026 |

