DOI:
10.1039/D5MA00936G
(Paper)
Mater. Adv., 2026,
7, 1825-1839
Condensation on soft substrates: a mesoscopic perspective
Received
20th August 2025
, Accepted 30th November 2025
First published on 8th December 2025
Abstract
We consider the condensation and evaporation of a volatile partially wetting liquid on a soft substrate in contact with a homogeneously saturated gas phase. Recent experiments demonstrated a strong dependence of nucleation density on the substrate softness. Motivated by these experiments, we approach the problem considering both macroscale and mesoscale models. On the macroscale, we employ thermodynamic considerations to determine the critical nuclei energies and the resulting nucleation probabilities in the limits of rigid and liquid substrates. On the mesoscale, we use a gradient dynamics model for a drop of volatile liquid on a soft substrate with Kelvin–Voigt viscoelasticity in Winkler-foundation form. The governing energy functional incorporates elastic and interface energies as well as bulk liquid energy. We show that nucleation probabilities obtained with the two models agree for small supersaturation, but display differences when drop nuclei are small. Finally, we use the mesoscopic model to investigate the condensation and evaporation dynamics of drops in the intermediate elastic regime and relate the results to the experimental findings.
1 Introduction
When breathing against a cold window pane, one notices how it becomes opaque. A close look reveals, that this results from a rather dense random arrangement of numerous tiny drops that scatter light. Such breath figures form on cool surfaces due to condensation of liquid from the adjacent vapor and are extensively investigated.1–5 Depending on the surface properties, the liquid condenses into droplets or into a uniform film. The spontaneous local gathering of vapor particles that initiate the formation of drops of another thermodynamic phase is called nucleation. While condensation, i.e., the clustering of vapor molecules into liquid drops, is accessible to observation and study, it is triggered by nucleation, a microscopic process that normaly occurs at scales that make it challenging to study. Yet nucleation plays a central role in a wide range of phenomena, from crystallization,6 electron condensation in solids,7 tectonic events such as earthquakes8 and volcanic eruptions,9 to meteorological processes like cloud formation, snow, and rainfall,10,11 pathological conditions such as decompression sickness,12 and even the formation of black holes.13 In general, nucleation is important for phase transitions of first order, which is a subject of great interdisciplinary interest and practical importance. Since Gibbs achieved the first insights into the matter14 various theories have been developed. The widely used classical nucleation theory (CNT)15–18 determines the energy cost of cluster formation based on purely macroscopic quantities such as interface and bulk energies. The CNT is extended, e.g., by the dynamic nucleation theory (DNT) and by the extended modified liquid drop (EMLD) model that incorporate translational motion and small fluctuations in the particle number, respectively.18–20 In contrast to these phenomenological approaches, kinetic theory calculates the energy of cluster formation by directly considering the molecular interactions on the microscale thereby avoiding the use of macroscopic quantities. Considering the particles to be hard shapes molecular dynamics (MD) and Monte Carlo simulations are often utilized.21–24 In contrast, density functional theory (DFT) describes the system in terms of a microscale ensemble-averaged density and is used, e.g., to consider colloidal crystals.25 The direct observation of nuclei of only a few molecules in size still remains an experimental challenge.18,20
Here, we consider how a soft substrate influences nucleation and growth of sessile drops of a partially wetting liquid from vapor, i.e., condensation onto soft substrates. It is known that the ability of a substrate to deform under external pressure crucially influences the nucleation density.26 This observation is confirmed by ref. 27 using MD simulations. There, it is further found that also condensation rate and heat transfer efficiency increase with the softness of the substrate. It also affects the condensation mode, i.e., whether drops or films are formed. Sharma et al.28 observe that even though the overall condensation of drops increases with the softness of the substrate, the growth of individual drops may be reduced by cloaking effects, e.g., by uncrosslinked PDMS chains leaking from the substrate. Further it is found that coalescence is significantly delayed as the substrate softness increases26,29 and it is confirmed by gradient dynamics models that as well the coarsening mode is affected by the substrate softness.30
Recently, experiments on dew formation presented in ref. 31 were performed on substrates of different softness. There, flat homogeneous layers (millimetric thickness) of silicone elastomers are deposited on a cooling stage in a chamber with controlled humidity (mixture of water vapor and N2) as illustrated in Fig. 1(a). Condensation is achieved by cooling down the gel while simultaneously fixing the chamber humidity and pressure until a phase transition is induced [see Appendix A]. The threshold of phase transition is referred to as saturation. The impact of substrate elasticity on dew formation is investigated by tuning the gel stiffness through its crosslinking density. The breath figures are recorded from above using a high resolution magnifying objective. Since the resolution of the objective is ≈1 µm the experiment does not directly record the nucleation process but rather the subsequent mesosopic dynamics. Fig. 1(c) provides examples of the resulting breath figures, each taken as soon as drops are visible, for decreasing substrate softness (from left to right) quantified by the shear storage modulus G′. As the latter increases, that is, with decreasing elasto-capillary length ℓec = γ/G′, the initial number of drops is found to decrease. Remarkably, once condensation has started, there are no further nuclei forming in the dry regions between the already growing drops, which is due to the decrease of vapor concentration below saturation in the proximity of the substrate as discussed in ref. 24 and 31. In Fig. 1(b) the drop density ψ is displayed as a function of ℓec for two different humidities, rH = 1.22 (△) and rH = 2.42 (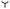 ).† Remarkably, while the drop density appears to be strongly affected by the substrate softness, i.e., it increases with ℓec, it is barely affected by changes in the supersaturation, that is the relative humidity rH at the substrate. Consider ref. 24 and 31 for a more extensive discussion regarding the later stages of droplet condensation.
).† Remarkably, while the drop density appears to be strongly affected by the substrate softness, i.e., it increases with ℓec, it is barely affected by changes in the supersaturation, that is the relative humidity rH at the substrate. Consider ref. 24 and 31 for a more extensive discussion regarding the later stages of droplet condensation.
 |
| | Fig. 1 (a) Schematic of the experimental setup. A gel substrate (red) is placed inside a controlled-humidity chamber and cooled down to Ts = 5 °C using a Peltier element (green). (b) Drop density ψ as a function of substrate softness quantified via the elasto-capillary length ℓec, based on data from ref. 31. The experiment used various PDMS gels – Sylgard 184 with mixing ratios ranging from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 80 1 to 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, CY52-276 (Dow Corning) with ratios of 1.3 1, CY52-276 (Dow Corning) with ratios of 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1 1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and PVS Elite16 (1 1, and PVS Elite16 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Measurements were conducted at two imposed relative humidities: rH = 2.42 ( 1). Measurements were conducted at two imposed relative humidities: rH = 2.42 (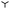 ) and rH = 1.22 (△). Horizontal lines indicate the limiting cases of a rigid substrate (red; nanometric PDMS brush grafted on a silicon wafer, see ref. 32) and a liquid-like substrate (blue; uncrosslinked PDMS). The color gradient from red to blue indicates the transition between these two limits. (c) Top-view images of breath figures formed on substrates with different softness levels, taken at the onset of drop visibility. The apparent nucleation density decreases with increasing substrate stiffness, characterized by the shear storage modulus G′. ) and rH = 1.22 (△). Horizontal lines indicate the limiting cases of a rigid substrate (red; nanometric PDMS brush grafted on a silicon wafer, see ref. 32) and a liquid-like substrate (blue; uncrosslinked PDMS). The color gradient from red to blue indicates the transition between these two limits. (c) Top-view images of breath figures formed on substrates with different softness levels, taken at the onset of drop visibility. The apparent nucleation density decreases with increasing substrate stiffness, characterized by the shear storage modulus G′. | |
Further, in ref. 33–36 it is predicted, that in the regime of intermediate softness the contact angles of steady drops transit smoothly between Young's and Neumann's laws, which is experimentally confirmed (see Fig. 2).‡ This transition in the contact angle is reminiscent of the transition observed in the drop density ψ when going from rigid to liquid-like substrates [cf.Fig. 1(b)]. The cross-over between the Young regime and the Neumann regime can be inferred from Fig. 2 to occur when the elasto-capillary length becomes comparable to the drop base radius ℓec ∼ R (cf.Fig. 3). In Fig. 1(b) the transition is found at ℓec ≈ 10 µm and thus elasticity is expected to play a role when ℓec ≈ R ≈ 10 µm. This observation is enigmatic for the typical nuclei size at the employed humidities is known to be R* ≪ 10 µm, i.e., too small to feel the elasticity of the substrate. As the drops grow larger, due to condensation, they automatically undergo a size-controlled transition in ℓec/R and elasticity gains impact. The transition shown in Fig. 2 may occur even before the diffusive boundary layer has formed.
 |
| | Fig. 2 Liquid–gas contact angle θlg relative to the horizontal as a function of the gel softness ℓec/R. Angles are measured on side-view images of droplets with radii ranging from R ≈ 10 µm to ≈1 mm, i.e., recorded at later stages, sitting on gels with storage modulus G′ ranging from 100 Pa to 106 Pa. The lightly shaded bands indicate the contact angles experimentally determined on short PDMS brushes, i.e., in the rigid limit (red), and on uncross-linked PDMS oligomers, representing the liquid-like limit (blue) for the same material. Again, the red to blue color gradient indicates the transition between these two limits. | |
 |
| | Fig. 3 Sketch of a radially symmetric drop of partially wetting liquid with base radius R. The spherical cap meets the elastic substrate along a circular three phase contact line. The macroscopic contact angle θ is governed by the energies γsv, γsl and γlv of the interfaces between the respective phases. The ratio of a surface element ds and its projection onto the (x, y)-plane defines the metric factor  of the respective profile ϕ(r). of the respective profile ϕ(r). | |
To investigate the role of elasticity in nucleation, we use a mesoscopic gradient dynamics model37 similar to the one presented in ref. 30, coupling a classic thin-film equation (TFE) for a simple liquid38,39 to the dynamics of the soft adaptive substrate employing a Kelvin–Voigt-type dynamics in Winkler-foundation form. In comparison to ref. 30, the model is extended to capture condensation and evaporation applying the one-sided approach of ref. 40–43 for evaporating sessile drops. Thereby, the saturation of the vapor phase is considered homogeneous as is the case in the very early stages of the experiment where the nucleated droplets are below the optical resolution of the equipment and therefore experimentally inaccessible. The advantage of the gradient dynamics approach is that it is derived directly from the governing energy functional, which makes it very versatile and easily adaptable to many scenarios. A somewhat similar model has been used in ref. 43 to study the dynamics of droplet growth and coalescence due to imposed local influx in dependence of the substrate softness and viscous damping. Here, the full curvature formulation37 is used which more exactly describes the static drop behavior, cf. ref. 44. The model is utilized to investigate the increase of nucleation density with increasing softness in an extended range of supersaturation that goes beyond the range considered in the experiment. In particular, we consider values where the size of the nuclei becomes comparable to the elasto-capillary length.
First, in Section 2 the macroscopic CNT is used to estimate the nucleation energy barrier in the limiting cases of perfectly rigid and liquid substrates, considering unstable steady macroscopic drops to represent the nuclei. In Section 3 the mesoscopic gradient dynamics model is used to investigate the critical nucleus in the regime of intermediate softness. We compare mesoscopic and macroscopic results in the liquid and rigid limits. Finally, the influence of substrate softness on the nucleation energy barrier is investigated in the context of the experimentally observed phenomena.
2 Macroscopic nuclei
According to CNT the change in energy associated with the creation of a new phase is given by the difference in Gibbs free energy  , implying constant temperature T, particle number N and external pressure p.18,45–48 The bulk contribution is given by the difference Δμ in chemical potentials, between initial and final state, to which the interface energies are added. In the present case of vapor condensing into liquid at a solid substrate, the change in Gibbs free energy is (see Appendix B for details)18,46–48
, implying constant temperature T, particle number N and external pressure p.18,45–48 The bulk contribution is given by the difference Δμ in chemical potentials, between initial and final state, to which the interface energies are added. In the present case of vapor condensing into liquid at a solid substrate, the change in Gibbs free energy is (see Appendix B for details)18,46–48| | 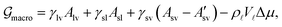 | (1) |
with γij and Aij respectively being the energies and areas of the liquid–vapor (lv), substrate–liquid (sl) and substrate–vapor (sv) interfaces and the difference in chemical potentials per particle is| | Δμ = μv − μℓ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(rH). ln(rH). | (2) |
The substrate–vapor interface area of the initial dry substrate state is  and ρℓ is the particle density of the liquid. The Gibbs free energy eqn (1) combines surface energy penalties, which in case of drop-like structures of size R scale with ∼R2, with the decrease in chemical potential per particle when changing from the vapor to the liquid phase, scaling with the created volume ∼R3. This balance results in an energy barrier
and ρℓ is the particle density of the liquid. The Gibbs free energy eqn (1) combines surface energy penalties, which in case of drop-like structures of size R scale with ∼R2, with the decrease in chemical potential per particle when changing from the vapor to the liquid phase, scaling with the created volume ∼R3. This balance results in an energy barrier  that must be overcome to nucleate and which defines a critical size R*. Since the nucleation of droplets on a substrate is a stochastic process driven by random fluctuations18 the nucleation probability P is estimated using a Boltzmann factor
that must be overcome to nucleate and which defines a critical size R*. Since the nucleation of droplets on a substrate is a stochastic process driven by random fluctuations18 the nucleation probability P is estimated using a Boltzmann factor
| |  | (3) |
The ratio in the exponent relates the energy barrier  to the thermal energy kBT. In the following, we calculate this energy barrier for a radially symmetric drop (w.r.t. the z-axis) of base radius R sitting on a deformable substrate, extended in the (x, y)-plane as shown in Fig. 3. In the limits of a perfectly rigid (ℓec = 0) and liquid-like (ℓec = ∞) substrate, elasticity can be neglected and the equilibrium drop shape is exclusively governed by the interface and bulk phase energies, i.e., it adapts spherical-cap shapes.
to the thermal energy kBT. In the following, we calculate this energy barrier for a radially symmetric drop (w.r.t. the z-axis) of base radius R sitting on a deformable substrate, extended in the (x, y)-plane as shown in Fig. 3. In the limits of a perfectly rigid (ℓec = 0) and liquid-like (ℓec = ∞) substrate, elasticity can be neglected and the equilibrium drop shape is exclusively governed by the interface and bulk phase energies, i.e., it adapts spherical-cap shapes.
2.1 Rigid limit
In the rigid limit the substrate is flat and the liquid–vapor interface of a drop or nucleus takes the shape of a spherical cap with curvature κlv as shown in Fig. 4(a). While the contact angle θY is given by the interface energies according to Young's law| | γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY + γsl = γsv, θY + γsl = γsv, | (4) |
the curvature depends on the volume of the nucleus which is yet to be determined. In terms of κlv and θY the volume is| |  | (5) |
while the interface areas are| |  | (6) |
 |
| | Fig. 4 Characteristic drop shapes of partially wetting liquid on substrates of different softness. (a) The substrate is rigid and very resistant against deformations, R ≫ ℓec. The drop adopts the shape of a spherical cap with curvature κlv and contact angle θY selected by Young's law. (b) The substrate is elastic and soft enough to allow for the formation of wetting ridges at the contact lines, R ≈ ℓec, but stiff enough to prevent the drop from sinking. The local angles at the tip of the wetting ridge are given by Neumann's law and as the softness increases the region rotates inwards such that the liquid–vapor contact angle and curvature increasingly deviate from those in the rigid case. (c) The substrate is so soft that it is considered liquid-like and elasticity is negligible, R ≪ ℓec. The drop resembles a liquid lens described by the intersection of two spherical caps with curvatures κlv and κsl. The angles at the three-phase contact are still related by Neumann's laws but the slope of the solid–liquid interface approaches zero. | |
Since the substrate is perfectly flat, the total area, that is the area  of the dry reference state, is
of the dry reference state, is  . With eqn (4)–(6) the energy (1) becomes
. With eqn (4)–(6) the energy (1) becomes
| |  | (7) |
With (2 + cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY
θY) (1 − cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY
θY)
2 = 2 − 3
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY
θY + cos
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY
θY we then find
| |  | (8) |
where the base radius
R = 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY
θY/
κlv has been introduced and the function
| | g(θ) = (2 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) (1 − cos θ) (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2/sin3 θ)2/sin3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (9) |
is a geometric prefactor that monotonically increases with
θ. Therefore, the energy barrier increases with increasing hydrophobicity of the substrate,
i.e. with increasing contact angle
θY.
The critical nucleus has to satisfy  and its resulting base radius is
and its resulting base radius is
| |  | (10) |
In consequence, at fixed Δμ a nucleated drop of base radius R < R* will shrink (evaporate) leaving behind the dry state, whereas a nucleus of base radius R > R* will grow (condense) without bound. The corresponding energy barrier is
| |  | (11) |
With
rH ≈ 2.41,
γlv = 70 × 10
−3 J m
−2,
ρℓ = 3.34 × 10
28 m
−3 and
θY = 70° the critical nucleus has a size of
R* ≈ 1.166 nm with an associated energy barrier

. Note, that the
θY-dependent factor of

in
eqn (11) increases monotonically from
g(
θY)sin(
θY)
3 = 0 in the complete wetting case (
θY = 0°) to
g(
θY)sin(
θY)
3 = 4 in the non-wetting case (
θY = 180°). In other words, low contact angles will drastically reduce the nucleation barrier.
2.2 Liquid-like limit
In the liquid-like case, i.e., for ℓec → ∞, the substrate is deformed under the influence of the Laplace pressure caused by the curved liquid–vapor interface until it is balanced by the Laplace pressure of the substrate–liquid interface. This results in the shape of a liquid lens as shown in Fig. 4(c) characterized by constant curvatures of both interfaces. While the drop sinks into the substrate the liquid–vapor and substrate–liquid interfaces form angles θlv and θsl w.r.t. the horizontal, respectively. The angles are again governed by the interface energies according to the components of Neumann's law:| | horizontal: γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlv + γsl θlv + γsl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsl = γsv, θsl = γsv, | (12) |
| | vertical: γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlv = γsl θlv = γsl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsl. θsl. | (13) |
Note, that the substrate beyond the drop is considered to remain perfectly horizontal. Similar to eqn (5) the lens volume can be expressed in terms of the curvatures and Neumann angles
| |  | (14) |
The balance of Laplace pressures results in a fixed ratio of curvatures given by the inverse ratio of the corresponding interface energies
| |  | (15) |
with the second equal sign resulting from
eqn (13). Note, that the curvature of a profile is considered negative if it is convex, as is the case for the substrate–liquid interface beneath the drop, and positive if it is concave, like the liquid–vapor interface (
cf.Fig. 4). In consequence, the difference in the Gibbs free energy
(1) becomes
| |  | (16) |
where
g(
θlv) +
g(
θsl) = 3
V/(π
R3). The critical radius and energy are then
| |  | (17) |
| |  | (18) |
respectively. Note, that the form of the expression for the critical radius
R* is identical in the rigid and liquid-like limit [
cf.eqn (10) and (17)] and that the energy for the case of a rigid substrate [
eqn (8)] is recovered from
eqn (16) in the limit
θlv =
θY and
g(
θsl) = 0. Further, the ratio

and depends only on the interface energies but not on supersaturation,
i.e., not on
R* and Δ
μ. For example, if the interface energies are
γlv = 70 × 10
−3 N m
−1,
γsl = 48 × 10
−3 N m
−1 and
γsv = 72 × 10
−3 N m
−1 the nucleation barrier differs by a factor

between the rigid and liquid-like case.
3 Mesoscopic model
In contrast to the rigid and liquid-like limit, in the intermediate elastic regime the substrate profile is not analytically known. We denote the corresponding radially symmetric height profiles by χ(r) for the liquid–vapor interface and ξ(r) for the substrate profile. The liquid layer thickness profile is then h(r) = χ(r) − ξ(r) (see Fig. 5). So far, only steady macroscopic drops have been considered. We now formulate a fully dynamic mesoscopic model that is applicable in the intermediate elastic regime as well as in the rigid and liquid-like limits. To do so, we include the mesoscopic wetting energy f(h) that governs the effective interaction of the solid–liquid and liquid–vapor interface. It is assumed to result from long-range van der Waals interactions and short-range repulsive interactions| |  | (19) |
 |
| | Fig. 5 Sketch of a mesoscopic radially symmetric drop of partially wetting liquid on an elastic substrate. The local liquid layer thickness and the substrate–liquid interface are described by scalar functions h(r) and ξ(r), respectively. Both resemble spherical caps centered at r = 0 and transit into the precursor layer of height h− (see the zoom) along a circular three phase contact region at r = R. The macroscopic base radius R is estimated by the position of maximal curvature of the liquid–vapor interface and the solid–gas interface energy is modeled by the wetting energy f(h). | |
The minimum of f(h) at h = ha [cf. thin lines in Fig. 6(a)] ensures that a macroscopically dry substrate is always covered by an ultra-thin adsorption layer of height ha, the energy of which has to be taken into account. The precise thickness h− of this layer depends on supersaturation and equals ha only for Δμ = 0 as will be further discussed in Section 3.1. In consequence, in the mesoscopic description, the macroscopic substrate–vapor interface energy is represented by the sum of the energies of the adsorption layer, substrate–liquid interface and liquid–vapor interface.
 |
| | Fig. 6 Dimensionless (a) wetting energy f and (b) Derjaguin (disjoining) pressure Π as functions of the film thickness h with Cθ = 1. Since Π = −∂hf the zeros of the Π correspond to the extrema of f and reflect steady film states. At saturation, i.e. p = 0 (thin lines), the functions allow for only one stable steady film state h− ( ). For p > 0, e.g., p = 0.1 (thick lines). A second unstable film state h+ (▼) exists. (c) With increasing p the two states approach each other and annihilate in a saddle-node bifurcation (✦). The sign of Π + p determines whether the film grows due to condensation or shrinks by evaporation (gray shaded), as indicated by the arrows for p = 0.1. ). For p > 0, e.g., p = 0.1 (thick lines). A second unstable film state h+ (▼) exists. (c) With increasing p the two states approach each other and annihilate in a saddle-node bifurcation (✦). The sign of Π + p determines whether the film grows due to condensation or shrinks by evaporation (gray shaded), as indicated by the arrows for p = 0.1. | |
Demanding consistency between the meso- and macroscopic descriptions at Δμ = 0 leads to the condition49
| | | γsv = γlv + γsl + f(ha). | (20) |
Then, together with Young's law (4), the Hamaker constant A corresponds to
| |  | (21) |
Further, the energy associated with the elastic deformation of the substrate is now taken into account. Employing the Winkler-foundation model50 it is given by
| |  | (22) |
with
S being an effective softness,
i.e., the inverse of the elastic stiffness. This formulation effectively describes the substrate as a continuous spring and follows from the fundamental solution for a finite-thickness layer with linear elasticity exposed to a localized force at the free surface. For a detailed discussion
cf. ref.
30.
The complete energy functional combines eqn (1) and (22), thereby expressing the interface areas and volumes in terms of h and ξ and the substrate–vapor interface energy γsv in terms of the wetting potential f [eqn (19) and (20)]. The energy  of a substrate with liquid coverage (drop or thick film) relative to the reference state of a macroscopically dry flat substrate is given by
of a substrate with liquid coverage (drop or thick film) relative to the reference state of a macroscopically dry flat substrate is given by
| |  | (23) |
with
| |  | (24) |
| |  | (25) |
where the domain has been restricted to a circular area of radius
L ≫
R. The dry substrate state is characterized by
h =
h−(Δ
μ). Note, that the constant
ρΔ
μ can either be seen as an imposed chemical potential (relative humidity) or as a Lagrange multiplier for volume conservation
| |  | (26) |
with
h0 being an arbitrary mean liquid layer thickness that is to be conserved.
The energy is extremized by calculating its variations w.r.t. the variables h and ξ yielding
| |  | (27) |
| |  | (28) |
with the local curvature

of a field
φ and the Derjaguin (disjoining) pressure
Π(
h) = −∂
hf(
h) (
cf.Fig. 6).
§ Note, that for
h ≫
ha one has
Π → 0 and
eqn (27) depends only on
χ =
h +
ξ, indicating that (at uniform supersaturation) the liquid–vapor interface of a steady drop always forms a spherical cap of curvature
κlv = −
ρℓΔ
μ/
γlv, entirely independent of elasticity. In consequence, at fixed contact angles also the volume of a steady drop is directly determined by the supersaturation.
To capture the time evolution we employ a gradient dynamics approach,30,37,51i.e., we use the kinetic equations
| |  | (29) |
| |  | (30) |
The dynamics of the liquid layer thickness h corresponds to a thin-film equation with mobility  and dynamic viscosity η52 which is extended by a non-conserved term that incorporates phase transition-limited mass exchange between liquid and vapor37,42,53 driven by the variation
and dynamic viscosity η52 which is extended by a non-conserved term that incorporates phase transition-limited mass exchange between liquid and vapor37,42,53 driven by the variation  with the transfer mobility M. For a discussion of other evaporation models see ref. 54. The dynamics of the substrate corresponds to the Kelvin–Voigt model and describes an exponential relaxation in time scaled by the effective substrate viscosity ζ.30 To reduce the number of parameters, the equations are non-dimensionalized using characteristic length and time scales
with the transfer mobility M. For a discussion of other evaporation models see ref. 54. The dynamics of the substrate corresponds to the Kelvin–Voigt model and describes an exponential relaxation in time scaled by the effective substrate viscosity ζ.30 To reduce the number of parameters, the equations are non-dimensionalized using characteristic length and time scales
| | t = T![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , r = ha , r = ha![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) , ξ = ha , ξ = ha![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e119.gif) , h = ha , h = ha![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) . . | (31) |
with
T = 3
ηha/
γlv. After dropping the tildes one obtains
| |  | (32) |
| |  | (33) |
with the dimensionless parameters
| |  | (34) |
Here,  is the predicted curvature of the liquid–vapor interface of the macroscopic critical nucleus [eqn (17)]. From here on, p refers to the (dimensionless) supersaturation, defined above. The thickness of the adsorption layer is chosen as the thermal capillary length
is the predicted curvature of the liquid–vapor interface of the macroscopic critical nucleus [eqn (17)]. From here on, p refers to the (dimensionless) supersaturation, defined above. The thickness of the adsorption layer is chosen as the thermal capillary length  , which is used in molecular kinetic theory (MKT) of wetting and capillary wave theory (CWT).55–57 It scales the thermal fluctuation of the liquid–vapor interface and in that sense the diffusivity of the latter. From an energetic perspective it defines the scale at which the thermal energy competes with the energy penalty associated with an increased interfacial area due to the interface tension γlvha2 = kBT. Hence, in the following all energies are expressed in terms of the thermal energy kBT. With
, which is used in molecular kinetic theory (MKT) of wetting and capillary wave theory (CWT).55–57 It scales the thermal fluctuation of the liquid–vapor interface and in that sense the diffusivity of the latter. From an energetic perspective it defines the scale at which the thermal energy competes with the energy penalty associated with an increased interfacial area due to the interface tension γlvha2 = kBT. Hence, in the following all energies are expressed in terms of the thermal energy kBT. With  and
and  it follows that
it follows that  . The elastocapillary length used in Fig. 4 is related to the softness s by30
. The elastocapillary length used in Fig. 4 is related to the softness s by30
| |  | (35) |
The shape of a steady drop sitting on an elastic substrate and the profile of the latter are usually characterized by the ratio of elastocapillary length to drop size, e.g., ℓec/R or  [cf.Fig. 4].¶
[cf.Fig. 4].¶
3.1 Steady film states
Before turning to the critical nuclei, we consider the case of a steady liquid layer of uniform thickness h(r) = h0 on an undisturbed flat substrate ξ(r) = 0. Then, the Laplace pressures vanish and the dimensionless total pressures [eqn (27) and (28)] reduce to| |  | (36) |
In Fig. 6(b) the total pressure  [eqn (36)] is shown as a function of uniform liquid layer thickness for p = 0.1. Fig. 6(a) displays the associated energy f(h) − ph. The respective thin lines give the case p = 0. According to eqn (36) a steady film state may only exist if the supersaturation is balanced by the Derjaguin pressure, leading to
[eqn (36)] is shown as a function of uniform liquid layer thickness for p = 0.1. Fig. 6(a) displays the associated energy f(h) − ph. The respective thin lines give the case p = 0. According to eqn (36) a steady film state may only exist if the supersaturation is balanced by the Derjaguin pressure, leading to
| |  | (37) |
Hence, two different steady film states may exist depending on the value of p, controlled by the relative humidity rH. The adsorption layer height h− represents the dry substrate state and corresponds to a minimum in the energy f(h) − ph, i.e., it is linearly stable [cf.Fig. 6(c)]. Note, that, as h− changes with p, the value of f(h−) changes as well resulting in turn in an increased substrate–vapor interface energy, according to the consistency condition (20).
From eqn (37) it is found, that in the limit p → 0 the liquid layer thickness either diverges to h+ → ∞ or becomes h− = 1, i.e., h− = ha in dimensional terms. From there, the two flat film states asymptotically follow h− ≈ 1 + p/3Cθ and h+ ≈ (Cθ/p)1/3. Increasing the supersaturation to p > 0 the pressure is correspondingly shifted while the energy is tilted by the linear term −ph. This results in a second zero crossing of the pressure, i.e., an additional maximum of the energy, associated with h+. The latter is hence unstable and represents a threshold similar to a nucleus but for uniform film states, that is, every uniform film of thickness h > h+ grows by condensation while for h < h+ it shrinks by evaporation until the dry state h− is reached. As p increases further, h− and h+ approach each other until they finally meet and vanish in a saddle-node bifurcation at pc = −Πmin = Cθ/4 where  [eqn (37)] as shown in Fig. 6(c). For p > −Πmin the Derjaguin pressure cannot compete with the supersaturation any more and nothing prevents the vapor from condensing into the liquid film.
[eqn (37)] as shown in Fig. 6(c). For p > −Πmin the Derjaguin pressure cannot compete with the supersaturation any more and nothing prevents the vapor from condensing into the liquid film.
3.2 Critical nuclei
3.2.1 Numerical approach and parameters.
The mesoscopic model is now utilized to explore the critical nuclei in the regime of intermediate elasticity by numerically solving eqn (32) and (33). To this end, the open source C++ library Oomph-lib58 is used to perform parameter continuation and time simulations. As discussed before, the critical nucleus is associated with a maximum of the Gibbs free energy  . Thus, in the mesoscopic model one has to solve
. Thus, in the mesoscopic model one has to solve  . To do so numerically, by using a Newton solver, a proper starting state is required, which has to closely resemble the final solution. While in the rigid and liquid-like limit the macroscopic spherical cap profiles might be sufficiently suited, this is usually not the case in the intermediate elastic regime 0 < s < ∞. Further the critical nucleus cannot be found using time simulations as it is associated with a maximum of the Gibbs free energy and thus unstable. Therefore, we make use of a trick; instead of an isothermal–isobaric ensemble, a canonical ensemble is considered. The drop state then corresponds to a minimum of the Helmholtz free energy and can thus be approached using time simulations. Thereby, the supersaturation is used as a Lagrange multiplier and adapts freely during the simulation to enforce conservation of an imposed volume V0. The stable steady drop found in the canonical ensemble exactly corresponds to a critical nucleus in the isothermal–isobaric ensemble if the supersaturation is set to
. To do so numerically, by using a Newton solver, a proper starting state is required, which has to closely resemble the final solution. While in the rigid and liquid-like limit the macroscopic spherical cap profiles might be sufficiently suited, this is usually not the case in the intermediate elastic regime 0 < s < ∞. Further the critical nucleus cannot be found using time simulations as it is associated with a maximum of the Gibbs free energy and thus unstable. Therefore, we make use of a trick; instead of an isothermal–isobaric ensemble, a canonical ensemble is considered. The drop state then corresponds to a minimum of the Helmholtz free energy and can thus be approached using time simulations. Thereby, the supersaturation is used as a Lagrange multiplier and adapts freely during the simulation to enforce conservation of an imposed volume V0. The stable steady drop found in the canonical ensemble exactly corresponds to a critical nucleus in the isothermal–isobaric ensemble if the supersaturation is set to  .
.
From this given critical nucleus, a continuation routine may be used to obtain the critical nucleus at a specific value of p. Such continuation techniques rely on the concept that small changes in a parameter, e.g., p, cause only small changes to a steady state in turn. Hence, if a steady state is known for a given parameter value p0, it is assumed to be well suited as initial condition to find the steady state at p = p0 + Δp if Δp is sufficiently small. This way, a steady state can be followed in parameter space.59–61
For all results the parameters are fixed to the values
| |  | (38) |
if not stated otherwise. The adsorption layer thickness is

. The corresponding values of the dimensionless parameters are
p ≈ 0.0226,
Cθ ≈ 2.2 and
σ ≈ 0.6857. Note, that in this setting a steady drop on a rigid substrate exhibits
θY = 70° and
R*/
ha ≈ 83.
3.2.2 Consistency in the rigid and liquid limit.
To validate our numerical results, first, the mesoscopic pendant of the macroscopic radius-dependent energy  [eqn (16)] is calculated for comparison. In the mesoscopic picture, the base radius R of a steady drop, i.e., a critical nucleus, is not known a priori. However, the macroscopic calculations in the rigid and liquid-like cases provide reasonable estimates also for the elastic regime, since R is assumed to transit monotonically between these two limits. Since there is no sharp three phase contact line in the mesoscopic description, the base radius is instead defined by the position R of maximal curvature of the liquid–vapor interface, i.e., κ(h + ξ)|r=R = max[κ(h + ξ)] (cf.Fig. 5), which is equivalent to Π(h)|r=R = min[Π(h)]. It is thus encoded in the profiles h and ξ such that
[eqn (16)] is calculated for comparison. In the mesoscopic picture, the base radius R of a steady drop, i.e., a critical nucleus, is not known a priori. However, the macroscopic calculations in the rigid and liquid-like cases provide reasonable estimates also for the elastic regime, since R is assumed to transit monotonically between these two limits. Since there is no sharp three phase contact line in the mesoscopic description, the base radius is instead defined by the position R of maximal curvature of the liquid–vapor interface, i.e., κ(h + ξ)|r=R = max[κ(h + ξ)] (cf.Fig. 5), which is equivalent to Π(h)|r=R = min[Π(h)]. It is thus encoded in the profiles h and ξ such that  can be seen as
can be seen as  . Note, that the adsorption layer height h− specifies a lower bound for the liquid layer thickness h, which in turn imposes a restriction to the minimal critical nucleus size min(R*) ∼ h−, in contrast to the macroscopic picture where no such limit exists. This restriction in turn sets a critical supersaturation pc, since R* ∼ p−1, beyond which no steady nucleus states are possible anymore. The energy
. Note, that the adsorption layer height h− specifies a lower bound for the liquid layer thickness h, which in turn imposes a restriction to the minimal critical nucleus size min(R*) ∼ h−, in contrast to the macroscopic picture where no such limit exists. This restriction in turn sets a critical supersaturation pc, since R* ∼ p−1, beyond which no steady nucleus states are possible anymore. The energy  can be calculated in two different ways:
can be calculated in two different ways:
(1) Quasi-static relaxation: in the first method, we consider the dynamics of a drop state as given by eqn (32) and (33) using a very small transfer mobility m such that all hydrodynamic relaxation processes due to capillarity and wettability (the conserved part of the dynamics) take place much faster than the exchange of mass between the phases. Starting from the critical nucleus state, the liquid height profile h is disturbed using white noise with a small positive or negative mean to nudge condensation or evaporation, respectively. While the drop then slowly shrinks or grows, the base radius and energy are calculated. Due to the very slow mass transfer, the drop is considered quasi-static during the process, which allows for  to be faithfully recovered.
to be faithfully recovered.
(2) Continuation: in the second method, continuation is used to trace the critical nucleus state over a range of p. As the size of the critical nucleus is R*(p) ∼ p−1, a continuation in p effectively corresponds to a continuation in R*. Inserting the p values from the continuation into eqn (24) and (25) along with the corresponding profiles h*(r;p) and ξ*(r;p) gives the nucleation energy barrier as a function of supersaturation or base radius  . However, right now we are not looking for the energy barrier
. However, right now we are not looking for the energy barrier  but for
but for  , the two of which differ only by the value of p used in the calculation, at otherwise fixed parameters. Basically we ask: How does the energy of the critical nucleus characterized by h* and ξ* look like, if we evaluate it at another value of p than the one at which it is a steady state? From eqn (24) and (25) it is seen, that the difference in
, the two of which differ only by the value of p used in the calculation, at otherwise fixed parameters. Basically we ask: How does the energy of the critical nucleus characterized by h* and ξ* look like, if we evaluate it at another value of p than the one at which it is a steady state? From eqn (24) and (25) it is seen, that the difference in  caused by a change Δp is given by
caused by a change Δp is given by
| |  | (39) |
Hence, the energy barriers  obtain for a set of values p during the continuation can be mapped to an arbitrary value
obtain for a set of values p during the continuation can be mapped to an arbitrary value ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) to obtain
to obtain
| |  | (40) |
Fig. 7 shows  as a function of drop radius in the liquid limit (blue), the rigid limit (red) and for an intermediate elastic case (purple). Both described methods are compared to the macroscopic result. While the mesoscopic values obtained by continuation (
as a function of drop radius in the liquid limit (blue), the rigid limit (red) and for an intermediate elastic case (purple). Both described methods are compared to the macroscopic result. While the mesoscopic values obtained by continuation (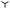 symbols) agree very well with the ones obtained by the quasi-static approach (solid lines), both are slightly smaller than the macroscopic analytical predictions (black dashed). This results from the differences between the macroscopic and mesoscopic nucleus profiles in the contact line region.|| More importantly, the positions of the energy maxima, i.e., the critical radii R* (marked by ▼), are correctly recovered. The overall agreement between macroscopic and mesoscopic model is quite satisfactory, allowing us to use the latter for exploring the critical nucleus characteristics in the elastic regime. The purple line in Fig. 7 shows the energy as obtained by the first method for an exemplary intermediate softness s = 103 and lies between the rigid and liquid-like limits, as expected.
symbols) agree very well with the ones obtained by the quasi-static approach (solid lines), both are slightly smaller than the macroscopic analytical predictions (black dashed). This results from the differences between the macroscopic and mesoscopic nucleus profiles in the contact line region.|| More importantly, the positions of the energy maxima, i.e., the critical radii R* (marked by ▼), are correctly recovered. The overall agreement between macroscopic and mesoscopic model is quite satisfactory, allowing us to use the latter for exploring the critical nucleus characteristics in the elastic regime. The purple line in Fig. 7 shows the energy as obtained by the first method for an exemplary intermediate softness s = 103 and lies between the rigid and liquid-like limits, as expected.
 |
| | Fig. 7 Comparison of the macroscopic energy  and mesoscopic energy and mesoscopic energy  as functions of the base radius R. The macroscopic energies are obtained analytically and plotted as dashed lines for the liquid-like (blue) and rigid (red) limit respectively. The mesoscopic energies are calculated using quasi-static time simulations (1st method, solid lines) and continuation (2nd method, as functions of the base radius R. The macroscopic energies are obtained analytically and plotted as dashed lines for the liquid-like (blue) and rigid (red) limit respectively. The mesoscopic energies are calculated using quasi-static time simulations (1st method, solid lines) and continuation (2nd method, 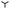 symbols). The critical radii and the energetic maxima are indicated by the ▼ symbols. The mesoscopic model is also used to capture the regime of intermediate elasticity, here the quasi-static method is used for s = 103 (dark purple curve). symbols). The critical radii and the energetic maxima are indicated by the ▼ symbols. The mesoscopic model is also used to capture the regime of intermediate elasticity, here the quasi-static method is used for s = 103 (dark purple curve). | |
3.2.3 Influence of supersaturation and elasticity.
Key to the investigation of the nucleation probability are the critical nuclei, i.e., the steady states corresponding to the maxima in Fig. 7. The corresponding results obtained from the continuation in supersaturation p as explained in Section 3.2.2, are shown in Fig. 8(a), giving the volume as a function of p on a log–log scale. The stable and unstable flat film states h− and h+ discussed in Section 3.1 are given as black solid and dashed lines, respectively. The volumes are given by V± = πh±L2. The volumes of the critical nuclei are shown for the rigid (red) and liquid (blue) limit. Thereby, the macroscopically obtained results (thin lines) [eqn (5) and (14)] are compared to the mesoscopically obtained ones (thick lines). The volumes are obtained by integration of the numerically determined thickness profiles,  . The volumes of all states, except for h−, increase with decreasing supersaturation p. In the low p limit, i.e., at large volumes, the macroscopic and mesoscopic critical nucleus states well agree and show the predicted scaling V ∼ p−3. As the nucleus size decreases (increasing p), the mesoscopic results deviate from the macroscopic predictions (see Section 3.2), approach Vdry = πh−L2, and eventually end in a pitchfork bifurcation, very close to the saddle-node bifurcation of the uniform states (♦ symbol). Note further, that the volumes of the mesoscopic states all depend on the system size L, since the adsorption layer, which is present in the macroscopically dry areas, contributes with a volume per unit area ha. Therefore, we also provide in the inset Fig. 8(b) the effective condensed volume
. The volumes of all states, except for h−, increase with decreasing supersaturation p. In the low p limit, i.e., at large volumes, the macroscopic and mesoscopic critical nucleus states well agree and show the predicted scaling V ∼ p−3. As the nucleus size decreases (increasing p), the mesoscopic results deviate from the macroscopic predictions (see Section 3.2), approach Vdry = πh−L2, and eventually end in a pitchfork bifurcation, very close to the saddle-node bifurcation of the uniform states (♦ symbol). Note further, that the volumes of the mesoscopic states all depend on the system size L, since the adsorption layer, which is present in the macroscopically dry areas, contributes with a volume per unit area ha. Therefore, we also provide in the inset Fig. 8(b) the effective condensed volume  for the mesoscopic states, i.e., the volume above the adsorption layer. This measure is independent of system size.
for the mesoscopic states, i.e., the volume above the adsorption layer. This measure is independent of system size.
 |
| | Fig. 8 Volume of the mesoscopic flat uniform steady film states (black) and of the critical nuclei in the rigid (red) and liquid-like (blue) limit as a function of the supersaturation p. (a) The total volume of the steady states, which in the mesoscopic picture includes the adsorption layer and therefor depends on system size. For small p the mesoscopic (thick lines) and macroscopic (thin lines) results agree and recover the scaling law V ∼ p−3. For larger p, the mesoscopic nuclei deviate form the macroscopic ones. All branches of mesoscopic states end at or near the saddle-node bifurcation of the film states (✦ symbol). (b) The inset gives the effective condensed volume, namely the volume above h−, as a function of p in the range close to the bifurcation shaded gray in (a). The numerical domain was restricted to circular region of radius L = 500ha. | |
Fig. 8(b) shows a better agreement of mesoscopic and macroscopic results that is maintained up to higher supersaturation. Only as pc = Cθ/4 is approached a clear deviation is visible. Linear stability analysis for an infinite domain size shows, that the bifurcation point where the branch of mesoscopic critical nuclei emerges coincides with the saddle-node bifurcation. For a finite domain, however, the bifurcation is shifted a bit along the h+ branch. Most remarkably, this bifurcation is then found at different positions (marked by 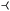 ) in the rigid and liquid-like limit. Again, the disagreement of macroscopic and mesoscopic model for p → Cθ/4 is assumably caused by the different nucleus shapes due to the diffuse contact region present in the latter, which gains impact as the nucleus size decreases.
) in the rigid and liquid-like limit. Again, the disagreement of macroscopic and mesoscopic model for p → Cθ/4 is assumably caused by the different nucleus shapes due to the diffuse contact region present in the latter, which gains impact as the nucleus size decreases.
In the same way, the nucleation barrier can be calculated from the mesoscopic profiles using eqn (24) and (25) and compared to the macroscopic prediction eqn (18). In Fig. 9 the energy barrier is shown as a function of supersaturation (using the same line styles as in Fig. 8). Again, both levels of description agree well in the small p limit, recovering the predicted power law  . The barrier increases with decreasing supersaturation in agreement with Section 3.2. Beyond that, the mesoscopic model estimates the energy barrier for p → pc to be up to several orders of magnitude smaller than the macroscopic value. This indicates, that the CNT, i.e., the employed macroscopic model, strongly underestimates the nucleation probability close to the critical point. In Fig. 10 a mesoscopic critical nucleus on a soft substrate is shown for p ≈ pc. At pc = Cθ/4 the mesoscopic nucleation energy barrier even vanishes, such that the vapor condenses uncontrollably into the liquid phase for p > pc. The dimensionless critical supersaturation pc = Cθ/4 translates to the critical relative humidity
. The barrier increases with decreasing supersaturation in agreement with Section 3.2. Beyond that, the mesoscopic model estimates the energy barrier for p → pc to be up to several orders of magnitude smaller than the macroscopic value. This indicates, that the CNT, i.e., the employed macroscopic model, strongly underestimates the nucleation probability close to the critical point. In Fig. 10 a mesoscopic critical nucleus on a soft substrate is shown for p ≈ pc. At pc = Cθ/4 the mesoscopic nucleation energy barrier even vanishes, such that the vapor condenses uncontrollably into the liquid phase for p > pc. The dimensionless critical supersaturation pc = Cθ/4 translates to the critical relative humidity
| |  | (41) |
which for the values given in
eqn (38) is
rcH ≈ 3.6553.
 |
| | Fig. 9 Nucleation energy barrier  as a function of supersaturation p. The presented data are the same as in Fig. 8. as a function of supersaturation p. The presented data are the same as in Fig. 8. | |
 |
| | Fig. 10 Shape of a mesoscopic critical nucleus on an elastic substrate for p ≈ pc = Cθ/4. The profiles h and ξ exhibit only slight modulations of 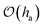 and barely resemble spherical caps. and barely resemble spherical caps. | |
Finally, the mesoscopic model is used to investigate the influence of elasticity on the nucleation probability. Once again, continuation is employed, however, this time we explore the substrate softness ℓec/R* at fixed supersaturation p. The resulting energy barrier is displayed in Fig. 11. With the transition from the rigid to the liquid-like limit, i.e. with increasing softness, the energy barrier decreases by a factor greater than 2. This decrease in the energy barrier is amplified through the Boltzmann exponent [eqn (3)], and may therefore strongly affect the nucleation probability and, consequently, the observed droplet density, (qualitatively) explaining recent observations in ref. 31. Note that the transition occurs approximately when R* ∼ ℓec.
 |
| | Fig. 11 Threshold energy as a function of substrate softness at fixed supersaturation p = 0.1. The energy barrier decreases with increasing softness, resulting in a strongly increased nucleation probability. Note, that the transition takes place at about ℓec ∼ R*. | |
4 Conclusion
Recent experiments showed that the nucleation density of dew is strongly affected by the softness of the elastic substrate controlled by the crosslinking ratio of a gel. The nucleation probability can be predicted as a Boltzmann factor and is therefore governed by the energy barrier  given by the critical nucleus. This barrier in Gibbs free energy has been calculated in the macroscopic picture in both, the rigid and the liquid-like limit. For the given interface energies the nucleation energy in the liquid-like limit is about half the one in the rigid limit. To further explore the regime of intermediate elasticity, a mesoscopic gradient dynamics model has been employed to determine the energy as a function of supersaturation p and softness ℓec/R*. The macroscopic and mesoscopic models were found to agree in the limit of rigid and liquid substrates, as long as the critical nucleus is of sufficiently large volume, i.e., when a relatively small supersaturation is considered. Both models predict a decrease in the energy barrier with increasing supersaturation, indicating an overall increased nucleation density at higher supersaturation. At large supersaturation, the macroscopic model considerably overestimates the energy barrier by several orders of magnitude as compared to the mesoscopic theory, resulting in an underestimated nucleation probability. This deviation is caused by the difference in nucleus shape; while mesoscopic nuclei exhibit diffuse contact regions that increasingly influence their shape as R* → h−, the shape of macroscopic nuclei is (in the rigid and the liquid-like limit) invariant under changes in size, which is most likely not justified as microscopic scales are approached. Next, the change of the energy barrier with increasing substrate softness at fixed supersaturation has been investigated using the mesoscopic model. The decrease in the energy barrier has been shown to coincide with the transition of contact angles from Young (rigid) to Neumann (liquid-like) at ℓec ∼ R*. However, in the experiments the increase in drop number occurred in the range 10−7 m < ℓec < 10−3 m and since the critical nuclei are considered to be of nanometer size, it is still unclear why nucleation depends on the substrate softness at all. Beyond that, the critical nucleus volume is found to decrease with the substrate softness, allowing for the formation of more nuclei if the vapor access is limited, e.g., by slow transport in the gas phase.
given by the critical nucleus. This barrier in Gibbs free energy has been calculated in the macroscopic picture in both, the rigid and the liquid-like limit. For the given interface energies the nucleation energy in the liquid-like limit is about half the one in the rigid limit. To further explore the regime of intermediate elasticity, a mesoscopic gradient dynamics model has been employed to determine the energy as a function of supersaturation p and softness ℓec/R*. The macroscopic and mesoscopic models were found to agree in the limit of rigid and liquid substrates, as long as the critical nucleus is of sufficiently large volume, i.e., when a relatively small supersaturation is considered. Both models predict a decrease in the energy barrier with increasing supersaturation, indicating an overall increased nucleation density at higher supersaturation. At large supersaturation, the macroscopic model considerably overestimates the energy barrier by several orders of magnitude as compared to the mesoscopic theory, resulting in an underestimated nucleation probability. This deviation is caused by the difference in nucleus shape; while mesoscopic nuclei exhibit diffuse contact regions that increasingly influence their shape as R* → h−, the shape of macroscopic nuclei is (in the rigid and the liquid-like limit) invariant under changes in size, which is most likely not justified as microscopic scales are approached. Next, the change of the energy barrier with increasing substrate softness at fixed supersaturation has been investigated using the mesoscopic model. The decrease in the energy barrier has been shown to coincide with the transition of contact angles from Young (rigid) to Neumann (liquid-like) at ℓec ∼ R*. However, in the experiments the increase in drop number occurred in the range 10−7 m < ℓec < 10−3 m and since the critical nuclei are considered to be of nanometer size, it is still unclear why nucleation depends on the substrate softness at all. Beyond that, the critical nucleus volume is found to decrease with the substrate softness, allowing for the formation of more nuclei if the vapor access is limited, e.g., by slow transport in the gas phase.
Finally, the nucleation energy barriers, even those predicted by the mesoscopic model, are about two orders of magnitude too large to satisfactorily explain the experimentally observed nucleation densities, even though the tendency with changing softness fits qualitatively. To appreciate the implications of such large energy barriers, we consider the resulting nucleation probabilities in the rigid and liquid-like regimes, for which the difference in energy barriers is about 50%. Using the Boltzmann factor to estimate the nucleation probability would for p = 0.1 yield
| |  | (42) |
A similar argument can be applied to the comparison of the energy barrier at different p, resulting in huge differences in the nucleation probability and indicating a strong dependence of the nucleation rate on the supersaturation, which could not be observed in the experiments. That being said, it was found that the mesoscopic nucleation energy barrier drastically decreases as pc is approached and reaches  at about
at about  which translates to rH ≈ 3.2657 or r0H = 1.2184. The behavior at large p depends strongly on the nucleus shape and, in turn, on the functional form of the wetting potential f(h) – many different forms are discussed in the literature.38–42,49,52–54,59 Further, the range of attractive microscopic interactions is determined by the rate at which f converges to zero as h increases. Increasing this range increases the width of the contact region, which in turn causes the energy barrier to fall off quicker as pc is approached.
which translates to rH ≈ 3.2657 or r0H = 1.2184. The behavior at large p depends strongly on the nucleus shape and, in turn, on the functional form of the wetting potential f(h) – many different forms are discussed in the literature.38–42,49,52–54,59 Further, the range of attractive microscopic interactions is determined by the rate at which f converges to zero as h increases. Increasing this range increases the width of the contact region, which in turn causes the energy barrier to fall off quicker as pc is approached.
All of this points towards the incompleteness of the procedure to estimate the nucleation probability using only the Boltzmann factor. As discussed in ref. 31 the relation between the observed drops and the nucleation rate is much more intricate than that. On the one hand, the classical nucleation theory is a strongly approximated description that considers macroscopic concepts like interface energies. The validity of the latter is at least questionable in the context of microscopic nuclei of only a few particles in size, which renders the entire CNT obsolete. Even though the mesoscopic model accounts for the influence of microscopic interactions in terms of the wetting potential, the use of a more advanced model, e.g., the dynamic nucleation theory (DNT) or the extended modified liquid drop (EMLD) model or both, might deliver more satisfying results. On the other hand, the experimental capabilities of capturing the nucleation process are strongly confined with regard to spatial as well as temporal resolution, both of which are of importance. In consequence, it cannot be ruled out that other physical processes are interfering. In particular, the halted nucleation of new drops in the dry regions of the initial breath figure is caused by the formation of a saturated diffusive boundary layer close to the substrate,24,31 which requires to spatially resolve the vapor density. A suspected cause that might enhance this effect is the cloaking of drops by liquids leaking from the substrate. This would alter the droplet shape and interface energy and therefore explain the discrepancy between experiments and theory. In addition the coarsening of drops was found to be suppressed on softer substrates both experimentally,26 and theoretically30 resulting in an increased drop density in turn. Finally, even though contaminants and impurities were ruled out as an additional source of nucleation in the experiments, there might still be microscopic heterogeneities present at the substrate surface, e.g., due to the molecular structure of the polymer network, which affect the nucleation rate. The impact of such effects is largely unknown and may be subject of future investigation.
Author contributions
Christopher Henkel: conceptualization, methodology, software, data curation, validation, formal analysis, investigation, visualization, writing – original draft, project administration; Ambre Bouillant: conceptualization, methodology, validation, formal analysis, investigation, writing – original draft; Jacco H. Snoeijer: conceptualization, methodology, writing – review & editing, supervision, funding acquisition; Uwe Thiele: conceptualization, methodology, writing – review & editing, supervision, project administration, funding acquisition.
Conflicts of interest
There are no conflicts to declare.
Data availability
The data presented in this article, including source codes of simulations, data set, data processing and plotting routines, are available via a Zenodo repository DOI: https://doi.org/10.5281/zenodo.16792688.
Appendices
A Temperature-induced condensation
The threshold of phase transition, i.e., saturation, can be predicted by the Clausius–Clapeyron relation. This relation is, however, often corrected to match experiments. For instance, the Rankine law introduces empirical constants to capture the temperature dependence of latent heat, while the Arden-Buck law further accounts for water vapor non-idealities over a wide temperature range.62 We adopt the latter semi-empirical law, which is widely used in meteorology and engineering for its accuracy and practicality| |  | (43) |
with T in °C and p in kPa and the empirical constants a ≈ 0.61121 kPa, b ≈ 18.678, c ≈ 234.5 °C and d ≈ 257.14 °C which are valid for T > 0 °C. For example, fixing the chamber humidity to r0H = 0.9 at the roof and cooling the gel from 20 °C to 5 °C, the relative humidity in the immediate vicinity of the substrate is rH ≈ 2.41.
B Classical nucleation theory
The transition of a particle from an initial phase to another one may occur spontaneously only if that process is associated with a decrease in free energy. This condition must be met also in the context of nucleation in order for a new phase to spontaneously emerge and grow. The formation of the latter, however, is always accompanied by the creation of an interface (with the surrounding initial phase), which represents an energy penalty. Assuming the new cluster to adapt a shape that minimizes the surface to volume ratio (provided the material is able to do that) the energy penalty is minimized as well. Since this ratio usually decreases further with increasing volume, the decrease in free energy per particle entering the new phase eventually predominates the penalty associated with the interface created in the same course. The minimal structure at which that happens corresponds to an energetic maximum and is referred to as a nucleus. It is these nuclei that initiate the formation of a new phase, once the associated energy barrier is overcome. In other words, the nucleus corresponds to a steady yet unstable threshold state, meaning that every smaller structure decays and every larger structure grows. The exact form of the governing energy and thus the characteristics of the nucleus crucially depend on the considered scenario. Two general cases are distinguished:
Homogeneous nucleation
A homogeneous initial phase, consisting of only one particle type, is considered. Due to thermal fluctuations these particles occasionally form small clusters of a new phase, that eventually start growing spontaneously if they exceed a critical size or particle number. In other words, these clusters of the same particle type may serve as nuclei. The energy penalty is exclusively governed by the interface energy between the initial and new phase and a lower bound may be estimated by assuming the nucleus to take a spherical shape.
Heterogeneous nucleation
The initial state is assumed heterogeneous in a sense that particles of different type may be present in some form ranging from microscopic impurities up to macroscopic structures (e.g. a solid substrate). If the interaction of the nucleating particle type with another type (expressed in terms of interface energies) is stronger than the interaction with its own type, nucleation is energetically favored wherever that other type is present. An example are the considered breath figures, where water vapor condenses to the liquid state at the surface of a cooled substrate. The energy penalty is then given by the interplay of interface energies between all the various phases.
The bulk energy gain associated with the nucleation is given by the difference in Gibbs free energy, and thus by the difference in chemical potentials, between initial and final state,18,45–48 implying constant temperature T, particle number N and external pressure p.** In the following we consider a small region in the immediate vicinity of the substrate such that the temperature in the gas phase is approximately constant and equal to the temperature of the substrate. The chemical potentials μℓ, μv of the liquid and vapor phase can be quantified either by employing a real gas theory, e.g. by considering a van der Waals gas, and performing a standard Maxwell construction or by assuming the vapor to behave like an ideal gas and fixing the chemical potential and particle density in the liquid. Following the latter route, the vapor obeys the corresponding equation of state pV = NkBT and its chemical potential is
| |  | (44) |
with Boltzmann constant
kB and the thermal wavelength
Λ,
i.e. the de Broglie wave length at thermal energy. Note, that the chemical potential is a function of temperature and pressure
μ(
T,
p)
via the equation of state. Consequently, chemical potential and pressure are not independent variables in an isothermal process. At equilibrium in an isothermal situation, the change in chemical potential associated with a change in pressure is determined by the Gibbs–Duhem relation
Including the ideal gas law and after integrating we find for the vapor
| |  | (46) |
with

being an arbitrary reference pressure. Assuming constant particle density in the liquid
ρℓ =
Nℓ/
Vℓeqn (45) becomes
| |  | (47) |
Then, the liquid pressure and chemical potential are directly related via the constant particle density. The difference in chemical potentials between liquid and vapor phase results to
| |  | (48) |
Demanding phase coexistence at a specific saturation pressure psatv, i.e. μℓ(psatv) = μv(psatv), the reference pressures have to be set to  , leading to
, leading to
| |  | (49) |
with the relative humidity
rH =
pv/
psatv. Fixing the chemical potential, and hence also the pressure, of the liquid to those of the vapor at saturation,
i.e. μℓ =
μv(
psatv) and
pℓ =
psatv, only the logarithmic term remains. If the gas phase is considered an ideal mixture of
K species (
e.g. water vapor in N
2) its total pressure
p is the sum of all partial pressures
pi according to Dalton's law

. The Gibbs–Duhem relation then writes
| |  | (50) |
Allowing only one component, e.g. i = v, to condense into a liquid phase coexistence requires μℓ(psat) = μv(psatv) where now  is the total pressure of the mixture at saturation of component v. In consequence, the reference pressures in eqn (48) have to be chosen differently, namely
is the total pressure of the mixture at saturation of component v. In consequence, the reference pressures in eqn (48) have to be chosen differently, namely  and
and  , yielding
, yielding
| |  | (51) |
According to classical thermodynamics the Gibbs free energy is given by  with Helmholtz free energy
with Helmholtz free energy  , the externally imposed total gas pressure p and the total volume V. The Gibbs free energies of the coexisting liquid and gas phase (including vapor) state
, the externally imposed total gas pressure p and the total volume V. The Gibbs free energies of the coexisting liquid and gas phase (including vapor) state  and the pure gas state
and the pure gas state  are given by
are given by
| |  | (52) |
and
| |  | (53) |
The energy difference then becomes
| |  | (54) |
For clarification the separate steps are explained: at 〈1〉 the volume of the coexistence state is divided into a liquid and a gas part V = Vℓ + Vg. Further, all components of the gas mixture share the same volume Vi = Vg = V − Vℓ and  , such that the respective partial pressure terms cancel with eqn (50). At 〈2〉 the particle conservation in the gas phase
, such that the respective partial pressure terms cancel with eqn (50). At 〈2〉 the particle conservation in the gas phase  is used for all components of the mixture i ≠ v. At 〈3〉 the global particle conservation of species v is used, i.e.
is used for all components of the mixture i ≠ v. At 〈3〉 the global particle conservation of species v is used, i.e. . At 〈4〉 eqn (50) is used again to eliminate the sum since dp = 0. Note, that not only the total pressure p but also the partial pressures
. At 〈4〉 eqn (50) is used again to eliminate the sum since dp = 0. Note, that not only the total pressure p but also the partial pressures  are held constant in the considered system. Hence, since chemical potential and pressure are not independent in an isotherm
are held constant in the considered system. Hence, since chemical potential and pressure are not independent in an isotherm  . The difference in chemical potentials is expressed using eqn (51) and finally the pressure difference commonly neglected.46,47 Finally, the energy gap is exclusively governed by the difference in chemical potentials. For rH > 1, i.e. pv > psatv, the difference in the Gibbs free energy is always negative such that a transition of particles from vapor to condensed state is always favorable. As mentioned above, this condition, referred to as supersaturation, is a prerequisite for spontaneous nucleation to occur and the new phase to grow. Finally, the change in Gibbs free energy associated with the creation of a liquid cluster of arbitrary shape from its own vapor in contact with a substrate is found by adding the interface energy penalties18,46–48
. The difference in chemical potentials is expressed using eqn (51) and finally the pressure difference commonly neglected.46,47 Finally, the energy gap is exclusively governed by the difference in chemical potentials. For rH > 1, i.e. pv > psatv, the difference in the Gibbs free energy is always negative such that a transition of particles from vapor to condensed state is always favorable. As mentioned above, this condition, referred to as supersaturation, is a prerequisite for spontaneous nucleation to occur and the new phase to grow. Finally, the change in Gibbs free energy associated with the creation of a liquid cluster of arbitrary shape from its own vapor in contact with a substrate is found by adding the interface energy penalties18,46–48
| |  | (55) |
with
γij and
Aij respectively being the energy and area of the liquid–vapor (lv), substrate–liquid (sl) and substrate–vapor (sv) interfaces and the prime referring to the pure gas state. This equation is the starting point for the modeling approach and corresponds to
eqn (1).
Acknowledgements
UT and JS acknowledges support by the Deutsche Forschungs-gemeinschaft (DFG) via Grants TH781/12 and SN145/1-1, respectively, within SPP 2171. AB acknowledges support from the French Agence Nationale de la Recherche (ANR JCJC MORNING). We are grateful to Bruno Andreotti, Jan Diekmann, Simon Hartmann for discussions.
Notes and references
- D. Beysens, C. R. Phys., 2006, 7, 1082–1100 CrossRef CAS.
- J. Guadarrama-Cetina, A. Mongruel, M. G. Medici, E. Baquero, A. Parker, I. Milimouk-Melnytchuk, W. González-Viñas and D. Beysens, Eur. Phys. J. E:Soft Matter Biol. Phys., 2014, 37, 1–6 CrossRef CAS PubMed.
- O. Al-Khayat, J. K. Hong, D. M. Beck, A. I. Minett and C. Neto, ACS Appl. Mater. Interfaces, 2017, 9, 13676–13684 CrossRef CAS PubMed.
- A. Katselas, R. Parin and C. Neto, Adv. Mater. Interfaces, 2022, 9, 2200246 CrossRef CAS.
-
D. Beysens, The physics of dew, breath figures and dropwise condensation, Springer, 2022 Search PubMed.
- G. Coquerel, Chem. Soc. Rev., 2014, 43, 2286–2300 RSC.
- B. Chakraverty, J. Non-Cryst. Solids, 1970, 3, 317–326 CrossRef CAS.
- J. B. Rundle, J. Geophys. Res.:Solid Earth, 1989, 94, 2839–2855 CrossRef.
- M. Blander, Adv. Colloid Interface Sci., 1979, 10, 1–32 CrossRef CAS.
-
H. R. Pruppacher, J. D. Klett and P. K. Wang, Microphysics of clouds and precipitation, Springer, Dordrecht, 2nd edn, 1998, p. 954 Search PubMed.
- S. T. Martin, Chem. Rev., 2000, 100, 3403–3454 CrossRef CAS PubMed.
- D. Yount and D. Hoffman, Aviat., Space Environ. Med., 1986, 57, 149–156 CAS.
- J. I. Kapusta, Phys. Rev. D:Part. Fields, 1984, 30, 831–832 CrossRef.
- J. W. Gibbs, Am. J. Sci., 1878, 3, 441–458 CrossRef.
- M. Volmer and A. Weber, Z. Phys. Chem., 1926, 119U, 277–301 CrossRef.
- R. Becker and W. Döring, Ann. Phys., 1935, 416, 719–752 CrossRef.
- J. Frenkel, J. Chem. Phys., 1939, 7, 538–547 CrossRef.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- G. K. Schenter, S. M. Kathmann and B. C. Garrett, Phys. Rev. Lett., 1999, 82, 3484–3487 CrossRef CAS.
- D. Reguera and H. Reiss, J. Phys. Chem. B, 2004, 108, 19831–19842 CrossRef CAS.
- M. Sekine, K. Yasuoka, T. Kinjo and M. Matsumoto, Fluid Dyn. Res., 2008, 40, 597–605 CrossRef.
- H.-M. Shim, J.-K. Kim, H.-S. Kim and K.-K. Koo, Cryst. Growth Des., 2014, 14, 5897–5903 CrossRef CAS.
-
D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Elsevier, 2023 Search PubMed.
- A. Bouillant, J. H. Snoeijer and B. Andreotti, Phys. Rev. Fluids, 2025, 10, 053605 CrossRef.
- R. M. Nyquist, V. Talanquer and D. W. Oxtoby, J. Chem. Phys., 1995, 103, 1175–1179 CrossRef CAS.
- M. Sokuler, G. K. Auernhammer, M. Roth, C. Liu, E. Bonacurrso and H. J. Butt, Langmuir, 2010, 26, 1544–1547 CrossRef CAS PubMed.
- Q. Che, Y. Lu, F. Wang and X. Zhao, Soft Matter, 2019, 15, 10055–10064 RSC.
- C. S. Sharma, A. Milionis, A. Naga, C. W. E. Lam, G. Rodriguez, M. F. Del Ponte, V. Negri, H. Raoul, M. D'Acunzi and H.-J. Butt,
et al.
, Adv. Funct. Mater., 2022, 32, 2109633 CrossRef CAS.
- R. Roy, R. Seiler, J. Weibel and S. Garimella, Adv. Mater. Interfaces, 2020, 7, 2000731 CrossRef CAS.
- C. Henkel, J. H. Snoeijer and U. Thiele, Soft Matter, 2021, 17, 10359–10375 RSC.
- A. Bouillant, C. Henkel, U. Thiele, B. Andreotti and J. H. Snoeijer, Phys. Rev. Lett., 2025, 134, 188204 CrossRef CAS PubMed.
- R. Lhermerout, H. Perrin, E. Rolley, B. Andreotti and K. Davitt, Nat. Commun., 2016, 7, 1–6 Search PubMed.
- L. Limat, Eur. Phys. J. E:Soft Matter Biol. Phys., 2012, 35, 134 CrossRef CAS PubMed.
- A. Marchand, S. Das, J. H. Snoeijer and B. Andreotti, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef PubMed.
- R. W. Style and E. R. Dufresne, Soft Matter, 2012, 8, 7177–7184 RSC.
- L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, J. Fluid Mech., 2014, 747, R1 CrossRef CAS.
- U. Thiele, Colloids Surf., A, 2018, 553, 487–495 CrossRef CAS.
- A. Oron, S. H. Davis and S. G. Bankoff, Rev. Mod. Phys., 1997, 69, 931–980 CrossRef CAS.
- R. V. Craster and O. K. Matar, Rev. Mod. Phys., 2009, 81, 1131–1198 CrossRef CAS.
- L. M. Pismen, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2004, 70, 021601 CrossRef PubMed.
- V. S. Ajaev, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2005, 72, 031605 CrossRef PubMed.
- U. Thiele, J. Phys.: Condens. Matter, 2010, 22, 084019 CrossRef CAS PubMed.
- F. Y. Leong and D.-V. Le, Phys. Fluids, 2020, 32, 062102 CrossRef CAS.
- C. Henkel, M. H. Essink, T. Hoang, G. J. van Zwieten, E. H. van Brummelen, U. Thiele and J. H. Snoeijer, Proc. R. Soc. London, Ser. A, 2022, 478, 20220132 CAS.
-
F. F. Abraham, Homogeneous nucleation theory, Elsevier, 1974 Search PubMed.
-
D. Kashchiev, Nucleation, Elsevier, 2000 Search PubMed.
- O. Pauluis, J. Atmos. Sci., 2011, 68, 91–102 CrossRef.
- R. P. Sear, J. Phys.: Condens. Matter, 2007, 19, 033101 CrossRef.
- P.-G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
-
K. L. Johnson, Contact Mechanics, Cambridge University Press, Cambridge, 1987 Search PubMed.
- M. Doi, J. Phys.: Condens. Matter, 2011, 23, 284118 CrossRef PubMed.
- V. S. Mitlin, J. Colloid Interface Sci., 1993, 156, 491–497 CrossRef CAS.
- A. V. Lyushnin, A. A. Golovin and L. M. Pismen, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 021602 CrossRef CAS PubMed.
- S. Hartmann, C. Diddens, M. Jalaal and U. Thiele, J. Fluid Mech., 2023, 960, A32 CrossRef.
- T. D. Blake, J. Colloid Interface Sci., 2006, 299, 1–13 CrossRef CAS PubMed.
- Y. Zhang, J. Sprittles and D. Lockerby, J. Fluid Mech., 2021, 915, A135 CrossRef CAS.
- R. Sedev, Adv. Colloid Interface Sci., 2015, 222, 661–669 CrossRef CAS PubMed.
- M. Heil and A. L. Hazel, Oomph-lib – an object-oriented multi-physics finite-element library, Lect. Notes Comput. Sci. Eng., 2006, 53, 75–198 Search PubMed.
- U. Thiele, M. G. Velarde and K. Neuffer, Phys. Rev. Lett., 2001, 87, 016104 CrossRef CAS PubMed.
-
Numerical Continuation Methods for Dynamical Systems, ed. B. Krauskopf, H. M. Osinga and J. Galan-Vioque, Springer, 2007 Search PubMed.
-
S. Engelnkemper, S. V. Gurevich, H. Uecker, D. Wetzel and U. Thiele, in Continuation for Thin Film Hydrodynamics and Related Scalar Problems, ed. A. Gelfgat, Springer International Publishing, Cham, 2019, pp. 459–501 Search PubMed.
- A. L. Buck, J. Appl. Meteorol. Climatol., 1981, 20, 1527–1532 CrossRef.
- A. J.-M. Yang, J. Chem. Phys., 1985, 82, 2082–2085 CrossRef CAS.
- D. Lee, M. Telo da Gama and K. Gubbins, J. Chem. Phys., 1986, 85, 490–499 CrossRef CAS.
Footnotes |
| † These values correspond to the relative humidity in the proximity of the substrate, that is at T = 5 °C and can be related to the relative humidity at different temperatures, e.g., T0 = 20 °C at the chamber roof, using eqn (43). |
| ‡ The droplets on which the angles are measured are above micron size and therefore not nuclei, but what they become after some time of condensation. |
| § Thereby, κ(h + ξ) corresponds to the curvature κlv and κ(ξ) to κsl. |
¶ It should be kept in mind, that at constant supersaturation p the volume V* and thus also the radius R* of the critical nucleus are unknown functions of the softness s. In consequence, the ratios ℓec/R* and  can not be assumed to be can not be assumed to be  in such a scenario. in such a scenario. |
| || This difference is constant and does not depend on drop size. It therefore becomes less important as the drop size and the associated energies increase. |
| ** In view of the experiments in ref. 31 the assumption of conserved particle number seems rather unjustified since the system has access to an infinite particle reservoir. In fact, it would be more convenient to consider fixed volume V and chemical potential μ instead. In other words, the system represents a realisation of a grand canonical ensemble and is driven by minimization of the corresponding grand canonical potential Ω (or Landau potential). It was shown, though, that the difference in grand potential associated with nucleus formation can be interpreted as a change in Gibbs free energy and is related to the change in Helmholtz free energy20,45,63,64 (see Appendix B.1). |
|
| This journal is © The Royal Society of Chemistry 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ambre
Bouillant
*a,
Ambre
Bouillant
 b,
Jacco H.
Snoeijer
b,
Jacco H.
Snoeijer
 c and
Uwe
Thiele
c and
Uwe
Thiele
 adef
adef
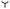 ).† Remarkably, while the drop density appears to be strongly affected by the substrate softness, i.e., it increases with ℓec, it is barely affected by changes in the supersaturation, that is the relative humidity rH at the substrate. Consider ref. 24 and 31 for a more extensive discussion regarding the later stages of droplet condensation.
).† Remarkably, while the drop density appears to be strongly affected by the substrate softness, i.e., it increases with ℓec, it is barely affected by changes in the supersaturation, that is the relative humidity rH at the substrate. Consider ref. 24 and 31 for a more extensive discussion regarding the later stages of droplet condensation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 80
1 to 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, CY52-276 (Dow Corning) with ratios of 1.3
1, CY52-276 (Dow Corning) with ratios of 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and PVS Elite16 (1
1, and PVS Elite16 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Measurements were conducted at two imposed relative humidities: rH = 2.42 (
1). Measurements were conducted at two imposed relative humidities: rH = 2.42 ( ) and rH = 1.22 (△). Horizontal lines indicate the limiting cases of a rigid substrate (red; nanometric PDMS brush grafted on a silicon wafer, see ref. 32) and a liquid-like substrate (blue; uncrosslinked PDMS). The color gradient from red to blue indicates the transition between these two limits. (c) Top-view images of breath figures formed on substrates with different softness levels, taken at the onset of drop visibility. The apparent nucleation density decreases with increasing substrate stiffness, characterized by the shear storage modulus G′.
) and rH = 1.22 (△). Horizontal lines indicate the limiting cases of a rigid substrate (red; nanometric PDMS brush grafted on a silicon wafer, see ref. 32) and a liquid-like substrate (blue; uncrosslinked PDMS). The color gradient from red to blue indicates the transition between these two limits. (c) Top-view images of breath figures formed on substrates with different softness levels, taken at the onset of drop visibility. The apparent nucleation density decreases with increasing substrate stiffness, characterized by the shear storage modulus G′. , implying constant temperature T, particle number N and external pressure p.18,45–48 The bulk contribution is given by the difference Δμ in chemical potentials, between initial and final state, to which the interface energies are added. In the present case of vapor condensing into liquid at a solid substrate, the change in Gibbs free energy is (see Appendix B for details)18,46–48
, implying constant temperature T, particle number N and external pressure p.18,45–48 The bulk contribution is given by the difference Δμ in chemical potentials, between initial and final state, to which the interface energies are added. In the present case of vapor condensing into liquid at a solid substrate, the change in Gibbs free energy is (see Appendix B for details)18,46–48
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(rH).
ln(rH). and ρℓ is the particle density of the liquid. The Gibbs free energy eqn (1) combines surface energy penalties, which in case of drop-like structures of size R scale with ∼R2, with the decrease in chemical potential per particle when changing from the vapor to the liquid phase, scaling with the created volume ∼R3. This balance results in an energy barrier
and ρℓ is the particle density of the liquid. The Gibbs free energy eqn (1) combines surface energy penalties, which in case of drop-like structures of size R scale with ∼R2, with the decrease in chemical potential per particle when changing from the vapor to the liquid phase, scaling with the created volume ∼R3. This balance results in an energy barrier  that must be overcome to nucleate and which defines a critical size R*. Since the nucleation of droplets on a substrate is a stochastic process driven by random fluctuations18 the nucleation probability P is estimated using a Boltzmann factor
that must be overcome to nucleate and which defines a critical size R*. Since the nucleation of droplets on a substrate is a stochastic process driven by random fluctuations18 the nucleation probability P is estimated using a Boltzmann factor
 to the thermal energy kBT. In the following, we calculate this energy barrier for a radially symmetric drop (w.r.t. the z-axis) of base radius R sitting on a deformable substrate, extended in the (x, y)-plane as shown in Fig. 3. In the limits of a perfectly rigid (ℓec = 0) and liquid-like (ℓec = ∞) substrate, elasticity can be neglected and the equilibrium drop shape is exclusively governed by the interface and bulk phase energies, i.e., it adapts spherical-cap shapes.
to the thermal energy kBT. In the following, we calculate this energy barrier for a radially symmetric drop (w.r.t. the z-axis) of base radius R sitting on a deformable substrate, extended in the (x, y)-plane as shown in Fig. 3. In the limits of a perfectly rigid (ℓec = 0) and liquid-like (ℓec = ∞) substrate, elasticity can be neglected and the equilibrium drop shape is exclusively governed by the interface and bulk phase energies, i.e., it adapts spherical-cap shapes.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY + γsl = γsv,
θY + γsl = γsv,

 of the dry reference state, is
of the dry reference state, is  . With eqn (4)–(6) the energy (1) becomes
. With eqn (4)–(6) the energy (1) becomes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY) (1 − cos
θY) (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY)2 = 2 − 3
θY)2 = 2 − 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY + cos3
θY + cos3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY we then find
θY we then find
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θY/κlv has been introduced and the function
θY/κlv has been introduced and the function![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) (1 − cos
θ) (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2/sin3
θ)2/sin3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and its resulting base radius is
and its resulting base radius is

 . Note, that the θY-dependent factor of
. Note, that the θY-dependent factor of  in eqn (11) increases monotonically from g(θY)sin(θY)3 = 0 in the complete wetting case (θY = 0°) to g(θY)sin(θY)3 = 4 in the non-wetting case (θY = 180°). In other words, low contact angles will drastically reduce the nucleation barrier.
in eqn (11) increases monotonically from g(θY)sin(θY)3 = 0 in the complete wetting case (θY = 0°) to g(θY)sin(θY)3 = 4 in the non-wetting case (θY = 180°). In other words, low contact angles will drastically reduce the nucleation barrier.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlv + γsl
θlv + γsl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsl = γsv,
θsl = γsv,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θlv = γsl
θlv = γsl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θsl.
θsl.




 and depends only on the interface energies but not on supersaturation, i.e., not on R* and Δμ. For example, if the interface energies are γlv = 70 × 10−3 N m−1, γsl = 48 × 10−3 N m−1 and γsv = 72 × 10−3 N m−1 the nucleation barrier differs by a factor
and depends only on the interface energies but not on supersaturation, i.e., not on R* and Δμ. For example, if the interface energies are γlv = 70 × 10−3 N m−1, γsl = 48 × 10−3 N m−1 and γsv = 72 × 10−3 N m−1 the nucleation barrier differs by a factor  between the rigid and liquid-like case.
between the rigid and liquid-like case.



 of a substrate with liquid coverage (drop or thick film) relative to the reference state of a macroscopically dry flat substrate is given by
of a substrate with liquid coverage (drop or thick film) relative to the reference state of a macroscopically dry flat substrate is given by





 of a field φ and the Derjaguin (disjoining) pressure Π(h) = −∂hf(h) (cf.Fig. 6).§ Note, that for h ≫ ha one has Π → 0 and eqn (27) depends only on χ = h + ξ, indicating that (at uniform supersaturation) the liquid–vapor interface of a steady drop always forms a spherical cap of curvature κlv = −ρℓΔμ/γlv, entirely independent of elasticity. In consequence, at fixed contact angles also the volume of a steady drop is directly determined by the supersaturation.
of a field φ and the Derjaguin (disjoining) pressure Π(h) = −∂hf(h) (cf.Fig. 6).§ Note, that for h ≫ ha one has Π → 0 and eqn (27) depends only on χ = h + ξ, indicating that (at uniform supersaturation) the liquid–vapor interface of a steady drop always forms a spherical cap of curvature κlv = −ρℓΔμ/γlv, entirely independent of elasticity. In consequence, at fixed contact angles also the volume of a steady drop is directly determined by the supersaturation.


 and dynamic viscosity η52 which is extended by a non-conserved term that incorporates phase transition-limited mass exchange between liquid and vapor37,42,53 driven by the variation
and dynamic viscosity η52 which is extended by a non-conserved term that incorporates phase transition-limited mass exchange between liquid and vapor37,42,53 driven by the variation  with the transfer mobility M. For a discussion of other evaporation models see ref. 54. The dynamics of the substrate corresponds to the Kelvin–Voigt model and describes an exponential relaxation in time scaled by the effective substrate viscosity ζ.30 To reduce the number of parameters, the equations are non-dimensionalized using characteristic length and time scales
with the transfer mobility M. For a discussion of other evaporation models see ref. 54. The dynamics of the substrate corresponds to the Kelvin–Voigt model and describes an exponential relaxation in time scaled by the effective substrate viscosity ζ.30 To reduce the number of parameters, the equations are non-dimensionalized using characteristic length and time scales![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) , r = ha
, r = ha![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) , ξ = ha
, ξ = ha![[small xi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e119.gif) , h = ha
, h = ha![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) .
.


 is the predicted curvature of the liquid–vapor interface of the macroscopic critical nucleus [eqn (17)]. From here on, p refers to the (dimensionless) supersaturation, defined above. The thickness of the adsorption layer is chosen as the thermal capillary length
is the predicted curvature of the liquid–vapor interface of the macroscopic critical nucleus [eqn (17)]. From here on, p refers to the (dimensionless) supersaturation, defined above. The thickness of the adsorption layer is chosen as the thermal capillary length  , which is used in molecular kinetic theory (MKT) of wetting and capillary wave theory (CWT).55–57 It scales the thermal fluctuation of the liquid–vapor interface and in that sense the diffusivity of the latter. From an energetic perspective it defines the scale at which the thermal energy competes with the energy penalty associated with an increased interfacial area due to the interface tension γlvha2 = kBT. Hence, in the following all energies are expressed in terms of the thermal energy kBT. With
, which is used in molecular kinetic theory (MKT) of wetting and capillary wave theory (CWT).55–57 It scales the thermal fluctuation of the liquid–vapor interface and in that sense the diffusivity of the latter. From an energetic perspective it defines the scale at which the thermal energy competes with the energy penalty associated with an increased interfacial area due to the interface tension γlvha2 = kBT. Hence, in the following all energies are expressed in terms of the thermal energy kBT. With  and
and  it follows that
it follows that  . The elastocapillary length used in Fig. 4 is related to the softness s by30
. The elastocapillary length used in Fig. 4 is related to the softness s by30
 [cf.Fig. 4].¶
[cf.Fig. 4].¶
 [eqn (36)] is shown as a function of uniform liquid layer thickness for p = 0.1. Fig. 6(a) displays the associated energy f(h) − ph. The respective thin lines give the case p = 0. According to eqn (36) a steady film state may only exist if the supersaturation is balanced by the Derjaguin pressure, leading to
[eqn (36)] is shown as a function of uniform liquid layer thickness for p = 0.1. Fig. 6(a) displays the associated energy f(h) − ph. The respective thin lines give the case p = 0. According to eqn (36) a steady film state may only exist if the supersaturation is balanced by the Derjaguin pressure, leading to
 [eqn (37)] as shown in Fig. 6(c). For p > −Πmin the Derjaguin pressure cannot compete with the supersaturation any more and nothing prevents the vapor from condensing into the liquid film.
[eqn (37)] as shown in Fig. 6(c). For p > −Πmin the Derjaguin pressure cannot compete with the supersaturation any more and nothing prevents the vapor from condensing into the liquid film. . Thus, in the mesoscopic model one has to solve
. Thus, in the mesoscopic model one has to solve  . To do so numerically, by using a Newton solver, a proper starting state is required, which has to closely resemble the final solution. While in the rigid and liquid-like limit the macroscopic spherical cap profiles might be sufficiently suited, this is usually not the case in the intermediate elastic regime 0 < s < ∞. Further the critical nucleus cannot be found using time simulations as it is associated with a maximum of the Gibbs free energy and thus unstable. Therefore, we make use of a trick; instead of an isothermal–isobaric ensemble, a canonical ensemble is considered. The drop state then corresponds to a minimum of the Helmholtz free energy and can thus be approached using time simulations. Thereby, the supersaturation is used as a Lagrange multiplier and adapts freely during the simulation to enforce conservation of an imposed volume V0. The stable steady drop found in the canonical ensemble exactly corresponds to a critical nucleus in the isothermal–isobaric ensemble if the supersaturation is set to
. To do so numerically, by using a Newton solver, a proper starting state is required, which has to closely resemble the final solution. While in the rigid and liquid-like limit the macroscopic spherical cap profiles might be sufficiently suited, this is usually not the case in the intermediate elastic regime 0 < s < ∞. Further the critical nucleus cannot be found using time simulations as it is associated with a maximum of the Gibbs free energy and thus unstable. Therefore, we make use of a trick; instead of an isothermal–isobaric ensemble, a canonical ensemble is considered. The drop state then corresponds to a minimum of the Helmholtz free energy and can thus be approached using time simulations. Thereby, the supersaturation is used as a Lagrange multiplier and adapts freely during the simulation to enforce conservation of an imposed volume V0. The stable steady drop found in the canonical ensemble exactly corresponds to a critical nucleus in the isothermal–isobaric ensemble if the supersaturation is set to  .
.

 . The corresponding values of the dimensionless parameters are p ≈ 0.0226, Cθ ≈ 2.2 and σ ≈ 0.6857. Note, that in this setting a steady drop on a rigid substrate exhibits θY = 70° and R*/ha ≈ 83.
. The corresponding values of the dimensionless parameters are p ≈ 0.0226, Cθ ≈ 2.2 and σ ≈ 0.6857. Note, that in this setting a steady drop on a rigid substrate exhibits θY = 70° and R*/ha ≈ 83.
 [eqn (16)] is calculated for comparison. In the mesoscopic picture, the base radius R of a steady drop, i.e., a critical nucleus, is not known a priori. However, the macroscopic calculations in the rigid and liquid-like cases provide reasonable estimates also for the elastic regime, since R is assumed to transit monotonically between these two limits. Since there is no sharp three phase contact line in the mesoscopic description, the base radius is instead defined by the position R of maximal curvature of the liquid–vapor interface, i.e., κ(h + ξ)|r=R = max[κ(h + ξ)] (cf.Fig. 5), which is equivalent to Π(h)|r=R = min[Π(h)]. It is thus encoded in the profiles h and ξ such that
[eqn (16)] is calculated for comparison. In the mesoscopic picture, the base radius R of a steady drop, i.e., a critical nucleus, is not known a priori. However, the macroscopic calculations in the rigid and liquid-like cases provide reasonable estimates also for the elastic regime, since R is assumed to transit monotonically between these two limits. Since there is no sharp three phase contact line in the mesoscopic description, the base radius is instead defined by the position R of maximal curvature of the liquid–vapor interface, i.e., κ(h + ξ)|r=R = max[κ(h + ξ)] (cf.Fig. 5), which is equivalent to Π(h)|r=R = min[Π(h)]. It is thus encoded in the profiles h and ξ such that  can be seen as
can be seen as  . Note, that the adsorption layer height h− specifies a lower bound for the liquid layer thickness h, which in turn imposes a restriction to the minimal critical nucleus size min(R*) ∼ h−, in contrast to the macroscopic picture where no such limit exists. This restriction in turn sets a critical supersaturation pc, since R* ∼ p−1, beyond which no steady nucleus states are possible anymore. The energy
. Note, that the adsorption layer height h− specifies a lower bound for the liquid layer thickness h, which in turn imposes a restriction to the minimal critical nucleus size min(R*) ∼ h−, in contrast to the macroscopic picture where no such limit exists. This restriction in turn sets a critical supersaturation pc, since R* ∼ p−1, beyond which no steady nucleus states are possible anymore. The energy  can be calculated in two different ways:
can be calculated in two different ways:
 to be faithfully recovered.
to be faithfully recovered. . However, right now we are not looking for the energy barrier
. However, right now we are not looking for the energy barrier  but for
but for  , the two of which differ only by the value of p used in the calculation, at otherwise fixed parameters. Basically we ask: How does the energy of the critical nucleus characterized by h* and ξ* look like, if we evaluate it at another value of p than the one at which it is a steady state? From eqn (24) and (25) it is seen, that the difference in
, the two of which differ only by the value of p used in the calculation, at otherwise fixed parameters. Basically we ask: How does the energy of the critical nucleus characterized by h* and ξ* look like, if we evaluate it at another value of p than the one at which it is a steady state? From eqn (24) and (25) it is seen, that the difference in  caused by a change Δp is given by
caused by a change Δp is given by
 obtain for a set of values p during the continuation can be mapped to an arbitrary value
obtain for a set of values p during the continuation can be mapped to an arbitrary value ![[p with combining tilde]](https://www.rsc.org/images/entities/i_char_0070_0303.gif) to obtain
to obtain
 as a function of drop radius in the liquid limit (blue), the rigid limit (red) and for an intermediate elastic case (purple). Both described methods are compared to the macroscopic result. While the mesoscopic values obtained by continuation (
as a function of drop radius in the liquid limit (blue), the rigid limit (red) and for an intermediate elastic case (purple). Both described methods are compared to the macroscopic result. While the mesoscopic values obtained by continuation ( symbols) agree very well with the ones obtained by the quasi-static approach (solid lines), both are slightly smaller than the macroscopic analytical predictions (black dashed). This results from the differences between the macroscopic and mesoscopic nucleus profiles in the contact line region.|| More importantly, the positions of the energy maxima, i.e., the critical radii R* (marked by ▼), are correctly recovered. The overall agreement between macroscopic and mesoscopic model is quite satisfactory, allowing us to use the latter for exploring the critical nucleus characteristics in the elastic regime. The purple line in Fig. 7 shows the energy as obtained by the first method for an exemplary intermediate softness s = 103 and lies between the rigid and liquid-like limits, as expected.
symbols) agree very well with the ones obtained by the quasi-static approach (solid lines), both are slightly smaller than the macroscopic analytical predictions (black dashed). This results from the differences between the macroscopic and mesoscopic nucleus profiles in the contact line region.|| More importantly, the positions of the energy maxima, i.e., the critical radii R* (marked by ▼), are correctly recovered. The overall agreement between macroscopic and mesoscopic model is quite satisfactory, allowing us to use the latter for exploring the critical nucleus characteristics in the elastic regime. The purple line in Fig. 7 shows the energy as obtained by the first method for an exemplary intermediate softness s = 103 and lies between the rigid and liquid-like limits, as expected. . The volumes of all states, except for h−, increase with decreasing supersaturation p. In the low p limit, i.e., at large volumes, the macroscopic and mesoscopic critical nucleus states well agree and show the predicted scaling V ∼ p−3. As the nucleus size decreases (increasing p), the mesoscopic results deviate from the macroscopic predictions (see Section 3.2), approach Vdry = πh−L2, and eventually end in a pitchfork bifurcation, very close to the saddle-node bifurcation of the uniform states (♦ symbol). Note further, that the volumes of the mesoscopic states all depend on the system size L, since the adsorption layer, which is present in the macroscopically dry areas, contributes with a volume per unit area ha. Therefore, we also provide in the inset Fig. 8(b) the effective condensed volume
. The volumes of all states, except for h−, increase with decreasing supersaturation p. In the low p limit, i.e., at large volumes, the macroscopic and mesoscopic critical nucleus states well agree and show the predicted scaling V ∼ p−3. As the nucleus size decreases (increasing p), the mesoscopic results deviate from the macroscopic predictions (see Section 3.2), approach Vdry = πh−L2, and eventually end in a pitchfork bifurcation, very close to the saddle-node bifurcation of the uniform states (♦ symbol). Note further, that the volumes of the mesoscopic states all depend on the system size L, since the adsorption layer, which is present in the macroscopically dry areas, contributes with a volume per unit area ha. Therefore, we also provide in the inset Fig. 8(b) the effective condensed volume  for the mesoscopic states, i.e., the volume above the adsorption layer. This measure is independent of system size.
for the mesoscopic states, i.e., the volume above the adsorption layer. This measure is independent of system size.
 ) in the rigid and liquid-like limit. Again, the disagreement of macroscopic and mesoscopic model for p → Cθ/4 is assumably caused by the different nucleus shapes due to the diffuse contact region present in the latter, which gains impact as the nucleus size decreases.
) in the rigid and liquid-like limit. Again, the disagreement of macroscopic and mesoscopic model for p → Cθ/4 is assumably caused by the different nucleus shapes due to the diffuse contact region present in the latter, which gains impact as the nucleus size decreases. . The barrier increases with decreasing supersaturation in agreement with Section 3.2. Beyond that, the mesoscopic model estimates the energy barrier for p → pc to be up to several orders of magnitude smaller than the macroscopic value. This indicates, that the CNT, i.e., the employed macroscopic model, strongly underestimates the nucleation probability close to the critical point. In Fig. 10 a mesoscopic critical nucleus on a soft substrate is shown for p ≈ pc. At pc = Cθ/4 the mesoscopic nucleation energy barrier even vanishes, such that the vapor condenses uncontrollably into the liquid phase for p > pc. The dimensionless critical supersaturation pc = Cθ/4 translates to the critical relative humidity
. The barrier increases with decreasing supersaturation in agreement with Section 3.2. Beyond that, the mesoscopic model estimates the energy barrier for p → pc to be up to several orders of magnitude smaller than the macroscopic value. This indicates, that the CNT, i.e., the employed macroscopic model, strongly underestimates the nucleation probability close to the critical point. In Fig. 10 a mesoscopic critical nucleus on a soft substrate is shown for p ≈ pc. At pc = Cθ/4 the mesoscopic nucleation energy barrier even vanishes, such that the vapor condenses uncontrollably into the liquid phase for p > pc. The dimensionless critical supersaturation pc = Cθ/4 translates to the critical relative humidity

 as a function of supersaturation p. The presented data are the same as in Fig. 8.
as a function of supersaturation p. The presented data are the same as in Fig. 8.
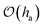 and barely resemble spherical caps.
and barely resemble spherical caps. given by the critical nucleus. This barrier in Gibbs free energy has been calculated in the macroscopic picture in both, the rigid and the liquid-like limit. For the given interface energies the nucleation energy in the liquid-like limit is about half the one in the rigid limit. To further explore the regime of intermediate elasticity, a mesoscopic gradient dynamics model has been employed to determine the energy as a function of supersaturation p and softness ℓec/R*. The macroscopic and mesoscopic models were found to agree in the limit of rigid and liquid substrates, as long as the critical nucleus is of sufficiently large volume, i.e., when a relatively small supersaturation is considered. Both models predict a decrease in the energy barrier with increasing supersaturation, indicating an overall increased nucleation density at higher supersaturation. At large supersaturation, the macroscopic model considerably overestimates the energy barrier by several orders of magnitude as compared to the mesoscopic theory, resulting in an underestimated nucleation probability. This deviation is caused by the difference in nucleus shape; while mesoscopic nuclei exhibit diffuse contact regions that increasingly influence their shape as R* → h−, the shape of macroscopic nuclei is (in the rigid and the liquid-like limit) invariant under changes in size, which is most likely not justified as microscopic scales are approached. Next, the change of the energy barrier with increasing substrate softness at fixed supersaturation has been investigated using the mesoscopic model. The decrease in the energy barrier has been shown to coincide with the transition of contact angles from Young (rigid) to Neumann (liquid-like) at ℓec ∼ R*. However, in the experiments the increase in drop number occurred in the range 10−7 m < ℓec < 10−3 m and since the critical nuclei are considered to be of nanometer size, it is still unclear why nucleation depends on the substrate softness at all. Beyond that, the critical nucleus volume is found to decrease with the substrate softness, allowing for the formation of more nuclei if the vapor access is limited, e.g., by slow transport in the gas phase.
given by the critical nucleus. This barrier in Gibbs free energy has been calculated in the macroscopic picture in both, the rigid and the liquid-like limit. For the given interface energies the nucleation energy in the liquid-like limit is about half the one in the rigid limit. To further explore the regime of intermediate elasticity, a mesoscopic gradient dynamics model has been employed to determine the energy as a function of supersaturation p and softness ℓec/R*. The macroscopic and mesoscopic models were found to agree in the limit of rigid and liquid substrates, as long as the critical nucleus is of sufficiently large volume, i.e., when a relatively small supersaturation is considered. Both models predict a decrease in the energy barrier with increasing supersaturation, indicating an overall increased nucleation density at higher supersaturation. At large supersaturation, the macroscopic model considerably overestimates the energy barrier by several orders of magnitude as compared to the mesoscopic theory, resulting in an underestimated nucleation probability. This deviation is caused by the difference in nucleus shape; while mesoscopic nuclei exhibit diffuse contact regions that increasingly influence their shape as R* → h−, the shape of macroscopic nuclei is (in the rigid and the liquid-like limit) invariant under changes in size, which is most likely not justified as microscopic scales are approached. Next, the change of the energy barrier with increasing substrate softness at fixed supersaturation has been investigated using the mesoscopic model. The decrease in the energy barrier has been shown to coincide with the transition of contact angles from Young (rigid) to Neumann (liquid-like) at ℓec ∼ R*. However, in the experiments the increase in drop number occurred in the range 10−7 m < ℓec < 10−3 m and since the critical nuclei are considered to be of nanometer size, it is still unclear why nucleation depends on the substrate softness at all. Beyond that, the critical nucleus volume is found to decrease with the substrate softness, allowing for the formation of more nuclei if the vapor access is limited, e.g., by slow transport in the gas phase.

 at about
at about  which translates to rH ≈ 3.2657 or r0H = 1.2184. The behavior at large p depends strongly on the nucleus shape and, in turn, on the functional form of the wetting potential f(h) – many different forms are discussed in the literature.38–42,49,52–54,59 Further, the range of attractive microscopic interactions is determined by the rate at which f converges to zero as h increases. Increasing this range increases the width of the contact region, which in turn causes the energy barrier to fall off quicker as pc is approached.
which translates to rH ≈ 3.2657 or r0H = 1.2184. The behavior at large p depends strongly on the nucleus shape and, in turn, on the functional form of the wetting potential f(h) – many different forms are discussed in the literature.38–42,49,52–54,59 Further, the range of attractive microscopic interactions is determined by the rate at which f converges to zero as h increases. Increasing this range increases the width of the contact region, which in turn causes the energy barrier to fall off quicker as pc is approached.


 being an arbitrary reference pressure. Assuming constant particle density in the liquid ρℓ = Nℓ/Vℓeqn (45) becomes
being an arbitrary reference pressure. Assuming constant particle density in the liquid ρℓ = Nℓ/Vℓeqn (45) becomes

 , leading to
, leading to
 . The Gibbs–Duhem relation then writes
. The Gibbs–Duhem relation then writes
 is the total pressure of the mixture at saturation of component v. In consequence, the reference pressures in eqn (48) have to be chosen differently, namely
is the total pressure of the mixture at saturation of component v. In consequence, the reference pressures in eqn (48) have to be chosen differently, namely  and
and  , yielding
, yielding
 with Helmholtz free energy
with Helmholtz free energy  , the externally imposed total gas pressure p and the total volume V. The Gibbs free energies of the coexisting liquid and gas phase (including vapor) state
, the externally imposed total gas pressure p and the total volume V. The Gibbs free energies of the coexisting liquid and gas phase (including vapor) state  and the pure gas state
and the pure gas state  are given by
are given by


 , such that the respective partial pressure terms cancel with eqn (50). At 〈2〉 the particle conservation in the gas phase
, such that the respective partial pressure terms cancel with eqn (50). At 〈2〉 the particle conservation in the gas phase  is used for all components of the mixture i ≠ v. At 〈3〉 the global particle conservation of species v is used, i.e.
is used for all components of the mixture i ≠ v. At 〈3〉 the global particle conservation of species v is used, i.e. . At 〈4〉 eqn (50) is used again to eliminate the sum since dp = 0. Note, that not only the total pressure p but also the partial pressures
. At 〈4〉 eqn (50) is used again to eliminate the sum since dp = 0. Note, that not only the total pressure p but also the partial pressures  are held constant in the considered system. Hence, since chemical potential and pressure are not independent in an isotherm
are held constant in the considered system. Hence, since chemical potential and pressure are not independent in an isotherm  . The difference in chemical potentials is expressed using eqn (51) and finally the pressure difference commonly neglected.46,47 Finally, the energy gap is exclusively governed by the difference in chemical potentials. For rH > 1, i.e. pv > psatv, the difference in the Gibbs free energy is always negative such that a transition of particles from vapor to condensed state is always favorable. As mentioned above, this condition, referred to as supersaturation, is a prerequisite for spontaneous nucleation to occur and the new phase to grow. Finally, the change in Gibbs free energy associated with the creation of a liquid cluster of arbitrary shape from its own vapor in contact with a substrate is found by adding the interface energy penalties18,46–48
. The difference in chemical potentials is expressed using eqn (51) and finally the pressure difference commonly neglected.46,47 Finally, the energy gap is exclusively governed by the difference in chemical potentials. For rH > 1, i.e. pv > psatv, the difference in the Gibbs free energy is always negative such that a transition of particles from vapor to condensed state is always favorable. As mentioned above, this condition, referred to as supersaturation, is a prerequisite for spontaneous nucleation to occur and the new phase to grow. Finally, the change in Gibbs free energy associated with the creation of a liquid cluster of arbitrary shape from its own vapor in contact with a substrate is found by adding the interface energy penalties18,46–48

 . Thereby, the last term refers to the Gibbs free energy of a pure gas state with the same total particle number of the components and at the same fixed chemical potentials μi. At 〈2〉 the Helmholtz free energy is expressed as
. Thereby, the last term refers to the Gibbs free energy of a pure gas state with the same total particle number of the components and at the same fixed chemical potentials μi. At 〈2〉 the Helmholtz free energy is expressed as  . At 〈3〉 the fixed volume V = V′ and the shared gas volume
. At 〈3〉 the fixed volume V = V′ and the shared gas volume  and Vi = V − Vℓ is used. At 〈4〉 eqn (50) is used to eliminate the sum since dp = 0. The difference in chemical potentials is expressed using eqn (49) and the pressure difference is neglected, as is common practice.46,47 This result is the same as eqn (54), hence
and Vi = V − Vℓ is used. At 〈4〉 eqn (50) is used to eliminate the sum since dp = 0. The difference in chemical potentials is expressed using eqn (49) and the pressure difference is neglected, as is common practice.46,47 This result is the same as eqn (54), hence  in this case (Fig. 12).
in this case (Fig. 12).



 can not be assumed to be
can not be assumed to be  in such a scenario.
in such a scenario.