Open Access Article
Open Access ArticleShort-time spreading dynamics of elastic drops
Surjyasish Mitra a,
A-Reum Kimb,
Boxin Zhao
a,
A-Reum Kimb,
Boxin Zhao b and
Sushanta K. Mitra
b and
Sushanta K. Mitra *a
*a
aDepartment of Mechanical & Mechatronics Engineering, Waterloo Institute for Nanotechnology, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. E-mail: skmitra@uwaterloo.ca
bDepartment of Chemical Engineering, Waterloo Institute for Nanotechnology, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. E-mail: zhaob@uwaterloo.ca
First published on 16th December 2025
Abstract
When a liquid drop makes first contact with any surface, the unbalanced surface tension force drives the contact line, causing spreading. For Newtonian or weakly elastic, non-Newtonian liquids, either liquid inertia or viscosity, or a combination of the two, resists spreading. In this work, we investigate how drop elasticity influences spreading dynamics. We conduct dynamical experiments with polyacrylamide drops of varying polymer concentrations to impart varying degrees of elasticity. Using high-speed imaging, we focus on the very first moments of spreading on glass substrates. For moderate and high Young's modulus values, we observe that the early-time spreading dynamics obey a viscous-capillary regime characterized by a power-law evolution of the spreading radius. However, the process transitions to a different regime on a timescale comparable to the characteristic viscoelastic relaxation timescale. We interpret this latter regime using a theoretical model invoking the standard linear model of viscoelasticity. For viscoelastic inks with moderate print speeds, the dynamical behavior investigated in this study can provide valuable insights into how to efficiently control such moving contact lines with non-trivial elasticity.
1 Introduction
When a liquid drop is gently deposited on any rigid substrate, it spreads spontaneously until equilibrium is reached.1,2 On the same substrate, a rigid sphere sits as deposited with a finite, small contact radius.3,4 These two extreme scenarios vis-a-vis wetting and contact adhesion have been treated independently using classical theories of Young5 and Hertz3/Johnson–Kendall–Roberts (JKR),4 respectively. However, between these two configurations lies a plethora of intermediate contact/wetting morphologies, primarily modulated by the substrate wettability and elasticity (Fig. 1). The effect of surface wettability is more pronounced for wetting than for contact adhesion, whereas modulating the surface's elastic modulus causes profound changes in both cases. For instance, making the substrate sufficiently soft enables a configuration where a sessile liquid drop exhibits deformation at the three-phase contact line, generating a wetting ridge structure.6–9 Similarly, increased indentation depths can be observed for contacts of rigid spheres on soft substrates.10 Despite such insights, many unanswered questions still remain. Primarily among them is the effect of the elasticity of the top pair. In recent studies using elastic hydrogel spheres, it was shown that configurations intermediate between wetting and contact emerge upon modulating the elastic modulus of the hydrogels.11,12 Typically, hydrogels consist of a solid network of crosslinked natural or synthetic polymers swollen with water.13,14 The primary polymer network imparts the desired elastic modulus of the hydrogel.13 By tuning the relative concentration of this primary polymer network in our earlier work, we prepared polyacrylamide hydrogels with Young's modulus varying from a few millipascals to hundreds of kilopascals and demonstrated how one can translate from a wetting-like morphology to a contact-like morphology upon contact with any substrate.11 Essentially, for weakly elastic hydrogels, a Newtonian-liquid-drop-like wetting morphology was observed, whereas for highly elastic hydrogels, a non-wetting, rigid-sphere-like contact morphology was observed.11 Furthermore, to interpret this transition from wetting to contact with increasing elasticity, we employed density functional theory.15 Consequently, it was shown that a switch from attractive to repulsive interaction potential between an elastic wedge and a rigid substrate enables this transition from wetting to contact with increasing Young's modulus.15 However, for any contacting system to reach equilibrium, it has to go through a finite transient stage. Typically, this transient dynamics on rigid and soft substrates16–19 is well studied for the wetting of liquids, i.e., spreading.For spreading of Newtonian liquid drops with well-defined liquid properties such as density, surface tension, and viscosity, the dynamics can be well defined using phenomenological scaling laws that account for the dominant driving and resistive forces.16–18,20 It is well understood that liquid surface tension drives the spreading process, whereas liquid inertia16,17,21 or viscosity18,20,22 opposes it. Consequently, we observe scaling laws representing the evolution of the drop-substrate footprint radius r as r ∼ tα, where the power-law exponent α typically assumes values of 1 (inertia-limited viscous,18,23,24 early), 0.5 (inertia,16,17,21 early), and 0.1 (contact line dissipation,25,26 late) depending on the dominant resistive force and the relevant stage of spreading. Furthermore, modulating the substrate properties, such as making the substrate hydrophobic, causes variation in the power-law exponent.17 In certain cases, deviations from power-law spreading are also observed. For instance, making the underlying substrate sufficiently soft causes the spreading radius to transition from the early-time inertial scaling law and follow a trajectory that can be best described using an exponential relaxation function.27 However, despite such extensive studies on the spreading dynamics with varying liquid and substrate properties, outstanding questions still remain. As mentioned previously, primarily among them is what happens when we impart elasticity to the drop phase. This dynamic elastowetting phenomenon is widely relevant for cell spreading, where cells are often modeled as elastic membrane-bound shells, whose early-time spreading behavior obeys power-law scaling.28
It is worth noting that existing literature mostly reports the spreading of viscoelastic liquids.29,30 These are either weakly elastic polymeric solutions, such as polyethylene oxide (PEO) and FLOPAM, or low concentrations of polyacrylamide (PAAm) and polyvinyl alcohol (PVA) solutions.29–31 For such cases, the shear storage modulus G′ is typically smaller than the shear loss modulus G″,31,32 and hence the materials behave more like viscous liquids rather than viscoelastic materials or even elastic solids. They are typically characterized using their zero-shear-rate or high-shear-rate viscosity obtained from shear-rate ramp measurements.29,30 For instance, Bouillant et al.29 and Yada et al.30 conducted spreading experiments with low concentrations of PEO solutions where the zero-shear-rate viscosity varied between 10 mPa s and 10 Pa s. Consequently, their early-time spreading behavior was found to mirror that of Newtonian liquids such as water. As a result, their spreading characteristics were described similarly using liquid inertia or rate-dependent viscosity (zero shear or high shear) since their elastic (or shear) modulus, often on the order of a few pascals, is not dominant. Consequently, the role of a non-trivial, finite elastic modulus in this transient dynamics remains elusive. In this work, we probe the spreading of elastic drops/spheres with Young's modulus varying between 0.1 kPa and 400 kPa on glass substrates.
The choice of the Young's modulus range is driven by the following factors. First, our previous work on the static morphologies of elastic drops/spheres indicated that such materials exhibit significant morphological changes in the aforementioned Young's modulus range.11 When the material's Young's modulus is on the order of tens of pascals or lower, they exhibit complete wetting configurations on substrates like glass, similar to a Newtonian liquid like DI water or weakly elastic polymeric liquids such as PEO.33 Furthermore, with increasing Young's modulus, the elastic drops bead up like glass spheres and beyond 500 kPa, they exhibit no discernible contact radius change.11 Second, for optimal print efficiency in many 3D printing applications using biomaterial inks, it is desired that the material is neither too elastic nor too viscous.34 Hence, our choice of PAAm Young's modulus perfectly fits that requirement.
2 Materials and methods
2.1 Fabrication of elastic drops
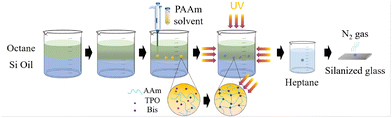
To enable broad control of Young's modulus E, we prepared 1 mm radius polyacrylamide (PAAm) drops/spheres, which behave as polymeric liquid drops at low polymer concentrations, exhibit intermediate morphologies at moderate concentrations, and behave as elastic spheres mimicking rigid beads at high concentrations.11 Briefly, the elastic drops were produced using an in-house recipe consisting of acrylamide (monomer), N,N′-methylene-bis-acrylamide (BIS) (crosslinker), and 2,4,6-tri-methyl benzoyldiphenylphosphine oxide (TPO) (initiator) (Fig. 2). The Young's modulus of the polyacrylamide drops was varied between 0.16 kPa and 366 kPa by varying the monomer weight percentage from 6.5 to 30, whereas the necessary spherical shapes of the drops were attained by suspending them in n-octane and silicone oil utilizing their density gradient (Fig. 2). Further details of the fabrication process can be found in our previous works.11,15,35 As our working substrates, we used microscope glass slides cleaned using acetone, IPA, and DI water before use.2.2 Rheology measurements
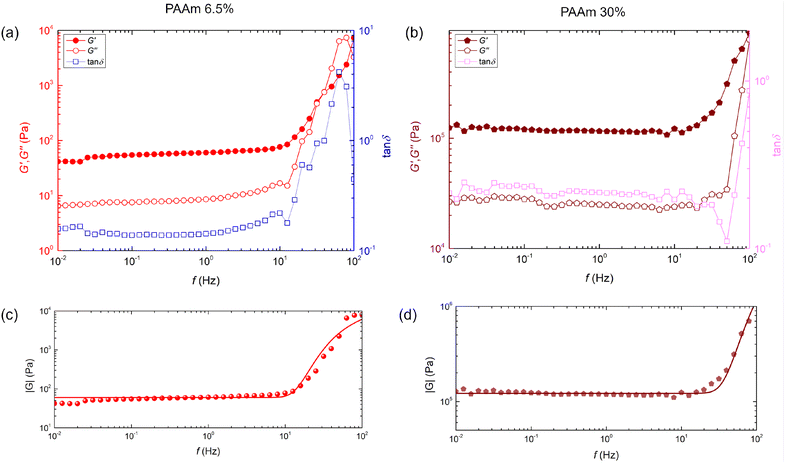
The elastic properties of the PAAm were characterized using a rheometer. For rheology measurements, each PAAm formulation was polymerized in a Petri dish with a thickness of 2 mm. The shear storage (G′) and loss (G″) moduli of the materials were measured by performing a frequency sweep test on a dynamic shear rheometer (AR 2000, TA Instruments and Kinexus Rotational Rheometer, Malvern Instruments) from 0.01 to 100 Hz at 1% strain and a normal force of 1 N. All measurements were performed at 25 °C using a 25 mm diameter plate as the test adapter. The measurements were taken after waiting 10 min for the polymer to stabilize. From the rheology measurements, it is evident that for PAAm with 6.5 wt% monomer, both G′ and G″ plateau to constant values at low frequency, where G′ ≫ G″, indicating solid-like behavior (Fig. 3a). However, at high frequency, we observed that G″ becomes equal to G′ and often exceeds it, indicating a transition to liquid-like behavior. However, for the stiffest PAAm, i.e., with 30 wt% monomer, we observed that G′ ≫ G″ across the entire frequency range (Fig. 3b). Note that due to limitations of the rheometer, the shear modulus at higher frequencies cannot be probed. Furthermore, note that additional rheology measurements, i.e., shear strain amplitude measurements, are included in the SI (see Fig. S1).Constitutive spring–dashpot models are often used to mimic the response of viscoelastic solids and liquids, where the spring represents an elastic solid with modulus G0 (or E0) and the dashpot represents a Newtonian fluid with viscosity μ0 (ref. 36) (Fig. 4a). The most common ones are the Maxwell model and the Kelvin–Voigt model (Fig. 4a). However, most real soft materials exhibit mechanical responses that can be best described using a combination of these two models.36 The simplest combinations are called the standard linear models.36–38 For instance, coupling a Maxwell element in parallel with another dashpot provides the well-known Oldroyd-B model, used extensively to model viscoelastic liquids39 (Fig. 4a). Variations of the Oldroyd-B model, for instance, the Saramito model, have also been used to model the flow and dynamical behavior of viscoelastic materials.40,41 These models inherently decouple the solvent and the polymer viscosities, μS and μP, respectively, using the two dashpots. However, for the present PAAm composition, the solvent (water) viscosity is significantly lower than the polymer viscosity, i.e., μS ≪ μP. Furthermore, due to the relatively higher elasticity of the materials and the dynamical nature of contact, we realized that the Oldroyd-B model is not suitable for our system. Hence, we used the standard linear model with a Kelvin–Voigt element in series with another spring. The rationale behind using this model is that it accurately maps the dynamics of the moving contact line as the elastic drops/spheres spread. Due to the finite velocity of the contact line, it is modeled using a spring with high-frequency modulus G∞ and the dashpot represents the viscosity μ0, whereas regions away from the contact line are modeled using a spring with relaxed modulus G0 (Fig. 4b). Furthermore, the high-frequency spring is either unrelaxed or in the process of relaxing, depending on the magnitude of the contact line velocity (Fig. 4b).
From existing literature,38 the relaxation function of the standard linear model can be represented as G(t) = G0 + (G∞ − G0)e−t/τ, where τ is the relaxation timescale and t is the temporal variable. From the G′ and G″ values measured from rheology, we first calculated the absolute shear modulus 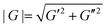 . Consequently, we used a fitting equation of the form G0 + (G∞ − G0)e−1/fτ to obtain the static shear modulus G0 and the relaxation timescale τ (see Table 1). Here, f = 1/t is the frequency. The elastic modulus of the materials was consequently calculated using the relation E0 = 2G0(1 + ν) = 3G0, i.e., considering Poisson's ratio ν = 1/2 (ref. 11) (see Table 1). The viscosity of the PAAm spheres was calculated using the relation μ0 = G0τ. Furthermore, note that other rheology models, such as the Chasset–Thirion relation,9,19 were found to be inappropriate for fitting the present rheology since in that model G″ decays following a power-law relation in f. In addition, due to the intermediate elasticity values of the prepared PAAm, conventional shear rate ramp measurements performed for non-Newtonian liquids or compression tests performed for stiff solids cannot be used to characterize these materials.
. Consequently, we used a fitting equation of the form G0 + (G∞ − G0)e−1/fτ to obtain the static shear modulus G0 and the relaxation timescale τ (see Table 1). Here, f = 1/t is the frequency. The elastic modulus of the materials was consequently calculated using the relation E0 = 2G0(1 + ν) = 3G0, i.e., considering Poisson's ratio ν = 1/2 (ref. 11) (see Table 1). The viscosity of the PAAm spheres was calculated using the relation μ0 = G0τ. Furthermore, note that other rheology models, such as the Chasset–Thirion relation,9,19 were found to be inappropriate for fitting the present rheology since in that model G″ decays following a power-law relation in f. In addition, due to the intermediate elasticity values of the prepared PAAm, conventional shear rate ramp measurements performed for non-Newtonian liquids or compression tests performed for stiff solids cannot be used to characterize these materials.
| Materials | E0 (kPa) | ρ (kg m−3) | γ (mN m−1) | τ (ms) |
|---|---|---|---|---|
| PAAm 6.5% | 0.16 | 1003.3 | 65.6 | 12.2 ± 1.6 |
| PAAm 30.0% | 366.6 | 1019.4 | 57.3 | 5.5 ± 0.3 |
For all the PAAm drops, the surface tension of each prepolymer solution was measured using the pendant drop technique on a drop-shape analyzer (DSA30, KRÜSS) under ambient conditions. To extract the surface tension, KRÜSS ADVANCE software's in-built Young-Laplace equation was used (see Table 1). Each measurement was repeated three times.
2.3 Imaging experiments
For static or equilibrium measurements, the PAAm drops/spheres were deposited on freshly cleaned glass substrates. Subsequently, side-view images were recorded under proper back-lit illumination using a camera (FASTCAM AX-200, Photron) coupled to a 4× objective lens and an adapter tube providing a spatial resolution of 4 µm per pixel. Static contact-angle measurements were performed using the sessile drop technique using a tangent fit in ImageJ.For spreading experiments, the spherical drops were held at the tip of a hydrophobic PTFE-coated stainless steel needle and gently lowered to make contact with the substrates positioned underneath on a stage. The lowering speed of the needle was maintained at a few µm s−1 to ensure minimal vibration upon contact. As the drop made contact with the substrate, the growth of the drop–substrate footprint radius, i.e., the spreading radius, was recorded using a high-speed camera (FASTCAM S12, Photron) at an acquisition rate of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames per second. The camera was equipped with a 10× long working-distance objective lens providing a spatial resolution of 2 µm per pixel. Due to the field of view restrictions imposed by the high magnification lens and the camera frame rate, the entire drop–substrate footprint radius is not captured, and we tracked the growth of the spreading radius on one side, specifically the right contact line. This is particularly true for the PAAm with 6.5 wt% where the spreading radius is large. The experimental videography was analyzed using a custom-built edge detection scheme on Python, whereby the radial location of the moving contact line was detected in each frame over the entire duration of the spreading event. Furthermore, using the information of the radial location, the dynamic contact angle in each frame was measured using either a tangent fit or a first-order polynomial fit. Each measurement was repeated 3–5 times to ensure consistency.
000 frames per second. The camera was equipped with a 10× long working-distance objective lens providing a spatial resolution of 2 µm per pixel. Due to the field of view restrictions imposed by the high magnification lens and the camera frame rate, the entire drop–substrate footprint radius is not captured, and we tracked the growth of the spreading radius on one side, specifically the right contact line. This is particularly true for the PAAm with 6.5 wt% where the spreading radius is large. The experimental videography was analyzed using a custom-built edge detection scheme on Python, whereby the radial location of the moving contact line was detected in each frame over the entire duration of the spreading event. Furthermore, using the information of the radial location, the dynamic contact angle in each frame was measured using either a tangent fit or a first-order polynomial fit. Each measurement was repeated 3–5 times to ensure consistency.
3 Results and discussion
3.1 Static morphology
In Fig. 5, we show the static or equilibrium configurations of these PAAm spheres/drops with varying Young's modulus. For low monomer wt%, i.e., low Young's modulus, the PAAm wets the glass substrates in a manner similar to Newtonian liquid drops such as water (Fig. 5, E0 = 5.7 Pa). Note that the equilibrium contact angle θE is approximately 20° for this liquid-like PAAm. With increasing Young's modulus, they exhibit intermediate wetting/contact morphologies with decreasing contact radius and increasing contact angles. For very stiff PAAm (Fig. 5, E0 = 366 kPa), the static configuration mimics that of a similarly sized glass sphere with θE ≈ 164°. From their equilibrium configurations, it is evident that, despite having similar surface tension values, they follow different trajectories upon initial deposition to arrive at different equilibrium contact radius/angle values. Consequently, we aim to resolve their spreading characteristics using our dynamic measurements. Note that the spreading of weakly elastic, polymeric liquid-like PAAm, i.e., PAAm with 4 wt% monomer, was reported in our previous work.33 Here, we focus on the spreading of PAAm having moderate and high Young's modulus values. | ||
| Fig. 5 Static configuration of (a) 1 mm radius water and PAAm with 4 wt% monomer drops on glass substrates, (b) 1 mm radius PAAm with 6.5 wt% monomer and PAAm with 10 wt% monomer drops on glass substrate, and (c) 1 mm radius PAAm with 30 wt% monomer spheres and glass beads on glass substrates. The elasticity E0 values are shown. Scale bars represent 1 mm. Certain sub-figures are reproduced from authors' previous works with permission from the Royal Society of Chemistry11 and the American Chemical Society, Copyright 2024.15,33 | ||
3.2 Spreading dynamics
In Fig. 6, we show the experimental snapshots of the early stages of contact of a moderately elastic PAAm (E0 = 0.16 kPa) and a stiff PAAm (E0 = 366 kPa) on glass substrates. It is evident that even when the Young's modulus is moderately high, the contact dynamics resemble spreading of liquids on partially wetting substrates, whereas for the stiffer PAAm, the dynamics remain in a JKR-type contact regime. Further, we observe that even though the dynamic contact angle for the moderately elastic PAAm gradually decreases during the course of spreading, for the stiffer one, it consistently remains high. Here, we will first elaborate on the dynamics of contact in terms of the dynamic spreading radius r(t) and dynamic contact angle θD (Fig. 6). In Fig. 7, we show the evolution of the PAAm–substrate footprint radius, i.e., the spreading radius r and the dynamic contact angle θD for PAAm 6.5 wt% (E0 = 0.16 kPa) on glass. From the observed trajectory, the spreading behavior can be categorized into two distinct regimes separated approximately at t = 10 ms. For t ≤ 10 ms, the growth of the spreading radius appears to obey a power-law behavior, r ∼ tα, where the exponent α needs to be analyzed. For t ≥ 10 ms, the spreading transitions to a different regime, which can be termed as arrested spreading or contact. This transition becomes more evident upon analyzing the evolution of the dynamic contact angle θD. For t ≤ 10 ms, we observe a monotonic decrease in θD, whereas for t ≥ 10 ms, we observe significant oscillations in θD. In the following sections, we will elaborate on these two distinct regimes observed.In Fig. 8, we show the comparison of the observed spreading behavior in regime I with both the inertial-capillary and viscous-capillary scaling laws. For comparison, we also show the spreading of 1 mm radius DI water drops on glass substrates. From Fig. 8, it is evident that for moderately elastic PAAm, the spreading radius obey the scaling law r ∼ (γR/μ)1/2t1/2, i.e., a regime where liquid capillarity is resisted primarily by PAAm viscosity. Thus, the behavior is similar to the spreading of a viscous liquid (Newtonian or shear-thinning). It may seem counterintuitive that viscosity plays a dominant role in such an elastic system, especially when the contact-line velocity is relatively high. Consequently, we analyze the relaxation timescale of the material. For PAAm 6.5%, τ = 12 ms, which is approximately the same as the spreading timescale in regime I, t0 ≈ 10–20 ms, around which the transition to regime II is observed. Thus, the characteristic Deborah number during regime I of spreading is De = τ/t0 ≈ 0.6–1.2 ≈ 1, and hence the material response should ideally be viscoelastic rather than purely viscous. To interpret the observed discrepancy, we highlight that, phenomenologically, the polymer chains are unrelaxed in this regime. Thus, they can neither resist deformation nor store energy. From a constitutive model point of view, the high-frequency spring G∞ is thus unrelaxed, and the system behaves as a Maxwell fluid where the viscous dashpot only contributes to the dissipation. At the same time, we note that for a purely viscous response to be effective, the spring with modulus G0 should not contribute to any form of dissipation and can only store a small fraction of the capillary energy. Furthermore, note that the characteristic viscous-capillary timescale tv = μR/γ ≈ 60 ms ≈ 4t0, reinforcing our conclusions that this regime is viscous-dominated. Alternatively, one can also look at the characteristic Ohnesorge number of the system, 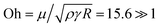 .
.
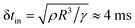 . Here, we do not observe such oscillations in regime I due to viscous damping, reinforcing our previous assertion of a purely viscous regime. However, in regime II, i.e., for t ≥ 10 ms, we observe oscillations with a typical duration of 500 ms. Additionally, the time periods of these oscillations are non-uniform and much greater than
. Here, we do not observe such oscillations in regime I due to viscous damping, reinforcing our previous assertion of a purely viscous regime. However, in regime II, i.e., for t ≥ 10 ms, we observe oscillations with a typical duration of 500 ms. Additionally, the time periods of these oscillations are non-uniform and much greater than 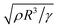 . We thus note that as polymers accumulate close to the moving contact line, they can be treated as a system of effective springs undergoing compression and relaxation, causing the observed oscillations in dynamic contact angles. Consequently, the high-frequency spring is relaxing and can resist deformation. Furthermore, G∞ can assume any value between G0 and βG0. Phenomenologically, the polymer accumulation close to the contact line is manifested by a distinct foot-like region that retards motion. The foot-like region grows in size until equilibrium is reached. Furthermore, the onset of the foot-like region highlights that the spreading loses its extensional character and shear effects need to be accounted for.
. We thus note that as polymers accumulate close to the moving contact line, they can be treated as a system of effective springs undergoing compression and relaxation, causing the observed oscillations in dynamic contact angles. Consequently, the high-frequency spring is relaxing and can resist deformation. Furthermore, G∞ can assume any value between G0 and βG0. Phenomenologically, the polymer accumulation close to the contact line is manifested by a distinct foot-like region that retards motion. The foot-like region grows in size until equilibrium is reached. Furthermore, the onset of the foot-like region highlights that the spreading loses its extensional character and shear effects need to be accounted for.To model the effect of elasticity and interpret the evolution of contact in this regime, we deviate from the conventional fluid mechanics approach. Thus, we first formulate the stress–strain relation relevant to this system: σ = G0e + μ0(de/dt′), where σ ∼ γR/r′2 is the Laplace pressure driving the contact line motion, and e is the strain. It is important to note that since both the relaxed spring G0 and the high-frequency spring G∞, contribute in this regime, the effective viscosity of the dashpot can be expressed as μ0 = (G∞ − G0)τ = β(G0 − 1)τ ≈ βG0τ since β ≫ 1. Furthermore, note that, for the ease of analysis, we consider a variable change: r′ = r − r0 and t′ = t − t0, where r0 and t0 are the spreading radius and time at the end of regime I (see inset of Fig. 9). Thus, the strain can be expressed as e ∼ r′/r0. Consequently, the force balance per unit area of the CL can be expressed as
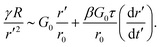 | (1) |
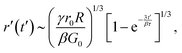 | (2) |
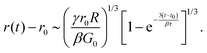 | (3) |
 | ||
| Fig. 9 Evolution of the spreading radius r for 1 mm radius PAAm 6.5% drops (E0 = 0.16 kPa) on glass substrates in regime II. The symbols represent experimental data, whereas the solid line represents the theoretical solution (eqn (3)). Here, the origin of the x-axis is at t = 10 ms. The inset shows the schematic of the spreading process, highlighting the different variables r, r′ and the radius at the end of regime I, r0. Error bars are omitted for clarity. | ||
Note that in solving eqn (3), we use our experimentally observed r0 and t0 as inputs. In Fig. 9, we show the comparison of our theoretical model with experimental data. A reasonably good agreement is observed for β = 50. Note that this β value deviates from that obtained from our rheology fitting, i.e., β = 200. Furthermore, we observe that using β = 200 to fit our experiments severely underestimates the data (see Fig. S3, SI). The discrepancy is likely due to the different dynamics involved in shear rheology and spreading. Furthermore, existing literature has typically used β ∼ 10–100 to model dynamic contact-line problems,46 and thus β = 50 is a reasonable assumption. Nevertheless, we highlight that our solution is extremely sensitive to β since it effectively prevents the exponential term in eqn (3) to go out of bounds. This also validates our assumption of using the standard linear model to represent the moving contact line, since for any other model, e.g., Maxwell (μ, G∞) or Kelvin–Voigt (μ, G0), the β factor does not appear within the exponential term of the final solution. Furthermore, we point out that the spreading radius continues to grow slowly beyond what is shown in Fig. 7 and 9, until equilibrium is reached. However, due to the limited field of view at the chosen frame rate and magnification, the entire process cannot be captured.
3.3 Dynamics of spreading for highly elastic drops
For the much stiffer PAAm (E0 = 366 kPa) sphere, we observe that the contact evolution is significantly slower with a much smaller final radius (Fig. 10). Qualitatively, the inherent characteristics remain the same: an initial regime obeying a power-law growth in the spreading radius, i.e., r ∼ t1/2, and a final regime with an exponential decay with a transition point around 7–8 ms (Fig. 10a and b). In other words, t0 = 7–8 ms, yielding the characteristic Deborah number of regime I, De = τ/t0 = 1.2–1.4 ≈ 1. Thus, similar to the softer PAAm, these conditions also signify a transition to regime II. Furthermore, note that, in comparing our experimental data in regime II with our model (eqn (3)), a β value of 10 was used, which is on par with the value obtained from rheology. Compared to the spreading of moderately elastic PAAm with E0 = 0.16 kPa, here the average contact-line velocity during regime I is vCL ≈ 8 mm s−1, which decays to approximately 0.1 mm s−1 during regime II. Additionally, we observe that there are significant phenomenological differences between the two cases. Notably, we observe uniform oscillations of the spreading radius in regime II, which were previously not observed. Repeated measurements confirmed that these oscillations are not artificially induced by image processing and are an inherent part of the dynamics. Thus, despite reasonable agreement between our theoretical model (eqn (3)) and the experimental data (Fig. 10b), we highlight that our governing equation does not contain a second-order derivative term to accurately model such oscillations in r.47 | ||
| Fig. 10 (a) Evolution of spreading radius r and dynamic contact angle θD for 1 mm radius PAAm 30% drops (E0 = 366 kPa) on glass substrates. The r ∼ t1/2 scaling law is shown for clarity. The error bars represent the standard deviation of multiple experimental runs. (b) Evolution of spreading radius r in regime II. The symbols represent experimental data, whereas the solid line represents the theoretical solution (eqn (3)). Here, the origin of the x-axis is at t = 7.5 ms. Error bars are omitted for clarity. (c) Evolution of the dynamic contact angle θD in regime II. δt represents the time period of oscillations. Here, the origin of the x-axis is at t = 7.5 ms. | ||
Phenomenologically, the observed oscillations are likely due to the high elasticity of the PAAm, rendering significant resistance to the moving contact line. Note that, here also, the deformation foot exists in regime II of spreading. However, due to the large elasticity, the foot dimensions are very small and are only evident during higher-magnification imaging. Additionally, oscillations of the dynamic contact angle θD are also observed, which were previously observed during the spreading of moderately elastic PAAm as well (Fig. 10c). However, compared to the oscillations observed for the spreading of PAAm 6.5 wt%, here we observe that the oscillations are more uniform. Both the oscillations in dynamic contact radius and dynamic contact angle have a uniform time period δt ≈ 30 ms (Fig. 10b and c). Considering capillarity and elasticity effects, the characteristic timescale of oscillations can be expressed as γ/G0vCL ≈ 60 ms, which is in reasonable agreement with our experimental data. Finally, we highlight that the significant error bars in Fig. 10a are due to the use of side-view imaging and a small contact radius involved at the early moments of contact. This can be circumvented by the use of bottom-view imaging.18,20
Combining eqn (3) with our experimental results has interesting implications. As t → ∞ and β → 1, r → (γr0R/G0)1/3 + r0. This limit can provide us with predictions of the equilibrium contact radius. For the spreading of PAAm 6.5 wt% (E0 = 0.16 kPa), r0 ≈ 0.4R (Fig. 7) and thus r → 0.7(γR2/G0)1/3 + 0.4R. However, for the spreading of PAAm 30 wt% (E0 = 366 kPa), r0 ≈ 0.06R (Fig. 10) and thus the second term can be neglected. Consequently, we have r → 0.4(γR2/G0)1/3 ∼ (γR2/G0)1/3, i.e., it recovers the JKR theory4 at equilibrium. Note that the small deviation from the JKR theory for the moderately elastic PAAm is reasonable since the strain involved at equilibrium is beyond the Hookean limit. Finally, we briefly comment on any possible dehydration of the polymer network, which can affect our experimental findings. Note that the PAAm spheres contain significant quantities of water. However, the characteristic diffusion coefficient, D ∼ 10−9 m s−1, renders the diffusion timescale to be around 1000 s.13 Since the characteristic timescale of early regimes of spreading is around 1 s, dehydration of the PAAm does not interfere with our experimental observations.
Here, we highlight the significance of these findings for 3D printing applications.34,48,49 In particular, during the deposition of the initial layer, the viscoelastic properties of the ink or resin are critical. Traditional materials research tends to emphasize ink rheology,50 with oscillatory shear rheology being a common tool. However, this method does not accurately replicate the dynamic conditions of 3D printing. Extensional rheology techniques, such as Capillary Breakup Extensional Rheology (CaBER), also have limitations, notably the absence of moving contact lines.51,52 Dynamic wetting studies, by contrast, offer a promising approach to simulate the interplay between viscoelasticity and contact-line motion.33,41,53 Notably, most commercial 3D printers, such as the Formlabs Form 4 and Uniz Slash Plus UDP, operate at speeds ranging from 0.01 to 100 mm s−1, which aligns well with our experimental conditions.54,55 Since both material viscoelasticity and printing speed jointly influence final print resolution, our work provides valuable insights for optimizing these parameters to achieve high-resolution prints.
4 Conclusions
In conclusion, using experiments and theory, we show the short-time spreading behavior of (visco)elastic drops across a wide range of Young's modulus, where both liquid-like wetting and solid-bead-like contact configurations are possible. For moderate to high Young's modulus values, we observe that the short-time spreading behavior is distinctly different from that observed for Newtonian liquid drops, such as water, or non-Newtonian, shear-thinning liquids, such as PEO and Carbopol. In particular, the dynamics exhibit two distinct regimes: an early viscous regime followed by a viscoelastic regime, with a crossover time dictated by the condition De ≈ 1. While the former shows a power-law evolution in the spreading radius, the latter exhibits an exponential decay. We interpret the former regime as a competition between the relevant capillary and viscous forces. The latter regime is interpreted using the standard linear model of viscoelasticity. Furthermore, our theoretical formulation leads to the JKR theory in the equilibrium limit and can, in principle, be used to construct a dynamic JKR theory. Additionally, we highlight how the rheology of the polymers validates our assumption of the standard linear model of viscoelasticity. Specifically, we observe that this model is better suited to explain dynamical polymeric systems like the present ones, compared to other constitutive models such as Kelvin–Voigt, Maxwell, Oldroyd-B, or Saramito. A similar model was used by de Gennes to describe the dynamics of crack propagation in soft adhesives, also referred to as de Gennes' trumpet model.37The findings presented here can be used to understand cell spreading, which involves similar elastic properties.56 Furthermore, they can provide a guiding principle for material selection in 3D printing using hydrogels and biomaterial inks,57,58 where viscoelasticity plays a key role in indicating the final achievable print resolution. Combined with the non-trivial contact velocity at which such printing processes typically operate, the present short-time spreading study offers routes to control print speeds for viscoelastic inks.
Author contributions
S. K. M. conceived the study. S. M. and A.-R. K. performed the experiments and analyzed the data. All authors discussed the results. S. M. wrote the manuscript with input from all the authors. B. Z. and S. K. M. supervised the research.Conflicts of interest
The authors declare no conflict of interest.Data availability
All data that support the findings of this study are included within the article.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ma00896d.
Acknowledgements
The authors are grateful to Lukas Bauman (Department of Chemical Engineering, University of Waterloo) for assistance with PAAm preparation and Prof. Michael K. C. Tam (Department of Chemical Engineering, University of Waterloo) for providing the dynamic shear rheometer. B. Z. acknowledges the support of NSERC RGPIN-2019-04650. S. K. M. acknowledges the support of the Discovery Grant (NSERC, RGPIN-2024-03729).References
- P.-G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 Search PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 Search PubMed.
- H. Hertz, J. für die reine Angew. Math., 1882, 92, 22 Search PubMed.
- K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 Search PubMed.
- T. Young, Philos. Trans. R. Soc. London, 1805, 65–87 CrossRef.
- E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 186103 Search PubMed.
- A. Marchand, S. Das, J. H. Snoeijer and B. Andreotti, Phys. Rev. Lett., 2012, 109, 236101 Search PubMed.
- S. J. Park, B. M. Weon, J. S. Lee, J. Lee, J. Kim and J. H. Je, Nat. Commun., 2014, 5, 4369 CrossRef CAS PubMed.
- S. Mitra, S. Misra, T. Tran and S. K. Mitra, Langmuir, 2022, 38, 7750–7758 Search PubMed.
- R. W. Style, C. Hyland, R. Boltyanskiy, J. S. Wettlaufer and E. R. Dufresne, Nat. Commun., 2013, 4, 2728 Search PubMed.
- A.-R. Kim, S. Mitra, S. Shyam, B. Zhao and S. K. Mitra, Soft Matter, 2024, 20, 5516–5526 Search PubMed.
- A. Chakrabarti, A. Porat, E. Raphaël, T. Salez and M. K. Chaudhury, Langmuir, 2018, 34, 3894–3900 Search PubMed.
- J. Yang, R. Bai, B. Chen and Z. Suo, Adv. Funct. Mater., 2020, 30, 1901693 Search PubMed.
- W. Zhang, R. Wang, Z. Sun, X. Zhu, Q. Zhao, T. Zhang, A. Cholewinski, F. K. Yang, B. Zhao and R. Pinnaratip, et al., Chem. Soc. Rev., 2020, 49, 433–464 Search PubMed.
- P. Chakraborty, S. Mitra, A.-R. Kim, B. Zhao and S. K. Mitra, Langmuir, 2024, 40, 7168–7177 CrossRef CAS PubMed.
- A.-L. Biance, C. Clanet and D. Quéré, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 016301 Search PubMed.
- J. C. Bird, S. Mandre and H. A. Stone, Phys. Rev. Lett., 2008, 100, 234501 Search PubMed.
- S. Mitra and S. K. Mitra, Langmuir, 2016, 32, 8843–8848 Search PubMed.
- Q. Vo, S. Mitra, M. Lin and T. Tran, J. Colloid Interface Sci., 2024, 664, 478–486 Search PubMed.
- A. Eddi, K. G. Winkels and J. H. Snoeijer, Phys. Fluids, 2013, 25, 013102 Search PubMed.
- K. G. Winkels, J. H. Weijs, A. Eddi and J. H. Snoeijer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 055301 Search PubMed.
- A. Carlson, G. Bellani and G. Amberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 045302 Search PubMed.
- J. D. Paulsen, J. C. Burton and S. R. Nagel, Phys. Rev. Lett., 2011, 106, 114501 Search PubMed.
- D. Debnath, P. Kumar and S. K. Mitra, Langmuir, 2021, 37, 14833–14845 CrossRef CAS PubMed.
- R. Cox, J. Fluid Mech., 1986, 168, 169–194 Search PubMed.
- L. Tanner, J. Phys. D: Appl. Phys., 1979, 12, 1473 CrossRef CAS.
- S. Chen, E. Pirhadi and X. Yong, J. Colloid Interface Sci., 2022, 618, 283–289 CrossRef CAS PubMed.
- D. Cuvelier, M. Théry, Y.-S. Chu, S. Dufour, J.-P. Thiéry, M. Bornens, P. Nassoy and L. Mahadevan, Curr. Bio., 2007, 17, 694–699 Search PubMed.
- A. Bouillant, P. J. Dekker, M. A. Hack and J. H. Snoeijer, Phys. Rev. Fluids, 2022, 7, 123604 Search PubMed.
- S. Yada, K. Bazesefidpar, O. Tammisola, G. Amberg and S. Bagheri, Phys. Rev. Fluids, 2023, 8, 043302 Search PubMed.
- S. C. Varma, A. Saha, S. Mukherjee, A. Bandopadhyay, A. Kumar and S. Chakraborty, Soft Matter, 2020, 16, 10921–10927 RSC.
- S. C. Varma, D. Dasgupta and A. Kumar, Phys. Fluids, 2022, 34, 093112 CrossRef CAS.
- S. Mitra, A.-R. Kim, B. Zhao and S. K. Mitra, Langmuir, 2024, 40, 18968–18976 CrossRef CAS PubMed.
- J. M. Townsend, E. C. Beck, S. H. Gehrke, C. J. Berkland and M. S. Detamore, Prog. Polym. Sci., 2019, 91, 126–140 CrossRef CAS PubMed.
- S. Mitra, A.-R. Kim, B. Zhao and S. K. Mitra, Soft Matter, 2025, 21, 4587–4595 RSC.
- I. M. Ward and J. Sweeney, Mechanical properties of solid polymers, John Wiley & Sons, 2012 Search PubMed.
- P.-G. de Gennes, Langmuir, 1996, 12, 4497–4500 CrossRef CAS.
- Y. M. Efremov, T. Okajima and A. Raman, Soft Matter, 2020, 16, 64–81 RSC.
- J. Hinch and O. Harlen, J. Non-Newtonian Fluid Mech., 2021, 298, 104668 CrossRef CAS.
- P. Saramito, J. Non-Newtonian Fluid Mech., 2007, 145, 1–14 CrossRef CAS.
- H. L. França, M. Jalaal and C. M. Oishi, Phys. Rev. Res., 2024, 6, 013226 CrossRef.
- S. Das, P. R. Waghmare and S. K. Mitra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 067301 CrossRef PubMed.
- T. Sridhar, V. Tirtaatmadja, D. Nguyen and R. Gupta, J. Non-Newtonian Fluid Mech., 1991, 40, 271–280 CrossRef CAS.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115–138 CrossRef CAS.
- A. Chowdhury, S. Misra, S. Mitra and S. K. Mitra, Langmuir, 2025, 41, 11358–11366 CrossRef CAS PubMed.
- S. Karpitschka, S. Das, M. van Gorcum, H. Perrin, B. Andreotti and J. H. Snoeijer, Nat. Commun., 2015, 6, 7891 CrossRef CAS PubMed.
- C.-A. Charles, A. Louhichi, L. Ramos and C. Ligoure, Soft Matter, 2021, 17, 5829–5837 RSC.
- R. C. Daniel and J. C. Berg, Adv. Colloid Interface Sci., 2006, 123, 439–469 CrossRef PubMed.
- M. T. Arango, Y. Zhang, C. Zhao, R. Li, G. Doerk, D. Nykypanchuk, Y. K. Chen-Wiegart, A. Fluerasu and L. Wiegart, Mater. Today Phys., 2020, 14, 100220 CrossRef.
- A. Corker, H. C.-H. Ng, R. J. Poole and E. Garca-Tuñón, Soft Matter, 2019, 15, 1444–1456 RSC.
- M. Rosello, S. Sur, B. Barbet and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2019, 266, 160–170 CrossRef CAS.
- O. Arnolds, H. Buggisch, D. Sachsenheimer and N. Willenbacher, Rheol. Acta, 2010, 49, 1207–1217 CrossRef CAS.
- J. van der Kolk, D. Tieman and M. Jalaal, J. Fluid Mech., 2023, 958, A34 CrossRef CAS.
- https://www.uniz.com/eu_en/3d-printers/slash-2.
- https://formlabs.com/3d-printers/professional.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327 CrossRef CAS.
- L. Bauman and B. Zhao, J. Colloid Interface Sci., 2023, 638, 882–892 CrossRef CAS PubMed.
- J. Li, C. Wu, P. K. Chu and M. Gelinsky, Mater. Sci. Eng., R, 2020, 140, 100543 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |