 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The levelized cost of exergy: a technoeconomic framework for energy system comparison
Jordan D.
Kocher
 *ab,
Aravindh
Rajan
c,
Jason
Woods
*ab,
Aravindh
Rajan
c,
Jason
Woods
 a,
Walter P.
Parker
Jr
ab,
Samuel
Woolsey
b and
Akanksha K.
Menon
*ab
a,
Walter P.
Parker
Jr
ab,
Samuel
Woolsey
b and
Akanksha K.
Menon
*ab
aNational Laboratory of the Rockies, Golden, CO, USA. E-mail: jordan.kocher@nrel.gov
bGeorge W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, USA. E-mail: akanksha.menon@me.gatech.edu
cOrca Sciences, Kirkland, WA, USA
First published on 29th December 2025
Abstract
While the levelized costs of electricity and heat have been quantified before, these two metrics cannot be directly compared, due to the different exergy content of heat and work. To address this, we develop a levelized cost of exergy (LCOEx) framework that enables direct comparisons between energy sources and processes. We find that moderate- and high-grade heat have an LCOEx that is comparable to electricity (5–10 ¢ per kWhex), while low-grade heat sources have much higher LCOEx values (>50 ¢ per kWhex). The LCOEx of a system's output is affected by (i) the LCOEx of the system input, (ii) the CAPEX of the system, and (iii) the exergetic efficiency of the system. We use our framework to identify which processes are already achieved with relatively high cost effectiveness (production of fuels, hydrogen, and ammonia) and which have room for improvement (dehumidification, food production).
Broader contextGrowing populations demand efficient and cost-effective sources of food, water, and energy. To quantify the cost to produce commodities, researchers have developed “levelized cost” metrics, including the levelized cost of electricity (LCOE), levelized cost of heat (LCOH), levelized cost of water (LCOW), and levelized cost of ammonia (LCOA). However, these quantities cannot be directly compared, given the different units of measure. Even LCOE and LCOH, which are both quantified in cost per unit energy, should not be compared, since one unit of electrical work is not thermodynamically equivalent to one unit of heat transfer. In this work, we develop a broadly applicable “levelized cost of exergy” (LCOEx) metric. Our framework allows a direct comparison between the cost of exergy (or “useful energy”) within different energy sources, chemicals, and foods. Applying the framework to an energy system reveals how the system's output is influenced by (i) the LCOEx of the system input, (ii) the exergetic efficiency of the system, and (iii) the system CAPEX. The framework then indicates which thermodynamic processes have room for cost reduction, as well as those which are already cost-optimized. Of those with room for improvement, cost reduction can be achieved by switching to a process that produces the same output with a cheaper exergy source, improving process efficiency, and/or reducing CAPEX. |
Introduction
As populations grow and urbanization intensifies, it becomes increasingly important to efficiently and cost-effectively utilize global energy resources. Low-grade heat, which for the purposes of this work is defined as heat delivered at temperatures ≤150 °C, is used in a variety of applications.1–6 For example, steam is used for sterilization,7–9 food and beverage processes,10,11 and thermal desalination.12–17 Hot water is used to heat buildings18,19 and regenerate liquid desiccants in dehumidifiers,20,21 and solar absorbers are used to regenerate sorbents in atmospheric water harvesting22–24 (AWH) and CO2 direct air capture25 (DAC) systems. Low-grade heat is often far cheaper (per unit energy) than electricity; for example, Gilbert et al. found that industrial steam (at 150 °C) generated with natural gas (NG) has a levelized cost of 1.25 ¢ per kWhth,26 while electricity produced by natural gas combined cycles (NGCC) often has a levelized cost around 6 ¢ per kWhe.27,28 Solar- and waste-heat also seem attractive, given that they have no fuel cost. However, Geffroy et al. showed that the necessary capital investment and low conversion efficiency of low-grade waste heat yield unfavorable economics when using this heat to produce electricity.1 Moderate-grade heat (above 150 °C) has more potential to generate electricity, in which case Rankine29 and organic Rankine cycles30 have proven cost-effective in valorizing waste heat. Beyond power generation, a broader technoeconomic analysis is needed to evaluate the viability of different energy sources (from electricity to low-grade and high-grade heat, hydrocarbon fuels, and more), which is the focus of the present work.On a per unit energy basis, heat and electricity cannot be directly compared. This is because heat has less potential to do work – not all of the energy transferred via heat is useful, and some of it must be rejected to the environment in accordance with the second law of thermodynamics. This has led to the development of the concept of “exergy”, which is the theoretical maximum amount of energy that can be converted to work when a system interacts with a specified reference environment.31–34 The flow of heat carries exergy, but the amount of exergy within the heat is less than the amount of energy being transferred. The higher the temperature at which heat is being transferred, the more exergy there is. In contrast, electrical energy is fully available as work; i.e., all of the energy is exergetic. Because low-grade heat sources have temperatures in the range of 80–150 °C, they carry far less exergy than electricity, so a comparison between the levelized costs per unit energy (heat or electricity) is not an appropriate one. Another comparison between heat- and work-driven systems that is often made in the literature is on the basis of “specific energy consumption” (SEC), which is defined as the energy consumption of a system, per unit output.12,35,36 However, for heat-driven systems, the SEC is far greater than for work-driven systems (for the exergetic-based reasons explained above). To remedy this, the SEC of the heat-driven system is often reported as an “equivalent” electric SEC, by multiplying it with an assumed heat conversion efficiency (usually around 30%12). This method is rather imprecise and does not consider the cost of the different energy sources. Thus, comparing the SEC (or other efficiency metrics like coefficient of performance) of work- and heat-driven systems is also not appropriate.
Framework
Comparing the thermodynamic and economic performance of systems on the basis of exergy allows for a direct comparison across systems with different energy sources. To quantify the costs associated with a particular exergy source, we introduce the levelized cost of exergy (LCOEx). The LCOEx quantifies the lifetime costs to produce exergy in a particular form (e.g., chemical exergy within a fuel, exergy transferred via heat, etc.), divided by the lifetime exergy production. The general expression for LCOEx is given in eqn (1), where CAPEX is the initial capital cost of the system, OPEXn is the variable operating cost associated with the system in year n, r is the discount rate, N is the lifetime of the system (in years), and Ex is the annual amount of exergy that the system produces. CRF is the capital recovery factor, which is defined in eqn (2). | (1) |
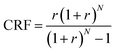 | (2) |
Generally, every system converts exergy input to exergy output, with an exergetic efficiency of ηex. Because the exergy input has some cost, the OPEX can be broken down into the cost of the exergy input (e.g., electricity cost), LCOExin/ηex, plus all other OPEX (e.g., maintenance costs), OPEXm. Then, the output LCOEx of a system can be written as shown in eqn (3).
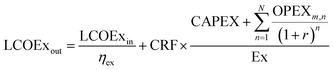 | (3) |
The amount of exergy per unit energy is sometimes referred to as the “exergy factor”, fe.37 For work, the exergy factor is unity. For heat flow, the exergy factor is simply the Carnot efficiency, given in eqn (4), where T0 is the ambient temperature and Td is the temperature of the heat being delivered. Notably, the temperature of heat supplied to a system will decrease from the source (T = TS) to the temperature at which it is delivered to the system (T = Td), resulting in a lower exergy factor at the point of delivery than at the source. For fuels, the exergy factor is simply the ratio of chemical exergy to heat of combustion.37
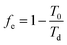 | (4) |
For any energy source, the LCOEx is equal to the levelized cost of energy divided by the exergy factor of the source. For electricity or mechanical work input, the LCOEx is simply equal to the LCOE, since the exergy factor of work is unity. For heat, the LCOEx is equal to the levelized cost of heat (LCOH) divided by the exergy factor of the heat, which is the Carnot efficiency.
In addition to the LCOEx, this framework compares heat- and work-driven systems on the basis of “specific exergy consumption”, Σ. The specific exergy consumption of a work-driven system is equal to the SEC, again because the exergy factor of work is unity. Meanwhile, the specific exergy consumption of a heat-driven system is the SEC multiplied by the exergy factor, which is given in eqn (5).
 | (5) |
Then, the quantity LCOExin × Σ is the cost of the energy needed to produce a unit output from the system. For example, for a desalination plant, LCOExin × Σ is the cost of the energy needed to produce one cubic meter of fresh water. As expected, LCOExin × Σ is equal to LCOEin × SEC for a work-driven system, but it is also equal to LCOHin × SEC for a heat-driven system (since the fe terms cancel out). Furthermore, the quantity LCOExin × Σ can be rewritten as LCOExin × Σrev/ηex, where Σrev is the reversible specific exergy consumption of a process, and ηex is the exergetic efficiency of the actual system that achieves said process.
Fundamentally, recasting the output cost in terms of LCOEx and exergetic efficiency does not change the end result of a cost analysis. Instead, it allows for more direct comparisons between two systems producing the same output using different energy inputs (e.g., work-driven, heat-driven with a high temperature source, heat-driven with a low temperature source, etc.). By writing the quantity in this way, the contribution to output cost can be broken down into three separate contributions: (i) the cost per unit exergy of the system input (LCOExin), (ii) how exergy intensive the process is (Σrev), which is independent of the system performance and only depends on the thermodynamics of the process, and (iii) how close the system gets to the reversible limit (ηex). This formulation is particularly useful as a litmus test for emerging concepts/processes: even in the reversible limit (ηex = 1), would the process use a high LCOEx input? Or does it have a high specific exergy consumption? If the answer to either of these questions is yes, then the unit output cost will be high.
To visualize how the LCOEx increases when going from energy input to output of a system (or series of systems), we introduce an LCOEx Sankey diagram; a generalized version is shown in Fig. 1. The overall illustration consists of two separate Sankey diagrams: the top one is for cost (in green), while the bottom one is for exergy (in yellow). The ratio of cost to exergy represents the LCOEx. When that ratio is calculated before the system boundary (left side of the figure), it represents the LCOEx of the system's energy source. For example, in the case of a reverse osmosis (RO) plant, this would be the LCOEx of the electricity input. For a NGCC power plant, it is the LCOEx of the NG fuel. When the cost to exergy ratio is calculated after the system boundary (right side of the figure), it represents the LCOEx of the system output. For the RO plant example, this would be the cost per unit exergy of the fresh water produced by the plant. For the NGCC power plant, it is the electricity produced. Notably, the LCOEx always increases from system input to system output, because exergy is destroyed in any real process. Furthermore, there are costs associated with building and maintaining the system (CAPEX), which must be added to the cost of the exergy source. For the LCOEx of the system output to be as low as possible, the Sankey diagram in Fig. 1 reveals that the system should have the following three attributes: (i) it should utilize an exergy source with a low LCOEx, (ii) the cost to build and maintain the system itself should be low, and (iii) the system should have a high exergetic efficiency. For a system with multiple subsystems, or for multiple different systems being used in series (e.g., a NGCC power plant generates electricity which is then used by an RO plant), the cost and exergy flow can be visualized through each of the systems sequentially, and the LCOEx at different points in the process can be calculated by taking the cost to exergy ratio before and after each system. The detailed methodology for constructing these diagrams with the appropriate units is described in Note S1.
Because Fig. 1 reveals that the LCOEx of a system's output largely depends on the LCOEx of the exergy source, we first present results for the LCOEx of various exergy sources, including electricity, high-grade and low-grade heat, fuels, and food. We then discuss which of these sources are used by different technologies, as well as the associated exergetic efficiencies. We then identify which processes and energy systems stand to benefit the most from switching to lower LCOEx sources and from exergetic efficiency improvements. Finally, we demonstrate that electrically-driven systems can reduce costs in certain cases (due to the relatively low LCOEx of electricity), while other systems will not benefit from using electricity as the energy source, due to high capital costs and/or low exergetic efficiencies.
Results
The LCOEx of heat
We apply our LCOEx framework first to heat as a source of exergy. We use the LCOH values that Gilbert et al.26 calculated for four different applications (industrial steam at 150 °C, a hot water heater at 80 °C, ethane cracking at 850 °C, and a glass furnace at 1200 °C). When NG is used as the heat source (and the cost of carbon is not considered), Gilbert et al. found the LCOH to be 1.25, 3.52, 3.70, and 5.94 ¢ per kWhth for steam, hot water, ethane cracking, and glass furnaces, respectively.26 In Fig. 2 we use these LCOH values to plot the LCOEx as a function of the temperature at which the heat is delivered. For example, steam generated using NG (in the industrial sector) has an LCOH of 1.25 ¢ per kWhth. At a temperature of 150 °C, it would have an LCOEx of 4.3 ¢ per kWhex (from Fig. 2). If that steam were then used as the energy source to heat feed water in a desalination system at 80 °C, the delivered heat would have an LCOEx of 8.3 ¢ per kWhex. Several major findings result from this analysis. First, electricity is usually a cheaper method of delivering exergy to a system than low-grade (i.e., ≤100 °C) heat. Second, the LCOEx from industrial steam is on-par with electricity, as is the heat used in ethane crackers (∼5 ¢ per kWhex) and glass melters (∼7 ¢ per kWhex). It is notable that, despite its lower exergy factor, steam at 150 °C is produced at a lower LCOEx than the high-grade heat applications. This is due to the lower CAPEX and higher thermal efficiency of the 150 °C steam boiler,26 giving electrically-driven heat little margin to compete with NG at these temperatures. Notably, the curves in Fig. 2 correspond to the particular assumptions made by Gilbert et al. regarding capacity factors, exergetic efficiencies, etc. Because these parameters vary by application and system design, Fig. 2 represents a common, but not comprehensive, range of LCOEx values for different heat sources. | ||
| Fig. 2 The levelized cost of exergy (LCOEx) of different heat sources, with different levelized costs of heat (LCOH), as a function of the heat delivery temperature. Curves correspond to LCOH values taken from Gilbert et al.26 for industrial steam (red curve), hot water heater (orange curve), ethane cracker (purple curve), and glass furnace (blue curve) with NG as the fuel source. The pink point corresponds to an incredibly simple (low CAPEX) solar thermal collector (see Note S3). The green band corresponds to the range of LCOEx for electricity from NGCC plants.28 | ||
Fig. 2 reveals that NG-fired hot water heaters produce heat at relatively high LCOEx values. This is partially due to the low temperatures of this heat: converting the chemical exergy of NG to heat at <100 °C is incredibly exergetically inefficient. This is also due to the fact that the hot water heater has a higher LCOH than the steam boiler. The high LCOH and low exergy factor of low-grade heat lead to LCOEx values in excess of 10 ¢ per kWhex at temperatures ≤80 °C. The hot water heater curve in Fig. 2 corresponds to heat as the end product. If creating hot water as the end product is expensive on a per unit exergy basis, then providing heat at similar temperatures to drive thermodynamic processes (e.g., desiccant regeneration) will also be expensive. Thus, low-grade heat is typically a high LCOEx energy source and end product; reducing its cost will be challenging. Converting high-exergy sources (fuels, electricity) to low-grade heat via exergetically inefficient methods (combustion, electric resistance heating) yields expensive low-grade heat. Heat pumps, whether driven by a fuel (sorption heat pumps) or electricity (vapor compression) have the opportunity to produce low-grade heat with a far higher exergetic efficiency than combustion or electric resistance heating, because they can convert a small amount of high-grade source energy into a large amount of low-grade thermal energy. However, further improvements in heat pump exergetic efficiency and reductions in CAPEX are required before they can produce low-grade heat with a low LCOEx. In many locations, current heat pump water heaters provide heat at a higher LCOH than natural gas water heaters.26,38 In Note S4, we discuss the nuance of the control volume boundary for a heat pump-driven system.
For steam and hot water, the LCOEx is dominated by the fuel cost. This prompts the question: would a solar-thermal collector without a fuel source (thus reducing OPEX) yield a lower cost? In fact, low-grade solar- and waste-heat have already been described as “free” in the literature,39,40 simply based on the fact that they require no fuel OPEX. Menon et al. performed a technoeconomic analysis of flat plate solar collectors, with generous assumptions (i.e., 5.5 hours of 1000 W m−2 solar absorption for 365 days per year, with 50% collector efficiency), yielding an LCOH of 1.3 ¢ per kWhth.36 Thus, despite having no OPEX, the solar collector has a nearly identical LCOEx as steam in Fig. 2, though the solar collector cannot produce heat at the temperatures that a NG boiler can. We performed a more detailed analysis of a flat plate solar collector (Note S2) and found that it would have an even higher LCOH than the one calculated by Menon et al.36 To evaluate if a solar collector with lower CAPEX could produce heat at a low LCOEx, we modeled a pipe painted black (Note S3). In this case, the collector produces heat at an LCOH < 1 ¢ per kWhth, but the heat is delivered at such a low temperature (41 °C) that it would barely have any exergy, leading to an LCOEx of 17.7 ¢ per kWhex and a large amount of heat needed to drive thermodynamic processes. This dispels the misconception that energy systems powered by low-grade heat will receive heat “for free”, or that these energy sources will be so much cheaper than electricity that they will enable otherwise impractical processes.
The LCOEx of fuel and fuels
Beyond heat and electricity, we also provide the cost per unit exergy of different fuels in Table 1. Wholesale fuel prices are used for the hydrocarbon fuels, largely from the same source, so these values represent market averages (as opposed to the outputs of specific systems or processes). Because these values are taken from wholesale prices, the LCOEx in Table 1 is not a true levelized cost of exergy, but rather the price per unit exergy to purchase these fuels wholesale and use them to drive a thermodynamic process. The true levelized cost to produce these fuels is somewhat lower than the price at which they are sold wholesale (though in competitive markets the price approaches the levelized cost41). Then, the values in Table 1 should not be seen as the costs per unit exergy at which these fuels could be produced (which will depend on plant size, technology type, etc.). Rather, these values represent the price per unit exergy of the current market, with current production capacities and technologies.| Fuel | Reaction | Specific exergy (kWhex kg−1) | Specific price (¢ per kg) | LCOEx (¢ per kWhex) |
|---|---|---|---|---|
| Natural gas | CH4 + 2O2 → CO2 + 2H2O | 14.3642 | 19.7343 | 1.37 |
| Gray hydrogen | H2 + 1/2O2 → H2O | 38.5044 | 100.045 | 2.60 |
| Blue hydrogen | H2 + 1/2O2 → H2O | 38.5044 | 152.045 | 3.95 |
| Green hydrogen | H2 + 1/2O2 → H2O | 38.5044 | 550.046 | 14.3 |
| Gray ammonia | NH3 + 3/4O2 → 1/2N2 + 1 1/2H2O | 5.5147 | 47.0048 | 8.53 |
| Green ammonia | NH3 + 3/4O2 → 1/2N2 + 1 1/2H2O | 5.5147 | 88.8049 | 16.1 |
| Gasoline | C8H18 + 12 1/2O2 → 8CO2 + 9H2O | 13.1750 | 63.7651 | 4.84 |
| Diesel | C12H23 + 17 3/4O2 → 12CO2 + 11 1/2H2O | 11.7450 | 67.3951 | 5.74 |
| Ethanol | C2H6O + 3 1/2O2 → 2CO2 + 3H2O | 8.1852 | 54.3653 | 6.65 |
| Jet A-1 | C11H23 + 16 3/4O2 → 11CO2 + 11 1/2H2O | 12.8254 | 70.0055,56 | 5.46 |
| Coal | C + O2 → CO2 | 7.3142 | 12.7857 | 1.75 |
| Wood | C6H12O6 + 9O2 → 6CO2 + 6H2O | 3.5742 | 25.5758 | 7.16 |
| Liquid water (avg.) | H2O (l) → H2O (v) | 0.015 | 0.1659 | 10.8 |
| Liquid water (Phoenix) | H2O (l) → H2O (v) | 0.051 | 0.1160 | 2.07 |
| Liquid water (Atlanta) | H2O (l) → H2O (v) | 0.017 | 0.2160 | 12.4 |
Notably, NG and coal have the lowest prices per unit exergy of the fuels we considered (<2 ¢ per kWhex). “Gray” hydrogen, which is usually produced via steam methane reforming (SMR), has an LCOEx of 2.60 ¢ per kWhex, while “gray” ammonia, produced from gray hydrogen, has an LCOEx of 8.53 ¢ per kWhex. This represents the costs incurred and exergetic losses that occur when going from NG (1.37 ¢ per kWhex) to hydrogen (2.60 ¢ per kWhex) to ammonia (8.53 ¢ per kWhex). The LCOEx of a system's output will always be greater than the exergy source, since the system has other costs (CAPEX and OPEX not associated with the exergy source), and because some of the exergy will always be destroyed, as shown in Fig. 1.
“Blue” hydrogen, which is produced via NG but includes carbon capture and storage (CCS) to offset emissions, has a higher LCOEx than gray hydrogen, because of the additional exergy input and component costs required for CCS. However, blue hydrogen still has an LCOEx that is relatively low when compared to electricity. Meanwhile, “green” hydrogen, which is produced via electrolysis of water, must have an LCOEx greater than the cost of electricity, because electricity is the exergy source (input), some of the exergy is destroyed, and additional costs are incurred (i.e., the cost to build and maintain the electrolysis plant). Thus, green hydrogen will always be more expensive than electricity on a per unit exergy basis. Likewise, green ammonia will always have a higher LCOEx than the green hydrogen used as the input to the Haber–Bosch process.
We also found that liquid water, which has exergy when the dead state is that of the water vapor in humid outdoor air (see Note S5), is incredibly cheap per unit mass, but also has very little exergy per unit mass. As a result, it has a price per unit exergy of 10.8 ¢ per kWhex (in the average case, where the outdoor air has a relative humidity of 68%). In theory, the exergy of liquid water could be used to drive locomotion or generate electricity,61–63 but the low price of liquid water is mitigated by its low exergy content, which hinders its potential in these applications. However, one application in which the exergy of liquid water has proven valuable is evaporative cooling.20,64,65 Cooling is used in residential (space cooling for thermal comfort), commercial (data center cooling) and industrial (power plant cooling towers) sectors, and cooling via sub-ambient temperatures requires an exergy source, such as electricity (for vapor compression refrigeration) or liquid water (for evaporative cooling). For data centers and power plants, the value of the exergy provided via sub-ambient evaporative cooling often outweighs the cost of the exergy input from liquid water,66 hence the ubiquity of evaporative cooling in these applications.67 In addition to the average LCOEx of water in Table 1 (which uses the U.S. average residential water price59 and global median humidity that we found in our prior work35), we also provide values for Phoenix and Atlanta, using local water prices60 and average annual specific exergy (from TMYx data68). In drier locations, the specific exergy of water is higher and (perhaps counterintuitively) the price of water is often lower,69 leading to a low LCOEx (hence its efficacy as an exergy source for evaporative cooling in these locations).
To illustrate the utility of this framework beyond energy systems, consider living beings that also need an exergy source in order to function: food. The macronutrients in food – protein, fat, and carbohydrates – contain the exergy that, when consumed, sustains life. Özilgen provides the chemical exergy content of these nutrients: 25.4 MJ kg−1 for food proteins, 39.6 MJ kg−1 for food fats, and 17.5 MJ kg−1 for food carbohydrates.70 From these values, Table 2 was constructed, which provides the specific exergy, price per unit mass, and LCOEx of various foods, based on current commodity market prices. Wheat, corn, and rice all have low LCOEx values, contributing to them being the most widely consumed foods around the world.71 In fact, the LCOEx of all the crops within Table 2 are within the range of the LCOEx of electricity. On the other end of the spectrum, the LCOEx of a chicken egg is very high. This is due to the low exergy content of the egg, which itself occurs because most of its weight is water72 (and water carries negligible chemical exergy, as seen in Table 1). The specific exergy of meat is low (as measured per kg of live animal), while the specific price is rather high, resulting in meat having a high LCOEx. Milk and butter again reveal the cost increase when going from an exergy source to an output. Milk is one of the exergy sources used to create butter, and because exergy is destroyed and other costs are incurred, the LCOEx of butter is greater than that of milk. Thus, the LCOEx framework can be used to determine which foods form the least expensive means of providing energy (and exergy) to people or livestock. Notably, our bodies also use water as an exergy source, but for processes like evaporative cooling, and not metabolic exergy.
| Food | Protein/fat/carbs in 1 kg of food (g) | Specific exergy (kWhex kg−1) | Specific price (¢ per kg) | LCOEx (¢ per kWhex) |
|---|---|---|---|---|
| Rice | 73/33/76773 | 4.61 | 28.5574 | 6.19 |
| Wheat | 137/25/71175 | 4.70 | 20.0076 | 4.26 |
| Oats | 125/58/69877 | 4.91 | 23.7778 | 4.84 |
| Corn | 88/23/69679 | 4.26 | 18.6980 | 4.34 |
| Soybeans | 348/182/29481 | 5.89 | 38.7982 | 6.59 |
| Sugar | 0/0/99683 | 4.84 | 40.4884 | 8.36 |
| Milk | 33/32/4685 | 0.81 | 40.0686 | 49.46 |
| Butter | 0/815/087 | 8.97 | 741.688 | 82.72 |
| Eggs | 126/95/789 | 1.97 | 380.790 | 193.2 |
| Poultry | 137/5/0 | 1.02 | 139.091 | 136.1 |
| Beef | 89/7/0 | 0.70 | 356.092 | 505.0 |
| Protein isolate | 883/5/26 | 6.41 | 236.693 | 36.91 |
Some additional insights can be derived from Table 2. Focusing on the high LCOEx of animal butter and protein isolate reveals an opportunity to develop alternative processes. For example, by leveraging the fact that electricity is a low-cost exergy source (Fig. 2) and combining it with an inexpensive carbon source, the LCOEx of fats94 and protein95,96 can be significantly reduced. The key to the success of such electrochemical synthetic food production97 lies in whether it can scale with sufficiently low CAPEX and high exergetic efficiency.
An investigation of algae also provides insight into the viability of certain non-traditional organic materials as fuels and/or food. The lower heating value of algae is ∼15 MJ kg−1 (4.17 kWh kg−1),98 which we approximate as being equal to the chemical exergy, given that the exergy factor of hydrocarbon fuels is typically ∼1.37 The current cost to produce 1 kg of dry algae is $2.57, while scaleup and locational favorability could further reduce costs to $0.85 per kg.99 Taking the latter value as a lower bound for cost, algae could approach an LCOEx of 20.4 ¢ per kWhex. While algae has been proposed as a biofuel,100 this LCOEx value is prohibitively high when compared to the fuels in Table 1. A good source of protein, algae has been proposed as an affordable and nutrient-dense food source,101 and its LCOEx is closer to parity with the foods in Table 2. However, it has an LCOEx ∼ 2–3× higher than the mass-produced crops, casting doubt on its viability as an economically-competitive vehicle for cheap nutrient delivery. Thus, algae would need a significantly lower specific cost (∼$0.30 per kg) or to provide some other benefit (e.g., aquaculture does not occupy habitable land like agriculture does) to compete with a food like soybeans (a similar crop in terms of nutritional content).
The prices of fuels in Table 1 and foods in Table 2 will fluctuate over time and vary with location. Thus, while we use these data to analyze general trends and provide benchmarks for the LCOEx of different commodities, these findings are not universal to every location or application.
Leveraging thermodynamics for economic benefits
Thermodynamically “unfavorable” processes (or in other words, processes that require significant energy input to produce a high-exergy output) are limited by the LCOEx of the exergy input, as well as the specific exergy of the output. Fig. 2 suggests that low-grade heat cannot serve as a significantly cheaper exergy source than electricity or the fuels in Table 1. As such, low-grade solar- and waste-heat will not significantly improve the economics of thermodynamically unfavorable processes.However, Fig. 3 illustrates that there are other methods of leveraging thermodynamics to improve a process’ economics. Using a chemical exergy input reduces the required energy input. For example, RO desalination uses seawater as its feed, while point-source carbon capture uses flue gas. Both of these feed streams have far higher concentrations (of water and CO2, respectively), and thus more exergy, than ambient air. Because much of their exergy input comes in the form of chemical exergy, RO and point-source carbon capture require far less energy input than AWH and DAC, respectively. Through the lens of the LCOEx framework, this means the total input LCOEx is less heavily weighted towards the LCOEx of the energy input. If the feed streams have a lower LCOEx than the energy source, then they effectively lower the overall LCOEx of the system input. In the case of RO and point source carbon capture, the system is receiving energy (heat or work) and chemical exergy, but it is only paying for the energy, as shown in Fig. 3. Because of the lower input LCOEx, desalination can produce water at lower costs than AWH, while point-source carbon capture can store carbon at lower costs than DAC.
Likewise, DAC via rock weathering (a recently proposed method of carbon sequestration102,103) uses rocks with chemical exergy as one of its inputs (along with ambient air). Furthermore, rock weathering produces an output with less exergy than conventional DAC. This is because rock weathering stores carbon as carbonates and/or bicarbonates, which have far less exergy than the compressed, concentrated stream of CO2 that a conventional DAC system outputs. Though still hypothetical, this “enhanced” rock weathering could leverage thermodynamics to reduce the LCOEx of sequestered carbon.
As another example, sulfur depolarized electrolysis104–106 is an alternative method of producing hydrogen that leverages both of these advantages: it uses a higher exergy input/feedstock (compared to near-dead state liquid water in conventional electrolysis) and produces a lower exergy output/product (co-production of hydrogen with sulfur dioxide or sulfuric acid; see Note S5 for output exergy calculations).47 Because sulfur depolarized electrolysis co-produces hydrogen (a precursor to ammonia) and sulfuric acid, which are both relevant for fertilizer production, it also has the advantage of distributing the CAPEX over two valuable products (instead of just hydrogen in conventional electrolysis).
Opportunities exist for electrically-driven systems to reduce cost
Following our analysis of exergy sources above, we now demonstrate the utility of the LCOEx framework in comparing systems that achieve the same process with different exergy sources. Due to its ubiquity as an energy source, the cost of electricity is a logical benchmark for LCOEx. Furthermore, electricity has a very competitive LCOEx compared to other energy sources (e.g., heat, hydrocarbon fuels, etc., shown in Fig. 2 and Table 1). One factor that has led to this is the high exergetic efficiency of NGCC power plants, which first convert the chemical exergy of NG to high-grade heat and then convert the heat to work, all with relatively low exergy destruction. Other electricity generation technologies must then compete with the LCOEx of NGCC electricity.In Fig. 4, the LCOEx framework is applied to a historical example – desalination – to illustrate how the cost of a commodity can be reduced. Per eqn (3), the LCOEx of the system output depends on two quantities: LCOExin/ηex, which represents the cost to convert the exergy input to output (if the system CAPEX were zero), and the actual (non-zero) system CAPEX. In Fig. 4(a), we plot historical desalination cost and efficiency data (see Methods). The LCOEx of fresh water produced with desalination is plotted against LCOExNG/ηex, where LCOExNG is the LCOEx of NG (1.37 ¢ per kWhex), and ηex is the exergetic efficiency if NG were used as the primary energy source (i.e., going from NG and saline water to clean water). A clear trend emerges: the older, heat-driven technology (multi-stage flash, MSF) was inefficient at converting the chemical exergy in NG to fresh water, because of losses incurred when NG is converted to low-grade heat and because of losses in the heat-driven desalination system itself. This led to a high LCOExNG/ηex value in 1970 (Fig. 4(b)), which in turn caused the desalinated water to be expensive.
 | ||
| Fig. 4 Comparison of work- and heat-driven desalination. (a) Plot of output (fresh water) LCOEx against the LCOEx of natural gas divided by exergetic efficiency. Desalination cost and efficiency data from Beltrán and Koo-Oshima.107 (b) Heat-driven system, where a boiler destroys a large portion of the exergy from the fuel source when producing low-grade steam, and the heat-driven desalination plant destroys additional exergy, producing little water per unit fuel input. (c) Work-driven system, where the exergy from the fuel source is converted to electrical work with little exergy destruction, and the desalination plant has a high exergetic efficiency, so it produces a large amount of water per unit fuel input. | ||
The first major improvement came when an electrically-driven technology was implemented (mechanical vapor compression, MVC), because the conversion of NG to electricity has a higher exergetic efficiency than NG to low-grade heat. Thus, using electricity as the exergy source improved the overall NG-to-water exergetic efficiency, which reduced LCOExNG/ηex. Upon switching from distillation to MVC, LCOExH2O was reduced by less than LCOExNG/ηex, indicating that the power plant + MVC combination had a higher CAPEX than the natural gas distillation system.
The next improvement came by increasing the exergetic efficiency of the desalination process itself, first by switching from MVC to RO, and then by improving the efficiency of RO (Fig. 4(c)). This highlights why (i) electricity is a favorable exergy source compared to low-grade heat, and (ii) processes that are exergetically efficient through the entire production chain (from primary energy source to final product) are usually preferable. This paradigm, revealed by the evolution of desalination, can serve as a roadmap to improve other processes. The exception, however, is when CAPEX is too high, which would result in a higher LCOExout, even with a lower LCOExin/ηex.
While desalination serves as an exemplary process for comparing work- and heat-driven technologies in the industrial sector, air conditioning can be used as a representative process in buildings. This is illustrated in the Sankey diagrams in Fig. 5. In Fig. 5(a), NG is used in a highly efficient power plant (61% exergetic efficiency for NGCC33,37) and electricity is transmitted with little loss (95% exergetic efficiency for transmission108) to a vapor compression refrigerator, which has an exergetic efficiency of 11% (Methods). Meanwhile, in Fig. 5(b), NG is used to directly heat an absorption refrigerator, where much of the NG chemical exergy is destroyed when converted to low-grade heat (assumed to be 90 °C109), and then most of the remaining exergy is destroyed because of the relatively low exergetic efficiency of the absorption refrigerator (assumed to be 11%, which is the same as the vapor compression refrigerator).
Similar to the conclusion for desalination, we find that work-driven refrigeration tends to have a lower LCOEx at the system output compared to absorption refrigeration, owing to fewer exergetic losses. If absorption refrigerators were designed to utilize very high-grade heat (as is used in power plants), then the overall exergetic efficiencies of vapor compression and absorption refrigeration would be comparable. However, engineering residential and commercial technologies to utilize this high-grade heat is unrealistic and would increase the CAPEX of absorption refrigeration. Instead, some absorption refrigerators utilize waste heat in large combined heat and power (CHP) plants;110 despite the low exergy factor of low-grade waste heat, the economics are favorable when the CAPEX of the heat exchanger to transfer this heat to the refrigerator is not too high. In the illustrative example in Fig. 5, it is assumed that both the vapor compression and absorption refrigeration systems have a CAPEX of $1000 per ton (which is likely a generous assumption for absorption refrigeration), a lifetime of 10 years, and a utilization factor of 20% (i.e., they run for 20% of the year). A discount rate of 7% was used to obtain the values in the illustration. The exergetic efficiency of 11% approximately corresponds to a COP of 4 for vapor compression and 0.7 for absorption refrigeration when the indoor temperature is 26.7 °C and the outdoor temperature is 35 °C.
Air conditioning111–113 (cooling) has seen electrically-driven systems become the dominant technology (i.e., vapor compression refrigeration) due to the paradigm mentioned above – the generation of electricity with high-grade heat is generally more exergetically efficient and cost-effective than using low-grade heat to power an absorption refrigeration cycle. However, the paradigm is somewhat different for heating in the built environment. As is the case with cooling, it is generally more exergetically efficient to generate electricity at a centralized power plant and then use that electricity to drive a heat pump than it is to burn natural gas to provide the low-grade heat needed in buildings. However, the low CAPEX of a NG furnace (compared to a heat pump) and the low cost of NG mean that, in certain cases, the less exergetically efficient method of burning NG to provide heat in buildings is still the more cost effective one. In other cases, such as in the southern U.S., where heating is not often needed and a vapor compression system is already required for cooling, the heat pump option may be preferable. In general, the LCOEx of the output heat of a natural gas furnace can be calculated, and if it is lower than the local electricity price, then there is no chance that the heat pump can compete (without subsidies or incentives). If, however, the LCOEx of the heat from a natural gas furnace is higher than the LCOEx of electricity, then the heat pump could be an attractive option (depending on the heat pump CAPEX and exergetic efficiency).
It is important to remember that both the LCOEx of a system's energy source and the exergetic efficiency of the system greatly affect the LCOEx of the system output. Perhaps no technology better demonstrates this than dehumidifiers. Currently, the vast majority of dehumidifiers use vapor compression refrigeration to condense moisture out of the supply air. This method is driven by electricity, which has a relatively low LCOEx; however, condensation dehumidification suffers from a very low exergetic efficiency.114,115 Thus, while the LCOEx of the energy source is low, the dehumidifier's low exergetic efficiency will cause the output LCOEx to be high. Researchers have explored heat-driven desiccant dehumidifiers as alternatives,116,117 but the LCOEx of low-grade heat input is high (Fig. 2), and desiccant systems sometimes have exergetic efficiencies that are not significantly greater than traditional air conditioning.118 Thus, there is an opportunity to lower the cost of dehumidification by creating systems that are driven by low LCOEx energy sources (such as electricity) but also have significantly higher exergetic efficiencies than current (electrically-driven) cold surface condensation dehumidifiers. Some liquid desiccant-based systems approach this by regenerating the desiccant with the heat from the condenser and cooling the supply air with the evaporator.21 Generally, the LCOEx framework favors this concept: these systems use existing vapor compression components that are already present in a traditional air conditioner (to avoid a significant CAPEX increase), while utilizing electricity as the energy source (low LCOEx input), and improving the COP over a traditional air conditioner (higher exergetic efficiency).
Certain processes are more likely to benefit from using electricity as the input
To understand where an electrically-driven process could compete with traditional heat- or fuel-driven alternatives, we present the regime maps in Fig. 6. This can be divided into 3 categories: (i) electrically-driven processes that cannot compete with conventional (e.g., thermochemical) processes, even when electricity is incredibly cheap (hydrocarbons and hydrogen), (ii) electrically-driven processes that can compete with traditional processes, but only if electricity becomes incredibly cheap (ammonia, moderate-grade heat), and (iii) electrically-driven processes that can already compete with traditional processes (high-grade heat). The regime maps also indicate whether the output cost of a given process is CAPEX-limited or efficiency-limited. For example, both green hydrogen and green ammonia are in the CAPEX-limited regime, such that improving the exergetic efficiency will have a negligible effect on cost.We first discuss the fuels – hydrocarbons (Fig. 6(a)), hydrogen (Fig. 6(b)), and ammonia (Fig. 6(c)). An electrically-driven system could produce any of these chemicals with the molecules present in the atmosphere: water vapor for hydrogen, CO2 for carbon, and air for nitrogen. Alternatively, liquid water could be used as the hydrogen source, though this would change the input LCOEx slightly, given its nonzero cost and exergy. NG is an incredibly cheap fuel, indicated by its low LCOEx. An unrealistically low CAPEX would be required to synthetically produce cost-competitive NG via electricity and feedstocks at the dead state (i.e., atmospheric) or near-dead state (i.e., low specific exergy, such as liquid water), even when electricity is incredibly cheap (1 ¢ per kWhe). Jet A-1, the most common jet fuel,119 has a higher LCOEx, but it will still be difficult for electricity to directly produce it at a competitive cost. A more feasible avenue for electricity to compete with fuels is as an energy source in the transportation sector (i.e., electric vehicles); the regime map for battery electric vehicles is given in Note S6.
Hydrocarbons are also used to produce plastics; for example, ethylene is the feedstock for polyethylene (∼$1 per kg cost120 and ∼12.8 kWhex kg−1 chemical exergy121). The question then arises as to whether the production of plastic feedstocks could switch to electricity as the energy source and use dead state hydrogen and carbon (i.e., atmospheric H2O and CO2) without a significant premium. While the LCOEx of polyethylene is somewhat more forgiving than NG, it would still require a relatively low CAPEX, revealing the challenges facing a hypothetical “electrically-driven atmospheric plastic production” process as a means of establishing a alternative plastic supply chain.
Green hydrogen production via electrolysis has been widely discussed in recent years. However, Fig. 6(b) casts doubt on its viability as an economically competitive fuel. Assuming an exergetic efficiency of 65% for electrically-produced hydrogen, the blue curve indicates the LCOEx of H2 produced with cheap electricity (1 ¢ per kWhe). If the electrolyzer CAPEX is $3 per W and the plant operates around the clock (i.e., a capacity factor of unity), then electrically-produced hydrogen will fail to compete with both SMR and methane pyrolysis, even when electricity is cheap. If the electrolyzer CAPEX is only $1.5 per W to the levelized cost of hydrogen, the electrically-produced hydrogen would be cheaper than methane pyrolysis but still more expensive than SMR.
Green ammonia (Fig. 6(c)), produced via electrolyzed hydrogen fed to a Haber–Bosch plant, has also been discussed as a potential fuel source and fertilizer. To evaluate the former use-case, the LCOEx of green ammonia should be compared to the LCOEx of other fuel sources. To evaluate the latter use-case, the LCOEx of green ammonia should be compared to that of grey ammonia. The CAPEX of a green ammonia plant can be approximated as that of a conventional (gray) ammonia plant, minus the CAPEX of the SMR portion of the plant, plus the CAPEX of an electrolyzer to replace the SMR. Thus, the “green premium” incurred on the ammonia CAPEX is less significant than in a green hydrogen plant, since it only affects a portion of the overall plant (and 1 kg of green hydrogen produces 5.63 kg of green ammonia). Regardless of whether the electrolyzer CAPEX is $1.5 per W or $3 per W, green ammonia would be cost competitive with grey ammonia if 1 ¢ per kWhe electricity were continuously available. This indicates a potential pathway for green ammonia to serve as a fertilizer. However, firm electricity at this cost will be difficult to produce. If the cheap electricity is only available intermittently, the capacity factor of the plant decreases, which increases the levelized CAPEX. As such, we have plotted points for a capacity factor of 0.25 (6 h of operation per day), which are significantly more expensive than conventionally-produced (gray) ammonia. Thus, green ammonia needs both very cheap and firm electricity to avoid a green premium. Furthermore, given the LCOEx of green ammonia – between 6 and 10 ¢ per kWhex – its use as a fuel source in the industrial and transportation sectors is not practical. It would be very cost ineffective to use 1 ¢ per kWhex electricity to produce green ammonia, an exergy/fuel source that is 6–10× more expensive than the electricity used to make it, and then use that ammonia to power some other system. Exergy is lost and cost is incurred by converting the cheap electricity into ammonia and then using that ammonia to power another process. Even green hydrogen, with an LCOEx of 4 ¢ per kWhex (when the CAPEX is $1 per kg and electricity is 1 ¢ per kWhe) would be an expensive exergy source relative to the electricity used to make it. Thus, our framework reveals the exergetic and economic inefficiencies associated with using electrically-produced fuels to power different sectors of the economy, though electrically-produced chemicals do have potential for other uses (e.g., as fertilizer).
While Fig. 6(a) reveals the significant challenges of using electricity to produce a cheap, high specific exergy fuel, Fig. 6(d) reveals a potential opportunity for electricity to produce the opposite – a more expensive, lower exergy material, such as protein. Poultry has a relatively high LCOEx, but electrochemically produced protein would likely not compete with meats, due to the fact that they are consumed in part for their taste. Instead, electrically-driven protein production would compete with protein isolates. Per Table 2, the specific cost of soybeans is 38.79 ¢ per kg, and there are 348 g of protein per kg of soybean, equating to a cost of $1.11 per kg of protein. Based on the exergy of protein, this corresponds to an LCOEx of ∼16 ¢ per kWhex for the protein within soybeans. However, Table 2 reveals that soy protein isolate has an LCOEx of ∼40 ¢ per kWhex; this increase in cost is due to the exergetic losses and costs incurred when going from soybean to soy protein isolate. This high LCOEx of protein isolate gives electrochemistry a chance to compete, and Fig. 6(d) sets the CAPEX values that must be met for it to do so. The exergetic efficiency of electricity to single-cell protein (SCP) biomass is approximated as 4% based on Wang et al.95 When the system CAPEX is high (>$10 per kg protein), the exergetic efficiency has little bearing on output cost. Conversely, if the system CAPEX is low (<$1 per kg protein), the exergetic efficiency has a significant effect on output cost, while a reduction in CAPEX would yield negligible benefits.
When utilizing intermittent electricity from renewable energy sources, “firmed” (or consistently available) requires some form of energy storage. Furthermore, the question remains as to whether this electrically-driven heat should be produced via dissipative heating (e.g., resistive heating) or via heat pumps. In Fig. 6(e) and (f), we investigate the LCOEx of firmed heat that is produced by an intermittent electricity source (with an LCOE of 1 ¢ per kWhe). In this case, we assume the electric resistance heater CAPEX is negligible, so we plot the LCOEx as a function of the CAPEX of the energy storage system. Fig. 6(e) reveals that, from an exergetic standpoint, high-grade heat will be the easiest to switch the exergy source to electricity (though practical challenges, such as durability at high temperatures, must be considered). This is because electric resistance heaters, which have a lower CAPEX than heat pumps, destroy little exergy when dissipating their electricity as heat at high temperatures. The combination of low CAPEX and high exergetic efficiency, and low input LCOEx of electric resistance heaters will allow the LCOEx of high temperature electric resistance heaters to approach that of the electricity input. Electricity at 1 ¢ per kWhe would thus lead to incredibly cheap high-grade industrial heat, but even electricity at 6 ¢ per kWhe would be close to the cost of high-grade industrial heat from NG (∼5 ¢ per kWhe). While electrochemical storage has a high CAPEX, thermal storage could enable low-cost electrically-driven heat if current cost targets are achieved122 as the technology readiness improves. Fig. 6(f) reveals that moderate-grade heat (150–400 °C) will be harder to source via electricity, for several reasons. First, NG has both lower LCOH and lower LCOEx values at these temperatures than high-grade heat (due to lower CAPEX and higher thermal efficiency26). Second, dissipative electric heaters will destroy far more exergy at these temperatures. For example, a dissipative heater (whether electric resistance or microwave) with a thermal efficiency of unity (the best-case scenario) would only have an exergetic efficiency of 20% at 100 °C and 55% at 400 °C. Fig. 6(f) shows that at 200 °C, electric resistance could compete with NG heat, but only if the cost of intermittent electricity input falls to 1 ¢ per kWhe. This indicates that the production of moderate-grade heat via electricity is feasible but difficult. At these temperatures, the less CAPEX-heavy electric resistance option has significantly more exergetic losses than when producing high-grade heat. Meanwhile, the more exergetically efficient heat pump option leads to a higher CAPEX, and the exergetic benefits are not as significant as when producing low-grade heat. So while electric resistance heating can be attractive for high-grade heat and heat pumps can be attractive for low-grade heat,38 it is unclear if either option can compete with NG for moderate-grade heat production.
Conclusions
The LCOEx framework enables a direct comparison between different energy sources, systems, and processes on a common basis ($ per kWhex). Among different energy sources, electricity delivers exergy at a relatively low cost, while low-grade heat does not carry much exergy per unit energy and thus has a relatively high LCOEx. In the theoretical ideal case, the LCOEx of a system's output would be equal to the LCOEx of the energy source/input, because there would be zero exergy destruction (reversible) and zero system CAPEX. However, any real system will have some capital cost and will destroy some of the input exergy, so the LCOEx of the output will always be greater. This highlights the importance of designing systems that:(i) Utilize low LCOEx energy sources.
(ii) Achieve high exergetic efficiency.
(iii) Have low CAPEX.
We use this work to demonstrate the new LCOEx framework, illustrate its utility through examples, and evaluate the price per unit exergy of different commodities (chemical fuels, electricity, water, heat, cooling, and food). Our analysis is not comprehensive given the wide breadth of processes to which it can be applied, and future studies can utilize the framework to analyze different commodities in greater depth.
Applying the LCOEx framework to different processes reveals which have significant room for improvement and which are already optimized, with LCOE values used as a benchmark for LCOEx. The opportunity to reduce cost should, however, be taken in context of the history of a given technology. For example, both air conditioning (∼173 ¢ per kWhex output per Fig. 5) and desalination (∼70 ¢ per kWhex output per Fig. 4) produce outputs with LCOEx values more than 10× that of electricity. This indicates room for improvement, but it is important to recognize that both processes are already electrically-driven, and they have experienced more than a century of engineering.123,124 As such, we believe it is unlikely that drastically higher exergetic efficiencies can be achieved without a significant increase in CAPEX.
Using the LCOEx metric not as a replacement for other levelized cost metrics, but rather as a complement to them, allows for a useful perspective. For example, the levelized cost of heat, water, hydrogen, ammonia, and energy storage are all useful metrics in assessing the economic viability of different energy systems, when compared to systems that produce the same output. These metrics, however, provide no insight into how fundamental thermodynamics influence the cost of an output, based on the cost of the inputs and the efficiency of the process. By combining conventional levelized cost metrics (i.e., the green portion of the Sankey diagram in Fig. 1) with exergy analysis (i.e., the yellow portion of the Sankey diagram in Fig. 1), a new perspective on the cost-effectiveness and efficiency of a thermodynamic process is gained.
The LCOEx framework is also useful in identifying fundamental cost bounds for different processes. For example, AWH is limited by the LCOEx of the exergy input and the specific exergy of the harvested water. AWH uses exergy sources with an LCOEx ∼ 6 ¢ per kWhex (e.g., electricity or heat) and the specific exergy consumption is high (∼80 kWhex m−3 for reversible operation in arid regions per Note S5). Thus, even when the CAPEX is negligible, the cost to produce water will be ∼$4.80 per m3, a value too high to compete with RO desalination (∼$1 per m3).35 In other cases, the reversible limit is potentially acceptable; for example, the reversible exergy consumption of DAC125 is ∼200 kWhex per ton of CO2, such that the reversible exergy input accounts for merely $12 per ton CO2 when the input LCOEx is 6 ¢ per kWhex. However, for processes like DAC, exergetic efficiencies and CAPEX hinder economic viability. These thermo-economically constrained processes need to leverage thermodynamic advantages to either lower the input LCOEx (e.g., point source carbon capture and hydrogen production via sulfur depolarized electrolysis105,106,126,127) or lower the specific exergy of the product (e.g., DAC via enhanced rock weathering). Otherwise, they will struggle to progress beyond lab-scale demonstrations and may never see meaningful market penetration.
Finally, we developed LCOEx regime maps for electrically-driven systems. By comparing the LCOEx of conventionally-produced commodities to electrically-driven alternatives, we identified (i) commodities that electricity would struggle to produce with cost parity (e.g., fuels), (ii) the CAPEX and exergetic efficiencies needed for emerging electrically-driven process (e.g., electrochemical protein synthesis), and (iii) for which processes electricity already makes sense as the exergy source (e.g., high-grade heat). We found that electrically-produced ammonia (specifically for fertilizers) and moderate-grade heat could reach cost parity if inexpensive electricity (1 ¢ per kWhe) becomes available, but if this electricity is intermittent the reduced capacity factor will make these electrically-driven commodities expensive. Alternatively, we believe that moderate-grade heat could be electrically-produced with more expensive electricity if better heat pumps are developed (i.e., lower CAPEX and higher exergetic efficiencies), but the margin for exergetic efficiency improvement that a heat pump presents over electric resistance heating is smaller at moderate-grade temperatures than with low-grade heat. Ultimately, while our analysis reveals the cost-effectiveness of electricity as an exergy source, further research is required to understand if the CAPEX and efficiency targets that we present for electrically-driven systems can be achieved. If these targets prove feasible, then the technology readiness of these emerging, electrically-driven processes must be addressed.
Methods
Calculating LCOEx and specific exergy content values in Table 2
The mass of protein, fat, and carbohydrates per kg of corn were calculated for a moisture content of 15.5%, which is the standard moisture content for a bushel of corn.128 The mass of protein, fat, and carbohydrates per kg of soybeans were calculated for a moisture content of 13%, which is the standard moisture content for a bushel of soybeans.129 For the protein, fat, and carbohydrates within wheat, USDA nutrition data for durum wheat was used, even though common wheat makes up the vast majority of global wheat production130 (because common wheat nutritional information was not given on the USDA website). For eggs, prices are reported in $ per dozen, and it was assumed that 1 dozen eggs weigh 1.5 lbs.For beef, the hot carcass weight was assumed to be 63% of the live weight, whereas the boneless trimmed beef weight is 40% of the live weight.131,132 The carcass contains fat which is discarded as a byproduct, and that fat contains some exergy, though that exergy is not considered in this work. Instead, we take the nutritional exergy of the boneless trimmed beef for our LCOEx value of beef in Table 2. Lean beef consists of 22.3% protein by weight and 1.8% fat by weight.133 Thus, 8.9% of the live animal weight is edible protein and 0.72% is edible fat.
For chicken, the edible share of live weight is 60%,132 and of this meat, 22.8% and 0.9% by weight are protein and fat, respectively.133 Thus, of the live animal weight, 13.7% is edible protein and 0.54% is edible fat.
For protein isolate, the bulk production cost per kg of soy protein isolate was used,93 along with soy protein isolate nutritional data.134
Historical desalination data
The desalination plot in Fig. 4 was created using historical data for seawater desalination in Spain, spanning from 1970 to 2005.12,107 The primary energy source (e.g., natural gas, coal, solar, wind) was not given for any of these systems, so it is impossible to know the true input LCOEx. Instead, we used the LCOEx of NG as a proxy, and we approximated the hypothetical NG-to-water exergetic efficiency to make a direct comparison between the heat- and work-driven technologies. For the heat-driven system (MSF), it was assumed that the reported SEC in the dataset was an “equivalent” electrical SEC, which is simply the thermal SEC multiplied by a factor of 0.3 (the standard power plant efficiency used to convert thermal SEC values to electrical SEC in desalination literature12). Thus, we took the reported SEC values from the dataset and divided by a factor of 0.3 to return the original thermal SEC (e.g., a reported SEC of 22 kWhe m−3 for MSF becomes 73.3 kWhth m−3). It was assumed that this SEC corresponds to the steam used to deliver heat to the MSF system; a boiler efficiency of 0.8 was assumed, such that the steam SEC was divided by 0.8 to return the amount of NG heat used to produce the steam that was used (e.g., the calculated steam SEC of 73.3 kWhth m−3 for MSF becomes 91.7 kWhth m−3). Then, to find the original exergy within the NG, the exergy factor of 1.03 (which corresponds to NG37) was used (e.g., the calculated NG thermal SEC of 91.7 kWhth m−3 for MSF becomes Σ = 94.4 kWhex m−3). Then, to find the exergetic efficiency, the minimum separation exergy for seawater desalination (∼0.9 kWhex m−3) was divided by the exergy input to find the exergetic efficiency (e.g., Σ = 94.4 kWhex m−3 becomes ηex = 9.5%).For the electrically-driven systems (MVC and RO), the hypothetical NG-to-water exergetic efficiency was found by first assuming that the electricity could be generated with a NGCC power plant possessing a thermal efficiency of 55% (slightly lower than the state of the art33). For example, a reported SEC of 3 kWhe m−3 for RO becomes 5.5 kWhth m−3 of heat from NG used to generate the electricity needed to drive RO. Then, the exergy factor of NG37 (1.03) was used to find the original exergy within the NG used to generate the electricity (e.g., the calculated NG thermal SEC of 5.5 kWhth m−3 for RO becomes Σ = 5.6 kWhex m−3). Finally, the minimum separation exergy for seawater desalination (∼0.9 kWhex m−3) was again divided by the exergy input to find the exergetic efficiency (e.g., Σ = 5.6 kWhex m−3 becomes ηex = 16.0%).
Air conditioning exergetic efficiency
To estimate the exergetic efficiency of air conditioning, we assumed that the vapor compression system has a COP of 4 (based on current SEER2 standards135) at the EER2 standard testing conditions of 80 °F indoor dry-bulb temperature and 95 °F outdoor dry-bulb temperature.136 At these standard testing conditions, the reversible COP would be 36. If the actual COP is 4 and the reversible COP is 36, then the exergetic efficiency is ∼11%.CAPEX and exergetic efficiency values in electrically-driven regime maps
For hydrogen electrolysis, we found that an LCOEx of 14.3 ¢ per kWhex ($5.50 per kg) results when the electrolyzer CAPEX contributes roughly $2 per kg of the levelized cost of hydrogen (assuming 65% exergetic efficiency during electrolysis and an input electricity cost of 6 ¢ per kWhe). This levelized CAPEX contribution of $2 per kgH2 corresponds to an electrolyzer cost of $3 per W (when a discount rate of 7% and electrolyzer lifetime of 14 years are assumed). While this agrees with some existing literature,137,138 an electrolyzer CAPEX contribution of $1 per kg ($1.5 per W) is also commonly reported.139 As such, we provided results for both values, for both hydrogen and ammonia. For both ammonia and hydrogen synthesis, we assumed the exergetic efficiency of electrically-driven synthesis is 65% (given that the hydrogen to ammonia exergetic efficiency is nearly unity140). For green ammonia plant CAPEX, we assume the NH3 and N2 subsystems CAPEX contribute a levelized cost of $0.10 per kg NH3, while the electrolyzer levelized CAPEX in units of $ per kg H2 can be converted into units of $ per kg NH3 by accounting for the fact that 1 kg of H2 produces 5.6 kg of NH3.For industrial heat, we used a thermal storage CAPEX of $5 per kWhth, based on values reported by Rondo for their thermal storage system.122 For electrochemical batteries, we used a CAPEX value of $100 per kWhe, which is typical for current Li-ion batteries.141
Author contributions
Conceptualization, J. D. K.; methodology, J. D. K.; investigation, J. D. K., A. R., W. P. P., and S. W.; writing – original draft, J. D. K.; writing – review & editing, J. D. K., A. R., J. W., W. P. P., S. W., and A. K. M.; funding acquisition, J. D. K., J. W., S. W., and A. K. M.; supervision, J. D. K. and A. K. M.Conflicts of interest
There are no conflicts to declare.Data availability
All data generated or analyzed during this study are included in the manuscript and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5ee05267j.Acknowledgements
This work was authored in part by the National Laboratory for the Rockies for the U.S. Department of Energy (DOE), operated under Contract No. DE-AC36-08GO28308. This work was supported by the Director's Fellowship Program in the Laboratory Directed Research and Development (LDRD) Program at the National Laboratory of the Rockies. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes. The authors would like to thank Mr Ahmed N. Mahfouz and Mr Preston Bohm for reviewing the manuscript and providing thoughtful insight.References
- C. Geffroy, D. Lilley, P. S. Parez and R. Prasher, Joule, 2021, 5, 3080–3096 CrossRef.
- Z. Y. Xu, R. Z. Wang and C. Yang, Energy, 2019, 176, 1037–1043 CrossRef.
- D. M. Warsinger, K. H. Mistry, K. G. Nayar, H. W. Chung and J. H. Lienhard, Entropy, 2015, 17, 7530–7566 CrossRef.
- W. P. Parker, J. D. Kocher and A. K. Menon, Desalination, 2024, 580, 117560 CrossRef.
- S. Garimella, K. Lockyear, D. Pharis, O. E. Chawa, M. T. Hughes and G. Kini, Joule, 2022, 6, 956–971 CrossRef CAS.
- A. Odukomaiya, J. Woods, N. James, S. Kaur, K. R. Gluesenkamp, N. Kumar, S. Mumme, R. Jackson and R. Prasher, Energy Environ. Sci., 2021, 14, 5315–5329 RSC.
- T. B. Magath, Ann. Med. Hist., 1937, 9, 338–344 Search PubMed.
- J. van Doornmalen and K. Kopinga, Am. J. Infect. Control, 2008, 36, 86–92 CrossRef PubMed.
- Z.-M. Zhao, L. Wang and H.-Z. Chen, Bioresour. Technol., 2015, 192, 547–555 CrossRef CAS.
- N. K. Sinha, Handbook of Food Products Manufacturing, John Wiley & Sons, 2007 Search PubMed.
- J. H. Billington, J. Inst. Brew., 1945, 51, 31–33 CrossRef.
- H. Nassrullah, S. F. Anis, R. Hashaikeh and N. Hilal, Desalination, 2020, 491, 114569 CrossRef CAS.
- K. H. Mistry, R. K. McGovern, G. P. Thiel, E. K. Summers, S. M. Zubair and J. H. Lienhard, Entropy, 2011, 13, 1829–1864 CrossRef CAS.
- I. Baniasad Askari and M. Ameri, Appl. Therm. Eng., 2021, 185, 116323 CrossRef CAS.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS.
- J. Eke, A. Yusuf, A. Giwa and A. Sodiq, Desalination, 2020, 495, 114633 CrossRef CAS.
- J. H. Lienhard, K. H. Mistry, M. H. Sharqawy and G. P. Thiel, in Desalination Sustainability: A Technical, Socioeconomic, and Environmental Approach, ed. H. A.Arafat, Elsevier Publishing Co., 2017, ch. 4 Search PubMed.
- M. Jangsten, J. Kensby, J.-O. Dalenbäck and A. Trüschel, Energy, 2017, 137, 292–301 CrossRef.
- T. T. Tasker, US Pat., US19591A, p. 1858.
- E. Kozubal, J. Woods, J. Burch, A. Boranian and T. Merrigan, NLR Report No. 1004010, 2011 DOI:10.2172/1004010.
- J. Woods, E. Kozubal, P. Luttik, D. Fox and J. Warner, Modeling and Experiments on a Dedicated Outdoor Air System Using Liquid Desiccant Heat and Mass Exchangers, Purdue University, West Lafayette, IN, 2022 Search PubMed.
- X. Li, B. El Fil, B. Li, G. Graeber, A. C. Li, Y. Zhong, M. Alshrah, C. T. Wilson and E. Lin, ACS Energy Lett., 2024, 9, 3391–3399 CrossRef CAS PubMed.
- A. LaPotin, Y. Zhong, L. Zhang, L. Zhao, A. Leroy, H. Kim, S. R. Rao and E. N. Wang, Joule, 2021, 5, 166–182 CrossRef CAS.
- J. Lord, A. Thomas, N. Treat, M. Forkin, R. Bain, P. Dulac, C. H. Behroozi, T. Mamutov, J. Fongheiser, N. Kobilansky, S. Washburn, C. Truesdell, C. Lee and P. H. Schmaelzle, Nature, 2021, 598, 611–617 CrossRef PubMed.
- S. Li, R. Chen, J. Wang, S. Deng, H. Zhou, M. Fang, H. Zhang and X. Yuan, npj Mater. Sustainability, 2024, 2, 11 CrossRef.
- T. Gilbert, A. K. Menon, C. Dames and R. Prasher, Joule, 2023, 7, 128–149 CrossRef CAS.
- LCOE U.S. H2 2023 by technology, https://www.statista.com/statistics/1427203/united-states-levelized-cost-of-electricity-by-technology/, (accessed December 20, 2024).
- 2023 Levelized Cost Of Energy+, https://www.lazard.com/research-insights/2023-levelized-cost-of-energyplus/, (accessed December 20, 2024).
- D.-H. Oh, C.-H. Lee and J.-C. Lee, ACS Omega, 2021, 6, 21043–21058 CrossRef CAS.
- G. Valencia Ochoa, J. Cárdenas Gutierrez and J. Duarte Forero, Resources, 2020, 9, 2 CrossRef.
- A. Bejan, Int. J. Energy Res., 2002, 26, 0–43 CrossRef.
- I. Dincer and M. A. Rosen, Exergy: Energy, Environment and Sustainable Development, Newnes, 2012 Search PubMed.
- J. D. Kocher and S. K. Yee, ASME J. Heat Mass Transfer, 2025, 147(2), 022901 CrossRef CAS.
- Z. Rant, Forsch. Geb. Ingenieurwes., 1956, 22, 36–37 Search PubMed.
- J. D. Kocher and A. K. Menon, Energy Environ. Sci., 2023, 16, 4983–4993 RSC.
- A. K. Menon, M. Jia, S. Kaur, C. Dames and R. S. Prasher, iScience, 2023, 26, 105966 CrossRef CAS.
- M. Gong and G. Wall, Energies, 2016, 9, 707 CrossRef.
- E. J. H. Wilson, P. Munankarmi, B. D. Less, J. L. Reyna and S. Rothgeb, Joule, 2024, 8, 1000–1035 CrossRef.
- K. Kaygusuz, Energy Sources, 1999, 21, 595–610 CrossRef CAS.
- N. A. S. Elminshawy, F. R. Siddiqui and G. I. Sultan, Energy Convers. Manage., 2015, 103, 28–35 CrossRef.
- J. Z. Klingensmith, Introduction to Microeconomics, Affordable Course Transformation: The Pennsylvania State University, University Park, 2019 Search PubMed.
- Z. Utlu and A. Hepbasli, Renewable Sustainable Energy Rev., 2007, 11, 603–634 CrossRef.
- Energy, https://www.bloomberg.com/energy, (accessed December 21, 2024).
- Z. Wu, S. Zhou and L. An, J. Sustainable Dev., 2011, 4, p. 260 Search PubMed.
- The Future of Hydrogen – Analysis, https://www.iea.org/reports/the-future-of-hydrogen, (accessed December 21, 2024).
- Executive summary – Global Hydrogen Review 2021 – Analysis, https://www.iea.org/reports/global-hydrogen-review-2021/executive-summary, (accessed January 8, 2025).
- J. Szargut, Egzergia: poradnik obliczania i stosowania, Wydawnictwo Politechniki Śląskiej, 2007 Search PubMed.
- Mike, Ammonia price index, https://businessanalytiq.com/procurementanalytics/index/ammonia-price-index/, (accessed January 13, 2025).
- Blue, green ammonia prices diverge as electrolysis power prices rise, natural gas falls, https://www.spglobal.com/commodity-insights/en/news-research/latest-news/energy-transition/031924-blue-green-ammonia-prices-diverge-as-electrolysis-power-prices-rise-natural-gas-falls, (accessed January 21, 2025).
- Z. Utlu and A. Hepbasli, Renewable Sustainable Energy Rev., 2007, 11, 1–29 CrossRef.
- Today in Energy Daily Prices – U.S. Energy Information Administration (EIA), https://www.eia.gov/todayinenergy/prices.php, (accessed December 21, 2024).
- C. A. Guerrero-Martin, J. S. Fernández-Ramírez, J. E. Arturo-Calvache, H. A. Milquez-Sanabria, F. A. da Silva Fernandes, V. J. Costa Gomes, W. Lima e Silva, E. Dutra Valente Duarte, L. E. Guerrero-Martin and E. F. Lucas, Energies, 2023, 16, 3502 CrossRef CAS.
- Ethanol – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/ethanol, (accessed December 21, 2024).
- H. Caliskan, S. Ekici and Y. Sohret, Propul. Power Res., 2022, 11, 391–400 CrossRef.
- Are aviation biofuels ready for take off?, https://www.iea.org/commentaries/are-aviation-biofuels-ready-for-take-off, (accessed June 24, 2025).
- USJP54, JET A1 price in United States 88.3 bbl/$ [24.06.2025], https://jet-a1-fuel.com/price/united-states, (accessed June 24, 2025).
- Coal – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/coal, (accessed December 21, 2024).
- Monthly Densified Biomass Fuel Report, https://www.eia.gov/biofuels/biomass/, (accessed December 21, 2024).
- Average monthly cost of water United States 2019, https://www.statista.com/statistics/720418/average-monthly-cost-of-water-in-the-us/, (accessed December 21, 2024).
- Water Pricing, https://www.circleofblue.org/waterpricing/, (accessed October 9, 2025).
- X. Chen, D. Goodnight, Z. Gao, A. H. Cavusoglu, N. Sabharwal, M. DeLay, A. Driks and O. Sahin, Nat. Commun., 2015, 6, 7346 CrossRef CAS PubMed.
- A.-H. Cavusoglu, X. Chen, P. Gentine and O. Sahin, Nat. Commun., 2017, 8, 617 CrossRef.
- N. G. Barton, ANZIAM J., 2008, 49, 503–524 CrossRef.
- E. Kozubal, J. Woods and R. Judkoff, US Pat., US9140471B2, 2015.
- M. Mumtaz, B. C. Pamintuan, A. J. Fix, J. E. Braun and D. M. Warsinger, Energy Convers. Manage., 2023, 294, 117547 CrossRef.
- K. F. Najjar, J. J. Shaw, E. E. Adams, G. H. Jirka and D. R. F. Harleman, Environmental and economic comparison of cooling-system designs for steam-electric power plants, Massachusetts Inst. of Tech., Cambridge (USA), 1978 Search PubMed.
- A. Shehabi, S. Smith, D. Sartor, R. Brown, M. Herrlin, J. Koomey, E. Masanet, N. Horner, I. Azevedo and W. Lintner, United States Data Center Energy Usage Report, Lawrence Berkeley National Laboratory (LBNL), Berkeley, CA (United States), 2016 Search PubMed.
- Repository of free climate data for building performance simulation, https://climate.onebuilding.org/, (accessed January 6, 2023).
- B. Walton, The Price of Water, https://www.circleofblue.org/2010/world/the-price-of-water-a-comparison-of-water-rates-usage-in-30-u-s-cities/, (accessed June 11, 2025).
- M. Özilgen, Renewable Sustainable Energy Rev., 2018, 96, 275–295 CrossRef.
- J. M. Awika, Advances in Cereal Science: Implications to Food Processing and Health Promotion, American Chemical Society, 2011, vol. 1089, pp. 1–13 Search PubMed.
- S. Réhault-Godbert, N. Guyot and Y. Nys, Nutrients, 2019, 11, 684 CrossRef.
- Rice, brown, long grain, unenriched, raw – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/2512380/nutrients, (accessed January 14, 2025).
- Rice – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/rice, (accessed January 13, 2025).
- Wheat, durum – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/169721/nutrients, (accessed January 14, 2025).
- Wheat – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/wheat, (accessed January 14, 2025).
- Oats, whole grain, steel cut – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/2346397/nutrients, (accessed January 14, 2025).
- Oat – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/oat, (accessed January 14, 2025).
- Corn, sweet, white, canned, whole kernel, regular pack, solids and liquids – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/168541/nutrients, (accessed January 14, 2025).
- Corn – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/corn, (accessed January 13, 2025).
- Soybeans, green, raw – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/169282/nutrients, (accessed January 14, 2025).
- Soybeans – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/soybeans, (accessed January 14, 2025).
- Sugars, granulated – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/746784/nutrients, (accessed January 14, 2025).
- Sugar – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/sugar, (accessed January 14, 2025).
- Milk, whole, 3.25% milkfat, with added vitamin D – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/746782/nutrients, (accessed January 14, 2025).
- Milk – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/milk, (accessed January 14, 2025).
- Butter, stick, unsalted – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/789828/nutrients, (accessed January 14, 2025).
- Butter – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/butter, (accessed January 14, 2025).
- Egg, whole, raw, fresh – USDA FoodData Central Food Details, https://fdc.nal.usda.gov/food-details/171287/nutrients, (accessed January 13, 2025).
- Eggs US – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/eggs-us, (accessed July 7, 2025).
- Poultry – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/poultry, (accessed January 13, 2025).
- Beef – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/beef, (accessed January 13, 2025).
- GC Protein Pricing Review Year End 2023, March 2024, https://greencirclecap.com/gcproteinpricing/, (accessed May 30, 2025).
- Savor, https://www.savor.it/home, (accessed May 29, 2025).
- Z. Wang, C. Zhang and F. Jiao, ACS Agric. Sci. Technol., 2025, 5, 681–686 CrossRef.
- E. C. Hann, S. Overa, M. Harland-Dunaway, A. F. Narvaez, D. N. Le, M. L. Orozco-Cárdenas, F. Jiao and R. E. Jinkerson, Nat. Food, 2022, 3, 461–471 CrossRef.
- S. J. Davis, K. Alexander, J. Moreno-Cruz, C. Hong, M. Shaner, K. Caldeira and I. McKay, Nat. Sustainability, 2024, 7, 90–95 CrossRef.
- N. Ripoll, C. Silvestre, E. Paredes and M. Toledo, Int. J. Hydrogen Energy, 2017, 42, 5513–5522 CrossRef.
- E. Koeleman, Algae cultivation profitable by 2025, https://www.allaboutfeed.net/animal-feed/raw-materials/algae-cultivation-profitable-by-2025/, (accessed May 29, 2025).
- W. de Queiróz Lamas, Fuel, 2025, 395, 134853 CrossRef.
- P. Procházka, J. Abrham, J. Cerveny, J. Soukupová, C. N. Ouma, K. J. Mullen, P. Sanova and L. Smutka, Front. Sustainable Food Syst., 2023, 7 DOI:10.3389/fsufs.2023.1256473.
- A. Vernon, A Review of Massively Scalable Enhanced Rock Weathering, https://austinvernon.substack.com/p/a-review-of-massively-scalable-enhanced, (accessed June 11, 2025) Search PubMed.
- A review of massively scalable enhanced rock weathering | Orca Notes, https://www.orcasciences.com/articles/a-review-of-massively-scalable-enhanced-rock-weathering, (accessed June 11, 2025).
- Z. Ying, A. Yang, M. Zhao, J. Yang, X. Zheng, B. Dou and G. Cui, J. Cleaner Prod., 2024, 435, 140590 CrossRef.
- S. Omelchenko, M. Shaner and I. McKay, US Pat., US20240271302A1, 2024 Search PubMed.
- Peregrine, https://peregrinehydrogen.com/#solution, (accessed June 12, 2025).
- J. M. Beltrán and S. Koo-Oshima, FAO Land and water discussion paper, 2006, vol. 5, p. 48 Search PubMed.
- How much electricity is lost in electricity transmission and distribution in the United States?, https://www.eia.gov/tools/faqs/faq.php?id=105&t=3, (accessed February 18, 2025).
- S. S. Alrwashdeh and H. Ammari, Case Stud. Therm. Eng., 2019, 16, 100559 CrossRef.
- Combined Heat and Power Technology Fact Sheet: Absorption Chillers for CHP Systems | Better Buildings Initiative, https://betterbuildingssolutioncenter.energy.gov/resources/combined-heat-and-power-technology-fact-sheet-absorption-chillers-chp-systems, (accessed July 12, 2025).
- P. E. Phelan, B. E. Phelan and A. Sharma, Front. Energy Effic., 2024, 2 DOI:10.3389/fenef.2024.1471628.
- J. D. Kocher, Int. J. Refrig., 2025, 169, 418–428 CrossRef.
- R. Gabbrielli, P. Castrataro and F. Del Medico, Energy Procedia, 2016, 91, 759–766 CrossRef.
- J. Woods, N. James, E. Kozubal, E. Bonnema, K. Brief, L. Voeller and J. Rivest, Joule, 2022, 6, 726–741 CrossRef.
- J. D. Kocher, S. K. Yee and R. Y. Wang, Energy Convers. Manage., 2022, 253, 115158 CrossRef.
- G. Angrisani, A. Capozzoli, F. Minichiello, C. Roselli and M. Sasso, Appl. Energy, 2011, 88, 1354–1365 CrossRef.
- Munters HCD desiccant dehumidifier | Munters, https://www.munters.com/en-us/products-cms/dehumidifiers/hcd-series/, (accessed July 15, 2025).
- F. Ge and C. Wang, Energy Convers. Manage., 2020, 224, 113343 CrossRef.
- What Are the Different Types of Aviation Fuel?, https://www.naa.edu/aviation-fuel/, (accessed June 24, 2025).
- Polyethylene – Price – Chart – Historical Data – News, https://tradingeconomics.com/commodity/polyethylene, (accessed June 24, 2025).
- Y. W. Huang, M. Q. Chen, Q. H. Li and W. Xing, Energy, 2018, 156, 548–554 CrossRef.
- Rondo Energy, https://www.rondo.com/, (accessed June 6, 2025).
- B. Zolghadr-Asli, N. McIntyre, S. Djordjević, R. Farmani and L. Pagliero, Water Supply, 2023, 23, 2517–2526 CrossRef.
- The Cool History of the Air Conditioner, https://www.popularmechanics.com/home/a7951/history-of-air-conditioning/, (accessed August 4, 2023).
- C. Cranmer, Energy Consumption of Direct Air Capture, https://large.stanford.edu/courses/2024/ph240/cranmer1/, (accessed June 13, 2025) Search PubMed.
- A. Biogradlija, Hydrogen Production Method Patented by Peregrine Hydrogen – Energy News, https://energynews.biz/hydrogen-production-method-patented-by-peregrine-hydrogen/, (accessed June 12, 2025) Search PubMed.
- C. E. Finke, US Pat., US20190376191A1, 2019.
- M. J. Mulvaney and P. Devkota, SS-AGR-443/AG442, https://edis.ifas.ufl.edu/publication/AG442, (accessed January 14, 2025) Search PubMed.
- S. M. Brouder, N. S. De Armond, R. F. Turco and J. J. Volenec, Purdue University Research Repository, 2014 DOI:10.4231/R7RN35SJ.
- The International Wheat Genome Sequencing Consortium (IWGSC), Science, 2014 Search PubMed.
- How Many Pounds of Meat Can We Expect From A Beef Animal? | UNL Beef | Nebraska, https://beef.unl.edu/beefwatch/2020/how-many-pounds-meat-can-we-expect-beef-animal/, (accessed February 17, 2025).
- V. Smil, IEEE Spectrum, 2019, https://spectrum.ieee.org/how-chicken-beat-beef-in-america Search PubMed.
- N. M. Soren and A. K. Biswas, in Meat Quality Analysis, ed. A. K. Biswas and P. K. Mandal, Academic Press, 2020, pp. 21–36 Search PubMed.
- Soy protein isolate, potassium type, crude protein basis, 1 oz, https://www.urmc.rochester.edu/encyclopedia/content?contenttypeid=76&contentid=16423-1, (accessed June 16, 2025).
- SEER2 New Efficiency Standards, https://seer2.com/, (accessed July 15, 2025).
- What's a Good SEER2 Rating?, https://www.trane.com/residential/en/resources/blog/whats-good-seer-rating/, (accessed July 15, 2025).
- Electrolyser cost | European Hydrogen Observatory, https://observatory.clean-hydrogen.europa.eu/hydrogen-landscape/production-trade-and-cost/electrolyser-cost, (accessed July 9, 2025).
- E. Doyle and E. Krasowski, Ramboll Group Whitepaper, 2023, https://www.ramboll.com/net-zero-explorers/what-will-it-take-to-reduce-capex-in-green-hydrogen-production.
- Electrolysers – Energy System, https://www.iea.org/energy-system/low-emission-fuels/electrolysers, (accessed July 9, 2025).
- C. Michalakakis, A. G. Hernandez, J. M. Cullen and B. Hallmark, Eceee Industrial Summer Study Proceedings, 2018.
- S. Orangi, N. Manjong, D. P. Clos, L. Usai, O. S. Burheim and A. H. Strømman, J. Energy Storage, 2024, 76, 109800 CrossRef.
| This journal is © The Royal Society of Chemistry 2026 |




