Open Access Article
Open Access ArticleUnsupervised and few-shot segmentation in photovoltaic electroluminescence images for defect detection via a novel enhanced iterative autoencoder with simple implementation
Ye
Lin†
 abe,
Pingyang
Sun†
abe,
Pingyang
Sun†
 *c,
Rongcheng
Wu†
*c,
Rongcheng
Wu†
 ab,
Shu
Geng
d,
Man Lung
Yiu
e,
Zhidong
Li
b,
Fang
Chen
b,
Yu
Gao
a,
Mingzhe
Wang
*f,
Kaiwen
Sun
ab,
Shu
Geng
d,
Man Lung
Yiu
e,
Zhidong
Li
b,
Fang
Chen
b,
Yu
Gao
a,
Mingzhe
Wang
*f,
Kaiwen
Sun
 *c and
Xiaojing
Hao
*c
*c and
Xiaojing
Hao
*c
aMolly Wardaguga Institute for First Nations Birth Rights, Faculty of Health, Charles Darwin University, Brisbane, QLD 4000, Australia. E-mail: yu.gao@cdu.edu.au
bThe Data Science Institute, University of Technology Sydney, Sydney, NSW 2007, Australia. E-mail: rongcheng.wu@student.uts.edu.au
cSchool of Photovoltaic and Renewable Energy Engineering, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: xj.hao@unsw.edu.au
dSchool of Chemical Engineering and Australian Centre for Nanomedicine (ACN), The University of New South Wales, Sydney, NSW 2052, Australia. E-mail: shu.geng@unsw.edu.au
eDepartment of Computing, The Hong Kong Polytechnic University, Hong Kong, 999077, China. E-mail: csmlyiu@polyu.edu.hk
fSchool of Computer Science and Technology, Xidian University, Xi’an, Shaanxi 710126, China. E-mail: wangmingzhe@xidian.edu.cn
First published on 26th November 2025
Abstract
Photovoltaic electroluminescence (PVEL) imaging captures material-level degradation in PV modules and offers high-resolution input for machine learning (ML) models to perform automated fault detection and health evaluation, reducing reliance on manual inspection. It is expected to have a simple and efficient defect detection ML model to achieve accurate segmentation for the fine-featured identification of defects in fabricated PV modules. This study proposes a novel enhanced iterative autoencoder (EI-AE), a completely new model that differs fundamentally from existing approaches which rely directly on classical ML models for defect detection. The proposed EI-AE, which for the first time introduces an iterative mechanism into the traditional AE framework, features a simple yet effective architecture and achieves accurate unsupervised pixel-level segmentation of all defect types using only normal PVEL images. In addition, few-shot learning can be realized by extending the unsupervised EI-AE with a small number of annotated masks, allowing more detailed functional defect detection while mitigating background interference. Theoretical proof demonstrates the benefits of the proposed EI-AE in improving defect detection compared to the conventional AE. Experimental results further validate its superiority, showing consistently better performance across multiple pixel-level metrics and outperforming both widely used unsupervised and few-shot baseline approaches.
Broader contextPhotovoltaic (PV) systems are expanding rapidly worldwide, making reliable and cost-effective maintenance increasingly important. PV electroluminescence (PVEL) imaging provides high-resolution visual data that reveal material-level degradation in PV modules. These images are particularly valuable for machine learning (ML)-based automated fault detection and health assessment, reducing reliance on manual inspection. Achieving accurate segmentation of minute defects in fabricated PV modules requires a defect detection model that is both simple and efficient. This study presents an enhanced iterative autoencoder (EI-AE), a fundamentally new model that, for the first time, incorporates an iterative mechanism into the conventional AE framework. Unlike existing methods that rely directly on classical ML architectures, EI-AE features a simple yet effective design capable of performing fully unsupervised, pixel-level segmentation of all defect types using only normal PVEL images. Furthermore, by extending the unsupervised EI-AE with a small set of annotated masks, the framework supports few-shot learning, enabling more detailed functional defect identification while suppressing background interference. |
1 Introduction
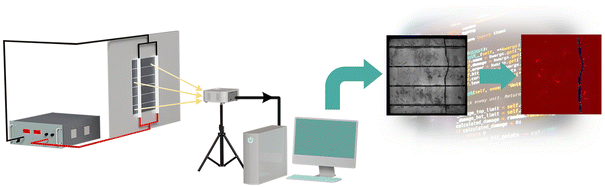
Photovoltaic electroluminescence (PVEL) imaging is a non-destructive technique for assessing PV module quality,1 revealing microscopic defects such as microcracks, inactive areas, broken fingers, shunts, and soldering issues that are often undetectable by visual inspection. It enables early detection of hidden defects during manufacturing, installation, or operation, supporting quality assurance, performance prediction, and reliability assessment.2 Due to the large volume and complexity of PVEL data, manual inspection is inefficient and error-prone, making automated defect detection algorithms3 essential for large-scale, reliable, and real-time assessment.4Machine learning (ML) can automatically detect defects in PVEL images by learning complex patterns,4,5 outperforming conventional image processing.6,7 While most ML methods address defect detection,8–13 advanced approaches perform defect segmentation to localize defective regions, as illustrated in Fig. 1. ML has been applied to (i) correlating defects with power output,14,15 (ii) detecting defects before lamination,16,17 (iii) enhancing image quality,18,19 and (iv) identifying defects in assembled modules.8,20–22 PVEL images of assembled PV modules contain rich spatial and intensity information that reflects subtle material and manufacturing defects, making them highly suitable for automated analysis.8 To identify defects in PVEL images of finished PV modules, three types of defect detection ML approaches can be utilized: (i) image-level binary and multi-class classification, (ii) bounding box-based object localization, and (iii) segmentation. This work focuses on the defect identification of fabricated PV modules, and adopts segmentation23 for pixel-level localization of complex defects to support automated EL image inspection.
Although image-level binary/multi-class classification is the most basic ML method for EL image defect detection, it assumes that all defect categories are fully defined and mutually exclusive. Convolutional neural networks (CNNs) dominate both tasks,8–10 employing architectures such as VGG16,11–13 high-resolution network (HRNet),9,10,24 and the combination of ResNet152, Xception, and coordinate attention (CA).25 Feature enhancement and model compression are achieved via the incorporation of histogram of oriented gradients (HoG)12 and knowledge distillation13 into VGG16. The current multi-class classification efforts mainly rely on CNN,20,26–36 support vector machine (SVM),26,30 and random forest (RF).30,37 In addition, transfer learning with compact architectures has been adopted to utilize pre-trained features,29 while architectural combinations33 and particle swarm optimization (PSO)35 further enhance accuracy and reduce model complexity. Other approaches include modified VGG19,28 unsupervised clustering,27 generative adversarial network (GAN)-based augmentation,32 fuzzy logic integration,34 and defect localization by YOLO.36 Unlike classification, bounding box methods detect multiple defects per module. Fusion of Faster regions with CNN features (R-CNN) and region-based fully convolutional network (R-FCN) outputs based on intersection over union (IoU) consistency improves accuracy and reduces false detections.21 Incorporating a complementary attention network (CAN) into a Faster R-CNN's region proposal network further enhances defect extraction.5 Mask R-CNN with a ResNet-101-FPN backbone detects fourteen defect types.38 However, the classification and bounding box-based defect localization tasks are often limited in providing detailed spatial information, which segmentation can overcome by delivering pixel-level defect mapping for precise assessment.
For the segmentation task, two paradigms can be utilized: (1) approaches that use a separate feature extractor followed by a segmentation procedure,22,39–41 and (2) end-to-end segmentation networks.42–46 Classification networks, such as ResNet1840 and ResNet50,22,41 can serve as backbone feature extractors, with their outputs passed to a segmentation head, such as autoencoder (AE)39 and DeepLabv3,41 for pixel-wise prediction. Instead of performing explicit segmentation, a ResNet-50 trained for classification is used to generate intermediate activation maps,22 whose spatial responses are interpreted as segmentation.
End-to-end segmentation networks are task-optimized for accurate, dense defect detection of PVEL images. A GAN is used to produce more realistic reconstructions of normal samples through adversarial training.42 However, GANs often suffer from training instability and typically require larger datasets, which limit their practicality in industrial settings. Different encoder–decoder NN architectures are also explored in PVEL image defect detection, including standard U-Net,44,46 U-Net with an attention mechanism,43 PSPNet46 and DeepLabv3+.46 Multiple combinations of encoder and decoder networks are explored,45 which are Mobile-net, ResNet, VGG-net, and U-net for the encoder part, while U-net, FCN-net, PSP-net, and SegNet for the decoder part. In addition, wavelet analysis is used to handle non-stationary textures in the segmentation of PVEL images,47 while K-Net has been used as a baseline method in segmentation tasks.48
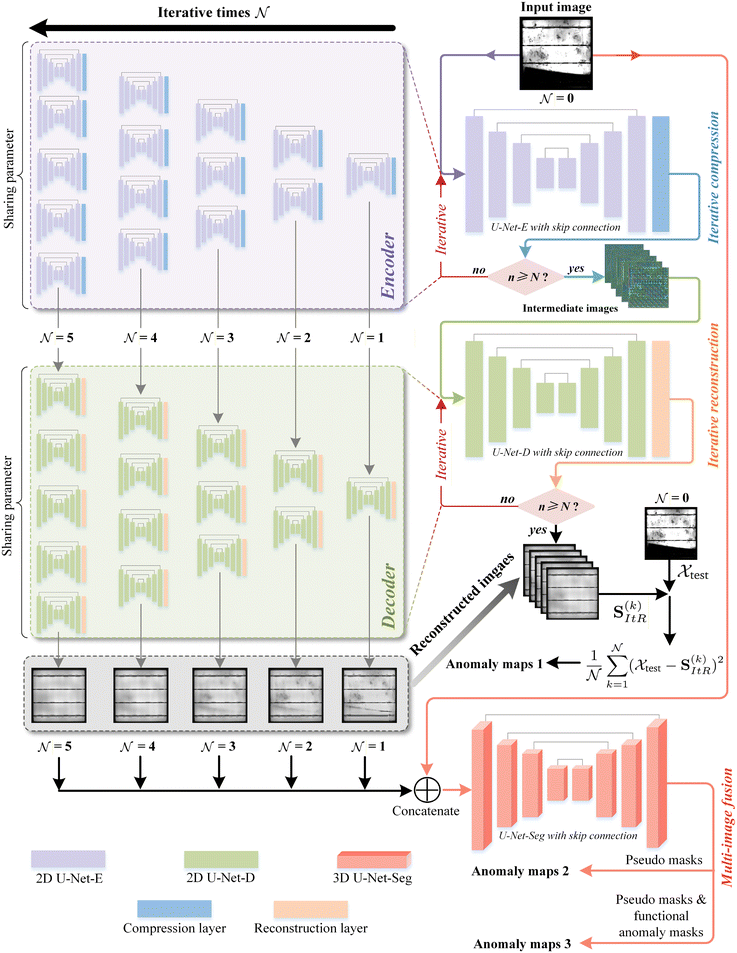
Nevertheless, the current studies on defect detection of PVEL images using end-to-end segmentation networks are still in the stage of direct use of classical NN models or their simple combinations. These approaches often lack adaptability to subtle or complex defect patterns, especially in cases involving irregular morphology or background interference. To address this limitation, a novel enhanced iterative autoencoder (EI-AE) is proposed in this study to achieve simple and accurate unsupervised defect segmentation of PVEL images using only normal samples during training. The proposed EI-AE utilizes U-Net49 as encoder and decoder blocks, while iterative operations50 are implemented in each encoder and decoder to significantly (i) expand function space constraints (enhancing the ability to generalize from normal PVEL image patterns), (ii) prevent defect memorization (avoiding the model from incorrectly learning and reconstructing latent defects in normal-looking PVEL images), and (iii) improve multi-scale information representation (accurately detecting defects of varying sizes in PVEL images). In addition, by incorporating a multi-image fusion structure, the proposed EI-AE can be adapted to detect more specific defects using a few-shot approach with only a limited number of annotated functional defect masks.
2 Description of datasets
In this work, we use the photovoltaic electroluminescence anomaly detection (PVEL-AD) dataset,51 which comprises 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 543 near-infrared images (11
543 near-infrared images (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353 good images) of solar cells featuring various internal defects and heterogeneous backgrounds. The dataset includes one defect-free category and 12 distinct defect types, namely black cores, corner defects, cracks (non-star), finger interruptions, fragments, horizontal dislocations, printing errors, scratches, short-circuit defects, star cracks, thick lines, and vertical dislocations (two images of each category are shown in Fig. 2). The PVEL-AD dataset, with its long-tail distribution of defect types, provides a challenging while realistic benchmark for evaluating unsupervised and few-shot learning approaches. It is particularly well-suited for testing models (e.g. the proposed EI-AE), which performs segmentation using only normal samples, and can be extended with limited annotations to detect rare functional defects, addressing the annotation bottleneck in practical PV quality inspection.
353 good images) of solar cells featuring various internal defects and heterogeneous backgrounds. The dataset includes one defect-free category and 12 distinct defect types, namely black cores, corner defects, cracks (non-star), finger interruptions, fragments, horizontal dislocations, printing errors, scratches, short-circuit defects, star cracks, thick lines, and vertical dislocations (two images of each category are shown in Fig. 2). The PVEL-AD dataset, with its long-tail distribution of defect types, provides a challenging while realistic benchmark for evaluating unsupervised and few-shot learning approaches. It is particularly well-suited for testing models (e.g. the proposed EI-AE), which performs segmentation using only normal samples, and can be extended with limited annotations to detect rare functional defects, addressing the annotation bottleneck in practical PV quality inspection.
Furthermore, to evaluate the segmentation performance under different settings of our proposed EI-AE, we manually annotated two types of segmentation masks (Mask A and Mask B) based on this dataset. All defects are captured in Mask A without explicitly defining the defect categories, while four specific defect types are annotated in Mask B. These additional annotations allow a more comprehensive assessment of segmentation accuracy and robustness.
2.1 All defect masks (Mask A)
In this setting, 30 masks are labelled for all observed defects, encompassing both functional and non-functional defects (18 images are shown in Fig. 3, while others are put in SI-S2). This comprehensive annotation strategy serves two main purposes. First, by including every visible defect, regardless of its specific impact on solar cell performance, we ensure that the segmentation model learns to detect a broad range of defect patterns. This coverage is especially relevant in real-world manufacturing contexts, where even minor or cosmetic defects (e.g., scratches or tiny surface inconsistencies) may indicate underlying process issues. Second, the inclusive nature of this mask annotation provides a more holistic evaluation of a model's capacity to identify and localize any deviation from the nominal appearance. Consequently, the “All defects” mask allows for a thorough assessment of segmentation performance, highlighting the robustness of the proposed EI-AE in scenarios where defect types or severities vary widely.2.2 Functional defect masks (Mask B)
In this setting, only defects that directly impact device performance are considered. Specifically, we use the bounding boxes provided by the PVEL-AD dataset to manually annotate high-resolution 438 masks within the testing set, targeting only functional defects. Although the PVEL-AD dataset51 contains 12 types of defects, four major categories, including cracks (non-star), finger interruptions, scratches, and star cracks, are utilized and manually annotated in this study to demonstrate the effectiveness of the proposed EI-AE. In addition, three representative images from each annotated category are shown in Fig. 4, while the remaining annotated images are provided in SI-S3. | ||
| Fig. 4 Functional defect masks by manual annotation (Mask B): (a) cracks (non-star), (b) finger interruptions, (c) scratches, and (d) star cracks. | ||
By refining the coarse bounding-box labels into pixel-precise segmentations, this annotation process ensures that our evaluations concentrate on those defects most critical to PV module reliability. Consequently, this approach enables an in-depth assessment of model performance in detecting and characterizing functionally significant defects, thereby facilitating more targeted strategies for quality control in smart manufacturing processes.
3 Proposed enhanced iterative autoencoder (EI-AE)
In this study, we propose a novel EI-AE unsupervised learning method for simple defect detection of PVEL images. The space of the PVEL input image can be expressed as![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) ⊂
⊂ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) h×w×c, where h, w, and c indicate the height, width, and number of channels, respectively. For the defect detection task, a training set
h×w×c, where h, w, and c indicate the height, width, and number of channels, respectively. For the defect detection task, a training set ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) train includes i normal EL images without abnormalities, while a test set
train includes i normal EL images without abnormalities, while a test set ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) test consists of t defective EL images, where
test consists of t defective EL images, where ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) train = {x1,x2,…,xi},
train = {x1,x2,…,xi}, ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) test = {x1,x2,…,xt}, and x ∈
test = {x1,x2,…,xt}, and x ∈ ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) . The learning objective aims to develop a model capable of performing pixel-level segmentation to detect defective regions within test images
. The learning objective aims to develop a model capable of performing pixel-level segmentation to detect defective regions within test images ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) test.
test.
3.1 Conventional autoencoder (AE)
Since the focus of this study is on 2D PVEL images, a traditional widely used convolutional AE for defect detection is first introduced in this section,52,53 following with its challenge explanations in high-precision defect identification.A convolutional AE is trained to minimize the reconstruction error Lrecon. on normal samples as:
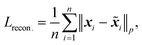 | (1) |
![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) i denotes the reconstruction of the input image xi, expressed as:
i denotes the reconstruction of the input image xi, expressed as:![[x with combining tilde]](https://www.rsc.org/images/entities/b_i_char_0078_0303.gif) i = fD(fE(xi)), i = fD(fE(xi)), | (2) |
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) →
→ ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ) that processes the input image to obtain a latent representation
) that processes the input image to obtain a latent representation ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (
(![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ⊂
⊂ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) h′×w′×c′, h′ < h, w′ < w, c′ ≥ c); fE is the decoder network (
h′×w′×c′, h′ < h, w′ < w, c′ ≥ c); fE is the decoder network (![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) →
→ ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) ), which takes the latent representation Z produced by the encoder and reconstructs the input image. A deep convolutional AE with depth N can be represented as:
), which takes the latent representation Z produced by the encoder and reconstructs the input image. A deep convolutional AE with depth N can be represented as:| FAE(x) = fD1(fD2(…fDN(fEN(…fE2(fE1(x)))))). | (3) |
Moreover, the parameters of each encoder and decoder block are given by 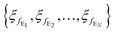 and
and 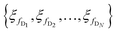 , respectively.
, respectively.
However, traditional AEs face several critical limitations when applied to industrial PVEL image defect detection:
(1) With a limited number of normal EL images, the AE is prone to overfitting, resulting in poor generalization.54 Although the training objective minimizes the reconstruction loss as eqn (1), the network will memorize training examples when the training set ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) train is small:
train is small:
fD(fE(xi)) ≈ xi, ∀xi ∈ ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) train. train. | (4) |
Since anomalies are absent in training, the model fails to generalize to unseen test samples ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) test ∉
test ∉ ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) train, making it unreliable for defect detection.
train, making it unreliable for defect detection.
(2) When a high representation capacity is present in the latent space, the AE reconstructs both normal and defective samples accurately, making defect detection ineffective.55 If the encoder fE maps inputs to a high-capacity latent space ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) , then for any input x, an expressive decoder can reconstruct it perfectly:
, then for any input x, an expressive decoder can reconstruct it perfectly:
| zi = fE(xi), xi ≈ fD(zi), | (5) |
Since defective data points xanom, are also mapped to similar latent representations, their reconstructions remain accurate:
| ‖xanom − fD(fE(xanom))‖p ≈ 0 | (6) |
This contradicts the assumption that anomalies should have high reconstruction errors and thus reduces the effectiveness of defect detection.
(3) A standard AE reconstructs anomalies in a single resolution scale, lacking multi-scale feature extraction, which limits their ability to differentiate complex anomalies from normal variations.56,57 The single encoding-decoding operation is expressed as:
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) i = fD(fE(xi)). i = fD(fE(xi)). | (7) |
3.2 Enhanced iterative autoencoder (EI-AE)
To address the potential issues of the conventional AE in the defect detection of PVEL images discussed in Section 3.1, this study proposes a novel EI-AE (Fig. 5) that utilizes iterative computation to achieve multi-step compression and reconstruction, improving parameter sharing and network representation capabilities. To be specific, the proposed EI-AE consists of two key stages: (i) a iterative compression encoder, and (ii) an iterative reconstruction decoder. These components jointly enhance function space constraints, prevent defect memorization, and improve multi-scale information representation, outperforming the conventional AE. This section presents the network architecture description of the proposed EI-AE, along with a detailed explanation of its improvements.![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) iterative iterations, while 5 iterations are used in this model.
iterative iterations, while 5 iterations are used in this model.
A modified U-Net is implemented as an encoder in the compression stage by replacing the output layer of the standard U-Net with a convolutional layer with kernel size 2 and stride 2, so that the spatial dimensions (height and width) of the original input are reduced by half. This process is similar to the encoder in a standard AE, where the input is compressed in the compression layer.
However, unlike a standard AE, our approach employs a modified U-Net (U-Net-E) that iteratively refines the encoding process through ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) self-iterations within the encoder, continuously compressing the input into a lower-dimensional representation while sharing a common encoder fE with parameters ξfE:
self-iterations within the encoder, continuously compressing the input into a lower-dimensional representation while sharing a common encoder fE with parameters ξfE:
S(j)ItC = fE(S(j−1)ItC;ξfE), j ∈ {1,2,3,…,![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) }, }, | (8) |
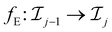 transforms the input from one resolution level to a lower one, where
transforms the input from one resolution level to a lower one, where  . The compression depth is limited to a maximum of
. The compression depth is limited to a maximum of ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) = 5 for 1024 × 1024 input images, as further downsampling leads to excessively small feature maps and prevents the model from functioning.
= 5 for 1024 × 1024 input images, as further downsampling leads to excessively small feature maps and prevents the model from functioning.
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )ItC in the iterative compression stage. Similar to the U-Net-E in the encoder, we also modify a standard U-Net to a new U-Net (U-Net-D) by replacing the output layer with a transposed convolution (deconvolution) layer with a kernel size of 2 and a stride of 2, upsampling the low-dimensional features back to the original input size.
)ItC in the iterative compression stage. Similar to the U-Net-E in the encoder, we also modify a standard U-Net to a new U-Net (U-Net-D) by replacing the output layer with a transposed convolution (deconvolution) layer with a kernel size of 2 and a stride of 2, upsampling the low-dimensional features back to the original input size.
Multiple self-iterations are performed in the new decoder to progressively upsample the low-dimensional features into high-dimensional representations, through ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) iterative iterations using a shared decoder fD with parameters ξfD:
iterative iterations using a shared decoder fD with parameters ξfD:
S(k)ItR = fD(S(k−1)ItR;ξfD), k ∈ {1,2,3,…,![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) }, }, | (9) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )ItC, and the spatial dimensions are gradually restored to the original resolution. The shared decoder
)ItC, and the spatial dimensions are gradually restored to the original resolution. The shared decoder 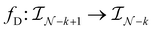 maps data from a lower resolution level to a higher one. By performing
maps data from a lower resolution level to a higher one. By performing ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) iterative reconstruction, the defective image will be reconstructed to their normal state S(
iterative reconstruction, the defective image will be reconstructed to their normal state S(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )ItR. Moreover, by successively subtracting the reconstructed normal images S(k)ItR from the input defective images in the test set
)ItR. Moreover, by successively subtracting the reconstructed normal images S(k)ItR from the input defective images in the test set ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) test, defect maps can be generated:
test, defect maps can be generated: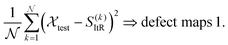 | (10) |
However, the current defect maps reflect all the defects (dark regions) in the PVEL images, which may not be ideal for industrial detection in specific scenarios. In practice, industrial detection often aims to focus on critical failures, such as significant cracks, fingers and scratch, while ignoring less significant defects. Simply subtracting the reconstructed normal image from the defective image results in the extraction of both true anomalies and background clutter (false positive). To prioritize true defects, multi-image fusion detection is further used, which can selectively emphasize significant anomolies while minimizing the impact of background-induced noise in the final defect maps. The implementation details are provided in the following section.
The reconstructed ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) images and the input image (in total
images and the input image (in total ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) + 1 images in each set) are fed into a 3D U-Net (U-Net-Seg), as shown in the red concatenation paths of Fig. 5 and can be expressed as:
+ 1 images in each set) are fed into a 3D U-Net (U-Net-Seg), as shown in the red concatenation paths of Fig. 5 and can be expressed as:
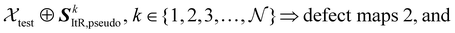 | (11) |
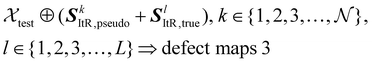 | (12) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) reconstructed images instead of a single one. This approach enhances structural consistency throughout the reconstruction process. The detailed configurations of pseudo masks and real functional defect masks are provided in Section 4.1.
reconstructed images instead of a single one. This approach enhances structural consistency throughout the reconstruction process. The detailed configurations of pseudo masks and real functional defect masks are provided in Section 4.1.
Enhancement of constraints in function space (advantage 1). The forward pass of the conventional deep AE with N encoder and decoder blocks is given by eqn (3) that FAE(x) = fD1(fD2(…fDN(fEN(…fE2(fE1(x)))))). It shows each encoder block fEi and decoder block fDi has its own corresponding parameters
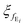 and
and 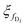 . However, the proposed EI-AE uses a shared encoder fE and a shared decoder fD, each applied
. However, the proposed EI-AE uses a shared encoder fE and a shared decoder fD, each applied ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) times:
times:FEI-AE(x) = f(k)D(f(j)E(x)) = f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )D(f( )D(f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) −1)D(…f(1)D(f( −1)D(…f(1)D(f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )E(f( )E(f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) −1)E(…f(1)E(x)))))), −1)E(…f(1)E(x)))))), | (13) |
| FEI-AE ⊂ FAE, | (14) |
In addition, shared parameters ξfE and ξfD are present in the shared encoder fEi and decoder fDi, respectively. Through gradient accumulation during backpropagation, the parameter sharing enforces constraints that ensure scale consistency:
iterative image compression:
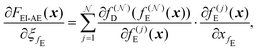 | (15) |
iterative image reconstruction:
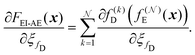 | (16) |
The gradients are computed for all iterations and then combined, guiding the learning process to ensure that the parameters learned by the model remain consistent across all layers. This forces the model to learn representations that are consistent in the function space, thereby avoiding overfitting to any particular scale.
Such analysis demonstrates that the function space in the proposed EI-AE is strictly smaller than that of the conventional AE, further effectively limiting its capacity to memorize arbitrary defect patterns.
Prevention of defect memorization (advantage 2). First, normal and defective image sets are defined as
![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) norm and
norm and ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) anom, respectively. The iterative architecture can be interpreted as utilizing regularization R(FEI-AE) on
anom, respectively. The iterative architecture can be interpreted as utilizing regularization R(FEI-AE) on ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) norm to step-by-step enforce consistency, ensuring stable feature representation across
norm to step-by-step enforce consistency, ensuring stable feature representation across ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) iterations:
iterations: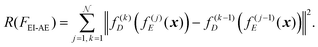 | (17) |
The expected reconstruction error for defective EL images in the proposed EI-AE, given by the expectation ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) x∈
x∈![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) anom and bounded below by:
anom and bounded below by:
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) x∈ x∈![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) anom[‖x − f( anom[‖x − f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )D(f( )D(f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )E(x;xfE);xfD)‖] ≥ c·min(d( )E(x;xfE);xfD)‖] ≥ c·min(d(![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) norm, norm,![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) anom)), anom)), | (18) |
![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) norm,
norm,![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) anom)) refers to the minimum distance between normal and defective distributions, and c is a positive constant (c > 0) that is a function of the number of iterations
anom)) refers to the minimum distance between normal and defective distributions, and c is a positive constant (c > 0) that is a function of the number of iterations ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) .
.
This sets a lower bound on the reconstruction error for anomalies, demonstrating that the used iterative architecture effectively prevents memorizing defective patterns without sacrificing the reconstruction of normal data. The detailed explanation is provided in S1.2 of the SI.
Improvement of multi-scale information representation (advantage 3). The iterative architecture with
![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) -step can capture multi-scale information with improved scale consistency. Starting from the iterative reconstruction stage S(k)ItR = f(k)D(f(
-step can capture multi-scale information with improved scale consistency. Starting from the iterative reconstruction stage S(k)ItR = f(k)D(f(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) )E(x)), the mutual information Info(·;·) between
)E(x)), the mutual information Info(·;·) between ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) reconstructions is:
reconstructions is:| Info(S(k)ItR;x) ≥ Info(SI(k−1)ItR;x), | (19) |
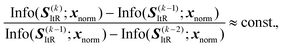 | (20) |
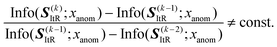 | (21) |
Therefore, the proposed EI-AE inherently captures hierarchical information through iterative operation, allowing it to differentiate between normal and defective patterns. A detailed theoretical explanation can be found in S1.3 of the SI.
4 Experimental verification
4.1 Training details
Our network consists of two main components: EI-AE and U-Net-Seg. The EI-AE is responsible for reconstructing a clean version of the input image by eliminating defects, while U-Net-Seg performs pixel-level segmentation to localize defects based on the reconstruction results.The U-Net-Seg network processes this 3D volume and outputs a single-channel prediction of shape h × w × 1, which is subsequently flattened to a 2D defect score map. The network is supervised using a pixel-wise ℓ1 loss between the predicted output and the GT mask, where pixels with value 1 indicate known defective regions. These ground truth masks are derived from the binary masks used for input corruption, guiding the model to focus on regions where the reconstruction deviates from expected normal patterns. In addition, 142 real functional defect masks (1.25% of good images) from the datasets described in Section 2.2 are included to achieve few-shot learning. These real masks will help U-Net-Seg selectively focus on the true defects.
P-AUROC measures the model's ability to distinguish between normal and defective pixels across all threshold values. P-AP is calculated as the area under the precision–recall (PR) curve, reflecting the trade-off between precision and recall. P-F1 is defined as the harmonic mean of precision and recall at the optimal threshold, providing a single-value summary of detection accuracy.
AUPRO evaluates detection performance across varying false positive rates by measuring how well predicted regions cover ground-truth defects. A-PRO calculates the proportion of ground-truth regions correctly detected, considering a prediction successful if the intersection over union (IoU) exceeds a predefined threshold (0.3 in this study).
4.2 Experiment 1 – unsupervised detection of all defects (No U-Net-Seg)
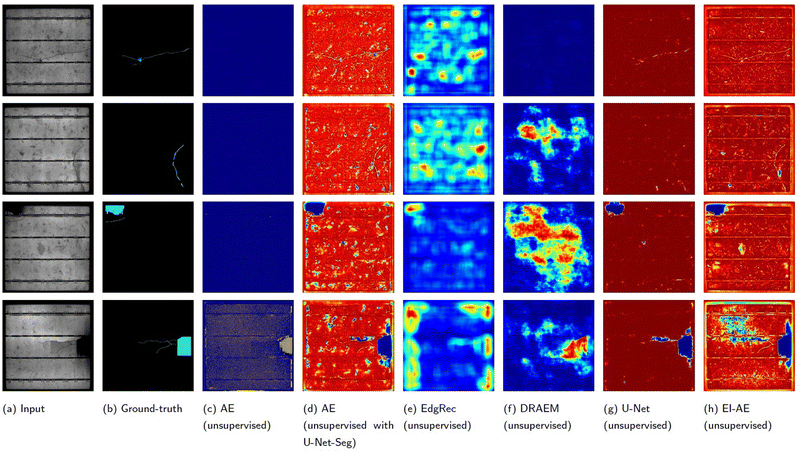
Fig. 6 (segmentation maps) and Table 1 (metrics) illustrate the comparison results, obtained by directly computing pixel-wise differences between the reconstructed images and their original counterparts. For performance evaluation, the GT is defined using the full defect masks (Mask A) as described in Section 2.1. Although EI-AE achieves slightly lower P-AP (0.6434) and P-F1 (0.6739) compared to DRAEM (0.7248 and 0.7206 respectively), it consistently outperforms all baseline methods in the remaining three metrics: P-AUROC (0.8800), AUPRO (0.4074), and A-PRO (0.8557). These results indicate that EI-AE provides stronger global discrimination capability and better robustness in identifying true functional defects across diverse pixel regions, while DRAEM tends to focus more on pixel-level differences, which may lead to higher precision in localized areas but lower overall consistency and generalization performance. The performance of the conventional AE is poorest because the model tends to take a shortcut during reconstruction by simply copying the input to the output. As a result, it also learns to reconstruct the defects, making it difficult to distinguish them from normal regions [eqn (5) and (6)]. In general, the results demonstrate the strong generalization capability of the proposed EI-AE in scenarios that demand comprehensive detection of diverse defect types in PVEL images.
| Methods | P-AUROC | P-AP | P-F1 | AUPRO | A-PRO |
|---|---|---|---|---|---|
| a U-Net is trained with functional defect masks (Mask B) to enable few-shot segmentation. | |||||
| AE (unsupervised) | 0.5772 | 0.2002 | 0.3757 | 0.0239 | 0.0212 |
| EdgRec (unsupervised) | 0.5448 | 0.2687 | 0.3099 | 0.1515 | 0.4060 |
| DRAEM (unsupervised) | 0.8596 | 0.7248 | 0.7206 | 0.1251 | 0.8202 |
| U-Net (unsupervised) | 0.5349 | 0.2449 | 0.3096 | 0.1232 | 0.3104 |
| U-Net (few-shot)a | 0.7571 | 0.5379 | 0.6207 | 0.1625 | 0.6939 |
| EI-AE (unsupervised) | 0.8800 | 0.6434 | 0.6739 | 0.4074 | 0.8557 |
Notably, the maximum feasible compression depth is ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) = 5, as it represents the limit imposed by the 1024 × 1024 input resolution and the downsampling factor of two per stage. Beyond this depth, the feature maps shrink to sizes below 32 × 32, potentially resulting in loss of spatial context, misalignment in the decoder, and numerical instability due to over-compression.
= 5, as it represents the limit imposed by the 1024 × 1024 input resolution and the downsampling factor of two per stage. Beyond this depth, the feature maps shrink to sizes below 32 × 32, potentially resulting in loss of spatial context, misalignment in the decoder, and numerical instability due to over-compression.
4.3 Experiment 2 – unsupervised defect detection using U-Net-Seg
By incorporating a segmentation head (referred to the multi-image fusion module, U-Net-Seg) and introducing annotated defect masks, the proposed EI-AE model is able to detect more specific defects in PVEL images. The test images are selected from the “Crack (non-star)” category in Mask B, as shown in Fig. 4(a), for evaluating the performance of all networks.Fig. 8 presents the segmentation results obtained by fusing the input image with five piecewise recovery images as input to U-Net-Seg, where only pseudo masks are used during training [eqn (11)]. Table 2 presents the quantitative comparison of different unsupervised methods for the “Crack (non-star)” category. The proposed EI-AE achieves the best overall performance, with the highest scores in P-AUROC (0.8868), AUPRO (0.6297), and A-PRO (0.8814), indicating superior pixel-wise discrimination and region-level defect localization. While P-AP (0.1428) and P-F1 (0.2076) are slightly lower than those of the U-Net baseline (0.2503 and 0.3355, respectively), EI-AE maintains a better balance across all metrics. This suggests that EI-AE avoids overfitting to local noise and generalizes better in complex surface defect scenarios. Although the integration of U-Net-Seg in the conventional AE significantly improves its performance, it still falls short of EI-AE, confirming the critical role of the embedded iterative operation in enhancing defect localization and suppression of irrelevant features.
| Methods | P-AUROC | P-AP | P-F1 | AUPRO | A-PRO |
|---|---|---|---|---|---|
| a Segmentation head (U-Net-Seg) is included in the conventional AE and the proposed EI-AE. | |||||
| AE (unsupervised) | 0.5108 | 0.0034 | 0.0074 | 0.5508 | 0.1512 |
| AE (unsupervised with U-Net-Seg)a | 0.8135 | 0.0651 | 0.1659 | 0.5508 | 0.7641 |
| EdgRec (unsupervised) | 0.6175 | 0.0068 | 0.0226 | 0.2534 | 0.4635 |
| DRAEM (unsupervised) | 0.6666 | 0.0491 | 0.1110 | 0.3368 | 0.5676 |
| U-Net (unsupervised) | 0.7353 | 0.2503 | 0.3355 | 0.4226 | 0.4985 |
| EI-AE (unsupervised)a | 0.8868 | 0.1428 | 0.2076 | 0.6297 | 0.8814 |
4.4 Experiment 3 – few-shot defect detection using U-Net-Seg
In the third experiment, true masks (functional defect masks – Mask B) are also included in the training process of the proposed EI-AE, in addition to the pseudo masks. A total of 142 real functional defect masks are randomly selected from the category groups of finger interruptions, scratches, and star cracks, while the non-star crack category group is used to evaluate the network performance.Despite comprising only 1.25% of the good images, the inclusion of true masks contributes to improved prediction accuracy and more precise defect segmentation with reduced background interference [Fig. 9(e)], as demonstrated in the comparison of EI-AE results in Experiment 2 [Fig. 8(h)]. An accuracy improvement of 3.04% is achieved in the few-shot setting (P-AUROC: 0.9138), compared to the baseline without few-shot learning (P-AUROC: 0.8868).
Table 3 compares the performance of AE, U-Net, and the proposed EI-AE in a few-shot defect segmentation setting. In terms of P-AUROC, EI-AE achieves the highest score of 0.9138, outperforming AE (0.8586) and U-Net (0.7923), indicating improved defect segmentation at the pixel level. For P-AP, EI-AE reaches 0.3425, which remains higher than that of U-Net (0.2870) and noticeably better than that of AE (0.2098), suggesting better precision–recall trade-off. The P-F1 of EI-AE is 0.4208, significantly higher than that of AE (0.3054) and slightly higher than that of U-Net (0.4205), reflecting more accurate segmentation boundaries. In terms of region-aware metrics, EI-AE also demonstrates competitive performance, achieving an AUPRO of 0.7576, slightly lower than that of AE (0.7916) but significantly higher than that of U-Net (0.5446). Similarly, the region-wise A-PRO of EI-AE reaches 0.8185, exceeding that of U-Net (0.6852) and only marginally lower than that of AE (0.8193). These results confirm the effectiveness of the enhanced iterative structure in improving segmentation accuracy and robustness with limited supervision.
To further illustrate how accuracy varies with different sampling sizes in the few-shot setting, we conduct an additional experiment testing 1-, 10-, and 50-shot scenarios, respectively. As shown in Table 4, the 1-shot case performs worse than the unsupervised one (0.8868) because a single labelled sample provides insufficient and potentially misleading supervision, disrupting the model's originally stable feature representation. However, as the number of shots increases, the accuracy improves rapidly and approaches saturation at 50-shot, demonstrating the model's strong few-shot learning capability.
| Methods | EI-AE (1-shot) (%) | EI-AE (10-shot) (%) | EI-AE (50-shot) (%) | EI-AE (142-shot) (%) |
|---|---|---|---|---|
| P-AUROC | 74.5 | 88.6 | 91.5 | 91.4 |
5 Implications and challenges in real-world manufacturing
The spatial distribution and trends of defects detected by the proposed EI-AE can be correlated with specific PV panel manufacturing steps (e.g., wafer cutting, cell soldering, encapsulation, lamination, or module assembly), serving as an effective quality control tool across various production stages. Moreover, the obtained defect maps can be integrated with statistical process control or optimization frameworks to quantitatively assess the impact of manufacturing parameters, enabling engineers to identify critical process stages and proactively guide process improvements.There are also some major challenges in practical deployment. First, building a larger set of high-quality PV-EL defect-free and defective images remains a challenge, especially for emerging PV materials such as perovskite and CIGS. Secondly, the current implementation does not explicitly distinguish defect types; integrating a dedicated classifier model would be a promising yet non-trivial step toward enabling automatic defect categorization. Lastly, in real production lines where PV panels may exhibit variations in shape, orientation, and layout, developing a model robust to such variations is still an open challenge. The proposed EI-AE paves the way for the development of more robust and adaptive models capable of handling these practical complexities.
6 Conclusion
Given that current PVEL anomaly detection methods predominantly apply classical segmentation networks with limited adaptability to subtle or complex defects, this study proposes a novel EI-AE framework to achieve more precise defect segmentation of complex anomalies in PV modules. Instead of relying on implementation-complex architectures, a simple yet effective iterative structure is adopted, introducing a small number of iterative steps within each encoder and decoder block to support effective deep feature extraction. Moreover, the proposed multi-image fusion structure concatenates the original inputs with all recovered images generated during the iterative process, achieving more precise segmentation of specific anomalies in PVEL images while using only a limited number of real labels.Three experiments, including (1) unsupervised detection of all defects, (2) unsupervised detection with segmentation head, and (3) few-shot detection with segmentation head, progressively demonstrate the superior performance of the proposed EI-AE over conventional methods. The proposed EI-AE reduces the need for extensive labelled data, making it highly suitable for large-scale PV module inspection in industrial settings. Its simple design and adaptability to complex defects also support efficient deployment in real-world manufacturing and maintenance scenarios.
Author contributions
Ye Lin: conceptualization, data curation, investigation, methodology, writing – original draft; Pingyang Sun: conceptualization, formal analysis, investigation, methodology, visualization, writing – original draft; Rongcheng Wu: conceptualization, data curation, methodology, software, validation, writing – original draft; Shu Geng: investigation, visualization, writing – review & editing; Man Lung Yiu: methodology, supervision, writing – review & editing; Zhidong Li: methodology, project administration, supervision; Fang Chen: project administration, supervision; Yu Gao: project administration, supervision; Mingzhe Wang: project administration, supervision, writing – review & editing; Kaiwen Sun: supervision, writing – review & editing; Xiaojing Hao: supervision, writing – review & editing.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the Photovoltaic Electroluminescence Anomaly Detection (PVEL-AD) dataset is used in this article: su binyi, Photovoltaic cell anomaly detection, https://kaggle.com/competitions/pvelad, 2022, Kaggle. In addition, the annotated masks in this paper have been included. Codes of the proposed EI-AE will be made publicly available on GitHub in the final version, https://github.com/rongcheng-wu/Abnormal-detection-in-Photovoltaic-Electroluminescence-Images. See DOI: https://doi.org/10.1039/d5ee05042a.Acknowledgements
This work is supported by the Australia – UK Renewable Hydrogen Innovation Partnerships (GA396723), funded by the Department of Climate Change, Energy, the Environment and Water, Australian Government. This work is also partly supported by the National Natural Science Foundation of China (No. 62306223), the China Postdoctoral Science Foundation (No. 2024M752533), the Young Talent Fund of Xi’an Association for Science and Technology (No. 959202413053), the Fundamental Research Funds for the Central Universities (No. XJSJ24020), and the Xiaomi Young Talents Program.References
- T. Fuyuki, H. Kondo, T. Yamazaki, Y. Takahashi and Y. Uraoka, Appl. Phys. Lett., 2005, 86, 262108 CrossRef.
- M. Köntges, S. Kurtz, C. E. Packard, U. Jahn, K. A. Berger, K. Kato, T. Friesen, H. Liu, M. Van Iseghem, J. Wohlgemuth, et al., Review of failures of photovoltaic modules, IEA International Energy Agency, https://iea-pvps.org/wp-content/uploads/2020/01/IEA-PVPS_T13-01_2014_Review_of_Failures_of_Photovoltaic_Modules_Final.pdf, 2014.
- G. Pang, C. Shen, L. Cao and A. V. D. Hengel, ACM Comput. Surv., 2021, 54, 1–38 CrossRef.
- B. Su, Z. Zhou and H. Chen, IEEE Trans. Industr. Inform., 2023, 19, 404–413 Search PubMed.
- B. Su, H. Chen, P. Chen, G. Bian, K. Liu and W. Liu, IEEE Trans. Industr. Inform., 2021, 17, 4084–4095 Search PubMed.
- S. Spataru, P. Hacke and D. Sera, 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), 2016, pp. 1602–1607.
- H. Chen, H. Zhao, D. Han and K. Liu, Opt. Lasers Eng., 2019, 118, 22–33 CrossRef.
- J. Balzategui, L. Eciolaza, N. Arana-Arexolaleiba, J. Altube, J.-P. Aguerre, I. Legarda-Ereno and A. Apraiz, 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), 2019, pp. 529–535.
- H. Munawer Al-Otum, Sol. Energy, 2024, 278, 112803 CrossRef.
- F. Demir, IEEE Access, 2025, 13, 58481–58495 Search PubMed.
- A. Bartler, L. Mauch, B. Yang, M. Reuter and L. Stoicescu, 2018 26th European Signal Processing Conference (EUSIPCO), 2018, pp. 2035–2039.
- H. Yousif and Z. Al-Milaji, Sol. Energy, 2024, 267, 112207 CrossRef.
- J. Zhang, X. Chen, H. Wei and K. Zhang, Appl. Energy, 2024, 355, 122184 CrossRef.
- J. Wu, E. Chan, R. Yadav, H. Gopalakrishna and G. TamizhMani, New Concepts in Solar and Thermal Radiation Conversion and Reliability, 2018, p. 1075915 Search PubMed.
- M. Dhimish and Y. Hu, Sci. Rep., 2022, 12, 12168 CrossRef CAS PubMed.
- D.-M. Tsai and J.-Y. Luo, IEEE Trans. Industr. Inform., 2011, 7, 125–135 Search PubMed.
- Y. Li, C. He, Y. Lyu, G. Song and B. Wu, NDT&E Int., 2019, 102, 129–136 CrossRef CAS.
- C. Mantel, S. Spataru, H. Parikh, D. Sera, G. A. D. R. Benatto, N. Riedel, S. Thorsteinsson, P. B. Poulsen and S. Forchhammer, 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), 2018, pp. 0433–0437.
- E. Sovetkin and A. Steland, Integr. Comput.-Aided Eng., 2019, 26, 123–137 Search PubMed.
- M. Sun, S. Lv, X. Zhao, R. Li, W. Zhang and X. Zhang, Defect Detection of Photovoltaic Modules Based on Convolutional Neural Network, Springer International Publishing, 2018, pp. 122–132 Search PubMed.
- X. Zhang, Y. Hao, H. Shangguan, P. Zhang and A. Wang, Infrared Phys. Technol., 2020, 108, 103334 CrossRef CAS.
- M. Mayr, M. Hoffmann, A. Maier and V. Christlein, 2019 IEEE International Conference on Image Processing (ICIP), 2019.
- Y. Guo, Y. Liu, T. Georgiou and M. S. Lew, Int. J. multimed. Inf. Retr., 2018, 7, 87–93 CrossRef.
- X. Zhao, C. Song, H. Zhang, X. Sun and J. Zhao, Energy, 2023, 267, 126605 CrossRef.
- J. Wang, L. Bi, P. Sun, X. Jiao, X. Ma, X. Lei and Y. Luo, Sensors, 2022, 23, 297 CrossRef PubMed.
- A. Ahmad, Y. Jin, C. Zhu, I. Javed, A. Maqsood and M. W. Akram, IET Renew. Power Gen., 2020, 14, 2693–2702 CrossRef.
- A. M. Karimi, J. S. Fada, J. Liu, J. L. Braid, M. Koyuturk and R. H. French, 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), 2018, pp. 0418–0424.
- S. Deitsch, V. Christlein, S. Berger, C. Buerhop-Lutz, A. Maier, F. Gallwitz and C. Riess, Sol. Energy, 2019, 185, 455–468 CrossRef.
- M. Demirci, N. Besli and A. Gümüşçü, Defective PV Cell Detection Using Deep Transfer Learning and EL Imaging, International Conference on Data Science, Machine Learning and Statistics - 2019 (DMS-2019), Van Yuzuncu Yil University, 2019 Search PubMed.
- A. M. Karimi, J. S. Fada, M. A. Hossain, S. Yang, T. J. Peshek, J. L. Braid and R. H. French, IEEE J. Photovolt., 2019, 9, 1324–1335 Search PubMed.
- W. Tang, Q. Yang and W. Yan, 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), 2019, pp. 1–5.
- W. Tang, Q. Yang, K. Xiong and W. Yan, Sol. Energy, 2020, 201, 453–460 CrossRef.
- M. Y. Demirci, N. Beşli and A. Gümüşçü, Expert Syst. Appl., 2021, 175, 114810 CrossRef.
- C. Ge, Z. Liu, L. Fang, H. Ling, A. Zhang and C. Yin, IEEE Trans. Parallel Distrib. Syst., 2021, 32, 1653–1664 Search PubMed.
- C. Huang, Z. Zhang and L. Wang, IEEE J. Photovolt., 2022, 12, 1550–1558 Search PubMed.
- X. Chen, T. Karin and A. Jain, Sol. Energy, 2022, 242, 20–29 CrossRef CAS.
- C. Mantel, F. Villebro, G. Alves Dos Reis Benatto, H. Rajesh Parikh, S. Wendlandt, K. Hossain, P. B. Poulsen, S. Spataru, D. Séra and S. Forchhammer, Appl. Mach. Learn., 2019, 1 Search PubMed.
- Y. Zhao, K. Zhan, Z. Wang and W. Shen, Prog. Photovoltaics Res. Appl., 2021, 29, 471–484 CrossRef.
- U. Otamendi, I. Martinez, M. Quartulli, I. G. Olaizola, E. Viles and W. Cambarau, Sol. Energy, 2021, 220, 914–926 CrossRef.
- A. Korovin, A. Vasilyev, F. Egorov, D. Saykin, E. Terukov, I. Shakhray, L. Zhukov and S. Budennyy, arXiv, 2022, preprint, arXiv:2208.05994 DOI:10.48550/arXiv.2208.05994.
- J. Fioresi, D. J. Colvin, R. Frota, R. Gupta, M. Li, H. P. Seigneur, S. Vyas, S. Oliveira, M. Shah and K. O. Davis, IEEE J. Photovolt., 2022, 12, 53–61 Search PubMed.
- C. Shou, L. Hong, W. Ding, Q. Shen, W. Zhou, Y. Jiang and C. Zhao, 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), 2020, pp. 312–317.
- M. R. U. Rahman and H. Chen, IEEE Access, 2020, 8, 40547–40558 Search PubMed.
- L. Pratt, D. Govender and R. Klein, Renewable Energy, 2021, 178, 1211–1222 CrossRef CAS.
- E. Sovetkin, E. J. Achterberg, T. Weber and B. E. Pieters, IEEE J. Photovolt., 2021, 11, 444–452 Search PubMed.
- L. Pratt, J. Mattheus and R. Klein, Syst. Soft Comput., 2023, 5, 200048 CrossRef.
- B. Yang, Z. Zhang and J. Ma, IEEE Sens. J., 2025, 25, 891–903 Search PubMed.
- R. Duan, Y. Wang, X. Chen and S. Li, Energy, 2025, 331, 136711 CrossRef.
- O. Ronneberger, P. Fischer and T. Brox, in U-Net: Convolutional Networks for Biomedical Image Segmentation, Springer International Publishing, 2015, pp. 234–241 Search PubMed.
- M. Burgin, Super-recursive algorithms, Springer Science & Business Media, 2006 Search PubMed.
- su binyi, Photovoltaic cell anomaly detection, https://kaggle.com/competitions/pvelad, 2022, Kaggle.
- D. Gong, L. Liu, V. Le, B. Saha, M. R. Mansour, S. Venkatesh and A. v d Hengel, IEEE Int. Conf. Comput. Vis. Workshops, 2019, 1705–1714 Search PubMed.
- P. Bergmann, K. Batzner, M. Fauser, D. Sattlegger and C. Steger, Int. J. Conf. Violence, 2022, 130, 947–969 Search PubMed.
- D. P. Kingma and M. Welling, et al., Foundations and Trends in Machine Learning, 2019, vol. 12, pp. 307–392 Search PubMed.
- P. Bergmann, S. Löwe, M. Fauser, D. Sattlegger and C. Steger, arXiv, 2018, preprint, arXiv:1807.02011 DOI:10.48550/arXiv.1807.02011.
- V. Zavrtanik, M. Kristan and D. Skocaj, Int. J. Conf. Violence, 2021, 8330–8339 Search PubMed.
- N.-C. Ristea, N. Madan, R. T. Ionescu, K. Nasrollahi, F. S. Khan, T. B. Moeslund and M. Shah, CVPR, 2022, 13576–13586 Search PubMed.
- S. Ji, W. Xu, M. Yang and K. Yu, IEEE Trans. Pattern Anal. Mach. Intell., 2012, 35, 221–231 Search PubMed.
- J. A. Hanley and B. J. McNeil, Radiology, 1983, 148, 839–843 CrossRef CAS PubMed.
- P. Bergmann, M. Fauser, D. Sattlegger and C. Steger, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 9592–9600.
- K. Roth, L. Pemula, J. Zepeda, B. Schölkopf, T. Brox and P. Gehler, Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2022, pp. 14318–14328.
- T. Liu, B. Li, Z. Zhao, X. Du, B. Jiang and L. Geng, arXiv, 2022, preprint, arXiv:2210.14485 DOI:10.48550/arXiv.2210.14485.
- V. Zavrtanik, M. Kristan and D. Skočaj, Proceedings of the IEEE/CVF international conference on computer vision, 2021, pp. 8330–8339.
Footnote |
| † Y. Lin, P. Sun and R. Wu contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |