Open Access Article
Open Access ArticleTransfer from lithium to sodium: promoting battery lifetime prognosis application
Jiahao
He
a,
Jiawei
Xiang
bd,
Shulei
Chou
 *ac,
Xin
Tan
*ac,
Xin
Tan
 *ac and
Dongzhen
Lyu
*bd
*ac and
Dongzhen
Lyu
*bd
aInstitute for Carbon Neutralization Technology, College of Chemistry and Materials Engineering, Wenzhou University, Wenzhou, Zhejiang 325035, China. E-mail: xintan@wzu.edu.cn; chou@wzu.edu.cn
bCollege of Mechanical and Electrical Engineering, Wenzhou University, Wenzhou, 325035, China. E-mail: lvdongzhen@yeah.net
cWenzhou Key Laboratory of Sodium-ion Batteries, Wenzhou University Technology Innovation Institute for Carbon Neutralization, Wenzhou, Zhejiang 325035, China
dZhejiang Key Laboratory of Equipment Monitoring and Intelligent Operation & Maintenance under Extreme Working Conditions, Wenzhou, Zhejiang 325035, China
First published on 17th November 2025
Abstract
Lithium-ion batteries (LIBs) have achieved substantial progress; however, the limited availability of lithium resources poses a significant challenge to their continued scalability. Sodium-ion batteries (SIBs) offer a promising, cost-effective alternative, yet their widespread adoption is hindered by limited research—particularly in performance degradation and health management. This knowledge gap reinforces a development bottleneck, in contrast to the extensive diagnostic and prognostic studies available for LIBs. To address this, we constructed a comprehensive SIB cycling lifedataset and propose a transfer learning-based prognostic framework. Our approach utilizes knowledge from LIBs to speed up prognostics development for SIBs, while enhancing modeling flexibility and prediction accuracy. Central to this method is a Dual-Dynamic Mode Decomposition (Dual-DMD) model that captures both shared degradation behaviors and battery-specific deviations. By extracting universal features from LIB data and modeling SIB-specific characteristics, effective knowledge transfer is achieved. An online transfer factor optimization mechanism further mitigates distributional discrepancies between LIBs and SIBs. Degradation trajectories are then predicted using an adaptive unscented Kalman filter (AUKF). The proposed Dual-DMD framework achieves high predictive accuracy, with average mean absolute percentage error (MAPE), mean absolute error (MAE), and root mean square error (RMSE) values of 3.73%, 4.6%, and 5.2%, respectively, across all SIB test samples.
Broader contextThe global shift toward sustainable energy demands efficient and safe storage solutions. Lithium-ion batteries (LIBs) are dominant due to their high energy density but face sustainability and safety challenges. Sodium-ion batteries (SIBs) offer a safer, resource-abundant alternative but currently lack comprehensive lifetime prediction methods. This research employs advanced transfer learning techniques, leveraging established LIB datasets to overcome data scarcity in SIBs. The proposed Dual-DMD model significantly improves accuracy and reliability in predicting SIB lifespans, contributing toward safer, sustainable, and cost-effective energy storage solutions. |
1. Introduction
Owing to LIBs’ excellent energy density, long cycle life, and versatile application potential, they have seen widespread adoption in areas including new energy vehicles, large-scale energy storage, and consumer electronic devices.1–6 As battery-powered transportation rapidly develops and the need for high-capacity energy storage continues to grow, LIBs have become a foundational technology driving the global shift toward sustainable energy. However, the raw materials required for LIBs—such as lithium, cobalt, and other critical minerals—are facing growing scarcity driven by surging demand.7–10 This resource constraint, coupled with environmental concerns associated with mineral extraction, raises questions about the long-term sustainability of lithium-ion battery technology.11,12 Moreover, LIBs are prone to safety risks, including thermal runaway under conditions such as overcharging, short-circuiting, or elevated temperatures, posing significant safety and environmental hazards.13,14 In light of these challenges, SIBs have garnered growing attention as a promising alternative to LIBs.Sodium, owing to its abundance and electrochemical similarity to lithium, represents a viable solution for future energy storage technologies.15 While LIBs are well known for delivering excellent energy performance, typically around 95%, SIBs exhibit a slightly lower efficiency of approximately 90%.16,17 Despite this modest efficiency gap, SIBs offer significant advantages, particularly in terms of thermal and operational safety. Compared to their lithium-based counterparts, SIBs are less prone to thermal runaway and related safety hazards, making them a safer and more stable choice for specific applications.18 Consequently, SIBs are increasingly regarded as an ideal solution for energy storage systems, especially in renewable energy applications and low-speed electric vehicles, where safety, cost-effectiveness, and resource sustainability are critical concerns. However, the long-term performance of SIBs is subject to degradation, leading to capacity fading and efficiency loss over time.19 Therefore, accurate prediction of their remaining useful life (RUL) is essential to prevent unexpected failures and minimize equipment damage.20
Estimating RUL has become a critical research focus within the field of battery technology,21,22 as accurate RUL estimation is essential for improving the performance, safety, and lifespan of batteries. RUL prediction methods are mainly classified into two types of approaches: physics-based models and data-driven methods.23,24 However, existing research efforts in both categories have predominantly focused on LIBs, with few studies addressing batteries with other chemistry, such as SIBs. The physics model-based approach provides a more intuitive prediction method by modeling the electrochemical reactions and degradation mechanisms of batteries; however, this approach often struggles to capture the nonlinear degradation behavior under complex, real-world conditions.25,26 In contrast, machine learning and deep learning techniques within data-driven approaches have achieved significant advancements in the past few years. They improve the accuracy of predictions by extracting degradation trends from extensive historical data.27,28 Algorithms based on machine learning—including support vector machines (SVM), random forests (RF), and decision trees (DT)—have demonstrated strong predictive performance across various applications, effectively capturing the nonlinear and complex characteristics of battery degradation processes.29,30 Meanwhile, deep learning approaches like convolutional neural networks (CNNs) and long short-term memory (LSTM) models, with their powerful feature extraction and modeling capabilities, have shown considerable advantages, especially when handling high-dimensional and sequential data.31,32 These methods enable more accurate modeling of complex degradation mechanisms through automated feature extraction and are extensively utilized across fields such as electric mobility and large-scale energy storage systems. However, it is important to note that most existing RUL prediction research has focused on LIBs underpinned by a wealth of publicly available datasets and extensive experimental validation. In contrast, the RUL prediction of SIBs remains largely unexplored, with systematic and dedicated studies still lacking. This research gap is primarily due to the relatively recent emergence of sodium-ion battery technology and the absence of long-term, large-scale degradation datasets under diverse operational scenarios. Given the similarities in electrochemical principles and degradation mechanisms between LIBs and SIBs, leveraging the well-established knowledge, methodologies, and predictive models developed for LIBs offers a compelling pathway to advance RUL prediction for SIBs.33,34 Such cross-domain transfer of knowledge can effectively address current challenges posed by limited sodium-ion battery datasets and modeling frameworks, thereby enhancing the accuracy, robustness, and generalization capability of RUL prediction models for SIBs.
We propose an innovative transfer-driven prediction approach, termed Dual-DMD, which integrates shared dynamic mode extraction with differential trajectory modeling, building upon state-of-the-art RUL prediction techniques developed for LIBs.35 The experimental analysis utilized 8 degradation datasets of LIBs and 7 degradation datasets of SIBs. The lithium-ion battery data and the sodium-ion battery data were obtained from cycling life tests, and SIBs were assembled using synthesized electrode materials. First, a time-delay (TD) module is embedded into dynamic mode decomposition (DMD) to extract the dynamic features of lithium battery degradation data. Based on these features, a differential modeling structure is constructed to capture the deviation between a reference lithium trajectory and the target sodium-ion battery. The resulting prediction model is then combined with an adaptive Kalman filter to estimate the degradation trend of the sodium-ion battery.
The main contributions of this study are summarized as follows:
1. A transfer learning approach that leverages rich LIB knowledge to accelerate prognostics application development for SIBs, enhancing modeling flexibility and improving prediction accuracy, is proposed.
2. A Dual-DMD framework is developed to separate shared degradation patterns from LIBs and SIB-specific variations, enabling efficient and interpretable cross-domain modeling.
3. A time-delay embedding mechanism is integrated to enhance the modeling of temporal dependencies and nonlinear degradation behavior within the Dual-DMD process.
4. An adaptive transfer factor strategy is proposed to reduce distribution gaps between LIB and SIB data, improving model robustness and prediction accuracy.
5. The integration of the Dual-DMD model with an adaptive unscented Kalman filter allows for accurate, real-time prognostics of SIB degradation trajectories.
By leveraging extensive LIB datasets to compensate for the limited availability of SIB data, our approach significantly improves the accuracy and generalization of remaining useful life predictions for sodium-ion batteries. This work thus offers a scalable and practical solution to advance health management in emerging sodium-ion battery technologies.
The remainder of this paper is organized as follows: Section 2 details the lithium-ion and sodium-ion battery datasets employed in this work and discusses the differences between capacity degradation in lithium-ion and sodium-ion batteries. Section 3 introduces the overall research methodology, including the proposed Dual-DMD and adaptive unscented Kalman filter-based transfer-driven prediction method, which establishes a high-precision cross-battery-type lifetime prediction approach. Section 4 comprehensively evaluates and discusses the performance of the proposed transfer-based prediction approach. Section 5 concludes the paper and provides perspectives for future research.
2. Description of experimental data
The lithium-ion and sodium-ion battery datasets utilized in this study are detailed below. The lithium-ion battery consists of cells with ternary lithium (NCM) cathodes, graphite anodes, and a polymer electrolyte. We employed eight lithium iron pouch cells (see Fig. S3), each with a nominal capacity of 0.8 Ah and a nominal voltage of 3.7 V. The battery was charged at a constant current of 1 C until the voltage reached 4.2 V and was held constant at 4.2 V. Charging was continued until the current dropped to 0.25 C, preventing overcharging. During discharge, the system applied a constant 1 C current until the voltage dropped to 2.7 V. Here, “C” denotes the current rate relative to the battery's nominal capacity. For instance, 1 C corresponds to a current of 0.8 A for a 0.8 Ah lithium-ion battery. The nominal configuration of each lithium-ion battery is shown in Fig. 1a, and details of the battery degradation testing platform are provided in Fig. S2. The lithium-ion battery dataset was selected as the source domain primarily because its degradation features are representative, the dataset size is moderate, and it contains enough lithium-ion samples to ensure effective transfer learning. | ||
| Fig. 1 Voltage and current responses during cycling: (a) lithium-ion batteries and (b) sodium-ion batteries. | ||
The target domain is a sodium-ion battery dataset (see Fig. S4). Such a cross-domain design facilitates assessment of the model's generalization capability and prediction accuracy. We constructed seven sodium-ion battery half-cells using an iron–manganese Prussian blue analogue as the cathode, hard carbon as the anode, and an electrolyte composed of 1 M NaClO4 in propylene carbonate with 1% vinylene carbonate (VC). Detailed morphological and structural characterization studies of the iron–manganese Prussian blue cathode material—including scanning electron microscopy (see Fig. S5), X-ray diffraction (see Fig. S6), thermogravimetric (see Fig. S7), and Fourier-transform infrared spectroscopy (see Fig. S8) analyses—were performed. The synthesis procedures, material characteristics, and electrochemical performance of these components have been thoroughly described in previous studies.36 Specifically, Prussian blue was synthesized via the co-precipitation method, and hard carbon was produced through high-temperature pyrolysis. Button cell assembly was carried out in a glove box under an argon atmosphere.37 After assembly, the sodium-ion battery half-cells were rested for 10 hours in a constant-temperature chamber to ensure full electrolyte infiltration. Then, we performed the charge/discharge test using a Neware CT-4008 Battery Test System. Charging was carried out at 0.5 C between 2.0 and 4.0 V, while discharging was performed at 1 C (1 C = 100 mAh g−1). The nominal configuration of each sodium-ion battery is shown in Fig. 1b, and details of the battery degradation testing platform are provided in Fig. S1. Specifications for the two battery types are provided in Table S1.
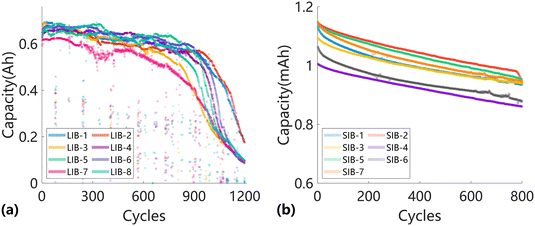
Fig. 2 presents the degradation trajectories of the eight LIBs and seven SIBs. Fig. 2a shows the capacity degradation curves of the lithium-ion batteries, with cycle lives of approximately 1200 cycles. The discrete outliers in the figure correspond to periodic checkpoints set by Lyu et al. In the early stages of cycling, the battery degradation trajectory follows a slow decline. Around the 900th cycle, the degradation rate becomes roughly linear, and subsequently, the degradation rate begins to accelerate. When the capacity degradation reaches around 1100 cycles, the rate of decline slows again. Overall, the battery's degradation rate exhibits an inverted S-shape. This dataset comes from the world's largest, longest-running, and most systematic battery performance degradation experiment.
The sodium-ion batteries in Fig. 2b exhibit nearly identical capacity degradation trends, due to the consistent materials, manufacturing processes, and testing protocols, all of which are from the same batch. The cycle lives of these batteries are approximately 1100 cycles, and we selected the first 800 cycles as the effective lifespan for analysis in the experiment. Lithium-ion and sodium-ion batteries have different capacity sizes: LIBs are usually measured in ampere-hours (Ah), while SIBs are measured in milliampere-hours (mAh). Moreover, LIBs are generally pouch-type cells, while SIBs are coin-type cells, leading to differences in capacity scale, thermal properties, and mechanical behavior. These disparities in unit scale, form factor, and cycling characteristics introduce variations in data scale and degradation distribution, which motivate the use of a transfer-driven modeling strategy capable of bridging such cross-domain inconsistencies. Importantly, the distinct structural and electrochemical characteristics between LIBs and SIBs provide a meaningful opportunity to rigorously evaluate the transferability of the proposed Dual-DMD framework. The successful knowledge transfer from pouch-type LIBs to coin-type SIBs thus serves as strong evidence of the model's capability to generalize across different chemistries and cell architectures, highlighting the robustness of the proposed cross-domain approach.
3. Research methods
3.1. Overview of the Dual-DMD prediction framework
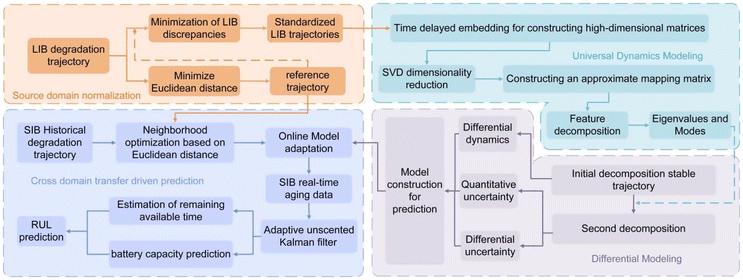
The proposed Dual-DMD framework aims to provide precise remaining useful life forecasts across multiple battery types with varying characteristics. The framework integrates two complementary modeling strategies: time-delay embedded dynamic mode decomposition (TD-DMD) and adaptive differential modeling decomposition (ADMD).27 Unlike traditional ensemble schemes that combine multiple model outputs through statistical weighting, the “linear combination” in Dual-DMD occurs within the dynamic state-evolution formulation. TD-DMD is employed to extract dominant and transferable degradation dynamics from time-series data, capturing universal patterns shared across different battery types as global features. In parallel, ADMD constructs a flexible differential modeling structure between a selected reference trajectory and each target trajectory, enabling the model to adaptively capture battery-specific degradation variations. The two modules are coupled inside the evolution equation rather than at the output level, forming a unified dynamics decomposition and reconstruction mechanism. The integration of these two modules forms the core of the Dual-DMD framework: TD-DMD ensures global generalization, while ADMD introduces localized adaptability. By anchoring the differential modeling process to TD-DMD-derived modes, the framework maintains consistency with fundamental degradation trends while accommodating inter-battery variability.Fig. 3 illustrates the proposed Dual-DMD framework, which consists of four main modules: normalization of source domain degradation trajectories; extraction of shared degradation features via TD-DMD; differential modeling for individualized adaptation; and cross-domain prediction through model fusion. Each module is described in detail in the following sections.
3.2. Source domain degradation normalization
Substantial variations are observed among the degradation trajectories of LIBs, as illustrated in Fig. 2a. To address this, we first use Euclidean distance to measure the similarity between all degraded trajectories in LIBs, and the degraded trajectory with the smallest cumulative deviation from other trajectories is selected as the reference trajectory (see Table S2 for symbols, acronyms, and definitions). For any two-dimensional coordinates (t1, z1) and (t2, z2), the Euclidean distance between the two is: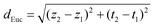 | (1) |
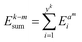 | (2) |
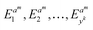 . The value
. The value 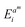 indicates the difference between the kth and mth LIB trajectories. It is the smallest Euclidean distance between the ith point
indicates the difference between the kth and mth LIB trajectories. It is the smallest Euclidean distance between the ith point 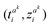 in the kth lithium-ion battery trajectory and all the points in the mth lithium-ion battery trajectory. After calculating the total Euclidean distance difference between any lithium-ion battery and the other lithium-ion battery, the reference trajectory Treref is selected from the lithium-ion battery domain. Compared to any other degradation trajectory of LIBs, the reference trajectory Treref has the smallest sum of total Euclidean distances with all other degradation trajectories.
in the kth lithium-ion battery trajectory and all the points in the mth lithium-ion battery trajectory. After calculating the total Euclidean distance difference between any lithium-ion battery and the other lithium-ion battery, the reference trajectory Treref is selected from the lithium-ion battery domain. Compared to any other degradation trajectory of LIBs, the reference trajectory Treref has the smallest sum of total Euclidean distances with all other degradation trajectories.
For each non-reference lithium-ion battery other than the reference degradation trajectory battery, a normalization coefficient Nr is sequentially set to normalize the rth non-reference lithium-ion battery. Normalization aims to minimize the Euclidean distance between each non-reference lithium-ion battery and the reference degradation trajectory battery. Taking the non-reference lithium-ion battery TreLi-r as an example, its normalized degradation data are:
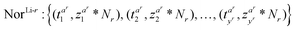 | (3) |
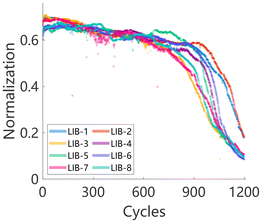
Fig. 4 presents the degradation curves of all LIBs after normalization based on their Euclidean distance similarity. Compared with Fig. 2a, the inter-cell differences are significantly reduced.
3.3. Universal feature extraction via TD-DMD
DMD is a widely used data-driven technique for analyzing the spatiotemporal evolution of dynamic systems.38 It decomposes sequential measurements into a set of characteristic modes, each associated with a specific temporal behavior defined by eigenvalues. Despite its success in approximating complex dynamics, standard DMD assumes linearity and requires full-state measurements, which limits its effectiveness in handling localized, nonlinear degradation in battery systems.39To overcome these limitations, we adopt TD-DMD,40 which enhances the dynamic observability of time-series data by constructing high-dimensional delay-coordinate matrices. This enables the model to extract dominant degradation patterns from partial measurements and improves prediction performance in low-frequency or local sampling scenarios.
TD-DMD is used to extract the main dynamic modes of battery degradation processes in the lithium-ion battery domain. Through the construction of a time-delay matrix, singular value decomposition (SVD), eigenvalue calculation, and mode selection, the main dynamic features of battery degradation trajectories are analyzed. The following is the detailed TD-DMD calculation process.
To effectively get the temporal dynamic characteristics of lithium-ion battery degradation, we construct a time delay matrix and convert the time series data into a high-dimensional embedding matrix, enabling the DMD method to identify the dynamic patterns of battery degradation. We use Z = [Z1, Z2, …, Zm]to represent any one of the battery degradation trajectories, where Zt represents the capacity of the lithium-ion battery in the tth cycle. m is the number of cycles. We construct delay matrices Y1 and Y2,
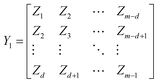 | (4) |
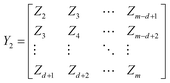 | (5) |
To reduce dimensionality and remove noise, we performed singular value decomposition on the time delay matrix Y1:
| Y1 = OVMT | (6) |
The optimal linear operator A establishes the relationship between the two data matrices as follows:
| Y2 = AY1 | (7) |
So, matrix A can be expressed by
| A = Y2MV−1OT | (8) |
A low-dimensional representation of A is obtained by retaining the first r modes from matrices O, M, and V. Then, A, Y1, and Y2 are projected onto the first r POD modes extracted from Y1,
| Ar = OTrYt−d+12MrVr−1 | (9) |
To perform dimensionality reduction, we select r as a truncation number. The eigen-decomposition of matrix Ar is defined as follows:
| Ar = GΛG−1 | (10) |
| ϕ = OG | (11) |
Then, the system state at any given time can be expressed as
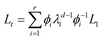 | (12) |
This formulation defines the DMD method in its discrete form, which can be represented as
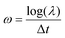 | (13) |
3.4. Individual degradation modeling via ADMD
The ADMD method is designed to capture the individual degradation dynamics of batteries by modeling the deviations between a reference trajectory and the target trajectory. The ADMD process consists of two key stages: first-stage decomposition and second-stage decomposition. The first-stage decomposition focuses on assessing uniform uncertainty in measurements and plays a key role in stabilizing the degradation trend, while the second-stage decomposition focuses on refining the model by capturing the nonlinear dynamic behavior of individual battery cells.The first-stage decomposition involves utilizing Euclidean distance-based normalization of the degradation trajectories of LIBs. This normalization reduces the variation among the degradation trajectories across different batteries, although significant fluctuations and noise may still exist in the data. To mitigate this, a smoothing spline is used to eliminate the measurement noise, leading to stabilized degradation trajectories. The relationship between the original degradation trajectory pt, the normalized trajectory Lt, and the measurement noise ut is expressed as:
| pt = Lt + ut | (14) |
The second-stage decomposition further refines the model by addressing the nonlinear dynamics and temporal relationships between the degradation states of the battery. The second-stage decomposition utilizes the differential dynamics between the target and reference trajectories, thereby offering a more reliable basis for precise prediction. The dynamic correlation between two consecutive degradation states can be expressed as:
| Lt+1 − Lt = f′(Lt, t) + ωt | (15) |
3.5. Fusion of universal and individual dynamics for RUL prediction
To achieve accurate and adaptable remaining useful life prediction across heterogeneous battery types, we propose a unified prediction formulation by integrating the global degradation dynamics extracted by TD-DMD with the individual degradation variations modeled by ADMD. Specifically, the predicted degradation state at time t + 1 is expressed as a combination of a shared dynamic component and an individual deviation component:| Lt+1 = fTD-DMD(Lt) + ΔfADMD(Lt) | (16) |
Dual-DMD fuses the TD-DMD and ADMD modules through a dynamics-level combination rather than output aggregation. The first term fTD-DMD(Lt) captures the dominant temporal degradation trends shared among batteries in the lithium-ion battery domain. Eqn (11) and (13) are used to realize the reconstruction, which is based on time-delay embedding and dynamic mode decomposition:
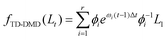 | (17) |
The second term ΔfADMD(Lt) characterizes the individual-specific degradation dynamics of the target battery by modeling the deviation from the reference trajectory. Such a dynamics-based coupling enables the model to maintain cross-system generality while capturing system-specific nonlinearities through the differential term, in contrast to conventional ensembles that combine outputs post hoc. It is formulated as a nonlinear differential model:
| ΔfADMD(Lt) = f′(Lt, t) + ωt. | (18) |
Moreover, the Dual-DMD framework leverages the global modal structure extracted from the entire LIB dataset rather than relying on a single reference trajectory. The reference trajectory only serves as a temporal alignment baseline for differential modeling, ensuring consistent performance across different selections within the same dataset. Localized irregularities in the reference data are effectively mitigated through the differential dynamics and adaptive filtering mechanisms.
3.6. Prediction of cross-battery type migration
Using the reference path taken from LIBs, where all data are available, we get the following form:
| Treref: {(tref1, zref1)(tref2, zref2), …, (trefm, zrefm)} | (19) |
The degradation trajectory of SIBs is represented as:
| Trepac,1:n = (tpac1, zpac1)(tpac2, zpac2), …, (tpacn, zpacn) | (20) |
We utilized a scale factor to normalize the degraded trajectory in the target domain, thereby reducing its deviation from the reference trajectory, and constructed a scale domain difference index:
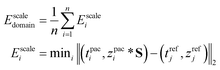 | (21) |
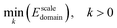 | (22) |
In order to solve this problem, we introduce the Lagrange function:
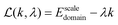 | (23) |
By calculating the first and second derivatives, 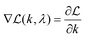 and
and 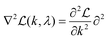 , we use Newton's method to iteratively update k:
, we use Newton's method to iteratively update k:
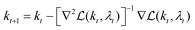 | (24) |
After obtaining a new target domain data point, this process can be executed once to dynamically adjust the transfer factor ki. Finally, the updated ki is applied to the capacity value of the target trajectory:
| yi = kt·yi | (25) |
The adjusted target trajectory will be used as input for the Dual-DMD model to enhance the precision and stability of cross-domain prediction.
The state update equation of the target domain sodium ion battery is defined as follows:
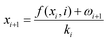 | (26) |
At each moment t, 2n + 1 sigma points are generated using the current state mean ut−1 and covariance matrix Pt−1:
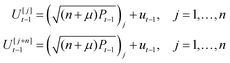 | (27) |
Within the UKF process, the battery status and covariance are updated over time. A single-step estimation of the system state ût and its corresponding covariance Pt is obtained based on the propagated sigma points.
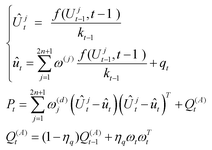 | (28) |
By recursively applying state transition functions, it is possible to predict the state distribution at any future time:
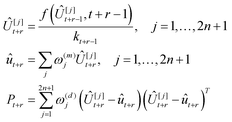 | (29) |
4. Results and discussion
This section aims to show a comprehensive evaluation of the proposed transfer-based prediction method. By extracting both intuitive and detailed degradation features from the lithium-ion battery domain, this approach seeks to ensure accurate and reliable predictions in the target domain. Specifically, the degradation data of lithium batteries are used as the source domain, while the degradation data of sodium batteries serve as the target domain. For this study, a Dual-DMD model is constructed and trained using the degradation data from eight lithium battery cells. Subsequently, this model is employed to predict the degradation processes of seven sodium battery cells, and the prediction results are thoroughly evaluated and discussed.The prediction performance of battery capacity degradation is quantitatively assessed using four commonly adopted metrics: absolute percentage error (PE), MAE, RMSE, and MAPE, which are defined as follows:
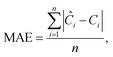 | (30) |
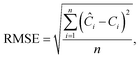 | (31) |
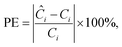 | (32) |
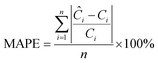 | (33) |
4.1. RUL prediction results of sodium ion batteries
The proposed method for predicting the capacity aging trajectory is iterative, wherein the model is progressively refined through continuous updates of actual lifespan data and sodium-ion battery characteristics. This iterative process optimizes the prediction outcomes and gradually approaches the battery's actual degradation behavior.Fig. 6 illustrates the predicted capacity degradation trajectories for SIBs 1 through 7, all of which rely on offline training data from the eight LIBs. The yellow line represents the actual measured cycle life, while the blue solid line depicts the predicted future trajectory. The light blue dotted line indicates the predicted confidence interval range, and the purple shaded area denotes the probability density function (PDF) of the battery's RUL prediction. The pink dotted line denotes the end-of-life threshold.
To ensure the general applicability of the proposed method, we evaluated its performance across different stages of battery aging. We considered three prediction starting points—namely the 100th, 450th, and 600th cycles, each starting point representing distinct stages of the battery lifecycle. The early stage (100th cycle) exhibited stable performance, while the middle stage (450th cycle) marked the onset of accelerated degradation. The late stage (600th cycle), on the other hand, highlighted a more pronounced acceleration of degradation, accompanied by an increased risk of failure. This varied selection of starting points provides a comprehensive perspective on battery degradation dynamics across different phases of their life.
In battery life prediction, the end-of-life threshold is a critical parameter, representing the point at which a battery is deemed to have reached the end of its usable life. For LIBs, the end-of-life threshold is usually set around 80% of the nominal capacity, reflecting their performance degradation due to capacity loss, internal resistance increase, and other aging factors. This threshold is a widely accepted industry standard, ensuring that batteries are replaced before their performance becomes unacceptable for most applications. In contrast, SIBs, which exhibit slower degradation rates and more stable cycling performance, have a higher end-of-life threshold, often set at 85%. This higher threshold reflects the generally more stable electrochemical behavior of SIBs, which allows them to retain a greater proportion of their capacity over time. By setting the end-of-life threshold at 85%, the prediction model accounts for the extended useful life and more gradual performance decline characteristics of SIBs, providing a more accurate estimation of their operational lifespan.
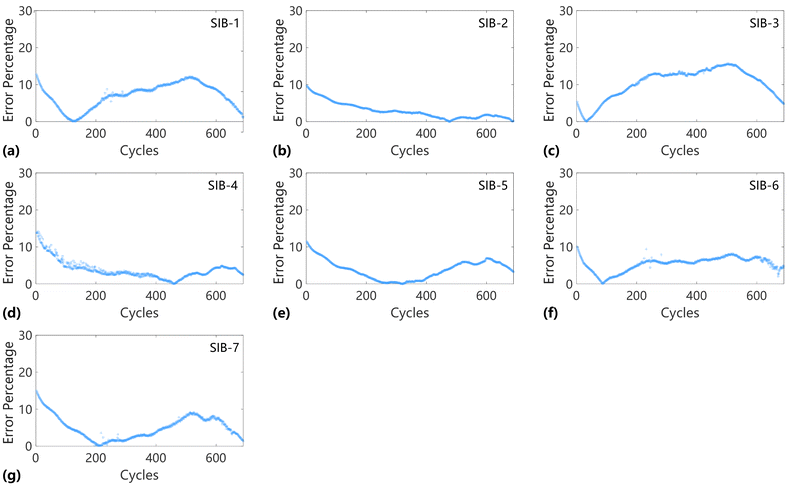
Fig. 6 presents the predicted degradation trajectories of SIBs 1–7. In this analysis, the prediction starting points are set at the 100th cycle for SIB-1, SIB-4 and SIB-6; at the 450th cycle for SIB-2 and SIB-5; and at the 600th cycle for SIB-3 and SIB-7. From a more detailed perspective, when the starting point is set at the 100th cycle, the probability density function (PDF) is narrower, and the initial predicted trajectory closely aligns with the actual degradation trajectory. Although there is a slight deviation between the 300th and 680th cycles, the method demonstrates a good short-to-medium term accuracy, indicating its applicability even with limited early data. Notably, in Fig. 6b and e, when the prediction starting point is set to the 450th cycle, the battery enters the mid-stage of degradation, where the rate of degradation begins to accelerate. At this stage, the model maintains strong predictive performance benefiting from well-formed degradation trends that align with the model's dynamic tracking capability. In contrast, Fig. 6c and g show that when the prediction starts at the 600th cycle, the degradation process becomes more unstable, resulting in a wider predicted confidence interval. This is attributed to the more obvious nonlinear dynamics and accelerated degradation occurring in the later stage of the battery life, which introduce greater uncertainty into the model's predictions. Despite this increased complexity, the model still successfully captures the overall degradation trend within an acceptable uncertainty range, demonstrating its stability under challenging conditions.
Then, to further assess the predictive performance of our method across various starting points, we present the distribution maps of percentage errors for the seven SIBs. These visualizations offer an in-depth evaluation of the method's accuracy over a range of prediction starting times. Fig. 7 illustrates the dynamic fluctuations in the absolute percentage errors observed across SIBs 1 through 7. Upon further analysis, a distinct pattern is observed: the maximum deviation between predicted and actual values remains approximately 10%, regardless of the specific characteristics of the individual batteries. The consistent error threshold observed across a range of cells highlights the underlying complexities inherent in battery prediction models. Although the variations are subtle, the 10% error margin consistently exists, emphasizing the challenges and limitations in achieving precise predictions within this field. As the prediction period extends, the prediction error initially decreases before subsequently increasing. For prediction periods up to 200 cycles, the prediction error remains below 16%. However, after 400 cycles, a significant increase in prediction error is observed, although it remains within 15%. These results demonstrate that the proposed method possesses robust long-term predictive capability, making it sufficient to provide detailed battery degradation information across various aging stages for battery management systems.
In this study, battery life is defined as the number of charge–discharge cycles until the capacity falls below 85% of its initial value, while the remaining useful life refers to the difference between the current cycle count and the total battery life. Fig. 8 illustrates the predicted RUL values for the seven SIBs. The light green line denotes the 95% confidence range, the blue dashed line denotes the actual RUL values, and the dark green solid line denotes the average RUL at each prediction starting point. As shown in the figure, the predicted RUL values closely align with the actual values. To quantitatively assess the comprehensive predictive performance of the model, several error metrics are employed, including MAPE, RMSE, and MAE. Lower metric values denote improved prediction accuracy. As depicted in Fig. 9, the proposed approach shows strong predictive performance, with average RMSE, MAPE, and MAE values of 5.28%, 3.73%, and 4.60%, respectively, over all battery samples.
Fig. 10 and 11 compare the predicted capacity trajectories of different methods at a prediction starting point of 100 cycles for the source and target domains, respectively. In the lithium-ion battery domain, almost all methods achieve excellent performance on LIB-1. However, the Long Short-Term Memory (LSTM) model performs poorly, exhibiting a larger deviation after 200 cycles. In the target domain, only the proposed Dual-DMD method demonstrates strong predictive performance. Using SIB-1 as an illustrative example in Fig. 12, the Dual-DMD method produces a predicted degradation path that not only closely matches the actual trend but also presents a confidence interval that entirely contains the random variations in the measured values. In contrast, other approaches display notable discrepancies between predicted and actual degradation paths, with prediction intervals unable to capture future degradation behavior accurately.
Fig. 12 presents the percentage errors in RUL predictions across the entire lifecycle. Among LIBs 1–8 in the lithium-ion battery domain, the performance differences between Dual-DMD, ADMD, and DMD are relatively minor, fluctuating around 8%. In the early stages of prediction, the predictive performance of FNN and ED is relatively stable. However, in the later stages, the predictive performance of FNN and ED may deteriorate, and the error may exceed 50%. The LSTM model shows unstable prediction behavior throughout the entire process, characterized by large fluctuations in the error curve. High variability in prediction results and weak performance in later cycles indicate that the two methods FNN and ED are not suitable for employment. For SIBs 1–7 in the target domain, the prediction accuracy of the differential model and ADMD has significantly deteriorated, increasing from 8% to over 30%. The predictive performance of FNN and ED for the sodium-ion batteries is also worse than that for the lithium-ion batteries. Notably, for the same dataset, our model exhibits superior estimation accuracy in the case of transition driven prediction from the lithium-ion batteries to the sodium-ion batteries. The prediction error for each sodium-ion battery is below 5.5%.
Tables 1 and 2 comprehensively compare the prediction performance of five methods across both source and target domains using MAPE, MAE, and RMSE metrics. In the lithium-ion battery domain, although several methods perform competitively, Dual-DMD consistently achieves lower error rates, demonstrating strong adaptability to lithium-ion battery degradation patterns. In the more challenging target domain involving SIBs, Dual-DMD outperforms all other methods by significant margins, especially in terms of its generalization ability under distribution shift. It yields the lowest MAPE, MAE, and RMSE values across most cases, highlighting its superiority in transfer-driven RUL prediction tasks. Specifically, Dual-DMD achieves an average MAPE of approximately 3.73%, MAE of 4.6%, and RMSE of 5.2% across all batteries, further confirming its robustness and accuracy in cross-domain scenarios.
| Battery | Dual-DMD | ADMD | DMD | ED | FNN | LSTM | |
|---|---|---|---|---|---|---|---|
| Source domain | LIB-1 | 7.14 | 8.56 | 7.08 | 9.07 | 14.65 | 17.92 |
| LIB-2 | 9.80 | 10.16 | 11.05 | 9.73 | 15.61 | 17.70 | |
| LIB-3 | 10.51 | 10.14 | 6.22 | 10.79 | 22.53 | 9.43 | |
| LIB-4 | 2.71 | 1.73 | 1.37 | 7.63 | 4.03 | 19.85 | |
| LIB-5 | 3.54 | 3.36 | 5.27 | 8.6 | 3.08 | 25.25 | |
| LIB-6 | 3.83 | 3.35 | 3.31 | 5.22 | 11.55 | 18.01 | |
| LIB-7 | 26.57 | 29.45 | 20.10 | 21.36 | 18.99 | 16.86 | |
| LIB-8 | 6.33 | 5.64 | 6.28 | 12.01 | 2.86 | 21.52 | |
| Target domain | SIB-1 | 4.67 | 22.09 | 18.32 | 39.10 | 19.43 | 39.39 |
| SIB-2 | 1.85 | 10.99 | 17.35 | 43.38 | 11.72 | 21.74 | |
| SIB-3 | 5.42 | 24.71 | 8.62 | 32.92 | 30.01 | 30.97 | |
| SIB-4 | 2.92 | 18.96 | 9.52 | 17.59 | 21.15 | 35.10 | |
| SIB-5 | 3.30 | 15.97 | 20.10 | 52.59 | 14.91 | 21.90 | |
| SIB-6 | 3.67 | 13.58 | 14.46 | 49.11 | 20.79 | 23.13 | |
| SIB-7 | 4.28 | 16.09 | 18.57 | 40.19 | 18.88 | 33.78 |
| Battery | Error (%) | Dual-DMD | ADMD | DMD | ED | FNN | LSTM | |
|---|---|---|---|---|---|---|---|---|
| Source domain | LIB-1 | MAE | 7.05 | 8.06 | 7.32 | 8.59 | 12.21 | 19.57 |
| RMSE | 7.37 | 8.56 | 7.70 | 9.57 | 12.83 | 24.10 | ||
| LIB-2 | MAE | 10.13 | 11.03 | 10.41 | 7.29 | 14.75 | 15.77 | |
| RMSE | 10.66 | 11.24 | 10.86 | 8.18 | 15.47 | 17.92 | ||
| LIB-3 | MAE | 7.77 | 6.08 | 7.26 | 4.61 | 1.91 | 13.00 | |
| RMSE | 8.25 | 6.61 | 7.77 | 5.71 | 2.32 | 16.74 | ||
| LIB-4 | MAE | 2.04 | 1.29 | 1.30 | 8.03 | 3.81 | 23.20 | |
| RMSE | 2.25 | 1.55 | 1.56 | 8.14 | 4.02 | 25.71 | ||
| LIB-5 | MAE | 4.08 | 3.12 | 2.82 | 9.66 | 2.62 | 23.66 | |
| RMSE | 4.44 | 3.52 | 3.24 | 9.98 | 2.91 | 28.14 | ||
| LIB-6 | MAE | 3.23 | 3.39 | 3.05 | 1.99 | 7.96 | 13.55 | |
| RMSE | 3.44 | 3.62 | 3.30 | 2.78 | 8.57 | 16.24 | ||
| LIB-7 | MAE | 13.95 | 14.10 | 13.34 | 9.92 | 9.97 | 18.83 | |
| RMSE | 14.97 | 15.02 | 14.34 | 10.90 | 10.60 | 23.11 | ||
| LIB-8 | MAE | 6.10 | 5.36 | 5.74 | 12.84 | 1.10 | 24.69 | |
| RMSE | 6.34 | 5.52 | 5.93 | 13.05 | 1.39 | 27.02 | ||
| Target domain | SIB-1 | MAE | 5.77 | 18.01 | 14.04 | 40.24 | 20.68 | 27.29 |
| RMSE | 6.39 | 19.43 | 16.77 | 44.35 | 22.39 | 30.29 | ||
| SIB-2 | MAE | 2.30 | 11.18 | 18.94 | 49.68 | 11.55 | 18.30 | |
| RMSE | 2.93 | 12.12 | 20.31 | 51.06 | 12.36 | 21.09 | ||
| SIB-3 | MAE | 8.74 | 21.16 | 9.37 | 33.11 | 21.61 | 29.87 | |
| RMSE | 9.44 | 23.15 | 11.81 | 37.64 | 23.39 | 33.28 | ||
| SIB-4 | MAE | 2.83 | 17.56 | 18.32 | 46.47 | 18.50 | 29.24 | |
| RMSE | 3.43 | 22.47 | 20.35 | 50.21 | 22.98 | 33.37 | ||
| SIB-5 | MAE | 3.33 | 13.31 | 17.04 | 45.06 | 15.78 | 25.97 | |
| RMSE | 4.12 | 14.25 | 19.36 | 48.59 | 16.69 | 29.37 | ||
| SIB-6 | MAE | 4.93 | 18.10 | 13.92 | 41.27 | 18.85 | 25.48 | |
| RMSE | 5.40 | 19.85 | 15.62 | 43.88 | 20.45 | 28.73 | ||
| SIB-7 | MAE | 4.31 | 14.93 | 17.25 | 44.83 | 18.18 | 24.94 | |
| RMSE | 5.19 | 16.03 | 19.90 | 48.67 | 19.86 | 27.77 |
5. Conclusions
This study has developed a new domain transfer strategy for RUL prediction of SIBs by utilizing the rich historical degradation data of LIBs. The primary contribution is the development of a Dual-DMD prediction model that achieves effective transfer from LIBs to SIBs. This model integrates TD-DMD to capture shared degradation dynamics and ADMD to characterize battery-specific degradation behaviors. An online adaptive transfer factor optimization mechanism is further introduced to reduce the distributional discrepancies between the two battery types, thereby enabling accurate and reliable prediction of sodium-ion battery degradation, even during the initial operational phase.Experimental results using degradation data from both LIBs and SIBs prove the proposed method's performance, as the average absolute percentage error for each SIB degradation trajectory remains below 3.8%. The proposed approach surpasses current methods with respect to prediction accuracy. Additionally, the method's capability to handle diverse battery types and varying operating conditions offers a significant advancement in the battery health management field. From a practical perspective, this study provides a robust framework for integrating SIBs into renewable energy systems.
However, the study is not without its limitations. The differences in cell formats (pouch full-cells vs. button half-cells) and capacity scales (Ah vs. mAh) may introduce variability in degradation mechanisms, which could affect the model's generalizability. The method relies on the availability of comprehensive degradation data from LIBs, which are not ensured to be accessible under practical operating conditions. The generalization of the model across diverse battery types and working environments has yet to be fully achieved. Additionally, the complexity of the degradation process, including non-linear behavior and varying environmental conditions, presents challenges in achieving universally high prediction accuracy. Nonetheless, these differences should not be viewed solely as limitations. In fact, the variations in chemistry, cell configuration, and capacity scale also provide a meaningful opportunity to evaluate the cross-domain transferability of the proposed Dual-DMD framework. The successful application of a LIB-trained model to predict the degradation trajectories of SIB cells demonstrates the framework's robustness and adaptability across distinct electrochemical systems. This finding underscores the potential of transfer learning strategies to bridge data gaps between mature and emerging battery technologies.
Future work should aim to broaden the dataset by adding cycling life data from sodium-ion batteries with different electrode materials and styles, thereby enhancing the model's adaptability across batteries with various chemistries, and further refining the transfer learning mechanism. Exploring the integration of uncertainty quantification techniques, such as Monte Carlo simulations, could also help in addressing the inherent uncertainty in battery lifespan predictions, thus enhancing the reliability of the proposed method in large-scale, real-world deployments.
Author contributions
Jiahao He: writing – original draft, validation, methodology, and conceptualization. Jiawei Xiang: resources and investigation. Shulei Chou: writing – review and editing, supervision, and funding acquisition. Xin Tan: writing – review and editing, supervision, and funding acquisition. Dongzhen Lyu: writing – review and editing, supervision, resources, and funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The dataset of sodium-ion batteries used in this work is available at https://github.com/lvdongzhen/Wenzhou-Sodium-ion-Battery-Degradation-Data. Proper attribution is required when using the data, citing it as "Wenzhou Sodium-ion Battery Degradation Data", and cite the source article: "Jiahao He, et al. Transfer from lithium to sodium: promoting battery lifetime prognosis application. EES Batteries, 2026". The dataset of Lithium-ion batteries used in this work is available at https://github.com/lvdongzhen/Wenzhou-Pack-Degradation-Data. Please name the data source as "Wenzhou Pack Degradation Data" and cite the source article: "Dongzhen Lyu, et al. Transfer-Driven Prognosis from Battery Cells to Packs: An Application with Adaptive Differential Model Decomposition. Applied Energy, 2025".Supplementary information (SI) includes details of the experimental setup, the testing platform, capacity degradation curves for LIBs and SIBs, material characterization data (SEM, XRD, TGA, and FTIR), and symbol definitions used in this study. See DOI: https://doi.org/10.1039/d5eb00215j.
Acknowledgements
This research was supported in part by the National Natural Science Foundation of China (Grant No. 52405126), Key Research and Development Program of Zhejiang (2024C01057), and the Zhejiang Provincial Natural Science Foundation of China (LMS26E050041).References
- X. Q. Zeng, M. Li, D. Abd El-Hady, W. Alshitari, A. S. Al-Bogami, J. Lu and K. Amine, Adv. Energy Mater., 2019, 9, 1900161 CrossRef.
- Y. L. Gao, Z. H. Pan, J. G. Sun, Z. L. Liu and J. Wang, Nano-Micro Lett., 2022, 14, 49 CrossRef.
- B. Diouf and R. Pode, Renewable Energy, 2015, 76, 375–380 CrossRef.
- D. Lyu, E. Liu, B. Zhang, E. Zio, T. Yang and J. Xiang, IEEE Trans. Syst. Man Cybern.: Syst., 2025, 55, 685–698 Search PubMed.
- D. Lyu, G. Niu, E. Liu, B. Zhang, G. Chen, T. Yang and E. Zio, Reliab. Eng. Syst. Saf., 2022, 226, 108686 CrossRef.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- E. A. Olivetti, G. Ceder, G. G. Gaustad and X. K. Fu, Joule, 2017, 1, 229–243 CrossRef.
- E. Shojaeddini, E. Alonso and N. T. Nassar, Resour., Conserv. Recycl., 2024, 207, 9 CrossRef.
- M. Dixit, B. Witherspoon, N. Muralidharan, M. M. Mench, C. B. M. Kweon, Y. K. Sun and I. Belharouak, ACS Energy Lett., 2024, 9, 3780–3789 CrossRef CAS PubMed.
- D. Lyu, G. Niu, E. Liu, T. Yang, G. Chen and B. Zhang, IEEE Trans. Ind. Electron., 2022, 69, 5235–5246 Search PubMed.
- E. S. Fan, L. Li, Z. P. Wang, J. Lin, Y. X. Huang, Y. Yao, R. J. Chen and F. Wu, Chem. Rev., 2020, 120, 7020–7063 CrossRef CAS PubMed.
- D. Lyu, G. Niu, B. Zhang, G. Chen and T. Yang, IEEE Trans. Ind. Electron., 2021, 68, 1591–1603 Search PubMed.
- S. Rana, R. Kumar and R. S. Bharj, Chem. Eng. J., 2023, 463, 29 CrossRef.
- D. Z. Lyu, B. Zhang, E. Zio and J. W. Xiang, Cell Rep. Phys. Sci., 2024, 5, 18 Search PubMed.
- Z. Xu and J. Wang, Adv. Energy Mater., 2022, 12, 33 Search PubMed.
- K. Chayambuka, G. Mulder, D. L. Danilov and P. H. L. Notten, Adv. Energy Mater., 2020, 10, 11 Search PubMed.
- P. K. Nayak, L. T. Yang, W. Brehm and P. Adelhelm, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- X. N. Guo, S. Guo, C. W. Wu, J. Y. Li, C. T. Liu and W. H. Chen, Adv. Energy Mater., 2023, 13, 19 Search PubMed.
- Y. Q. Chen, S. M. Yan, L. Chen, D. Zhao, Y. Ding, Y. B. Zeng and Z. X. Chen, Small, 2025, 21, 18 Search PubMed.
- Y. H. Che, X. S. Hu, X. K. Lin, J. Guo and R. Teodorescu, Energy Environ. Sci., 2023, 16, 338–371 RSC.
- H. Rauf, M. Khalid and N. Arshad, Renewable Sustainable Energy Rev., 2022, 156, 27 CrossRef.
- L. Sugiarto, Z. J. Huang and Y. C. Lu, Energy Environ. Sci., 2025, 18, 2511–2523 RSC.
- H. Q. Li, Z. X. Zhang, T. M. Li and X. S. Si, Mech. Syst. Signal Process., 2024, 209, 32 Search PubMed.
- L. Q. Y. Xu, F. Wu, R. J. Chen and L. Li, Energy Storage Mater., 2023, 59, 34 Search PubMed.
- W. Deng, H. Le, K. T. P. Nguyen, C. Gogu, K. Medjaher, J. Morio and D. Wu, Appl. Energy, 2025, 384, 125314 CrossRef.
- A. H. Tang, Y. C. Xu, Y. Z. Hu, J. P. Tian, Y. W. Nie, F. W. Yan, Y. Tan and Q. Q. Yu, Appl. Energy, 2024, 370, 16 CrossRef.
- M. F. Ng, J. Zhao, Q. Y. Yan, G. J. Conduit and Z. W. Seh, Nat. Mach. Intell., 2020, 1, DOI:10.1038/s42256-020-0191-4.
- C. Ferreira and G. Goncalves, J. Manuf. Syst., 2022, 63, 550–562 CrossRef.
- M. W. Ahmad, J. Reynolds and Y. Rezgui, J. Cleaner Prod., 2018, 203, 810–821 CrossRef.
- P. S. Yu, T. C. Yang, S. Y. Chen, C. M. Kuo and H. W. Tseng, J. Hydrol., 2017, 552, 92–104 CrossRef.
- L. Alzubaidi, J. L. Zhang, A. J. Humaidi, A. Al-Dujaili, Y. Duan, O. Al-Shamma, J. Santamaría, M. A. Fadhel, M. Al-Amidie and L. Farhan, J. Big Data, 2021, 8, 74 CrossRef.
- S. F. Ahmed, M. S. B. Alam, M. Hassan, M. R. Rozbu, T. Ishtiak, N. Rafa, M. Mofijur, A. Ali and A. H. Gandomi, Artif. Intell. Rev., 2023, 56, 13521–13617 CrossRef.
- Q. Mayemba, A. Li, G. Ducret and P. Venet, J. Energy Storage, 2024, 83, 25 Search PubMed.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring, D. Fraggedakis, M. Z. Bazan, S. J. Harris, W. C. Chueh and R. D. Braatz, Nat. Energy, 2019, 4, 383–391 CrossRef.
- D. Lyu, E. H. Liu, H. L. Chen, B. Zhang and J. W. Xiang, Appl. Energy, 2025, 377, 12 CrossRef.
- W. J. Li, C. Han, G. Cheng, S. L. Chou, H. K. Liu and S. X. Dou, Small, 2019, 15, 21 Search PubMed.
- R. G. Cao, K. Mishra, X. L. Li, J. F. Qian, M. H. Engelhard, M. E. Bowden, K. S. Han, K. T. Mueller, W. A. Henderson and J. G. Zhang, Nano Energy, 2016, 30, 825–830 CrossRef CAS.
- P. J. Schmid, Annu. Rev. Fluid Mech., 2022, 54, 225–254 CrossRef.
- S. S. Cao, Z. F. Zhang, Q. Z. Zhang and Y. S. He, Nonlinear Dyn., 2024, 112, 11265–11281 CrossRef.
- Y. Yuan, K. Zhou, W. Zhou, X. Wen and Y. Liu, Phys. Fluids, 2021, 33, 095109 CrossRef CAS.
- M. Khodarahmi and V. Maihami, Arch. Comput. Methods Eng., 2023, 30, 727–747 CrossRef.
- W. D. Wang, X. T. Wang, C. L. Xiang, C. Wei and Y. L. Zhao, IEEE Access, 2018, 6, 35957–35965 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |