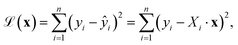From handbooks to high-throughput: rule-based prediction of electronic absorption maxima from SMILES with ChromoPredict

Abstract

Accurate prediction of electronic absorption spectra is essential for the rational design of photofunctional molecules. While ab initio quantum chemical methods provide reliable results, their high computational cost often precludes their application in high-throughput or resource-constrained screening workflows. Data-driven alternatives can offer improved efficiency but typically require large, high-quality datasets and may lack interpretability. In this work, we present a low-cost, interpretable approach for predicting absorption maxima (λ_max) based on digitized and extended empirical rules originally proposed by R. B. Woodward, M. Fieser, L. Fieser and H. Kuhn. These rule sets estimate ππ* transition energies through additive contributions from base chromophores and position dependent contributions of certain structural features and substituents. Our implementation enables direct prediction of λ_max from SMILES input for three representative compound classes: (i) α, β-unsaturated carbonyl compounds, for which we introduce a refined rule set, (ii) dienes and polyenes, and (iii) 3,4,6-substituted coumarin derivatives. For the latter, we define an entirely new set of empirical rules based on literature data. The resulting workflow offers a computationally efficient and chemically interpretable alternative for early-stage molecular screening and design, bridging historical empirical knowledge with modern cheminformatics.

---

1 Introduction

The correlation between molecular structure and electronic ultraviolet-visible (UV-vis) absorption spectra is central to the design and interpretation of photofunctional molecules, like dyes, photosensors, photosensitizers, and photocatalysts. For these applications, it is often crucial to excite specific types of electronic states, such as ππ* or charge-transfer states, since their nature largely determines the resulting photophysical and photochemical behavior. The energies of these transitions, experimentally reflected in the positions of their corresponding absorption bands, define the optical window in which a molecule can be effectively photoexcited. Consequently, accurate prediction and interpretation of UV-vis absorption maxima (λ_max) is a key requirement in the rational design and tuning of photoactive compounds.

One common approach for predicting absorption properties involves ab initio quantum chemical simulations, which give rise to vertical excitation energies, oscillator strengths, and the character of electronic transitions and thus enable a direct assignment of experimental absorption bands.^1,2 Among these, time-dependent density functional theory (TD-DFT) has emerged as the workhorse, particularly in the context of data-driven photochemistry, due to its favorable balance between accuracy and computational cost.^3–5 This is reflected in the widespread use of TD-DFT for generating datasets of UV-vis absorption properties.^6–14

Despite their success in generating high-quality datasets, ab initio methods remain computationally demanding, particularly for large-scale screening or rapid exploration of chemical space during early-stage molecular design. This limitation has motivated the development of fast alternatives, such as machine learning models, which leverage structural representations, such as SMILES, molecular fingerprints or graph-based matrix descriptors, to predict λ_max from structure-property relationships.^10–19 While these models can achieve high accuracy at low computational cost, their black-box nature limits interpretability, reducing their utility for rational design where understanding the influence of specific substituents or electronic effects is crucial.¹⁹ Recent studies have employed Shapley additive explanations (SHAP) to identify molecular descriptors governing absorption and emission properties.^20–22 These analyses revealed that features such as the number of aliphatic heterocycles, the fraction of sp³-hybridized carbons, the presence of primary amine groups, and fingerprints of specific structural fragments contribute significantly to the optical properties and improve model transparency. Nevertheless, these descriptor-level insights do not explicitly relate the identified features to their spatial or electronic context within the molecule, which limits their relevance for rational molecular design.

Empirical rules offer a solution that retains the advantages of low computational costs and fast predictions while providing distinct chemical insights. Among the earliest and most influential of these are the additive rules developed by R. B. Woodward, M. Fieser, L. Fieser, and H. Kuhn in the mid-20^th century.^23–29 These rules relate specific structural features, such as the number of conjugated double bonds and the nature of substituents, to shifts in λ_max (cf. Section 2). Formulated for dienes, α, β-unsaturated carbonyls, and linear polyenes with more than four conjugated double bonds, the Woodward–Fieser (WF)^23–26 and Fieser–Kuhn (FK)^27,28 rules have historically offered chemists a simple and interpretable heuristic framework for estimating λ_max of low-energy ππ* absorption bands of conjugated organic chromophores.

These additive rules represent an early example of empirical modeling, grounded in well-curated experimental data and systematic analysis – a principle that underlies many modern cheminformatics and machine learning approaches. Despite their interpretability and demonstrated predictive utility, the WF and FK rules remain largely absent from contemporary computational workflows, being primarily applied in educational contexts where predictions are performed manually using tabulated values from textbooks.^28,30,31 Notably, to the best of our knowledge, they have not been integrated as features, priors, or constraints in data-driven models, although conversely, a few studies have suggested that their data-driven approaches would have the potential to inform the development of rules for calculating λ_max based on substructures.^18,19 Of particular note in this context is the approach taken by Joung et al.,¹⁹ who draw inspiration from the WF framework to develop an interpretable deep learning model that can predict a range of optical properties, including λ_max, emission maxima, quantum yields and excited state lifetimes. Their model quantitatively reproduced classical substituent increments, for example, predicting contributions of ethyl (+5 nm), methoxy (+4 nm), and ethylamine (+70 nm) in cyclohexane, closely matching the original WF values of +5, +6, and +60 nm for diene systems (see Table 1 in Section 2).^19,26 While the model captures the electronic effects of substituents, it accounts for the position of substituents indirectly. For example, to quantify the effect of the cyano group in 3-hydroxy-7-cyano-coumarin, a reference molecule (3-hydroxy-coumarin) is required to isolate the substituent contribution. In contrast, the WF framework incorporates these effects systematically through position and type dependent increments. Thus, although this approach illustrates the enduring value of chemically interpretable additive models, it does not explicitly extend, refine or digitize the WF rules themselves.

Table 1 Summary of the Woodward–Fieser rules for predicting λ_max for enones and dienes. The columns distinguish base values, increment values for conjugated features beyond the base chromophore and the position-dependent increments to account for substituent effects

Enones ([#6]=[#6]–[#6]=[#8])
Compound category	Base value	Conjugated features	Increment	Substituent	α	β	γ	>γ
α, β-Unsaturated aldehyde	210 (218)	Conjugated double bond	+30	–Alkyl	+10 (+11)	+12 (+19)	+18	+18
α, β-Unsaturated ketone	215 (212)	Exocyclic double bond	+5	–Cl	+15 (+28)	+12 (+22)	+12	+12
α, β-Unsaturated acid	195 (196)	Homoannular cyclodiene	+39	–Br	+25 (+38)	+30 (+33)	+0	+0
α, β-Unsaturated ester	195			–OH	+35 (+38)	+30 (+14)	+50	+0
Cyclohexenone	215 (206)			–O-alkyl	+35 (+29)	+30 (+22)	+17	+31
Cyclopentenone	202 (191)			–O-acyl	+12	+12	+12	+12

---

Dienes ([#6]=[#6]–[#6]=[#6])
Compound category	Base value	Conjugated features	Increment	Substituent	Increment
Acyclic diene	217	Additional double bond	+30	–Alkyl	+5
Homoannular cyclic diene	253	Exocyclic double bond	+5	–Cl/–Br	+10
Heteroannular cyclic diene	214			–O-alkyl	+6
				–N(alkyl)2	+60
				–O-phen	+18
				–S-alkyl	+30

---

We attribute this limitation to the lack of programmatic, high-throughput implementations of the WF and FK rules: manual lookup and structural interpretation impede their use in automated workflows and large-scale screening. To address this, we introduce ChromoPredict, a Python package that encodes the WF and FK rules for direct estimation of λ_max from SMILES inputs (see Section 3.1). By formalizing these empirical rules digitally, ChromoPredict preserves their inherent interpretability, providing transparent insights into how specific substituents and structural motifs modulate absorption maxima.

Herein, we systematically evaluate and refine the empirical rules using a curated computational dataset of 720 α, β-unsaturated carbonyl compounds, including aldehydes, ketones, carboxylic acids, cyclopentenones, and cyclohexenones, and experimental datasets of additional 28 enones and 36 coumarins, with the individual molecules in both datasets bearing methyl, methoxy, hydroxy, chloro, or bromo substituents (see Section 3.2). WF predictions for α, β-unsaturated carbonyl compounds generated with ChromoPredict are benchmarked against TD-DFT reference calculations (see Section 3.2.1), and the refined rules are further compared to random forest models trained on molecular fingerprints (see Section 3.2.2). This analysis delineates the predictive strengths and limitations of additive rules and highlights opportunities for hybrid approaches that integrate mechanistic insight with data-driven modeling. Finally, we extend the WF rules to 3-, 4-, or 6-substituted coumarin derivatives, illustrating the flexibility and scalability of ChromoPredict (see Section 3.2.3).

2 The Woodward–Fieser and Fieser–Kuhn rules

Empirical attempts to predict ππ* UV-vis absorption maxima (λ_max) of organic molecules can be traced back to the work of Woodward²³ and Fieser et al.,²⁶ which were focused on terpenoid systems such as cholestenone, corticosterone, pregna- and cholestadienes, and related steroid derivatives.^23,26 Their work culminated in the so-called Woodward–Fieser (WF) rules, which relate λ_max to chromophore type, substitution pattern, and solvent effects.^23,25,26 These additive scheme achieves remarkable predictive accuracy (±5–10 nm) and laid the foundation for systematic spectral analysis of simple carbonyl-containing chromophores and dienes.

The earliest systematic work was carried out by Robert B. Woodward in the 1940s, who focused on α, β-unsaturated carbonyl compounds, including acyclic enals, ketones, acids, esters, as well as cyclic enones such as cyclopentenone and cyclohexenone.^23,25,29 Based on the analysis of numerous UV-vis spectra, Woodward identified clusters of λ_max corresponding to the degree and position of substitution: α- or β-mono-substituted (225 ± 5 nm), α, β- or β, β′-di-substituted (239 ± 5 nm), and α, β, β′-tri-substituted (254 ± 5 nm) systems.²³ Subsequent refinements classified di- and tri-substituted molecules according to the presence of exocyclic bonds.²⁵ In parallel, Woodward extended his analysis to normal conjugated dienes, defining base values for symmetric dienes (e.g., butadiene: 217 nm) and introducing additive increments of +5 nm for each substituent or exocyclic double bond. The λ_max of asymmetric dienes was then estimated as the average of the corresponding symmetric systems.²⁴

Building on Woodward's foundation, Louis and Mary Fieser introduced a systematic increment scheme to predict λ_max for α, β-unsaturated carbonyls and conjugated dienes.²⁶ Their approach assigned base values to core chromophores (see left column in Table 1) and increment values for substituents, distinguishing contributions according to type (e.g., alkyl, chloro, bromo, hydroxy, alkoxy, acyloxy) of substituent and for α, β-unsaturated carbonyl compounds also on the position of substituents (α, β, γ, or higher).²⁶ Additional increments accounted for extended conjugation: linear double bonds (+30 nm), homoannular cyclodienes (+39 nm), and exocyclic double bonds (+5 nm).^25,26 An overview of base values and increments of the WF rules is summarized in Table 1, with representative structures and calculation examples illustrated in Fig. 1, S2 and S3.

As the study of molecular systems expanded, particularly in the context of natural pigments like β-carotin, the limitations of the original WF rules became evident. These rules, while effective for small chromophores, were not suited for extended polyene systems containing five or more conjugated double bonds. To address this gap, Louis Fieser and Harold Kuhn, developed the Fieser–Kuhn (FK) rules specifically for linear polyenes with extended conjugation.^27,28

Unlike the earlier chromophore-specific formulations, the Fieser–Kuhn rules adopt a parametric approach, allowing λ_max to be estimated based on structural features that scale with conjugation length. The empirical model predicts λ_max as

λ_max = 114 + 5m + 48n(1 − 1.7n) − 16.5⋅R_endo − 10⋅R_exo,

where m is the number of alkyl substituents, n is the number of conjugated double bonds, R_endo denotes the count of endocyclic double bonds, and R_exo accounts for the number of exocyclic double bonds. Example simulations are shown in Fig. S4.

3 ChromoPredict

The Woodward–Fieser and Fieser–Kuhn rules provide a simple yet powerful empirical framework to estimate ππ* UV-vis absorption maxima (λ_max) in conjugated organic molecules.^23–26,29 They define a base chromophore with an associated value and assign additive increments for structural features, capturing the influence of substituent type and position on electronic transitions. ChromoPredict provides a digital implementation of these rules, enabling automated prediction of λ_max directly from molecular structure. We first outline the implementation and usage of the package (Section 3.1), then describe applications that revisit, refine, and extend the Woodward–Fieser framework using modern computational data (Section 3.2).

3.1 Implementation and usage

The Woodward–Fieser (WF) and Fieser–Kuhn (FK) rules follow a common additive framework correlating molecular structure with absorption maxima. In ChromoPredict (cp), predictions proceed sequentially via cp.predict (see GitHub tutorial³²). The workflow, summarized in Fig. S1, mirrors the original stepwise logic of the empirical rules:

3.1.1 Rule set selection. The input structure, provided as a SMILES string, is matched against predefined SMARTS patterns stored in the chrombase library. This procedure identifies the appropriate chromophore class: Woodward–Fieser systems (α, β-unsaturated carbonyl compounds: [#6]=[#6]–[#6]=[#8]), Fieser systems (dienes: [#6]=[#6]–[#6]=[#6]) and Fieser–Kuhn systems (polyenes with at least four conjugated C=C double bonds: [#6]=[#6]–[#6]=[#6]–[#6]=[#6]–[#6]=[#6]). The base chromophore is automatically detected for the inputed SMILES. Alternative formulations (e.g., the original WF rules, the extended rules by Kang and co-workers,^17,33,34 or the refined rules introduced herein) can be explicitly requested through the chromlib parameter. For example, cp.predict(smiles = ”C=CC(=O)C″, chromlib = ”woodward_extended”) predicts the λ_max of but-3-en-2-one (E01, Table S2) with the Kang extension.³⁴

3.1.2 Base value assignment. Each chromophore class carries a characteristic base absorption, representing the minimal conjugated core. Examples include 215 nm for α, β-unsaturated ketones, 253 nm for homoannular dienes, and 114 nm for tetraenes in the FK model. In cp, these assignments are handled by the woodwardfieser, fieser, and fieserkuhn modules, where substructure matches are linked to tabulated base values (Table 1). During this step, the subgraph corresponding to the base chromophore is tagged for further processing.

3.1.3 Structural features. Incremental corrections are applied for conjugation-related features directly extending from the tagged chromophore. These include additional double bonds (+30 nm), exocyclic double bonds (+5 nm), and homoannular ring closures (+39 nm). Identification is streamlined by searching the neighborhood of the chromophore subgraph, a task performed by the strucfeatures module, which like in step 2, further tags the identified structural features in the molecular graphs.

3.1.4 Substituent increments. To account for the different electronic nature of substituents, all rule sets apply type-dependent increments that reflect mesomeric and inductive effects. In the WF scheme rules, these increments are further position-specific, distinguishing α-, β-, γ-, and more remote substituents relative to the chromophore. By contrast, for dienes and polyenes only substituent contributions solely dependent on the type enter the calculation. In cp, the corresponding increments are retrieved from the tabulated values (Table 1) and assigned to the tagged chromophore and its structural extensions.

3.1.5 Solvent corrections (optional). Finally, empirical offsets may be introduced to account for solvatochromic shifts. Polar solvents often stabilize the ground state relative to the excited state, resulting in hypsochromic shifts. The respective approximate empirical corrections as implemented in cp are listed in Table S1.^23,28

Stepwise example calculations illustrating base value assignment (Step 2), structural features (Step 3), and substituent increments (Step 4) are shown for representative α, β-unsaturated ketones and conjugated dienes in Fig. 1 and S2–S4.

Fig. 1 Rule-based prediction of π–π* absorption maxima (λ_max) for enones (left) and dienes (right) using the Woodward–Fieser (WF) rules. Structural contributions are color-coded: base chromophore (purple), additional conjugated double bonds (blue), substituents (gray), and exocyclic double bonds (yellow). For dienes, all substituent increments are summed, whereas for enones (and more generally α, β-unsaturated carbonyls) only the largest contribution per position is applied (cf. gray highlighted substituents).

3.2 Woodward–Fieser rules today: reviewing, reinterpreting, and refining

The Woodward–Fieser (WF) rules were originally developed from limited experimental data and have not been systematically validated on diverse, large datasets. Using our digitized implementation (ChromoPredict, cp) and curated datasets, we present herein the refinement, validation, and extension of these rules. The following sections cover rule refinement (Section 3.2.1), comparison to machine learning (Section 3.2.2), and extension to coumarins (Section 3.2.3).

3.2.1 Refining the Woodward–Fieser rules. The WF rules were originally derived from experimental data on α, β-unsaturated carbonyl compounds and dienes, primarily within the terpenoid chemical space.^23–26 As a result, they suffer from two key limitations: a rather narrow substance scope and systematic stereochemical constraints imposed by double bonds embedded in ring systems. Within this restricted domain, the rules achieve an accuracy of about ±10 nm, but, to the best of our knowledge, they have not been validated against a large and systematically varied dataset.

Only a few studies have partially addressed this gap.^33–36 Kang and co-workers^33–35 proposed extended WF rules for enones, expressing λ_max as a function of the number of substituents and exocyclic double bonds. Their study, however, was limited to 17 enones bearing only alkyl and O-acyl substituents, which contribute similar increments in the original formulation – explaining the observed linear relationship. As a result, the derived expression is applicable only within an even narrower chemical space. In another effort by Wathelet et al.,³⁶ TD-DFT calculations were performed for 213 systematically generated α, β-unsaturated aldehydes, ketones, and acids with bromo, chloro, hydroxy, alkoxy, or methyl substituents. Although substitution patterns included mono- (α or β), di- (α, β or β, β′), and tri- (α, β, β′), only uniform substitution was considered. This precluded analysis of mixed substitution effects, such as the interplay of resonance and inductive contributions from methoxy and chloro groups.

Here, we extend these efforts by combining 213 mono-substituted molecules reported by Wathelet et al.³⁶ with 435 compounds bearing mixed substitution patterns and 72 cyclic enones. From these, we assembled a comprehensive dataset of SMILES strings and corresponding ππ* absorption maxima obtained at the TD-DFT level of theory (Section 4.1), explicitly considering cis/trans isomers where applicable. This dataset was used to evaluate and refine the original WF rules for predicting λ_max.

For each molecule, the base chromophore type, α- and β-substituents, and stereochemistry were extracted. Two approaches were analyzed: one in which stereochemical information was explicitly encoded in the base chromophore definition (e.g., cis-aldehyde), and another in which stereochemistry was not considered in defining the base structure. The corresponding refined increment values for the base chromophores and α/β-substituents are reported in Table 1 (parentheses) and summarized in Fig. S9 for the stereochemistry-explicit approach. Across all 720 reference compounds, the refined rules reduced the mean absolute error (MAE) to 8 nm, compared to 13 nm for the original WF formulation (see Fig. S6).

Fig. 2 shows violin plots of the prediction accuracy for the two refined schemes: following the original WF framework (purple) and with explicit stereochemical encoding (green), separated by compound class (α, β-unsaturated aldehydes, acids, ketones, as well as cyclopentenones and cyclohexenones). As evident, explicit inclusion of double-bond stereochemistry – omitted in the original WF rules – does not substantially improve accuracy, with both approaches yielding comparable MAEs (Fig. S6–S8). For example, the MAE across all trans-configured compounds is 7 nm following both approaches (Fig. S7).

Fig. 2 Violin plots comparing the prediction accuracy of two refined Woodward–Fieser (WF) models for predicting the absorption maxima of α, β-unsaturated aldehydes, acids, linear ketones, cyclopentenones, and cyclohexenones (see structures on the abscissa). The purple model (WFR) refines base chromophores and α/β substituent increments against TD-DFT data for 720 compounds. The green model (WFR-stereo) further accounts for α, β-double bond stereochemistry by distinguishing base values into cis, trans, and undefined classes (no stereochemistry). Across the 720 structures, WFR and WFR-stereo achieve mean absolute errors (MAEs) of 8 nm, each, compared to 13 nm for the original WF rules.

This finding can be rationalized by the original rules' implicit treatment of stereochemistry. In Woodward's formulation, the β-substituent is defined as the group with the larger increment on the same side as the carbonyl group.^23,25,26 Consequently, depending on the nature of the α-substituent, the resulting base values already represent a statistical mixture of cis and trans isomers. Any mismatch between the assumed and actual stereochemistry is therefore random rather than systematic. As such, explicitly encoding stereochemistry does not improve predictive performance, as this variability is already embedded in the empirical design of the original rules. Our global optimization including stereochemistry further shows that the base values of the isomers are nearly identical (e.g., 214 nm for trans-enones, 211 nm for cis-enones, and 215 nm otherwise), yielding an average of 213 nm that aligns closely with the stereochemistry-independent refined enone base value of 212 nm (cf. values in Table 1a and Fig. S9).

In summary, the digital implementation of the WF rules in cp enabled a systematic and efficient refinement, yielding improved predictive accuracy across the explored chemical space (cf.Fig. 3a). All subsequent analyses are therefore based on these refined WF increments (Section 3.2.2). The refined rules have been integrated into cp and can be accessed via the chromlib = ’woodward_refine’ option in the cp.predict function (cf. Section 3.1).

Fig. 3 Predicted absorption maxima (λ_max) from the original Woodward–Fieser rules (WF, filled symbols) and the refined rules (WFR, open symbols), compared with TD-B3LYP/def2-TZVP/D4 reference values (a). The 288 enones are colored in purple, while the data points of the α, β-unsaturated aldehydes and acids (#432) are shown in gray. Distribution of predicted λ_max values, with TD-B3LYP in gray and WFR in purple (b). Comparison of WFR (purple triangles) and random forest (RF, green filled symbols) predictions with experimental λ_max values for the 27 test molecules E01–E27 (c). The RF model was trained on 230 enones using Morgan fingerprints (FMFP, radius 2, 1024 bits). RF predictions based solely on FMFP descriptors (green circles) versus an augmented model incorporating FMFP and WF-derived features (green triangles, (d); features: increments of exocyclic double bonds, α- and β-substituents, and total substituent count). Molecular structures of E18, E20, and E26 (e–g). In the top row, the WF base chromophore (light purple) and substituents (dark purple) are highlighted. In the bottom row, the α-carbon environment (radius 2) contributing to Morgan fingerprint bits is shown. Below each structure, experimental (left) and predicted λ_max values are reported (top: RF with WF + FMFP, (d); bottom: RF with FMFP, (c).

3.2.2 Predicting λ_max: empirical rules vs. machine learning. The absorption maxima of conjugated chromophores are often governed by localized substructures rather than the overall molecular framework. In their original studies, Woodward and Fieser analyzed terpenoid and steroid derivatives, where the chromophore constitutes only a small fraction of the molecule while bulky substituents or annulated rings remain spectroscopically irrelevant. Consequently, the WF rules explicitly capture such chromophoric contributions in α, β-unsaturated carbonyls and dienes.^23,26 By contrast, data-driven chemoinformatics approaches typically rely on molecular fingerprints or other global encodings, which represent the entire molecular graph and whose predictive accuracy depends critically on descriptor choice.

To benchmark whether machine learning (ML) models trained on molecular fingerprints can reproduce the classic scenario described by Woodward and Fieser – where a chromophore embedded in a larger molecular framework retains local control over the absorption – we compared the refined WF rules with random forest (RF) regression models. RF was chosen based on previous studies demonstrating its effectiveness for predicting λ_max from structural descriptors.^17,20 For training and testing, we used 288 enones from TD-B3LYP calculations (see Fig. 3a), comprising mono-, di-, and tri-substituted acyclic enones, cyclopentenones, and cyclohexenones (Sections 3.2.1 and 4.1). The RF models were trained on 80 % of this dataset using four distinct encodings: topological torsion fingerprints (TTFP, 2048 bits), feature Morgan fingerprints (FMFP, radius 2, 1024 bits), MACCS keys, and rooted fingerprints (RFP). The latter restricts TTFP generation to α, β-unsaturated carbonyls and their substituents, thereby paralleling the scope of the WF rules. To probe generalizability, we curated an inference set of 26 enones (E01–E26, see Fig. S10) from experimental data (see values in Table S2).^35–38 These compounds feature fused rings and bulky substituents but no additional conjugated double bonds relative to the enone core and thus display λ_max in the same range as the training and test data (see Fig. 3b).

On the enone test set, all RF models achieved mean absolute errors (MAEs) between 9 and 12 nm, comparable to the refined WF rules (MAE: 8 nm, see Fig. S11a–d). On the inference set, however, performance diverged: the RF models yielded MAEs of 16 nm (RFP and MACCS), 10 nm (TTFP), and 8 nm (FMFP), whereas the WF rules maintained a substantially lower MAE of 5 nm (see Fig. S11e–h). Thus, among purely fingerprint-based models, FMFP proved most robust (see Fig. 3c).

To assess whether explicit rule-based descriptors enhance fingerprint models, we augmented FMFP with WF-derived features (increments for exocyclic double bonds, α- and β-substituents, and the total number of substituents). This hybrid model reduced the MAE to 8 nm on the test set, but showed slightly decreased accuracy on the inference set (11 nm, see Fig. 3d and S12). Closer inspection revealed that for molecules E04, E06, E20, and E26, the hybrid model outperformed the models trained on FMFP alone. These systems bear bulky substituents (e.g., isopropyl or spiropyran groups) that do not contribute to the chromophore absorption, suggesting that fingerprint encodings of these groups introduced spurious correlations leading to underestimation of λ_max. Noteworthy, RF models trained exclusively on WF-derived features achieved superior accuracy for half of the inference molecules compared to the hybrid models (see Fig. 3d and S12), including comparably accurate predictions (within ±5 nm) for bulky systems (E04, E06, E26) and α, β, β′-substituted cases (E18, E21 and E22). The latter underscores the importance of substituent-counting features, consistent with the extended WF rule formulations by Kang and co-workers.^33–35

To contextualize the efficiency and accuracy of the WF predictions, we compared them against ab initio results. Structures of compounds E01–E26 were optimized at either the B3LYP^39,40 or xTB⁴¹ level, followed by linear-response TD-B3LYP simulations to determine the λ_max of the π–π* transition. These calculations required in total approximately 700–3000 CPU hours, highlighting the substantial computational cost compared to the near-instantaneous predictions of ChromoPredict (≈0 CPU hours). Despite their simplicity, the refined WF rules yielded mean absolute errors (MAEs) within the historical uncertainty reported by Woodward and Fieser (±5 nm).^23,26 Random forest models trained on 230 data points achieved comparable accuracy, while incorporating WF-derived features further improved performance for systems with bulky or non-conjugated substituents. In contrast, TD-DFT-predicted λ_max values exhibited broader error distributions, with MAEs of roughly 15 nm (see Fig. S14). These results underscore that explicit chromophore-based descriptors remain both computationally efficient and chemically interpretable, maintaining robustness in off-domain regimes and providing a valuable complement to data-driven and ab initio approaches.

3.2.3 Extending rule-based predictions: case study on substituted coumarins. To assess the transferability of the Woodward–Fieser (WF) rules to a new chemical domain, we examined coumarin chromophores, which contain an α, β-unsaturated ester moiety embedded in a fused benzene ring, i.e., an enone substructure, yet are not explicitly covered by the original WF rule sets.

The unsubstituted coumarin core (C01) displays the characteristic enone ππ* absorption maximum (λ_max,1) at approximately 311 nm (generally between 300 and 330 nm) and a stronger benzoid ππ* absorption band between 250 and 300 nm (λ_max,2).^42,43 This suggests that the WF-based predictions can be used to estimate λ_max,1, but deviations due to ring conjugation and substitution patterns required a detailed analysis of the experimental trends:^42,43 Substituents in the benzene ring (5-, 7-, or 8-position) with positive mesomeric effects (+M) generally induce bathochromic shifts of λ_max,1, with the effect being most pronounced at the 7-position due to extended conjugation in the para-position relative to the enone. Substituents at the 6-position shift λ_max,1 bathochromically regardless of electronic character, without substantially affecting λ_max,2. Substituents at the α- and β-positions (3- and 4-positions) affect λ_max,1 depending on their electronic properties: substituents that withdraw electron density from the carbonyl carbon by mesomeric or inductive mechanism (−M or –I effect) induce bathochromic shifts, whereas electron-donating groups with +M or + I effect lead to hypsochromic shifts due to destabilization of the π*-acceptor orbital. Steric interactions at positions 4 and 5 further modulate both bands, often resulting in hypsochromic shifts.

Guided by these trends, we focused on coumarins substituted exclusively at the 3-, 4-, and 6-positions, corresponding to the α-, β-, and higher substituent sites influencing the enone chromophore, while excluding substitutions at positions 5, 7, and 8, which introduce steric or extended conjugation effects not captured by standard WF increments. Applying these criteria, we constructed a dataset of 36 mono-, di-, and tri-substituted coumarins, combining experimentally reported λ_max,1 values from the literature^43–55 with corresponding TD-B3LYP predictions of their absorption maxima (see Tables S4, S5, Fig, S13, S14 and Section 4.2).

Using the experimental λ_max,1 values of coumarins C01–C26 (Table S3 and Fig. S10), we refined the WF increments with the unsubstituted coumarin (C01) as the reference chromophore, defining the base structure (SMARTS: [#6]1=[#6][#6]=[#6]2[#6](=[#6]1)[#6]=[#6][#6]([#8]2)=[#8]) and base value (312 nm). To capture both hypsochromic and bathochromic shifts relative to C01, positive and negative contributions were allowed during global optimization, which was performed for substituents at the α (3-), β (4-), and higher (6-) positions, considering chloro, bromo, hydroxy, methoxy, and methyl groups (15 parameters in total). The refined increments are summarized in Table S5.

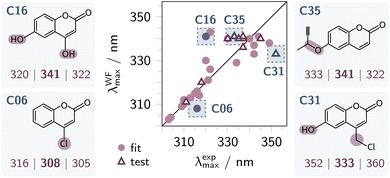
Fig. 4 displays the correlation between WF-predicted and experimental λ_max,1 values, with an analogous pairplot and violin plots including the TD-B3LYP predicted values provided in Fig. S17. For the fitted compounds C01–C26, the mean absolute error (MAE) is 4 nm (purple filled circles in Fig. 4), while application to the ten unseen coumarins C27–C36 yields a MAE of 5 nm (purple triangles). This analysis demonstrates that the refined increments capture the dominant electronic effects of substituents on the coumarin chromophore. The largest deviations arise for hydroxy- and alkoxy-substituted coumarins at the 6-position (see structures C16, C31, C35 in Fig. 4), which are underrepresented in the training set (three hydroxy- and five alkoxy-substituted analogues). Notably, TD-DFT predictions also overestimate the bathochromic shifts induced by hydroxy or alkoxy groups at the 6-position (Tables S3 and S4).

Fig. 4 Correlation between Woodward–Fieser-type rule-predicted and experimental λ_max values for coumarins C01–C35. Filled circles (26 points, C01–C26, see Table S3 and Fig. S15) indicate the dataset used to optimize substituent parameters, while open triangles (10 points, C27–C36, see Table S4 and Fig. S16) show predictions for unseen test structures. Representative examples of overestimation (C16 and C35) and underestimation (C06 and C31) are shown on the left (training set) and right (test set), respectively. For these four molecules, experimental, rule-predicted, and B3LYP-calculated absorption maxima are displayed below the structural formulas, with substituents contributing to the absorption beyond the coumarin core highlighted.

In direct comparison with TD-DFT (cf. Fig. S17), the refined WF rules reflect important substituent effects with greater accuracy. For example, the rules assign increments of −1 and +3 for a hydroxy group in the α (3-) and β (4-) positions, respectively. This is consistent with the stronger destabilization of the carbonyl π* orbital in 3-hydroxycoumarin (C13, λ_exp: 310 nm) compared to 4-hydroxycoumarin (C12, λ_exp: 317 nm).⁴³ In contrast, TD-B3LYP predicts maxima at 304 nm (C13) and 287 nm (C12), thereby inverting the experimental trend. A similar inversion occurs for methoxy substitution: TD-B3LYP predicts λ_max values of 303 nm (C18) and 284 nm (C17) for the 3- and 4-methoxy derivatives, respectively. Thus, TD-B3LYP overestimates the +M effect of the methoxy and hydroxy groups on the enon moeiety at the α-position and underestimates it at the β-position. By contrast, both WF and TD-DFT reproduce the experimental λ_max trends for the structurally more complex coumarins C27–C36 (Table S4).

Overall, the error distribution of the TD-B3LYP predictions for C01–C36 is larger than for the WF estimations, as reflected in the violin plots in Fig. S17 and an MAE of 9 nm, which is comparable to the WF estimates (5 nm) that were fitted to C01–C26 and thus are expected to have a smaller MAE. This demonstrates that the refined WF scheme reliably predicts λ_max,1 for simple 3-, 4-, and 6-substituted coumarins. Moreover, it reproduces all experimental trends covered by C01–C36, including 3-/4-methoxy and hydroxy derivatives, for which TD-DFT gives incorrect estimates of the absorption energies.

4 Materials and methods

4.1 Dataset of α, β-unsaturated carbonyl compounds

To construct a chemically diverse and systematically varied dataset of simple α, β-unsaturated carbonyl compounds, we generated molecular structures for ketones (linear α, β-unsaturated methyl ketones as well as cyclopentenone- and cyclohexenone-derivatives), aldehydes, and carboxylic acids using combinatorial substitution based on a core enone motif defined by the SMARTS pattern [#6](=[#8])–[#6]=[#6], allowing substitution at the α- and the (two) β-position(s). Substituents were selected from six chemically relevant groups considered in the Woodward rules: methyl (C), methoxy (OC), chloro (Cl), bromo (Br), hydroxy (O), and hydrogen (H).

A total of 720 molecules were generated: 216 per acyclic compound class (ketone, aldehyde, and carboxylic acid), and 36 per cyclic enone (see Fig. S5). For the acyclic compounds, all possible permutations of mono- (α or β), di- (α, β), and tri-substitution (α, β, β′) were systematically constructed. Where applicable, both cis/trans stereoisomers were explicitly included, specifically for β-, α, β-, and β, β′-substituted derivatives. For the cyclic enones, due to the presence of only one accessible β-position, mono- and di-substitution patterns were generated, covering α-, β-, and α, β-substitution. All possible combinations of the selected substituents across the available positions were enumerated and represented as isomeric SMILES, ensuring that E/Z-isomerism was captured.

For the resulting SMILES, 3D molecular geometries were generated using the Experimental-Torsion basic Knowledge Distance Geometry (ETKDG) method⁵⁶ as implemented in RDKit, followed by geometry optimization using density functional theory (DFT) at the B3LYP^39,40/def2-TZVP⁵⁷/D4 (ref. 58 and 59) level of theory. Subsequently, time-dependent DFT (TD-DFT) calculations were performed to simulate the 10 lowest singlet excited states. The S1 and S2 states were assigned as nπ* and ππ^* states, respectively. In accordance with the scope of the Woodward rules, only the vertical excitation energies of the S0 → S2 (ππ*) transitions were considered for further analysis. Nonetheless, the information on the first five excitations and their oscillator strengths are available in the dataset provided with the ChromoPredict code on Github.³² All (TD-)DFT simulations were performed using the VeloxChem software.⁶⁰

4.2 Dataset of coumarins

To extend the WF rules to coumarins, we assembled a dataset of 36 mono-, di-, and tri-substituted derivatives bearing hydroxy, chloro, benzo, alkyl, or alkoxy groups at the 3-, 4-, and 6-positions.^43–55 Reported absorption maxima, SMILES representations, and references are summarized in Tables S3 and S4, with molecular structures shown in Fig. S10 and S11.

SMILES strings were converted to 3D structures using the ETKDG algorithm.⁵⁶ Geometry optimizations were carried out at B3LYP/def2-TZVP/D4 (ref. 40 and 57–59) level of theory. Vertical excitation energies and oscillator strengths of the lowest 10 singlet states were obtained from TD-DFT calculations at the same level of theory. In all calculations solvent effects (ethanol, ε = 24.852) were modeled using the conductor-like polarizable continuum model (CPCM).⁶¹ Analyses focused on the lowest-energy absorption maximum with predominant ππ* character (S₀ → S₂ transitions).

4.3 Parameterization of the Woodward–Fieser rules

To improve the classical Woodward–Fieser rules for α, β-unsaturated carbonyl compounds and develop a tailored parameter set for coumarins, we employed a numerical optimization strategy based on the dual annealing algorithm. This procedure was applied to the previously described computational Woodward–Fieser (see Section 4.1) and experimental coumarin dataset (see Section 4.2).

Each enone molecule was encoded using three categorical descriptors: the base chromophore, the α-substituent, and the β-substituent. For coumarins, an additional descriptor was included to account for substitution at the 6-position, denoted by the categorical variable higher. To incorporate stereochemical influences, which are absent from the original formulation, we extended the base chromophore category to distinguish between aldehydes, ketones, and carboxylic acids, each further subdivided into cis, trans, or non-stereospecific configurations. Initial estimates for these base chromophore values were adopted from classical Woodward–Fieser increments (e.g., 210 nm for aldehydes), assigning equivalent starting values to all stereoisomeric variants.

All categorical features were one-hot encoded to preserve the independence of the base and substituent values and construct a design matrix X, with corresponding target values ŷ representing vertical excitation energies derived either from TD-DFT calculations (for enones) or from experimental absorption maxima (for coumarins). The model assumes a linear additive form, ŷ = X·x, where x is the vector of unknown coefficients representing the contributions of each feature (X). Parameter estimation was formulated as a minimization problem over the sum of squared residuals:

where n is the number of molecules and ŷ_i the rule determined absorption wavelength of the ith molecule.

To retain the interpretability of rule-based additive values, the coefficient vector x was constrained to integer values through rounding within the loss function. Optimization was carried out using the global optimization using the dual annealing algorithm as implemented in SciPy, which is well-suited for navigating non-convex parameter landscapes.

Parameter bounds were informed by chemical considerations. In enones, all substituents are known to induce bathochromic shifts, whereas in coumarins, both bathochromic and hypsochromic shifts can occur, depending on substituent type and position. Accordingly, for enones, base chromophore values were restricted to the range between 150 and 300 nm, hydrogen substituents were fixed to zero, and remaining substituent increments were allowed to vary between 1 and 70 nm. For the coumarins, the base chromophore value was fixed to 312 nm, hydrogen substituents were fixed to zero, and remaining substituent increments were allowed to vary between −70 and 70 nm.

5 Conclusions

We present ChromoPredict, a Python package for the automated application of the Woodward–Fieser and Fieser–Kuhn rules to predict the low-energy ππ* absorption maxima (λ_max) of α, β-unsaturated carbonyl compounds, dienes, and linear polyenes. By the digitization of these rules, we have enabled systematic refinement using a curated TD-DFT dataset, which shows that stereochemistry within α, β-unsaturated carbonyl compounds plays a negligible role, as it is largely intrinsically encompassed by the original rule formulation. The refinement improves prediction accuracy compared to classical increments and TD-DFT results. Furthermore, the rule-based predictions exhibit higher transferability and accuracy in out-of-domain regimes than random forest models trained on the same dataset. In particular, the inclusion of rule-derived descriptors as features in machine learning models can further improve their predictive performance, underscoring the value of chemically interpretable, chromophore-based features for data-driven approaches. Building on this framework, we have derived new empirical rules for 3-, 4- and 6-substituted coumarins that accurately reproduce experimental substitution trends and, in some cases, outperform TD-B3LYP, especially when DFT misestimates substituent effects. Overall, this work creates a practical, interpretable, and robust framework that combines classical empirical rules with modern computer-aided and machine learning approaches and supports rapid structural analysis.

Author contributions

C. F. implemented the Woodward–Fieser, Fieser, and Fieser–Kuhn rules in ChromoPredict. C. M. curated the experimental and computational datasets, carried out the technical validation and application studies of the Woodward rules, and conceptualized and supervised the project. Both authors contributed to writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data and the ChromoPredict Python code are openly available on Zenodo (https://doi.org/10.5281/zenodo.17520032).⁶² The package includes a predict function for estimating λ_max values of α, β-unsaturated carbonyl compounds, dienes, polyenes, and coumarins, with automatic detection of chromophore type and application of the corresponding rule sets. Required dependencies (numpy, pandas, pillow, rdkit, etc.) are listed in the accompanying requirements.txt file.³² A step-by-step tutorial in the form of a Jupyter notebook is also provided on the repository.³²

Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00382b.

Acknowledgements

We thank Philipp Marx for his valuable feedback on the coding aspects of this work. C. M. gratefully acknowledges financial support from the Emerging Talents Initiative (ETI) of Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and from the FAU Competence Center Engineering of Advanced Materials (FAU EAM) through an EAM Starting Grant. High-performance computations were carried out at the Erlangen National High Performance Computing Center (NHR@FAU).

Notes and references

1. S. Mai and L. González, Angew. Chem., Int. Ed., 2020, 59, 16832–16846.
2. L. González and R. Lindh, Quantum Chemistry and Dynamics of Excited States: Methods and Applications, John Wiley & Sons, 2020.
3. A. D. Laurent, C. Adamo and D. Jacquemin, Phys. Chem. Chem. Phys., 2014, 16, 14334–14356.
4. C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856.
5. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
6. D. Jacquemin, J. Preat and E. A. Perpète, Chem. Phys. Lett., 2005, 410, 254–259.
7. M. Pinheiro Jr, S. Zhang, P. O. Dral and M. Barbatti, Sci. Data, 2023, 10, 95.
8. Y. Zhu, M. Li, C. Xu and Z. Lan, Sci. Data, 2024, 11, 948.
9. R. Gómez-Bombarelli, J. Aguilera-Iparraguirre, T. D. Hirzel, D. Duvenaud, D. Maclaurin, M. A. Blood-Forsythe, H. S. Chae, M. Einzinger, D.-G. Ha and T. Wu, et al. , Nat. Mater., 2016, 15, 1120–1127.
10. E. J. Beard, G. Sivaraman, Á. Vázquez-Mayagoitia, V. Vishwanath and J. M. Cole, Sci. Data, 2019, 6, 307.
11. K. Ghosh, A. Stuke, M. Todorović, P. B. Jørgensen, M. N. Schmidt, A. Vehtari and P. Rinke, Adv. Sci., 2019, 6, 1801367.
12. K. P. Greenman, W. H. Green and R. Gómez-Bombarelli, Chem. Sci., 2022, 13, 1152–1162.
13. J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427–438.
14. S. G. Jung, G. Jung and J. M. Cole, J. Chem. Inf. Model., 2024, 64, 1486–1501.
15. M. Hussain Tahir, S. Naeem, A. Y. Elnaggar and M. Mahmoud, Chem. Phys., 2025, 588, 112476.
16. H. Ochiai and H. Kaneko, ACS Omega, 2025, 10, 665–672.
17. B. Kang, C. Seok and J. Lee, J. Chem. Inf. Model., 2020, 60, 5984–5994.
18. F. Urbina, K. Batra, K. J. Luebke, J. D. White, D. Matsiev, L. L. Olson, J. P. Malerich, M. A. Z. Hupcey, P. B. Madrid and S. Ekins, Anal. Chem., 2021, 93, 16076–16085.
19. J. F. Joung, M. Han, M. Jeong and S. Park, J. Chem. Inf. Model., 2022, 62, 2933–2942.
20. R. C. Souza, J. C. Duarte, R. R. Goldschmidt and I. J. Borges, J. Chem. Inf. Model., 2025, 65, 3270–3281.
21. R. C. Souza, J. C. Duarte, R. R. Goldschmidt and I. Borges Jr, J. Braz. Chem. Soc., 2025, 36, 20250037.
22. M. M. Hasan, O. Tarkhaneh, S. D. Bungay, R. A. Poirier and S. M. Islam, J. Chem. Inf. Model., 2025, 65, 9497–9515.
23. R. B. Woodward, J. Am. Chem. Soc., 1941, 63, 1123–1126.
24. R. B. Woodward, J. Am. Chem. Soc., 1942, 64, 72–75.
25. R. B. Woodward, J. Am. Chem. Soc., 1942, 64, 76–77.
26. L. F. Fieser, M. Fieser and S. Rajagopalan, J. Org. Chem., 1948, 13(6), 800–806.
27. L. F. Fieser, J. Org. Chem., 1950, 15, 930–943.
28. L. F. Fieser, M. Fieser and H. R. Hensel, Lehrbuch der organischen Chemie (Organic Chemistry, dt.) Uebers. u. bearb. von Hans Ruprecht Hensel, 1954.
29. R. B. Woodward and A. Clifford, J. Am. Chem. Soc., 1941, 63, 2727–2729.
30. L. B. Slater, Stud. Hist. Phil. Sci. A, 2002, 33, 1–33.
31. A. I. Scott, Interpretation of the Ultraviolet Spectra of Natural Products: International Series of Monographs on Organic Chemistry, Elsevier, 2013, vol. 7.
32. ChromoPredict, 2025, https://github.com/CompPhotoChem/ChromoPredict.
33. Y. Kang and F.-A. Kang, Tetrahedron Lett., 2011, 52, 6679–6681.
34. Y. Kang and F.-A. Kang, Tetrahedron Lett., 2012, 53, 1928–1932.
35. G. Kang, Y. Kang and F.-A. Kang, J. Phys. Org. Chem., 2021, 34, e4186.
36. V. Wathelet, J. Preat, M. Bouhy, M. Fontaine, E. A. Perpète, J.-M. André and D. Jacquemin, Int. J. Quantum Chem., 2006, 106, 1853–1859.
37. R. C. Cambie, P. A. Craw, R. J. Hughes, P. S. Rutledge and P. D. Woodgate, Aust. J. Chem., 1982, 35, 2111–2130.
38. J. A. Marshall and D. J. Schaeffer, J. Org. Chem., 1965, 30, 3642–3646.
39. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
41. C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, WIREs Comput. Mol. Sci., 2021, 11, e1493.
42. K. V. Masrani, H. S. Rama and S. L. Bafna, J. Appl. Chem. Biotechnol., 1974, 24, 331–341.
43. A. Mangini and R. Passerini, Gazz. Chim. Ital., 1957, 87, 243–266.
44. T. S. Reddy, H. Moon and M.-S. Choi, New J. Chem., 2020, 44, 4992–5000.
45. W. W. Mantulin and P.-S. Song, J. Am. Chem. Soc., 1973, 95, 5122–5129.
46. J. Kolodziejczyk-Czepas, S. Kozachok, Ł. Pecio, S. Marchyshyn and W. Oleszek, Phytochemistry, 2021, 190, 112861.
47. J. Avó, S. Martins, A. J. Parola, J. C. Lima, P. S. Branco, J. P. Ramalho and A. Pereira, ChemPlusChem, 2013, 78, 789–792.
48. F. Celikezen, C. Orek, A. Parlak, K. Sarac, H. Turkez and Ö. Ö. Tozlu, J. Mol. Struct., 2020, 1205, 127577.
49. W. Chen, G. Wang, K. Mei and J. Zhu, Rec. Nat. Prod, 2021, 15, 356–362.
50. A. O. Obaseki, J. E. Steffen and W. R. Porter, J. Heterocycl. Chem., 1985, 22, 529–533.
51. G. Wang, S. B. Adhikari, P. Aryal, I. Okafor, A. Chen and A. Duffney, Carbohydr. Res., 2025, 109526.
52. C. Loarueng, B. Boekfa, S. Jarussophon, P. Pongwan, N. Kaewchangwat, K. Suttisintong and N. Jarussophon, Arkivoc, 2019, 6, 116–127.
53. T. Eckardt, V. Hagen, B. Schade, R. Schmidt, C. Schweitzer and J. Bendig, J. Org. Chem., 2002, 67, 703–710.
54. K. C. Majumdar and P. Chatterjee, J. Chem. Res., 1996,(10), 462–463.
55. D. P. Kranz, A. G. Griesbeck, R. Alle, R. Pérez Ruiz, J. M. Neudörfl, K. Meerholz and H.-G. Schmalz, Angew. Chem., Int. Ed., 2012, 51, 6000–6004.
56. S. Riniker and G. A. Landrum, J. Chem. Inf. Model., 2015, 55, 2562–2574.
57. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
58. E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112.
59. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
60. Z. Rinkevicius, X. Li, O. Vahtras, K. Ahmadzadeh, M. Brand, M. Ringholm, N. H. List, M. Scheurer, M. Scott, A. Dreuw and P. Norman, WIREs Comput. Mol. Sci., 2020, 10, e1457.
61. A. W. Lange and J. M. Herbert, J. Chem. Phys., 2010, 133, 244111.
62. C. Forster and C. Müller, CompPhotoChem/ChromoPredict: ChromoPredict (v1), 2025,  DOI:10.5281/zenodo.17520032.

---