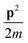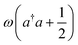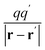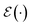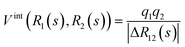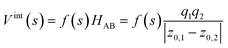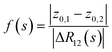Open Access Article
Open Access ArticleChemically motivated simulation problems are efficiently solvable on a quantum computer
Philipp
Schleich
 *ab,
Lasse Bjørn
Kristensen
*ab,
Lasse Bjørn
Kristensen
 acd,
Jorge A.
Campos-Gonzalez-Angulo
bc,
Abdulrahman
Aldossary
bc,
Davide
Avagliano
ce,
Mohsen
Bagherimehrab
ac,
Christoph
Gorgulla
fg,
Joe
Fitzsimons
h and
Alán
Aspuru-Guzik
abcijklm
acd,
Jorge A.
Campos-Gonzalez-Angulo
bc,
Abdulrahman
Aldossary
bc,
Davide
Avagliano
ce,
Mohsen
Bagherimehrab
ac,
Christoph
Gorgulla
fg,
Joe
Fitzsimons
h and
Alán
Aspuru-Guzik
abcijklm
aDepartment of Computer Science, University of Toronto, Toronto, ON M5S 3G4, Canada. E-mail: aspuru@utoronto.ca; philipps@cs.toronto.edu
bVector Institute of Artificial Intelligence, Toronto, ON M5G 1M1, Canada
cDepartment of Chemistry, University of Toronto, Toronto, ON M5S 3H6, Canada
dDepartment of Computer Science, University of Copenhagen, Copenhagen, DK-2100, Denmark. E-mail: lakr@di.ku.dk
eChimie ParisTech, PSL University, CNRS, Institute for Life and Health Sciences (iCLeHS UMR 8060), 75005 Paris, France
fDepartment of Structural Biology, St. Jude Children's Research Hospital, Memphis, TN 38105, USA
gDepartment of Physics, Harvard University, Cambridge, MA 02138, USA
hHorizon Quantum Computing, Singapore 138565
iDepartment of Chemical Engineering & Applied Chemistry, University of Toronto, Toronto, ON M5S 3E5, Canada
jDepartment of Materials Science & Engineering, University of Toronto, Toronto, ON M5S 3E4, Canada
kAcceleration Consortium, Toronto, ON M5S 3H6, Canada
lCanadian Institute for Advanced Research, Toronto, ON M5G 1Z8, Canada
mNVIDIA, 431 King St W #6th, Toronto, ON M5V 1K4, Canada
First published on 27th November 2025
Abstract
Simulating chemical systems is highly sought after and computationally challenging, as the number of degrees of freedom increases exponentially with the size of the system. Quantum computers have been proposed as a computational means to overcome this bottleneck, thanks to their capability of representing this amount of information efficiently. Most efforts so far have been centered around determining the ground states of chemical systems. However, hardness results and the lack of theoretical guarantees for efficient heuristics for initial-state generation shed doubt on the feasibility. Here, we propose a heuristically guided approach that is based on inherently efficient routines to solve chemical simulation problems, requiring quantum circuits of size scaling polynomially in relevant system parameters. If a set of assumptions can be satisfied, our approach finds good initial states for dynamics simulation by assembling them in a scattering tree. In particular, we investigate a scattering-based state preparation approach within the context of mergo-association. We discuss a variety of quantities of chemical interest that can be measured after the quantum simulation of a process, e.g., a reaction, following its corresponding initial state preparation.
1. Introduction
The idea of using quantum computers for the simulation of quantum systems goes back to the first proposals of quantum computing by Benioff, Feynman, and Manin.1–3 This idea has generated substantial effort toward applying quantum computing to chemical problems, as conventional quantum many-body simulations for chemistry are inherently limited by the curse of dimensionality and constitute a significant portion of current supercomputing usage. This effort has largely focused on two problems: quantum simulation of dynamics (also known simply as Hamiltonian simulation or quantum simulation in the field of quantum computing) and the ground-state preparation problem. Quantum simulation4–8 describes the problem of time-evolving an initial state according to the Schrödinger equation under a Hamiltonian. The relevant Hamiltonians for chemical and most physical processes can be efficiently computed, and the corresponding time evolution, governed by the Schrödinger equation, is probably within the computational complexity class BQP (bounded-error quantum polynomial-time). This class encompasses decision problems that a quantum computer can solve in polynomial time with a bounded error probability.6,9 In contrast, the problem of determining the ground state – formulated as the local Hamiltonian problem in quantum complexity theory – is complete for the class Quantum Merlin-Arthur (QMA),9–11 a larger class sometimes compared to the classical complexity class NP. More recently, it was shown that simulating Schrödinger operators of the form −Δ + V with some restrictions regarding smoothness and boundedness on V and without particle exchange symmetries, a slight restriction compared to general local Hamiltonians, is also BQP-complete, and the ground-state problem for such operators is StoqMA-hard,12 namely Merlin-Arthur for Hamiltonians without a sign problem (stoquastic Hamiltonians).13 As a result, it is not clear whether ground state problems can be solved efficiently, even on a quantum computer.Ground-state search and Hamiltonian simulation are often used jointly. Simulation algorithms serve as a subroutine to find the ground-state energy (e.g., via phase estimation10,14–16), in the elucidation of reaction mechanisms described in ref. 17 or for free energy calculations in ref. 18, while ground states can be input states for performing quantum dynamics. State-of-the-art implementations of Hamiltonian simulation can be categorized into several classes. One is the class of algorithms based on Trotter–Suzuki formulae,9,19 which split the exponential of a sum into products of exponentials. Another class is based on “qubitization”,20,21 which makes use of quantum signal processing22 to encode the simulation in a quantum walk. Additionally, there are randomized algorithms such as QDRIFT23 and its extensions.24,25 Each of these approaches has its advantages in different scenarios,26,27 and methods based on product formulae in particular can make the evolution of perturbative systems, as often present in chemistry and physics, even more efficient.28,29 However, as they all lead to polynomially sized circuits for Hamiltonians of constant sparsity, we refrain from going into details here and refer to the relevant literature. A good overview can be found in ref. 30, with additional recent theoretical progress reported in ref. 31 and 32 and experimental progress reported in ref. 33 and 34.
We propose a departure from the current mainstream approach of the quantum computing community to chemistry, moving beyond the 1950s' computational chemist's way of thinking,35,36 which has been shaped by the limitations of classical computing to use the ground-state as the starting point of computations, to a new era. With the advent of fault-tolerant quantum computers, dynamical simulation of quantities that a practicing chemist might care about is within reach. Specifically, we argue that a wide set of relevant quantum chemistry problems are inherently addressable through dynamical evolution alone, leading to efficient quantum algorithms for these problems. This holds, e.g., for the determination of reaction rates, photochemistry, or spectroscopy. Examples of such problems and strategies for how to extract relevant quantities are summarized in Section 1.2.
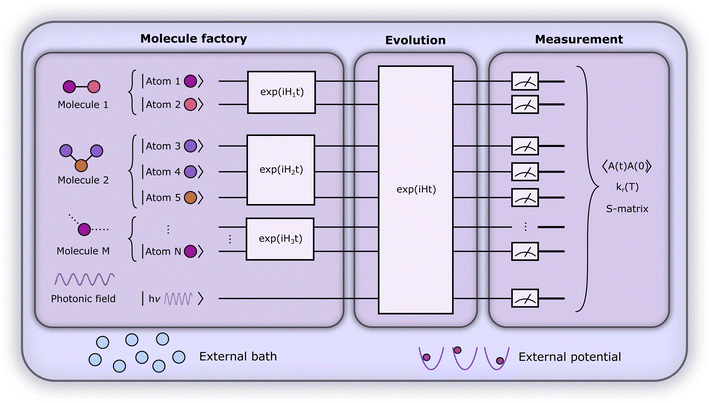
A central requirement for such dynamics-based approaches is having techniques for preparing chemically relevant initial states. For this state preparation, our proposed framework employs a limited set of attainable atomic initial states and then dynamically prepares input states for a reaction of interest through a scattering process. Particularly, our main contribution is the approach to prepare molecular states by hierarchically ‘combining’ atomic ones – here specifically by scattering them. This allows for a heuristic state preparation that is guided by chemical intuition. Then, another dynamical evolution embodies a reaction, and a broad set of relevant quantities can be measured. Under certain assumptions on what constitutes relevant initial states, the ensuing algorithm is not limited by the QMA-hardness of preparing ground states and thermal states. Similarly, the focus on less restrictive initial states and more general observables means we can circumvent an orthogonality catastrophe, namely, a vanishing success probability to retrieve a ground state. As has been recently shown,37 this orthogonality catastrophe is why exponential speedups for ground-state energy estimation of molecular Hamiltonians on quantum computers may be hard to attain as the (state-of-the-art) methods considered for state preparation fail to produce reliable overlaps for molecules of increasing size. However, a distinction to make is that our methodology is based on heuristic physical intuition, which makes it not directly comparable to methods like QPE from a complexity-theoretic perspective. Furthermore, a method was proposed recently that is able to address the orthogonality catastrophe in some cases with a divide and conquer approach.38 Similar to our ‘molecule factory’ in Fig. 3 where we split the problem into fragments based on chemical intuition (which can e.g. be guided by knowledge from retrosynthesis in certain cases), they use a tree decomposition of the Hamiltonian.
Two observations are at the foundation of our approach. First, the simulation of k-local Hamiltonians is achievable by polynomial-size quantum circuits. Hamiltonians that stem from chemical problems are 2-local due to the nature of the Coulomb interaction and, thus, also have finite locality when represented as quantum operations on qubits. Including photons to simulate light–matter interactions in the computation increases the maximum support of operations but not beyond a constant factor. The second observation is that we can aim to simulate processes corresponding to experiments that can be performed in a lab in finite time, i.e., problems that are, in some sense, experimentally verifiable. Molecular ground states, as viewed from the perspective of computational chemistry, which implies a frozen molecular geometry at absolute-zero temperature, do not necessarily represent a system's thermal equilibrium state and hence do not belong to the class of problems corresponding to experiments that can be carried out in finite time. Specifically, this encompasses situations when the Born–Oppenheimer approximation fails, and when effects such as nonadiabatic coupling and anharmonicity are not negligible, or the problem requires treatment through thermal states. We propose to simulate the process of producing reactants with a hierarchical scattering process. First, we prepare the ground states of atoms by quantum phase estimation – this does not fall under the orthogonality catastrophe, as atoms are finite-sized and state preparation feasible as long as we stay within the regime where efficient heuristics for initial state preparation are available – and then use a simple scattering process to produce molecular reactants. Our method integrates artificial potentials and photonic fields to induce the success of scatterings, leading to a lower-bounded probability of success. Specifically, mergo-association, as discussed in Section 3, is a promising avenue to realize this. This lower bound means that a fixed number of repetitions of a weak measurement scheme to herald success – see Section 3.2 – will suffice to ensure the success of intermediary scattering processes. Thus, meaningful molecular input states, which do not need to be ground states, are efficiently prepared. Our framework facilitates the modeling of complex chemical reactions by hierarchically operating the scattering with N atoms to create M reactants, which can then undergo a quantum simulation corresponding to a reaction, followed by measurements of reaction rates and time correlation functions.
1.1. Hamiltonian simulation and complexity considerations
We continue by discussing relevant complexity classes for the problems we consider and the efficiency of their solutions. The complexity class BQP (bounded-error quantum polynomial-time) is oftentimes considered the quantum generalization of the complexity class P (polynomial time), or, more precisely, its probabilistic extension BPP (bounded-error probabilistic polynomial-time). Polynomial complexity is usually considered efficient as the increase in cost when scaling relevant parameters is somewhat moderate. Problems from QMA (Quantum Merlin-Arthur), in contrast, can be considered “hard”; QMA is the quantum analog of NP (non-deterministic polynomial time) or, more precisely, the probabilistic class MA (Merlin-Arthur). QMA describes promise problems with solutions that can be verified in polynomial time with bounded error probability. However, there is no guarantee of efficiency in finding their solution.39–41Our argument is that a large class of chemically relevant phenomena can be addressed by algorithms solving efficiently solvable problems, which is grounded on the following conjectural, intuitive argumentation: namely, that phenomena that occur in finite time in a chemical laboratory can be simulated in finite time, and, moreover, that the gap between time in nature and time on a quantum computer is only polynomially sized.
Our argument is that a large class of chemically relevant phenomena can be addressed by algorithms for efficiently solvable problems. More precisely, our central hypothesis is that phenomena that occur in finite time in a chemical laboratory can be simulated in finite time, while the gap between time in nature and time on a quantum computer is only polynomially-sized. In other words, we conjecture that the relevant system sizes and time scales for observable chemistry phenomena often grow at most polynomially with system size, allowing for in principle efficient quantum simulations. For instance, while undergoing chemical reactions, systems such as those discussed in Section 1.2 do not typically cool down to their electronic ground state, making thermal states or efficiently reachable metastable states42 more relevant.
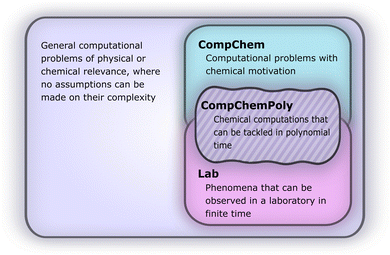
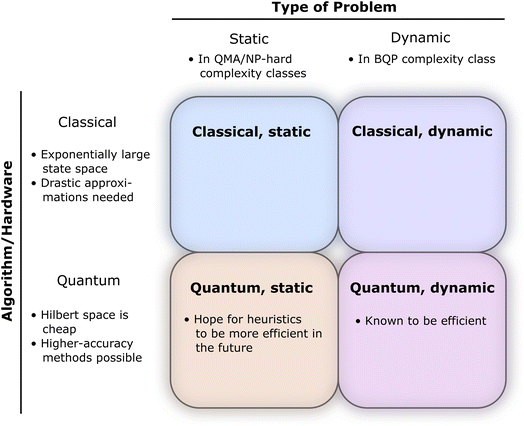
Here, we can draw a distinction between problems of polynomial complexity, such as those from BQP, and QMA-hard problems, such as the local Hamiltonian problem. We note that the QMA-hardness of the local Hamiltonian problem is not sufficient to infer the same complexity for a molecular Hamiltonian with the continuous two-body Coulomb interaction term, although folklore oftentimes considers this to be the case. Therefore, we envision a fundamental change in the way chemistry problems on quantum computers are typically approached, and we display this in Fig. 1. We denote by COMPCHEM the set of computational problems of chemical relevance – including phenomena like ground states. Note that these are not necessarily decision problems; our argumentation is based on circuit fragments that stem from known complexity results rather than decision problems and the language of complexity theory. The set that we call COMPCHEMPOLY represents the focal set of problems within this work; namely, problems of relevance to chemistry and that have polynomial complexity. Our conjecture here is thus that chemical problems that are feasible in a laboratory, LAB in Fig. 1, have non-trivial overlap with chemical simulation problems that can be simulated efficiently, COMPCHEMPOLY. Our present study highlights a wide set of chemically interesting problems involving simulation as a subroutine yet avoiding subroutines and decision problems which are known to be hard. Many approaches in chemistry that involve searching for the ground state are related to problems which are QMA-, StoqMA or NP-hard;12,43–45 examples of tasks that fall into this category are finding the universal functional in density functional theory or the Hartree–Fock problem. Significant progress was made in solving the latter numerically, to the point that it is mostly seen as “solved” despite the formal hardness. This view results in hope about tackling the ground-state problem as well. Yet, at this point, we seem far from similar success in chemistry ground-state search, and hope for solving practical chemical problems may thus lie in dynamics.
To represent chemical systems, we choose molecular Hamiltonians that are not necessarily restricted to the Born–Oppenheimer (BO) approximation. Non-BO was previously explored in the split-operator formalism on quantum computers, where kinetic and potential dynamics are factored.46,47 While it was argued in ref. 46 that the non-BO approach is more efficient than implementing the BO procedure, there have been recent advances that render BO more efficient thanks to a fully coherent implementation.48 Hamiltonians occurring in chemistry are composed of the operators laid out in Table 1, from which locality is an obvious consequence, as k-locality follows from the 2-body nature of the interactions.
Our framework is independent of the choice of basis used to represent the Hamiltonian numerically and the choice between the first and second quantization. Asymptotically, a first-quantized representation tends to be more efficient for fault-tolerant quantum algorithms with an abundant number of logical qubits, as the number of required qubits grows linearly with the number of particles and logarithmically with the number of basis functions (since one stores the basis information for every particle), as opposed to the linear dependence in the number of basis functions for second quantization, where one stores occupation for each basis function.30,31,49–53 In this work, we restrict ourselves to the first-quantized representation for concrete examples. For a circuit to have polynomially-sized complexity, it is further necessary that the operator norm of the simulated Hamiltonian, or rather, its individual terms acting on at most k qubits, grow at most polynomially in the number of qubits used to represent them.7–9 Energy is an extensive thermodynamic property, so it grows roughly linearly by increasing the system size (i.e., the number of particles). Therefore, the thermodynamic relation between the amount of matter and internal energy is linear.†
1.2. Measuring dynamical quantities of interest and a review of exemplary applications
While more details about the framework will be provided below, here, we first provide a brief motivation and review of some of the potential applications. Simulating the dynamics of molecular processes provides access to meaningful information about the rearrangements of atomic nuclei and electrons and their interactions with electromagnetic fields as they unfold. Already with classical resources, time-dependent approaches offer numerous advantages over time-independent ones, as the former are more amenable to handling the continuum portion of the spectrum and grant access to the relevant elements of the scattering matrix‡ over a meaningful range of energies. We provide an overview of chemical problems, with time-dependent versus stationary quantities, solved on different hardware, in Fig. 2.Measuring observables in a dynamical picture requires considering the time evolution of a wave packet, i.e., a superposition of solutions of the time-dependent Schrödinger equation (TDSE). Most measurements of dynamical quantities can be phrased in terms of wave packet correlation functions, whose calculation fits perfectly into our framework. Transition amplitudes are measured, e.g., using a Hadamard test.46,54,55 We can follow the scheme introduced in ref. 56, which is capable of obtaining two-point correlation functions, or the cumulative correlation function method in ref. 57. This scheme is extendable to the S-matrix and to n-point correlators by additional time-evolutions and block encodings, similarly to the linear response framework in ref. 55. If results at more than two times are required, we can use a history state encoding following the conditional time evolutions of the quantum circuit of quantum phase estimation, similar to the construction in ref. 58, which also considers observables measured across various time-steps. To that end, we add a clock register 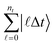 so that ntΔt = t. Then, instead of a direct time evolution of the overall system, we split the evolution into chunks of Δt and condition on the clock register to produce a superposition of the state at different evolution time steps. Furthermore, if needed, applying a quantum Fourier transform before measurement is straightforward and does not compromise the overall efficiency of the algorithm. While this framework could be interpreted as purely theoretical, we can easily show that this approach covers a vast range of contexts, extending from nature to chemical laboratories.
so that ntΔt = t. Then, instead of a direct time evolution of the overall system, we split the evolution into chunks of Δt and condition on the clock register to produce a superposition of the state at different evolution time steps. Furthermore, if needed, applying a quantum Fourier transform before measurement is straightforward and does not compromise the overall efficiency of the algorithm. While this framework could be interpreted as purely theoretical, we can easily show that this approach covers a vast range of contexts, extending from nature to chemical laboratories.
2. Computational framework
In what follows, we describe the computational framework in more detail – i.e., a dynamics-based state-preparation scheme that serves as input for a “main” quantum dynamics routine, preceding measurement. Our overall idea is based on the experiment in ref. 74, where molecules were “built” using two atoms with finite success probability, as well as a mergo-association scheme that merges atoms, e.g. Rb and Cs, using a trap potential.75–77 The chemical dynamics we aim to simulate to extract chemical properties requires a sensible initial state for the time evolution. This state must reproduce a natural one to faithfully extract the desired properties. Depending on the process under consideration, good candidates could be found among ground states, or perturbed ground states, such as those obtained by laser excitation. However, as previously argued, general molecular ground states are hard to access. Nevertheless, preparing the ground states of atoms is feasible – the lighter the atom, the easier – and can be done efficiently as constant overlap for heuristic input states is expected.37 For this reason, we propose to follow a hierarchical approach, as outlined in Fig. 3. All processes generating the reactants and products are carried out through Hamiltonian simulation with local Hamiltonians, including molecular and external field components. After using this technique to generate initial states, we aim to measure observables, e.g., reaction rates according to the scheme in ref. 46 and 54 or auto-correlation functions,55 as outlined in the previous section.We start with a state representing N atoms, all of which are assumed to be in their ground states or another state of interest ρ(atom)i, such as a thermal state. The preparation of these states can be achieved by existing algorithms for ground-state10,78–81 and thermal-state preparation82,83 followed by amplitude amplification to enhance the probability of obtaining the desired state. For generality, we represent both pure and mixed states using density-matrix notation. Since the atoms are all finitely sized, and we can prepare an initial state with a significant overlap with the desired state for each atom, any amplitude amplification costs are constant with respect to overall system size. The overall cost to prepare the atomic initial states is 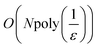 , with ε being the accuracy in preparing the atomic states. Using these atoms encoded as a state ρ(atom)1ρ(atom)2⋯ρ(atom)N, we seek to create M molecular reactants ρ(mol)1ρ(mol)2⋯ρ(mol)M. For this step to produce a molecular state from atomic states, appropriate (anti)symmetrization is essential too; see also the discussion in Appendix A.2.2.
, with ε being the accuracy in preparing the atomic states. Using these atoms encoded as a state ρ(atom)1ρ(atom)2⋯ρ(atom)N, we seek to create M molecular reactants ρ(mol)1ρ(mol)2⋯ρ(mol)M. For this step to produce a molecular state from atomic states, appropriate (anti)symmetrization is essential too; see also the discussion in Appendix A.2.2.
Based on these initial states, we next prepare the reactants by a scattering process mimicking a physical experiment. In other words, we jointly evolve a set of atoms meant to form a reactant molecule. We discuss the modeling and treatment of a bath that allows exchanging energy with an environment further below.
Consider one of the reactant molecules to be prepared. We combine the constituent atoms by successively scattering in a tree-like manner, as in Fig. 3, until the desired molecular state is attained. In the worst case, each molecule is generated by combining only two participants at a time, leading to a binary scattering tree, and thus an overall number of scatterings that is quasi-linear in the number of input atoms. It is essential to ensure a high overlap with the desired intermediate state at each level in this procedure. Otherwise, the overlap would decrease at each combination step. For instance, with an initial overlap of (1 − δ), the overlap would drop exponentially to (1 − δ)n after n steps. A seemingly obvious choice for mitigating this problem would be to use oblivious amplitude amplification.84 However, in our case, the open-system character of the simulation and the fact that the abstract angle to be amplified is not independent of the (unknown) input state are major roadblocks for this approach, which we leave up to future research. Instead, we propose the following approach towards bounded success probability. Inspired by the nanoreactor approach in ref. 85 and the mergo-association scheme from ref. 75–77, we introduce artificial potentials that confine the products to be combined in each scattering step, as well as an additional photonic field as an energy source and a bath as an energy sink. Following the procedure we propose in Section 3.1, mergo-association shows more promise in terms of suitability for simulation on the molecular scale at this point as we can confine individual, small systems without the need for large ensembles in high-pressure and high-temperature regimes. Using this framework, we show that, heuristically, we can expect a constant lower bound P on the probability of success for certain types of bonds for the chemical formation of reactants. Such a lower bound is an important assumption in the procedure and also highlights its heuristic nature. For the example of mergo-association, we show that the existence of a constant lower bound on the success probability for certain types of bonds, such as covalent bonds, is reasonable; cf. Section 3.1. The intuition we observe there is that given a certain order of magnitude of bonding energy (say, the typical regime of covalent bonds of approximately 30–180 kcl mol−1), a requirement of simulating potentials of similar magnitude may lead to a substantial constant factor in the simulation cost, but the scaling with respect to system size of this cost would heuristically be only polynomial in the combined nuclear masses, not exponential.
Suppose the scattering is organized as a binary (or higher-order, ternary, …) tree. For each node in the tree, there is a simulation channel  , parametrized by the subsystem size, dissipation model (bath), and confinement properties (artificial potentials). Then, we may assume that this channel produces a state of the kind
, parametrized by the subsystem size, dissipation model (bath), and confinement properties (artificial potentials). Then, we may assume that this channel produces a state of the kind
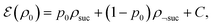 | (1) |
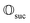 that allows us to distinguish between the subspaces spanned by ρsuc and ρ¬suc by weak measurements, which enables the heralding of the scattering success and projecting the state into the successful subspace. The presence of a coherence C does not influence measurement outcomes of
that allows us to distinguish between the subspaces spanned by ρsuc and ρ¬suc by weak measurements, which enables the heralding of the scattering success and projecting the state into the successful subspace. The presence of a coherence C does not influence measurement outcomes of 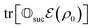 ; see Appendix A.2.3. Using these two building blocks, we will now outline the simulation strategy of each node, as depicted in Fig. 4. As depicted in this figure, we propose alternating simulations and weak measurements of
; see Appendix A.2.3. Using these two building blocks, we will now outline the simulation strategy of each node, as depicted in Fig. 4. As depicted in this figure, we propose alternating simulations and weak measurements of 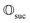 , terminating on the heralding of a successful reaction and the corresponding projection on ρsuc. Note that said measurement of
, terminating on the heralding of a successful reaction and the corresponding projection on ρsuc. Note that said measurement of 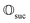 , even if carried out weakly, could disturb the state such that it does not describe a realistic state encountered in nature any more after the measurement, especially in the case of the successful outcome. However, we assume that the simulation channel
, even if carried out weakly, could disturb the state such that it does not describe a realistic state encountered in nature any more after the measurement, especially in the case of the successful outcome. However, we assume that the simulation channel 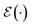 , such as the one devised below through mergo-association, does resemble a process in nature. Thus, it tends to make states decay towards such physically meaningful states, and another application of the channel will, therefore, map us back into a state resembling those in nature,
, such as the one devised below through mergo-association, does resemble a process in nature. Thus, it tends to make states decay towards such physically meaningful states, and another application of the channel will, therefore, map us back into a state resembling those in nature,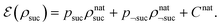 | (2) |
If the molecule is unstable, but the reacted state is desired, we may simply skip this reapplication and proceed. Hence, if measuring 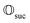 yields a positive outcome, generating meaningful states with a high success rate seems plausible. Further, we can use the following strategy to ensure success even if
yields a positive outcome, generating meaningful states with a high success rate seems plausible. Further, we can use the following strategy to ensure success even if 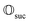 shows that scattering was unsuccessful. Although the state is projected towards the unsuccessful subspace (see Appendix A.2.3 for details), failure is heralded. Therefore, we can apply another simulation channel
shows that scattering was unsuccessful. Although the state is projected towards the unsuccessful subspace (see Appendix A.2.3 for details), failure is heralded. Therefore, we can apply another simulation channel  , which may be slightly modified from
, which may be slightly modified from  (e.g., stronger confinement or dissipation), leading to
(e.g., stronger confinement or dissipation), leading to
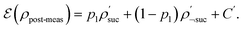 | (3) |
This assumption is similar to that in ref. 79 in that we expect a redistribution of probability toward the state of interest. We can then redo the measurement and iterate between measurements of 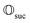 and (progressively more) modified simulation channels until success occurs.
and (progressively more) modified simulation channels until success occurs.
To summarize, we can use the above strategy to create a tree-like sequence of scatterings so that, at each step, the success probability at each of the nodes in the tree is bounded by, say, 1 ≥ P > 0. As we can herald success, at most O(1/P) repetitions are required per node. Since P is assumed to be fixed, the number of repetitions per node is O(1). Furthermore, since failure does not require a restart from the leaves of the tree, the complexities of individual nodes straightforwardly add up. Hence, the number of repetitions grows linearly with the number of nodes in the tree, which, with N initial constituents, goes at most as O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(N)). In Section 3.2 and Appendix A.2, we provide a more detailed discussion of the construction of the weak measurements.
log(N)). In Section 3.2 and Appendix A.2, we provide a more detailed discussion of the construction of the weak measurements.
We leverage parallels to optical tweezers86,87 or molecular beams88,89 that are used in physical experiments to engineer the aforementioned artificial potentials to boost the success probability of scatterings. Before we go into details regarding a specific instance in terms of mergo-association in Section 3.1, we first outline more general approaches here. Molecular beams offer well-established success rates, though they require an abundance of particles and, hence, an abundance of available qubits. On the other hand, traps via artificial potentials – e.g., adding to the Hamiltonian a harmonic potential term confined to a specific region as done in eqn (4) – can considerably boost success without high additional space requirement. Many of the applications we will discuss benefit from reactant states in a form resembling nuclear wave packets. To that end, consider the input states for the scattering process to be prepared as such. Then, the said process supported by artificial potentials would, in most physical cases, largely preserve the locality in configuration space and maintain the wave-packet-like nature of the states. At this point, one may choose to induce a reaction by explicitly modeling a photonic reservoir to excite the reactants.90 Additionally, an explicit register for a bath can be used to absorb excess energy once the reaction has occurred, allowing the products to relax. Alternatively, instead of explicitly tracing out a subsystem here, post-selection on a ‘successful’ reaction, as described later in Section 3.2, can serve to model energy moving out of the system. Finally, energy dissipation can be implemented using Markovian open-system simulation methods, as discussed in more detail below.
Beyond the scattering approach, one could think of using a molecular Hartree–Fock (HF) state as an alternative heuristic for an initial state for the reaction dynamics under investigation. One can expect the efficacy of this approach to be limited to cases where the Hartree–Fock state as input to a simulation channel is close enough to the manifold of physically meaningful states so that convergence to a desired state as input to a reaction happens in controllable time, such as in systems with low static correlation. While such systems tend to be amenable to classical treatment, they may be candidates for early experiments of our approach on quantum devices, as it is likely that using an HF initial state has considerably lower constant factors than the scattering approach. In contrast, the scattering approach will apply to more general states (such as those where Hartree–Fock does not provide a sufficient heuristic).
As mentioned above, the embedding of processes into a larger environment play an important role in the framework during the molecular preparation stage. The ability to dissipate excess energy is essential for both the probability of successfully forming stable bound states and the ability of the dynamics to emulate the open-system evolution of chemical experiments. Recently proposed methods for simulating the weak coupling to a large, memory-less (i.e., Markovian) environment modelled by a Lindbladian operator91,92 can be used to model the presence of such a dissipative bath.82,83,93–95 This simulation is efficient in the size of the system and for some methods is shown to converge to a thermal state.82,83 The only parameter of this procedure that does not scale polynomially with system size is the thermalization time, which is difficult to predict and can, in principle, grow exponentially with system size. However, our observation is that slowly thermalizing systems in our simulation correspond to systems that also thermalize slowly in nature. Thus, for physically motivated open-system models, we would expect to produce either thermalized, metastable, or slowly thermalizing states, depending on which ones are prevalent in nature. A good example of these types of systems would be a glassy molecular mixture. From this perspective, we conjecture that polynomial-time simulations are sufficient to reach all chemically relevant states.
One thing to note is that the system on which the readout is to be performed may need to include some degrees of freedom surrounding the molecule, e.g., if solvent effects, photon or phonon couplings, or non-Markovian dynamics96 are important. The preparation of this more explicit bath follows the same framework as the main molecular degrees of freedom.
3. A scattering-based state-preparation step
With a conceptual framework in mind, in this section, we discuss a specific instance of a single scattering step. The approach is based on an external-potential assisted merging of molecular fragments and the construction of a success-heralding measurement oracle. In the first part, we discuss the coherent part of the simulation of the merging. Part of the open-system character of the approach in Fig. 3 is brought into play by means of the measurement oracle outlined in the second part of this section.3.1. Molecular states by mergo-association
A promising approach to realize the assemblage of molecular wavefunctions in Fig. 3 is mergo-association, as considered in ref. 75–77. Here, optical tweezers confine two fragments – e.g., two hydrogen atoms – to form a bond.To mimic this, we propose to carry out the simulation in the following way. We consider a real-space first-quantized representation the most convenient with oracles for the repeat-until-success procedure. We closely follow the implementation put forward in ref. 30 to represent the Hamiltonian. However, note that the core building block is open-system simulation, e.g., implemented by combining the methods of ref. 30 with open-system techniques, as proposed in ref. 82. Then, we place the two participating systems at a reasonable estimate for a bonding distance. For dihydrogen, this is well known; for more involved systems, a heuristic guess needs to be found. Initially, we implement their dynamics according to two independent Hamiltonians, HA on subsystem A and HB on subsystem B. Then, we slowly turn on inter-system Coulomb interactions HAB = Vint together with trapping potentials Vtrap, according to
| H(s) = HA + HB + f(s)HAB + g(s)Vtrap. | (4) |
For the example of two nuclei, modeling the trap by a harmonic potential acting on nuclear coordinates R1, R2, its functional form is given simply by75–77
| Vtrap(R1, R2) = Vtrap1(R1) + Vtrap2(R2), | (5) |
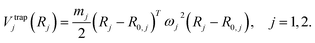 | (6) |
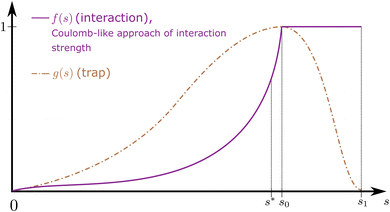
More details on this are provided in Appendix A.1.1. A qualitative choice of f, g is displayed in Fig. 5. After the merging (s ≥ s0), the trap is re-released (s0 ≤ s ≤ s1), while the interaction stays on. With a certain probability of success, the state will not undergo a diabatic transition into a higher-lying excited state, meaning a successful merger has occurred. The specific design of scheduling functions is left up to further research. However, in order to mimic mergo-association, we propose the use of an f(s) that schedules the inter-species interactions to resemble the trajectory of a Coulomb potential. More details on a quantum encoding of the trap potential can be found in Appendices A.1 and A.1.1.
Equivalently to the adiabatic evolution in s, one may put system A and system B at initial distance z* and move their centers of masses together at a predetermined rate 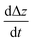 until the bonding length is reached. Hence, the scheduling functions f(s), g(s) are not present in the Hamiltonian anymore, and naturally the strength of the interactions is implicitly determined by distance, recovering the procedure of mergo-association.
until the bonding length is reached. Hence, the scheduling functions f(s), g(s) are not present in the Hamiltonian anymore, and naturally the strength of the interactions is implicitly determined by distance, recovering the procedure of mergo-association.
The mergo-association scheme we follow relies on assumptions from scattering theory. The setup in scattering theory is that two scattered objects, situated beyond a certain scattering length, can be modeled as free particles. Within the scattering length, the scattered product is considered as ‘one’. Conceptually, this is analogous to the ‘molecule factory’ in Fig. 3. The scattering length, or harmonic length, is defined as 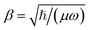 with a frequency ω and relative mass µ = m1m2/(m1 + m2) and induces a notion of a bonding energy via ℏω. As we are interested in chemical bonds, a proxy for this scattering frequency can be the most weakly bound state or the highest-lying bonded vibrational excited state.
with a frequency ω and relative mass µ = m1m2/(m1 + m2) and induces a notion of a bonding energy via ℏω. As we are interested in chemical bonds, a proxy for this scattering frequency can be the most weakly bound state or the highest-lying bonded vibrational excited state.
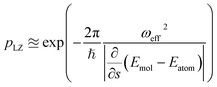
The key aspect of such a mergo-association is the choice of trap frequency ω and the consequences on the diabatic transition probability. Here, we work with an isotropic trap for simplicity, hence eqn (6) is described by a single trap frequency ω. Successful, in our case, means that a (e.g., covalent) bond has been formed and that there is no diabatic transition beyond a certain vibrational frequency of the trapped system, say ωa. Then, it is possible to approximate the probability of success by using the Landau–Zener probability,97
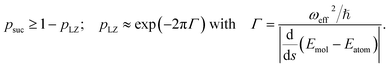 | (7) |
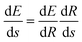 . More details are given in the caption of Fig. 5. Defining the velocity
. More details are given in the caption of Fig. 5. Defining the velocity 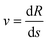 and using the shorthand ∂Emol, ∂Eatom for the energy derivatives, this gives
and using the shorthand ∂Emol, ∂Eatom for the energy derivatives, this gives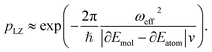 | (8) |
A more detailed discussion can be found in Appendix A.1.2, and we continue by presenting a simplified final expression. We start by the observation in [ref. 76, eqn (54)] that
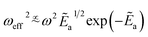 | (9) |
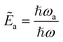 as a ‘relative bonding energy’. Together with expressions for energy derivatives from eqn (A16) and an approximation to eqn (9) we can obtain a bound on pLZ,
as a ‘relative bonding energy’. Together with expressions for energy derivatives from eqn (A16) and an approximation to eqn (9) we can obtain a bound on pLZ,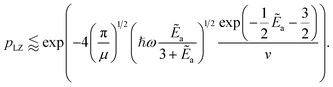 | (10) |
Ideally, we want pLZ to be close to zero so that psuc is close to one. Then, up to the speed of evolution v and effective mass µ, this depends on the ratio of binding energy compared to trap energy, Ẽa ∼ ωa/ω. The inner exponential is closer to one (which means smaller pLZ) for small Ẽa and thus for ω as large as possible relative to ωa. Beyond this, for fixed ℏωa, the other term depending on frequencies, 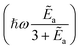 , is also maximal for large trap strength ω. However, there is a trade-off in maximizing this probability of success versus minimizing the cost factor of the block-encoding of the operator. The latter represents the cost of representing the potential in the block-encoding access model, and is quantified by the operator one-norm of the potential, αtrap. Generally, we would aim to keep the frequency no larger than necessary to keep the block-encoding cost low. Additionally, we can look at the system of interest in ref. 75–77, namely Rb and Cs. They use ω = 150 kHz for all of their simulations and experiments. This order of magnitude is about the same as the appearing ωa, which is roughly 110 kHz; the scattering length (regarding binding energy) for this system in a weakly bonded regime is approximately 645a0.98 This setup allows75 high probabilities of success to be observed (see [ref. 75, Fig. 4], close to 80%).
, is also maximal for large trap strength ω. However, there is a trade-off in maximizing this probability of success versus minimizing the cost factor of the block-encoding of the operator. The latter represents the cost of representing the potential in the block-encoding access model, and is quantified by the operator one-norm of the potential, αtrap. Generally, we would aim to keep the frequency no larger than necessary to keep the block-encoding cost low. Additionally, we can look at the system of interest in ref. 75–77, namely Rb and Cs. They use ω = 150 kHz for all of their simulations and experiments. This order of magnitude is about the same as the appearing ωa, which is roughly 110 kHz; the scattering length (regarding binding energy) for this system in a weakly bonded regime is approximately 645a0.98 This setup allows75 high probabilities of success to be observed (see [ref. 75, Fig. 4], close to 80%).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 frequency for ωa (approx. 1012 kHz). Therefore, we expect the required ω to be, in general, vastly larger than 150 kHz; however, the hope is that the remaining behavior will carry over, and we only need to scale it according to the relative difference in bonding energy. Then, in fact, Ea = ℏωa can remain bounded in the two-atom/molecule scatterings and effectively act as a constant in an asymptotic sense. This means for pLZ to be bounded as well, ω incurs a (likely substantial) constant factor through Ea and then scales as O(µ) for
000 cm−1 frequency for ωa (approx. 1012 kHz). Therefore, we expect the required ω to be, in general, vastly larger than 150 kHz; however, the hope is that the remaining behavior will carry over, and we only need to scale it according to the relative difference in bonding energy. Then, in fact, Ea = ℏωa can remain bounded in the two-atom/molecule scatterings and effectively act as a constant in an asymptotic sense. This means for pLZ to be bounded as well, ω incurs a (likely substantial) constant factor through Ea and then scales as O(µ) for 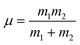 . Therefore, since at the last scattering stage in the “molecule factory”, µ ∼ Nnuc, we can roughly estimate ω in the expression of αtrap by a linear factor Nnuc and a system-dependent constant factor for the binding energy of covalent bonds. Using this in our asymptotic expression for the block-encoding factor of the trap,
. Therefore, since at the last scattering stage in the “molecule factory”, µ ∼ Nnuc, we can roughly estimate ω in the expression of αtrap by a linear factor Nnuc and a system-dependent constant factor for the binding energy of covalent bonds. Using this in our asymptotic expression for the block-encoding factor of the trap,| αtrap ≈ O(Nnuc3Ωtrap2/3). | (11) |
We want to compare this result with the corresponding sub-normalization factors of the kinetic energy, 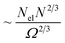 , where N is the number of basis functions across three dimensions and Ω the volume of the simulation box, and the Coulomb energies,
, where N is the number of basis functions across three dimensions and Ω the volume of the simulation box, and the Coulomb energies,  .30 If the density of grid points grows linearly with the number of particles, then the encoding costs of these operators increase roughly with power
.30 If the density of grid points grows linearly with the number of particles, then the encoding costs of these operators increase roughly with power 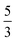 or
or 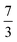 of the system size, whereas the cost of the trap scales cubically. It also grows with the volume Ω2/3 rather than with the inverse grid density. A more accurate representation will need a finer grid spacing, increasing the cost of representation for the Coulomb potentials. For the trap potential, the box size matters, which will need to increase for larger systems, although there is no increase in cost for increasing accuracy through a finer grid spacing.
of the system size, whereas the cost of the trap scales cubically. It also grows with the volume Ω2/3 rather than with the inverse grid density. A more accurate representation will need a finer grid spacing, increasing the cost of representation for the Coulomb potentials. For the trap potential, the box size matters, which will need to increase for larger systems, although there is no increase in cost for increasing accuracy through a finer grid spacing.
This necessary increase in the number of basis functions has direct consequences on the implementation cost, through query complexity as outlined in the paragraphs above, but also through constant factors.
The constant factor Toffoli complexity regarding the implementation of phase estimation of a Born–Oppenheimer Hamiltonian is reported in [ref. 30, theorems 4 and 5]. Parameters affected by discretization in this expression are the block-encoding factor (in our work α, in ref. 30λ) and the number of bits used to store the number of plane-waves used for discretization np.
We first discuss the impact by np. It appears with terms growing at most quadratically; the same scaling would hold when using a grid. Using the fact from above that a grid for protons would need to be roughly 260 times as dense as one for electrons, np(proton) ≈ np(electron) + [log2(260)] ⪅ np(electron) + 9, with the np parameter appearing in linear and quadratic order in the cost for both qubitization and interaction picture simulation. Therefore, we can expect the Toffoli count following [ref. 30, theorems 4 and 5] to only grow modestly even though the grid needs to be significantly denser. Additionally, the subnormalization factor of the block-encoding of the Hamiltonian terms may depend on the number of grid-points or basis functions N that is chosen; see eqn (11) and below it. These terms are linear (potential energy) and quadratic (kinetic energy) in the number of grid points per dimension; a roughly 6.38-fold increase as discussed above would thus lead to a 6.38 times higher subnormalization of the potential energy terms as well as a roughly 40.7 times higher subnormalization for the kinetic energy. As we point out in the previous paragraph, the simulation of the trap itself does not depend on the grid density. Hence overall, we expect a rather low impact of non-BO simulation on the constant factors in the simulation beyond the subnormalization factor; the latter grows linear/quadratic with finer discretization and polynomial in the particle number. Gate counts related to creating superpositions over the grid, etc. depend poly-logarithmically on the chosen discretization.
The non-BO simulation approach would be necessary in order to properly represent the mergo-association approach. Our state-preparation therefore would incur slightly higher simulation costs for systems that are sufficiently well represented by the BO approximation. Note that following the algorithms in ref. 18 and 48 as an alternative pathway to implement a mergo-association-like process, i.e., resolving the nuclear dynamics classically and only the electrons quantumly, may incur similar block-encoding costs that would similarly need to be considered.
3.2. Measurement oracles for success heralding
Suppose now that after a scattering step, we aim to herald success according to eqn (2) and (3). To that end, we need a measurement operator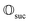 able to give the desired partitioning. A more detailed discussion of the following outline can be found in Appendix A.2.
able to give the desired partitioning. A more detailed discussion of the following outline can be found in Appendix A.2.
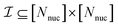 , then
, then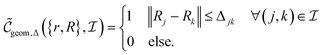 | (12) |
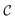 returns 1. Note that we choose to restrict the evaluation to nuclear coordinates as the relative position of nuclei within a bonded state is essentially stationary compared to the electrons. The definition in eqn (12) is classical and assumes direct access to {Rj}j∈[Nnuc], whereas types of states we encode are superpositions of tensor products across basis state labels,
returns 1. Note that we choose to restrict the evaluation to nuclear coordinates as the relative position of nuclei within a bonded state is essentially stationary compared to the electrons. The definition in eqn (12) is classical and assumes direct access to {Rj}j∈[Nnuc], whereas types of states we encode are superpositions of tensor products across basis state labels, 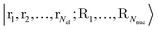 . More generally, we can think of what happens to a mixed state when going through the success heralding. Then, we consider states of the form
. More generally, we can think of what happens to a mixed state when going through the success heralding. Then, we consider states of the form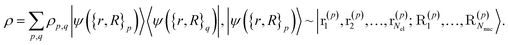 | (13) |
The set 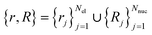 denotes a nuclear and electronic configuration, and {r, R}j denotes an instance as the pth term of the superposition. Configurations include a spin degree of freedom. Hence the range of p, q is the number of possible basis states labeling the grid points.
denotes a nuclear and electronic configuration, and {r, R}j denotes an instance as the pth term of the superposition. Configurations include a spin degree of freedom. Hence the range of p, q is the number of possible basis states labeling the grid points.
Now, we assume that there is a quantum circuit that can achieve the action of  efficiently, namely a
efficiently, namely a  that takes the state ρ plus an ancilla and stores success in the ancilla, according to the following sets:
that takes the state ρ plus an ancilla and stores success in the ancilla, according to the following sets:
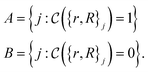 | (14) |
The crucial part here is that such a criterion induces a bi-partition of the Hilbert space, splitting the set of states into two groups. Specifically, every state of the form |ψ({r, R}j)〉 either corresponds to a configuration with 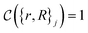 or a configuration with
or a configuration with 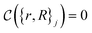 . The set A enumerates the states the oracle accepts as merged, and B enumerates the states that the oracle rejects. For convenience we will denote |ψj〉:= |ψ({r, R}j)〉 from now on. With this bi-partition, a general input state can now be written as
. The set A enumerates the states the oracle accepts as merged, and B enumerates the states that the oracle rejects. For convenience we will denote |ψj〉:= |ψ({r, R}j)〉 from now on. With this bi-partition, a general input state can now be written as
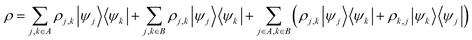 | (15) |
Weak measurement of this oracle and thus flagging of a successful merging can be implemented following the subsequent operations based on work in ref. 100–103:
(1) Append an ancilla qubit, qa,1, and perform the unitary 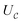 on the joint system. This stores the ‘success value’ in the ancilla.
on the joint system. This stores the ‘success value’ in the ancilla.
(2) Append a second ancilla, qa,2, and perform a controlled rotation CRy(δ) gate on qa,2 conditioned on qa,1.
(3) Perform 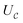 on the input state and qa,1, resetting qa,1.
on the input state and qa,1, resetting qa,1.
(4) Measure qa,2 in the computational basis and reset it for later use. The measurement on qa,2 is then used as a result flag of a successful merger.
Finally, we can conclude that the measurement oracle 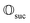 is composed of the circuit
is composed of the circuit 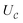 and the weak measurement scheme above. More details are given in Appendix A.2.3.
and the weak measurement scheme above. More details are given in Appendix A.2.3.
An important aspect to consider in constructing these measurements is that the wavefunctions encoded, even when expressed as a mixed state, need to satisfy the necessary exchange symmetry (antisymmetric for fermions, symmetric for bosons). Ongoing measurement induces the risk of compromising such symmetries. Thus, the measurement needs to be adapted to satisfy that. A detailed discussion is provided in Appendix A.2.2.
 by a check of whether the obtained state is in the correct spin state. Suppose we have access to an implementation of the time-evolution of the (normalized) spin operator S2. Then, one step of quantum phase estimation allows storing in an ancilla qubit whether there is a singlet (0) or triplet (1) state. Augmentation to higher-order spin states (such as doublets, quadruplets, etc.) follows simply by augmenting the ancilla register of the QPE circuit to represent the appropriate spin numbers. Based on this result, we can accept or reject according to the obtained outcome and thus effectively have a scheme that projects into the desired spin state. Therefore, this yields an implementation of a projection into the correct spin state; this requires nontrivial knowledge about the expected spin state. One can draw from ideas in ref. 104 to deal with more complicated ensembles of spin states. A detailed procedure in case of lack of knowledge or intuition about the expected spin state is subject to further research.
by a check of whether the obtained state is in the correct spin state. Suppose we have access to an implementation of the time-evolution of the (normalized) spin operator S2. Then, one step of quantum phase estimation allows storing in an ancilla qubit whether there is a singlet (0) or triplet (1) state. Augmentation to higher-order spin states (such as doublets, quadruplets, etc.) follows simply by augmenting the ancilla register of the QPE circuit to represent the appropriate spin numbers. Based on this result, we can accept or reject according to the obtained outcome and thus effectively have a scheme that projects into the desired spin state. Therefore, this yields an implementation of a projection into the correct spin state; this requires nontrivial knowledge about the expected spin state. One can draw from ideas in ref. 104 to deal with more complicated ensembles of spin states. A detailed procedure in case of lack of knowledge or intuition about the expected spin state is subject to further research.
We remark that construction of the S2 operator is simple given an encoding as in eqn (13), as then it simply translates to its form as Pauli operators acting on the spin degree of freedom.
4. Conclusion and outlook
We have provided an algorithmic framework that, in principle, can solve a broad set of chemically relevant problems using inherently efficient building blocks. To that end, we considered that, while general ground states are hard to obtain, we may assume we are able to prepare atomic ones as a single-cost effort that can enable a building block library. A scattering process, implemented by simulating dynamics and boosted by artificial potentials, can produce a molecular input state for a subsequent dynamical simulation, which is then followed by the measurement of dynamical quantities. Preparing molecular states via mergo-association is a particularly promising candidate here, which we discussed in detail. We provide examples of applications from, e.g., spectroscopy, photochemistry, and beyond.Future work remains to build upon this approach and provide a more general and detailed analysis of mergo-association and numerical experiments of this approach, e.g., to gauge the feasibility of the procedure with respect to constant factors and to investigate the more precise costs arising from choosing specific problem instances and methodologies. Another interesting extension would be the inclusion of other modeling tools used in classical simulation, such as the Nosé–Hoover thermostat.105 Additionally, an interesting avenue would be to consider additional classical dynamical simulation such as more molecular dynamics (e.g., studied in the context of protein modeling in ref. 106), in particular in the case when conservation laws (such as energy conservation) allow direct mappings to Hamiltonian simulation.107 One can also think of incorporating different notions of how to distinguish bonded states in molecules, e.g., grounding on the notion of molecular structure in ref. 108.
A common focal point in quantum chemistry is finding ground state energies, a problem known to be QMA-complete for local Hamiltonians like those seen in molecular systems. We should not restrict ourselves to that perspective, which focuses on a problem known to be hard, and looks for paths that allow using dynamics more directly. Additionally, for situations when the ground state is of interest, it may prove useful to give up the search for exact solutions to a hard problem and look at heuristics. The Hartree–Fock problem is known to be NP-hard yet practically efficient, thanks to approximations.44 Attempts based on open-system dynamics such as in ref. 79 and 109 may be a promising path towards quantum heuristics for ground states. Nevertheless, we call upon what dynamical quantum simulation offers for chemistry.
Author contributions
Conceptualization: AAG, JF, PS; methodology: PS, LBK, AA, JCGA, DA, MB, CG; investigation: PS, LBK, AA, JCGA, DA, MB; visualization: DA, PS, CG, MB; funding acquisition: AAG; project administration: PS; supervision: AAG, JF; writing – original draft: PS, LBK; writing – review & editing: PS, AAG, AA, LBK, JCGA, DA, MB, CG, JF.Conflicts of interest
There are no conflicts to declare.Data availability
No software or code has been included, and no new data were generated or analysed as part of this study. All results are part of the document.A. Appendices
A.1. Scattering molecules via mergo-association
This section includes more details on merging molecules by mergo-association as described in Section 3.1.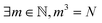 ,
, | (A1) |
The associated volume box 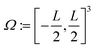 . Exemplarity for dihyodrogen with Nel = 2, Nnuc = 2, and an estimated volume of |Ω| = L3 = (10a0)3 is expected to suffice, where a0 is the Bohr radius. With a grid spacing of ∼0.1a0, this volume would lead to N ∼ 106. Then, upon defining the size of the simulation box, it is straightforward to map every p ∈ G to a coordinate,
. Exemplarity for dihyodrogen with Nel = 2, Nnuc = 2, and an estimated volume of |Ω| = L3 = (10a0)3 is expected to suffice, where a0 is the Bohr radius. With a grid spacing of ∼0.1a0, this volume would lead to N ∼ 106. Then, upon defining the size of the simulation box, it is straightforward to map every p ∈ G to a coordinate, 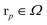 for electrons and
for electrons and 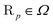 for nuclei.
for nuclei.
The following is needed to describe the desired dynamics: Hamiltonians describing the isolated hydrogen atoms, interactions between the hydrogen atoms, and a ‘trap potential’ modeled by a harmonic oscillator potential. The system Hamiltonian without a trap is given by
| Hsys = Tel + Tnuc + Unuc–el + Vee + Vnn. | (A2) |
As the initial state to the simulation, we assume access to a product state of the ground states of the hydrogen atom, respectively,
| |ψ0,H〉|ψ0,H〉. | (A3) |
From ref. 30, we know the sub-normalization factors (which we will repeat further below) to encode these in real space, together with estimates for the cost of Hamiltonian simulation algorithms. The placement of the individual |ψ0,H〉 should follow a guess for the desired molecular distance so that the relaxation through the trap potential induces a more accurate placement for the bonded state.
The harmonic trap potential from ref. 76 and 77 is
| Vtrap(R1,R2) = Vtrap1(R1) + Vtrap2(R2), | (A4) |
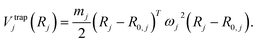 | (A5) |
We may neglect electronic mass and coordinates for the trap parameters given the large discrepancy between electronic and nuclear mass; the confinement is a heuristic approach nonetheless. The positions R0,j define the center of the two traps. For single-particle nuclei, such as dihydrogen, the determination of trap centers is straightforward; in contrast, for larger systems, center-of-mass and relative coordinates need to be considered.77 The frequencies ωj2, in general, make up positive, diagonal matrices; the expression above describes the strength of the trap, which may not be spherically symmetric. For the sake of our discussion here, we will assume the trap to be isotropic, and then the trap frequency can be described by a scalar ωj. The role of these frequencies and relevant energy scales will be discussed further below in Appendix A.1.2.
Next, we discuss a quantum implementation of the trap potential. We reformulate eqn (A5) to
 | (A6) |
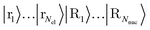 . A state called |rj〉 or |Rk〉 will hold the explicit coordinate information. This requires log(N) qubits per particle to represent its position on the grid. For dihydrogen, overall Nnuc = Nel = 2, so we need 4 × log2(number of grid-points) qubits to encode the grid; with the estimated 106 grid points from above, that makes roughly 80 qubits for the |p〉 register.
. A state called |rj〉 or |Rk〉 will hold the explicit coordinate information. This requires log(N) qubits per particle to represent its position on the grid. For dihydrogen, overall Nnuc = Nel = 2, so we need 4 × log2(number of grid-points) qubits to encode the grid; with the estimated 106 grid points from above, that makes roughly 80 qubits for the |p〉 register.
The procedure that is simulated is described using scheduling functions as mentioned above in eqn (4), so that f(s) introduces the inter-atomic Coulomb interactions and g(s) guides the strength of the trap. As a consequence, implementing this scattering follows evolution across 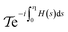 , with H(s) from eqn (4). The truncated Dyson series algorithm in ref. 110 can serve as a way to implement this. A necessary requirement is then to have access to the potentials as a HAM-T oracle, which we outline for Vtrap:
, with H(s) from eqn (4). The truncated Dyson series algorithm in ref. 110 can serve as a way to implement this. A necessary requirement is then to have access to the potentials as a HAM-T oracle, which we outline for Vtrap:
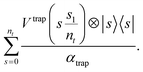 | (A7) |
Using this, we can simulate over s across the scheduling functions so that the inter-species interactions remain and the trap has fully decayed, i.e., until s1. This operation can be constructed easily given the LCU outlined in eqn (A8) and (A10) together with oracular access to the scheduling functions from eqn (A9) and an appropriate superposition over |s〉, s = 0, …, nt. To construct superpositions over where nt is not a power of two, see e.g. [ref. 30, Appendix J]. The equivalent construction is necessary for the interaction term together with f(s); see eqn (4), and encodings for the Coulomb-term in the literature [ref. 30, Appendix K]. There is an argument to make here about the (a) diabaticity of this evolution, which will be part of Appendix A.1.2.
We continue by outlining an LCU encoding of Vtrap(s′) for a specific 0 ≤ s′ ≤ s1. Coordinate directions are denoted by {x, y, z} ∼ {0, 1, 2} and we use the usual LCU notation of PREP and SEL operations so that 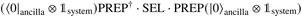 block-encodes the desired operator. The state we are acting on is assumed to be a superposition over |p〉|s′〉, with the state |p〉 representing a spatial part and |s′〉 the current step in the evolution of the merging. The PREP step involves preparing a superposition across nuclei and coordinate directions, weighted by the square root of the interaction strength at that point:
block-encodes the desired operator. The state we are acting on is assumed to be a superposition over |p〉|s′〉, with the state |p〉 representing a spatial part and |s′〉 the current step in the evolution of the merging. The PREP step involves preparing a superposition across nuclei and coordinate directions, weighted by the square root of the interaction strength at that point:
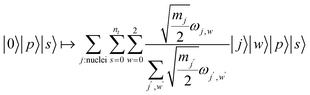 | (A8) |
Next, we illustrate the SEL operation, where we omit amplitudes and explicit sums for clarity. The goal here is to compute state-dependent interaction strengths on the fly. Namely, we aim to prepare a register that contains (Rpi,w − R0;w)2, and another containing g(s) to multiply the latter, so that we can use e.g. ref. 111 to move information from the state into the amplitude. Consequently, access to oracles Of and Og that represent the scheduling is required,
| Of/g : |0〉|s〉 → |f/g(s)〉|s〉. | (A9) |
The oracular access to the scheduling function and the label-to-coordinate mapping may be realized with classical data encodings, e.g., a QROM or other techniques.51,112,113 Using a number of ancillas given by nanc initialized in zero, and assuming a state that encodes the relative center of the trap R0,
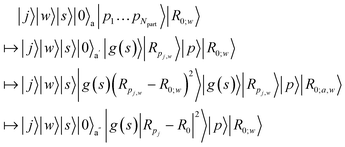 | (A10) |
The size of the necessary ancillary register |0〉a that is used to store intermediary and final results scales linearly in the bits of precision used for numerical representation (to store g(s), Rpj,w and perform multiplication and sum-of-squares). As mentioned above, to finalize the SEL operation, the state information in |g(s)|Rpj − R0|2〉 needs to be moved into the amplitude. There are multiple ways to do so, such as the inequality-testing approach in ref. 111, or, the conceptually simplest would be controlled rotations, conditioned on |g(s)|Rpj − R0|2〉 and applied to the system register.
We refrain from analyzing exact Toffoli or gate counts as done in ref. 30, expecting that the addition of the trap potentials would not add a significant change here per single query to involved oracles and circuits as the appearing arithmetic operations are comparable to the usual potentials in the Hamiltonian. The factor that may make the trap potentials more costly and needs to be studied more closely is its sub-normalization factor. This factor captures the number of necessary queries for a successful block-encoding. We recall the sub-normalization factors from [ref. 30, Appendix K],
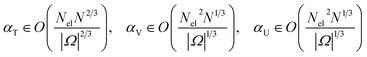 | (A11) |
The block-encoding factor of the trap potential may be upper-bounded by  . Then,
. Then, 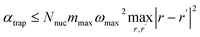 . In the present discretization,
. In the present discretization, 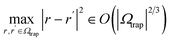 , where Ωtrap ⊆ Ω is the part of the domain the trap potential is defined on. Most of the mass of particles under such a potential will be incentivized to be close to the center; therefore, an upper bound that puts the maximum mass at a maximum distance will not be very tight in most scenarios, and a smaller αtrap may be sufficient. One could further think about designing the shape of the trap potential to be decaying for larger distances to reduce the encoding cost or oscillatory as in optical tweezers, such that the maximum amplitude is always within reach – we leave concrete specifications up to future work. The maximum nuclear mass
, where Ωtrap ⊆ Ω is the part of the domain the trap potential is defined on. Most of the mass of particles under such a potential will be incentivized to be close to the center; therefore, an upper bound that puts the maximum mass at a maximum distance will not be very tight in most scenarios, and a smaller αtrap may be sufficient. One could further think about designing the shape of the trap potential to be decaying for larger distances to reduce the encoding cost or oscillatory as in optical tweezers, such that the maximum amplitude is always within reach – we leave concrete specifications up to future work. The maximum nuclear mass 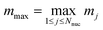 can be treated as a constant factor attached to the nuclei. Then, we have that
can be treated as a constant factor attached to the nuclei. Then, we have that
| αtrap ∈ O(ωmax2Nnuc|Ωtrap|2/3). | (A12) |
Up to the frequency ωmax, the sub-normalizations of the present procedure in eqn (A11) compared to the trap potential inhibit a few key differences. Because the strength of the trap depends on a maximum distance, there is no notion of ‘grid density’ in the cost. Therefore, the factors in eqn (A11) increase when a lower target accuracy is desired. The trap encoding is not directly dependent on accuracy, though it is more pronounced on system size. The system size of the trap may be upper-bounded with the overall system studied, as present at the last scattering stage before ‘evolution’ in Fig. 3.
Therefore, it is key to understand the role of ωmax in the scattering and whether there is a way to relate this quantity to the system size.
 | (A13) |
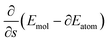 , as a consequence of the chain rule, as |∂Emol − ∂Eatom|v. Here, ∂E are energy derivatives near the initial configuration with respect to the internuclear distance and v, the speed of the evolution along the scheduling function.
, as a consequence of the chain rule, as |∂Emol − ∂Eatom|v. Here, ∂E are energy derivatives near the initial configuration with respect to the internuclear distance and v, the speed of the evolution along the scheduling function.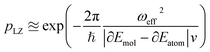 | (A14) |
Thus, the success probability of the mergo-association, so that the merging happens without transitioning into a higher vibrational state of the trapped system as desired, is
| psuc ∼ 1 − pLZ. | (A15) |
As we pointed out in the previous section, this means that the type of evolution we call successful here is adiabatic. It is important to note that this is not adiabatic ground-state preparation, which is explicitly beyond the scope of our work. Following another discussion in the preceding section, the threshold to success here considers molecular bound states, so the ‘upper limit’ for adiabaticity would be the highest-lying vibrational bound state. One way or another, a practical implementation will need to consider this. This still poses limits on the speed of evolution (given by v in eqn (A14)). Then, 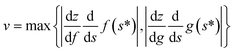 , where z is the considered internuclear distance.
, where z is the considered internuclear distance.
Looking at eqn (A14), we can identify that the stronger (“steeper”) the potential as described by the effective frequency, the higher the success, and the faster the merging proceeds, the less likely. This conclusion is consistent with intuition.
We continue by breaking down the quantities that appear. Following ref. 76, ∂Eatom ≈ 0, as it is reasonable to assume the energy surface for separated atoms is flat. Taking a harmonic oscillator approximation to the relative motion of the nuclei, [ref. 76, eqn (37)] obtains an approximation to the gradient, ∂Emol ≈ µω2z*, where z* is the point of contact of the avoided crossing between the two states. In terms of the scheduling functions that we envision, this corresponds to the state at s = s*, 0 < s* < s0 < s1 (Fig. 5): briefly before both interaction and trap are ‘fully acting’. Assuming an isotropic potential, the spatial coordinate is approximated as 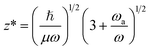 so that [ref. 76, eqn (35)]
so that [ref. 76, eqn (35)]
| ∂Emol ≈ (ℏµ)1/2ω(3ω + ωa)1/2, | (A16) |
To estimate ωeff, we can also follow [ref. 76, eqn (52)]:
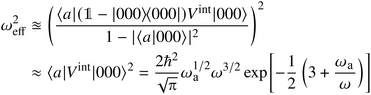 | (A17) |
States “000” describe the vibrational ground-state, “a” an excited vibrational state, and ω is the frequency of the harmonic oscillator trap. The approximation to only look at the transition element itself is investigated in [ref. 76, Fig. 6] – for a merely qualitative argument, this is a sufficient choice. The choice for ωa in our case is an estimate for an upper threshold of the respective bonded vibrational energy subspace. Introducing a ‘binding energy’-quantity Ea = ℏωa, we can rewrite ωeff2 to be approximately proportional to [ref. 76, eqn (54)],
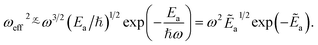 | (A18) |
In the latter equation, we introduce the relative binding energy Ẽa = Ea/(ℏω), defined in relation to the trap energy. Then,
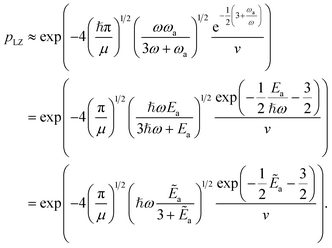 | (A19) |
A.2. Construction of measurement oracles for certifying reactions
For this oracle construction, we assume a first-quantized real space implementation. The choice of representation in first-quantization on real space makes the construction of the following oracle easier; of course, plane-wave or plane-wave dual bases52 are possible too and can be translated to with appropriate transformations. The encoded quantum states are linear combinations of wavefunctions with fermionic (antisymmetric) and bosonic (symmetric) parts. Within such a combination, a single component looks like a tensor product over electronic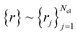 and nuclear
and nuclear 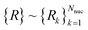 grid labels (represented on the grid eqn (A1)),
grid labels (represented on the grid eqn (A1)),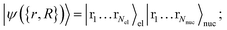 | (B1) |
We further remember that the above collapsed notation that also contains spin information in an extra qubit, i.e., 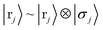 with σj ∈ {↑, ↓}, and analogous for nuclei if desired. Then, a density matrix formulation of linear combinations of such a state is
with σj ∈ {↑, ↓}, and analogous for nuclei if desired. Then, a density matrix formulation of linear combinations of such a state is
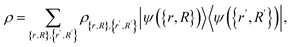 | (B2) |
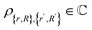 . The goal of this section is to construct an oracle that can distinguish the ‘good’, reacted components of such a state from the ‘bad’, non-reacted components. Given a state representing two molecular fragments that have evolved for some time, we want to distinguish the parts of the wavefunction that correspond to the fragments having reacted to form a single molecule from those where they are still separate unbound fragments.
. The goal of this section is to construct an oracle that can distinguish the ‘good’, reacted components of such a state from the ‘bad’, non-reacted components. Given a state representing two molecular fragments that have evolved for some time, we want to distinguish the parts of the wavefunction that correspond to the fragments having reacted to form a single molecule from those where they are still separate unbound fragments.
As we consider linear transformations, it suffices to study the effect on the individual components from eqn (B1) to draw conclusions for a general state in eqn (B2). Therefore, we first focus on a single position-basis state |ψ({r, R})〉 in the upcoming Appendix A.2.1 before we consider exchange symmetry in Appendix A.2.2 and more general superpositions in Appendix A.2.3.
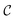 for whether a given configuration corresponds to a desired molecule can then be constructed,
for whether a given configuration corresponds to a desired molecule can then be constructed,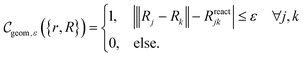 | (B3) |
Note that evaluating this criterion is classically efficient with respect to the number of bits devoted to the constituent quantities, scaling no worse than O(Nnuc2) in the number of nuclei and no worse than quadratically in the bit-precision due to a product and a square root in the evaluation of the norm. In other words, evaluating this function is classically efficient in the size of the molecule as long as the bit-precision only grows polynomially, corresponding to the requirement that the number of grid points in the simulation should not grow faster than exponential in the involved particle number.
In some cases, it may be possible to devise more accurate criteria, such as by comparing the angles between inter-nuclear distances to desired bond angles. On the other hand, there may be cases where less is known about the target structure. Then, the best that one can hope for is to check that the two fragments are at least spatially adjacent, corresponding to the looser requirement
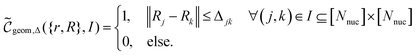 | (B4) |
 , in which we only check a subset of the encoded locations regarding proximity. There are many ways this type of geometric requirement could be mixed and matched, e.g., utilizing different levels of knowledge or different precisions ε for different groups of atoms. Either way, common to these approaches is the fact that the classical evaluation of the criterion is efficient under the mild restrictions to the grid resolution outlined above.
, in which we only check a subset of the encoded locations regarding proximity. There are many ways this type of geometric requirement could be mixed and matched, e.g., utilizing different levels of knowledge or different precisions ε for different groups of atoms. Either way, common to these approaches is the fact that the classical evaluation of the criterion is efficient under the mild restrictions to the grid resolution outlined above.
A result of this classical efficiency is that a corresponding unitary to perform the computation can also be implemented efficiently on a quantum computer using reversible logic. Specifically, for a given efficient criterion  of the form considered here, the following unitary can be implemented:
of the form considered here, the following unitary can be implemented:
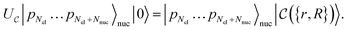 | (B5) |
Thus, extracting information about the criterion into an ancilla qubit for easy access is possible. Using a measurement of this ancilla then allows for a projection onto the good 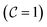 subspace, heralded by an outcome “1” of the measurement. However, the outcome “0” similarly fully projects the state into the bad subspace
subspace, heralded by an outcome “1” of the measurement. However, the outcome “0” similarly fully projects the state into the bad subspace  . Furthermore, care needs to be taken to avoid either kind of projection destroying physically important symmetries of the state, including fermionic and bosonic particle-exchange symmetries. Mitigating each of these potential problems will be the topics of the following two sections.
. Furthermore, care needs to be taken to avoid either kind of projection destroying physically important symmetries of the state, including fermionic and bosonic particle-exchange symmetries. Mitigating each of these potential problems will be the topics of the following two sections.
A.2.2.1 Symmetrization of the wavefunction. Recall that the wavefunctions we encode are given as superpositions of position-labelling basis states,
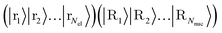 | (B6) |
We repeat that by  we mean the labels for grid points and spin rather than the resolved coordinates and choose this notation as it is more illustrative in the context of (anti)symmetrization of the wavefunctions. For fermionic (indistinguishable) particles, the wavefunction needs to be anti-symmetrized with respect to the indistinguishable degrees of freedom. Formally, this can be done by applying the antisymmetrization operator
we mean the labels for grid points and spin rather than the resolved coordinates and choose this notation as it is more illustrative in the context of (anti)symmetrization of the wavefunctions. For fermionic (indistinguishable) particles, the wavefunction needs to be anti-symmetrized with respect to the indistinguishable degrees of freedom. Formally, this can be done by applying the antisymmetrization operator  . Using the electronic degrees of freedom as an example, and with σ a permutation from the permutation group over Nel elements, SNel:
. Using the electronic degrees of freedom as an example, and with σ a permutation from the permutation group over Nel elements, SNel:
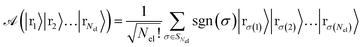 | (B7) |
Similarly, bosonic degrees of freedom will be symmetric with respect to exchange, described by symmetrization 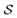 of the general form
of the general form
 | (B8) |
In general, a set of nuclei to be modeled as indistinguishable will correspond to a subset of nuclear registers to be (anti)symmetrized. Thus, the desired symmetry properties are characterized by sets of registers to be symmetrized,  , and sets of registers to be anti-symmetrized,
, and sets of registers to be anti-symmetrized, 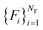 . Denoting which basis states an operator acts on by a subscript, one gets the following anti-symmetrized state:
. Denoting which basis states an operator acts on by a subscript, one gets the following anti-symmetrized state:
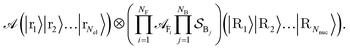 | (B9) |
A.2.2.2 Illustrative example: H2O2. To elucidate our notation, consider the molecule H2O2, and assume that the non-symmetrized positions are encoded as
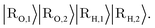 | (B10) |
In this case, the oxygen nuclei are spin-0 nuclei, meaning they should be symmetrized. On the other hand, the hydrogen nuclei are spin-1/2 particles, meaning they should be anti-symmetrized. We can represent this by the following two sets:
| B1 = {1,2}, F1 = {3,4}. | (B11) |
The first tells us to symmetrize the oxygen registers (1 and 2), and the second tells us to anti-symmetrize the hydrogen registers (3 and 4). The state after symmetrization is therefore
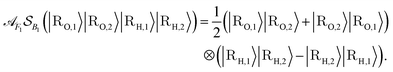 | (B12) |
The encoded molecular state will generally be a superposition of states of form in eqn (B9), i.e., the tensor products of an antisymmetric wavefunction, a symmetric wavefunction, and possibly a non-symmetrized component. Then, for the remainder, it suffices to discuss the oracle's effect on one term of the superposition. To see what symmetry implies for the construction of oracles, consider again the example of H2O2. Looking at the form of the wavefunction in eqn (B10) and the equilibrium geometry of the molecule, one might be tempted to define a criterion of the form
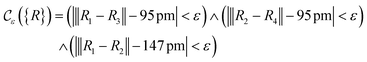 | (B13) |
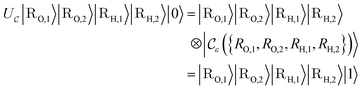 | (B14) |
 | ||
| Fig. 6 Equilibrium configuration of a H2O2 molecule, with oxygen nuclei marked in red and hydrogen nuclei marked in grey. | ||
However, the same cannot be said for states where the positions are permuted. For instance, swapping the oxygen positions, the evaluation of the oracle reads
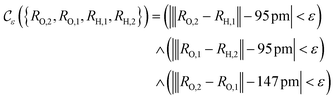 | (B15) |
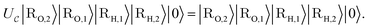 | (B16) |
Considering the full symmetrized wavefunction, one finds
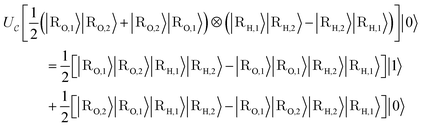 | (B17) |
Despite all four components corresponding to the same molecule (just with particle labeling altered), only two of them have been certified by the oracle. Furthermore, if the ancilla is measured, the resulting projected state is no longer of the symmetric form described in eqn (B9), and direct inspection shows that it is neither symmetric nor anti-symmetric upon permutations among the nuclear coordinates.
One possible response to this problem might be simply re-applying an (anti-)symmetrization step whenever a projection occurs. In principle, this operation scales linearly (up to logarithmic factors) in the system size;114,115 thus, it would not change the polynomial runtime of the algorithm. However, existing algorithms require a particular structure on the input state, a requirement that is linked to unitarity114 and thus likely challenging to lift. Furthermore, even with a hypothetical generalization of the algorithm, the present work proposes a quasi-continuous weak-measurement strategy for monitoring the reaction criteria. Since this entails frequent (weak) measurements during the simulation run, it is likely to lead to a high total number of measurements, scaling extensively with the simulation time. Restoring symmetry after each measurement could, therefore, add significant complexity to the algorithm, even if a fast and applicable symmetrization algorithm is available. Therefore, we next discuss a more comprehensive approach to address these shortcomings.
A.2.2.3 Symmetry of states. To build certification oracles that are valid under the correct exchange symmetry, we will first formalize the symmetrization requirement for the states of the system. Consider first a single set of identical particles, represented by a set of indices
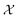 . The group of permutations of this set is characterized by the symmetric group,
. The group of permutations of this set is characterized by the symmetric group, 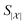 , and for each permutation
, and for each permutation 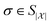 , we can define a unitary consisting of SWAP gates that implements the permutation of our registers:
, we can define a unitary consisting of SWAP gates that implements the permutation of our registers: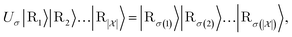 | (B18) |
| Uσ|ψ{r, R}〉 = |ψ[σ{r, R}]〉 | (B19) |
 onto the space of states. In terms of these constructions, the symmetrization requirement is
onto the space of states. In terms of these constructions, the symmetrization requirement is | (B20) |
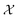 are fermions or bosons.
are fermions or bosons.
Generalizing this construction to multiple sets of bosonic and fermionic particles, the symmetry group takes the form of a product group of the individual bosonic and fermionic symmetries,
| S = SB ⊗ SF | (B21) |
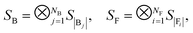 | (B22) |
| Uσ|ψ〉 = sgn(σF)|ψ〉 ∀σ ∈ S. | (B23) |
A.2.2.4 Symmetry of oracles. Using the notation introduced above, we can now state the requirement that a reaction criterion
 needs to fulfill to respect the symmetry defined in the previous section. Specifically, we will say that a criterion
needs to fulfill to respect the symmetry defined in the previous section. Specifically, we will say that a criterion  respects symmetry when a projective measurement of
respects symmetry when a projective measurement of  on a symmetrized state produces post-measurement states that are still correctly symmetrized. Below, we will show that this property holds if and only if
on a symmetrized state produces post-measurement states that are still correctly symmetrized. Below, we will show that this property holds if and only if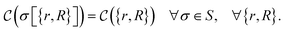 | (B24) |
To see that this is sufficient criteria, consider the projection operators related to the readout of 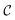 using an ancilla qubit:
using an ancilla qubit:
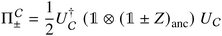 | (B25) |
 | (B26) |
Looking at the constituent operators, we can note that
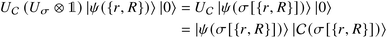 | (B27) |
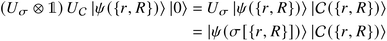 | (B28) |
Thus, if the relation in eqn (B24) holds, it implies that
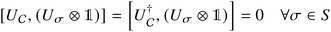 | (B29) |
Therefore, the projectors also commute with the permutations,
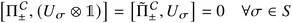 | (B30) |
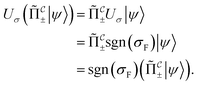 | (B31) |
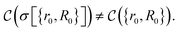 | (B32) |
However, suppose for contradiction that the projectors related to 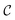 still map (anti)symmetrized states to (anti)symmetrized states. Under this assumption, consider a state |ψ〉 formed by the (anti)symmetrization of |ψ({r0, R0})〉. By definition, this state has a non-zero overlap with |ψ({r0, R0})〉. Writing the decomposition of the state in terms of positions,
still map (anti)symmetrized states to (anti)symmetrized states. Under this assumption, consider a state |ψ〉 formed by the (anti)symmetrization of |ψ({r0, R0})〉. By definition, this state has a non-zero overlap with |ψ({r0, R0})〉. Writing the decomposition of the state in terms of positions,
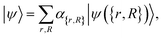 | (B33) |
Assume now without loss of generality that 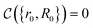 , and consider
, and consider
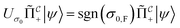 | (B34) |
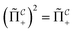 ,§ this implies
,§ this implies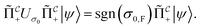 | (B35) |
Therefore, the norms of the left-hand and right-hand sides above are also equal. Using the following sets
A={{r, R}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C({r, R}) = 0} C({r, R}) = 0} | (B36) |
Bσ0 = {{r, R}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C(σ0[{r, R}])=0} C(σ0[{r, R}])=0} | (B37) |
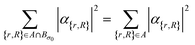 | (B38) |
Note that basic set theory implies that A∩Bσ0 ⊆ A, meaning every term in the left-hand sum is also present in the right-hand sum. Subtracting these common terms, this implies
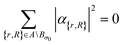 | (B39) |
There can be no nonzero amplitude for any configurations in A\Bσ0. However, by assumption  , meaning {r0, R0} ∈ A. Furthermore, eqn (B32) implies that C(σ0[{r, R}]) ≠ 0, meaning {r0, R0} ∉ Bσ0. Thus, {r0, R0} ∈ A\Bσ0 and |α{r0,R0}|2 > 0. We have, in other words, arrived at a contradiction. For a criterion
, meaning {r0, R0} ∈ A. Furthermore, eqn (B32) implies that C(σ0[{r, R}]) ≠ 0, meaning {r0, R0} ∉ Bσ0. Thus, {r0, R0} ∈ A\Bσ0 and |α{r0,R0}|2 > 0. We have, in other words, arrived at a contradiction. For a criterion  that does not fulfill eqn (B24), configurations necessarily exist where measuring
that does not fulfill eqn (B24), configurations necessarily exist where measuring 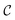 breaks symmetrization.
breaks symmetrization.
Note that all arguments above apply equally to other groups of spatial transformations under which the wave function should be invariant (up to a phase), for instance, SO(3). They also may be extended to other operators that commute with the Hamiltonian, such as total spin. In general, one should construct criteria that are maximally invariant under trivial transformations. One will otherwise discard components that correspond to desired configurations, yielding artificially low success probabilities (e.g., 50% in the case of fully formed H2O2).
We recall the form of a general input state,
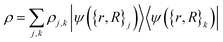 | (B40) |
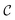 and a unitary implementation
and a unitary implementation 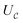 , as discussed in Section 1.2.1. Further, we recall the definition of the set of ‘successful states’ marked by A and ‘unsuccessful states’ marked by B from the main text as:
, as discussed in Section 1.2.1. Further, we recall the definition of the set of ‘successful states’ marked by A and ‘unsuccessful states’ marked by B from the main text as: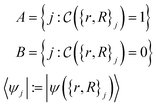 | (B41) |
Then, the input state from above can be rewritten to account for the ‘successful’ and ‘unsuccessful’ subspaces as
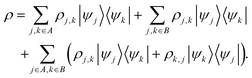 | (B42) |
Below, we will go through each step outlined in the main text in Section 3.2.1, discussing motivation and relevant considerations.
A.2.3.1 Step 1: first application of
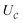 .
This step aims to extract the information represented by the oracle into an ancilla for easy access. Using the definition of the sets A and B, the state resulting from this step can be explicitly written as
.
This step aims to extract the information represented by the oracle into an ancilla for easy access. Using the definition of the sets A and B, the state resulting from this step can be explicitly written as | (B43) |
At this stage, a measurement of the ancilla qubit would project the state onto either the first or the second term in this sum. In the case of projection onto the first term (i.e., a measurement outcome of ‘1’), this projection would correspond to a heralded projection onto the desired set of states, as identified by the oracle. However, such a measurement would come with a risk of a projection onto the space that does not correspond to success. Thus, a full measurement risks projecting the state out of the desired space, and repeated measurements would risk a Zeno-effect-like freezing of the dynamics in the B subspace.
A.2.3.2 Steps 2 + 3: preparation for weak measurement. To avoid the problems discussed above, this step partially extracts the information stored in the first ancilla into a second ancilla, then resets the first ancilla using a second application of
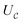 . For ease of notation, we combine these two steps here and omit the first ancilla (now unentangled and in the state |0〉〈0|) from the expression:
. For ease of notation, we combine these two steps here and omit the first ancilla (now unentangled and in the state |0〉〈0|) from the expression: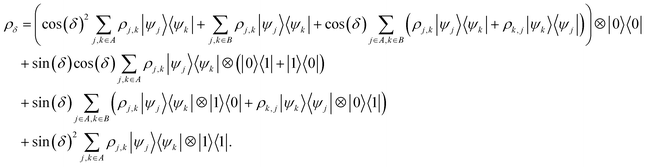 | (B44) |
Note that only the first and last of these expressions will be relevant once the ancilla is measured.
A.2.3.3 Step 4: measurement and heralding. We are now ready to see the effect of a measurement of the second ancilla and to understand the role played by the parameter δ. Consider first the projectors corresponding to the two measurement outcomes of the projective measurement:
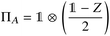 | (B45) |
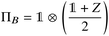 | (B46) |
Assume now that the measurement yields a ‘1’ outcome. The probability of this event is
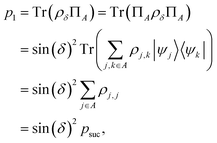 | (B47) |
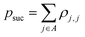 is the probability of the system having transitioned to a state labeled by the criteria as successfully merged. Assuming p1 is nonzero, the state after the measurement is given by
is the probability of the system having transitioned to a state labeled by the criteria as successfully merged. Assuming p1 is nonzero, the state after the measurement is given by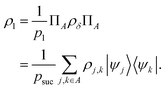 | (B48) |
Thus, this measurement outcome is the desirable one: it heralds that the state has been projected onto the desired subspace. Furthermore, the probability of getting this outcome depends both on the overlap of the input state with the desired subspace and the parameter δ, with values of  maximizing the probability.
maximizing the probability.
Consider now instead the ‘0’ outcome. The probability for this outcome is
| p0 = 1 − p1 = 1 − sin(δ)2psuc | (B49) |
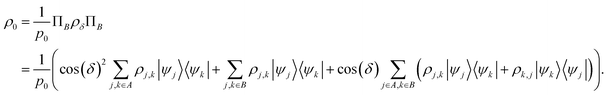 | (B50) |
Note that this state closely resembles the input state from eqn (B42), except the components related to the A subspace have decreased in magnitude by a factor of cos(δ) and a renormalization by 1/p0 has occurred. To better understand this measurement-induced perturbation, we can define the following normalized states and coefficients
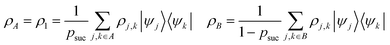 | (B51) |
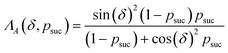 | (B52) |
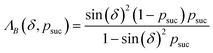 | (B53) |
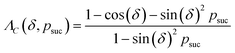 | (B54) |
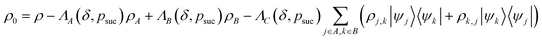 | (B55) |
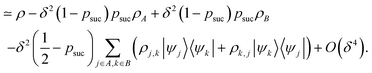 | (B56) |
Thus, receiving a measurement result of ‘0’ implies that the state has been left mostly unchanged, except primarily for two effects: the desired components related to ρA have decreased by an amount ΛAρA, while the unwanted components related to ρB have increased by an amount ΛBρB. In other words, the measurement has caused a shift towards the subspace of undesired states, with the magnitude of the shift depending on δ and psuc. From this, we see a trade-off in play when picking the parameter δ. As shown above, the largest probability of successful heralded projection requires  , but in this case the desired A part of the state is completely lost whenever the measurement outcome ‘0’ occurs (see eqn (B50)). On the other hand, a small value of δ implies a small probability of successful heralded projection but also a small state perturbation in the case of the outcome ‘0’, with both scaling as δ2 in the small-δ limit. In this sense, δ represents the power of the measurement, with strong measurements yielding a higher chance of detecting a successful molecular merger but also a higher disruptive impact of the measurement on the state. Picking good schedules for adjusting δ has previously been studied in the context of Grover search,101–103 and will likely also play a significant role in determining the performance of the simulation approaches presented here.
, but in this case the desired A part of the state is completely lost whenever the measurement outcome ‘0’ occurs (see eqn (B50)). On the other hand, a small value of δ implies a small probability of successful heralded projection but also a small state perturbation in the case of the outcome ‘0’, with both scaling as δ2 in the small-δ limit. In this sense, δ represents the power of the measurement, with strong measurements yielding a higher chance of detecting a successful molecular merger but also a higher disruptive impact of the measurement on the state. Picking good schedules for adjusting δ has previously been studied in the context of Grover search,101–103 and will likely also play a significant role in determining the performance of the simulation approaches presented here.
Acknowledgements
The authors thank Juan Bernardo Perez Sanchez, Kouhei Nakaji, Mohammad Ghazi Vakili, FuTe Wong, and Sumner Alperin-Lea for helpful discussions and comments. We further thank Jakob S. Kottmann for confirming that LBK is always right. JACGA acknowledges support from the National Institute of Advanced Industrial Science and Technology of Japan (AIST). AA gratefully acknowledges King Abdullah University of Science and Technology (KAUST) for the KAUST Ibn Rushd Postdoctoral Fellowship. LBK acknowledges support from the Carlsberg Foundation. This research was developed with funding from the Defence Advanced Research Projects Agency (DARPA) and the Department of the Navy, Office of Naval Research. The views, opinions, and/or findings expressed are those of the authors and should not be interpreted as representing the official views or policies of the Department of Defense or the U.S. Government. AAG acknowledges support from the NSERC Industrial Research Chairs Program and the Canada 150 Research Chairs. This work is supported by the Novo Nordisk Foundation, grant number NNF22SA0081175, NNF Quantum Computing Programme. Resources used in preparing this research were provided, in part, by the Province of Ontario, the Government of Canada through CIFAR, and companies sponsoring the Vector Institute (https://vectorinstitute.ai/partnerships/current-partners/).References
- P. Benioff, J. Stat. Phys., 1980, 22, 563 CrossRef.
- R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467 CrossRef.
- Y. Manin, Computable and Uncomputable, Sovetskoye Radio, Moscow, 1980, vol. 28, p. 128 Search PubMed.
- C. Zalka, Proc. R. Soc. London, Ser. A, 1998, 454, 313 CrossRef.
- S. Wiesner, arXiv, 1996, preprint, arXiv:quant-ph/9603028, DOI:10.48550/arXiv.quant-ph/9603028.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1997, 79, 2586 CrossRef CAS.
- D. Aharonov and A. Ta-Shma, in Proceedings of the thirty-fifth annual ACM symposium on Theory of computing, STOC ’03, Association for Computing Machinery, New York, NY, USA, 2003, pp. 20–29 Search PubMed.
- D. W. Berry, G. Ahokas, R. Cleve and B. C. Sanders, Commun. Math. Phys., 2007, 270, 359 CrossRef.
- S. Lloyd, Science, 1996, 273, 1073 CrossRef CAS PubMed.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1999, 83, 5162 CrossRef CAS.
- J. Kempe, A. Kitaev, and O. Regev, in FSTTCS 2004: Foundations of Software Technology and Theoretical Computer Science, Lecture Notes in Computer Science, ed. K. Lodaya and M. Mahajan, Springer, Berlin, Heidelberg, 2005, pp. 372–383 Search PubMed.
- Y. Zheng, J. Leng, Y. Liu, and X. Wu, arXiv, 2024, preprint, arXiv:2411.05120, DOI:10.48550/arXiv.2411.05120.
- S. Bravyi, A. J. Bessen, and B. M. Terhal, arXiv, 2006, preprint, arXiv:quant-ph/0611021, DOI:10.48550/arXiv.quant-ph/0611021.
- A. Y. Kitaev, arXiv, 1995, preprint, arXiv:quant-ph/9511026, DOI:10.48550/arXiv.quant-ph/9511026.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704 Search PubMed.
- J. D. Whitfield, J. Biamonte and A. Aspuru-Guzik, Mol. Phys., 2011, 109, 735 CrossRef CAS.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555 CrossRef CAS PubMed.
- P.-W. Huang, G. Boyd, G.-L. R. Anselmetti, M. Degroote, N. Moll, R. Santagati, M. Streif, B. Ries, D. Marti-Dafcik, H. Jnane, et al., arXiv, 2025, preprint, arXiv:2508.16719, DOI:10.48550/arXiv.2508.16719.
- A. M. Childs, Y. Su, M. C. Tran, N. Wiebe and S. Zhu, Phys. Rev. X, 2021, 11, 011020 CAS.
- G. H. Low and I. L. Chuang, Quantum, 2019, 3, 163 CrossRef.
- D. W. Berry, C. Gidney, M. Motta, J. R. McClean and R. Babbush, Quantum, 2019, 3, 208 CrossRef.
- D. Motlagh and N. Wiebe, PRX Quantum, 2024, 5, 020368 CrossRef.
- E. Campbell, Phys. Rev. Lett., 2019, 123, 070503 CrossRef CAS PubMed.
- K. Nakaji, M. Bagherimehrab and A. Aspuru-Guzik, PRX Quantum, 2024, 5, 020330 CrossRef.
- M. Pocrnic, M. Hagan, J. Carrasquilla, D. Segal and N. Wiebe, Phys. Rev. Res., 2024, 6, 013224 CrossRef CAS.
- A. Rajput, A. Roggero and N. Wiebe, Quantum, 2022, 6, 780 CrossRef.
- M. Hagan and N. Wiebe, Quantum, 2023, 7, 1181 CrossRef.
- M. Bagherimehrab, L. M. Calderon, D. W. Berry, P. Schleich, M. G. Vakili, A. Aldossary, J. A. C. G. Angulo, C. Gorgulla, and A. Aspuru-Guzik, Faster algorithmic quantum and classical simulations by corrected product formulas, arXiv, 2024, preprint, arXiv:2409.08265 [quant-ph], DOI:10.48550/arXiv.2409.08265.
- J. L. Bosse, A. M. Childs, C. Derby, F. M. Gambetta, A. Montanaro and R. A. Santos, Nat. Commun., 2025, 16(1), 2673 CrossRef CAS PubMed.
- Y. Su, D. W. Berry, N. Wiebe, N. Rubin and R. Babbush, PRX Quantum, 2021, 2, 040332 CrossRef.
- T. N. Georges, M. Bothe, C. Sünderhauf, B. K. Berntson, R. Izsák and A. V. Ivanov, npj Quantum Inf., 2025, 11, 55 CrossRef.
- A. Caesura, C. L. Cortes, W. Pol, S. Sim, M. Steudtner, G.-L. R. Anselmetti, M. Degroote, N. Moll, R. Santagati and M. Streif, et al. , PRX Quantum, 2025, 6, 030337 CrossRef.
- V. C. Olaya-Agudelo, B. Stewart, C. H. Valahu, R. J. MacDonell, M. J. Millican, V. G. Matsos, F. Scuccimarra, T. R. Tan and I. Kassal, Phys. Rev. Res., 2025, 7, 023215 CrossRef CAS.
- N. Maskara, S. Ostermann, J. Shee, M. Kalinowski, A. McClain Gomez, R. Araiza Bravo, D. S. Wang, A. I. Krylov, N. Y. Yao, M. Head-Gordon, M. D. Lukin and S. F. Yelin, Nat. Phys., 2025, 21, 289–297 Search PubMed.
- P.-O. Löwdin, in Advances in Chemical Physics, John Wiley & Sons, Ltd, 1958, pp. 207–322 Search PubMed.
- P.-O. Löwdin, Int. J. Quantum Chem., 1995, 55, 77 CrossRef.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, Nat. Commun., 2023, 14, 1952 CrossRef CAS PubMed.
- S. Simon, G.-L. R. Anselmetti, R. Santagati, M. Degroote, N. Moll, M. Streif, and N. Wiebe, arXiv, 2025, preprint, arXiv:2504.03465, DOI:10.48550/arXiv.2504.03465.
- A. Ambainis, in 2014 IEEE 29th Conference on Computational Complexity (CCC), 2014, pp. 32–43, iSSN: 1093-0159 Search PubMed.
- J. D. Watson and J. Bausch, arXiv, 2021, preprint, arXiv:2105.13350, DOI:10.48550/arXiv.2105.13350.
- J. Bausch, T. S. Cubitt and J. D. Watson, Nat. Commun., 2021, 12, 452 CrossRef CAS PubMed.
- C.-F. Chen, H.-Y. Huang, J. Preskill, and L. Zhou, in Proceedings of the 56th Annual ACM Symposium on Theory of Computing, 2024, pp. 1323–1330 Search PubMed.
- N. Schuch and F. Verstraete, Nat. Phys., 2009, 5, 732 Search PubMed.
- J. D. Whitfield, P. J. Love and A. Aspuru-Guzik, Phys. Chem. Chem. Phys., 2012, 15, 397 RSC.
- B. O'Gorman, S. Irani, J. Whitfield and B. Fefferman, PRX Quantum, 2022, 3, 020322 CrossRef.
- I. Kassal, S. P. Jordan, P. J. Love, M. Mohseni and A. Aspuru-Guzik, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18681 CrossRef CAS PubMed.
- H. H. S. Chan, R. Meister, T. Jones, D. P. Tew and S. C. Benjamin, Sci. Adv., 2023, 9, eabo7484 CrossRef CAS PubMed.
- S. Simon, R. Santagati, M. Degroote, N. Moll, M. Streif and N. Wiebe, PRX Quantum, 2024, 5, 010343 Search PubMed.
- R. Babbush, D. W. Berry, I. D. Kivlichan, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, New J. Phys., 2016, 18, 033032 CrossRef.
- I. D. Kivlichan, J. McClean, N. Wiebe, C. Gidney, A. Aspuru-Guzik, G. K.-L. Chan and R. Babbush, Phys. Rev. Lett., 2018, 120, 110501 CrossRef CAS PubMed.
- R. Babbush, C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler and H. Neven, Phys. Rev. X, 2018, 8, 041015 CAS.
- R. Babbush, N. Wiebe, J. McClean, J. McClain, H. Neven and G. K.-L. Chan, Phys. Rev. X, 2018, 8, 011044 Search PubMed.
- J. R. McClean, F. M. Faulstich, Q. Zhu, B. O'Gorman, Y. Qiu, S. R. White, R. Babbush and L. Lin, New J. Phys., 2020, 22, 093015 CrossRef CAS.
- J. S. Pedernales, R. Di Candia, I. L. Egusquiza, J. Casanova and E. Solano, Phys. Rev. Lett., 2014, 113, 020505 CrossRef CAS PubMed.
- E. Kökcü, H. A. Labib, J. Freericks and A. F. Kemper, Nat. Commun., 2024, 15, 3881 CrossRef PubMed.
- F. Tacchino, A. Chiesa, S. Carretta and D. Gerace, Adv. Quantum Technol., 2020, 3, 1900052 CrossRef.
- L. Lin and Y. Tong, PRX Quantum, 2022, 3, 010318 CrossRef.
- N. L. Diaz, P. Braccia, M. Larocca, J. M. Matera, R. Rossignoli and M. Cerezo, Phys. Rev. Res., 2025, 7(3), 033294 CrossRef CAS.
- P. J. Ollitrault, G. Mazzola and I. Tavernelli, Phys. Rev. Lett., 2020, 125, 260511 CrossRef CAS PubMed.
- H. Liu, G. H. Low, D. S. Steiger, T. Häner, M. Reiher and M. Troyer, Mater. Theory, 2022, 6, 11 CrossRef.
- R. Bhuyan, J. Mony, O. Kotov, G. W. Castellanos, J. Gómez Rivas, T. O. Shegai and K. Börjesson, Chem. Rev., 2023, 123, 10877 CrossRef CAS PubMed.
- B. F. E. Curchod and T. J. Martínez, Chem. Rev., 2018, 118, 3305 Search PubMed.
- D. Motlagh, R. A. Lang, P. Jain, J. A. Campos-Gonzalez-Angulo, W. Maxwell, T. Zeng, A. Aspuru-Guzik and J. M. Arrazola, Quantum Sci. Technol., 2025, 10(4), 045048 Search PubMed.
- D. J. Tannor, Introduction to Quantum Mechanics, University Science Books, 2007 Search PubMed.
- V. Vitale, J. Dziedzic, S. M.-M. Dubois, H. Fangohr and C.-K. Skylaris, J. Chem. Theory Comput., 2015, 11, 3321 Search PubMed.
- N. T. Hunt, Chem. Soc. Rev., 2009, 38, 1837 RSC.
- I. Noda, Appl. Spectrosc., 1990, 44, 550 CrossRef CAS.
- L. Bassman Oftelie, K. Klymko, D. Liu, N. M. Tubman and W. A. de Jong, Phys. Rev. Lett., 2022, 129, 130603 CrossRef CAS PubMed.
- J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe and S. Lloyd, Nature, 2017, 549, 195 CrossRef CAS PubMed.
- M. Cerezo, G. Verdon, H.-Y. Huang, L. Cincio and P. J. Coles, Nat. Comput. Sci., 2022, 2, 567 CrossRef CAS PubMed.
- H.-Y. Huang, M. Broughton, J. Cotler, S. Chen, J. Li, M. Mohseni, H. Neven, R. Babbush, R. Kueng, J. Preskill and J. R. McClean, Science, 2022, 376, 1182 CrossRef CAS PubMed.
- A. Angulo, L. Yang, E. S. Aydil and M. A. Modestino, Digital Discovery, 2022, 1, 35 RSC.
- J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427 Search PubMed.
- L. R. Liu, J. D. Hood, Y. Yu, J. T. Zhang, N. R. Hutzler, T. Rosenband and K.-K. Ni, Science, 2018, 360, 900 CrossRef CAS PubMed.
- D. K. Ruttley, A. Guttridge, S. Spence, R. C. Bird, C. R. Le Sueur, J. M. Hutson and S. L. Cornish, Phys. Rev. Lett., 2023, 130, 223401 Search PubMed.
- R. C. Bird, C. R. Le Sueur and J. M. Hutson, Phys. Rev. Res., 2023, 5, 043086 Search PubMed.
- R. C. Bird and J. M. Hutson, Phys. Rev. Res., 2025, 7(3), 033022 Search PubMed.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704 CrossRef CAS PubMed.
- Z. Ding, C.-F. Chen and L. Lin, Phys. Rev. Res., 2024, 6, 033147 CrossRef CAS.
- D. W. Berry, Y. Tong, T. Khattar, A. White, T. I. Kim, G. H. Low, S. Boixo, Z. Ding, L. Lin, S. Lee and G. K. L. Chan, PRX Quantum, 2025, 6(2), 020327 CrossRef.
- W. J. Huggins, O. Leimkuhler, T. F. Stetina and K. B. Whaley, PRX Quantum, 2025, 6(2), 020319 CrossRef.
- C.-F. Chen, M. J. Kastoryano, F. G. Brandão, and A. Gilyén, arXiv, 2023, preprint, arXiv:2303.18224, DOI:10.48550/arXiv.2303.18224.
- M. Hagan and N. Wiebe, arXiv, 2025, preprint, arXiv:2502.03410, DOI:10.48550/arXiv.2502.03410.
- D. W. Berry, A. M. Childs, R. Cleve, R. Kothari, and R. D. Somma, in Proceedings of the 46th Annual ACM Symposium on Theory of Computing – STOC ’14, ACM Press, New York, USA, 2014, pp. 283–292 Search PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martínez, Nat. Chem., 2014, 6, 1044 CrossRef CAS PubMed.
- P. A. M. Neto and H. M. Nussenzveig, Europhys. Lett., 2000, 50, 702 CrossRef.
- J. E. Molloy and M. J. Padgett, Contemp. Phys., 2002, 43, 241 CrossRef CAS.
- P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355 CrossRef CAS.
- S. Y. T. van de Meerakker, H. L. Bethlem and G. Meijer, Nat. Phys., 2008, 4, 595 Search PubMed.
- C. Cohen-Tannoudji, J. Dupont-Roc, and G. Grynberg, Photons and Atoms: Introduction to Quantum Electrodynamics, Wiley, 1st edn, 1997 Search PubMed.
- G. Lindblad, Commun. Math. Phys., 1976, 48, 119 Search PubMed.
- J. Mehra and E. Sudarshan, Il Nuovo Cimento, 1972, 11, 215 Search PubMed.
- R. Cleve and C. Wang, in 44th International Colloquium on Automata, Languages, and Programming (ICALP 2017) (Schloss-Dagstuhl-Leibniz Zentrum für Informatik), 2017 Search PubMed.
- Z. Ding, M. Junge, P. Schleich and P. Wu, Commun. Math. Phys., 2025, 406, 60 Search PubMed.
- M. Pocrnic, D. Segal and N. Wiebe, J. Phys. A:Math. Theor., 2025, 58(30), 305302 Search PubMed.
- X. Dan, E. Geva and V. S. Batista, J. Chem. Theory Comput., 2025, 1530–1546 CrossRef CAS PubMed.
- C. Wittig, J. Phys. Chem. B, 2005, 109, 8428 Search PubMed.
- T. Takekoshi, M. Debatin, R. Rameshan, F. Ferlaino, R. Grimm, H.-C. Nägerl, C. R. Le Sueur, J. M. Hutson, P. S. Julienne and S. Kotochigova, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 032506 CrossRef.
- M. Bagherimehrab and A. Aspuru-Guzik, Quantum Sci. Technol., 2024, 9, 035010 CrossRef.
- A. Lund, New J. Phys., 2011, 13, 053024 CrossRef.
- P. Andrés-Martínez and C. Heunen, Quantum Sci. Technol., 2022, 7, 025007 CrossRef.
- B. Yan, S. Wei, H. Jiang, H. Wang, Q. Duan, Z. Ma and G.-L. Long, Sci. Rep., 2022, 12, 14339 CrossRef CAS PubMed.
- A. Mizel, Phys. Rev. Lett., 2009, 102, 150501 Search PubMed.
- D. M. Jackson, U. Haeusler, L. Zaporski, J. H. Bodey, N. Shofer, E. Clarke, M. Hugues, M. Atatüre, C. Le Gall and D. A. Gangloff, Phys. Rev. X, 2022, 12, 031014 CAS.
- W. G. Hoover, Computational Statistical Mechanics, Elsevier, 1st edn, 1991 Search PubMed.
- Z. Liu, X. Li, C. Wang, and J.-P. Liu, arXiv, 2024, preprint, arXiv:2411.03972, DOI:10.48550/arXiv.2411.03972.
- R. Babbush, D. W. Berry, R. Kothari, R. D. Somma and N. Wiebe, Phys. Rev. X, 2023, 13, 041041 Search PubMed.
- L. Lang, H. M. Cezar, L. Adamowicz and T. B. Pedersen, J. Am. Chem. Soc., 2024, 146, 1760 CrossRef CAS PubMed.
- H. E. Li, Y. Zhan and L. Lin, npj Quantum Inf., 2025, 11(1), 183 CrossRef.
- G. H. Low and N. Wiebe, arXiv, 2018, preprint, arXiv:1805.00675, DOI:10.48550/arXiv.1805.00675.
- Y. R. Sanders, G. H. Low, A. Scherer and D. W. Berry, Phys. Rev. Lett., 2019, 122, 020502 CrossRef CAS PubMed.
- X.-M. Zhang and X. Yuan, npj Quantum Inf., 2024, 10, 42 Search PubMed.
- Z. Sun, G. Boyd, Z. Cai, H. Jnane, B. Koczor, R. Meister, R. Minko, B. Pring, S.C. Benjamin and N. Stamatopoulos, Low-depth phase oracle using a parallel piecewise circuit, Physical Review A, 2025, 111(6), 062420, DOI:10.1103/m32k-7nq2.
- D. W. Berry, M. Kieferová, A. Scherer, Y. R. Sanders, G. H. Low, N. Wiebe, C. Gidney and R. Babbush, npj Quantum Inf., 2018, 4, 1 CrossRef.
- Z. Liu, A. M. Childs, and D. Gottesman, arXiv, 2024, preprint, arXiv:2411.04019, DOI:10.48550/arXiv.2411.04019.
Footnotes |
| † Note that energy scales in general also depend on the fidelity of the problem representation, e.g., the resolution of the discretization or the size of the plane-wave basis.30 Thus, a polynomial scaling of these quantities is implicitly assumed in this argument. |
| ‡ The S-matrix has transition elements concerning a process represented by the evolution step in Fig. 3, independent of the state preparation scheme in the molecule factory part. |
| § To see this in the case of the tilded operators, compare their effects on states from the complete basis {|ψ({r, R})〉}. |
| This journal is © The Royal Society of Chemistry 2026 |