Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Toward accelerating rare-earth metal extraction using equivariant neural networks
Ankur K.
Gupta†
 *,
Caitlin V.
Hetherington†‡
*,
Caitlin V.
Hetherington†‡
 and
Wibe A.
de Jong
and
Wibe A.
de Jong
 *
*
Applied Mathematics and Computational Research Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: ankur@lbl.gov; wadejong@lbl.gov
First published on 26th November 2025
Abstract
The separation of rare-earth metals, vital for numerous advanced technologies, is hampered by their similar chemical properties, making ligand discovery a significant challenge. Traditional experimental and quantum chemistry approaches for identifying effective ligands are often resource-intensive. We introduce a machine learning protocol based on an equivariant neural network, Allegro, for the rapid and accurate prediction of binding energies in rare-earth complexes. Key to this work is our newly curated dataset of rare-earth metal complexes—made publicly available to foster further research—systematically generated using the Architector program. This dataset distinctively features functionalized derivatives of proven rare-earth-chelating scaffolds, hydroxypyridinone (HOPO), catecholamide (CAM), and their thio-analogues, selected for their established efficacy in binding these elements. Trained on this valuable resource, our Allegro models demonstrate excellent performance, particularly when trained to directly predict DFT-level binding energies, yielding highly accurate results that closely correlate with theoretical calculations on a diverse test set. Furthermore, this strategy exhibited strong out-of-sample generalization, accurately predicting binding energies for an isomeric HOPO-derivative ligand not seen during training. By substantially reducing computational demands, this machine learning framework, alongside the provided dataset, represent powerful tools to accelerate the high-throughput screening and rational design of novel ligands for efficient rare-earth metal separation.
1 Introduction
Rare-earth elements (REEs) (namely, Sc, Y, and lanthanides (La–Lu)) are indispensable in numerous advanced technologies and modern applications due to their unique properties.1,2 They are critical components in clean energy technologies, such as hybrid batteries and permanent magnets, and are essential in light-emitting materials such as in displays and various imaging technologies.3 REEs are vital in hundreds of products, ranging from high-tech consumer goods to critical defense applications.4 Their growing demand across industries has placed significant pressure on the supply chain, necessitating an accelerated development of strategies for their recovery and separation from diverse sources.5–7 However, their extraction and separation pose challenges due to their similar chemical and physical properties, arising from their stable, comparably sized trivalent ions.8,9 These similarities make the separation process more complex, time-consuming, and expensive compared to that of other elements.10 Consequently, research efforts have focused on improving separation methods to efficiently recycle REEs, ensuring a more sustainable and reliable supply of these critical elements. Solvent extraction is seen as the most efficient way to separate REEs at industrial scale,11–13 involving selectively binding a specific REE with suitable ligands to form discrete REE-ligand complexes which then aggregate in an organic phase that can be extracted from an aqueous phase. However, since the suitable ligands require high and selective binding affinities towards specific REEs, this process is still inefficient, requires multiple steps, and generates a large amount of waste and pollutants, which is both economically and environmentally costly.14,15In the same context, selective precipitation16,17 has emerged as a promising strategy for separating REEs. This approach involves precipitating individual REEs from aqueous mixtures by binding them with organic ligands (or complexing agents), followed by isolation through filtration. The success of this method hinges on discovering novel ligands that bind to REEs with high specificity and selectivity. While hydroxypyridinone (HOPO) based ligands have demonstrated serendipitous success, the vast chemical space remains largely unexplored, offering significant potential for the discovery of more efficient ligands that could revolutionize rare-earth separation processes.18–22
To address the need for efficacious ligands for REE extraction and separation, the exploration of the vast chemical space via a high-throughput screening approach is essential. A key factor in determining a ligand's efficacy in REE separation is its binding affinity to a given REE, which can be deduced experimentally through titration techniques and subsequently quantified using the resultant equilibrium constants and IC50 values.23 However, the synthesis and experimental evaluation of thousands of novel ligands for REE separation are time-consuming, resource-intensive, and cost-prohibitive, rendering wet-lab-based high-throughput screening impractical. Calculated metal–ligand binding energies are thermodynamically related to equilibrium constants; for a given metal and ligand series, a more negative binding energy implies a favorable exchange toward that ligand and thus greater extraction efficacy.23 Our study focuses on the computational prediction of binding energy, serving to rank and prioritize the most promising ligand candidates for subsequent, targeted experimental validation through techniques such as spectrofluorimetric titration. Thus, quantum chemistry-based calculations offer a viable alternative for high-throughput screening of unexplored ligands through a virtual platform. This approach allows precise control over molecular structures and parameters, such as charge, oxidation state, and ligand properties, irrespective of their complexity or synthetic accessibility. However, for accurate computation of rare-earth complex (REC) properties, the choice of theoretical method is crucial due to their complex electronic structure arising from the involvement of f-electrons. This complexity results in varied spin multiplicities, polarization effects,24 and multi-reference character across the REE series. While computationally intensive correlated wave function theory (e.g., CCSD(T)) and multi-reference methods (e.g., CASSCF) offer higher accuracy, density functional theory (DFT) with a reasonably sized basis set provides a practical balance between cost and accuracy for computing reliable binding energies and other properties for RECs. Nevertheless, applying DFT to potentially hundreds of thousands of RECs remains computationally challenging, particularly since RECs can exhibit noisy and prolonged self-consistent field (SCF) convergence, further exacerbating computational time and resource demands. Static correlation could also be incorporated during dataset generation for RECs using correction methods over DFT, such as DFT + U or static correlation correction (SCC),25,26 though, while relatively cost-effective, additional accuracy challenges could arise.
In response to the computational challenges posed by quantum chemistry calculations, machine learning techniques offer a promising avenue for rapid and cost-effective predictions of REC properties. However, the success of any machine learning method fundamentally depends on the quality and breadth of the dataset on which it is trained. Despite the potential of machine learning, the field is currently hampered by a significant lack of datasets that are specifically curated for REC structures and properties, as most existing datasets mainly focus on organic or main group elements.27 To bridge this gap, we propose and develop a rigorous protocol to generate datasets targeting RECs, particularly those involving ligands known to be effective in REE separation. Additionally, we demonstrate various machine learning strategies, utilizing state-of-the-art equivariant neural networks, to predict REC binding energies, paving the way for accelerated property prediction and ultimately, the discovery of novel ligands for efficient REE separation through the application of molecular inverse design algorithms.
2 Methods
2.1 Data curation
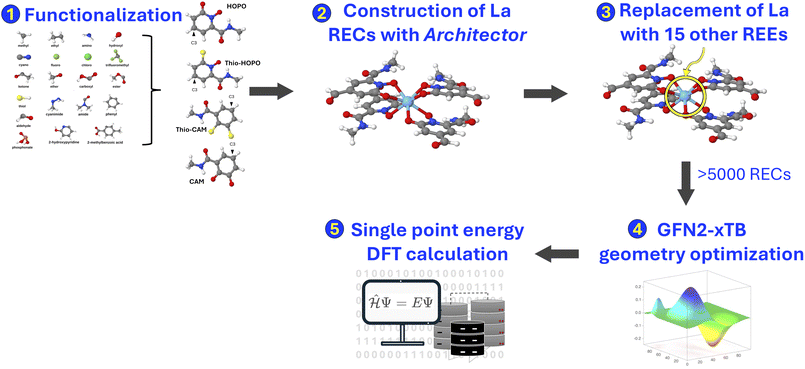
Hydroxypyridinone (HOPO) and catecholamide (CAM) ligands, along with their sulfur analogues, thio-HOPO and thio-CAM (Fig. 1), have been experimentally identified to exhibit strong binding affinity to REEs,23,28–30 making them promising candidates for REE separation. However, existing datasets incorporating these critical ligands are scarce, underscoring the need for curated representative datasets. We therefore designed a high-throughput computational approach to efficiently identify the most promising ligand candidates from a vast chemical space, thereby guiding and prioritizing subsequent experimental synthesis and validation efforts. By strategically focusing on derivatives of experimentally validated scaffolds like HOPO and CAM, and by using the calculated binding energy as a direct proxy for binding affinity, our workflow provides a direct link between fundamental quantum chemical properties and the practical goal of discovering new, more effective ligands for real-world separation applications. Given the structural complexity of RECs, manual generation of a large, diverse, and accurate dataset is impractical and error-prone. To address this challenge, we utilized the recently developed Architector program (version 0.0.10)31 to design an automated, high-throughput protocol (Fig. 2) for generating 3D structures of RECs. Architector enables the in silico design of mononuclear organometallic complexes, leveraging metal-center symmetry to generate diverse 3D conformers from minimal 2D inputs, such as ligand SMILES (Simplified Molecular Input Line Entry System)—a line notation used to represent a chemical structure as a text string—metal oxidation state, and spin state. This facilitated the creation of a wide range of metal-complex configurations, while affording precise control over specific complex and ligand structural properties. The resulting 3D REC structures served as the foundation for our curated dataset, enabling accurate quantum chemistry-based property computations, as detailed below. Since these systems contain ligand derivatives from experimentally identified rare-earth extraction systems, we would expect them to exhibit similar properties and those found to have the highest binding affinities could inform the use of the particular ligand for selective extraction of specific REEs from complex solutions.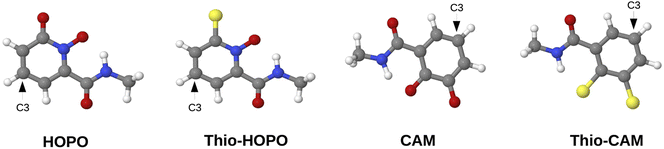 | ||
| Fig. 1 Molecular geometries of HOPO, thio-HOPO, CAM, and thio-CAM ligands (grey: C, red: O, blue: N, yellow: S, white: H). Functionalization was carried out at the C3 position. | ||
The data curation protocol comprised of five steps, as illustrated in Fig. 2. The first step involved functionalizing HOPO- and CAM-based ligands (Fig. 1) with diverse substituents at position C3, i.e. diametrically opposite the metal coordinating atom that is adjacent to the side chain (Fig. 2, step 1). This diversification of the dataset enabled the investigation of the influence of various chemical and electronic environments on REE binding affinities. The selected substituents (Fig. 3) were all uncharged and encompassed a range of electron-donating groups (e.g., alcohols, amines) and electron-withdrawing groups (e.g., carboxylic acids, esters), allowing for the exploration of ligand polarity effects on REE binding affinity. Furthermore, to examine how different heteroatoms modulate metal–ligand binding strength, we included substituents containing nitrogen (e.g., amino), oxygen (e.g., hydroxyl), sulfur (e.g., thiol), and phosphorus (e.g., phosphonate). Substituent size and complexity were systematically varied, ranging from simple methyl groups to larger, more complex moieties like 2-methylbenzoic acid, to generate a diverse array of ligand sizes and shapes. Halogen substituents, such as chloride and fluoride, were also incorporated to investigate their impact on REC acidity. Notably, due to its higher electronegativity, fluoride increases the complex's acidity (lower pKa) compared to chloride through inductive electron withdrawal. Furthermore, the dataset focused exclusively on mononuclear RECs, with the central metal atom being the sole heavy metal present in the complexes.
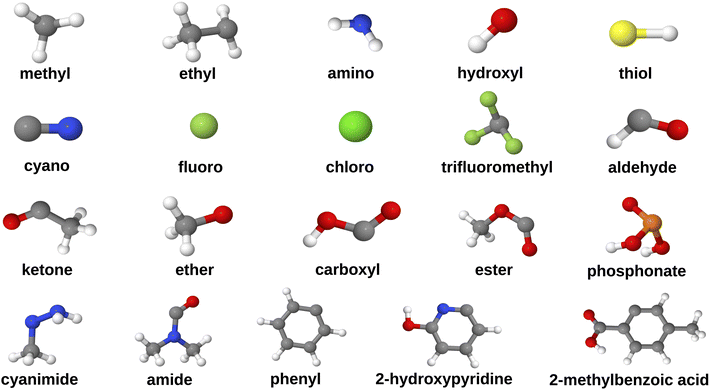 | ||
| Fig. 3 Geometries of substituents that are attached to the ligands (grey: C, red: O, blue: N, yellow: S, white: H, pale green: F, bright green: Cl). | ||
In the second step, 3D geometries of RECs were generated using Architector. Each complex consisted of the previously discussed ligands (Fig. 1) attached to a REE metal center, and identical ligands were used for each individual REC. This process utilized the SMILES strings of the ligands and Architector-specific parameters as input (Fig. 2, step 2). The Architector setup involved determining the optimal metal center symmetry and 3D ligand geometry to generate a diverse set of REC conformers. The following settings were employed: GFN2-xTB32 (version 6.6.0) for structure optimization and energy-based ranking of the generated structures, and a coordination number of eight for all complexes, consistent with common coordination environments observed for RECs.33 Up to ten different metal-centered symmetries were explored during the generation and optimization of multiple conformers. To enhance conformational sampling and ensure identification of the most stable structures, the Conformer-Rotamer Ensemble Sampling Tool (CREST, version 2.12)34 integrated into Architector was employed in conjunction with GFN2-xTB. CREST initiated a further search for lower-energy conformations, starting from the lowest-energy REC conformer obtained in the previous step. This approach facilitated a more thorough exploration of the conformational space. The resulting lowest-energy conformer from the CREST protocol was then utilized in subsequent steps, as detailed below.
To optimize computational efficiency and minimize processing time, only lanthanum (La) complexes were initially constructed during the REC structure generation step. La serves as an excellent representative for the entire series of REEs due to their shared chemical properties. The selection of La as the starting point for generating RECs was motivated by two primary factors. Firstly, La possesses the largest atomic radius among REEs, facilitating greater adaptability when subsequently replacing La with other REEs in each REC structure. This allowed for structural modifications without significantly altering metal–ligand coordination behavior. Secondly, La's natural and only stable oxidation state of +3 is universally accessible across all REEs, ensuring consistency in electronic configuration throughout the REE series.
To simulate a realistic aqueous environment while ensuring computational feasibility, we employed a hybrid solvation strategy. In addition to an implicit model for the bulk solvent, we explicitly included water molecules in the primary coordination sphere to model the crucial competition for metal binding. To capture the diversity of potential coordination environments, we generated four distinct types of REC geometries by varying the ratio of bidentate ligands to explicit water molecules, all while maintaining a coordination number of eight (Fig. 4). This approach not only enhanced the physical realism of our models but also increased the overall diversity and size of the dataset. The first geometry type consisted of four bidentate ligands attached to the metal center (Fig. 4a). The remaining three types of complexes incorporated water molecules, reflecting their potential to bind to the metal in aqueous media. The second geometry type featured three ligands and two water molecules (Fig. 4b), while the third type comprised two ligands and four water molecules (Fig. 4c). The final geometry type included one ligand and six water molecules coordinated to the metal center (Fig. 4d). This comprehensive set of geometries allowed for a thorough exploration of various ligand–water combinations in the coordination sphere, providing a more realistic representation of RECs in aqueous environments.
Following the CREST search, the lowest-energy lanthanum (La)-ligand complexes were used as templates for further exploration. La was systematically substituted with 15 other REEs (Fig. 2, step 3): yttrium (Y), cerium (Ce), praseodymium (Pr), neodymium (Nd), promethium (Pm), samarium (Sm), europium (Eu), gadolinium (Gd), terbium (Tb), dysprosium (Dy), holmium (Ho), erbium (Er), thulium (Tm), ytterbium (Yb), and lutetium (Lu). This substitution strategy expanded the dataset, essential for developing robust machine learning models. Throughout this process, the ligand identity and molecular charge remained unchanged; only the spin multiplicity was adjusted to reflect the properties of the substituted REEs. Since the ligands are closed-shell, the spin multiplicity of each complex was assigned based on the corresponding isolated REE ion in its +3 oxidation state.
All generated structures were optimized using the GFN2-xTB32 method, employing the analytical linearized Poisson–Boltzmann (ALPB) implicit water solvation model35 to better simulate experimental conditions (Fig. 2, step 4). This computationally efficient semiempirical method was chosen to balance geometric accuracy with the high-throughput demands of generating several thousand optimized complex structures.27 To ensure high-quality data for the machine learning model, a quality control procedure was also implemented. During GFN2-xTB geometry optimizations, some RECs underwent changes in atom connectivity, potentially leading to incorrect ligand valencies. To identify and exclude such erroneous structures, we converted the ligands into their hashed International Chemical Identifiers (InChIKeys).36 As InChIKeys function as unique molecular identifiers, a complex was retained only if the InChIKeys of its ligands matched those of the corresponding free ligands; otherwise, it was excluded. Only a small number of complexes were filtered out during this process, yielding a total number of 5356 complexes.
Despite being robust for the structure optimization of large transition-metal complexes,37 xTB has limited applicability to REEs in which f-electrons play a crucial role in determining their properties, due to its semi-empirical and highly parameterized nature, leading to reduced accuracy. A notable limitation of the current GFNn-xTB methods is their lack of spin-dependent energy expressions, which prevents proper differentiation between high-spin and low-spin states. Therefore, to achieve higher fidelity in energy calculations, we computed single-point energies and gradients using density functional theory (DFT) at the B3LYP-D438,39 level of theory. The def2-SVPD40 basis set was used for the ligands, and the def2-TZVP basis set was employed for the metals, utilizing the ORCA41,42 program (version 5.0.4). Effective Core Potentials43 (ECPs) were applied to account for the core electrons of the metals. The RIJCOSX approximation was employed to efficiently compute Coulomb integrals and perform numerical integration for Hartree–Fock exchange. Additionally, the SMD44 implicit solvation model was used to simulate aqueous conditions more accurately.
To quantify the affinity of a ligand to the metal in RECs, we calculated the metal–ligand binding energies using the absolute energies obtained from DFT. Theoretically computed binding affinities are thermodynamically related to equilibrium constants (ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K)). Here binding energy is evaluated with matched fragment stoichiometry, charge, and spin (and consistent protonation states), providing a robust proxy for the free energy when comparing ligand efficacy for metal extraction. Thus, the binding energy (Ebinding) for an REC can be defined as
ln(K)). Here binding energy is evaluated with matched fragment stoichiometry, charge, and spin (and consistent protonation states), providing a robust proxy for the free energy when comparing ligand efficacy for metal extraction. Thus, the binding energy (Ebinding) for an REC can be defined as
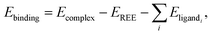 | (1) |
2.2 Model architecture and training
For predicting the binding energies of rare-earth complexes (RECs), we employed the Allegro architecture,45 an E(3) equivariant deep neural network. While classical machine learning techniques have been explored for predicting predominantly experimental properties of RECs,46–48 to our knowledge, this work is among the first to apply an E(3) equivariant model like Allegro to predict metal–ligand interactions for these f-block element complexes.An equivariant neural network is a model that respects the physical symmetries of a molecule by operating directly on 3D atomic coordinates. Its internal representations are designed to transform consistently with the molecule's rotation or translation, ensuring that predicted scalar properties (like energy) remain unchanged (invariant), while predicted vector properties (e.g. forces, dipoles) transform in the exact same way as the molecule (equivariant). This approach has been shown to significantly improve data efficiency and accuracy for property prediction. The inherent E(3) equivariance of the Allegro framework is key to its exceptional performance, allowing it to achieve high accuracy with less training data—a crucial benefit when using datasets derived from computationally expensive, high-fidelity quantum chemical calculations. We also note that while architectures like Allegro are often used as interatomic potentials, their design as general-purpose equivariant networks makes them highly adept for direct property prediction tasks,49 as demonstrated in this work.
For model development, a standard data partitioning strategy of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 was implemented, randomly allocating samples for the training, validation, and test sets, respectively. All Allegro models were configured with a 6 Å radial cutoff. This cutoff was chosen to effectively capture the relevant atomic interactions within the metal complexes, encompassing both the primary coordination sphere interactions and pertinent secondary non-covalent effects. The training process utilized the mean absolute error (MAE) in energy as the loss function. Parameter optimization was performed using the Adam algorithm, coupled with a ReduceLROnPlateau learning rate scheduler that initiated at a rate of 0.01. Training for each model proceeded until the learning rate adaptively decreased to 10−5, signaling convergence. Comprehensive hyperparameter specifications for the Allegro models tested are detailed in Table S3 of the SI.
10 was implemented, randomly allocating samples for the training, validation, and test sets, respectively. All Allegro models were configured with a 6 Å radial cutoff. This cutoff was chosen to effectively capture the relevant atomic interactions within the metal complexes, encompassing both the primary coordination sphere interactions and pertinent secondary non-covalent effects. The training process utilized the mean absolute error (MAE) in energy as the loss function. Parameter optimization was performed using the Adam algorithm, coupled with a ReduceLROnPlateau learning rate scheduler that initiated at a rate of 0.01. Training for each model proceeded until the learning rate adaptively decreased to 10−5, signaling convergence. Comprehensive hyperparameter specifications for the Allegro models tested are detailed in Table S3 of the SI.
3 Results and discussion
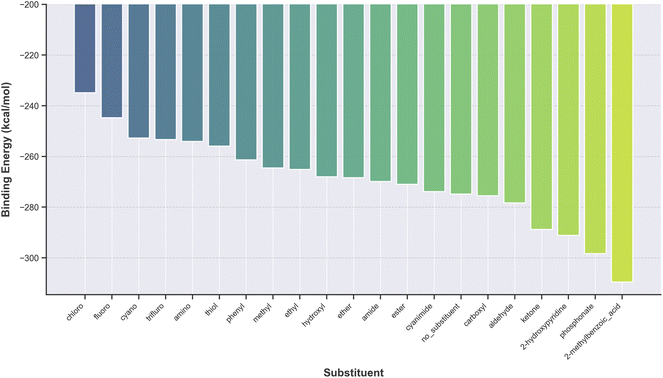
Each metal complex studied comprised a single metal atom coordinated by identical ligands. We systematically introduced various substituents to the base ligands—HOPO, CAM, thio-HOPO, and thio-CAM—to investigate how electronic properties, such as electron-donating and electron-withdrawing effects, along with steric factors, influence ligand–metal binding strengths. Fig. 5 exemplifies this, showing the binding energies of Eu-CAM complexes arranged in ascending order. Notably, complexes substituted with smaller electron-withdrawing groups, such as chloro and fluoro, exhibited the weakest binding energies. In contrast, bulkier substituents, including phosphonate and 2-methylbenzoic acid, resulted in relatively higher binding energies. This variation in binding strengths, spanning from approximately 230 to 300 kcal mol−1, highlights the importance of substituent selection in optimizing ligand design. Identifying substituents that maximize binding affinity could enhance selective extraction of specific REEs from complex solutions. A primary outcome of our high-throughput screening is the identification of guiding principles for the rational design of novel ligands. Our results consistently show that the CAM and thio-CAM scaffolds provide a more promising backbone for strong chelation than their HOPO counterparts. Across all scaffolds, binding affinity was most significantly enhanced by functionalization with bulky substituents, particularly the phosphonate, 2-hydroxypyridine, and 2-methylbenzoic acid groups. This suggests that combining a CAM-based scaffold with one of these high-performing substituents represents a top-tier candidate for experimental synthesis and validation. Furthermore, the predicted differential affinities across the REE series, for example, the consistently stronger binding of lanthanides like Ytterbium (Yb) and Gadolinium (Gd), provide a thermodynamic basis for designing selective separation strategies. However, while thermodynamics governs the ultimate binding preference, it is important to note that kinetic factors may also play a crucial role in the rate of metal exchange and the overall efficiency of a practical separation process.We evaluated two distinct modeling strategies using the Allegro architecture (detailed in Section 2.2) to predict the binding energies of the RECs. The first approach, hereafter referred to as Strategy 1, involved training the ML model on the absolute energies of the complexes computed via DFT. The binding energies were then derived from the model's predicted absolute energies using eqn (1), requiring separate DFT calculations for the energies of the isolated metal ions and ligands performed at the same level of theory. The second approach, termed Strategy 2, trained the ML model to predict the binding energies directly, using pre-computed binding energies as target labels, thus eliminating the need for post-processing calculations.
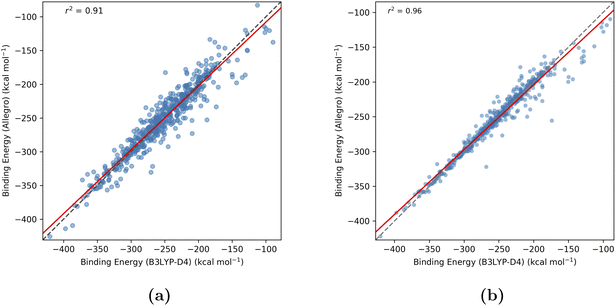
Fig. 6 presents parity plots comparing the DFT-calculated (ground truth) binding energies with the Allegro-predicted values for both strategies on the test set. While Strategy 1 (predicting absolute energies) yielded a strong correlation with a coefficient of determination (r2) of 0.91 and a mean absolute error (MAE) of 11.3 kcal mol−1 (Fig. 6a), Strategy 2 (predicting binding energies directly) proved superior. The direct prediction method employed in Strategy 2 achieved both a higher correlation (r2 = 0.96) and a significantly lower MAE of 6.1 kcal mol−1 (Fig. 6b), indicating it provides more accurate binding energy predictions for RECs. Results obtained with a simpler Allegro architecture (employing only 2 tensor features), are presented in Fig. S1 of the SI. This simpler model variant yields lower performance for Strategy 1 (absolute energy prediction, r2 = 0.85), while Strategy 2 (direct binding energy prediction) maintains comparable accuracy (r2 = 0.96).
Overall, the model employing 4 tensor features and trained using Strategy 2 is well-suited for its primary purpose of high-throughput virtual screening, a context where the ability to correctly rank potential ligands is the most critical metric. Its high correlation with DFT reference data (r2 = 0.96) demonstrates a strong capacity to reliably distinguish between strong and weak binders, enabling the rapid down-selection of promising candidates from vast chemical libraries for more rigorous and costly evaluation.
3.1 Evaluation of Δ-ML strategies
To potentially enhance the prediction accuracy for the target DFT-level energies, we extended the two modeling strategies by incorporating a delta machine learning (Δ-ML) approach.50,51 The Δ-ML technique often improves energy predictions by learning the correction needed to elevate results from a cost-effective baseline theory to a more accurate, high-cost target level of theory. This strategy leverages the typically systematic nature of the errors between the two methods, aiming to reduce these errors and potentially capture longer-range interactions more effectively than models trained solely on absolute energies or properties from the target level.50,52 Due to the cancellation of systematic errors, we expect to observe an improvement in the predictive accuracy of the Δ-ML model, enabling the trained model to be used to correct the calculated GFN2-xTB energies and to achieve DFT-like accuracy during inference. Note that since the training phase for Δ-ML requires energies from both DFT and GFN2-xTB methods, the training cost itself is not reduced.In this study, we employed the semi-empirical GFN2-xTB method as the low-cost baseline and DFT (B3LYP-D4) as the high-cost target level. Within the Δ-ML framework, the energy at the target DFT level (EML-DFT) is estimated by adding an ML-predicted correction (ΔML) to the baseline GFN2-xTB energy (EGFN2-xTB),
| EML-DFT = EGFN2-xTB + ΔML. | (2) |
The correction term, ΔML, represents the learned difference between the high-fidelity DFT energy (EDFT) and the low-fidelity GFN2-xTB energy,
| ΔML = EDFT − EGFN2-xTB. | (3) |
We applied this Δ-ML concept to our two primary modeling strategies:
• Strategy 1 (Δ-ML on absolute energies): the Allegro ML model was trained to predict the difference in absolute energies between DFT and GFN2-xTB (ΔML from eqn (3)). The predicted ΔML for the test set complexes was added to their GFN2-xTB energies (calculated separately) according to eqn (2) to estimate the absolute DFT energies. Subsequently, binding energies were calculated using eqn (1), requiring the corresponding isolated metal and ligand energies at the DFT level.
• Strategy 2 (Δ-ML on binding energies): this approach offers a more direct route to the target property. The Allegro model was trained to learn the difference between the binding energies calculated at the DFT level and the GFN2-xTB level (ΔEbinding = Ebinding,DFT − Ebinding,GFN2-xTB). The predicted ΔEbinding for the test set complexes was then added to their GFN2-xTB binding energies (calculated separately) to estimate the binding energy at the DFT level.
Fig. 7 displays the parity plots comparing the Δ-ML predicted binding energies against the ground truth DFT values for the test set. Applying Δ-ML to the first strategy (absolute energies, Fig. 7a) resulted in an r2 of 0.92 and an MAE of 9.9 kcal mol−1. This represents a modest improvement in the metrics compared to the direct approach for Strategy 1 (r2 = 0.91, MAE = 11.3 kcal mol−1, Fig. 6a). For the second strategy (direct binding energy prediction, Fig. 7b), the Δ-ML approach yielded an r2 of 0.95 and an MAE of 6.6 kcal mol−1. Compared to the direct prediction of binding energies without the delta correction (Strategy 2: r2 = 0.96, MAE = 6.1 kcal mol−1, Fig. 6b), the Δ-ML approach in this case resulted in a slightly lower correlation and a slightly higher MAE, indicating a comparable but not superior performance for REC binding energy predictions. Fig. S2 in the SI details the performance of a simplified Allegro model variant with 2 tensor features, where Strategy 2 (direct binding energy prediction) sustains a similar level of accuracy (r2 = 0.95), while Strategy 1 (absolute energy prediction) experiences a notable decrease in performance (r2 = 0.83).
3.2 Out-of-sample generalization with an isomeric ligand
To further assess the generalizability of our trained models to previously unseen ligand environments, their performance was evaluated on RECs formed with an out-of-sample ligand not included in the original training datasets. We therefore built an out-of-sample dataset of RECs containing the ligand HDEV, a positional isomer of HOPO. In HDEV, the positions of the N-hydroxy (–N–OH) and carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups are interchanged relative to HOPO. Under our binding conditions, the N-hydroxy is deprotonated (–N–O−), and coordination remains O,O-bidentate via the deprotonated N-hydroxy oxygen and the carbonyl oxygen (see Fig. 8 for structure).53 The structural alteration in HDEV creates a chemical environment distinct from the ligands (HOPO, CAM, and their thio-analogues from Fig. 1) used in the model's training set, making it well-suited for this validation. Additionally, HDEV has been identified experimentally for its selective binding to REEs, establishing its relevance as a candidate for synthetically feasible rare-earth separation.53 For this out-of-sample evaluation, 325 RECs without any coordinated water molecules, featuring HDEV—functionalized at the C3 position with the same range of substituents shown in Fig. 3—were generated using the high-throughput protocol detailed in Section 2.1 and illustrated in Fig. 2. These HDEV complexes formed a dedicated out-of-sample test set, and binding energy predictions for these complexes were made using the Allegro models previously trained on 80% of the original dataset (which excluded any HDEV complexes).
O) groups are interchanged relative to HOPO. Under our binding conditions, the N-hydroxy is deprotonated (–N–O−), and coordination remains O,O-bidentate via the deprotonated N-hydroxy oxygen and the carbonyl oxygen (see Fig. 8 for structure).53 The structural alteration in HDEV creates a chemical environment distinct from the ligands (HOPO, CAM, and their thio-analogues from Fig. 1) used in the model's training set, making it well-suited for this validation. Additionally, HDEV has been identified experimentally for its selective binding to REEs, establishing its relevance as a candidate for synthetically feasible rare-earth separation.53 For this out-of-sample evaluation, 325 RECs without any coordinated water molecules, featuring HDEV—functionalized at the C3 position with the same range of substituents shown in Fig. 3—were generated using the high-throughput protocol detailed in Section 2.1 and illustrated in Fig. 2. These HDEV complexes formed a dedicated out-of-sample test set, and binding energy predictions for these complexes were made using the Allegro models previously trained on 80% of the original dataset (which excluded any HDEV complexes).
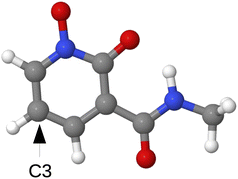 | ||
| Fig. 8 Optimized geometry of HDEV (grey: C, red: O, blue: N, white: H). Functionalization was carried out at the C3 position. | ||
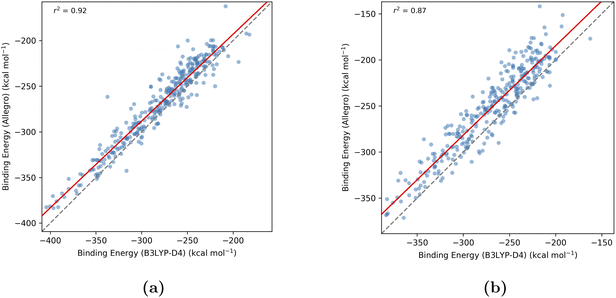
The predictive performance of the different modeling strategies on this HDEV test set is illustrated by the parity plots in Fig. 9, which compare Allegro-predicted binding energies against the ground truth DFT values. When employing Strategy 2 (direct prediction of binding energies), the model demonstrated excellent correlation for the HDEV complexes. As shown in Fig. 9a, this approach yielded an r2 of 0.92 and an MAE of 9.4 kcal mol−1. These results indicate that directly training on precomputed binding energies enables robust predictions for RECs with ligands not encountered during training. In stark contrast, Strategy 1 (predicting absolute energies first) proved less effective for generalizing to new, unseen RECs. This approach yielded a significantly lower r2 value of 0.10 (refer to Fig. S3a in the SI) and exhibited a large deviation from the ideal y = x correlation. This shift from ground truth binding energies may stem from inconsistencies between the ML-predicted absolute energies of the RECs and the DFT-calculated absolute energies of the free ligands used to compute the final binding energies.
We also tested the Δ-ML approach where the model learns the difference in binding energies (ΔEbinding) between DFT and GFN2-xTB (Δ-ML Strategy 2). The results for this strategy, depicted in Fig. 9b, show an r2 of 0.87 and an MAE of 19.7 kcal mol−1. While still showing a reasonable correlation, this Δ-ML strategy was less accurate for the HDEV test set compared to the ML model trained directly on binding energies (Fig. 9a). Furthermore, Δ-ML Strategy 1, which predicts absolute energy differences, showed improved correlation over the original Strategy 1 with an r2 of 0.34 (Fig. S3b in the SI) but remained insufficiently accurate for practical applications. Overall, the high accuracy achieved with the HDEV out-of-sample test set, particularly by the Strategy 2 model trained directly on precomputed binding energies, underscores the model's generalizability and its promising potential for reliable high-throughput screening of novel ligand candidates.
3.3 Comparison with a universal foundation model
The recent emergence of large-scale, pre-trained foundation models for chemistry raises the question of their out-of-the-box applicability to specialized chemical domains. To investigate this, we tested a state-of-the-art universal potential, the MACE-OMOL (extra-large; MACE v0.3.14) foundation model,54–57 on a representative complex from our dataset, [Y(HOPO-hydroxyl)4]−1. The pre-trained model, which references the wB97M-V level of theory, predicted a binding energy of −1050.54 kcal mol−1. This value is in stark contrast to our B3LYP-D4 reference value of −278.85 kcal mol−1, a discrepancy of over 770 kcal mol−1 that represents an overestimation of the binding strength by a factor of nearly four. While acknowledging the different DFT functionals, this large error suggests that even advanced universal models may not yet possess the required accuracy for electronically complex systems like rare-earth coordination chemistry without domain-specific training or fine-tuning. Due to the vastness of chemical space, curated datasets for novel chemical domains will therefore remain highly relevant for improving model generalizability. These foundation models can serve as an excellent starting point, and fine-tuning them on domain-specific datasets, such as the one presented here, offers a computationally efficient path toward developing highly accurate potentials for specialized applications.4 Conclusions
The critical role of REEs in clean energy and advanced technologies necessitates more efficient and rapid methods for their separation and extraction. This study addressed this challenge by developing and validating an equivariant neural network model, leveraging the Allegro architecture, for the accurate prediction of binding energies in RECs. Alongside the development of the ML model, a key contribution of this work was our systematic data curation protocol. Employing the Architector program, this protocol enabled the generation of a new, diverse dataset of over 5000 RECs, which is being made publicly available to the scientific community. This dataset was strategically focused on functionalized derivatives of hydroxypyridinone (HOPO), catecholamide (CAM), and their thio-analogues—ligand families chosen for their established efficacy and promising interactions with REEs—thereby forming a robust and relevant foundation for both the current study and future machine learning endeavors in this field.Key findings indicate that machine learning models, even when trained on moderately sized datasets, can achieve strong correlations with high-fidelity DFT calculations. Specifically, we demonstrated that training the ML model to predict binding energies directly is more effective and accurate (r2 = 0.96, MAE = 6.1 kcal mol−1 on the initial test set) than predicting absolute energies first. While the Δ-ML approach, learning the correction between GFN2-xTB and DFT, showed promise by improving upon the absolute energy prediction strategy, it did not surpass the performance of directly predicting DFT-level binding energies for our primary test sets. Crucially, the model predicting binding energies directly also exhibited encouraging out-of-sample generalization when tested on complexes with the isomeric HDEV ligand (r2 = 0.92, MAE = 9.4 kcal mol−1), highlighting its potential for broader applicability in screening novel candidates.
Despite these promising results, certain limitations warrant acknowledgment. While Architector aids in generating diverse structures, the vastness of chemical space means our current dataset, though substantial, represents only a fraction of potential ligand motifs and substituent combinations. Future investigations should aim to broaden the scope and robustness of these predictive models. Extending the dataset with a wider array of ligand backbones, diverse functional groups, and potentially different metal oxidation states or molecular charges would be beneficial. A particularly exciting avenue for future work lies in the development of self-supervised foundation models.56–59 By training on large-scale datasets of REC geometries—which can be generated more readily using tools like Architector without the immediate need for computationally expensive DFT labels—these models could learn fundamental representations of metal–ligand interactions, potentially enhancing transferability and applicability to a wider range of systems and tasks with minimal fine-tuning. Additionally, while this study has focused on the prediction of static binding energies, we envision this work as a foundational step toward the development of a full interatomic potential (IP). Such a model, trained on forces from intermediate geometries, would enable dynamic simulations and geometry optimizations. The high accuracy achieved here validates the use of equivariant models for this chemical space and provides a clear path for prioritizing promising candidates for which the significant computational investment required to develop a full IP is warranted.
In summary, this work demonstrates the significant potential of equivariant neural networks to accelerate the computational screening of ligands for REE extraction. The developed models and insights pave the way for integration into high-throughput virtual screening workflows and, ultimately, toward the inverse design of novel, highly selective ligands, thereby contributing to more sustainable and efficient REE separation technologies.
Conflicts of interest
There are no conflicts to declare.Data availability
The complete dataset generated and analyzed during this study, comprising the geometries and final energies for all rare-earth complexes in XYZ format, is available in the Figshare repository at https://doi.org/10.6084/m9.figshare.29430059. The custom code used for model training and evaluation has been archived on Zenodo and is available at https://doi.org/10.5281/zenodo.17666661. The underlying equivariant neural network architecture, Allegro, is open-source and available at https://github.com/mir-group/allegro.Supplementary information (SI): tables of ligand charges and rare-earth element spin states (Tables S1 and S2); table of hyperparameters used in Allegro models (Table S3); parity plots for Allegro models (features = 2) for both direct binding energy and Δ-ML prediction approaches (Fig. S1 and S2); results for Strategy 1 (absolute energy prediction) applied to the HDEV out-of-sample complexes (Fig. S3); schematic of a graph neural network for chemistry (Fig. S4). Scripts and instructions for model training and evaluation can be found at: https://github.com/cvhetherington/Rare-Earth-Net. See DOI: https://doi.org/10.1039/d5dd00286a.
Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division, through the Rare Earth Project in the Separations Program, at the Lawrence Berkeley National Laboratory under Contract DE-AC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy Office of Science User Facility using NERSC award BES-ERCAP0031712. This research used the Lawrencium computational cluster resource provided by the IT Division at the Lawrence Berkeley National Laboratory.References
- V. Balaram, Rare earth elements: A review of applications, occurrence, exploration, analysis, recycling, and environmental impact, Geosci. Front., 2019, 10, 1285–1303 CrossRef CAS.
- E. Alonso, A. M. Sherman, T. J. Wallington, M. P. Everson, F. R. Field, R. Roth and R. E. Kirchain, Evaluating rare earth element availability: A case with revolutionary demand from clean technologies, Environ. Sci. Technol., 2012, 46, 3406–3414 CrossRef CAS.
- G. Charalampides, K. I. Vatalis, B. Apostoplos and B. Ploutarch-Nikolas, Rare earth elements: industrial applications and economic dependency of Europe, Procedia Econ. Finance, 2015, 24, 126–135 CrossRef.
- D. A. Atwood, The rare earth elements: fundamentals and applications, John Wiley & Sons, 2013 Search PubMed.
- A. Golev, M. Scott, P. D. Erskine, S. H. Ali and G. R. Ballantyne, Rare earths supply chains: Current status, constraints and opportunities, Resour. Policy, 2014, 41, 52–59 CrossRef.
- V. Fernandez, Rare-earth elements market: A historical and financial perspective, Resour. Policy, 2017, 53, 26–45 CrossRef.
- W. Hou, H. Liu, H. Wang and F. Wu, Structure and patterns of the international rare earths trade: A complex network analysis, Resour. Policy, 2018, 55, 133–142 CrossRef.
- T. Liu and J. Chen, Extraction and separation of heavy rare earth elements: A review, Sep. Purif. Technol., 2021, 276, 119263 CrossRef CAS.
- E. O. Opare, E. Struhs and A. Mirkouei, A comparative state-of-technology review and future directions for rare earth element separation, Renew. Sustain. Energy Rev., 2021, 143, 110917 CrossRef CAS.
- M. Asadollahzadeh, R. Torkaman and M. Torab-Mostaedi, Extraction and separation of rare earth elements by adsorption approaches: current status and future trends, Separ. Purif. Rev., 2021, 50, 417–444 CrossRef CAS.
- F. Xie, T. A. Zhang, D. Dreisinger and F. Doyle, A critical review on solvent extraction of rare earths from aqueous solutions, Miner. Eng., 2014, 56, 10–28 CrossRef CAS.
- K. L. Nash and M. P. Jensen, Analytical-scale separations of the lanthanides: A review of techniques and fundamentals, Sep. Sci. Technol., 2001, 36, 1257–1282 CrossRef CAS.
- M. K. Jha, A. Kumari, R. Panda, J. R. Kumar, K. Yoo and J. Y. Lee, Review on hydrometallurgical recovery of rare earth metals, Hydrometallurgy, 2016, 165, 2–26 CrossRef CAS.
- P. S. Arshi, E. Vahidi and F. Zhao, Behind the scenes of clean energy: the environmental footprint of rare earth products, ACS Sustain. Chem. Eng., 2018, 6, 3311–3320 CrossRef CAS.
- J. C. Lee and Z. Wen, Pathways for greening the supply of rare earth elements in China, Nat Sustainability, 2018, 1, 598–605 CrossRef.
- B. V. Hassas, Y. Shekarian and M. Rezaee, Selective precipitation of rare earth and critical elements from acid mine drainage-Part I: Kinetics and thermodynamics of staged precipitation process, Resour. Conserv. Recycl., 2023, 188, 106654 CrossRef.
- B. V. Hassas and M. Rezaee, Selective precipitation of rare earth and critical elements from acid mine drainage-Part II: Mechanistic effect of ligands in staged precipitation process, Resour. Conserv. Recycl., 2023, 188, 106655 CrossRef.
- J. A. Rees, G. J.-P. Deblonde, D. D. An, C. Ansoborlo, S. S. Gauny and R. J. Abergel, Evaluating the potential of chelation therapy to prevent and treat gadolinium deposition from MRI contrast agents, Sci. Rep., 2018, 8, 4419 CrossRef.
- T. A. Choi, A. M. Furimsky, R. Swezey, D. I. Bunin, P. Byrge, L. V. Iyer, P. Y. Chang and R. J. Abergel, In vitro metabolism and stability of the actinide chelating agent 3, 4, 3-LI (1, 2-HOPO), J. Pharmaceut. Sci., 2015, 104, 1832–1838 CrossRef CAS PubMed.
- M. Sturzbecher-Hoehne, T. A. Choi and R. J. Abergel, Hydroxypyridinonate complex stability of group (IV) metals and tetravalent f-block elements: The key to the next generation of chelating agents for radiopharmaceuticals, Inorg. Chem., 2015, 54, 3462–3468 CrossRef.
- G. J. Deblonde, M. Sturzbecher-Hoehne and R. J. Abergel, Solution thermodynamic stability of complexes formed with the octadentate hydroxypyridinonate ligand 3, 4, 3-LI (1, 2-HOPO): a critical feature for efficient chelation of lanthanide (IV) and actinide (IV) ions, Inorg. Chem., 2013, 52, 8805–8811 CrossRef CAS PubMed.
- M. Sturzbecher-Hoehne, C. N. P. Leung, A. D’Aléo, B. Kullgren, A.-L. Prigent, D. K. Shuh, K. N. Raymond and R. J. Abergel, 3, 4, 3-LI (1, 2-HOPO): In vitro formation of highly stable lanthanide complexes translates into efficacious in vivo europium decorporation, Dalton Trans., 2011, 40, 8340–8346 RSC.
- R. M. Pallares, M. Charrier, S. Tejedor-Sanz, D. Li, P. D. Ashby, C. M. Ajo-Franklin, C. Y. Ralston and R. J. Abergel, Precision engineering of 2D protein layers as chelating biogenic scaffolds for selective recovery of rare-earth elements, J. Am. Chem. Soc., 2022, 144, 854–861 CrossRef CAS PubMed.
- E. Furet, K. Costuas, P. Rabiller and O. Maury, On the sensitivity of f electrons to their chemical environment, J. Am. Chem. Soc., 2008, 130, 2180–2183 CrossRef CAS.
- V. Anisimov and O. Gunnarsson, Density-functional calculation of effective Coulomb interactions in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7570 CrossRef CAS.
- Y. Wang, Z. Lin, R. Ouyang, B. Jiang, I. Y. Zhang and X. Xu, Toward Efficient and Unified Treatment of Static and Dynamic Correlations in Generalized Kohn–Sham Density Functional Theory, JACS Au, 2024, 4, 3205–3216 CrossRef CAS.
- C. Hölzer, I. Gordiy, S. Grimme and M. Bursch, Hybrid DFT Geometries and Properties for 17k Lanthanoid Complexes The LnQM Data Set, J. Chem. Inf. Model., 2024, 64, 825–836 CrossRef.
- C. J. Jocher, E. G. Moore, J. Xu, S. Avedano, M. Botta, S. Aime and K. N. Raymond, 1, 2-Hydroxypyridonates as contrast agents for magnetic resonance imaging: TREN-1, 2-HOPO, Inorg. Chem., 2007, 46, 9182–9191 CrossRef CAS.
- A. Ricano, I. Captain, K. P. Carter, B. P. Nell, G. J.-P. Deblonde and R. J. Abergel, Combinatorial design of multimeric chelating peptoids for selective metal coordination, Chem. Sci., 2019, 10, 6834–6843 RSC.
- S. Singh, N. Kumari, B. K. Kanungo and M. Baral, Hydroxypyridinone based chelators: a molecular tool for fluorescence sensing and sensitization, Sens. Diagn., 2024, 3, 968 RSC.
- M. G. Taylor, D. J. Burrill, J. Janssen, E. R. Batista, D. Perez and P. Yang, Architector for high-throughput cross-periodic table 3D complex building, Nat. Commun., 2023, 14, 2786 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- J. K. Burdett, R. Hoffmann and R. C. Fay, Eight-coordination, Inorg. Chem., 1978, 17, 2553–2568 CrossRef CAS.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Ehlert, M. Stahn, S. Spicher and S. Grimme, Robust and efficient implicit solvation model for fast semiempirical methods, J. Chem. Theory Comput., 2021, 17, 4250–4261 CrossRef CAS.
- S. R. Heller and A. D. McNaught, The IUPAC international chemical identifier (InChI), Chem. Int., 2009, 31, 7 CAS.
- M. Bursch, H. Neugebauer and S. Grimme, Structure optimisation of large transition-metal complexes with extended tight-binding methods, Angew. Chem., Int. Ed., 2019, 58, 11078–11087 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96, 2155–2160 CrossRef CAS.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, The ORCA program system, WIRES Comput. Molec. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, Software update: the ORCA program system, version 5.0, WIRES Comput. Molec. Sci., 2022, 12, e1606 CrossRef.
- X. Cao and A. Weigand, Relativistic pseudopotentials and their applications, Comput. Methods Lanthanide Actinide Chem., 2015, 147–179 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning local equivariant representations for large-scale atomistic dynamics, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed.
- J. Li, J. Li, Z. Liu and D. Wang, Prediction of Actinide–Ligand Complex Stability Constants by Machine Learning, J. Phys. Chem. A, 2025, 129, 4611–4623 CrossRef CAS PubMed.
- T. Liu, K. R. Johnson, S. Jansone-Popova and D.-e. Jiang, Advancing rare-earth separation by machine learning, JACS Au, 2022, 2, 1428–1434 CrossRef CAS PubMed.
- S. Chaube, S. Goverapet Srinivasan and B. Rai, Applied machine learning for predicting the lanthanide-ligand binding affinities, Sci. Rep., 2020, 10, 14322 CrossRef CAS.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csanyi, Evaluation of the MACE force field architecture: From medicinal chemistry to materials science, J. Chem. Phys., 2023, 159, 044118 CrossRef PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Big data meets quantum chemistry approximations: the Δ-machine learning approach, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- M. Ruth, D. Gerbig and P. R. Schreiner, Machine learning of coupled cluster (T)-energy corrections via delta (Δ)-learning, J. Chem. Theory Comput., 2022, 18, 4846–4855 CrossRef CAS.
- A. K. Gupta, M. M. Stulajter, Y. Shaidu, J. B. Neaton and W. A. de Jong, Equivariant neural networks utilizing molecular clusters for accurate molecular crystal lattice energy predictions, ACS Omega, 2024, 9, 40269–40282 CAS.
- J. J. Nelson, T. Cheisson, H. J. Rugh, M. R. Gau, P. J. Carroll and E. J. Schelter, High-throughput screening for discovery of benchtop separations systems for selected rare earth elements, Commun. Chem., 2020, 3, 7 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, MACE: Higher order equivariant message passing neural networks for fast and accurate force fields, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, The design space of E (3)-equivariant atom-centred interatomic potentials, Nat. Mach. Intell., 2025, 7, 56–67 CrossRef.
- D. S. Levine, M. Shuaibi, E. W. C. Spotte-Smith, M. G. Taylor, M. R. Hasyim, K. Michel, I. Batatia, G. Csányi; M. Dzamba, P. Eastmanet al., The Open Molecules 2025 (OMol25) Dataset, Evaluations, and Models, arXiv, 2025, preprint, arXiv:2505.08762, DOI:10.48550/arXiv.2505.08762.
- I. Batatia, P. Benner, Y. Chiang, A. M. Elena, D. P. Kovács, J. Riebesell, X. R. Advincula, M. Asta, M. Avaylon, W. J. Baldwinet al., A foundation model for atomistic materials chemistry, arXiv, 2023, preprint, arXiv:2401.00096, DOI:10.48550/arXiv.2401.00096.
- F. Cai, K. Hanna, T. Zhu, T.-R. Tzeng, Y. Duan, L. Liu; S. Pilla, G. Li and F. Luo, A Foundation Model for Chemical Design and Property Prediction, arXiv, 2024, preprint, arXiv:2410.21422, DOI:10.48550/arXiv.2410.21422.
- O. Méndez-Lucio, C. A. Nicolaou and B. Earnshaw, MolE: a foundation model for molecular graphs using disentangled attention, Nat. Commun., 2024, 15, 9431 CrossRef.
Footnotes |
| † Ankur K. Gupta (AKG) and Caitlin V. Hetherington (CVH) contributed equally to this work. |
| ‡ Present address: Institute for Advanced Computational Science and Department of Chemistry, Stony Brook University, Stony Brook, New York 11794, USA. |
| This journal is © The Royal Society of Chemistry 2026 |