Open Access Article
Open Access ArticleEfficient symmetry-aware materials generation via hierarchical generative flow networks
Tri Minh
Nguyen
 *,
Sherif Abdulkader
Tawfik
*,
Sherif Abdulkader
Tawfik
 ,
Truyen
Tran
,
Sunil
Gupta
,
Santu
Rana
and
Svetha
Venkatesh
,
Truyen
Tran
,
Sunil
Gupta
,
Santu
Rana
and
Svetha
Venkatesh
Applied Artificial Intelligence Institute, Deakin University, 75 Pigdons Rd, Waurn Ponds, VIC, Australia. E-mail: tri.nguyen1@deakin.edu.au; s.abbas@deakin.edu.au; truyen.tran@deakin.edu.au; sunil.gupta@deakin.edu.au; santu.rana@deakin.edu.au; svetha.venkatesh@deakin.edu.au
First published on 2nd October 2025
Abstract
Discovering new solid-state materials requires rapidly exploring the vast space of crystal structures and locating stable regions. Generating stable materials with desired properties and compositions is extremely difficult as we search for very small isolated pockets in the exponentially many possibilities, considering elements from the periodic table and their 3D arrangements in crystal lattices. Materials discovery necessitates both optimized solution structures and diversity in the generated material structures. Existing methods struggle to explore large material spaces, outside the training space, and generate diverse samples with desired properties and requirements. We propose the Symmetry-aware Hierarchical Architecture for Flow-based Traversal (SHAFT), a novel generative model employing a hierarchical exploration strategy to efficiently exploit the symmetry of the materials space to generate crystal structures with desired properties. In particular, our model decomposes the exponentially large materials space into a hierarchy of subspaces consisting of symmetric space groups, lattice parameters, and atoms. To benchmark our approach, we first develop a novel, non-hierarchical GFlowNet for complete crystal structure generation. We then introduce SHAFT, a more expressive hierarchical model that leverages its architecture and increased model capacity to more efficiently explore the materials space. We demonstrate that SHAFT significantly outperforms the flat GFlowNet baseline and other state-of-the-art methods like CDVAE and DiffCSP in generating valid, stable, and diverse crystal structures.
1 Introduction
Discovering new solid-state materials plays a central role in advancing multiple critical industries, including energy generation and storage, and semiconductor electronics.1,2 Each unique crystal structure exhibits properties useful for specific applications. For example, superconductive perovskite structures are used in circuit board elements for computers. Generating material structures that meet given property requirements poses a set of unique challenges. The key challenge is generating crystal structures that exhibit a repeating arrangement of atoms in three-dimensional space. A crystal structure is determined by how atoms are arranged within the unit cell specified by its lengths and angles. However, the inter-atom interactions are not confined within the unit cell but also occur with adjacent unit cells. These characteristics make the search space of crystal structures significantly larger and more complex compared to well-studied molecular search spaces. The number of known crystal structures, both experimental and hypothetical, is around 3 million curated from AFLOW3–5 and the Materials Project,6 which is tiny compared to billions of molecules from the ZINC dataset.7 The limited data undermine modern data-driven methods to learn the crystal structure representation.8,9We address the complexity associated with the large search space by proposing a new generative model termed Symmetry-aware Hierarchical Architecture for Flow-based Traversal (SHAFT). SHAFT explores the vast search space in an efficient way. The key insight for solving the large state space problem is breaking space exploration into more meaningful hierarchical sub-tasks. Here the higher-level tasks explore actions that are closely related to the reward function, while lower-level tasks handle the configuration adjustment corresponding to the actions taken at higher-level tasks. Since the exploration starts at a highly general concept level, it can learn a more meaningful policy that corresponds to the target reward function. With more meaningful actions taken at a higher level, the policy networks can focus on searching the actions in a significantly smaller sub-space that corresponds to the actions of high-level tasks instead of exploring the whole space.
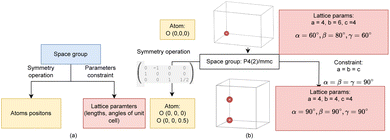
Three key concepts can help generative models search the material space effectively. First, the crystal structure class imposes symmetry operations and geometrical characteristics on atom positions and lattice parameters, as seen in Fig. 1, effectively reducing the material search space. Second, searching for stable structures on the non-smooth energy landscape defined by quantum mechanics requires generative models to explore and generate diverse sample sets. This approach helps avoid getting stuck in a single mode or local minima. Third, we apply bond constraints on atom pairs in the generated crystals, ensuring that atoms are not closer to each other than specific bond thresholds. These thresholds are obtained using all materials in the Materials Project database. Given the diversity of materials in this database, it's reasonable to assume that minimum distances derived from it are threshold distances for the ground state structure of the respective atoms in any new crystal structure. By incorporating these concepts, generative models can more effectively navigate the complex material space and produce stable, diverse, and physically realistic crystal structures.
We model the entire material space in a hierarchical structure. The highest level is the crystal structure class, which is related to relevant material properties. Exploring this class can efficiently lead to more optimal properties of the generated structure. Specifically, we use the space group of the crystal structure to effectively reduce the 3D atom space exploration to a more meaningful high-level exploration and generate a high-symmetry crystal structure. The next level searches for the unit cell lattice parameters and atom configurations, given the space group. The space group imposes constraints on these parameters and atom positions, thus reducing the search space. Choosing positions one by one creates a long-horizon trajectory, making it difficult to learn a policy that generates high-symmetry structures proportional to the reward function. By leveraging the space group's symmetry operations, we can immediately replicate atoms over the unit cell. This approach reduces the trajectory length, making it easier for the policy network to learn how to generate a high-symmetry crystal structure.
While deep generative models have shown promise, the immense complexity and size of the material search space remain a formidable barrier. Prior methods using Generative Flow Networks (GFlowNets), such as Crystal-GFN,10 have successfully generated crystal parameters like space groups and lattice constants, but stop short of generating the complete crystal structure, omitting the explicit placement of atoms. Our work addresses this complete generation problem.
Our work first addresses this complete generation problem by developing a novel, non-hierarchical or “flat”, GFlowNet that generates the full crystal—space group, lattice, and atomic coordinates—within a single, monolithic policy framework. This in itself is a significant advance for creating full atomic structures with GFlowNets. However, we hypothesize that such a flat approach struggles to efficiently navigate the intricate, long-horizon dependencies inherent in crystal design. To overcome this, we then introduce SHAFT, a hierarchical model that decomposes the generation problem to improve learning efficiency and exploration. The comparison between SHAFT and our flat GFlowNet baseline is therefore designed specifically to isolate and quantify the benefits of this hierarchical decomposition.
Our main contributions are:
(1) We propose a generative model that can search effectively in a large search space, even outside the observed training dataset space, by modeling the state space in a hierarchical structure.
(2) We incorporate the physical knowledge curated from the large material databases into our generative model to generate more stable structures.
(3) We validate the hierarchical structure state space and physics priors of our proposed generative model in the crystal structure generation task to show the efficiency in material space exploration as well as the stability of the generated structures.
2 Related studies
There are three main approaches to crystal structure generation. (1) The first is element substitution. Given a crystal template,11 the elements are substituted with other elements having similar properties.12–14 This approach is computationally expensive and relies on domain knowledge in element substitution. (2) The second strategy is distribution sampling. Deep generative models learn from the distribution of known stable crystal structures to sample new structures, such as those generated by Variational AutoEncoders (VAEs),2,15,16 Generative Adversarial Networks (GANs),17,18 symmetry-aware diffusion models,19 and periodic-E(3)-equivariant denoising model.20 Recent advances in generative modeling for materials design include SymmCD's symmetry-preserving crystal generation,21 GNoME's large-scale discovery of stable inorganic materials using graph neural networks,22 and MatterGen's diffusion-based model capable of generating novel,23 stable materials under diverse structural and property constraints. This data-driven approach has difficulty generating high symmetry structures and performing out-of-distribution generalization. Also, the generation process is solely based on learning from the known data, leaving minimal room for domain knowledge and human intervention during the generation process. And finally, (3) iterative generation: crystal structures can be decomposed into compositional objects, and constructed step by step using reinforcement learning (RL).24 Crystal-GFN10 uses GFlowNet to generate crystal structure parameters such as space group, lattice lengths, and angles, but it does not generate the complete structure with atoms' coordinates. Crystal-GFN uses GFlowNet to determine crystal parameters via a fixed, linear sequence of actions (space group, then composition, and then lattice parameters), but it does not generate the complete structure with atoms' coordinates. This contrasts with our framework, which employs an iterative refinement process where the space group, lattice, and atomic placements can be dynamically updated throughout the generation trajectory. Our work is the first to apply the RL-based technique to explore the entire material and atom space. The key advantage of this RL-based approach is that it allows the incorporation of domain knowledge into the action and state space and shaping the reward function. RL can generalise to hierarchical RL which solves the long horizon trajectory problem by designing sub-goals.25,26 By exploiting high-level crystal structure classes such as space groups, SHAFT creates a sub-goal for low-level policies, helping them to learn the atom coordinate space more effectively.Generative Flow Networks (GFlowNets) are generative models designed to sample candidates proportional to their target rewards. The framework has been successfully applied to many fields such as molecular discovery,27 protein sequence discovery,28 causality,29 and continuous control.30 Jiangyan et al.31 integrated symmetries into GFlowNets with equivalent actions. LS-GFN32 explores the local neighborhood to avoid the over-exploration in GFlowNet. Our SHAFT is a generalization of GFlowNets for more efficient sampling by modelling the hierarchy of the search space. When applied to crystal structure generation, SHAFT also exploits the group symmetry unique to this domain.
3 Preliminaries
3.1 Crystallographic space group
The crystal structure is the repeating arrangement of the atoms within a unit cell in 3D. Formally, the unit cell of N atoms is a triplet (L, A, X) of lattice parameters L, atom list A, and atom coordinates X. There are 6 lattice parameters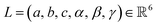 describing 3 lengths and 3 angles of the unit cell, respectively. The atoms list A = (a1, …, aN) describes the elements. The atoms' coordinates
describing 3 lengths and 3 angles of the unit cell, respectively. The atoms list A = (a1, …, aN) describes the elements. The atoms' coordinates 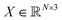 describe the positions of the atoms within the unit cell, which can be Cartesian or fractional.
describe the positions of the atoms within the unit cell, which can be Cartesian or fractional.
The space group of a crystal structure consists of a list of symmetry transformations applied to the atoms within the unit cell. In crystallography, there are 230 space groups.33 Each space group has geometrical characteristics defined in lattice angles and lengths that can be used as constraints to limit the parameter search space. The list of geometrical characteristics is provided in SI Appendix Section A.1. Given the space group Gs, the elements of the space group g ∈ Gs are a set of symmetry operations. A crystallographic orbit of an atom o = (xo, ao) with coordinate xo and element ao is defined as OGs(xo) = {g·xo∣g ∈ Gs}, where g·xo denotes the application of the symmetry operation g on the atom o within the unit cell. From a reference atom o, we can obtain a set OGs of equivalent points.
3.2 Generative flow network
GFlowNet models the sampling process of the compositional object s as the directed acyclic graph (DAG) G = (S, A), where S is the set of states and A is the state transition which is the subset of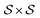 . The sampling process starts with the initial state vertex s0 ∈ S with no incoming edge and stops at the sink state vertex sn ∈ S, where n is the sampling trajectory length, with no outgoing edge. GFlowNet learns a policy function π that can sample the object x with a probability proportional to the non-negative reward function. GFlowNets construct the object step by step, from the initial state s0 to the sink state sn, forming a trajectory τ = s0, …, sn, τ ∈ τ where τ is the trajectory set. For any state s in the trajectory, we can define the flow of the state as
. The sampling process starts with the initial state vertex s0 ∈ S with no incoming edge and stops at the sink state vertex sn ∈ S, where n is the sampling trajectory length, with no outgoing edge. GFlowNet learns a policy function π that can sample the object x with a probability proportional to the non-negative reward function. GFlowNets construct the object step by step, from the initial state s0 to the sink state sn, forming a trajectory τ = s0, …, sn, τ ∈ τ where τ is the trajectory set. For any state s in the trajectory, we can define the flow of the state as 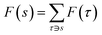 and the flow of the edge s → s′ as
and the flow of the edge s → s′ as 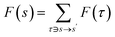 .27 The forward policy that maps the probability of transition from the current state s to the next state s′ is given by
.27 The forward policy that maps the probability of transition from the current state s to the next state s′ is given by 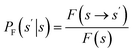 . The backward policy mapping probability transition to the previous state s given the current state s′ is given by
. The backward policy mapping probability transition to the previous state s given the current state s′ is given by 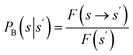 . The training objective of the GFlowNets is flow-matching consistency where the incoming flow is equal to the outgoing flow,
. The training objective of the GFlowNets is flow-matching consistency where the incoming flow is equal to the outgoing flow, 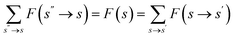 , for all states. Ref. 34 proposes trajectory balance to deal with the long trajectory credit assignment problem. Given the trajectory τ = (s0 → s1 → … → sn), the forward probability of a trajectory is defined as
, for all states. Ref. 34 proposes trajectory balance to deal with the long trajectory credit assignment problem. Given the trajectory τ = (s0 → s1 → … → sn), the forward probability of a trajectory is defined as 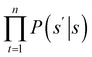 . The trajectory balance constraint is defined as
. The trajectory balance constraint is defined as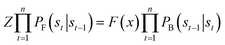 | (1) |
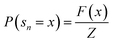 and Z = F(s0) represents the initial state flow. Then the trajectory balance objective is defined as:
and Z = F(s0) represents the initial state flow. Then the trajectory balance objective is defined as: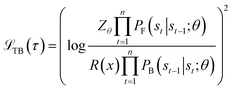 | (2) |
4 Methods
To best leverage the group symmetry in the crystal structure space, here we propose SHAFT (Symmetry-aware Hierarchical Architecture for Flow-based Traversal), a generic flow-based generative model that explores the space in a hierarchical manner. In SHAFT, the lower states represent discrete concepts constrained by the higher states that represent more abstract concepts. When applied to crystal structure generation, SHAFT makes use of the group symmetry in the space. See Fig. 1 for the overall structural state design.4.1 Hierarchical policy
A standard, or “flat”, GFlowNet-based approach to crystal generation would treat the entire process as a single sequence of actions managed by one monolithic policy network. This policy would be responsible for every decision, from selecting a space group to specifying the precise fractional coordinates of each atom. While feasible, this approach faces significant challenges: it must learn the complex interplay between all degrees of freedom simultaneously from a unified and vast action space. The critical, high-level decision of choosing a space group is diluted among many low-level, continuous decisions, making it difficult for the agent to attribute a high final reward to a good initial space group choice.To address this, SHAFT introduces a hierarchical policy structure that decomposes the generation process into two distinct, more manageable sub-tasks, as illustrated in Fig. 2. This design is motivated by the natural hierarchy present in crystal structures themselves. SHAFT generalises GFlowNets to accommodate a policy hierarchy of two levels: the high-level decision-making policy operating on the space groups, and the low-level execution policy operating on the atom–lattices (see Fig. 2). The space group policy chooses the space group and applies corresponding constraints on the atom–lattice policy actions. The corresponding hierarchical state space is decomposed as s = (ssg, sal), where ssg is the space group state and sal is the atom–lattice state. The latter consists of lattice parameters slp, atom coordinate sac, and atom type sat states.
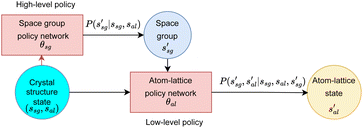 | ||
Fig. 2 Hierarchical policy for the crystal structure state. First, the crystal structure graph state s is decomposed into space group state ssg and atom-lattice state sal. Then the transition probability 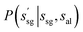 in eqn (4) is given by the space group policy network θsg. The transition probability in eqn (4) is given by the space group policy network θsg. The transition probability 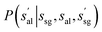 in eqn (4) is given by the atom-lattice policy network θal. in eqn (4) is given by the atom-lattice policy network θal. | ||
Then we define the probability of transitions as:
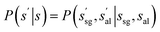 | (3) |
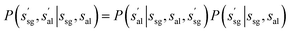 | (4) |
Then given the trajectory τ = (s0 → s1 → … → sn), we have the trajectory balance constraint (eqn (1)) with the decomposed state as:
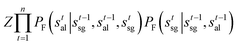 | (5) |
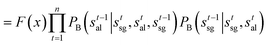 | (6) |
The space group forward and backward transition probabilities PF(stsg|st−1) and PB(st−1sg|st) are parameterized by the multinoulli distribution defined by the logits output of the space group policy networks. The lattice parameter state slp transition probability is parameterized by the Gaussian distribution defined by the mean µ and variance σ2. The atom fractional coordinate state sac transition probability is parameterized by the multivariate Gaussian distribution defined by the mean µ and covariance matrix Σ. The atom type state sat transition probability is parameterized by the multinoulli distribution.
The sampling process is described in Algorithm 1. The lattice sampling process starts with the state s0 which has lattice parameters a = b = c = 4 and α = β = γ = 90°, space group 1, and an empty crystal graph at state 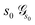 . The state at any point, s = (ssg, sal), represents the crystal structure accumulated up to that step. Initially, at s0, the crystal is empty. At each subsequent step t, the algorithm performs space group proposal and incremental construction. In the space group proposal, the high-level policy, θsg, proposes a new space group,
. The state at any point, s = (ssg, sal), represents the crystal structure accumulated up to that step. Initially, at s0, the crystal is empty. At each subsequent step t, the algorithm performs space group proposal and incremental construction. In the space group proposal, the high-level policy, θsg, proposes a new space group, 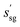 . This proposed space group governs the symmetry rules for the current step. It is used by the low-level policy, θal, to apply symmetry operations to the new reference atom being added. The choice of
. This proposed space group governs the symmetry rules for the current step. It is used by the low-level policy, θal, to apply symmetry operations to the new reference atom being added. The choice of 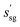 can also impose new constraints on the crystal's lattice parameters, refining the overall structure. In the incremental construction, the low-level policy adds a new reference atom to the existing structure. The symmetry operations of the currently proposed space group,
can also impose new constraints on the crystal's lattice parameters, refining the overall structure. In the incremental construction, the low-level policy adds a new reference atom to the existing structure. The symmetry operations of the currently proposed space group,  , are applied to this new atom and all previously placed reference atoms in the structure. The resulting state at the end of the step,
, are applied to this new atom and all previously placed reference atoms in the structure. The resulting state at the end of the step, 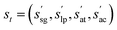 , is an augmentation of the previous state, st−1. It incorporates the newly added atom (and its symmetric equivalents) and reflects the space group that is now governing the structure's symmetry. This step-by-step refinement ensures the DAG property of the generation process (more details in SI Appendix Section A.2).
, is an augmentation of the previous state, st−1. It incorporates the newly added atom (and its symmetric equivalents) and reflects the space group that is now governing the structure's symmetry. This step-by-step refinement ensures the DAG property of the generation process (more details in SI Appendix Section A.2).
A key aspect of this sampling process is the implicit handling of Wyckoff positions. SHAFT does not require the explicit selection of a Wyckoff position. Instead, the low-level policy learns to place reference atoms at specific fractional coordinates. If these coordinates correspond to a special Wyckoff position for the given space group, the application of symmetry operations generates a set of symmetrically equivalent atoms, some of which will overlap. These overlapping sites are then merged using a standard distance tolerance (0.01 Å via the pymatgen). If the coordinates correspond to a general Wyckoff position, a larger set of symmetrically equivalent atoms will be generated.
The policy is guided by a reward function that favors the generation of stable, low-energy structures. The policy learns to propose reference atom positions that result in favorable crystal structures, which may indirectly lead it to utilize Wyckoff positions commonly found in stable materials. This is an emergent behavior rather than an explicit design constraint.
The consistency between the space group, atom positions, and composition is maintained throughout this process. The atom positions are, by definition, consistent with the chosen space group because they are generated by its symmetry operations. The overall composition is managed incrementally. At each step, the model chooses an atom type, and a composition-related reward (Rcomp(x)) guides the policy towards chemically valid structures. Furthermore, as shown in Algorithm 1, the choice of elements can be restricted using a validity mask based on compositional constraints, ensuring that the generated structures adhere to desired chemical formula.
4.2 Physics-informed reward function
At the terminal state x = sMt of the trajectory, a reward is returned by a non-negative function R(x), providing feedback on the generated crystal structure, especially its validity and stability. To achieve these goals, we design the reward function to include the following key elements:The formation energy term dictates that a stable crystal structure will have a negative formation energy, defined as Re(x) = e−E(x)/T where E(x) is the predicted formation energy per atom given by the prediction model (SI Appendix Section A.4.7), and T is the normalization term.
The bond length preference term Rb encourages the bond lengths of the input crystal structure to agree with the empirical lengths retrieved from the database. First, for each atom ai in the crystal structure x, we search all its neighbors nei(ai) within a radius cutoff of 4.0 Å. The neighbors can also include atoms from adjacent unit cells. We retrieve the minimum and average bond distances of all bond types existing in x from the Materials Project database (e.g. the minimum bond distance of Li–O is 1.63 and the average bond distance of Li–O is 3.02). Then the difference between the bond length d(ai, aj), aj ∈ nei(ai) with minimum dmin(ai, aj) and the average bond distance davg(ai, aj) of the (ai, aj) bond type is given by
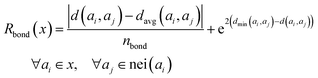 | (7) |
The density term RP encourages the optimal structure density. Because the bond distance preference term applies a strict penalty for structures violating the minimum distance constraint, the generative model tends to generate a structure with long distances between atom pairs with only a few neighboring atoms. This leads the model to generate gas-like structures with low density rather than solid-state density. On the other hand, structures with very high density (i.e. larger than 10) are unlikely to be realistic as the unit cells are crowded with atoms causing a very high formation energy. We measure the generated structure density P(x) (SI Appendix Section A.4.5) and define the density term as a Gaussian function of structure density: 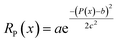 .
.
The composition validity term is defined as Rcomp(x) = 1 for valid composition and Rcomp(x) = 0 otherwise. We follow composition validity as determined by the charge neutrality check.35 Finally, the physics-informed reward function is composed as:
| R(x) = weRe(x) + wpRP(x) + wbRbond(x) + wcRcomp(x) | (8) |
4.3 State representation
The crystal structure state must capture all relevant information about the crystal, including its atomic arrangement and lattice parameters. We represent the crystal unit cell (L, A, X) described in Section 3.1 as a directed graph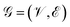 with node feature matrix
with node feature matrix 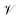 and edge matrix
and edge matrix 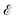 . The node features include the atom's atomic number and its fractional coordinates within the unit cell. The edges are determined using k-nearest neighbors with the maximum number of neighbors being 12 and the radius cut-off is 8.0 Å. The graph representation of the crystal structure is learned using a MatErials Graph Network (MEGNet) model36 (details in SI Appendix Section A.4.2) to satisfy the periodic invariance and E(3) invariance of the crystal structure.
. The node features include the atom's atomic number and its fractional coordinates within the unit cell. The edges are determined using k-nearest neighbors with the maximum number of neighbors being 12 and the radius cut-off is 8.0 Å. The graph representation of the crystal structure is learned using a MatErials Graph Network (MEGNet) model36 (details in SI Appendix Section A.4.2) to satisfy the periodic invariance and E(3) invariance of the crystal structure.
Lattice parameters are encoded using a multi-layer perceptron as:
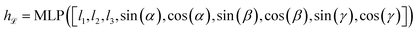 | (9) |
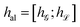 . The encoded crystal structure state hM is later used as the representation of the hierarchical state space sM.
. The encoded crystal structure state hM is later used as the representation of the hierarchical state space sM.
5 Experiments
Our SHAFT can be applied to any crystal discovery tasks given a set of elements. The main bottleneck is the prohibitive cost of validation of the generated structures. We will first focus on a constrained generation task with careful DFT validation (Section 5.1). Then we demonstrate the scalability of SHAFT on nearly unconstrained generation tasks (Section 5.3).Baselines: we compare our SHAFT with SOTA techniques including CDVAE,15 DiffCSP20 and GFlowNet, which is a flat version of our method. CDVAE is a diffusion model that uses SE(3) equivariant GNNs adapted for periodicity. We train CDVAE and DiffCSP on the MP-battery dataset for the battery material discovery task (based on requirements in Section 5.1, more details in SI Appendix Section A.5) and the MP-20 dataset6 for general crystal generation (Section 5.3). We report the top-K (K = 100) results ranked by eqn (8). For CDVAE and DiffCSP, we sample 100 samples three times and report the mean and standard deviation. We follow recent work on continuous GFlowNet37 to operate in the continuous space of the atoms' coordinates and lattice parameters. The model has a single-level policy network that outputs the space group, lattice parameters, atom coordinates, and atom types. Note that this is the first time GFlowNet has been applied successfully to complete crystal generation.
5.1 Constrained generation: battery materials discovery
For concreteness, we focus on battery material discovery, the most fundamental task in the battery industry worth hundreds of billions of dollars, and of great importance for securing a green energy future. The challenge is to generate stable structures with specific formulae and elements.Motivated by the search for light-weight, transition-metal free cation materials, we explore the space of possible materials that can be made from the light elements Be, B, C, N, O, Si, P, S, and Cl, and one of the three alkali metals Li, Na and K. This space of materials constitutes materials that can be utilised in lithium-ion, sodium-ion, and potassium-ion battery materials, respectively. We discuss further the motivation for the experiments in SI Appendix Section A.3.
| Method | Structure ↑ | Composition ↑ |
|---|---|---|
| CDVAE | 0.66 ± 0.03 | 0.73 ± 0.090 |
| DiffCSP | 0.86 ± 0.03 | 0.59 ± 0.005 |
| GFlowNet | 0.98 ± 0.03 | 1.00 ± 0.000 |
| SHAFT | 0.99 ± 0.01 | 1.00 ± 0.000 |
| Method | Crystal family ↑ | Composition ↑ | Structure ↑ |
|---|---|---|---|
| CDVAE | 0.15 ± 0.09 | 1859.07 ± 199.28 | 0.43 ± 0.004 |
| GFlowNet | 1.97 ± 0.15 | 165.13 ± 32.55 | 0.84 ± 0.03 |
| DiffCSP | 1.23 ± 0.09 | 2360.97 ± 110.37 | 0.57 ± 0.06 |
| SHAFT | 2.19 ± 0.06 | 147.80 ± 15.81 | 0.89 ± 0.05 |
SHAFT demonstrates superior performance in generating a broad range of crystal families (Shannon–Wiener index of 2.19) and structurally distinct materials (structure diversity of 0.89), outperforming all baselines.
Conversely, for compositional diversity, we observe that the scores for GFlowNet (165.13) and SHAFT (147.80) are lower than those for CDVAE (1859.07) and DiffCSP (2360.97). This difference is an important and expected consequence of their fundamentally different generative approaches. CDVAE and DiffCSP are trained to replicate the distribution of the training data, and their high compositional diversity reflects the breadth of compositions present in the source dataset. In contrast, SHAFT and our GFlowNet baseline are reward-driven agents designed to actively seek candidates that maximize a physics-informed reward function. This reward-guided exploration inherently focuses the search on compositional regions that yield high-reward structures—those with high stability and validity—within the constrained chemical space of the battery discovery task.
This represents a critical trade-off: while diffusion models may explore a wider range of compositions, this often comes at the cost of lower stability and validity, as shown by our results in Tables 1 and 3. SHAFT, by design, prioritizes finding high-quality candidates within promising compositional niches, leading to a more targeted but less compositionally diverse set of outputs in this specific metric. This focus on high-reward regions is a key feature of our approach for efficient materials discovery, trading exhaustive compositional breadth for a higher yield of stable and valid material candidates.
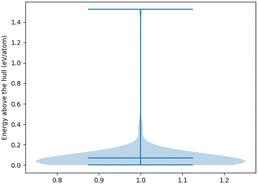
| Method | Energy ↓ | % Energy < 0 ↑ | E hull ↓ |
|---|---|---|---|
| CDVAE | −0.318 ± 0.080 | 74.6 ± 8.6 | 1.04 ± 0.24 |
| DiffCSP | 0.120 ± 0.108 | 45.5 ± 6.3 | 0.55 ± 0.04 |
| GFlowNet | −1.014 ± 0.003 | 98.6 ± 1.6 | 0.32 ± 0.02 |
| SHAFT | −1.241 ± 0.097 | 99.5 ± 0.8 | 0.29 ± 0.03 |
As illustrated in Fig. 4a, SHAFT demonstrates significantly faster mode discovery than the baseline flat GFlowNet. This enhanced efficiency is a direct consequence of its hierarchical policy structure. The high-level policy, θsg, learns to strategically prune the vast search space by first proposing promising crystallographic space groups that are historically more likely to yield stable materials. This high-level decision provides a strong structural constraint. Consequently, the low-level policy, θal, is tasked with a more focused and tractable problem: arranging atoms and defining lattice parameters within the pre-selected, promising symmetric framework. By contrast, a flat GFlowNet must inefficiently explore all parameters simultaneously, making it slower to escape regions of the search space that lead to invalid or unstable structures. The discovery of nearly 30 unique modes after evaluating 105 candidates underscores the immense and sparse nature of the de novo materials design space. The vast majority of potential atomic combinations are unstable or physically invalid. The critical insight from this experiment is that SHAFT's hierarchical decomposition of the problem allows it to navigate this complex landscape more efficiently, identifying the rare, high-reward modes with substantially fewer samples than its non-hierarchical counterpart.
Diffusion models like CDVAE and DiffCSP are trained to be expert replicators, learning the distribution of known, stable materials from a database. Their ability to generate stable structures is largely inherited from these high-quality training data. In contrast, RL-based models like SHAFT are trained as systematic explorers, designed to search the entire chemical space to find novel, high-reward structures. This process necessarily involves learning from a large number of low-reward samples to map out the vast, unstable regions of the search space, thus again highlighting the immense and sparse nature of the de novo materials design space.
The average reward per epoch in Fig. 4b shows that SHAFT not only speeds up the mode discovery but also discovers higher reward structures. The formation energy, bond length preferences, density, and composition validity terms improving over epochs (see SI Fig. 9) show that the model can learn to embed the physical constraints into the policy network. SI Fig. 10 showing the shift of the distribution of reward function terms from the random initialization of an untrained SHAFT crystal structure to trained SHAFT further proves this point.
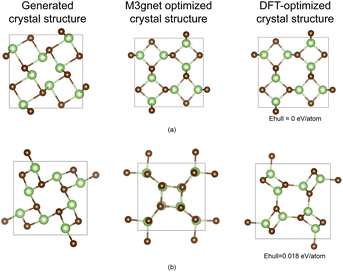 | ||
| Fig. 3 Examples of two configurations ((a) and (b)) of (LiBr)x generated by SHAFT and the corresponding structure optimized by the M3GNet framework38 and DFT. | ||
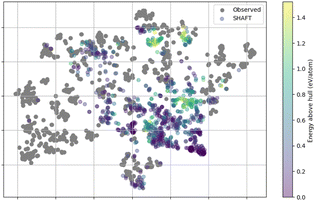 | ||
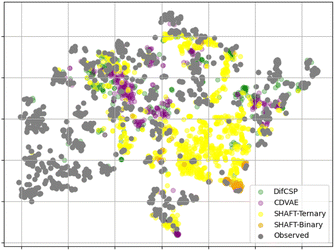
| Fig. 6 Distributions of the sampled crystal structures from the observed crystal structures (MP-battery dataset) and SHAFT in terms of energy above hull, plotted using t-SNE. | ||
Match rate: we follow the previous work in ref. 39 to evaluate the match rate of crystal structure relaxation. A structure m and its optimized structure m′ are considered matched if their atoms' translations and angles are within tolerance thresholds, indicating that the generated structure is close to the optimum, and thus is more stable. We use the matching algorithm provided by the pymatgen library43 in StructureMacher with 10° angle tolerance, 1.0 fractional length tolerance, and 1.0 site tolerance. The match rate is the fraction of matched structures over the total number of generated structures.
The results reported in Table 4 show that our proposed method can produce more structures (at a rate of 0.82) that are nearly optimal in terms of total energy compared to GFlowNets and CDVAE.
| Methods | Match rate ↑ | RMS displacement ↓ |
|---|---|---|
| CDVAE | 0.46 ± 0.03 | 0.287 ± 0.0133 |
| DiffCSP | 0.33 ± 0.04 | 0.335 ± 0.041 |
| GFlowNet | 0.80 ± 0.01 | 0.174 ± 0.019 |
| SHAFT | 0.82 ± 0.02 | 0.161 ± 0.020 |
We also report the match rate of structures generated by SHAFT with their DFT-optimized structures (reported in Section 5.1.7) instead of M3GNet-optimized structures. In stark contrast, when comparing the as-generated structures to their DFT-relaxed ground truths, the match rate drops to 0.042 and the RMS displacement increases to 0.297 Å.
This discrepancy is expected and highlights a key characteristic of surrogate-model-guided generation. The high match rate with M3GNet-relaxed structures validates that SHAFT effectively optimizes its outputs for its given reward function—the M3GNet potential energy surface (PES). The model learns to produce structures that are already near a local minimum on this surrogate PES.
However, the M3GNet potential, while highly accurate, is an approximation of the true quantum mechanical landscape described by DFT. The lower match rate with DFT-relaxed structures quantifies the inherent gap between the surrogate model and the ground truth. The larger structural rearrangement required during DFT optimization is a necessary step to move the structure from the surrogate's predicted minimum to the true ground-state configuration. This also illustrates a common challenge known as “reward hacking”: the model becomes highly proficient at generating structures that minimize the energy of the surrogate M3GNet potential, which is an accurate but imperfect proxy for the true quantum mechanical landscape described by DFT.
Ultimately, this analysis reinforces the power of the hierarchical generation and validation workflow. SHAFT, guided by the M3GNet surrogate, is exceptionally effective at identifying promising regions of the vast chemical space that contain verifiably stable materials. The results confirm that while a final DFT refinement is essential for achieving ground-truth accuracy, SHAFT's approach is highly successful for the critical initial discovery phase.
5.2 Generating stable structures with target properties
Our proposed framework, SHAFT, offers the flexibility to optimize multiple objectives via the reward function. We conduct experiments to generate stable structures with low band gaps. The experiment setup is similar to the battery material discovery task (Section 5). While the ideal band gap depends on the specific battery component, a low or zero band gap is highly advantageous for electrode materials. High electronic conductivity is critical for enabling fast charge-transfer kinetics and improving charge/discharge rates, and thus by targeting a near-zero band gap in this experiment, our goal is to discover novel candidates for battery electrodes. We add the following band gap term for the near zero band gap constraint: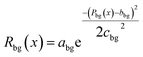 | (10) |
| R(x) = weRe(x) + wbgRbg(x) + wpRP(x) + wbRbond(x) + wcRcomp(x) | (11) |
We set weights as we = wbg = 0.1, wp = 0.1, wb = 0.5, and wc = 0.1. To demonstrate that the generated structures are stable and have near zero band gap, we present the average formation energy and band gap in Table 5.
| Method | Energy ↓ | % Energy < 0 ↑ | Band gap ↓ |
|---|---|---|---|
| CDVAE | −0.82 | 83.33 | 0.45 |
| DiffCSP | −0.96 | 86.74 | 0.48 |
| GFlowNet | −0.63 | 90.91 | 0.08 |
| SHAFT | −0.84 | 100.00 | 0.04 |
5.3 Exploring a very large element space
To further demonstrate the ability to generalize across the whole chemical space, we train our proposed method on 89 elements from H to Pu. Because we have 89 elements instead of 12, the compositional diversity is higher than that in the experiment, as shown in Table 2. As shown in Tables 6 and 7, our proposed method maintains a high percentage of stable structures and low formation energies.| Methods | Crystal family diversity ↑ | Composition diversity ↑ | Structure diversity ↑ |
|---|---|---|---|
| CDVAE | 0.95 | 1857.31 | 0.74 |
| DiffCSP | 2.60 | 1812.25 | 0.93 |
| GFlowNet | 2.37 | 1399.59 | 0.99 |
| SHAFT | 2.32 | 1471.59 | 1.01 |
| Methods | Comp. val. | Struct. val. | Avg. form. E | % E < 0 | Match rate ↑ | RMS dis. ↓ |
|---|---|---|---|---|---|---|
| CDVAE | 0.86 | 1.00 | −0.84 | 58 | 0.71 | 0.14 |
| DiffCSP | 0.83 | 1.00 | −0.85 | 90 | 0.94 | 0.06 |
| GFlowNet | 1.00 | 1.00 | −0.89 | 72 | 0.66 | 0.18 |
| SHAFT | 1.00 | 0.97 | −1.14 | 87 | 0.71 | 0.19 |
6 Conclusion
We have proposed SHAFT, a hierarchical generative flow network for crystal structure generation, aiming at rapid exploration of the exponential crystal space while simultaneously satisfying physical constraints. SHAFT is built on a hierarchical state space, allowing multi-level policy networks to operate on abstracted actions. It effectively exploits the high-symmetry in the crystal structure space, defining space transformation groups. The framework is flexible for domain experts to embed domain knowledge to guide the generation process through space structure design and reward engineering. SHAFT demonstrates its superiority in efficiency in exploration, diversity, and stability of the generated crystal structures.While this work has primarily focused on generating stable crystal structures with desirable formation energies and targeted band gaps, the SHAFT framework offers inherent flexibility for broader applications in materials discovery. In principle, additional material properties, such as mechanical characteristics (e.g., hardness and elastic moduli) or specific optical responses (e.g., refractive index and absorption spectra), could be seamlessly integrated into the generative process. This would typically involve incorporating corresponding terms into the reward function, guided by accurate and computationally efficient surrogate models capable of predicting these properties from structural inputs. However, expanding to multiple target properties introduces further considerations. The primary challenge lies in navigating the complexities of multi-objective optimization, particularly when objectives are conflicting, which may necessitate sophisticated strategies beyond simple weighted-sum approaches to effectively explore the Pareto front.44 Furthermore, the computational overhead of evaluating an increasing number of property predictors must be carefully managed to maintain the efficiency of the generation process. Future work could explore advanced multi-objective SHAFT algorithms and the development of robust surrogate models for a wider range of material characteristics to fully exploit SHAFT's potential in designing novel, multi-functional materials.
Conflicts of interest
There are no conflicts to declare.Data availability
The implementation and data (MP-battery, sampled crystal structures, and their DFT-optimized structures) are available at https://github.com/ngminhtri0394/SHAFT.CCDC 2409676–2409705 contain the supplementary crystallographic data for this paper.45a–ad
Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d4dd00392f.
References
- L. I. Berger, Semiconductor Materials, CRC Press, 2020 Search PubMed.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Matter, 2019, 1, 1370–1384 CrossRef.
- M. J. Mehl, D. Hicks, C. Toher, O. Levy, R. M. Hanson, G. Hart and S. Curtarolo, Comput. Mater. Sci., 2017, 136, S1–S828 CrossRef.
- D. Hicks, M. J. Mehl, E. Gossett, C. Toher, O. Levy, R. M. Hanson, G. Hart and S. Curtarolo, Comput. Mater. Sci., 2019, 161, S1–S1011 CrossRef.
- D. Hicks, M. J. Mehl, M. Esters, C. Oses, O. Levy, G. L. Hart, C. Toher and S. Curtarolo, Comput. Mater. Sci., 2021, 199, 110450 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 1–12 Search PubMed.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177–182 CrossRef PubMed.
- S. Chithrananda, G. Grand and B. Ramsundar, Machine Learning for Molecules Workshop, NeurIPS, Online, 2020 Search PubMed.
- Y. Liu, M. Ott, N. Goyal, J. Du, M. Joshi, D. Chen, O. Levy, M. Lewis, L. Zettlemoyer, V. Stoyanov and P. G. Allen, arXiv, 2019, preprint, arXiv:1907.11692, DOI:10.48550/arXiv.1907.11692.
- M. AI4Science, A. Hernandez-Garcia, A. Duval, A. Volokhova, Y. Bengio, D. Sharma, P. L. Carrier, Y. Benabed, M. Koziarski and V. Schmidt, arXiv, 2023, preprint, arXiv:2310.04925, DOI:10.48550/arXiv.2310.04925.
- A. Belkly, M. Helderman, V. L. Karen and P. Ulkch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Inorg. Chem., 2011, 50, 656–663 CrossRef PubMed.
- H. C. Wang, S. Botti and M. A. Marques, npj Comput. Mater., 2021, 7(1), 1–9 CrossRef.
- L. Wei, N. Fu, E. M. Siriwardane, W. Yang, S. S. Omee, R. Dong, R. Xin and J. Hu, Inorg. Chem., 2022, 61, 8431–8439 CrossRef PubMed.
- T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, Proceeding of International Conference on Learning Representations, 2022 Search PubMed.
- C. J. Court, B. Yildirim, A. Jain and J. M. Cole, J. Chem. Inf. Model., 2020, 60, 4518–4535 CrossRef PubMed.
- Y. Zhao, M. Al-Fahdi, M. Hu, E. M. D. Siriwardane, Y. Song, A. Nasiri and J. Hu, Adv. Sci., 2021, 8, 2100566 CrossRef PubMed.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420 CrossRef PubMed.
- Y. Luo, C. Liu and S. Ji, Proceedings of Conference on Neural Information Processing Systems, 2023 Search PubMed.
- R. Jiao, W. Huang, P. Lin, J. Han, P. Chen, Y. Lu and Y. Liu, Proceedings of the Advances in Neural Information Processing Systems, 2023 Search PubMed.
- D. Levy, S. S. Panigrahi, S.-O. Kaba, Q. Zhu, M. Galkin, S. Miret and S. Ravanbakhsh, The AI for Accelerated Materials Discovery (AI4Mat) Workshop, 2024 Search PubMed.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef PubMed.
- C. Zeni, R. Pinsler, D. Zügner, A. Fowler, M. Horton, X. Fu, A. Shysheya, J. Crabbé, L. Sun, J. Smith, B. Nguyen, H. Schulz, S. Lewis, C.-W. Huang, Z. Lu, Y. Zhou, H. Yang, H. Hao, J. Li, R. Tomioka and T. Xie, Nature, 2023, 639(8055), 624–632 CrossRef PubMed.
- E. Zamaraeva, C. M. Collins, D. Antypov, V. V. Gusev, R. Savani, M. S. Dyer, G. R. Darling, I. Potapov, M. J. Rosseinsky and P. G. Spirakis, Digital Discovery, 2023, 2(6), 1831–1840 RSC.
- O. Nachum, G. Brain, S. Gu, H. Lee and S. Levine, Conference on Neural Information Processing Systems, 2018 Search PubMed.
- Z. Wen DeepMind, D. Precup DeepMind, M. Ibrahimi DeepMind, A. Barreto DeepMind, B. Van Roy DeepMind and S. Singh DeepMind, Conference on Neural Information Processing Systems, 2020 Search PubMed.
- E. Bengio, M. Jain, M. Korablyov, D. Precup and Y. Bengio, Adv. Neural Inf. Process. Syst., 2021, 33, 27381–27394 Search PubMed.
- M. Jain, E. Bengio, A.-H. Garcia, J. Rector-Brooks, B. F. P. Dossou, C. Ekbote, J. Fu, T. Zhang, M. Kilgour, D. Zhang, L. Simine, P. Das and Y. Bengio, Proceeding of International Conference on Machine Learning, 2022 Search PubMed.
- T. Deleu, A. Góis, C. Emezue, M. Rankawat, S. Lacoste-Julien, S. Bauer and Y. Bengio, Proceedings of the Conference on Uncertainty in Artificial Intelligence, 2022 Search PubMed.
- Y. Li, S. Luo, H. Wang and J. HAO, CFlowNets: Continuous control with Generative Flow Networks, 2023 Search PubMed.
- J. Ma, E. Bengio, Y. Bengio and D. Zhang, NeurIPS AI for Science Workshop, 2023 Search PubMed.
- M. Kim, T. Yun, E. Bengio, D. Zhang, Y. Bengio, S. Ahn and J. Park, Proceeding of International Conference on Learning Representations, 2024 Search PubMed.
- M. Glazer, G. Burns and A. N. Glazer, Space groups for solid state scientists, 2012 Search PubMed.
- N. Malkin, M. Jain, E. Bengio, C. Sun and Y. Bengio, Proceedings of Advances in Neural Information Processing Systems, 2022 Search PubMed.
- D. Davies, K. Butler, A. Jackson, J. Skelton, K. Morita and A. Walsh, J. Open Source Softw., 2019, 4, 1361 CrossRef.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 Search PubMed.
- S. Lahlou, T. Deleu, P. Lemos, D. Zhang, A. Volokhova, A. Hernández-García, L. Néhale Ezzine, Y. Bengio and N. Malkin, Proceedings of the International Conference on Machine Learning, 2023 Search PubMed.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2(11), 718–728 Search PubMed.
- Y. Zhao, E. M. Siriwardane, Z. Wu, N. Fu, M. Al-Fahdi, M. Hu and J. Hu, npj Comput. Mater., 2023, 9(1), 1–12 Search PubMed.
- H. Pan, A. M. Ganose, M. Horton, M. Aykol, K. A. Persson, N. E. Zimmermann and A. Jain, Inorg. Chem., 2021, 60, 1590–1603 Search PubMed.
- C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 379–423 Search PubMed.
- L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef.
- M. Jain, S. C. Raparthy, A. Hernandez-Garcia, J. Rector-Brooks, Y. Bengio, S. Miret and E. Bengio, Proceedings of the 40th International Conference on Machine Learning, 2023 Search PubMed.
- (a) CCDC 2409676: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwghg; (b) CCDC 2409677: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgjh; (c) CCDC 2409678: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgkj; (d) CCDC 2409679: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwglk; (e) CCDC 2409680: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgml; (f) CCDC 2409681: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgnm; (g) CCDC 2409682: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgpn; (h) CCDC 2409683: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgqp; (i) CCDC 2409684: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgrq; (j) CCDC 2409685: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgsr; (k) CCDC 2409686: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgts; (l) CCDC 2409687: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgvt; (m) CCDC 2409688: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgwv; (n) CCDC 2409689: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgxw; (o) CCDC 2409690: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgyx; (p) CCDC 2409691: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwgzy; (q) CCDC 2409692: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh00; (r) CCDC 2409693: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh11; (s) CCDC 2409694: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh22; (t) CCDC 2409695: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh33; (u) CCDC 2409696: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh44; (v) CCDC 2409697: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh55; (w) CCDC 2409698: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh66; (x) CCDC 2409699: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh77; (y) CCDC 2409700: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh88; (z) CCDC 24096701: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwh99; (a a) CCDC 2409702: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwhbb; (a b) CCDC 2409703: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwhcc; (a c) CCDC 2409704: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwhdd; (a d) CCDC 2409705: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2lwhff.
| This journal is © The Royal Society of Chemistry 2026 |