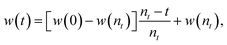Particle swarm optimization in the realm of chemistry: from theory to applications
Megha
Rajeevan
 a,
Niha
a,
Niha
 a,
Chris
John
a,
Chris
John
 b,
Shobhita
Mani
b,
Shobhita
Mani
 a and
Rotti Srinivasamurthy
Swathi
a and
Rotti Srinivasamurthy
Swathi
 *a
*a
aSchool of Chemistry, Indian Institute of Science Education and Research Thiruvananthapuram (IISER TVM), Thiruvananthapuram 695 551, India. E-mail: swathi@iisertvm.ac.in
bDipartimento di Chimica e Chimica Industriale, Università di Pisa, via G. Moruzzi 13, 56124 Pisa, Italy
First published on 14th November 2025
Abstract
In this tutorial review, we introduce the reader to one of the most cited stochastic global optimization methods in chemistry, namely, particle swarm optimization (PSO). Beginning with a detailed description of the basic PSO algorithm, we explore how the algorithm has evolved over time to address increasingly complex chemical problems. The importance of the different aspects of the algorithm, its possible modifications and variants, and hybrid swarm intelligence techniques are presented as we navigate through various chemical applications of PSO reported in current literature. Overall, this review is intended to equip novices with a fundamental understanding of the PSO algorithm to intelligently approach any chemistry-based optimization problem they desire to explore using PSO.
Key learning points(1) Introduction to global optimization and its taxonomy(2) Algorithmic framework of particle swarm optimization (PSO) (3) Algorithmic variants of PSO (4) Applications of PSO in chemistry (5) A roadmap for performing optimizations using PSO |
1. Introduction
The world of computational chemistry is central to optimization problems of diverse complexities, from geometry optimization of simple noble gas dimers to wavefunction optimization in multireference methods. Mathematically, an optimization problem consists of an objective function, with one or more variables, which is to be minimized or maximized, subject to a set of constraints.1 Depending on the problem, this could either be a search for a local extremum (local optimization) or a global extremum (global optimization) within the parameter space. Conventionally, owing to their smaller search space, local optimization problems are dealt with using rigorous and complete deterministic methods that guarantee exact solutions. For complex global optimization problems, the search space is so huge, increasing exponentially with the dimensionality of the problem, that employing a deterministic method, which covers the entire search space, is impractical. Deterministic methods can be employed for global optimization problems, provided the problem is simple and unimodal, or sufficient prior information about the search space is available to be exploited as in, for example, the branch-and-bound method.2 However, chemically relevant global optimization problems have such highly complex and rugged search space that it becomes impractical to use these deterministic strategies. Such problems must be efficiently tackled by algorithms which intelligently probe the search space without requiring much mathematical or computational efforts. Toward this end, a plethora of optimization algorithms, falling under the broad umbrella of non-deterministic global optimization methods, have been developed in the past few decades. These algorithms do not cover the entire search space and herein lies their biggest advantage and disadvantage. Unlike deterministic methods, these methods avoid a complete exploration, and hence cannot guarantee that their solution is indeed the global optimum. However, for this same reason, they are more successful in probing for optimal solutions of real-world problems of quite large dimensions, where employing a deterministic method is not feasible.One way to classify these non-deterministic techniques is to segregate them into heuristic, metaheuristic, and hyperheuristic methods.3 Heuristic and metaheuristic techniques provide solutions to the optimization problems with a systematic evaluation incorporating stochasticity.4,5 Heuristic methods are problem-dependent while metaheuristic methods are problem-independent, making the latter more reliable for all kinds of complex optimization problems.6 Lastly, hyperheuristic approach, a relatively new approach in the area of global optimization, automatically selects and combines various low-level heuristic methods to solve hard computational problems.7 Within the above outlined classification, in the realm of chemistry, most of the problems addressed using global optimization techniques utilize metaheuristic approaches. The popularity of metaheuristic techniques originates from their flexibility, adaptability, and extensive search capacity. There are a wide variety of metaheuristic techniques like particle swarm optimization (PSO),8 genetic algorithm,9 differential evolution,10 ant colony algorithm,11 tabu search,12 and basin hopping,13 to name a few. These algorithms can be further classified based on the number of search agents involved in the optimization process, i.e., into population-based (PSO, genetic algorithm, differential evolution etc.) and trajectory-based algorithms (simulated annealing, tabu search etc.).14
In the current review, we focus on one of the most popular metaheuristic algorithms, namely PSO, which falls under the taxonomy of population-based algorithms. Proposed by James Kennedy and Russell Eberhart in 1995,8,15 the study was first initiated to model the social behavior of birds within a flock which they quoted as “the graceful but unpredictable choreography of a bird flock”. However, in the process of simulating the flock's search of a cornfield, they adopted the concept of a swarm, which later led them to the formulation of a simple yet effective optimization algorithm. PSO is known for its robustness, efficiency, fast convergence, and low computational cost. A major advantage of the PSO algorithm is its ease of parallelization owing to its population-based nature. The fewer number of parameters and ease of implementation make PSO more attractive when compared to other metaheuristic global optimization algorithms. However, the algorithm also possesses some demerits such as challenges associated with parameter initialization, premature convergence, and local minima entrapment, which may be fixed by modifying the algorithm. Herein, with the intention of guiding a novice in this area to the fundamentals of the PSO algorithm and the ability to approach chemistry-based optimization problems using the same, we present a review of the relevant applications of PSO in chemistry. We begin with a description of the algorithmic framework of PSO and some initial modifications to the algorithm to deal with different challenges. Subsequently, we delve into the various modifications to the basic PSO algorithm and hybrid approaches that have been developed and employed in chemistry for various applications, namely structure prediction, development of force fields and quantum-based methods, kinetics, and electrochemistry (Fig. 1).
2. PSO algorithm
The idea behind PSO is to “fly” a group of agents, called the particle swarm, across the search space associated with the optimization problem.8 Each particle, i, represents a potential solution to the problem at hand and its position, xi, corresponds to a point in the solution space. During each iteration, the particles of the swarm communicate with each other and move towards better solutions. The strategy of communication depends on the neighborhood topology adopted in the algorithm. Common topologies include the von Neumann topology, star topology, and ring topology. The basic PSO algorithm uses a star topology, wherein all particles can communicate with all the other particles of the swarm and the best fitness value attained among the entire swarm is kept in the memory of all particles as the global best (gbest), i.e., all particles possess the same gbest. On the other hand, in a ring topology, the neighborhood is defined in such a way that the particles are lying on a ring, and each particle communicates only to its immediate neighbours based on the particle indices. The gbest in this case will be dependent on the particle, with the gbest of each particle being the best position in its corresponding neighborhood. Note that the choice of topology can significantly control the exploration and exploitation ability of the algorithm and hence must be decided based on the optimization problem. Each particle also keeps in its memory the position corresponding to the best fitness it has achieved so far, termed as personal best (pbest). At each iteration, a particle updates its velocity using the equation| vi(t + 1) = vi(t) + c1r1(t)(pbesti(t) − xi(t)) + c2r2(t)(gbest(t) − xi(t)), | (1) |
| xi(t + 1) = xi(t) + vi(t + 1). | (2) |
Hence, for every iteration, each particle of the swarm updates its position by changing its velocity based on the direction of its previous position, the pbest position, and the gbest position (Fig. 2). The ability of the algorithm to stochastically revert to best positions in past iterations is the feature that reflects its similarity to the social behavior of bird flocks. Through each position and velocity update, the particles explore the search space until the termination criterion is met. Unlike deterministic methods, PSO cannot have convergence criteria based on the full coverage of the entire search space. The commonly used termination criteria for PSO include termination at a maximum number of iterations, termination upon the observation of no improvement in the global minimum solution over a number of iterations, and termination at near-zero value of the normalized swarm radius.16 For problems with prior knowledge of the optimal solutions, termination at an acceptable error level is also considered.16 Since non-deterministic methods do not cover the entire search space, the final solution is considered as the putative global optimum. Considering the randomness of the PSO algorithm, different runs with same parameters can result in different solutions. Hence, it is necessary to perform various PSO runs until concordant values are obtained with a good success rate to establish the reliability of the result.
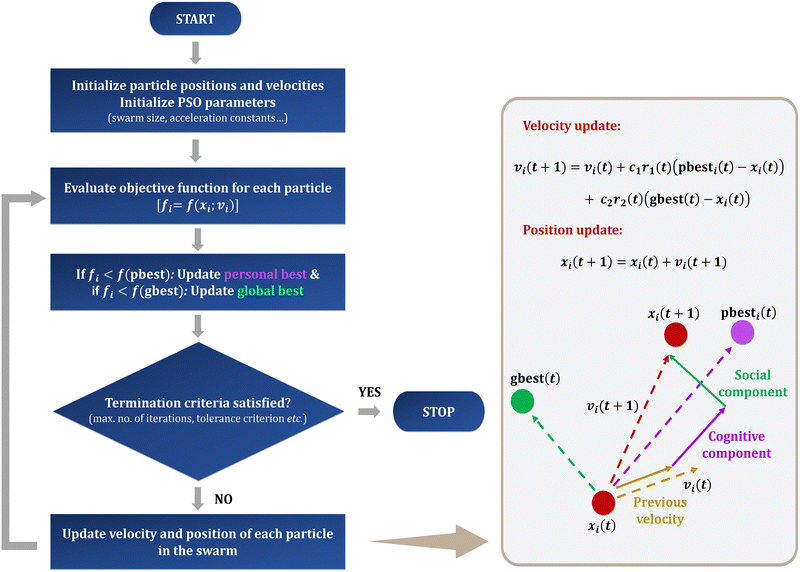 | ||
| Fig. 2 A schematic representation of the PSO algorithm along with an illustration of the position and velocity update equations of a particle. | ||
At the time of the initial proposal of the PSO algorithm, c1 and c2 were assigned a value of 2.0, as such a choice makes the mean weights for cognitive and social components to 1.0. This version of PSO algorithm was found optimal for the training of neural network weights.8 However, the authors remarked on the dependence of the acceleration constants on the optimization problem and varied their numerical values in later studies. It is important to judiciously choose the values of c1 and c2, since low values result in exploration of regions far from the target before converging to the optimum, while high values can make the particles fly toward or past the target abruptly. Additionally, the efficiency of the algorithm can be enhanced by clamping the positions and velocities of the particles to a fixed range as it prevents them from flying away from the desired search space.17 The first time such an implementation was carried out, they assigned a cut-off for the maximum velocity (vmax) achievable by a particle. The choice of vmax is to be carefully considered, since too high a value can make the particles overshoot past regions containing good solutions, and too low a value may not result in exploring locally good regions.
The three terms of the velocity update equation (eqn (1)) together enable the PSO algorithm to perform both a local and a global search of the function space. Without the first term (vi(t)) in the velocity update equation, the algorithm would reduce to a local search (exploitation) and the quality of solution would largely depend on the quality of initial population. It is the presence of this first term that provides the algorithm the exploration capacity that is associated with a global search. Hence, by adding a weightage to vi(t), a better balance can be achieved between the exploration and exploitation abilities of the algorithm. Thus, Eberhart and co-workers introduced the concept of inertia weight,18w, into the velocity update equation as follows:
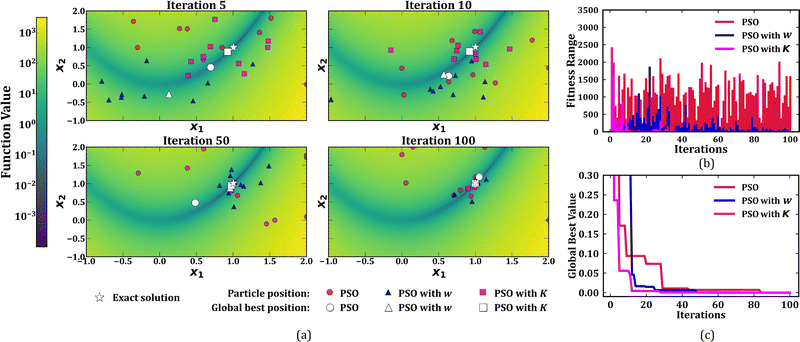
Case study: finding the global minimum of the Rosenbrock function using PSOHere, we illustrate the performance of PSO in finding the global minimum of the Rosenbrock function,
(i) Basic PSO algorithm: using acceleration constants, c1 = c2 = 2.0. (ii) PSO with inertia weight (w): using acceleration constants, c1 = c2 = 2.0, and a linearly decreasing inertia weight defined as (iii) PSO with constriction factor (K): using acceleration constants c1 = c2 = 2.05, and a constriction factor K = 0.729. All the three PSO implementations are performed with a swarm of size 10 for a total of 100 iterations. The search is carried out in the range [−1.0, 2.0] for both the variables, x1 and x2. The particle velocities in all cases are clamped between vmax and vmin, whose values are the same as those of xmax (2.0) and xmin (−1.0), respectively. Scatter plots representing the evolution of particles across the iterations for all the three cases are provided in Fig. 3(a). The ability of PSO, in general, to navigate the swarm towards the global minimum is evident from the figure. As observed by Eberhart and Shi,22 PSO with constriction factor converged faster compared to the basic PSO and the PSO with inertia weight. This difference in performance of the three algorithms can also be seen from the variation of the range of objective function values (fitness range) and the global best values of the swarm across the iterations (Fig. 3(b) and (c)). |
| vi(t + 1) = wvi(t) + c1r1(t)(pbesti(t) − xi(t)) + c2r2(t)(gbest(t) − xi(t)). | (3) |
Subsequently, another modification was proposed to the PSO algorithm by Clerc in 1999,21 wherein a constriction factor, K was introduced to the velocity update equation as expressed below:
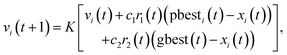 | (4) |
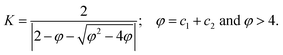 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, the average number of iterations for PSO-II was consistently lower. However, the variance in obtained global best over the trials was high for the case of PSO-II. This prompted the authors to try PSO-II with vmax = xmax for the same functions, and interestingly, they observed an improvement in the convergence of the PSO algorithm with this slight modification. Nonetheless, a closer look at eqn (3) and (4) reveals that both the equations are in-principle the same, provided we use the appropriate coefficients. Hence, in this case, a choice of w = 0.729 and c1 = c2 = 1.49445 provides same result as that obtained by a PSO with a constriction factor of 0.729.
000, the average number of iterations for PSO-II was consistently lower. However, the variance in obtained global best over the trials was high for the case of PSO-II. This prompted the authors to try PSO-II with vmax = xmax for the same functions, and interestingly, they observed an improvement in the convergence of the PSO algorithm with this slight modification. Nonetheless, a closer look at eqn (3) and (4) reveals that both the equations are in-principle the same, provided we use the appropriate coefficients. Hence, in this case, a choice of w = 0.729 and c1 = c2 = 1.49445 provides same result as that obtained by a PSO with a constriction factor of 0.729.
So far, we have discussed the basic PSO algorithm and some modifications to it that were reported during the early stages of its development. However, over the years, many new variants of PSO have been proposed in literature.23–26 Below, through some interesting chemical applications of PSO, we discuss few of these variants and other possible improvements in the algorithm.
3. PSO for structure prediction
In chemistry, the structure of a molecule plays a key role in defining its chemical and physical properties. A molecule tends to adopt the structure with minimum energy, and this structure influences everything, including reactivity, binding affinity, and electronic and optical behavior. However, identifying a molecule's global minimum energy structure is challenging. This is because the number of possible configurations grows exponentially with system size, causing a corresponding exponential increase in computational effort. As a result, geometry optimization and structure prediction are considered nondeterministic polynomial-time hard (NP-hard) problems.27,28 For instance, for a medium-sized Lennard-Jones (LJ) cluster of 55 atoms (LJ55), the number of distinct minima was estimated to be of the order of 1021. Assuming that evaluating each local minimum requires 1 second of calculation, the overall computational time would amount to 1021 seconds, which is significantly greater than the estimated age of our universe (approximately 1.383×1010 years!).29,30 Locating the global minimum among these many local minima is a daunting task. To tackle this challenge, chemists often use global optimization algorithms such as basin hopping,13,31–33 simulated annealing,34 differential evolution,35–38 genetic algorithm,28,39–41 and PSO.42,43 Additionally, it is not just the size of the search space that matters, but the overall “shape” and navigability of the search spaces also play an important role in deciding the complexity of the problem. For example, finding the global minimum of the LJ38 cluster is much harder compared to the above discussed, LJ55 despite its estimated 1021 minima. Although smaller than LJ55, the potential energy surface (PES) of LJ38 is highly deceptive, with its global minimum residing in a narrow funnel, while rest of its PES is dominated by structures very different from the global minimum.13 Therefore, the choice of the global optimization technique is highly problem-dependent, and one method that works for a certain subset of problems may not be great for another subset. Herein, we focus on some of the interesting structure prediction problems that have been successfully solved by PSO, in increasing order of complexity (Fig. 4). Usually in these scenarios, each particle represents a candidate configuration of the molecular system and the objective function considered is the total intermolecular interaction energy. Through iterative updating of their positions and velocities, the particles search for low-energy structures and the final minimum-energy structure identified by PSO is expected to correspond to the global minimum of the PES.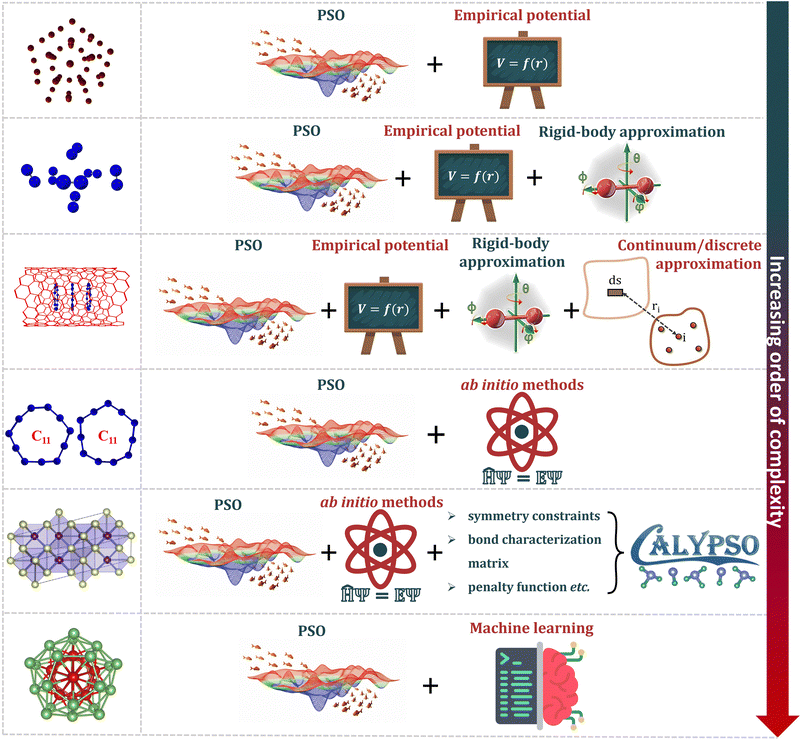 | ||
| Fig. 4 A schematic illustrating the hierarchy of PSO implementations in structure prediction. The hierarchy is guided by the complexity of the objective function in PSO. Sub-images are reproduced from ref. 58 with the permission of American Chemical Society, copyright 2021, ref. 67 with the permission of American Chemical Society, copyright 2023, ref. 92 with the permission of American Chemical Society, copyright 2020, ref. 76 and ref. 86 with the permission of Elsevier, copyright 2016. | ||
A common test set used for benchmarking optimization algorithms are the LJ clusters.13,44,45 Putative global minima of LJ clusters containing up to at least 1610 atoms are well-known.39,46–49 Interactions within LJ clusters are calculated by a simple mathematical model, the LJ potential, and the total interaction energy is given by the expression
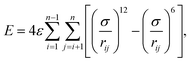 | (6) |
In addition to exploring bare atomic clusters, PSO has also been used to study clusters under confinement. In our group, we have employed PSO to investigate the encapsulation of noble gas clusters within various carbon nanostructures such as fullerenes and carbon nanotubes (CNTs).57,58 Using a continuum approximation that exploits the symmetry of these nanostructures along with the PSO algorithm, we were able to save significant computational time in the search of the optimal confined geometries. Such a combined approach was successful in determining confinement features, packing capacities, and adsorption sites for a variety of noble gases. Meanwhile, with the help of a discrete approximation in conjunction with PSO, we also explored the adsorption of noble gases on graphynes (GYs).59,60 Employing a PSO algorithm with a constriction factor of 0.729, we explored the adsorption of noble gases on monolayer GYs and the intercalation of the same within bilayer GYs.59,60 In all the confinement studies carried out in our group, we integrated the standard PSO with a local optimization strategy, namely, limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method61 in order to ensure the optimality of the obtained putative global minima.
PSO, when implemented for molecular cluster optimization, is often combined with a rigid-body approximation to ease the complexity of the problem (Fig. 4). Within this approximation, a group of atoms belonging to a molecule is translated and rotated as a single unit such that the distance between any two points within this unit does not change.62 This reduces the dimensionality of the optimization problem. For a molecule with n atoms (normally described by 3n Cartesian coordinates), the rigid-body approximation reduces the degrees of freedom to six – 3 translational degrees of freedom (the coordinates of the center of mass: X, Y, Z), and 3 rotational degrees of freedom (the Euler angles: θ, ψ, φ). Within rigid-body approximation, the Cartesian coordinate of the ith atom of a molecule is given by
| ri = rCOM + R−1(θ, ψ, φ)rrel,i, | (7) |
Very recently, we used PSO in conjunction with empirical force fields and rigid-body approximation, to locate the global minima of unary and binary clusters of CO2 and N2 adsorbed on various γ-GY surfaces.63 Three systems were examined: (i) bare CO2 clusters, (ii) bare CO2–N2 binary clusters, and (iii) their adsorbed counterparts on GYs. The electrostatic interactions were treated using Coulomb's law, and the non-electrostatic interactions were modelled using the LJ potential for CO2 clusters, the Buckingham potential for N2 clusters, and the improved Lennard-Jones (ILJ) potential for CO2–N2 clusters. The ILJ potential was also used to describe the cluster–GY interactions in the adsorbed systems, where the GY structures were first optimized using density functional theory (DFT) to provide realistic starting configurations. As in the previous cases, PSO was combined with a local search using the L-BFGS method. Furthermore, instead of employing a standard velocity update (c1 = c2 = 2.05), constriction factors (0.729) were used alongside dynamic velocity clamping to improve the exploration of the algorithm. The upper velocity bound was set to half the difference between the minimum and maximum values of the corresponding position, and the negative of this term was defined as the lower velocity bound. As the search progressed, we employed a dynamic velocity clamping, where at each iteration t, both the lower and the upper bound of the velocity component were multiplied by a factor of 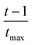 , tmax being the total number of iterations. With the help of this modified PSO, we were able to perform a thorough analysis of the selectivity of various γ-GYs for CO2/N2 adsorption as well as understand the influence of the γ-GY pore size towards the same. In a similar way, we have also explored the intercalation of N2 molecules within bilayer graphene and water molecules within multilayer GYs.67,68 There are related studies where PSO has been employed to study confinement of molecular clusters wherein intervening interactions are described using empirical formulations. For instance, in a study by Fukuura and co-workers, a PSO-LJ method was applied to investigate π-conjugated molecules confined within CNTs and explore the configurational space of confined systems.69
, tmax being the total number of iterations. With the help of this modified PSO, we were able to perform a thorough analysis of the selectivity of various γ-GYs for CO2/N2 adsorption as well as understand the influence of the γ-GY pore size towards the same. In a similar way, we have also explored the intercalation of N2 molecules within bilayer graphene and water molecules within multilayer GYs.67,68 There are related studies where PSO has been employed to study confinement of molecular clusters wherein intervening interactions are described using empirical formulations. For instance, in a study by Fukuura and co-workers, a PSO-LJ method was applied to investigate π-conjugated molecules confined within CNTs and explore the configurational space of confined systems.69
The accuracy of the minimum energy geometry determined by PSO in the above cases depends on the accuracy of the chosen potentials. However, when the number of atoms is small, one could alternatively employ more accurate ab initio methods for the energy evaluation steps (Fig. 4).70–73 Call and co-workers, in 2006,42 employed for the first time, ab initio integrated PSO to predict structures of silicon hydride and triply-hydrated hydroxide ion. The single-point energy evaluations were performed using DFT. They implemented a few modifications to the standard PSO algorithm along with the rigid-body approximation. In their PSO implementation, the search began with the generation of an initial population of random structures, where each structure consisted of rigid groups of atoms. These structures were either fragments, partially connected, or fully-connected structures. Each rigid unit had two types of velocity vectors, one for translation and one for rotation, whose bounds were defined based on the problem. A minimum distance constraint was also enforced between atoms to prevent the generation of chemically irrelevant configurations. The algorithm also switched between two phases, attraction and repulsion, to improve the exploration and avoid premature convergence. When the population was too uniform, the algorithm switched to the repulsion phase, encouraging particles to move away from the best-known solution to explore new regions of the configuration space. This was accomplished by introducing a direction parameter, d, which switches between attraction (+1) and repulsion (−1) in the velocity update equation.
| vi(t + 1) = wvi(t) + dc1r1(t)(pbesti(t) − xi(t)) + dc2r2(t)(gbest(t) − xi(t)), | (8) |
This switching between repulsion and attraction phases was based on a metric which measured the diversity in the population. This metric was calculated as the average pairwise root-mean-squared deviation between particles' distance matrices. When the diversity was below a user-defined threshold, the algorithm switched to the repulsion phase to promote exploration. To further promote diversity and avoid premature convergence, the authors also implemented a local-neighborhood strategy, where each particle is influenced not by the global best but by the best solution within its structural neighborhood. Their modified PSO algorithm successfully identified the global minimum structures for both systems, consistent with earlier findings reported by Pak et al.74 for Si2H5− and Robertson et al.75 for OH−(H2O)3.
The study by Chattaraj and co-workers76 on carbon clusters is yet another example that showcases the effectiveness of a PSO algorithm when implemented together with DFT. Unlike other studies where symmetry constraints are used, the authors of this work demonstrated how randomly generated structures can be used to find the global minima of Cn clusters. The process began with the generation of a set of completely random carbon structures – each structure treated as a swarm particle in a multidimensional space. The particles were assigned initial positions and velocities within a range of −3.0 to 3.0. At each iteration of a standard PSO, the energy of each structure was determined using a single-point DFT calculation. Though this is computationally expensive, it provides accurate energy estimates. These energies were then used to determine improved cluster configurations. These steps were repeated until a convergence criterion was met. The authors made sure that the algorithm could regenerate new initial structures based on previously found solutions to restart the search from appropriate regions of the PES. Once a low-energy structure was found via PSO, it was further optimized using DFT to ensure that the final geometry was a physically valid minimum of the actual PES.
Beyond atomic and molecular geometry optimizations, one of the major applications of PSO in chemistry is in crystal structure prediction (Fig. 4). In the 1990s, crystal structure predictions were considered impossible, with growing concerns over the need for systematic search algorithms and accurate intermolecular potentials to capture subtle noncovalent interactions governing crystal packing and polymorphism in molecular solids.77 The most stable structure of a crystal is the one with the lowest Gibbs free energy (G) at a given pressure and temperature. In practice, when temperature and pressure are neglected, crystal structure prediction simplifies to identifying the structure with the lowest energy.78 However, theoretical prediction of crystal structures is extremely difficult due to the large number of energy minima on the lattice energy surface.79 But now, owing to the advancements in computational power, it is possible to predict crystal structures with decent accuracy using computational tools. One of the most popular algorithms among these is the Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO), developed by Ma and co-workers.43 In CALYPSO, the developers have integrated techniques like symmetry constraints, bond characterization matrix, penalty function, etc., with the PSO algorithm. Although the core idea was introduced in an earlier work by the same group,79 this method was refined and systematized in the CALYPSO framework. The algorithm starts with a population of random structures restricted to the 230 known crystallographic space groups to ensure symmetry and reduce configurational search space. The candidate structures thus generated are then optimized through ab initio and force-field computational packages such as VASP,80,81 SIESTA,82 CASTEP,83,84 GULP,85etc. and their enthalpies are calculated as the fitness criteria for selection. The structure with the lowest enthalpy is selected as gbest. During subsequent iterations, the PSO algorithm governs the evolution of the structures. The position and velocity of each particle are updated according to the equations of a PSO algorithm with inertia weight. They employ a dynamic inertia weight that varies as follows:
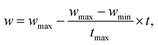 | (9) |
4. PSO for force field development
As mentioned in the previous section, the high computational cost associated with ab initio calculations has resulted in an increased reliability on force fields for molecular modeling. However, the accuracy of the geometries and their respective energies computed from force fields highly depend on the parameters of the potentials used. These parameters are often obtained via fitting the potentials against accurate reference data. The reference data may be taken from either experimental studies or high-level theoretical calculations. A majority of studies employ binding energies obtained using ab initio methods as reference data for force field parametrization. In such cases, the aim is to find a set of force field parameters, a = (a0, a1, a2, …, am), such that| VFF(rj1, rj2, … rjn; a) = Ejref, | (10) |
One of the first implementations of PSO in force field parametrization for chemical systems was by González et al. in 2014.94 By employing PSO, the authors parametrized (i) the LJ potential, (ii) a 6-parameter pair potential for argon, and (iii) the Sutton–Chen potential (an embedded atom potential) for copper. They used an improved PSO algorithm, wherein, in addition to incorporating an inertia weight (w = 0.7, c1 = c2 = 1.4), the swarm was perturbed by randomizing the particle positions whenever the global best minimum gets stuck in the same position for Ns steps. The value of Ns was chosen as 10 times the number of parameters to be optimized. In the study, the LJ potential and the 6-parameter pair potential were parametrized against the already known LJ potential of argon. Using a swarm of 500 particles, the PSO algorithm was able to retrieve the parameters of the LJ potential within 1300 iterations, while for the 6-parameter pair potential, the same algorithm took 9000 steps. Similarly, when employed for optimizing the Sutton–Chen parameters for copper, PSO with a swarm of size 800 particles was able to predict parameter values very close to the reference values within ∼190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Clearly, this increase in the number of iterations is a reflection of the increased complexity of the potential function. Having established the efficiency of PSO, the authors reparametrized the Sutton–Chen potential for copper against DFT data from three thermodynamic phases obtained from molecular dynamics simulations. The reparametrized potential was successful in reproducing the ab initio generated radial distribution function and diffusion coefficient of liquid copper at 2070
000 steps. Clearly, this increase in the number of iterations is a reflection of the increased complexity of the potential function. Having established the efficiency of PSO, the authors reparametrized the Sutton–Chen potential for copper against DFT data from three thermodynamic phases obtained from molecular dynamics simulations. The reparametrized potential was successful in reproducing the ab initio generated radial distribution function and diffusion coefficient of liquid copper at 2070![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, demonstrating the effectiveness of PSO in finding the optimal parameters.
K, demonstrating the effectiveness of PSO in finding the optimal parameters.
Soon after the first implementation of PSO for parametrization, Stinson et al., in 2015, used PSO for parametrizing a two-state empirical valence bond potential describing the interaction between molecular clusters of sulfuric acid and water.95 In a later study, Hase and co-workers focused on the parametrization of an analytical potential that describes the intermolecular interaction between I− and H2O in the I−(H2O) system with the help of PSO.96 The potential was a combination of the well-known LJ and Buckingham potentials with a total of 8 parameters (including both linear and nonlinear parameters). The parametrization was carried out for two models of water: a 3-site model and a 4-site model (ghost atom model). Using as an objective function, the root-mean-square-error (RMSE) of the interaction energies obtained using the analytical potential and the reference DFT calculation at the B97-1/ECP/d level of theory, the authors performed standard PSO calculations with inertia weight and velocity clamping to determine the parameter values. The reference data comprised potential energy profiles evaluated for various orientations of I−—H2O. To improve the flexibility of the PSO algorithm, the values of the inertia weight and the acceleration constants were randomly chosen from uniform distributions within the ranges [0.4, 1.0] and [1.4, 2.0], respectively. For clamping the velocity, vmax was chosen such that it is one-tenth of the domain size considered for each parameter. In addition to these, the authors also implemented a multi-start approach, wherein, multiple PSO runs were repeated by assigning the optimal solution of the previous run as the gbest of the upcoming run. A total of 100 runs with 500 iterations per run were performed for the parametrization. Besides this, for each PSO implementation, a second termination criterion was applied wherein the algorithm stopped after 100 iterations if no significant progress in global minimum was seen. To ensure the local refinement of the solution obtained, they used a local optimization method namely, cyclic ordinate descent, in between two consecutive runs. Such a strategy enhanced the exploration–exploitation trade-off of the PSO implementation, and thereby improved the efficiency of the search. Meanwhile, the same parametrization when performed using genetic/non-linear least square algorithm, produced larger RMSE values while taking ten times the computational cost of PSO. Note that this performance comparison is specific to the problem in hand and does not necessarily mean that PSO will always outperform genetic algorithms in other contexts because the performance of an algorithm is highly problem-dependent.
Beyond the empirical potentials discussed so far, PSO has also been employed in the parametrization of reactive force fields (ReaxFF).103 ReaxFF can model the breaking and formation of chemical bonds as they incorporate bonding and non-bonding interactions. Due to the hundreds of parameters that need to be optimized in ReaxFF, they require an optimization procedure that overcomes premature convergence. The first time PSO was employed in parametrizing ReaxFF, the authors, Furman et al., parametrized only the parameters of the low-gradient (lg) dispersion interaction model that describes organic crystals.98 The reference data for parametrization consisted of DFT-generated equations of state of various hydrocarbon crystals and energetic crystals, and dissociation and expansion curves of various non-covalent dimers of the S66 database. The objective function for minimization was the weighted sum of squares of the deviation of the ReaxFF data from the reference data. The authors employed an enhanced PSO with linearly decreasing inertia weight and Gaussian mutation for minimization. A mutation is a perturbation that is applied on a particle's trajectory in order to avoid it from getting trapped in local minima and thereby diversifying the swarm. In their PSO implementation, the authors employed a Gaussian mutation to the particle when its number of failures (fi) was greater than 1. A failure indicates a less favorable fitness value than the one obtained in the previous iteration. With mutation, a particle is replaced with a mutated version of the global best position as follows:
xi(t + 1) = gbest(t) + γG(0,1)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) i(t + 1), i(t + 1), | (11) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) is a unit vector. A schematic illustration of this algorithm is provided in Fig. 5a. Additionally, this PSO framework was integrated with a local optimization strategy, namely, sequential one-parameter parabolic interpolation method. The parameters obtained using such an implementation showed better agreement to DFT predictions than the original parametrization of ReaxFF-lg. Moreover, the authors noted that, for this particular problem, the PSO implementation led to better performance when compared to a genetic algorithm-based optimization technique for reactive force fields such as GARFfield.104 While, in the above study, PSO was employed in parametrizing a part of ReaxFF (the dispersion model), PSO has also been employed for the parametrization of the whole ReaxFF parameter set. For example, very recently, in 2025, Sun et al. were successful in parametrizing ReaxFF of hydrogen and sulfur atoms using a hybrid algorithm combining simulated annealing and PSO.105 Hybrid PSO formalisms like these are increasingly being used to meet the demands of complex parametrization problems.105,106
is a unit vector. A schematic illustration of this algorithm is provided in Fig. 5a. Additionally, this PSO framework was integrated with a local optimization strategy, namely, sequential one-parameter parabolic interpolation method. The parameters obtained using such an implementation showed better agreement to DFT predictions than the original parametrization of ReaxFF-lg. Moreover, the authors noted that, for this particular problem, the PSO implementation led to better performance when compared to a genetic algorithm-based optimization technique for reactive force fields such as GARFfield.104 While, in the above study, PSO was employed in parametrizing a part of ReaxFF (the dispersion model), PSO has also been employed for the parametrization of the whole ReaxFF parameter set. For example, very recently, in 2025, Sun et al. were successful in parametrizing ReaxFF of hydrogen and sulfur atoms using a hybrid algorithm combining simulated annealing and PSO.105 Hybrid PSO formalisms like these are increasingly being used to meet the demands of complex parametrization problems.105,106
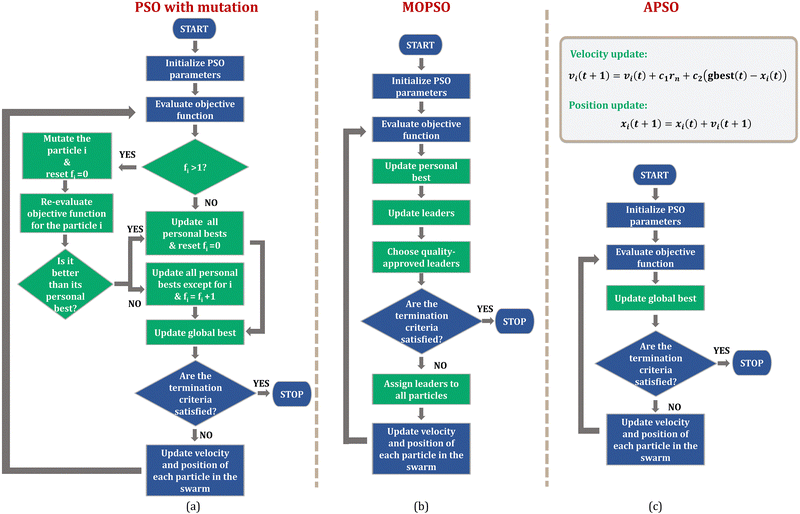 | ||
| Fig. 5 The algorithmic frameworks of three PSO variants: (a) PSO with mutation, (b) MOPSO, and (c) APSO. Steps deviating from the standard PSO algorithm are highlighted in green. | ||
5. PSO for parametrization and basis set optimization in quantum-based methods
In recent years, PSO has also been employed for developing quantum-based methodologies. One such application is the parametrization of a semiempirical methodology, namely, the density functional tight-binding (DFTB) method.107 As previously explained, the high computational cost of ab initio methods prevents their application to large chemical systems, thereby setting classical methods as the default choice for computational modeling. However, such models, when employed in classical molecular dynamics, fail to accurately capture energies and chemical processes like bond breaking and bond forming. In such scenarios, a semiempirical methodology like DFTB offers a better alternative.In the DFTB method, the two-center overlap and Hamiltonian integrals are precomputed and tabulated in the so-called Slater–Koster (SK) files along with other relevant parameters.107 This reduces the computational time by three orders of magnitude when compared to traditional DFT methods. However, the accuracy and transferability of the DFTB method depends on the SK parameters. Although many initial studies performed manual parametrization, computational time and effort for the same are enormous. Thus, researchers have focused on developing automatic development of SK files. One such study by Chou et al. reported the first implementation of PSO in DFTB parametrization,108 with the authors developing a DFTB parametrization toolkit based on PSO. The PSO algorithm employed in the study incorporates a linearly decreasing inertia weight (0.9 to 0.4) with acceleration coefficients c1 = 1.5 and c2 = 2.0. The main goal of the study was to develop a set of optimal DFTB parameters that could reproduce DFT data corresponding to various physical properties of solid silicon, methanol, and hydrogen peroxide. Since the parameters need to be transferable across different properties, the optimization has to be carried out for more than one objective function. For example, in the case of methanol, objectives that needed to be considered were equilibrium geometry, atomization energy, dimer binding energy, and vibrational harmonic frequencies.108 Such problems are termed as multi-objective optimization problems. Though these problems can be conveniently solved by adopting an aggregating function, for example, weighted sums of all the objectives as a single function, the accuracy of the parameters depends on the weightage factors used for the individual objectives.108 Therefore, the authors instead used, along with the standard PSO, an alternative algorithm called multi-objective PSO (MOPSO).109,110 The fitness function of a MOPSO with m number of objective functions is given as
![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) ( (![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) = [f1( ) = [f1(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ), f2( ), f2(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ), … fm( ), … fm(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) )]. )]. | (12) |
In MOPSO, instead of a single solution, a set of non-dominated solutions called Pareto-optimal solutions are generated.111 A solution is considered as a non-dominated solution if no other solution outperforms it in all the objectives simultaneously. From the obtained non-dominated solutions, the most suitable solution is selected as the final solution. The generation of Pareto-optimal solutions is achieved by considering a set of leaders (non-dominated solutions) in the PSO algorithm with respect to which the particles update their positions. The choice of leader for each particle in each iteration is decided based on some quality measurements on the leader. This set of leaders is typically stored in an external archive, and these leaders are updated in each iteration based on the updated particles. The positions corresponding to the leaders at the end of the PSO calculation are considered as the desired set of solutions. A schematic representation of the basic MOPSO algorithm is provided in Fig. 5b. In most MOPSO algorithms, mutation operators are also applied in order to prevent premature convergence on local minima. More details regarding the MOPSO algorithm and its variants can be found in ref. 111. Soon after the development of the automatic toolkit by Chou et al.,108 Hutama et al. employed the same for developing DFTB parameters for bulk zirconia.112,113
Other varieties of PSO, besides MOPSO, have also been successfully employed to solve the multi-objective DFTB parametrization problem. In a recent study by Aguirre et al., the authors parametrized self-consistent charge DFTB (SCC-DFTB) for organic molecules consisting of hydrogen, carbon, nitrogen, and oxygen using similarity measurements quantifying the desired molecular properties.114 They used a single-objective function defined as (1 − S), where S is a function that measures the similarity of the molecular descriptors obtained using DFTB with respect to those obtained using the reference method, which in this case was DFT. The molecular descriptors included binding energies, atomic forces, success in determining the lowest energy isomer, and the relative energetic order of all isomers. The optimization was performed in two steps: (i) parametrization of DFTB to maximize the similarity in the binding energies and atomic forces to the reference DFT values, and (ii) optimization of the total similarity with a search starting from the solution of the first step. To perform the two-step optimization, authors employed two different PSO techniques: (i) a modified version of PSO, namely accelerated PSO (APSO)115 (Fig. 5c), and (ii) the standard PSO. The APSO algorithm is a simpler version of PSO wherein the contribution of cognitive component to velocity is ignored. However, in the study, the APSO was implemented by gradually decreasing the coefficient of the cognitive component, c1, across iterations thereby reducing the influence of the cognitive component on the total velocity. This acceleration was initiated only when 10% of the particles were found far from the swarm. This fastened the convergence of the algorithm and reduced the computational cost. However, as the authors indicate a word of caution, there is an increased probability of getting trapped in a local minimum.
More recently, a high-end application of PSO in the world of quantum chemistry was reported, wherein, the authors employed PSO for the first time for basis set optimization.116 They developed polarization-consistent basis sets with incorporation of relativistic effects for astatine (At). Astatine being biologically relevant, the authors wanted to develop a force field describing the intermolecular interactions in the astatine anion–water system. The accuracy of the force fields depends on the reference data against which they are parametrized. Since astatine is a heavy element with inherent relativistic effects, relativistic DFT was found to be a suitable methodology to generate reference data. However, the known exchange–correlation functionals and basis sets do not guarantee the accuracy for such heavy elements. Hence, to circumvent the issue, the authors developed accurate basis sets for astatine detangling the errors associated with the choice of exchange–correlational functional and basis sets arising when applied to heavy elements. As a part of this process, PSO was employed to optimize the exponents in the primitive Gaussian-type orbitals for the given uncontracted basis sets, which are then used for the generation of compact basis sets using suitable contraction schemes. Parametrization was performed for three uncontracted basis sets of varying sizes: (i) PSO-L (largest), (ii) PSO-M (medium), and (iii) PSO-S (smallest). The larger basis set (PSO-L) ensures high accuracy and flexibility, while the smallest one (PSO-S) reduces the computational cost. The authors employed a basic PSO algorithm with a swarm of size 15, an inertia weight of 0.829, and acceleration constants c1 and c2 of 1.49445. For the optimization of exponents in the primitive basis sets, authors incorporated a modification in the PSO algorithm by constraining the value of the exponent to be always positive and within the values of neighboring exponents. Note that each exponent value corresponds to an element of the position of a particle in PSO. The parametrization was carried out against the binding energies of At, At+, At−, At2, and HAt (equilibrium and non-equilibrium configurations of At2 and HAt) obtained using HF and PBE0 at complete basis set limit incorporating relativistic effects. PSO exhibited high efficiency in reducing the mean absolute error (MAE) significantly for all the three uncontracted basis sets considered. The MAE corresponding to PSO-L was less than 1%, reaching chemical accuracy, and for PSO-S, the MAE was close to chemical accuracy. When contracted, these basis sets provided relatively accurate basis sets for astatine, though the MAEs are 20–50% larger than those obtained for uncontracted basis sets. A two-component relativistic DFT calculation with PBE0 exchange–correlation functional for describing the At−–H2O interaction gave more accurate binding energy profiles with the contracted basis set generated from PSO-L, when compared to several other basis sets specific to relativistic DFT. The obtained binding energy profiles were very close to the CCSD(T) binding profiles, thus establishing the efficiency of PSO in basis set optimization.
6. PSO for kinetic model parameter estimation
The search for optimal parameters is a common problem encountered in other fields of chemistry as well. In chemical kinetics, reaction mechanisms depend on kinetic parameters such as rate constants and activation energies. These parameters are often estimated using kinetic models that simulate the behavior of chemical systems. However, due to uncertainties in these parameters and the challenges associated with obtaining them experimentally, it is difficult to build accurate kinetic models. As a result, inverse modeling techniques, where the parameters of the model are determined from experimental data have become essential. This is where PSO comes into play. In 2016, Kazantsev et al. utilized a PSO method with inertia weight to solve the inverse chemical kinetics problem for the process of n-hexane isomerization into iso-hexanes catalyzed by sulfated zirconia.117 After a preliminary analysis, they fixed their PSO parameters to w = 0.8, c1 = 0.7, and c2 = 0.8. The objective function considered was a sum of squares of deviations between the calculated and experimental concentrations of isomers. Their results highlighted that despite minimal individual effects, the combined optimization of parameters doubled the probability of achieving the best solution. In 2021, El Rassy et al. also analyzed the performance of PSO in a kinetic mechanism optimization problem, where 14 strategies were considered by taking various combinations of PSO coefficients.118 Their final results suggested better convergence rate for the implemented PSO algorithms compared to genetic algorithm. We would like to reiterate that this does not necessarily mean superior performance of PSO compared to the genetic algorithm for other cases unless verified. They also observed that strategies with a greater importance to inertia weight provided poorer results, while those that assigned a greater importance to the cognitive component positively influenced the optimization process. Nevertheless, all strategies tested in the kinetic model contributed to an improvement in model quality. PSO has also proven to be efficient in estimating the kinetic parameters of other reactions such as biomass pyrolysis,119 combustion and reaction behavior of syngas,120 reaction mechanisms in dimethyl ether–air systems,121 skeletal oxidation of diesel surrogate fuels,122 and reactions of ammonia.123 In the study by Zhang and co-workers,123 PSO technique was utilized to optimize the kinetic parameters in the ammonia/air combustion model, improving the accuracy of laminar flame speed predictions under varying pressures and equivalence ratios. They adopted weighted velocity update equation, with the acceleration coefficients, c1 = c2 = 1.49445. The inertia weight, w is updated with the following equation: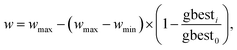 | (13) |
7. PSO for battery model optimization
Another domain of chemistry where PSO has been employed is in the development of battery models. Battery models are broadly classified into three categories: equivalent circuit models, data-driven models, and electrochemical models.124 Among these, electrochemical models are more accurate in representing internal battery dynamics. However, the complexity of the derivatives included in electrochemical models increases the computational effort significantly, making it difficult to estimate the model parameters directly. The large number of parameters to be optimized further increases the computational burden. Additionally, these parameters can vary significantly under different operating conditions, and the complex, high-dimensional nature of these models often leads to overparametrization, where different parameter sets yield similar outputs, complicating parameter identification.124,125 To overcome these issues, optimization techniques such as PSO are used for efficient and robust parameter estimation in battery modeling. In a recent study, PSO demonstrated accuracy and efficiency, consistently identifying the global minima for battery parameter identification, especially in cases when no prior knowledge of the battery parameters was known.126 In a 2016 work by Rahman et al., a PSO framework was employed to identify four critical parameters in a Li-ion battery model.127 The objective function considered was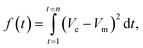 | (14) |
| vi(t + 1) = |r1|(pbesti(t) − xi(t)) + |r2|(gbest(t) − xi(t)), | (15) |
8. ML-integrated PSO
Like in most areas of research in the past few decades, there has been a growing interest in the use of ML for global optimization problems in chemistry as well. ML techniques like Bayesian optimization have been highly successful in the field of materials research.136 More interestingly, one can combine different ML methods with metaheuristic algorithms to create powerful and efficient strategies to solve complex high-dimensional problems. One of the major focuses in this regard has been in the use of ML to cut down the computational cost of function evaluation in optimization techniques using surrogate models.137–139 Common surrogate models include polynomial regression, radial basis functions, support vector regression, and Kriging-based models. For instance, by replacing time-consuming function evaluations or pre-screening for promising particles that require exact function evaluations, surrogate-assisted PSO has shown to considerably reduce the computational time and provide a better balance between exploration and exploitation.137–139 Other ML methods like Bayesian techniques and reinforcement learning have also been used along with PSO for obtaining enhanced performance.140–142 Zhang et al., have combined PSO with a Bayesian technique that adjusts the inertia weight based on past particle positions to improve its exploration capability.140 Similarly, reinforcement learning has been used to tune the PSO parameters during its execution to enhance its convergence.142 Reinforcement learning based dynamic topology, velocity vector generation, and tunable local search to accompany PSO have all been reported in recent years.141,143,144Although the integration of PSO with ML has garnered considerable attention, ML-integrated PSO for chemical applications is a relatively unexplored area. One area where this has been successfully implemented is in the field of structure prediction. Just as other ML-integrated optimization strategies such as genetic algorithm,145 covariance matrix adaptation-evolution strategy,145 Bayesian optimization,145,146 and random searching,146 are currently reported for improved crystal structure prediction, ML-aided PSO has also been developed for the same. As mentioned in Section 3, Ma and co-workers used a ML potential, namely Gaussian approximation potential, to replace the DFT calculations within the CALYPSO framework for predicting large boron clusters.91 Their method was able to reproduce known experimental structures of B36 and B40, and they even proposed a new stable structure for the B84 cluster. More importantly, they were able to reduce the computational time by ∼1–2 orders of magnitude.91 In another study on structure prediction, the authors employed a topology-ML-PSO-DFT protocol that analyses the structure-energy relationships to arrive at the geometries of Li clusters.92 They employed an ML model within the PSO algorithm to eliminate identical structures and predict the three lowest energy geometries from each PSO iteration, which were then used as starting structures for DFT optimization. Out of all the DFT-optimized geometries at each iteration, the one with the lowest energy was considered as the global minimum geometry. Mitra and co-workers have also proposed an approach combining a convolutional neural network (CNN) and PSO93 for predicting the energy of cluster units containing both metal and non-metal elements, including C5, N2−4, N4−6, Aun (n = 2–8), and AunAgm (2 ≤ n + m ≤ 8).
The integration of ML with PSO was also reported for the parametrization of the DFTB method to model lithium-intercalated graphite.147 The authors used a ML potential to describe the repulsive potential in the formulation of the total DFTB energy, and then employed the PSO algorithm proposed by Chou et al., for the DFTB parametrization, as discussed in Section 5.108 In another recent study, PSO integrated with ML was employed for predicting the efficiency of MXene membranes in desalination.148 The ML prediction model served as the objective function from which PSO selected potential desalination candidate membranes. Later, the same group extended the study by integrating ML with hybrid variants of PSO including PSO-differential evolution and PSO-genetic algorithm, as well as a multi-objective PSO algorithm called the nondominated sorting PSO.149 The study showed improved performance of the hybrid and multi-objective PSO algorithms compared to the single-objective algorithms when used for predicting desalination membranes.
The above examples constitute one side of PSO-ML implementations in chemistry where ML has been used within PSO implementation to solve chemically relevant optimization problems. There exists another equally important side to PSO-ML integration; one in which PSO is employed to optimize the parameters of the ML models. For instance, PSO has been used to optimize the parameters of an ML model called Kriging, which estimates atomic multipole moments of oxygen in the central water molecule of a water cluster.150 Another example is a study wherein ML integrated with PSO was employed to optimize and predict biomass pyrolysis process based on the biomass properties and process operating conditions.151
9. Beginner's guide to PSO
The take-home message from all the examples discussed above is the importance to customize the PSO algorithm to suit the problem of choice. Customizing one's algorithm is central to these types of global optimization techniques, as the method needs to adapt itself to the search space of the problem. As we have seen, the performance of the PSO algorithm highly depends on the choice of the different PSO parameters such as the acceleration constants, number of iterations, and swarm size. Further, as the complexity of the problem increases, it might even become necessary to use variants or hybrid formalisms of PSO. Therefore, we present below a checklist for beginners to help them tailor the PSO algorithm to their needs.Did you check the quality of your acceleration coefficients?
An appropriate choice of c1 and c2 is essential to balance the exploration and exploitation abilities of the PSO algorithm. For example, by testing different sets of acceleration constants, we were able to tune the performance of the PSO algorithm in predicting the optimal cluster geometry of Ne10 when described using an ILJ potential.59 The test calculations performed by varying c1 and c2 from 1.9 to 2.1 with an increment of 0.05 within a PSO calculation with a constriction factor and velocity clamping showed that the most stable cluster geometry was predicted when c1 + c2 > 4 (Fig. 6a). Hence, as a first step, it is always best to check the quality of the acceleration constants used in the PSO algorithm through some preliminary tests.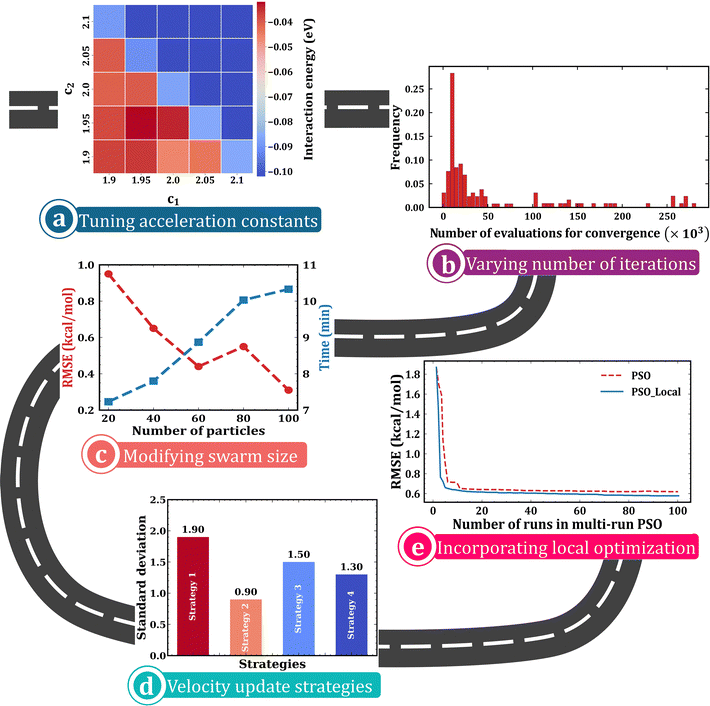 | ||
| Fig. 6 A roadmap to customizing the PSO algorithm: plots representing (a) the variation in the interaction energy of Ne10 cluster obtained using PSO with various combinations of acceleration constants, data obtained from ref. 59, (b) number of iterations until convergence for DFTB parametrization using PSO, reproduced from ref. 114 with the permission of American Chemical Society, copyright 2020, (c) the influence of swarm size on the RMSE of force field fits obtained using PSO and the corresponding computational cost, data obtained from ref. 96, (d) the influence of various PSO strategies on the optimization of an altered version of a methane combustion mechanism, namely GRI-Mech mechanism using PSO, reproduced from ref. 118 with the permission of American Chemical Society, copyright 2021, and (e) the improvement in the accuracy of force field parametrization with the incorporation of local optimization in the PSO framework, reproduced from ref. 96 with the permission of American Chemical Society, copyright 2018. | ||
What is the termination criterion used?
The number of iterations and the convergence criteria used will have a large impact on the computational overhead of PSO calculations. Therefore, the maximum number of iterations must be chosen based on the computational resources at hand and the accuracy one aims to achieve. In the study by Aguirre et al.,114 discussed in Section 5, the authors employed PSO calculations until all the particles reached the same point within 0.01% precision in both parameters and objective function. The calculations took around 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 evaluations to converge in most cases, except a few, where it exceeded 200
000 evaluations to converge in most cases, except a few, where it exceeded 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 evaluations (Fig. 6b). Such an analysis helps in saving considerable computational time by identifying the least number of iterations required to reach the accuracy one desires.
000 evaluations (Fig. 6b). Such an analysis helps in saving considerable computational time by identifying the least number of iterations required to reach the accuracy one desires.
Is your swarm size optimal?
The choice of swarm size is another deciding factor of the algorithm's performance. In the study by Hase and co-workers on the parametrization of force fields96 (Section 4), they assessed the influence of swarm size on the performance of the PSO algorithm. As the swarm size was increased, an increase in computational cost and decrease in RMSE were observed (Fig. 6c), suggesting a swarm size of 50–100 to be optimal for similar problems. Since the better exploration capacity of a large swarm comes at a high computational cost, it is ideal to perform trial runs with varying sizes of population before you finalize the swarm size for your calculation.Did you try alternative velocity strategies?
If the basic PSO algorithm is not providing you the optimal solutions, it is time to fine-tune your algorithm by incorporating modifications like constriction factor, inertia weight, and velocity clamping. You may either use constant values for these parameters or dynamically vary them across iterations. One can even use dynamic acceleration constants, as reported in literature, to improve the performance of the algorithm.118 However, choosing a suitable strategy requires additional test calculations as these factors are problem-dependent. In the previously mentioned study by El Rassy et al. (Section 6), authors demonstrated notable variations in PSO performance for optimization of kinetic mechanism when employing fourteen different parameter strategies,118 including PSO with a fixed constriction factor (strategy 1), PSO with fixed constriction factor but varying acceleration constants (strategy 2), PSO with constant inertia weight and varying acceleration constants (strategy 3), and PSO with varying inertia weight and acceleration constants (strategy 4). Among these, the lowest standard deviation was exhibited by the second strategy (Fig. 6d); however, the fourth strategy showed the best performance when mean error percentage was also taken into account.Is the algorithm still not providing optimal solutions? Did you try local optimization?
As the PSO algorithm is stochastic, there is always a possibility of converging at a wrong point before reaching an extremum. Hence, a local optimization can be performed at the end of the PSO calculations to aid in better exploitation of the search space. For instance, as we mentioned in Section 4, Hase and co-workers96 employed a local optimization using cyclic coordinate descent in between their consecutive PSO runs in multirun PSO to enhance the performance of their algorithm, as observed in Fig. 6e. So, if your algorithm lacks exploitation features, the ideal solution is to integrate it with a local optimization strategy.Still unable to optimize?
If the optimization problem is highly complex, a basic PSO algorithm or its primitive variations may not suffice. In such cases, one can try advanced versions or hybrid formalisms of PSO. For example, you can try a PSO algorithm with mutation, or, if the problem consists of multiple objectives, as seen in the study by Chou et al. for DFTB parametrization108 discussed in Section 5, you can choose a PSO variant like MOPSO.Are you able to reproduce your result?
Remember that the stochastic nature of PSO demands the user to run the algorithm multiple times to assess the reliability of the results. Computing the success rate of the algorithm for your specific problem can be one way to ensure your result is indeed the desired global optimum.10. Conclusions and outlook
In summary, with the help of some interesting and relevant case studies, we have highlighted the performance and applications of particle swarm optimization (PSO) in the field of chemistry. PSO, being efficient and easy-to-implement, has been applied in various regimes of chemistry, including structure prediction, force field parametrization, development of semiempirical and ab initio techniques, and so on. Starting with a detailed description of the PSO algorithm with an illustrative example for a beginner-level understanding, we have discussed, through various literature reports, the importance of fine-tuning the different parameters of the algorithm. Care should be taken while deciding the swarm size, the number of iterations, and other parameters of PSO in order to avoid premature convergence and avoid excess use of computational resources. Moreover, to help a first-time user to decide on the choice of algorithm suitable for problem in hand, we have presented a variety of PSO algorithms implemented in chemistry, from the basic PSO algorithm to APSO for enhanced convergence, and MOPSO for multi-objective optimizations.Currently, there is a lot of interest in the topic of hybrid global optimization techniques aimed at improving the existing algorithms. Very recently, employing a hybrid algorithm combining PSO, Latin hypercube design, backtracking search optimization, and genetic algorithm, researchers were able to develop an accurate reactive force field applicable for Fe/Ni transition metals and alloys.106 Similarly, a hybrid algorithm proposed by Waller and co-workers employed PSO for optimizing the parameters of ant colony algorithm, which after training on a small set of difluorinated polyenes, was employed for successful optimization of a set of 102 highly flexible molecular balances.152 Researchers have also started to incorporate ML techniques to enhance the efficiency of these global optimization methods. A major time-limiting step in an optimization algorithm is function evaluation. With the help of ML, however, one can easily cut down the computational time required for the evaluation of objective function, thereby making it easier for the optimization algorithm to explore a larger search space and perform an efficient search. Such studies have already begun in the field of geometry optimization, wherein, a swarm navigating through the potential energy surface described by newly-developed ML potentials is able to locate the global minimum more quickly and precisely.91,93 The efficiency of these algorithms further opens up the possibility for faster and accurate geometry optimization of large chemical systems. Metaheuristic-aided ML methods also have a huge scope in molecular designing and discovery. De novo drug design is one such area where PSO, when combined with ML, can identify optimal candidate drugs as reported by Winter et al.153 With its ability to handle multiple objectives, PSO when combined with ML, can search a latent space representation of compounds from millions of chemicals and identify a molecule that best satisfies a set of targets and has the desired pharmacokinetics-related properties.
Finally, we would like to reiterate that, like other metaheuristic optimization methods, it is impossible to assess the suitability of PSO for the problem at hand a priori. Therefore, it's appropriate to start with an algorithmic framework that has been successfully employed for a related problem and then customize it further. Alternatively, the user can also employ other global optimization techniques and compare their performance with that of PSO.
Author contributions
The manuscript was written through contributions of all the authors. All the authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Data availability
The Python code executing global optimization of Rosenbrock function and Lennard-Jones cluster configurations using particle swarm optimization can be found at the GitHub repository https://github.com/SMMACG-IISER/PSO-LJ-Rosenbrock.Acknowledgements
R. S. S. acknowledges the Science and Engineering Research Board (SERB), Government of India for financial support of this work, through the SERB Core Research Grant (CRG/2022/006873). R. S. S. also acknowledges the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) and the Indian Department of Science and Technology (DST) for financial support through IRTG 2991 ‘Photoluminescence in Supramolecular Matrices’ – Project numbers 517122340 (DFG) and INT/FRG/IRTG/01/2024 (DST). M. R. and S. M. thank IISER TVM and Niha thanks DST-INSPIRE for the fellowships. C. J. acknowledges the Italian Ministry of University and Research for the funding provided by the European Union-NextGenerationEU-PNRR, Mission 4 Component 2 Investment line 1.2 (CUP: I53C24002030006). The authors thank the reviewers for their suggestions, which have added significant value to the quality of the article.References
- J. Nocedal and S. J. Wright, Numerical Optimization, Springer, New York, 1999 Search PubMed.
- R. Horst and H. Tuy, in Global Optimization: Deterministic Approaches, ed. R. Horst and H. Tuy, Springer, Berlin, Heidelberg, 1996, ch. 4, pp. 115–178 Search PubMed.
- J. Stork, A. E. Eiben and T. Bartz-Beielstein, Nat. Comput., 2022, 21, 219–242 CrossRef.
- J. Pearl, Heuristics: Intelligent Search Strategies for Computer Problem Solving, Addison-Wesley Longman Publishing Co., Inc., Massachusetts, 1984 Search PubMed.
- E.-G. Talbi, Metaheuristics: From Design to Implementation, John Wiley & Sons, New Jersey, 2009 Search PubMed.
- K. Sörensen, Int. Trans. Oper. Res., 2015, 22, 3–18 CrossRef.
- P. Cowling, G. Kendall and E. Soubeiga, A Hyperheuristic Approach to Scheduling a Sales Summit, Springer, Berlin, Heidelberg, 2001 Search PubMed.
- J. Kennedy and R. Eberhart, Particle Swarm Optimization, IEEE, Perth, 1995 Search PubMed.
- J. H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, The MIT Press, Massachusetts, 1992 Search PubMed.
- R. Storn and K. Price, J. Global Optim., 1997, 11, 341–359 CrossRef.
- M. Dorigo, V. Maniezzo and A. Colorni, IEEE Trans. Syst. Man Cybern., Part B, 1996, 26, 29–41 CAS.
- F. Glover, ORSA J. Comput., 1989, 1, 190–206 CrossRef.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- K. Rajwar, K. Deep and S. Das, Artif. Intell. Rev., 2023, 56, 13187–13257 CrossRef.
- R. C. Eberhart and Y. Shi, Particle Swarm Optimization: Developments, Applications and Resources, IEEE, Seoul, 2001 Search PubMed.
- A. P. Engelbrecht, Computational Intelligence: An Introduction, Wiley Publishing, 2007 Search PubMed.
- R. Eberhart and J. Kennedy, A New Optimizer Using Particle Swarm Theory, IEEE, Nagoya, 1995 Search PubMed.
- Y. Shi and R. Eberhart, A Modified Particle Swarm Optimizer, IEEE, Alaska, 1998 Search PubMed.
- Y. Shi and R. C. Eberhart, Parameter Selection in Particle Swarm Optimization, Springer, Berlin, Heidelberg, 1998 Search PubMed.
- Y. Shi and R. C. Eberhart, Empirical Study of Particle Swarm Optimization, IEEE, Washington, 1999 Search PubMed.
- M. Clerc, The Swarm and the Queen: Towards a Deterministic and Adaptive Particle Swarm Optimization, IEEE, Washington, 1999 Search PubMed.
- R. C. Eberhart and Y. Shi, Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization, IEEE, California, 2000 Search PubMed.
- R. Poli, J. Kennedy and T. Blackwell, Swarm Intell., 2007, 1, 33–57 CrossRef.
- D. Wang, D. Tan and L. Liu, Soft Comput., 2018, 22, 387–408 CrossRef.
- M. N. Ab Wahab, S. Nefti-Meziani and A. Atyabi, PLoS One, 2015, 10, e0122827 CrossRef PubMed.
- M. Clerc, Particle Swarm Optimization, John Wiley & Sons, UK, 2010 Search PubMed.
- L. T. Wille and J. Vennik, J. Phys. A: Math. Gen., 1985, 18, L419 CrossRef CAS.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS.
- Y. Wang, J. Lv, P. Gao and Y. Ma, Acc. Chem. Res., 2022, 55, 2068–2076 CrossRef CAS PubMed.
- N. Doraiswamy and L. D. Marks, Philos. Mag. B, 1995, 71, 291–310 CrossRef CAS.
- L. Zhan, J. Z. Y. Chen, W.-K. Liu and S. K. Lai, J. Chem. Phys., 2005, 122, 244707 CrossRef.
- R. H. Leary, J. Global Optim., 2000, 18, 367–383 CrossRef.
- H. G. Kim, S. K. Choi and H. M. Lee, J. Chem. Phys., 2008, 128, 144702 CrossRef PubMed.
- L. T. Wille, Chem. Phys. Lett., 1987, 133, 405–410 CrossRef CAS.
- Z. Chen, X. Jiang, J. Li, S. Li and L. Wang, J. Comput. Chem., 2013, 34, 1046–1059 CrossRef CAS PubMed.
- Y.-H. Yang, X.-B. Xu, S.-B. He, J.-B. Wang and Y.-H. Wen, Comput. Mater. Sci., 2018, 149, 416–423 CrossRef CAS.
- T.-E. Fan, G.-F. Shao, Q.-S. Ji, J.-W. Zheng, T.-D. Liu and Y.-H. Wen, Comput. Phys. Commun., 2016, 208, 64–72 CrossRef CAS.
- Z. Chen, W. Jia, X. Jiang, S.-S. Li and L.-W. Wang, Comput. Phys. Commun., 2017, 219, 35–44 CrossRef CAS.
- B. Hartke, J. Phys. Chem., 1993, 97, 9973–9976 CrossRef CAS.
- B. Hartke, Chem. Phys. Lett., 1995, 240, 560–565 CrossRef CAS.
- D. M. Daven, N. Tit, J. R. Morris and K. M. Ho, Chem. Phys. Lett., 1996, 256, 195–200 CrossRef.
- S. T. Call, D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 1177–1186 CrossRef CAS PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- R. Gong and L. Cheng, Comput. Theor. Chem., 2016, 1082, 41–48 CrossRef CAS.
- G. Mai, Y. Hong, S. Fu, Y. Lin, Z. Hao, H. Huang and Y. Zhu, Swarm Evol. Comput., 2020, 57, 100710 CrossRef.
- B. Hartke, The Genetic and Evolutionary Computation Conference, GECCO-2001, Morgan Kaufmann, San Francisco, 2001 Search PubMed.
- K. Yu, X. Wang, L. Chen and L. Wang, J. Chem. Phys., 2019, 151, 214105 CrossRef PubMed.
- Y. Xiang, L. Cheng, W. Cai and X. Shao, J. Phys. Chem. A, 2004, 108, 9516–9520 CrossRef CAS PubMed.
- Y. Xiang, H. Jiang, W. Cai and X. Shao, J. Phys. Chem. A, 2004, 108, 3586–3592 CrossRef CAS.
- R. J. W. Hodgson, Particle Swarm Optimization Applied to the Atomic Cluster Optimization Problem, ACM, New York, 2002 Search PubMed.
- W. Cai, H. Jiang and X. Shao, J. Chem. Inf. Comput. Sci., 2002, 42, 1099–1103 CrossRef CAS PubMed.
- R. H. Leary and J. P. K. Doye, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, R6320–R6322 CrossRef CAS.
- J. Lee, I.-H. Lee and J. Lee, Phys. Rev. Lett., 2003, 91, 080201 CrossRef PubMed.
- Y. Zhou, Z. Zhao and D. Cheng, Comput. Phys. Commun., 2020, 247, 106945 CrossRef CAS.
- Y. Tsuji, Y. Yoshioka, M. Hori and K. Yoshizawa, Top. Catal., 2022, 65, 215–227 CrossRef CAS.
- J.-C. Zhou, W.-J. Li and J.-B. Zhu, Trans. Nonferrous Met. Soc. China, 2008, 18, 410–415 CrossRef.
- C. Owais, C. John and R. S. Swathi, Phys. Chem. Chem. Phys., 2020, 22, 20693–20703 Search PubMed.
- C. John, C. Owais, A. James and R. S. Swathi, J. Phys. Chem. C, 2021, 125, 2811–2823 CrossRef CAS.
- M. Rajeevan and R. S. Swathi, Artif. Intell. Chem., 2024, 2, 100048 CrossRef.
- C. John, M. Rajeevan and R. S. Swathi, Chem. – Asian J., 2022, 17, e202200625 CrossRef CAS.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- J. L. Llanio-Trujillo, J. M. C. Marques and F. B. Pereira, J. Phys. Chem. A, 2011, 115, 2130–2138 CrossRef CAS PubMed.
- M. Rajeevan, C. John and R. S. Swathi, Phys. Chem. Chem. Phys., 2024, 26, 23152–23167 RSC.
- G. Chen, B. Xiong and X. Huang, Precis. Eng., 2011, 35, 505–511 CrossRef.
- Y. Chen, J. Yan, J. Feng and P. Sareh, Acta Mech., 2020, 231, 1485–1501 CrossRef.
- V. S. Kaza, P. R. Anisha and C. K. K. Reddy, in Next-Generation Cybersecurity: AI, ML, and Blockchain, ed. K. Kaushik and I. Sharma, Springer Nature Singapore, Singapore, 2024, ch. 17, pp. 369–417 Search PubMed.
- C. John and R. S. Swathi, J. Phys. Chem. A, 2023, 127, 4632–4642 CrossRef CAS.
- M. Rajeevan and R. S. Swathi, Phys. Chem. Chem. Phys., 2025, 27, 17598–17614 RSC.
- S. Fukuura, Y. Nishidate and T. Yumura, J. Phys. Chem. A, 2024, 128, 5054–5064 CrossRef CAS.
- Z. Deng, Y. Zhou, L. Zhao and D. Cheng, Mol. Simul., 2022, 48, 891–901 CrossRef CAS.
- Y. Tsuji, Y. Yoshioka, K. Okazawa and K. Yoshizawa, ACS Omega, 2023, 8, 30335–30348 CrossRef CAS PubMed.
- L. Li, X.-H. Cui, H.-B. Cao, Y. Jiang, H.-M. Duan, Q. Jing, J. Liu and Q. Wang, Chin. Phys. B, 2020, 29, 077101 CrossRef CAS.
- M. Tang, C.-E. Hu, Z.-L. Lv, X.-R. Chen and L.-C. Cai, J. Phys. Chem. A, 2016, 120, 9489–9499 CrossRef CAS PubMed.
- C. Pak, J. C. Rienstra-Kiracofe and H. F. Schaefer, J. Phys. Chem. A, 2000, 104, 11232–11242 CrossRef CAS.
- W. H. Robertson, E. G. Diken, E. A. Price, J. W. Shin and M. A. Johnson, Science, 2003, 299, 1367–1372 CrossRef CAS.
- G. Jana, A. Mitra, S. Pan, S. Sural and P. K. Chattaraj, Front. Chem., 2019, 7, 485 CrossRef CAS.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS.
- Y. Wang and Y. Ma, J. Chem. Phys., 2014, 140, 040901 CrossRef PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415 CrossRef CAS.
- X. Luo, J. Yang, H. Liu, X. Wu, Y. Wang, Y. Ma, S.-H. Wei, X. Gong and H. Xiang, J. Am. Chem. Soc., 2011, 133, 16285–16290 CrossRef CAS PubMed.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 015503 CrossRef PubMed.
- Y. Wang, H. Liu, J. Lv, L. Zhu, H. Wang and Y. Ma, Nat. Commun., 2011, 2, 563 CrossRef.
- G.-J. Li, Y.-J. Gu, Z.-G. Li, Q.-F. Chen and X.-R. Chen, RSC Adv., 2020, 10, 26443–26450 RSC.
- Q. Tong, L. Xue, J. Lv, Y. Wang and Y. Ma, Faraday Discuss., 2018, 211, 31–43 RSC.
- X. Chen, D. Chen, M. Weng, Y. Jiang, G.-W. Wei and F. Pan, J. Phys. Chem. Lett., 2020, 11, 4392–4401 CrossRef CAS.
- A. Mitra, G. Jana, R. Pal, P. Gaikwad, S. Sural and P. K. Chattaraj, Theor. Chem. Acc., 2021, 140, 30 Search PubMed.
- D. González and S. Davis, Comput. Phys. Commun., 2014, 185, 3090–3093 CrossRef.
- J. L. Stinson, M. K. Kathmann and I. J. Ford, Mol. Phys., 2016, 114, 172–185 CrossRef CAS.
- H. N. Bhandari, X. Ma, A. K. Paul, P. Smith and W. L. Hase, J. Chem. Theory Comput., 2018, 14, 1321–1332 CrossRef CAS.
- X. Ma, N. Yang, M. A. Johnson and W. L. Hase, J. Chem. Theory Comput., 2018, 14, 3986–3997 CrossRef CAS.
- D. Furman, B. Carmeli, Y. Zeiri and R. Kosloff, J. Chem. Theory Comput., 2018, 14, 3100–3112 CrossRef CAS.
- M. Majumder, H. N. Bhandari, S. Pratihar and W. L. Hase, J. Phys. Chem. C, 2018, 122, 612–623 CrossRef CAS.
- H. Kim, H. N. Bhandari, S. Pratihar and W. L. Hase, J. Phys. Chem. A, 2019, 123, 2301–2309 CrossRef CAS.
- Z. Liu, Q. Han, Y. Guo, J. Lang, D. Shi, Y. Zhang, Q. Huang, H. Deng, F. Gao, B. Sun and S. Du, J. Alloys Compd., 2019, 780, 881–887 CrossRef CAS.
- R. Christensen, S. S. Sørensen, H. Liu, K. Li, M. Bauchy and M. M. Smedskjaer, J. Chem. Phys., 2021, 154, 134505 CrossRef CAS PubMed.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- A. Jaramillo-Botero, S. Naserifar and W. A. Goddard, III, J. Chem. Theory Comput., 2014, 10, 1426–1439 CrossRef CAS PubMed.
- Q. Sun, J. Zhong, P. Shi, H. Xu and Y. Wang, Comput. Mater. Sci., 2025, 251, 113776 CrossRef CAS.
- M. Shi, X. Jiang, Y. Hu, L. Ling and X. Wang, Comput. Mater. Sci., 2023, 221, 112083 CrossRef CAS.
- D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947–12957 CrossRef CAS PubMed.
- C.-P. Chou, Y. Nishimura, C.-C. Fan, G. Mazur, S. Irle and H. A. Witek, J. Chem. Theory Comput., 2016, 12, 53–64 CrossRef CAS PubMed.
- J. Moore and R. Chapman, Application of Particle Swarm to Multiobjective Optimization, Technical Report, Department of Computer Science and Software Engineering, Auburn University, 1999 Search PubMed.
- M. F. Leung, S. C. Ng, C. C. Cheung and A. K. Lui, A New Strategy for Finding Good Local Guides in MOPSO, IEEE, Beijing, 2014 Search PubMed.
- M. Reyes-Sierra and C. C. Coello, Int. J. Comput. Intell. Res., 2006, 2, 287–308 Search PubMed.
- A. S. Hutama, Y. Nishimura, C.-P. Chou and S. Irle, Development of density-functional tight-binding repulsive potentials for bulk zirconia using particle swarm optimization algorithm, AIP Conference Proceedings, Greece, 2017 Search PubMed.
- A. S. Hutama, C.-P. Chou, Y. Nishimura, H. A. Witek and S. Irle, J. Phys. Chem. A, 2021, 125, 2184–2196 CrossRef CAS.
- N. F. Aguirre, A. Morgenstern, M. J. Cawkwell, E. R. Batista and P. Yang, J. Chem. Theory Comput., 2020, 16, 1469–1481 CrossRef CAS.
- X.-S. Yang, in Engineering Optimization, ed. X.-S. Yang, John Wiley & Sons, Inc., New Jersey, 2010, ch. 15, pp. 203–211 Search PubMed.
- K. J. Rueda Espinosa, A. A. Kananenka and A. A. Rusakov, J. Chem. Theory Comput., 2023, 19, 7998–8012 CrossRef CAS PubMed.
- K. V. Kazantsev, L. I. Bikmetova, O. V. Dzhikiya, M. D. Smolikov and A. S. Belyi, Procedia Eng., 2016, 152, 34–39 CrossRef CAS.
- E. El Rassy, A. Delaroque, P. Sambou, H. K. Chakravarty and A. Matynia, J. Phys. Chem. A, 2021, 125, 5180–5189 CrossRef CAS PubMed.
- Y. Ding, W. Zhang, L. Yu and K. Lu, Energy, 2019, 176, 582–588 CrossRef CAS.
- H. Wang, C. Sun, O. Haidn, A. Aliya, C. Manfletti and N. Slavinskaya, Fuel, 2023, 332, 125945 CrossRef CAS.
- Y. Li, S. Su, L. Wang, J. Yin and S. Idiaba, Int. J. Chem. Kinet., 2022, 54, 142–153 CrossRef CAS.
- W. Chen, X. Fang, C. Zhu, X. Qiao and D. Ju, Proc. Inst. Mech. Eng., Part A, 2020, 234, 1147–1160 CrossRef.
- Y. Hu, J. Li, H. Chen, K. Li, L. Wang and F. Zhang, Fuel, 2024, 363, 131019 CrossRef CAS.
- W. Zhou, Y. Zheng, Z. Pan and Q. Lu, Processes, 2021, 9, 1685 CrossRef CAS.
- E. Miguel, G. L. Plett, M. S. Trimboli, L. Oca, U. Iraola and E. Bekaert, J. Energy Storage, 2021, 44, 103388 CrossRef.
- F. Guo, L. Couto and G. Thenaisie, Efficiency and Optimality in Electrochemical Battery Model Parameter Identification: A Comparative Study of Estimation Techniques, IEEE, Almeria, 2024 Search PubMed.
- M. A. Rahman, S. Anwar and A. Izadian, J. Power Sources, 2016, 307, 86–97 CrossRef CAS.
- X. Hu, S. Li and H. Peng, J. Power Sources, 2012, 198, 359–367 CrossRef CAS.
- Y. Wang and Z. Cai, Front. Comput. Sci. China, 2009, 3, 38–52 CrossRef.
- R. A. Krohling and L. D. S. Coelho, IEEE Trans. Syst. Man Cybern., Part B, 2006, 36, 1407–1416 Search PubMed.
- Y. Zou, S. E. Li, B. Shao and B. Wang, Appl. Energy, 2016, 161, 330–336 CrossRef CAS.
- J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313 CrossRef.
- T. Mesbahi, F. Khenfri, N. Rizoug, P. Bartholomeüs and P. L. Moigne, IEEE Trans. Sustainable Energy, 2017, 8, 59–73 Search PubMed.
- T. Mesbahi, F. Khenfri, N. Rizoug, K. Chaaban, P. Bartholomeüs and P. Le Moigne, Electr. Power Syst. Res., 2016, 131, 195–204 CrossRef.
- I. Jarrraya, L. Degaa, N. Rizoug, M. H. Chabchoub and H. Trabelsi, J. Energy Storage, 2022, 50, 104424 CrossRef.
- Y. Wu, A. Walsh and A. M. Ganose, Digital Discovery, 2024, 3, 1086–1100 RSC.
- C. Fan, B. Hou, J. Zheng, L. Xiao and L. Yi, Appl. Soft Comput. J., 2020, 91, 106242 CrossRef.
- Y. Cui, X. Meng and J. Qiao, Appl. Intell., 2024, 54, 11649–11671 CrossRef.
- F. Li, W. Shen, X. Cai, L. Gao and G. Gary Wang, Appl. Soft Comput. J., 2020, 92, 106303 CrossRef.
- L. Zhang, Y. Tang, C. Hua and X. Guan, Appl. Soft Comput. J., 2015, 28, 138–149 CrossRef.
- W. Li, P. Liang, B. Sun, Y. Sun and Y. Huang, Swarm Evol. Comput., 2023, 78, 101274 CrossRef.
- S. Yin, M. Jin, H. Lu, G. Gong, W. Mao, G. Chen and W. Li, Complex Intell. Syst., 2023, 9, 5585–5609 CrossRef.
- H. Samma, C. P. Lim and J. Mohamad Saleh, Appl. Soft Comput. J., 2016, 43, 276–297 CrossRef.
- Y. Xu and D. Pi, Neural Comput. Appl., 2020, 32, 10007–10032 CrossRef.
- J. Hu, W. Yang, R. Dong, Y. Li, X. Li, S. Li and E. M. D. Siriwardane, CrystEngComm, 2021, 23, 1765–1776 RSC.
- G. Cheng, X.-G. Gong and W.-J. Yin, Nat. Commun., 2022, 13, 1492 CrossRef CAS PubMed.
- C. Panosetti, S. B. Anniés, C. Grosu, S. Seidlmayer and C. Scheurer, J. Phys. Chem. A, 2021, 125, 691–699 CrossRef CAS PubMed.
- X. Ma, C. Lan, H. Lin, Y. Peng, T. Li, J. Wang, J. Azamat and L. Liang, J. Membr. Sci., 2024, 702, 122803 CrossRef CAS.
- H. Lin, M. Wu, Z. Zhao, F. Zhang, C. Zhou, D. Yang, Y. Fu, K. Feng and L. Liang, ACS Appl. Mater. Interfaces, 2025, 17, 49533–49555 CrossRef CAS.
- N. Di Pasquale, S. J. Davie and P. L. A. Popelier, J. Chem. Theory Comput., 2016, 12, 1499–1513 CrossRef CAS PubMed.
- Z. U. Haq, H. Ullah, M. N. A. Khan, S. Raza Naqvi, A. Ahad and N. A. S. Amin, Bioresour. Technol., 2022, 363, 128008 CrossRef CAS PubMed.
- T. Dresselhaus, J. Yang, S. Kumbhar and M. P. Waller, J. Chem. Theory Comput., 2013, 9, 2137–2149 CrossRef CAS.
- R. Winter, F. Montanari, A. Steffen, H. Briem, F. Noé and D.-A. Clevert, Chem. Sci., 2019, 10, 8016–8024 RSC.
| This journal is © The Royal Society of Chemistry 2026 |