Confinement effects on molecular diffusion in zeolites: mechanisms and perspectives
Lei
Zhao†
ab,
Jiamin
Yuan†
c,
Youdong
Xing
ab,
Ji
Qi
ab,
Peng
Peng
ab,
Zhiqiang
Liu
*ab and
Anmin
Zheng
 *abc
*abc
aInterdisciplinary Institute of NMR and Molecular Sciences, State Key Laboratory of Advanced Refractories, Wuhan University of Science and Technology, Wuhan 430081, P. R. China. E-mail: zqliu_wh@wust.edu.cn; zam@wust.edu.cn
bHubei Province for Coal Conversion and New Carbon Materials, School of Chemistry and Chemical Engineering, Wuhan University of Science and Technology, Wuhan 430081, P. R. China
cState Key Laboratory of Magnetic Resonance Spectroscopy and Imaging, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, 430071 Wuhan, P. R. China
First published on 3rd November 2025
Abstract
Zeolites exemplify a quintessential class of confined systems, where well-defined molecular-scale channels impose precise spatial constraints on guest species, profoundly altering their diffusion behavior and catalytic properties. This review systematically examines confinement effects on molecular diffusion in zeolites, elucidating fundamental mechanisms such as orders-of-magnitude variations in diffusivity, the reconstruction of diffusion pathways, and emergent phenomena including the levitation effect, molecular trajectory control, the molecular trapdoor effect, and thermal resistance effects, among others. We summarize the synergistic effects of framework topology, guest molecular conformation, acid-site interactions, loading, and temperature on diffusion within these confined environments. Furthermore, we highlight the critical interplay between diffusion and catalytic performance, emphasizing confinement-driven shape selectivity and reaction enhancement. Finally, we outline key challenges and opportunities in designing zeolites with tailored diffusion properties for advanced applications in catalysis, separation, and energy conversion. By bridging atomic-scale mechanistic insights with practical implications, this comprehensive analysis provides a roadmap for the development of next-generation zeolite catalysts.
1. Introduction
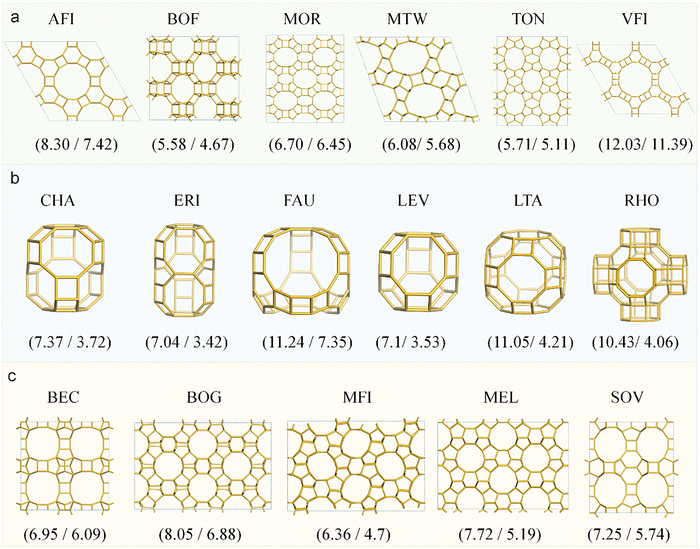
Zeolites represent a quintessential class of confined systems, characterized by well-defined, molecular-scale channels that exert precise spatial constraints on guest species.1–6 Their nanoporous architecture not only exhibits intrinsic catalytic activity but also governs molecular diffusion and reaction kinetics, endowing zeolites with shape-selective catalytic functionality—a hallmark of these materials. When molecules, ions, or nanoparticles enter size-matched nanochannels or cavities, their physicochemical properties (e.g., diffusion coefficient, reaction activity, and electronic structure) undergo significant alterations due to confinement effects.2,7 This confinement phenomenon is widely regarded as the key factor governing the unique physicochemical behaviors of zeolites in catalysis, separation, and energy-related applications.3,8–13In both catalytic and separation processes, assessing molecular accessibility to zeolite pores is a fundamental design criterion. For catalytic applications, key considerations include: (i) the effective diffusion of reactants to active sites within the pore network, and (ii) the subsequent desorption of products from the confined channels. These transport (or diffusion) properties can be approximated by correlating molecular kinetic diameters with the intrinsic pore dimensions of the zeolite framework.14–18 A representative example is the screening of suitable zeolite catalysts for propane dehydrogenation to propene. This process involves first strategically selecting a zeolite with pore sizes >4 Å (larger than the kinetic diameter of propane), a criterion that not only ensures unrestricted transport of reactants but also maintains efficient diffusion of products.16 Analogously, separation processes require careful matching between target molecule dimensions and zeolite pore architecture.19–21 These fundamental principles underscore the necessity of correlating molecular kinetic diameters (Table 1)22–24 with key structural parameters of zeolites, particularly, pore opening size or the maximum diameter of a freely diffusing sphere (Df).25–28 As illustrated in Fig. 1, the Df values for typical zeolites predominantly fall within the 3–8 Å range, which primarily governs their diffusion characteristics. For comprehensive analysis of adsorption behavior and reaction intermediate accommodation, the largest included sphere diameter (Di), spanning 4–11 Å, provides additional structural insight.28
| Molecule | Molecular formula | Kinetic diameters σ (Å) |
|---|---|---|
| a Parts A, B, and C correspond to ref. 22–24, respectively. | ||
| Part A22 | ||
| Helium | He | 2.55 |
| Neon | Ne | 2.82 |
| Argon | Ar | 3.54 |
| Krypton | Kr | 3.66 |
| Xenon | Xe | 4.05 |
| Deuterium | D2 | 2.83–2.89 |
| Hydrogen bromide | HBr | 3.35 |
| Carbonyl sulfide | COS | 4.13 |
| Nitrogen trifluoride | NF3 | 3.62 |
| Methyl chloride | CH3Cl | 4.18 |
| Carbon tetrachloride | CCl4 | 5.95 |
| Carbon tetrafluoride | CF4 | 4.66 |
| Hexafluoroethane | C2F6 | 5.10 |
| cis-2-Butene | C4H8 | 4.23 |
| 1,3-Butadiene | C4H6 | 5.20 |
| Isopentane | C5H12 | 5.00 |
| Neopentane | C5H12 | 6.20–6.46 |
| Perfluorohexane | C6F14 | 7.00 |
| n-Heptane | C7H16 | 4.30 |
| 2,2,4-Trimethylpentane | C8H18 | 6.20 |
| Part B23 | ||
| α-D-Glucose | C6H12O6 | 8.60 |
| β-D-Glucose | C6H12O6 | 8.60 |
| Cellulose | (C6H10O5)n | 8.60 |
| Cellubiose | C12H22O11 | 6.60 |
| Acetic acid | C2H4O2 | 4.40 |
| Formic acid | CH2O2 | 4.00 |
| 5-Hydroxymethyl furfural (HMF) | C6H6O3 | 6.20 |
| Hydroxylacetylaldehyde | C2H4O2 | 4.80 |
| Furfural | C5H4O2 | 5.50 |
| 2-Methyl furan | C5H6O | 5.30 |
| Furan | C4H4O | 5.10 |
| 4-Methyl furfural | C6H6O2 | 5.90 |
| 2-Furanmethanol | C5H6O2 | 5.70 |
| Levoglucosan | C6H10O5 | 6.70 |
| Indane | C9H10 | 6.30 |
| 1,2,3-TMB | C9H12 | 6.60 |
| 2-Ethyl toluene | C9H12 | 6.60 |
| 3-Ethyl toluene | C9H12 | 6.60 |
| 4-Ethyl toluene | C9H12 | 6.60 |
| Naphthalene | C10H8 | 6.20 |
| 1-Methyl naphthalene | C11H10 | 6.80 |
| 1,5-Dimethylnaphthalene | C12H12 | 7.70 |
| 1,6-Dimethylnaphthalene | C12H12 | 7.70 |
| 2,6-Dimethylnaphthalene | C12H12 | 7.20 |
| Anthracene | C14H10 | 6.96 |
| Pyrene | C16H10 | 7.24 |
| Phenanthrene | C14H10 | 6.96 |
| Part C24 | ||
| Water | H2O | 2.60, 2.70, 3.20 |
| Carbon monoxide | CO | 3.30, 3.80 |
| Oxygen | O2 | 3.50 |
| Hydrogensulfide | H2S | 3.60 |
| Hydrochloric acid | HCl | 3.20, 3.30 |
| Carbon dioxide | CO2 | 3.30 |
| Sulfur dioxide | SO2 | 3.60, 4.10 |
| Tetrachloroethylene | C2Cl4 | 6.60 |
| Methane | CH4 | 3.80, 3.90, 4.10–4.30 |
| Acetylene | C2H2 | 3.30 |
| Ethylene | C2H4 | 3.90, 4.20 |
| Methanol | CH4O | 3.40, 3.60, 4.30 |
| Propyne | C3H4 | 4.10 |
| Propene | C3H6 | 4.00, 4.50, 4.70 |
| Propane | C3H8 | 4.30, 4.30–5.10 |
| Trifluoromethane | CHF3 | 4.70 |
| Carbon disulfide | CS2 | 3.60, 4.50 |
| Sulfur hexafluoride | SF6 | 5.10, 5.50 |
| Dichloromethane | CH2Cl2 | 3.30, 4.90 |
| Tris([1,1′-biphenyl]-4-yl) phosphine (TPPP) | C36H27P | 15.40 |
| 2,6-Dimethylpyridine (2,6-Lutidine) | C7H9N | 6.70, 7.00 |
| Chloroform | CHCl3 | 5.40, 5.70 |
| Iodomethane | CH3I | 5.00–6.00 |
| Pyridine | C5H5N | 5.10, 5.30–5.90, 6.50 |
| 2,4,6-Trimethylpyridine | C8H11N | 7.20–7.40 |
| (2,4,6-Collidine) | ||
| 2,6-Di-tert-butylpyridine (DTBpy) | C13H21N | 7.90, 8.00, 8.30, 10.50 |
| 2,4,6-Tri-tert-butyl-pyridine (TTBpy) | C17H29N | 11.00 |
| Ammonia | NH3 | 2.40, 2.60, 2.90, 3.70 |
| 1-Propanol | C3H8O | 4.60 |
| Isopropylalcohol | C3H8O | 4.70, 4.90 |
| Diethyl ether | C4H10O | 4.60 |
| 2,2-Dimethylbutane | C6H14 | 5.60, 6.20, 6.30 |
| 2,3-Dimethylbutane | C6H14 | 5.80 |
| 3-Methylpentane | C6H14 | 5.00, 5.40, 5.50 |
| Decane | C10H22 | 4.30 |
| Tetrahydrofuran | C4H8O | 6.30 |
| Benzene | C6H6 | 3.70, 5.30–5.90, 6.60 |
| Cyclohexane | C6H12 | 4.80, 6.00–6.20, 6.60 |
| Toluene | C7H8 | 5.30, 5.90–6.60 |
| o-Xylene | C8H10 | 6.30, 6.80, 7.30 |
| m-Xylene | C8H10 | 6.30, 6.80, 7.30 |
| p-Xylene | C8H10 | 5.70, 5.80, 5.90, 6.60 |
| Isopropylbenzene (Cumene) | C9H12 | 6.80 |
| 1,3,5-Triisopropylbenzene | C15H24 | 9.50 |
| Ethanol | C2H6O | 4.40–4.50 |
| Dimethyl ether | C2H6O | 4.10, 4.30, 4.70 |
| Isobutylene | C4H8 | 4.80 |
| Triethylamine | C6H15N | 7.80 |
| Lepidine (4-Methylquino line) | C10H9N | 7.30 |
| 2,4-Dimethylquinoline | C11H11N | 9.10 |
| Tributylamine | C12H27N | 8.10–11.0 |
| Trihexylamine | C18H39N | 13.0 |
| Perfluorotributylamine | C12F27N | 9.40 |
| Trimethylphosphine (TMP) | C3H9P | 5.50 |
| Triphenylphosphine (TPP) | C18H15P | 7.20, 10.00–10.80 |
| Tricyclohexylphosphine | C18H33P | >9.90 |
| Tris(4-methoxyphenyl)-phosphine (TMPP) | C21H21O3P | 13.00 |
| Butyldi-1-adamantylphosphine | C24H39P | 9.80–11.80 |
| Trimethylphosphine oxide (TMPO) | C3H9PO | 5.50 |
| Triethylphosphine oxide (TEPO) | C6H15PO | 6.00 |
| Tributylphosphine oxide (TBPO) | C12H27PO | 8.20 |
| Triphenylphosphine oxide (TPPO) | C18H15PO | 11.00 |
| Trioctylphosphine oxide (TOPO) | C24H51PO | 11.00 |
| The kinetic diameter values of the following molecules have been reported in multiple literatures. Superscripts A, B, and C denote data obtained from ref. 22–24, respectively. | ||
| Hydrogen | H2 | 2.83–2.89A, 2.90C |
| Bromine | Br2 | 4.30A, 3.50C |
| Nitrous oxide | N2O | 3.83A, 3.30C |
| Ethane | C2H6 | 4.44A, 4.10- 4.40C |
| Isobutane | C4H10 | 5.28A, 5.00–5.30C |
| Ethyl benzene | C8H10 | 6.00B, 5.80–6.00C |
| 1,2,4-Trimethylbenzene | C9H12 | 7.60B,C |
| n-Pentane | C5H12 | 4.50A,C |
| n-Octane | C8H18 | 4.30A,C, 4.50–5.90C |
| Nitrogen | N2 | 3.64–3.80A, 3.10C, 3.60–3.70C |
| Chlorine | Cl2 | 4.22A, 3.20C |
| Nitric oxide | NO | 3.49A, 3.20C |
| Dichlorodifluoromethane | CCl2F2 | 5.00A, 4.40–5.00C |
| Cyclopropane | C3H6 | 4.23–4.81A, 4.20–4.80C |
| 2-Methylpentane | C6H14 | 5.50A, 5.40C |
| n-Butane | C4H10 | 4.69A, 4.50C, 0.43–4.70C |
| 1,3,5-Trimethylbenzene | C9H12 | 0.86B, 7.70–8.60C |
| n-Hexane | C6H14 | 4.30A, 4.30–4.90C |
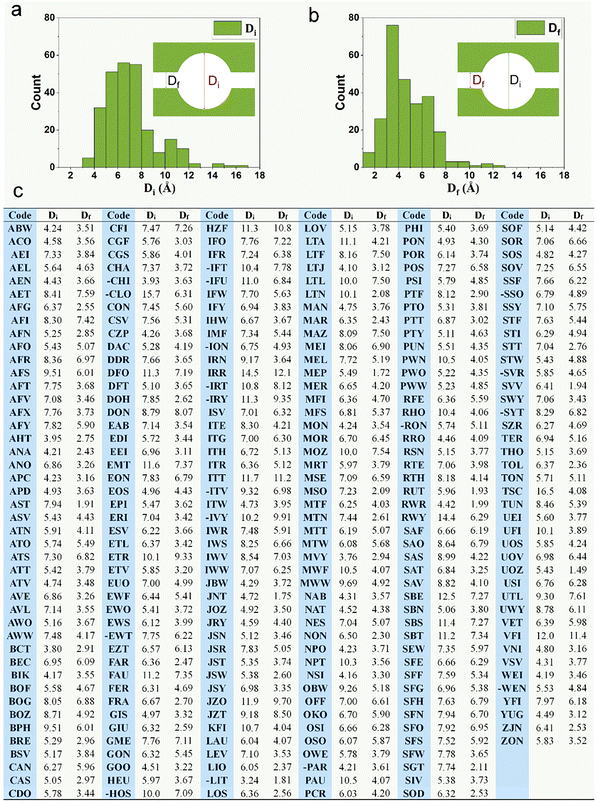 | ||
| Fig. 1 The diameter distribution of (a) the largest included sphere Di, and (b) the largest free sphere Df that can diffuse. (c) Di and Df for the about 260 known zeolite frameworks. | ||
Diffusion in zeolites is governed by a complex interplay between guest molecule properties and host framework characteristics.29,30 While the aforementioned methods enable preliminary assessment of diffusion behavior, quantitative determination of diffusion coefficients becomes essential when molecular dimensions approach those of the pore channels.29 Moreover, for non-spherical molecules or non-circular zeolite channels, such estimates may carry a risk of inaccuracy. For instance, although the kinetic diameter of p-xylene is larger than 5.70 Å and the freely diffusing sphere of MFI zeolite is only about 4.70 Å, experimental evidence confirms that p-xylene can nevertheless diffuse effectively within the MFI framework.31 In addition, the dynamic nature of both guest molecules (conformational flexibility) and zeolite frameworks (structural flexibility), coupled with reaction-specific temperature and pressure conditions, necessitates deeper mechanistic insights into confined diffusion behavior.32–35 Furthermore, the unique pore architectures of zeolites impose spatial constraints on guest molecules, leading to diffusion behaviors that differ significantly from those in bulk phases, and thus a comprehensive understanding of these factors is essential for optimizing zeolite-based applications in catalysis and separation.29,36–39
Experimental techniques for measuring diffusion are primarily categorized into macroscopic and microscopic methods. Macroscopic techniques typically employ a bed of zeolite crystals or a zeolite membrane and monitor the system's response to changes in adsorbate concentration within the gas phase. Macroscopic techniques include intelligent gravimetric analysis (IGA), temporal analysis of products (TAP), zero-length column (ZLC), tapered element oscillating microbalance (TEOM), tracer exchange-positron emission profiling (TEX-PEP), frequency response (FR), Fourier-transform infrared (FTIR) spectroscopy, chromatography, and uptake methods.37 The measurement ranges of some techniques are illustrated in Fig. 2.40 In contrast, microscopic techniques probe adsorbate mobility over significantly shorter time and length scales. These approaches can track molecular propagation within individual zeolite crystals and provide direct insight into the fundamental microscopic mechanisms of diffusion. For fast diffusion processes (10−8 to 10−12 m2 s−1), techniques such as pulsed field gradient nuclear magnetic resonance (PFG-NMR) and quasi-elastic neutron scattering (QENS) are typically employed, whereas slow diffusion is commonly investigated using exchange NMR spectroscopy.41 Other microscopic experimental methods include interference microscopy (IFM), infrared microscopy (IRM), single-molecule fluorescence microscopy (SMFM), and single-molecule localization microscopy (SMLM). As different techniques are suitable for specific diffusion regimes, method selection should be made with careful consideration. For a detailed introduction to diffusion measurement methods, including principles, parameter settings, and limitations of these methods, we refer readers to the work of Kärger.42
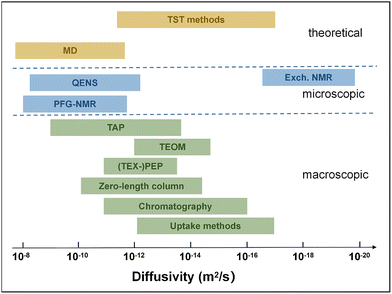 | ||
| Fig. 2 Measurable range of diffusivities that can be determined with different methods. The measurable range for some techniques depends on zeolite crystal size; a uniform crystal size of 10 μm was assumed in this comparison. The full names of some of the methods are provided below: TST, Transition state theory; MD, molecular dynamics; QENS, Quasi-elastic neutron scattering; Exch. NMR, exchange nuclear magnetic resonance; PFG-NMR, pulsed-field gradient nuclear magnetic resonance; TAP, temporal analysis of products; TEOM, tapered element oscillating microbalance; TEX-PEP, tracer exchange-positron emission profiling. Reproduced from the concept from ref. 40. | ||
Diffusion can be quantitatively characterized by diffusion coefficients, which can be classified into Fick (or transport), Maxwell–Stefan (corrected, or collective), and self-diffusion coefficient (Ds).30,43–46 The Ds, as an intrinsic transport property of matter, provides direct insight into molecular dynamic behavior under zero net chemical potential gradient (∇μ = 0), offering distinct advantages by eliminating external interference from concentration gradients. This makes it particularly valuable for investigating intrinsic transport mechanisms in confined systems (e.g., zeolites and MOFs); dynamic properties of pure substances or homogeneous systems; and fundamental relationships between molecular motion and thermodynamic parameters (temperature/pressure). This study primarily focuses on self-diffusion within zeolites, specifically the intrinsic diffusion inside the crystalline framework. The self-diffusion coefficient can be experimentally measured using PFG-NMR47,48 and QENS.49,50 As PFG-NMR and QENS techniques face inherent experimental limitations in diffusion studies (including zeolite morphology constraints, high-temperature/pressure conditions, and measurable diffusion coefficient ranges), alternative approaches (zero-length column, chromatography, and uptake methods) are often employed to enable qualitative assessment of diffusion trends.42 With the advancement of computer technology, theoretical methods, such as molecular dynamics (MD) simulations,29,30 as well as ab initio molecular dynamics (AIMD) combined with enhanced sampling techniques34,51 have also been applied to diffusion measurements. MD simulation calculates the diffusion coefficient by numerically solving Newton's equations of motion to track the trajectories of every atom/molecule within a system as they evolve on a potential energy surface, thereby directly “observing” their diffusive behavior. AIMD combines with enhanced sampling techniques by applying a restraining potential to divide the diffusion path (reaction coordinate) into multiple windows for sampling, thereby enabling the calculation of the free energy surface and dynamical properties for diffusion processes that overcome high energy barriers. These theoretical approaches not only enable the observation of microscopic molecular behaviors that are difficult to visualize experimentally, but also provide crucial supplementation and predictions for experimental studies. In addition, other diffusion measurement approaches exist, such as transition state theory (TST) methods, which are commonly combined with MD simulations to characterize slow diffusion processes with coefficients below 10−12 m2 s−1.51,52
Unlike existing reviews that focus on experimental techniques for diffusion measurement,42,53,54 theoretical and computational approaches,30,33,51,55–57 or material properties that enhance diffusion,58–60 this review provides a comprehensive overview of diffusion phenomena through a molecular- and atomic-scale analysis, with a particular focus on how nanoconfinement effects fundamentally govern diffusion mechanisms. Special emphasis is placed on elucidating how spatial constraints imposed by zeolitic frameworks modify molecular diffusion pathways, energy barriers, and dynamic behaviors. By bridging fundamental confinement principles with practical diffusion characteristics, we hope that this review can serve not only as an authoritative introduction for researchers entering this field but also as a critical reference for establishing structure—diffusion relationships in confined systems. Fig. 3 shows the characteristics of zeolite frameworks that are frequently discussed in this review. Unless otherwise specified, the diffusion coefficients presented in this review were obtained from MD simulations.
The remainder of this review is structured as follows: in Section 2, we provide a comprehensive review of fundamental mechanisms and microscopic phenomena governing confined diffusion in zeolites. Section 3 highlights recent advances in understanding diffusion-reaction coupling. Finally, Section 4 summarizes the key insights and outlines emerging challenges and future research directions in the field.
2. Confined diffusion in zeolite
The pore confinement effect in zeolites exerts multidimensional influences on molecular diffusion behavior, which can be categorized into four aspects: (1) nanoconfinement-induced persistent molecule-wall collisions dramatically shorten molecular mean free paths, causing diffusivity variations spanning orders of magnitude; (2) framework-generated potential fields reconstruct diffusion pathways, creating pronounced diffusion anisotropy; (3) coupled flexibility effects—where confined molecular conformations and framework vibrations mutually adapt—collectively regulate transport dynamics; (4) counterintuitive diffusion regimes emerge when molecules and zeolites reach specific matching conditions, resulting in novel transport phenomena that deviate from classical diffusion models.2.1. Confinement effects lead to orders-of-magnitude variations in diffusion coefficients
The most striking feature of molecular diffusion under zeolitic confinement is its orders-of-magnitude deviation from bulk-phase behavior (e.g., gases and liquids). Remarkably, even minor variations in zeolite pore geometry can lead to drastic alterations in diffusion coefficients, a characteristic that fundamentally enables zeolites’ renowned shape-selective functionality in catalysis and molecular separation.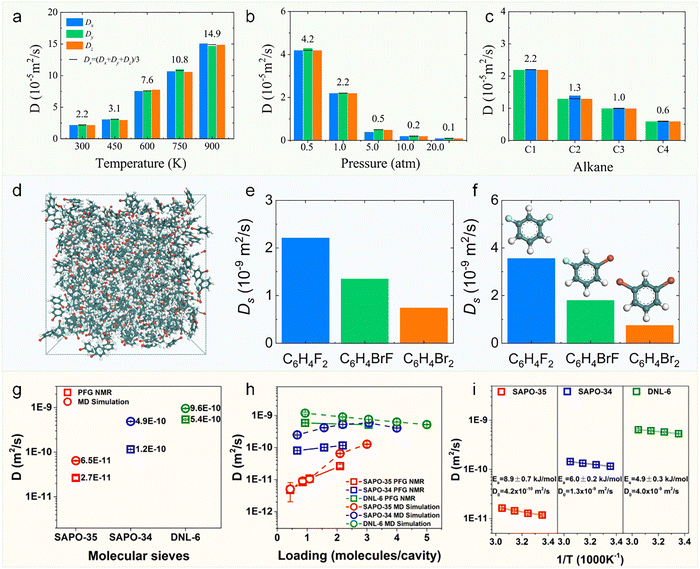 | ||
| Fig. 4 Self-diffusion coefficients (Ds) of various molecules in zeolites under different conditions. (a)–(c) Ds from MD simulations: (a) Ds of methane at various temperature, (b) pressure, and (c) Ds of alkanes at ambient conditions in gas phase.38 Reproduced from ref. 38 with permission from (John Wiley and Sons), copyright 2020. (d) Structures of C6H4BrF in the liquid-phase. Ds for various halogenated benzenes in the liquid-phase by (e) MD simulation and (f) PFG-NMR technique.61 Reproduced from ref. 61, licensed under CC BY 4.0. (g) Comparison of Ds for methane in SAPO-35 (LEV), SAPO-34 (CHA), and DNL-6 (RHO) zeolites at a loading of two molecules per cavity and 298 K, measured by PFG-NMR and MD simulations. (h) Loading dependence of experimental and simulated Ds for methane in cavity-type zeolites at 298 K. (i) Temperature dependence of Ds on the log-linear scale for methane within cavity-type zeolites by PFG-NMR.62 Reproduced from ref. 62 with permission from (Elsevier), copyright 2019. | ||
When the molecular dimensions approach the pore size of zeolites, steric hindrance becomes pronounced, leading to dramatically reduced mobility. This is exemplified by the diffusion of ethane and propane molecules in CHA: 6.0 × 10−12 and 5.4 × 10−13 m2 s−1, respectively.62 For systems exhibiting extremely low diffusivity (Ds < 10−12 m2 s−1), conventional MD simulations often require augmentation with enhanced sampling techniques.68,69 A representative study by Sholl and coworkers successfully addressed this challenge by combining standard MD with transition path sampling (TPS) methodology. Their investigations revealed the Ds of propane and n-butane in LTA at 300 K are 2.30 × 10−13 and 7.1 × 10−16 m2 s−1, respectively.70 This approach demonstrates the necessity of advanced sampling methods when studying strongly confined molecular systems where conventional simulations become computationally prohibitive. These slow diffusion processes stand in stark contrast to the rapid diffusion observed in other zeolite systems. For example, MD simulations demonstrate that methane (kinetic diameter: 3.8 Å) diffuses remarkably fast in ATO-type zeolites (pore size: 5.5 Å), with a diffusion coefficient as high as 1.9 × 10−7 m2 s−1.38 The observed order-of-magnitude variation in diffusivity (10−7 to 10−16 m2 s−1) underscores the critical role of pore confinement effects in molecular transport within zeolitic systems.
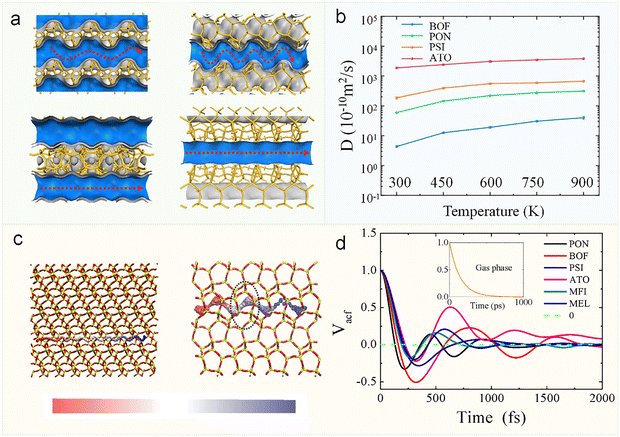 | ||
| Fig. 5 Molecular diffusion of methane in one-dimensional zeolite channels with varying curvature. (a) Structures of four one-dimensional zeolite channels, showing tortuous pores (PON, top left; BOF, top right) and straight pores (PSI, bottom left; ATO, bottom right). (b) Diffusion coefficients of methane as a function of temperature by MD simulation. (c) Trajectory of a methane molecule inside ATO (left) and BOF (right). The trajectories are colored with time proceeding (red-white-blue). (d) Velocity autocorrelation function of methane in various zeolites and in gas phase.38 Reproduced from ref. 38 with permission from (John Wiley and Sons), copyright 2020. | ||
It is particularly noteworthy that the VACF relaxation time of methane differs dramatically between gaseous and confined environments. While methane in the gas phase exhibits a relaxation time of approximately 1000 ps, this value decreases to less than 1 ps when confined within zeolitic frameworks (Fig. 5d). This striking contrast (three orders of magnitude difference) demonstrates that the collision frequency of methane molecules is significantly enhanced in confined spaces compared to the gas phase. The confined environment of zeolites substantially increases molecular collision rates, thereby reducing both the mean free path and consequently, the diffusion coefficient. However, a comprehensive understanding of the diffusivity differences among various guest molecules in distinct zeolitic frameworks requires further investigation from multiple perspectives, including zeolite topology, diffusion pathway, molecular flexibility, framework flexibility, acid sites, host–guest interactions, and free energy landscapes.29,30
2.2. Confinement effects reconstruct diffusion pathways
Zeolite-confined diffusion exhibits a defining characteristic that distinguishes it from homogeneous-phase transport: the framework-directed restructuring of molecular trajectories. This pathway reconstruction is fundamentally governed by the atomic-level topological features of zeolite architecture, giving rise to unique diffusion phenomena unobserved in unconfined systems.75–77 Moreover, the interaction potential imposed by the zeolite framework is highly sensitive to guest molecular species, framework topology, chemical composition, and acid site distribution,78 thereby enabling strategic modulation of local residence times to direct diffusion. External parameters such as concentration and temperature further exert substantial influence on diffusion behavior. In the gas phase, where intermolecular distances are large, molecules predominantly undergo linear motion until collision-induced trajectory changes occur (Fig. 6a).38,73 In contrast, the liquid phase exhibits stronger intermolecular interactions and enhanced confinement effects, resulting in complex dynamics involving rotational motion and spatial hopping (Fig. 6b).74 Within zeolite frameworks, guest molecules display even greater diffusion complexity—their transport behavior is not only dictated by guest–guest interactions but also critically regulated by guest-framework interactions.30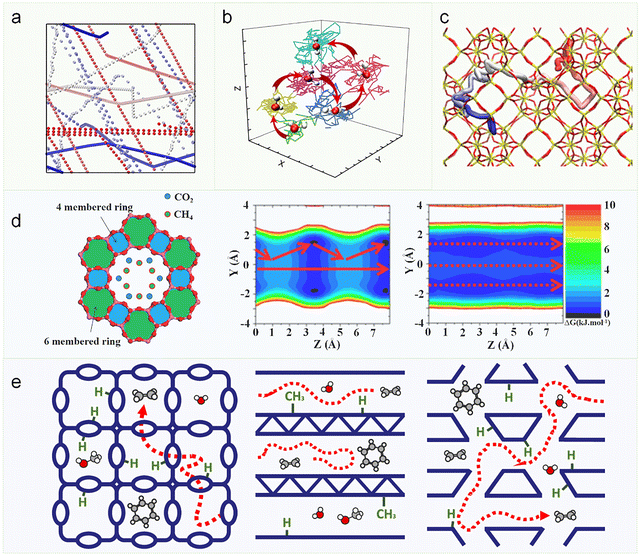 | ||
| Fig. 6 Diffusion trajectories of guest molecules in (a) gas phase, (b) liquid phase,74 Reproduced from ref. 74, licensed under CC BY 4.0. and (c) zeolites.75 Reproduced from ref. 75 with permission from (American Chemical Society), copyright 2022. The trajectories were colored with time proceeding (red-white-blue). (d) Preferential positions of the center of mass of CH4 and CO2 in the AlPO4-5 (AFI) channel (left) and cumulated densities in the YZ plane for the single components CH4 (middle), as well as CO2 (right).79 Reproduced from ref. 79 with permission from (American Chemical Society), copyright 2013. (e) Schematic representation of various zeolites having different topologies, characterized either by spacious cages with windows (left), channels in one direction (middle), or various channel systems (right).34 Reproduced from ref. 34, licensed under CC BY 4.0. | ||
For different guest molecules, diffusion trajectories may vary significantly. Maurin et al. investigated the diffusion behaviors of CO2 and CH4 in AlPO4-5 zeolite, revealing that CO2 exhibits stronger interactions with the pore walls, causing it to reside closer to the zeolite framework (Fig. 6d, left). Spatial density probability analysis demonstrates that CH4 follows more tortuous diffusion pathways (Fig. 6d, middle), while CO2 adopts straighter and shorter trajectories (Fig. 6d, right).79 Furthermore, the zeolite framework topology, active sites, and loading govern molecular diffusion trajectories by creating distinct interaction potentials (Fig. 6e).34,75 This confinement effect leads to considerably more complex diffusion behavior compared to homogeneous systems. A comprehensive understanding of these processes requires systematic investigation of multiple governing factors, including energetics, acid site characteristics, temperature, and concentration effects.
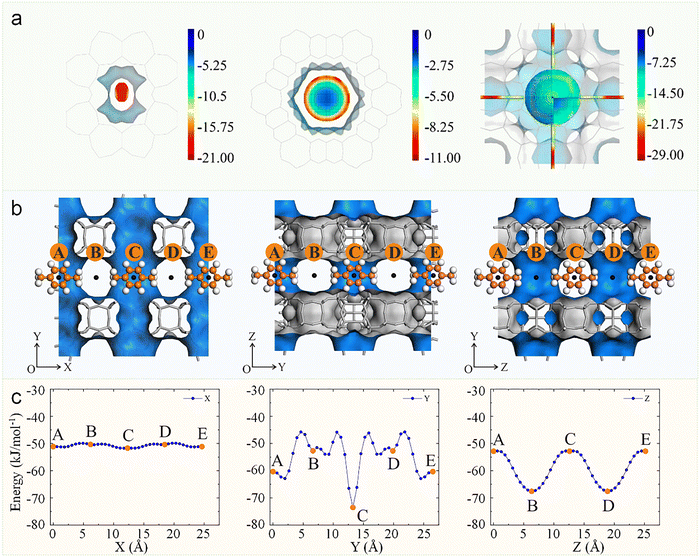 | ||
| Fig. 7 Potential energy landscapes and directional diffusion in zeolites. (a) Potential energy profile for methane in TON with small pore (left), VFI with large pore (middle), and RHO with large cage (right).75 Reproduced from ref. 75 with permission from (American Chemical Society), copyright 2022. (b) Definition of p-xylene (center of mass) diffusion pathways (points A to E) along the X (left), Y (middle), and Z directions (right) in SCM-15 (SOV) zeolite. (c) Interaction energy profiles of p-xylene along the X (left), Y (middle), and Z directions (right) in SCM-15 zeolite.80 Reproduced from ref. 80, licensed under CC BY 4.0. | ||
Among various zeolites, the ZSM-5 (MFI topology) zeolite with intersecting straight (5.3 × 5.6 Å) and sinusoidal channels (5.1 × 5.5 Å), represents both the most prominent anisotropic diffusion system and one of the most industrially important zeolites, serving as a paradigm for structure-diffusion relationship studies (Fig. 8a).82,84–86 Fuchs et al. conducted a systematic investigation into the diffusion behavior of linear alkanes with varying chain lengths in silicalite-1 zeolite by MD simulation, revealing pronounced diffusion anisotropy.83 Their study demonstrated that under different adsorption concentrations, alkane molecules consistently exhibit distinct anisotropic diffusion, with the diffusion coefficients following a consistent trend: Dy (straight channels) > Dx (sinusoidal channels) > Dz (Fig. 8b). Notably, the diffusion anisotropy was more pronounced in longer-chain alkanes compared to their shorter-chain counterparts. For instance, the Dy/Dx ratios for methane and n-butane were 1.6 and 5.5, respectively. In contrast, as the chain length increased, n-hexane and n-octane exhibited substantially higher ratios of 11.1 and 31.3, clearly demonstrating the strong dependence of diffusion anisotropy on molecular chain length.
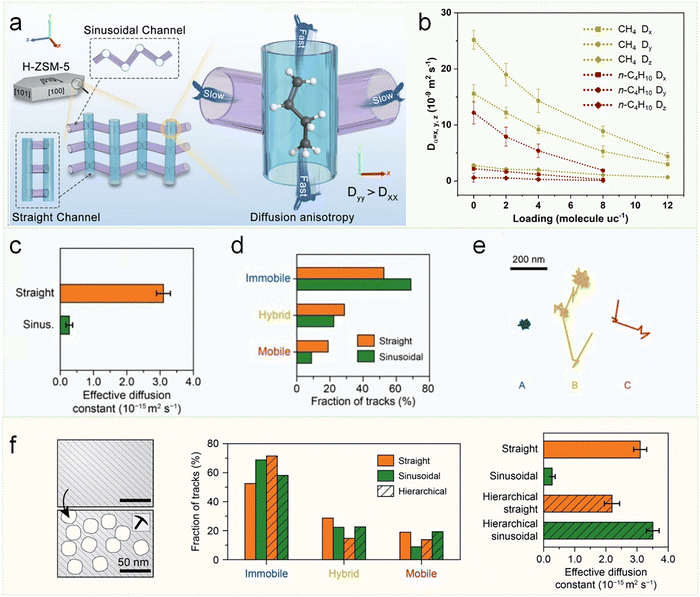 | ||
| Fig. 8 Diffusion anisotropy and the effect of secondary porosity in ZSM-5 zeolite. (a) Framework and diffusion model of ZSM-5 (MFI) zeolite, which is composed of straight channels running along the Y-axis and sinusoidal channels in the XZ-plane, featuring similar opening sizes but different geometries.82 Reproduced from ref. 82, licensed under CC BY 4.0. (b) The concentration-dependent diffusion anisotropy of alkanes in ZSM-5 zeolite exhibits distinct chain-length dependence as derived from data analysis by MD simulation.83 Reproduced from ref. 83 with permission from (Royal Society of Chemistry), copyright 2004. (c) The effective diffusion coefficients of the straight and sinusoidal zeolite channels. (d) The fraction of each type of trajectory within the straight and sinusoidal zeolite channels, and (e) diffusion patterns of three representative trajectories with immobile, hybrid, and mobile motion types. (f) Schematic representation of the introduction of secondary pore networks into zeolites (left), the fraction of each type of trajectory within the straight and sinusoidal zeolite channels with secondary porosity (middle), and the effective diffusion coefficients for the straight and sinusoidal zeolite channels with secondary porosity (right).84 Reproduced from ref. 84, licensed under CC BY 4.0. | ||
In addition to theoretical calculations, experimental studies have confirmed diffusion anisotropy in ZSM-5 zeolite too. For example, PFG-NMR measurements reveal that the diffusivity of n-butane in the straight channel is nearly an order of magnitude higher than in the sinusoidal channel, indicating its preferential diffusion pathway.67 Recently, Weckhuysen et al. employ single-molecule localization microscopy to systematically investigate diffusion anisotropy in ZSM-5 zeolite's sinusoidal (a-axis) and straight (b-axis) channels. The results reveal significant anisotropic diffusion behavior dictated by channel geometry: molecules in straight channels diffuse approximately ten times faster (3.10 ± 0.21 × 10−15 m2 s−1) than those in sinusoidal channels (0.27 ± 0.10 × 10−15 m2 s−1) (Fig. 8c). This disparity stems from distinct molecular motion patterns—the linear architecture of straight channels facilitates rapid molecular transport, while the tortuous sinusoidal channels enhance guest–host interactions (Fig. 8d), resulting in higher immobile fractions (Fig. 8e). Notably, hierarchical pore network introduction dramatically modified this anisotropy: sinusoidal channels showed an order-of-magnitude enhancement in effective diffusivity (from 0.27 × 10−15 to 3.51 × 10−15 m2 s−1), whereas straight channels experienced a slight reduction due to compromised connectivity (Fig. 8f). These findings provide molecular-level insights into structure-diffusivity relationships, offering critical guidance for designing zeolite materials with optimized transport properties. The work establishes single-molecule tracking as a powerful approach for characterizing diffusion heterogeneity in porous materials.84 In addition, Weckhuysen and coworkers employed confocal laser scanning microscopy (CLSM) to directly visualize the anisotropic diffusion behavior of resorufin molecules along the straight channels of zeolite-β crystals. Quantitative analysis revealed a diffusion coefficient of 3 × 10−15 m2 s−1. More importantly, their real-time imaging unambiguously demonstrated the existence of diffusion barriers originating from the interfaces between crystalline subunits (subunit boundaries) within the zeolite framework – specifically at the junctions where pyramidal and side subunits meet.87
Besides MFI and SOV, the diffusion anisotropy has also been found in zeolites with BOG, CON, DFO, ITG, ITN, IWR, IWW, MSE, OKO, PUN, SEW, SFS, SFV, UOV, USI, and UWY,76,77 as well as BEC and POS.80,88 However, due to the morphological characteristics of zeolite materials and the limitations of current anisotropic diffusion measurement techniques, research on anisotropic diffusion in zeolites has primarily focused on theoretical simulations. There is an urgent need to develop more advanced experimental methods to expand the study of anisotropic diffusion behavior across different zeolite systems. Moreover, as will be discussed in detail in later sections, the distribution and concentration of acid sites in zeolites also play a critical role in influencing diffusion anisotropy.
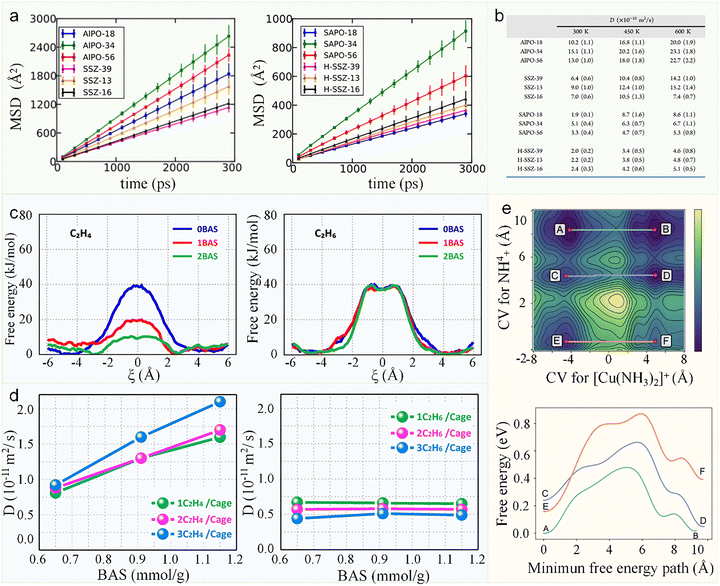 | ||
| Fig. 9 The influence of acid sites on molecular diffusion in zeolites. (a) Mean square displacement (MSD) of ethene at 300 K in zeolites without acids (left) and in acidic zeolites (right). (b) Ethene diffusion coefficient at various temperatures, derived from MD simulations by fitting the MSD curves.78 Reproduced from ref. 78 with permission from (American Chemical Society), copyright 2015. (c) Free energy profile for ethene (left) and ethane (right) diffusion at 600 K through an 8-ring window of SAPO-34 containing 0, 1, or 2 BASs. (d) Self-diffusion coefficients of ethene (left) and ethane (right) at 295 K in H-SAPO-34 with varying BAS density, measured by 1H PFG-NMR for loadings of 1–3 molecules per cage.90 Reproduced from ref. 90, licensed under CC BY 4.0 (e) Two-dimensional metadynamics simulation for the movement of [Cu(NH3)2]+ and NH4+ ions with the embedding network having a Si/Al ratio of 13 and Cu/Al of 0.25 (top). Selected free energy barriers along the minimum energy path between different stable sites (bottom).91 Reproduced from ref. 91, licensed under CC BY 4.0. | ||
Consequently, intracrystalline diffusion is critically dependent on acid site concentration, strength, and spatial distribution. A notable example is the work by Masuda et al.,92 who studied MFI-type zeolites with varying acid densities by MD simulation. At low temperatures, diffusivities of benzene, toluene, and p-xylene decreased markedly with increasing acid content, whereas at high temperatures, diffusion coefficients became insensitive to acidity. This dichotomy arises from molecule–acid site interactions. At low-temperature regime, molecules frequently adsorb at acid sites, immobilizing temporarily before desorbing and migrating to adjacent sites. This “hopping” mechanism introduces diffusion resistance, explaining the inverse correlation between acid content and mobility. The critical temperature (Tc), marking the transition between regimes, increases with acid density due to stronger retention effects. In contrast, at high-temperature regime, enhanced thermal energy overcomes adsorption barriers, reducing residence times at acid sites and rendering diffusivity nearly independent of acidity.
Moreover, the influence of Brønsted acid sites (BASs) on guest molecule diffusion in zeolites exhibits pronounced site dependence and molecular selectivity. Van Speybroeck and co-workers90 systematically investigated the differential effects of acid site concentration on the diffusion of alkenes versus alkanes, uncovering the underlying mechanistic origin. Their results demonstrate that BAS exert a significantly stronger influence on alkene diffusion than on alkanes, displaying a unique concentration dependence: as the number of BAS increases, the diffusion barrier for alkenes decreases anomalously (Fig. 9c). This counterintuitive trend arises from the precise positioning of BAS along the diffusion pathway—when located at the free energy maximum (e.g., the 8-MR window), the stable H–π interaction93 between the BAS and the alkene molecule acts as a driving force to facilitate diffusion. For instance, the diffusion barrier for ethene decreases markedly from 38 kJ mol−1 (no BAS) to 20 kJ mol−1 (1 BAS) and further to 10 kJ mol−1 (2 BAS). In contrast, when BAS are positioned away from key diffusion channels (e.g., 6-MR), they exhibit negligible impact on diffusion. For alkanes, which interact primarily through van der Waals forces with the zeolite framework, the presence of BAS has minimal effect on their diffusion barriers (∼40 kJ mol−1). These mechanistic insights were corroborated experimentally by PFG-NMR measurements, which revealed a substantial increase in ethene diffusivity with rising BAS concentration at room temperature, while ethane diffusion remained largely unaffected (Fig. 9d). Similarly, the Xie group employed homemade time-resolved in situ Fourier transform infrared spectroscopy to demonstrate that H-π interactions also facilitate the rapid diffusion of olefins toward acid sites in MFI-type zeolites.94
In addition to van der Waals and H–π interactions, hydrogen bonding can also significantly influence molecular diffusion. Leeuw and co-workers demonstrated that BAS in zeolites prolong methanol's residence time near active centers through hydrogen-bonding interactions, consequently retarding its diffusion in both H-MFI and H-Beta frameworks.95 O’Malley and co-workers revealed that BAS in HY zeolites can form hydrogen bonds with water molecules, thereby impeding molecular diffusion.96,97 The effect of hydrogen bonding on diffusion is summarized in detail in Section 2.2.5. Beyond BAS, surface hydroxyl groups were also found to significantly influence diffusion dynamics.96,98 Moreover, acid site distribution significantly influences molecular diffusion. As demonstrated by Grönbeck and co-workers, two-dimensional metadynamics simulations can precisely resolve the diffusion free energy landscapes along distinct transport pathways, offering a novel strategy for probing diffusion mechanisms (Fig. 9e).91 In general, the influence of acid sites on diffusion depends on multiple factors, including the type of acid sites, their spatial distribution, and the nature of the guest molecules. Typically, acid sites exhibit a weaker effect on the diffusion of alkanes than on that of olefins (due to H–π interactions), alcohols, and water molecules (governed by hydrogen bonding). Additionally, the specific location of acid sites along the diffusion pathway plays a critical role. Furthermore, when investigating the influence of acid sites on diffusion, careful consideration must be given to force field selection, as certain force fields used in MD may fail to adequately capture H–π interactions.35 These aspects warrant further systematic investigation.
Kärger and co-workers systematically categorized the concentration dependence of diffusion coefficients in zeolites into five distinct types (Type 1–Type 5), as illustrated in Fig. 10a.99 Among these classifications, Type 1 and Type 4 represent the most commonly observed behaviors, corresponding to channel-type/intersecting channel-type and cage-type zeolites, respectively.101 Numerous experimental investigations and computational simulations consistently confirm that zeolites with MFI topology (intersecting channel) display Type 1 concentration-dependent diffusion behavior.102,103 In 2006, Beerdsen et al. employed one-dimensional free energy analysis to elucidate the concentration dependence of molecular diffusion using MD simulations. They conducted a systematic investigation of methane diffusion across ten zeolite frameworks (LTA, CHA, ERI, SAS, AFI, MTW, LTL, MFI, BOG, and BEC), categorizing them into three distinct classes based on pore topology: (i) cage-type, (ii) channel-type, and (iii) intersecting channel-type (Fig. 10b). Their study revealed a striking correlation between pore architecture and diffusion-concentration dependence. For cage-type zeolites, a type 4 diffusion-concentration relationship was predominantly observed. The narrow windows connecting cages introduced substantial free-energy barriers. At low concentrations, each additional methane molecule filled the potential well, lowered the effective energy barrier and increased the diffusion coefficient. However, at high densities, steric crowding and diminished free volume suppressed diffusivity (Fig. 10c, left). In contrast, channel-type zeolites primarily exhibited type 1 diffusion-concentration behavior. Here, the diffusion coefficient monotonically decreased with loading due to pronounced molecular congestion, as the lower energy barriers offered less resistance to intermolecular interactions (Fig. 10c middle). Intersecting channel-type zeolites displayed hybrid characteristics, blending features of both cage- and channel-type systems. The diffusion energy barrier in these frameworks was governed by the relative volume of channel intersections compared to the overall pore structure (Fig. 10c, right).101 In addition, Van Speybroeck employed AIMD combined with umbrella sampling, revealing that increasing propene concentration in SAPO-34 zeolite reduced the free energy barrier for inter-cage diffusion of guest molecules, thereby facilitating their migration to adjacent cages (Fig. 10d).35
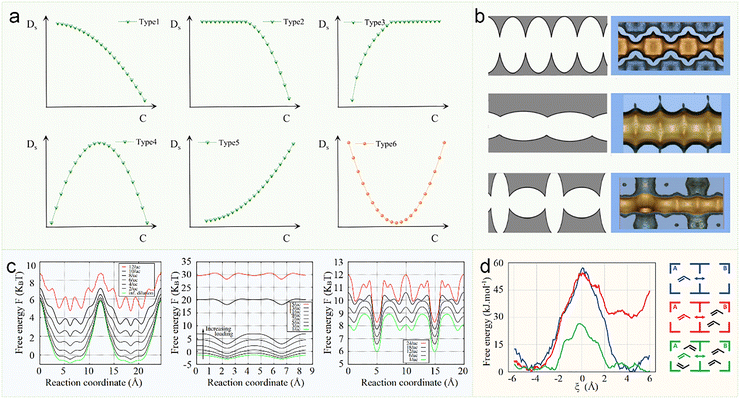 | ||
| Fig. 10 Loading dependence of diffusion in different zeolite topologies. (a) Types of the loading dependence of Ds in zeolites. C, concentration.99,100 Reproduced from ref. 100 with permission from (American Chemical Society), copyright 2025. (b) Three ways to connect ellipsoids cage-type (top), channel-type (middle), and intersecting channel-type (bottom).101 (c) Free-energy profiles as a function of loading for cage-type LTA (left), channel-type AFI (middle), and intersecting channel-type MFI (right), at 300 K.101 Reproduced from ref. 101 with permission from (Elsevier), copyright 2006. (d) Free energy profiles for propene diffusion of SAPO-34 at 600 K with different propene loadings in the cages from AIMD combined with umbrella sampling.35 Reproduced from ref. 35, licensed under CC BY 4.0. | ||
Recent work by Zheng et al. uncovered a novel concentration-dependent diffusion trend characterized by an initial decrease followed by subsequent increase in diffusion coefficients, governed by a “self-gating” diffusion mechanism.100 While RHO and LTA zeolites share similar topological features (both containing lta cages), they differ in their connecting units—LTA features single 8-MR whereas RHO contains double 8-MR connections (Fig. 11a). Intriguingly, these two frameworks exhibit completely opposite concentration-dependent diffusion trends (Fig. 11b). Molecular trajectory analysis reveals that diffusion in both frameworks occurs via cage-to-cage hopping, with RHO showing shorter diffusion distances than LTA over 100 ns timescales, consistent with their respective diffusion coefficients (Fig. 11c). Through the continuous-time random-walk coarse-graining method, the diffusion coefficient differences were attributed primarily to variations in cage-hopping frequencies (Fig. 11d). Three-dimensional free energy analysis further demonstrated that molecular diffusion follows a pathway where molecules move between double 8-MR units along the lta cage walls, with the double 8-MR serving as the diffusion-limiting unit (Fig. 11e, top). At low concentrations, molecules diffuse freely. As concentration increases, the strong adsorption energy of double 8-MR causes preferential molecular accumulation at these sites. A further increase in concentration leads to molecular self-gating at the double 8-MR, raising the free energy barrier for cage-to-cage hopping and consequently decreasing diffusion coefficients. However, beyond a critical concentration threshold, cooperative molecular collisions overcome this gating effect, reducing residence times in both cages and double 8-MR connections, thereby lowering the diffusion free energy barrier (Fig. 11e, bottom) and increasing diffusion coefficients. This comprehensive study systematically elucidates concentration-driven diffusion mechanisms in confined spaces (Fig. 11f), establishing a new paradigm for understanding concentration effects on molecular diffusion processes.
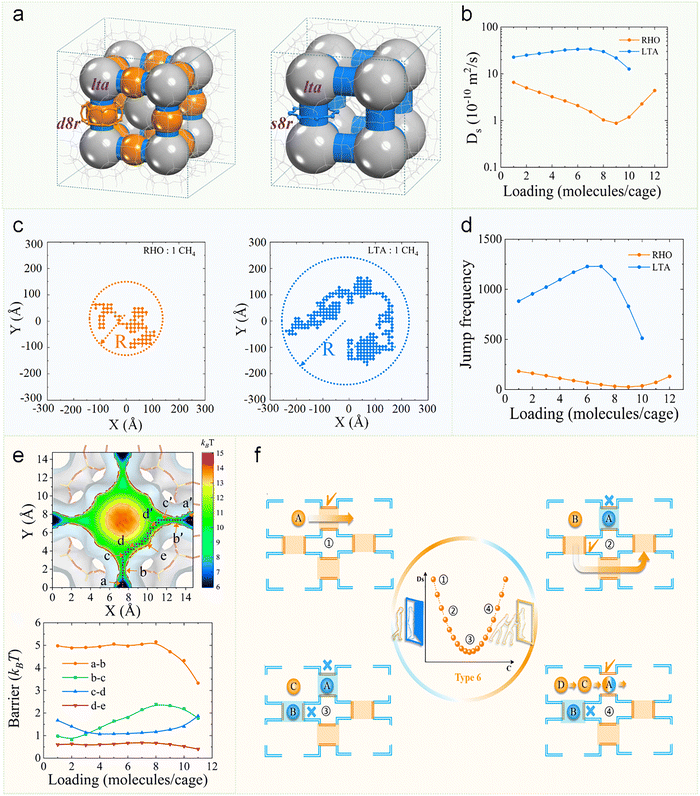 | ||
| Fig. 11 Loading-dependent self-gating diffusion in RHO and LTA zeolites. (a) Framework structures of RHO-type (left) and LTA-type (right) zeolites. Both contain lta cages (silver), but are interconnected through double eight-member rings (d8r, orange) in RHO and single eight-member rings (s8r, blue) in LTA. (b) Ds of methane inside RHO and LTA zeolite as a function of loading at 298 K by MD simulation. (c) Trajectories of one representative methane diffusion in RHO (left) and LTA (right) zeolite in the XY plane at the loading of 1 molecule per cage during 100 ns. (d) Jump frequency in zeolites as a function of loading at 298 K. (e) 2D free energy of diffusion extracted from 3D free energy map (top). Free energy barriers for varied loadings in RHO zeolite at 298 K (bottom). (f) Mechanism of molecular self-gating controlled diffusion in RHO zeolite at various loading.100 Reproduced from ref. 100 with permission from (American Chemical Society), copyright 2025. | ||
The unique and fascinating aspect of water diffusion lies in its ability to form hydrogen bonds, as well as strong interactions with cations present within the zeolite framework. Wang and coworkers investigated the diffusion behavior of water molecules in NaA-type zeolite using molecular simulations.114 Their findings revealed that H2O diffusion does not occur via direct passage through the α-cages but rather through hopping between adjacent 8-membered oxygen rings (Fig. 12a). A comparison of NaA with and without Na+ revealed that Na+ ions, as key components of the water channels, enhance water adsorption and reduce the diffusion energy barrier. Additionally, water molecules were observed to fill the NaA zeolite framework in a layer-by-layer manner. Furthermore, Suffritti and co-workers identified a cooperative diffusion mechanism in zeolites NaA and NaCaA, involving the coordinated motion of water molecules and cations (Fig. 12b). Analysis of simulated trajectories indicated that this process is facilitated by transient hydrogen bonds, which enable both species to jump between equilibrium sites (Fig. 12c).115 Regarding hydrogen bond lifetime, Subramanian et al. employed MD simulations and found that in pure-silica FAU zeolite, aluminosilicate FAU zeolite, and bulk liquid water, the hydrogen bond lifetimes of water molecules were 26.3, 47.1, and 164.4 ps, respectively. These results demonstrate that the confinement effect of zeolites significantly influences hydrogen bond stability.117 Not only can water molecules form hydrogen bonds with each other, but they can also establish hydrogen bonds with acid sites on the zeolite framework, leading to the protonation of water.105 Typically, a single water molecule interacts with the Brønsted acid site in zeolites primarily through hydrogen bonding, and proton transfer from the zeolite framework to the water molecule is rarely observed. In contrast, when two or more water molecules are present, the proton can migrate from the framework to the water cluster, leading to the formation of hydrated hydronium ions. Parrinello and colleagues utilized AIMD in combination with well-tempered metadynamics to quantitatively determine the free energy associated with water protonation as a function of hydration number. Their results are consistent with the findings discussed above.5 Mei and co-workers also applied AIMD combined with an enhanced sampling technique to investigate the protonation behavior of water clusters. They demonstrated that in a monohydrate system, proton hopping occurs primarily among oxygen atoms near acid sites. In contrast, systems containing two or more water molecules exhibit a pronounced tendency for facile proton transfer, indicating that the presence of additional water molecules significantly promotes proton dissociation and mobility.118 These findings have been corroborated by experimental techniques such as two-dimensional infrared spectroscopy (2D IR),116 inelastic neutron scattering (INS),119 and solid-state nuclear magnetic resonance (NMR) spectroscopy.120
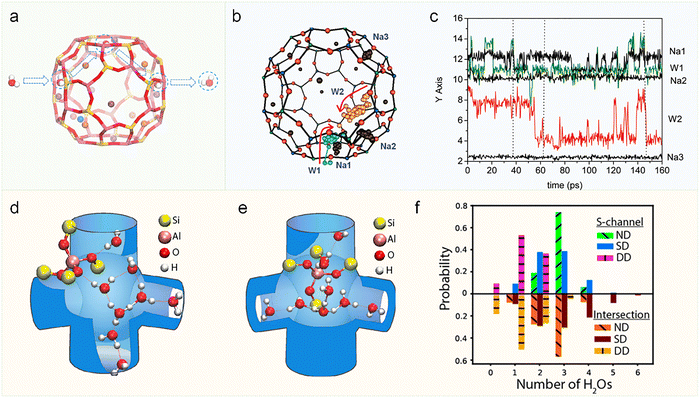 | ||
| Fig. 12 Mechanisms of water diffusion and hydrogen bonding in zeolites. (a) Diffusion pathway of a water molecule through the α-cage of zeolite NaA.114 Reproduced from ref. 114 with permission from (Elsevier), copyright 2021. (b) Intra-cage diffusion mechanism of water molecules in zeolite NaA. W1 (green) and W2 (pink) represent water molecules, while the black spheres denote different Na ions. (c) The time evolution of the most significant coordinate of the involved molecules and cations.115 Reproduced from ref. 115 with permission from (American Chemical Society), copyright 2010. Representative trajectory snapshots of the protonated water cluster configurations with the Al T-site located at (d) the straight channel (S-channel) and (e) the intersection with the zigzag channel (Z-channel), dashed red lines in (d) and (e) depict H-bonds. (f) Statistical distribution of H-bonding configurations for water molecules: double donor (DD), single donor (SD) and no donor (ND).116 Reproduced from ref. 116 with permission from (American Chemical Society), copyright 2021. | ||
Tokmakoff and colleagues combined ultrafast two-dimensional infrared (2D IR) spectroscopy with AIMD simulations to investigate water confined in the pores of highly hydrated HZSM-5 zeolite. Their findings indicate that the hydrated proton predominantly exists in the form of H+(H2O)8.116 AIMD simulation results reveal that when the Al T-site is located in the straight channel (S-channel, Fig. 12d), the water cluster adopts an elongated configuration, wherein two to three water molecules bridge the deprotonated Brønsted acid site and the water molecules accumulated at the channel intersection. In contrast, when the Al T-site is situated at the intersection itself (Fig. 12e), the cluster becomes more compact, with three to four water molecules extending into the adjacent straight and zigzag channels. Fig. 12f quantifies the hydrogen-bonding configurations of water molecules in HZSM-5 zeolite pores. This distribution highlights the prevalence of weakly bonded water under confinement, as evidenced by the lower population of double-donor (DD) configurations. Interestingly, Van Speybroeck et al. used machine learning potentials and path integral molecular dynamics to show that nuclear quantum effects lower the activation energy for proton hopping in H-SSZ-13 zeolites. The calculated activation energy decreased from 67.1 kJ mol−1 without nuclear quantum effects to 55.8 kJ mol−1 when they were included.121 Currently, studying the diffusion of hydrated protons over long timescales (nanoseconds) using ab initio molecular dynamics (AIMD) remains challenging, which creates an opportunity for methods based on machine learning potential methods.33,34,121
2.3. Framework and molecular flexibility dictate diffusion under confinement
The pioneering computational studies necessarily approximated zeolite frameworks as rigid structures, a simplification motivated by the dual challenges of unavailable flexible force fields and constrained computational capabilities. However, emerging experimental evidence has revealed significant intrinsic framework flexibility in zeolites.31,122 The rapid advancement of computational technology, coupled with the development of sophisticated flexible force fields—particularly when combined with AIMD methods—has enabled systematic investigation of pore flexibility effects on diffusion processes. This paradigm shift in research methodology has not only enhanced the accuracy of computational simulations but, more importantly, provided a more physically realistic representation of actual diffusion mechanisms.Early attempts to characterize framework flexibility in zeolites utilized MD simulations with flexible models, enabling the reconciliation of experimental and theoretical diffusion coefficients for alkanes.134–137 Generally, the framework flexibility does not significantly affect the diffusion of molecules that are significantly smaller than the pore size of the zeolite, while it is observed to play a role if the adsorbate fits tightly in the zeolite pore.70,136–140 Krishna et al. suggested that framework flexibility can be effectively taken into account by performing simulations with a different rigid structure, the so-called time averaged (TA) structure. They concluded that TA structure is sufficient to capture the effect of framework flexibility.137 Rousseau et al. have shown that the effect of framework flexibility depends on the sorbate length and loading in silicalite. Diffusion is enhanced in flexible frameworks only for the shortest alkanes (Fig. 13a; e.g. methane and n-butane) and at low loadings. At low loadings, the enhancement of diffusion is caused by a weak modification of sorbate-zeolite potential energy surface. Therefore, a flexible framework is required for quantitative studies of self-diffusion at low loading. At high loadings, diffusion is mostly controlled by sorbate-sorbate interactions and the sorbate-zeolite interaction modifications caused by flexibility become negligible (Fig. 13b).83 Vlugt et al. systematically investigate how framework flexibility influences the diffusion of aromatic molecules in MFI-type zeolites (Fig. 13c). Notably, flexibility reduces free-energy barriers between adsorption sites (Fig. 13d), enhancing diffusion rates by several orders of magnitude in the straight channels (Fig. 13e).133 However, due to the lack of accurate and universal flexible force fields, as well as the computational cost associated with their implementation, rigid force fields remain the prevailing choice in current studies. There is an urgent need to develop high-precision and universal force fields based on ab initio calculations with experimental validation. Fortunately, machine learning potentials (MLPs) trained on density functional theory (DFT) offer a promising pathway toward flexible force field development. For instance, Kulkarni et al. constructed MLPs trained on 219 zeolite structures from the IZA database,141 while Boronat et al. employed a machine-learning interatomic potential to investigate the diffusion of Cu+ species in Cu-CHA.142 With new MLPs continually emerging,34,121,143–145 significant opportunities are arising for advancing the study of diffusion processes in zeolites.
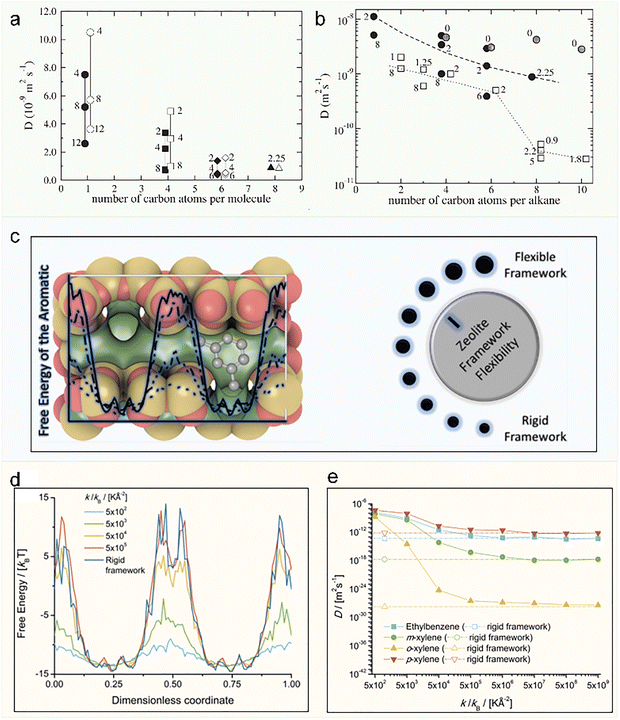 | ||
| Fig. 13 The influence of framework flexibility on molecular diffusion in MFI zeolite. (a) Ds of methane and n-alkanes in silicalite calculated using both rigid (full symbol), flexible DHFF framework (empty symbols). Numbers on the plot indicate loadings in molecule per unit cell. (b) Chain length and loading dependences of the Ds of alkanes ranging from methane to decane by MD simulation.83 Reproduced from ref. 83 with permission from (Royal Society of Chemistry), copyright 2004. (c) Correlation diagram of MFI zeolite framework structure, flexibility, and diffusion. (d) Free-energy profiles in the b-crystallographic axis for m-xylene at infinite dilution in an MFI-type at 353 K, varying framework flexibility k. (e) Ds for ethylbenzene and xylene isomers in the straight channel of an MFI type zeolite at 353 K, varying framework flexibility k.133 Reproduced from ref. 133, licensed under CC BY 4.0. | ||
Recent groundbreaking work by Wei and colleagues has employed in situ electron microscopy to directly observe subcell topological flexibility in MFI-type zeolites during benzene adsorption (Fig. 14a and b).31 While the MFI framework maintains remarkable macroscopic rigidity (<0.5% unit-cell deformation), local pore channels exhibit substantial anisotropic deformation, stretching up to 15% along adsorbed benzene molecules. Complementary AIMD simulations demonstrate that benzene adsorption induces characteristic pore deformation in ZSM-5, elongating channels by approximately 0.6 Å while simultaneously suppressing thermal fluctuations (Fig. 14c–e). This flexibility originates from dynamic Si–O–Si angle variations (135°–153°), while the SiO4 tetrahedra themselves maintain structural rigidity (Fig. 14f–h).31 These findings provide fundamental insights into how subcell topological flexibility mediates molecular diffusion through dynamic pore size modulation, profoundly influencing adsorption and catalytic behavior in microporous materials. The role of framework flexibility has become increasingly recognized as a critical design parameter for molecular sieving, enabling exquisite control over gas diffusion and separation processes. A paradigm-shifting example is the flexible pure-silica zeolite ITQ-55 reported by Corma and coworkers, where precise modulation of framework flexibility achieves exceptional ethene/ethane separation selectivity approaching 100.146 The framework flexibility-guest interaction paradigm extends further to cation-gating mechanisms in materials such as K-CHA and Na-RHO. In these systems, extra-framework cations undergo reversible relocation to dynamically regulate pore accessibility, enabling remarkable discrimination of molecules with near-identical dimensions (e.g., N2/CH4 and CH4/CO2).147–149 These collective advances underscore the imperative to incorporate framework flexibility as a key design consideration in developing next-generation molecular sieves, opening new avenues for precision separation technologies.
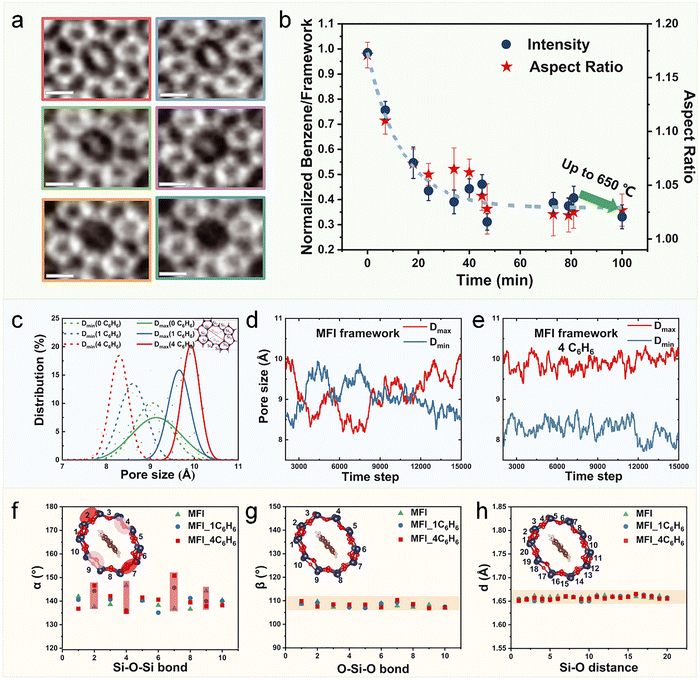 | ||
| Fig. 14 Framework flexibility of MFI zeolite during benzene adsorption/desorption. (a) Integrated differential phase contrast scanning transmission electron microscopy (iDPC-STEM) snapshots of a benzene@MFI specimen along the [010] projection at different stages during the cyclic benzene desorption process. (b) Evolution of the normalized benzene/zeolite framework contrast ratio and corresponding aspect ratios of Si10 opening pores during the in situ benzene uptake and release process. (c) Distributions of pore size for benzene (C6H6) molecule adsorption with different loadings as calculated from AIMD simulations. Pore size evolution with time for (d) 0, and (e) 4C6H6 molecules adsorbed inside MFI zeolite. Statistical results for the (f) Si–O–Si angle, (g) O–Si–O angle, and (h) Si–O bond length indicating a loose network composed of rigid tetrahedral SiO4 and soft hinges at the oxygen atoms.31 Reproduced from ref. 31 with permission from (American Association for the Advancement of Science), copyright 2022. | ||
Yuan et al. systematically investigated the diffusion behaviors of short- and long-chain alkanes in MFI zeolite (Fig. 15a) under varying temperatures. Their study revealed a distinct temperature dependence: while the diffusion coefficients of short-chain alkanes (e.g., C1, C4) increased with temperature, long-chain alkanes (e.g., n-dodecane) exhibited an opposite trend (Fig. 15b). Energy analysis demonstrated that this phenomenon correlates strongly with molecular strain energy—elevated temperatures induce greater bending conformations in long-chain alkanes (Fig. 15c), enhancing molecular flexibility which consequently increases steric hindrance and diffusion barriers (Fig. 15d). Further investigation showed that when considering only molecular flexibility (while neglecting bond length/angle variations), all alkanes displayed increased diffusion coefficients with temperature, with long-chain alkanes demonstrating significantly stronger dependence on flexibility (Fig. 15e) than their short-chain counterparts (Fig. 15f). Notably, this anomalous negative temperature dependence of diffusion coefficients for long-chain alkanes was exclusively observed in narrow-pore zeolites (e.g., MTW, TON), but not in large-pore structures (e.g., AFI, VFI), highlighting the crucial role of confinement effects (Fig. 15g). Based on these findings, the authors defined this temperature-induced increase in diffusion resistance for long-chain molecules (approaching that of branched alkanes) as the “thermal resistance effect” (Fig. 15h).153 Furthermore, the research team discovered that selecting zeolites with tailored pore sizes can effectively modulate the conformational freedom of long-chain molecules, maintaining their linear configuration within the confined space to achieve ultrafast diffusion. Through systematic infrared spectroscopic measurements, they quantitatively characterized the bending angle variations of these molecules in different zeolite frameworks. The experimental results conclusively demonstrate that spatial constraints of the confinement environment significantly alter molecular flexibility, thereby governing their diffusion dynamics.66
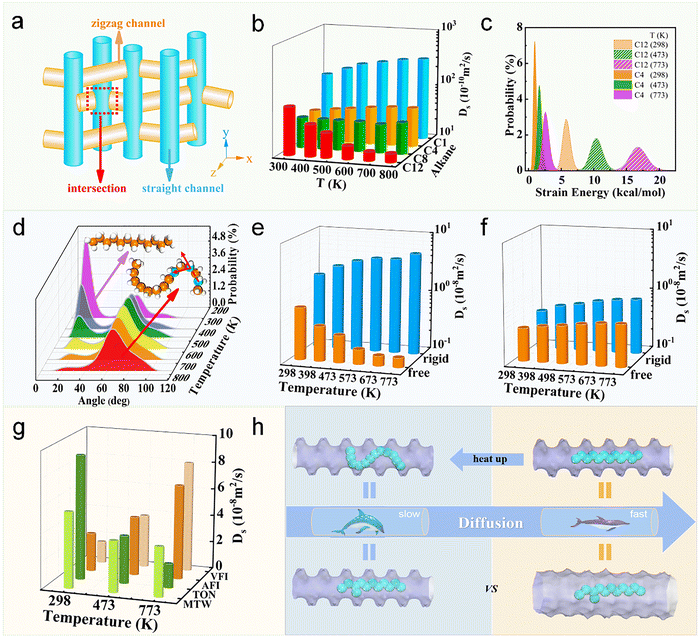 | ||
| Fig. 15 Conformational flexibility and the thermal resistance effect of n-alkanes in zeolites. (a) Three-dimensional channels of MFI zeolite. (b) Ds of methane (C1), n-butane (C4), n-octane (C8), and n-dodecane (C12) in MFI zeolite at different temperatures by MD simulation. (c) Distributions of strain energy for alkane molecules at 298, 473, and 773 K. (d) Distributions of distorted angle for n-dodecane at various temperatures. (e) Ds of rigid C12 and free C12. (f) Ds of rigid C4 and free C4. (g) Ds of C12 inside MTW, TON, AFI, and VFI zeolites. (h) The scheme of thermal resistance effect (TRE) for C12 molecule diffused inside zeolite channels at low and high temperatures. The diffusion resistance of linear-chain molecules at high temperatures is equivalent to that of the branched-chain configuration, which induces slow diffusion under confinement.153 Reproduced from ref. 153, licensed under CC BY 4.0. | ||
While experimental techniques can characterize the flexibility of both molecules and zeolites, quantitatively assessing their impact on diffusion remains highly challenging. Theoretical calculations offer distinct advantages in investigating how molecular and framework flexibility influence diffusion behavior. Future studies should integrate both experimental and computational approaches to precisely quantify the respective contributions of molecular flexibility and framework flexibility to diffusion processes.
2.4. Emergent diffusion mechanisms under confinement
Beyond classical diffusion mechanisms, the nanoconfined environments of zeolites give rise to unconventional and often counterintuitive transport phenomena that challenge traditional theoretical frameworks. Notable examples include the levitation effect,154 molecular path control,155 molecular traffic control,156,157 single-file diffusion,158 resonant diffusion,159 incommensurate diffusion,52,150 thermal resistance effect,153 molecular trapdoor,147 and so on.61,160 These emergent behaviors arise from complex guest–host interactions within the intricate structural landscapes of zeolitic frameworks, showcasing the remarkable diversity of molecular motion under nanoconfinement. In the following sections, we present a review of these anomalous diffusion mechanisms, addressing their fundamental origins and implications for both diffusion science and the rational design of nanoporous materials.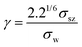 | (1) |
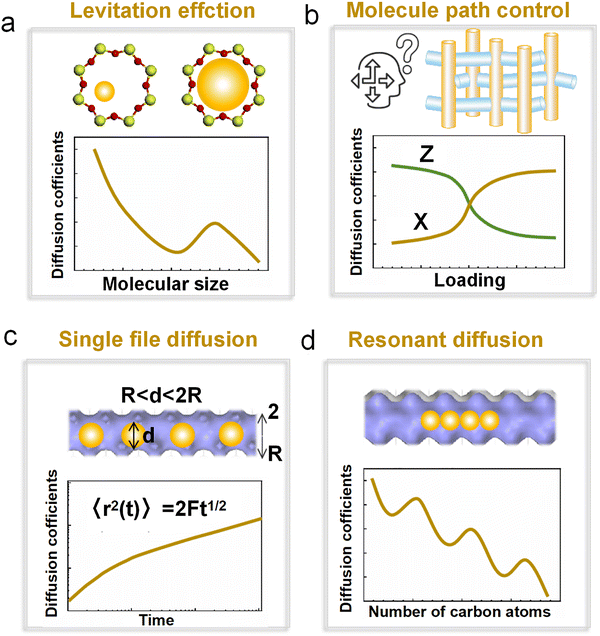 | ||
| Fig. 16 Schematic illustrations of unconventional diffusion phenomena in zeolite-confined spaces: (a) levitation effect; (b) molecular path control; (c) single-file diffusion; (d) resonant diffusion. | ||
Here, σsz represents the sorbate-zeolite Lennard-Jones interaction diameter, and σw corresponds to the window diameter (defined as the oxygen center-to-center distance). As shown in Fig. 17a, the diffusion coefficient exhibits a pronounced maximum when γ ≈ 1, confirming the existence of the levitation effect (also termed the “ring effect”) where molecular transport is optimized. In a comprehensive follow-up study, Yashonath et al. extended this analysis to VPI-5 and silicalite zeolites, comparing their results with Derouane's original framework.162 While the precise γ value for maximal diffusion varied between different zeolite topologies, the fundamental relationship between diffusion enhancement and molecular confinement remained consistent. This systematic investigation validated Derouane's conceptual model as a universal principle governing molecular transport across diverse zeolitic frameworks, independent of their specific structural characteristics.
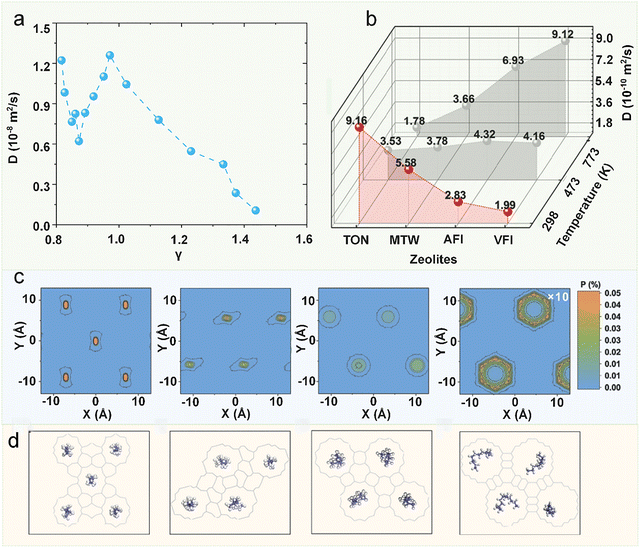 | ||
| Fig. 17 The levitation effect in zeolites. (a) Plot of the diffusion coefficient vs. γ in silicalite zeolite.162 Reproduced from ref. 162 with permission from (American Chemical Society), copyright 1995. (b) Diffusion coefficients of n-C12H26 in 1D channel zeolites by MD simulation. (c) The probability of n-C12H26 molecule distribution in the radial plane of the zeolite channel. (d) Corresponding structure diagram of a random frame of n-dodecane diffusion in zeolite, with TON, MTW, AFI, and VFI zeolite from left to right.66 Reproduced from ref. 66, licensed under CC BY 4.0. | ||
Both the “floating molecule” concept and levitation effect underscore the critical role of size matching between adsorbates and zeolite frameworks in governing confined diffusion. Since its discovery, the levitation effect has been widely explored and utilized in molecular separation processes. In 1997, Yashonath and coworkers systematically examined the impact of temperature163 and concentration164 on levitation-mediated diffusion by molecular simulation. Their work revealed that temperature serves as a crucial regulatory parameter, enabling selective control over the transport of differently sized molecules. This finding established thermal modulation as a potential switching mechanism for molecular separations. Further expanding this paradigm, the same group demonstrated in 2010 that branched pentane isomers exhibit anomalously higher diffusivity than linear n-pentane—a counterintuitive behavior explained within the levitation effect framework through a combination of QENS experiments and MD simulations.165 These collective findings not only validate the universality of size-dependent diffusion in zeolites but also highlight its practical implications for designing selective separation processes.
However, for long-chain molecules, their structural flexibility leads to continuous bending and deformation during diffusion, making it challenging to match their size with the pore dimensions to satisfy the conditions for levitation diffusion. Addressing this issue, Yuan et al.66 in 2023 proposed a strategy to limit the bending deformation of long-chain molecules by precisely regulating the pore size of zeolites, thereby enabling ultrafast diffusion in confined channels (Fig. 17b). Zeolites with smaller pore sizes facilitate the maintenance of linear configurations in long-chain alkanes, confining their movement to the center of the pores. In contrast, larger pore size leads to increased molecular bending and deformation, resulting in strong adsorption to the pore walls and significant tilting (Fig. 17c and d). Consequently, long-chain alkanes exhibit faster diffusion in zeolites with smaller pore sizes. This result was further validated using uptake curve measurements and infrared spectroscopy.
In conclusion, diffusion within confined spaces is strongly correlated with the match between the pore dimensions and the size of the adsorbed molecules. To achieve ultrafast diffusion, it is essential to identify the optimal balance, which requires in-depth mechanistic studies. This underscores the importance of understanding the interplay between molecular diffusion and pore structure in designing advanced materials for efficient molecular separation and transport.
Similar MPC phenomena have also been observed in the novel SCM-15 zeolite system.80 The SCM-15 zeolite exhibits exceptional connectivity characteristics (Fig. 18a): while the Y/Z channels intersect with the X channels but remain disconnected from each other (forming discrete intersecting channels), the X-direction maintains continuous connectivity with both Y and Z channels, with all atomic sites located at channel intersections-hence termed as “continuum intersecting” channels. This unique architecture gives rise to concentration-dependent diffusion path switching: at low concentrations, molecules preferentially diffuse along the discrete channels (Z-direction), whereas high concentrations favor transport through the continuum intersecting channels (X-direction) (Fig. 18b). The diffusion process is fundamentally governed by the energy landscape along different pathways. Generally, more uniform channel structures correspond to smoother potential energy profiles and lower diffusion barriers, consequently enabling faster molecular transport. In SCM-15, the continuum X-direction channels demonstrate remarkable structural uniformity, exhibiting smooth potential energy curves and exceptionally low diffusion barriers (Fig. 7c left), thereby facilitating rapid diffusion. In contrast, the discontinuous Z-direction channels show structural heterogeneity with strong adsorption sites, resulting in significantly higher diffusion barriers (Fig. 7c, right) and consequently slower molecular transport.
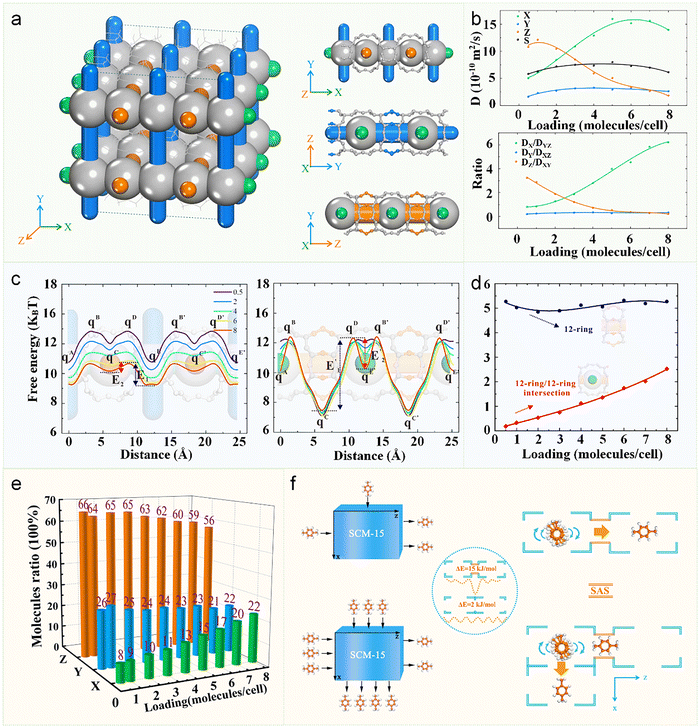 | ||
| Fig. 18 Molecular path control of p-xylene in SCM-15 zeolite. (a) 3D channels in the SCM-15 zeolite (left). 1D channels along the X (top), Y (middle), and Z directions (bottom). The small blue and orange balls represent atoms in the Y and Z channels, respectively. (b) Variations in the anisotropic diffusivity of p-xylene molecules inside the SCM-15 zeolite as a function of loading along the X, Y, and Z directions and as a function of total loading at 298 K (top), and variations in anisotropic diffusion coefficient ratio of p-xylene molecules as a function of loading (bottom) by MD simulation. (c) Free energy profiles of p-xylene diffusion along the X and Z directions. (d) Variations in the free energy barriers as a function of loading along the Z directions. (e) Molecular percentage of p-xylene molecules located in X, Y, and Z channels at different loadings. (f) Mechanism of p-xylene diffusion in SCM-15 zeolite.80 Reproduced from ref. 80 with permission from (American Association for the Advancement of Science), copyright 2021. | ||
Free energy analysis reveals concentration-dependent diffusion trends. As concentration increases, the X-direction diffusion barrier decreases (Fig. 18c, left), enhancing diffusivity. The Z-direction exhibits minimal change across 12-MR (Fig. 18c, right) but a rising barrier at intersecting pores, reducing diffusivity (Fig. 18d). The three-dimensional distribution of molecules across different channel types plays a pivotal role in determining the overall diffusion coefficients (Fig. 18e). Taking p-xylene as an example, the discrete channels (Y/Z) exhibit stronger adsorption affinity, leading to predominant molecular occupancy at low concentrations. However, with increasing concentration, the continuous X-direction channels demonstrate progressively greater molecular uptake (from 8% to 22% relative distribution), while maintaining their intrinsic diffusion advantage through: (1) increasing molecular population ratio and (2) persistently low diffusion barriers. The synergy between these two factors enables the X-direction to maintain superior diffusion performance across a wide concentration range (Fig. 18f). The phenomenon extends to diverse molecules (methane, n-alkanes, xylenes), with selectivity tunable via pore size matching and framework flexibility. These insights provide a blueprint for designing new zeolites, where concentration-gated diffusion optimizes separations and catalysis.80
The diffusion of molecules in porous materials typically exhibits an inverse correlation with molecular size, primarily due to stronger adsorption energies and increased steric hindrance for larger molecules. Gao et al. employed PFG-NMR to quantify alkane diffusion in DNL-6 zeolite, observing the expected size-dependent trend: CH4 > C2H6 > C3H8.62 Comparative studies revealed significantly slower diffusion for branched alkanes compared to their linear counterparts, highlighting the impact of molecular geometry.174–176 DeLuca and other groups predicted diffusion based on adsorption energetics, adsorption entropies and diffusion barriers. These predictions confirmed that diffusion is slower for larger molecules in more strongly confining systems.177–180
Nevertheless, such size-dependent diffusion trends may deviate under strong confinement conditions. “Resonance diffusion” phenomena exhibit characteristic periodicity in alkane transport properties, showing alternating diffusivity patterns with incremental CH2 unit additions (Fig. 16d).159,181,182 In addition, rotation can also contribute to diffusion.183–185 Kolokathis et al. combined QENS and MD simulations to investigate aromatic diffusion in silicalite-1. Their study revealed an unexpected trend: p-xylene exhibited faster diffusivity than benzene, which they attributed to reduced entropic barriers for the more elongated p-xylene molecule within the zeolite channels.160 Liu and coworkers systematically investigated the diffusion of meta-difluorobenzene (C6H4F2), meta-fluorobromobenzene (C6H4FBr), and meta-dibromobenzene (C6H4Br2) in both liquid-phase (Fig. 4d) and zeolites (Fig. 19a).61 Their study revealed a striking contrast in diffusion behavior between these environments: Liquid-phase diffusion followed the conventional trend of decreasing mobility with increasing molecular size and intermolecular interactions (Fig. 4e: C6H4F2 > C6H4FBr > C6H4Br2). Zeolite-confined diffusion exhibited a counterintuitive sequence: C6H4F2 > C6H4Br2 > C6H4FBr (Fig. 19b). MD simulations traced this anomaly to asymmetric molecular rotation (Fig. 19c), where: non-symmetric molecule-zeolite interactions drive asymmetric molecular rotation in confinement. 2D free energy landscapes revealed that such rotation suppresses translational diffusion (Fig. 19d). In narrow AFI channels, confinement effects selectively restrict C6H4Br2 rotation, paradoxically enhancing its mobility over C6H4FBr. This phenomenon was exclusive to confined spaces (Fig. 19e; AFI, MAZ) and corroborated by uptake rate experiments (Fig. 19f) and 2H solid-state NMR spectra (Fig. 19g), which directly linked rotational symmetry to diffusion differences. Although theoretical simulations have revealed intriguing diffusion phenomena in zeolites, experimental validation has so far been limited to certain cases, as detecting anomalous diffusion experimentally remains a significant challenge.54,186
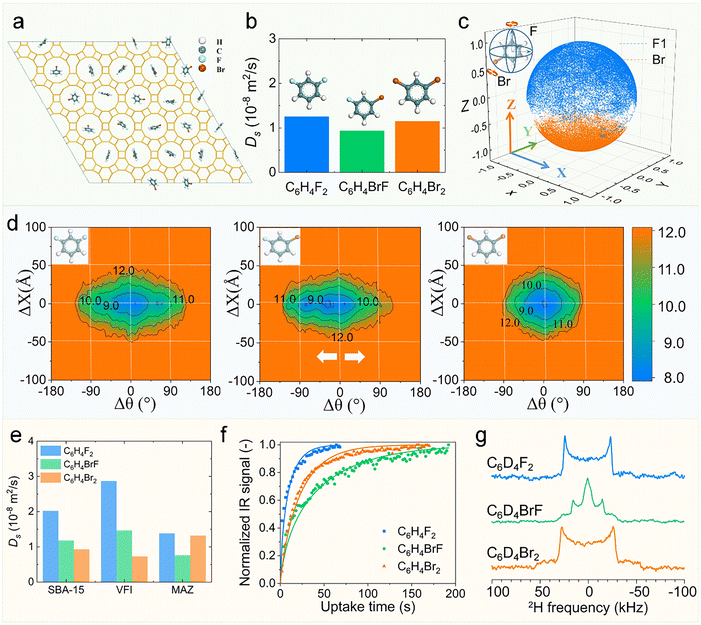 | ||
| Fig. 19 Effects of molecular symmetry on diffusion under confinement. (a) Initial structures of C6H4BrF inside AFI zeolite. (b) Ds for various molecules inside AFI zeolite by MD simulation at 298 K. (c) Three-dimensional trajectory of normalized C–F and C–Br bond vector for C6H4BrF in AFI zeolite. (d) Two-dimensional free energy contour plots correlate rotational angle difference (Δθ) and translational displacement (ΔX) for C6H4F2, C6H4BrF, and C6H4Br2 in AFI zeolite, at a time interval of 100 ps. (e) Ds for C6H4F2, C6H4BrF, and C6H4Br2 inside SBA-15 model, microporous zeolites with VFI and MAZ topologies at 298 K by MD simulation. (f) Uptake rate curves of C6H4F2, C6H4Br2 and C6H4BrF molecules at 298 K by synchrotron radiation-based infrared microscope (SR-IRM). (g) 2H solid-state NMR spectra of C6D4F2, C6D4BrF and C6D4Br2 in AlPO4-5 at 298 K.61 Reproduced from ref. 61, licensed under CC BY 4.0. | ||
The trapdoor effect of zeolites was first observed in a small-pore chabazite (CHA) zeolite that can even perform “size-inverse” separation.147 Cs-CHA exhibits significant CO2 adsorption at 195 K despite negligible CH4/N2 uptake below their critical temperatures (Tc = 343 K and 333 K, respectively). This deviation from classical adsorption-temperature trends led to the “molecular trapdoor” mechanism, where selectivity arises from cation dynamics rather than static pore exclusion. In CHA frameworks, Cs+ or K+ occupy SIII’ sites in the 8-MR windows (3.8 × 3.8 Å), narrowing apertures to <3.3 Å due to their large ionic radii (Cs+: 3.34 Å). While this would block CO2 (3.3 Å) statically, CO2's polarizability induces transient cation displacement: adsorption weakens the potential well anchoring Cs+, enabling partial migration toward the 8-MR interface. This metastable “open” state permits CO2 diffusion into supercages before cation reversion—a trapdoor-like gating process (Fig. 20a). The mechanism redefines molecular transport in zeolites, linking selectivity to dynamic cation-gated diffusion rather than rigid pore geometry. Its efficacy hinges on cation identity and process conditions (temperature, pressure), motivating fundamental studies into the interplay of cation mobility, guest interactions, and system thermodynamics—key to tailoring next-generation separations.147
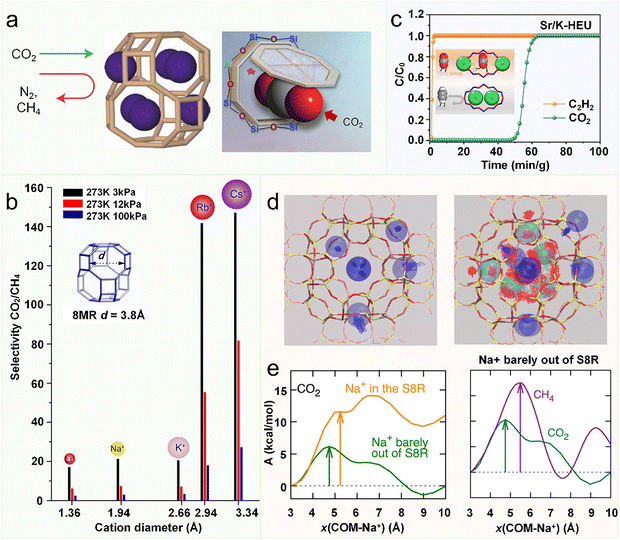 | ||
| Fig. 20 The molecular trapdoor mechanism in cation-containing zeolites. (a) Schematic illustration of the “molecular trapdoor” mechanism.147 Reproduced from ref. 147 with permission from (American Chemical Society), copyright 2012. (b) Adsorption selectivity of CO2/CH4 on Si/Al ratio = 2 chabazites with different cation types derived from equal molar single component adsorption isotherms, at 273 K and variable pressures.191 Reproduced from ref. 191 with permission from (American Chemical Society), copyright 2013. (c) Column breakthrough curves of CO2/C2H2/He over a fixed-bed reactor packed with Sr/K-HEU at 298 K.194 Reproduced from ref. 194 with permission from (John Wiley and Sons), copyright 2025. (d) The traces of cations in a simulation without adsorbates (on the left) and the traces of cations and CO2 molecules in a simulation with 15 molecules of CO2 (on the right). (e) Free energy profile for a guest molecule entering the single 8-ring (S8R) of RHO by AIMD simulation.189 Reproduced from ref. 189 with permission from (American Chemical Society), copyright 2017. | ||
Gate-keeping cations act as pivotal determinants in selective adsorption and diffusion within molecular trapdoor systems. Webley and colleagues191 conducted systematic mapping of compositional thresholds for trapdoor effects in chabazite zeolites, demonstrating that cation size and density govern accessibility to zeolitic supercages. Their investigation of alkali and alkaline-earth cation-exchanged variants revealed that only cations with ionic radii matching or exceeding K+ (e.g., Rb+, Cs+, and divalent Ba2+) achieve effective 8-MR aperture blocking while permitting CO2-triggered transient displacements, as evidenced by adsorption selectivities of CO2/CH4 (Fig. 20b). Smaller cations such as Na+ or Li+ predominantly occupy intra-cage positions rather than 8-MR centers, allowing unimpeded diffusion of nonpolar species like N2 and CH4, leading to a low selectivity. This size-dependent selectivity stems from coordination preferences: K+ and larger ions stabilize at 8-MR sites through optimized electrostatic interactions with framework oxygens, while smaller cations migrate to lower-energy positions within supercages. The study further established a quantitative design principle—effective trapdoor functionality requires a minimum of nine univalent cation equivalents per unit cell (Si/Al < 3) for complete 8-MR occupation. This criterion is mathematically expressed as 1 ≥ Y ≥ 0.25X + 0.25 (X = Si/Al ratio; Y = fraction of door-keeping cations), delineating a compositional regime where each aperture remains cation-guarded. These findings highlight the necessity for dual optimization of cation dimensions and spatial distribution to achieve precise molecular differentiation.
Recent advancements have extended cation-mediated trapdoor effects to highly challenging separations involving gas pairs with overlapping physical properties, such as CO2–C2H2 (similar kinetic diameters, polarizabilities, and boiling points). Pioneering work by Li and coworkers194 demonstrated reverse-selective CO2–C2H2 separation in Sr/K-HEU zeolites via molecular trapdoor mechanisms, achieving record selectivity (48.0) through Sr2+ cation gating (Fig. 20c). Three-dimensional electron diffraction (3D ED) and DFT calculations elucidated Sr2+ dynamics in 10-MR channels (Channel A) and interaction disparities with gas species. Sr2+ resides in channel A, forming a gated structure. Strong CO2–Sr2+ interactions (dipole-cation forces) induce transient Sr2+ displacement, opening the channel for CO2 ingress, followed by rapid cation repositioning to seal the pore. In contrast, C2H2's lower polarity and planar molecular geometry weaken interactions with Sr2+, creating an insurmountable energy barrier (>200 kJ mol−1 by DFT) for gate activation. Notably, residual K+ in Sr/K-HEU partially offsets selectivity by enabling minor C2H2 diffusion. This study exemplifies how rational cation engineering—harnessing ionic size and charge synergistically—enables trapdoor systems to address intricate separations where conventional size-sieving fails due to molecular property convergence.
Early mechanistic models attributed trapdoor effects to direct guest–cation interactions, as previously discussed, proposing that strongly adsorbing species like CO2 physically “pull” cations away from pore apertures. However, AIMD simulations by Coudert and Kohen189 challenged this explanation and proposed a “swinging door” mechanism. Their results revealed that CO2 permeation arises from electrostatic interactions with the framework and the exploitation of transient pore openings created by the thermal motion of the cations. Their simulations (Fig. 20d, CO2-free system) demonstrated intrinsic thermal fluctuations of Na+ cations near S8R and S6R sites, with trajectory analysis showing ∼1 Å displacements independent of CO2 presence—evidence that cation dynamics occur spontaneously without guest triggering. In CO2-loaded systems (Fig. 20d), CO2 preferentially adsorbed at S8R sites, forming stabilized Na+–CO2 pairs (shortened interatomic distances), yet Na+ positions shifted minimally (0.5 Å average displacement), contradicting the “cation-pulling” hypothesis. Free energy analysis for S8R permeation revealed a critical coupling mechanism: when Na+ thermally deviates from its equilibrium position (constraint radius shifts from 5.76 Å to 4.68 Å), CO2's diffusion energy barrier drops from 48.5 kJ mol−1 to 25.9 kJ mol−1, indicating cation fluctuations create transient opportunities for CO2 ingress (Fig. 20e). Under identical conditions, methane demonstrates a substantially higher diffusion energy barrier (∼75.2 kJ mol−1) compared to CO2, owing to its lack of strong electrostatic interactions with S8R sites and incapacity to utilize transiently opened pores. This work atomically unravels the coupling mechanism between cation thermal fluctuations and molecular diffusion that advances the design of selective adsorbents and highlights AIMD's utility in unraveling complex dynamic processes.
External stimuli such as temperature and pressure critically govern molecular diffusion to enable efficient separations in the trapdoor zeolites. Temperature-regulated adsorption in zeolites manifests as a gate-opening phenomenon where gas molecule access to internal pores requires surpassing a critical threshold temperature (T0). May et al. developed a theoretical framework describing thermally activated guest admission, revealing that thermal fluctuations of pore-guarding cations (e.g., K+ in CHA) enable transient doorway opening via dynamic displacement from equilibrium positions when exceeding T0.126 Li and coworkers recently demonstrated that K-ZSM-25 zeolite exhibits a unique “molecular trapdoor” mechanism for selective N2/CH4 separation, driven by temperature-regulated diffusion dynamics.149 The accessibility of 8-MR pores is controlled by the thermal oscillation of “gate-keeping” K+ cations. Below 173 K, restricted K+ mobility blocks pore access, while increasing temperature enhances K+ vibrations, gradually opening diffusion pathways (Fig. 21a). Structural analysis reveals four distinct diffusion channels in ZSM-25, each formed by interconnected cages through 8-MR windows (Fig. 21b). Among these, the first channel—comprising grc-opr and pau-opr cages—emerges as the primary diffusion pathway due to its lower energy barrier (109 kJ mol−1 for K+ displacement in pau-opr vs. 164 kJ mol−1 in other channels) (Fig. 21c). The pau-opr cage acts as the rate-limiting step, requiring sufficient thermal energy to overcome K+ blocking. DFT calculations show that N2, with its smaller kinetic diameter (3.64 Å), permeates with minimal K+ displacement (2.8 Å) at 173 K, overcoming a modest diffusion barrier (95.5 kJ mol−1) (Fig. 21d and e). In contrast, CH4 (3.8 Å) demands higher temperature (353 K) and greater K+ displacement (3.1 Å) to surmount a 111.9 kJ mol−1 barrier. This temperature-dependent sieving enables K-ZSM-25 to achieve exceptional N2/CH4 selectivity (up to 34) within an industrially viable range (240–300 K), bypassing energy-intensive cryogenic distillation. Beyond temperature, external stimuli such as pressure gradients and electric fields have emerged as additional control parameters for tuning trapdoor-mediated diffusion, expanding the toolbox for designing adaptive separation systems.193,196,197
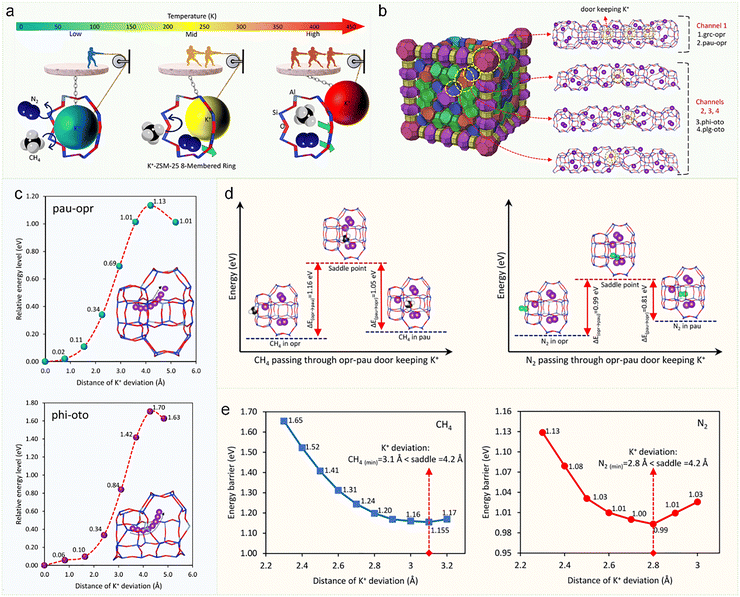 | ||
| Fig. 21 Molecular trapdoor mechanism in ZSM-25. (a) Schematic illustration of the “molecular trapdoor” mechanism for temperature-regulated diffusion. (b) 3D view of the ZSM-25 and four unique channels connected through 8-MR as the main routes for gas diffusion consisting of four double-connected cages. (c) Minimum energy pass of door-keeping K+ movement from its most stable site to the nearest secondary stable site in pau-opr (top) and phi-oto (bottom). (d) DFT-calculated energy barriers of the gas molecule passing through blocked opr-pau cages. Energy level for forward and reverse movement of CH4 (left) and N2 (right) through double-connected cages. (e) Energy barrier of gas diffusion as a function of K+ deviation for CH4 (left) and N2 (right).149 Reproduced from ref. 149 with permission from (American Chemical Society), copyright 2021. | ||
Although the existence of surface barriers and their impact on membrane separation and catalysis have been well demonstrated experimentally and computationally, the origin and mechanism of these barriers remain controversial.37,42 This is basically because the surface barrier is highly sensitive to the imperfection of crystal surface originating from its physical and chemical properties such as terminal silanol groups, defect sites, etc.203,214 Besides, even some gentle modifications like SiO2 introduction and/or fluoride etching can greatly alter the surface barriers of the zeolites. Peng et al. proposed that this is just one of the reasons why the reaction performance of zeolites changes after they are transformed into industrial catalysts through forming techniques.60,215 Furthermore, the complexity of surface barrier nature also stems from its high diversity at single crystal scale. Kärger et al. recorded the methanol intracrystalline concentration profiles of two similar SAPO-34 at single-crystal scale via interference microscopy technique (IFM), and the results revealed that the surface barrier of every zeolite crystal is highly individualization.216
Fan et al.202,217–219 proposed three paradigmatic physical models to rationalize the surface barrier diffusion (Fig. 22a). Generally, the total diffusion process can be regarded as a linear combination of both intracrystalline diffusion and the diffusion through the surface, and each of them obeys Arrhenius relationship. (1) For Pore Narrowing Model: the zeolitic micropore mouths at the outer surface are assumed to be narrowed or partially clogged. When the guest molecules traverse such surface layer, more activation energy has to be consumed. Therefore, the key point of such mechanism is an increased surface diffusion energy, which is the origin of this type of surface barrier model; (2) For Pore Blocking Model: given the zeolitic pore mouths have been totally blocked in this mechanism model, the guest molecules have to bounce back at the choked pore mouth, and continue to diffusion within the zeolitic microporous framework near the surface until finding out another open pore mouth. Obviously, the diffusion activation remains unchanged because the micropore mouth aperture does not change. The surface barrier can be regarded as the consumption for such additional intracrystalline diffusion. Since both of the aforementioned mechanistic models are related to changes in the structural properties of the zeolite micropores near the pore mouths on the surface, they are also referred to as “Structural Surface Barriers”. (3) Kinetic Desorption Model: in contrast to the two structural surface barrier models, the Kinetic Desorption Model, as the non-structural surface barrier model, emphasizes the effects of strong adsorptive interaction between zeolite crystal surface and guest molecules. For some types of the adsorbate molecules, their surface interaction is so high that the probability of the guest molecules to escape to the guest phase is rather rare. Instead, they have to diffuse along the external surface of the zeolite crystal and may re-enter the microporous framework, restarting a new round of attempt journey to desorb from the microporous zeolitic crystal into the gas phase. In this case, the kinetic desorption process is rate-determining, constituting the origin of the “Non-Structural Surface Barriers”.
 | ||
| Fig. 22 Surface barriers and their modification in zeolite membranes. (a) Schematic models for surface barriers in zeolite materials.219 Reproduced from ref. 219 with permission from (American Chemical Society), copyright 2019. (b) The permeation frontiers (inferred by dash-dot lines) for the 0, 20%, 40%, 60%, and 80% of amino silane coupling agent (ASCA) modified DD3R zeolite membrane materials.234 (c) The wetting modes for the unmodified DD3R zeolite membrane materials.234 Reproduced from ref. 234 with permission from (Elsevier), copyright 2025. | ||
As a classical application where diffusion is of vital importance, zeolite membrane has been recruited in many adsorptive separation occasions,220 such as removal of CO2 or H2 from gas mixtures,221–226 zeolitic membrane reactor for selective CO2 conversion to methanol,227,228 separation of xylene isomer,229 enrichment of radioactive krypton-85 isotope,230 separation of SO2/NO2,231,232etc. The gas diffusion behavior in zeolite membrane systems differs significantly from other types of membrane materials since surface barrier plays pivotal roles in controlling the permeability.233 Both structural and non-structural surface barriers control the permeability and separation selectivity of zeolite membrane. For example, Tu et al.234 reported theoretical research on explaining the transformation mechanism of ZSM-5 zeolite membrane from hydrophilicity to hydrophobicity by applying amino silane coupling agent (ASCA) as surface modifier at molecular scale, which can be seen as a case to showcase the influence of structural surface diffusion barrier. The simulation results indicate that the water flux (indexed as the permeation frontiers) of ZSM-5 zeolite membrane gradually decreases with increasing coverage due to ASCA surface modification (Fig. 22b). The authors elaborated on the aforementioned issues from the alteration of water storage property, surface wettability, and the interaction between water molecules and zeolitic surface atoms: the water storage capacity of zeolites originates from the presence of surface cavities, as they increase the adsorption sites for water molecules. Additionally, the existence of polar oxygen atoms is responsible for the hydrophilic nature of the bare ZSM-5 zeolite surface. Wetting process is characterized by water molecule filling, spreading, and the alteration thereof (Fig. 22c). During this process, the interconnected channel system of the zeolite allows further penetration of water molecules, thereby further enhancing its water absorption potential. However, when ASCA modifier is introduced, it inherently introduces hydrophobic alkyl groups on one hand, and reduces the exposed pore area on the zeolite surface on the other hand. These changes significantly weaken the water storage and wetting capabilities of the surface modified zeolites. Moreover, the O and N atoms in ASCA modifier can form hydrogen-bonding networks with water molecules, which further restricts the movement of liquid droplets, retarding the water molecule permeation.
3. Confined diffusion affects catalytic performance
The confinement-mediated diffusion mechanisms discussed above extend their influence on catalysis, where controlled transport of reaction species through the pore architecture enables fine-tuning of shape selectivity30,235–237 and sorption equilibrium238 at the molecular level.3.1. Diffusion-controlled shape selectivity
Shape-selective catalysis relies on the synergy between zeolites’ well-defined pore structures and molecular diffusion dynamics to control reaction outcomes.239 The diffusion of reactants, intermediates, and products plays a pivotal role in product shape selectivity.236,240 Reactants must effectively diffuse to active sites to undergo catalytic conversion, while products require efficient diffusion away from active sites to prevent pore blocking and enable continuous production (Fig. 23a).62,241 The SAPO-34 zeolite exhibits excellent selectivity for ethene and propene, while demonstrating remarkably low yields of C4+ products (e.g., butene).242 Van Speybroeck and coworkers systematically investigated diffusion phenomena during MTO conversion, revealing distinct diffusion barriers of 20 kJ mol−1 for propene and 40 kJ mol−1 for ethene in SAPO-34, with ethene displaying faster diffusion kinetics (Fig. 23b left). Notably, the formation of aromatic hydrocarbon species within the zeolite framework dramatically increases the diffusion barrier for propene to >150 kJ mol−1 (Fig. 23b right). This dual diffusion limitation explains the scarcity of 1-butenes in the product distribution: 1-butenes as products face significant diffusion resistance, and propene encounters difficulties diffusing to active sites for further chain growth to form 1-butenes.35 | ||
| Fig. 23 Diffusion-mediated shape selectivity in zeolite-catalyzed reactions. (a) Schematic of shape selectivity in the methanol-to-olefins (MTO) process, illustrating how product distribution is governed by cavity-controlled diffusion.62 Reproduced from ref. 62 with permission from (Elsevier), copyright 2019. (b) Free energy profiles for ethene/propene diffusion through SAPO-34 (left) and for propene diffusion through an 8-ring of H-SAPO-34 with cage B contains a hydrocarbon pool species.34 Reproduced from ref. 34, licensed under CC BY 4.0. (c) Schematic shown diffusion-improved selectivity of ethene.243 Reproduced from ref. 243, licensed under CC BY 4.0. (d) Free energy profile of the movement of the acylium ion from the side pocket to the 12-MR channel without MeOH or DME in the 12-MR channel (left), previously occupied by DME and the further formation of MAMe+ (middle), and previously occupied by MeOH and the further formation of MAH+ (right).244 Reproduced from ref. 244, licensed under CC BY 4.0. | ||
Recent studies employing advanced computational and experimental techniques have also reported similar hydrocarbon pool (HCP)-induced diffusion behavior that can change the reaction pathway of MTH. Yang et al. demonstrated that the nonuniform mesoscale spatial distribution of aromatic HCP species in SAPO-34 zeolite critically modulates olefin selectivity during MTO processes (Fig. 23c). Ethene, with a lower diffusion energy barrier, exhibits faster transport compared to propene, leading to prolonged retention of propene within channels. This extended residence time facilitates secondary reactions such as methylation or coke formation, thereby indirectly enhancing ethene selectivity. Kinetic Monte Carlo simulations using a simplified cubic mesoscale model revealed that increasing the proportion of aromatic layers (0.1–0.7) exacerbates the diffusion time disparity between propene and ethene. Phenanthrene exhibited the highest propene-to-ethene diffusion time ratio (24.0), due to its bulky polycyclic structure. Spatial analysis further indicated preferential accumulation of aromatics at the zeolite periphery, creating interfacial diffusion bottlenecks that couple reaction and transport processes. This spatial confinement promotes cyclization of retained olefins into polyaromatic hydrocarbons (PAHs), consistent with experimental observations of edge-dominated aromatic deposition in SAPO-34 and accelerated catalyst deactivation via coke formation.243 Based on the transition state theory, Gao et al. proposed a model, which considers the molecular translation and rotation within nano-channel and overcoming the energy barrier of nano-window, to accurately predict the intracrystalline diffusivity of molecules within different zeolites.177 In addition, combining this model with reaction kinetics, the shape selectivity of MTH reactions can be forecasted.245,246 Intriguingly, reactant (e.g., ethanol) diffusion was found to facilitate the transport of intermediates (e.g. acylium ion) by effectively lowering their diffusion energy barriers, thereby promoting product (e.g. methyl acetate formation) shape selectivity during the carbonylation in mordenite (MOR) zeolite (Fig. 23d).244
Besides SAPO-34, HZSM-5 also exhibits remarkable shape selectivity due to its unique pore structure featuring both straight channels and sinusoidal channels with distinct dimensional characteristics. This has made the highly selective production of p-xylene (while minimizing m-xylene and o-xylene formation) in toluene alkylation reactions one of the few persistent industrial challenges in the chemical field.247 Ma et al. addressed this issue by developing an HZSM-5 zeolite with an inverse aluminum zoning distribution, where the sinusoidal channels primarily open to the crystal surface, thereby maximizing their shape-selective effect. Their synthesized twinned HZSM-5_T crystals exhibit an acid site density gradient that decreases from the core to the surface. In this “acid-core” structured HZSM-5_T, xylene molecules must diffuse through the sinusoidal channels, preferentially forming p-xylene molecules. The scarcity of acid sites on the external surface and near pore openings creates a deficiency of active reaction centers, effectively suppressing non-shape-selective reactions. This structural characteristic proves crucial for achieving high p-xylene selectivity in the final product.248
Yang et al. further employed AIMD simulations and free energy sampling methods to investigate toluene methylation with methanol in HZSM-5 zeolites. Their study examined the role of diffusion in determining p-xylene selectivity, revealing how diffusion barriers compete with isomerization to dictate product distribution. The key reaction steps and intermediates are illustrated in Fig. 24a and b. The results demonstrate that the straight channels of the zeolite facilitate the diffusion of p-xylene (PX) and m-xylene (MX), with diffusion barriers of 19.4 kJ mol−1 and 23.2 kJ mol−1, respectively (Fig. 24c). However, in the zigzag (sinusoidal) channels, MX exhibits a significantly higher diffusion barrier (46.8 kJ mol−1) compared to PX (15.9 kJ mol−1). Moreover, a dynamic competition arises between diffusion and isomerization processes at active sites. For p-xylene, isomerization presents a much higher energy barrier than diffusion in HZSM-5, causing PX to preferentially diffuse out of the zeolite rather than undergo isomerization (Fig. 24d, left). In contrast, m-xylene faces a diffusion barrier along the zigzag channel that is substantially higher than its isomerization barrier (Fig. 24d, right). As a result, MX tends to isomerize into PX rather than diffuse. Thus, enhancing the sinusoidal (zigzag) channel structure favors higher PX selectivity.249
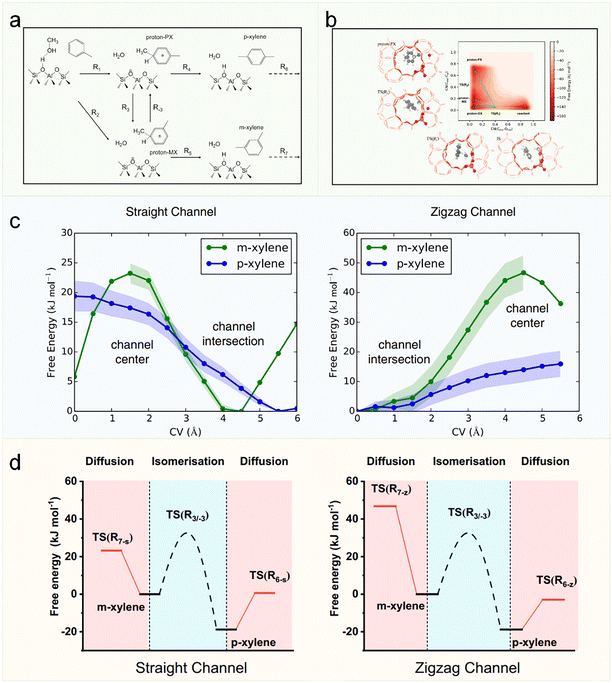 | ||
| Fig. 24 Reaction and diffusion pathways for shape-selective xylene production in HZSM-5. (a) Reaction pathways of toluene methylation in the pores of HZSM-5. (b) Two-dimensional free energy profile of the methylation of toluene. (c) Free energy profiles with a standard deviation of p-xylene and m-xylene diffusing along straight channel (left) and along zigzag channel (right) obtained from blue-moon simulations. (d) The simplified mechanistic framework of toluene methylation to p-xylene and m-xylene by combining the isomerization and diffusion along straight and zigzag channels.249 Reproduced from ref. 249, licensed under CC BY 4.0. | ||
3.2. Concentration-enhanced reaction
Beyond controlling product shape selectivity, the pore confinement effect can spatially concentrate reactants and intermediates near active sites, thereby increasing effective collision frequency and substantially enhancing catalytic performance.179 Early studies demonstrated that the pore confinement effect in zeolites enables methane enrichment concentrations exceeding 10 times ambient levels under standard temperature and pressure conditions.12,38 Mason et al. demonstrated that Silicalite-1 can selectively enrich oxygen when immersed in an aqueous solution (water).250 The confined spaces within zeolite frameworks not only facilitate directional diffusion of guest molecules along pore walls, but also significantly enhance contact probability and collision frequency between reactive species and active sites.75 This unique molecular transport behavior contributes to superior catalytic performance in zeolite-mediated reactions. Liu et al. demonstrated that the confined 8-MR pockets in MOR zeolites facilitate reactant (i.e., CO) enrichment, which promotes molecular collisions at active centers and consequently elevates carbonylation activity.251The most representative enrichment strategy involves the construction of “molecular fences” that create spatial confinement, effectively trapping key reactive species near active centers by strategically restricting their outward diffusion pathways. Xiao et al. developed an innovative “molecular fence” catalyst design strategy to address the challenge of low-temperature methane oxidation (Fig. 25a). By engineering a zeolite-encapsulated metal nanoparticle catalyst with a molecular-scale hydrophobic shell, they discovered that controlling the diffusion of hydrogen peroxide (H2O2) intermediates was critical for enhancing reaction efficiency. This unique architecture selectively confines H2O2 within nanoscale compartments while permitting unimpeded methane access, thereby promoting continuous methanol production through sustained in situ reactions.252
 | ||
| Fig. 25 (a) Molecular fence strategy: gaseous reactants/products diffuse freely, while H2O2 intermediates are concentrated to boost reactivity (top), and a scheme shows the molecular diffusions in the methane oxidation process. The thickness of the arrows represents the diffusion amount (bottom).252 Reproduced from ref. 252 with permission from (American Association for the Advancement of Science), copyright 2020. (b) Number of ethene molecules in free space and zeolite during the diffusion process (left) and adsorption structure and energy of ethene in S1 and S1-OH zeolites (right). (c) Kinetic reaction order in olefin (left) and CO (right).253 Reproduced from ref. 253, licensed under CC BY 4.0. (d) Calculation results of diffusion coefficients in gas (left), toluene and mesitylene (middle), and zeolite region in toluene and mesitylene (right) by MD simulation.254 Reproduced from ref. 254 with permission from (American Chemical Society), copyright 2025. | ||
In addition to intermediate accumulation, the inherent adsorption-diffusion characteristics of zeolites enable spatial concentration gradients of reactants, which significantly enhance catalytic efficiency through increased active site accessibility. The strategic incorporation of hydroxyl nests in Rh/S-1 zeolites enhances hydroformylation TOF, showcasing microenvironment control in Rh catalysis. MD simulations reveal ethene's preferential partitioning into silanol-rich zeolite regions (90% enrichment, Fig. 25b left), driven by stronger adsorption energies (−56.9 kJ mol−1vs. −36.7 kJ mol−1 in silanol-free pores, Fig. 25b right) through hydrogen-π interactions. Despite enrichment, ethene maintains high mobility (Ds = 4.1 × 10−9 m2 s−1 at 110 °C), ensuring efficient transport to Rh sites. Kinetic studies demonstrate saturated ethene coverage on Rh/S-1-OH (zero-order, k = 0.15 ± 0.11) versus first-order dependence on Rh/S-1 (k = 1.10 ± 0.08, Fig. 25c, left), while CO kinetics remain unaffected (1.01 ± 0.10 vs. 0.88 ± 0.13, Fig. 25c, right). This selective olefin enrichment-effect microenvironment exemplifies a new paradigm for regulating substrate availability in zeolite-confined metal catalysis.253
Furthermore, Xiao et al. reported that the solvophobic catalyst with gas-filled micropores could enrich enormous amounts of gas molecules to accelerate Rh@S-1 zeolite catalyzed hydroformylation (Fig. 25d).254 Adsorption measurements revealed that S-1 zeolite in mesitylene solvent dramatically increased gas uptake compared to toluene systems, particularly for hydrogen (50 μmol g−1vs. 17 μmol g−1). This enhancement followed a linear relationship with zeolite content, confirming the micropores’ role as gas reservoirs. MD simulations and methanol displacement experiments provided direct evidence of gas storage within the hydrophobic micropores. Diffusion coefficients calculated through MD simulations showed striking differences between gas, wet and dry zeolite systems. The rapid molecular diffusion in the gas phase is very fast (Fig. 25d, left, 10−5–10−6 m2 s−1). In mesitylene (dry pores), H2, CO, and C2H4 exhibited diffusion coefficients of 1.3 × 10−7, 2.2 × 10−8, and 1.1 × 10−8 m2 s−1 respectively (Fig. 25d, middle)- orders of magnitude higher than in toluene-wetted pores (Fig. 25d, right, 1.1 × 10−8, 8.2 × 10−11, and 5.8 × 10−11 m2 s−1). This accelerated transport in gas-filled pores reduced mass transfer limitations, as evidenced by the higher slope (0.95 vs. 0.80) in the reaction rate vs. catalyst weight relationship. The combined effects of enhanced adsorption and diffusion led to reduced apparent activation energy and altered kinetic reaction orders in mesitylene systems. Notably, the negative ethene reaction order suggested preferential adsorption in micropores over H2 and CO. These findings establish that solvophobic micropores create efficient gas transport pathways while maintaining high gas concentrations near active sites, overcoming traditional limitations in triphase reactions. The hollow zeolite variant further amplified these effects through increased gas storage volume, achieving record productivity.254 Intriguingly, beyond conventional catalysis, zeolites demonstrate remarkable potential in daily-life applications through their molecular enrichment capabilities. A prime example is that H-SSZ-13 zeolite facilitates greenhouse CO2 enrichment, boosting tomato photosynthesis and fruit quality.255
3.3. Product diffusion-governed reaction enhancement
Enhanced product diffusion not only facilitates active site regeneration by rapid product desorption, but also minimizes unwanted product-active site interactions that promote side reactions (e.g., coke formation). Common strategies to optimize diffusion include fabricating nanosheet-assembled zeolites13,256 and engineering hierarchical pore architectures.29,37,59,60 These structural modifications reduce the mean residence time and diffusion path length of reaction species, thereby significantly improving diffusion properties. An alternative effective strategy involves in situ product removal via selective adsorption, which shifts the reaction equilibrium by modulating reactant concentrations, thereby thermodynamically driving the forward reaction.238Early studies primarily focused on qualitative analyses of the interplay between nanosized zeolite dimensions, diffusion properties, and catalytic performance.13 Recently, Pan et al. have established quantitative correlations among zeolite thickness, molecular diffusion rates, and catalytic efficiency metrics by applying the Thiele modulus. Thiele modulus (φ) is a dimensionless index defined by the following equation:  , where L and Deff represent the diffusion length and effective diffusivity, respectively. It reflects the influence of diffusion properties. In contrast, n, cAs, and k denote the reaction order, the concentration at the acidic active sites, and the intrinsic reaction rate constant based on catalyst volume, respectively, accounting for the contribution of the intrinsic kinetics of the studied reaction. Obviously, Thiele modulus reflects the relative contributions between intrinsic kinetics and diffusion properties. Considering that the reacting species can be assumed following the same reaction pathway occurring at specific active sites under the same reaction conditions, allowing the aforementioned intrinsic kinetic parameters to be treated as constants, the Thiele modulus can serve as a quantitative tool for comparing and correlating the molecular diffusion rates with different zeolite sizes. The higher the overall diffusion property parameter
, where L and Deff represent the diffusion length and effective diffusivity, respectively. It reflects the influence of diffusion properties. In contrast, n, cAs, and k denote the reaction order, the concentration at the acidic active sites, and the intrinsic reaction rate constant based on catalyst volume, respectively, accounting for the contribution of the intrinsic kinetics of the studied reaction. Obviously, Thiele modulus reflects the relative contributions between intrinsic kinetics and diffusion properties. Considering that the reacting species can be assumed following the same reaction pathway occurring at specific active sites under the same reaction conditions, allowing the aforementioned intrinsic kinetic parameters to be treated as constants, the Thiele modulus can serve as a quantitative tool for comparing and correlating the molecular diffusion rates with different zeolite sizes. The higher the overall diffusion property parameter 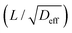 , the higher the φ. When φ > 4.0, it can be considered that the catalytic reaction is strongly controlled by diffusion resistance.37,60 Pan et al. found that shorter 12-MR channels (e.g., 60 nm) in MOR zeolites drastically enhance mass transfer, reducing diffusion limitations (Thiele modulus φ = 0.92) and improving acid site accessibility. This boosts CO conversion (33%) and ethene selectivity (69%) in syngas reactions, while longer channels (φ = 5.19) suffer transport constraints, lowering performance.257 Similarly, hierarchical zeolites can be rationally designed following Murray's law to optimize mass transport properties, thereby maximizing catalytic efficiency.60,258 Liu et al. discovered that the 16-MR channels of ZEO-1 zeolite exhibit exceptional diffusion properties, which significantly facilitate the catalytic performance in dimethoxymethane (DMM) carbonylation reactions.259
, the higher the φ. When φ > 4.0, it can be considered that the catalytic reaction is strongly controlled by diffusion resistance.37,60 Pan et al. found that shorter 12-MR channels (e.g., 60 nm) in MOR zeolites drastically enhance mass transfer, reducing diffusion limitations (Thiele modulus φ = 0.92) and improving acid site accessibility. This boosts CO conversion (33%) and ethene selectivity (69%) in syngas reactions, while longer channels (φ = 5.19) suffer transport constraints, lowering performance.257 Similarly, hierarchical zeolites can be rationally designed following Murray's law to optimize mass transport properties, thereby maximizing catalytic efficiency.60,258 Liu et al. discovered that the 16-MR channels of ZEO-1 zeolite exhibit exceptional diffusion properties, which significantly facilitate the catalytic performance in dimethoxymethane (DMM) carbonylation reactions.259
Controlled product removal through surface desorption provides another viable approach to drive reactions forward by dynamically maintaining favorable adsorption equilibria. Xiao's group pioneered a diffusion-control approach using layered zeolites to optimize intermediate transport in polyethylene conversion.260 They elucidate the cooperative diffusion-reaction mechanism in ZSM-5 zeolites. Their key findings reveal that the diffusivity of intermediates (modeled by 1-hexene) in zeolite micropores (Ds = 14.7 × 10−10 m2 s−1) decreases with increasing concentrations of cracking products (propene). When the intracrystalline propene population rises from 32 to 128 molecules, Ds drops to 8.4 × 10−10 m2 s−1 (Fig. 26a). By constructing multi-layered zeolite models, they demonstrate that reducing b-axis thickness (80–100 nm) significantly enhances mass transport: propene diffusion coefficients reach 10.0 × 10−9 and 4.8 × 10−9 m2 s−1 in 1-layer and 8-layer unit models, respectively (Fig. 26b and c). This optimized diffusion pathway enables rapid transport of surface-generated intermediates, preventing accumulation and coke formation while achieving kinetic matching for cracking reactions. Remarkably, hydrogen participation lowers the energy barrier (40.5 kJ mol−1) for converting active carbocations (C6H13+) to alkanes, effectively suppressing polycyclic species formation and maintaining micropore accessibility (Fig. 26d and e). The revealed diffusion-reaction coupling mechanism provides fundamental insights for low-temperature polyethylene conversion, establishing a new design principle for zeolite catalysts in polyolefin upgrading.260
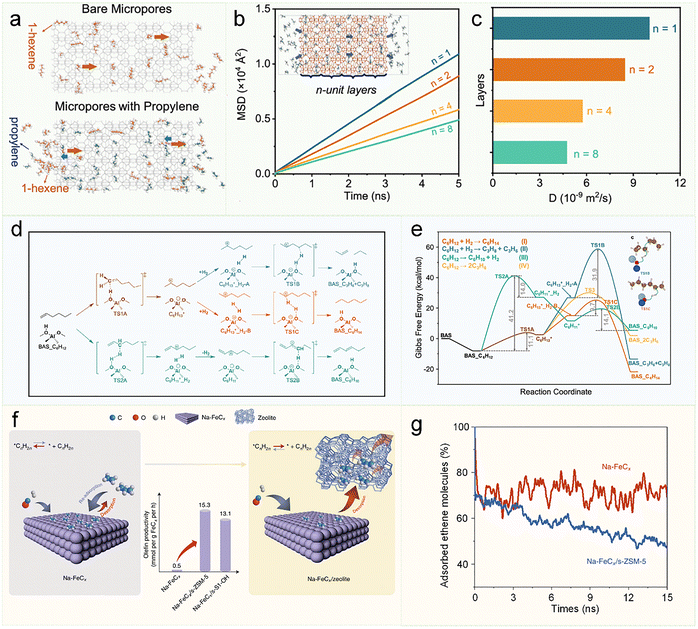 | ||
| Fig. 26 Enhanced diffusion and reaction efficiency. (a) Schematic illustration of the diffusion of 1-hexene through the zeolite crystals with bare micropores and micropores containing propene. (b) MSD of propene molecules diffusing in s-ZSM-5 zeolites with different unit layers. (c) Data of propene Ds in the s-ZSM-5 zeolite micropores with different unit layers. (d) Proposed pathways of 1-hexene hydrogenolysis, hydrogenation, and dehydrogenation over the ZSM-5 catalyst. (e) Gibbs free energy surface (280 °C) of different reaction pathways.260 Reproduced from ref. 260 with permission from (American Chemical Society), copyright 2022. (f) Schematic showing the strategy to boost the FTO via shifting the chemical equilibrium on the catalyst surface. (g) Percentage of ethene molecules adsorbed on the Na–FeCx surface during the desorption process over Na–FeCx and Na–FeCx/s-ZSM-5.261 Reproduced from ref. 261 with permission from (Springer Nature), copyright 2022. | ||
In the Fischer–Tropsch to Olefins (FTO) reaction, diffusion processes exhibit a profound correlation with catalytic performance. Recent studies demonstrate that MFI zeolite nanosheets significantly enhance reaction efficiency through optimized diffusion pathways:261 (i) diffusion-promoted product desorption: When olefins form on Fe5C2 catalyst surfaces, s-ZSM-5 zeolites with short b-axis thickness (90–110 nm) rapidly adsorb olefin molecules through their microporous structure, accelerating desorption from active sites (Fig. 26f). (ii) Diffusion-mediated selectivity control: MD simulations indicate that the thin-layer architecture of zeolites shortens olefin diffusion paths. For instance, ethene diffusion coefficients in monolayer s-ZSM-5 (2.6 × 10−8 m2 s−1) double those in eight-layer structures. This enhanced diffusion suppresses secondary adsorption and over-hydrogenation of long-chain hydrocarbons, achieving 72% selectivity for C2–C10 olefins (Fig. 26g). (iii) Synergistic diffusion-reaction equilibrium: theoretical calculations reveal that zeolite micropores capture gas-phase olefins via H–π interactions (adsorption energy: −75.3 kJ mol−1), disrupting the adsorption–desorption equilibrium on catalyst surfaces and driving the reaction toward product formation. Collectively, zeolites establish a “fast diffusion-desorption” mechanism that optimizes both reaction kinetics and thermodynamic equilibrium, enabling high CO conversion (82.5%) and olefin productivity (15.3 mmolg−1·h−1) at low temperatures (260 °C). These findings provide novel design principles for high-performance diffusion-reaction coupled catalytic systems.
Furthermore, suppression of side reactions represents an additional effective strategy to enhance catalytic performance. Previous studies have revealed that the 8-MR channels in MOR primarily facilitate carbonylation reactions, while BAS within the 12-MR predominantly catalyze undesirable side reactions that accelerate deactivation.262–264 To optimize catalytic performance, strategic suppression of 12-MR acidity is essential. Two effective mitigation approaches have been demonstrated: (i) direct inhibition of framework aluminum in 12-MR channels through controlled synthesis or post-synthetic modification,265–268 and (ii) selective poisoning of 12-MR acid sites via pre-adsorption of pyridine or other ions, which sterically prevents dimethyl ether (DME) diffusion to these active sites, thereby suppressing parasitic reactions.269–272
Water is ubiquitous in most catalytic reactions, where it not only competes with reactants for adsorption sites—promoting undesirable side reactions—but also interacts with the metal surface, leading to the blockage of active sites and subsequent catalyst deactivation.274–277 Xiao et al. discovered that physically mixing the catalyst with a hydrophobic polymer enhances CO hydrogenation by facilitating water removal. Water exhibits stronger interactions with hydrophilic surfaces (Fig. 27a), and its diffusion rate is significantly slower on hydrophilic surfaces (Ds = 2.2 × 10−7 m2 s−1) compared to hydrophobic surfaces (Fig. 27b, Ds = 4.7 × 10−7 m2 s−1). In a non-equilibrium diffusion process, the introduction of hydrophobic materials (Fig. 27c) creates a concentration gradient that enables rapid water diffusion away from the catalyst surface. This hydrophobic modification effectively promotes water displacement from active sites (Fig. 27d), thereby exposing more catalytic centers and favoring the forward reaction.273 Ding et al. developed a bifunctional catalytic system comprising hydrophobic FeNa@Si-c and HZSM-5 zeolite. The catalyst demonstrated exceptional performance with merely 14.3% CO2 selectivity at 49.8% CO conversion, while achieving a remarkable 62.5% selectivity toward gasoline-range hydrocarbons in the total products. MD simulations combined with model experiments revealed distinct water diffusion behaviors: bidirectional diffusion in hydrophilic catalysts versus unidirectional diffusion in hydrophobic catalysts. This fundamental difference in diffusion characteristics plays a pivotal role in modulating the water–gas shift reaction and effectively suppressing CO2 formation. Their findings provide novel mechanistic insights into the function of hydrophobic modification in catalysts for syngas conversion.278 Furthermore, regulating surface diffusion barriers can effectively suppress side reactions while promoting product desorption, thereby enhancing overall catalytic performance.209,214,233
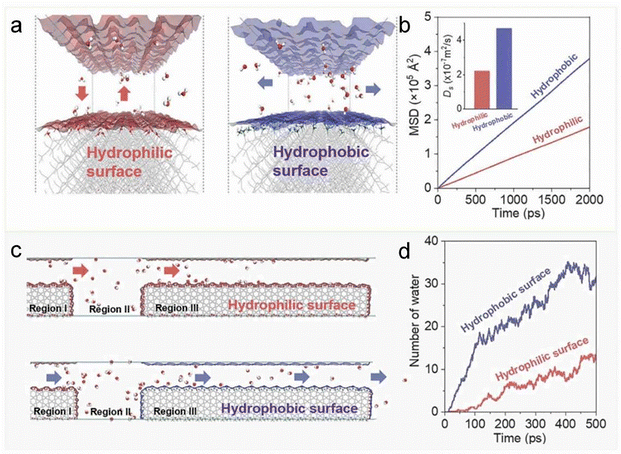 | ||
| Fig. 27 Facilitating byproduct diffusion enhances catalytic activity. (a) Models showing the water diffusion within regions surrounded by hydrophilic (left) and hydrophobic (right) surfaces. (b) Mean square displacement (MSD) and diffusion coefficient (Ds) showing the water diffusion efficiency at 250 °C. (c) Models showing the water escape through different regions. The regions I are hydrophilic and the regions III are hydrophilic (top) and hydrophobic (bottom), respectively. (d) The number of water molecules that escaped from region III from an initial state with 100 water molecules on region I as a function of time.273 Reproduced from ref. 273 with permission from (American Association for the Advancement of Science), copyright 2022. | ||
4. Conclusions and future prospects
This review provides a comprehensive molecular-level perspective on diffusion phenomena in zeolitic systems, addressing how nanoconfinement fundamentally modifies transport mechanisms compared to bulk-phase behavior. The intricate interplay among pore topology, framework dynamics, and guest–host interactions is summarized, while quantitatively evaluating the influence of key external parameters—including acidity, concentration, and temperature—on diffusional processes. The unique diffusion behaviors arising from optimal guest–host-environment matching offer novel design principles for precise molecular transport regulation. Particularly relevant are the mechanistic insights into diffusion-mediated shape-selective catalysis, where we highlight three governing factors: localized reactant enrichment at active sites driven by preferential adsorption, enhanced product egress through structurally optimized pore channels, and suppression of side reactions via molecular-level confinement effects. These insights establish fundamental structure-diffusion-function relationships that are pivotal for rational catalyst design.While current research predominantly focuses on small-molecule diffusion, industrial applications frequently encounter diffusion limitations with long-chain or bulky molecules (e.g., long-chain alkanes, aromatic compounds). The diffusion mechanisms of these molecules remain insufficiently understood, necessitating systematic investigation. Although over 260 microporous zeolite topologies have been developed, comprehensive studies on the diffusion behavior of various guest molecules under different temperatures, concentrations, and pore environments remain incomplete. Establishing a systematic zeolite diffusion database (encompassing structure-diffusion-environment parameter relationships) will form a critical foundation for rational material design, with significant implications for gas adsorption/separation and catalytic applications.
Hierarchical porous zeolites demonstrate exceptional diffusion performance due to their unique micro-/meso-/macroporous architectures.279–281 However, research on their diffusion characteristics remains fragmented. The complex mass transfer pathways in hierarchical pore systems (e.g., micro–meso/meso–macro pore synergies, surface diffusion) pose challenges in establishing quantitative structure–performance relationships. It should be noted that current theoretical simulations of confined diffusion in zeolites primarily rely on MD methods. The computational accuracy and reliability critically depend on the appropriate selection of several parameters, including the degrees of freedom,282 the treatment of framework flexibility,283 and the duration of simulation time to ensure computational accuracy and reliability.
Notably, current studies often examine zeolite-confined diffusion and catalytic reactions in isolation, whereas in practice they exhibit dynamic coupling (e.g., diffusion-controlled reaction intermediates, localized concentration gradient effects). Future work should focus on uncovering the dynamic cross-talk behaviors and mechanisms among time-dependent material, diffusion and reaction.32 The coupling of metal cluster active sites with zeolite frameworks has emerged as a highly promising and important direction in zeolite catalysis research.284,285 A key challenge for future investigations lies in establishing quantitative correlations between catalyst deactivation and the complex interplay of pore architecture, active centers, mass transport, and reaction kinetics—an area that warrants in-depth fundamental studies. Furthermore, methodologies better approximating real-world industrial conditions (high temperature/pressure, multicomponent competitive adsorption) must be developed. Elucidating the fundamental diffusion mechanisms in zeolites offers critical theoretical foundations for designing next-generation zeolite catalysts that simultaneously achieve superior activity, exceptional selectivity, and prolonged operational stability. Machine learning is poised to play a pivotal role in predicting diffusion properties and elucidating structure-performance relationships in zeolites. While several outstanding studies have already demonstrated its potential in zeolite adsorption286 and related fields,145,287 as well as prediction of Ds in pure liquids288 or other materials,289 broader applications in diffusion prediction and mechanistic analysis remain an exciting frontier for future research.
Conflicts of interest
The authors declare no competing financial interest.Data availability
This article is a review and does not report any new primary data. All data discussed and analysed herein are derived from previously published research articles, which are cited throughout the text. The original data supporting the findings presented in this review are available in the respective cited publications and their supplementary information files (where applicable). Readers are directed to the cited references for access to the underlying datasets.Acknowledgements
This work was supported by the National Key R&D Program of China (2022YFE0116000, and 2021YFA1502600), the National Natural Science Foundation of China (22472125, 22402211, 22241801, 22032005, 22125304), the Natural Science Foundation of Hubei Province (2024AFA054, 2025AFA008), and the Natural Science Foundation of Wuhan (2024040701010058), Postdoctoral Fellowship Program of CPSF (GZC20241291). We thank anonymous reviewers for very insightful comments on how to improve this review.References
- G. Sastre and A. Corma, J. Mol. Catal. A:Chem., 2009, 305, 3–7 CrossRef CAS.
- Y. Chai, W. Dai, G. Wu, N. Guan and L. Li, Acc. Chem. Res., 2021, 54, 2894–2904 CrossRef CAS PubMed.
- Y. Li and J. Yu, Chem. Rev., 2014, 114, 7268–7316 CrossRef CAS PubMed.
- S. Wu, X. Yang and C. Janiak, Angew. Chem., Int. Ed., 2019, 58, 12340–12354 CrossRef CAS PubMed.
- E. Grifoni, G. Piccini, J. Lercher, V. Glezakou, R. Rousseau and M. Parrinello, Nat. Commun., 2021, 12, 2630 CrossRef CAS.
- W. Chen, X. Yi, Z. Liu, X. Tang and A. Zheng, Chem. Soc. Rev., 2022, 51, 4337–4385 RSC.
- E. Garcia, J. Perez-Pellitero, C. Jallut and G. Pirngruber, Phys. Chem. Chem. Phys., 2013, 15, 5648–5657 RSC.
- B. Yue, S. Liu, Y. Chai, G. Wu, N. Guan and L. Li, J. Energy Chem., 2022, 71, 288–303 CrossRef CAS.
- R. Bai, X. Song, W. Yan and J. Yu, Nat. Sci. Rev., 2022, 9, nwac064 CrossRef CAS.
- A. Primo and H. Garcia, Chem. Soc. Rev., 2014, 43, 7548–7561 RSC.
- M. Mondal, B. Biswas, S. Garai, S. Sarkar, H. Banerjee, K. Brahmachari, P. Bandyopadhyay, S. Maitra, M. Brestic, M. Skalicky, P. Ondrisik and A. Hossain, Agronomy, 2021, 11, 448 CrossRef CAS.
- E. Perez-Botella, S. Valencia and F. Rey, Chem. Rev., 2022, 122, 17647–17695 CrossRef CAS.
- X. Wang, Y. Ma, Q. Wu, Y. Wen and F. Xiao, Chem. Soc. Rev., 2022, 51, 2431–2443 RSC.
- P. Cao, W. Zheng, W. Sun and L. Zhao, Chem. Eng. Sci., 2021, 245, 116966 CrossRef CAS.
- B. Li, P. Huang, P. Cao, W. Gao, W. Zheng, C. Lian, W. Sun and L. Zhao, Microporous Mesoporous Mater., 2022, 341, 112040 CrossRef CAS.
- Q. Zhao, L. Chen, S. Ma and Z. Liu, Nat. Commun., 2025, 16, 3720 CrossRef CAS.
- C. Chizallet, C. Bouchy, K. Larmier and G. Pirngruber, Chem. Rev., 2023, 123, 6107–6196 CrossRef CAS.
- J. Tan, H. Liang, W. Chen, J. Yuan, W. Dong, W. Liu, X. Yu, H. Shi and A. Zheng, Microporous Mesoporous Mater., 2024, 365, 112887 CrossRef CAS.
- J. Kim, M. Abouelnasr, L. Lin and B. Smit, J. Am. Chem. Soc., 2013, 135, 7545–7552 CrossRef CAS PubMed.
- D. Hewitt, T. Pope, M. Sarwar, A. Turrina and B. Slater, Chem. Sci., 2022, 13, 13178–13186 RSC.
- J. Crum, J. Crum, C. Taylor and W. Schneider, Microporous Mesoporous Mater., 2023, 351, 112466 CrossRef CAS.
- J. Li, R. Kuppler and H. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504 RSC.
- J. Jae, G. Tompsett, A. Foster, K. Hammond, S. Auerbach, R. Lobo and G. Huber, J. Catal., 2011, 279, 257–268 CrossRef CAS.
- K. Gugeler, J. Kästner and M. Dyballa, ACS Catal., 2025, 15, 4798–4816 CrossRef CAS.
- T. Willems, C. Rycroft, M. Kazi, J. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS.
- A. Vasudevan, J. Prieto, S. Zorkaltsev and M. Haranczyk, Comput. Phys. Commun., 2024, 305, 109344 CrossRef CAS.
- D. Bermúdez and G. Sastre, Theor. Chem. Acc., 2017, 136, 116 Search PubMed.
- Database of zeoltie structures, https://america.iza-structure.org/IZA-SC/ftc_table.php, (accessed August 2025).
- B. Bukowski, F. Keil, P. Ravikovitch, G. Sastre, R. Snurr and M. Coppens, Adsorption, 2021, 27, 683–760 CrossRef CAS.
- B. Smit and T. Maesen, Chem. Rev., 2008, 108, 4125–4184 CrossRef CAS PubMed.
- H. Xiong, Z. Liu, X. Chen, H. Wang, W. Qian, C. Zhang, A. Zheng and F. Wei, Science, 2022, 376, 491–496 CrossRef CAS.
- S. Lin, Y. Zhi, Z. Liu, J. Yuan, W. Liu, W. Zhang, Z. Xu, A. Zheng, Y. Wei and Z. Liu, Natl. Sci. Rev., 2022, 9, nwac151 CrossRef CAS.
- L. Li, X. Xu, M. Ye and Z. Liu, J. Phys. Chem. C, 2024, 129, 24–36 CrossRef.
- V. Van Speybroeck, M. Bocus, P. Cnudde and L. Vanduyfhuys, ACS Catal., 2023, 13, 11455–11493 CrossRef.
- P. Cnudde, R. Demuynck, S. Vandenbrande, M. Waroquier, G. Sastre and V. Van Speybroeck, J. Am. Chem. Soc., 2020, 142, 6007–6017 CrossRef CAS PubMed.
- J. Kärger, D. Ruthven and R. Valiullin, Adsorption, 2020, 27, 267–281 CrossRef.
- X. Liu, C. Wang, J. Zhou, C. Liu, Z. Liu, J. Shi, Y. Wang, J. Teng and Z. Xie, Chem. Soc. Rev., 2022, 51, 8174–8200 RSC.
- Z. Liu, J. Zhou, X. Tang, F. Liu, J. Yuan, G. Li, L. Huang, R. Krishna, K. Huang and A. Zheng, AIChE J., 2020, 66, e16269 CrossRef CAS.
- P. Huang, Z. Yin, Y. Tian, J. Yang, W. Zhong, C. Li, C. Lian, L. Yang and H. Liu, Chem. Eng. Sci., 2021, 246, 116995 CrossRef CAS.
- S. Danny, Diffusion in Zeolites: Towards a Microscopic Understanding, Eindhoven University of Technology, 2002.
- P. Magusin, D. Schuring, E. Van Oers, J. De Haan and R. Van Santen, Magn. Reson. Chem., 1999, 37, S108–S117 CrossRef CAS.
- J. Kärger, R. Valiullin, S. Brandani, J. Caro, C. Chmelik, B. Chmelka, M. Coppens, S. Farooq, D. Freude, H. Jobic, M. Kruteva, E. Mangano, R. Pini, W. Price, A. Rajendran, P. Ravikovitch, G. Sastre, R. Snurr, A. Stepanov, S. Vasenkov, Y. Wang and B. Weckhuysen, Pure Appl. Chem., 2025, 97, 1–89 CrossRef.
- J. Kärger and D. Ruthven, Diffusion in Zeolites and other Microporous Solids, Wiley, New York, 1992 Search PubMed.
- R. Krishna and J. van Baten, J. Phys. Chem. B, 2005, 109, 6386–6396 CrossRef CAS.
- R. Krishna, Chem. Soc. Rev., 2012, 41, 3099–3118 RSC.
- R. Krishna, Microporous Mesoporous Mater., 2014, 185, 30–50 CrossRef CAS.
- J. Kärger, M. Avramovska, D. Freude, J. Haase, S. Hwang and R. Valiullin, Adsorption, 2021, 27, 453–484 CrossRef.
- J. Kärger, D. Freude and J. Haase, Processes, 2018, 6, 147 CrossRef.
- H. Jobic and D. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- M. Kruteva, Adsorption, 2021, 27, 875–889 CrossRef CAS.
- V. Van Speybroeck, K. Hemelsoet, L. Joos, M. Waroquier, R. Bell and C. Catlow, Chem. Soc. Rev., 2015, 44, 7044–7111 RSC.
- D. Dubbeldam and B. Smit, J. Phys. Chem. B, 2003, 107, 12138–12152 CrossRef CAS.
- J. Kärger and R. Valiullin, Chem. Soc. Rev., 2013, 42, 4172–4197 RSC.
- J. Kärger, Adsorption, 2003, 9, 29–35 CrossRef.
- D. Dubbeldam and R. Snurr, Mol. Simul., 2007, 33, 305–325 CrossRef CAS.
- A. Schlaich, J. Barrat and B. Coasne, Chem. Rev., 2025, 125, 2561–2624 CrossRef CAS PubMed.
- D. Cai, H. Xiong, C. Zhang and F. Wei, Small, 2020, 16, 1901979 CrossRef CAS.
- D. Schneider, D. Mehlhorn, P. Zeigermann, J. Kärger and R. Valiullin, Chem. Soc. Rev., 2016, 45, 3439–3467 RSC.
- M. Hartmann, A. Machoke and W. Schwieger, Chem. Soc. Rev., 2016, 45, 3313–3330 RSC.
- P. Peng, X. Gao, Z. Yan and S. Mintova, Nat. Sci. Rev., 2020, 7, 1726–1742 CrossRef.
- Z. Liu, X. Kan, M. Gao, Y. Ji, F. Ye, J. Tan, F. Liu, J. Yuan, X. Tang, H. Li, P. Gao, J. Xue, Q. Cai, N. Osti, N. Jalarvo, C. Li, Y. Zou, Y. Li, S. Xu, G. Hou, M. Ye, F. Liu and A. Zheng, Nat. Commun., 2025, 16, 2018 CrossRef CAS PubMed.
- S. Gao, Z. Liu, S. Xu, A. Zheng, P. Wu, B. Li, X. Yuan, Y. Wei and Z. Liu, J. Catal., 2019, 377, 51–62 CrossRef CAS.
- E. Cussler, Multicomponent Diffusion, Elsevier, Amsterdam, 1976 Search PubMed.
- S. Mitra, V. Sharma and R. Mukhopadhyay, Rep. Prog. Phys., 2021, 84, 066501 CrossRef CAS.
- M. Holz, S. Heil and A. Sacco, Phys. Chem. Chem. Phys., 2020, 2, 4740–4742 RSC.
- J. Yuan, M. Gao, Z. Liu, X. Tang, Y. Tian, G. Ma, M. Ye and A. Zheng, Nat. Commun., 2023, 14, 1735 CrossRef CAS PubMed.
- S. Zeng, S. Xu, S. Gao, M. Gao, W. Zhang, Y. Wei and Z. Liu, ChemCatChem, 2020, 12, 463–468 CrossRef CAS.
- R. Nagumo, H. Takaba and S. Nakao, Chem. Phys. Lett., 2008, 458, 281–284 CrossRef CAS.
- E. Beerdsen, B. Smit and D. Dubbeldam, Phys. Rev. Lett., 2004, 93, 248301 CrossRef CAS.
- S. Boulfelfel, P. Ravikovitch and D. Sholl, J. Phys. Chem. C, 2015, 119, 15643–15653 CrossRef CAS.
- J. Liu, Z. Cheng, J. Wei, Q. Zhang, X. Chen, Y. Cen and L. Li, Chem. Eng. Sci., 2017, 172, 117–124 CrossRef CAS.
- F. Keil, R. Krishna and M. Coppens, Rev. Chem. Eng., 2000, 16, 71–197 CAS.
- D. Tsalikis, V. Mavrantzas and S. Pratsinis, Phys. Fluids, 2023, 35, 097131 CrossRef CAS.
- Q. Zhang, T. Wu, C. Chen, S. Mukamel and W. Zhuang, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10023–10028 Search PubMed.
- W. Rao, J. Yuan, X. Tang, K. Lin, X. Xu, H. Xia, Y. Jiang, A. Zheng and Z. Liu, J. Phys. Chem. Lett., 2022, 13, 2808–2813 CrossRef CAS PubMed.
- J. Toda, A. Corma and G. Sastre, J. Phys. Chem. C, 2016, 120, 16668–16680 CrossRef CAS.
- J. Toda and G. Sastre, J. Phys. Chem. C, 2018, 122, 7885–7897 CrossRef CAS.
- A. Ghysels, S. Moors, K. Hemelsoet, K. De Wispelaere, M. Waroquier, G. Sastre and V. Van Speybroeck, J. Phys. Chem. C, 2015, 119, 23721–23734 CrossRef CAS.
- S. Rives, H. Jobic, A. Beale and G. Maurin, J. Phys. Chem. C, 2013, 117, 13530–13539 CrossRef CAS.
- Z. Liu, J. Yuan, J. van Baten, J. Zhou, X. Tang, C. Zhao, W. Chen, X. Yi, R. Krishna, G. Sastre and A. Zheng, Sci. Adv., 2021, 7, eabf0775 CrossRef CAS PubMed.
- S. Gao, J. Yuan, Z. Liu, C. Lou, Z. Yu, S. Xu, A. Zheng, P. Wu, Y. Wei and Z. Liu, J. Phys. Chem. C, 2021, 125, 6832–6838 CrossRef CAS.
- X. Liu, J. Shi, G. Yang, J. Zhou, C. Wang, J. Teng, Y. Wang and Z. Xie, Commun. Chem., 2021, 4, 107 CrossRef CAS.
- F. Leroy, B. Rousseau and A. Fuchs, Phys. Chem. Chem. Phys., 2004, 6, 775–783 RSC.
- D. Fu, J. Maris, K. Stanciakova, N. Nikolopoulos, O. van der Heijden, L. Mandemaker, M. Siemons, D. Salas Pastene, L. Kapitein, F. Rabouw, F. Meirer and B. Weckhuysen, Angew. Chem., Int. Ed., 2021, 61, e202114388 CrossRef.
- J. Tong, T. Miyakage, T. Toyao and K. Shimizu, Catal. Sci. Technol., 2024, 14, 1902–1910 RSC.
- L. Bu, M. Nimlos, D. Robichaud and S. Kim, J. Phys. Chem. C, 2017, 121, 500–510 CrossRef CAS.
- J. Erik Maris, L. Parker, K. Stanciakova, N. Nikolopoulos, K. Berendsen, A. van Blaaderen, F. Meirer, F. Rabouw and B. Weckhuysen, Chem. – Eur. J., 2024, 30, e202302553 CrossRef CAS.
- W. Rao, X. Tang, K. Lin, X. Xu, H. Xia, Y. Jiang, Z. Liu and A. Zheng, J. Phys. Chem. Lett., 2023, 14, 3567–3573 CrossRef CAS PubMed.
- S. Se, H. Wang, J. Zhou, Q. Li, Y. Qin and L. Song, J. Mater. Sci., 2024, 59, 16501–16519 CrossRef CAS.
- P. Cnudde, E. Redekop, W. Dai, N. Porcaro, M. Waroquier, S. Bordiga, M. Hunger, L. Li, U. Olsbye and V. Van Speybroeck, Angew. Chem., Int. Ed., 2021, 133, 10104–10110 CrossRef.
- J. Bjerregaard, M. Votsmeier and H. Grönbeck, Nat. Commun., 2025, 16, 603 CrossRef CAS PubMed.
- T. Masuda, Y. Fujikata, T. Nishida and K. Hashimoto, Microporous Mesoporous Mater., 1998, 23, 157–167 CrossRef CAS.
- C. Blaeker, V. Mauer, C. Pasel, F. Dreisbach and D. Bathen, Adsorption, 2024, 30, 1547–1564 CrossRef CAS.
- X. Liu, Y. Wang, J. Teng, Y. Wang and Z. Xie, ChemCatChem, 2025, 17, e202401144 CrossRef CAS.
- C. Botchway, R. Tia, E. Adei, A. O'Malley, N. Dzade, C. Hernandez-Tamargo and N. de Leeuw, Catalysts, 2020, 10, 1342 CrossRef CAS.
- A. Porter and A. O’Malley, J. Phys. Chem. C, 2021, 125, 11567–11579 CrossRef CAS.
- A. Porter, S. McHugh, T. Omojola, I. Silverwood and A. O'Malley, Microporous Mesoporous Mater., 2023, 348, 112391 CrossRef CAS.
- A. Misturini, O. Altundal, P. García-Aznar, S. Kariminasab and G. Sastre, Chem. Ing. Tech., 2023, 95, 1768–1776 CrossRef CAS.
- J. Kärger and H. Pfeifer, Zeolites, 1987, 7, 90–107 CrossRef.
- Z. Liu, C. Lou, J. Yuan, X. Tang, Y. Fan, J. Qi, R. Zhang, P. Peng, G. Liu, S. Xu and A. Zheng, J. Am. Chem. Soc., 2025, 147, 6126–6136 CrossRef CAS PubMed.
- E. Beerdsen, D. Dubbeldam and B. Smit, Phys. Rev. Lett., 2006, 96, 044501 CrossRef CAS.
- W. Kellouai, P. Judeinstein, M. Plazanet, J. Zanotti, Q. Berrod, M. Drobek, A. Julbe and B. Coasne, Microporous Mesoporous Mater., 2025, 381, 113305 CrossRef CAS.
- E. Beerdsen, D. Dubbeldam and B. Smit, Phys. Rev. Lett., 2005, 95, 164505 CrossRef CAS PubMed.
- D. Resasco, S. Crossley, B. Wang and J. White, Catal. Rev., 2021, 63, 302–362 CrossRef CAS.
- Q. Liu and J. van Bokhoven, Chem. Soc. Rev., 2024, 53, 3065–3095 RSC.
- K. Stanciakova and B. Weckhuysen, Trends Chem., 2021, 3, 456–468 CrossRef CAS.
- Y. Hu, R. Liu, K. Lu, D. Wu, P. Gao, G. Hou, H. Zhang and W. Dai, Nat. Commun., 2025, 16, 5851 CrossRef PubMed.
- T. Wang, H. Iriawan, J. Peng, R. Rao, B. Huang, D. Zheng, D. Menga, A. Aggarwal, S. Yuan and J. Eom, Chem. Rev., 2025, 125, 1420–1467 CrossRef CAS.
- K. Han, S. Bernardi, L. Wang and D. Searles, J. Membr. Sci., 2015, 495, 322–333 CrossRef CAS.
- R. Valiullin, J. Kärger, K. Cho, M. Choi and R. Ryoo, Microporous Mesoporous Mater., 2011, 142, 236–244 CrossRef CAS.
- A. Porter, S. McHugh, T. Omojola, I. Silverwood and A. O'Malley, Microporous Mesoporous Mater., 2023, 348, 112391 CrossRef CAS.
- K. Joshi, G. Psofogiannakis, A. Van Duin and S. Raman, Phys. Chem. Chem. Phys., 2014, 16, 18433–18441 RSC.
- C. Parravano, J. Baldeschwieler and M. Boudart, Science, 1967, 155, 1535–1536 CrossRef CAS PubMed.
- C. Qiu, S. Deng, X. Sun, Y. Gao, Z. Yao, G. Zhuang, S. Wang and J. Wang, J. Membr. Sci., 2021, 635, 119462 CrossRef CAS.
- P. Demontis, J. Gulin-Gonzalez, H. Jobic and G. Suffritti, J. Phys. Chem. C, 2010, 114, 18612–18621 CrossRef CAS.
- J. Hack, J. Dombrowski, X. Ma, Y. Chen, N. Lewis, W. Carpenter, C. Li, G. Voth, H. Kung and A. Tokmakoff, J. Am. Chem. Soc., 2021, 143, 10203–10213 CrossRef CAS.
- S. Ahsan, G. Reddy, S. Durani and Y. Subramanian, J. Phys. Chem. C, 2024, 128, 9229–9246 CrossRef CAS.
- P. Liu and D. Mei, J. Phys. Chem. C, 2020, 124, 22568–22576 CrossRef CAS.
- M. Jiménez-Ruiz, D. Gahle, T. Lemishko, S. Valencia, G. Sastre and F. Rey, J. Phys. Chem. C, 2020, 124, 5436–5443 CrossRef.
- M. Wang, N. Jaegers, M. Lee, C. Wan, J. Hu, H. Shi, D. Mei, S. Burton, D. Camaioni and O. Gutiérrez, J. Am. Chem. Soc., 2019, 141, 3444–3455 CrossRef CAS.
- M. Bocus, R. Goeminne, A. Lamaire, M. Cools-Ceuppens, T. Verstraelen and V. Van Speybroeck, Nat. Commun., 2023, 14, 1008 CrossRef CAS PubMed.
- S. Ghojavand, E. Dib and S. Mintova, Chem. Sci., 2023, 14, 12430–12446 RSC.
- B. Ilić and S. Wettstein, Microporous Mesoporous Mater., 2017, 239, 221–234 CrossRef.
- M. Treacy, C. Dawson, V. Kapko and I. Rivin, Philos. Trans. R. Soc., A, 2014, 372, 20120036 CrossRef CAS PubMed.
- S. Kuznicki, V. Bell, S. Nair, H. Hillhouse, R. Jacubinas, C. Braunbarth, B. Toby and M. Tsapatsis, Nature, 2001, 412, 720–724 CrossRef CAS.
- G. Li, J. Shang, Q. Gu, R. Awati, N. Jensen, A. Grant, X. Zhang, D. Sholl, J. Liu, P. Webley and E. May, Nat. Commun., 2017, 8, 15777 CrossRef.
- V. Kapko, C. Dawson, M. Treacy and M. Thorpe, Phys. Chem. Chem. Phys., 2010, 12, 8531–8541 RSC.
- E. Verheyen, L. Joos, C. Martineau, C. Dawson, C. Weidenthaler, W. Schmidt, R. Yuan, E. Breynaert, V. Van Speybroeck, M. Waroquier, F. Taulelle, M. Treacy, J. Martensa and C. Kirschhock, Mater. Horizons, 2014, 1, 582–587 RSC.
- S. Wells, K. Leung, P. Edwards, M. Tucker and A. Sartbaeva, R. Soc. Open Sci., 2017, 4, 170757 CrossRef.
- C. Dawson, V. Kapko, M. Thorpe, M. Foster and M. Treacy, J. Phys. Chem. C, 2012, 116, 16175–16181 CrossRef CAS.
- V. Kapko, C. Dawson, I. Rivin and M. Treacy, Phys. Rev. Lett., 2011, 107, 164304 CrossRef CAS PubMed.
- R. Fletcher, S. Wells, K. Leung, P. Edwards and A. Sartbaeva, Acta Crystallogr., Sect. B, 2015, 71, 641–647 CrossRef CAS.
- S. Caro-Ortiz, E. Zuidema, M. Rigutto, D. Dubbeldam and T. Vlugt, J. Phys. Chem. C, 2020, 124, 24488–24499 CrossRef CAS.
- E. Clatworthy, S. Moldovan, K. Nakouri, S. Gramatikov, F. Dalena, M. Daturi, P. Petkov, G. Vayssilov and S. Mintova, J. Am. Chem. Soc., 2023, 145, 15313–15323 CrossRef CAS PubMed.
- H. Shi, A. Migues and S. Auerbach, Green Chem., 2014, 16, 875–884 RSC.
- A. Garcia-Sanchez, D. Dubbeldam and S. Calero, J. Phys. Chem. C, 2010, 114, 15068–15074 CrossRef CAS.
- R. Krishna and J. van Baten, J. Phys. Chem. C, 2010, 114, 18017–18021 CrossRef CAS.
- R. Krishna and J. van Baten, Microporous Mesoporous Mater., 2011, 137, 83–91 CrossRef CAS.
- R. Awati, P. Ravikovitch and D. Sholl, J. Phys. Chem. C, 2013, 117, 13462–13473 CrossRef CAS.
- J. Toda, A. Corma, R. Abudawoud, M. Elanany, I. Al-Zahrani and G. Sastre, Mol. Simul., 2015, 41, 1438–1448 CrossRef CAS.
- T. Sours and A. Kulkarni, J. Phys. Chem. C, 2023, 127, 1455–1463 CrossRef CAS.
- R. Millan, E. Bello-Jurado, M. Moliner, M. Boronat and R. Gomez-Bombarelli, ACS Cent. Sci., 2023, 9, 2044–2056 CrossRef CAS PubMed.
- K. Wan, J. He and X. Shi, Adv. Mater., 2024, 36, 2305758 CrossRef CAS.
- L. Brugnoli, M. Ducamp and F. Coudert, J. Phys. Chem. C, 2024, 128, 20512–20522 CrossRef CAS.
- S. Ma and Z. Liu, Chem. Sci., 2022, 13, 5055–5068 RSC.
- P. Bereciartua, A. Cantín, A. Corma, J. Jordá, M. Palomino, F. Rey, S. Valencia, E. Corcoran, P. Kortunov, P. Ravikovitch, A. Burton, C. Yoon, Y. Wang, C. Paur, J. Guzman, A. Bishop and G. Casty, Science, 2017, 358, 1068–1071 CrossRef CAS.
- J. Shang, G. Li, R. Singh, Q. Gu, K. Nairn, T. Bastow, N. Medhekar, C. Doherty, A. Hill, J. Liu and P. Webley, J. Am. Chem. Soc., 2012, 134, 19246–19253 CrossRef.
- M. Lozinska, J. Mowat, P. Wright, S. Thompson, J. Jorda, M. Palomino, S. Valencia and F. Rey, Chem. Mater., 2014, 26, 2052–2061 CrossRef CAS.
- J. Zhao, S. Mousavi, G. Xiao, A. Mokarizadeh, T. Moore, K. Chen, Q. Gu, R. Singh, A. Zavabeti, J. Liu, P. Webley and G. Li, J. Am. Chem. Soc., 2021, 143, 15195–15204 CrossRef CAS PubMed.
- D. Dubbeldam, S. Calero, T. Maesen and B. Smit, Phys. Rev. Lett., 2003, 90, 245901 CrossRef CAS.
- H. Jobic, A. Méthivier, G. Ehlers, B. Farago and W. Haeussler, Angew. Chem., Int. Ed., 2004, 43, 364–366 CrossRef CAS.
- J. Dunn, J. Crossley-Lewis, A. McCluskey, F. Jackson, C. Buda, G. Sunley, A. Mulholland and N. Allan, Catal. Sci. Technol., 2024, 14, 3674–3681 RSC.
- J. Yuan, Z. Liu, Y. Wu, J. Han, X. Tang, C. Li, W. Chen, X. Yi, J. Zhou, R. Krishna, G. Sastre and A. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2102097118 CrossRef CAS.
- S. Yashonath and P. Santikary, J. Phys. Chem., 1994, 98, 6368–6376 CrossRef CAS.
- D. Dubbeldam, E. Beerdsen, S. Calero and B. Smit, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12317–12320 CrossRef CAS PubMed.
- E. Derouane and Z. Gabelica, J. Catal., 1980, 65, 486–489 CrossRef CAS.
- L. Clark, G. Ye and R. Snurr, Phys. Rev. Lett., 2000, 84, 2893–2896 CrossRef CAS PubMed.
- K. Hahn, J. Kärger and V. Kukla, Phys. Rev. Lett., 1996, 76, 2762–2765 CrossRef CAS.
- E. Ruckenstein and P. Lee, Phys. Lett. A, 1976, 56, 423–424 CrossRef.
- P. Kolokathis, G. Káli, H. Jobic and D. Theodorou, J. Phys. Chem. C, 2016, 120, 21410–21426 CrossRef CAS.
- E. Derouane, J. Andre and A. Lucas, J. Catal., 1988, 110, 58–73 CrossRef CAS.
- S. Bandyopadhyay and S. Yashonath, J. Phys. Chem., 1995, 99, 4286–4292 CrossRef CAS.
- S. Yashonath and C. Rajappa, Faraday Discuss., 1997, 106, 105–118 RSC.
- C. Rajappa and S. Yashonath, J. Phys. Chem. B, 1997, 101, 8035–8037 CrossRef CAS.
- B. Borah, H. Jobic and S. Yashonath, J. Chem. Phys., 2010, 132, 144507 CrossRef PubMed.
- V. Gupta, S. Nivarthi, D. Keffer, A. McCormick and H. Davis, Science, 1996, 274, 164 CrossRef CAS.
- V. Kukla, J. Kornatowski, D. Demuth, I. Girnus, H. Pfeifer, L. Rees, S. Schunk, K. Unger and J. Kärger, Science, 1996, 272, 702–704 CrossRef CAS.
- G. Sastre and A. Corma, Top. Catal., 2003, 24, 7–12 CrossRef CAS.
- A. Vogl, Diffusion Spreading in Nature, Technology and Society, Springer Nature, Cham, 2007 Search PubMed.
- A. Smit and T. Maesen, Chem. Rev., 2008, 108, 4125–4184 CrossRef PubMed.
- S. Bhide and S. Yashonath, J. Am. Chem. Soc., 2003, 125, 7425–7434 CrossRef CAS PubMed.
- K. Czaplewski, T. Reitz, Y. Kim and R. Snurr, Microporous Mesoporous Mater., 2002, 56, 55–64 CrossRef CAS.
- M. Schenk, S. Calero, T. Maesen, L. van Benthem, M. Verbeek and B. Smit, Angew. Chem., Int. Ed., 2002, 41, 2499–2502 CrossRef CAS.
- H. Jobic, J. Mol. Catal. A:Chem., 2000, 158, 135–142 CrossRef CAS.
- J. van Baten and R. Krishna, Microporous Mesoporous Mater., 2005, 84, 179–191 CrossRef CAS.
- D. Schuring, A. Koriabkina, A. de Jong, B. Smit and R. van Santen, J. Phys. Chem. B, 2001, 105, 7690–7698 CrossRef CAS.
- M. Gao, H. Li, M. Ye and Z. Liu, AIChE J., 2020, 66, e16991 CrossRef CAS.
- M. DeLuca and D. Hibbitts, Microporous Mesoporous Mater., 2022, 333, 111705 CrossRef CAS.
- C. Wang, Z. Liu, L. Wang, X. Dong, J. Zhang, G. Wang, S. Han, X. Meng, A. Zheng and F. Xiao, ACS Catal., 2017, 8, 474–481 CrossRef.
- H. Matsubara, F. Pichierri and K. Kurihara, Phys. Rev. Lett., 2012, 109, 197801 CrossRef.
- R. Tsekov and P. Smirniotis, J. Phys. Chem. B, 1998, 102, 9385–9391 CrossRef CAS.
- R. Runnebaum and E. Maginn, J. Phys. Chem. B, 1997, 101, 6394–6408 CrossRef CAS.
- A. Rybakov, A. Larin and D. Vercauteren, Phys. Chem. Chem. Phys., 2017, 19, 20930–20940 RSC.
- A. Khudozhitkov, H. Jobic, D. Freude, J. Haase, D. Kolokolov and A. Stepanov, J. Phys. Chem. C, 2016, 120, 21704–21709 CrossRef CAS.
- P. Ghorai and S. Yashonath, J. Chem. Phys., 2004, 120, 5315–5321 CrossRef CAS.
- S. Brandani, S. Hwang, J. Kärger and E. Mangano, Nat. Commun., 2024, 15, 5721 CrossRef CAS.
- K. Chen, S. Mousavi, R. Singh, R. Snurr, G. Li and P. Webley, Chem. Soc. Rev., 2022, 51, 1139–1166 RSC.
- M. Lozinska, E. Mangano, J. Mowat, A. Shepherd, R. Howe, S. Thompson, J. Parker, S. Brandani and P. Wright, J. Am. Chem. Soc., 2012, 134, 17628–17642 CrossRef CAS.
- F. Coudert and D. Kohen, Chem. Mater., 2017, 29, 2724–2730 CrossRef CAS.
- X. Wang, N. Yan, M. Xie, P. Liu, P. Bai, H. Su, B. Wang, Y. Wang, L. Li, T. Cheng, P. Guo, W. Yan and J. Yu, Chem. Sci., 2021, 12, 8803–8810 RSC.
- J. Shang, G. Li, R. Singh, P. Xiao, J. Liu and P. Webley, J. Phys. Chem. C, 2013, 117, 12841–12847 CrossRef CAS.
- T. Du, X. Fang, L. Liu, J. Shang, B. Zhang, Y. Wei, H. Gong, S. Rahman, E. May, P. Webley and G. Li, Chem. Commun., 2018, 54, 3134–3137 RSC.
- K. Chen, S. Mousavi, Z. Yu, L. Zhang, Q. Gu, R. Snurr, P. Webley, N. Sun and G. Li, ACS Appl. Mater. Interfaces, 2024, 16, 51129–51138 CrossRef CAS.
- J. Jia, N. Yan, X. Lian, S. Liu, B. Yue, Y. Chai, G. Wu, J. Xu and L. Li, Angew. Chem., Int. Ed., 2025, 64, e202419091 CrossRef CAS PubMed.
- C. Zhao, J. Yuan, X. Tang, W. Chen, X. Yi, H. Xia, W. Liu, A. Zheng and Z. Liu, Chem. Commun., 2021, 57, 4170–4173 RSC.
- K. Chen, Z. Yu, S. Mousavi, R. Singh, Q. Gu, R. Snurr, P. Webley and G. Li, Nat. Commun., 2023, 14, 5479 CrossRef CAS.
- J. Shang, A. Hanif, G. Li, G. Xiao, J. Liu, P. Xiao and P. Webley, Ind. Eng. Chem. Res., 2020, 59, 7857–7865 CrossRef CAS.
- J. Kärger, D. Ruthven and D. Theodorou, Diffusion in nanoporous materials, Wiley Online Library, 2012 Search PubMed.
- J. Kärger, M. Bülow, G. Millward and J. Thomas, Zeolites, 1986, 6, 146–150 CrossRef.
- O. Gobin, S. Reitmeier, A. Jentys and J. Lercher, J. Phys. Chem. C, 2009, 113, 20435–20444 CrossRef CAS.
- M. Krutyeva, S. Vasenkov, X. Yang, J. Caro and J. Kärger, Microporous Mesoporous Mater., 2007, 104, 89–96 CrossRef CAS.
- A. Teixeira, C. Chang, T. Coogan, R. Kendall, W. Fan and P. Dauenhauer, J. Phys. Chem. C, 2013, 117, 25545–25555 CrossRef CAS.
- M. Gao, H. Li, M. Yang, S. Gao, P. Wu, P. Tian, S. Xu, M. Ye and Z. Liu, Commun. Chem., 2019, 2, 43 CrossRef.
- D. Ruthven, J. Kärger, S. Brandani and E. Mangano, Adsorption, 2021, 27, 787–799 CrossRef CAS.
- G. Sastre, J. Kärger and D. Ruthven, J. Phys. Chem. C, 2019, 123, 19596–19601 CrossRef CAS.
- G. Sastre, J. Kärger and D. Ruthven, J. Phys. Chem. C, 2018, 122, 7217–7225 CrossRef CAS.
- A. Thomas and Y. Subramanian, J. Chem. Phys., 2018, 149, 064702 CrossRef.
- A. Thomas and Y. Subramanian, J. Phys. Chem. C, 2019, 123, 16172–16178 CrossRef CAS.
- J. Zhou, W. Fan, Y. Wang and Z. Xie, Natl. Sci. Rev., 2020, 7, 1630–1632 CrossRef.
- S. Hu, J. Liu, G. Ye, X. Zhou, M. Coppens and W. Yuan, Angew. Chem., Int. Ed., 2021, 60, 14394–14398 CrossRef CAS PubMed.
- S. Peng, M. Gao, H. Li, M. Yang, M. Ye and Z. Liu, Angew. Chem., Int. Ed., 2020, 132, 22129–22132 CrossRef.
- S. Rao, E. Saraçi, R. Gläser and M. Coppens, Chem. Eng. J., 2017, 329, 45–55 CrossRef CAS.
- P. Peng, D. Stosic, A. Aitblal, A. Vimont, P. Bazin, X. Liu, Z. Yan, S. Mintova and A. Travert, ACS Catal., 2020, 10, 6822–6830 CrossRef CAS.
- M. Gao, H. Li, Y. Tian, J. Yu, M. Ye and Z. Liu, ACS Catal., 2023, 13, 11598–11609 CrossRef CAS.
- Y. Xu, P. Peng, H. Wang, H. Xiong, Z. Xu, X. Chen, Y. Li, A. Zheng, Y. Wei and Z. Yan, J. Am. Chem. Soc., 2025, 147, 18550–18562 CrossRef CAS PubMed.
- J. Remi, A. Lauerer, C. Chmelik, I. Vandendael, H. Terryn, G. Baron, J. Denayer and J. Kärger, Nat. Mater., 2016, 15, 401–406 CrossRef CAS.
- P. Bai, E. Haldoupis, P. Dauenhauer, M. Tsapatsis and J. Siepmann, ACS Nano, 2016, 10, 7612–7618 CrossRef CAS PubMed.
- V. Vattipalli, X. Qi, P. Dauenhauer and W. Fan, Chem. Mater., 2016, 28, 7852–7863 CrossRef CAS.
- X. Qi, V. Vattipalli, K. Zhang, P. Bai, P. Dauenhauer and W. Fan, Langmuir, 2019, 35, 12407–12417 CrossRef CAS PubMed.
- Z. Kang, H. Guo, L. Fan, G. Yang, Y. Feng, D. Sun and S. Mintova, Chem. Soc. Rev., 2021, 50, 1913–1944 RSC.
- X. Tan, S. Robijns, R. Thür, Q. Ke, N. De Witte, A. Lamaire, Y. Li, I. Aslam, D. Van Havere and T. Donckels, Science, 2022, 378, 1189–1194 CrossRef CAS PubMed.
- P. Du, Y. Zhang, X. Wang, S. Canossa, Z. Hong, G. Nenert, W. Jin and X. Gu, Nat. Commun., 2022, 13, 1427 CrossRef CAS.
- H. Guo, G. Kong, G. Yang, J. Pang, Z. Kang, S. Feng, L. Zhao, L. Fan, L. Zhu and A. Vicente, Angew. Chem., Int. Ed., 2020, 132, 6343–6347 CrossRef.
- X. Jin, S. Wang, Y. Zhao, L. Liu, X. Gao and X. Gu, J. Membr. Sci., 2024, 706, 122929 CrossRef CAS.
- A. Aydani, A. Brunetti, H. Maghsoudi and G. Barbieri, Sep. Purif. Technol., 2021, 256, 117796 CrossRef CAS.
- D. Fu and M. Davis, Chem. Soc. Rev., 2022, 51, 9340–9370 RSC.
- W. Yue, Y. Li, W. Wei, J. Jiang, J. Caro and A. Huang, Angew. Chem., Int. Ed., 2021, 60, 18289–18294 CrossRef CAS.
- Z. Wang, J. Xu, S. Pati, T. Chen, Y. Deng, N. Dewangan, L. Meng, J. Lin and S. Kawi, AIChE J., 2020, 66, e16278 CrossRef CAS.
- C. Shen, M. Xue, H. Qiu and W. Guo, J. Am. Chem. Soc., 2024, 146, 13276–13281 CrossRef CAS PubMed.
- X. Wang, T. Zhou, P. Zhang, W. Yan, Y. Li, L. Peng, D. Veerman, M. Shi, X. Gu and F. Kapteijn, Angew. Chem., Int. Ed., 2021, 60, 9032–9037 CrossRef CAS PubMed.
- Z. Li, J. Li, H. Rong, J. Zuo, X. Yang, Y. Xing, Y. Liu, G. Zhu and X. Zou, J. Am. Chem. Soc., 2022, 144, 6687–6691 Search PubMed.
- Z. Li, X. Liu, Y. Deng, X. Yang, Y. Guan, J. Wu, J. Dong, Z. Chang and X. Zou, J. Membr. Sci., 2024, 709, 123097 Search PubMed.
- S. Xu, K. Zheng, C. Boruntea, D. Cheng, F. Chen, G. Ye, X. Zhou and M. Coppens, Chem. Soc. Rev., 2023, 52, 3991–4005 RSC.
- M. Fang, J. Jing, T. Guo, J. Feng, C. Wang, Y. Ji, H. Zang, Y. Tu and G. Sas, J. Membr. Sci., 2025, 733, 124357 CrossRef CAS.
- J. Dai and H. Zhang, Small, 2021, 17, 2005334 CrossRef CAS.
- B. Smit and T. Maesen, Nature, 2008, 451, 671–678 CrossRef CAS.
- J. Han, Z. Liu, H. Li, J. Zhong, W. Zhang, J. Huang, A. Zheng, Y. Wei and Z. Liu, ACS Catal., 2020, 10, 8727–8735 CrossRef CAS.
- H. Wang, H. Li, J. Duan, L. Wang and F. Xiao, Acc. Chem. Res., 2025, 58, 440–451 CrossRef CAS PubMed.
- L. Zhang, N. Liu, C. Dai, R. Xu, G. Yu, B. Chen and N. Wang, Chem. Synth., 2023, 3, 2 CrossRef CAS.
- W. Zhang, S. Lin, Y. Wei, P. Tian, M. Ye and Z. Liu, Nat. Sci. Rev., 2023, 10, nwad120 CrossRef CAS PubMed.
- S. Gao, F. Ye, S. Xu, Y. Wei and Z. Liu, Chem. Commun., 2025, 61, 3636–3648 RSC.
- J. Li, Y. Wei, J. Chen, S. Xu, P. Tian, X. Yang, B. Li, J. Wang and Z. Liu, ACS Catal., 2015, 5, 661–665 CrossRef.
- Q. Chen, J. Liu and B. Yang, JACS Au, 2025, 5, 1791–1802 CrossRef CAS PubMed.
- W. Chen, K. Tarach, X. Yi, Z. Liu, X. Tang, K. Góra-Marek and A. Zheng, Nat. Commun., 2022, 13, 7106 CrossRef CAS.
- M. Gao, H. Li, J. Yu, M. Ye and Z. Liu, AIChE J., 2023, 69, e17881 CrossRef CAS.
- M. Gao, H. Li, W. Liu, Z. Xu, S. Peng, M. Yang, M. Ye and Z. Liu, Nat. Commun., 2020, 11, 3641 CrossRef CAS PubMed.
- P. Wright, Microporous framework solids, Royal Society of Chemistry, Cambridge, 2008 Search PubMed.
- C. Wang, L. Zhang, X. Huang, Y. Zhu, G. Li, Q. Gu, J. Chen, L. Ma, X. Li, Q. He, J. Xu, Q. Sun, C. Song, M. Peng, J. Sun and D. Ma, Nat. Commun., 2019, 10, 4348 CrossRef PubMed.
- Q. Chen, J. Liu and B. Yang, Nat. Commun., 2021, 12, 3725 CrossRef CAS.
- D. Erdosy, M. Wenny, J. Cho, C. DelRe, M. Walter, F. Jimenez-Angeles, B. Qiao, R. Sanchez, Y. Peng, B. Polizzotti, M. de la Cruz and J. Mason, Nature, 2022, 608, 712–718 CrossRef CAS.
- Z. Liu, X. Yi, G. Wang, X. Tang, G. Li, L. Huang and A. Zheng, J. Catal., 2019, 369, 335–344 CrossRef CAS.
- Z. Jin, L. Wang, E. Zuidema, K. Mondal, M. Zhang, J. Zhang, C. Wang, X. Meng, H. Yang, C. Mesters and F. Xiao, Science, 2020, 367, 193–197 CrossRef CAS.
- Y. Liu, Z. Liu, Y. Hui, L. Wang, J. Zhang, X. Yi, W. Chen, C. Wang, H. Wang, Y. Qin, L. Song, A. Zheng and F. Xiao, Nat. Commun., 2023, 14, 2531 CrossRef CAS.
- Y. Wu, Z. Liu, H. Wang, H. Shi, W. Yuan, Y. Wang, Y. Liu, Y. Lv, X. Qin, A. Zheng, L. Wang and F. Xiao, J. Am. Chem. Soc., 2025, 147, 11301–11308 CrossRef CAS.
- A. Wang, H. Wang, J. Lv, X. Liang, H. Ying, L. Wang, J. Yu, F. Xiao and K. Shi, J. Clean. Prod., 2024, 444, 141276 CrossRef CAS.
- W. Tai, W. Dai, G. Wu and L. Li, Chem. Synth., 2023, 3, 38 CAS.
- H. Wang, F. Jiao, J. Feng, Y. Zhang, Z. Xu, X. Pan and X. Bao, Angew. Chem., Int. Ed., 2025, 137, e202424946 CrossRef.
- M. Sun, S. Gao, Z. Hu, T. Barakat, Z. Liu, S. Yu, J. Lyu, Y. Li, S. Xu, L. Chen and B. Su, Nat. Sci. Rev., 2022, 9, nwac236 CrossRef CAS.
- S. Gao, P. Lu, L. Qi, Y. Wang, H. Li, M. Ye, V. Valtchev, A. Bell and Z. Liu, Chin. J. Catal., 2025, 68, 230–245 CrossRef.
- J. Duan, W. Chen, C. Wang, L. Wang, Z. Liu, X. Yi, W. Fang, H. Wang, H. Wei, S. Xu, Y. Yang, Q. Yang, Z. Bao, Z. Zhang, Q. Ren, H. Zhou, X. Qin, A. Zheng and F. Xiao, J. Am. Chem. Soc., 2022, 144, 14269–14277 CrossRef CAS PubMed.
- C. Wang, W. Fang, Z. Liu, L. Wang, Z. Liao, Y. Yang, H. Li, L. Liu, H. Zhou, X. Qin, S. Xu, X. Chu, Y. Wang, A. Zheng and F. Xiao, Nat. Nanotechnol., 2022, 17, 714–720 CrossRef CAS.
- W. Chen, G. Li, X. Yi, S. Day, K. Tarach, Z. Liu, S. Liu, S. Edman Tsang, K. Góra-Marek and A. Zheng, J. Am. Chem. Soc., 2021, 143, 15440–15452 CrossRef CAS.
- A. Bhan, A. Allian, G. Sunley, D. Law and E. Iglesia, J. Am. Chem. Soc., 2007, 129, 4919–4924 CrossRef CAS PubMed.
- P. Cheung, A. Bhan, G. Sunley and E. Iglesia, Angew. Chem., Int. Ed., 2006, 45, 1617–1620 CrossRef CAS.
- R. Liu, B. Fan, W. Zhang, L. Wang, L. Qi, Y. Wang, S. Xu, Z. Yu, Y. Wei and Z. Liu, Angew. Chem., Int. Ed., 2022, 61, e202116990 CrossRef CAS.
- R. Liu, S. Zeng, T. Sun, S. Xu, Z. Yu, Y. Wei and Z. Liu, ACS Catal., 2022, 12, 4491–4500 CrossRef CAS.
- Y. Li, M. Yu, K. Cai, M. Wang, J. Lv, R. Howe, S. Huang and X. Ma, Phys. Chem. Chem. Phys., 2020, 22, 11374–11381 RSC.
- M. Wang, S. Huang, J. Lu, Z. Cheng, Y. Li, S. Wang and X. Ma, Chin. J. Catal., 2016, 37, 1530–1538 CrossRef CAS.
- J. Liu, H. Xue, X. Huang, P. Wu, S. Huang, S. Liu and W. Shen, Chin. J. Catal., 2010, 31, 729–738 CrossRef CAS.
- S. Liu, X. Fang, Y. Liu, H. Liu, X. Ma, W. Zhu and Z. Liu, Catal. Commun., 2020, 147, 106161 CrossRef CAS.
- K. Cao, D. Fan, L. Li, B. Fan, L. Wang, D. Zhu, Q. Wang, P. Tian and Z. Liu, ACS Catal., 2020, 10, 3372–3380 CrossRef CAS.
- X. Fang, F. Wen, X. Ding, H. Liu, Z. Chen, Z. Liu, H. Liu, W. Zhu and Z. Liu, Angew. Chem., Int. Ed., 2022, 61, e202203859 CrossRef CAS PubMed.
- W. Fang, C. Wang, Z. Liu, L. Wang, L. Liu, H. Li, S. Xu, A. Zheng, X. Qin, L. Liu and F. Xiao, Science, 2022, 377, 406–410 CrossRef CAS.
- M. Wang, G. Zhang, H. Wang, Z. Wang, Y. Zhou, X. Nie, B. Yin, C. Song and X. Guo, Chem. Rev., 2024, 124, 12006–12085 CrossRef CAS.
- S. Teong, S. Chan, X. Li, J. Wang and Y. Zhang, Green Chem., 2025, 27, 547–559 RSC.
- Y. Hui, L. Wang and F. Xiao, ACS Nano, 2025, 19, 7617–7633 CrossRef CAS PubMed.
- Y. Xu and M. Ding, Chem. Soc. Rev., 2025, 54, 2881–2905 RSC.
- Y. Xu, H. Liang, R. Li, Z. Zhang, C. Qin, D. Xu, H. Fan, B. Hou, J. Wang, X. Gu and M. Ding, Angew. Chem., Int. Ed., 2023, 62, e202306786 CrossRef CAS.
- L. Chen, M. Sun, Z. Wang, W. Yang, Z. Xie and B. Su, Chem. Rev., 2020, 120, 11194–11294 CrossRef CAS.
- M. Sun, J. Zhou, Z. Hu, L. Chen, L. Li, Y. Wang, Z. Xie, S. Turner, G. Van Tendeloo and T. Hasan, Matter, 2020, 3, 1226–1245 CrossRef.
- S. Yu, L. Chen, M. He and B. Su, Natl. Sci. Rev., 2025, 12, nwaf258 CrossRef PubMed.
- H. Xu, R. Cabriolu and B. Smit, J. Chem. Theory, 2022, 18, 2826–2835 CrossRef CAS.
- P. Demontis and G. Suffritti, Microporous Mesoporous Mater., 2009, 125, 160–168 CrossRef CAS.
- Z. Xu, M. Gao, Y. Wei, Y. Yue, Z. Bai, P. Yuan, P. Fornasiero, J. Basset, B. Mei, Z. Liu, H. Zhu, M. Ye and X. Bao, Nature, 2025, 643, 691–698 CrossRef CAS PubMed.
- Y. Wu, P. Deng, L. Liu, J. Zhang, H. Liu, X. Gao, F. Xiao and L. Wang, Chem. Soc. Rev., 2025, 54, 4745–4762 RSC.
- C. Rzepa, D. Dabagian, D. Siderius, H. Hatch, V. Shen, J. Mittal and S. Rangarajan, JACS Au, 2024, 4, 4673–4690 CrossRef CAS PubMed.
- M. Ducamp and F. Coudert, J. Phys. Chem. C, 2022, 126, 1651–1660 CrossRef CAS.
- J. Allers, C. Priest, J. Greathouse and T. Alam, J. Phys. Chem. B, 2021, 125, 12990–13002 CrossRef CAS PubMed.
- M. Zhou and J. Wu, ACS Appl. Nano Mater., 2021, 4, 5394–5403 CrossRef CAS.
Footnote |
| † L.Z. and J.Y. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2026 |