Harnessing magnetic, photo, and thermal fields and their synergistic interactions for enhanced electrocatalytic oxygen evolution reaction
Yuan
Cao†
 a,
Linfeng
Gao†
a,
Linfeng
Gao†
 a,
Yijiang
Liu
*ab and
Zhiqun
Lin
a,
Yijiang
Liu
*ab and
Zhiqun
Lin
 *a
*a
aDepartment of Chemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, Singapore 117585, Singapore. E-mail: z.lin@nus.edu.sg
bCollege of Chemistry, Key Lab of Environment-Friendly Chemistry and Application in Ministry of Education, Xiangtan University, Xiangtan 411105, Hunan Province, P. R. China. E-mail: liuyijiang84@xtu.edu.cn
First published on 27th November 2025
Abstract
The oxygen evolution reaction (OER) constitutes a critical half-reaction in electrochemical water splitting and plays a central role in sustainable energy conversion systems. This review commences with an overview of the fundamental principles governing the OER, serving as the conceptual basis for understanding the influence of external physical fields on catalytic behaviour. The individual effects of magnetic, photo, and thermal fields on OER kinetics and mechanisms are systematically examined, followed by an exploration of the coupling phenomena that arise from their concurrent application. Building on these mechanistic insights, we further discuss catalyst design strategies that exploit both isolated and synergistic external field effects, as reported in recent studies. Advances in computational screening and descriptor-guided design methodologies are also reviewed. Finally, we outline critical future directions, including the optimization of performance trade-offs among activity, stability, and energy efficiency, the development of standardized evaluation protocols, and the integration of theoretical modelling to guide rational catalyst development. Collectively, this review provides a comprehensive framework for advancing OER catalysis through the strategic application of external physical fields.
1. Introduction
The oxygen evolution reaction (OER) represents the kinetic bottleneck in water splitting and related electrochemical energy conversion processes due to the sluggish four-electron transfer and high overpotential requirements.1–3 Conventional strategies such as optimizing morphology, composition, and electronic structure have achieved notable improvements in catalytic performance, but these approaches are now approaching their intrinsic limits in activity enhancement.4,5 Overcoming such limitations requires new strategies that can dynamically modulate catalytic energetics during operation rather than relying solely on static material design.In this context, the application of external physical stimuli has emerged as a powerful paradigm for electrocatalyst regulation. External fields can introduce new degrees of freedom that reshape charge, spin, and lattice dynamics, thereby enabling kinetic pathways that are inaccessible under conventional conditions.6–8 Among them, magnetic, photo, and thermal fields have demonstrated complementary effects in accelerating OER kinetics by modulating interfacial environments and reaction energetics. Understanding how each of these stimuli affects the reaction mechanism provides a crucial foundation for designing next-generation catalytic systems.
Beyond their individual roles, these external fields can act cooperatively, producing synergistic effects that transcend the sum of their independent contributions (Fig. 1). For example, coupling thermal and photo fields enables thermally assisted excitation and charge separation, where moderate heating releases electrons trapped in defect states and drives them toward the conduction band, thereby increasing carrier density and sustaining photocatalytic activity even under weak illumination.9 In magneto-photo systems, Zeeman splitting under an external magnetic field generates spin-polarized charge carriers, which suppresses spin-forbidden recombination and facilitates spin-allowed O–O bond formation during OER.10,11 In addition, thermal-magnetic coupling offers an effective means to regulate spin alignment, because thermal activation near the Curie temperature can reorient magnetic domains and modulate spin transport, whereas a moderate temperature helps preserve long-range spin ordering and enhances spin-selective charge transfer.12 These representative examples illustrate that cooperative modulation of light, heat, and magnetic fields can reshape interfacial energetics, redistribute carrier populations, and open reaction pathways that are inaccessible under single-field conditions, thereby enabling dynamically optimized OER kinetics.
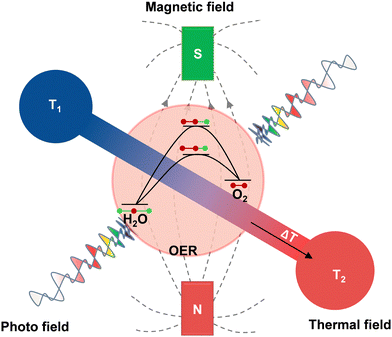 | ||
| Fig. 1 Schematic of multi-field-coupled OER. OER is intrinsically uphill. Synergistic magnetic, photo, and thermal fields reshape the reaction coordinate and lower the effective barrier. | ||
These findings establish external field modulation as a frontier strategy to overcome the intrinsic limitations of conventional OER catalysts. In this review, we first introduce the fundamental principles of OER, followed by the underlying physics and chemistry of individual external fields, including magnetic, photo, and thermal stimuli. We then discuss how these external fields interact through electron, phonon, and spin interactions, giving rise to synergistic effects that enhance catalytic activity. Subsequently, design strategies that exploit single-field and multi-field effects, together with theoretical insights obtained from density functional theory (DFT), are systematically summarized. Finally, perspectives are provided on future opportunities and challenges for developing efficient and durable field-driven electrocatalytic systems.
2. Fundamentals of OER
A comprehensive understanding of the fundamental principles of OER is crucial to fully appreciate the impact of external field enhancement. The OER involves the oxidation of water (in acidic or neutral media) or hydroxide ions (in alkaline media) to produce molecular oxygen.1,4,13Acidic medium:
| 2H2O(l) → O2(g) + 4H+(aq) + 4e− | (1) |
Alkaline medium:
| 4OH−(aq) → O2(g) + 2H2O(l) + 4e− | (2) |
Although the overall stoichiometry appears simple, OER is mechanistically complex, involving four coupled proton–electron transfers. Three primary pathways have been established: the adsorbate evolution mechanism (AEM), the lattice oxygen-mediated mechanism (LOM), and the oxide path mechanism (OPM).
Adsorbate evolution mechanism (AEM)
Under alkaline conditions, the AEM proceeds through four sequential electron-transfer steps at an active catalytic site (*):| * + OH− → *OH + e− | (3) |
| *OH + OH− → *O + H2O + e− | (4) |
| *O + OH− → *OOH + e− | (5) |
| *OOH + OH− → * + O2 + H2O + e− | (6) |
Among these elementary steps, the overall efficiency is usually dictated by the rate-determining step (RDS), namely the slowest and energetically most demanding transformation. In most cases, the *O → *OOH conversion is the bottleneck, though the exact RDS can shift depending on catalyst composition, local environment, and applied potential.5,14–16 According to the Sabatier principle, optimal OER activity requires a balance between adsorption and desorption of oxygen intermediates.17 However, density functional theory (DFT) studies reveal a widely acknowledged scaling relationship between *OH and *OOH adsorption energies (ΔG*OOH − ΔG*OH ≈ 3.2 ± 0.2 eV), which intrinsically constrains the minimum theoretical overpotential of AEM-based catalysts to ∼0.37 V.4,18–24
Overcoming this barrier is central to catalyst design, though it introduces trade-offs. Stronger adsorption can accelerate early steps but hampers *OOH formation, while weaker adsorption facilitates desorption yet destabilizes *OH formation. Moreover, catalysts optimized solely for activity often suffer from stability issues, such as dynamic surface reconstruction, cation leaching, or amorphization, which compromise long-term performance.25–27
To clarify when AEM dominates, it is generally favored in systems where the metal–oxygen bond is moderately strong and oxygen-vacancy formation is energetically unfavorable, thus preventing lattice-oxygen participation. In such cases, O2 evolves exclusively via surface-adsorbed intermediates (*OH, *O, *OOH) without isotope exchange with lattice oxygen. Representative AEM-type catalysts include RuO2, where operando isotope labelling and on-line electrochemical mass spectrometry confirm that the evolved O2 originates solely from electrolyte-derived oxygen.28 Likewise, NiFe and NiCoFe-based layered double hydroxides typically operate via the AEM pathway, as demonstrated by 18O-labeling and in situ Raman studies showing no lattice-oxygen incorporation.29 Therefore, AEM predominates on surfaces with low O 2p-metal 3d hybridization, limited oxygen-vacancy formation, and kinetically accessible *OOH formation.
Lattice oxygen-mediated mechanism (LOM)
The lattice oxygen mechanism (LOM) represents one of the major OER pathways.30 Like AEM, it begins with hydroxide adsorption and deprotonation, but the O–O bond forms differently: instead of proceeding through *OOH, adjacent *O species couple directly, with lattice oxygen actively participating in the redox cycle.31–34The likelihood of LOM is strongly influenced by metal–oxygen covalency. High orbital overlap between metal and oxygen facilitates lattice oxygen involvement, enabling O–O bond formation without reliance on the scaling-constrained *OOH intermediate.30,35,36 In this way, LOM provides a pathway to higher activity. However, lattice oxygen participation often raises stability concerns, as repeated oxygen extraction can induce structural distortions, oxygen vacancy accumulation, or irreversible phase transitions.37–39
LOM typically dominates when the metal–oxygen bond exhibits high covalency and the O-2p band approaches the Fermi level, enabling partial oxidation of lattice oxygen during OER. This electronic configuration facilitates charge delocalization across M–O bonds and reduces the energy required for oxygen vacancy formation. Canonical 18O isotope labeling studies on perovskites such as SrCoO3−δ and related families provide direct evidence that evolved O2 contains lattice-derived oxygen.30 In NiFe-based (oxy)hydroxides, Mo doping can increase oxygen-vacancy concentration and enhance metal–oxygen covalency, thereby shifting the reaction pathway from AEM to LOM.40
AEM and LOM offer complementary frameworks for understanding OER catalysis. Yet both face intrinsic trade-offs between activity and durability. These mechanistic insights underscore the importance of innovative strategies, such as external field modulation, to reshape reaction energetics and stabilize dynamic active sites, thereby transcending the limitations of conventional catalyst design.
Oxide path mechanism (OPM)
The oxide path mechanism (OPM) has recently emerged as a dual-site OER pathway that directly couples two adsorbed oxygen species (*O–O*), thereby bypassing *OOH and avoiding lattice-oxygen participation.41,42 By doing so, OPM circumvents the AEM scaling relation and mitigates LOM-induced structural instability, offering a route to combine high activity with durability.41,43,44 This dual-site coupling pathway effectively decouples the adsorption energies of intermediates and mitigates the activity-stability trade-off that plagues AEM- and LOM-based catalysts. Operando and theoretical studies now provide direct evidence for OPM, including the spectroscopic observation of *O–O* formation and free-energy profiles favouring dual-site coupling over *OOH routes.43Mechanistically, the OPM proceeds through two possible proton-coupled electron transfer (PCET) routes: (i) a stepwise proton removal pathway (*OH, *O, O*–OH*, O*–O*), and (ii) a continuous dehydrogenation route (OH(I)*–OH(II)*, O*–OH*, O*–O*). Both pathways culminating in adjacent-site *O–O* coupling. Critically, geometric proximity of dual sites is required. Dual metal centres must be close enough to enable orbital overlap for O–O bond formation.41
Compared with AEM and LOM systems, OPM-based catalysts exhibit significantly lower overpotentials and superior durability under both alkaline and acidic conditions.42,43,45,46 These features establish OPM as a balanced mechanism that unifies activity and stability. OPM has been successfully activated in various systems, including perovskites,45 layered double hydroxides,47 molecular catalysts (MOFs/COFs),42,45 and atomically dispersed catalysts with well-defined dual-atom48,49 or atom-array structures.50,51
Key performance metrics for OER electrocatalysts
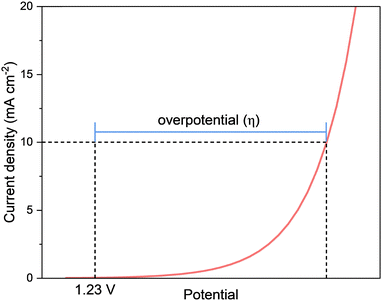
In the pursuit of advanced OER electrocatalysts, conventional benchmarking metrics remain indispensable. Yet, when catalysts operate under external stimuli, such as magnetic, photo, and thermal fields, the interpretation of these metrics acquires added depth. To rigorously evaluate such improvements and disentangle intrinsic effects from field-induced contributions, a standardized set of performance metrics is essential. These benchmarks extend beyond simple thermodynamic requirements to quantify efficiency, kinetics, and durability under realistic operating conditions. A comprehensive assessment requires a multidimensional perspective, as no single parameter suffices to capture the overall catalytic performance.Overpotential (η)
The most fundamental and widely reported metric for OER is the overpotential (η). It quantifies the extra potential required beyond the thermodynamic equilibrium potential to drive the reaction at a desired rate. The OER equilibrium potential of 1.23 V is defined with respect to the reversible hydrogen electrode (RHE). RHE represents the equilibrium of the hydrogen redox couple (2H+ + 2e− ⇌ H2). Because the RHE potential intrinsically compensates for the pH-dependent term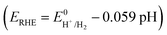 , the OER equilibrium potential remains constant at 1.23 V vs. RHE across different pH electrolytes.
, the OER equilibrium potential remains constant at 1.23 V vs. RHE across different pH electrolytes.
Mathematically:
| η = Eapplied − 1.23 V | (7) |
Tafel slope (b)
The relationship between the applied overpotential (η) and the resulting current density (j) is fundamental for evaluating catalytic performance. It is formally described by the Butler–Volmer equation:56,57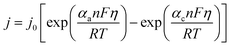 | (8) |
For OER, which occurs at a significant positive overpotential, the cathodic term becomes negligible, simplifying the equation to:
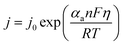 | (9) |
Taking the logarithm yields Tafel equation:
| η = b × log(j) + a | (10) |
Faradaic efficiency (FE)
Faradaic efficiency assesses selectivity by quantifying the fraction of charge that contributes to O2 evolution. It is defined as the ratio of experimentally measured O2 to the theoretical O2 expected from total charge transfer. An FE of 100% indicates perfect selectivity, whereas deviations reflect parasitic reactions such as catalyst self-oxidation, electrolyte degradation, or peroxide formation.61 FE is typically determined by coupling electrochemical data with gas quantification methods such as gas chromatography. For example, Ram et al. reported a delaminated CoWO4 catalyst whose FE for O2 generation was 96.6 ± 5.2% at 10 mA cm−2 over 160 min, demonstrating high selectivity under steady-state conditions.62Turnover frequency (TOF) and electrochemically active surface area (ECSA)
To isolate intrinsic activity from morphological contributions, normalization is essential.63 The turnover frequency (TOF) quantifies the number of O2 molecules generated per active site per unit time, providing a molecular-level measure of efficiency. For example, Chong et al. assessed the intrinsic activity of La- and Mn-codoped porous cobalt spinel fibers, which exhibited a high TOF of 0.079 ± 0.011 s−1 at an overpotential of 370 mV, underscoring their superior intrinsic kinetics.3 Accurate TOF calculation requires reliable estimation of active sites, which is often challenging. A widely used proxy for estimating the number of accessible active sites is the electrochemically active surface area (ECSA), commonly derived from double-layer capacitance (Cdl).64 For instance, Li et al. conducted cyclic voltammetry in the non-faradaic region of an atomically dispersed iridium oxide catalyst at scan rates from 0.002 to 0.05 V s−1. By plotting the anodic and cathodic charging currents at 1.30 V vs. RHE against the scan rate, they extracted the Cdl value, which was divided by a specific capacitance of 0.035 mF cm−2 in 1 M H2SO4 to obtain the ECSA.65However, for poorly conductive transition-metal oxides and hydroxides, the Cdl approach often fails to provide a reliable ECSA estimation. This unreliability stems from their strong dielectric behavior, where the measured capacitive current primarily reflects dielectric polarization rather than genuine double-layer charging.66 Additional factors, including pseudocapacitance from surface ion coordination or intercalation, chemical capacitance from trap-state occupation, and residual charge-transfer processes, further distort the Cdl response and lead to substantial uncertainty in the calculated ECSA.
To overcome these limitations, alternative or complementary approaches such as Ni redox charge integration and electrochemical quartz crystal microbalance (EQCM) measurements have been employed.67–69 The Ni redox charge method directly correlates the integrated charge of pre-OER Ni2+/Ni3+ redox peaks with the number of accessible active sites, provided that scan rate, potential window, and current overlap are carefully controlled. EQCM, in contrast, offers in situ tracking of mass changes during redox cycling, enabling correlation between charge transfer and the mass of active species. Reliable interpretation requires rigid film-substrate coupling and the exclusion of mass contributions from solvent or ion adsorption.
Given the inherent limitations of individual methods, combining multiple complementary techniques, including Cdl analysis, Ni redox charge integration, and EQCM, provides a more rigorous framework for accurately quantifying ECSA. Cross-validation enhances reliability and enables deeper insight into the intrinsic activity of oxide and hydroxide catalysts.
3. Fundamentals of external fields coupling in OER
3.1. Individual external field effects and their mechanistic principles
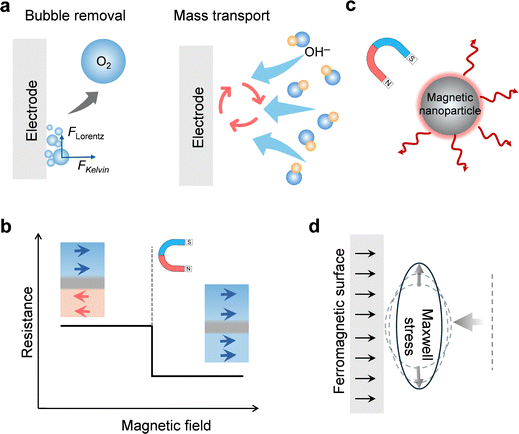
Magnetohydrodynamic (MHD) effect. The application of an external magnetic field to an electrochemical system can induce fluid motion through a phenomenon known as the magnetohydrodynamic (MHD) effect (Fig. 3a).6,70,71 This effect is governed by the Lorentz force (FLorentz = J × B, where J is the current density and B is the magnetic field), which acts on charged particles moving within a magnetic field.72 In the context of OER, the electrolyte contains mobile ions, such as hydroxide (OH−) or hydronium (H3O+) ions, as well as supporting electrolyte ions, which are all in motion under the influence of the applied electric potential. When an external magnetic field is applied perpendicular to the direction of ion movement (i.e., the current), a Lorentz force is exerted on these charge carriers. This force, acting on the bulk electrolyte, generates a convective flow or stirring effect at the microscale, fundamentally altering the mass transport regime near the electrode surface.73–79 This magnetically induced convection supplements the standard modes of mass transport (diffusion and natural convection), providing a powerful, non-intrusive method to manipulate the local environment of the electrocatalyst.
For OER, these magnetic effects offer solutions to key kinetic bottlenecks, most notably those related to mass transport and gas bubble management.70,80–83 OER is an archetypal gas-evolving reaction where the product, O2 gas, forms bubbles directly on the catalyst's active sites. These bubbles often adhere to the surface, masking active areas, impeding reactant transport, and increasing local ohmic resistance. The MHD-induced convection, driven by the Lorentz force, creates micro-vortices that exert a drag force on these bubbles, promoting their detachment. Furthermore, a secondary magnetic force, the Kelvin force, comes into play.77,84,85 The Kelvin force originates from the magnetic field gradient (∇B) that forms at the interface between the electrolyte and ferromagnetic or ferrimagnetic electrodes such as Ni or γ-Fe2O3@NF.86
When these magnetic electrodes are placed in an external magnetic field, they redistribute the local magnetic flux: the field becomes stronger near the electrode edges and weaker above and below the surface, creating a pronounced magnetic-field gradient at the electrode/electrolyte interface. This gradient exerts an outward Kelvin force on the paramagnetic O2 bubbles, directed toward the region of higher magnetic flux density. As a result, the bubbles experience an additional driving force that facilitates their detachment and release from the electrode surface, thereby enhancing mass transport and maintaining a refreshed reaction interface.
The Kelvin force can be expressed as:
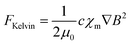 | (11) |
The performance enhancements stemming from these combined magnetic phenomena are directly observable in key OER metrics. By accelerating the removal of O2 bubbles through both convective drag (Lorentz force) and direct magnetic attraction (Kelvin force), and by enhancing the transport of reactants to the electrode surface, the overall process becomes more efficient. This significantly reduces both concentration polarization and the overpotential associated with surface passivation by gas bubbles. Consequently, this translates to a lower total overpotential required to achieve a target current density and can lead to a substantial increase in the limiting current density. By maintaining a more accessible catalyst surface and mitigating harsh local pH gradients, these magnetic forces can offer a distinct physical pathway to overcome the intrinsic sluggishness of the OER.
Magnetoresistance effect. Beyond influencing the bulk electrolyte, an external magnetic field can directly alter the intrinsic electronic properties of the electrocatalyst material itself through the magnetoresistance (MR) effect (Fig. 3b). Magnetoresistance is defined as the change in a material's electrical resistance in response to an applied magnetic field.87,88 This is a solid-state phenomenon, fundamentally different from the MHD effect, as it pertains to charge transport within the catalyst rather than ion transport in the electrolyte. The magnitude and sign of the MR effect, whether the resistance increases (positive MR) or decreases (negative MR), are intrinsic properties determined by the material's crystal structure, magnetic ordering, and the interaction between charge carriers (electrons or holes) and local magnetic moments.87,89 For OER catalysts, this effect introduces a tunable electronic parameter that can directly impact the overall efficiency of the electrochemical process.
The primary consequence of the MR effect on OER performance is its influence on the ohmic overpotential. The total potential applied to an electrochemical cell is partitioned into several components: the thermodynamic potential, the activation overpotential, the concentration overpotential, and the ohmic drop (IR drop). A portion of this ohmic drop occurs within the catalyst material itself as electrons travel from the active sites to the current collector. If a catalyst exhibits negative magnetoresistance, its internal electrical resistance decreases under a magnetic field. This reduction in resistance leads to a smaller internal ohmic drop for any given current density. As a result, a larger fraction of the applied potential is available as effective overpotential at the catalyst–electrolyte interface, where it can drive the charge-transfer reactions of the OER. This manifests as a lower measured overpotential for the system, effectively making the catalyst appear more active.
Furthermore, the MR effect may have more subtle and profound implications tied to the spin-dependent nature of the OER mechanism itself.6,90–92 The overall reaction requires the conversion of spin-singlet reactants (H2O or OH−) into a spin-triplet product (ground-state O2), a transition that creates a kinetic barrier. In magnetic catalysts, the application of a magnetic field can influence the spin alignment of the d-electrons that constitute the active sites. This spin polarization of the catalyst surface could act as a “spin filter”, potentially lowering the activation energy for the spin-forbidden steps by facilitating spin-selective electron transfer. In this scenario, the MR effect is not just a measure of changing resistance but is a macroscopic signature of the underlying spin-dependent scattering processes that could be directly modulating the intrinsic catalytic activity, offering a pathway to lower the activation overpotential in addition to the ohmic overpotential.
In the La1−xSrxMnO3 system, the application of a DC magnetic field aligns the spins along the Mn–O–Mn double-exchange pathways, thereby suppressing spin-disorder-induced electron scattering. Electrochemical impedance spectroscopy shows a pronounced decrease in Rct under the magnetic field, and the authors conclude that the magnetoresistance (MR) effect plays a dominant role in decreasing spin electron-dependent scattering after applying an external DC magnetic field, which in turn facilitates electron transfer and effectively lowers the resistivity.93
Here, MR quantifies the change in electrical resistance under an external magnetic field, is defined as
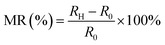 | (12) |
Beyond the La1−xSrxMnO3 system, similar magnetoresistance-driven enhancement of the OER has also been reported for Ni-based catalysts under external magnetic fields.94 In this study, the field-induced reduction in overpotential closely followed the magnitude of negative MR across Ni(OH)2, NiO, and Ni catalysts. The authors attributed this improvement to magnetic-field-induced alignment of magnetic domains inside the ferromagnetic catalysts, which reduces spin-dependent scattering at domain boundaries and enhances spin-polarized charge transfer during the first electron-transfer step of OER. This MR-governed spin-alignment mechanism directly modifies the intrinsic electronic conductivity of the catalyst, thereby accelerating the reaction kinetics without changing the reaction pathway.
Magnetothermal effect. The magnetothermal effect describes the phenomenon where a material's temperature changes in response to a magnetic field, providing a direct pathway to influence reaction kinetics through localized heating (Fig. 3c).95 The primary mechanism underpinning this is the magnetocaloric effect (MCE), an intrinsic property of magnetic materials where the application or removal of a magnetic field alters the material's magnetic entropy. To conserve total entropy, this change is compensated by an opposite change in the lattice vibrational entropy, resulting in a temperature increase or decrease.96,97 In the context of OER, catalysts designed with a significant MCE can be locally heated by applying a magnetic field.98–100 This offers a distinct advantage over conventional bulk heating, as it concentrates the thermal energy precisely at the catalyst–electrolyte interface where the reaction occurs, improving energy efficiency and minimizing heat loss to the surrounding system.
The enhancement of OER kinetics via the magnetothermal effect is rooted in the fundamental relationship between temperature and reaction rate, as described by the Arrhenius equation. The multi-step OER process is characterized by significant activation energy barriers (Ea) for its elementary steps, which is a primary reason for its sluggishness. By inducing localized heating, the magnetothermal effect provides the necessary thermal energy to help the system overcome these barriers more easily. This directly accelerates the rate of the charge-transfer steps, leading to a substantial increase in the reaction's intrinsic rate constant. Consequently, this mechanism primarily targets the reduction of the activation overpotential, allowing the reaction to proceed more rapidly at a given applied potential. Furthermore, the localized increase in temperature can also enhance the local diffusion rates of reactant ions (e.g., OH−) and facilitate the desorption of O2 product bubbles, further contributing to improved mass transport.101–103
The practical impact of the magnetothermal effect on OER performance is multifaceted and significant. The most direct outcome is a reduction in the overpotential required to achieve benchmark current densities, as the thermally accelerated kinetics make the catalyst intrinsically more active. This can also be reflected in a more favorable Tafel slope, indicating that the reaction rate becomes more sensitive to changes in applied potential. Importantly, the magnetothermal effect opens up powerful synergistic possibilities. It can be combined with photothermal effects, where a magnetic field might enhance a material's ability to convert light into heat, or with other magnetic phenomena like the magnetoresistance effect.104,105 By providing a non-contact method to precisely control the local thermal environment of the catalyst, the magnetothermal effect represents a sophisticated strategy for rationally designing highly efficient OER systems.
Maxwell stress. The Maxwell stress is a surface force that arises at the interface between two media with different electrical or magnetic properties when subjected to an electromagnetic field (Fig. 3d). It can be conceptualized as the “pressure” or “tension” exerted by the field itself. In the context of OER, this force becomes relevant at two key interfaces: the electrode–electrolyte interface and, more significantly, the gas bubble–electrolyte interface. Unlike the Lorentz force, which is a body force acting on moving charges within the bulk electrolyte, the Maxwell stress acts directly on the boundary surface due to discontinuities in electric permittivity and magnetic permeability. This provides another distinct physical mechanism through which an external magnetic field can manipulate the electrochemical environment.
The primary role of Maxwell stress in enhancing OER is its ability to influence gas bubble dynamics. An O2 gas bubble has a much lower dielectric constant and different magnetic susceptibility compared to the surrounding aqueous electrolyte. When an electric and/or magnetic field permeates this system, the field lines are distorted at the bubble's surface, creating a non-uniform field distribution that results in a net force described by the Maxwell stress tensor. This force can deform the bubble and, more importantly, exert a physical push or pull on it, promoting its detachment from the catalyst surface. By actively dislodging bubbles, the Maxwell stress helps to keep the catalyst's active sites clear and accessible to reactants, thereby mitigating the performance losses associated with bubble adhesion.
While its effect on bubble management is the most direct contribution, the Maxwell stress may also have more subtle impacts. The force exerted at the electrode–electrolyte interface could potentially induce localized surface strain or even restructuring in soft or nanoscale catalyst materials, thereby modulating their intrinsic electronic properties and catalytic activity. It is crucial to recognize that the Maxwell stress does not act in isolation; it coexists and interacts synergistically with the Lorentz force, Kelvin force, and other magnetic phenomena. The overall observed enhancement is a complex interplay of these forces, where Maxwell stress contributes a unique surface-acting component that complements the body forces and paramagnetic attractions, collectively leading to a more efficient and stable OER process.
Spin state reconfiguration. When an external magnetic field (B) is imposed on magnetic catalysts such as Fe-, Co-, or Ni-based oxides, it reorganizes the spins and electronic structure at the active sites. This reconfiguration modulates the adsorption energetics of reaction intermediates, the kinetics of interfacial charge transfer, and the energy profiles of elementary steps. In this regard, the magnetic field serves as an effective external parameter that controls both spin polarization and orbital occupation, thereby offering an effective approach to tailor surface electronic structures and reaction energetics in electrocatalysis.
At the atomic and surface level, the magnetic field aligns magnetic domains within the catalyst, generating a spin-polarized surface where electrons share a unified spin orientation. This alignment enables oxygen intermediates (*OH, *O, *OOH) to couple more readily into triplet O2, a step that is normally spin-forbidden, effectively lowering the O–O formation barrier. Such enhancement is observed only for ferromagnetic or ferrimagnetic catalysts like NiZnFe4Ox, while non-magnetic IrO2 shows negligible change, confirming a spin-origin mechanism.106,107 Meanwhile, the magnetic field strengthens exchange coupling between the ferromagnetic lattice and the surface oxyhydroxide layer, allowing the substrate's ordered spins to “pin” the spin orientation of oxygen intermediates during the first electron-transfer step.91 This interfacial spin pinning facilitates spin-consistent charge transport and improves kinetics, often observed as a reduction in Tafel slope and enlarged magnetic coercivity.90
Beyond spin alignment, the magnetic field also subtly modulates the electronic configuration of transition-metal centres. The external field affects the relative energies of spin sublevels within the d orbitals, leading to a redistribution of electrons among them. Such field-induced splitting of spin states (known as Zeeman splitting) can shift the equilibrium between high-spin (HS) and low-spin (LS) configurations, thereby tuning the occupancy of antibonding eg(σ*) orbitals.108,109 The eg filling level directly determines metal–oxygen bond strength: too low causes overly strong adsorption, too high weakens binding, while eg ≈ 1 achieves an ideal balance.110 Magnetic fields thus serve as fine regulators of eg filling, M–O covalency, and charge-transfer energy, lowering activation barriers and optimizing catalytic performance.111–113
In summary, the magnetic field synchronizes spin alignment, stabilizes interfacial spin exchange, and fine-tunes orbital electron occupancy, synergistically promoting faster electron transfer and more favourable intermediate binding to accelerate oxygen evolution.
Photothermal effect. The photothermal effect refers to the temperature rise of a material upon absorbing light. The efficiency of converting light into heat varies among materials and is determined by how their electronic or band structures respond to electromagnetic (EM) radiation. Three main physical pathways are responsible for this light-to-heat conversion: plasmonic localized heating, nonradiative relaxation in semiconductors, and thermally activated molecular vibrations.
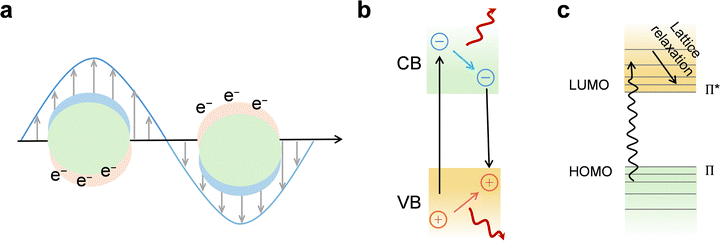
Plasmonic localized heating: in metallic nanostructures with subwavelength dimensions, localized surface plasmon resonance (LSPR) is a dominant mechanism for photothermal conversion (Fig. 4a). Under resonant illumination, conduction electrons collectively oscillate at the surface, strongly confining the incident EM field to the nanoscale. This resonance not only amplifies local electric fields but also significantly enhances optical absorption and scattering cross-sections, enabling efficient energy capture. The photothermal process proceeds through sequential steps: (i) excitation of LSPR by photons whose energy matches the plasmon band;114 (ii) ultrafast dephasing and decay of plasmons via either radiative photon re-emission or nonradiative Landau damping;115,116 (iii) generation of highly energetic, nonthermal “hot” electrons within tens to hundreds of femtoseconds;117 (iv) energy redistribution through electron–electron collisions (∼100 fs – 1 ps) followed by electron–phonon coupling (ps – hundreds of ps), leading to lattice heating;118 and (v) dissipation of heat to the surrounding medium via phonon–phonon scattering on the 100 ps – 10 ns timescale. This cascade transforms photon energy into localized thermal energy, making plasmonic nanostructures exceptionally effective nanoscale heat sources.119
Nonradiative relaxation in semiconductors: in nonplasmonic semiconductors, photothermal heating can originate from direct interband or intraband electronic transitions (Fig. 4b). When incident photons have energy exceeding the bandgap, they generate electron–hole pairs. These carriers can lose energy radiatively by emitting photons, or nonradiatively by transferring it to the lattice.120,121 The latter pathway, mediated by phonon emission, results in localized heating. Two principal nonradiative mechanisms dominate: Shockley–Read–Hall (SRH) recombination and Auger recombination.122,123 SRH recombination, often associated with defects or impurities, involves carrier capture by mid-gap trap states followed by relaxation to the opposite band, with the process accompanied by phonon release.124 Auger recombination, more significant in narrow-bandgap materials, involves three carriers, where the recombination energy of an electron–hole pair is transferred to a third carrier, which then thermalizes via lattice vibrations. Both mechanisms ultimately convert carrier energy into lattice heat, with efficiencies dependent on intrinsic material properties and defect densities.
Thermal vibrations in molecules: certain carbon-based materials and organic polymers also exhibit strong photothermal responses, largely through molecular vibration-electron coupling (Fig. 4c). Although σ–σ* transitions in bonds like C–C, C–O, and C–H require high excitation energies, π electrons in conjugated or aromatic systems can be excited from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) under relatively low-energy illumination.125,126 Following electronic excitation, relaxation back to the ground state occurs via vibrational pathways, releasing energy as heat. Extended π-conjugation reduces the HOMO–LUMO gap, enhancing light absorption in the visible to near-infrared range and improving photothermal conversion efficiency. Hyperconjugation and delocalization effects further facilitate these low-energy transitions, making such materials competitive candidates for photothermal applications.127,128
The photothermal effect occurs when a catalyst absorbs light and converts part of the photon energy into heat rather than using it for electronic excitation. In metals, plasmonic nanostructures, or strongly absorbing semiconductors, absorbed photons can relax through non-radiative pathways, where the excited electrons transfer their excess energy to the lattice via electron–phonon coupling. This process leads to localized heating at the catalyst–electrolyte interface, with temperature increases often confined to nanometer-scale regions. The magnitude of the effect depends on the material's optical absorption properties, the presence of plasmonic resonances, and the efficiency of heat dissipation to the surrounding medium.119,129,130
To decouple the intertwined contributions of thermal and photo effects during photo-assisted OER, several experimental “handles” have been established. Thermal effects can be modulated by controlling the reaction temperature or adjusting the infrared absorption of the catalyst layer.131 A common approach is to perform dark-light switching experiments under constant temperature, using a thermostated electrochemical cell to ensure identical bulk and interfacial temperatures in both illuminated and dark states.132,133 This allows researchers to isolate the portion of activity enhancement solely attributed to photothermal heating.
Complementary tools such as infrared thermography and micro-thermocouples can further quantify local surface temperature differences.134,135 While wavelength-dependent illumination provides mechanistic insight, if near-infrared (NIR) light, which has insufficient photon energy for electronic excitation, still enhances activity, the effect is dominantly photothermal.136,137 Moreover, constructing Arrhenius plots of log(current) versus 1/T under light and dark conditions can verify whether the enhancement follows classical thermal kinetics.138,139
In contrast, photo-induced effects arise from photo-driven charge redistribution or electronic excitation. They can be tuned by varying the photon energy or illumination intensity and identified by monochromatic excitation and isothermal photoelectrochemical measurements.67,140 When illumination with photon energies above the bandgap yields enhanced current under a constant temperature, the improvement originates from genuine photoexcitation rather than heating.141,142 Additionally, chopped-light transient photocurrent or EIS measurements provide direct evidence of photo-carrier participation: a fast, reversible current response upon light on/off indicates non-thermal electron–hole dynamics.143,144
Overall, thermal effects primarily accelerate reaction kinetics by increasing temperature: they reduce apparent activation barriers, enhance ionic conductivity and mass transport, and thus increase the reaction rate at a given applied potential. By contrast, in a more general sense, photo effects mainly originate from the generation of photogenerated charge carriers and the associated photovoltage under illumination. This additional driving force effectively reduces the overpotential that must be supplied by the external bias, raises the steady-state carrier density at the catalyst–electrolyte interface, and thereby boosts the apparent OER kinetics. Consequently, carefully designed isothermal photoelectrochemical measurements combined with dark heating controls are indispensable to disentangle thermal acceleration from genuine photoinduced driving forces, and to rationally design multi-field-coupled OER systems that exploit both temperature and photovoltage in a controllable manner.
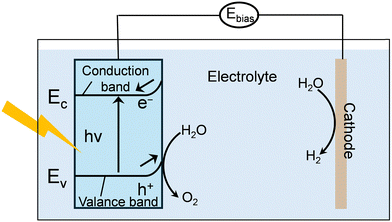
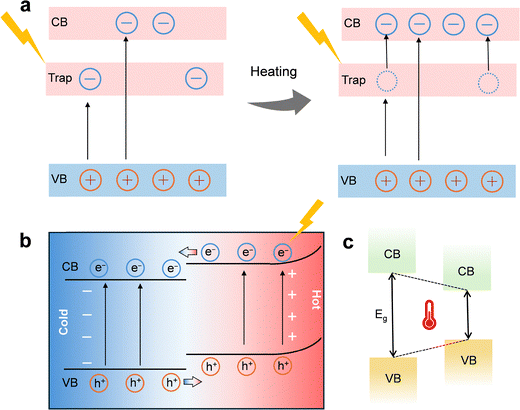
Photoelectric effect. The photoelectric effect in OER, refers to the direct conversion of photon energy into mobile charge carriers within a semiconductor catalyst (Fig. 5).145 This principle underpins photoelectrochemical (PEC) water splitting. Unlike the photothermal effect, which transforms light into heat and indirectly influences reaction kinetics, the photoelectric effect uses photons to excite electrons across the semiconductor bandgap (E ≥ Eg), generating electron–hole pairs.
When a semiconductor photoanode absorbs light, electrons are promoted from the valence band (VB) to the conduction band (CB), leaving behind positively charged holes (h+). A built-in electric field in the space-charge region at the semiconductor–electrolyte interface drives these carriers apart: photogenerated holes migrate toward the surface to participate in oxidation, while electrons are swept into the bulk and collected by the external circuit. At the anode surface, the highly oxidizing holes directly drive the multi-step OER, effectively substituting for the external current required in conventional electrocatalysis.
The efficiency of this process hinges on minimizing recombination losses, both within the bulk and at the surface, as any recombination converts the absorbed photon energy into heat or luminescence.145–147 Strategies such as constructing heterojunctions, introducing co-catalysts, or engineering surface passivation layers are commonly employed to enhance charge separation.
A key manifestation of the photoelectric effect is the generation of photocurrent and the associated photovoltage. Under illumination, the absorbed photons provide part of the reaction driving force, resulting in a cathodic shift of the OER onset potential compared to dark conditions. In ideal cases, this enables water oxidation at little or no external bias, with light supplying a substantial fraction of the required energy. This synergy between light absorption and electrochemical bias directly enhances the energy efficiency of PEC water splitting and is central to achieving high solar-to-hydrogen (STH) conversion efficiencies.
Despite significant advances, PEC water splitting still faces several intrinsic limitations that hinder its large-scale application. First, inefficient charge separation and transport severely restrict quantum efficiency. In many semiconductors such as Fe2O3 and Cr2O3, photogenerated carriers undergo rapid bulk and interfacial recombination due to short diffusion lengths and sluggish charge mobility, leading to low photocurrents even under strong illumination.148,149 For instance, hematite photoanodes typically exhibit hole diffusion lengths below 4 nm,150,151 much shorter than the light absorption depth, resulting in excessive recombination losses.
Second, chemical and photoelectrochemical instability remains a major obstacle. Narrow-bandgap materials such as CdS, GaP, and Si are prone to photocorrosion or oxidation in aqueous electrolytes, leading to rapid degradation of photocurrent.152–154 Protective overlayers (e.g., TiO2, Al2O3, or NiOx) and catalyst coatings can slow the deterioration but often introduce additional interfacial resistances.155,156
Finally, low solar-to-hydrogen (STH) efficiency persists at the device level. Even with tandem PEC architectures, practical efficiencies rarely exceed 10%, as energy losses from sub-bandgap photons and overpotentials at the oxygen and hydrogen evolution interfaces remain substantial.157 Consequently, rational band engineering, interface passivation, and hybrid photoelectrocatalytic-photothermal systems are being explored to overcome these fundamental constraints and approach scalable, stable solar fuel generation.158–161
Plasmonic hot carrier generation. In plasmonic materials such as Au, Ag, and Cu, illumination at resonant wavelengths excites localized surface plasmon resonances (LSPR), which are collective oscillations of conduction electrons. These plasmons can decay radiatively, emitting photons, or non-radiatively, producing hot electrons and hot holes with excess energies relative to the Fermi level. The hot carriers can transfer to adjacent semiconductor bands or directly to adsorbed molecules, provided they have sufficient energy to overcome interfacial barriers. The short lifetimes of these carriers (femtoseconds to picoseconds) make their capture efficiency dependent on ultrafast interfacial transfer processes.114,162,163
Photoinduced surface state modulation. Light irradiation can dynamically alter the surface chemistry of a catalyst by creating or annihilating defect states such as oxygen vacancies, hydroxyl groups, or cation vacancies. This process often involves the trapping of photogenerated carriers at the surface, which changes local charge density, modifies bonding configurations, and shifts the Fermi level. Such changes can influence the local electric field at the interface and modify the adsorption energy of reaction intermediates. These surface state modifications can be reversible, depending on illumination conditions and reaction environment164,165
Photo-induced phase transition. High-energy photons or hot carriers can trigger structural and electronic transformations in a catalyst, resulting in changes to crystal phase, oxidation state, or coordination environment. In layered transition metal dichalcogenides, for example, light can induce a semiconducting 2H phase to transform into a metallic 1T phase through carrier injection and bond rearrangement. Similar transformations can occur in metal oxides, where light exposure changes the oxidation state of surface atoms. These transitions can be reversible or irreversible, depending on the energy input and material stability, and they often lead to significant changes in electronic properties.166,167
The thermal-induced strain effect arises in heterogeneous catalyst systems, particularly where an active material is anchored to a substrate or support.168–170 This effect is driven by the mismatch in the coefficient of thermal expansion (CTE) between the two different materials.171,172 When the system is heated, either through an external source or via localized photothermal or magnetothermal effects, the catalyst and its underlying support attempt to expand at different rates. Because they are physically bound at an interface, this differential expansion creates significant mechanical stress. This stress results in lattice strain (Fig. 6b), which is a physical distortion of the catalyst's crystal structure. Depending on the relative CTEs, the catalyst can be subjected to either tensile strain (stretching) or compressive strain (squeezing), providing a dynamic and tunable method for manipulating its atomic arrangement.173
This mechanically induced strain directly modulates the electronic properties of the catalyst's active sites, which is the core of its mechanism for enhancing OER.174,175 According to the d-band center theory, the catalytic activity of transition metals is strongly correlated with the energy level of their d-electron states.176,177 Lattice strain alters the interatomic distances, which in turn modifies the overlap between electron orbitals and shifts the d-band center.178 For instance, tensile strain typically weakens orbital overlap, narrowing the d-band and shifting its center upwards, which often leads to stronger binding of reaction intermediates.174 Conversely, compressive strain increases orbital overlap, broadening the d-band and shifting its center downwards, leading to weaker binding. By carefully engineering the CTE mismatch, the binding energies of key OER intermediates (*OH, *O, *OOH) can be fine-tuned to more closely match the optimal values predicted by the Sabatier principle.
The practical consequence of this strain-induced electronic tuning is a direct reduction in the activation energy for the rate-determining step of the OER. This translates into superior catalytic performance, observable as a lower overpotential and potentially a more favorable Tafel slope. Crucially, the thermal-induced strain effect represents a powerful synergistic mechanism. When a catalyst is heated via photothermal or magnetothermal means, the performance boost is not solely due to the Arrhenius-type thermal acceleration of kinetics. It is a dual enhancement, where the heat simultaneously provides thermal energy and induces beneficial strain. This integrated effect, where a single stimulus triggers two distinct enhancement pathways, offers a more potent strategy for overcoming the intrinsic limitations of OER catalysis.
3.2. Cross-field interactions and coupling phenomena
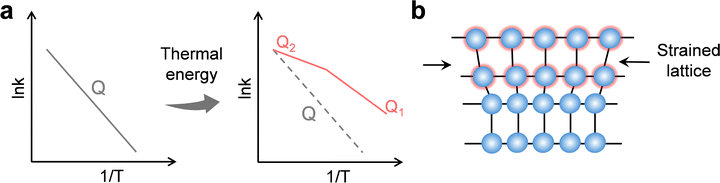
Thermal energy can expand carrier generation beyond direct bandgap transitions. In oxygen-deficient TiO2, moderate heating promotes electrons trapped at vacancy states into the conduction band,9,184 increasing the density of active carriers for surface reactions (Fig. 7a). Narrow-bandgap semiconductors such as Ti2O3 can convert nearly all absorbed photons into heat,185,186 enabling continuous thermally assisted excitation under broadband solar input. Pyroelectric materials like ZnSnO3 use temperature cycling to induce spontaneous polarization and internal electric fields that facilitate photoexcitation; under UV light and thermal cycling between 20–65 °C, RhB degradation reached nearly 98%, surpassing photocatalysis (∼77%) or pyroelectric catalysis (∼20%) alone.187 These findings highlight that coupling defect engineering or pyroelectric effects with broadband absorption can unlock carrier reservoirs inaccessible to pure photoexcitation.
Temperature gradients can be converted into internal electric fields via the Seebeck or pyroelectric effect,188,189 which drive electrons and holes apart to suppress recombination (Fig. 7b). In plasmonic systems, localized heating combined with interfacial engineering, such as in Au@CdS core–shell architectures190 or Au/TiO2 with ultrathin dielectric layers,191 extends hot-carrier lifetimes and increases steady-state charge density. Nonplasmonic systems also benefit from pyroelectric-assisted separation; for example, CdS nanorods modified with 2-mercaptobenzimidazole achieved over a fourfold enhancement in hydrogen evolution at 25–55 °C compared with pristine CdS,192 with improvements persisting under weak illumination. These results demonstrate that controlled thermal gradients can function as an internal “driving field” for carrier separation, particularly valuable under low-light or fluctuating sunlight conditions.
Thermal activation further improves carrier mobility by lowering energy barriers across interfaces or defect sites. In oxygen-deficient WO3/CdS core–shell structures, the WO3 core harvests photons across UV-vis-NIR wavelengths, storing electrons that are subsequently thermally transferred to the CdS shell for hydrogen generation.193 Similarly, CdS-based composite microfibers,194 when exposed to infrared light, developed pyroelectric fields in their substrate that boosted water-splitting rates by more than fivefold and delivered an average apparent quantum efficiency close to 17%.195,196Operando monitoring confirmed that the thermoelectric output generated during reaction directly correlated with enhanced carrier migration toward reactive sites. This clear link between temperature control and directional carrier transport highlights a powerful strategy for next-generation solar-fuel devices.
Temperature also influences recombination dynamics in both beneficial and detrimental ways. Moderate heating accelerates surface reaction steps, effectively depleting carriers before recombination. For example, in oxygen-deficient TiO2, heating releases electrons trapped at oxygen vacancies to reactive surface states, thereby accelerating electron transfer to adsorbed CO2 and boosting multi-electron reduction pathways.9,197 Conversely, excessive heating increases phonon and carrier-carrier scattering, activating SRH/Auger non-radiative channels and shortening carrier lifetimes,198,199 while in plasmonic systems, prolonged strong heating can damage active sites.200 Coupling pyroelectric polarization with plasmonic structures has further been shown to locally tune hot-carrier densities, enhancing both surface reactions and optical responses.201,202 These observations underscore the importance of precise thermal-field control, balancing beneficial carrier activation with the risks of accelerated recombination or catalyst degradation.
Another fundamental thermal-photo coupling mechanism arises from the temperature dependence of semiconductor band gaps (Fig. 7c). As temperature increases, enhanced phonon interactions cause band-gap narrowing, which extends light absorption toward longer wavelengths and modifies the generation of electron–hole pairs.203 In this way, thermal excitation complements photoexcitation by reshaping carrier energetics and supporting more efficient utilization of incident light.
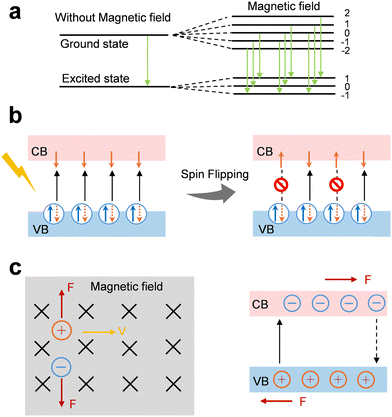
Recently, Zeeman effect has been introduced into the electrocatalysis sysytem to explain the magnetic-field influence on reaction kinetics. When a magnetic field is applied, spin-up and spin-down energy levels are separated, leading to a population imbalance that promotes electron transfer through spin-favored channels. This spin selectivity reduces the probability of opposite-spin recombination and accelerates spin-matched O–O bond formation steps. Both theoretical and experimental studies have demonstrated that the Zeeman effect can modulate adsorbate energetics, tuning activation barriers and improving reaction rates. For instance, Yao et al. linked the enhanced performance to magnetic-field-induced reconfiguration of interfacial water and Zeeman splitting of hydrogen atoms, both of which accelerate interfacial charge-transfer kinetics. A 50 mV drop in overpotential at 10 mA cm−2 was observed under a 1 T field in the HER system.213 Nguyen et al. provided direct EPR evidence that Zeeman interactions govern the spin-level splitting and transition probabilities of oxygen molecules under magnetic fields, thus offering measurable confirmation of magnetic field-driven spin conversion during OER.214 Xia et al. further demonstrated that the Zeeman effect amplifies spin-polarized band splitting in magnetic semiconductors, prolonging carrier lifetimes and enhancing catalytic rates.206 More importantly, Huang et al. found that applying a 0.4 T magnetic field to CoFe2O4, the overpotential at 10 mA cm−2 reduced by 39 mV and the Tafel slope reduced from 92 mV to 83 mV dec−1, with no detectable structural changes.92 The authors attributed this remarkable enhancement to magnetic effect-induced spin polarization, a behaviour that is consistent with the role of Zeeman splitting in redistributing spin populations under an external magnetic field. This promotes spin-selective electron transfer and promotes spin-aligned electron involvement in M–O and O–O coupling, thereby reducing spin–flip barriers and accelerating OER kinetics. Collectively, these findings indicate that the Zeeman effect provides foundation for understanding and designing spin-sensitive electrocatalysts with magnetically tunable OER activity.
In addition to spin regulation, magnetic fields also act directly on charge carrier trajectories. Under a magnetic field, photogenerated electrons and holes experience Lorentz forces that deflect their paths, leading to spatial separation of carriers both in the bulk and at interfaces (Fig. 8c).215,216 This effective charge separation reduces recombination losses and increases the probability that carriers reach active sites. The asymmetric motion further establishes local potential gradients at catalyst surfaces, which drive carriers directionally toward reactive centers.217 In liquid-phase photocatalytic systems, Lorentz forces can additionally enhance mass transport by enriching oppositely charged reactants near the catalyst surface, thereby raising their collision frequency and overcoming diffusion limitations.218
Beyond these effects on spin and orbital motion, magnetic fields also regulate charge transport kinetics through magnetoresistance. By altering the resistivity of semiconductors, magnetic fields can tune carrier mobility and interfacial transfer rates. Negative magnetoresistance decreases resistive losses, accelerating carrier migration to surface-active sites while minimizing energy dissipation. In contrast, positive magnetoresistance may be advantageous in some cases by suppressing premature recombination.219,220 Such transport modulation is especially critical at heterojunction interfaces or in defect-rich regions, where conductive pathways are complex and easily disrupted. Optimizing magnetoresistance in these environments ensures that a higher proportion of photogenerated carriers contribute to productive redox reactions at the surface.212,215,221
Within an optimal temperature range, thermally induced adjustments of electronic states and variations in orbital interactions can enhance spin coherence at interfaces, enabling spin-polarized carriers to maintain higher directionality and selectivity during transport. This, in turn, improves both carrier mobility and stability. However, excessive heating can disrupt spin alignment, alter magnetic anisotropy, and reduce performance associated with magnetic ordering. In multiphase composite or core–shell architectures, a strongly magnetic core can help sustain interfacial spin alignment even when the outer layer loses long-range order, thereby extending the magnetic responsiveness of the material under external perturbations.
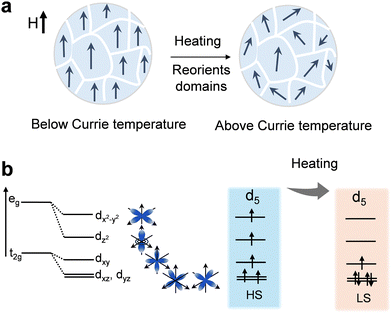
Besides, thermally induced spin-state transitions provide an effective strategy to regulate the electronic configuration of transition-metal catalysts and thereby optimize their OER activity. In a d5 configuration, heating can drive the system from a high-spin (HS) to a low-spin (LS) state (Fig. 9b),12 which alters the occupancy of eg orbitals and modifies the metal–oxygen bonding strength at the active sites. This transition reduces the energy mismatch between metal d orbitals and oxygen intermediates, improving charge transfer and lowering the kinetic barrier for O–O bond formation. Unlike static structural modifications, spin-state transitions offer a dynamic and reversible means of tuning catalytic behaviour under operating conditions, providing a new design principle for thermally responsive OER electrocatalysts.
The interplay between temperature and magnetic ordering offers a controllable physical lever for tuning spin alignment. By precisely setting the operating temperature close to, but below, the magnetic phase transition point, it is possible to introduce moderate thermal excitation while preserving high spin ordering, achieving a dual optimization of spin transport efficiency and energy-state regulation. This regulation strategy is not limited to specific magnetic catalytic systems but can also be generalized to a broader class of multifunctional materials in multi-field coupling scenarios, providing new design guidelines for next-generation energy conversion and transport devices.
4. Design strategies for enhancing OER via external fields and their synergistic effects
4.1. Single field enhancement
In contrast, the Lorentz force generated by the interaction of current and magnetic field can induce magnetohydrodynamic (MHD) convection, enhancing electrolyte circulation and gas-bubble detachment. In microgravity environments, the combined Lorentz-driven MHD flow and magnetic buoyancy arising from magnetic susceptibility differences between diamagnetic water and paramagnetic oxygen effectively replace gravitational convection, leading to rapid bubble release, thinner diffusion layers, and up to ∼23% higher current density for OER.231
Additionally, Lorentz-force-induced transverse ion convection can occur even in the absence of magnetic catalysts. A uniform magnetic field acting on ionic currents was reported to generate vortex-like motion in the electrolyte, enhancing mass transport and increasing the diffusion-limited current by over 50% in diffusion-limited reactions.83
Recently, it has attracted increasing attention that the spin configuration of OH−/H2O is different from that of O2. Specifically, the OH−/H2O is in spin singlet state with all electrons paired. However, the O2 is in spin triplet state with two unpaired electrons.232–234 The difference between the spin configurations of reactants and products will cause spin transition during the OER. Thus, additional energy will be consumed during the reaction, which will lead to excessive overpotential. Then, external magnetic field was added to facilitate the polarization of oxygen intermediates.
The spin configurations of electrocatalysts have been found to have a close relationship with their OER performance.240–244 A compelling demonstration of spin-configuration control affecting OER activity comes from the formation of high-spin Co3+ in cobalt oxyhydroxides. In the study by Zhang et al., the authors show that deliberately inducing a high-spin configuration (eg2 t2g4) for Co3+ in CoOOH leads to enhanced water-oxidation kinetics.241 By correlating operando spectroscopic evidence of spin-state transitions with electrochemical metrics, they attribute the higher activity to increased Co–O covalency, optimized adsorbate binding strengths, and improved charge transfer kinetics under the high-spin state. This work establishes that the spin configuration of the active metal center is a direct parameter to tune OER performance. In perovskite LaCoO3, decreasing particle size from bulk crystals to nanosized (∼80 nm) particles induces a surface spin-state transition of Co3+ and drives the eg occupancy from ∼1.0 toward the “optimal” ≈1.2, thereby placing the *O/*OH/*OOH binding energies in a near-ideal window and delivering a marked activity gain. This is an experimental validation of the eg descriptor concept, where the spin configuration determines the eg occupation and thus governs adsorption strength of key intermediates.245Operando spectroscopic evidence further reveals that Fe-doped CoOOH preserves an intermediate-spin (eg1t2g5) Co3+ configuration under OER conditions, which strengthens Co–O covalency and optimizes proton-coupled electron-transfer energetics relative to low- or high-spin pathways, yielding higher activity and durability. Together, these cases illustrate that tuning spin configurations of active phase to a favorable state can improve OER performance.246 However, manipulating the spin configurations of electrocatalyst cannot be easily realized by traditional electrocatalysts synthesis strategies. Recently, it was found that under an alternating magnetic field before OER, magnetic metal ions in metal–organic frameworks (MOFs) can realize spin-state reconfiguration with magnetothermal effects (Fig. 10a). The spin state rearranged MOF achieves a remarkable mass activity of 3514.7 A gmetal−1 at 1.5 V, representing a 21.1-fold improvement over the pristine MOF. Compared with traditional heating method, the magnetothermal effect in MOFs can confine heat around magnetic metal ions because different layers of MOFs-based electrocatalysts were connected by organic molecules with low thermal conductivity.235 Thus, it can exclude the influence from thermal strain disturbance. In addition, the spin reconfiguration is permanent and the reconstructed spin states of active sites can be maintained when the altering magnetic field was removed and it can stay stable in long-term OER process.
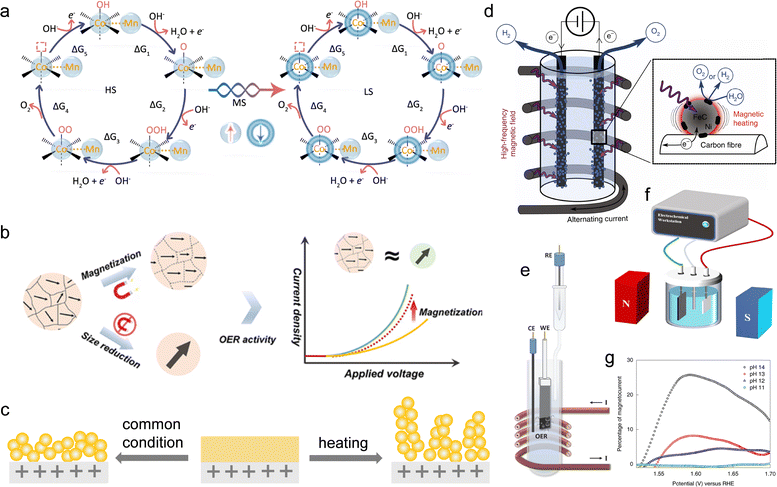 | ||
| Fig. 10 (a) The spin states of Co–Mn based MOFs were modulated under an alternating magnetic field through magnetically induced thermal effects. Reproduced with permission from ref. 235 Copyright 2021 Springer Nature. (b) Illustration showing the influence of magnetic domain structures on OER activity. When ferromagnetic particles are downsized into the single-domain regime, they inherently achieve complete spin alignment, exhibiting catalytic behaviour equivalent to that of magnetized multi-domain particles. As a result, additional external magnetic fields no longer provide further enhancement for single-domain catalysts, since their spins are already fully aligned. Reproduced with permission from ref. 236 Copyright 2023 John Wiley & Sons. (c) Schematic illustration of surface structural reconstruction during CV activation in the presence and absence of an external magnetic field. Reproduced with permission from ref. 230 Copyright 2024 John Wiley & Sons. (d) Schematic depiction of an alkaline water electrolysis (AWE) cell positioned within a coil that produces an alternating magnetic field (AMF). Reproduced with permission from ref. 237 Copyright 2018 Springer Nature. (e) Schematic illustration of the electrochemical setup used for the alternating magnetic field-assisted OER. Reproduced with permission from ref. 238 Copyright 2025 John Wiley & Sons. (f) Schematic illustration of the electrochemical setup used for the static magnetic field-assisted OER. Reproduced with permission from ref. 239 Copyright 2023 American Chemical Society. (g) Variation of magnetically induced current response with electrolyte pH. The external magnetic field was generated by placing an Nd magnet near the electrochemical cell. The magnetocurrent density was determined by taking the difference between the LSV curves recorded under magnetic field (magnet ON) and those obtained in its absence (magnet OFF). Reproduced with permission from ref. 106 Copyright 2019 Springer Nature. | ||
Magnetic enhancement strategy can also be realized without applying an external field by tailoring the intrinsic domain structure of catalysts. Specifically, the single-domain CoFe2O4 exhibits a TOF of 0.309 s−1, slightly higher than that of the multi-domain CoFe2O4 (0.291 s−1) under an applied magnetic field.236 Reducing the particle size of ferromagnetic materials into the single-domain regime enables persistent spin polarization, leading to water oxidation activity comparable to that of multi-domain catalysts under external magnetization (Fig. 10b). This approach demonstrates that size engineering to achieve single-domain ferromagnetism provides an effective route to exploit spin-polarized OER pathway. Another distinctive magnetic strategy utilizes gradient magnetic fields to guide in situ reconstruction of precatalysts.230 In a CoFe2O4@CoBDC core–shell system, the presence of a spatially varying magnetic field produces a Kelvin force that steers the reconstruction pathway (Fig. 10c). This regulation promotes a higher content of Co2+ species in the resulting CoOxHy, thereby delivering superior OER activity compared with reconstruction performed without magnetic field assistance. Specifically, the current density at 1.63 V increased by approximately 128%, accompanied by a 28 mV reduction in overpotential.
Recent studies have revealed that the magnetic proximity effect can induce interfacial spin interactions in heterostructure catalysts.247 When a paramagnetic OER-active layer is coupled with a ferromagnetic substrate, the interfacial spin exchange leads to ferromagnetic ordering within the paramagnetic catalyst via the spin pinning effect. This induced magnetic ordering can modulate the spin state of reaction intermediates, thereby enhancing the OER activity.
The application of a high-frequency alternating magnetic field to electrodes modified with magnetic nanoparticles has been demonstrated to significantly enhance OER performance.237 The magnetic flux of the alternating magnetic field oscillates periodically with time, usually produced by a solenoid or dual-coil system powered by an alternating current source. During operation, the electrochemical cell or the working electrode region is placed within or near the center of the coil, allowing the oscillating field to dynamically interact with the catalyst surface (Fig. 10d and e). Such AMF-integrated electrolysis systems have been widely demonstrated and are clearly presented with schematic diagrams and experimental photographs in previous studies.98,230,238 Notably, although the actual bulk temperature increase was only about 5 °C, the observed activity enhancement corresponded to that expected from a temperature rise of approximately 200 °C. This discrepancy is attributed to the localized magnetic heating effect in core–shell structured FeC–Ni nanoparticles, where the magnetic FeC core acts as an efficient nanoscale heater under the alternating field, while the Ni shell provides the catalytic active sites (Fig. 10d). This finding highlights the substantial potential of magnetic-induced local heating in advancing electrocatalytic water oxidation. Moreover, when magnetic cobalt single-atom catalysts are anchored onto monolayer MoS2 (Co@MoS2), room-temperature ferromagnetism can be induced due to strong hybridization between Co atoms and neighboring Mo/S atoms.98 This ferromagnetic ordering is believed to facilitate the parallel spin alignment of oxygen intermediates, thereby promoting the OER process. Additionally, under an alternating magnetic field, the ferromagnetic Co single atoms undergo spin flipping, which generates a localized magnetothermal effect, further accelerating the reaction kinetics and enhancing the overall OER performance. The overpotential decreased from 317 mV to 250 mV at 10 mA cm−2.
Beyond alternating magnetic fields, static magnetic fields have also been reported to significantly enhance OER performance. In a static magnetic field configuration (Fig. 10f), the magnetic field remains constant over time and is typically generated by permanent magnets or electromagnets placed around the electrochemical cell. The magnets are arranged so that the magnetic flux passes parallel or perpendicular to the electrode surface. Depending on the experimental purpose, the magnetic field can either cover the entire cell or be localized near the working electrode to strengthen the interaction between the field and catalytic interface. This arrangement enables direct coupling between the magnetic field and the reaction zone.106,239 For instance, ferromagnetic catalysts supported on Ni-based substrates exhibited reduced overpotentials and lower Tafel slopes when placed between neodymium permanent magnets. Control experiments excluded mass transport, heating, and electrode artifacts as the sources of enhancement, while pH-dependence and catalyst magnetism dependence indicated an intrinsic magnetic contribution (Fig. 10g). These findings suggest that the applied magnetic field promotes spin-aligned O–O bond formation, accelerating the rate-determining step of OER. This underlines the critical role of spin-state engineering via static field-induced magnetization in catalyst design.106
Beyond macroscopic magnetic enhancement effects, recent studies have delved deeper into the microscopic spin dynamics underlying OER under magnetic fields. In particular, attention has shifted toward how magnetically induced spin polarization and interfacial spin alignment influence the elementary steps of O–O bond formation and oxygen evolution kinetics. These insights provide a theoretical and mechanistic foundation for the rational design of spin-regulated electrocatalysts. The magnetic-field-facilitated O–O coupling process has been further elucidated by several studies.90–92,248–250 It was found that ferromagnetically ordered catalysts can be spin-polarized under a constant magnetic field. According to the principle of spin angular momentum conservation, spin polarization occurs at the initial step of the four-electron transfer process in OER.94 Subsequently, the spin-polarized catalysts can rapidly exchange spin with adsorbed oxygen intermediates, enhancing reaction kinetics through a spin-selective pathway.90
Beyond bulk magnetization effects, recent advances have focused on manipulating spin states of reaction intermediates as a strategy to enhance OER under external magnetic fields. Ferromagnetic catalysts can be spin-polarized under a static magnetic field, promoting spin-aligned reaction pathways in accordance with spin angular momentum conservation principles.94 The spin-polarized surface further enables exchange interactions with adsorbed oxygen intermediates, thus lowering the kinetic barriers for O–O bond formation.90
To address the challenge that many active OER species are not intrinsically ferromagnetic, an effective strategy involves constructing ferromagnet/oxyhydroxide heterostructures that leverage the spin pinning effect.91 In this approach, a ferromagnetic substrate is first synthesized, followed by surface reconstruction to form an oxyhydroxide layer under operating conditions. The resulting interface enables localized spin alignment, which can be further reinforced by an external magnetic field. This promotes parallel spin alignment of oxygen radicals formed during *OH dehydrogenation, thereby reducing the energy barrier for the O–O coupling step and accelerating the OER kinetics. Another design strategy exploits the alignment of internal magnetic domains under external fields to facilitate spin-oriented charge transfer.90 Under alkaline conditions, the formation of metal–oxyl (M–O˙) species allows for spin exchange between the active metal sites and the oxyl radicals. Magnetic polarization favors parallel spin alignment of neighboring M–O˙ units, promoting triplet oxygen evolution.
Furthermore, dynamic interface engineering via controlled surface reconstruction has proven effective in optimizing spin interactions.246,251,252 For example, SmCo5 particles can be transformed into a SmCo5/CoOxHy core–shell structure under mild electrochemical pretreatment.253 The ferromagnetic core induces interfacial spin polarization via spin pinning, which is further enhanced under magnetic fields. Consequently, the 1.1 T-magnetized SmCo2/CoOxHy exhibits a TOF of ∼1.90 s−1 at 1.58 V. This remarkable activity originates from spin-selective charge transfer facilitated by the ferromagnetic core, demonstrating a viable route toward high-efficiency magnetic-field-assisted OER.
The above strategies primarily focus on spin-related charge transfer processes occurring at the electrode–electrolyte interface, where magnetic fields modulate interfacial spin states and reaction kinetics. However, magnetic fields can also independently influence both the electrode and the electrolyte, offering additional avenues for performance enhancement.94 In particular, mobile ions and electrons in the electrolyte experience a Lorentz force when subjected to a magnetic field. This deflects their original migration paths, inducing localized magnetically driven convection near the electrode surface.254 The resulting fluid flow enhances electrolyte circulation, accelerates the removal of oxygen bubbles, and improves overall mass transport. This effect, referred to MHD, is strongly dependent on magnetic field strength but largely independent of the electrode material, making it a versatile strategy for promoting OER across a wide range of systems. In addition, in order to exclude spin-related effects, P. Vensaus et al. use non-magnetic electrodes as the research subject. They confirmed that magnetic fields enhance OER primarily by Lorentz force-induced convection, which improves electrolyte flow and accelerates reactant/product transport. The effect was modest under kinetically favorable conditions, indicating its greater relevance in diffusion-limited OER systems.83
Another important consideration for magnetic-field-assisted strategies is the dependence of catalytic enhancement on electrolyte conditions.106 Previous studies have revealed that magnetic-field-induced OER enhancement exhibits a strong pH dependence. Garcés-Pineda et al. first established the critical phenomenological evidence that the magnetocurrent improvement is remarkable only under highly alkaline conditions, maximized at pH 14 and almost disappearing below pH 11, which cannot be explained by mass transport or thermal influences such as mass transport or heat effects.106 This indicates that the rate-limiting step under low pH is not spin-restricted, in contrast to strong alkaline media. Subsequent mechanistic investigations clarified the reason behind this behaviour. Wu et al. proposed that high pH facilitates the deprotonation of surface M–OH groups to generate M–O˙ oxyl radicals containing unpaired electrons, which engage in spin-allowed O–O coupling and therefore respond strongly to magnetic spin polarization.91 At moderately alkaline pH, insufficient oxyl species weaken the contribution of the spin-selective pathway, resulting in limited magnetic enhancement. Chen et al. further confirmed that these oxyl radicals possess parallel spin alignment between metal 3d and oxygen 2p orbitals under magnetic polarization, which promotes the formation of triplet O2 with reduced spin-conversion barriers, while M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O species dominant at lower pH contain paired electrons that fail to engage in the spin-related reaction pathway.253 Overall, only when strongly alkaline conditions enable abundant oxyl radicals does magnetic modulation effectively accelerate the spin-matched O–O bond formation step, establishing a clear mechanistic correlation between pH regulation and spin-dependent kinetics.
O species dominant at lower pH contain paired electrons that fail to engage in the spin-related reaction pathway.253 Overall, only when strongly alkaline conditions enable abundant oxyl radicals does magnetic modulation effectively accelerate the spin-matched O–O bond formation step, establishing a clear mechanistic correlation between pH regulation and spin-dependent kinetics.
It should be emphasized that the influence of an external magnetic field on electrochemical systems is strongly influenced by magnet-electrode geometry. While properly aligned magnetic fields can facilitate mass transport and bubble detachment through MHD effects, improper configurations may have the opposite impact, raising the operating voltage and reducing conductivity. For instance, Li et al. systematically examined different magnet-electrode geometries during water electrolysis and observed that when a vertical electrode directly faced a magnet, allowing the magnetic field lines to pass across the electrode surface, the cell voltage at current density of 200 mA cm−2 increased from 11.1 V to 12.5 V,80 and the conductivity dropped from 0.45 to 0.40 S, compared with the field-free case. The authors attributed this deterioration to hindered bubble detachment and accumulation near the electrode surface, which increased ohmic resistance. Moreover, Chen et al. reported that when the magnetic field oriented perpendicular to the electrode surface with large electrode spacing between anode and cathode (50 mm) did not enhance performance and even reduced conductivity at the electrode edges, owing to non-uniform field gradients and hindered ion transport.255 These results demonstrate that the influence of a magnetic field on electrocatalytic performance varies with reaction environment. When the Lorentz force acts opposite to the upward flow of bubbles or the main electrolyte circulation, it suppresses bubble detachment and promotes gas accumulation on the electrode surface, thereby increasing the ohmic resistance and polarization losses. Therefore, careful optimization of the magnetic-electric geometry, electrode spacing, and field orientation is essential to avoid such undesirable effects and to harness the magnetic field effectively. Such negative effects highlight the necessity of precise field alignment and rational magnetic design in future magneto-electrocatalytic systems, ensuring that the magnetic field serves as a beneficial rather than interfering factor.
Building on this concept, recent efforts have focused on structural designs that maximize localized photothermal effects. An innovative design strategy draws inspiration from the greenhouse effect to amplify photothermal responses (Fig. 11a). Specifically, the approach involves constructing a Ni@P-SiO2 core–shell structure, where the Ni nanocrystal core converts incident light into heat via non-radiative relaxation, while the nanoporous SiO2 shell provides thermal insulation and infrared shielding to prevent heat loss.256 Through this cooperative architecture, localized heating is effectively confined, giving rise to a “super-photothermal effect” that elevates the interfacial temperature by approximately 60 K and consequently enhances the catalytic performance by about 12.3 fold.
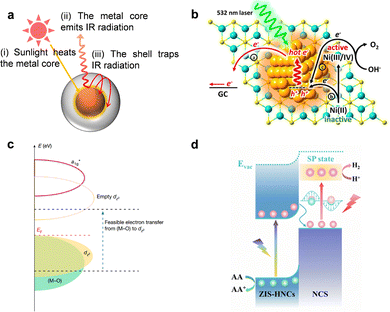 | ||
| Fig. 11 (a) Schematic of the nanoscale greenhouse effect. Light enters through a porous shell and heats the core. The shell traps heat, enhancing local temperature. Reproduced with permission from ref. 256 Copyright 2021 Springer Nature. (b) Depiction of the electron transfer pathways within the Ni(OH)2–Au electrode subjected to 532 nm laser irradiation. Reproduced with permission from ref. 257 Copyright 2016 American Chemical Society. (c) The essence of the coupled evolution mechanism lies in the electron transfer from (M–O) states into the dz2 orbital, which is facilitated by the presence of a non-overlapping region formed through the partial interaction between the vacant dz2 orbital and the a1g* band. Reproduced with permission from ref. 2 Copyright 2022 Springer Nature. (d) Mechanism of hot electron generation in ZIS-HNCs under light. Light scattering and S vacancies enhance absorption and electron transfer to NCS, where hot electrons are produced via LSPR and transferred excitation. Reproduced with permission from ref. 258 Copyright 2023 Royal Society of Chemistry. | ||
Unlike conventional heating methods that raise the temperature of the entire electrolyte system, photo-induced localized heating enables precise thermal modulation confined to the catalyst surface. Under light irradiation, electrocatalysts can convert incident photons directly into heat, eliminating the need for additional external heating devices. This localized photothermal effect allows for more accurate control of temperature at the working electrode, improving intrinsic activity, accelerating charge transfer, and potentially stabilizing active sites during operation.
Such a strategy not only reduces energy consumption associated with bulk heating but also expands the material design space by integrating light-absorbing components into the catalytic system for self-regulated thermal enhancement under solar or artificial illumination.
Designing electrocatalysts capable of converting visible or near-infrared light into localized heat offers an efficient photo-field enhancement strategy. By integrating plasmonic metals, carbon-based absorbers, or narrow-bandgap semiconductors, localized photothermal effects can be confined to the catalyst surface, lowering activation barriers, accelerating charge transfer, and minimizing energy loss associated with bulk heating.105,259–261 This enables precise thermal modulation under solar or LED illumination without additional external heaters.262 A practical photo-field enhancement strategy involves designing electrocatalysts that can convert light into localized heat to dynamically activate surface reconstruction. For instance, NiFe2O4-based electrodes were shown to absorb near-infrared (NIR) light and generate sufficient localized heating under illumination.134 This photothermal response facilitated the in situ transformation of the catalyst surface into highly active oxyhydroxide phases, as confirmed by operando Raman spectroscopy. The reconstructed layer exhibited improved OER kinetics, delivering a remarkably low overpotential of 309 mV at 100 mA cm−2, outperforming many earth-abundant systems. This approach demonstrates a strategy of coupling photothermal materials with dynamic phase evolution, enabling on-demand generation of active sites and enhanced catalytic activity under light exposure. To amplify high photothermal conversion efficiency, Cao et al. developed a villous carbon framework (VCF) embedded with FeNi3 alloy, inspired by the thermal insulation of polar bear fur. The villous morphology and embedded alloy synergistically enhanced light-to-heat conversion, thereby boosting OER performance. Under 0.25 W cm−2 illumination, the VCF achieved 100 mA cm−2 at only 194 mV overpotential and >300 mA cm−2 at 1.45 V, which is 8.5 times higher than in the dark.263 Similarly, Xu et al. designed the graphene-encapsulated CoNi nanocages (CoNi@Gr), combining 98% full-spectrum absorption and 97% STC efficiency. CoNi–carbon interactions enhance graphene's broadband light absorption, while the hierarchical nanocage architecture induces light trapping. Photothermally induced high surface temperatures form a vapor layer and three-phase interface, lowering the OER potential over 240 mV and the free energy of O* → OOH* from 2.51 to 1.75 eV.264 In addition, Wu et al. enhanced photothermal conversion by integrating in situ formed Ni0.91Mo0.09 alloy nanoparticles, which exhibit strong broadband light absorption and efficient light-to-heat conversion, with vertically aligned MoO2 nanorods that suppress diffuse reflection and improve light harvesting, enabling efficient localized heating at the catalytic sites.265 When assembled into an anion exchange membrane (AEM) electrolyzer, the catalyst can deliver a current of 0.45 A under 1.6 V, demonstrating outstanding photothermal-assisted water splitting performance. In summary, for photothermal-assisted catalysts, enhancing light absorption, improving light-harvesting capability, and reducing thermal-radiation losses of the material are crucial.
Leveraging localized surface plasmon resonance (LSPR) represents an effective photo-field enhancement strategy for OER. When the frequency of incident photons resonates with the collective oscillation of conduction electrons in plasmonic metals (e.g., Au), intense localized electromagnetic fields are generated at the metal–semiconductor interface.266 These fields can trigger both thermal and non-thermal excitation pathways, enabling strong coupling with nearby catalytic components. In particular, Au nanoparticles embedded in Ni(OH)2 matrices have been shown to induce LSPR under light illumination, which facilitates electronic interactions between Au and Ni species. This interaction promotes the oxidation of Ni3+ to catalytically active Ni4+, thereby 4-fold enhancing the intrinsic OER activity (Fig. 11b).257 The strategy of integrating plasmonic metals with redox-active transition metal hydroxides provides a powerful platform for light-responsive electronic tuning, enabling dynamic modulation of catalyst valence states under irradiation. Another viable strategy to enhance plasmonic effects in OER photocatalysts is to integrate plasmonic metals with semiconductor hosts via heterojunction engineering. For example, Ag/CoV-LDH@G nanohybrids couple a Mott–Schottky interface.267 The heterojunction optimizes interfacial charge distribution, shifts the Fermi level, and lowers the d-band center from −0.89 to −0.93 eV, which reduces the OER energy barrier and strengthens light absorption. This synergistic modulation of electronic structure and photothermal/electronic plasmonic effects provides a generalizable approach for boosting plasmon-assisted OER performance. Liu et al. enhanced photothermal catalysis by integrating broadband solar absorption with selective suppression of thermal-radiation loss,268 achieving near-complete utilization of the solar spectrum while minimizing heat dissipation at high temperatures. The design employs a tailored absorber structure and plasmonic components to concentrate light, strengthen electromagnetic fields, and maximize light-to-heat conversion efficiency, thereby achieving a high temperature of 345.2 °C at catalytic sites.
For plasmonic effects, the lifetime of hot electrons is critical. They enhanced the plasmonic effect by constructing a strongly coupled NiCo2S4/ZnIn2S4 heterostructure, where high-density photogenerated electrons are efficiently transferred and accumulated on the NiCo2S4 surface.258 The localized surface plasmon resonance (LSPR) of NiCo2S4 then excites these electrons into hot electrons, and the continuous electron supply from ZnIn2S4 sustains the excitation, thereby increasing LSPR intensity and significantly extending hot-electron lifetime.
Beyond plasmonic enhancement via localized electromagnetic fields, recent studies have explored more intrinsic light-induced transformations in catalyst structure and electronic configuration, even in the absence of traditional plasmonic materials (Fig. 11c).2 These phenomena reveal new opportunities for photo-field-driven catalytic optimization based on strain, symmetry, and oxygen redox chemistry.
A recent study demonstrated that strain-stabilized non-nickel oxyhydroxides exhibit significantly enhanced OER activity under light illumination, which gradually diminishes upon removal of the light source.2 Detailed characterization confirmed that this enhancement was not due to conventional photothermal effects, resistance change, grain growth, or photo-excited carriers.
Instead, operando X-ray absorption spectroscopy revealed that light irradiation induces a reduction in the oxidation state of Ni, which acts as a redox mediator during the deprotonation step. Simultaneously, a photo-induced phase transition from octahedral NiO6 to planar NiO4 was observed, accompanied by the emergence of non-bonding oxygen species, suggesting that lattice oxygen itself serves as an active redox center during the O–O bond formation. This is consistent with growing evidence in the field supporting oxygen redox contributions to OER catalysis.111
These findings led to a novel design strategy: leveraging light-responsive electronic reconfiguration to optimize charge transfer pathways in strained oxyhydroxide systems. Specifically, under illumination, metal centers participate in initial proton-coupled electron transfer (PCET), while oxygen anions take over as redox-active sites during the O–O coupling step. This dual redox-site mechanism, metal–oxygen redox synergy, minimizes reaction energy barriers and enhances catalytic efficiency in a dynamically light-tunable fashion. Related work on light-induced M–O reconfiguration can also be found in Mn-, Co-, and Ni-based layered oxides.269,270
Finally, photo-enhancement can also be achieved through structural and interfacial engineering.258 Hollow nanostructures promote multiple scattering to boost light absorption, ultrathin layers accelerate carrier migration, and the deliberate introduction of vacancies broadens the absorption range while reinforcing interfacial coupling with plasmonic domains. Together, these effects enable hot-electron generation from both plasmonic excitation and transferred photogenerated carriers, providing a general route to enhance charge separation and catalytic efficiency (Fig. 11d).
From a kinetic perspective, elevated temperatures enhance reaction rates by reducing activation energy, as described by the Arrhenius relationship. In electrochemical systems, moderate heating can not only accelerate ionic mobility and reduce electrolyte viscosity, facilitating mass transport, but also can promote charge transfer between the electrode and redox species. In addition, it can also lower the kinetic barrier of critical steps such as OH− deprotonation and O–O bond formation.
Beyond these general kinetic effects, thermal fields can also be harnessed in a more targeted manner through strain engineering. A distinct design strategy involves exploiting thermally induced strain to dynamically tune the electronic structure of catalysts.173 For example, in Sr2IrO4, heating generates anisotropic thermal expansion that introduces compressive strain in IrO6 units. This strain downshifts the d-band center, optimizes the binding strength between OER intermediates and Ir active sites, and thereby accelerates OER kinetics (Fig. 12a). Unlike conventional approaches that impose constant lattice strain, the temperature-dependent strain effect can be readily adjusted in real time, offering a flexible route to enhance catalytic performance beyond the traditional thermal diffusion contribution.
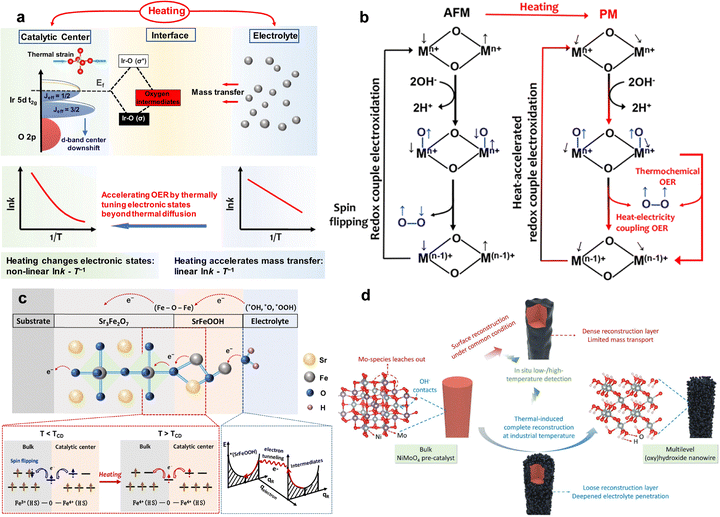 | ||
| Fig. 12 (a) Thermal effects on OER: heating accelerates mass transport and induces strain in IrO6 octahedra, downshifting the d-band centre and tuning Ir–O bonding. In low-spin Ir4+, strong spin–orbit coupling splits the t2g states into Jeff = 3/2 and Jeff = 1/2 sub-bands. Diffusion-driven kinetics follow a linear Arrhenius relation, while strain-induced band shifts lead to nonlinear behaviour. Reproduced with permission from ref. 173 Copyright 2024 Springer Nature. (b) Schematic illustrating that heating drives AFM NiFeOOH toward PM states, where spin alignment shifts the pathway from singlet O2 (↑O–O↓) to the lower-energy triplet O2 (↑O–O↑). Reproduced with permission from ref. 272 Copyright 2022 American Chemical Society. (c) Schematic of interfacial electron transfer in OER, where intermediates couple with SrFeOOH active sites via resonant tunnelling and electrons transfer through unoccupied eg orbitals of Fe4+ in Fe–O–Fe chains at the Sr3Fe2O7@SrFeOOH interface. Reproduced with permission from ref. 273 Copyright 2024 National Academy of Sciences. (d) Schematic illustration of the distinct reconstruction pathways of NiMoO4 precatalysts under electro-oxidation at different temperatures. Reproduced with permission from ref. 274 Copyright 2020 John Wiley & Sons. | ||
In addition to strain regulation, thermal fields can also be utilized to dynamically tune spin configurations at catalyst interfaces, thereby reducing interfacial electron transfer barriers.275 This strategy is particularly relevant for magnetic heterostructures, where spin misalignment across interfaces can impose significant resistance to charge transport. A recent study revealed that FeNiOxHy undergoes a ferrimagnetic-to-paramagnetic transition when heated to 70 °C, leading to the emergence of low-spin Fe3+ species with enhanced electron mobility.276 This thermal spin transition not only promotes more efficient electron transfer during the Ni2+/Ni3+ pre-oxidation step, but also facilitates the subsequent OER process. As a result, the potential mismatch between these two steps is reduced, improving the overall energy efficiency of water splitting, achieving a current density of 100 mA cm−2 at an overpotential of only 221 mV under 90 °C. This strategy highlights the potential of temperature-induced spin modulation as a design principle, leveraging thermal fields to reshape electronic structures and create low-barrier charge transport pathways in active catalytic phases. In another case, NiFeN@NiFeOOH core–shell catalysts exhibit a spin–flip barrier at the ferromagnetic-antiferromagnetic interface, which hinders charge flow.272 Upon heating to 55–70 °C, both core and shell undergo magnetic phase transitions to paramagnetic states, forming a spin-aligned interface that facilitates electron transfer (Fig. 12b). This approach demonstrates how thermally induced spin reconfiguration can serve as an effective strategy to optimize interfacial transport in multi-phase OER catalysts. Building on the role of thermal fields in tuning spin states, recent studies have further demonstrated that temperature can also modulate the bulk electronic structure of transition-metal oxides by suppressing charge instabilities, offering an additional pathway to enhance electron transport. In Fe-based perovskite oxides with negative charge transfer energy, low temperatures can induce charge disproportionation (2Fe4+ → Fe3+ + Fe5+), which impairs electronic conductivity. Heating above the disproportionation threshold stabilizes Fe4+ (t2g3eg1), preserving unoccupied eg orbitals as effective channels for interfacial charge transfer (Fig. 12c).273 In systems such as Sr3Fe2O7@SrFeOOH, this thermal control promotes efficient electron transport without spin flipping, demonstrating a strategy that couples thermal excitation with orbital tuning to improve OER performance. Furthermore, thermal fields can also drive structural transformations that unlock durable and active catalytic phases under operating conditions. Specifically, thermal fields can promote surface reconstruction, forming stable active phases with improved performance and durability (Fig. 12d).274 A multilevel reconstructed catalyst maintained low overpotential (282.3 mV at 20 mA cm−2) for over 250 hours at 25–52 °C. The presence of boundaries and vacancies lowered the OER energy barrier, as confirmed by theoretical analysis. This demonstrates a strategy where heat-induced structural evolution enables both high activity and long-term stability under practical conditions.
4.2. Synergistic coupling of different external fields
For example, Ma et al.277 designed a hybrid electrocatalyst by combining Co3O4, a material with strong photothermal conversion ability, and CoFe2O4, which exhibits spin polarization and magnetoresistance. The Co3O4 component converts light into localized heat, enhancing conductivity and reaction kinetics, while CoFe2O4 reduces resistance through the giant magnetoresistive effect and facilitates spin-aligned oxygen intermediate formation (Fig. 13a). This work exemplifies a strategy of functionally partitioned hybrid design, in which distinct roles for light and magnetic responses are assigned to specific material components, achieving a synergistic activation pathway under dual-field stimulation. This work illustrates a promising strategy to integrate light-induced thermal modulation with magnetic spin control, enabling highly efficient OER with an exceptional overpotential of 172.4 mV at 10 mA cm−2.
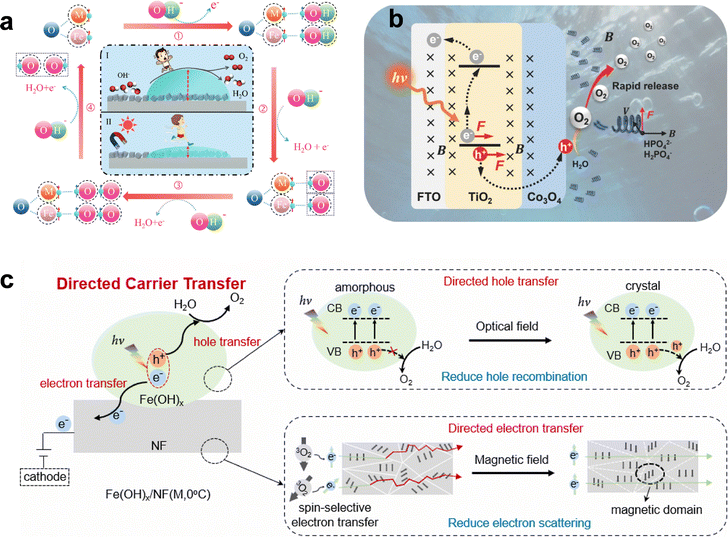 | ||
| Fig. 13 (a) Spin-polarized OER pathway driven by magnetic-photothermal coupling. Reproduced with permission from ref. 277 Copyright 2023 John Wiley & Sons. (b) Proposed mechanism for the magnetic field-driven enhancement of PEC activity in Co3O4/TiO2 systems. The experiment is conducted under AM 1.5 G light irradiation and an applied magnetic field of 140 mT. Reproduced with permission from ref. 278 Copyright 2024 Springer Nature. (c) Schematic illustration of Fe(OH)x/NF under external magnetic and photo fields, where directional carrier transfer is promoted to enhance electrocatalytic activity. Reproduced with permission from ref. 279 Copyright 2024 American Chemical Society. | ||
In addition to hybrid designs with functionally partitioned components, another representative strategy emphasizes direct photo-magnetic coupling to enhance OER performance. In this approach, the magnetic field works in tandem with photoexcitation:278 the Lorentz force drives photogenerated electrons and holes in opposite directions, suppressing recombination and improving charge migration to the electrode surface. Simultaneously, magnetic Co3O4 nanoparticles interacting with the external field strengthen interfacial charge transfer, while Lorentz-force-induced ion motion in the electrolyte generates local convection that accelerates oxygen release (Fig. 13b). The current density can increase from 0.29 to 0.65 mA cm−2 at 1.23 V vs. RHE. This integration of photogenerated carrier dynamics with magnetic-field-driven processes exemplifies a synergistic photo-magnetic design.
Another study introduces a material design strategy that leverages magnetic field-assisted crystallization and ferromagnetic substrate engineering to enable directional carrier dynamics under photo-magnetic dual fields.279 The key innovation lies in using a low-temperature magnetic field during electrodeposition to promote the growth of highly crystalline Fe(OH)x on a ferromagnetic Ni foam substrate. This architecture simultaneously fulfills the requirements for both efficient photogenerated hole transport, facilitated by the long-range order in the Fe(OH)x lattice, and spin-aligned electron transfer, guided by the magnetic domain orientation of the Ni substrate under an external magnetic field. The resulting directional transport of carriers, with holes migrating toward the surface and electrons toward the external circuit, forms a dual-pathway transport framework that significantly lowers interfacial resistance and suppresses charge recombination (Fig. 13c). This strategy reduces the OER overpotential by 63 mV (from 285 to 222 mV) and enhances reaction kinetics beyond what can be achieved by individual external fields.
This strategy highlights that rational control over crystallinity and substrate magnetism is essential for constructing electrocatalysts with intrinsic compatibility toward dual-field synergy, and provides a generalized design route for future multifunctional OER systems.
The synergistic enhancement arising from photo-magnetic coupling is sustained only within a physically compatible regime of magnetic flux and optical intensity. To maintain spin coherence, the incident light intensity should be controlled so that the resulting photothermal temperature remains below the Curie or Néel temperature of the magnetic component, beyond which thermally assisted demagnetization and collapses of magnetic ordering occur.280 For common ferrite electrocatalysts, keeping the applied field in a moderate regime helps avoid magnetostrictive strain large enough to compromise interfacial integrity.281
It is worth noting that under illumination, photothermal assistance may also induce photocatalytic or photoelectrochemical oxygen evolution. To accurately distinguish photothermal effects from genuine photocatalytic contributions under illumination, recent studies have established several diagnostic strategies. One widely adopted approach is dark-light switching under isothermal conditions, in which the electrode surface temperature is maintained constant (using external heaters or thermostatic liquid circulation) while alternately turning the light source on and off.282,283 If the catalytic current enhancement persists in the dark at the same temperature, it can be attributed to photothermal heating, whereas an immediate current drop upon light-off at constant temperature indicates a photoexcitation-driven contribution. Complementary insights can be obtained from wavelength-dependent measurements performed at constant absorbed power (P),284,285 where the incident light intensity is adjusted so that P remains constant across wavelengths. A reaction rate or current density that scales uniformly with total absorbed power, independent of wavelength, reveals a thermal origin. In contrast, spectral features that follow the semiconductor bandgap indicate true photocatalytic participation.
Recent studies have revealed that the enhancement of OER activity under external magnetic fields is highly dependent on the thermal environment. For example, Ren et al. showed that in ferromagnetic catalysts such as CoFe2O4, the spin-polarization effect induced by an external magnetic field can significantly accelerate OER kinetics at room temperature. However, this enhancement diminishes progressively as the temperature rises from 298 K to 328 K (Fig. 14a), due to thermal disruption of long-range magnetic order and the consequent loss of magnetization. These observations suggest a key design strategy: to maintain effective magnetic-field-induced spin polarization, catalysts must retain robust magnetic ordering within the operational temperature range. This calls for the development of materials with high Curie temperatures, strong magnetic anisotropy, or thermally stable magnetic domains, ensuring that spin-mediated charge transfer can be sustained under realistic reaction conditions. Accordingly, magnetic-assisted OER systems should be designed with consideration of both their intrinsic magnetic properties and their thermal response, enabling reliable and durable performance under coupled thermal-magnetic fields.90
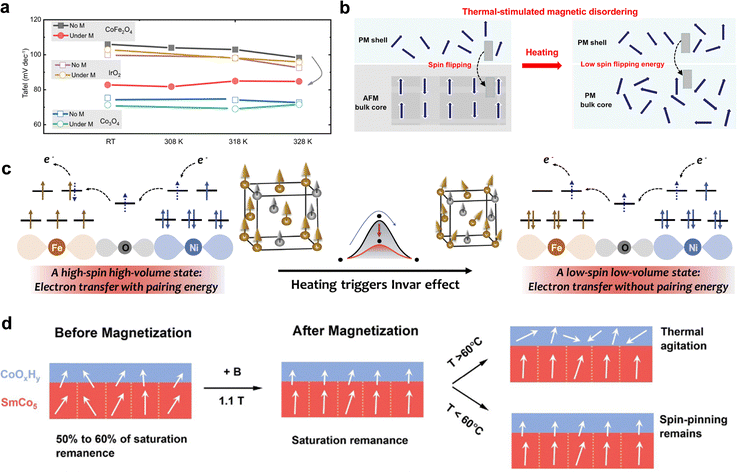 | ||
Fig. 14 (a) Tafel curves of different ferromagnetic catalysts recorded in O2-saturated 1 M KOH under constant magnetic field (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe) and non-magnetic conditions at various operating temperatures (room temperature, 308 K, 318 K, and 328 K). Reproduced with permission from ref. 90 Copyright 2021 Springer Nature. (b) Schematic of an antiferromagnetic core-paramagnetic shell, where heating-induced spin disorder enables low-barrier electron transfer. Reproduced with permission from ref. 286 Copyright 2025 Royal Society of Chemistry. (c) Schematic illustration of how the thermal Invar effect promotes electron transport. Reproduced with permission from ref. 12 Copyright 2024 American Physical Society. (d) Scheme of spin alignment in SmCo5/CoOxHy. Magnetization induces remanence, preserved by spin pinning below 60 °C but disrupted by thermal agitation above 60 °C. Reproduced with permission from ref. 253 Copyright 2021 John Wiley & Sons. 000 Oe) and non-magnetic conditions at various operating temperatures (room temperature, 308 K, 318 K, and 328 K). Reproduced with permission from ref. 90 Copyright 2021 Springer Nature. (b) Schematic of an antiferromagnetic core-paramagnetic shell, where heating-induced spin disorder enables low-barrier electron transfer. Reproduced with permission from ref. 286 Copyright 2025 Royal Society of Chemistry. (c) Schematic illustration of how the thermal Invar effect promotes electron transport. Reproduced with permission from ref. 12 Copyright 2024 American Physical Society. (d) Scheme of spin alignment in SmCo5/CoOxHy. Magnetization induces remanence, preserved by spin pinning below 60 °C but disrupted by thermal agitation above 60 °C. Reproduced with permission from ref. 253 Copyright 2021 John Wiley & Sons. | ||
To overcome this limitation, recent efforts have shifted toward designing catalysts whose magnetic properties can be adaptively tuned by temperature, enabling cooperative thermal-magnetic modulation rather than mutual interference. A representative strategy for realizing thermal-magnetic synergy in OER catalysis involves designing materials that undergo temperature-triggered magnetic phase transitions. Yan et al. demonstrated that incorporating an antiferromagnetic (AFM) core with a thermally tunable transition to a paramagnetic (PM) state can effectively modulate spin dynamics at the catalyst interface.286 In their system, the YFe1−xMnxO3@YFeOOH core–shell structure enabled a progressive AFM → weak ferromagnetic → PM transition under thermal excitation. This magnetic disordering reduces spin-flipping energy barriers, thereby accelerating interfacial electron transfer (Fig. 14b). Simultaneously, the thermally induced spin-state perturbation also reconfigures the electronic structure of the shell layer, enhancing the adsorption of key OER intermediates and substantially lowering the reaction energy barrier. Notably, the OER activity exhibited a distinct deviation from linear Arrhenius-type behavior, indicating that the improvement stemmed not solely from thermal diffusion but from a synergistic reorganization of magnetic and electronic states. By tuning the Mn doping level, the magnetic transition temperature can be precisely adjusted, enabling the rational control of thermal response windows. This strategy highlights the potential of coupling thermal activation with field-responsive magnetic ordering to unlock new reactivity pathways and guide the design of high-performance, multi-field-responsive OER catalysts. Beyond phase-level magnetic ordering, recent advances also explore thermally induced spin-state transitions as a subtler yet effective means to regulate interfacial electron transport. A distinct strategy to couple thermal fields with magnetic-related spin dynamics was recently reported via the use of Invar alloys. In this work, Fe64Ni36, known for its negative thermal expansion (Invar effect), undergoes a temperature-triggered spin transition from high-spin (HS) to low-spin (LS) Fe states. This transition creates a larger number of unoccupied 3d orbitals in the bulk Fe64Ni36, which serve as efficient electron acceptor channels at the interface with the FeNiOxHy catalytic layer. As a result, the thermally stimulated spin switching significantly reduces the interfacial electron transfer barrier without requiring a macroscopic magnetic phase transition (Fig. 14c). This mechanism leads to a non-Arrhenius enhancement in OER kinetics, including lower overpotentials, reduced charge-transfer resistance, and faster quasi-Fermi level decay. Compared to conventional heating, which accelerates kinetics via mass transport or reaction rates alone, this strategy enables thermally adaptive modulation of electronic states. It provides a powerful means to dynamically activate interfacial electron transport by spin state engineering, paving the way for multi-field responsive catalyst designs that exploit intrinsic material physics instead of relying solely on composition or nanostructure.12
Building on this concept, a thermal-magnetic coupling strategy has been demonstrated by constructing a SmCo5/CoOxHy core–shell catalyst that exploits interfacial spin pinning.253 The ferromagnetic SmCo5 core stabilizes spin polarization at the interface with the CoOxHy shell, enabling spin-selective electron transfer and improved OER performance. This interfacial spin polarization can be maintained up to 60 °C, ensuring catalytic efficiency under elevated operating temperatures relevant to practical applications. However, at higher temperatures, thermal effects disrupt interfacial spin order, diminishing the magnetic contribution (Fig. 14d). This strategy demonstrates how combining magnetic spin pinning with thermal stability can guide the design of OER catalysts for real-world conditions.
Similar to photo-magnetic coupling, magnetic-thermal systems must operate within a compatible window of temperature and magnetic field strength, ensuring that the working temperature remains safely below the magnetic transition point and that the applied field is moderate enough to maintain magnetic and structural stability.
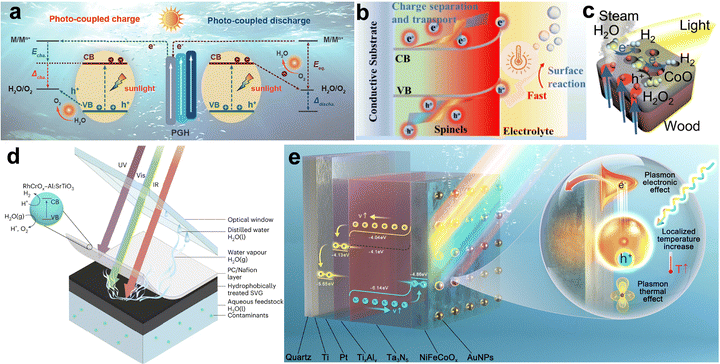 | ||
| Fig. 15 (a) Synergistic photoelectric and photothermal effects of PGH under AM 1.5 G illumination (100 mW cm−2) reduce the charge–discharge voltage gap by enhancing charge transport and reaction kinetics. Reproduced with permission from ref. 287 Copyright 2025 John Wiley & Sons. (b) Schematic depiction of light-induced heating regulating charge carriers and interfacial reactions. Reproduced with permission from ref. 291 Copyright 2025 Royal Society of Chemistry. (c) Schematic illustration of the preparation of a wood-based photocatalyst structure that produces water vapor and drives its photolysis for hydrogen generation under AM 1.5 G illumination (100 mW cm−2). Reproduced with permission from ref. 289 Copyright 2021 Springer Nature. (d) Schematic of the SVG-PC sheet architecture and its operation mechanism under AM 1.5 G illumination (100 mW cm−2). Reproduced with permission from ref. 160 Copyright 2023 Springer Nature. (e) Schematic diagram and mechanism of electron/hole transfer of AuNPs@NiFeCoOx/Ta3N5/TixAly photoanode under AM 1.5 G illumination (100 mW cm−2). Synergistic plasmonic thermal and electronic effects boost OER efficiency. Reproduced with permission from ref. 292 Copyright 2021 Elsevier. | ||
Wang et al. revealed that in TiO2-based photo-oxidation, the rate-determining step shifts with light intensity, from hole generation and diffusion at low light, to slow thermally activated steps (e.g., O–O bond formation and proton release) at high light. This indicates that excess photogenerated carriers may not improve performance if thermal steps become limiting. Therefore, effective thermal-photo coupling strategies should not only promote charge generation, but also accelerate surface thermal kinetics and prevent intermediate buildup (Fig. 15b). Designing catalysts with heat-localizing structures and low-barrier active sites is essential to maintain kinetic balance under variable illumination.288
Besides, recent efforts have explored designs that couple photothermal conversion with interfacial regulation. Guo et al. devised a photothermally induced biphase photocatalytic platform by loading particulate catalysts onto a charred-wood, broadband light-absorbing floater at the air–water interface (Fig. 15c). Under AM 1.5 G illumination, the wood drives photothermal transpiration to generate water steam and create a gas/solid biphase microenvironment. This gas–solid configuration improves interfacial thermodynamics and mass transport. The hydrogen-release resistance drops by nearly two orders of magnitude compared with liquid-immersed systems, which mitigates bubble blockage.289 In addition, rational structural design is also crucial for improving the efficiency of thermal-photo coupled catalysis. Pornrungroj et al. significantly improve the efficiency and stability of solar-driven water splitting via rational integration of photothermal and photocatalytic processes, combined with interface engineering (Fig. 15d).160 In this design, a porous carbon-based solar vapor generator (SVG) absorbs visible and infrared light and converts it into heat, driving localized water evaporation to produce water vapor. A UV-active photocatalyst (RhCrOx–Al:SrTiO3) positioned above the SVG utilizes ultraviolet light to split the generated vapor into hydrogen and oxygen, thereby maximizing utilization of the full solar spectrum. Importantly, the photocatalyst is physically isolated from liquid water and exposed only to vapor, which prevents catalyst poisoning and deactivation caused by impurities in liquid water. This physical isolation design not only enhances anti-fouling capability but also enables prolonged operation, maintaining stable performance for up to 154 hours even with seawater or other non-pure water sources. By coupling photothermal-driven vapor generation with UV-driven gas–solid photocatalysis, this system achieves high efficiency, long-term durability, and broad water-source adaptability for sustainable hydrogen production. Similarly, Z et al. adopted a photothermal-photocatalysis coupling strategy analogous to the RhCrOx–Al:SrTiO3/SVG system, integrating a broadband-absorbing photothermal layer with a floating photocatalyst layer.290 The photothermal component harvests visible and NIR light to generate localized heating and drive continuous water vapor evaporation, while the photocatalyst, contacting only the vapor phase, avoids liquid-phase contamination and benefits from improved mass transfer. This gas–solid interface design expands light utilization and enhances photocatalytic hydrogen evolution efficiency, achieving a solar-to-hydrogen (STH) conversion efficiency of 2.06%.
First-principles molecular dynamics and microkinetic analysis have shown that elevated temperatures reshape the water/TiO2 interface by forming a gas–liquid–solid (bubble–water–TiO2) three-phase environment. This thermally induced interfacial state weakens the hydrogen-bond network, reducing the energetic barrier for forming the semi-hydrophobic ˙OH intermediate, which is otherwise hindered by surrounding water molecules. At the same time, proton transfer remains active within the loosened network. As a result, the oxygen evolution activity is enhanced by nearly 25-fold. These findings highlight a strategy of engineering interfacial environments, via heat, nanostructuring, or hydrophobic modification, to stabilize key intermediates and accelerate OER kinetics under light-driven conditions.293
Besides, another paper highlights a thermal-photo coupling strategy: Au nanoparticles on a semiconductor photoanode harness localized surface plasmon resonance to generate both photothermal heating and hot-electron injection (Fig. 15e).292 The photothermal effect raises the local electrode temperature, lowering activation barriers and speeding up oxygen evolution with a current density of 12.1 mA cm−2, while the electronic effect produces high-energy electrons that improve charge separation and reduce recombination. The synergy of these two light-driven effects greatly accelerates photoelectrocatalysis. Quantitative analysis shows that at high irradiance the electronic contribution (69.4%) dominates, yet the added heat still enhances kinetics. For catalyst design, this suggests tailoring plasmonic nanostructures to absorb a broad spectrum, tuning their size and composition to maximize both hot-electron generation and localized heating, and balancing the thermal and electronic contributions to achieve the optimal reaction rate. From the perspective of thermal-photo coupling, the resonant excitation of localized surface plasmon resonance (LSPR) in plasmonic nanocrystals induces both photothermal heating and the generation of energetic hot electrons and holes via nonradiative decay. These hot carriers can be injected into the molecular orbitals of adsorbed reactants, enabling surface chemical transformations. However, during charge transport within the nanocrystal, hot carriers rapidly relax into lower-energy states, with much of their energy dissipated as heat into the lattice, raising the local temperature rather than directly contributing to reaction pathways. This interplay imposes a fundamental challenge for efficient solar-to-chemical energy conversion. To address this, one effective thermal-photo coupling strategy involves constructing heterojunctions by anchoring Au nanocrystals onto n-type semiconductors. The resulting Schottky barrier at the metal/semiconductor interface facilitates spatial separation of hot electrons and holes, effectively extending hot-electron lifetimes and enhancing their participation in slower catalytic processes. This approach demonstrates how tailored interfacial architectures can simultaneously harness photothermal and hot-carrier effects to improve photocatalytic efficiency.294
To fully exploit the infrared portion of the solar spectrum, long neglected due to its low photon energy and enhance photocatalytic performance, the authors proposed a design that couples photothermal and pyroelectric effects.195 Infrared light accounts for ∼50% of the solar spectrum but cannot directly drive photocatalytic reactions. Photothermal technology can efficiently convert infrared light into heat (conversion efficiency up to 85%), while ferroelectric materials can generate positive and negative pyroelectric fields in response to temperature variations, effectively regulating charge-carrier migration. Based on this concept, integrating photothermal materials with pyroelectric materials and photocatalysts enables the construction of a pyroelectric-photothermal-photocatalytic system that efficiently utilizes infrared light and leverages built-in pyroelectric fields to promote charge separation. Guided by this strategy, the research team designed and fabricated PVDFHFP/CNT/CdS composite microfibers, which realize infrared-responsive pyroelectric fields and achieve more than a fivefold enhancement in photocatalytic hydrogen evolution efficiency, with an average apparent quantum efficiency of ∼16.9%.
A thermal-photo coupling strategy was demonstrated using a flexible P(VDF-TrFE)/g-C3N4 composite film, where both light and thermal fluctuations synergistically enhance catalysis.295 Temperature-induced pyroelectric fields from the P(VDF-TrFE) component promote charge separation and prolong carrier lifetimes in the g-C3N4 matrix, suppressing recombination of carrier and boosting catalysis efficiency. This concept highlights the potential of integrating pyroelectric materials into electrocatalytic OER system, to leverage dynamic thermal stimuli for improved carrier dynamics and catalytic performance.
While the photothermal effect offers a favorable route for harnessing near-infrared light, excessively high temperatures can increase carrier collision rates within photocatalysts, promoting recombination and thus reducing activity. A 3D porous honeycomb-like carbon framework with excellent thermal insulation preserves localized photothermal effects and amplifies temperature fluctuations, creating favorable conditions for the pyroelectric effect.296 Bi2S3 serves as both a photothermal and pyroelectric component, absorbing NIR light, converting it into heat, and generating pyroelectric fields during temperature oscillations to release surface charges. When coupled with CdS nanoparticles, these charges suppress electron–hole recombination, markedly enhancing photocatalytic hydrogen evolution to reach 5.88 mmol g−1 h−1. This thermal-photo-electric synergistic design maximizes NIR light utilization and improves overall photocatalytic performance.
To harness the full solar spectrum for water splitting, a thermal-photo coupling strategy was developed by integrating a UV-responsive photocatalyst (RhCrOx–Al:SrTiO3) with a porous carbon-based solar vapor generator (SVG). While the photocatalyst utilizes UV light to drive water splitting, the SVG absorbs visible and infrared light, typically underutilized, and converts it into heat, rapidly generating water vapor. This vapor-phase feedstock enhances the reactivity and enables the photocatalyst to operate more efficiently. The spatial and functional separation of light absorption (SVG) and catalytic conversion (photocatalyst) allows for synergistic utilization of solar thermal and photo energy. This approach highlights a general design principle: combining photothermal materials with spectrally selective light absorbers can expand the usable range of solar energy, offering a pathway toward high-efficiency, full-spectrum solar-driven catalysis.160
Similar to other multi-field systems, thermal-photo coupling requires careful control of both illumination and temperature to maintain balanced charge and thermal dynamics. Excessive photothermal heating can shift the reaction from a photo-driven to a thermally dominated regime, leading to carrier recombination and catalyst degradation.259,260,297 Therefore, operating within a moderate illumination-temperature range is essential to preserve efficient charge separation and stable catalytic performance.
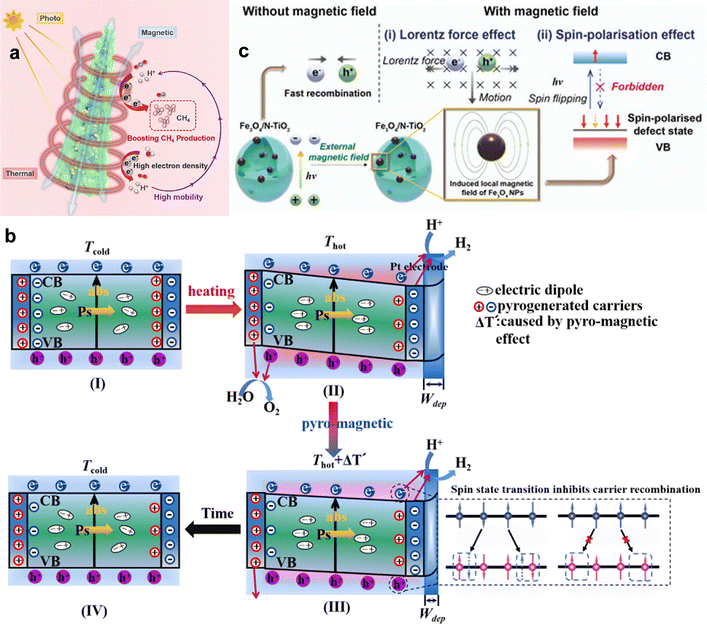 | ||
| Fig. 16 (a) Synergistic photo-thermal-magnetic coupling enhances photocatalysis by increasing carrier density and mobility, suppressing recombination, and accelerating reaction kinetics for improved efficiency and selectivity. Reproduced with permission from ref. 298 Copyright 2022 Elsevier. (b) Schematic of magnetic-thermal-photo coupling in PEC water splitting. Magnetic-thermal coupling induces a pyro-magnetic effect that suppresses non-radiative recombination, enhancing carrier separation and boosts PEC water-splitting performance. Reproduced with permission from ref. 299 Copyright 2023 Elsevier. (c) Schematic illustration of the POWS system, where photoexcitation and the induced magnetic field act synergistically to promote charge separation. Reproduced with permission from ref. 300 Copyright 2022 Royal Society of Chemistry. | ||
Harnessing the synergistic effects of thermal, photo, and magnetic fields offers a powerful route to enhance water-splitting catalysis by simultaneously modulating charge generation, transport, and reaction kinetics. Using a NaNbO3 semiconductor with a noncentrosymmetric crystal structure as a model system, it was shown that magnetic-field assistance alone had limited impact on purely photoelectric performance, likely due to Lorentz-force-constrained suppression of nonradiative recombination. In contrast, combining magnetic fields with thermally driven pyroelectric polarization markedly boosted catalytic performance by enhancing carrier separation and overcoming recombination limits (Fig. 16b). Under simultaneous thermal, photo, and magnetic stimulation, the photoanode achieved a current density of 0.45 mA cm−2 at 1.23 V, which is three times higher than with light alone. Computational modeling (DFT and COMSOL) confirmed that the multi-field coupling promotes spin-polarized carrier transport, reinforces pyroelectric fields, and accelerates interfacial reaction steps. These results point to a design strategy that integrates pyroelectric materials with strong spin–orbit coupling and light-absorbing capability, enabling simultaneous harvesting of thermal fluctuations, photon energy, and magnetic-field-induced spin alignment to maximize overall catalytic efficiency.299,301
In a particulate photocatalytic overall water-splitting (POWS) system, the synergistic coupling of thermal, photo, and magnetic fields was realized by integrating superparamagnetic Fe3O4 nanoparticles with nitrogen-doped TiO2 (N-TiO2). Under visible-light illumination (437 nm) and elevated temperature (270 °C), an external weak magnetic field (180 mT) induced intense localized magnetic flux around Fe3O4. The photo field generated electron–hole pairs in N-TiO2, the thermal field provided activation energy to accelerate interfacial reactions, and the magnetic field enhanced charge dynamics through Lorentz-force-driven carrier separation and strong spin polarization, both of which prolonged exciton lifetimes and suppressed recombination (Fig. 16c). The cooperative action of these three fields enabled stoichiometric H2 and O2 generation from pure water with an apparent quantum efficiency of 88.7%-without sacrificial agents-and established alternative carrier relaxation pathways for rapid water decomposition. This demonstrates that embedding superparamagnetic components into light-absorbing semiconductors can effectively harness thermal-photo-magnetic multi-field coupling to optimize carrier dynamics and maximize solar-to-hydrogen conversion efficiency.300
As the boundary conditions for photo-magnetic, magnetic-thermal, and thermal-photo coupling have been discussed above, the operational range for triple-field (photo-thermal-magnetic) coupling can be regarded as the combined constraint of these individual regimes. In practice, stable operation requires maintaining the temperature, illumination intensity, and magnetic field strength within the previously defined ranges, ensuring preserved magnetic ordering, moderate photothermal effects, and well-balanced charge-transport kinetics.
4.3. Theoretical investigations using density functional theory (DFT)
Density functional theory (DFT) has become an indispensable tool for probing the fundamental mechanisms of OER. By providing quantitative insights into electronic structure, adsorption energetics, and reaction pathways at the atomic scale, DFT bridges experimental observations with theoretical understanding. The incorporation of external fields such as light, heat, and magnetism adds new layers of complexity, as these stimuli modulate charge density, orbital hybridization, and spin configurations beyond conventional catalytic environments. Consequently, theory-guided simulations play a vital role in disentangling these effects and identifying rational design principles.For example, Gao et al.134 combined operando Raman spectroscopy with DFT+U calculations to reveal that photothermal excitation drives active-site reconstruction on NiFe2O4, specifically the surface conversion to (Ni,Fe) oxyhydroxides. This transformation significantly lowers reaction barriers and enhances OER activity under light illumination, highlighting how photo-driven thermal effects couple with lattice reconfiguration. Building on such insights, Yang et al.302 employed computational simulations to demonstrate that reducing mid-infrared emissivity by 70% for a catalyst could elevate surface temperature by nearly 228 K. Guided by this principle, they experimentally realized a Janus-type Ti3C2Tx catalyst exhibiting ∼88% solar absorptivity and ∼21% mid-infrared emissivity, where the close match between predicted and measured temperature rise validated the accuracy of computation-driven design strategies.
Magnetic-field effects have also been elucidated by DFT calculations.303,304 Ren et al.90 showed that the increased magnetic moment of the ligand hole enhances 3d–2p hybridization in ferromagnetic CoFe2O4, directly influencing spin-selective charge transfer during the OER. Their findings established a positive correlation between magnetization-induced spin alignment and catalytic activity, suggesting that magnetic moment could serve as a predictive descriptor for ferromagnetic OER catalysts. Similarly, thermal modulation introduces unique lattice perturbations. Du et al.173 demonstrated that thermal modulation introduces strain into Sr2IrO4 through its anisotropic lattice expansion, thereby generating compressive stress within the crystal. This thermally induced strain perturbs the orbital overlap between Ir 5d and O 2p states, leading to a downshift of the d-band center. The shift weakens the binding of oxygen intermediates, lowers the energy barrier for OER elementary steps, and ultimately accelerates the reaction kinetics. By altering the electronic free-energy, this effect also disrupts the conventional linear Arrhenius relationship and improves energy conversion efficiency.
Despite these advances, most theoretical investigations remain limited to the effect of a single external field at a time. Reports that attempt to capture multi-field coupling are extremely scarce. This gap is largely due to the formidable challenge of modeling several fields simultaneously within a DFT framework: each field alters the system's electronic, structural, and spin states in distinct, often non-linear ways. Coupling these perturbations creates a vast, high-dimensional parameter space, pushing beyond the capabilities of conventional DFT approaches. Moreover, the lack of benchmark datasets under multi-field conditions further hampers validation. As a result, while single-field studies provide critical mechanistic insights, a comprehensive theoretical description of synergistic field effects remains an open frontier.
To move toward such a general framework, recent theoretical progress has focused on extending DFT to explicitly describe how catalysts respond to external potentials, magnetic fields, and spin–orbit interactions.
Conventional ground-state calculations can reproduce the intrinsic vibrational frequencies of catalysts and assist in interpreting Raman spectra, yet they fail to account for potential-dependent peak shifts or intensity changes observed under electrochemical operation. To overcome this limitation, new frameworks combine grand-canonical DFT, which determines vibrational frequencies and Stark tuning rates at different electrode potentials,311 with time-dependent Raman theory, which connects electronic excitation and molecular vibration to estimate excited-state Raman intensities.312 Integrating these methods allows both Raman peak positions and strengths to be simulated more realistically, providing a theoretical bridge to operando spectroscopy.
Beyond electrochemical potential, similar methodological advances have enabled the explicit inclusion of magnetic fields within first-principles frameworks. Finite magnetic field implementations in DFT permit a uniform magnetic field to be applied directly in the simulation cell, making it possible to examine how external magnetism modifies electronic levels, charge distribution, and spin alignment of active sites.313 When the field is allowed to interact in a coherent way with both spin and orbital magnetic moments, the resulting Zeeman splitting and orbital responses can be benchmarked against the Berry-phase theory of orbital magnetization.314 These developments open the door to quantifying external fields-induced modifications of adsorption energies and reaction barriers.
At the same time, the role of spin–orbit coupling (SOC) has gained increasing attention in OER modelling. For heavy transition-metal oxides such as Ir- and Pt-based systems, SOC strongly influences band splitting, orbital occupancy, and metal-oxygen covalency. Neglecting it can therefore cause large errors in predicted reaction energetics. In Sr2IrO4, SOC divides the t2g5 manifold into two sub-bands with effective orbital angular momentum Jeff = 1/2 and 3/2.315 In IrO2, only SOC-included simulations reproduce experimental optical spectra.316 Incorporating SOC explicitly, often in combination with correlation-corrected or hybrid functionals, has thus become essential for obtaining reliable adsorption and free-energy profiles of key OER intermediates.
Together, these emerging computational advances provide a foundation for capturing the interplay of potential, external fields and their relativistic effects in electrocatalysis. They not only deepen the microscopic understanding of OER under complex external stimuli but also set the stage for future multi-field theoretical frameworks capable of treating coupled photo, thermal, and magnetic field-assisted electrocatalytic processes in a unified manner.
DFT is not merely a computational aid to experimental results but a central theoretical framework for uncovering the intrinsic mechanism of catalysis. In particular, DFT enables quantitative visualization of how multiple microscopic degrees of freedom, such as electronic, lattice (phononic), and spin, are mutually coupled and jointly determine the macroscopic kinetics of the oxygen evolution reaction (OER). This section now provides a more detailed picture of these interactions and how their feedback governs the overall catalytic behavior. Acting as a microscopic bridge between atomic-scale electronic processes and observable catalytic behavior, DFT uncovers that these three fundamental modes are dynamically coupled rather than independent. During OER, electronic redistribution, lattice vibrations, and spin alignment continuously interact and evolve together under realistic operating conditions, collectively shaping the activity and stability of the catalyst.19,30,110
DFT and density functional perturbation theory (DFPT) calculations reveal that lattice vibrations directly affect the local electronic environment of active sites. When catalysts are heated or illuminated, the oscillation of metal–oxygen bonds dynamically modulates orbital overlap between metal 3d and oxygen 2p states, instantly changing charge density and adsorption strength. This process lowers the reaction barriers of oxygen intermediates and promotes fast O–O coupling. Operando Raman and DFT studies on NiFe2O4 have shown that vibrational softening and surface reconstruction of NiFeOOH layers correlate with improved OER activity,134 directly linking lattice dynamics to catalytic kinetics. Alongside recent work that demonstrates how dynamic structural regulation of active sites can break the universal linear-scaling relationships in OER, through coordination changes and electronic-structure modulation during operation.317,318 Further DFT-EXAFS combined investigations reveal reversible oscillations of [Ni–O–Fe] units under operating potentials, can help stabilize high-valent oxyhydroxide phases and maintain strong catalytic performance.40 These findings highlight that electron–phonon coupling serves as a key microscopic mechanism linking lattice dynamics to electronic reorganization, which governs the evolution of active-site geometry and ultimately dictates OER kinetics.
DFT calculations have revealed that the spin state of a catalyst and its electronic structure are closely linked through the interaction between neighbouring metal atoms and oxygen, known as the super-exchange effect.319 When the angle of metal–oxygen–metal bonds or the distance between atoms changes slightly during operation, the overlap between electronic orbitals is altered, which in turn adjusts how spins on adjacent metal centers interact and align with each other. Such structural responses continuously influence the local electronic distribution and the spin polarization of active sites, thereby modifying the electron transfer behavior in the oxygen evolution reaction.320
Together, these findings illustrate that DFT provides a clear microscopic picture of how electron-spin coupling operates, showing that magnetic ordering and spin alignment can dynamically reshape the electronic environment of catalytic sites, open up spin-allowed charge-transfer pathways, and ultimately accelerate the spin-mediated steps of the OER.
DFT studies reveal that lattice vibrations can strongly influence magnetic interactions through spin–phonon coupling. In magnetic oxides such as NiO, small structural distortions. For example, changes in metal–oxygen–metal bond angles modify the overlap between metal d and oxygen p orbitals, thereby tuning the super-exchange interactions between neighboring metal ions and affecting their spin alignment.305,306 First-principles calculations reveal that small atomic vibrations in NiO can change both the magnetic exchange strength and the frequencies of lattice vibrations. This demonstrates that spin and lattice motions are closely linked, providing microscopic evidence for spin-phonon coupling in magnetic oxides.307
In OER systems, spin-polarized DFT studies, together with first-principles analyses of lattice distortions, indicate that the coupling between spin states and local lattice motions can modulate adsorption energetics and reaction barriers, thereby influencing catalytic kinetics. For instance, Li et al. employed DFT to show that tensile strain in 2D CoOOH reshapes the local Co–O coordination, drives a low-spin to high-spin transition of Co3+, and markedly lowers the OER overpotential by facilitating O2 release. Similarly, spin-polarized DFT calculations on transition-metal-based catalysts further show that spin states and the accompanying lattice distortions jointly regulate adsorption energetics, reaction free-energy profiles, and overpotentials, thereby directly influencing catalytic kinetics.308 Besides, experimental and spin-polarized DFT studies on LaCoO3-based perovskite cobaltites indicate that lattice and phonon-related distortions of the Co–O framework can drive spin-state changes and modify super-exchange interactions.309 These changes improve spin ordering and eg occupation at catalytically relevant Co sites and correlate with enhanced OER activity.240
Overall, these studies demonstrate that spin-phonon coupling acts as a crucial microscopic bridge between lattice flexibility and magnetic ordering. Lattice vibrations can tune magnetic exchange pathways and spin polarization at catalytic sites, while spin reordering in turn modulates phonon characteristics.310 This mutual regulation enables more efficient spin-polarized electron transfer and ultimately enhances the overall activity of OER catalysts.
In summary, the DFT analysis clarifies that superior OER performance arises not from a single factor but from the cooperative evolution and coupling of electron, phonon, and spin components. By capturing these interdependent effects within a unified quantum framework, DFT provides a crucial microscopic foundation for understanding how thermal, magnetic, and structural fields synergistically enhance catalytic activity.
5. Conclusions and outlook
The application of external physical fields, including magnetic, photo, and thermal fields, has emerged as a powerful paradigm for overcoming the intrinsic limitations of conventional OER catalyst design. Each field regulates catalytic activity through distinct mechanisms: magnetic fields induce magnetohydrodynamic, magnetoresistance, and magnetothermal effects; photo fields give rise to photothermal, photoelectric, and localized surface plasmon resonance effects; thermal fields introduce lattice strain and promote phase transitions. Importantly, synergistic coupling of these fields can generate cooperative effects that exceed the sum of their individual contributions. For example, thermal-light interplay provides unique opportunities to modulate photogenerated charge dynamics. Thermal energy not only complements photoexcitation by releasing carriers from defect states, extending hot-carrier lifetimes, and enhancing interfacial mobility, but also introduces additional driving forces through thermoelectric or pyroelectric effects to promote carrier separation. When coupled with plasmonic or defect-engineered systems, localized heating amplifies hot-spot formation and sustains charge density, while pyroelectric-assisted separation supports operation under weak or fluctuating illumination. Nevertheless, excessive heating can accelerate non-radiative recombination and catalyst degradation, highlighting the importance of precise control. Overall, thermal-light synergy represents a critical design principle for next-generation photo(electro)catalytic OER systems.The synergy between magnetic and photo fields lies in their combined ability to regulate the generation, separation, and utilization of photogenerated charge carriers. Magnetic fields influence photoexcitation via Zeeman splitting and spin polarization, increasing the proportion of long-lived parallel-spin carriers. Concurrently, the Lorentz force deflects electron and hole trajectories, promoting spatial separation and guiding carriers toward catalytic sites. In plasmonic systems, magnetic fields can further tune resonance conditions and hot-electron distributions, while facilitating spin-aligned electron transfer and prolonging carrier lifetimes. Collectively, these mechanisms demonstrate that magnetic-light coupling enhances charge generation, separation, and utilization, offering an effective strategy for multi-field-assisted catalyst design.
Thermal-magnetic synergy provides an indirect yet effective approach to control spin-dependent transport through modulation of magnetic ordering. Moderate heating strengthens orbital interactions and interfacial spin coherence, allowing spin-polarized carriers to maintain mobility and stability, while excessive heating disrupts long-range magnetic order and reduces performance.
Recent studies have demonstrated diverse strategies to harness these effects in OER catalysts. Rational design approaches for field-responsive catalysts can be grouped into magnetic, photo, thermal, and multi-field categories. Magnetic strategies include magnetothermal spin-state reconfiguration, interfacial spin pinning, localized magnetic heating in core–shell structures, construction of ferromagnet/oxyhydroxide heterostructures, dynamic interface reconstruction, and Lorentz force-driven convection. Photo strategies encompass photothermal materials with thermal management design, incorporation of plasmonic nanostructures, heterojunction and Schottky interface engineering, broadband light absorbers, and light-induced structural reconfiguration. Thermal strategies involve temperature-triggered spin transitions, bulk electronic modulation by heating, and heat-driven surface reconstruction. Beyond single-field designs, dual-field couplings have been explored: photo-magnetic designs employ materials with both photo-responsive and magnetic components; thermal-magnetic approaches use high Curie temperature materials, magnetic phase transition structures, and spin-switching alloys with thermal sensitivity; thermal-photo designs rely on photothermal absorbers with thermal management design, integration of pyroelectric and light-absorbing materials, spectral separation systems combining photothermal layers with UV-responsive photocatalysts, and gradient homojunction structures. At the frontier, multi-field integration combines light absorbers, photothermal units, and magnetic components, often with pyroelectric or thermally responsive materials, to achieve coordinated regulation of charge generation, spin states, and interfacial structures.
In parallel, descriptor-based computational frameworks, including magnetic moment of the ligand hole, wavelength, and thermally induced strain, are increasingly employed to guide material screening and prediction or evaluation of field-dependent catalytic behavior. These advances expand the design space and provide a theoretical basis for integrating multi-field effects into electrocatalyst optimization.
Research on magnetic, photo, and thermal fields, as well as their synergistic interactions, has accelerated and yielded promising gains in OER performance. Yet the field remains nascent, and several gaps must be closed to translate proof-of-concept advances into robust technologies.
(1) Trade-offs in activity, stability, and energy input. A central challenge in OER catalyst design lies in navigating the intrinsic trade-off between catalytic activity and operational stability. To move beyond qualitative assessments of this compromise, rigorous analytical frameworks such as Techno-Economic Analysis (TEA) and Life Cycle Assessment (LCA) are indispensable. While high activity reduces the energy cost of driving the reaction, it often comes at the expense of rapid degradation, necessitating frequent catalyst replacement. TEA translates this dilemma into quantifiable operational costs, balancing the immediate savings from high activity against the long-term expenses of material replenishment and system downtime. In parallel, LCA evaluates the environmental consequences of this cycle, accounting for the resource consumption and waste generation associated with repeated catalyst synthesis and disposal. Thus, an ideal catalyst is not simply the most active, but one that achieves a balance of activity and stability that is both economically favorable (as confirmed by TEA) and environmentally sustainable (as verified by LCA).
The incorporation of external energy fields-such as photo, heat, and magnetic forces-introduces a critical third dimension to this analysis: the cost and impact of energy input. The sustainability of these enhancements fundamentally depends on the origin of the external energy supply. If the photo, thermal, or magnetic fields are powered by electricity generated from fossil fuels, the apparent performance gains may come with hidden environmental costs, thereby diminishing the true sustainability advantage. In this context, TEA becomes vital for a holistic cost-benefit evaluation, carefully considering the capital and operational expenditures of auxiliary systems (e.g., solar concentrators and heating devices) alongside the energy consumed by these external stimuli. These costs must be weighed against the economic benefits of reduced electrical overpotential. Complementing this, LCA scrutinizes the cradle-to-grave footprint of the system, encompassing not only catalyst production but also the manufacturing of auxiliary equipment and, importantly, the origin of the external energy supply. For instance, a photo-assisted OER system powered by fossil-fuel-based electricity would compromise its sustainability claims, a limitation that only a comprehensive LCA can adequately expose.
Ultimately, the synergistic application of multiple external fields, guided by predictive TEA and LCA, represents the most promising path toward practical OER systems. By combining stimuli, it may be possible to achieve high performance under milder, less energy-intensive conditions, thereby optimizing the complex interplay between activity, stability, and energy input. For instance, preliminary TEA models can guide researchers toward synergistic combinations that minimize the projected Levelized Cost of Hydrogen (LCOH), steering experimental efforts away from scientifically interesting but economically unviable pathways. Likewise, early-stage LCA can identify potential environmental hotspots, such as the use of rare or toxic elements in a catalyst that is only effective under specific magnetic or thermal conditions. In this paradigm, TEA and LCA are no longer post-mortem evaluation tools but are integrated into the research and development process, driving the design of OER technologies that are not only scientifically advanced but also truly sustainable and scalable.
(2) Standardization of performance metrics for field-assisted catalysis. While numerous reports have demonstrated that external fields-such as photo, magnetic, and thermal stimuli-can enhance the apparent activity of OER catalysts, the majority of studies quantify these effects solely in terms of overpotential reduction or current density increase. These metrics, although intuitive, do not account for the energy cost of generating the external field, making it impossible to judge whether the enhancement is energetically and practically meaningful. A high apparent activity gain may, in fact, come at the expense of disproportionate external energy consumption, leading to negligible or even negative net benefits in real applications.
To address this gap, we propose that energy-conversion efficiency (ηfield) should be adopted as a standardized figure-of-merit for field-assisted OER. This metric quantitatively relates the useful catalytic performance improvement to the external energy supplied for generating the field, enabling fair comparison across different field types, catalyst systems, and experimental setups. The general definition is:
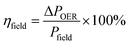 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1). Besides, Pfield is the average power required to sustain the external field (W).
485 C mol−1). Besides, Pfield is the average power required to sustain the external field (W).
For photo field,
| Plight = Iirr × Aillum | (14) |
For magnetic field,
| Pmag = Vcoil × Icoil | (15) |
For thermal field, Pheat from an external heater or photothermal/magnetothermal source.
Adopting ηfield provides a unified, quantitative basis for evaluating external field-assisted OER. This metric normalizes performance enhancement to actual energy investment, allowing fair cross-field comparisons (photo, magnetic, thermal), assessing scalability for industrial applications, and guiding the identification of field-catalyst combinations that deliver the highest catalytic return per unit of external energy. From a cost-benefit perspective, the practicality of field-assisted catalysis can be greatly improved if the external energy source is low-cost or waste-derived, such as utilizing solar energy for the photo field, permanent magnets for the magnetic field, or industrial waste heat for the thermal field.
To further enhance comparability and reproducibility among studies, we recommend that reports on field-assisted catalysis include a standardized checklist of key experimental parameters, summarized below:
(i) Light intensity and illuminated area for photo-assisted systems.
(ii) Temperature measurement method (bulk versus local, steady-state or transient) for thermal or photothermal systems.
(iii) iR compensation and resistance-correction procedure for electrochemical data.
(iv) Basis for current normalization (geometric area or electrochemical surface area, ECSA).
(v) Mass transport parameters, such as stirring rate or rotating-electrode speed.
(vi) Energy consumption of the applied field (e.g., coil current or power supply) or magnet type (electromagnet versus permanent magnet).
(vii) Substrate electrode type and pretreatment, including material (e.g., glassy carbon, Ni foam, or carbon paper) and surface preparation details.
Adhering to this checklist can ensure that improvements in overpotential or current density are interpreted within a consistent energy and experimental framework, thereby strengthening cross-study comparability and reproducibility.
(3) The integration of external fields such as light irradiation and thermal activation into OER systems presents new opportunities to overcome the intrinsic limitations of conventional electrocatalysts. While descriptors like eg occupancy, oxygen vacancy concentration, and ΔG(OH*) remain useful under standard electrochemical conditions, field-assisted catalysis requires descriptors that explicitly capture coupled multi-field effects. For example, how simultaneous light absorption, thermal excitation, and magnetic spin alignment interact to regulate carrier dynamics, adsorption energetics, and reaction pathways. Density functional theory (DFT), in combination with in situ spectroscopy and machine learning (ML), provides a robust platform to establish such descriptors and enable computational screening of optimal catalysts. A related example is the work of Shabbir et al.,321 who developed a high-throughput ML framework for extreme ultraviolet detectors, correlating external-field parameters, material descriptors, and device configuration with detector responsivity, and successfully identifying α-MoO3 as a high-performance material. Although beyond catalysis, this paradigm illustrates how correlation models between field parameters, electronic descriptors, and performance metrics can guide ML-assisted prediction and validation of catalysts under specific external stimuli.
Despite these advances, no OER study has yet demonstrated a workflow in which ML first predicts field-specific materials or parameters and subsequently validates them under external fields, highlighting a clear gap for future research. Furthermore, most descriptors are still adapted from zero-field electrocatalysis and fail to incorporate parameters relevant to multi-field coupling. Current computational models also rarely consider dynamic conditions like pulsed illumination, spatial temperature gradients, or magnetization switching, and no unified framework exists to quantify cooperative or antagonistic effects among multiple fields, limiting systematic comparison across conditions.
Looking forward, the development of field-specific descriptors that reflect multi-field coupling will be crucial for accelerating material discovery in photo-, thermal-, and magnetic-assisted OER. Promising candidates include photo-coupled descriptors (e.g., hot-electron injection yield, photo absorption efficiency, exciton dissociation probability) and thermal descriptors (e.g., entropy-corrected adsorption free energy, temperature-dependent prefactor, activation energy reduction), which need to be extended toward multi-field conditions. Progress will depend on multi-scale modeling that bridges ab initio DFT with continuum simulations capable of simultaneously describing photo, thermal, and magnetic field transport, thereby capturing realistic interactions among external fields, catalysts, and electrolytes. In addition, integrating cost-performance considerations (such as sunlight as a light source, industrial waste heat as a thermal source, and permanent magnets as magnetic sources) will help identify catalyst systems that are not only efficient but also practical for large-scale applications.
Conflicts of interest
There are no conflicts to declare.Data availability
This review does not report any original research data, software, or code. No new datasets were generated or analyzed in the course of this work. Additional information related to the review can be obtained from the authors upon reasonable request.Acknowledgements
The authors acknowledge the financial support by the Ministry of Education (MOE), Singapore, under its Academic Research Fund Tier 2 program (T2EP50123-0010, T2EP50224-0011, and T2EP50125-0032) and Agency for Science, Technology and Research (A*STAR) under its RIE2025 MTC IRG program (M23M6c0106). This work is also supported by the National Natural Science Foundation of China (52173207) and the Science Fund for Distinguished Young Scholars of Hunan Province of China (2023JJ10040).References
- T. E. Jones, D. Teschner and S. Piccinin, Chem. Rev., 2024, 124, 9136–9223 CrossRef CAS PubMed
.
- X. Wang, S. Xi, P. Huang, Y. Du, H. Zhong, Q. Wang, A. Borgna, Y.-W. Zhang, Z. Wang, H. Wang, Z. G. Yu, W. S. V. Lee and J. Xue, Nature, 2022, 611, 702–708 CrossRef CAS
.
- L. Chong, G. Gao, J. Wen, H. Li, H. Xu, Z. Green, J. D. Sugar, A. J. Kropf, W. Xu, X. M. Lin, H. Xu, L. W. Wang and D. J. Liu, Science, 2023, 380, 609–616 CrossRef CAS PubMed
.
- L. Gao, X. Cui, C. D. Sewell, J. Li and Z. Lin, Chem. Soc. Rev., 2021, 50, 8428–8469 RSC
.
- K. S. Exner, Acc. Chem. Res., 2024, 57, 1336–1345 CrossRef CAS
.
- A. Yu, Y. Zhang, S. Zhu, T. Wu and Z. J. Xu, Nat. Energy, 2025, 10, 435–447 CrossRef
.
- C. Hu, Y. Dong, Q. Shi, R. Long and Y. Xiong, Chem. Soc. Rev., 2025, 54, 524–559 RSC
.
- B. Liu, H. Zhong, J. Liu, J. Yu, Q. Zhang, J. R. Loh, L. Zhao, P. Zhang, L. Gao and J. Xue, ACS Nano, 2025, 19, 5110–5130 CrossRef CAS PubMed
.
- F. Yu, C. Wang, Y. Li, H. Ma, R. Wang, Y. Liu, N. Suzuki, C. Terashima, B. Ohtani, T. Ochiai, A. Fujishima and X. Zhang, Adv. Sci., 2020, 7, 2000204 CrossRef CAS PubMed
.
- U. E. Steiner and T. Ulrich, Chem. Rev., 2002, 89, 51–147 CrossRef
.
- B. Dai, J. Guo, C. Gao, H. Yin, Y. Xie and Z. Lin, Adv. Mater., 2023, 35, e2210914 CrossRef
.
- M. Lu, Y. Du, S. Yan, T. Yu and Z. Zou, Phys. Rev. Lett., 2024, 133, 258001 CrossRef CAS PubMed
.
- J. Du, F. Li and L. Sun, Chem. Soc. Rev., 2021, 50, 2663–2695 RSC
.
- J. Li, Nano-Micro Lett., 2022, 14, 112 CrossRef CAS
.
- K. S. Exner, ChemCatChem, 2020, 12, 2000–2003 CrossRef CAS
.
- E. Romeo, F. Illas and F. Calle-Vallejo, Chem. Sci., 2023, 14, 3622–3629 RSC
.
- D. Y. Kuo, H. Paik, J. Kloppenburg, B. Faeth, K. M. Shen, D. G. Schlom, G. Hautier and J. Suntivich, J. Am. Chem. Soc., 2018, 140, 17597–17605 CrossRef CAS PubMed
.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Norskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed
.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS
.
- J. H. Montoya, L. C. Seitz, P. Chakthranont, A. Vojvodic, T. F. Jaramillo and J. K. Norskov, Nat. Mater., 2016, 16, 70–81 CrossRef
.
- R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, J. Phys. Chem. C, 2016, 120, 24910–24916 CrossRef CAS
.
- F. Calle-Vallejo, A. Krabbe and J. M. Garcia-Lastra, Chem. Sci., 2017, 8, 124–130 RSC
.
- Y. Wang, W. Qiu, E. Song, F. Gu, Z. Zheng, X. Zhao, Y. Zhao, J. Liu and W. Zhang, Natl. Sci. Rev., 2018, 5, 327–341 CrossRef CAS
.
- K. S. Exner, Chem Catal., 2021, 1, 258–271 CAS
.
- S. Chen, L. Ma, Z. Huang, G. Liang and C. Zhi, Cell Rep. Phys. Sci., 2022, 3, 100729 CrossRef CAS
.
- F. Dionigi, Z. Zeng, I. Sinev, T. Merzdorf, S. Deshpande, M. B. Lopez, S. Kunze, I. Zegkinoglou, H. Sarodnik, D. Fan, A. Bergmann, J. Drnec, J. F. Araujo, M. Gliech, D. Teschner, J. Zhu, W. X. Li, J. Greeley, B. R. Cuenya and P. Strasser, Nat. Commun., 2020, 11, 2522 CrossRef CAS PubMed
.
- S. Samira, J. Hong, J. C. A. Camayang, K. Sun, A. S. Hoffman, S. R. Bare and E. Nikolla, JACS Au, 2021, 1, 2224–2241 CrossRef CAS
.
- K. A. Stoerzinger, O. Diaz-Morales, M. Kolb, R. R. Rao, R. Frydendal, L. Qiao, X. R. Wang, N. B. Halck, J. Rossmeisl, H. A. Hansen, T. Vegge, I. E. L. Stephens, M. T. M. Koper and Y. Shao-Horn, ACS Energy Lett., 2017, 2, 876–881 CrossRef CAS
.
- S. Lee, K. Banjac, M. Lingenfelder and X. Hu, Angew. Chem., Int. Ed., 2019, 58, 10295–10299 CrossRef CAS
.
- A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y. L. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Nat. Chem., 2017, 9, 457–465 CrossRef CAS PubMed
.
- Z. Wang, W. A. Goddard, 3rd and H. Xiao, Nat. Commun., 2023, 14, 4228 CrossRef CAS
.
- Y. Pan, X. Xu, Y. Zhong, L. Ge, Y. Chen, J. M. Veder, D. Guan, R. O'Hayre, M. Li, G. Wang, H. Wang, W. Zhou and Z. Shao, Nat. Commun., 2020, 11, 2002 CrossRef CAS PubMed
.
- K. Schweinar, B. Gault, I. Mouton and O. Kasian, J. Phys. Chem. Lett., 2020, 11, 5008–5014 CrossRef CAS PubMed
.
- Z. Shi, Y. Wang, J. Li, X. Wang, Y. Wang, Y. Li, W. Xu, Z. Jiang, C. Liu, W. Xing and J. Ge, Joule, 2021, 5, 2164–2176 CrossRef CAS
.
- J. Hwang, R. R. Rao, L. Giordano, Y. Katayama, Y. Yu and Y. Shao-Horn, Science, 2017, 358, 751–756 CrossRef CAS
.
- W. T. Hong, R. E. Welsch and Y. Shao-Horn, J. Phys. Chem. C, 2015, 120, 78–86 CrossRef
.
- X. Ping, Y. Liu, L. Zheng, Y. Song, L. Guo, S. Chen and Z. Wei, Nat. Commun., 2024, 15, 2501 CrossRef CAS PubMed
.
- A. Loncar, D. Escalera-Lopez, S. Cherevko and N. Hodnik, Angew. Chem., Int. Ed., 2022, 61, e202114437 CrossRef CAS PubMed
.
- F.-Y. Chen, Z.-Y. Wu, Z. Adler and H. Wang, Joule, 2021, 5, 1704–1731 CrossRef CAS
.
- Z. He, J. Zhang, Z. Gong, H. Lei, D. Zhou, N. Zhang, W. Mai, S. Zhao and Y. Chen, Nat. Commun., 2022, 13, 2191 CrossRef CAS PubMed
.
- S. Xu, S. Feng, Y. Yu, D. Xue, M. Liu, C. Wang, K. Zhao, B. Xu and J. N. Zhang, Nat. Commun., 2024, 15, 1720 CrossRef CAS PubMed
.
- C. T. He, L. H. Yu, H. Liu, Q. Wang, Z. M. Ye, J. Zhang, L. D. Wang, M. Q. He, X. F. Zhang, H. G. Du, Z. W. Lu, J. Yang, H. H. Huang and X. M. Chen, Nat. Commun., 2025, 16, 4389 CrossRef CAS PubMed
.
- Q. Ji, B. Tang, X. Zhang, C. Wang, H. Tan, J. Zhao, R. Liu, M. Sun, H. Liu, C. Jiang, J. Zeng, X. Cai and W. Yan, Nat. Commun., 2024, 15, 8089 CrossRef CAS PubMed
.
- Z. H. Yin, H. Liu, J. S. Hu and J. J. Wang, Natl. Sci. Rev., 2024, 11, nwae362 CrossRef CAS
.
- C. Rong, X. Huang, H. Arandiyan, Z. Shao, Y. Wang and Y. Chen, Adv. Mater., 2025, 37, e2416362 CrossRef
.
- F. Qian, D. Cao, S. Chen, Y. Yuan, K. Chen, P. J. Chimtali, H. Liu, W. Jiang, B. Sheng, L. Yi, J. Huang, C. Hu, H. Lei, X. Wu, Z. Wen, Q. Chen and L. Song, Nat. Commun., 2025, 16, 6894 CrossRef CAS PubMed
.
- Z. Li, D. Wang, H. Kang, Z. Shi, X. Hu, H. Sun and J. Xu, J. Mater. Chem. A, 2025, 13, 587–594 RSC
.
- T. Zhang, J. Jiang, W. Sun, S. Gong, X. Liu, Y. Tian and D. Wang, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2317247121 CrossRef CAS
.
- Q. Zhou, W. Xue, X. Cui, P. Wang, S. Zuo, F. Mo, C. Li, G. Liu, S. Ouyang, S. Zhan, J. Chen and C. Wang, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2404013121 CrossRef CAS PubMed
.
- C. Lin, J.-L. Li, X. Li, S. Yang, W. Luo, Y. Zhang, S.-H. Kim, D.-H. Kim, S. S. Shinde, Y.-F. Li, Z.-P. Liu, Z. Jiang and J.-H. Lee, Nat. Catal., 2021, 4, 1012–1023 CrossRef CAS
.
- P. Ma, J. Xue, J. Li, H. Cao, R. Wang, M. Zuo, Z. Zhang and J. Bao, Nat. Commun., 2025, 16, 2573 CrossRef CAS PubMed
.
- S. B. Scott, R. R. Rao, C. Moon, J. E. Sorensen, J. Kibsgaard, Y. Shao-Horn and I. Chorkendorff, Energy Environ. Sci., 2022, 15, 1977–1987 RSC
.
- C. C. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed
.
- A. Peugeot, C. E. Creissen, D. Karapinar, H. N. Tran, M. Schreiber and M. Fontecave, Joule, 2021, 5, 1281–1300 CrossRef CAS
.
- J. Zhao, Y. Guo, Z. Zhang, X. Zhang, Q. Ji, H. Zhang, Z. Song, D. Liu, J. Zeng, C. Chuang, E. Zhang, Y. Wang, G. Hu, M. A. Mushtaq, W. Raza, X. Cai and F. Ciucci, Nat. Nanotechnol., 2025, 20, 57–66 CrossRef CAS PubMed
.
-
J. Newman and N. P. Balsara, Electrochemical Systems, John Wiley & Sons, 2021 Search PubMed
.
-
A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical methods: fundamentals and applications, John Wiley & Sons, 2022 Search PubMed
.
- O. van der Heijden, S. Park, R. E. Vos, J. J. J. Eggebeen and M. T. M. Koper, ACS Energy Lett., 2024, 9, 1871–1879 CrossRef CAS
.
- P. Khadke, T. Tichter, T. Boettcher, F. Muench, W. Ensinger and C. Roth, Sci. Rep., 2021, 11, 8974 CrossRef CAS
.
- X. Wang, Q. Yang, S. Singh, H. Borrmann, V. Hasse, C. Yi, Y. Li, M. Schmidt, X. Li, G. H. Fecher, D. Zhou, B. Yan and C. Felser, Nat. Energy, 2024, 10, 101–109 CrossRef
.
- P. A. Kempler and A. C. Nielander, Nat. Commun., 2023, 14, 1158 CrossRef CAS
.
- R. Ram, L. Xia, H. Benzidi, A. Guha, V. Golovanova, A. Garzon Manjon, D. Llorens Rauret, P. Sanz Berman, M. Dimitropoulos, B. Mundet, E. Pastor, V. Celorrio, C. A. Mesa, A. M. Das, A. Pinilla-Sanchez, S. Gimenez, J. Arbiol, N. Lopez and F. P. Garcia de Arquer, Science, 2024, 384, 1373–1380 CrossRef CAS PubMed
.
- C. Wei, S. Sun, D. Mandler, X. Wang, S. Z. Qiao and Z. J. Xu, Chem. Soc. Rev., 2019, 48, 2518–2534 RSC
.
- D. M. Morales and M. Risch, J. Phys.: Energy, 2021, 3, 034013 CAS
.
- A. Li, S. Kong, K. Adachi, H. Ooka, K. Fushimi, Q. Jiang, H. Ofuchi, S. Hamamoto, M. Oura, K. Higashi, T. Kaneko, T. Uruga, N. Kawamura, D. Hashizume and R. Nakamura, Science, 2024, 384, 666–670 CrossRef CAS PubMed
.
- S. Jung, C. C. L. McCrory, I. M. Ferrer, J. C. Peters and T. F. Jaramillo, J. Mater. Chem. A, 2016, 4, 3068–3076 RSC
.
- M. B. Stevens, L. J. Enman, A. S. Batchellor, M. R. Cosby, A. E. Vise, C. D. M. Trang and S. W. Boettcher, Chem. Mater., 2016, 29, 120–140 CrossRef
.
- M. D. Obradović and S. L. Gojković, J. Electroanal. Chem., 2022, 918, 116479 CrossRef
.
- R. Martínez-Hincapié, J. Wegner, M. U. Anwar, A. Raza-Khan, S. Franzka, S. Kleszczynski and V. Čolić, Electrochim. Acta, 2024, 476, 143663 CrossRef
.
- Y. Zhang, C. Liang, J. Wu, H. Liu, B. Zhang, Z. Jiang, S. Li and P. Xu, ACS Appl. Energy Mater., 2020, 3, 10303–10316 CrossRef CAS
.
- T. Z. Fahidy, J. Appl. Electrochem., 1983, 13, 553–563 CrossRef CAS
.
- L. M. A. Monzon and J. M. D. Coey, Electrochem. Commun., 2014, 42, 38–41 CrossRef CAS
.
- X. Ye, J. Yang, W. Yang, T. Chen, W. Li and Y. Liu, Corros. Sci., 2025, 255, 113082 CrossRef CAS
.
- L. Zhang, T. Dang, Z. Zhao, H. Liu, M. Wang and X. Yang, Sustainable Mater. Technol., 2025, 45, e01455 CrossRef CAS
.
- J. Liu, C. Li, G. Shi, R. Wang and X. Han, Appl. Phys. A: Mater. Sci. Process., 2025, 131, 728 CrossRef CAS
.
- C. Machado Fernandes, E. M. Rodrigues, O. C. Alves, F. Garcia, Y. Xing, M. C. dos Santos and J. C. M. Silva, Appl. Catal. O: Open, 2025, 205, 207052 CAS
.
- S. Luo, K. Elouarzaki and Z. J. Xu, Angew. Chem., Int. Ed., 2022, 61, e202203564 CrossRef CAS PubMed
.
- O. Lioubashevski, E. Katz and I. Willner, J. Phys. Chem. B, 2004, 108, 5778–5784 CrossRef CAS
.
- V. Gatard, J. Deseure and M. Chatenet, Curr. Opin. Electrochem., 2020, 23, 96–105 CrossRef CAS
.
- Y. H. Li and Y. J. Chen, Sci. Rep., 2021, 11, 9346 CrossRef CAS
.
- D. Baczyzmalski, F. Karnbach, G. Mutschke, X. Yang, K. Eckert, M. Uhlemann and C. Cierpka, Phys. Rev. Fluids, 2017, 2, 093701 CrossRef
.
- Y. Liu, S. Li, H. Wu and Y. Shi, J. Electroanal. Chem., 2023, 945, 117679 CrossRef CAS
.
- P. Vensaus, Y. Liang, J. P. Ansermet, G. Soler-Illia and M. Lingenfelder, Nat. Commun., 2024, 15, 2867 CrossRef CAS PubMed
.
- L. M. A. Monzon and J. M. D. Coey, Electrochem. Commun., 2014, 42, 42–45 CrossRef CAS
.
- A. P. Wills and L. G. Hector, Phys. Rev., 1924, 23, 209–220 CrossRef CAS
.
- X. Li, C. Hao, Y. Du, Y. Lu, Y. Fan, M. Wang, N. Wang, R. Meng, X. Wang, Z. J. Xu and Z. Cheng, Chin. J. Catal., 2023, 55, 191–199 CrossRef CAS
.
- M. N. Baibich, J. M. Broto, A. Fert, F. Nguyen Van Dau, F. Petroff, P. Etienne, G. Creuzet, A. Friederich and J. Chazelas, Phys. Rev. Lett., 1988, 61, 2472–2475 CrossRef CAS
.
- J. S. Moodera, L. R. Kinder, T. M. Wong and R. Meservey, Phys. Rev. Lett., 1995, 74, 3273–3276 CrossRef CAS
.
- B. Raveau, A. Maignan, C. Martin and M. Hervieu, Chem. Mater., 1998, 10, 2641–2652 CrossRef CAS
.
- X. Ren, T. Wu, Y. Sun, Y. Li, G. Xian, X. Liu, C. Shen, J. Gracia, H.-J. Gao, H. Yang and Z. J. Xu, Nat. Commun., 2021, 12, 2608 CrossRef CAS PubMed
.
- T. Wu, X. Ren, Y. Sun, S. Sun, G. Xian, G. G. Scherer, A. C. Fisher, D. Mandler, J. W. Ager, A. Grimaud, J. Wang, C. Shen, H. Yang, J. Gracia, H. J. Gao and Z. J. Xu, Nat. Commun., 2021, 12, 3634 CrossRef CAS
.
- C. Y. Huang, H. A. Chen, W. X. Lin, K. H. Chen, Y. C. Lin, T. S. Wu, C. C. Chang, C. W. Pao, W. T. Chuang, J. C. Jan, Y. C. Shao, N. Hiraoka, J. W. Chiou, P. C. Kuo, J. Shiue, S. K. D. Vishnu, R. Sankar, Z. W. Cyue, W. F. Pong and C. W. Chen, J. Am. Chem. Soc., 2025, 147, 13286–13295 CrossRef CAS PubMed
.
- J. Qian, H. Zhang, G. Li, L. Jia, X. Peng, C. Zhong, F. Li, D. Chao and D. Gao, Adv. Funct. Mater., 2023, 34, 2305621 CrossRef
.
- Y. Zhang, P. Guo, S. Li, J. Sun, W. Wang, B. Song, X. Yang, X. Wang, Z. Jiang, G. Wu and P. Xu, J. Mater. Chem. A, 2022, 10, 1760–1767 RSC
.
-
A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, CRC Press, 2016 Search PubMed
.
- V. K. Pecharsky and J. K. A. Gschneidner, Phys. Rev. Lett., 1997, 78, 4494–4497 CrossRef CAS
.
- K. A. Gschneidner and V. K. Pecharsky, Annu. Rev. Mater. Sci., 2000, 30, 387–429 CrossRef CAS
.
- X. Gong, Z. Jiang, W. Zeng, C. Hu, X. Luo, W. Lei and C. Yuan, Nano Lett., 2022, 22, 9411–9417 CrossRef CAS PubMed
.
- Y. L. Wang, T. H. Yang, S. Yue, H. B. Zheng, X. P. Liu, P. Z. Gao, H. Qin and H. N. Xiao, ACS Appl. Mater. Interfaces, 2023, 15, 11631–11641 CrossRef CAS
.
- H. B. Zheng, Y. L. Wang, J. W. Xie, P. Z. Gao, D. Y. Li, E. V. Rebrov, H. Qin, X. P. Liu and H. N. Xiao, ACS Appl. Mater. Interfaces, 2022, 14, 34627–34636 CrossRef CAS
.
- R. E. Zeebe, Geochim. Cosmochim. Acta, 2011, 75, 2483–2498 CrossRef CAS
.
- H. Su, J. Sun, C. Wang and H. Wang, Ultrason. Sonochem., 2024, 102, 106734 CrossRef CAS
.
- A. Babich, A. Bashkatov, M. Eftekhari, X. Yang, P. Strasser, G. Mutschke and K. Eckert, PRX Energy, 2025, 4, 013011 CrossRef
.
- M. Lázaro, Á. V. Delgado and G. R. Iglesias, J. Magn. Magn. Mater., 2024, 591, 171718 CrossRef
.
- X. Cui, Q. Ruan, X. Zhuo, X. Xia, J. Hu, R. Fu, Y. Li, J. Wang and H. Xu, Chem. Rev., 2023, 123, 6891–6952 CrossRef CAS
.
- F. A. Garcés-Pineda, M. Blasco-Ahicart, D. Nieto-Castro, N. López and J. R. Galán-Mascarós, Nat. Energy, 2019, 4, 519–525 CrossRef
.
- Z. Chen, X. Li, H. Ma, Y. Zhang, J. Peng, T. Ma, Z. Cheng, J. Gracia, Y. Sun and Z. J. Xu, Natl. Sci. Rev., 2024, 11, nwae314 CrossRef CAS PubMed
.
- X. Han, J. Chen, P. He and J. Lu, Natl. Sci. Rev., 2024, 11, nwae217 CrossRef CAS PubMed
.
- X. Wang, X. J. Gao, L. Qin, C. Wang, L. Song, Y. N. Zhou, G. Zhu, W. Cao, S. Lin, L. Zhou, K. Wang, H. Zhang, Z. Jin, P. Wang, X. Gao and H. Wei, Nat. Commun., 2019, 10, 704 CrossRef CAS PubMed
.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS
.
- A. Grimaud, A. Demortière, M. Saubanère, W. Dachraoui, M. Duchamp, M.-L. Doublet and J.-M. Tarascon, Nat. Energy, 2017, 2, 16189 CrossRef CAS
.
- W. T. Hong, K. A. Stoerzinger, Y.-L. Lee, L. Giordano, A. Grimaud, A. M. Johnson, J. Hwang, E. J. Crumlin, W. Yang and Y. Shao-Horn, Energy Environ. Sci., 2017, 10, 2190–2200 RSC
.
- Y. Zhang, Q. Wu, J. Z. Y. Seow, Y. Jia, X. Ren and Z. J. Xu, Chem. Soc. Rev., 2024, 53, 8123–8136 RSC
.
- M. L. Brongersma, N. J. Halas and P. Nordlander, Nat. Nanotechnol., 2015, 10, 25–34 CrossRef CAS
.
- J. G. Liu, H. Zhang, S. Link and P. Nordlander, ACS Photonics, 2017, 5, 2584–2595 CrossRef
.
- M. Bernardi, J. Mustafa, J. B. Neaton and S. G. Louie, Nat. Commun., 2015, 6, 7044 CrossRef CAS PubMed
.
- A. Manjavacas, J. G. Liu, V. Kulkarni and P. Nordlander, ACS Nano, 2014, 8, 7630–7638 CrossRef CAS PubMed
.
- S. Linic, U. Aslam, C. Boerigter and M. Morabito, Nat. Mater., 2015, 14, 567–576 CrossRef CAS
.
- G. Baffou and R. Quidant, Laser Photonics Rev., 2012, 7, 171–187 CrossRef
.
- M. Gao, L. Zhu, C. K. Peh and G. W. Ho, Energy Environ. Sci., 2019, 12, 841–864 RSC
.
- W. W. Gärtner, Phys. Rev., 1961, 122, 419–424 CrossRef
.
- W. Shockley and W. T. Read, Phys. Rev., 1952, 87, 835–842 CrossRef CAS
.
- M. Ghoussoub, M. Xia, P. N. Duchesne, D. Segal and G. Ozin, Energy Environ. Sci., 2019, 12, 1122–1142 RSC
.
- L. B. Hoch, P. Szymanski, K. K. Ghuman, L. He, K. Liao, Q. Qiao, L. M. Reyes, Y. Zhu, M. A. El-Sayed, C. V. Singh and G. A. Ozin, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E8011–E8020 CrossRef CAS PubMed
.
- W. He, L. Zhou, M. Wang, Y. Cao, X. Chen and X. Hou, Sci. Bull., 2021, 66, 1472–1483 CrossRef CAS
.
- D. Xu, Z. Li, L. Li and J. Wang, Adv. Funct. Mater., 2020, 30, 2000712 CrossRef CAS
.
- Y. Wang, H.-M. Meng, G. Song, Z. Li and X.-B. Zhang, ACS Appl. Polym. Mater., 2020, 2, 4258–4272 CrossRef CAS
.
- C. Yu, L. Xu, Y. Zhang, P. S. Timashev, Y. Huang and X.-J. Liang, ACS Appl. Polym. Mater., 2020, 2, 4289–4305 CrossRef CAS
.
- L. Zhou, Y. Tan, D. Ji, B. Zhu, P. Zhang, J. Xu, Q. Gan, Z. Yu and J. Zhu, Sci. Adv., 2016, 2, e1501227 CrossRef
.
- X. Chen, Y. Chen, M. Yan and M. Qiu, ACS Nano, 2012, 6, 2550–2557 CrossRef CAS
.
- B. Jin, Y. Li, J. Wang, F. Meng, S. Cao, B. He, S. Jia, Y. Wang, Z. Li and X. Liu, Small, 2019, 15, e1903847 CrossRef PubMed
.
- C. Zhou, L. Zhang, X. Tong and M. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 61227–61236 CrossRef CAS
.
- L. Shi, S. Zhuo, M. Abulikemu, G. Mettela, T. Palaniselvam, S. Rasul, B. Tang, B. Yan, N. B. Saleh and P. Wang, RSC Adv., 2018, 8, 29179–29188 RSC
.
- L. Gao, X. Cui, Z. Wang, C. D. Sewell, Z. Li, S. Liang, M. Zhang, J. Li, Y. Hu and Z. Lin, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2023421118 CrossRef CAS
.
- Z. Lin, Q. Gao and P. Diao, J. Colloid Interface Sci., 2023, 638, 54–62 CrossRef CAS
.
- M. Zhao, T. Chen, B. He, X. Hu, J. Huang, P. Yi, Y. Wang, Y. Chen, Z. Li and X. Liu, J. Mater. Chem. A, 2020, 8, 15976–15983 RSC
.
- Y. Liang, Y. Zhang, X. Wang, J. Zhou, Z. Cao, M. Huang and H. Jiang, Mater. Today Energy, 2022, 25, 100966 CrossRef CAS
.
- E. Nurlaela, T. Shinagawa, M. Qureshi, D. S. Dhawale and K. Takanabe, ACS Catal., 2016, 6, 1713–1722 CrossRef CAS
.
- H. Yang, Y. Liu, Y. Ding, F. Li, L. Wang, B. Cai, F. Zhang, T. Liu, G. Boschloo, E. M. J. Johansson and L. Sun, Nat. Commun., 2023, 14, 5486 CrossRef CAS
.
- T. Yao, X. An, H. Han, J. Q. Chen and C. Li, Adv. Energy Mater., 2018, 8, 1800210 CrossRef
.
- D. J. Martin, P. J. Reardon, S. J. Moniz and J. Tang, J. Am. Chem. Soc., 2014, 136, 12568–12571 CrossRef CAS
.
- S. Chen, Y. Qi, T. Hisatomi, Q. Ding, T. Asai, Z. Li, S. S. K. Ma, F. Zhang, K. Domen and C. Li, Angew. Chem., Int. Ed., 2015, 54, 8498–8501 CrossRef CAS
.
- E. Kecsenovity, B. Endrodi, P. S. Toth, Y. Zou, R. A. W. Dryfe, K. Rajeshwar and C. Janaky, J. Am. Chem. Soc., 2017, 139, 6682–6692 CrossRef CAS
.
- Q. Meng, B. Zhang, L. Fan, H. Liu, M. Valvo, K. Edström, M. Cuartero, R. de Marco, G. A. Crespo and L. Sun, Angew. Chem., Int. Ed., 2019, 58, 19027–19033 CrossRef CAS PubMed
.
- T. Hisatomi and K. Domen, Nat. Catal., 2019, 2, 387–399 CrossRef CAS
.
- K. Sivula and R. van de Krol, Nat. Rev. Mater., 2016, 1, 15010 CrossRef CAS
.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS
.
- M. Sachs, L. Harnett-Caulfield, E. Pastor, B. Davies, D. J. C. Sowood, B. Moss, A. Kafizas, J. Nelson, A. Walsh and J. R. Durrant, Nat. Chem., 2025, 17, 1348–1355 CrossRef CAS PubMed
.
- F. F. Abdi, T. J. Savenije, M. M. May, B. Dam and R. van de Krol, J. Phys. Chem. Lett., 2013, 4, 2752–2757 CrossRef CAS
.
- H.-J. Ahn, M.-J. Kwak, J.-S. Lee, K.-Y. Yoon and J.-H. Jang, J. Mater. Chem. A, 2014, 2, 19999–20003 RSC
.
- V. Nair, C. L. Perkins, Q. Lin and M. Law, Energy Environ. Sci., 2016, 9, 1412–1429 RSC
.
- X. Zheng, Y. Song, Q. Gao, J. Lin, J. Zhai, Z. Shao, J. Li, D. Wu, X. Shi, W. Liu, X. Tian and Y. Liu, Adv. Funct. Mater., 2025, 35, 2506159 CrossRef CAS
.
- G. Xie, S. U. Jan, Z. Dong, Y. Dai, R. Boddula, Y. Wei, C. Zhao, Q. Xin, J.-N. Wang, Y. Du, L. Ma, B. Guo and J. R. Gong, Chin. J. Catal., 2020, 41, 2–8 CrossRef CAS
.
- Á. Balog, E. Kecsenovity, G. F. Samu, J. He, D. Fekete and C. Janáky, Nat. Catal., 2024, 7, 522–535 CrossRef
.
- D. H. Wi, K. Ishisone, Z. Xi, Z. Ye, D. Seo, J. Zhan, X. Tong, M. Liu, G. Galli and K. S. Choi, J. Am. Chem. Soc., 2025, 147, 30851–30862 CrossRef CAS PubMed
.
- J. Tan, B. Kang, K. Kim, D. Kang, H. Lee, S. Ma, G. Jang, H. Lee and J. Moon, Nat. Energy, 2022, 7, 537–547 CrossRef CAS
.
- M. Arunachalam, R. S. Kanase, K. Zhu and S. H. Kang, Nat. Commun., 2023, 14, 5429 CrossRef CAS
.
- H. Zhang, C. Li, F. Lang, M. Li, H. Liu, D. C. Zhong, J. S. Qin, Z. Di, D. H. Wang, L. Zeng, J. Pang and X. H. Bu, Angew. Chem., Int. Ed., 2024, 64, e202418017 CrossRef PubMed
.
- T. Xu, J. Shi, K. S. Peng, Y. H. Hsu, Y. C. Liu, S. Wang, H. Zhang, Y. Wang, G. Zhang, S. F. Hung, K. Liu and X. Wang, Angew. Chem., Int. Ed., 2025, 64, e202513029 CrossRef CAS PubMed
.
- C. Pornrungroj, A. B. Mohamad Annuar, Q. Wang, M. Rahaman, S. Bhattacharjee, V. Andrei and E. Reisner, Nat. Water, 2023, 1, 952–960 CrossRef CAS
.
- M. Gao, T. Zhang, S. W. L. Ng, W. Lu, G. Tian, W. L. Ong, S. M. Kozlov and G. W. Ho, Adv. Energy Mater., 2025, 15, 2404198 CrossRef CAS
.
- C. Clavero, Nat. Photonics, 2014, 8, 95–103 CrossRef CAS
.
- L. Zhou, Q. Huang and Y. Xia, Chem. Rev., 2024, 124, 8597–8619 CrossRef CAS PubMed
.
- S. Bai, N. Zhang, C. Gao and Y. Xiong, Nano Energy, 2018, 53, 296–336 CrossRef CAS
.
- C. Yuan, H. Yin, J. Li, Y. Zhang, H. Chen, D. Xiao, Q. Wang, Y. Zhang and Q. K. Xue, Nat. Commun., 2025, 16, 6607 CrossRef CAS PubMed
.
- J. Lim, J. I. Lee, Y. Wang, N. Gauriot, E. Sebastian, M. Chhowalla, C. Schnedermann and A. Rao, Nature, 2024, 633, 83–89 CrossRef CAS
.
- D. Voiry, A. Mohite and M. Chhowalla, Chem. Soc. Rev., 2015, 44, 2702–2712 RSC
.
- T. Nilsson Pingel, M. Jorgensen, A. B. Yankovich, H. Gronbeck and E. Olsson, Nat. Commun., 2018, 9, 2722 CrossRef
.
- Z. Hou, C. Cui, Y. Li, Y. Gao, D. Zhu, Y. Gu, G. Pan, Y. Zhu and T. Zhang, Adv. Mater., 2023, 35, e2209876 CrossRef PubMed
.
- A. R. Passos, A. Rochet, L. M. Manente, A. F. Suzana, R. Harder, W. Cha and F. Meneau, Nat. Commun., 2020, 11, 4733 CrossRef CAS
.
- O. Matvienko, O. Daneyko, T. Kovalevskaya, A. Khrustalyov, I. Zhukov and A. Vorozhtsov, Metals, 2021, 11, 279 CrossRef CAS
.
- A. Moridi, H. Ruan, L. C. Zhang and M. Liu, Int. J. Solids Struct., 2013, 50, 3562–3569 CrossRef
.
- Y. Du, F. Xie, M. Lu, R. Lv, W. Liu, Y. Yan, S. Yan and Z. Zou, Nat. Commun., 2024, 15, 1780 CrossRef CAS PubMed
.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef
.
- J. R. Petrie, H. Jeen, S. C. Barron, T. L. Meyer and H. N. Lee, J. Am. Chem. Soc., 2016, 138, 7252–7255 CrossRef CAS PubMed
.
-
B. Hammer and J. K. Nørskov, Advances in Catalysis, Academic Press, 2000, vol. 45, pp. 71–129 Search PubMed
.
- J. K. Norskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef CAS PubMed
.
- E. Hassan, S. A. K. Navodye and G. T. K. K. Gunasooriya, Ind. Eng. Chem. Res., 2025, 64(34), 16531–16543 CrossRef CAS
.
- T. Salavati-fard and B. Wang, ACS Catal., 2022, 12, 12869–12878 CrossRef CAS
.
- G. Ghimire, J. Guo, R. Halmagian and J. He, Angew. Chem., Int. Ed., 2023, 62, e202302215 CrossRef CAS PubMed
.
- S. Mahapatra, D. Liu, C. Siribaddana, K. Wang, L. Li and N. Jiang, Chem. Phys. Rev., 2023, 4, 021301 CrossRef CAS
.
- J. Khurgin, A. Y. Bykov and A. V. Zayats, eLight, 2024, 4, 15 CrossRef
.
- J. N. G. Stanley, I. García-García, T. Perfrement, E. C. Lovell, T. W. Schmidt, J. Scott and R. Amal, Chem. Eng. Sci., 2019, 194, 94–104 CrossRef CAS
.
- A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 085212 CrossRef
.
- J. Wang, Y. Li, L. Deng, N. Wei, Y. Weng, S. Dong, D. Qi, J. Qiu, X. Chen and T. Wu, Adv. Mater., 2017, 29, 1603730 CrossRef PubMed
.
- Y. Cai, H. Zhu, Q. Shi, Y. Cheng, L. Chang and W. Huang, iScience, 2022, 25, 103661 CrossRef CAS PubMed
.
- J. Chen, W. Luo, S. Yu, X. Yang, Z. Wu, H. Zhang, J. Gao, Y.-W. Mai, Y. Li and Y. Jia, Ceram. Int., 2020, 46, 9786–9793 CrossRef CAS
.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS
.
- A. Zevalkink, D. M. Smiadak, J. L. Blackburn, A. J. Ferguson, M. L. Chabinyc, O. Delaire, J. Wang, K. Kovnir, J. Martin, L. T. Schelhas, T. D. Sparks, S. D. Kang, M. T. Dylla, G. J. Snyder, B. R. Ortiz and E. S. Toberer, Appl. Phys. Rev., 2018, 5, 021303 Search PubMed
.
- H. Dong, J. Feng, J. Liu, X. Wan, J. Zhang, Z. Wang, H. Chen and Y.-X. Weng, J. Phys. Chem. C, 2021, 125, 19906–19913 CrossRef CAS
.
- B. Ostovar, S. A. Lee, A. Mehmood, K. Farrell, E. K. Searles, B. Bourgeois, W. Y. Chiang, A. Misiura, N. Gross, A. Al-Zubeidi, J. A. Dionne, C. F. Landes, M. Zanni, B. G. Levine and S. Link, Sci. Adv., 2024, 10, eadp3353 CrossRef CAS
.
- M. Zhang, Q. Hu, K. Ma, Y. Ding and C. Li, Nano Energy, 2020, 73, 104810 CrossRef CAS
.
- Y. Lu, Y. Li, Y. Wang and J. Zhang, Appl. Catal., B, 2020, 272, 118979 CrossRef CAS
.
- M. Sachs, J. S. Park, E. Pastor, A. Kafizas, A. A. Wilson, L. Francas, S. Gul, M. Ling, C. Blackman, J. Yano, A. Walsh and J. R. Durrant, Chem. Sci., 2019, 10, 5667–5677 RSC
.
- B. Dai, J. Fang, Y. Yu, M. Sun, H. Huang, C. Lu, J. Kou, Y. Zhao and Z. Xu, Adv. Mater., 2020, 32, e1906361 CrossRef PubMed
.
- T. Lv, J. Li, N. Arif, L. Qi, J. Lu, Z. Ye and Y.-J. Zeng, Matter, 2022, 5, 2685–2721 CrossRef CAS
.
- Y. Ji and Y. Luo, J. Am. Chem. Soc., 2016, 138, 15896–15902 CrossRef CAS
.
- O. Rubel, S. D. Baranovskii, K. Hantke, B. Kunert, W. W. Rühle, P. Thomas, K. Volz and W. Stolz, Phys. Rev. B:Condens. Matter Mater. Phys., 2006, 73, 233201 CrossRef
.
- N. Medvedev and I. Milov, Phys. Rev. B:Condens. Matter Mater. Phys., 2020, 102, 064302 CrossRef CAS
.
- M. Gerhard, B. Louis, R. Camacho, A. Merdasa, J. Li, A. Kiligaridis, A. Dobrovolsky, J. Hofkens and I. G. Scheblykin, Nat. Commun., 2019, 10, 1698 CrossRef
.
- Q. Wang, C. R. Bowen and V. K. Valev, Adv. Funct. Mater., 2024, 34, 2312245 CrossRef CAS
.
- H. You, S. Li, Y. Fan, X. Guo, Z. Lin, R. Ding, X. Cheng, H. Zhang, T. W. B. Lo, J. Hao, Y. Zhu, H. Y. Tam, D. Lei, C. H. Lam and H. Huang, Nat. Commun., 2022, 13, 6144 CrossRef CAS PubMed
.
- K. P. O’Donnell and X. Chen, Appl. Phys. Lett., 1991, 58, 2924–2926 CrossRef
.
- R. F. C. Claridge and B. M. Peake, Mol. Phys., 1970, 18, 137–139 CrossRef CAS
.
- C. M. Marian, WIREs Comput. Mol. Sci., 2011, 2, 187–203 CrossRef
.
- S. Xia, X. Yin, Y. Chen, L. Zhang, J. Yu, B. Ding and J. Yan, ACS Nano, 2025, 19, 1519–1529 CrossRef CAS
.
- Y. Zhang, Y. Tang, X. Yang, D. Feng, B. Feng, R. Guan and G. Che, Small Methods, 2025, 9, e2402041 CrossRef PubMed
.
- Z. G. Sheng, M. Nakamura, W. Koshibae, T. Makino, Y. Tokura and M. Kawasaki, Nat. Commun., 2014, 5, 4584 CrossRef CAS
.
- Y.-Z. Sun, J.-H. Liu, Z. Li, L.-P. Qiu, J.-B. Song, S.-J. Wang, Z. Zhang, R. Li, H.-D. Zhang, W.-P. Han, J. Zhang and Y.-Z. Long, npj Clean Water, 2025, 8, 58 CrossRef CAS
.
- M. Ai, L. Pan, C. Shi, Z. F. Huang, X. Zhang, W. Mi and J. J. Zou, Nat. Commun., 2023, 14, 4562 CrossRef CAS
.
- H. Gajapathy, S. Bandaranayake, E. Hruska, A. Vadakkayil, B. P. Bloom, S. Londo, J. McClellan, J. Guo, D. Russell, F. M. F. de Groot, F. Yang, D. H. Waldeck, M. Schultze and L. R. Baker, Chem. Sci., 2024, 15, 3300–3310 RSC
.
- S. He, Y. Chen, J. Fang, Y. Liu and Z. Lin, Chem. Soc. Rev., 2025, 54, 2154–2187 RSC
.
- X. Yao, J. Guo, Z. Wang, G. Qian, X. Wang, D. Wang and X. Gong, JACS Au, 2025, 5, 3926–3943 CrossRef CAS
.
- T. T. Nguyen, R. I. Sayler, A. H. Shoemaker, J. Zhang, S. Stoll, J. R. Winkler, R. D. Britt and B. M. Hunter, J. Am. Chem. Soc., 2024, 146, 15019–15026 CrossRef CAS
.
- R. Li, L. P. Qiu, S. Z. Cao, Z. Li, S. L. Gao, J. Zhang, S. Ramakrishna and Y. Z. Long, Adv. Funct. Mater., 2024, 34, 2316725 CrossRef CAS
.
- W. Gao, J. Lu, S. Zhang, X. Zhang, Z. Wang, W. Qin, J. Wang, W. Zhou, H. Liu and Y. Sang, Adv. Sci., 2019, 6, 1901244 CrossRef CAS
.
- Z. Wang, Y. Li, C. Wu and S. C. E. Tsang, Joule, 2022, 6, 1798–1825 CrossRef CAS
.
- C. Li, G. Liao and B. Fang, Chem Catal., 2022, 2, 238–241 CAS
.
- F. L. Bloom, W. Wagemans, M. Kemerink and B. Koopmans, Phys. Rev. Lett., 2007, 99, 257201 CrossRef CAS PubMed
.
- J. D. Bergeson, V. N. Prigodin, D. M. Lincoln and A. J. Epstein, Phys. Rev. Lett., 2008, 100, 067201 Search PubMed
.
- Y. Xu, J. Qin, F. Wang and H. Wang, Green Chem., 2025, 27, 4489–4503 RSC
.
- G. Armelles, A. Cebollada, A. García-Martín and M. U. González, Adv. Opt. Mater., 2013, 1, 10–35 Search PubMed
.
- V. V. Temnov, Nat. Photonics, 2012, 6, 728–736 CrossRef CAS
.
- K. Uchida, H. Adachi, D. Kikuchi, S. Ito, Z. Qiu, S. Maekawa and E. Saitoh, Nat. Commun., 2015, 6, 5910 CrossRef CAS
.
- D. O'Connor, P. Ginzburg, F. J. Rodriguez-Fortuno, G. A. Wurtz and A. V. Zayats, Nat. Commun., 2014, 5, 5327 CrossRef
.
- A. H. MacDonald, H. C. Oji and S. M. Girvin, Phys. Rev. Lett., 1985, 55, 2208–2211 CrossRef CAS
.
- G. Sukhodub, F. Hohls and R. J. Haug, Phys. Rev. Lett., 2004, 93, 196801 Search PubMed
.
- G. E. Bauer, E. Saitoh and B. J. van Wees, Nat. Mater., 2012, 11, 391–399 CrossRef CAS
.
- K. Uchida, S. Takahashi, K. Harii, J. Ieda, W. Koshibae, K. Ando, S. Maekawa and E. Saitoh, Nature, 2008, 455, 778–781 CrossRef CAS PubMed
.
- S. Ma, K. Wang, M. Rafique, J. Han, Q. Fu, S. Jiang, X. Wang, T. Yao, P. Xu and B. Song, Angew. Chem., Int. Ed., 2024, 63, e202412821 CrossRef CAS
.
- O. Akay, M. Monfort-Castillo, T. Francis, J. Becker, S. Saravanabavan, A. Romero-Calvo and K. Brinkert, Nat. Chem., 2025, 17, 1673–1679 CrossRef CAS
.
- W. T. Borden, R. Hoffmann, T. Stuyver and B. Chen, J. Am. Chem. Soc., 2017, 139, 9010–9018 CrossRef CAS
.
- C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1757 CrossRef CAS PubMed
.
- M. Braunstein, R. Panfili, R. Shroll and L. Bernstein, J. Chem. Phys., 2005, 122, 184307 CrossRef CAS PubMed
.
- G. Zhou, P. Wang, H. Li, B. Hu, Y. Sun, R. Huang and L. Liu, Nat. Commun., 2021, 12, 4827 CrossRef CAS
.
- J. Ge, X. Ren, R. R. Chen, Y. Sun, T. Wu, S. J. H. Ong and Z. J. Xu, Angew. Chem., Int. Ed., 2023, 62, e202301721 CrossRef CAS PubMed
.
- C. Niether, S. Faure, A. Bordet, J. Deseure, M. Chatenet, J. Carrey, B. Chaudret and A. Rouet, Nat. Energy, 2018, 3, 476–483 CrossRef CAS
.
- J. L. Del Rio-Rodriguez, S. Gutierrez-Tarrino, I. Marquez, A. Gallo-Cordova, M. A. Molina, J. S. Martinez, J. J. Calvente, C. Cerezo-Navarrete, A. M. Beale, M. D. P. Morales, J. L. Olloqui-Sariego and P. Ona-Burgos, Small, 2025, 21, e2503871 CrossRef PubMed
.
- Y. Yuan, Z. Jiang, M. Li and K. Peng, ACS Appl. Energy Mater., 2023, 6, 7865–7876 CrossRef CAS
.
- Y. Tong, Y. Guo, P. Chen, H. Liu, M. Zhang, L. Zhang, W. Yan, W. Chu, C. Wu and Y. Xie, Chem, 2017, 3, 812–821 CAS
.
- X. Zhang, H. Zhong, Q. Zhang, Q. Zhang, C. Wu, J. Yu, Y. Ma, H. An, H. Wang, Y. Zou, C. Diao, J. Chen, Z. G. Yu, S. Xi, X. Wang and J. Xue, Nat. Commun., 2024, 15, 1383 CrossRef CAS
.
- L. Li, J. Zhou, X. Wang, J. Gracia, M. Valvidares, J. Ke, M. Fang, C. Shen, J. M. Chen, Y. C. Chang, C. W. Pao, S. Y. Hsu, J. F. Lee, A. Ruotolo, Y. Chin, Z. Hu, X. Huang and Q. Shao, Adv. Mater., 2023, 35, e2302966 CrossRef PubMed
.
- Y. Sun, X. Ren, S. Sun, Z. Liu, S. Xi and Z. J. Xu, Angew. Chem., Int. Ed., 2021, 60, 14536–14544 CrossRef CAS
.
- J. Huang, C. N. Borca, T. Huthwelker, N. S. Yuzbasi, D. Baster, M. El Kazzi, C. W. Schneider, T. J. Schmidt and E. Fabbri, Nat. Commun., 2024, 15, 3067 CrossRef CAS
.
- S. Zhou, X. Miao, X. Zhao, C. Ma, Y. Qiu, Z. Hu, J. Zhao, L. Shi and J. Zeng, Nat. Commun., 2016, 7, 11510 CrossRef CAS
.
- W. H. Lee, M. H. Han, Y. J. Ko, B. K. Min, K. H. Chae and H. S. Oh, Nat. Commun., 2022, 13, 605 CrossRef CAS PubMed
.
- Z. Xiong, C. Hu, X. Luo, W. Zhou, Z. Jiang, Y. Yang, T. Yu, W. Lei and C. Yuan, Nano Lett., 2021, 21, 10486–10493 CrossRef CAS PubMed
.
- L. Lin, Y. Xu, Y. Han, R. Xu, T. Wang, Z. Sun and Z. Yan, J. Am. Chem. Soc., 2024, 146, 7363–7372 CrossRef CAS
.
- C. A. Mesa, F. A. Garcés-Pineda, M. García-Tecedor, J. Yu, B. Khezri, S. Plana-Ruiz, B. López, R. Iturbe, N. López, S. Gimenez and J. R. Galan-Mascaros, APL Energy, 2024, 2, 016106 CrossRef CAS
.
- H. Dong, L. Luo, S. Zhou, L. Chen, X. Wu, Y. Yang, Z. Liao, L. Fu, M. Chen, Y. Zhu, P. Su, H. Jiang, Z. Sun, L. Lin and Q. Hua, Adv. Sci., 2025, 12, e2415525 CrossRef
.
- T. Wu, Y. Sun, X. Ren, J. Wang, J. Song, Y. Pan, Y. Mu, J. Zhang, Q. Cheng, G. Xian, S. Xi, C. Shen, H. J. Gao, A. C. Fisher, M. P. Sherburne, Y. Du, J. W. Ager, J. Gracia, H. Yang, L. Zeng and Z. J. Xu, Adv. Mater., 2023, 35, e2207041 CrossRef
.
- J. Wang, Chem, 2023, 9, 1645–1657 Search PubMed
.
- R. R. Chen, G. Chen, X. Ren, J. Ge, S. J. H. Ong, S. Xi, X. Wang and Z. J. Xu, Angew. Chem., Int. Ed., 2021, 60, 25884–25890 CrossRef CAS PubMed
.
- Y. Liu, L.-m Pan, H. Liu, T. Chen, S. Yin and M. Liu, Int. J. Hydrogen Energy, 2019, 44, 1352–1358 CrossRef CAS
.
- Y.-J. Chen, Y.-H. Li and C.-Y. Chen, Magnetochemistry, 2023, 9, 233 CrossRef CAS
.
- M. Cai, Z. Wu, Z. Li, L. Wang, W. Sun, A. A. Tountas, C. Li, S. Wang, K. Feng, A.-B. Xu, S. Tang, A. Tavasoli, M. Peng, W. Liu, A. S. Helmy, L. He, G. A. Ozin and X. Zhang, Nat. Energy, 2021, 6, 807–814 CrossRef CAS
.
- G. Liu, P. Li, G. Zhao, X. Wang, J. Kong, H. Liu, H. Zhang, K. Chang, X. Meng, T. Kako and J. Ye, J. Am. Chem. Soc., 2016, 138, 9128–9136 CrossRef CAS
.
- Y. Guo, J. Sun, Y. Tang, X. Jia, Y. Nie, Z. Geng, C. Wang, J. Zhang, X. Tan, D. Zhong, J. Ye and T. Yu, Energy Environ. Sci., 2023, 16, 3462–3473 RSC
.
- R. Verma, G. Sharma and V. Polshettiwar, Nat. Commun., 2024, 15, 7974 CrossRef CAS
.
- D. Mateo, J. L. Cerrillo, S. Durini and J. Gascon, Chem. Soc. Rev., 2021, 50, 2173–2210 RSC
.
- B. Xie, D. Hu, P. Kumar, V. V. Ordomsky, A. Y. Khodakov and R. Amal, Joule, 2024, 8, 312–333 CrossRef CAS
.
- D. Yao, W. Hao, S. Weng, M. Hou, W. Cen, G. Li, Z. Chen and Y. Li, Small, 2022, 18, e2106868 CrossRef
.
- Y. Cao, L. Gao, B. Wang, Y. Yao, C. Wu, Q. Shen, J. Feng, Y. Zhou, Z. Li and Z. Zou, ACS Mater. Lett., 2022, 4, 1912–1920 CrossRef CAS
.
- M. Xu, Q. Bing, Y. Tu, Y. Zhang, M. Zhang, Y. Cai, J. Li, X. Meng, J. Zhu, L. Yu and D. Deng, Angew. Chem., Int. Ed., 2024, 63, e202412049 CrossRef CAS
.
- L. Wu, W. Lu, W. L. Ong, A. S. W. Wong, Y. Zhang, T. Zhang, K. Zeng, Z. Ren and G. W. Ho, Nat. Commun., 2025, 16, 3098 CrossRef CAS PubMed
.
- Z. Geng, Y. Yu, A. J. Offen and J. Liu, Nat. Catal., 2023, 6, 1241–1247 CrossRef CAS
.
- X. Lu, Z. Ma, Y. Chang, S. Wang, X. Li, D. Xu, J. Bao and Y. Liu, Adv. Mater., 2024, 36, e2313057 CrossRef
.
- S. Liu, X. Wang, Y. Chen, Y. Li, Y. Wei, T. Shao, J. Ma, W. Jiang, J. Xu, Y. Dong, C. Wang, H. Liu, C. Gao and Y. Xiong, Adv. Mater., 2024, 36, e2311957 CrossRef
.
- Q. Zhao, L. Liu, J. Yin, J. Zheng, D. Zhang, J. Chen and L. A. Archer, Angew. Chem., Int. Ed., 2020, 59, 3048–3052 CrossRef CAS PubMed
.
- J. Hu, L. Yu, J. Deng, Y. Wang, K. Cheng, C. Ma, Q. Zhang, W. Wen, S. Yu, Y. Pan, J. Yang, H. Ma, F. Qi, Y. Wang, Y. Zheng, M. Chen, R. Huang, S. Zhang, Z. Zhao, J. Mao, X. Meng, Q. Ji, G. Hou, X. Han, X. Bao, Y. Wang and D. Deng, Nat. Catal., 2021, 4, 242–250 CrossRef CAS
.
- K. Zeng and D. Zhang, Prog. Energy Combust. Sci., 2010, 36, 307–326 CrossRef CAS
.
- M. Lu, G. Li, S. Yan, L. Zhang, T. Yu and Z. Zou, Nano Lett., 2022, 22, 9131–9137 CrossRef CAS PubMed
.
- M. Lu, Y. Du, S. Yan, T. Yu and Z. Zou, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2316054120 CrossRef CAS PubMed
.
- X. Liu, R. Guo, K. Ni, F. Xia, C. Niu, B. Wen, J. Meng, P. Wu, J. Wu, X. Wu and L. Mai, Adv. Mater., 2020, 32, e2001136 CrossRef
.
- F. Mekhaldi, R. Muscheler, F. Adolphi, A. Aldahan, J. Beer, J. R. McConnell, G. Possnert, M. Sigl, A. Svensson, H. A. Synal, K. C. Welten and T. E. Woodruff, Nat. Commun., 2015, 6, 8611 CrossRef CAS PubMed
.
- D. Liu, M. Lu, D. Liu, S. Yan, W. Zhou, L. Zhang and Z. Zou, Adv. Funct. Mater., 2022, 32, 2111234 CrossRef CAS
.
- Y. Ma, Y. Zhou, C. Wang, B. Gao, J. Li, M. Zhu, H. Wu, C. Zhang and Y. Qin, Adv. Mater., 2023, 35, e2303741 CrossRef
.
- Z.-E. Zhou, Y. Lu, Y.-X. Liu, S. Cao, G. Tian, Z.-Y. Hu, L. Shen, S.-M. Wu, J. Ying, W. Geng and X.-Y. Yang, Sci. China Mater., 2024, 67, 3167–3175 CrossRef CAS
.
- H. Wang, Y. Dong, J. Ying, Y. Feng, Z.-H. Zhu, Y.-X. Xiao, G. Tian, L. Shen, W. Geng, Y. Lu, S.-M. Wu and X.-Y. Yang, ACS Catal., 2024, 14, 17664–17674 CrossRef CAS
.
- A. Kirilyuk, A. V. Kimel and T. Rasing, Rev. Mod. Phys., 2010, 82, 2731–2784 CrossRef
.
- P. N. Anantharamaiah, H. M. Shashanka, S. Srinivasan, D. Das, A. A. El-Gendy and C. V. Ramana, ACS Omega, 2022, 7, 43813–43819 CrossRef CAS PubMed
.
- J. H. Kim, J. Seo, D. Lim, J. Lee, J. Kim, J. U. Lee, J. A. Moon, J. Jeong, S. M. Zakeeruddin, H. Lee, S. Cho, M. Graetzel, H. Lim, J. S. Lee and J. Y. Kim, Nat. Commun., 2025, 16, 7003 CrossRef CAS
.
- J. Cheng, L. Wu and J. Luo, Nat. Commun., 2023, 14, 7228 CrossRef CAS
.
- S. Liu, Z. Wu, Z. Zhu, K. Feng, Y. Zhou, X. Hu, X. Huang, B. Zhang, X. Dong, Y. Ma, K. Nie, J. Shen, Z. Wang, J. He, J. Wang, Y. Ji, B. Yan, Q. Zhang, A. Genest, X. Zhang, C. Li, B. Wu, X. An, G. Rupprechter and L. He, Nat. Commun., 2025, 16, 2245 CrossRef CAS PubMed
.
- X. Tao, H. Zhou, C. Zhang, N. Ta, R. Li and C. Li, Adv. Mater., 2023, 35, e2211182 CrossRef PubMed
.
- F. Xie, Y. Du, M. Lu, S. Yan and Z. Zou, Energy Environ. Sci., 2025, 18, 1972–1983 RSC
.
- Y. Lin, F. Yang, X. Wang, L. Zhong and D. Yu, Adv. Mater., 2025, 37, e2415608 CrossRef PubMed
.
- P. Wang, G. Benitez and F. A. Houle, ACS Catal., 2025, 15, 7653–7665 CrossRef CAS
.
- S. Guo, X. Li, J. Li and B. Wei, Nat. Commun., 2021, 12, 1343 CrossRef CAS PubMed
.
- S. Zhao, C. Zhang, S. Wang, K. Lu, B. Wang, J. Huang, H. Peng, N. Li and M. Liu, Nanoscale, 2023, 16, 152–162 RSC
.
- W. Li, G. Lv, M. Liu, F. Zhao, Z. He, G. Li, W. Wang, D. Chen and L. Liao, J. Mater. Chem. A, 2025, 13, 21389–21420 RSC
.
- Y. Liu, P.-F. Sui, Y.-C. Wang, Y. Wei, C. Xu, Y. Zhang and J.-L. Luo, Appl. Catal., B, 2025, 374, 125391 CrossRef CAS
.
- G. Ren, M. Zhou, P. Hu, J. F. Chen and H. Wang, Nat. Commun., 2024, 15, 2346 CrossRef CAS PubMed
.
- Y. Hu, N. Wijerathne, M. Y. Pabel, D. K. Arachchige and W. D. Wei, Acc. Chem. Res., 2025, 58, 2562–2572 CrossRef CAS
.
- B. Dai, C. Gao, J. Guo, M. Ding, Q. Xu, S. He, Y. Mou, H. Dong, M. Hu, Z. Dai, Y. Zhang, Y. Xie and Z. Lin, Nano Lett., 2024, 24, 4816–4825 CAS
.
- M. Li, J. Sun, G. Chen, S. Wang and S. Yao, Adv. Powder Mater., 2022, 1, 100032 CrossRef
.
- G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Light: Sci. Appl., 2020, 9, 108 CrossRef
.
- Z. Tang, F. Zhu, J. Zhou, W. Chen, K. Wang, M. Liu, N. Wang and N. Li, Appl. Catal., B, 2022, 309, 121267 CrossRef CAS
.
- T. Li, Y. Zou and Z. Liu, Appl. Catal., B, 2023, 328, 122486 CrossRef CAS
.
- Y. Li, Z. Wang, Y. Wang, A. Kovács, C. Foo, R. E. Dunin-Borkowski, Y. Lu, R. A. Taylor, C. Wu and S. C. E. Tsang, Energy Environ. Sci., 2022, 15, 265–277 RSC
.
- H. Wei, L. Zhou, F. Cao, Y. Chen, B. Li, J. Kou, C. Lu and Z. Xu, Nano Energy, 2024, 129, 110064 CrossRef CAS
.
- Z. Yang, Z. Y. Wu, Z. Lin, T. Liu, L. Ding, W. Zhai, Z. Chen, Y. Jiang, J. Li, S. Ren, Z. Lin, W. Liu, J. Feng, X. Zhang, W. Li, Y. Yu, B. Zhu, F. Ding, Z. Li and J. Zhu, Nat. Commun., 2024, 15, 7599 CrossRef CAS
.
- T. Sun, Z. Tang, W. Zang, Z. Li, J. Li, Z. Li, L. Cao, J. S. Dominic Rodriguez, C. O. M. Mariano, H. Xu, P. Lyu, X. Hai, H. Lin, X. Sheng, J. Shi, Y. Zheng, Y. R. Lu, Q. He, J. Chen, K. S. Novoselov, C. H. Chuang, S. Xi, X. Luo and J. Lu, Nat. Nanotechnol., 2023, 18, 763–771 CrossRef CAS
.
- L. Wang, X. Zhou, Z. Luo, S. Liu, S. Yue, Y. Chen and Y. Liu, Adv. Funct. Mater., 2024, 34, 2408870 CrossRef CAS
.
- Y. Tian, S. Shen, J. Cong, L. Yan, Y. Chai and Y. Sun, Chin. Phys. B, 2016, 25, 017601 CrossRef
.
- M. T. Escote, V. B. Barbeta, R. F. Jardim and J. Campo, J. Phys.:Condens. Matter, 2006, 18, 6117–6132 CrossRef CAS
.
- J. Ss and D. Bansal, Phys. Rev. B, 2025, 111, 104306 CrossRef CAS
.
- E. Batsaikhan, M. Hayashi and B. Sainbileg, Phys. Chem. Chem. Phys., 2025, 27, 11700–11707 RSC
.
- G. J. Shu, P. C. Wu and F. C. Chou, RSC Adv., 2020, 10, 43117–43128 RSC
.
- E. Aytan, B. Debnath, F. Kargar, Y. Barlas, M. M. Lacerda, J. X. Li, R. K. Lake, J. Shi and A. A. Balandin, Appl. Phys. Lett., 2017, 111, 252402 CrossRef
.
- M. Weng, N. Bonnet, O. Andreussi and N. Marzari, arXiv, 2025, preprint, arxiv:2509.10307 DOI:10.48550/arXiv.2509.10307.
- A. Baiardi, J. Bloino and V. Barone, J. Chem. Theory Comput., 2018, 14, 6370–6390 CrossRef CAS PubMed
.
- C. Lü, Y. Chen, Y. Wang, Z. Dai, Z. Fang, X.-G. Gong, Q. Wu and H. Xiang, Phys. Rev. Lett., 2025, 135, 196401 CrossRef
.
- D. Ceresoli, U. Gerstmann, A. P. Seitsonen and F. Mauri, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 060409 CrossRef
.
- B. J. Kim, H. Jin, S. J. Moon, J. Y. Kim, B. G. Park, C. S. Leem, J. Yu, T. W. Noh, C. Kim, S. J. Oh, J. H. Park, V. Durairaj, G. Cao and E. Rotenberg, Phys. Rev. Lett., 2008, 101, 076402 CrossRef CAS
.
- S. K. Panda, S. Bhowal, A. Delin, O. Eriksson and I. Dasgupta, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 155102 CrossRef
.
- Z. Zhang, H. Zhao, S. Xi, X. Zhao, X. Chi, H. Bin Yang, Z. Chen, X. Yu, Y. G. Wang, B. Liu and P. Chen, Nat. Commun., 2025, 16, 1301 CrossRef CAS PubMed
.
- H. Ding, H. Liu, W. Chu, C. Wu and Y. Xie, Chem. Rev., 2021, 121, 13174–13212 CrossRef CAS
.
- P. Huang, M. Meng, G. Zhou, P. Wang, W. Wei, H. Li, R. Huang, F. Liu and L. Liu, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2219661120 CrossRef CAS
.
- D. V. Sosnovsky and K. L. Ivanov, Phys. Rev. B, 2021, 103, 014403 CrossRef CAS
.
- R. A. W. Ayyubi, M. X. Low, S. Salimi, M. Khorsandi, M. M. Hossain, H. Arooj, S. Masood, M. H. Zeb, N. Mahmood, Q. Bao, S. Walia and B. Shabbir, Nat. Commun., 2025, 16, 6265 CrossRef CAS
.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2026 |