Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The product of NH3 loss from gas phase protonated tyrosine
Griffin
Loebsack†
 abc,
Neville J. A.
Coughlan†
ab,
Lara
van Tetering
abc,
Neville J. A.
Coughlan†
ab,
Lara
van Tetering
 de,
Yuting
Li
ab,
Nour
Mashmoushi
ab,
Yiming
Xiao
a,
Mircea
Guna
f,
Bradley B.
Schneider
f,
J. C. Yves
Le Blanc
f,
Jonathan
Martens
de and
W. Scott
Hopkins
*abc
de,
Yuting
Li
ab,
Nour
Mashmoushi
ab,
Yiming
Xiao
a,
Mircea
Guna
f,
Bradley B.
Schneider
f,
J. C. Yves
Le Blanc
f,
Jonathan
Martens
de and
W. Scott
Hopkins
*abc
aDepartment of Chemistry, University of Waterloo, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada. E-mail: scott.hopkins@uwaterloo.ca
bWaterloo Institute of Nanotechnology, University of Waterloo, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada
cWaterFEL Free Electron Laser Laboratory, University of Waterloo, 200 University Avenue West, Waterloo, Ontario N2L 3G1, Canada
dHFML-FELIX, Toernooiveld 7, 6525 ED Nijmegen, the Netherlands
eInstitute for Molecules and Materials, Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, the Netherlands
fSCIEX, Four Valley Drive, Concord, Ontario L4K V48, Canada
First published on 5th January 2026
Abstract
The lowest energy unimolecular dissociation product channel of protonated tyrosine, [Tyr + H]+, is loss of NH3. The structure of the [Tyr − NH3 + H]+ ion is still debated; past calculations suggest that the global minimum benzyl cation form is only accessible via a relatively high barrier and that a lower energy pathway to formation of the higher-energy phenonium isomer is likely to occur via collision-induced dissociation (CID). To resolve this open question, [Tyr − NH3 + H]+ was studied computationally and experimentally using ion mobility spectrometry, ultraviolet photodissociation (UVPD) spectroscopy, and infrared ion spectroscopy (IRIS). Traveling wave ion mobility spectrometry (TWIMS) yields a collision cross section of ΩN2 = 130.0 ± 1.4 Å2, which compares favorably with computed values of 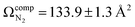 and
and 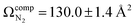 for the benzyl cation and phenonium products, respectively. Differential mobility spectrometry and mass spectrometry were used to mobility- and mass-select [Tyr + H]+ prior to producing [Tyr − NH3 + H]+via CID and subsequently measuring its UVPD spectrum. Similarly, [Tyr − NH3 + H]+ was produced via CID prior to measuring its IRIS spectrum. The UVPD and IRIS spectra indicate that the phenonium ion is the major product formed via CID.
for the benzyl cation and phenonium products, respectively. Differential mobility spectrometry and mass spectrometry were used to mobility- and mass-select [Tyr + H]+ prior to producing [Tyr − NH3 + H]+via CID and subsequently measuring its UVPD spectrum. Similarly, [Tyr − NH3 + H]+ was produced via CID prior to measuring its IRIS spectrum. The UVPD and IRIS spectra indicate that the phenonium ion is the major product formed via CID.
Introduction
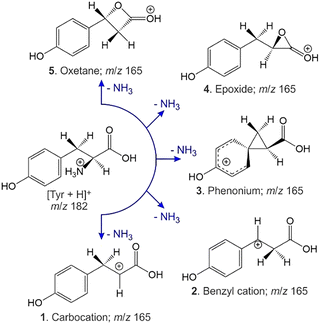
The dissociation reactions of protonated amino acids have attracted substantial attention in great part due to the use of these species as models for the fragmentation of protonated peptides.1–29 In contrast with the aliphatic, acidic, and hydroxylic species, aromatic amino acids (except for histidine) exhibit loss of NH3 as a major product channel.27,29,30 Energy-resolved collision-induced dissociation (CID) experiments demonstrated that for protonated tyrosine, [Tyr + H]+, and protonated tryptophan, [Trp + H]+, elimination of NH3 has the lowest energy threshold.27,29–32 Analogous experiments for protonated phenylalanine, [Phe + H]+, revealed that the threshold for loss of NH3 is slightly higher in energy than concomitant loss of (H2O + CO).27,29,30With respect to the NH3 loss mechanism from [Tyr + H]+, Harrison et al. proposed migration of the phenolic group to form a phenonium ion (see Fig. 1, product 3).30 In their work, Rogalewicz et al. invoked this mechanism, emphasizing the stabilizing effect of the electron-donating OH group.27 El Aribi et al. similarly invoked this interpretation when they demonstrated that the loss of NH3 is approximately 5× more favoured for [Tyr + H]+ than for [Phe + H]+.29 However, calculations by Shoeib et al. indicate that a benzyl cation product (Fig. 1, product 2) is significantly more thermodynamically stable than the phenonium product ion. En route to the benzyl cation, though, is a barrier associated with a 1,2-hydride shift, which potentially exceeds the energy requirement of the (essentially barrierless, they propose) phenyl shift pathway.33 In addition to the pathways leading to products 2 and 3, one could also envision formation of epoxide or oxetane products (Fig. 1, products 4 and 5, respectively). Moreover, although loss of the α-amino group is believed to involve nucleophilic attack of the α-carbon by neighboring groups,30,33 formation of carbocation 1 has yet to be discounted. Conclusive evidence for any of these products is currently lacking.
Mass spectrometry (MS) combined with action spectroscopy can be a powerful tool to study the vibronic structures of ions in the gas phase.34–40 For example, Matthews and Dessent demonstrated that the two tautomers of protonated 4-aminobenzoic acid, which were promoted by two different ESI solvents, were distinguishable using multi-wavelength ultraviolet photodissociation (UVPD), as their UV photodepletion spectra illustrated different band characters.34 Marlton and coworkers took this workflow a step further by implementing high field asymmetric waveform ion mobility spectrometry (FAIMS) to separate tautomers of protonated nicotine prior to spectroscopic characterization.35 The spectroscopic properties of the aromatic amino acids have also been investigated using MS-UVPD. The aromatic amino acids undergo intense π to π* transitions in the UV region near 270 nm which have been explored using photofragment mass spectrometry by several teams.41–45 Boyarkin and coworkers reported the electronic spectra of [Tyr + H]+ obtained at both ∼298 K and 10 K, and found that the cooler multipole ion trap led to higher spectral resolution because low temperatures prevented the appearance of hot-band features and suppressed spectral broadening by restricting vibrational and rotational motion.42 Pereverzev and colleagues measured the photofragmentation spectra of [Tyr + H]+ with an Orbitrap mass analyzer and a DUV/UV optical parametric oscillator (OPO).44 Protonated aromatic amino acids were shown to absorb photons in the region of 190 to 290 nm, with significant absorption observed at ∼280 nm for [Trp + H]+, and ∼230 nm and ∼275 nm for [Tyr + H]+. With respect to infrared ion spectroscopy (IRIS), McMahon et al. investigated the protonation sites and structures of protonated amino acids by infrared multiple-photon dissociation (IRMPD) and by electronic-structure calculations.46 Protonated aromatic amino acids were shown to have bands in the 1174 and 1183 cm−1 regions arising from carboxylic acid and hydroxyl bending as well as in the ∼1450 cm−1 region due to NH3 umbrella vibrations.
In this study, we characterize the deamidation product of [Tyr + H]+. We employ differential mobility spectrometry (DMS) and mass spectrometry to isolate [Tyr + H]+, which subsequently undergoes CID with background gases to yield [Tyr − NH3 + H]+. These ions are then trapped in the third quadrupole (Q3) of our customized triple quadrupole instrument, where they are irradiated with tunable photons from an Nd:YAG-pumped OPO, as described in a previous study.36 We similarly produce and study [Tyr − NH3 + H]+via IRIS at the FELIX free electron laser laboratory, and we use traveling wave ion mobility spectrometry (TWIMS) to measure the collision cross section of the deamidation product following in-source production. Supporting electronic structure calculations were conducted to model fragmentation pathways and vibrational spectra, and vibronic transitions were modelled using vertical gradient Franck–Condon (VG|FC) factors for the analysis of experimental UVPD spectra.
Experimental section
DMS-MS and UVPD experiments
The DMS-MS UVPD instrumentation employed in this study has been described elsewhere; additional details are provided in Section S1 in the supplementary information.36,47–49 During the DMS-MS experiments, the SV was scanned from 0–3000 V in 500 V increments, and from 3000–4000 V in 200 V increments. At each SV step, the CV was scanned in 0.1 V increments from 25 V to −60 V. Mass spectra were recorded using mass axial ejection from Q3,50 and the ion intensities recorded as a function of SV and CV for display as ionograms and dispersion plots. This procedure revealed only a single ionogram feature for [Tyr + H]+, indicating that only a single prototropic isomer was present in the probed ensemble. For UVPD experiments, ion populations of [Tyr + H]+ were gated at the CV transmission maximum at SV = 3000 V, mass-selected in Q1 and stored in the Q3 linear ion trap. To further confirm the identity of [Tyr + H]+, the trapped m/z 182 parent ions were irradiated by light from an OPO to induce wavelength-dependent photodissociation.36 Laser wavelengths were scanned from λ = 208–350 nm in increments of 1 nm. At each wavelength step, ions were accumulated in Q3 trap for 3–5 ms prior to irradiation. The intensities of any resulting photofragments and the parent ion were recorded at each wavelength. The experimental UVPD spectra were generated by monitoring the fragmentation efficiency as a function of wavelength I(λ), as described in eqn (1):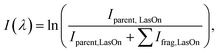 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LasOn is the intensity of precursor ion and ΣIfrag,
LasOn is the intensity of precursor ion and ΣIfrag,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LasOn is the sum of the intensities of the fragment ions produced during laser irradiation. Fragmentation efficiency was normalized with respect to the OPO output power, which was measured at each wavelength.
LasOn is the sum of the intensities of the fragment ions produced during laser irradiation. Fragmentation efficiency was normalized with respect to the OPO output power, which was measured at each wavelength.
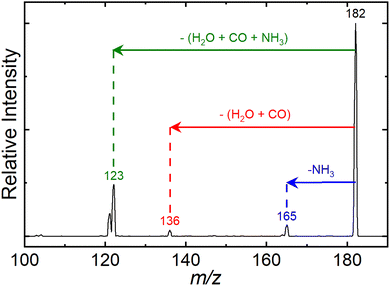
The process described by eqn (1) does not account for precursor ion fragmentation by CID in Q3; these background processes could be monitored in the absence of laser irradiation. In-trap CID to yield [Tyr − NH3 + H]+ at m/z 165 was especially prominent and enabled mass isolation and subsequent UVPD of the deamidation product. In fact, the m/z 165 product was also produced via in-source fragmentation following ESI in our UVPD apparatus and in our Waters Synapt G2Si, enabling travelling-wave ion mobility spectrometry (TWIMS) measurements and collision cross section (CCS) determination (described below). All experiments were repeated multiple times on different days to ensure reproducibility.
TWIMS-MS experiments
A Waters Synapt G2-Si HDMS mass spectrometer (Waters Corporation, Milford, MA, USA) equipped with a TWIMS cell was used to measure the collision cross sections (CCSs) of [Tyr + H]+ and [Tyr − NH3 + H]+. The [Tyr − NH3 + H]+ deamination product was generated in-source via CID in the StepWave region of the instrument prior to transfer to the TWIMS cell. The instrument operated in positive ionization mode with an m/z acquisition range of 50–1350, calibrated using sodium formate. CCS calibration curves were generated using the Waters Major Mix and wave height settings of 36 V, 38 V, and 40 V while maintaining a wave velocity of 500 m s−1, as recommended by Gabelica et al.51 The collision cross calibration was performed with Anglient Tuning Mix (G1969-8500, Agilent, Santa Clara, CA, USA). CCSs were measured at the same wave height settings as were used for the calibration and arrival time distributions exhibited single peaks for both [Tyr + H]+ and [Tyr − NH3 + H]+. The source parameters were as follows: capillary voltage, 3 kV; sampling cone, 20 V; source offset, 80 V; source temperature, 100 °C; desolvation temperature, 400 °C; cone gas flow, 100 L h−1; desolvation gas flow, 500 L h−1; and nebulizer gas pressure, 6.5 bar.IRIS experiments
Following electrospray ionization, [Tyr + H]+ was mass selected and fragmented via CID to yield [Tyr − NH3 + H]+ using a modified quadrupole ion trap mass spectrometer (Bruker Amazon) that is interfaced with the output of the FELIX IR beam. The experimental apparatus used for these studies has been described in detail previously.52 The nascent deamidated product ions were then irradiated and fragmented via IRMPD across the 800–3700 cm−1 region. The vibrational spectrum was acquired by recording the precursor fragmentation efficiency as a function of the tunable laser output. FELIX provided IR radiation in the form of 10 µs macropulses at 10 Hz, each carrying an energy of 20–110 mJ depending on the frequency, with a spectral bandwidth of ∼0.5% of the central frequency. Wavelength calibration was performed with a grating spectrometer and a linear correction was applied to account for frequency-dependent variations in the laser pulse energy.Computational methods
The global geometry optimization and ensemble generator (GOAT) module of ORCA was employed to identify conformers of [Tyr + H]+ and the isomers of [Tyr − NH3 + H]+ (i.e., products 1–5),53 using the GFN2-xTB semiempirical tight-binding model.54,55 The geometry of each conformer was then optimized at the ωB97X-D3/Def2-TZVPP level of theory using the RIJCOSX approximation and Def2/J auxiliary basis set.56–65 Normal mode analyses were conducted to ensure that all optimized geometries were minima on the potential energy surface (i.e., no imaginary frequencies), to compute vibrational spectra, and to compute thermochemical corrections. By default in ORCA, computed vibrational lines are convoluted with a Gaussian function of width 15 cm−1. Atomic partial chargers were also calculated via the CHELPG partition scheme using a 0.1 Å grid, with grid points being at most 3.0 Å from the closest atom in the molecule.66 All calculations were carried out using ORCA version 6.0.1,53,67–69 and the analysis of computation results was facilitated by the Pythonic Orca Data Processing and Analysis Libraries (PodPals) GUI. Complete input/output files are available via the ioChem-BD database associated with this manuscript (https://dx.doi.org/10.19061/iochem-bd-6-600).The first ten vertical excitation energies were calculated for the lowest energy conformer of [Tyr + H]+ and for the lowest energy conformer of each isomer of [Tyr − NH3 + H]+ using time-dependent density functional theory (TD-DFT)70–72 at the ωB97X-D3/Def2-TZVPP level of theory. TD-DFT excitation energies and the ground state Hessians were then employed in vertical gradient Franck–Condon (VG|FC) simulations to compute electronic absorption spectra.73–75 By default in ORCA, computed vibronic lines are convoluted with a Lorentzian function of width 50 cm−1. We also calculated ion-neutral collision cross sections (CCSs) for each ion at T = 298 K in N2 using the parallelized trajectory method as implemented in MobCal-MPI 2.0.75–77 CCS calculations employed DFT-optimized geometries and CHELPG atomic partial charges, and consisted of 10 full trajectory cycles with 108 velocity integration points and 512 impact parameter integration points.
Results and discussion
Characterization of [Tyr + H]+
To first confirm the identity of the [Tyr + H]+ parent ion, a combination of DMS-MS and UVPD spectroscopy was employed. The combination of DMS-MS with UVPD yields an analytical advantage by providing orthogonal probes for ion samples potentially composed isobaric or isomeric mixtures. The DMS cell can be utilized to separate isomeric ions in the gas phase by exploiting differences in their differential mobilities. The full potential of UVPD for structural assignment of gas-phase ions can then be realized since DMS-MS gating ensures clean populations of target ion populations. UVPD action spectra directly probe the vibronic structures of target molecules, and therefore are sensitive to subtle structural differences, and in certain cases small configurational changes lead to different excited state dynamics that are manifested in individual fragmentation channel patterns.The ionogram for [Tyr + H]+ in an N2 environment at SV = 3000 V (shown in Fig. S1A) shows a single peak centered around CV = −1 V, suggesting the presence of a single prototropic isomer of [Tyr + H]+. As determined by calculations and reported by others,43,45,78,79 the most likely protonation site of Tyr is on the basic amine group; protonation at other sites is thermodynamically unfavorable and therefore we would not expect to see a significant population of alternative prototropic isomers in the gas phase. Our GOAT/DFT method to map the reaction pathway revealed 39 conformers associated with three prototropic isomers for [Tyr + H]+. The lowest energy geometries of the three prototropic isomers (i.e., N-protonated, carbonyl O-protonated, and hydroxy O-Protonated) are shown in Fig. S2. The recorded dispersion plot in Fig. S1B shows a single Type B curve for [Tyr + H]+, demonstrating that at no point are isomeric (or isobaric) species separated from the ion ensembled and indicating a relatively weak interaction between a highly charged site on the protonated tyrosine ions and neutral N2 carrier gas molecules.80,81
Having established ideal DMS conditions for transmission of [Tyr + H]+ ions (SV = 3000 V, CV = –1.0 V), we set Q1 to transmit ions with m/z 182 (i.e., precursor ion mass), which were then trapped in Q3 and irradiated with UV light to measure the action spectrum of the gas phase [Tyr + H]+ ensemble. Fig. S3A shows the recorded UVPD action spectrum for [Tyr + H]+ in the λ = 200–340 nm region; the observed spectrum is in excellent agreement with that reported in the literature (see Fig. S3B).43,45 This spectrum was recorded by monitoring the depletion of the parent ion and the enhancement of the product ion signals as a function of laser wavelength. Table 1 provides the observed UVPD product channels of [Tyr + H]+ and the corresponding neutral losses. Fig. S4 shows the computed vibronic spectra for the three lowest energy prototropic isomers (i.e., protomers) of [Tyr + H]+; the agreement between experiment and theory for the N-protonated protomers (see Fig. S2 and S4), indicates that protonation occurs on the amino moiety (as expected). Fig. S5 displays the transition orbitals for the electronic excitations contributing to the observed vibronic spectrum.
| m/z | Product |
|---|---|
| 165 | [M + H − NH3]+ |
| 147 | [M + H − NH3 − H2O]+ |
| 136 | [M + H − CO − H2O]+ |
| 123 | [M + H − NH3 − CH2CO]+ |
| 119 | [M + H − CO − H2O − NH3]+ |
| 107 | [M + H − CO − H2O − HCN − H2]+ |
| 95 | [M + H − NH3 − CO − CH2CO]+ |
| 91 | [M + H − NH3 − H2O − CO − CO]+ |
Owing to the mass-selectivity of our instrument, we could examine the UVPD spectrum of [Tyr + H]+ as it appears in each product channel. In general, the spectra across the various product channels are similar one another, but the m/z 147 channel (loss of NH3 + H2O) does exhibit a substantial increase in the relative intensity of the band feature near λ ≈ 270 nm (see Fig. S6). This considered alongside the fact that the spectrum observed via the m/z 165 channel was very noisy led us to hypothesize that, upon formation, the m/z 165 product resonantly absorbed UV photons and subsequently fragmented to yield the m/z 147 product.
Upon revisiting the mass spectrum recorded following trapping of [Tyr + H]+ in Q3 (but without laser irradiation), we observed the formation of product ions at m/z 123, 136, and 165 as shown in Fig. 2. These products, which become more abundant with trapping time, are likely formed via collision with background gases during trapping in Q3, and they correspond to the lowest energy CID product channels of [Tyr + H]+.29,82 Given the presence of these product ions, the UVPD action spectra of [Tyr + H]+ likely represents a convolution of the photodissociation of the parent and these two in-trap CID products. However, given their relative abundances, we expect the contribution of these product ions to be a minor contribution to the spectrum of [Tyr + H]+ and again note the excellent agreement of our measured UVPD spectrum of [Tyr + H]+ (considering all fragment ions) with that reported by Pereverzev and coworkers44 and with the tandem mass spectrometry data reported by Zhang and coworkers.82 These experiments instill confidence in our subsequent analysis of the m/z 165 product (vide infra).
Characterization of [Tyr − NH3 + H]+
To characterize the product corresponding to loss of NH3 from [Tyr + H]+, we first conducted travelling wave ion mobility spectrometry (TWIMS) experiments to measure collision cross sections (CCSs). Owing to the fragility of [Tyr + H]+ and the fact that loss of NH3 is the lowest energy product channel, CID to yield the m/z 165 ion occurs within the StepWave sector of the TWIMS instrument. Consequently, we were able to measure the CCSs of both [Tyr + H]+ (ΩN2 = 142.7 ± 1.6 Å2) and the m/z 165 product ion (ΩN2 = 130.0 ± 1.4 Å2), whose mobiligrams are both shown in Fig. S7A and B, respectively. With respect to [Tyr + H]+, although our computed value of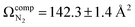 accords well with experiment, our measured and computed values are slightly less than the literature values of 145.5 ± 0.4 Å2,83 146.0 ± 0.5 Å2,84 and 148.5 ± 0.1 Å2.85 We are unaware of any report of the CCS for [Tyr − NH3 + H]+.
accords well with experiment, our measured and computed values are slightly less than the literature values of 145.5 ± 0.4 Å2,83 146.0 ± 0.5 Å2,84 and 148.5 ± 0.1 Å2.85 We are unaware of any report of the CCS for [Tyr − NH3 + H]+.
To compute possible geometries of the m/z 165 product, we conducted GOAT searches and subsequent DFT geometry optimizations for each of the product isomers shown in Fig. 1. We found that conformers of product 5 (oxetane formation) were unstable and optimized to conformers of product 2 (benzyl cation). Conformers of product 1 were also unstable under the model chemistry employed and reverted to products 2 and 3. Conformers associated with epoxide formation (product 4) were found to be more than 280 kJ mol−1 above the global minimum product (i.e., product 2; benzyl cation), and the lowest energy conformer of the phenonium product (product 3) was computed to lie 40.5 kJ mol−1 above the global minimum. To compute CCSs of the various m/z 165 product isomers/conformers, we employed MobCal-MPI 2.0.75–77 The lowest energy conformers of products 2 and 3 yielded 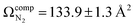 and
and 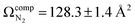 , respectively (see Fig. 3). The lowest energy conformer of product 4 yielded a computed CCS of
, respectively (see Fig. 3). The lowest energy conformer of product 4 yielded a computed CCS of 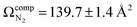 , which is 7.5% larger than the measured value. When considered in concert with their relatively high energies, the CCS value for the epoxide product indicates that these species are not in the probed ensemble. Interestingly, despite its relatively high energy, the CCS of the phenonium product is in better agreement with theoretical predictions than is the benzyl cation product, supporting the hypothesis that formation of the benzyl cation is kinetically disfavored by the presence of a high-energy barrier associated with a 1,2-hydride shift.33
, which is 7.5% larger than the measured value. When considered in concert with their relatively high energies, the CCS value for the epoxide product indicates that these species are not in the probed ensemble. Interestingly, despite its relatively high energy, the CCS of the phenonium product is in better agreement with theoretical predictions than is the benzyl cation product, supporting the hypothesis that formation of the benzyl cation is kinetically disfavored by the presence of a high-energy barrier associated with a 1,2-hydride shift.33
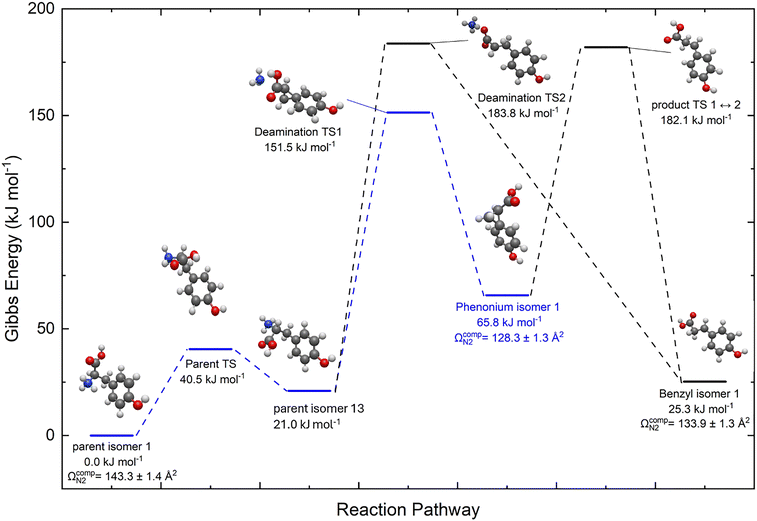
We further explored the apparent gas phase ion chemistry by computing the reaction pathway for loss of NH3 from [Tyr + H]+ to yield the benzyl and phenonium [Tyr − NH3 + H]+ products. The lowest energy path required that the global minimum parent ion first undergo conformational change to adopt a geometry ΔG° = +21.0 kJ mol−1 higher in energy. From this structure, the phenonium ion is produced via impulsive dissociation of the C–N bond via a barrier at ΔG° = +151.5 kJ mol−1. To generate the benzyl cation product, a concerted 1,2-hydride shift and loss of NH3 must occur via a barrier at ΔG° = +183.8 kJ mol−1. Alternatively, the lowest energy phenonium product can undergo ring opening and a 1,2-hydride shift to produce the lowest energy benzyl cation via a barrier at ΔG° = +182.1 kJ mol−1. Thus, the computed reaction pathway indicates that production of the phenonium ion is strongly favoured kinetically.
To conduct UVPD action spectroscopy experiments on the m/z 165 product, DMS- and mass-selected [Tyr + H]+ was subjected to CID in the Q2 ion trap to yield the [Tyr − NH3 + H]+ deamidation product, which was subsequently transferred to Q3 for interrogation. This procedure generated substantially more m/z 165 product ions than could be produced via in-trap CID of [Tyr + H]+ with the background gases in Q3. To record the UVPD spectrum of [Tyr − NH3 + H]+, we monitored depletion of the m/z 165 signal and enhancement of the m/z 147 signal, corresponding to the [Tyr − NH3 − H2O + H]+ ion, which was the dominant UVPD product channel observed. The UVPD action spectrum for [Tyr − NH3 + H]+ is plotted in Fig. 4(A); distinct spectral features are observed at λ ≈ 250 nm (ca. 5 eV) and at λ ≈ 290 nm (ca. 4.3 eV). Note that both [Tyr + H]+ and [Tyr − NH3 + H]+ absorb in the λ ≈ 260 − 290 nm region (see Fig. S8). This suggests that the m/z 165 product generated via in-trap CID could indeed contribute to production of the m/z 147, thus slightly impacting the measured UVPD spectrum of [Tyr + H]+ and contributing to the distinct spectrum observed in the m/z 147 product channel.
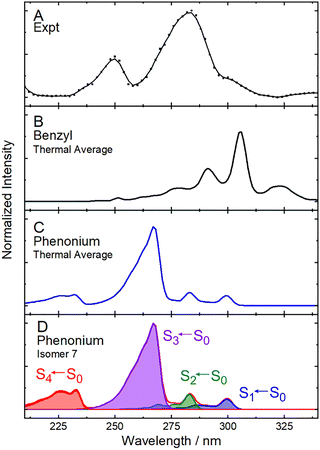 | ||
| Fig. 4 (A) The UVPD action spectrum of [Tyr − NH3 + H]+ as monitored in the m/z 165 → m/z 147 product channel. The thermally-averaged (T = 298 K) calculated VG|FC vibronic spectra for the lowest energy conformers of (B) phenonium isomer and (C) the benzyl isomer of [Tyr − NH3 + H]+. (D) The VG|FC spectrum for isomer 7, the second-lowest energy phenonium structure; assignments for the vibronic band systems are provided. Calculations were conducted at the ωB97X-D3BJ/def2-TZVPP level of theory. A spectra shift of –0.3 eV was applied for the VG|FC predictions, in accordance with shifts typically applied in the literature.86–89 | ||
Fig. 4(B) and (C) show the thermally-averaged VG|FC vibronic spectra for the benzyl cation and phenonium isomers of the [Tyr − NH3 + H]+ deamidation product. The method of thermal averaging assumes a localized Boltzmann distribution within the region of the potential energy surface (PES) associated with each isomeric structure (i.e., benzyl versus phenonium) but not for the entire PES. In other words, such an approach assumes a thermalized distribution for the conformers of the kinetically trapped phenonium isomer. By inspection, the computed spectrum of the phenonium isomer (i.e., product 3; Fig. 4(C)) yields the best match with experiment based on the spectral features. However, the features of the phenonium ion spectrum are shifted to higher energy of the observed bands (whereas the benzyl ion spectral features are shifted to lower energy). Unlike the benzyl ion conformers, both isomer 6 and isomer 7, the two lowest energy conformers of the phenonium geometry, exhibit band intensity in the 210–240 nm region (although the band is somewhat more intense for isomer 7; see Fig. 4(D)). All four of the band systems in this region are associated with π → π* excitations that transfer electron density from the phenyl ring to mixed anti-bonding phenyl and carbonyl orbitals. The computed spectrum of the benzyl cation (i.e., product 2; Fig. 4(B)) is a very poor match with experiment, but we cannot completely discount the presence of the benzyl species since it could be contributing to the shoulder at ∼300 nm in the experimental spectrum.
To further test our hypothesis that the phenonium ion is indeed the major deamidation product of [Tyr + H]+, we measured the infrared ion spectrum of [Tyr − NH3 + H]+ (shown in Fig. 5(A)). When comparing the computed vibrational spectra of the benzyl and phenonium ions, we could identify a diagnostic band at ∼950 cm−1. This band, which is present in both the experimental and computed phenonium ion spectrum, is associated with the CH2 twisting motion of the three-membered carbon ring. To estimate the population of the phenonium ion relative to other product ions, a population analysis was performed via the ∼950 cm−1 band (Fig. S10).90 The analysis revealed that this band rapidly depletes to zero with increasing IR laser pulses, indicating that it likely corresponds to only the phenonium ion. Given the computed energetics and the results of our CCS, UVPD spectroscopy, and IR spectroscopy experiments, we conclude with reasonable certainty that the phenonium ion is the predominant product in the probed ensembles.
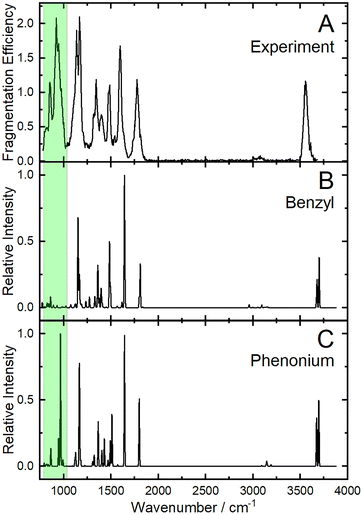 | ||
| Fig. 5 (A) The experimental IRIS spectrum of [Tyr − NH3 + H]+ as monitored via the fragmentation channels given in Table 1. The calculated harmonic vibronic spectra for (B) the global minimum benzyl product and (C) the lowest energy phenonium product. Calculations were conducted at the ωB97X-D3BJ/def2-TZVPP level of theory and a scaling factor of 0.97 was applied.91 | ||
Conclusions
The deamidation product of protonated tyrosine, [Tyr − NH3 + H]+ (m/z 165), was investigated using ion mobility spectrometry, mass spectrometry, UVPD spectroscopy, IR spectroscopy, and quantum chemical calculations. In-source CID was employed to produce the m/z 165 ion for characterization using TWIMS. CCS measurements indicated that the product ion adopts a phenonium structure, rather than the global minimum benzyl cation, which is only accessible via a relatively high-energy barrier associated with concerted NH3 loss and a 1,2-hydride shift. To further probe the product structure, the m/z 165 ion was subjected to UVPD spectroscopy and IR spectroscopy. In UVPD experiments, [Tyr + H]+ was mobility- and mass-selected prior to undergoing CID to yield the m/z 165 ion. Subsequent UVPD interrogation of the nascent [Tyr − NH3 + H]+ across the range λ = 210–330 nm revealed an action spectrum that matched the VG|FC simulation for the phenonium product reasonably well, though the benzyl cation could not be entirely discounted as a possible minor contributor to the experimental spectrum. The IR spectrum of the m/z 165 ion was in excellent agreement with the spectrum computed for the phenonium ion, but again the presence of the benzyl cation could not be completely discounted owing to the absence of diagnostic features for this structural motif.This work underscores the challenge of assigning structure (viz. geometry) to the product ions generated in tandem mass spectrometry. CID can provide diagnostic molecular fingerprints to resolve parent molecular structures via library search, but this process increasingly relies on in silico-generated MSN spectra as a reference for de novo identification. Underpinning the predicted MSN spectra are in silico-generated product ion structures. Recently, an infrared ion spectroscopy study of three dozen product ion structures from five precursor molecules revealed that virtually all fragment ion structure annotations for these species in the HMDB, METLIN, and mzCloud databases are incorrect.92 This study of the deamidation product of protonated tyrosine further highlights the ambiguity that exists with respect to the structures of product ions – ambiguity that significantly impacts the accuracy of ML-driven models for structure annotation. A thorough and comprehensive database including the combination of ion mobility spectrometry, mass spectrometry, and ion spectroscopy could help resolve this issue.
Author contributions
NJAC and YL conducted UVPD experiments, NM conducted DMS experiments, and GL and YX conducted TWIMS experiments as well as VG|FC calculations. LT and JM conducted IRIS experiments. MG, JCYL, and BBS advised on optimizing hardware configuration and aided in the repositioning of the linac at Q3. WSH conducted electronic structure calculations, MobCal-MPI calculations, and conceptualized the project. NJAC, GL, YL, and WSH conducted the analysis and prepared the manuscript.Conflicts of interest
The authors declare no conflicts of interest to report.Data availability
The data for this article, including the energy calculations for each reactant and product isomers are openly available in ioChem-BD at https://doi.org/10.19061/iochem-bd-6-600.Supporting information: experimental details and characterization of [Tyr + H]+ (ionogram, dispersion plot, mobiligram, protomer geometries, protomer UVPD experimental and calculated spectra), calculated transition orbitals associated with Sn → S0 transitions for N-protonated [Tyr + H]+, UVPD action spectra for [Tyr + H]+ product channels, calculated harmonic vibronic spectra of benzyl cation and phenonium isomers, and IRIS isomer population analysis. See DOI: https://doi.org/10.1039/d5cp04446d.
Acknowledgements
WSH acknowledges financial support from the Natural Sciences and Engineering Research Council (NSERC) in the form of a Discovery (RGPIN-03501-2023) and Alliance Grants (ALLRP-571095-2021). WSH also acknowledges financial support from the Mitacs Accelerate program (project IT23591) as well as support from the Digital Research Alliance of Canada in the form of access to high performance computing infrastructure. NJAC acknowledges NSERC funding in the form of a Vanier-Banting postdoctoral fellowship.References
- K. Biemann and J. A. McCloskey, J. Am. Chem. Soc., 1962, 84, 3192–3193 CrossRef.
- G. Junk and H. Svec, J. Am. Chem. Soc., 1963, 85, 839–845 Search PubMed.
- K. Heyns and H.-Fr Grützmacher, Liebigs Ann. Chem., 1963, 667, 194 Search PubMed.
- W. Vetter, in Biochemical Applications of Mass Spectrometry, ed. G. R. Waller, Wiley, New York, 1972; p. 387; 1980; Suppl. Vol. 1, p 439 Search PubMed.
- G. W. A. Milne, T. Axenrod and H. M. Fales, J. Am. Chem. Soc., 1970, 92, 5170–5175 CrossRef PubMed.
- M. Meot-Ner and F. H. Field, J. Am. Chem. Soc., 1973, 95, 7207–7211 CrossRef PubMed.
- P. A. Leclercq and D. Desiderio, Org. Mass Spectrom., 1973, 7, 515–533 CrossRef.
- C. W. Tsang and A. G. Harrison, J. Am. Chem. Soc., 1976, 98, 1301–1308 CrossRef PubMed.
- D. F. Hunt, J. Shabanowitz and F. K. Botz, Anal. Chem., 1977, 49, 1160–1163 CrossRef.
- R. J. Beuhler, E. L. Flanigan, L. J. Greene and L. Friedman, J. Am. Chem. Soc., 1974, 96, 3990–3999 CrossRef PubMed.
- D. Volgt and J. Schmidt, Biomed. Mass Spectrom., 1978, 5, 44–46 CrossRef PubMed.
- M. Vairamani, R. Srinivas and G. K. Viswanadha Rao, Indian J. Chem., Sect. B: Org. Chem. Incl. Med. Chem., 1988, 27, 284–285 Search PubMed.
- M. Eckersley, J. H. Bowie and R. N. Hayes, Int. J. Mass Spectrom. Ion Processes, 1989, 93, 199–213 CrossRef.
- H. U. Winkler and H. D. Beckey, Org. Mass Spectrom., 1972, 6, 855–860 CrossRef.
- A. Benninghoven, D. Jaspers and W. Sichtermann, Appl. Phys., 1976, 11, 35–39 Search PubMed.
- A. Benninghoven and W. Sichtermann, Anal. Chem., 1978, 50, 1180–1184 CrossRef PubMed.
- L. K. Liu, K. L. Busch and R. G. Cooks, Anal. Chem., 1981, 53, 109–113 CrossRef.
- J. J. Zwinselman, N. M. M. Nibbering, J. Van der Greef and M. C. Ten Noever de Brauw, Org. Mass Spectrom., 1983, 18, 525–529 CrossRef.
- J. Van der Greef, M. C. Ten Noever de Brauw, J. J. Zwinselman and N. M. M. Nibbering, Org. Mass Spectrom., 1982, 17, 274–276 CrossRef.
- W. Kulik and W. Heerma, Biomed. Mass Spectrom., 1988, 15, 419–427 Search PubMed.
- M. A. Posthumus, P. G. Kistemaker, H. L. C. Meuzelaar and M. C. Ten Noever de Brauw, Anal. Chem., 1978, 50, 985–991 CrossRef.
- C. Schiller, D. Kupka and F. Hillenkamp, Fresenius’ Z. Anal. Chem., 1981, 308, 304–308 CrossRef.
- T. P. Fan, E. D. Hardin and M. L. Vestal, Anal. Chem., 1984, 56, 1870–1876 CrossRef PubMed.
- C. D. Parker and D. M. Hercules, Anal. Chem., 1985, 57, 698–704 CrossRef.
- C. D. Parker and D. M. Hercules, Anal. Chem., 1986, 58, 25–30 CrossRef.
- S. Bouchonnet, J.-P. Denhez, Y. Hoppilliard and C. Mauriac, Anal. Chem., 1992, 64, 743–754 CrossRef.
- F. Rogalewicz, Y. Hoppilliard and G. Ohanessian, Int. J. Mass Spectrom., 2000, 195–196, 565–590 CrossRef.
- G. E. Reid, R. J. Simpson and R. A. J. O’Hair, J. Am. Soc. Mass Spectrom., 2000, 11, 1047–1060 CrossRef.
- H. El Aribi, G. Orlova, A. C. Hopkinson and K. W. M. Siu, J. Phys. Chem. A, 2004, 108, 3844–3853 CrossRef.
- N. N. Dookeran, T. Yalcin and A. G. Harrison, J. Mass Spectrom., 1996, 31, 500–508 CrossRef.
- H. Lioe and A. J. O’Hair, J. Am. Soc. Mass Spectrom., 2004, 15(1), 65–76, DOI:10.1016/j.jasms.2003.09.011.
- W. K. J. Mino, K. Gulyuz, D. Wang, C. N. Stedwell and N. C. Polfer, J. Phys. Chem. Lett., 2011, 2(4), 299–304, DOI:10.1021/jz1017174.
- T. Shoeib, A. Cunjie, A. C. Hopkinson and K. W. M. Siu, J. Am. Soc. Mass Spectrom., 2002, 13, 408–416 CrossRef CAS PubMed.
- E. Matthews and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2017, 19, 17434–17440 RSC.
- S. J. P. Marlton, et al. , Faraday Discuss., 2019, 217, 453–475 RSC.
- N. J. A. Coughlan, P. J. J. Carr, S. C. Walker, C. Zhou, M. Guna, J. L. Campbell and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2020, 31(2), 405–410, DOI:10.1021/jasms.9b00039.
- N. J. A. Coughlan, W. Fu, M. Guna, B. B. Schneider, J. C. Y. Le Blanc, J. L. Campbell and W. S. Hopkins, Phys. Chem. Chem. Phys., 2021, 23, 20607–20614 RSC.
- J. Martens, et al. , Anal. Chim. Acta, 2020, 1093, 1–15, DOI:10.1016/j.aca.2019.10.043.
- Kj Houthuijs, G. Berden, U. F. H. Engelke, V. Gautam, D. S. Wishart, R. A. Wevers, J. Martens and J. Oomens, Anal. Chem., 2023, 95, 8998–9005, DOI:10.1021/acs.analchem.3c01078.
- J. Martens, et al. , Anal. Chim. Acta, 2020, 1093, 1–15 CrossRef CAS PubMed.
- F. O. Talbot, T. Tabarin, R. Antoine, M. Broyer and P. Dugourd, J. Chem. Phys., 2005, 122, 3–7 CrossRef PubMed.
- O. V. Boyarkin, S. R. Mercier, A. Kamariotis and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 2816–2817 CrossRef CAS.
- G. Grégoire, et al. , Eur. Phys. J. D, 2009, 51, 109–116 CrossRef.
- A. Y. Pereverzev, V. Kopysov and O. V. Boyarkin, Angew. Chem., Int. Ed., 2017, 56, 15639–15643 CrossRef CAS PubMed.
- D. Nolting, C. Marian and R. Weinkauf, Phys. Chem. Chem. Phys., 2004, 6, 2633–2640 RSC.
- R. Wu and T. B. McMahon, ChemPhysChem, 2008, 9, 2826–2835 CrossRef CAS PubMed.
- B. B. Schneider, T. R. Covey, S. L. Coy, E. V. Krylov and E. G. Nazarov, Anal. Chem., 2010, 82, 1867–1880 CrossRef CAS.
- J. L. Campbell, J. C. Y. Le Blanc and B. B. Schneider, Anal. Chem., 2012, 84, 7857–7864 CrossRef CAS PubMed.
- J. L. Campbell, M. Zhu and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2014, 25, 1583–1591 CrossRef CAS.
- F. A. Londry and J. W. Hager, J. Am. Soc. Mass Spectrom., 2003, 14, 1130–1147 CrossRef CAS PubMed.
- V. Gabelica, A. A. Shvartsburg, C. Afonso, P. Barran, J. L. P. Benesch, C. Bleiholder, M. T. Bowers, A. Bilbao, M. F. Bush and J. L. Campbell, et al. , Mass Spectrom. Rev., 2019, 38(3), 291–320, DOI:10.1002/mas.21585.
- J. Martens, G. Berden, C. R. Gebhardt and J. Oomens, Rev. Sci. Instrum., 2016, 87, 103108 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606, DOI:10.1002/WCMS.1606.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15(3), 1652–1671, DOI:10.1021/acs.jctc.8b01176.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11(2), e1493, DOI:10.1002/WCMS.1493.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065, 10.1039/b515623h.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/b508541a.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- R. Izsák, F. Neese and W. Klopper, J. Chem. Phys., 2013, 139(9), 094111, DOI:10.1063/1.4819264/315430.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135(14), 144105, DOI:10.1063/1.3646921/190211.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155(10), 104109, DOI:10.1063/5.0058766/1013244.
- D. Bykov, T. Petrenko, R. Izsák, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113(13–14), 1961–1977, DOI:10.1080/00268976.2015.1025114.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356(1–3), 98–109, DOI:10.1016/J.CHEMPHYS.2008.10.036.
- F. Neese, J. Comput. Chem., 2003, 24(14), 1740–1747, DOI:10.1002/JCC.10318.
- D. Bykov, T. Petrenko, R. Izsák, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113(13–14), 1961–1977, DOI:10.1080/00268976.2015.1025114.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11(3), 361–373, DOI:10.1002/jcc.540110311.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78, DOI:10.1002/wcms.81.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152(22), 224108, DOI:10.1063/5.0004608/1061982.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327, DOI:10.1002/wcms.1327.
- B. De Souza, G. Farias, F. Neese and R. Izsák, J. Chem. Theory Comput., 2019, 15(3), 1896–1904, DOI:10.1021/acs.jctc.8b00841.
- B. De Souza, F. Neese and R. Izsák, J. Chem. Phys., 2018, 148(3), 034104, DOI:10.1063/1.5010895/195946.
- F. Neese and G. Olbrich, Chem. Phys. Lett., 2002, 362(1–2), 170–178, DOI:10.1016/S0009-2614(02)01053-9.
- J. P. Götze, B. Karasulu and W. Thiel, J. Chem. Phys., 2013, 139(23), 234108, DOI:10.1063/1.4844055.
- J. D. Alia and J. A. Flack, RSC Adv., 2020, 10(70), 43153–43167, 10.1039/D0RA06774A.
- C. Ieritano, J. Crouse, J. L. Campbell and W. S. Hopkins, Analyst, 2019, 144(5), 1660–1670, 10.1039/c8an02150c.
- A. Haack, C. Ieritano and W. S. Hopkins, Analyst, 2023, 148, 3257–3273, 10.1039/d3an00545c.
- C. Ieritano, MobCal-MPI Analysis GUI., 2024 DOI:10.5281/zenodo.11426096.
- G. Féraud, M. Broquier, C. Dedonder, C. Jouvet, G. Grégoire and S. Soorkia, J. Phys. Chem. A, 2015, 119(23), 5914–5924, DOI:10.1021/jp5065837.
- J. Zhao, T. Shoeib and A. C. Hopkinson, Int. J. Mass Spectrom., 2006, 265, 255–256 Search PubMed.
- C. Ieritano and W. S. Hopkins, Phys. Chem. Chem. Phys., 2022, 24, 20594–20615, 10.1039/D2CP02540J (Perspective).
- B. B. Schneider, E. G. Nazarov, F. Londry, P. Vouros and T. R. Covey, Mass Spectrom. Rev., 2016, 35, 687–737, DOI:10.1002/mas.21453.
- P. Zhang, W. Chan and I. L. Ang, et al. , Sci. Rep., 2019, 9, 6453, DOI:10.1038/s41598-019-42777-8.
- C. M. Nichols, J. N. Dodds, B. S. Rose, J. A. Picache, C. B. Morris, S. G. Codreanu, J. C. May, S. D. Sherrod and J. A. McLean, Anal. Chem., 2018, 90(24), 14484–14492 CrossRef PubMed.
- S. M. Stow, T. J. Causon, X. Zheng, R. T. Kurulugama, T. Mairinger, J. C. May, E. E. Rennie, E. S. Baker, R. D. Smith and J. A. McLean, et al. , Anal. Chem., 2017, 89(17), 9048–9055, DOI:10.1021/acs.analchem.7b01729.
- X. Zheng, N. Aly, Y. Zhou, K. Dupuis, A. Bilbao, V. Paurus, D. J. Orton, R. Wilson, S. Payne and R. D. Smith, et al. , Chem. Sci., 2017, 8(11), 7724–7736 RSC.
- A. Sirohiwal, R. Berraud-Pache, F. Neese, R. Izsák and D. A. Pantazis, J. Phys. Chem., 2020, 124(40), 8761–8771, DOI:10.1021/ACS.JPCB.0C05761.
- V. Barone, M. Biczysko, M. Borkowska-Panek and J. Bloino, ChemPhysChem, 2014, 15(15), 3355–3364, DOI:10.1002/CPHC.201402300.
- V. Barone, S. Alessandrini, M. Biczysko, J. R. Cheeseman, D. C. Clary, A. B. McCoy, R. J. DiRisio, F. Neese, M. Melosso and C. Puzzarini, Nat. Rev. Methods Primers., 2021, 1(1), 1–27, DOI:10.1038/s43586-021-00034-1.
- C. Ieritano, A. N. Fry, J. N. Dodds, E. S. Baker and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2025, 36(9), 1889–1901, DOI:10.1021/jasms.5c00130.
- F. A. M. G. van Geenen, R. F. Kranenburg, A. C. van Asten, J. Martens, J. Oomens and G. Berden, Anal. Chem., 2021, 93, 2687–2693, DOI:10.1021/acs.analchem.0c05042.
- R. D. Johnson, K. K. Irikura, R. N. Kacker and R. Kessel, J. Chem. Theory Comput., 2010, 6(9), 2822–2828, DOI:10.1021/ct100244d.
- L. Tetering, S. Spies, Q. Wildeman, K. Houthuijs, R. Outersterp, J. Martens, R. Wevers, D. Wishart, G. Berden and J. Oomens, Commun. Chem., 2024, 7(1), 30, DOI:10.1038/s42004-024-01112-7.
Footnote |
| † Co-first authors. |
| This journal is © the Owner Societies 2026 |