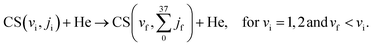Open Access Article
Open Access ArticleVibrational relaxation rate coefficients in CS–He collisions up to the dissociation limit: mixed quantum-classical calculations and neural network predictions
Marco Pezzella a,
Fernando Pirani
a,
Fernando Pirani b,
Massimiliano Bartolomei
b,
Massimiliano Bartolomei c,
Qizhen Hong
c,
Qizhen Hong d,
François Lique
d,
François Lique e,
Loriano Storchi
e,
Loriano Storchi *a and
Cecilia Coletti
*a and
Cecilia Coletti *a
*a
aDipartimento di Farmacia, Universitá G. d'Annunzio Chieti-Pescara, Via dei Vestini, 66100 Chieti, Italy. E-mail: cecilia.coletti@unich.it; loriano.storchi@unich.it
bDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, via Elce di Sotto 8, 06123 Perugia, Italy
cInstituto de Física Fundamental – CSIC, C/Serrano 123, Madrid, Spain
dState Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, 100190 Beijing, China
eUniv Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251, 35000 Rennes, France
First published on 8th January 2026
Abstract
Rate coefficients for the process CS(v) + He → CS(v–Δv) + He with Δv = 1, 2, 3 and for v up to 45 were calculated in the 80–5000 K temperature using a mixed quantum-classical (MQC) method. The dataset was then completed using a Neural Network (NN) model, trained on the MQC rate coefficients. The reliability of the MQC method was first verified by comparing the new MQC results with initially state-selected ro-vibrational rate coefficients up to v = 2 computed with the vibrational close-coupling infinite-order sudden (VCC-IOS) method [F. Lique and A. Spielfiedel, Astron. Astrophys., 2007, 462, 1179] employing the same potential energy surface (PES). To enable calculations for higher vibrationally excited states, a new analytical PES was developed that is suitable even under large bond distortions.
1 Introduction
The study of inelastic molecular collisions is essential for modelling non-equilibrium physical environments, from plasmas and (exo)planetary atmosphere composition and dynamics to the characterisation of the interstellar medium (ISM).1–8 Non-local thermal equilibrium (non-LTE) conditions require models that rely on extensive sets of state-to-state collisional data, which are usually impossible to obtain from experiments alone.9Therefore, the theoretical approach is the necessary way to proceed: collisional information is obtained from molecular dynamics simulations using accurate potential energy surfaces (PESs), which describe the interactions between colliding particles. When available, these theoretical results can be compared with experimental data to assess the reliability of the adopted computational methods. A variety of techniques can be used to describe nuclear motion and compute state-to-state collisional cross sections and rate coefficients. Full quantum methods represent the gold standard as they incorporate all possible quantum effects. However, these methods are computationally expensive and their cost increases dramatically with the number of molecular quantum states considered in the calculation, restricting their application to systems where few quantum states are accessible or when the excitation of small and medium sized rigid molecules is induced by light colliders such as He or H2, unless approximations are introduced. Methods based on classical mechanics, mostly quasi-classical trajectory approaches (QCT), are often the alternative. They can be readily scaled for large systems and are easily parallelisable. Nevertheless, these methods inherently neglect quantum effects and schemes for the assignment of the final quantum states need to be applied, whose accuracy, particularly for vibrational states, is still debated.10,11
The mixed quantum-classical (MQC) approach12,13 represents an effective compromise between fully quantum and classical methodologies. In this framework, the degrees of freedom exhibiting the most significant quantum behaviour are treated quantum mechanically, while the remaining ones are treated classically. This enables the inclusion of the quantum effects of interest with a consistent reduction in computational cost. In recent years, the original MQC formalism has been further developed and refined, in applications where rotations (e.g. ref. 14 and references therein) or vibrations (e.g. ref. 15 and references therein) constitute the quantum subset.
In the modelling of ISM or exoplanet atmospheres, there is a growing need to extend the database of available rotationally resolved rate coefficients data for collision-induced transitions between ro-vibrational levels across a large number of species. Indeed, results from full quantum simulations have been obtained for a variety of systems,16–21 but are often limited to cold temperature conditions, mainly addressing the quenching of rotational states in the ground vibrational state. However, recent years have seen the detection of a growing number of vibrationally excited molecules, making the availability of comprehensive vibrational quenching and excitation rate coefficients an urgent requirement. Indeed, in the past decade, we have undergone a revolution in our ability to observationally study the molecular Universe. The high resolution of new telescopes such as Atacama Large Millimeter/submillimeter array (ALMA) and James Webb Space Telescope (JWST) enables very detailed observations of small astrophysical bodies such as planetary atmospheres, cometary comae, and exoplanets as well as interstellar environments such as molecular clouds and protoplanetary disks. In particular, infrared observations of vibrational molecular signatures, boosted by the MIRI and NIRSPEC instruments on JWST, are flourishing.
Using MQC methods, where the vibrational motions are treated quantum mechanically while rotations and translations are described classically, can be highly effective in such cases. Indeed, this approach has been used to successfully reproduce and extend experimental results on the vibrational quenching of Earth's atmospheric species (N2, CO, and O2) through collisions with atoms and diatomic molecules.22–26
Among diatomic molecules frequently detected in astrophysical environments, carbon monosulfide (CS) is of particular interest, as it has been detected in interstellar molecular clouds, circumstellar envelopes and protoplanetary disks.27–33 More recently, CS has also been identified in exoplanetary atmospheres as an intermediate species in the photochemical formation of SO2.34 Molecular collisions involving CS have been studied by Lique and coworkers (CS–He collisions),35,36 and by different groups (CS–H2 collisions).37–40 The results from Lique and coworkers for CS–He collisions are especially relevant, as they provide detailed insights into ro-vibrational excitation processes: first they developed an intermolecular PES to study rotational quenching of CS,35 and then extended their work to include the first two excited vibrational states (this work will be referred as 07LiSp hereafter).36 Rate coefficients for inelastic collisions were calculated using the vibrational close-coupling infinite-order sudden approximation (VCC-IOS) quantum method41,42 and made available through the BaseCol database.43
In this work we focus on CS–He inelastic collisions. We take on the PES developed in ref. 36, briefly described in Section 3, and apply the MQC method, described in Section 2, to calculate the rate coefficients for the same vibrational transitions for which VCC-IOS results are available. This enables us to directly compare the performance of the MQC and VCC-IOS scattering approaches (Section 5.1). We then develop a new intermolecular analytical PES, based on the Improved Lennard-Jones model44 (Section 3.2), which can describe larger deformations of the CS molecule. This new PES can therefore be used to obtain vibration-to-translation/rotation (V–T/R) rate coefficients for highly vibrationally excited states of CS, approaching its dissociation limit. Using the ILJ PES we construct a comprehensive dataset of V–T/R rate coefficients covering all CS vibrational levels up to 45, explicitly calculated by the MQC method and completed using a Neural Network (NN) model (Section 4).
It is worth noting that, while the MQC method can yield state-to-state rate coefficients for specific ro-vibrational transitions (see Section 5.1), the primary objective of this study is to calculate a comprehensive dataset of rotationally averaged rate coefficients for the collisional quenching of vibrationally excited CS by He (see Section 5.2). This dataset includes all rate coefficients for the following processes:
| CS(v) + He → CS(v–Δv) + He, with Δv = 1, 2, 3 |
2 MQC collisional cross sections and rate coefficients
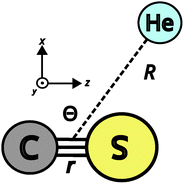
Our MQC implementation for vibrational energy transfer in atom–diatom collisions simultaneously solves the time-dependent Schrödinger equation for the vibrational degree of freedom and ro-vibrational coupling, and the classical equations of motion for the other degrees of freedom (rotation and translation). The total Hamiltonian (H) of the system in Jacobi coordinates (see Fig. 1) can be written as:
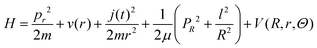 | (1) |
The quantum Hamiltonian is composed by the first three terms of eqn (1). The rotational contribution 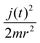 is present in the quantum and in the classical Hamiltonian, and, together with the effective potential Veff introduced in the following, defines their interaction.
is present in the quantum and in the classical Hamiltonian, and, together with the effective potential Veff introduced in the following, defines their interaction. 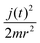 and the remaining terms compose the classical Hamiltonian. The Ehrenfest averaged potential, Veff(R, Θ), is used instead of V(r, R, Θ) in the classic Hamiltonian and also couples the two Hamiltonians:45
and the remaining terms compose the classical Hamiltonian. The Ehrenfest averaged potential, Veff(R, Θ), is used instead of V(r, R, Θ) in the classic Hamiltonian and also couples the two Hamiltonians:45
| Veff(r, Θ) = 〈Ψ|V(R, r, Θ)|Ψ〉 | (2) |
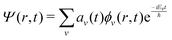 | (3) |
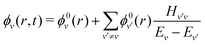 | (4) |
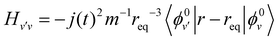 | (5) |
The coefficients av are obtained by plugging eqn (3) and (4) into the time-dependent Schrödinger equation, and propagating in time the following set of coupled equations together with the classical equations:
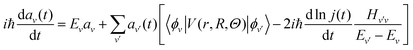 | (6) |
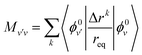 | (7) |
The probability for the vibrational transition vi → vf can be obtained as Pvi→vf = |avf(∞)|2 and depends on the initial conditions (i.e. the initial random values of angle and action) of the particular trajectory considered.
The total energy conservation and micro-reversibility principle imposing that Pvi→vf(E) = Pvf→vi(E) are guaranteed by the utilisation of a symmetrisation procedure13 which assigns a total energy E to a specific transition, so that:
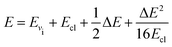 | (8) |
If we consider a specific initial ro-vibrational state (vi, ji) we can obtain the probability of the collisional transition to a final vibrational state vf, by averaging over a number of trajectories N allowing a statistical sampling over the initial conditions:
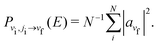 | (9) |
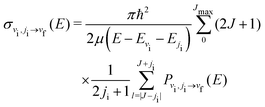 | (10) |
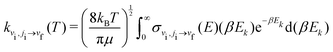 | (11) |
In many applications, we are interested in rate coefficients for vibrational transitions averaged over the initial rotational quantum numbers ji. This approach is especially suitable for heavy molecules such as CS, for which rotational spacings are small and many rotational states contribute to the relaxation process over the temperature range considered here. Under these conditions, statistical effects are expected to reduce the sensitivity of vibrational relaxation rates to the specific initial rotational state. It is therefore important to evaluate the validity of this approximation under the conditions relevant to astrochemical observations. While laboratory experiments have accessed rotational states as high as j = 113,46,47 astrochemical detections remain limited to much lower excitation. In high-excitation regions such as Orion KL, the highest detected transition of CS is j = 26–25,48 and in colder dense cores rotational levels with j < 10 are typically observed. In these environments, the gas density often exceeds the critical density for rotational transitions, ensuring that the rotational population follows a Boltzmann distribution. Nevertheless, in extreme non-LTE or very low-density environments (e.g., cometary comae) state-specific rotational effects may become more important. However, as recently discussed by Bowesman et al.,49 approaches assuming rotational LTE and vibrational (or vibronic) non-LTE are expected to capture the dominant non-LTE effects observable with the James Webb Space Telescope, particularly in view of the computational infeasibility of treating the full set of rovibrational transitions explicitly. Furthermore, radiative-transfer models generally require the inclusion of higher-lying rotational levels that may be weakly populated, even if not directly observed, as neglecting them can affect the excitation balance and lead to biased physical conditions.
To determine rotationally averaged rate coefficients, it is convenient to calculate rotationally averaged “cross sections” σvi→vf(Ecl, Tref):
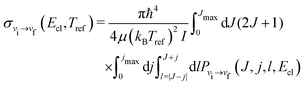 | (12) |
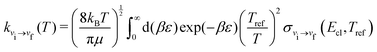 | (13) |
In the following, we calculated the rate coefficients using eqn (11) to compare the coefficients obtained by the MQC method with those obtained by the VCC-IOS approach,36 and then using eqn (13) to produce the dataset of V–T/R rate coefficients for vibrational quenching in a wide temperature range. In both cases, adequate coverage of the energy spectrum is important for good sampling, which can be achieved by using denser sampling of low energies to describe low temperatures and including a representative number of points at higher energies.
We solved the combined classical and quantum coupled equations using a variable-order, variable-step Adams predictor–corrector integrator, imposing an accuracy of 1 × 10−8.
3 Potential energy surfaces
3.1 CS intramolecular potential and vibrational wavefunctions
The evaluation of the matrix coupling elements in eqn (7), the vibrational wavefunction (eqn (3)) and the vibrational energy levels requires the use of the rotationless vibrational wavefunctions ϕj=0v(r, t) for the isolated CS molecule.Initially, to enable comparison with the results of ref. 36, we used the same matrix elements and vibrational energy levels. These were obtained using the vibrational wavefunctions evaluated by the Fourier Grid Hamiltonian (FGH) method,50 which is based on a CS potential energy function derived from a Rydberg–Klein–Rees (RKR) curve51 and using the experimental spectroscopic constants from Bogey et al.52 The work reports matrix elements for the ground state and the first two excited vibrational states.
To determine collisional vibrational transition rate coefficients for highly excited states, we employed CS vibrational wavefunctions obtained from the recent spectroscopic model, developed by Paulose et al. (hereafter referred to as JnK).53 This model starts from Coxon & Hajigeorgiou potential energy curve,54 with refined parameters that yield improved agreement with experimental data. Experimental vibrational energy levels were used when available through the measured active rotation–vibration energy levels procedure.55 The model consists of 50 vibrational states up to the dissociation limit, with rotational states ranging up to j = 257 for v = 0. The energy levels for the first three vibrational states obtained by the two models agree within 0.1 cm−1.
The matrix elements 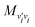 were generated using the vibrational wavefunction from Level16 program,56 on a grid spanning 0.75 < r (Å) < 8.0 with a step size of 0.05 Å. The resulting values differ from those reported by Lique and Spielfiedel36 by less than 4%, which is well within the expected 10% accuracy of the method.
were generated using the vibrational wavefunction from Level16 program,56 on a grid spanning 0.75 < r (Å) < 8.0 with a step size of 0.05 Å. The resulting values differ from those reported by Lique and Spielfiedel36 by less than 4%, which is well within the expected 10% accuracy of the method.
3.2 CS–He intermolecular potential: a new analytical PES
The quality of scattering cross sections and rate coefficients critically depends on the quality of the PES describing the interaction potential both at short and long range. In particular, long-range interactions play a fundamental role at low temperatures, where orientation effects—which originate at large intermolecular separations—can significantly influence the dynamics and outcomes of the collisions.We again start by using the intermolecular PES developed by Lique and Spielfiedel,36 obtained through an analytical fit to ab initio points calculated at the coupled cluster level with single and double excitations and perturbative triples [CCSD(T)], using Dunning's augmented correlation-consistent quadruple-zeta basis set57 (aug-cc-pVQZ) further augmented with diffuse [3s3p2d2f1g] bond functions. Basis set superposition error (BSSE) corrections were included following the procedure of Werner et al.58 The dependence on the carbon–sulfur bond length r was explicitly incorporated by evaluating the potential at three geometries, 2.4, 2.9, and 3.4 bohr. This makes the potential energy surface reliable for vibrational levels up to v = 2.
Throughout this work, the CS–He potential is described using a Jacobi coordinate system, where r represents the carbon–sulfur bond length, R is the distance between the He atom and the CS centre of mass, and Θ is the angle between these two vectors (Fig. 1).
To address higher vibrationally excited states, we have also developed a new potential energy surface designed to be reliable for larger distortions of the CS bond.
As in previous works,15,26,59 where we determined large datasets of rate coefficients for vibrational energy transfer, we adopt an analytical model that provides a reliable representation of the interaction, both at equilibrium and for large distortions of the CS bond. This model is expressed as a combination of effective contributions, whose basic parameters have clear physical interpretations in terms of the fundamental properties of the interacting species—such as the static dipole polarizability, the number of outer-shell electrons determining its magnitude, and the permanent electric dipole moment. The numerical values of these parameters were adjusted against accurate ab initio interaction energies for the CS–He ground singlet state computed for a wide range of intermolecular distances using the CCSD(T) approach in the complete basis set (CBS) limit.
In such computations, counterpoise-corrected60 interaction energies obtained using the aug-cc-pVQZ and aug-cc-pV5Z57 basis sets have been properly combined61,62 to obtain reliable extrapolated CBS values. To also probe the dependence of the intermolecular potential on the stretching of the CS bond length beyond its equilibrium value rCSeq = 2.9 bohr, two further values (3.19 and 3.335 bohr) were considered. Furthermore, ab initio estimations of the CS permanent dipole moment and static dipole polarizability, which are quantities needed for the analytical representation of the global PES (see below), have been obtained as previously done63–66 for different monomers at the multireference ACPF (Averaged Coupled Pair functional) level in combination with the aug-cc-pV5Z basis set and as a function of the internuclear distance. In particular, the natural molecular orbitals in the ACPF calculations were those from the complete active space self-consistent field reference wave functions. The active space (CAS) considered here is defined by distributing 18 electrons in the orbitals indicated as (2, 3, 4)σg (2, 3, 4)σu (1, 2)πu (1, 2)πg. The 1σg 1σu core molecular orbitals were constrained to be doubly occupied and excluded from the used CAS while also being fully optimised. Additional estimations of the CS dipole polarizability have been carried out at the CCSD(T)/aug-cc-pV5Z level of theory. All electronic structure calculations were carried out by using the Molpro 2012.1 package.67
The complete formulation of the analytical PES is provided in Appendix A, and the corresponding computational subroutine is available in the SI.
Fig. 2 and 3 present several comparisons between the new analytical PES and the ab initio PES derived in ref. 36 for CS at its equilibrium bond length. The contour plot shown in Fig. 2 indicates that the two PESs exhibit a very similar overall topology, with only minor differences in the shape of the potential minimum for certain orientations. The potential cuts shown in Fig. 3 demonstrate excellent agreement between the current ab initio estimations (calculated at the CCSD(T)/CBS level) and the two PESs for the three dimer configurations considered (top three panels). Both PESs accurately reproduce the predicted position and depth of the potential well, with minor discrepancies, below 0.5 meV, occurring for Vanal. The two bottom panels of the same figure illustrate the corresponding angular dependence of the interaction energy at fixed intermolecular distance R values (R = 4 Å and R = 5 Å). In all cases, the quantitative differences in the attractive region are very small (ca. 0.1 meV) and limited to a few specific orientations. This also constitutes a validation of the new analytical PES for small distortions of CS bond length. Indeed, such good agreement between the analytical PES and the ab initio points is remarkable. While this level of agreement is expected for the V07LiSp PES, which was constructed by fitting a large number of ab initio points at the CS equilibrium bond length, the analytical PES relies solely on a limited number of physically motivated parameters. The last condition is basic to formulate a PES reliable in the full range of accessible molecular orientations and in an extended range of molecular deformations.
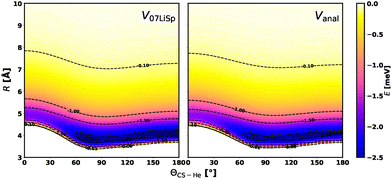 | ||
| Fig. 2 Contour plots of the new analytical potential energy surface, Vanal (right panel), and of the V07LiSp PES36 (left panel), both evaluated at the equilibrium bond length r = rCSeq. The minimum of Vanal is located at Θ = 78° and R = 3.90 Å, with a well depth of −2.61 meV, while for V07LiSp the minimum occurs at Θ = 75°, R = 3.84 Å, and −2.70 meV. | ||
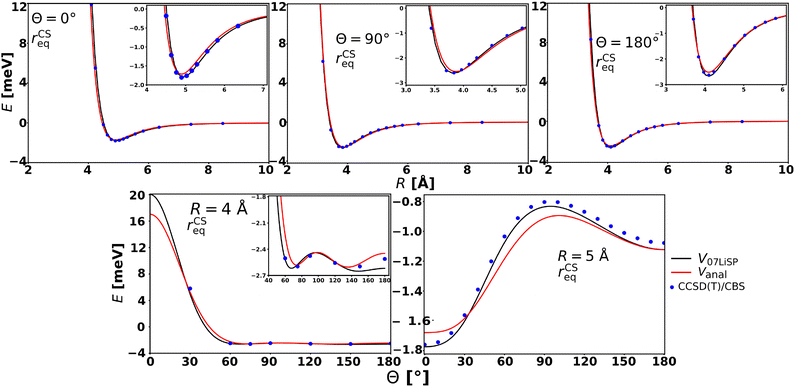 | ||
| Fig. 3 Potential energy cuts at the equilibrium bond length r = rCSeq comparing the results from the V07LiSp PES,36 the present analytical potential Vanal, and the CCSD(T)/CBS ab initio points. | ||
Direct comparison with the ab initio data computed at the CCSD(T)/CBS level is feasible only for small deviations from the equilibrium bond length (see Fig. S1 in the SI, corresponding to a 15% CS bond elongation). A more extensive comparison would require accounting for the increasing multireference character of the electronic wavefunction at larger distortions, which lies beyond the scope of the present work. The figure shows that the position of the potential minimum is satisfactorily reproduced, with a maximum discrepancy in the well depth of approximately 0.5 meV.
Overall, the accuracy of the analytical PES, based on comparison with ab initio points, is expected to be within 10% for small deformations of the CS bond and within 30% for the largest deformations.
4 The neural network model
In recent years, machine learning (ML) techniques have been increasingly employed to predict cross sections and rate coefficients from a limited set of computed values. The requirement for extensive state-to-state datasets, often spanning wide temperature ranges, makes data-driven prediction from a restricted number of computationally expensive calculations an appealing approach. Consequently, rate coefficients derived from QCT and MQC simulations for both reactive and inelastic scattering have been modelled using Neural Networks (NN) and Gaussian Process Regression (GPR) methods.25,68–71 Both techniques have demonstrated comparable predictive performance, provided they are applied within the interpolation domain of the training data. However, differences in training efficiency can arise depending on the size of the dataset and the dimensionality of the feature space.69In this work, we construct the dataset directly starting from rate coefficients rather than on cross sections, since the rotationally averaged cross sections (eqn (12)), which depend on the reference temperature, do not represent intrinsic collision properties. In contrast, rate coefficients can be straightforwardly related to physically relevant observables, such as collisional excitation and relaxation rates. Besides, we verified that building the dataset starting from cross sections or from rate coefficients leads to negligible differences in the final results.
Here, an NN model was selected over a GPR one, as a comparative evaluation demonstrated its superior performance on our specific datasets. To ensure a fair comparison, both models first underwent hyperparameter optimization via an extensive grid search. For the GPR model, we optimized parameters including the value of ν (nu) when using the (Matérn kernel). For the NN model, we optimised the architecture by varying the number of dense layers and the number of neurons per layer. The performance of the optimised models was then evaluated using a Leave-One-Out Cross-Validation (LOOCV) strategy. This was applied to the three datasets of rotationally averaged rate coefficients for the CS(v) + He → CS(v–Δv) + He transitions, corresponding to Δv = 1, 2, and 3. In this procedure, the model is trained on all data points in a set except one, which is kept out for testing. This process is repeated for every data point, enabling us to judge the overall effectiveness of each model. The ANN model consistently produced better predictive accuracy in these tests, resulting in its selection as the optimal model for this study.
Following this initial step, the optimal neural network architecture was identified through a two-stage grid search process designed to balance the accuracy of the predictions with the physical plausibility of the resulting output surface. In the first stage, a conventional grid search was performed on a wide range of model hyperparameters, using a standard LOOCV strategy to evaluate performance and select a smaller subset of promising candidates. The second stage involved a more refined evaluation focused on the smoothness of the final interpolated surface. To achieve this, the training data points – consisting here of all the computed rate coefficients values for each Δv – were combined with the model predictions to create a complete surface representation. The smoothness of this surface was then assessed quantitatively by calculating the mean absolute Laplacian. This metric was derived by first interpolating the scattered data points onto a regular grid and then applying a Laplacian kernel via 2D convolution to approximate the surface curvature at each point. Ultimately, models that produced a lower mean absolute Laplacian value were favoured, as this indicates a smoother and less erratic surface. This ensures that the final selection is accurate and generates physically realistic outputs. All codes can be retrieved at ref. 72.
This two-stage optimisation process led to the selection of our final model configuration. The optimal architecture identified was a three-layer network with 256 neurons per layer ([256, 256, 256]). The model was trained using the Adam optimiser with the mean squared error (MSE) loss function. Training was run for 1000 epochs for all datasets, and the model weights from the epoch that achieved the minimum training MSE were selected for the final model. The optimisation process also indicated different optimal batch sizes: a batch size of 50 was used for the Δv = 1 dataset and a batch size of 256 was employed for both the Δv = 2 and Δv = 3 datasets.
5 Results and discussion
5.1 Comparison between MQC and VCC-IOS rate coefficients
The availability of the results for the CS–He ro-vibrational de-excitation cross sections and rate coefficients in ref. 36 gives us the opportunity to compare these quantities using two completely different methods: the time-independent quantum VCC-IOS of ref. 36, and the time-dependent MQC approach of the present work.The results by Lique and Spielfiedel36 cover ro-vibrational transitions for v = 0, 1, and 2, ranging from j = 0 to j = 37. The reported accuracy is within a factor of 2–3 for the ro-vibrational excitation and within a factor of 1.5 for pure rotational excitation within one vibrational manifold.
Those rate coefficients were compared with the corresponding MQC values calculated using eqn (11) obtained by running 5000 trajectories for each of the 34 initial classical energy values Ecl, in the interval 50–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, selected on an unevenly distributed energy grid, with a higher density of points at lower energies. These settings should ensure an accuracy of the MQC method within 20%. An initial separation of R = 20 Å was adopted which reflects the coordinate space extension used in Lique and Spielfiedel.36 As mentioned in Section 2, the present implementation of the MQC method does not explicitly select the final rotational state jf of the CS molecule. However, since the VCC-IOS data include rotational states only up to j = 37, a histogram binning procedure was applied to enable a meaningful comparison. Specifically, the cross sections (eqn (10)) were computed by including only those trajectories leading to a final rotational energy equal to or lower than that corresponding to jf = 37. Accordingly, the rate coefficients can be compared for the following process:
000 cm−1, selected on an unevenly distributed energy grid, with a higher density of points at lower energies. These settings should ensure an accuracy of the MQC method within 20%. An initial separation of R = 20 Å was adopted which reflects the coordinate space extension used in Lique and Spielfiedel.36 As mentioned in Section 2, the present implementation of the MQC method does not explicitly select the final rotational state jf of the CS molecule. However, since the VCC-IOS data include rotational states only up to j = 37, a histogram binning procedure was applied to enable a meaningful comparison. Specifically, the cross sections (eqn (10)) were computed by including only those trajectories leading to a final rotational energy equal to or lower than that corresponding to jf = 37. Accordingly, the rate coefficients can be compared for the following process:
Calculations were performed for initial rotational states ji = 0, 1, 2, 5, 10, and 30 with vi = 1, and for ji = 0, 5, 10, and 30 with vi = 2, coupling only the first three vibrational levels. The results for these selected transitions are presented in Fig. 4, while a detailed quantitative comparison of the corresponding rate coefficients is provided in Table S1 of the SI. Fig. S2 in the SI further illustrates the comparison in terms of the ratio between the MQC and VCC-IOS rate coefficients.
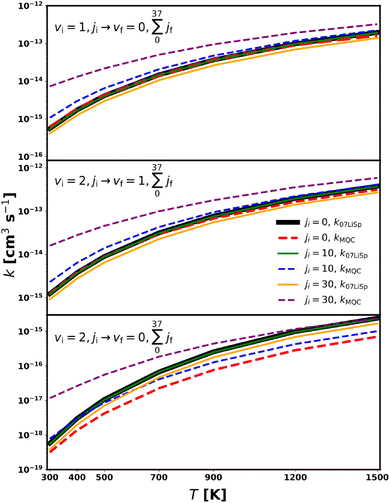 | ||
Fig. 4 MQC (dashed lines) and VCC-IOS36 (solid lines) rate coefficients for the  transition as a function of temperature. transition as a function of temperature. | ||
For processes with Δv = 1 (upper panels in Fig. 4), the agreement is excellent for the lowest initial rotational quantum numbers, regardless of the initial vibrational state and across the entire temperature range. For ji ≤ 5, the maximum deviation remains below 50%, which is well within the combined numerical uncertainties of both methods. The main difference between VCC-IOS and MQC data is that VCC-IOS rate coefficients are basically independent on the initial rotational excitation whereas MQC values show an increase as ji grows, an effect which decreases with temperature. As a result, MQC and VCC-IOS rate coefficients match very well (i.e. differences are below the methods accuracy) for at least ji ≤ 10 in the low temperature range and nearly for all the considered ji's for the highest temperature. This behaviour may be partly attributed to the imposed constraint of jf ≤ 37. Considering the rotational state distribution within the investigated temperature range, and the known propensity of vibrational relaxation processes to favour transitions with Δj = jf − ji = 0, with the probability decreasing rapidly as |Δj| increases, particularly at low temperatures, this limitation is expected to have only a minor effect for the lowest ji values. In contrast, for the highest ji levels, where transitions populating high rotational states is more likely, an accurate description of the final rotational distribution becomes increasingly important.
It is worth noting, however, that ro-vibrational excitation rate coefficients calculated using the full close-coupling (CC) method for CO–He collisions73 show a similar trend, with a slight increase as the initial rotational excitation of the molecule rises in the 1000–1500 K temperature range, even though those calculations are limited to jf ≤ 14. This behaviour suggests that a comparable dependence may also apply to the CS–He system as captured by the MQC-calculated rate coefficients.
The process involving the loss of two vibrational quanta shows a comparable behaviour; however, in this case, the best agreement is observed for ji > 10 and discrepancies tend to be larger.
Although the level of agreement with the results of Lique and Spielfiedel36 varies with the initial rotational quantum number, the fact that the present work focuses on producing a dataset of rotationally averaged vibrational de-excitation rate coefficients ensures that these differences remain within the expected accuracy of the VCC-IOS results.
5.2 Dataset of vibrational excitation rate coefficients
The rotationally averaged de-excitation rate coefficients for the process CS(v) + He → CS(v–Δv) + He, for vibrational levels up to v = 45, were calculated using eqn (13) and the new analytical PES. The accuracy of the results, considering the combined uncertainties of the PES and of the MQC method, is expected to lie within 25–30% for the transitions involving lower vibrational states and within 50% for the highest ones. Fig. 5 compares the MQC-calculated rate coefficients for the CS(v = 1) + He → CS(v = 0) + He transition obtained with the new Vanal and the 07LiSp PESs. Both surfaces yield similar temperature dependencies, while the new PES systematically predicts values larger by approximately a factor of two. This systematic increase may be related to the slightly earlier onset of the repulsive wall in the analytical PES compared to the V07LiSp PES for collisions occurring within the acceptance angular cone Θ < 90° (Fig, 3), corresponding to He approaching CS from the carbon side (Θ = 0°). Given the larger distance of the carbon atom from the molecular center of mass, such collisions are expected to be more effective in inducing vibrational energy transfer.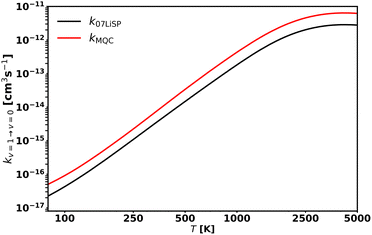 | ||
| Fig. 5 MQC rate coefficients for CS(v = 1) + He → CS(v = 0) + He calculated using the new Vanal (black curve) and the 07LiSp PESs (red curve) as a function of temperature. | ||
MQC de-excitation rate coefficients were calculated for the first three vibrational states and, starting from vi = 5, every five levels up to vi = 45. Above this level, the predissociative character of the vibrations caused numerical instabilities in the simulations. For each calculation, all vibrational levels within a 7000 cm−1 interval from vi were coupled. The temperature range of 80–5000 K was chosen to ensure good coverage of environments ranging from the interstellar medium (ISM) to hot exoplanetary atmospheres. A total of 5000 trajectories were computed for each of the 37 values of Ecl, spanning the 50–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 interval on an uneven energy grid with a higher point density at low energies. All trajectories were initiated at a separation of R = 50 Å. Vibrational energy levels were taken from the JnK model,53 and matrix coupling elements were obtained from the vibrational wavefunctions following the procedure described by Hong et al.15
000 cm−1 interval on an uneven energy grid with a higher point density at low energies. All trajectories were initiated at a separation of R = 50 Å. Vibrational energy levels were taken from the JnK model,53 and matrix coupling elements were obtained from the vibrational wavefunctions following the procedure described by Hong et al.15
Fig. 6 presents the collisional relaxation rate coefficients corresponding to the loss of one (top panel), two (middle panel), and three (bottom panel) vibrational quanta over the studied temperature range. As expected, in all cases the rate coefficients increase with both the initial vibrational level—owing to the decreasing energy gap—and temperature. The latter dependence is more pronounced at low temperatures and for low vibrational states: the rate coefficients reach a plateau at progressively lower temperatures as vi increases. Consequently, vibrational relaxation proceeds more rapidly for highly excited vibrational states at low temperatures (as expected from the stronger direct coupling between such states), while becoming nearly independent of vi at high temperature. This temperature trend becomes increasingly pronounced as Δv grows, and the corresponding rate coefficients decrease in magnitude. The combined effect of these behaviours produces a larger variation in the rate coefficients across the temperature range for the lowest vibrational states, as illustrated in Fig. S3 in SI.
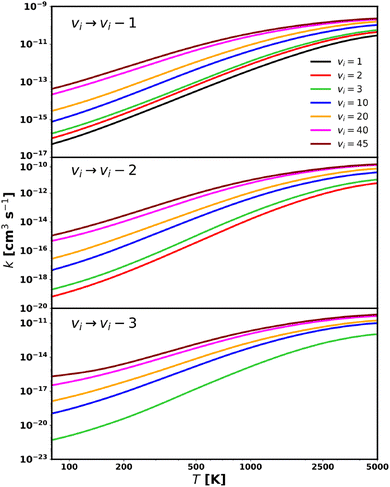 | ||
| Fig. 6 MQC rate coefficients for CS(v) + He → CS(v–Δv) + He calculated for selected v as a function of temperature. | ||
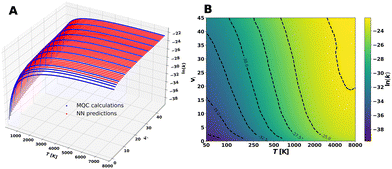
The dataset was completed by using the NN model as described in Section 4. Panel A of Fig. 7 shows both the MQC calculated and the predicted NN rate coefficients for the CS(vi) + He → CS(vi − 1) + He transitions, while panel B shows the corresponding contour plot, illustrating that the NN predicted values smoothly fill in the calculated ones across the full vibrational range. Similar plots for the vi → vi − 2 and vi → vi − 3 transitions are provided in the SI (Fig. S4 and S5) and exhibit the same overall behaviour. All the rate coefficients are available, together with the NN models, at ref. 74.
6 Conclusions and further remarks
In this work, we employed a mixed quantum–classical (MQC) approach combined with a neural network (NN) scheme to construct a complete dataset for the vibrational relaxation of the CS molecule in collisions with He atoms over the 80–5000 K temperature range. Selected vibrational transitions were explicitly calculated using the MQC method, whose performance was preliminarily assessed by comparison with ro-vibrational rate coefficients obtained from the VCC-IOS approach. The agreement between the two methods is generally good, particularly for low initial rotational states. The main difference lies in their dependence on the initial rotational excitation: while VCC-IOS rate coefficients are largely independent of the initial rotational quantum number, the MQC results exhibit a moderate increase with rotational excitation.A new analytical potential energy surface (PES) was developed using physically meaningful parameters and is expected to remain reliable even for highly excited vibrational states. The MQC-calculated rate coefficients display the expected physical behaviour, increasing with both temperature and initial vibrational level. The NN approach was then applied to extend and complete the MQC dataset, yielding a smooth and physically consistent representation across the full vibrational and temperature ranges.
The resulting MQC + NN dataset provides a coherent description of CS–He collisional vibrational relaxation under a wide range of conditions relevant to astrophysical and (exo)planetary environments. This work highlights the potential of hybrid MQC (or semiclassical) and machine-learning strategies for producing accurate and comprehensive collisional datasets for complex molecular systems.
Future studies will explore the application of this approach to generate large datasets of rotationally state-resolved rate coefficients for vibrational transitions, particularly in regimes where the rotational dynamics exhibit predominantly classical behaviour.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
The data supporting this article, including the routine for the analytical PES, are available as part of the supplementary information (SI) or can be found in the following repositories: Neural Network codes: CurveFittingML, 2022, https://github.com/lstorchi/CurveFittingML. Trained Neural Network models and rate coefficient datasets: M. Pezzella, F. Pirani, M. Bartolomei, Q. Hong, F. Lique, L. Storchi and C. Coletti, DATA related to: Vibrational relaxation rate coefficients in CS–He collisions up to the dissociation limit: mixed quantum-classical calculations and neural network predictions, 2025, https://doi.org/10.5281/zenodo.17554162. Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04424c.Appendix
Appendix A: Formulation of the analytical PES
The analytical semi-empirical potential, Vanal, is made of three components:| Vanal = Vind + VILJ + Vrep. | (14) |
The first term describes the induction contribution (Vind) that arises from the interaction between the permanent dipole of CS (μCS) and the induced dipole on helium that depends on its polarizability (αHe). This contribution is represented by the following semiempirical formula:75
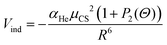 | (15) |
| μCS = 0.7758 − 1.45Δr + 0.3Δr2 + 0.45Δr3 − 0.17Δr4 | (16) |
VILJ represents the contribution to the interaction arising from the balance between the short-range atom-molecule size repulsion and the long-range dispersion attraction. It has been modelled according to the improved Lennard-Jones (ILJ) formulation.44
The VILJ contribution is expressed as the sum of pairwise interactions between He with C and S atoms. For each component, it takes the following form:
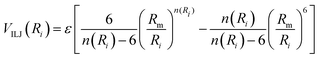 | (17) |
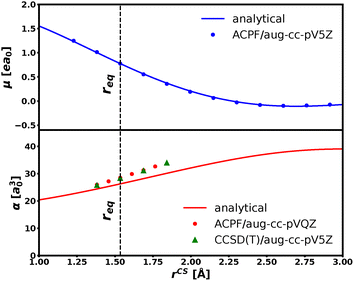 | ||
| Fig. 8 CS dipole moment (upper panel) and molecular polarizability (lower panel) as a function of the intramolecular distance. Solid lines correspond to the analytical expressions (see text). | ||
The term n(Ri) is:
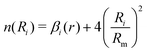 | (18) |
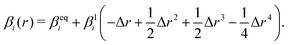 | (19) |
CS is characterized by a very large equilibrium distance. Its outer electronic charge distribution is highly anisotropic, defining the strength of the repulsion at each orientation angle Θ, and it cannot be represented as a combination of two spheres contributions related to the size of the two atoms. Accordingly, the sum of the two VILJ(Ri) components, characterizing previous formulations, has been corrected here with the addition of the term Vrep(r, Θ), which varies significantly with both the intermolecular distance and the molecular orientation:
Vrep(r, Θ) = crepe−3R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin6(Θ). sin6(Θ).
| (20) |
For the two interacting pairs, the adopted ε and Rm, evaluated at the equilibrium distance req, and the other potential parameters are given in Table 1. Note that the zeroth order values of ε and Rm, predicted by the atomic polarizabilities of the interacting pairs, have been fine-tuned (Rm by 2–3% and ε by 10–15%) to achieve the best comparison with the ab initio points.
| Parameter | Value |
|---|---|
| rCSeq (Å) | 1.5346 |
| μrCSeq (ea0) | 0.7758 |
| RS–Hem (Å) | 3.74 |
| RC–Hem (Å) | 3.85 |
| εS–He (meV) | 2.00 |
| εC–He (meV) | 1.28 |
| βeqS–He | 8.0 |
| βeqC–He | 8.2 |
| β1S–He | 2.0 |
| β1C–He | 6.0 |
| crep (meV) | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
The new PES behaves correctly upon deformation of the CS bond thanks to the physically meaningful parameters of its formulation. This is clear from the trend of the analytical expressions for the CS polarizability and dipole moment as a function of r (Fig. 8). These values are in good agreement with the ab initio predictions.
Acknowledgements
L. S., M. P. and C. C. acknowledge support by Fondazione ICSC, Spoke 3 Astrophysics and Cosmos Observations. National Recovery and Resilience Plan (Piano Nazionale di Ripresa e Resilienza, PNRR) Project ID CN_00000013 “Italian Research Center on High-Performance Computing, Big Data and Quantum Computing” funded by MUR Missione 4 Componente 2 Investimento 1.4: Potenziamento strutture di ricerca e creazione di “campioni nazionali di R&S (M4C2-19)” – Next Generation EU (NGEU) and the CINECA award under the ISCRA C initiative, grant IsCc7, for granting the high performance computing resources. M. B. acknowledges the Grant No. PID2024-155666NB-I00 of the Ministerio de Ciencia, Innovación y Universidades (Spain) for funding. Q. H. acknowledges funding from the Chinese Academy of Sciences Project for Young Scientists in Basic Research (Grant No. YSBR-107). F. L. thanks financial support the PNP program (INSU CNRS).References
- I. V. Adamovich and W. R. Lempert, Plasma Phys. Controlled Fusion, 2014, 57, 014001 CrossRef.
- R. Celiberto, I. Armenise, M. Cacciatore, M. Capitelli, F. Esposito, P. Gamallo, R. K. Janev, A. Laganà, V. Laporta, A. Laricchiuta, A. Lombardi, M. Rutigliano, R. Sayós, J. Tennyson and J. M. Wadehra, Plasma Sources Sci. Technol., 2016, 25, 033004 CrossRef.
- C. D. Pintassilgo and V. Guerra, J. Phys. Chem. C, 2016, 120, 21184–21201 CrossRef CAS.
- A. V. Pavlov, Geomagn. Aeron., 2011, 51, 143–169 CrossRef.
- V. Yankovsky and E. Vorobeva, Atmosphere, 2020, 11, 116 CrossRef CAS.
- M. Keidar, Plasma Sources Sci. Technol., 2015, 24, 033001 CrossRef.
- E. Roueff and F. Lique, Chem. Rev., 2013, 113, 8906–8938 CrossRef CAS PubMed.
- J. Tennyson, S. N. Yurchenko, J. Zhang, C. A. Bowesman, R. P. Brady, J. Buldyreva, K. L. Chubb, R. R. Gamache, M. N. Gorman, E. R. Guest, C. Hill, K. Kefala, A. Lynas-Gray, T. M. Mellor, L. K. McKemmish, G. B. Mitev, I. I. Mizus, A. Owens, Z. Peng, A. N. Perri, M. Pezzella, O. L. Polyansky, Q. Qu, M. Semenov, O. Smola, A. Solokov, W. Somogyi, A. Upadhyay, S. O. Wright and N. F. Zobov, J. Quant. Spectrosc. Radiat. Transfer, 2024, 326, 109083 CrossRef CAS.
- M. Capitelli, I. Armenise, E. Bisceglie, D. Bruno, R. Celiberto, G. Colonna, G. D’Ammando, O. De Pascale, F. Esposito and C. Gorse, et al., Plasma Chem. Plasma Process., 2012, 32, 427–450 CrossRef CAS.
- M. González-Martínez, W. Arbelo-González, J. Rubayo-Soneira, L. Bonnet and J.-C. Rayez, Chem. Phys. Lett., 2008, 463, 65–71 CrossRef.
- D. S. Lambrecht, G. N. I. Clark, T. Head-Gordon and M. Head-Gordon, J. Phys. Chem. A, 2011, 115, 5928–5935 CrossRef CAS PubMed.
- G. D. Billing, Comput. Phys. Commun., 1984, 32, 45–62 CrossRef CAS.
- G. D. Billing, Comput. Phys. Rep., 1984, 1, 237–296 CrossRef CAS.
- B. Mandal, D. Bostan, C. Joy and D. Babikov, Comput. Phys. Commun., 2024, 294, 108938 CrossRef CAS.
- Q. Hong, L. Storchi, Q. Sun, M. Bartolomei, F. Pirani and C. Coletti, J. Chem. Theory Comput., 2023, 19, 8557–8571 CrossRef CAS PubMed.
- M. Kirste, L. Scharfenberg, J. Kłos, F. Lique, M. H. Alexander, G. Meijer and S. Y. T. van de Meerakker, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 042717 CrossRef.
- Y. Ajili, K. Hammami, N. E. Jaidane, M. Lanza, Y. N. Kalugina, F. Lique and M. Hochlaf, Phys. Chem. Chem. Phys., 2013, 15, 10062–10070 RSC.
- F. Daniel, M. Gérin, E. Roueff, J. Cernicharo, N. Marcelino, F. Lique, D. C. Lis, D. Teyssier, N. Biver and D. Bockelée-Morvan, Astron. Astrophys., 2013, 560, A3 CrossRef.
- T. Stoecklin, O. Denis-Alpizar and P. Halvick, Mon. Not. R. Astron. Soc., 2015, 449, 3420–3425 CrossRef CAS.
- O. Denis-Alpizar and T. Stoecklin, Mon. Not. R. Astron. Soc., 2015, 451, 2986–2990 CrossRef CAS.
- O. Denis-Alpizar, T. Stoecklin, A. Dutrey and S. Guilloteau, Mon. Not. R. Astron. Soc., 2020, 497, 4276–4281 CrossRef CAS.
- Q. Hong, M. Bartolomei, C. Coletti, A. Lombardi, Q. Sun and F. Pirani, Molecules, 2021, 26, 7152 CrossRef CAS PubMed.
- Q. Hong, Q. Sun, M. Bartolomei, F. Pirani and C. Coletti, Phys. Chem. Chem. Phys., 2020, 22, 9375–9387 RSC.
- Q. Hong, Q. Sun, F. Pirani, M. A. Valentín-Rodríguez, R. Hernández-Lamoneda, C. Coletti, M. I. Hernández and M. Bartolomei, J. Chem. Phys., 2021, 154, 064304 CrossRef CAS PubMed.
- Q. Hong, L. Storchi, C. Coletti, J. Li, Q. Sun and J. Li, J. Chem. Phys., 2024, 160, 084305 CrossRef CAS PubMed.
- Q. Hong, M. Bartolomei, F. Pirani, Q. Sun and C. Coletti, J. Chem. Phys., 2025, 162, 114308 CrossRef CAS PubMed.
- A. Penzias, P. Solomon, R. Wilson and K. Jefferts, Astrophys. J., 1971, 168, L53 CrossRef CAS.
- R. N. Martin and A. H. Barrett, Astrophys. J. Lett., 1975, 202, L83–L86 CrossRef CAS.
- C. Henkel and J. Bally, Astron. Astrophys., 1985, 150, L25–L27 CAS.
- K. Drdla, G. R. Knapp and E. F. van Dishoeck, Astrophys. J., 1989, 345, 815 CrossRef CAS.
- C. Sánchez Contreras, V. Bujarrabal and J. Alcolea, Astron. Astrophys., 1997, 327, 689–698 Search PubMed.
- M. Agúndez, J. P. Fonfría, J. Cernicharo, C. Kahane, F. Daniel and M. Guélin, Astron. Astrophys., 2012, 543, A48 CrossRef.
- R. Le Gal, K. I. Öberg, R. A. Loomis, J. Pegues and J. B. Bergner, Astrophys. J., 2019, 876, 72 CrossRef CAS.
- S.-M. Tsai, E. K. Lee, D. Powell, P. Gao, X. Zhang, J. Moses, E. Hébrard, O. Venot, V. Parmentier and S. Jordan, et al., Nature, 2023, 617, 483–487 CrossRef CAS PubMed.
- F. Lique, A. Spielfiedel and J. Cernicharo, Astron. Astrophys., 2006, 451, 1125–1132 CrossRef CAS.
- F. Lique and A. Spielfiedel, Astron. Astrophys., 2007, 462, 1179–1185 CrossRef CAS.
- O. Denis-Alpizar, T. Stoecklin, P. Halvick, M.-L. Dubernet and S. Marinakis, J. Chem. Phys., 2012, 137, 234301 CrossRef PubMed.
- O. Denis-Alpizar, T. Stoecklin, P. Halvick and M.-L. Dubernet, J. Chem. Phys., 2013, 139, 204304 CrossRef PubMed.
- O. Denis-Alpizar, T. Stoecklin, S. Guilloteau and A. Dutrey, Mon. Not. R. Astron. Soc., 2018, 478, 1811–1817 CrossRef CAS.
- B. Yang, P. Zhang, C. Qu, P. C. Stancil, J. M. Bowman, N. Balakrishnan and R. C. Forrey, Phys. Chem. Chem. Phys., 2018, 20, 28425–28434 RSC.
- R. Goldflam, D. J. Kouri and S. Green, J. Chem. Phys., 1977, 67, 5661–5675 CrossRef CAS.
- R. Goldflam, S. Green and D. Kouri, J. Chem. Phys., 1977, 67, 4149–4161 CrossRef CAS.
- M. L. Dubernet, C. Boursier, O. Denis-Alpizar, Y. A. Ba, N. Moreau, C. M. Zwölf, M. A. Amor, D. Babikov, N. Balakrishnan, C. Balança, M. Ben Khalifa, A. Bergeat, C. T. Bop, L. Cabrera-González, C. Cárdenas, A. Chefai, P. J. Dagdigian, F. Dayou, S. Demes, B. Desrousseaux, F. Dumouchel, A. Faure, R. C. Forrey, J. Franz, R. M. García-Vázquez, F. Gianturco, A. Godard Palluet, L. González-Sánchez, G. C. Groenenboom, P. Halvick, K. Hammami, F. Khadri, Y. Kalugina, I. Kleiner, J. Klos, F. Lique, J. Loreau, B. Mandal, B. Mant, S. Marinakis, D. Ndaw, P. Pirlot Jankowiak, T. Price, E. Quintas-Sánchez, R. Ramachandran, E. Sahnoun, C. Santander, P. C. Stancil, T. Stoecklin, J. Tennyson, F. Tonolo, R. Urzúa-Leiva, B. Yang, E. Yurtsever and M. Zóltowski, Astron. Astrophys., 2024, 683, A40 CrossRef CAS.
- F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- P. Ehrenfest, Z. Phys., 1927, 45, 455–457 CrossRef.
- R. Ram, P. Bernath and S. Davis, J. Mol. Spectrosc., 1995, 173, 146–157 CrossRef CAS.
- H. Uehara, K. Horiai and Y. Sakamoto, J. Mol. Spectrosc., 2015, 313, 19–39 CrossRef CAS.
- N. R. Crockett, E. A. Bergin, J. L. Neill, C. Favre, P. Schilke, D. C. Lis, T. A. Bell, G. Blake, J. Cernicharo, M. Emprechtinger, G. B. Esplugues, H. Gupta, M. Kleshcheva, S. Lord, N. Marcelino, B. A. McGuire, J. Pearson, T. G. Phillips, R. Plume, F. van der Tak, B. Tercero and S. Yu, Astrophys. J., 2014, 787, 112 CrossRef.
- C. A. Bowesman, S. N. Yurchenko, A. Al-Refaie and J. Tennyson, TIRAMISU: Non-LTE radiative transfer for molecules in exoplanet atmospheres, 2025, https://arxiv.org/abs/2508.12873 Search PubMed.
- C. C. Marston and G. G. Balint-Kurti, J. Chem. Phys., 1989, 91, 3571–3576 CrossRef CAS.
- R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 158–166 CrossRef CAS.
- M. Bogey, C. Demuynck and J. Destombes, J. Mol. Spectrosc., 1982, 95, 35–42 CrossRef CAS.
- G. Paulose, E. J. Barton, S. N. Yurchenko and J. Tennyson, Mon. Not. R. Astron. Soc., 2015, 454, 1931–1939 CrossRef CAS.
- J. A. Coxon and P. G. Hajigeorgiou, Chem. Phys., 1992, 167, 327–340 CrossRef CAS.
- T. Furtenbacher, A. G. Császár and J. Tennyson, J. Mol. Spectrosc., 2007, 245, 115–125 CrossRef CAS.
- R. J. Le Roy, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 167–178 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- H.-J. Werner, B. Follmeg and M. H. Alexander, J. Chem. Phys., 1988, 89, 3139–3151 CrossRef CAS.
- J. Yang, Q. Hong, M. Bartolomei, C. Coletti, F. Pirani, Q. Sun and J. Li, Phys. Rev. A, 2025, 111, 032804 CrossRef CAS.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1999, 302, 437–446 CrossRef CAS.
- M. Bartolomei, E. Carmona-Novillo, M. I. Hernández, J. Campos-Martínez and R. Hernández-Lamoneda, J. Comput. Chem., 2011, 32, 279–290 CrossRef CAS PubMed.
- M. Bartolomei, F. Pirani, A. Laganà and A. Lombardi, J. Comput. Chem., 2012, 33, 1806–1819 CrossRef CAS PubMed.
- A. Lombardi, F. Pirani, A. Laganà and M. Bartolomei, J. Comput. Chem., 2016, 37, 1463–1475 CrossRef CAS PubMed.
- A. Lombardi, F. Pirani, M. Bartolomei, C. Coletti and A. Laganà, Front. Chem., 2019, 7, 309 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby, M. Schütz, P. Celani, T. Korona, G. Rauhut, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni and T. Thorsteinsson, MOLPRO, Version 2012.1, a Package of Ab Initio Programs, 2012, see https://www.molpro.net Search PubMed.
- J. Arnold, J. C. San Vicente Veliz, D. Koner, N. Singh, R. J. Bemish and M. Meuwly, J. Chem. Phys., 2022, 156, 034301 CrossRef CAS PubMed.
- Q. Hong, L. Storchi, M. Bartolomei, F. Pirani, Q. Sun and C. Coletti, Eur. Phys. J. D, 2023, 77, 128 CrossRef CAS.
- J. Yang, J. Li, J. Li and J. Li, J. Phys. Chem. A, 2024 Search PubMed.
- D. Bossion, G. Nyman and Y. Scribano, Artif. Intell. Chem., 2024, 2, 100052 CrossRef.
- L. Storchi, CurveFittingML, 2022, https://github.com/lstorchi/CurveFittingML Search PubMed.
- D. R. Flower, Mon. Not. R. Astron. Soc., 2012, 425, 1350–1356 CrossRef CAS.
- M. Pezzella, F. Pirani, M. Bartolomei, Q. Hong, F. Lique, L. Storchi and C. Coletti, DATA related to: Vibrational relaxation rate coefficients in CS–He collisions up to the dissociation limit: mixed quantum-classical calculations and neural network predictions, 2025, DOI:10.5281/zenodo.17554162.
- G. C. Maitland, M. Rigby, E. B. Smith and W. A. Wakeham, Intermolecular Forces: Their Origin and Determination, Clarendon Press, Oxford, 1987 Search PubMed.
- R. Cambi, D. Cappelletti, G. Liuti and F. Pirani, J. Chem. Phys., 1991, 95, 1852–1861 CrossRef CAS.
- T. N. Olney, N. Cann, G. Cooper and C. Brion, Chem. Phys., 1997, 223, 59–98 CrossRef CAS.
- M. Capitelli, D. Cappelletti, G. Colonna, C. Gorse, A. Laricchiuta, G. Liuti, S. Longo and F. Pirani, Chem. Phys., 2007, 338, 62–68 CrossRef CAS.
| This journal is © the Owner Societies 2026 |