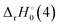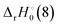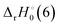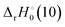Thermodynamic insight into AnO2+ bonding from ThH+/UH+ reactions studied by inductively coupled plasma tandem mass spectrometry
Received
14th November 2025
, Accepted 12th January 2026
First published on 22nd January 2026
Abstract
The bonding mechanisms of actinides have been a focus of fundamental research over the past few decades. In the present study, reactions of the simplest actinide-containing species, ThH+ and UH+, with O2 and CO2 are investigated by inductively coupled plasma tandem mass spectrometry. The reactions of ThH+ and UH+ with O2 are efficient, and the reactions of ThH+ and UH+ with CO2 display reduced reaction efficiencies. For both reactions involving CO2, ThO2+ and UO2+ are observed; however, there is a clear barrier to ThO2+ formation whereas UO2+ forms through an exothermic, barrierless process. The experimental observations and available thermodynamic information are used to predict the outcomes of reactions involving the later AnH+. The anticipated reaction enthalpies for Pa–Am display a clear correlation with the promotion energy of An+ to a 6d2 electronic configuration, Ep(6d2), although a shift in the slope of the correlation of reaction enthalpies and Ep(6d2) suggests that there is likely a change in bonding mechanism that starts with Np+. Similar shifts have also been noted in previous studies. Beginning with Np+, the 6d orbitals become less accessible than they are for the earlier An+ as measured by Ep(6d2), and this accessibility of the 6d orbitals may drive actinide bonding.
Introduction
The actinides (An) are commonly associated with nuclear applications, but from a fundamental perspective, An compose the bottom edge of the periodic table and display complex chemical behavior that is still not well understood. Experimental investigations of the factors that guide An reactivity and bonding remain limited. Gas-phase studies offer a direct route to examine the intrinsic chemistry of the actinides (free of perturbative solvent effects) that can provide and explain trends in bonding and reactivity across the An series.1
The simplest actinide-containing species, An–H, has been studied using several gas-phase techniques. Surface ionization mass spectrometry was used for the isotopic analysis of U and Pu and led to the observation of UH+ and PuH+,2 where the bond dissociation energy of UH+, D0(U+–H) was estimated to be 3.3 ± 0.5 eV. Early ion beam mass spectrometry enabled an examination of the energy dependences of the reactions of U+ with D2 and CD4 leading to the formation of UD+.3 The bond dissociation energy of UH+ was measured and reported as D0(U+–H) = 2.9 ± 0.2 eV. The infrared spectra of ThH and UH in noble gas matrices have also been reported, and complementary density functional theory (DFT) calculations included in those studies were used to characterize and assign the observed bands as well as provide mechanistic insight into product formation and reaction energetics.4,5
Fourier transform ion cyclotron resonance mass spectrometry (FTICR-MS) experiments enabled the formation of UH+, NpH+, PuH+, AmH+, and CmH+ as minor products in reactions of An2+ with various hydrocarbons.6 A subsequent study presented theoretical potential energy surfaces (PES) that mostly explained the observations noted in the FT-ICR MS experiments.7 Guided ion beam tandem mass spectrometry (GIBMS) was used to study the reactions of Th+ with CH4 and H2O.8,9 ThH+ was observed as a high energy product in both studies. Subsequent GIBMS studies of the reactions of Th+ and U+ with H2 led to the determination of the BDEs of ThH+ and UH+, D0(Th+–H)10 = 2.45 ± 0.07 eV and D0(U+–H)11 = 2.48 ± 0.06 eV. Experimental measurements of the electron affinities of ThH− and UH− accompanied by high level theoretical calculations have indicated that there is a 0.37 eV discrepancy between the theoretical and experimental D0(Th+–H) value.12,13 The reason for the discrepancy is unclear and remains an open investigation. Results from additional theoretical calculations for AnH0/+/− (An = Ac, Pa, Np, Pu) species have also been reported.12–15 Most recently, the BDEs of AnH+ (An = Th–Am) were experimentally measured by examining the kinetic energy dependence of the reaction An+ + CH4 → AnH+ + CH3.16 Table 1 summarizes the AnH+ thermochemistry published to date. Notably, experimental measurables, like BDEs, can be a key benchmark to help validate computational methods, and these computational methods will likely prove crucial to understanding An bonding.
Table 1 Experimental and theoretical bond dissociation energies (BDE) of AnH+ (in eV)
| D0(An+–H) |
Ep(6d)a |
Experimentalb |
Theoreticalc |
Modeld |
| Ref. 17. Unless noted otherwise ref. 16. FPD calculations of AnH+ BDEs compiled in ref. 15. See also ref. 12–14. Intrinsic BDE model assuming bonding between An+ 6d and H 1s electrons. Presented in ref. 10. Ref. 11. Ref. 3. |
| Th |
0.00 |
2.96 ± 0.81, 2.45 ± 0.07d |
2.82 |
2.45 |
| Pa |
0.10 |
2.94 ± 0.54 |
2.54 |
2.35 |
| U |
0.04 |
2.82 ± 0.71, 2.48 ± 0.06,e 2.9 ± 0.3f |
2.51 |
2.41 |
| Np |
0.00 |
2.87 ± 0.51 |
2.08 |
2.45 |
| Pu |
1.08 |
1.27 ± 0.83 |
0.94 |
1.37 |
| Am |
1.76 |
0.92 ± 0.74 |
|
0.69 |
A key finding of the previous experimental work is that the AnH+ BDEs are correlated to the promotion energy from the ground state to the first state that populates a 6d orbital, Ep(6d),10,16 which mirrors earlier findings that indicate that that D0(Ann+–O) for n = 0–2 are correlated to Ep(6d2).10,16,17 The BDEs of AnF+ also display some correlation to Ep(6d),18 which follows an earlier argument by Cox, Armentrout, and de Jong using previously reported ThF+, UF+, and PuF+ values.10 Recent inductively coupled plasma tandem mass spectrometry (ICP-MS/MS) work has indicated that D0(An+–CH2)16 and D0(An+–N)19 are also correlated to Ep(6d2). The latter had previously been speculated by Armentrout and coworkers.20,21 While this does not rule out the involvement of 5f or 7s orbitals, the 6d orbitals are clearly important to forming actinide-ligand (AnL) bonds.
Notably, the An species described in the previous paragraph have formal oxidation states (II–IV). Theoretical studies have concluded that the 5f orbitals are more active for An in higher oxidation states.22–25 Classic examples include the linear OAnO+ (V) species. Although the electrons of Th+ do not populate the 5f orbitals in the ground state, NBO analyses have shown that 5f orbitals contribute to bonding in OThO+.22 Recent work has suggested that reaction kinetics may be influenced by the participation of 5f orbitals in transient species.26 In that study, the comparison of the reaction kinetics between Pu+/Nd+/Sm+ + NO/CO2 were used to infer 5f orbital participation in the NPuO+ intermediate with corroborating theoretical potential energy surfaces (PES). Likewise, observing the reactions starting from diatomic An species (i.e. AnL+) may shed additional light on when the 5f orbitals are active in AnL bonding.
There are several reports of the reactions of AnO+ with a variety of co-reactants.22,25,27–31 Generally, AnO+ species are less reactive than their An+ counterparts. This may be explained by the reduced availability of electrons because two An+ valence electrons are involved in the robust AnO+ triple bond. Alternatively, AnO+ is likely to have increased steric restrictions compared to An+ and AnH+. AnH+ bonding employs one of the 6d electrons of An+. It is of interest to study the reactions of AnH+ to better understand the role of An+ valence electrons and assess the impact of reduced 6d electron availability upon the observed chemistry. For the simplest polyatomic, AnH+, the reactions of UH+ with background gases32 and nitriles33 have been reported in MSn experiments by Terhorst et al. However, hydrides, like UH+, are a known interference for analytical ICP-MS experiments.34 Here we take advantage of the inductively coupled plasma's (ICP) propensity to create hydrides in the ion source to study the reactions of ThH+ and UH+ with O2 and CO2. We also compare the observed reactions to the analogous AnOn+x (x = 0–1, n = 1–2) reactions to help determine the role of oxidation states in the observed chemistry. Likewise, we discuss the implications of observed thermochemical trends on An bonding.
Experimental and theoretical methods
CAUTION: the An used in this study are all radioisotopes with varying activities and half-lives. All work was done within the radiological protection controls of specialized laboratories at Pacific Northwest National Laboratory.
ICP-MS/MS
Experiments were conducted using an Agilent 8900 ICP-MS/MS located within the physical sciences facility at Pacific Northwest National Laboratory.35 This instrument utilizes an ICP ion source equipped with a quartz double-pass spray chamber and 100 µL min−1 perfluoroalkoxy alkane (PFA) nebulizer. Hydrides are formed within the plasma source, and the resulting ions are focused through an initial quadrupole mass filter where the reactant AnH+ are selected. The reactant ions are then focused into a collision reaction cell containing an octopole ion guide which can be pressurized with a neutral reactant gas, O2 (Oxarc, 99.999%) or CO2 (Oxarc, 99.999%). Residual reactant and product ions are radially confined within the octopole and drift to the exit aperture. Ions are subsequently focused through a second quadrupole mass filter to identify product ions and counted at a standard electron multiplier detector.
Stock multi-element standard solutions containing 10 ng g−1 of Th and U in 2% HNO3 were prepared. Oxygen and carbon dioxide were used as reactant gases. The flow rates of O2 and CO2 were 0.09 and 0.18 mL min−1, and 0.06 and 0.12 mL min−1, respectively. Tuning parameters were optimized to provide maximum sensitivity using a 10 ng g−1 232Th and 238U solution, with focus on increasing hydride formation. The octopole bias was adjusted in 1 V intervals from +7 V to −78 V while keeping other cell parameters constant: octopole RF peak-to-peak voltage of 180 V, axial acceleration of 0 V, and a kinetic energy discrimination (KED, the voltage difference between the octopole bias in the collision reaction cell and the second quadrupole) of −7.0 V. Data were acquired using 3 replicates, 10 sweeps/replicate and 1 s acquisition times.
Absolute reaction cross sections (σ) are calculated from the raw signal intensities using eqn (1)36
where
I is the reactant ion intensity exiting the collision cell,
I0 is the reactant ion intensity entering the collision cell,
ρ is the number density of the neutral reactant in the collision cell, and
l is the effective length of the collision cell. For this work
I0 is estimated as the sum of all observed ions from quadrupole 2. The physical length of the collision cell in the Agilent 8900, 10 cm, is used for
l, although this is not strictly accurate because the pressure gradient will extend beyond the boundaries of the collision cell. The difference is expected to be ≤20% and is included in the total uncertainties reported herein. Individual product ion cross sections (
e.g., MO
+) are calculated as a percentage of the overall reaction cross section. Because the Agilent 8900 operates under multi-collision conditions, to compare the observed cross sections to the reaction collision limit, the cross sections observed at 1.5 and 3.0 mTorr for O
2 and 1.4 and 2.8 mTorr for CO
2 were extrapolated to zero pressure to reflect rigorous single collision conditions. Previously, we have discussed the influences on the expected number of collisions for a given neutral reactant gas and pressure.
31 Following this analysis, the most probable number of collisions is 2–3 at the lowest energies. Although less than ideal, the two-point extrapolation was chosen to balance instrument time and operator exposure while still executing the experiment. Absolute uncertainties in the cross sections are estimated to be ±50% with relative uncertainties of ±20%.
The energy in the laboratory frame is estimated from the octopole bias by eqn (2)37
| | |
ELab = Vp + (m/mAr)(5/2)kBTp − Voct
| (2) |
where
Vp is the plasma potential (∼2 V),
m is the mass of the M
+ reactant ion,
mAr is the mass of argon (the flow gas in the ICP),
kB is Boltzmann's constant,
Tp is the ion electronic temperature entering the octopole, and
Voct is the octopole bias. The temperature of the ion exiting the plasma is expected to be the plasma temperature, 8000–10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 K. Previous work
16,38,39 has indicated that
Tp is between 1000–10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 K for atomic cations. For polyatomic cations, it is less clear what the electronic distribution may be. Presumably, some excess electronic energy from the atomic cations in the source is consumed to create AnH
+, and the electronic state density is likely less dense than the atomic electronic state density.
10–13 Consequently, the average electronic energy available is expected to be less than that available for atomic cations. An assumption is made that there are sufficient crossings between potential energy surfaces that a pathway exists between excited state reactants and ground state products so that excess electronic energy can be treated as energy available for reaction. Theoretical calculations were previously used to examine the low-lying electronic states of ThH
+ and UH
+.
11,13 Based on this work, the electronic energy,
Eel, is
Eel(ThH
+) = 0.37 eV and
Eel(UH
+) = 0.12 eV at 5000 K.
The energy in the center-of-mass (ECM) frame represents the kinetic energy available for a chemical reaction. The relationship between ELAB and ECM is described by eqn (3)36
| | |
ECM = ELAB × M/(M + m)
| (3) |
where
M is the mass of the neutral reactant partner, O
2 (32.00 amu) or CO
2 (44.01) and
m is the mass of the reactant metal hydride ion, ThH
+ (233.04 amu) or UH
+ (239.04 amu).
Experimental results
AnH+ + O2
Fig. 1 displays the absolute reaction cross section of ThH+ with O2 as a function of kinetic energy. Fig. 2 displays the UH+ + O2 cross section. Reactions (4)–(7) were observed:| | |
AnH+ + O2 → AnO+ + OH
| (4a) |
Reactions (4)–(6) are observed as barrierless exothermic processes. The reaction efficiencies (k/kcol) compared to the Su–Chesnavich semiclassical trajectory collision limit cross section40 are k/kcol(ThH+) = 1.52 ± 0.76 and k/kcol(UH+) = 1.26 ± 0.63 calculated as an average from all energies <1 eV. To our knowledge, k/kcol has not been reported for the reactions of ThH+ and UH+ with O2. Guided ion beam tandem mass spectrometry (GIBMS) experiments have reported reaction efficiencies of k/kcol = 1.21 ± 0.24 for Th+ + O241 and k/kcol = 1.1 ± 0.2 for U+ + O2.42 FTICR-MS experiments by Santos et al.27 reported k/kcol = 0.86 ± 0.43 and k/kcol = 0.68 ± 0.34, for the reactions of Th+ and U+ with O2, respectively. Earlier FTICR-MS studies of the same reactions from Cornehl et al.43 reported k/kcol = 1.12 ± 0.45 and k/kcol = 1.17 ± 0.47 for Th+ and U+, respectively. The reaction (4) (ThH+) rate does not appear to be significantly hindered by the H-ligand compared to the atomic rate. A comparison of AnH+ k/kcol to that for An+ and AnO+ is summarized in Table 2.
 |
| | Fig. 1 The absolute reaction cross section of ThH+ + O2 as a function of kinetic energy in the laboratory frame (upper x axis) and center-of-mass frame (lower x axis). The sum of the product cross sections (σtot) is represented by a solid gray line. Individual products are ThO+ (red circles), HThO+ (blue squares), Th+ (green diamonds), and ThO2+ (purple triangles). The Su–Chesnavich semi-classical trajectory (σtraj) collision limit40 is represented by a solid black line. | |
 |
| | Fig. 2 The absolute reaction cross section of UH+ + O2 as a function of kinetic energy in the laboratory frame (upper x axis) and center-of-mass frame (lower x axis). The sum of the product cross sections (σtot) is represented by a solid gray line. Individual products are UO+ (red circles), HUO+ (blue squares), U+ (green diamonds), and UO2+ (purple triangles). The Su–Chesnavich semi-classical trajectory (σtraj) collision limit40 is represented by a solid black line. | |
Table 2 A comparison of Ann+ (An = Th, U; n = 1, 2) and ThL+ and UL+ (L = H, O) reaction efficiencies (k/kcol)a
| AnL+ + OR |
ICP-MS/MSb |
GIBMSc |
FTICR-MSd |
| Reaction efficiencies are calculated relative to the Su–Chesnavich semiclassical trajectory collision limit. See ref. 40. This work for AnH+. Ref. 39 for An+. U2+ can be found in the SI Section. Ref. 22, 25, 31, 41 and 42. Ref. 27, 43 and 44. NR = no observed reaction at lowest energy studied. Calculated from ref. 25. |
| Th+ + O2 |
|
1.21 ± 0.24 |
0.86 ± 0.43; 1.12 ± 0.45 |
| Th2+ + O2 |
|
|
0.56 ± 0.28 |
| ThH+ + O2 |
1.52 ± 0.76 |
|
|
| ThO+ + O2 |
|
NRe |
NRe |
| U+ + O2 |
|
1.1 ± 0.2 |
0.68 ± 0.34; 1.17 ± 0.47 |
| U2+ + O2 |
|
|
0.53 ± 0.26 |
| UH+ + O2 |
1.26 ± 0.63 |
|
|
| UO+ + O2 |
|
1.16 ± 0.23 |
0.45 ± 0.23; 0.95 ± 0.38 |
| Th+ + CO2 |
1.19 ± 0.60 |
0.88 ± 0.18 |
0.35 ± 0.18; 0.95 ± 0.33 |
| Th2+ + CO2 |
|
|
0.55 ± 0.28 |
| ThH+ + CO2 |
0.49 ± 0.25 |
|
|
| ThO+ + CO2 |
|
NRe |
NRe |
| U+ + CO2 |
0.93 ± 0.47 |
1.18 ± 0.24 |
0.29 ± 0.15; 1.02 ± 0.36 |
| U2+ + CO2 |
0.72 ± 0.36 |
|
0.38 ± 0.17 |
| UH+ + CO2 |
0.36 ± 0.18 |
|
|
| UO+ + CO2 |
|
0.02 ± 0.01f |
0.004 ± 0.002; 0.002 ± 0.001 |
The product distribution is also different between ThH+ and UH+. For ThH+ at the lowest energy, the dominant product is ThO+ (reaction (4)). ThO2+ (reaction (6)) is the second most abundant product, while [Th, O, H]+ (reaction (5)) is a minor product. Note that previous theoretical work9,45,46 indicates that [Th, O, H]+ is likely HThO+. This structure will be adopted for future discussion of [An, O, H]+. At slightly higher energies (∼0.5–1.0), HThO+ becomes the second most abundant product. For UH+ at the lowest energy, the dominant product is UO2+ (reaction (6)). UO+ (reaction (4)) is the second most abundant product, while HUO+ (reaction (5)) is a minor product. Product branching remains relatively consistent for energies below 1 eV. Differences in the product distributions likely result from thermodynamic drivers. For example, D0(OU+–O) = 7.56 ± 0.12 eV25 ≫ D0(OTh+–O) = 4.87 ± 0.04 eV,22 so reaction (6) is significantly favored for UH+ compared to ThH+. Reaction thermodynamics are discussed in greater detail below. Product branching ratios are summarized in Table 3. Fig. S1–S4 also break down the branching ratios as a function of kinetic energy.
Table 3 Product branching ratios at select energies ≤1 eV. Relative uncertainty is ±10%
| Reaction |
Product |
0.1 eV |
0.5 eV |
1 eV |
| ThH+ + O2 → |
ThO+ |
0.70 |
0.81 |
0.79 |
| HThO+ |
0.09 |
0.13 |
0.10 |
| ThO2+ |
0.21 |
0.06 |
0.11 |
| |
| UH+ + O2 → |
UO+ |
0.31 |
0.26 |
0.32 |
| HUO+ |
0.04 |
0.04 |
0.06 |
| UO2+ |
0.65 |
0.70 |
0.62 |
| |
| ThH+ + CO2 → |
ThO+ |
0.45 |
0.47 |
0.47 |
| HThO+ |
0.55 |
0.53 |
0.53 |
| ThO2+ |
0.00 |
0.00 |
0.00 |
| |
| UH+ + CO2 → |
UO+ |
0.28 |
0.31 |
0.40 |
| HUO+ |
0.47 |
0.51 |
0.60 |
| UO2+ |
0.25 |
0.18 |
0.00 |
At higher energies the product An+ is observed with apparent thresholds of 1.5 eV for Th+ and 0.8 eV for U+. This likely can be attributed to reaction (7a), which is a collision induced dissociation (CID) reaction. GIBMS work indicates that the threshold for this process should be ≈2.5 eV for both ThH+ and UH+ (see Table 1).10,11,16 Alternatively, the hydroperoxyl radical could be formed through reaction (7b). Given D0(O2–H) = 2.24 ± 0.01 eV, the reaction (7b) threshold should be ≈0.25 eV for both ThH+ and UH+. Exact assignment of the reaction is difficult because the ICP-MS/MS data is extrapolated from multicollisional conditions to “zero pressure” single collision conditions. Previous work has indicated that while this extrapolation is reasonable, the cross section may retain some multicollisional character.16,39 Multicollision conditions may lead to observable artifacts such as an apparent threshold that is shifted to lower energies relative to the thermodynamic threshold. Furthermore, AnH+ can be partially activated upon collision storing some energy within rovibrational modes so that subsequent collisions may remove the ligand at lower energies. By contrast, competition with the more favorable reactions (4)–(6) may also delay the onset of reaction (7b). Consequently, An+ may be formed through either mechanism; nevertheless, the observed thresholds in Fig. 1 and 2 are consistent with D0(Th+–H) = 2.45 ± 0.07 eV and D0(U+–H) = 2.48 ± 0.06 eV reported in GIBMS studies.10,11
AnH+ + CO2
Fig. 3 and 4 display the absolute reaction cross section of ThH+ and UH+ with CO2 as a function of kinetic energy. Reactions (8)–(11) were observed:| | |
AnH+ + CO2 → AnO+ + OCH
| (8a) |
The observed reaction efficiencies are k/kcol(ThH+) = 0.49 ± 0.25 and k/kcol(UH+) = 0.36 ± 0.18. Like AnH+ + O2, the reaction of AnH+ with CO2 has not been previously reported. The reactions of An+ + CO2 have been previously reported for ICP-MS/MS, GIBMS, and FTICR-MS.25,27,30,31,39 Reaction efficiencies are listed in Table 2. For the atomic cations, ICP-MS/MS,39 GIBMS,31 and FTICR-MS43 reported values agree very well with the exception of the FTICR-MS efficiencies reported by Santos et al.27 The AnH+ reaction efficiencies are significantly reduced from the atomic reaction efficiencies. Table 2 also lists k/kcol for AnO+ reported from GIBMS and FTICR-MS experiments.25,27,31,43,44 While k/kcol(AnH+) is significantly reduced from k/kcol(An+), k/kcol(AnH+) ≫ k/kcol(AnO+), see Table 2. For ThO+ + CO2, D0(OTh+–O) = 4.87 ± 0.04 eV22 < D0(OC–O) = 5.45 eV,47 so no reaction is expected. However, D0(OU+–O) = 7.56 ± 0.12 eV25 ≫ D0(OC–O) = 5.45 eV, so thermodynamics do not explain the low reaction efficiency. Note also that by GIBMS,31 which measures the reaction energy dependence, the observed reaction threshold (E0) for ThO+ + CO2 did not match the thermodynamic threshold, which indicates the presence of some barrier to reaction.
 |
| | Fig. 3 The absolute reaction cross section of ThH+ + CO2 as a function of kinetic energy in the laboratory frame (upper x axis) and center-of-mass frame (lower x axis). The sum of the product cross sections (σtot) is represented by a solid gray line. Individual products are ThO+ (red circles), HThO+ (blue squares), Th+ (green diamonds), and ThO2+ (purple triangles). The Su–Chesnavich semi-classical trajectory (σtraj) collision limit40 is represented by a solid black line. | |
 |
| | Fig. 4 The absolute reaction cross section of UH+ + CO2 as a function of kinetic energy in the laboratory frame (upper x axis) and center-of-mass frame (lower x axis). The sum of the product cross sections (σtot) is represented by a solid gray line. Individual products are UO+ (red circles), HUO+ (blue squares), U+ (green diamonds), and UO2+ (purple triangles). The Su–Chesnavich semi-classical trajectory (σtraj) collision limit40 is represented by a solid black line. | |
Unlike AnH+ + O2, the primary reaction observed with CO2 was reaction (9). For ThH+, HThO+ was slightly favored by HThO+/ThO+ = 55/45 for all energies ≤1 eV. For UH+, the branching is HUO+/UO+ = 60/40 (note UO2+ has been removed for two energies, see Table 3) for all energies ≤1 eV. Reaction (10) was observed for UH+ at the lowest energies, but this product was no longer observed by 1 eV with a rapid decline occurring at ≈0.4 eV. A slight increase in the reaction (8) cross section occurs in this region, which may suggest a connection between the two channels, possibly loss of an O ligand from AnO2+, but the energy resolution in Fig. 4 is not sufficient to definitively establish this argument. Reaction (10) is not observed until higher energies for ThH+ with an apparent threshold of 2 eV. Reaction (11) is presumably a CID reaction, although the formation of HCO2 is conceivably possible. Apparent thresholds of 1.5 and 1 eV were observed for ThH+ and UH+, respectively. Despite the possible multicollisional character retained in the reaction (11) cross sections, these observed thresholds are likely consistent with the established BDEs of ThH+ and AnH+.
Discussion
Comparison of reaction rates
The reaction efficiencies of Ann+ (An = Th, U; n = 1, 2) and AnL+ (L = H, O) with O2 and CO2 from ICP-MS/MS,39 GIBMS,22,25,31,41,42 and FTICR-MS27,43,44 reactions are listed in Table 2. For these reactions, the precursor ion includes An in nominal oxidation states of I–III. ICP-MS/MS data available for the reaction U2+ + CO2 is also included in Table 2. The cross section for this reaction can be found in Fig. S5 in the SI Section.
In general, the observed ICP-MS/MS k/kcol for atomic cations matches reasonably well with the GIBMS measurements within experimental uncertainty. Likewise, the observed efficiencies from ICP-MS/MS are consistent with the Cornehl et al. FTICR-MS43 results. The FTICR-MS results from Gibson and coworkers are an average factor of 3 ± 1 times lower than the GIBMS and ICP-MS/MS values, Table 3. The difference between GIBMS and FTICR-MS k/kcol have been noted previously.31 Discrepancies between the reaction efficiencies reported by ICP-MS/MS, GIBMS, and FTICR-MS can likely be attributed to differences in the starting electronic energy distributions and collision conditions achieved by each of the methods.
The FTICR-MS work from Gibson and coworkers27,44 are the most complete for An (I–III) starting oxidation states. For the reactions ThO+ + O2/CO2, no reaction was observed. This result is not surprising because both reactions are endothermic as confirmed by GIBMS experiments.22,31 All other reactions were observed by FTICR-MS. For Ann+ + O2 (n = 1, 2) the reaction efficiency decreases slightly with increasing oxidation state (although with overlapping uncertainty). For UO+ + O2, the reaction efficiency also decreases slightly but is still within uncertainty of both Un+ (n = 1, 2) reactions. By contrast, the efficiency of UOx+ (x = 0, 1) + O2 measured by GIBMS are identical within experimental uncertainty.42 The FTICR-MS reaction trend for Ann+ (n = 1, 2) + CO2 appears to be reversed, yet the efficiency for UO+ + CO2 is significantly reduced compared to Un+ + CO2. This result is echoed in the GIBMS report.25
At present, a complete reaction set is not available for ICP-MS/MS. Assuming that the ICP-MS/MS reaction efficiencies are similar to those reported by GIBMS, then the reaction efficiency may increase slightly for AnH+ + O2 compared to An+ + O2 but would be within the combined experimental uncertainties. A similar result may be expected for An2+ given the historical differences between FTICR-MS, GIBMS, and ICP-MS/MS. Reaction enthalpies calculated from AnOn+x (n = 0–2; x = 1, 2) values compiled by Marçalo and Gibson17 indicate that all the O2 reactions in Table 2 will have similar thermodynamic drivers (except ThO+ + O2). Likewise, Table 4 indicates that the thermodynamics associated with AnH+ reactions with O2 will be similar. For the CO2 reactions in Table 2, there is a substantial difference between An+ + CO2 and AnH+ + CO2 reaction efficiencies. Table 4 indicates ≈0.5 eV difference in reaction enthalpies.
Table 4 Bond dissociation energies of X–L and LX–O (X = C, O, An+, L = H, O) and reaction enthalpies in eV
| X |
D0(X–H)a |
D0(X–O)b |
D0(OX–H)c |
D0(OX–O)b |
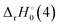
d |
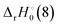
e |
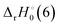
f |
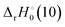
g |
| Ref. 16 unless indicated otherwise. Ref. 17 unless indicated otherwise. NIST Chemistry Webbook unless indicated otherwise. See eqn (12). See eqn (13). See eqn (16). See eqn (17). Ref. 10. Ref. 41. Ref. 22. Ref. 11. Ref. 42. Ref. 25. |
| C |
3.53c |
11.09c |
1.81 |
5.45c |
|
|
|
|
| O |
4.44c |
5.11c |
2.24 |
|
|
|
|
|
| Th+ |
2.45 ± 0.07h |
8.57 ± 0.14i |
|
4.87 ± 0.04j |
−5.45 ± 0.16 |
−2.48 ± 0.16 |
−5.88 ± 0.16 |
2.02 ± 0.16 |
| Pa+ |
2.94 ± 0.54 |
8.29 ± 0.52 |
|
8.08 ± 0.30 |
−4.68 ± 0.75 |
−1.71 ± 0.75 |
−8.33 ± 0.81 |
−0.43 ± 0.81 |
| U+ |
2.48 ± 0.06k |
8.01 ± 0.13l |
|
7.56 ± 0.12m |
−4.87 ± 0.15 |
−1.90 ± 0.15 |
−7.99 ± 0.19 |
−0.09 ± 0.19 |
| Np+ |
2.87 ± 0.51 |
7.88 ± 0.10 |
|
6.32 ± 0.23 |
−4.34 ± 0.52 |
−1.37 ± 0.52 |
−6.22 ± 0.57 |
1.68 ± 0.57 |
| Pu+ |
1.27 ± 0.83 |
6.75 ± 0.20 |
|
5.28 ± 0.39 |
−4.81 ± 0.85 |
−1.84 ± 0.85 |
−5.64 ± 0.94 |
2.26 ± 0.94 |
| Am+ |
0.92 ± 0.74 |
5.80 ± 0.29 |
|
4.25 ± 0.58 |
−4.21 ± 0.79 |
−1.24 ± 0.79 |
−4.02 ± 0.98 |
3.88 ± 0.98 |
The thermodynamics of the reactions observed in this work are discussed in greater detail in the next section. Table S1 also compiles the thermodynamic information for the reactions listed in Table 2. For An ≥ Np+, there is a significant difference in thermodynamics between oxidation states. Marçalo and Gibson tie this difference to Ep(6d2).17 Because Ep(6d2) are a rough measure of the energy of the 6d orbitals relative to the 5f orbitals populated in most Ann+ ground states, the difference between reactivity observed in Table 2 may be a function of the accessibility of the 6d orbitals. Conversely, the difference between An reactivity with O2 and CO2 follow similar trends regardless of the An oxidation state. The reduced reactivity of CO2 has been discussed in greater detail previously but has been tied to the weak interaction of a late intermediate along the potential energy surface.26,31,39,48
An+ thermochemistry
Most observed reactions are clearly exothermic reactions that seemingly will only provide upper or lower limits to BDEs. Nevertheless, the reactions here may refine existing or provide new thermodynamic values. The expected reaction enthalpies are discussed below.
The reaction enthalpy 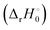 for the ligand exchange reactions, reactions (4) and (8), are:
for the ligand exchange reactions, reactions (4) and (8), are:
| |
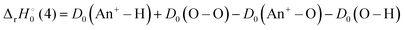 | (12) |
| |
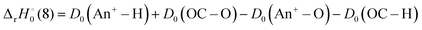 | (13) |
Existing thermochemical values are listed in
Table 4. Both reaction (4) and (8) are quite exothermic.
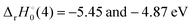
for ThH
+ and UH
+, respectively, while
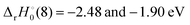
. For the other An, the more discerning reaction (8) should be exothermic if
D0(An
+–O) ≥
D0(An
+–H) + 3.64 eV. From
D0(An
+–H) listed in
Table 4, reaction (8) should be exothermic for An
+ = Th
+–Am
+.
For reactions (5) and (9), the reaction enthalpies are:
| |
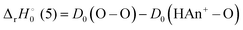 | (14) |
| |
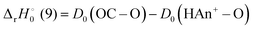 | (15) |
Consequently,
reactions (5) and (9) are exothermic if
D0(HAn
+–O) ≥
D0(O–O)/
D0(OC–O).
Fig. 3 and 4 indicate that
D0(HAn
+–O) ≥
D0(OC–O) = 5.45 eV for both Th
+ and U
+. The branching ratios may provide additional information to refine
D0(HAn
+–O). Assuming that the primary driver to the branching ratios is the reaction enthalpy, then °
Δr H
0°(9) ≤ °
ΔrH
0°(8) = −2.48 and −1.90 eV for ThH
+ and UH
+. This is true for
D0(HTh
+–O) ≥ 7.93 and
D0(HU
+–O) ≥ 7.38 eV. Because reaction dynamics are controlled by more than the thermodynamic driver, the BDEs may not be this large. Nevertheless, comparison of theoretical bond distances
9 r(Th
+–O) = 1.79 Å and
r(HTh
+–O) = 1.80 Å indicates that both the ThO
+ and HThO
+ BDEs are likely of similar strength, consistent with
D0(HTh
+–O) ≥ 7.93 eV.
For reaction (6) and (10), the reaction enthalpies are:
| |
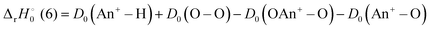 | (16) |
| |
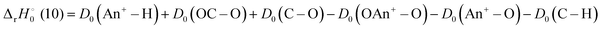 | (17) |
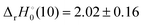
and −0.09 ± 0.19 eV for ThH
+ and UH
+, respectively. The apparent threshold observed for reaction (10) in
Fig. 3 is consistent with
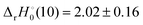
. Likewise, the observation of a barrierless exothermic reaction for reaction (10) in
Fig. 4 is also consistent with
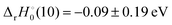
. Notably,
eqn (17) requires that
D0(OAn
+–O) +
D0(An
+–O) −
D0(An
+–H) ≥ 13.01 eV for reaction (10) to be exothermic.
Table 4 indicates that this may only be true for PaH+ and UH+, although the high uncertainty in 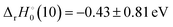 may indicate otherwise for PaH+. Observation of the energy dependence of reaction (10) may refine some of the uncertainty in the reported Pa+ BDEs.
may indicate otherwise for PaH+. Observation of the energy dependence of reaction (10) may refine some of the uncertainty in the reported Pa+ BDEs.
There is a noticeable change in the reaction (10) thermochemistry after UH+, as detailed in Table 4. While it has been clearly demonstrated that the 5f orbitals contribute to bonding in linear OAnO+, the primary participants in bonding are the 6d orbitals. Promotion energies to a state with one unpaired 6d electron are nearly equivalent in the early series Ep(6d) Th+ ≈ Ep(6d) Pa+ ≈ Ep(6d) U+ ≈ Ep(6d) Np+ ≪ Ep(6d) Pu+ ≪ Ep(6d) Am+. For Ep(6d2), Ep(6d2) Th+ < Ep(6d2) Pa+ ≈ Ep(6d2) U+ < Ep(6d2) Np+ ≪ Ep(6d2) Pu+ ≪ Ep(6d2) Am+. This appears to lead to a shift in the reaction (10) enthalpy after U to a new trend as observed in Fig. 5. Note that Th+ is excluded from this analysis because it lacks the four valence electrons to form strong dioxide bonds.
 |
| | Fig. 5 The correlation between Ep(6d2) and the reaction (10) enthalpy calculated using the values found in Table 4 and eqn (17). The solid line represents the least square linear regression trend line (−0.5 + (1.3 ± 0.3)Ep(6d2), r2 = 0.87). | |
Promotion energies, Ep(6d) and Ep(6d2), to some extent represent the accessibility of the 6d orbitals for bonding. Comparing these promotion energies to the 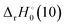 indicates how influential the 6d orbitals may be in forming OAnO+ bonds. Assuming similar driving forces across the An series to OAnO+ bonding, the trend should be linear. Fig. 5 does indicate a relatively linear correlation, yet a clear difference between the early and latter An is observed. This mirrors observations in other single ligand systems that may have deviations in observed trends between Np+ and Pu+.16,19 This trend may suggest that there is a difference in bonding mechanism (i.e. orbital participation) for NpO2+–AmO2+. Considering only spatial overlap as the driving force to molecular orbital formation, Fig. 5 is consistent with 5f orbital participation where the 5f orbitals are spatially larger for the early An. Armentrout and coworkers22,25 have demonstrated 5f orbital participation for ThO2+ and UO2+. 5f orbital participation in hydrocarbon activation in the early An has also been argued previously to interpret FTICR-MS studies of the reactions of An+ with hydrocarbons of varying lengths.49 Nevertheless, 5f orbital participation in the early An cannot explain the trend observed in Fig. 5. A natural bond order analysis of AnO2+ (An = U–Am) presented by Feng, Glendening, and Peterson50 indicates that the 5f and 6d orbital participation in both the σ and π bonding orbitals remains consistent across the four An at 50% 6d and 50% 5f (df hybrid orbital) and 50% 6d and 35% 5f (pd3f2 hybrid orbital), respectively. Computational studies51 utilizing B3LYP indicate two σ and two π bonding orbitals for neutral AnO2. σg and πg orbitals were characterized as having major contributions from the O 2p orbitals with minor contributions from the An 6d/7s orbitals. By contrast the σu and πu orbitals were characterized by major An 5f and minor O 2p orbital contributions. For the early An, the gerade orbitals are lower in energy, but this shifts between Am and Cm. The shift in the relative energy between the 5f and 6d orbitals is possibly the driving force to the shift in bonding. Between Np+ and Pu+ is where the 6d orbitals become less accessible. This concept can be observed in Table 1 where the Ep(6d) values are listed and Table S2 where Ep(6d2) are listed. For both promotion energies, there is a clear escalation in energies from Np+ to Pu+. Since the 5f/6d orbital participation does not seem to vary significantly according to theoretical observations, it is plausible that how the participation is incorporated shifts (i.e. orbital overlap vs. energy driven degeneracy).
indicates how influential the 6d orbitals may be in forming OAnO+ bonds. Assuming similar driving forces across the An series to OAnO+ bonding, the trend should be linear. Fig. 5 does indicate a relatively linear correlation, yet a clear difference between the early and latter An is observed. This mirrors observations in other single ligand systems that may have deviations in observed trends between Np+ and Pu+.16,19 This trend may suggest that there is a difference in bonding mechanism (i.e. orbital participation) for NpO2+–AmO2+. Considering only spatial overlap as the driving force to molecular orbital formation, Fig. 5 is consistent with 5f orbital participation where the 5f orbitals are spatially larger for the early An. Armentrout and coworkers22,25 have demonstrated 5f orbital participation for ThO2+ and UO2+. 5f orbital participation in hydrocarbon activation in the early An has also been argued previously to interpret FTICR-MS studies of the reactions of An+ with hydrocarbons of varying lengths.49 Nevertheless, 5f orbital participation in the early An cannot explain the trend observed in Fig. 5. A natural bond order analysis of AnO2+ (An = U–Am) presented by Feng, Glendening, and Peterson50 indicates that the 5f and 6d orbital participation in both the σ and π bonding orbitals remains consistent across the four An at 50% 6d and 50% 5f (df hybrid orbital) and 50% 6d and 35% 5f (pd3f2 hybrid orbital), respectively. Computational studies51 utilizing B3LYP indicate two σ and two π bonding orbitals for neutral AnO2. σg and πg orbitals were characterized as having major contributions from the O 2p orbitals with minor contributions from the An 6d/7s orbitals. By contrast the σu and πu orbitals were characterized by major An 5f and minor O 2p orbital contributions. For the early An, the gerade orbitals are lower in energy, but this shifts between Am and Cm. The shift in the relative energy between the 5f and 6d orbitals is possibly the driving force to the shift in bonding. Between Np+ and Pu+ is where the 6d orbitals become less accessible. This concept can be observed in Table 1 where the Ep(6d) values are listed and Table S2 where Ep(6d2) are listed. For both promotion energies, there is a clear escalation in energies from Np+ to Pu+. Since the 5f/6d orbital participation does not seem to vary significantly according to theoretical observations, it is plausible that how the participation is incorporated shifts (i.e. orbital overlap vs. energy driven degeneracy).
An alternate explanation could be that NpO2+ is unusual. Removing the NpO2+ from the trend in Fig. 5 (r2 = 0.87) results in an improved linear correlation (Fig. S6, r2 = 0.99). This correlation excluding NpO2+ is stronger than both of the linear trends displayed in Fig. S7 (r2 = 0.95 for both trends). NpO2+ may be an outlier because the electronic configuration of Np+ is unusual for the early An series and has a 7L5 (5f46d7s) ground level with a low lying 5I4 (5f47s2, 0.003 eV) level.52 Pa+ (n= 4) and U+ (n = 5) both have 5fn−27s2 ground configurations, although the 5fn−26d7s configurations are very low lying at 0.10 and 0.04 eV, respectively. Pu+ (n =7) and Am+ (n = 8) both have 5fn−17s ground configurations. The 5f, 6d, and 7s orbitals of ground state Np+ are occupied, which may suggest that they are also similar in energy. This energy similarity may drive a bonding mechanism (orbital participation) for Np+ that is different from the other An+, although theoretical calculations indicate minimal differences in the bonding orbital contribution.50 Np+ also has a low lying j = (5/2, 1/2) 5f57s level at 0.01 eV, so if the ground electronic configuration is related to the observed trend in Fig. 5, then Np+ can be grouped with both Pa+/U+ and Pu+/Am+. The experimental uncertainty limits the conclusions that can be drawn because the trend excluding NpO2+ (Fig. S6) and the split trend (Fig. S7) are both reasonable. Additional experimental work is necessary to provide support for the validity of either argument.
Conclusion
The reactions of AnH+ + O2/CO2 (An+ = Th, U) may provide additional insight into An bonding. Observed reactions, in particular reaction (8), are consistent with thermochemistry derived from previous reports.16,17 Extending these results to the additional An in the series indicates that there may be a change in bonding mechanism that starts at Np+, Fig. 5. Notably, at Np+ the 6d orbitals become less accessible than the earlier An+ as measured by Ep(6d2). Computational studies,50 however, suggest that there is minimal change in the orbitals involved in AnO2+ bonding. Because the 5f orbitals contract with increasing atomic number, the consistent composition of the An bonding orbitals may be indicative of the newer concept of energy driven covalency.53 This concept is far from proven, but observed shifts in bonding in gas phase experiments16,19 are consistent with an energy driven covalency model. Although much of the focus of An chemistry has been on when and why the 5f orbitals participate in bonding, these may be the wrong questions to ask. It appears that there may be a fundamental shift in bonding mechanism between early and latter An. Additional studies should be focused on understanding that difference.
Conflicts of interest
There are no conflicts to declare.
Data availability
All data used within this document are available within this document, the accompanying supplementary information (SI), or the manuscripts referenced in this document. Supplementary information: tabulated thermochemistry values, product branching ratios as a function of kinetic energy, kinetic energy dependence absolute reaction cross section of U2+ + CO2. See DOI: https://doi.org/10.1039/d5cp04417k.
Acknowledgements
The experimental data was collected with support from the Open Call Initiative under the Laboratory Directed Research and Development (LDRD) Program at Pacific Northwest National Laboratory (PNNL). Interpretation of this experimental data and writing this manuscript was supported by a U.S. Department of Energy, Office of Science, Early Career Research Program award in the Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Heavy Element Chemistry program under FWP 81364. PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RL01830.
References
- M. C. Heaven and K. A. Peterson, Probing Actinide Bonds in the Gas Phase: Theory and Spectroscopy, in Experimental and Theoretical Approaches to Actinide Chemistry, ed. J. K. Gibson and W. A. de Jong, John Wiley & Sons Ltd, Oxford, 2018 Search PubMed.
- P. E. Moreland, D. J. Rokop and C. M. Stevens, Mass-Spectrometric Observations of Uranium and Plutonium Monohydrides Formed by Ion—Molecule Reaction, Int. J. Mass Spectrom. Ion Phys., 1970, 5(1), 127–136 CrossRef CAS.
- P. B. Armentrout, R. V. Hodges and J. L. Beauchamp, Endothermic Reactions of Uranium Ions with N2, D2, and CD4, J. Chem. Phys., 1977, 66(10), 4683 CrossRef CAS.
- P. F. Souter, G. P. Kushto, L. Andrews and M. Neurock, Experimental and Theoretical Evidence for the Isolation of Thorium Hydride Molecules in Argon Matrices, J. Phys. Chem. A, 1997, 101(7), 1287–1291 Search PubMed.
- X. Wang, L. Andrews and L. Gagliardi, Infrared Spectra of ThH2, ThH4, and the Hydride Bridging ThH4(H2)x (x = 1–4) Complexes in Solid Neon and Hydrogen, J. Phys. Chem. A, 2008, 112(8), 1754–1761 CrossRef CAS PubMed.
- J. Marcalo, M. Santos and J. K. Gibson, Gas-phase Reactions of Doubly Charged Actinide Cations with Alkanes and Alkenes-Probing the Chemical Activity of 5f Electrons from Th to Cm, Phys. Chem. Chem. Phys., 2011, 13(41), 18322–18329 RSC.
- E. Di Santo, M. Santos, M. C. Michelini, J. Marçalo, N. Russo and J. K. Gibson, Gas-Phase Reactions of the Bare Th2+ and U2+ Ions with Small Alkanes, CH4, C2H6, and C3H8: Experimental and Theoretical Study of Elementary Organoactinide Chemistry, J. Am. Chem. Soc., 2011, 133(6), 1955–1970 CrossRef CAS PubMed.
- R. M. Cox, P. B. Armentrout and W. A. de Jong, Activation of CH4 by Th+ as Studied by Guided Ion Beam Mass Spectrometry and Quantum Chemistry, Inorg. Chem., 2015, 54(7), 3584–3599 CrossRef CAS PubMed.
- R. M. Cox and P. B. Armentrout, Activation of Water by Thorium Cation: A Guided Ion Beam and Quantum Chemical Study, J. Am. Soc. Mass Spectrom., 2019, 30(10), 1835–1849 CrossRef CAS PubMed.
- R. M. Cox, P. B. Armentrout and W. A. de Jong, Reactions of Th+ + H2, D2, and HD Studied by Guided Ion Beam Tandem Mass Spectrometry and Quantum Chemical Calculations, J. Phys. Chem. B, 2016, 120, 1601–1614 CrossRef CAS PubMed.
- W.-J. Zhang, M. Demireva, J. Kim, W. A. de Jong and P. B. Armentrout, Reactions of U+ with H2, D2, and HD Studied by Guided Ion Beam Tandem Mass Spectrometry and Theory, J. Phys. Chem. A, 2021, 125(36), 7825–7839 CrossRef CAS.
- G. F. de Melo, M. Vasiliu, M. Marshall, Z. Zhu, B. A. Tufekci, S. M. Ciborowski, M. Blankenhorn, R. M. Harris, K. H. Bowen and D. A. Dixon, Experimental and Computational Description of the Interaction of H and H− with U, J. Phys. Chem. A, 2022, 126(27), 4432–4443 CrossRef CAS PubMed.
- M. Vasiliu, K. A. Peterson, M. Marshall, Z. Zhu, B. A. Tufekci, K. H. Bowen and D. A. Dixon, Interaction of Th with H0/−/+: Combined Experimental and Theoretical Thermodynamic Properties, J. Phys. Chem. A, 2022, 126(2), 198–210 CrossRef CAS PubMed.
- G. F. de Melo and D. A. Dixon, Protactinium and Actinium Monohydrides: A Theoretical Study on Their Spectroscopic and Thermodynamic Properties, J. Phys. Chem. A, 2022, 126(36), 6171–6184 CrossRef CAS PubMed.
- G. F. de Melo and D. A. Dixon, Energetic and Electronic Properties of NpH0/+/− and PuH0/+/−, J. Phys. Chem. A, 2023, 127(14), 3179–3189 CrossRef CAS PubMed.
- A. R. F. Bubas, D. Amanda, K. M. Melby, M. J. Rodriguez and R. M. Cox, The Balance of Orbital Overlap and Orbital Energy in the Activation of Methane by Actinide Cations: Insights from Inductively Coupled Plasma Tandem Mass Spectrometry, Inorg. Chem. Front., 2025, 12, 1503–1516 RSC.
- J. Marçalo and J. K. Gibson, Gas-Phase Energetics of Actinide Oxides: An Assessment of Neutral and Cationic Monoxides and Dioxides from Thorium to Curium, J. Phys. Chem.
A, 2009, 113(45), 12599–12606 CrossRef PubMed.
- J. K. Gibson, Bond Dissociation Energies Reveal the Participation of d Electrons in f-Element Halide Bonding, J. Phys. Chem. A, 2022, 126(2), 272–285 CrossRef CAS PubMed.
- R. M. Cox, A. R. Bubas, K. M. Melby, A. D. French, M. J. Rodriguez, M. P. Prange, N. Govind, K. A. Peterson and P. B. Armentrout, The Reactions of An+ (An+ = Th+, U+–Am+) + NO Reactions Observed by Inductively Coupled Plasma Tandem Mass Spectrometry, 2025, in progress.
- R. M. Cox, A. Kafle, P. B. Armentrout and K. A. Peterson, Bond Energy of ThN+: A Guided Ion Beam and Quantum Chemical Investigation of the Reactions of Thorium Cation with N2 and NO, J. Chem. Phys., 2019, 151(3), 034304 CrossRef PubMed.
- A. R. Bubas, A. Kafle, B. C. Stevenson and P. B. Armentrout, The Bond Energy of UN+: Guided Ion Beam Studies of the Reactions of U+ with N2 and NO, J. Chem. Phys., 2024, 160, 164305 CrossRef CAS PubMed.
- P. B. Armentrout and K. A. Peterson, Guided Ion Beam and Quantum Chemical Investigation of the Thermochemistry of Thorium Dioxide Cations: Thermodynamic Evidence for Participation of f Orbitals in Bonding, Inorg. Chem., 2020, 59(5), 3118–3131 CrossRef CAS PubMed.
- K. S. Otte, J. E. Niklas, C. M. Studvick, C. L. Montgomery, A. R. C. Bredar, I. A. Popov and H. S. La Pierre, Proton-Coupled Electron Transfer at the Pu5+/4+ Couple, J. Am. Chem. Soc., 2024, 146, 21859–21867 Search PubMed.
- J. E. Niklas, K. S. Otte, C. M. Studvick, S. Roy Chowdhury, B. Vlaisavljevich, J. Bacsa, F. Kleemiss, I. A. Popov, H. S. La Pierre and A. Tetrahedral, Neptunium(V) Complex, Nat. Chem., 2024, 16(9), 1490–1495 CrossRef CAS PubMed.
- A. R. Bubas, W.-J. Zhang, P. B. Armentrout and A. Guided Ion Beam Investigation, of UO2+ Thermodynamics and f orbital Participation: Reactions of U+ + CO2, UO+ + O2, and UO+ + CO, J. Chem. Phys., 2023, 159(24), 244305 CrossRef CAS.
- R. M. Cox, A. R. Bubas, K. M. Melby, A. D. French, M. J. Rodriguez, M. P. Prange and N. Govind, The Curious Case of Pu+: Insight on 5f Orbital Activity from Inductively Coupled Plasma Tandem Mass Spectrometry (ICP-MS/MS) Reactions, Inorg. Chem., 2024, 63(43), 20617–20624 CrossRef CAS.
- M. Santos, J. Marçalo, A. P. D. Matos, J. K. Gibson and R. G. Haire, Gas-Phase Oxidation Reactions of Neptunium and Plutonium Ions Investigated via Fourier Transform Ion Cyclotron Resonance Mass Spectrometry, J. Phys. Chem. A, 2002, 106, 7190–7194 Search PubMed.
- M. Santos, A. P. d Matos, J. Marcüalo, J. K. Gibson, R. G. Haire, R. Tyagi and R. M. Pitzer, Oxidation of Gas-Phase Protactinium Ions, Pa+ and Pa2+: Formation and Properties of PaO22+(g), Protactinyl, J. Phys. Chem. A, 2006, 110, 5751–5759 Search PubMed.
- M. Santos, J. Marçalo, J. P. Leal, A. P. D. Matos, J. K. Gibson and R. G. Haire, FTICR-MS Study of the Gas-phase Thermochemistry of Americium Oxides, Int. J. Mass Spectrom., 2003, 228, 457–465 CrossRef CAS.
- P. B. Armentrout and J. L. Beauchamp, Reactions of U+ and UO+ with O2, CO, CO2, COS, CS2 and D2O, Chem. Phys., 1980, 50, 27–36 Search PubMed.
- R. M. Cox, K. Harouaka, M. Citir and P. B. Armentrout, Activation of CO2 by Actinide Cations (Th+, U+, Pu+, and Am+) as Studied by Guided Ion Beam and Triple Quadrupole Mass Spectrometry, Inorg. Chem., 2022, 8168–8181 Search PubMed.
- J. G. Terhorst, T. A. Corcovilos and M. J. van Stipdonk, Conversion of a UO22+ Precursor to UH+ and U+ Using Tandem Mass Spectrometry to Remove Both “yl” Oxo Ligands, J. Am. Soc. Mass Spectrom., 2023, 34(11), 2439–2442 CrossRef CAS PubMed.
- J. G. Terhorst, T. A. Corcovilos, S. J. Lenze and M. J. van Stipdonk, Synthesis of Organo-Uranium(II) Species in the Gas-Phase using Reactions Between [UH]+ and Nitriles, Dalton Trans., 2025, 54(1), 231–238 RSC.
- K. P. Hobbs, A. D. French, K. M. Melby, E. J. Bylaska, K. Harouaka, R. M. Cox, I. J. Arnquist and C. L. Beck, Assessing Gas-Phase Ion Reactivity of 50 Elements with NO and the Direct Application for 239Pu in Complex Matrices Using ICP-MS/MS, Anal. Chem., 2024, 96(15), 5807–5814 CrossRef CAS PubMed.
- K. Harouaka, C. Allen, E. Bylaska, R. M. Cox, G. C. Eiden, M. L. D. Vacri, E. W. Hoppe and I. J. Arnquist, Gas-Phase Ion-Molecule Interactions in a Collision Reaction Cell with Triple Quadrupole-Inductively Coupled Plasma Mass Spectrometry: Investigations with N2O as the Reaction Gas, Spectrochim. Acta, Part B, 2021, 186, 106309 Search PubMed.
- P. B. Armentrout, Mass Spectrometry – Not Just a Structural Tool: The Use of Guided Ion Beam Tandem Mass Spectrometry to Determine Thermochemistry, J. Am. Soc. Mass Spectrom., 2002, 13(5), 419–434 Search PubMed.
- N. Yamada, Kinetic Energy Discrimination in Collision/Reaction Cell ICP-MS: Theoretical Review of Principles and Limitations, Spectrochim. Acta, Part B, 2015, 110, 31–44 CrossRef CAS.
- A. R. Bubas, R. M. Cox, K. M. Melby, A. D. French, M. J. Rodriguez, M. P. Prange, N. Govind and P. B. Armentrout, The Reactions of Ln+ (Ln+ = Ce+, Pr+, Nd+, Sm+, Eu+) + NO Reactions Observed by Inductively Coupled Plasma Tandem Mass Spectrometry, J. Chem. Phys., 2025 Search PubMed , submitted.
- R. M. Cox, K. M. Melby, A. D. French and M. J. Rodriguez, f-Block Reactions of Metal Cations with Carbon Dioxide Studied by Inductively Coupled Plasma Tandem Mass Spectrometry, Phys. Chem. Chem. Phys., 2024, 26(1), 209–218 RSC.
- T. Su and M. T. Bowers, Ion-Polar Molecule Collisions: The Effect of Ion Size on Ion-Polar Molecule Rate Constants: The Parameterization of the Average Dipole Orientation Theory, Int. J. Mass Spectrom. Ion Phys., 1973, 12, 347–356 Search PubMed.
- R. M. Cox, M. Citir, P. B. Armentrout, S. R. Battey and K. A. Peterson, Bond Energies of ThO+ and ThC+: A Guided Ion Beam and Quantum Chemical Investigation of the Reactions of Thorium Cation with O2 and CO, J. Chem. Phys., 2016, 144, 184309 Search PubMed.
- W. Zhang, A. R. E. Hunt, M. Demireva, J. Kim, K. A. Peterson and P. B. Armentrout, Bond Energies of UO+ and UC+: Guided Ion Beam and Quantum Chemical Studies of the Reactions of Uranium Cation with O2 and CO, Isr. J. Chem., 2023, e202300026 CrossRef CAS.
- H. H. Cornehl, R. Wesendrup, M. Diefenbach and H. Schwarz, A Comparative Study of Oxo-Ligand Effects in the Gas-Phase Chemistry of Atomic Lanthanide and Actinide Cations, Chem. – Eur. J., 1997, 3(7), 1083–1090 Search PubMed.
- J. K. Gibson, R. G. Haire, M. Santos, J. Marcalo and A. Pires de Matos, Oxidation Studies of Dipositive Actinide Ions, An2+ (An = Th, U, Np, Pu, Am) in the Gas Phase: Synthesis and Characterization of the Isolated Uranyl, Neptunyl, and Plutonyl Ions UO22+(g), NpO22+(g), and PuO22+(g), J. Phys. Chem. A, 2005, 109(12), 2768–2781 Search PubMed.
- G. Mazzone, M. d C. Michelini, N. Russo and E. Sicilia, Mechanistic Aspects of the Reaction of Th+ and Th2+ with Water in the Gas Phase, Inorg. Chem., 2008, 47(6), 2083–2088 Search PubMed.
- J. Zhou and H. B. Schlegel, Ab Initio Molecular Dynamics Study of the Reaction between Th+ and H2O, J. Phys. Chem. A, 2010, 114(33), 8613–8617 Search PubMed.
- R. D. Johnson III, NIST Computational Chemistry Comparison and Benchmark Database. https://cccbdb.nist.gov/ (accessed April 12, 2018).
- P. B. Armentrout and R. M. Cox, Potential Energy Surface for Reaction of Sm+ + CO2 → SmO+ + CO: Guided Ion Beam and Theoretical Studies, Phys. Chem. Chem. Phys., 2017, 19, 11075–11088 Search PubMed.
- J. K. Gibson, R. G. Haire, J. Marçalo, M. Santos, A. Pires de Matos, M. K. Mrozik, R. M. Pitzer and B. E. Bursten, Gas-Phase Reactions of Hydrocarbons with An+ and AnO+ (An = Th, Pa, U, Np, Pu, Am, Cm): The Active Role of 5f Electrons in Organoprotactinium Chemistry, Organometallics, 2007, 26(16), 3947–3956 CrossRef CAS.
- R. Feng, E. D. Glendening and K. A. Peterson, Actinyl Cation-Cation Interactions in the Gas Phase: An Accurate Thermochemical Study, Phys. Chem. Chem. Phys., 2019, 21(15), 7953–7964 Search PubMed.
- A. Kovacs, P. Pogany and R. J. M. Konings, Theoretical Study of Bond Distances and Dissociation Energies of Actinide Oxides AnO and AnO2, Inorg. Chem., 2012, 51(8), 4841–4849 CrossRef CAS PubMed.
- J. E. Sansonetti and W. C. Martin, NIST Standard Reference Database 108. https://www.nist.gov/pml/handbook-basic-atomic-spectroscopic-data.
- J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, Energy-Degeneracy-Driven Covalency in Actinide Bonding, J. Am. Chem. Soc., 2018, 140(51), 17977–17984 Search PubMed.
|
| This journal is © the Owner Societies 2026 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Amanda R. Bubas
*,
Amanda R. Bubas and
Amanda D. French
and
Amanda D. French
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Previous work16,38,39 has indicated that Tp is between 1000–10
000 K. Previous work16,38,39 has indicated that Tp is between 1000–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for atomic cations. For polyatomic cations, it is less clear what the electronic distribution may be. Presumably, some excess electronic energy from the atomic cations in the source is consumed to create AnH+, and the electronic state density is likely less dense than the atomic electronic state density.10–13 Consequently, the average electronic energy available is expected to be less than that available for atomic cations. An assumption is made that there are sufficient crossings between potential energy surfaces that a pathway exists between excited state reactants and ground state products so that excess electronic energy can be treated as energy available for reaction. Theoretical calculations were previously used to examine the low-lying electronic states of ThH+ and UH+.11,13 Based on this work, the electronic energy, Eel, is Eel(ThH+) = 0.37 eV and Eel(UH+) = 0.12 eV at 5000 K.
000 K for atomic cations. For polyatomic cations, it is less clear what the electronic distribution may be. Presumably, some excess electronic energy from the atomic cations in the source is consumed to create AnH+, and the electronic state density is likely less dense than the atomic electronic state density.10–13 Consequently, the average electronic energy available is expected to be less than that available for atomic cations. An assumption is made that there are sufficient crossings between potential energy surfaces that a pathway exists between excited state reactants and ground state products so that excess electronic energy can be treated as energy available for reaction. Theoretical calculations were previously used to examine the low-lying electronic states of ThH+ and UH+.11,13 Based on this work, the electronic energy, Eel, is Eel(ThH+) = 0.37 eV and Eel(UH+) = 0.12 eV at 5000 K.




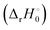 for the ligand exchange reactions, reactions (4) and (8), are:
for the ligand exchange reactions, reactions (4) and (8), are: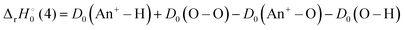
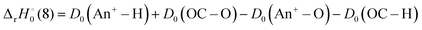
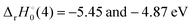 for ThH+ and UH+, respectively, while
for ThH+ and UH+, respectively, while 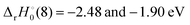 . For the other An, the more discerning reaction (8) should be exothermic if D0(An+–O) ≥ D0(An+–H) + 3.64 eV. From D0(An+–H) listed in Table 4, reaction (8) should be exothermic for An+ = Th+–Am+.
. For the other An, the more discerning reaction (8) should be exothermic if D0(An+–O) ≥ D0(An+–H) + 3.64 eV. From D0(An+–H) listed in Table 4, reaction (8) should be exothermic for An+ = Th+–Am+.
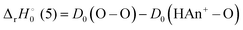
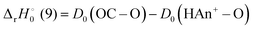
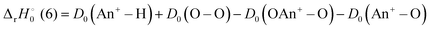
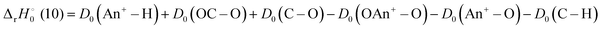
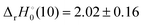 and −0.09 ± 0.19 eV for ThH+ and UH+, respectively. The apparent threshold observed for reaction (10) in Fig. 3 is consistent with
and −0.09 ± 0.19 eV for ThH+ and UH+, respectively. The apparent threshold observed for reaction (10) in Fig. 3 is consistent with 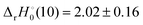 . Likewise, the observation of a barrierless exothermic reaction for reaction (10) in Fig. 4 is also consistent with
. Likewise, the observation of a barrierless exothermic reaction for reaction (10) in Fig. 4 is also consistent with 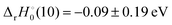 . Notably, eqn (17) requires that D0(OAn+–O) + D0(An+–O) − D0(An+–H) ≥ 13.01 eV for reaction (10) to be exothermic.
. Notably, eqn (17) requires that D0(OAn+–O) + D0(An+–O) − D0(An+–H) ≥ 13.01 eV for reaction (10) to be exothermic.
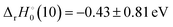 may indicate otherwise for PaH+. Observation of the energy dependence of reaction (10) may refine some of the uncertainty in the reported Pa+ BDEs.
may indicate otherwise for PaH+. Observation of the energy dependence of reaction (10) may refine some of the uncertainty in the reported Pa+ BDEs.
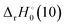 indicates how influential the 6d orbitals may be in forming OAnO+ bonds. Assuming similar driving forces across the An series to OAnO+ bonding, the trend should be linear. Fig. 5 does indicate a relatively linear correlation, yet a clear difference between the early and latter An is observed. This mirrors observations in other single ligand systems that may have deviations in observed trends between Np+ and Pu+.16,19 This trend may suggest that there is a difference in bonding mechanism (i.e. orbital participation) for NpO2+–AmO2+. Considering only spatial overlap as the driving force to molecular orbital formation, Fig. 5 is consistent with 5f orbital participation where the 5f orbitals are spatially larger for the early An. Armentrout and coworkers22,25 have demonstrated 5f orbital participation for ThO2+ and UO2+. 5f orbital participation in hydrocarbon activation in the early An has also been argued previously to interpret FTICR-MS studies of the reactions of An+ with hydrocarbons of varying lengths.49 Nevertheless, 5f orbital participation in the early An cannot explain the trend observed in Fig. 5. A natural bond order analysis of AnO2+ (An = U–Am) presented by Feng, Glendening, and Peterson50 indicates that the 5f and 6d orbital participation in both the σ and π bonding orbitals remains consistent across the four An at 50% 6d and 50% 5f (df hybrid orbital) and 50% 6d and 35% 5f (pd3f2 hybrid orbital), respectively. Computational studies51 utilizing B3LYP indicate two σ and two π bonding orbitals for neutral AnO2. σg and πg orbitals were characterized as having major contributions from the O 2p orbitals with minor contributions from the An 6d/7s orbitals. By contrast the σu and πu orbitals were characterized by major An 5f and minor O 2p orbital contributions. For the early An, the gerade orbitals are lower in energy, but this shifts between Am and Cm. The shift in the relative energy between the 5f and 6d orbitals is possibly the driving force to the shift in bonding. Between Np+ and Pu+ is where the 6d orbitals become less accessible. This concept can be observed in Table 1 where the Ep(6d) values are listed and Table S2 where Ep(6d2) are listed. For both promotion energies, there is a clear escalation in energies from Np+ to Pu+. Since the 5f/6d orbital participation does not seem to vary significantly according to theoretical observations, it is plausible that how the participation is incorporated shifts (i.e. orbital overlap vs. energy driven degeneracy).
indicates how influential the 6d orbitals may be in forming OAnO+ bonds. Assuming similar driving forces across the An series to OAnO+ bonding, the trend should be linear. Fig. 5 does indicate a relatively linear correlation, yet a clear difference between the early and latter An is observed. This mirrors observations in other single ligand systems that may have deviations in observed trends between Np+ and Pu+.16,19 This trend may suggest that there is a difference in bonding mechanism (i.e. orbital participation) for NpO2+–AmO2+. Considering only spatial overlap as the driving force to molecular orbital formation, Fig. 5 is consistent with 5f orbital participation where the 5f orbitals are spatially larger for the early An. Armentrout and coworkers22,25 have demonstrated 5f orbital participation for ThO2+ and UO2+. 5f orbital participation in hydrocarbon activation in the early An has also been argued previously to interpret FTICR-MS studies of the reactions of An+ with hydrocarbons of varying lengths.49 Nevertheless, 5f orbital participation in the early An cannot explain the trend observed in Fig. 5. A natural bond order analysis of AnO2+ (An = U–Am) presented by Feng, Glendening, and Peterson50 indicates that the 5f and 6d orbital participation in both the σ and π bonding orbitals remains consistent across the four An at 50% 6d and 50% 5f (df hybrid orbital) and 50% 6d and 35% 5f (pd3f2 hybrid orbital), respectively. Computational studies51 utilizing B3LYP indicate two σ and two π bonding orbitals for neutral AnO2. σg and πg orbitals were characterized as having major contributions from the O 2p orbitals with minor contributions from the An 6d/7s orbitals. By contrast the σu and πu orbitals were characterized by major An 5f and minor O 2p orbital contributions. For the early An, the gerade orbitals are lower in energy, but this shifts between Am and Cm. The shift in the relative energy between the 5f and 6d orbitals is possibly the driving force to the shift in bonding. Between Np+ and Pu+ is where the 6d orbitals become less accessible. This concept can be observed in Table 1 where the Ep(6d) values are listed and Table S2 where Ep(6d2) are listed. For both promotion energies, there is a clear escalation in energies from Np+ to Pu+. Since the 5f/6d orbital participation does not seem to vary significantly according to theoretical observations, it is plausible that how the participation is incorporated shifts (i.e. orbital overlap vs. energy driven degeneracy).