 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Correlation between information entropy and pore connectivity in oxidic materials with random disordered porosity
Antigoni G. Margellou a,
Gerasimos S. Armatasb,
Konstantina Koloniacd and
Philippos J. Pomonis
a,
Gerasimos S. Armatasb,
Konstantina Koloniacd and
Philippos J. Pomonis *c
*c
aDepartment of Chemistry, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
bDepartment of Materials Science and Engineering, University of Crete, 70013 Heraklion, Crete, Greece
cDepartment of Chemistry, University of Ioannina, 45110 Ioannina, Greece. E-mail: ppomonis@uoi.gr
d5th Junior High School, Zefirou 20, Palaio Faliro, 17564 Athens, Greece
First published on 9th January 2026
Abstract
Pore connectivity is a crucial structural characteristic of porous solids that governs the mass transfer and diffusion of fluids through them. Information entropy, on the other hand, is a statistical property that can be estimated for any distribution, including the size distribution of pores in solids. In this work, we present the first comprehensive study investigating the correlation between the pore connectivity and the Shannon information entropy of classical pore size distributions of inorganic porous materials. Experimental data are based on sixteen reported oxidic alumino–phosphoro–vanadate porous solids. All studied materials exhibit random disordered porosity, as determined by standard nitrogen porosimetry. Pore connectivity was estimated using the Seaton method, which is based on the hysteresis loop of nitrogen adsorption–desorption isotherms. Results demonstrate a linear and robust correlation between the binary information entropy and binary logarithm of pore connectivity. This relationship can be rationalized by considering the statistical information entropy of independent pore mixing. The physical origin of the correlation between information entropy and average pore connectivity is attributed to the random packing of pores, analogous to the classical problem of random packing of particles. The statistical base is the heteroscedasticity between the variance and mean parameters of pore size distributions: variance drives information entropy, while the mean drives pore connectivity, as described by the model of random packing.
Introduction
Pore labyrinths in solids are typical examples of complex systems consisting of minute voids up to several quadrillions per unit of surrounding mass. Such pores of variable sizes and shapes are interconnected in a complex network, and the connectivity between them governs the mass transfer that occurs within the internal space of porous materials. Extensive information about such complex systems has been compiled by experts in two collective multivolume editions: the “Handbook of Porous Solids” published in 20021 and the “Handbook of Porous Materials” published in 2021.2 The articles in these handbooks contain copious data on primary synthesis routes, specific material properties, virtual modelling of porous substances, and their applications in separation technologies, adsorption and heterogeneous catalysis, along with extensive relevant literature.Pore connectivity (c) has garnered limited attention in the above-mentioned review articles and specialized studies, and its potential relationship with the information entropy (IE) of pore size distributions (PSDs) is practically absent from the literature. Nevertheless, there are compelling reasons to pursue this investigation. Specifically, the structural property of pore connectivity is critical in fields such as chemical engineering3–7 and geoscience.8–12 In chemical engineering, c controls mass transfer and fluid diffusion through pore networks, especially in adsorbents and heterogeneous catalysts,3–5 which are two areas of considerable importance for chemo-technological applications.6,7 In geoscience, research has largely focused on the relationship between soil pore connectivity (and, in some cases, soil entropy) and properties such as water permeability, pollutant diffusion and microbial ecology, all of which influence remediation outcomes.8–12 However, a possible correlation between c and IE has not yet been systematically investigated in geoscience or chemical engineering.
In the present study, we restrict our focus to porous adsorbents. Although the calculation of pore connectivity for such materials is not straightforward,13–17 the statistical measure of IE can be determined through a relatively simple procedure.18,19 Thus, exploring the potential correlation between IE and c could enable the estimation of a difficult-to-measure property through a more convenient approach. Intuitively, a narrow pore size distribution, for instance, in mesoporous MCM-type materials with uniformly sized pores, would exhibit limited pore connectivity. This narrow distribution would also correspond to low information entropy, and the reverse would be expected for broader distributions. However, a quantitative relationship between c and IE remains unresolved. The present work addresses this gap by investigating the correlation between pore connectivity and information entropy of representative PSDs of materials with random disordered porosity, characterized using standard nitrogen physisorption measurements.20,21
The article has the following structure: in Section 2, Background information, we provide important aspects and methodologies employed for calculating the pore connectivity and information entropy of PSDs. In Section 3, Experimental, we describe the preparation methods and material characterization by nitrogen porosimetry. In Section 4, Results, we compare the values of information entropy and the related nanopore entropy obtained from experimental PSD plots to Seaton's average pore connectivity (caverage). In Section 5, Discussion, we explore the correlation between information entropy and nanopore entropy, elucidating their direct relationship with pore connectivity. Additionally, we present a statistical expression for the entropy of pore mixing, which is analogous to the well-established concept of mixing in solutions and propose an explanation for the observed correlation between pore connectivity and information entropy based on the random packing of particles (RPP) model. Finally, in Section 6, Conclusions, we provide a concise summary of the physical implications, consequences, practical applications, and limitations of the study.
Background information
Pore connectivity
Pore connectivity (c) is a comprehensive physical property of porous substances that quantifies the number of empty paths (pore channels) connected to a single void. Its determination for chemically homogeneous substances (such as porous silica and alumina) with structured porosity was not feasible until the early 1990s. Then, Seaton and co-workers proposed a tractable method for determining average c values based on the hysteresis loop observed during nitrogen physisorption measurements.20,21 Other methods for assessing pore connectivity were developed based on computer models that constructed viral pore networks in accordance with experimental nitrogen physisorption data. For example, Mayagoitia et al.16,17 proposed the dual-site-bond model (DSBM) that provides the distribution of connectivities among the pores of various sizes. It has been demonstrated by Armatas and Pomonis5 that the mean connectivity (cmean) of the pore networks of silicate materials, calculated using computer models such as DSBM, closely aligns with the average pore connectivity (caverage) determined via Seaton's method. For this interrelation, see S.I.-1. Relevant studies have typically focused on the effect of pore connectivity on the apparent diffusion coefficients of molecules absorbed into porous solids. For instance, Meyers et al.6 demonstrated that the pore diffusivity of ribonuclease through silica particles in liquid chromatography separation columns is correlated with the pore connectivity of silica.In the present work, the average pore connectivities of sixteen (16) alumino–phosphoro–vanadate mixed oxidic porous solids22–24 are estimated using the Seaton's method.13–15 Details about the estimation of relevant pore connectivities and their similarities with those observed in trees and neurons are provided in ref. 23 and 24.
Information entropy
This concept, initially proposed by Shannon in 1948,18 is a mathematical/statistical expression that can be applied to any distribution, quantifying its dispersity.
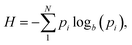 | (1) |
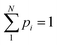 . The original study investigated the propagation of an electromagnetic telecommunication signal, and it was observed that as the signal travelled away from the emission point, it became progressively broader and more entropic. The choice of logarithmic base b may vary depending on the application. Base “2” corresponds to units of “bits” (or “shannons”), base “e” to “nats” (or “natural units”), and base “10” to “dits” (or “decimal digits”). Interconversion is trivial because 1 dit = 1.44 nats = 3.32 bits.
. The original study investigated the propagation of an electromagnetic telecommunication signal, and it was observed that as the signal travelled away from the emission point, it became progressively broader and more entropic. The choice of logarithmic base b may vary depending on the application. Base “2” corresponds to units of “bits” (or “shannons”), base “e” to “nats” (or “natural units”), and base “10” to “dits” (or “decimal digits”). Interconversion is trivial because 1 dit = 1.44 nats = 3.32 bits.
The fundamental concept of information entropy, which is applicable to a wide range of problems beyond information theory, quantifies the level of uncertainty associated with an event. Rare or unlikely events (e.g., an earthquake) are more surprising and therefore more informative than that of routine ones (e.g., tomorrow's sunrise). Alternatively, rare events, being less certain, require more information to be understood than common occurrences:
Low probability event  Surprising event
Surprising event  Valuable new information
Valuable new information  High information entropy.
High information entropy.
High probability event  Unsurprising event
Unsurprising event  Limited new information
Limited new information  Low information entropy.
Low information entropy.
Fhionnlaoich and Guldin19 proposed a thoughtful modification of formula (1) to obtain an assumption-free nanoparticle entropy (E), which is suitable for describing a wide range of nanoparticle size distributions. They introduced formula (2) to account for the width of measuring bin and nullify its influence on H.
| E = eH × bin width | (2) |
The significance of this correction lies in the fact that as the bin width decreases, the number of observations (i) in formula (1) increases, and, as a result, the values of H increase exponentially. The application of formula (2) eliminates such effects, provided that the number of observations (i) is sufficiently large. In the present work, the calculation of information entropy (H) and the corresponding nanopore entropy (E) was performed using formulae (1) and (2) applied to the PSDs of the studied porous solids.
Experimental
Preparation of materials
The porous materials used here have been studied before and include sixteen (16) mesoporous alumino–phosphoro–vanadate mixed oxides of the general formula Al100PxVy, where x, y = 0, 5, 10, and 20.22–24 The full formula involves substantial amounts of oxygen to balance the valencies of Al, P and V, but a precise oxide-based formula is not fully established, and thus, the abbreviated version is more convenient to use. All materials Al100PxVy with some of their properties are shown in Table 1. S.I.-2 has some additional informative properties of these materials.| Sample | Connectivity caverage | H(2) (48–0.5) (bits) | E(2) = eH(2)·0.5 (nm) |
|---|---|---|---|
| Al100P0V0 | 6.5 | 3.70 | 20.22 |
| Al100P5V0 | 12.3 | 3.81 | 22.58 |
| Al100P10V0 | 11.2 | 4.59 | 49.25 |
| Al100P20V0 | 14.0 | 5.06 | 78.80 |
| Al100P0V5 | 5.8 | 3.42 | 15.28 |
| Al100P5V5 | 7.0 | 3.84 | 23.26 |
| Al100P10V5 | 9.1 | 4.58 | 48.76 |
| Al100P20V5 | 9.6 | 4.97 | 72.01 |
| Al100P0V10 | 5.8 | 3.26 | 13.02 |
| Al100P5V10 | 7.8 | 4.04 | 28.41 |
| Al100P10V10 | 10.5 | 4.86 | 64.51 |
| Al100P20V10 | 15.0 | 5.40 | 110.70 |
| Al100P0V20 | 10.6 | 4.80 | 60.75 |
| Al100P5V20 | 9.0 | 4.53 | 46.38 |
| Al100P10V20 | 10.9 | 5.03 | 76.47 |
| Al100P20V20 | 15.2 | 5.41 | 111.82 |
The method of preparation is as follows: calculated amounts of Al(NO3)3·9H2O, H3PO4 and V2O5 (dissolved in 10 mL of NH4OH) were dissolved in 120 mL of water, and ammonia was added while stirring until a pH of 9.5 was attained. The formed gel was then dried slowly at 110 °C for 24 h, cooled, ground and finally heated at 600 °C for 6 h. For more details, see ref. 22–24. The parent material Al100P0V0 has the typical structure of amorphous Al2O3, and the addition of P at a constant concentration of V, and vice versa, noticeably increases the specific surface area and specific pore volume (see Table in S.I.-2). This enlargement of surface area is due to the heteroatoms of P and V that disrupt the crystallization habit of alumina, and as a result, the materials develop an amorphous structure with enhanced porosity. This in turn influences the pore connectivity (c), as shown in Table 1.
Characterization by nitrogen porosimetry
Specific surface area (Sp) (m2 g−1) and specific pore volume (Vp) (cm3 g−1) were determined by standard nitrogen adsorption–desorption porosimetry at 77 K, measured over the relative pressure range 0 < (P/P0) < 1, as described previously.23,24 The corresponding adsorption–desorption isotherms, e.g. VN2,ads = f(P/P0) and VN2,des = f(P/P0), are reproduced in S.I.-2. The standard BET (Braunauer–Emmett–Teller) methodology was employed for the estimation of surface area (Sp), and the BJH (Barrett–Joyner–Halenda) algorithm was used for calculating PSD, i.e., (dV/dD) (cc g−1 nm−1) = f(D) (nm), as shown in Table S.I.-2. Details about nitrogen porosimetry and the BET and BJH methods can be found in literature.20,21Pore connectivities
The average pore connectivities (caverage) for the sixteen Al100PxVy (x, y = 0, 5, 10, and 20) materials are given in S.I.-2 and reproduced in Table 1. They were estimated from the hysteresis loops of the nitrogen adsorption–desorption isotherms shown in S.I.-2, using the method proposed by Seaton and co-workers.13–15 Some short relevant comments and typical fitting results in the range of 0.3 < (P/P0) < 0.6 are shown in S.I.-3 and discussed more extensively in ref. 23 and 24.Information entropy
Information entropy H(2) and nanopore entropy E(2) were calculated according to formulae (1) and (2) using the binary logarithmic base (b) = 2 (indicated by the number in parentheses). For H(2), we employed forty-eight (n = 48) points in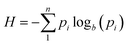 , chosen as follows: across the D axis of desorption isotherms dV/dD = f(D) shown in S.I.-2, forty eight equidistant points were selected in the range 2.5 < D < 26.5 (nm). This corresponds to a bin width, BW = (26.5 − 2.5)/48 = 0.5 nm. A measuring stick of size 0.5 nm was chosen purposely since it corresponds roughly to the size of N2 molecule, which upon adsorption covers 0.162 nm2 or a circle with a diameter of 0.45 nm.
, chosen as follows: across the D axis of desorption isotherms dV/dD = f(D) shown in S.I.-2, forty eight equidistant points were selected in the range 2.5 < D < 26.5 (nm). This corresponds to a bin width, BW = (26.5 − 2.5)/48 = 0.5 nm. A measuring stick of size 0.5 nm was chosen purposely since it corresponds roughly to the size of N2 molecule, which upon adsorption covers 0.162 nm2 or a circle with a diameter of 0.45 nm.
At each of those 48 Di values, e.g. D1, D2, D3 …D48, there are 48 values of (dV/dD)i, e.g. (dV/dD)1, (dV/dD)2, (dV/dD)3, ……. (dV/dD)48. Then ratios of 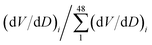 are the pi values, that is, the fractional probability of each component of distribution subject to the constrain
are the pi values, that is, the fractional probability of each component of distribution subject to the constrain 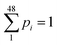 . The values of nanopore entropy (E) were calculated according to formula (2). The results for both H(2) and E(2) are summarized in Table 1. It is noted that E has units similar to bin width, i.e., nanometres (nm), while H is dimensionless, but depending on the logarithmic base b, it may be expressed in “bits” (for b = 2), nats (for b = e) or “dits” (for b = 10).
. The values of nanopore entropy (E) were calculated according to formula (2). The results for both H(2) and E(2) are summarized in Table 1. It is noted that E has units similar to bin width, i.e., nanometres (nm), while H is dimensionless, but depending on the logarithmic base b, it may be expressed in “bits” (for b = 2), nats (for b = e) or “dits” (for b = 10).
Additionally, we calculated two sets of H and E values using logarithmic base b = 10 (dits) and b = e (nats) with similar bin width of 0.5 nm for comparison purposes. These additional values are mentioned as H(10), E(10) for b = 10 and H(e), E(e) for b = e. Additionally, for b = e (nats), we estimated additional sets of H′(e) and E(e) values with bin width = 1 nm (not 0.5 nm). In that case, 24 equidistant points were chosen across the D axis and B.W = (26.5 − 2.5)/24 = 1 nm, 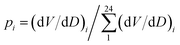 and
and 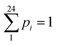 . Rest calculations of H's and E's are as above. All additional results are collected in Table S.I.-4. It is observed that the two datasets for b = e (nats) in Table S.I.-4, estimated for n = 48 pi values and bin width = 0.5 nm, on the one hand, and n = 24 pi values and bin width = 1.0 nm, on the other hand, exhibit a difference between the H(e) and H′(e) values since the number of employed points is different, i.e., 48 for H(e) and 24 for H′(e). The difference is nullified for E(e) and E′(e), as anticipated from formula (2). This exercise of alternative calculations shows that the obtained results are free of miscalculations due to the number of employed measurements.
. Rest calculations of H's and E's are as above. All additional results are collected in Table S.I.-4. It is observed that the two datasets for b = e (nats) in Table S.I.-4, estimated for n = 48 pi values and bin width = 0.5 nm, on the one hand, and n = 24 pi values and bin width = 1.0 nm, on the other hand, exhibit a difference between the H(e) and H′(e) values since the number of employed points is different, i.e., 48 for H(e) and 24 for H′(e). The difference is nullified for E(e) and E′(e), as anticipated from formula (2). This exercise of alternative calculations shows that the obtained results are free of miscalculations due to the number of employed measurements.
It is mentioned that the calculation of PSDs and of pore connectivity is performed by considering cylindrical, random, and disordered pore geometries that are common for inorganic materials like aluminates or silicates.20,21 Besides, the present Al–P–V materials are neither expected to provide nor have they provided any indications of elongated or ordered pore geometry in previous studies22–24). It is understood that, as suggested by Seaton,14a switching from a cylindrical to a slit-pore model may shift the absolute values of PSD (mean size and spread) and connectivity in a uniform fashion. However, this is not expected to fundamentally alter the qualitative correlation between the obtained data. Besides, such a switch has no physical basis in the present case and may only apply to carbons or pillared clays possessing slit-like pores.
Results
In Table 1, the values of the pore connectivity (caverage), information entropy H(2) and nanopore entropy E(2) are listed for the sixteen (16) porous materials Al100PxVy (x, y = 0, 5, 10, an d 20). Fig. 1 presents the values of H(2) (upper part) and E(2) (lower part) as a function of pore connectivity (c), i.e. H(2) = f(c)-upper part and E(2) = f(c)-lower part. | ||
Fig. 1 Variation in information entropy (H(2)) (upper part) and nanopore entropy (E(2)) (lower part) as a function of pore connectivity (c). Data are taken from Table 1. The regression lines read H(2) = 2.58 + 0.19·c (dashed red line  with R2 = 0.68) and E(2) = −36.54 + 8.90·c, (dashed red line with R2 = 0.68) and E(2) = −36.54 + 8.90·c, (dashed red line  with R2 = 0.73). If the outlier points are excluded, the fitting lines (not shown) remain almost similar but the correlation coefficients improve; H(2) = 2.46 + 0.21c, (R2 = 0.86) and E(2) = −42.21 + 9.82c, (R2 = 0.91). with R2 = 0.73). If the outlier points are excluded, the fitting lines (not shown) remain almost similar but the correlation coefficients improve; H(2) = 2.46 + 0.21c, (R2 = 0.86) and E(2) = −42.21 + 9.82c, (R2 = 0.91). | ||
Similar graphs to those in Fig. 1 are presented in S.I.-5 for all H(10), E(10) = f(c) and E(e), E(e) = f(c) relationships for comparison purposes.
As can be seen in Fig. 1, both H(2) and E(2) show a strong positive correlation with pore connectivity, indicating that as the pore network becomes more interconnected, both the information entropy (H(2)) and the corresponding nanopore entropy (E(2)) increase. The corresponding first-order linear fittings exhibited H(2) = 2.58 + 0.19c, (R2 = 0.68) and E(2) = −36.54 + 8.90c, (R2 = 0.73). If the outlier points are excluded, the linear fitting lines (not shown) remain more or less similar but the correlation coefficients improve noticeably, such as H(2) = 2.46 + 0.21c, (R2 = 0.86) and E(2) = −42.21 + 9.82c, (R2 = 0.91). In any case, the relationship is stronger for E(2), suggesting it may be more sensitive to connectivity variations. Similar correlations are apparent for the data plots H(10) = f(c); E(10) = f(c); H(e) = f(c) and E(e) = f(c) and are shown in S.I.-5 for comparison. These results indicated a strong dependence between the compared parameters. The subtle physical meaning of this dependence will be discussed in the next section.
Discussion
As shown in Fig. 1, there is a discreet correlation between pore connectivity (c) and information entropy (H) or nanopore entropy (E), expressed in bits. In Table 2, we transcribed the numerical data of Table 1 in binary logarithmic values (logarithmic base b = 2). Specifically, the values of pore connectivity (c), information entropy (H(2)) and nanopore entropy (E(2)) were expressed as log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, log2
c, log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2), and H(2) → log2
E(2), and H(2) → log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) − log2 (bin width) = log2
E(2) − log2 (bin width) = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) − logb (0.5) = log2
E(2) − logb (0.5) = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) + 1.
E(2) + 1.
| Sample | Log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
E(2) | Log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) E(2) |
H(2) = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) + 1.0 E(2) + 1.0 |
|---|---|---|---|---|
| Al100P0V0 | 2.70 | 20.22 | 4.34 | 5.34 |
| Al100P5V0 | 3.62 | 22.58 | 4.50 | 5.50 |
| Al100P10V0 | 3.49 | 49.25 | 5.62 | 6.62 |
| Al100P20V0 | 3.81 | 78.80 | 6.30 | 7.30 |
| Al100P0V5 | 2.54 | 15.28 | 3.93 | 4.93 |
| Al100P5V5 | 2.81 | 23.26 | 4.54 | 5.54 |
| Al100P10V5 | 3.19 | 48.76 | 5.61 | 6.61 |
| Al100P20V5 | 3.26 | 72.01 | 6.17 | 7.17 |
| Al100P0V10 | 2.54 | 13.02 | 3.70 | 4.70 |
| Al100P5V10 | 2.96 | 28.41 | 4.83 | 5.83 |
| Al100P10V10 | 3.39 | 64.51 | 6.01 | 7.01 |
| Al100P20V10 | 3.91 | 110.70 | 6.79 | 7.79 |
| Al100P0V20 | 3.41 | 60.75 | 5.92 | 6.92 |
| Al100P5V20 | 3.17 | 46.38 | 5.54 | 6.54 |
| Al100P10V20 | 3.45 | 76.47 | 6.26 | 7.26 |
| Al100P20V20 | 3.93 | 111.82 | 6.81 | 7.81 |
The same transcription of data was also applied to the values of information entropy H(10)–H(e) and nanopore entropies E(10)–E(e) in Table S.I.-4. The new results are presented in Table S.I.-6.
In Fig. 2, we plotted the data in Table 2. The corresponding first-order fitting relationships are given by formulae (3) and (4) with a very strong correlation coefficient R2 = 0.924. The single out-of-trend point at the right-middle section of all sub-figures has not been considered. This outlier corresponds to sample Al100P5V0, exhibiting higher c and lower H values. This can be attributed to its lower-than-expected Dmax and FWHM, as seen in Table S.I.-2 and Fig. 5.24 This, in turn, leads to a lower entropy value. This discrepancy may originate from some experimental mishap during sample preparation. The plots for the remaining 15 samples fifteen samples follow the below relationships:
Log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = −1.276 + 2.091·log2 E(2) = −1.276 + 2.091·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c
| (3) |
H(2) = −0.277 + 2.092·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c
| (4) |
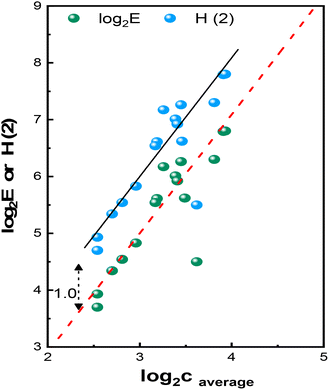 | ||
Fig. 2 Plots obtained from the data in Table 2. The regression lines have the form log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = −1.276 + 2.091·log2 E(2) = −1.276 + 2.091·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, (dashed red line c, (dashed red line  with R2 = 0.924) and H(2) = −0.277 + 2.092·log2 with R2 = 0.924) and H(2) = −0.277 + 2.092·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, (black line c, (black line  with R2 = 0.924). The out-of-trend point in the right-low-middle section has not been considered. with R2 = 0.924). The out-of-trend point in the right-low-middle section has not been considered. | ||
The above relationships (plots based on log2) exhibit very a strong correlation coefficient of R2 = 0.924. Similar results (R2 = 0.921 for plots based on log10 and R2 = 0.926 for plots based on loge) are obtained if decadic or natural logarithms are used instead of binary logarithm, as shown in Fig. S.I.-7. All R2 values are practically similar as expected, with differences attributable to the rounding of decimal points during calculations. The outcome establishes a strong correlation between the logarithm of pore connectivity (logb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) and information entropy H(b) as well as the logarithm of nanopore entropy log
c) and information entropy H(b) as well as the logarithm of nanopore entropy log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(b) expressed in logarithmic base b = 10 (dits), e (nats) or 2 (bits).
E(b) expressed in logarithmic base b = 10 (dits), e (nats) or 2 (bits).
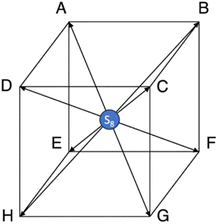
Nevertheless, although correlations based on b = 10 (dits) and e (nats) are mathematically as good as the ones based on b = 2 (bits), the latter offers a more profound interpretation of the relationship between connectivity and entropy. For instance, it reflects the binary questions Q a lilliputian traveller (say a nitrogen molecule) in the pore labyrinth needs to ask the Genie to find its way at a crossroad (site) with c connections (bonds). This is equivalent to counting the number of connections. The number of binary questions Q is related to c by the simple formula Q = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, as exemplified in Fig. 3. If the connections are c = 8 = 23, then three questions are needed. Similarly, for c = 16 = 24, four questions are necessary, for c = 4 = 22, two questions and finally for c = 2 = 21, just one question is needed.
c, as exemplified in Fig. 3. If the connections are c = 8 = 23, then three questions are needed. Similarly, for c = 16 = 24, four questions are necessary, for c = 4 = 22, two questions and finally for c = 2 = 21, just one question is needed.
By introducing Q = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, formulae (3) and (4) can be re-written as follows:
c, formulae (3) and (4) can be re-written as follows:
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = −1.28 + 2.09·log2 E(2) = −1.28 + 2.09·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = −1.28 + 2.09 Q ∼ 2Q − 1 c = −1.28 + 2.09 Q ∼ 2Q − 1
| (5) |
H(2) = −0.28 + 2.09·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = −0.28 + 2.09 Q ∼ 2Q c = −0.28 + 2.09 Q ∼ 2Q
| (6) |
The above results show that for porous materials, like the ones in the present case, the estimation of information entropy (H) and nanopore entropy € also yields the value of pore connectivity (c). This relationship becomes apparent irrespective of the expression of H, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E and log
E and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c in the logarithmic form of base b = 10, e, or 2. By employing base b = 2, an additional opportunity arises to formulate binary questions Q (yes–no) for counting c and establishing a relationship between c and information entropy parameters E and H. These experimental findings are modelled as follows.
c in the logarithmic form of base b = 10, e, or 2. By employing base b = 2, an additional opportunity arises to formulate binary questions Q (yes–no) for counting c and establishing a relationship between c and information entropy parameters E and H. These experimental findings are modelled as follows.
If a porous sample exhibits an average pore connectivity of c = 8 = 23, as illustrated in Fig. 3, which is a typical value for the present materials (see Table 1), the corresponding logarithm of binary nanopore entropy would be log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = 4.99 (as per formula (5)). Similarly, the binary information entropy of PSD is H(2) = 5.99 (as per formula (6)) and the binary questions are Q = 3. Similarly, if c = 16 = 24, the binary questions are Q = 4, while log2
E(2) = 4.99 (as per formula (5)). Similarly, the binary information entropy of PSD is H(2) = 5.99 (as per formula (6)) and the binary questions are Q = 3. Similarly, if c = 16 = 24, the binary questions are Q = 4, while log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = 7.07 and H(2) = 8.01. For c = 4 = 22, Q = 2, log2
E(2) = 7.07 and H(2) = 8.01. For c = 4 = 22, Q = 2, log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = 2.90 and H(2) = 3.89. Finally, for c = 2 = 21, Q = 1, log2
E(2) = 2.90 and H(2) = 3.89. Finally, for c = 2 = 21, Q = 1, log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = 0.81 and H(2) = 1.80. These results are summarized in Table 3.
E(2) = 0.81 and H(2) = 1.80. These results are summarized in Table 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, binary questions Q, binary information entropy H(2), and binary logarithm of nanopore entropy log2
c, binary questions Q, binary information entropy H(2), and binary logarithm of nanopore entropy log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2)
E(2)
| Pore connectivity c = 2n | Binary logarithm log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Binary questions Q | Information entropy H(2) (bits) | Binary logarithm of nanopore entropy log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) E(2) |
|---|---|---|---|---|
| 16 = 24 | 4 | 4 | 8.01–8 | 7.07–7 |
| 8 = 23 | 3 | 3 | 5.99–6 | 4.99–5 |
| 4 = 22 | 2 | 2 | 3.89–4 | 2.90–3 |
| 2 = 21 | 1 | 1 | 1.80–2 | 0.81–1 |
The corresponding idealized linear relationships H(2) = f(log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c), log2
c), log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = f(log2
E(2) = f(log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) and Q = f(log2
c) and Q = f(log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) are as follows:
c) are as follows:
Log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2) = −1.27 + 2.073 × log2 E(2) = −1.27 + 2.073 × log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c
| (7 ≃ 5) |
H(2) = −0.26 + 2.07 × log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c
| (8 ≃ 6) |
Q = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, c,
| (9) |
Q ≈ H(2)/2 ≈ log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(2)/2 + 0.5 E(2)/2 + 0.5
| (10) |
Entropy of pore mixing
Formula (1) that provides the values of information entropy (H) bears similarities with the well-known relationship describing the entropy of mixing (ΔSmixing) in solutions.25 When various independent components (A, B,…) are mixed to form a solution, the entropy of mixing is given by
ΔSmixing = −R(xA × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xA + xB × ln xA + xB × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xB + …) = −RΣxi × ln xB + …) = −RΣxi × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xi xi
| (11) |
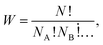 | (12) |
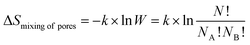 | (13) |
Formula (13) is the classical Boltzmann's equation that expresses the change in thermodynamic entropy during mixing processes. After applying a simplifying technique, which includes the Stirling's approximation and multiplication by the number of particles N, we can calculate the change in the entropy of the entire system compared with that of the unmixed case.
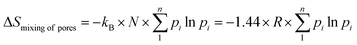 | (14) |
The above thermodynamic entropy for i = 1…. n groups of species of total number N is analogous to the binary information entropy (H(2)) of the same distribution of species. While the thermodynamic entropy is due to the positional uncertainty of species, the Shannon information entropy, given by formula (1), describes the compositional uncertainty of the N collection of species. Thus, the similarity between formulae (1) and (14) may be expressed in the form:
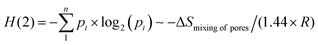 | (15) |
The H(2) parameter for the present collection of porous materials is given by the relation 6 ≃ 8; for instance, H(2) = −0.26 + 2.07·log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c. If this formula is simplified to the form of H(2) ∼ 2
c. If this formula is simplified to the form of H(2) ∼ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, then formula (15) can be expressed in the following form:
c, then formula (15) can be expressed in the following form:
H(2) ∼ 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2 log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c ∼ −ΔSmixing c ∼ −ΔSmixing![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pores/(1.44 × R) or −ΔSmixing pores/(1.44 × R) or −ΔSmixing![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pores ∼ 2.88·R × log2 pores ∼ 2.88·R × log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c
| (16) |
All parameters in formula (16) are in binary form. Conversion into the natural logarithm form yields a simpler formula:
2R × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c = R × H(e) ∼ or −ΔSmixing c = R × H(e) ∼ or −ΔSmixing![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pores pores
| (17) |
A similar relationship S = k × H is established in statistical mechanics, linking the macroscopic properties of a system to the microstates of its constituent particles. Information entropy quantifies the uncertainty of these microstates. In the present case, for c = 16, 8, 4 and 2; H(2) = 8, 6, 4, and 2 bits (see Table 3); H(e) = 2.30 × H(2) = 18.4, 9.2, 4.6 and 2.3 nats, and the entropy of pore mixing −ΔS = 46.1, 34.6, 23.1 and 11.5 J K−1, respectively, which are reasonable outcomes. Unfortunately, as far as we know, there are no relevant theoretical or experimental values in the literature for comparison.
Explanation of the relationship between connectivity and information entropy
An explanation for the observed correlation between pore connectivity and information entropy of PSD may be traced in the field of statistical physics, referred to as the random packing of particles (RPP). The relevant literature is extensive. This operation reflects too the entropy of random pore mixing described in the previous section. Hence, we focus here on some works referred to the effect of particle size26–29 and the spread of particle distribution30,31 on the number of neighbouring particles (n).As shown by Liu et al.,26 in a random collection of spherical particles, a robust correlation exists between the average number of neighbouring particles (n) and normalized particle size (r) (see Fig. 3). This analysis compiled data from multiple studies28–30 based on the collections of spherical particles with normal (N) or log-normal (LN) distributions, different distribution widths (σ) and varying strengths of interparticle adhesion (Ad). Remarkably, regardless of the distribution type (N or LN), its spread (σ), or adhesion strength (Ad), the neighbour number scales with the particle size according to n ∼ rk. This result reflects the fact that large particles have more neighbours (connections) than small ones.
Similar findings were reported by O'Donovan et al.,27 where theoretical calculations showed that the average contact number z (∼connections) of spherical particles of a certain size follows systematic relationships with normalized radius (r), area (a ∼ r2) and volume (v ∼ r3) across different size distributions (monodispersed, bidispersed, uniform, Gaussian and log-normal). The resulting scaling formulae take the form: (number of normalized neighbours or contacts) ≈ f(normalized radius)a ≈ f(normalized area)b ≈ f(normalized volume)c, where exponents a > 1, b ∼ 1 and c < 1.
These results can be summarized as follows: a random collection of spherical particles, initially isolated, gradually approach each other until contact is established. Each contact point represents a connection c. Naturally, larger spheres form more connections due to their greater surface area. If Di denotes the diameter of the i-th sphere, with surface area Ai ∝ Di2, and the connectivity depends solely on the exposed surface area, then one would expect c(Di) ∝ kDi2. However, not all surface area is available for contact; hence, the relationship is generally expressed as c(Di) ∝ kDαi with α < 2 or in logarithmic form log(c) ≈ α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(D).
log(D).
By replacing random spherical particles with a distribution of random-size spherical pores, the above arguments lead to the same outcome: large pores exhibit more connections, whereas smaller pores exhibit fewer connections. In other words, materials with a larger maximum diameter (Dmax) in their PSD are expected to show a higher average connectivity. In the present case, the experimental data between the average pore connectivity (caverage) (Table 1) and the maximum diameter (Dmax, nm) of PSD (Table in S.I.-1) are related by a power law (formula (18)), such as c ∝ kDα, predicted theoretically.
| c = 0.98 (Dmax)1.07 | (18) |
With a very strong correlation coefficient R2 = 0.897. The relevant plot is shown in Fig. 4-upper left. The exponent 1.07 appears smaller than the exponents obtained in previous studies26,27 referring to solid particles. In those cases, the surrounding medium (assumed air or vacuum) does not influence the packing. However, in porous materials, the medium surrounding the pores is a solid mass forming pore walls. Therefore, the available packing space for smaller pores around a larger one is diminished. Consequently, formula (18) expresses the fact that the values of pore connectivity (c) correspond roughly to Dmax expressed in nm. For example, if Dmax = 1, then c ≈ 0.98, if Dmax = 2, then c ≈ 2.06, if Dmax = 4, then c ≈ 4.32, if Dmax = 8, then c ≈ 9.07 and if Dmax = 16, c ≈ 17.04.
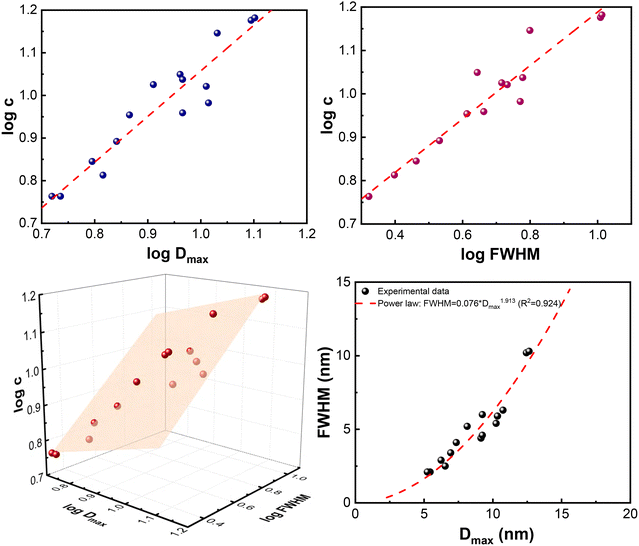 | ||
| Fig. 4 Graphical presentation of regression results described by formulae (18), (19), (20), and (21): upper left: log(c) = 1.07·log (Dmax) − 0.01, (R2 = 0.897); upper right: log(c) = 0.62·log (FWHM) + 0.57, (R2 = 0.929); lower left: log(c) = 0.42 + 0.28·log(Dmax) + 0.46·log(FWHM) (R2 = 0.933). The plane tilts more strongly along the FWHM axis, confirming that log (FWHM) is the dominant predictor of log(c); and lower right: FWHM = 0.076·(Dmax)1.913 (R2 = 0.924). | ||
Another important parameter of particle size distribution is the standard deviation σ. Its effect on the number of neighbouring particles (n) in packed particle studies remains ambiguous26 and depends on the model applied. In relevant works of Clusel et al.31 and Cronin et al.,32 there is a discussion on the effect of the spread of log-normal packing distributions on the resulting number of neighbouring particles (see Fig. 9 in ref. 32). Theoretical results, obtained from molecular dynamics simulations and model predictions,31 show that the probability of the density of neighbours for packings with log-normal size distributions of mean = 1 becomes wider and flatter and its maximum moves to larger values as the standard deviation (σ) increases from 0.01 to 0.3. This means that as sigma increases, there are more neighbours of variable sizes next to each other.
In the present case of pores, the FWHM of PSD is strongly related to pore connectivity (c) according to formula (19)
| c = 3.72 × (FWHM)0.62 | (19) |
| c = 2.63 × (Dmax)0.28 × (FWHM)0.46 | (20) |
The strong interdependence between Dmax and FWHM is critical for establishing the relationship between pore connectivity and information entropy. This dependence is described by the formula (21):
| FWHM = 0.076 × (Dmax)1.913 | (21) |
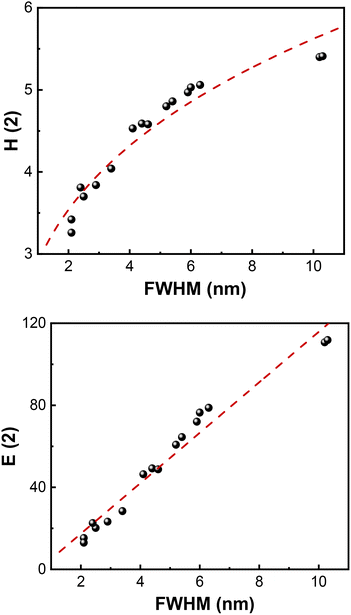
Indeed, as shown in Fig. 5, binary information entropy (H(2)) and FWHM are related by a strong power law H(2) = 2.90 × (FWHM)0.289 with correlation coefficient R2 = 0.933. The binary nanopore entropy (E(2)) is also related to FWHM via an excellent linear relationship E(2) = −7.19 + 12.30·(FWHM) with R2 = 0.96.
The net result is that the pore connectivity of random-size pores and the entropy of their distribution move in a parallel way and their interrelation is physically justified.
Heteroscedasticity
In statistics, the parallel growth in variance with the mean of a distribution is termed heteroscedasticity and is common in natural growth processes, fragmentation and aggregation systems.32,33 In the present case, as the pore domain size increases, the distribution broadens, which means that larger pore sizes are less uniform and show greater size dispersion.In Fig. 6-upper part, the general concept of heteroscedasticity is depicted in a simplified version. In Fig. 6-lower part, the heteroscedasticity of the experimental data Dmax and the range of FWHM (not its single value) are shown.
In conclusion, the increase in Dmax drives connectivity, as shown by formula (18). The parallel increase in FWHM (Fig. 4) drives information entropy as per formula (1). As a result, the two parameters move in tandem as expressed by formulae (5) and (6) as long as the corresponding PSDs exhibit heteroscedasticity.
The above discussion leaves several questions unanswered. These include the kind of relation between pore connectivity and pore entropy in materials with ordered or quasi-ordered porosity, which often exhibit homoscedasticity, that is, a similar mean but different variance of pore size distributions. Another point of interest is the relationship(s) between pore connectivity and pore anisotropy and/or pore length. A methodology for estimating these two quantities has been detailed previously by our team and can be found in the relevant bibliography. Additionally, there is a possible relationship between (pore) entropy and (pore) anisotropy, a dependence that has emerged in different systems and fields like geology, medicine and astronomy. These queries necessitate further research work.
Conclusions
In this study, we demonstrated that the Shannon information entropy (H) of pore size distributions in oxidic alumino–phosphoro–vanadate porous solids with random disordered porosity is strongly correlated with the average pore connectivity (c) of the porous network. Pore connectivity was estimated using the Seaton's method, which relies on the hysteresis loop of nitrogen adsorption–desorption isotherms. The relationship between H and c becomes apparent when expressed in the binary logarithmic form H(2) = A + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2(c). The results are consistent for other logarithmic bases b = 10 or e. However, employing the binary base (b = 2) offers a conceptual advantage since binary (yes–no) questions Q can be used to count the number of connections (Q = log2(c)). The outcome aligns with the statistical expression of the thermodynamic entropy of pore mixing (ΔSmixing
log2(c). The results are consistent for other logarithmic bases b = 10 or e. However, employing the binary base (b = 2) offers a conceptual advantage since binary (yes–no) questions Q can be used to count the number of connections (Q = log2(c)). The outcome aligns with the statistical expression of the thermodynamic entropy of pore mixing (ΔSmixing![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of
of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pores), which parallels the classical paradigm of mixing in solutions. While thermodynamic entropy (ΔS) reflects the positional uncertainty of species, information entropy (H) describes their compositional uncertainty.
pores), which parallels the classical paradigm of mixing in solutions. While thermodynamic entropy (ΔS) reflects the positional uncertainty of species, information entropy (H) describes their compositional uncertainty.
The physical meaning of this correlation lies in the analogy between a random collection of connected pores and the well-established models of random packing of spherical particles. Importantly, the proposed relationship suggests that pore connectivity, a property that is difficult to determine, can be conveniently estimated via information entropy (H) or nanopore entropy (E), which can be derived from any pore size distribution plot. This is valid only for truly disordered pore systems.
The statistical base of the correlation between information entropy (IE) of pore size distributions with average pore connectivity (caverage) is the heteroscedasticity observed between the variance (≈ full width at half maximum, FWHM) and the mean (≈ maximum diameter, Dmax) of pore size distributions: the variance (≈ FWHM) directly affects information entropy (IE). The mean (≈ Dmax) directly affects pore connectivity, as revealed by the model of random packing of spherical particles.
Extension of similar studies to materials with ordered porosity, such as MCMs, zeolites or MOFs, or even with semi-ordered porosity, that represent most non-ordered systems, as well as in materials possessing slit-like pores like carbons of pillared clays, is needed in order to understand the application and the limits of the present observations.
Author contributions
Antigoni G. Margellou: data curation, formal analysis, writing – original draft. Gerasimos S. Armatas: data curation, formal analysis, investigation, writing – original draft, review and editing. Konstantina Kolonia: data curation, formal analysis, investigation. Philippos J. Pomonis: conceptualization, formal analysis, investigation, writing – original draft, review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp04416b.References
- F. Schüth, K. S. W. Sing and J. Weitkamp, Handbook of porous solids, Wiley-VCH, Weinheim, 2002, vol. 4 Search PubMed.
- V. Gitis and G. Rothenberg, Handbook of porous materials: synthesis, properties, modeling and key applications, World Scientific Publishing Co. Pte. Ltd., Singapore, 2021 Search PubMed.
- R. L. Portsmouth and L. F. Gladden, Determination of pore connectivity by mercury porosimetry, Chem. Eng. Sci., 1991, 46, 3023–3036 CrossRef CAS.
- R. Aris, The mathematical theory of diffusion and reaction in permeable catalysts, Clarendon Press, Oxford, 1975, vol. 1, p. 25 Search PubMed.
- G. S. Armatas and P. J. Pomonis, A Monte Carlo pore network for the simulation of porous characteristics of functionalized silica: pore size distribution, connectivity distribution and mean tortuosities, Chem. Eng. Sci., 2004, 59, 5735–5749 CrossRef CAS.
- J. J. Meyers, S. Nahar, D. K. Ludlow and A. I. Liapis, Determination of the pore connectivity and pore size distribution and pore spatial distribution of porous chromatographic particles from nitrogen sorption measurements and pore network modelling theory, J. Chromatogr. A, 2001, 907, 57–71 CrossRef CAS PubMed.
- R. Mann, in Structured Catalysts and Reactors, ed. A. Cybulski and J. A. Moulijn, Marcel Dekker, 1998 Search PubMed.
- B. Ghanbarian and H. Daigle, Permeability in two-component porous media: Effective-medium approximation compared with Lattice-Boltzmann simulations, Vadose Zone J., 2016, 15, 1–10 CrossRef.
- J. K. Carson, V. Gonzalez-Quinones, D. V. Murphy, C. Hinz, J. A. Shaw and D. B. Gleeson, Low pore connectivity increases bacterial diversity in Soil, Appl. Environ. Microbiol., 2010, 76(12), 3936–3942 CrossRef CAS PubMed.
- C. C. Ezeuko, A. Sen, A. Grigoryan and I. D. Gates, Pore-network modelling of biofilm evolution in porous media, Biotechnol. Bioeng., 2011, 108, 2413–2423 CrossRef CAS PubMed.
- S. W. Yoon and D. Giménez, Entropy characterization of soil pore systems derived from soil-water retention curves, Soil Sci., 2012, 177(6), 361–368 CrossRef CAS.
- T. Klöffel, N. Jarvis, S. W. Yoon, J. Barron and D. Giménez, Relative entropy as an index of soil structure, Eur. J. Soil Sci., 2022, 73(3), e13254 CrossRef.
- N. A. Seaton, Determination of the connectivity of porous solids from nitrogen sorption measurements, Chem. Eng. Sci., 1991, 46, 1895–1909 CrossRef CAS.
- (a) H. Liu, L. Zhang and N. A. Seaton, Determination of the connectivity of porous solids from nitrogen sorption measurements-II. Generalisation, Chem. Eng. Sci., 1992, 47, 4393–4404 CrossRef CAS; (b) H. Liu, L. Zhang and N. A. Seaton, Analysis of Sorption Hysteresis in Mesoporous Solids Using a Pore Network Model, J. Colloid Interface Sci., 1993, 156, 285–293 CrossRef CAS; (c) H. Liu, L. Zhang and N. A. Seaton, Sorption hysteresis as a probe of pore structure, Langmuir, 1993, 9, 2576–2582 CrossRef CAS.
- H. Liu and N. A. Seaton, Determination of the connectivity of porous solids from nitrogen sorption measurements-III. Solids containing large mesopores, Chem. Eng. Sci., 1994, 49, 1869–1878 CrossRef CAS.
- V. Mayagoitia, F. Rojas, I. Kornhauser, G. Zgrablich, R. J. Faccio, B. Gilot and C. Guiglion, Refinements of the Twofold Description of Porous Media, Langmuir, 1996, 12, 211–216 CrossRef CAS.
- V. Mayagoitia, F. Rojas, I. Kornhauser and H. Pérez-Aguilar, Modelling of Porous Media and Surface Structures:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Their True Essence as Networks, Langmuir, 1997, 13, 1327–1331 CrossRef CAS.
Their True Essence as Networks, Langmuir, 1997, 13, 1327–1331 CrossRef CAS. - C. E. Shannon, A Mathematical Theory of Communication, Bell Syst. Tech. J., 1948, 27, 379–423 CrossRef . ibib, 1948, 27, 623–656.
- N. Mac Fhionnlaoich and S. Guldin, Information Entropy as a Reliable Measure of Nanoparticle Dispersity, Chem. Mater., 2020, 32, 3701–3706 CrossRef CAS PubMed.
- S. J. Gregg and K. S. W. Sing, Adsorption, surface area, and porosity, Academic Press, London, 2nd edn, 1982 Search PubMed.
- F. Rouquerol, J. Rouquerol and K. S. W. Sing, Adsorption by Powders and Porous Solids, Academic Press, San Diego, 1999 Search PubMed.
- R. D. Gourgeon, P. R. Bodart, R. K. Harris, D. M. Kolonia, D. E. Petrakis and P. J. Pomonis, Solid-state NMR study of mesoporous phosphoro-vanado-aluminas, Phys. Chem. Chem. Phys., 2000, 2, 5286–5292 RSC.
- P. J. Pomonis, K. M. Kolonia and G. S. Armatas, Relationship between Pore Connectivity and Mean Pore Size in Modulated Mesoporous Vanado-Phosphoro-Aluminates and Some Similarities with the Branching of Trees, Langmuir, 2001, 17, 8397–8404 CrossRef CAS.
- G. S. Armatas, K. M. Kolonia and P. J. Pomonis, Morphometry of Porous Solids:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Lacunarity, Fractal Dimensions, Connectivity, and Some Topological Similarities with Neurons, Langmuir, 2002, 18, 10421–10429 CrossRef CAS.
Lacunarity, Fractal Dimensions, Connectivity, and Some Topological Similarities with Neurons, Langmuir, 2002, 18, 10421–10429 CrossRef CAS. - P. W. Atkins and J. De Paula, Atkins’ Physical Chemistry, W.H. Freeman, New York, 2006 Search PubMed.
- W. Liu, S. Chen, C. Wu and S. Li, Unifying size-topology relations in random packings of dry adhesive polydisperse sphere, Phys. Rev. E, 2019, 99, 022901 CrossRef CAS PubMed.
- C. B. O’Donovan, E. I. Corwin and M. E. Mobius, Mean-field granocentric approach in 2D & 3D polydisperse, frictionless packings, Philos. Mag., 2013, 93, 31–33 CrossRef.
- V. Baranau and U. Tallarek, Random-close packing limits for monodisperse and polydisperse hard spheres, Soft Matter, 2014, 10, 3826–3841 RSC.
- E. Kyeyune-Nyombi, F. Morone, W. Liu, S. Li, M. L. Gilchrist and H. A. Makse, High-resolution of particle contacts via fluorophore exclusion in deep-imaging of jammed colloidal packings, Phys. A, 2018, 490, 1387–1395 CrossRef.
- M. Clusel, E. I. Corwin, A. O. Siemens and J. Brujić, A ‘granocentric’ model for random packing of jammed emulsions, Nature, 2009, 460, 611–615 CrossRef.
- E. I. Corwin, M. Clusel, A. Siemens and J. Brujić, Model for random packing of polydisperse frictionless spheres, Soft Matter, 2010, 6(13), 2949–2959 RSC.
- K. Cronin and F. J. Gutiérrez Ortiz, The Evolution of Variance and Entropy of the Granule Size Distribution in Fluidized Bed Agglomeration, Processes, 2023, 11(8), 2247 CrossRef.
- E. K. O. Hellén, T. P. Simula and M. J. Alava, Dynamic scaling in one-dimensional cluster-cluster aggregation, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 4752 CrossRef PubMed.
| This journal is © the Owner Societies 2026 |

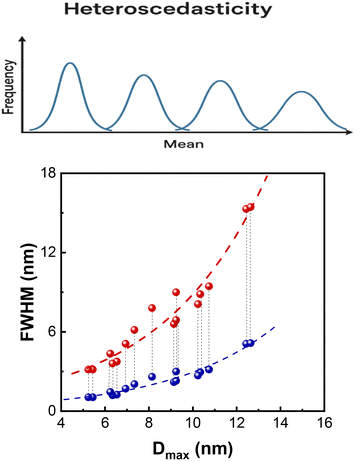

![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ). The cone-shaped scatterplot is characteristic of heteroscedasticity and defined by the low and upper limits of FWHM. The two dashed red (
). The cone-shaped scatterplot is characteristic of heteroscedasticity and defined by the low and upper limits of FWHM. The two dashed red (
