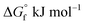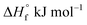Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phase equilibria and thermodynamic properties of the nickel(II) methanesulfonate–methanesulfonic acid–water system
Femke Derison a,
Xu Jia
a,
Xu Jia b,
Luc Van Meervelt
b,
Luc Van Meervelt b,
Koen Binnemans
b,
Koen Binnemans a and
Rayco Lommelen
a and
Rayco Lommelen *a
*a
aKU Leuven, Department of Chemistry, Solvomet Group, Celestijnenlaan 200F, box 2404, B-3001 Leuven, Belgium. E-mail: rayco.lommelen@kuleuven.be
bKU Leuven, Department of Chemistry, Biomolecular Architecture, Celestijnenlaan 200F, box 2404, B-3001 Leuven, Belgium
First published on 20th January 2026
Abstract
Methanesulfonic acid (MSA) is a promising reagent for hydrometallurgy, but the fundamental chemistry of methanesulfonate salts remains largely underexplored. Given the important role of nickel in cathode-active materials of lithium-ion batteries, the solubility of nickel(II) methanesulfonate and the influence of MSA on the solubility of this salt were studied. Solid–liquid equilibria of Ni(CH3SO3)2–H2O–MSA systems were investigated by the isothermal solubility method, followed by water activity and density measurements on the saturated aqueous solutions. Solid phases of different hydrates were formed and identified by thermogravimetric analysis and single-crystal X-ray diffraction, showing the presence of three hydrates: Ni(CH3SO3)2·2H2O, Ni(CH3SO3)2·6H2O and Ni(CH3SO3)2·12H2O. The solubility behavior of nickel(II) methanesulfonate in mixtures of MSA and H2O shows a decrease in solubility with increasing acid concentration, reaching a minimum at 95 wt% MSA. Experimental data were obtained over a wide range of Ni(CH3SO3)2 and MSA concentrations at different temperatures and used to build a thermodynamic model with the mixed-solvent-electrolyte (MSE) thermodynamic framework by OLI Systems. Thermodynamic properties of the different hydrates and interaction parameters for the aqueous phase were optimized.
Introduction
Hydrometallurgical flowsheets for metal recovery typically focus on conventional acids such as sulfuric acid and hydrochloric acid, as both systems are well-established, highly reliable, and widely used in the industry.1–4 However, these acids have several inherent shortcomings, such as corrosivity and poor solubility of certain metals, that could be mitigated by using an alternative acid.4,5A promising alternative acid for hydrometallurgy is methanesulfonic acid (MSA, CH3SO3H). This acid has long seen only limited industrial applications and research interest in hydrometallurgy, which is therefore a lesser known reagent. MSA and its advantages were first presented by Gernon et al. (1999).5 These authors demonstrated the useful properties of MSA as a replacement for HBF4 and H2SiF6 in electrochemical applications. Unlike other organic acids, MSA is a very strong acid (pKa = −1.9). It has a good chemical and electrochemical stability, and is only weakly oxidizing. Its environmental impact is considered low due to its biodegradability and low toxicity, and hence it is considered as a green acid. In addition to these advantages, another remarkable property is the high solubility of some methanesulfonate salts compared to the corresponding salts of other acids. Consequently, MSA has experienced a recent surge in research interest in the field of hydrometallurgy.1,4 Despite its extensive use in organic synthesis and the tin plating industry, the chemistry of methanesulfonate salts remains insufficiently explored. Therefore, deeper study on the chemistry of these systems would facilitate the application of MSA in hydrometallurgy, particularly in solvent extraction and leaching processes.
Further optimization of this MSA-based processes is required, which is often a demanding task due to the many parameters involved.6 Use of a computational model could reduce the required time and resources, as less experimental work is necessary and the effect of various flowsheet configurations and process parameters can rapidly be assessed. Building and using these models can also provide a better view and understanding of the chemistry and interactions in these systems. Accurate and predictive models are crucial and they should be capable to handle the increasing complexity of mixed-solvent systems with various species and deviations from thermodynamically ideal behavior.7–10
Various modeling approaches exist, each with their distinct strengths and limitations. The simplest models are empirical and are based solely on experimental data to which arbitrary mathematical functions are fitted. Empirical models lack chemical insight and have limited accuracy and predictive power outside the range of experimental conditions.11,12 Chemistry-based models incorporate chemical reaction equilibria and generally use concentrations as variables. The latter can be inadequate for systems showing non-ideal thermodynamic behavior, which is the case for highly concentrated electrolyte solutions or high loadings of the organic phase in solvent extraction processes. Therefore, effective concentrations, or activities, should be used. Neglecting activity corrections not only leads to the introduction of fictitious species in a model, but also results in significant errors in the calculation of solubilities and distribution ratios. This outcome should be avoided to enhance the model's ability to provide meaningful insights and reliable predictions. Semi-empirical models combine a chemical foundation with a theoretical framework, in which adjustable interaction parameters are optimized through regression of activity equations against experimental data. These models require a robust thermodynamic framework capable of handling the complexity of the system to ensure sufficient accuracy and predictability. To construct such models, relevant data must be obtained from experimental studies of the systems in question. For the model to perform well, it must accurately represent the chemistry of these systems. In contrast, purely theoretical models are based on first principles, fundamental physical laws and statistical thermodynamics. However, their practical application in hydrometallurgical processes is constrained by the high computational costs.11,13,14
The currently available thermodynamic models for the Ni(CH3SO3)2–MSA–H2O system have several shortcoming that hamper their application in hydrometallurgy.15,16 First, they are not able to calculate mass density of the solutions, although knowledge of the density is essential for the conversion of mass- and mole-based units in the thermodynamic framework to the volumetric units typically used in hydrometallurgy. Secondly, incorporating the acid–base equilibrium of MSA in the model would allow to calculate the behavior of more concentrated MSA solutions and to improve the reliability of the model over the whole MSA concentration range.17,18 Third, a model using the Gibbs free energy of formation, enthalpy of formation and the entropy would have a more sound thermodynamic basis compared to models using temperature-corrected equilibrium constants.
This study employs a semi-empirical thermodynamic model based on the OLI mixed-solvent electrolyte (OLI-MSE) thermodynamic framework.19,20 This type of model has successfully been applied to model solvent extraction processes of relevance for hydrometallurgy.21,22 The successful development of thermodynamic models for other acids demonstrates the feasibility of extending this approach to MSA, whose inclusion could provide substantial advantages in accurately describing the system.8
To construct the model, experimental data on metal–H2O–MSA systems are required. Although only limited experimental data are available as yet, Belova et al. have reported solubility and phase diagram data for several metal methanesulfonate salt–water systems (e.g. Zn, Cu, Co, Mn, Ni) in water up to 44 °C, with some limited extension to H2O–MSA systems.15,16,23–26 However, a more extensive characterization of MSA salt chemistry in MSA-containing systems over the whole MSA–H2O concentration range is required to understand and calculate MSA-based systems in the context of hydrometallurgy. Our study aims to investigate the Ni(CH3SO3)2–MSA–H2O systems over a broad range of temperatures and concentrations. To provide a comprehensive description of the equilibrium behavior, we include isothermal solubility measurements as well as determinations of water activity, density, precipitate speciation and water content. In addition, literature data reported by Belova et al. are incorporated to complement and validate our findings.15,16
The focus is on nickel due to its relevance in battery-related hydrometallurgical flowsheets. The aqueous chemistry of Ni(CH3SO3)2–H2O–MSA systems was investigated, as these experimental data are essential for developing a thermodynamic model that incorporate the aqueous Ni(CH3SO3)2–MSA chemistry and interactions, enabling the calculation of solid–liquid equilibria and aqueous chemistry of Ni(CH3SO3)2 systems. This will be the foundation for later thermodynamic models to be used to describe solvent extraction of transition metals from MSA media. The software used for this thermodynamic model is provided by OLI Systems, which employs the OLI-MSE thermodynamic framework. The constructed model is a semi-empirical model that uses experimental data and the theoretical framework to optimize interaction parameters and thermodynamic properties. This method, from experimental setup to the modeling procedure, can be extended to battery metals other than nickel.
The goal of this study is to generate experimental data for the Ni(CH3SO3)2–MSA–H2O system and use it to develop a robust semi-empirical thermodynamic model within the OLI-MSE framework. This includes a detailed investigation of solid–liquid equilibria and aqueous speciation, which are essential for accurately describing the system's behavior. The resulting model will serve as a foundation for future modeling of solvent extraction processes involving nickel and other battery-relevant metals in MSA-based media.
Experimental
Chemicals
Nitric acid (68–70%) and nickel(II) oxide (NiO, general purpose grade) were purchased from Fisher Scientific (Merelbeke, Belgium). Methanesulfonic acid (99.5%) was purchased from Carl Roth GmbH (Karlsruhe, Germany). Imidazole (99%) was obtained from Acros Organics (Geel, Belgium). The ICP standards of nickel, cobalt and manganese (each 1000 mg L−1 in 3–5% HNO3), were obtained from ChemLab (Zedelgem, Belgium). All chemicals were used as received, without any further purification. Ultrapure water was used, prepared by a Merck Millipore Milli-Q® Reference A+ system, deionized to a conductivity of less than 18.2 MΩ cm at 298.15 K.Nickel(II) methanesulfonate was synthesized by reaction of nickel(II) oxide with MSA in water (eqn (1)).27 A twofold excess of the oxide was used to ensure prevent contamination of the final product with unreacted MSA.
| NiO(s) + 2CH3SO3H(aq) → Ni(CH3SO3)2(aq) + H2O | (1) |
This reaction was magnetically stirred overnight at 500 rpm at a temperature of 70 °C. The mixture was filtered twice using a Büchner filter and glass fiber filtration paper (pore size: 1.6 µm), ensuring removal of all NiO residues. Subsequently, water was evaporated from the aqueous solution using a rotary evaporator, at a final pressure below 1 mbar. Then, the contents of the flask were further dried on a Schlenk line overnight under vacuum at 70 °C. The final product was a pale green salt, which was characterized by TGA and ICP–OES analysis (see Results and discussion) to determine the degree of hydration. The compound was identified as the dihydrate, Ni(CH3SO3)2·2H2O.
Isothermal solubility method
To determine the solubilities of different systems, an isothermal solubility method was used. Stock aqueous solutions of 0, 10, 30, 50, 70, 80, 85, 90, 95 and 100 wt% MSA were prepared and aliquots (5 mL) were added to 20 mL glass vials. These were subsequently saturated with synthesized Ni(CH3SO3)2 salt, by addition of a weighed excess of Ni(CH3SO3)2 under magnetic stirring. The samples were stirred isothermally at 500 rpm at the targeted temperature (25, 50 or 70 °C) in an aluminum heating block with a temperature uncertainty of ±0.5 °C. The stirring was stopped after 48 hours, and the solution was left to stand for an additional 48 hours to ensure that equilibrium was attained and the phases well separated.28,29 The supernatant was then sampled for ICP–OES analysis to measure the nickel concentration. The saturated samples were carefully separated for further individual analysis. For the liquid phase, density, water activity and water content of the liquid samples were measured, while for the solid phase the number of water molecules of hydration were determined. To assess the experimental uncertainty, triplicate measurements were performed for samples at 25 °C. Subsequent experiments at elevated temperatures were conducted without replication.Aqueous chemistry experiments
To obtain data on the water activity, density and viscosity below saturation level, samples were prepared with varying concentrations of Ni(CH3SO3)2, all below the saturation level determined during the saturation experiments. Again, the MSA concentration (0 to 50 wt% MSA) was varied and analysis was executed at two temperatures (25 and 50 °C). The solubility of Ni(CH3SO3)2 in solutions containing more than 50 wt% MSA is too low to justify additional experiments below saturation level, as they would not yield new useful data beyond what was already obtained through the isothermal solubility method. Different Ni(CH3SO3)2 concentrations were used, depending on the maximum solubility at a specified MSA concentration, from 0.2 to 2 mol L−1. The samples were stirred at 500 rpm at room temperature for 2 hours prior to the measurements. After all the measurements at 25 °C had been executed, the samples were stirred for another 2 hours at 50 °C before analysis. ICP-OES analysis was used to determine the exact nickel concentration in solution.Chemical analysis of liquid phase – ICP–OES
Metal concentrations were determined by inductively coupled plasma–optical emission spectroscopy (ICP–OES) using a PerkinElmer Avio 500 spectrometer, equipped with an axial/radial dual plasma view, a GemCone High Solids nebulizer, a baffled cyclonic spray chamber, and a demountable quartz torch featuring a 2.0 mm internal diameter alumina injector. Samples, calibrations and quality checks were all diluted with 2 vol% HNO3 and all ICP–OES spectra were measured in triplicate. The error on the triplicate measurements was less than 5%. Calibration curves were constructed using solutions containing 0.1, 0.5, 1, 3, 6, 9 ppm of nickel. Additional quality checks, using a blank sample and a 2 ppm nickel solution, were added after 10 samples to verify the instrument's performance during the measurement. Cobalt (5 ppm) was used as an internal standard and added to all samples, calibration standards and quality checks.Water activity – Density/viscosity – Karl Fischer analysis
For the saturation samples, water activity, density/viscosity and water content could be determined only for the samples at 25 °C. At higher temperatures, precipitation occurred upon cooling of the samples during handling, resulting in inaccurate measurements. Below saturation, density/viscosity and water activity of the aqueous samples were measured at 25 and 50 °C.The water activity (aw) of the aqueous phase was measured using a water activity meter (AQUALAB TDL by METER). Calibration was performed prior to each measurement using AQUALAB's own standards, with water activities ranging from 0.250 to 1.000. Approximately 5 mL of the sample was placed in a sample cup inside the instrument's chamber to measure its water activity from the vapor above the liquid surface at the desired temperature.
Densities and viscosities of the solutions were measured using an Anton Paar DMA 4500M densitometer. The density was measured by injecting 1 mL of the liquid in the density chamber at the desired temperature, up until 50 °C. Simultaneously, the viscosity was determined in the capillary chamber based on Hoeppler's falling-ball principle.
The water content of the saturation samples was measured using a METTLER TOLEDO V30S volumetric Karl Fischer titrator with HYDRANAL™ – composite 5 titrant. Acidic samples cannot be measured directly by the Karl Fischer method. Therefore, the MSA was neutralized by addition of an excess (2 g) of imidazole to the titration vessel. Samples (0.05 to 0.5 mL) were directly injected in the titration vessel to determine the water content.
Thermal analysis
The synthesized salt was measured by thermogravimetric analysis (TGA) on a TA Instruments TGA Q500 thermogravimeter to determine its hydration state. Where possible, solid phases from the isothermal solubility experiments were analyzed by TGA to determine the hydrates present.Differential scanning calorimetry (DSC) was performed with a METTLER TOLEDO DSC 1 instrument to determine the specific heat capacity (Cp) of the three hydrates. The hydrates were stored in sealed vials to prevent exposure to a changing ambient humidity and to avoid changes in hydration. The ASTM E1269-11 sapphire method was used for Cp determination, according to the standard method, by measuring a blank, a sapphire standard and the sample itself. DSC calibration was performed with indium and zinc standards to ensure correct enthalpy and temperature measurements. Standard aluminum 40 µL pans with lid were used, and all measurements and calibrations were performed under a 30 mL min−1 helium atmosphere. The solids were slightly pressed into the pan using a Teflon stamper to ensure good thermal contact with the bottom of the aluminum pan, while minimizing any risk of altering the hydration state.
Powder X-ray diffraction
The synthesized salt was characterized by a powder X-ray diffraction (XRD) analysis, performed on a Bruker D2 phaser Diffractometer with Cu-Kα radiation (30 kV, 10 mA, step size of 0.05°, a counting time of 0.5 s per step in the measurement range 2θ between 7 and 50° 2Θ). Data processing was done with the Bruker DIFFRAC.EVA software.Single-crystal X-ray crystallography
A good quality single crystal was obtained in the 0 wt% MSA sample and the X-ray diffraction data were collected at 21(2) °C on an Agilent SuperNova diffractometer with Eos CCD detector using MoKα radiation. Crystal data, data collection parameters and refinement statistics are given in the SI (see SI single-crystal X-ray crystallography and Table S2). The CCDC deposition number is 2484546.Microcalorimetry
Microcalorimetric measurements were conducted using a TA Instruments Thermal Activity Monitor (TAM) IV microcalorimeter equipped with a SolCal module for the determination of dissolution enthalpy. For each experiment, 300 mg of salt was placed into a stainless steel sample holder, which was sealed using two thin glass windows, also called the crushing ampoule. This ampoule was then inserted into a 100 mL SolCal reaction vessel filled with water. The vessel, which is integrated with thermistors and calibration heaters, is connected to the calorimeter. At the base of the vessel, a sapphire tip is positioned to crush the ampoule during the experiment, but the ampoule remains suspended above the tip until the dissolution step is initiated.The assembled module was placed into the thermostat, and thermal equilibrium was achieved after approximately 40 minutes, indicated by a stable baseline signal. The experimental procedure starts with a pre-calibration step, wherein a controlled amount of heat, comparable to the expected heat of dissolution, was applied. Following each section, a 5-minute pause took place to re-stabilize the baseline. The dissolution enthalpy was then measured by mechanically breaking the ampoule, initiating the reaction. Subsequently, a post-calibration was performed. The enthalpy of dissolution was calculated by integrating the temperature signal over time. The enthalpy value derived from the post-calibration was used for analysis, as it offers improved accuracy due to the similarity in conditions between the dissolution and calibration phases.
Thermodynamic modeling
The MSE framework (version 12) by OLI Systems Inc. (Parsippany NJ, USA) was used to build the thermodynamic model for the solid–liquid equilibria and aqueous chemistry of Ni(CH3SO3)2 in MSA–water systems. The software packages OLI Studio 12, OLI Databook 12, and OLI Chemistry Wizard 12 of OLI Systems Inc. were used.Standard Gibbs free energies are insufficient to describe the thermodynamic properties of solutions at high concentrations or high ionic strengths. Deviations from ideal behavior are captured by the excess Gibbs free energy term, which consists of three contributions corresponding to interactions occurring at different distances: short-range (SR), medium-range (MR), and long-range (LR) interactions (see eqn (2)):19
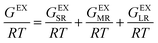 | (2) |
The long-range electrostatic interaction parameters are represented by an extension of the Debye–Hückel equation, proposed by Pitzer.30 This term depends on the charges present in solution, and therefore on the ionic strength and dielectric constant of the solution. The dielectric constants of solutions are calculated in OLI, based on a framework that incorporates the dielectric constant of the pure solvent adjusted for mixing and ionic strength effects.19,31 Therefore, no additional interaction parameter optimization is required.
The mid-range interaction term is described by a symmetrical second virial coefficient-type equation and is used for ion/ion and ion/neutral interactions not included in the long-range interactions, particularly at higher ionic strengths.19 This term uses ionic-strength-independent (bij) and ionic-strength-dependent (cij) binary interaction parameters between species i and j to describe interactions at higher ionic strengths.
These interaction parameters are calculated by fitting the activity equations to experimental data via regression. For this, the OLI regression tool was used. To support the fitting process, appropriate system data are essential. While activity data for all present species would be ideal, obtaining such data aside from water is often practically challenging or even impossible. Therefore, different data on speciation, solubility, density and water activity cover many of the equilibria aspects and are considered sufficient.
In thermodynamic modeling, the choice of the reference state plays a crucial role in defining solution behavior and calculating activities. Two commonly used reference states are based on either Raoult's law and on Henry's law. Raoult's law defines ideal behavior based on the pure solute as the reference state, making it suitable for concentrated solutions where the solute is the dominant component. In contrast, Henry's law defines ideality at infinite dilution, which is more appropriate for dilute systems where solute–solvent interactions dominate. Selecting the appropriate reference state ensures consistency in activity calculations and improves the reliability of equilibrium and speciation predictions. Both reference states are useful for describing ideal solution behavior, but each is most effective within its respective concentration range. It is important to handle thermodynamic calculations with care, as the interpretation of properties depends on the reference state being applied. Within the framework used here, a normalization of the mole fraction is applied to all species, resembling Raoult's law.19,32
The thermodynamic model presented below was built upon the general OLI-MSE database, which is available in the OLI software package. This general OLI-MSE database already contains the thermodynamic values and interaction parameters required to calculate the chemistry of water and MSA–water systems. The performance of the general OLI-MSE database for the MSA–water system was validated with literature data for acid dissociation, water activity and solution density (SI, Fig. S8).
Chemical species that are present in the system were added to OLI Databook and required values for thermodynamic properties, such as standard state Gibbs free energy of formation 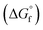 , enthalpy of formation
, enthalpy of formation 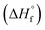 , entropy (S°) and specific heat capacity
, entropy (S°) and specific heat capacity 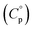 . The formation reaction of the different hydrates can be described using eqn (3), with x representing the amount of hydration water. A first estimate for the
. The formation reaction of the different hydrates can be described using eqn (3), with x representing the amount of hydration water. A first estimate for the 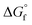 of each hydrate was calculated from the solubility product for each hydrate using eqn (4) and (5).32 This
of each hydrate was calculated from the solubility product for each hydrate using eqn (4) and (5).32 This 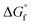 value was optimized later, since the solubility product (Ksp) cannot be determined at standard conditions of infinite dilution. The entropy was calculated from the formation reaction of the hydrates, similar to the Gibbs free energy calculation, by assuming that standard entropy of reaction
value was optimized later, since the solubility product (Ksp) cannot be determined at standard conditions of infinite dilution. The entropy was calculated from the formation reaction of the hydrates, similar to the Gibbs free energy calculation, by assuming that standard entropy of reaction 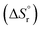 equals 0, as shown in eqn (6). Further conversion of standard entropy of formation
equals 0, as shown in eqn (6). Further conversion of standard entropy of formation 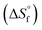 to S° was done by eqn (7) and using standard thermodynamic values for the elemental species. Standard thermodynamic values for Ni2+ and H2O were taken from the literature, while values for MSA were obtained from OLI Studio.33–36 The enthalpy of formation can then be calculated using eqn (8).
to S° was done by eqn (7) and using standard thermodynamic values for the elemental species. Standard thermodynamic values for Ni2+ and H2O were taken from the literature, while values for MSA were obtained from OLI Studio.33–36 The enthalpy of formation can then be calculated using eqn (8).
| Ni(CH3SO3)2·xH2O → Ni2+ + 2CH3SO3− + xH2O | (3) |
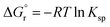 | (4) |
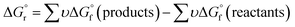 | (5) |
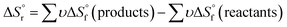 | (6) |
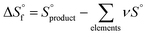 | (7) |
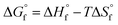 | (8) |
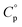 values of each of the three hydrates were determined by DSC measurements, within the temperature range at which they were present. The
values of each of the three hydrates were determined by DSC measurements, within the temperature range at which they were present. The 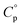 values obtained for the hydrates were as follows: Ni(CH3SO3)2·2H2O = 1.59 ± 0.08 J g−1 K−1, Ni(CH3SO3)2·6H2O = 1.93 J g−1 K−1, Ni(CH3SO3)2·12H2O = 2.44 ± 0.41 J g−1 K−1. The small standard deviation observed for the dihydrate is attributed to the ease of handling its powder form, which allowed for good contact with the sample pan and hence improved the thermal conduction and measurement accuracy. In contrast, the larger crystals of the dodecahydrate posed challenges during measurement as particle size reduction risked altering the hydration state, contributing to the larger standard deviation. The hydration state of Ni(CH3SO3)2·12H2O was verified by TGA after the heat capacity measurements under conditions where a change in hydration could occur, but no change was observed. The
values obtained for the hydrates were as follows: Ni(CH3SO3)2·2H2O = 1.59 ± 0.08 J g−1 K−1, Ni(CH3SO3)2·6H2O = 1.93 J g−1 K−1, Ni(CH3SO3)2·12H2O = 2.44 ± 0.41 J g−1 K−1. The small standard deviation observed for the dihydrate is attributed to the ease of handling its powder form, which allowed for good contact with the sample pan and hence improved the thermal conduction and measurement accuracy. In contrast, the larger crystals of the dodecahydrate posed challenges during measurement as particle size reduction risked altering the hydration state, contributing to the larger standard deviation. The hydration state of Ni(CH3SO3)2·12H2O was verified by TGA after the heat capacity measurements under conditions where a change in hydration could occur, but no change was observed. The 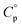 value of the hexahydrate was estimated by interpolation from the other hydrates, as isolating and handling this phase for direct measurement was not feasible in practice.
value of the hexahydrate was estimated by interpolation from the other hydrates, as isolating and handling this phase for direct measurement was not feasible in practice.
The enthalpy of dissolution of Ni(CH3SO3)2·12H2O was measured using a TAM IV microcalorimeter and converted to the 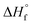 using eqn (9).
using eqn (9).
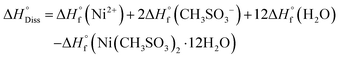 | (9) |
The dissolution enthalpy 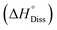 of Ni(CH3SO3)2·12H2O was found to be 57.86 kJ mol−1. This value, together with
of Ni(CH3SO3)2·12H2O was found to be 57.86 kJ mol−1. This value, together with 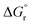 derived from the measured solubility, served as experimental constraints for calculating
derived from the measured solubility, served as experimental constraints for calculating 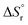 . Therefore, these values were coupled during the initial optimization so that no individual variation was possible. Only at the end of the fitting procedure, individual optimization of
. Therefore, these values were coupled during the initial optimization so that no individual variation was possible. Only at the end of the fitting procedure, individual optimization of 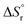 was performed to further finetune the model and to extrapolate the
was performed to further finetune the model and to extrapolate the 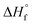 based on the calorimetric dissolution value at finite concentration (3 g L−1) to infinite dilution.
based on the calorimetric dissolution value at finite concentration (3 g L−1) to infinite dilution.
The experimental data were organized into structured datasets within a model input file, alongside interaction parameters and thermodynamic properties requiring optimization. This optimization procedure uses chemical speciation together with the thermodynamic framework to fit the thermodynamic values and interaction parameters to the experimental data.
The chemical species present in the system studied here can be split up between the aqueous phase and the solid phase. The aqueous phase consists of H2O, H3O+, Ni(II) (mainly as Ni2+), CH3SO3H (MSA), and CH3SO3− species, all of which were already present in the OLI database. For Ni(II), the OLI software also predicts minor amounts of nickel(II) hydroxide species in solution, typically less than 1%. To improve the accuracy of the model, additional interaction parameters between Ni2+ and CH3SO3− species were included in the optimization. The solid–liquid equilibria show a variety of Ni(CH3SO3)2 hydrates present in the solid phase, none of which were present in the OLI database. Therefore, these hydrates were included with initially estimated thermodynamic properties and were later subjected to optimization. The hydrates (Ni(CH3SO3)2·2H2O, Ni(CH3SO3)2·6H2O and Ni(CH3SO3)2·12H2O) were added as solids in the OLI database.
Modeling solid–liquid equilibria requires knowledge of both liquid and solid phases formed at equilibrium. Experimental difficulties in determining the full equilibrium composition of both phases may result in insufficient experimental data being available to build a model that can accurately predict the chemistry of both phases.37 Constructing diverse types of datasets, along with additional speciation datasets, can help to mitigate this problem. To enhance the accuracy of the thermodynamic calculations, integrated speciation and solubility datasets were constructed, allowing for constraints on the formation of specific hydrates. These datasets were constructed based on the experimental conditions of each sample, combined with the corresponding analytical results for nickel concentration and density. Since water content in the liquid phase was not initially available, additional Karl Fischer (KF) titration analyses were performed to establish complete mass balances for all relevant species. From the mass balance of MSA, Ni(CH3SO3)2, and water, the quantity of solid phase formed was calculated. This approach enabled indirect determination of the yield of solid, which could not be measured experimentally with sufficient precision.
Results and discussion
Solid–liquid equilibria
The synthesized Ni(CH3SO3)2 salt was characterized using ICP–OES, powder XRD and TGA analysis. Fig. 1 shows that the thermal decomposition of the salt occurs in different steps. The mass loss due to water of hydration is of particular interest. TGA analysis showed a 13.70% mass loss up to 200 °C, which is in good agreement with the theoretical mass loss value of 12.65% for 2 water molecules from the dihydrate Ni(CH3SO3)2·2H2O. The mass decrease between 400 and 500 °C can be attributed to thermal decomposition of the compound, accompanied by the release of volatile decomposition products, primarily SO2 and CO.38 The final black solid residue is most likely nickel sulfide, as decomposition of other methanesulfonate salts under inert atmospheres has been shown to yield sulfide products, as reported by Charbonnier et al.38–41 A slight excess of water detected by TGA and ICP–OES indicated the presence of a few percent of the hexahydrate, resulting in an estimated purity of approximately 96% Ni(CH3SO3)2·2H2O with 4% Ni(CH3SO3)2·6H2O. The powder XRD diffractogram of Ni(CH3SO3)2·2H2O is provided in the SI (Fig. S1). This dihydrate salt was used to perform all experiments. It became evident that different ways of drying the synthesized salt leads to the formation of other hydrates and even mixtures of hydrates. To ensure consistency of the starting material, the salt was dried on a Schlenk line to guarantee that the dihydrate form was consistently used as starting material.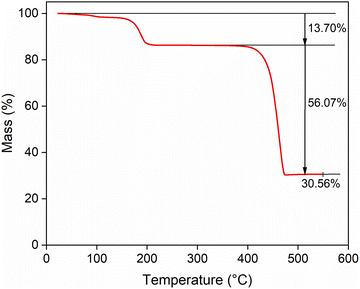 | ||
| Fig. 1 Thermogravimetric curve for Ni(CH3SO3)2·2H2O synthesized salt during heating with a heating rate of 5 °C min−1 in nitrogen atmosphere at 60.0 mL min−1 flow rate. | ||
Experimental data on the Ni(II) solubility of the different Ni(CH3SO3)2–MSA–H2O systems are given in Fig. 2. The solubility decreases upon increasing the MSA concentration. At the highest concentrations of MSA, almost no Ni(CH3SO3)2 is dissolved and the minimum solubility that could be experimentally measured was 0.0064 ± 0.0005 mol L−1. This decrease in solubility can be attributed to the amount of free water present in the solution. To keep nickel(II) ions in solution, sufficient hydration is needed, which becomes problematic at high concentrations of MSA with only a small amount of water present.4 As MSA is known to be hygroscopic, the activity of the remaining water molecules is reduced by their involvement in the solvation of MSA. While solubility often increases with temperature, this trend plateaus beyond approximately 50 °C, as evidenced by the negligible difference between the solubility measurements at 50 °C and 70 °C. The data point obtained at room temperature and 0 wt% MSA by Belova et al. (2.31 mol L−1) is within the error margin of the data presented in our work (2.34 ± 0.047 mol L−1), indicating good compatibility of both data.15,16 Additionally, Gernon et al. reported a solubility of 2.13 mol L−1 for Ni(CH3SO3)2 in water.5 This slightly lower value might be explained by the lower temperature of 22 °C used in that work. More recent work by Belova et al. reports additional Ni(CH3SO3)2 solubility data in MSA–water mixtures and their data also show good agreement with our results.15 For instance, Belova obtained solubilities of 1.88, 1.02, and 0.247 mol L−1 at 22.23, 38.41, and 60.31 wt% MSA, respectively. In the same concentration range, though not at exactly the same MSA values, our measurements at 21.82, 38.78, and 66.19 wt% MSA are 1.89 ± 0.17, 1.11 ± 0.08, and 0.110 ± 0.007 mol L−1, respectively. All values agree within their error ranges except for the point at 60.31 wt% MSA. This deviation can be explained by the higher MSA concentration of our corresponding data point (66.19 wt%), which accounts for the lower solubility observed in this work.
 | ||
| Fig. 2 Solubility of Ni(CH3SO3)2 as a function of the MSA concentration at different temperatures, measured by the isothermal solubility method. The X-axis depicts wt% MSA at equilibrium. | ||
Therefore, the promising advantage of high solubilities of metals in MSA as reported by Gernon et al., appears to hold true for the nickel–MSA system, but only at lower concentrations of MSA.5 However, a similar trend is observed for the NiSO4–H2SO4–H2O system shown in Fig. 3 where the Ni(CH3SO3)2 solubility data are plotted together with the NiSO4 solubilities in function of the acid mole fraction of MSA and H2SO4. Here also, the solubility in the sulfate system steeply decreases with increasing acid concentrations, showing both minimal solubilities at approximately 0.4 mole fraction of acid.42–44 In H2SO4 media, the solubility curve exhibits lower values within the acid concentration range of 0.05 to 0.15 mole fraction. Within this range, the solubility of nickel remains higher in the MSA system, whereas in H2SO4 media, the nickel concentration decreases to less than 1 mol L−1. This lower acid concentration range is particularly relevant for hydrometallurgical applications, where minimizing free acid and avoiding excess sulfate from other cationic salts is preferred due to economic, safety, and operational considerations. Therefore, this shows a distinct advantage of the MSA system over the sulfuric acid system in terms of solubility of nickel.
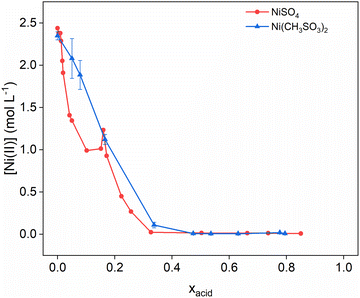 | ||
| Fig. 3 Solubility of Ni(CH3SO3)2 (blue) and NiSO4 (red) as a function of the equilibrium acid concentration, for water–MSA and water–H2SO4 systems at 25 °C. The solubility data for NiSO4 were taken from Addlestone et al.43 | ||
Additional data on the water activity, density and water content are given in Table S3 for 25, 50 and 70 °C. The experimental data are consistent with the trends and estimations observed in related systems, indicating their reliability and relevance. As such, they provide a solid foundation for the construction of a thermodynamic model that accurately describes the behavior of the system. A detailed overview of all input streams and equilibrium outcomes is provided in the SI Table S3.
The solid phases in the samples used for solubility measurements already showed major differences in visual appearance as their color shifted from a dark green to a yellowish light green upon increasing the MSA concentration (Fig. 4). The crystal habit of the solid varied likewise from larger crystalline pieces at low MSA concentrations to a fine powder at high MSA concentrations. This indicates the formation of different hydrates upon increasing the MSA concentration. At 0 wt% MSA and 25 °C, large crystals could be obtained. A crystal of sufficient quality for single-crystal X-ray diffraction structural analysis could be isolated. The crystal structure confirmed the formation of the dodecahydrate Ni(CH3SO3)2·12H2O. The crystal structure was determined at 21 ± 2 °C (SI Fig. S7) and supports the DSC results obtained by Belova et al. that no phase transition occurs between −163 and 27 °C.16 The Ni–O bond is 2.0352(12) Å, comparable to 2.037(1) Å reported by Belova et al. at −173 °C. The crystal structure determination of Ni(CH3SO3)2·12H2O at ambient temperature, compared to the low temperature measurement from Belova et al. adds structural insight beyond previous studies, more relevant for practical applications. When the temperature was reduced from 21 ± 2 to −173 °C, a volume contraction of 2.3% was observed, mainly caused by a shrinkage of the cell parameters a and b. Additionally, TGA analysis confirmed the presence of Ni(CH3SO3)2·12H2O. TGA analysis was used to identify the solid phases in the other samples, because the other crystals were too small for single-crystal X-ray diffraction. TGA analysis was feasible until 30 wt% MSA (SI Fig. S2–S5). Beyond 30 wt% MSA, TGA analysis became less reliable due to challenges in solid–liquid separation. Additionally, drying the solid phase at these concentrations poses a risk of altering its hydration state. At 70 °C TGA measurements were only feasible at the lowest concentration. At MSA concentrations above 30 wt%, the light green color resembles that of the dried, synthesized Ni(CH3SO3)2·2H2O, providing a visual indication of the conditions in which the formation of Ni(CH3SO3)2·2H2O is dominant. At the highest MSA concentration, the light green color faded to a more yellowish color. Here, the amount of water present could be too low even for the formation of the dihydrate, resulting in a possible monohydrate or anhydrous solid. Above 30 °C, the hexahydrate would be formed at 0 wt% MSA according to Belova et al.16 A cooled, crystallized solubility sample from the 70 °C series with 10 wt% MSA was analyzed using TGA, confirming the formation of a hexahydrate under these conditions (SI Fig. S6). Similar to observations made at 25 °C, a color change was noted at higher MSA concentrations, indicating that a lower hydrate had formed. The different hydrates are shown in the last column of Table S3, for the samples where TGA and/or visual identification of the hydrate was possible.
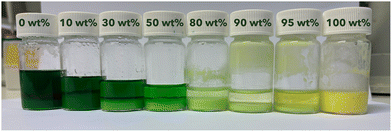 | ||
| Fig. 4 Samples saturated with Ni(CH3SO3)2 at 70 °C with varying initial MSA concentration from 0 wt% MSA (left) to 100 wt% MSA (right). | ||
Water activity and density measurements were not feasible due to a small decrease in temperature during sample handling for analysis, inducing precipitation (see Experimental). Therefore, water activity and density analyses at lower Ni(CH3SO3)2 concentrations and elevated temperatures were crucial to enable accurate modeling under these conditions.
Aqueous Ni(CH3SO3)2 samples
Samples with varying Ni(CH3SO3)2 concentrations below saturation levels were made and analyzed. Water activity measurements showed a decrease with increasing MSA and Ni(CH3SO3)2 concentrations, (Fig. 5). Density data at 25 and 50 °C are shown in Fig. 6, displaying a strong increase in density at higher MSA and Ni(CH3SO3)2 concentrations. At a higher temperature, lower densities were measured for similar conditions because of volume expansion. Viscosity data at 25 and 50 °C are shown in Fig. 7, which follow the same trends as for the density: lower viscosities at higher temperatures.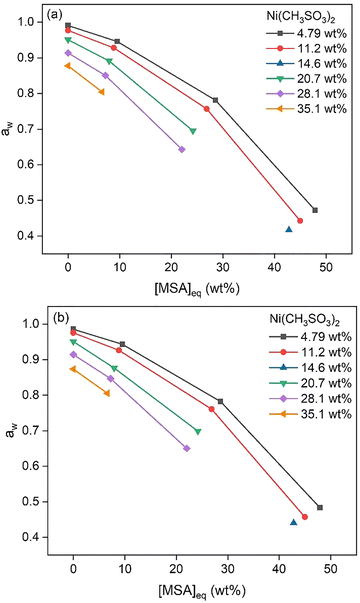 | ||
| Fig. 5 Water activity of samples with different Ni(CH3SO3)2 concentrations as a function of the MSA concentration, at 25 °C (a) and 50 °C (b). | ||
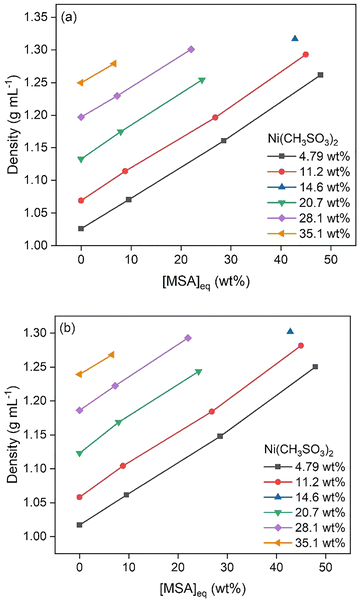 | ||
| Fig. 6 Density of samples with different Ni(CH3SO3)2 concentrations as a function of MSA concentration, at 25 °C (a) and 50 °C (b). | ||
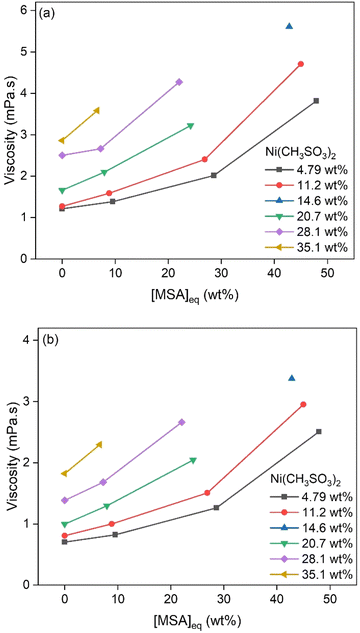 | ||
| Fig. 7 Viscosity of samples with different Ni(CH3SO3)2 concentrations as a function of MSA concentration, at 25 °C (a) and 50 °C (b). | ||
Thermodynamic modeling
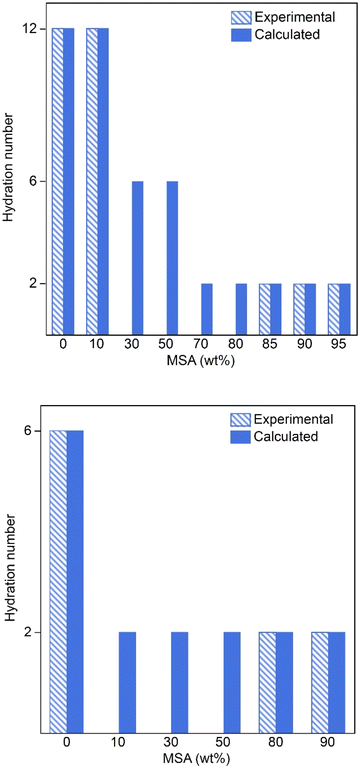
The aqueous chemistry of the system was optimized by incorporating MIDRANGE binary interaction parameters between ionic nickel(II) and methanesulfonic acid (MSA) species. At higher MSA concentrations, neutral MSA species interactions were also included. These parameters were fitted using available experimental data on water activity, density, and solubility at 25 and 50 °C. Additional data for the water activity and density of undersaturated samples were integrated, alongside published data of Belova et al.16,26 The solid–liquid equilibria were dependent on the thermodynamic stability of various hydrates in the system. Gibbs free energy minimization (GEM) was employed to determine the relative stability of these hydrates, incorporating entropy contributions to account for the temperature dependence. The initial estimates of thermodynamic parameters were refined by fitting to solubility and speciation data for different temperatures.Challenges in simultaneously optimizing solubility and speciation data for the hydrates were addressed by introducing combined solubility and speciation datasets. The final optimized thermodynamic values for the hydrates are presented in Table 1. Speciation calculations revealed a transition from the dodecahydrate to the dihydrate via the intermediate hexahydrate in the solubility samples. The model accurately calculates the speciation of saturation samples at 25 and 50 °C. These results are illustrated in Fig. 8 and are consistent with the expected speciation behavior from visual observations and TGA measurements.
Experimental data obtained in this study, along with solubility data at various temperatures in water, as reported by Belova et al.,16 are compared with model calculations in Fig. 9. In the low-temperature region, where the dodecahydrate dominates the speciation, the calculated values show minimal deviation from the experimental results and align well with the data reported by Belova et al. At temperatures above approximately 30 °C, the hexahydrate Ni(CH3SO3)2·6H2O starts to form, leading to a shift in speciation. In this higher-temperature region, larger deviations are observed between calculated and experimental solubility values. Attempts to improve the fit for this region led to increased deviations in other datasets, particularly those at elevated temperatures and higher MSA concentrations. In addition, higher temperatures may introduce additional experimental challenges, such as increased measurement uncertainty and reduced reliability of supporting data such as density. Together, these factors contribute to the observed discrepancies between the model predictions and experimental results in this part of the system.
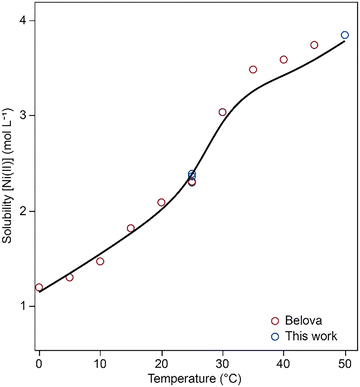 | ||
| Fig. 9 Model fit (solid line) to experimental data (open markers) of the solubility of Ni(CH3SO3)2 in water as a function of the temperature. | ||
Fig. 10 compares the experimental solubility data of Ni(CH3SO3)2 at 25 °C and 50 °C with the values predicted by the thermodynamic model, plotted as a function of the equilibrium MSA concentration. A good agreement between the experimental results and the calculated values is observed at both temperatures, confirming that the model allow to accurately describe the solubility behavior under the studied conditions.
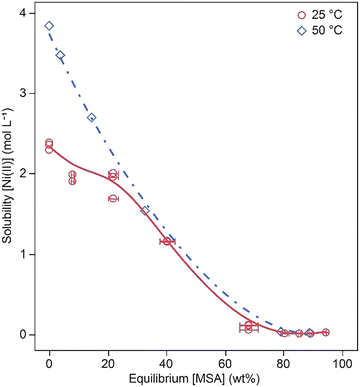 | ||
| Fig. 10 Model fit (line) to experimental solubility data from this work (open markers) for Ni(CH3SO3)2 as a function of equilibrium MSA concentration at 25 °C (red circles) and 50 °C (blue diamonds). | ||
Density parameters were initially optimized using undersaturation density data collected between 15 and 50 °C.26 To achieve an accurate fit, both ionic-strength-independent and -dependent parameters, as well as temperature-independent and -dependent parameters, were introduced (Table 2). These density parameters were later refined together with the other parameters during the final optimization steps. For water activity data, both temperature-dependent and -independent MIDRANGE binary interaction parameters were required to improve the agreement between model and experimental data. The MIDRANGE binary energy and density interaction parameters were essential for accurately modeling the aqueous chemistry. The final set of optimized parameters is presented in Table 2.
| Species | MIDRANGEa | MIDRANGE densityb | |
|---|---|---|---|
| bij | cij | dij | |
a Mid-range binary interaction parameters: 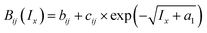 .b Mid-range binary density interaction parameters: .b Mid-range binary density interaction parameters: 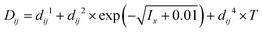 .c .c 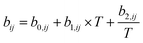 . . |
|||
| Ni2+–CH3SO3− (0) | −71.35187 | 1.646710 | |
| Ni2+–CH3SO3− (1)bc | 7.6610450 × 10−2 | 7.8421665 × 10−2 | 1.280136 |
| Ni2+–CH3SO3− (2)bc | −2.157762 | ||
| Ni2+–CH3SO3− (4)b | −2.7534679 × 10−4 | ||
| Ni2+–CH4SO3 (0) | −28.64634 | 21.44289 | |
| Ni2+–CH4SO3 (1)bc | −3.1201256 × 10−2 | 4.2655301 × 10−2 | −0.1040064 |
To statistically evaluate the performance of the thermodynamic model in describing various aspects of the solid–liquid equilibria in the Ni(CH3SO3)2–MSA–H2O system, quality-of-fit (QoF) plots were constructed for each type of dataset used in the optimization procedure. Due to uncertainty regarding the hydrate speciation of the data points at 95 wt% MSA, and the possibility of lower hydration states introducing larger deviations in solubility and water activity calculations, these points were excluded from the QoF analysis. Density and water activity QoF plots are presented in Fig. 11, while solubility QoF is shown in Fig. 12. Calculated values are compared with experimental data points in these plots, alongside an ideal fit line (y = 1x + 0, dashed black) representing a perfect agreement between model calculations and experimental data.
In Fig. 11, the 95% confidence interval overlaps with the ideal fit line in the lower value range for water activity and in the middle range for density, indicating good agreement. At higher water activities and at both lower and higher density ranges, a slight lack of fit is observed, primarily due to model overestimation at saturation conditions. For the density, the deviations are more pronounced at elevated temperatures, which can be attributed to the limited availability of experimental density data in this region. The root mean square error (RMSE) and the 95% prediction intervals provide insight into the expected error range of the model. The RMSE value represents the level of accuracy with which the model can predict values. A range of two times the RMSE corresponds to a 95% confidence level for prediction. The model predicts mean density and water activity values within ±0.06 and ±0.06 units, respectively, from the linear regression line, indicating strong predictive accuracy in these regions. This non-zero error value highlights the limitations of the current model and potential experimental uncertainties.
Similarly, the solubility QoF plots in Fig. 12 provide insight into the model's performance for the different MSA concentration ranges, for all tested temperatures. The solubility data show a good overall agreement between calculated and experimental values. Nevertheless, assessing model accuracy across the full concentration range within a single QoF plot is challenging due to solubility differences exceeding one order of magnitude. On a linear scale, the larger absolute experimental errors at high solubility values result in an overestimation of the deviations between the model and experiments at low solubilities. Conversely, on a log scale, higher relative experimental errors at low solubility values lead to an overestimation of the deviation between the model and experiments at high solubilities. To address this, the QoF plot is split in a high-solubility and low-solubility plot or low (0–10 mol L−1, Fig. 11 top) and high (≥10 mol L−1, Fig. 11 bottom) MSA concentration plot, respectively.
In the QoF plot for MSA concentrations up to 10 mol L−1 (Fig. 12, top), the highest solubility values show a slight lack of fit. This deviation is primarily due to the underestimation of the solubility at elevated temperatures, particularly in the presence of the hexahydrate, as discussed in Fig. 9. Below 27 °C, no significant lack of fit is observed. The RMSE analysis indicates that at low MSA concentrations, the mean solubility is predicted within ±0.163 mol L−1 of the experimental values at a 95% confidence level. Above 10 mol L−1 MSA (Fig. 12, bottom), the very low solubility values pose challenges for experimental analysis, increasing the likelihood of measurement errors. These uncertainties make it more difficult for the model to accurately reproduce the experimental data. Nevertheless, a slight lack of fit is present, and the RMSE indicates that the mean solubility is predicted within ±0.0098 mol L−1 of the experimental values in this region.
Conclusions
Experimental data were obtained for the Ni(CH3SO3)2–MSA–H2O system over a broad range of conditions. Isothermal solubility experiments were conducted between 25 and 70 °C, over the whole MSA–H2O concentration range. These data were supplemented by additional water activity, viscosity, and liquid density measurements at and below saturation to expand the dataset. Hydrate speciation revealed the presence of at least three distinct hydrates of nickel(II) methanesulfonate, depending on the experimental conditions.The solubility behavior of nickel(II) methanesulfonate in mixtures of MSA and H2O is similar to that observed for nickel(II) sulfate in sulfuric acid media, namely a decrease in solubility with increasing acid concentrations. A decline in solubility occurs with increasing MSA concentration, reaching a minimum at 95 wt% MSA. Although both systems exhibit similar trends at high acid concentrations, the steep decrease in nickel(II) sulfate occurs at lower sulfuric acid concentrations. This difference is relevant for hydrometallurgical applications, where lower acid concentrations are often preferred, highlighting the potential advantages of MSA in such processes.
The experimental results were used to build a semi-empirical thermodynamic model, using the OLI-MSE framework, with the objective to describe the aqueous chemistry and solid–liquid equilibria of the Ni(CH3SO3)2–MSA–H2O system. The model successfully integrated solid-phase speciation, solubility, water activity, and density, with calculated values showing strong agreement with experimental data across a range of experimental conditions. The model demonstrated a robust predictive capability, and RMSE values indicate that density and water activity can be predicted at 95% certainty within ±0.06 and ±0.06 units, respectively, and solubility within ±0.163 mol L−1 at low MSA concentrations and ±0.0098 mol L−1 at high MSA concentrations. These small error margins confirm the reliability of the model and its suitability for application in hydrometallurgical process design and optimization.
Author contributions
Femke Derison: conceptualization, investigation, methodology, formal analysis, visualization, software, writing – original draft. Rayco Lommelen: conceptualization, supervision, formal analysis, software, writing – review & editing. Xu Jia: investigation, formal analysis. Luc Van Meervelt: investigation, formal analysis, writing. Koen Binnemans: conceptualization, supervision, writing – review & editing, resources, funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
All experimental data are available in the supplementary information (SI). The SI provides the powder X-ray diffractogram, thermogravimetric analysis (TGA) results, a comprehensive table of experimental conditions and corresponding results, detailed data from single-crystal X-ray crystallography, and an overview of the performance of the general OLI-MSE database for the MSA-water system. See DOI: https://doi.org/10.1039/d5cp03992d.CCDC 2484546 contains the supplementary crystallographic data for this paper.45
Acknowledgements
This work was funded by the European Union (ERC, CIRMET, project number 101093943). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. The authors would like to thank Dr Stijn Raiguel (KU Leuven) for his valuable support and insightful contributions during the experimental investigation. The authors want to acknowledge Elewout Swinnen for providing assistance with JMP software and graphical data representation. LVM and KB thank the Hercules Foundation for supporting the purchase of the diffractometer through project AKUL/09/0035.References
- K. Binnemans and P. T. Jones, Methanesulfonic Acid (MSA) in Hydrometallurgy, J. Sustainable Metall., 2023, 9(1), 26–45, DOI:10.1007/s40831-022-00641-6.
- A. Porvali, M. Aaltonen, S. Ojanen, O. Velazquez-Martinez, E. Eronen, F. Liu, B. P. Wilson, R. Serna-Guerrero and M. Lundström, Mechanical and Hydrometallurgical Processes in HCl Media for the Recycling of Valuable Metals from Li-Ion Battery Waste, Resour., Conserv. Recycl., 2019, 142, 257–266, DOI:10.1016/j.resconrec.2018.11.023.
- X. Chen, Y. Chen, T. Zhou, D. Liu, H. Hu and S. Fan, Hydrometallurgical Recovery of Metal Values from Sulfuric Acid Leaching Liquor of Spent Lithium-Ion Batteries, Waste Manage., 2015, 38, 349–356, DOI:10.1016/j.wasman.2014.12.023.
- K. Binnemans and P. T. Jones, Methanesulfonic Acid (MSA) in Clean Processes and Applications: A Tutorial Review, Green Chem., 2024, 26(15), 8583–8614, 10.1039/D4GC02031F.
- M. D. Gernon, M. Wu, T. Buszta and P. Janney, Environmental Benefits of Methanesulfonic Acid. Comparative Properties and Advantages, Green Chem., 1999, 1(3), 127–140, 10.1039/A900157C.
- J. Rydberg and G. R. Choppin, Solvent Extraction Principles and Practice, CRC Press, New York, 2004, vol. Second Edt Search PubMed.
- H. Chen, A. J. Masters, R. Taylor, M. Jobson and D. Woodhead, Application of SAFT-VRE in the Flowsheet Simulation of an Advanced PUREX Process, Ind. Eng. Chem. Res., 2019, 58(9), 3822–3831, DOI:10.1021/acs.iecr.8b05606.
- R. Lommelen and K. Binnemans, Molecular Thermodynamic Model for Solvent Extraction of Mineral Acids by Tri-n-Butyl Phosphate (TBP), Sep. Purif. Technol., 2023, 313, 123475, DOI:10.1016/j.seppur.2023.123475.
- X. Lin, P. Ning, W. Xu, H. Cao and Y. Zhang, Thermodynamic Models Based on Pitzer-NRTL and Pitzer-Margules Equations for the Extraction of Tungstic Acid with Primary Amine N1923, Sci. China: Technol. Sci., 2015, 58(5), 935–942, DOI:10.1007/s11431-015-5819-y.
- C. O. Iloeje, J. Colón, F. Carlos., J. Cresko and D. J. Graziano, Gibbs Energy Minimization Model for Solvent Extraction with Application to Rare-Earths Recovery, Environ. Sci. Technol., 2019, 53(13), 7736–7745, DOI:10.1021/acs.est.9b01718.
- J.-L. Rivail, Molecular Modelling. Semi-Empirical and Empirical Methods of Theoretical Chemistry, in Computational Advances in Organic Chemistry: Molecular Structure and Reactivity, ed. C. Ögretir and I. G. Csizmadia, Springer, Netherlands, Dordrecht, 1991, pp. 229–259. DOI:10.1007/978-94-011-3262-6_4.
- M. W. Wadsley, Computational Analysis in Hydrometallurgy, Proceedings of the International Sympos, 2005, vol. Thermodynamically consistent versus completely empirical property models in process simulation, pp. 311–326 Search PubMed.
- S. Dash and S. Mohanty, Mathematical Modeling Aspect in Solvent Extraction of Metals, Sep. Purif. Rev., 2021, 50(1), 74–95, DOI:10.1080/15422119.2019.1648294.
- A. Klamt, The COSMO and COSMO-RS Solvation Models, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1338, DOI:10.1002/wcms.1338.
- E. V. Belova, A. S. Kapelushnikov, A. A. Novikov, R. Chen and I. A. Uspenskaya, Phase Equilibria in Water–Methanesulfonic Acid–Nickel (Cobalt) Methanesulfonate Systems: Experiment and Modeling, J. Chem. Eng. Data, 2025, 70(6), 2505–2514, DOI:10.1021/acs.jced.5c00059.
- E. V. Belova, J. D. Shakirova, K. A. Lyssenko, I. V. Mikheev, A. S. Maliutin, N. A. Kovalenko and I. A. Uspenskaya, Phase Equilibria, Structural and Thermodynamic Properties of Phases in the Nickel (II) Methanesulfonate – Water, Cobalt (II) Methanesulfonate – Water and Manganese (II) Methanesulfonate – Water Systems, J. Chem. Thermodyn., 2023, 182, 107049, DOI:10.1016/j.jct.2023.107049.
- A. K. Covington and R. Thompson, Ionization of Moderately Strong Acids in Aqueous Solution. Part III. Methane-, Ethane-, and Propanesulfonic Acids at 25 °C, J. Solution Chem., 1974, 3(8), 603–617, DOI:10.1007/BF00650404.
- A. K. Covington and T. H. Lilley, Ionization of Methanesulphonic Acid in Aqueous Solution at 25 °C by Proton Magnetic Resonance Measurements, Trans. Faraday Soc., 1967, 63, 1749–1753, 10.1039/TF9676301749.
- P. Wang, A. Anderko and R. D. Young, A Speciation-Based Model for Mixed-Solvent Electrolyte Systems, Fluid Phase Equilib., 2002, 203(1–2), 141–176, DOI:10.1016/S0378-3812(02)00178-4.
- P. Wang, A. Anderko, R. D. Springer and R. D. Young, Modeling Phase Equilibria and Speciation in Mixed-Solvent Electrolyte Systems: II. Liquid–Liquid Equilibria and Properties of Associating Electrolyte Solutions, J. Mol. Liq., 2006, 125(1), 37–44, DOI:10.1016/j.molliq.2005.11.030.
- R. Lommelen, B. Dewulf, J. Bussé and K. Binnemans, Predictive Thermodynamic Model for Solvent Extraction of Iron(III) by Tri-n-Butyl Phosphate (TBP) from Chloride Media, Sep. Purif. Technol., 2024, 348, 127708, DOI:10.1016/j.seppur.2024.127708.
- R. Lommelen and K. Binnemans, Thermodynamic Modeling of Salting Effects in Solvent Extraction of Cobalt(II) from Chloride Media by the Basic Extractant Methyltrioctylammonium Chloride, ACS Omega, 2021, 6(17), 11355–11366, DOI:10.1021/acsomega.1c00340.
- E. V. Belova, V. S. Krasnov, A. B. Ilyukhin and I. A. Uspenskaya, Solid-Liquid Phase Equilibrium in the Water–Zn(II) Methanesulfonate and Water–Cu(II) Methanesulfonate Systems, Thermochim. Acta, 2018, 668, 46–57, DOI:10.1016/j.tca.2018.08.004.
- E. V. Belova, A. S. Kapelushnikov, A. A. Novikov, Z. Sun and I. A. Uspenskaya, Phase Equilibria in Water–Methanesulfonic Acid–Copper (Zinc) Methanesulfonate: Experiments and Modeling, J. Chem. Eng. Data, 2024, 69(3), 1347–1356, DOI:10.1021/acs.jced.3c00646.
- E. V. Belova, A. S. Kapelushnikov and A. L. Voskov, Phase Equilibria in H2O–CH3SO3H System: Experiment and Thermodynamic Modeling, Russ. J. Phys. Chem. A, 2023, 97(7), 1354–1360, DOI:10.1134/S0036024423070038.
- E. V. Belova, Yu. D. Shakirova and V. V. Epishev, Volume Properties of Solutions in Water–Methanesulfonic Acid–Nickel (Cobalt) Methanesulfonate Systems, Russ. J. Phys. Chem. A, 2022, 96(7), 1498–1505, DOI:10.1134/S0036024422070081.
- J. Sniekers, K. Verguts, N. R. Brooks, S. Schaltin, T. H. Phan, T. M. Trung Huynh, L. Van Meervelt, S. De Feyter, J. W. Seo, J. Fransaer and K. Binnemans, Liquid Nickel Salts: Synthesis, Crystal Structure Determination, and Electrochemical Synthesis of Nickel Nanoparticles, Chem. – Eur. J., 2016, 22(3), 1010–1020, DOI:10.1002/chem.201504123.
- E. Königsberger, Editorial: Guidelines for the Measurement of Solid–Liquid Solubility Data at Atmospheric Pressure, J. Chem. Eng. Data, 2019, 64(2), 381–385, DOI:10.1021/acs.jced.8b01263.
- Z. Li and G. P. Demopoulos, Solubility of CaSO4 Phases in Aqueous HCl + CaCl2 Solutions from 283 K to 353 K, J. Chem. Eng. Data, 2005, 50(6), 1971–1982, DOI:10.1021/je050217e.
- K. S. Pitzer, Thermodynamics of Electrolytes. I. Theoretical Basis and General Equations, J. Phys. Chem., 1973, 77(2), 268–277, DOI:10.1021/j100621a026.
- P. Wang and A. Anderko, Computation of Dielectric Constants of Solvent Mixtures and Electrolyte Solutions, Fluid Phase Equilib., 2001, 186(1–2), 103–122, DOI:10.1016/S0378-3812(01)00507-6.
- J. M. Prausnitz; R. N. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice-Hall international series in the physical and chemical engineering sciences, Prentice Hall PTR, Upper Saddle River, N.J, 3rd edn, 1999 Search PubMed.
- D. G. Archer, Thermodynamic Properties of Import to Environmental Processes and Remediation. II. Previous Thermodynamic Property Values for Nickel and Some of Its Compounds, J. Phys. Chem. Ref. Data, 1999, 28(5), 1485–1507, DOI:10.1063/1.556044.
- J. D. Cox; D. D. Wagman and V. A. Medvedev, CODATA Key Values for Thermodynamics, Hemisphere Publishing Corporation, New York, 1984 Search PubMed.
- N. A. Lange, Lange's Handbook of Chemistry, 15, in McGraw-Hill handbooks, ed. J. A. Dean, McGraw-Hill, New York, NY, 1999 Search PubMed.
- K. G. Joback and R. C. Reid, Estimation of Pure-Component Properties from Group-Contributions, Chem. Eng. Commun., 1987, 57(1–6), 233–243, DOI:10.1080/00986448708960487.
- H. Veith, C. Luebbert and G. Sadowski, Correctly Measuring and Predicting Solubilities of Solvates, Hydrates, and Polymorphs, Cryst. Growth Des., 2020, 20(2), 723–735, DOI:10.1021/acs.cgd.9b01145.
- F. Charbonnier, Thermal Behavior of Some Compounds of Methanesulfonic Acid with Transition Metals, Thermochim. Acta, 1979, 33, 31–39, DOI:10.1016/0040-6031(79)87027-6.
- J. Tian, H. Jiang, H. Gong and Z. Sun, Research of Thermal Decomposition of Hydrated Methanesulfonates, J. Therm. Anal. Calorim., 2004, 77(3), 825–831, DOI:10.1023/B:JTAN.0000041661.57570.83.
- M. Wang, Z. G. Song, H. Jiang and H. Gong, Thermal Decomposition of Metal Methanesulfonates in Air, J. Therm. Anal. Calorim., 2009, 98(3), 801–806, DOI:10.1007/s10973-009-0119-z.
- F. Charbonnier, Thermal Analysis of Some Hydrated Cobalt(II) Alkanesulfonates, Thermochim. Acta, 1973, 7(3), 217–224, DOI:10.1016/0040-6031(73)85058-0.
- P. M. Kobylin, H. Sippola and P. A. Taskinen, Thermodynamic Model for Acidic Ni(II) Sulfate from Solubility Data, Calphad, 2013, 40, 41–47, DOI:10.1016/j.calphad.2012.10.002.
- J. A. Addlestone, The System Nickel Sulfate – Sulfuric Acid – Water at 25 °C. and 0 °C, J. Phys. Chem., 1938, 42(3), 437–440, DOI:10.1021/j100898a014.
- E. J. Reardon, Ion Interaction Model Applied to Equilibria in the Nickel(II) Sulfate-Sulfuric Acid-Water System, J. Phys. Chem., 1989, 93(11), 4630–4636, DOI:10.1021/j100348a045.
- CCDC 2484546: Experimental Crystal Structure Determination, 2025 DOI:10.5517/ccdc.csd.cc2pdcn4.
| This journal is © the Owner Societies 2026 |