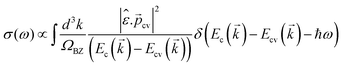Pressure-induced tunability and conductivity minimum in 3C-SiC for optoelectronic applications

Abstract

This study unveils the pressure-induced tuning of the optoelectronic properties of cubic silicon carbide (3C-SiC) through a novel synergic approach that combines Hirshfeld topological analysis (HTA) with first-principles calculations. Our simulations reveal a systematic compression of the crystal lattice, with the lattice parameter decreasing from 4.380 Å to 4.088 Å as pressure increases to 65.6 GPa. This structural evolution drives significant blueshifts in the complex dielectric function and reflectivity. The key finding is the discovery of a distinct minimum in the electrical conductivity at a critical pressure of 26.6 GPa. Crucially, HTA provides the microstructural rationale, correlating this minimum with the evolution of void spaces (e.g., Hirshfeld volume of ∼348.4 ų, and void volume of 49.92 ų). This phenomenon demonstrates the potential of 3C-SiC for designing highly sensitive pressure sensors and tunable optoelectronic devices that operate in extreme environments. This work establishes a framework for optimizing functional materials through targeted manipulation of their topological properties.

---

1. Introduction

Cubic silicon carbide (3C-SiC) is a pivotal semiconductor material, renowned for its exceptional mechanical strength, high thermal conductivity, and wide band gap, which make it a leading candidate for next-generation optoelectronic and high-power electronic devices.^1–6 Its performance in extreme environments, particularly under high pressure, is critical for applications ranging from high-pressure sensors to protective coatings.^7–9

In our recent study,¹⁰ we employed a synergic Hirshfeld topological analysis (HTA) and first-principles approach to comprehensively investigate the mechanical and structural response of 3C-SiC to pressures up to 65.6 GPa. That work established a detailed picture of its mechanical stability, elastic anisotropy, and the evolution of bond lengths and Hirshfeld topological geometries (HTGs) under compression. However, while the mechanical properties under pressure are now well-characterized, a fundamental question remains: how does this controlled compression, which we have shown to systematically alter the crystal's structure and bonding, modulate its core optoelectronic functionality.

The interplay between pressure-induced structural changes and optoelectronic properties is a rich area of study, facilitated by advanced experimental techniques like high-pressure XRD and Raman spectroscopy,^11–13 and increasingly accurate ab initio computational methods.^14,15 While the thermodynamic and elastic behaviors of 3C-SiC have been explored,¹⁶ a detailed and systematic theoretical investigation of its pressure-dependent optical constants and electronic conductivity—correlated directly with topological changes in the electron density—is conspicuously absent from the literature. This gap is significant, as the ability to tune a material's dielectric function, absorption, and conductivity through external pressure is a powerful tool for designing advanced optoelectronic devices.

This paper extends our previous work by shifting the focus from mechanical to optoelectronic properties. We leverage the same robust synergic methodology—integrating HTA with density functional theory (DFT) calculations—to unravel the fundamental optoelectronic behavior of 3C-SiC under elevated pressures. Where standard DFT calculations provide the electronic structure, HTA offers a unique, visual, and quantitative perspective on how intermolecular interactions and void spaces evolve with pressure, providing a direct structural link to the observed macroscopic properties.

Specifically, we present a comprehensive analysis of the complex dielectric function, reflectivity, absorption spectrum, and complex conductivity of 3C-SiC across a wide pressure range. Our investigation reveals a surprising and novel phenomenon: a distinct minimum in the electrical conductivity at approximately 26.6 GPa. This non-monotonic behavior, which we correlate directly with the evolving Hirshfeld surfaces and void volumes, demonstrates that external pressure can be used as a precise tool to fine-tune the optoelectronic response of 3C-SiC. This discovery opens new avenues for the development of pressure-sensitive optoelectronic devices and provides a deeper understanding of the structure–property relationships in this technologically critical material.

2. Calculations methodology

2.1. The CASTEP computational procedure under elevated pressure

The process begins with importing the initial structure of the unit cell, often obtained experimentally from a Crystallographic Information File (CIF),^12–14 into CASTEP code.¹⁵ This initial configuration serves as a starting point for simulations at zero pressure. Then, this initial configuration was used to optimize the unit cell at elevated pressures (see below). The determination of electrical and optical behavior involved the utilization method based on the DFT is described in comprehensive details in ref. 16–20.

Briefly, the software navigated the intricate domain of computational methodology, integrating the generalized gradient approximation (GGA)¹⁶ within the expansive landscape of the full potential linearized augmented plane wave's technique. Augmented plane waves, seamlessly integrated into the intricate of the CASTEP code, played a pivotal role in unraveling the structural, electrical, and optical hallmarks. The GGA which is implemented in the modern DFT, embarked on a quest to refine the local density approximation, put on the Perdew–Burke–Ernzerhof (PBE) scheme.^17,19 The utilization of an ultra-soft pseudo-potential emerged as a time-saving routine, bestowing computational efficiency while keeping the computational accuracy at maximum. To pursuit the elusive 3C-SiC crystal structure with least energy, under varied pressures, the geometry optimization is invoked through the Broyden–Fletcher–Goldfarb–Shanno (BFGS) iterations.²¹ Cut-off energy of 630 eV presided over the plane-wave expansion, while the Brillouin zone, subjected to the Monkhorst–Pack mesh's different choreography k-points to achieve the best geometry optimization for SiC crystal at different pressures.¹⁵ The valence electron configuration is set to be: pseudo atomic calculation for the C-atom: 2s2 2p2, and Si-atom: 3s2 3p2 which is in turn converged in 19 iterations to total energies of −145.716 eV and −101.648 eV, respectively. Geometry optimization was done utilizing the total energy convergence tolerance of 10⁻⁶ eV per atom, maximum lattice point displacement within 10⁻³ Å, maximum ionic Hellmann–Feynman force within 0.03 eV Å⁻¹ and maximum stress tolerance of 0.01 GPa, with finite basis set corrections. Also, the none-periodic dipole correction, purely density-mixing, and charge density mixing g-vector = 1.500 Å⁻¹ schemes were adopted for the rest of calculations. These chosen levels of tolerances are consistent approximations of structural, opto-electric hallmarks with optimized computing times.²¹

The calculation of crystal lattice constants and bonding distances between atoms after optimization involves post-processing analyses of the optimized geometry. After the geometry optimization, the software provides the optimized unit cell parameters, including lattice constants (a, b, c) and angles (α, β, γ) that define the shape, and size of the unit cell in three-dimensional space. Then the software computes the direct lattice vectors (a, b, c) and reciprocal lattice vectors (a*, b*, c*) from optimized unit cell parameters. These vectors are fundamental in describing the crystal structure and are essential for subsequent calculations. Also, the optimized atomic positions within the unit cell are determined after the geometry optimization. The software calculates the distances between pairs of atoms based on their optimized positions. These distances provide information about the bonding arrangement in the material.¹⁹

The single crystal 3C-SiC calculations of the optical and electrical properties of cubical structure with space group crystal: F4̄3m (#216) was conducted through a systematic approach known as the stress and strain approach.^22,23 In electronic properties calculation, the crystal undergoes a series of analyses to unveil its behavior under elevated pressure. Initially, the geometry optimization phase refines the crystal structure, seeking the most stable atomic arrangement amidst heightened pressure conditions. Subsequently, employing DFT, CASTEP delves into the electronic structure of the crystal, unraveling the energies and wavefunctions of electrons within the material. Through band structure analysis, the computation reveals intricate details of the crystal's energy levels and permissible electronic states, pivotal for grasp electrical conductivity and other electronic phenomena. Moreover, CASTEP carefully considers the influence of elevated pressure on the electronic structure, adeptly adjusting the unit cell volume and atomic positions to reflect these effects.¹⁵

Meanwhile, in the optical properties calculation, CASTEP explores on a nuanced exploration of the crystal's interaction with light under elevated pressure. It initiates by computing the complex dielectric function 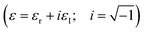, a cornerstone in understanding how the crystal interfaces with electromagnetic fields, crucial for discerning its response to light and other electromagnetic radiation forms. Leveraging insights from the dielectric function, CASTEP proceeds to determine the complex refractive index (n* = n + iκ; n: refractive index, κ: extinction coefficient) of the crystal, shedding light on the extent to which light is refracted as it traverses through the material. Further, by simulating the absorption spectrum, CASTEP unveils the wavelengths of light absorbed by the crystal, pivotal for applications such as photovoltaic and optical devices. Notably, CASTEP also factors in pressure-induced changes in optical properties, providing invaluable insights into alterations in the material's behavior under light during processing. By precisely examining both electronic and optical properties, CASTEP equips researchers with a holistic understanding of how a single crystal responds to elevated pressure and elucidates the consequent shifts in its electronic and optical behaviors.¹⁵

The decision to employ specific pressure conditions stems from the desire to emulate real-world scenarios or to explore the material's behavior under extreme conditions that may achievable in experimental setups.^7,8 High pressure can induce significant changes in the crystal structure, electronic properties, and optical behaviors, offering insights into novel phenomena or potential applications of the material under extreme environments. Furthermore, by varying the pressure range, researchers can systematically investigate the pressure-dependent responses of the material, contributing to a comprehensive understanding of its behavior across a wide range of conditions. Thus, the rationale behind selecting high pressure values is crucial for contextualizing the simulation results and elucidating their significance in the broader scientific context.^6–10

2.2. The generation of 3C-SiC single crystal's CIF at elevated pressures using the zero pressure-based crystal CIF data

The experimentally 3C-SiC single crystal's properties at diverse external stresses are selected and compared with that found in ref. 8. Their density, lattice-parameter a (in Å), and unit-cell volume (in ų) are displayed in Table 1. This particular report used and analyzed the CFI data from Cambridge-Structural-Database (i.e., CSD).¹⁴ This study has only used the CIF (refcode: 1747966¹⁴) for the single crystal structure at zero pressure as an input file in CASTEP computational code whereas other cubical crystal's CIF's at elevated pressures were optimized using the CASTEP code as describes below. These optimized structures are then used for the subsequent calculations to gain insights about the EoS, structure and elastic properties of a single SiC crystal.

Table 1 The 3C-SiC crystal applied stress along with the CIF and other unit cell parameter a (in Å) and unit cell volume (ų). The C⋯Si, Si⋯Si, and C⋯C bond length (Å) is also depicted in the table. The experimental data were also shown for comparison as detailed in.⁸ The used refcode in this study is 1747966¹⁴

Pressure (GPa)	a (Å) (This work)	a (Å) (Experimental)^a	C⋯Si (Å)	Si⋯Si (Å)	C⋯C (Å)	V (Å^3) (This work)	V (Å^3) (Experimental)^a
a The data taken from ref. 8.
0	4.3804	4.3618	1.89871	—	—	84.0523	82.9846
2.0	4.3712	4.3486	1.89278	—	—	83.522138	82.2334
6.4	4.3427	4.3204	1.88794	—	—	81.902360	80.6440
16.4	4.2855	4.2651	1.85570	—	—	78.708281	77.5868
26.6	4.2353	4.2165	1.83393	2.99479	2.99479	75.970447	74.9646
35.6	4.1958	4.1786	1.81683	2.96687	2.96687	73.864985	72.9613
45.8	4.1556	4.1396	1.79941	2.93843	2.93843	71.761163	70.9374
56.9	4.1164	4.1008	1.78243	2.91070	2.91070	69.748987	68.9614
65.6	4.0878	4.0729	1.77019	2.89070	2.89070	68.306113	68.3076

---

2.3. CrystalExplorer software: Hirshfeld surface analysis

Analysis of small molecule crystal's configurations has traditionally centered on identifying hydrogen bonding patterns.^22,23 The spatially arrangement of the atoms in a crystal is crucial, especially under high pressure, leading to significant topological distortions. To visualize intermolecular contacts, the molecular HS is calculated, providing a three-dimensional representation. Using CrystalExplorer21 (https://crystalexplorer.net/), Hirshfeld surfaces and 2D fingerprints are easily generated from the single crystal XRD studies. The parameter d_norm, reflecting distances and van der Waals radii, helps highlight closest contacts in red or van der Waals contacts in white and blue. The 2D fingerprint plots depict various intermolecular interactions.¹³

3. Results and discussion

3.1. Structural properties at elevated pressures

The 3C-SiC crystal adopts a cubic zinc blende structure (space group F4̄3m, #216), as illustrated in Fig. 1. The Si and C atoms occupy the Wyckoff positions (0, 0, 0) and (1/4, 1/4, 1/4), respectively, within the unit cell.¹⁷ Visualization via VESTA software²⁴ confirms the unit cell comprises four silicon and four carbon atoms, forming a structure with 56 bonds and 14 polyhedra.

Fig. 1 Schematic 3D crystal structure of silicon carbide (SiC) crystal: (left) Ball- and-stick (right) polyhedra representation. The crystallographic principle axial directions in the crystal are also indicated. The structure exhibits a space group: F4̄3m (#216).

Our DFT-calculated structural parameters under elevated pressure are summarized in Table 1, alongside available experimental data for comparison.^6–8,25,26 The results demonstrate the expected compression of the lattice under hydrostatic stress. Specifically, the C–Si bond length contracts from 1.89971 Å at 0 GPa to 1.77019 Å at 65.6 GPa. Similarly, the Si–Si and C–C bond lengths both decrease from 2.99479 Å to 2.89070 Å over the same pressure range. This bond compression drives a concomitant reduction in the lattice parameter a, and the unit cell volume.

These calculated trends are in excellent agreement with previous experimental work. For instance, Zhuravlev et al.⁸ reported a lattice parameter reduction from 4.3618 Å to 4.0729 Å for 3C-SiC under pressures exceeding 65 GPa using simultaneous XRD and IR measurements, closely matching our computational results.

While the compressibility of 3C-SiC is well-documented,^25–28 significant gaps remain in understanding its full suite of properties under extreme conditions. Notably, studies by Ghebouli et al.²⁹ and Drissi et al.³⁰ indicate no phase transition occurs in the 40–70 GPa range, even at high temperatures, confirming the stability of the cubic phase within our studied pressure regime. However, a scarcity of data persists concerning the detailed thermodynamic and functional properties—particularly optoelectronic behavior—of cubic 3C-SiC under high pressure at ambient temperature. It is this critical gap in fundamental understanding that the present work aims to address, providing essential insights for advancing the material's technological applications in high-pressure environments.

3.2. Electronic and optical properties at elevated pressures

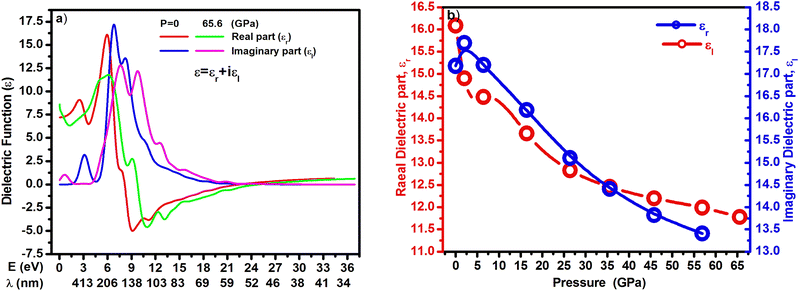
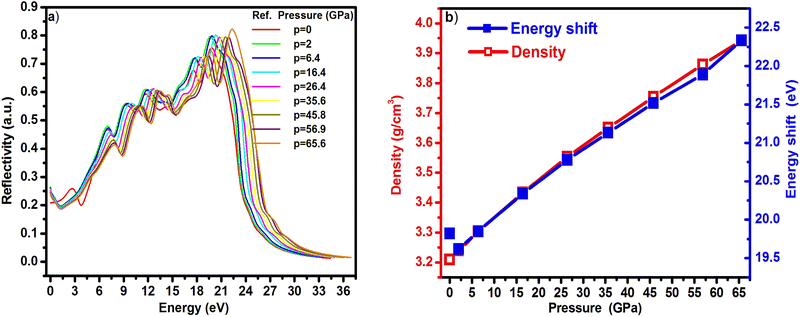
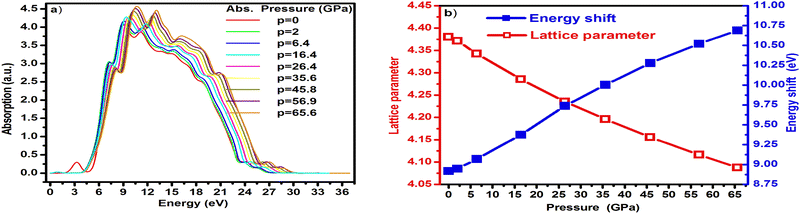
The application of pressure induces significant changes in the electronic and optical response of 3C-SiC, directly stemming from the structural compression detailed in Section 3.1. The complex dielectric function, ε(ω) = ε_r + iε_I, is a fundamental property that dictates the material's interaction with light. Fig. 2a presents this function across a photon energy range of 0–36 eV for low (0 GPa) and high (65.6 GPa) pressures, revealing a pronounced pressure-induced shift in the peaks of both its real and imaginary components.

Fig. 2 (a) Variation of the complex dielectric function ε (i.e., ε = ε_r + iε_I) versus incoming photon energy (in eV) at two selected (p = 0 GPa) and high (p = 65.6 GPa) pressures applied on the silicon carbide (SiC) crystal. (b) The maximum values of the real and imaginary part of the complex dielectric function as a function of the applied stress on the SiC crystal. These peaked values are obtained from curves similar to that presented in panel (a). The figure shows both parts are decreasing while elevating the stress on the crystal.

This systematic shift, quantified in Fig. 2b, shows the dielectric peaks decreasing in value with increasing pressure, a direct consequence of the reducing unit cell volume (Table 1). This modification of the dielectric landscape has an immediate cascading effect on other optical properties. As shown in Fig. 3a, the crystal's reflectivity is altered, with its peak values increasing and shifting to higher photon energies—a total shift of approximately 3 eV is observed between ambient and high pressure (Fig. 3b). A similar blueshift and enhancement are observed in the absorption spectrum (Fig. 4).

Fig. 3 The calculated reflectivity as a function of photon energy (0 < E < 36 eV) at different applied external pressure on the silicon carbide (SiC) crystal (a), and the energy shift at maximum reflectivity gained from the SiC crystal (b). The figure shows that the applied pressure induces an energy shift in the peaked reflectivity.

Fig. 4 The calculated absorption as a function of photon energy (0 < E < 36 eV) at different applied external pressure on the silicon carbide (SiC) crystal (a), and the energy shift at maximum absorption gained from the SiC crystal (b). The figure shows that the applied pressure induces an energy shift at maximum absorption while the lattice parameter decreases as the applied external pressure is elevated.

The complex refractive index (n* = n + iκ) follows this trend, with both components declining from n = 4.15, κ = 4.05 at 0 GPa to n =3.35, κ = 2.68 at 65.6 GPa (Fig. 5a and b). Most significantly, the analysis of the complex conductivity (σ = σ_r + iσ_I) reveals a striking phenomenon. While the spectra shift (Fig. 6a and b), the key finding is the evolution of the total conductivity with pressure, detailed in Fig. 7. Contrary to a monotonic increase, the total conductivity exhibits a clear and distinct minimum at 26.6 GPa. This non-monotonic behavior demonstrates that external pressure is not merely a direct tool for increasing conductivity but a precise means to fine-tune the electrical (and thus optoelectronic) properties of 3C-SiC for specific applications. The observed behavior in 3C-SiC can be understood as follow: the complex conductivity is intrinsically linked to the joint density of states (JDOS) and the probability of optical transitions between the valence and conduction bands. In a perfect crystal, these electronic states are organized into well-defined energy bands (E(k⃑)) that are periodic in the reciprocal space (the Brillouin zone). The optical conductivity, σ(ω), is calculated from the integral over all possible electronic transitions across the Brillouin zone:

where p⃑_c is the momentum matrix element, E_c and E_v are the conduction and valence band energies, and [small epsilon, Greek, circumflex] is the polarization vector. Thus, the observed “periodic” peaks and valleys in the conductivity spectrum arise due to the following reasons. Firstly, the electronic density of states exhibits sharp features, known as Van Hove singularities,¹ at critical points in the Brillouin zone where the gradient of (E(k⃑)) vanishes (i.e., (∇_k⃑E = 0)). At these specific photon energies, the JDOS becomes very large, leading to prominent peaks in the optical conductivity. The sequence of peaks in Fig. 6 corresponds to a series of these singularities at different high-symmetry points in the Brillouin zone of 3C-SiC (e.g., Γ, X, L). Thus, the “periodic curve” seen here is the characteristic fingerprint of 3C-SiC's electronic band structure. The pressure-induced changes we observe—namely the blueshift and reshaping of these peaks—are direct computational evidence of the systematically alters the underlying band energies and the probabilities of interband transitions due to compression.

Fig. 5 (a) Variation of the complex index of refraction n* (n* = n + iκ) versus incoming photon energy (in eV) at two selected (p = 0 GPa) and high (p = 65.6 GPa) pressures applied on the silicon carbide (SiC) crystal. (b) The maximum values of the real and imaginary part of the complex index of refraction as a function of the applied stress on the SiC crystal. These peaked values are obtained from curves similar to that presented in panel (a). The figure shows both parts are decreasing while elevating the stress on the crystal.

Fig. 6 (a) Variation of the complex conductivity (i.e., σ = σ_r + iσ_I) and (b) the total conductivity versus incoming photon energy (in eV) at two selected (p = 0 GPa) and high (p = 65.6 GPa) pressures applied on the silicon carbide (SiC) crystal. The inset shows the total conductivity variation between 5.5 < E < 12.0 eV. Also, the graph shows a decrease in the maximum conductivity as a function of applied external pressure (see next figure for details).

Fig. 7 The maximum values of the total conductivity as a function of the applied stress on the SiC crystal. These peaked values are obtained from curves similar to that presented in Fig. 6b. The figure shows that the conductivity attains its minimum value at pressure = 26.6 GPa; simultaneously the energy shift keeps increasing while elevating the stress on the crystal.

This tunability can be understood through pressure's effect on the electronic band structure. Lattice contraction enhances the overlap of electronic orbitals, which leads to a systematic reduction of the band gap⁸ as confirmed by our calculations (see Table 3). The evolution of electrical conductivity, however, reveals a more nuanced picture than a simple monotonic increase. The presence of a well-defined conductivity minimum at 26.6 GPa (Fig. 7) signifies a complex interplay between competing mechanisms. Our analysis reveals that this non-monotonic behavior arises from the competition between a steadily increasing carrier concentration, driven by band gap closure, and a non-monotonic change in carrier mobility, governed by pressure-dependent effective masses. Specifically, both electron and hole effective masses reach a maximum at the critical pressure of 26.6 GPa (Table 3), leading to a minimum in mobility that temporarily overcomes the effect of rising carrier concentration. Following this minimum, the steep rise in conductivity is driven by the continued band gap reduction coupled with a decrease in carrier effective masses, significantly enhancing semiconducting behavior. Thus, this occurs without a transition to metallic character, as the band gap remains finite (1.165 eV at 65.6 GPa). This finding moves beyond the established literature on pressure-induced metallization^29–31 and highlights a new regime for precisely manipulating the electronic transport in 3C-SiC by targeting specific band structure configurations.

Table 2 Evolution of Hirshfeld topological geometries for 3C-SiC under hydrostatic pressure. The systematic reduction in void volume and surface area quantifies the lattice densification. The conductivity minimum at 26.6 GPa occurs at a critical void volume of 49.92 ų, providing the microstructural link to the electronic transition

Pressure (GPa)	Hirshfeld volume (Å^3)	Void's volume (Å^3)	Hirshfeld surface (Å^2)	Void's surface (Å^2)
0	380.74	59.53	299.81	64.36
2.0	383.75	58.63	301.49	64.18
6.4	380.74	57.91	299.81	64.05
16.4	361.1	53.02	288.76	63.17
26.6	348.43	49.92	281.54	62.49
35.6	338.29	47.33	275.7	61.78
45.8	328.39	44.88	269.95	61.08
56.9	318.85	42.45	264.34	60.09
65.6	312.13	40.73	260.38	59.1

---

Table 3 Electronic properties and Hirshfeld void volume of 3C-SiC under hydrostatic pressure. The conductivity minimum at 26.6 GPa correlates with maxima in both electron (0.114 m_e) and hole (0.476 m_h) effective masses, occurring at a specific Hirshfeld void volume of 49.92 ų. The band gap shows monotonic closure from 1.378 eV to 1.165 eV, demonstrating competing effects of increasing carrier concentration and decreasing carrier mobility

Pressure (GPa)	Band gap (eV)			Hirshfeld void volume (Å^3)	Conductivity (S m^−1)
0	1.378	0.11362	0.44032	59.53	15.27629
2	1.372	0.11236	0.43931	58.63	15.21897
6.4	1.361	0.11135	0.43924	57.91	15.04915
16.4	1.315	0.1097	0.43276	53.02	14.62027
26.6	1.283	0.11385	0.47551	49.92	14.17069
35.6	1.254	0.11003	0.47294	47.33	14.34581
45.8	1.231	0.1066	0.46995	44.88	14.46946
56.9	1.188	0.09171	0.46798	42.45	14.57395
65.6	1.165	0.08467	0.46247	40.73	14.67255

---

3.3. Correlating Hirshfeld topological evolution with optoelectronic properties

The evolution of the HTSs and their associated voids under pressure provides the critical microstructural link to the macroscopically observed optoelectronic trends discussed in Section 3.2. This analysis moves beyond standard DFT by offering a quantitative, visual framework to understand how compression alters electron density distributions and intermolecular interactions, which ultimately govern the material's functional properties.

As shown in Fig. 8, the HTGs offer a detailed view of the electron density around atoms. The distinct colors on these surfaces map regions of close interatomic contact: red craters signify strong repulsive interactions, while blue humps indicate attractive forces. The dominant interaction is the Si⋯C bond (85.3%), with smaller contributions from C⋯C (6.4%) and Si⋯Si (8.3%) contacts as addressed in details by Khattari et al.¹⁰ Under increasing pressure, the HTS morphology transforms from a rounded-cubical shape to a more compact, elongated-edged cubical configuration by 65.6 GPa (see SI), indicating a redistribution of electron density and a strengthening of intermolecular interactions, even as the relative percentages of contact types remain constant.¹⁰

Fig. 8 The Hirshfeld topological geometry volumes (in ų) and surfaces (in Ų) as a function of the total conductivity of the silicon carbide crystal. The figure shows that the minimum conductivity is assumed at specific Hirshfeld topological geometries as the pressure is increased on the crystal. The Hirshfeld topological geometries while the voids are generated at 0.05, 0.08 e.a.u.⁻³ respectively as input parameters in the software Crystal Explorer. See text for more discussions.

Concurrently, the void spaces within the crystal lattice, visualized in Fig. 8, undergo a significant transformation. For instance, the HTS area contracts from 302 Ų to 260 Ų, and the void surface area from 64.4 Ų to 59.0 Ų between 0 and 65.6 GPa (see Table 2). This quantifiable densification of the crystal structure is a key driver of the changing optoelectronic response.

Most importantly, the HTA directly explains the non-monotonic behavior of the total conductivity, particularly the minimum observed at 26.6 GPa. Fig. 8 depicts the total conductivity as a function of key Hirshfeld parameters. The conductivity minimum occurs simultaneously at specific critical values: a Hirshfeld volume of ∼350.0 ų and a void volume of ∼50.0 ų, corresponding to a Hirshfeld surface area of ∼282 Ų and a void surface area of ∼62.5 Ų (see Table 2).

This correlation reveals the elaborated interplay between external pressure, microscopic structure, and electronic properties:

• Enhanced intermolecular interactions: pressure reduces interatomic distances, leading to a stronger overlap of electron clouds. This directly affects the electronic structure by modifying the bandgap and altering charge carrier mobility, mechanisms crucial for the observed shifts in conductivity and optical absorption (see discussions below).

• Reduction of void spaces: the systematic collapse of void spaces (Table 2) increases the crystal's density. This densification modifies the polarizability of the material and how it interacts with electromagnetic light, leading to the documented increases in the refractive index, dielectric function, and optical absorption (see discussions below).

Thus, the HTA is not merely a complementary technique but the cornerstone of our synergic approach. It provides a direct, quantitative connection between the pressure-induced structural compaction—evidenced by evolving surfaces and shrinking voids—and the macroscopic tuning of 3C-SiC's optoelectronic properties. These microscopic changes in electron density distribution and intermolecular space are the fundamental drivers behind the ability to precisely fine-tune this material's functionality for advanced device applications.

3.4 The origin of the conductivity minimum

Our combined DFT and HTA reveal the precise physical mechanism behind the anomalous conductivity minimum in 3C-SiC under pressure. The electrical conductivity, plotted in Fig. 7, exhibits a clear minimum at 26.6 GPa. This behavior arises from a complex competition between two pressure-induced phenomena: a monotonic increase in intrinsic carrier concentration due to band gap closure, and a non-monotonic change in carrier mobility governed by pressure-dependent effective masses.

Contrary to a simple metallization scenario, our results show that the band gap closes gradually from 1.378 eV at 0 GPa to 1.165 eV at 65.6 GPa (Table 3). This steady reduction should, in isolation, lead to a monotonic increase in carrier concentration and conductivity. The observed minimum, therefore, must be driven by a countervailing effect on carrier transport.

The key insight comes from our calculated carrier effective masses. As shown in Table 3, both the electron (m_e) and hole (m_h) effective masses reach distinct maxima precisely at 26.6 GPa. The electron effective mass peaks at 0.114 m_e, while the hole effective mass shows a more pronounced increase, peaking at 0.476 m_e. This simultaneous mass enhancement for both carriers directly explains the mobility minimum, as mobility is inversely proportional to effective mass (μ ∝ 1/m*).¹

This electronic transition is rooted in the structural evolution quantified and visualized by our HTA. As vividly illustrated in Fig. 9, the internal void spaces undergo a significant transformation, evolving from a rounded shape to a compressed, leaflet-like ellipsoid as pressure increases to 65.6 GPa. This visual evidence of densification is quantified in Table 2, which shows the Hirshfeld void volume decreasing monotonically with pressure from 59.53 ų to 40.73 ų. Crucially, the conductivity minimum and effective mass maxima (Table 3) do not occur at the point of maximum compression, but at a specific, critical void volume of 49.92 ų, corresponding to the lattice configuration at 26.6 GPa. This indicates that the electronic response is not a simple function of compression degree, but is highly sensitive to the specific atomic-scale environment achieved at this critical pressure.

Fig. 9 Evolution of Hirshfeld surfaces (left) and void spaces (right) in 3C-SiC under representative pressures. The surfaces are mapped with the normalized contact distance d_norm, where red regions indicate interatomic distances shorter than the sum of van der Waals radii (close contacts), blue regions indicate longer distances (void spaces), and white regions represent contacts at the van der Waals separation. The progressive compression from 0 GPa to 65.6 GPa leads to a systematic reduction and reshaping of the internal void spaces (highlighted in blue), correlating with the increasing lattice densification. The critical configuration at 26.6 GPa, associated with the conductivity minimum, occurs at a specific void volume of 49.92 ų, illustrating the direct link between microscopic topology and macroscopic electronic response.

The band structures in Fig. 10 visually confirm this, showing pronounced flattening of both the valence and conduction bands at 26.6 GPa compared to other pressures, which is the direct origin of the increased effective masses. Complementary evidence from the density of states (Fig. 11) further elucidates this electronic transition. The progressive closure of the band gap is apparent, and at 26.6 GPa, sharp peaks emerge in the DOS near both band edges, directly manifesting the band flattening observed in the electronic structure.

Fig. 10 Electronic band structure of 3C-SiC at representative pressures. (a) 0 GPa shows the semiconducting ground state. (b) At 26.6 GPa, band flattening occurs in both conduction and valence bands, corresponding to the maxima in both electron and hole effective masses and the conductivity minimum (c); and (d)  At 65.6 GPa, continued band evolution is observed as the gap narrows to 1.165 eV.

Fig. 11 Density of states (DOS) evolution of 3C-SiC under hydrostatic pressure. (a) 0 GPa shows the semiconducting ground state with clear band gap. (b) At 16.4 GPa, initial band gap reduction begins. (c) At 26.6 GPa, pronounced band flattening occurs, evidenced by sharp DOS peaks near both valence and conduction band edges, corresponding to maxima in carrier effective masses and the conductivity minimum. (d) At 65.6 GPa, continued band evolution accompanies gap closure to 1.165 eV. The total DOS (green line) and projected s-(blue) and p-orbital (red) contributions reveal the orbital basis of pressure-induced electronic restructuring. Vertical lines indicate the Fermi level (E_F).

Therefore, the conductivity minimum at 26.6 GPa represents a transition point where the suppression of carrier mobility, due to maximal band effective masses, temporarily overcomes the enhancement of carrier concentration from band gap reduction. This transition is triggered when the lattice compression, evidenced by the evolving void spaces in Fig. 9, tunes the crystal to the specific configuration where the band structure is optimally flat. Before this pressure, the effect of increasing carrier concentration dominates. After this pressure, the combined effect of resumed band steepening (decreasing effective masses) and continued gap closure drives the conductivity upward once more. This work establishes a robust structure–property relationship in 3C-SiC, demonstrating that targeted lattice compression can be used to tune optoelectronic performance through deliberate band structure engineering.

Finally, the interplay of these factors is powerfully summarized in the 2D heatmap of Fig. 12, which visualize the coupled evolution of the band gap and carrier effective masses with pressure and void volume, clearly highlighting the anomalous maxima at the critical point. These two-dimensional coupling maps showing the simultaneous variation of (a) band gap, (b) electron effective mass (m*/m_e), and (c) hole effective mass (m*/m_h) as a function of applied pressure and Hirshfeld void volume. The color scale represents the magnitude of each property. The maps visually demonstrate how the progressive reduction of void space (i.e, structural compression) is directly linked to band gap closure and the non-monotonic evolution of carrier effective masses, with a distinct maximum in both 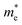and 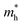occurring at a critical void volume of ∼50 ų. This provides a concise overview of the fundamental structure–property relationship governing the electronic behavior of 3C-SiC under pressure.

Fig. 12 Three 2D heatmap summarize how band gap (left), electron effective mass (m*/m_e) (middle), and hole effective mass (m*/m_h) (right) vary as a function of applied pressure (GPa) and void volume (ų). The color scale in each panel represents the magnitude of the corresponding property, allowing direct visual comparison of their sensitivities to compression. As pressure increases and the internal volume contracts, the band gap shows a gradual reduction, while the electron and hole effective masses exhibit distinct trends linked to changes in the curvature of the conduction- and valence-band edges. Together, these maps highlight the coupling between structural compression and charge-carrier dynamics, providing a concise overview of the electronic behavior evolves under moderate pressure conditions.

3.5. Limitations and future perspectives

This study provides a foundational understanding of the hydrostatic pressure-dependent optoelectronic properties of 3C-SiC through a novel Hirshfeld-DFT synergic approach. However, the work naturally suggests several promising avenues for future research to explore more complex and application-relevant scenarios.

1. Polytypism and anisotropy: our investigation focused on the isotropic cubic polytype (3C-SiC) to establish a clear baseline. Future work should extend this methodology to anisotropic polytypes like 4H-SiC and 6H-SiC.^7–9 Their hexagonal symmetry will introduce direction-dependent responses to pressure, likely leading to anisotropic shifts in optical properties and conductivity, presenting a rich area for exploration. While this requires more complex modeling to account for directional dependencies,¹⁰ it is essential for a comprehensive understanding of the SiC family.

2. Beyond hydrostatic pressure: the effect of shear stress in our model assumes ideal hydrostatic conditions. In real-world applications, such as device fabrication or mechanical processing, materials often experience non-hydrostatic (e.g., uniaxial or biaxial) stress. As demonstrated in other systems like SiO₂,³² such anisotropic pressure can induce direction-dependent properties, potentially leading to different bandgap modifications and optical anisotropies in 3C-SiC. Developing models to simulate these complex stress states, though computationally demanding, would provide invaluable insights for practical device design under operational conditions.

3. The role of defects, impurities, and doping: real-world crystals are never perfect. The intentional introduction of dopants or the unintentional presence of defects and impurities can drastically alter optoelectronic properties by creating localized states in the band structure, modifying carrier concentrations, and changing scattering mechanisms.^2,3 The interplay between these atomic-scale imperfections and high pressure remains largely unexplored. Future studies employing large supercell models could investigate how specific defects (e.g., vacancies, substitutional atoms) modulate the pressure response of 3C-SiC, which is critical for predicting the performance of engineered materials in extreme environments.

4. Conclusion

The study focused on the elaborated pressure-dependent behavior of 3C-SiC through a novel synergy of Hirshfeld topological analysis and first-principles calculations. Our work confirms the stability of the cubic phase under compression and goes beyond structural analysis to reveal a fundamental optoelectronic transition point.

The key discovery is a distinct minimum in electrical conductivity at 26.6 GPa. The study demonstrate that this phenomenon is not a simple structural effect but is governed by a direct competition in the electronic band structure: a steady rise in carrier concentration due to band gap closure is temporarily overcome by a sharp drop in carrier mobility, which is correlated with a maximum in both electron and hole effective masses at the critical pressure.

Crucially, the Hirshfeld analysis provides the missing microstructural link, showing that this electronic transition occurs at a specific Hirshfeld void volume of ∼50 ų. This direct correlation between a topological descriptor and a quantum mechanical property underscores the power of our synergistic approach.

This work provides a new design principle for tuning 3C-SiC's functionality, moving beyond mere compression and towards targeted band structure engineering. The identified transition point opens avenues for developing highly sensitive pressure-switching devices and establishes a framework for optimizing functional materials by linking their macroscopic properties to nanoscale topological and electronic evolution.

Conflicts of interest

There are no conflicts to declare.

Data availability

The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request. All relevant computational input files, raw data, and processed results will be shared with editors or reviewers if required for verification purposes.

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03752b.

Acknowledgements

The authors thank The Hashemite University for the financial support. During the preparation of this work the authors used ChatGPT/Open AI in order to improve the manuscript English language and grammar. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

References

1. H. T. Grahn, Introduction to Semiconductor Physics, World Scientific Publishing Co. Pte. Ltd., Singapore, 1999.
2. P. Vashishta, R. K. Kalia, A. Nakano and J. P. Rino, Interaction Potential for Silicon Carbide: A Molecular Dynamics Study of Elastic Constants and Vibrational Density of States for Crystalline and Amorphous Silicon Carbide, J. Appl. Phys., 2007, 101(10), 103515.
3. X. Dong and Y. C. Shin, Multiscale Modeling for Predicting the Mechanical Properties of Silicon Carbide Ceramics, J. Am. Ceram. Soc., 2016, 99(3), 1006–1014.
4. Q. Zheng, C. Li, A. Rai, J. H. Leach, D. A. Broido and D. G. Cahill, Thermal Conductivity of GaN, 71GaN, and SiC from 150 K to 850 K, Phys. Rev. Mater., 2019, 3(1), 014601.
5. V. V. Sobolev and A. N. Shestakov, Optical Spectra and Electronic Structure of Cubic Silicon Carbide, Semiconductors, 2000, 34, 433–443.
6. Q. Fan, C. Chai, J. Zhang, J. Zhang, Q. Zhang, X. Shen, W. Fan, Y. Liu and W. Lei, The Mechanical and Electronic Properties of Carbon-Rich Silicon Carbide, Materials, 2016, 9(5), 333.
7. I. Peivaste, G. Alahyarizadeh, A. Minuchehr and M. Aghaie, Comparative Study on Mechanical Properties of Three Different SiC Polytypes (3C, 4H and 6H) under High Pressure: First-Principle Calculations, Vacuum, 2018, 154, 37–43.
8. K. K. Zhuravlev, A. F. Goncharov, S. N. Tkachev, P. Dera and V. B. Prakapenka, Vibrational, Elastic, and Structural Properties of Cubic Silicon Carbide under Pressure up to 75 GPa: Implication for a Primary Pressure Scale, J. Appl. Phys., 2013, 113, 113503.
9. E. Konstantinova, M. J. V. Bell and V. Anjos, Ab Initio Calculations of Some Electronic and Elastic Properties for SiC Polytypes, Intermetallics, 2008, 16, 1040–1042.
10. Z. Y. Khattari, S. Al-Omari and F. Afaneh, Multi-Scale Investigation of the Mechanical-Structural Hallmarks of Cubic-Silicon-Carbide under Elevated Pressures: Hirshfeld Topological Surfaces-First Principles Synergic Approach, Mater. Today Commun., 2024, 39, 108776.
11. Y. Azzaz, M. Benouis, N. Moulay, A. Zennati, Y. Massim, O. Arbouche, D. Bensaid and M. Ameri, Electronic and Magnetic Properties of MAX Phase Cr₂SiC with GGA + U Approximation, J. Solid State Chem., 2022, 308, 122870.
12. S. R. Hall, F. H. Allen and I. D. Brown, The Crystallographic Information File (CIF): A New Standard Archive File for Crystallography, Acta Crystallogr., Sect. A: Found. Crystallogr., 1991, 47, 655–685.
13. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer: A Program for Hirshfeld Surface Analysis, Visualization and Quantitative Analysis of Molecular Crystals, J. Appl. Crystallogr., 2021, 54, 1006–1011.
14. Crystallographic Information File (CIF); CCDC Software: Cambridge, U.K. https://www.ccdc.cam.ac.uk/solutions/software/csd/.
15. Materials Studio CASTEP Manual; Accelrys Software Inc.: San Diego, CA, 2010. https://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/CASTEP.html (accessed [Insert Current Month Year]).
16. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
17. D. Vanderbilt, Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
18. T. H. Fischer and J. Almlof, General Methods for Geometry and Wave Function Optimization, J. Phys. Chem., 1992, 96, 9768–9774.
19. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
20. G. P. Francis and M. C. Payne, Finite Basis Set Corrections to Total Energy Pseudopotential Calculations, J. Phys.: Condens. Matter, 1990, 2, 4395–4404.
21. R. Fletcher, Practical Methods of Optimization, John Wiley & Sons, New York, 2nd edn, 1987. p. 436.
22. M. A. Spackman and D. Jayatilaka, Hirshfeld Surface Analysis, CrystEngComm, 2009, 11, 19–32.
23. M. A. Spackman and J. J. McKinnon, Fingerprinting Intermolecular Interactions in Molecular Crystals, CrystEngComm, 2002, 4, 378–392.
24. K. Momma and F. Izumi, VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
25. F. Shariatmadar Tehrani, M. Fakhredin and M. J. Tafreshi, The Optical Properties of Silicon Carbide Thin Films Prepared by HWCVD from Pure Silane and Methane under Various Total Gas Partial Pressure, Mater. Res. Express, 2019, 6, 086469.
26. S. Daoud, N. Bouarissa, H. Rekab-Djabri and F. S. Saoud, Structural and Thermo-Physical Properties of 3C-SiC: High-Temperature and High-Pressure Effects, Silicon, 2022, 14, 6299–6309.
27. E. A. Ekimov, V. S. Krivobok, M. V. Kondrin, D. A. Litvinov, L. N. Grigoreva, A. V. Koroleva, D. A. Zazymkina, R. A. Khmelnitskii, D. F. Aminev and S. N. Nikolaev, Structural and Optical Properties of Silicon Carbide Powders Synthesized from Organosilane Using High-Temperature High-Pressure Method, Nanomaterials, 2021, 11, 3111.
28. J. P. Watt, Hashin-Shtrikman Bounds on the Effective Elastic Moduli of Polycrystals with Orthorhombic Symmetry, J. Appl. Phys., 1979, 50, 6290–6295.
29. M. A. Ghebouli, B. Ghebouli, M. Fatmi and A. Bouhemadou, Theoretical Prediction of the Structural, Elastic, Electronic and Thermal Properties of the MAX Phases X₂SiC (X = Ti and Cr), Intermetallics, 2011, 19, 1936–1942.
30. L. B. Drissi, N. Bouarissa and F. Jomni, Optical Properties and Chemical Bonding of 3C-SiC under High-Pressure, Optik, 2020, 202, 163613.
31. M. Perani, D. Cavalcoli, M. Canino, M. Allegrezza, M. Bellettato and C. Summonte, Electrical Properties of Silicon Carbide/Silicon Rich Carbide Multilayers for Photovoltaic Applications, Sol. Energy Mater. Sol. Cells, 2015, 135, 29–34.
32. Z. Y. Khattari, S. Al-Omari and F. Afaneh, Optical and Electrical Properties of SiO₂ under Uniaxial, Biaxial, and Isotropic Pressure: A First Principles Study, Silicon, 2024, 16, 4713–4722.

---