Dissecting reactions with the independent gradient model: the case of the stereoselective insertion of a Fischer-type carbene ligand into a Mn–C bond

Abstract

The Independent Gradient Model, applied to the dynamics of carbene ligand insertion into a C–Mn bond, reveals details of electron density redistribution events, challenging earlier assumptions. The unique stereoselectivity of the reaction is rationalised by the joint use of the new Steric-Exclusion Localisation Function.

---

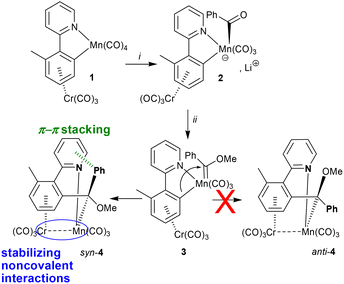
The independent gradient model^1–4 (IGM) is a method for analysing electron density (ED) gradients to characterise and quantify chemical interactions between atoms or groups of atoms, even when those interactions involve weak ED. This feature is missing from QTAIM,⁵ for example. Chemical interactions and bonds can therefore be categorised into three main groups based on the value of the intrinsic bond strength index² (IBSI) noted ι: interatomic interactions are categorised from IBSI ι values as follows: noncovalent when ι ≤ 0.15, coordination bond when 0.15 ≤ ι ≤ 0.60 or covalent bond when ι ≥ 0.15.² For instance, another descriptor is Δg^inter,² which enables the quantification of the interaction between user-defined fragments, making it beneficial for characterising non-covalent interactions. Other descriptors, such as the degree of interaction (DOI) of a target atom and the related atomic contributions (AtC) of neighbouring atoms,⁶ enable the precise tracking of density sharing contributions from surrounding nuclear centres. This is particularly suited to the changes occurring at a metal centre during a reaction when the metal is the centre of reactive events, e.g. by staging its surrounding ligands, like in many organometallic reactions. Unlike QTAIM,⁵ which targets bond paths, or URVA,⁷ which provides a rigorous but less accessible analysis focusing on vibrational mode contributions, IGM describes the spatial extent and evolution of electron-density contragradience around the metal, capturing atom-resolved electronic rearrangements in a more accessible density-based framework. Like other analytical approaches of reaction dynamics such as the URVA,⁷ the reaction force^8,9 or the reaction electronic flux,¹⁰ reactions can be investigated by applying the IGM analysis to the full reaction path generated by intrinsic reaction coordinate (IRC) routines. In this communication, we present an example of applying IGM to reaction dynamics, demonstrating its potential over a straightforward reaction involving the stereo-selective insertion of a transient manganese-bound Fischer-type phenyl,methoxymethylidene ligand into the C–Mn bond of a tricarbonyl complex {[2-(η⁶-phenylene)tricarbonylchromium] pyridine, κ^C,N} published¹¹ by some of us in 1998. It was further demonstrated that similar carbene insertion reactions, involving Mn(I) or Re(I) tetracarbonyl metallacycles, could be achieved by condensing aryl-substituted diazoalkanes giving rise to analogs of 4.^11–16 This chemistry attracted our attention due to the apparent coordinative unsaturation of the Mn(I) centre in product 4, which suggested the unusual stabilization of the metal complex by noncovalent interactions with the Cr(CO)₃ moiety.¹⁷

The concept of a noncovalent stabilization of a formally unsaturated metal centre by noncovalent interactions (NCI) and other weak fluxional¹⁸ covalent interactions with the neighbouring Cr(CO)₃ moiety was further confirmed with other metals,¹⁹ giving birth to the concept of “hemichelation”.²⁰

The centre of interest of the present theoretical study† is the conversion of 3 into syn-4 and the origin of its stereoselectivity (Scheme 1). The two reaction paths leading to syn-4 or anti-4 from rotamers syn-3 or anti-3, respectively, were computed using an IRC search from the fully optimised transition states TS-syn and TS-anti. In 3, two groups of atoms are subject to significant internal motion: the Cr(CO)₃ group, which is a swift rotor with a weak barrier²¹ to rotation when mechanically unhindered,²² and the carbene ligand Ph(MeO)C:, which rotates around the Mn–C1 axis.²³

Scheme 1 The synthesis of syn-4 from the sequential treatment of 1 with (i) PhLi at sub-ambient temperature in tetrahydrofuran or 1,2-dimethoxyethane and (ii) MeOTf.

The conformation of the Cr(CO)₃ moiety was kept static and set to anti-eclipsed like in product 4, and was allowed to adapt to changes occurring during the IRC scans. Note that in a ¹³CO-labelled sample of syn-4, the rotational Gibbs energy barrier (298.15 K) of Cr(CO)₃ was experimentally estimated²⁴ to be ∼15 kcal mol⁻¹. The rotational barriers of the Ph(MeO)C: ligand in 3 were assessed at 3 and 5 kcal mol⁻¹ relative to the syn-3 rotamer, which was found to be more stabilised than anti-3 by only 1 kcal mol⁻¹. Applying clockwise and counterclockwise rotations around the Mn–C axis of syn-3 led to two distinct rotational energy maxima, TSrot+ and TSrot−, in which one carbene substituent eclipses the chelate's carbon with either the methoxy or the phenyl group. This rotational feature is essential because it requires the cis-migration of the C2′ atom onto C1 to pass through the “reactant rotamers” syn-3 and anti-3, in which the carbene ligand is ideally oriented to interact with the aryl moiety. This allows the vacant p orbital of the Fischer-type carbene ligand to interact with the sigma orbital of the chelate's carbanionic carbon, forming the C–C bond in 4 with an exothermicity of approximately −14 kcal mol⁻¹. The activation enthalpy for passing through TS-syn from syn-3 is 3 kcal mol⁻¹ lower than that for passing through TS-anti from anti-3.

To further trace key events and assess whether additional information could be obtained on the factors differentiating the syn and anti paths, IGM analysis was applied to highly sampled reaction pathways (382 and 685 individual transient geometries in the syn and anti paths, respectively). The entire study was referenced against the reaction path curvature (abbreviated RPC, in Fig. 2), whose peaks have been shown to correlate with ED redistribution acceleration events occurring during the reaction and represent an internal control of the pertinence of IGM descriptors in revealing remarkable events.⁶Fig. 2 displays the graphs of the electronic energy paths for the syn and anti reaction paths, overlaid over the respective associated RPC curves, and the graphs of DOI(Mn). The DOI is described in the IGM as a measure of the interaction of an atom (here Mn) with the rest of the system. Here, it serves as a sensor of significant ED changes induced by the bonding transformations that occur around the metal. Remarkably, the DOI(Mn) increases along the reaction path from a starting value of ∼4.55 in 3 to a final value of ∼4.85 in 4 for both syn and anti paths, which challenges the categorisation of syn-4 as a “coordinatively unsaturated” Mn(I) complex as compared, say to 3 or even 1: this increase of DOI(Mn), in the contrary, suggests a coordinative saturation thanks to collective weak electron density sharing²⁵ and noncovalent interactions (NCI) components with Cr(CO)₃.

Local maxima or peaks (noted PD) and minima or valleys (noted VD) of DOI(Mn) appearing along the reaction path reveal specific ED redistribution events occurring at the Mn centre (Fig. 2). They can be analysed through the associated structures, the positions of which lie around 0.5 Å along the length of the reaction path, and correlate directly with a broad peak of mid-intensity of the RPC. PD and VD geometries are in the stiff descending slope of the reaction energy curve, leading to 4, and are considered as dynamic transients. In both DOI(Mn) plots, the PD and VD appear after the transition state (called TS), which also correlates with a pretty intense peak in the RPC plot in both reaction paths. The most reasonable interpretation of PD is that it corresponds to the new consolidation of the C1–C2′ bond upon the insertion of the carbene in the C2′–Mn bond, which forces the under-coordinated Mn to increase its interaction with the benzylidene fragment, which in turn becomes nearly η⁵-bonded to the Cr(CO)₃ moiety. The VD structure, according to its associated structures, is related to the start of the disruption of the latter interaction of the Mn centre with the benzylidene ligand and the migration of the same metal towards the Cr(CO)₃ moiety for the final stabilisation of 4, which is illustrated by a plateau of maximum DOI(Mn) value. It is noteworthy that TS corresponds to a shoulder to the PD in the DOI(Mn) curve in both syn and anti paths. Interestingly, sourcing down the origin of DOI(Mn) variations can be done easily by extracting the so-called atomic contributions to the DOI noted AtC_DOI(Mn) (atom). For example, the AtC analysis (cf. SI) indicates clearly that the significant raise of DOI(Mn) occurring after VD is primarily due to an increase of the interactions with Cr, and with the two vicinal Cr-bound carbonyl ligand carbons C1* and C2*. The AtC analysis (see SI for detailed analyses) of PD reveals that, on both paths, in this transitory situation, as a consequence of the undercoordination of the metal centre, the Mn-bound carbonyl atoms, C2 and C3 (Fig. 1), make their highest contribution to DOI(Mn), which eventually recedes after VD (see SI).

Fig. 1 (a) Singlet ground state geometries of rotamers syn-3 and anti-3 optimized at the COSMO(THF)-ZORA-PBE-D4(EEQ)/all electron TZP level. (b) Rotational equilibrium related to the Ph(MeO)C: ligand at 3.

Fig. 2 Electronic reaction energy profiles of the syn and anti paths (black curve in kcal mol⁻¹vs. path length in Å) overlaid with the plots of the degree of interaction DOI(Mn) (blue curve in a₀⁻¹) and the reaction path curvature (RPC, grey curve in amu^−1/2a₀⁻¹).

This is confirmed by the progression of the Δg^inter score for the interaction between the Mn centre and its bonded three carbonyl ligands (Table 1, entries 11 and 12). The Δg^inter score quantifies the strength of interactions between user-defined molecular fragments and can be calculated at will to characterise any intramolecular interaction. Table 1 lists selected interactions characterised by their Δg^inter score along the reaction paths. Interestingly, the plot of DOI(Cr) (cf. SI) also shows a clear peak slightly before TS in both paths, which may be related to the strengthening of the bonding of the phenylene moiety to Cr in its preparation to migrate onto the carbene ligand. DOI(Cr) exhibits a decrease at VD, from which it increases again quite significantly as the Mn(CO)₃ moiety relaxes towards it to afford 4. The Δg^inter score for the Mn/Cr(CO)₃ interaction evolves similarly in both paths, δg^inter isosurfaces (cf. the SI) for the syn path clearly show an attractive interaction between the Mn and Cr atoms as well as with C1* and C2* arising from VD-syn. In fact, several descriptors such as DOI(Mn), their associated AtC, IBSI (not detailed here, cf. SI) and the Δg^inter scores of interactions located in the coordination sphere of both metals, for both syn and anti paths, show similar features of almost identical intensity, and the detailed analyses of the AtC to DOI(Mn) converge in both cases, suggesting that the origin of the stereoselectivity leading experimentally to the exclusive formation of syn-4 lies elsewhere. Although a closer examination of the structure resolved by X-ray diffraction of syn-4 initially suggested that π–π might be responsible for the observed stereoselectivity, a closer examination of the ED contragradience reveals a different picture. Although the syn path displays larger absolute Δg^inter scores (Table 1, entries 1 and 2), the accumulation of ED contragradience from reactant to TS is actually greater for the anti path (+0.844 vs. +0.714 kcal mol⁻¹), which would contradict a purely attractive NCI-based discrimination favouring syn. To resolve this apparent paradox, an analysis of the steric exclusion localisation function (SELF)²⁶ was performed to quantify steric repulsion between the [Ph(MeO)] and 2-phenylenepyridine fragments. The results unambiguously show that the anti pathway accumulates significantly more steric clash during the reaction (+181.2 kcal mol⁻¹) compared to the syn pathway (+144.7 kcal mol⁻¹). As illustrated in Fig. 3, the SELF-coloured δg^IGM/ρ isosurfaces reveal progressively intensifying steric repulsion exclusively in the anti approach. SELF atomic decomposition (cf. SI) shows that the methoxy group shows comparable steric accumulation in both pathways. At the same time, the phenyl moiety of Ph(MeO)C is clearly discriminant (+33.7 syn vs. +51.1 anti). On the opposite fragment, both pyridine and phenyl units undergo greater steric hindrance in the anti approach, collectively accounting for the observed stereoselectivity.

Table 1 List of Δg^inter scores computed for various interactions between user-defined fragments of 3, TS, PD, VD and 4 for both syn and anti paths

			Δg^inter (a0^−1)
Entry	Interacting fragments	Path	3	TS	PD	VD	4
a This is the interaction between the Mn atom and the three Mn-bound carbonyl ligands.
1	Ph(MeO)C/phpy	syn	0.875	1.589	1.909	2.196	2.226
2		anti	0.555	1.399	1.831	2.010	2.110
3	Mn/Ph(MeO)C	syn	0.812	0.757	0.733	0.672	0.590
4		anti	0.814	0.762	0.720	0.673	0.593
5	Mn/phpy	syn	1.186	1.039	1.007	0.986	1.045
6		anti	1.204	1.043	1.009	0.999	1.066
7	Mn/Cr(CO)3	syn	0.075	0.149	0.180	0.225	0.432
8		anti	0.073	0.156	0.208	0.237	0.437
9	Ph/phpy	syn	0.560	0.662	0.686	0.717	0.608
10		anti	0.119	0.312	0.344	0.363	0.324
11	Mn/(CO)3^a	syn	2.822	2.933	2.954	2.957	2.990
12		anti	2.813	2.929	2.952	2.956	2.973

---

Fig. 3 Steric analysis²⁶ of (a) syn-3 and TS-syn, and (b) anti-3 and TS-anti. Fragment 1 = Ph(MeO)C, fragment 2 = phpy. The isosurface of the δg^inter/ρ IGM descriptor (0.79 bohr⁻¹) highlights electronic clashes between fragments, with colours representing the SELF values to quantify the steric effect. A Blue-Green-Red colour scale is applied to represent the SELF descriptor values (blue = no steric interaction, red = large steric interaction). The same isovalue and colour range (0 : 5.8 kcal mol⁻¹ bohr⁻³) were used for each structure to ensure consistent comparison of the steric interactions. The integrated iSELF score is reported in kcal mol⁻¹.

Conclusions

The present study is a simple example of an application of the IGM. It reveals transient events and allows tracing how ED variations and redistributions occur in the various phases of the reaction. In this study, it appears that the initial qualification of “coordination unsaturation” at the Mn centre of syn-4, from the application of the 18-electron rule is a simplification that overlooks the delocalized interaction of the Mn centre with its coordination environment: DOI(Mn) and DOI(Cr) suggest a strengthening of the multiple interactions of the Mn and Cr centres with their immediate environment as syn-4 is being formed. Counterintuitively, the new SELF analysis shows that the stereoselectivity of this insertion reaction stems from differences in steric clashes that favour the syn path over the anti path, rather than from an exclusive control by so-called π–π interactions.

Author contributions

All authors contributed equally to this article, reviewed the results and approved the final version of the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: computational details and a comparative benchmark of methods, T1 diagnostics, additional plots, Cartesian coordinates for all considered geometries, energies. See DOI: https://doi.org/10.1039/d5cp03547c.

Acknowledgements

The CNRS, the International Centre for Frontier Research in Chemistry and the University of Strasbourg are thanked for their financial support. S. F. d. A. M. gratefully acknowledges the International Center for Frontier Research in Chemistry (ICFRC) / Fondation Jean-Marie Lehn (project ‘Quantified Noncovalent Interactions for the Prediction of Reactivity’) for financially supporting her associate research position.

Notes and references

1. C. Lefebvre, J. Klein, H. Khartabil, J.-C. Boisson and E. Hénon, J. Comput. Chem., 2023, 44, 1750–1766.
2. J. Klein, H. Khartabil, J.-C. Boisson, J. Contreras-García, J.-P. Piquemal and E. Hénon, J. Phys. Chem. A, 2020, 124, 1850–1860.
3. C. Lefebvre, G. Rubez, H. Khartabil, J.-C. Boisson, J. Contreras-García and E. Hénon, Phys. Chem. Chem. Phys., 2017, 19, 17928–17936.
4. E. Hénon, IGMPlot website, https://igmplot.univ-reims.fr/.
5. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15.
6. C. Lefebvre, H. Khartabil and E. Hénon, Phys. Chem. Chem. Phys., 2023, 25, 11398–11409.
7. S. Nanayakkara and E. Kraka, Phys. Chem. Chem. Phys., 2019, 21, 15007–15018.
8. P. Politzer, A. Toro-Labbé, S. Gutiérrez-Oliva and J. S. Murray, in Advance Quantun Chemistry, ed. J. R. Sabin and E. J. Brändas, Academic Press, 2012, vol. 64, pp. 189–209.
9. A. Toro-Labbé, S. Gutiérrez-Oliva, J. S. Murray and P. Politzer, J. Mol. Model., 2009, 15, 707–710.
10. E. Echegaray and A. Toro-Labbé, J. Phys. Chem. A, 2008, 112, 11801–11807.
11. J.-P. Djukic, A. Maisse, M. Pfeffer, K. H. Dötz and M. Nieger, Eur. J. Inorg. Chem., 1998, 1781–1790.
12. J.-P. Djukic, C. Michon, D. Heiser, N. Kyritsakas-Gruber, A. de Cian, K. H. Dötz and M. Pfeffer, Eur. J. Inorg. Chem., 2004, 2107–2122.
13. J.-P. Djukic, K. H. Dötz, M. Pfeffer, A. De Cian and J. Fischer, Inorg. Chem., 1998, 37, 3649–3651.
14. J.-P. Djukic, K. H. Dötz, M. Pfeffer, A. De Cian and J. Fischer, Organometallics, 1997, 16, 5171–5182.
15. J.-P. Djukic, A. Maisse-François, M. Pfeffer, K. H. Dötz, A. De Cian and J. Fischer, Organometallics, 2000, 19, 5484–5499.
16. C. Michon, J.-P. Djukic, Z. Ratkovic, J.-P. Collin, M. Pfeffer, A. de Cian, J. Fischer, D. Heiser, K. H. Dötz and M. Nieger, Organometallics, 2002, 21, 3519–3535.
17. I. Hyla-Kryspin, S. Grimme and J.-P. Djukic, Organometallics, 2009, 28, 1001–1013.
18. N. Sieffert, Dalton Trans., 2018, 47, 8906–8920.
19. Y. Cornaton and J.-P. Djukic, Acc. Chem. Res., 2021, 54, 3828–3840.
20. C. Werlé, C. Bailly, L. Karmazin-Brelot, X.-F. Le Goff, L. Ricard and J.-P. Djukic, J. Am. Chem. Soc., 2013, 135, 17839–17852.
21. A. Elass, J. Brocard, G. Surpateanu and G. Vergoten, J. Mol. Struct. THEOCHEM, 1999, 466, 35–48.
22. P. A. Downton, B. Mailvaganam, C. S. Frampton, B. G. Sayer and M. J. McGlinchey, J. Am. Chem. Soc., 1990, 112, 27–32.
23. F. J. Manganiello, M. D. Radcliffe and W. M. Jones, J. Organomet. Chem., 1982, 228, 273–279.
24. J.-P. Djukic, M. Pfeffer and K. H. Dötz, C. R. Acad. Sci. – Ser. IIC – Chemistry, 1999, 2, 403–408.
25. C. Foroutan-Nejad, Angew. Chem., Int. Ed., 2020, 59, 20900–20903.
26. G. Hénon-Just, C. Lefebvre, A. Rajamani, H. Khartabil, J. Pilmé and E. Hénon, ChemRxiv, 2025, preprint DOI:10.26434/chemrxiv-2025-br97q.
27. W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theor. Comput., 2012, 8, 460–468.

---

Footnote

† The validity of the single-reference approach was verified by determining the Frobenius norm T1-diagnostic²⁷ for all key structures (3, TS and 4) (cf. SI).

---