A computational protocol for ¹⁵N NMR parameter prediction in aqueous peptide ensembles using optimized DFT methods

Abstract

Accurate prediction of ¹⁵N NMR chemical shifts in flexible peptide systems remains challenging. We present an ensemble-based computation protocol combining density functional theory with replica-exchange molecular dynamics. This approach outperformed single-structure predictions with deviations of 2.5–5.6 ppm for most residues and 1.1 ppm for leucine in a model peptide.

---

Nuclear magnetic resonance (NMR) spectroscopy stands as one of the most powerful analytical techniques for elucidating molecular structure and dynamics at the atomic level. Among the various NMR-active nuclei, nitrogen-15 (¹⁵N) provides particularly valuable structural information for biomolecular systems, especially proteins, through its exceptional sensitivity to local electronic environments and hydrogen bonding patterns.^1,2

However, experimental acquisition of ¹⁵N NMR data faces significant challenges due to low natural abundance (0.365%) and relatively small gyromagnetic ratio, resulting in poor sensitivity compared to proton detection.³ Recent advances in density functional theory (DFT) have enabled increasingly accurate predictions of NMR chemical shifts across diverse molecular systems.^4–6 AI-based tools have also demonstrated high accuracy in chemical shift prediction in previous studies.^7–10 However, these AI-based approaches face inherent limitations in accurately incorporating specific solvent environments into their predictive models, whereas DFT-based methodologies enable explicit consideration of solvation effects through quantum mechanical calculations.

Computational frameworks specifically designed for nitrogen nuclei in aqueous environments remain largely underexplored. While reliable scaling factors for ¹⁵N chemical shift predictions have been established, these calibrations primarily relied on gas-phase calculations or non-aqueous solvation models.^11–15 Therefore, the development of a comprehensive methodology specifically validated for aqueous systems is crucial for practical applications in water-based biological systems. The challenge becomes even more complex when dealing with intrinsically disordered proteins (IDPs), which lack rigid three-dimensional structures and exhibit dynamic conformational variability. These proteins exist as ensembles of multiple conformers, with observed NMR signals representing ensemble-averaged value over all accessible conformations.¹⁶ Our investigation focuses on the short model peptide, Asp–Gln–Leu–Gly–Lys (DQLGK), corresponding to residues 98–102 of α-synuclein IDP (Fig. 1).

Fig. 1 Molecular structure of a short model peptide, Asp–Gln–Leu–Gly–Lys, with an acetylated N-terminus and an amidated C-terminus. (a) Line structure and (b) stick representation of the pentapeptide. In panel (b), the structure is displayed with standard atom coloring (carbon: green, nitrogen: blue, oxygen: red).

This pentapeptide is expected to form an ensemble of multiple conformers. Boltzmann-weighted averaging is therefore anticipated to improve the accuracy of chemical shift predictions for such flexible systems.

In this study, we first establish an optimal computational protocol by systematically evaluating¹⁷ 882 functional/basis set combinations across 19 small organic molecules (43 nitrogen datapoints) in water³ to determine accurate scaling factors for aqueous environments. Using this optimized protocol, we predict Boltzmann-averaged ¹⁵N chemical shifts for a pentapeptide and validate their accuracy against experimental data. Representative conformers composing the ensemble are derived from replica-exchange molecular dynamics (REMD)¹⁸ simulations, and the chemical shifts are calculated with density functional theory (DFT). This approach ensures reliable predictions for flexible peptide systems in biologically relevant conditions.

To obtain experimental ¹⁵N chemical shift for the pentapeptide, we performed ¹H–¹⁵N HSQC, ¹H–¹H TOCSY, and ¹H–¹H NOESY experiments. All NMR experiments in this work were performed on a 600 MHz NMR spectrometer equipped with a z-gradient cryoprobe. ¹⁵N chemical shifts of backbone amides were measured from the HSQC spectrum (Fig. S1, SI), and the five peaks were assigned to each residue by TOCSY (Fig. S2, SI) and NOESY (Fig. S3, SI) spectra. All samples were 6 mM peptides (without ¹⁵N enrichment) in 20 mM sodium phosphate (pH 6.0), 20 mM sodium chloride, 5% D₂O, and measured at 20 °C.

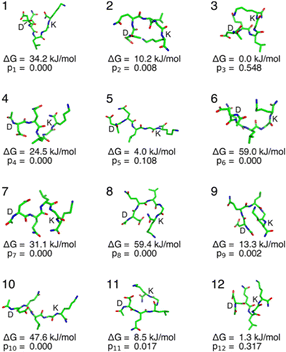
The conformational ensemble of the pentapeptide was derived via REMD simulation in GROMACS 24.02.^19–26 The simulation employed the AMBER99SB force field²⁷ and the SPC/E water model.²⁸ Simulations were run for 40 ns with a 2 fs time step. Trajectories were clustered with the GROMOS method,²⁹ yielding 12 clusters. The lowest-energy frame from each cluster was selected as its representative conformer.

Each conformer was first geometry optimized and then subjected to ¹⁵N chemical shift calculations, using the same DFT functional/basis set identified as optimal during the scaling factor optimization. Then, Gibbs free energy was calculated using DFT B3LYP^30–32/6-31G(d,p).^33–35 All DFT calculations were performed using Gaussian16 Rev. A.03³⁶ on the NURION supercomputer (KISTI) using Knights Landing nodes with Intel Xeon Phi 7250 processors (68 cores, 96 GB RAM).

Geometry optimization was the most time-consuming step, with CPU times ranging from 40 to 100 days, and up to 200 days for the representative conformer of the second cluster. In contrast, NMR calculations typically required CPU time about 7 hours, and frequency calculations took approximately 8 days on average.

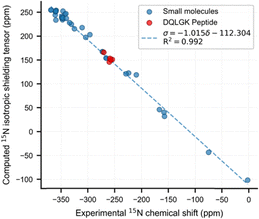
Scaling factor optimization used datasets of small molecules (Table S1, SI). The isotropic shielding tensors were calculated with a broad range of DFT methods. For geometry optimization, 3 functional/basis set were employed, whereas the NMR calculations explored 294 combinations (49 functionals × 6 basis sets) (Tables S2–S4, SI). Subsequently, we carried out linear regressions between the experimental chemical shifts and the computed shielding tensors for each case (Tables S5–S7, SI). The optimal scaling factor were adopted for the peptide study.

Through systematic evaluation, we establish an optimal computational protocol specifically calibrated for aqueous environments (Fig. 2); B3LYP[GD3BJ]^30–32,37/6-311++G(d,p)^38–46 for geometry optimization and LC-ωHPBE^47–50/6-31+G(d,p)^{33–35,38,39,51–55} for NMR calculations. The linear regression yielded σ = −1.015δ − 112.304 with R² = 0.992, demonstrating excellent agreement between the fitted slope −1.015 and the theoretical slope −1 in δ_sample = σ_ref − σ_sample.⁵⁶

Fig. 2 Correlation between experimental ¹⁵N chemical shifts and computed ¹⁵N isotropic shielding tensors in aqueous solution. Neat-nitromethane chemical shift of 380.3 ppm (Fig. S4, SI) was set to 0 ppm. Because the experimental shifts differ from the neat-nitromethane reference according to δ_ref − δ_exp > 0, δ_exp have negative values.

Thermodynamic analysis using DFT-calculated Gibbs free energies revealed substantial differences in conformer stability. The three most populated conformers represent 54.75%, 31.73%, and 10.76% of the ensemble, respectively, amounting to 97.24% of the total population (Fig. 3).

Fig. 3 Optimized 3D structures of the 12 representative conformers obtained from REMD. Each conformer is labeled with its relative Gibbs free energy (ΔG) in kJ mol⁻¹ and Boltzmann population (p_i). The backbone nitrogen atoms of aspartic acid and lysine are denoted as D and K, respectively. The structures are displayed in stick representation with standard atom coloring (carbon: green, nitrogen: blue, oxygen: red). The corresponding 2D structures are provided in Fig. S5.

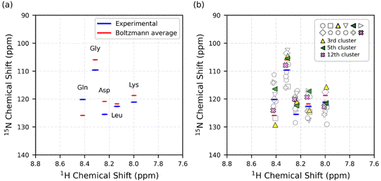
The calculation of ensemble-averaged ¹⁵N chemical shifts involved Boltzmann-weighted averaging of individual conformer contributions according to their thermodynamic populations. Comparison between calculated ensemble-averaged chemical shifts and experimental values obtained from ¹H–¹⁵N HSQC spectroscopy showed good agreement (Fig. 4).

Fig. 4 (a) ¹H–¹⁵N HSQC spectrum for the experimental pentapeptide spectrum (blue contours) with the Boltzmann-weighted theoretical spectrum (red contours). Proton chemical shifts were made identical. Each peak is labeled with its corresponding three-letter amino acid code based on the assignment results. (b) Calculated chemical shift from individual cluster are denoted by distinct symbols, where the 3rd, 5th and 12th cluster are highlighted to underscore its dominant population within the ensemble.

Ensemble averaging improved prediction accuracy compared to using only the dominant 3rd cluster's chemical shifts. (Fig. S6, SI) While the 3rd cluster exhibited an MAE (Mean Absolute Error) of 5.1 ppm, the ensemble-averaged chemical shifts yielded a reduced MAE of 3.6 ppm. This finding supports the view that the peptide exists as a dynamic mixture of interconverting conformers and that the experimentally observed chemical shifts represent an ensemble-averaged property.

The computational predictions showed deviations ranging from 2.5 to 5.6 ppm for most backbone nitrogen atoms (Asp, Gln, Gly, Lys), with all calculated values appearing up-field relative to experimental measurements, except for glutamine. Notably, the leucine residue demonstrated exceptional agreement with only 1.1 ppm deviation from the experimental value. Averaged ¹⁵N shift deviations of 3.6 ppm is slightly smaller than those reported in prior ¹⁵N DFT study – averaged deviation of 4.0 in ubiquitin and 4.6 ppm in GB3.⁵⁷

In contrast to the four residues, the central residue exhibits accurate prediction results. The accuracy of quantum calculations for peptides in aqueous solution is critically dependent on the proper treatment of solvent system. For terminal residues, particularly the charged aspartic acid and lysine residues, implicit solvation models may inadequately capture the specific hydrogen bonding networks and electrostatic interactions with water molecules. Recent computational studies have demonstrated that explicit solvation models are essential for accurate description of peptide-solvent interactions, particularly for systems involving strong hydrogen bonding and charged residues.^58,59 The central leucine residue, being surrounded by neighbouring residues and possessing a hydrophobic side chain, experiences less solvent interaction, making implicit solvation models more suitable for this residue.

In conclusion, we have successfully determined scaling factors for NMR chemical shift calculations in aqueous environments, demonstrating their reliability and accuracy for both small molecule and peptide systems. This systematic validation provides a robust framework for future applications in predicting NMR parameters of biomolecules in their aqueous environment.

The Boltzmann-weighted averaging of ¹⁵N chemical shifts from 12 representative conformers yielded good agreement with experimental HSQC measurements, with deviations of 2.5–5.6 ppm for most residues and an improved accuracy (1.1 ppm) for leucine. These results validate the ensemble approach for capturing the dynamic nature of intrinsically disordered proteins and demonstrate that experimental chemical shifts represent population-weighted averages over accessible conformational states.

The computational protocol developed in this work provides a reliable foundation for future investigations of larger and more flexible systems, bridging the gap between theoretical predictions and experimental NMR observations. This methodology offers valuable insights into how conformational dynamics modulate ¹⁵N chemical shifts in biomolecules for which conformational flexibility is central to biological function.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03354c.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (no. RS-2025-005194288, NRF-2022R1I1A2073122, and RS-2024-00459815).

Notes and references

1. H. Le and E. Oldfield, J. Phys. Chem., 1996, 100, 16423–16428.
2. J. Cavanagh, W. J. Fairbrother, A. G. Palmer, M. Rance and N. J. Skelton, in Protein NMR Spectroscopy, ed. J. Cavanagh, W. J. Fairbrother, A. G. Palmer, M. Rance and N. J. Skelton, Academic Press, Burlington, 2nd edn, 2007, ch. 10, pp. 781–817.
3. R. Gupta and M. Lechner, Chemical shifts and coupling constants for Fluorine-19 and Nitrogen-15, Springer Berlin, Heidelberg, 1998.
4. Q. Gao, S. Yokojima, T. Kohno, T. Ishida, D. G. Fedorov, K. Kitaura, M. Fujihira and S. Nakamura, Chem. Phys. Lett., 2007, 445, 331–339.
5. X. Yi, L. Zhang, R. A. Friesner and A. McDermott, J. Phys. Chem. Lett., 2024, 15, 2270–2278.
6. Q. N. N. Nguyen, J. Schwochert, D. J. Tantillo and R. S. Lokey, Phys. Chem. Chem. Phys., 2018, 20, 14003–14012.
7. J. Li, J. Liang, Z. Wang, A. L. Ptaszek, X. Liu, B. Ganoe, M. Head-Gordon and T. Head-Gordon, J. Chem. Theory Comput., 2024, 20, 2152–2166.
8. S. Liu, J. Li, K. C. Bennett, B. Ganoe, T. Stauch, M. Head-Gordon, A. Hexemer, D. Ushizima and T. Head-Gordon, J. Phys. Chem. Lett., 2019, 10, 4558–4565.
9. W. Gerrard, L. A. Bratholm, M. J. Packer, A. J. Mulholland, D. R. Glowacki and C. P. Butts, Chem. Sci., 2020, 11, 508–515.
10. C. Yiu, B. Honoré, W. Gerrard, J. Napolitano-Farina, D. Russell, I. M. L. Trist, R. Dooley and C. P. Butts, Chem. Sci., 2025, 16, 8377–8382.
11. V. A. Semenov, D. O. Samultsev and L. B. Krivdin, J. Phys. Chem. A, 2019, 123, 8417–8426.
12. P. Gao, X. Wang and H. Yu, Adv. Theory Simul., 2019, 2, 1800148.
13. D. Xin, C. A. Sader, U. Fischer, K. Wagner, P.-J. Jones, M. Xing, K. R. Fandrick and N. C. Gonnella, Org. Biomol. Chem., 2017, 15, 928–936.
14. S. E. Soss, P. F. Flynn, R. J. Iuliucci, R. P. Young, L. J. Mueller, J. Hartman, G. J. O. Beran and J. K. Harper, ChemPhysChem, 2017, 18, 2225–2232.
15. J. D. Hartman and G. J. O. Beran, Solid State Nucl. Magn. Reson., 2018, 96, 10–18.
16. E. Delaforge, T. N. Cordeiro, P. Bernadó and N. Sibille, in Modern Magnetic Resonance, ed. G. A. Webb, Springer International Publishing, Cham, 2018, pp. 381–399 DOI:10.1007/978-3-319-28388-3_52.
17. E. Benassi, J. Comput. Chem., 2022, 43, 170–183.
18. Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151.
19. H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56.
20. E. Lindahl, B. Hess and D. van der Spoel, Mol. Model. Annu., 2001, 7, 306–317.
21. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718.
22. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
23. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
24. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
25. M. Abraham, A. Alekseenko, V. Basov, C. Bergh, E. Briand, A. Brown, M. Doijade, G. Fiorin, S. Fleischmann, S. Gorelov, G. Gouaillardet, A. Gray, M. E. Irrgang, F. Jalalypour, J. Jordan, C. Kutzner, J. A. Lemkul, M. Lundborg, P. Merz, V. Miletic, D. Morozov, J. Nabet, S. Pall, A. Pasquadibisceglie, M. Pellegrino, H. Santuz, R. Schulz, T. Shugaeva, A. Shvetsov, A. Villa, S. Wingbermuehle, B. Hess and E. Lindahl, Zenodo, 2024.
26. S. Páll, M. J. Abraham, C. Kutzner, B. Hess and E. Lindahl, in Solving Software Challenges for Exascale, ed. S. Markidis and E. Laure, Springer International Publishing, Cham, 2015, pp. 3–27.
27. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinform., 2006, 65, 712–725.
28. H. J. Berendsen, J.-R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
29. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed., 1999, 38, 236–240.
30. A. D. Becke, J. Chem. Phys., 1986, 84, 4524–4529.
31. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
32. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
33. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
34. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
35. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
36. M. J. Frisch, et al., Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
38. R. C. Binning Jr and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216.
39. J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021.
40. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
41. K. Raghavachari and G. W. Trucks, J. Chem. Phys., 1989, 91, 1062–1065.
42. A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036.
43. P. J. Hay, J. Chem. Phys., 1977, 66, 4377–4384.
44. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
45. M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511–516.
46. L. A. Curtiss, M. P. McGrath, J. P. Blaudeau, N. E. Davis, R. C. Binning, Jr. and L. Radom, J. Chem. Phys., 1995, 103, 6104–6113.
47. T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, J. Chem. Phys., 2009, 131, 044108.
48. O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109.
49. O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109.
50. O. A. Vydrov, J. Heyd, A. V. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106.
51. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
52. P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214.
53. M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163–168.
54. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229.
55. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
56. J. C. Facelli, Prog. Nucl. Magn. Reson. Spectrosc., 2011, 58, 176–201.
57. A. S. Larsen, L. A. Bratholm, A. S. Christensen, M. Channir and J. H. Jensen, PeerJ, 2015, 3, e1344.
58. T. Zhu, J. Z. H. Zhang and X. He, J. Chem. Theory Comput., 2013, 9, 2104–2114.
59. K. Scholten and C. Merten, Phys. Chem. Chem. Phys., 2022, 24, 3611–3617.

---