A theoretical study on the mechanism of C₂H_3–5 oxidation by N₂O

Abstract

Nitrous oxide fuel blend (NOFBX), consisting of nitrous oxide and small hydrocarbons like ethane and ethene, offers potential for green propellants and optimized propulsion systems. This study investigates the oxidation reaction pathways of N₂O with C₂H_3–5 using G4 and CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP methods. The oxidation typically begins with addition reactions at N or O atomic sites, or the H-abstraction reaction by N₂O, followed by hydrogen transfer and bond dissociation, leading to stable molecules and free radicals. Additionally, RRKM/ME theory was applied to calculate the reaction rate constants and branching ratios for N₂O + C₂H_3–5 over a temperature range of 300–3000 K and pressures of 1–100 atm. A comparative analysis identified the dominant reaction pathways for N₂O with CH components. Simulations incorporating detailed reaction mechanisms and kinetic data improved predictions of ignition delay times for both N₂O/C₂H₄ and N₂O/C₂H₆ systems. The new model also shows higher/lower fuel conversion below/above ∼1000 K. Sensitivity analysis indicates that direct reactions between N₂O and CH components have minimal impact on model accuracy at temperatures above the ignition point, becoming stronger near ∼1200 K before weakening at higher temperatures. The results provide essential data for refining kinetic models of N₂O/C₂H₄ and N₂O/C₂H₆ systems and offer a theoretical basis for designing and optimizing NOFBX propellants.

---

1. Introduction

Conventional hydrazine-based propellants – such as hydrazine, methylhydrazine, and unsymmetrical dimethylhydrazine – are expected to face increasingly strict restrictions due to their high toxicity, corrosiveness, and complex safety handling requirements.¹ As such, the development of green alternatives has become a key concern. Among the candidates, nitrous oxide fuel blend (NOFBX), a single-component propellant composed of nitrous oxide (N₂O) and small hydrocarbons,² and particularly C₂-based fuels,^3,4 has attracted growing attention due to its non-toxic nature, high performance and low cost. However, the use of premixed NOFBX brings challenges, such as high flame temperature and increased risk of backfire, necessitating more precise control and understanding of the combustion process. In this context, in-depth studies on the combustion kinetics of NOFBX propellants are crucial for their practical applications.

Kinetic studies of NOFBX generally fall into three categories: (1) the conventional chemistry of small hydrocarbons, (2) the decomposition of the oxidant N₂O, and (3) the direct reactions between N₂O and the hydrocarbon components. N₂O easily forms complex couplings with free radicals in hydrocarbon fuels, increasing the difficulty of kinetic research on such processes.^5–8 In the emission control of NO_x pollutants, the interaction between N₂O and the fuel also warrants consideration.^9,10 Numerous detailed mechanisms for small hydrocarbons have been developed, including GRI-Mech 3.0,¹¹ Aramco-Mech 2.0,¹² USC-II,¹³ and the latest NUIG-Mech 1.3 mechanism.¹⁴ The thermal decomposition of N₂O into N₂ and O₂ has also been investigated.^15,16 In these mechanism models, C₂ species act not only as core intermediates in the oxidative decomposition of hydrocarbon fuels (especially acetylene, ethylene-based fuels, and cracking products of higher carbon number fuels) but also as key participants in the formation of soot precursors (e.g., polycyclic aromatic hydrocarbons, PAHs). Therefore, research on the relevant kinetics of their reaction with N₂O is of great significance for model optimization. Wang et al.¹⁷ studied laminar flames and developed a chemical kinetic model of N₂O/C₂H₄ based on the USC-II mechanism, refining the kinetic parameters of eight key elementary reactions. However, they did not delve into the direct reactions between N₂O and the hydrocarbon components. Zheng et al.¹⁸ proposed a kinetic model for the N₂O–C₂ system, validated in the range of 110–1700 K, 0.1–1.6 MPa, and equivalence ratios of 0.5–2.0. In this model, four new elementary reactions for the interactions between N₂O and C₂H₃/C₂H₄ were incorporated. These pathways were derived by analogy with known O radical reactions with C₂H₃/C₂H₄ in the USC-II model¹³ and N₂O reactions with C₂H₃/C₂H₂ from the Konnov model.¹⁹ Zhang et al.²⁰ conducted autoignition experiments in a rapid compression machine (RCM) with N₂O/C₂H₄ over a temperature range of 885–940 K, pressures of 2.5–4.3 MPa and equivalence ratios of 1.05 and 1.35. They found that the decomposition of N₂O dominated at high temperatures, while its direct interaction with hydrocarbons became more significant at low temperatures. They further emphasized the need for more accurate low-temperature oxidation mechanisms and high-level theoretical data to improve combustion modeling.

From an atmospheric chemistry perspective, N₂O is also a potent greenhouse gas,²¹ and its reactions with small organic radicals are of significant interest. Moreover, the oxidation of C₂H_3–5 radicals by N₂O is mechanistically relevant to coal combustion because such reactions govern whether N₂O, formed as an intermediate during fuel-nitrogen conversion, decomposes benignly to N₂ or further oxidizes to NO, thus directly influencing NO_x emissions. As early as 1959, Kenwright et al.²² reported rate constants for reactions between ethane radical (C₂H₅) and N₂O at temperatures of 826–861 K. Tang et al.²³ reviewed the combustion chemistry of unsaturated and oxygenated hydrocarbons in the presence of NO, NO₂ and N₂O, summarizing earlier findings of RH–N₂O reactions since 1950s. Only a few studies, such as that by Trenwith et al.,²⁴ provided experimental rate constants of the reaction of C₂H₄ + N₂O → CH₃CHO + N₂ at 828–863 K. Li et al.²⁵ used the B3LYP/6-31++G** method to investigate the oxidation mechanism of the N₂O/C₂H₄ system, and obtained the reaction pathways of N₂O and C₂H₄ that generated acetaldehyde and N₂, with the former further decomposed into CH₃ and CHO. They also estimated the activation energies and energetics of the subsequent steps leading to CO₂ and H₂O. Despite the above efforts, a comprehensive kinetic analysis of the N₂O + C₂H₄ reaction has not been conducted.

To sum up, the direct reactions of N₂O with C₂H₃, C₂H₄ and C₂H₅ radicals still lack systematic study, despite their relevance to both NOFBX combustion modeling and atmospheric chemistry, and hence require further investigation. To address this gap, the present study has two main objectives: (1) to elucidate the reaction mechanisms between N₂O with C₂H_3–5 components and provide accurate kinetic data using high-precision quantum methods, and (2) to evaluate the impact of these reactions on the overall N₂O–C₂ model through comparisons of ignition delay times and sensitivity analyses, thereby providing a solid foundation for future kinetic model development.

2. Computational methods

2.1. Quantum chemistry calculations

Geometrical optimizations and frequency analyses of all reactants, intermediates (IMs), transition states (TSs), and products on the potential energy surfaces (PESs) of the reactions between N₂O and C₂H₃, and C₂H₄ and C₂H₅ were carried out using the M06-2X(D3)/def2-TZVP method.^26–29 The validity of each transition state was confirmed by verifying the presence of a single imaginary frequency and ensuring that the corresponding vibrational mode connects the intended reactants and products. Additionally, intrinsic reaction coordinate (IRC) calculations were performed to further verify that the transition states correctly connect the associated minima on the PESs. Single-point energy for each species at 0 K were calculated using the CCSD(T)/cc-pVQZ method, with errors less than ± 1 kcal mol⁻¹. However, for the reaction path of N₂O + C₂H₃, the CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP method produced unreasonable energy values. To address this issue and enable comparison, the reactions of N₂O + C₂H_3–5 series were also computed using the G4 method.³⁰ All electronic structure calculations for the PESs were conducted using the Gaussian 16 program.³¹ Additionally, T₁ diagnostics was performed using the CCSD(T)/cc-pVQZ method to assess the potentially strong influence of a strong electron correlation. For reaction pathways with T₁ values greater than 0.045, a multi-reference method was employed. Consequently, based on the geometries optimized using the G4 method, single-point energies were recalculated using the multi-reference CASPT2(7e,7o)/cc-pVQZ method,³² implemented via the Mokit interface³³ with the Molpro software.³⁴ For the system N₂O + C₂H₃, the main types of orbitals considered for the activation space include the π and π* orbitals of the N–N bond, the π and π* orbitals of the C–C bond, the π and π* orbitals of the entire structure, and the free radical orbitals of the CH part. For the system N₂O + C₂H₅, 7e and 7o were selected. These mainly come from the bonding and non-bonding orbitals of the methyl part in C₂H₅, the π and π* orbitals of the N–N bond in the bonding direction, the π and π* orbitals in the p direction, and the free radical orbitals of the methylene part in C₂H₅.

2.2. Kinetic methods

The rate constants for the different reaction pathways of N₂O + C₂H_3–5 at 1–100 atm and 300–3000 K were calculated using the RRKM/master equation method,³⁵ implemented via the kinetic calculation program MESS.³⁶ Argon (Ar) was used as the bath gas, and the calculated intermediate IM1 was taken as the reactant. The critical temperature T_c and critical pressure P_c of IM1 were calculated using the Joback formula.³⁷ The Lennard-Jones (L-J) parameters required calculating the collisional deactivation rate constants and were estimated from empirical equations:³⁸σ = 2.44(T_c/P_c)^1/3 and ε/k_b = 0.77T_c. The obtained L-J parameters were as follows: σ = 5.68 Å and ε/k_b = 441.57 K for the N₂O + C₂H₃ system; σ = 5.87 Å and ε/k_b = 508.35 K for N₂O + C₂H₄; σ = 5.63 Å and ε/k_b = 440.88 K for N₂O + C₂H₅; and σ = 3.55 Å and ε/k_b = 116.16 K for Ar. The average energy transferred per deactivating collision, which determines the collisional efficiency and plays an important role in the attenuation effect, was expressed by a simple power law: ΔE_down = Θ(T/300)^0.80 cm⁻¹,³⁹ where the empirical parameter Θ was estimated to be 250 cm⁻¹ in this work. Due to the small molecular weight of the investigated system and the presence of multiple unsaturated bonds in the molecules, the anharmonic effect of the low-frequency torsion was not considered. The effect of one-dimensional (1-D) asymmetric Eckart tunneling⁴⁰ is also taken into account in the MESS software.³⁶ All vibrational modes were treated as resonances, and their frequencies were scaled by a factor of 0.984, as appropriate for the M06-2X(D3)/def2-TZVP method.⁴¹

3. Results and discussion

The reactions of N₂O with three CH species–C₂H₃, C₂H₄ and C₂H₅–are illustrated in Fig. 1–4 through their PESs, where intermediates and transition states are distinguished by subscript labels (a)–(c) for each system. For the N₂O + C₂H₃ system, all energy values are provided at the G4 level. For the N₂O + C₂H₄ and N₂O + C₂H₅ systems, energies are given at both the G4 level and the CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP level, with the latter shown in parentheses. Species with T₁ diagnostic values exceeding 0.045 at the CCSD(T)/cc-pVQZ level are highlighted in red to indicate possible multi-reference characters. Detailed structural parameters and vibrational frequency data for the PES are provided in Tables S1 and S2 of SM1. Fig. 5–7 present the calculated rate constants for the three reaction systems, identifying the dominant reaction pathways between N₂O and each CH species. The corresponding fitted rate constants are provided in Tables S4–S6. The PESs for the N₂O + C₂H₃/N₂O + C₂H₅ calculated using the CASPT2/cc-pVQZ//B3LYP/6-31G(2df,p) (G4 optimization method) method are provided in Fig. S1 and S2. The herein obtained kinetic data are incorporated into a reaction model, which was used to simulate ignition delay times (IDTs) and perform sensitivity analyses for the N₂O/C₂H₄ system (Fig. 8 and 9), with additional IDT data for N₂O/C₂H₆ provided in Fig. S3.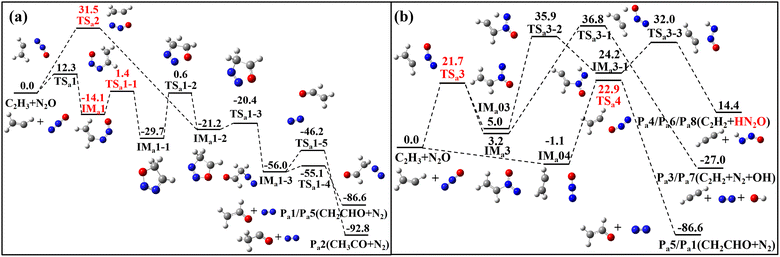

Fig. 1 PES of the addition reaction channel for the N₂O + C₂H₃ at 0 K calculated at the G4 level (in kcal mol⁻¹).

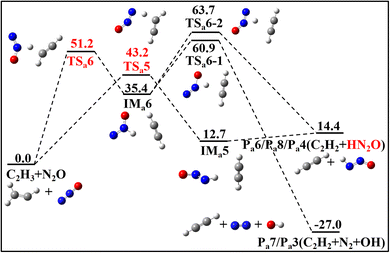Fig. 2 PES of the H-abstraction reaction channel for the N₂O + C₂H₃ at 0 K calculated at the G4 level (in kcal mol⁻¹).

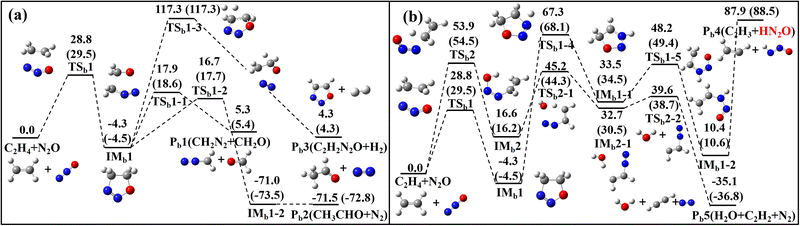Fig. 3 PES for the N₂O + C₂H₄ reaction channels at 0 K, calculated at the G4 level, with CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP values provided in parentheses (in kcal mol⁻¹)

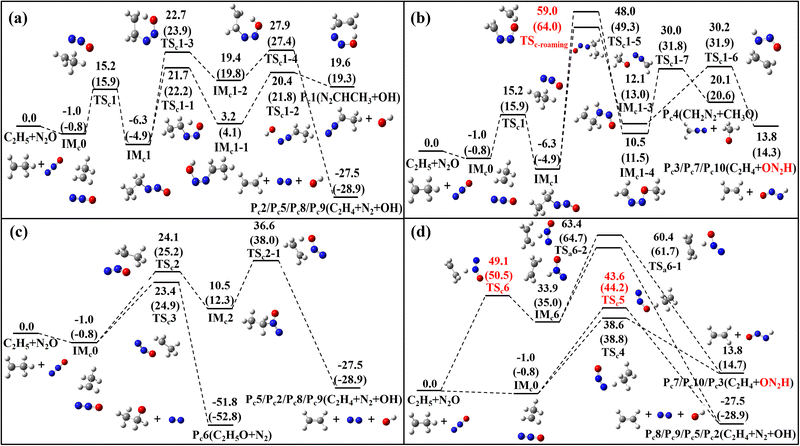Fig. 4 PES for the N₂O + C₂H₅ reaction channels at 0 K, calculated at the G4 level, with CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP values provided in parentheses (in kcal mol⁻¹).

Fig. 5 (a) Rate constants for different reaction pathways of N₂O + C₂H₃ (G4 method: solid lines, CASPT2/cc-pVQZ//B3LYP/6-31G(2df,p) method: short dashed lines); (b) branching ratios of products for different reaction pathways.

Fig. 6 (a) Rate constants for different reaction pathways of N₂O + C₂H₄ (G4 method: solid lines, CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP method: short dashed lines); (b) branching ratios of products for different reaction pathways.

Fig. 7 (a) Rate constants for different reaction pathways of N₂O + C₂H₅; (b) branching ratios of products for different reaction pathways (G4 method: solid lines, CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP method: dashed lines, CASPT2/cc-pVQZ//B3LYP/6-31G(2df,p) method: short dashed lines).

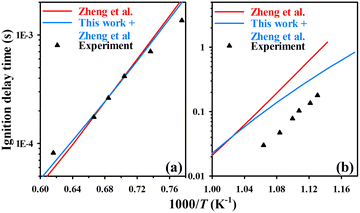Fig. 8 Predicted (lines, using the original model of ref. 18 with and without the N₂O + C₂H_3–5 reactions of this work) and experimental (symbols) results of ignition delay times for the N₂O/C₂H₄/Ar mixture of (a) equivalence ratio 0.5 and at 4 atm pressure⁴² and (b) equivalence ratio 1.05 and at 30 bar pressure.¹⁸

Fig. 9 Normalized sensitivity coefficients to C₂H₄ of the 5 most important elementary reactions among the N₂O–C₂H_3–5 system during the oxidation of a stoichiometric N₂O/C₂H₄ mixture at atmospheric pressure and different temperatures using Ansys Chemkin Pro 2022.

3.1. Potential energy surfaces

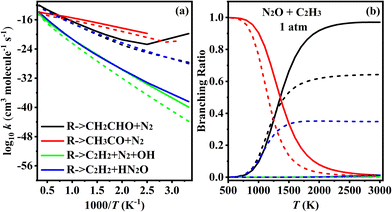
The PES for the reaction between N₂O and C₂H₃ is depicted in Fig. 1 and 2. This reaction proceeds via five addition pathways and three hydrogen abstraction pathways, ultimately yielding four products: P_a1/P_a5 (CH₂CHO + N₂), P_a2 (CH₃CO + N₂), P_a3/P_a7 (CH₂CH₂ + N₂ + OH), and P_a4/P_a6/P_a8 (C₂H₂ + HN₂O). As illustrated in Fig. 1a, the C₂H₃ adds directly to the terminal nitrogen atom of N₂O, forming a C-N bond. This adduct undergoes torsional rotation to form a five-membered ring intermediate, IM_a1-1, which can then experience hydrogen migration between C-C bonds to form intermediate IM_a1-2. Alternatively, C₂H₃ and N₂O may form IM_a1-2 directly through the transition state TS_a2. Subsequent cleavage of the N–O bond leads to ring-opening and the formation of IM_a1-3, which has two possible bond-breaking channels: in the first, direct C–N bond cleavage yields CH₂CHO and N₂; in the second, the C–N bond cleaves while hydrogen transfer occurs between the C–C bonds, producing CH₃CO and N₂. Comparison reveals that the second product is more exothermic. The C₂H₃ radical may also add to the central nitrogen atom (via TS_a3) or to the terminal oxygen atom (via TS_a4), as shown in Fig. 1b. Addition to the central nitrogen yields two distinct intermediates, differing by 1.8 kcal mol⁻¹ in energy. These intermediates subsequently undergo intramolecular hydrogen transfer, in which a hydrogen atom from the CH₂ group migrates through a five-membered ring transition state to the O or N atom, respectively, leading to decomposition and the formation of products P_a3 and P_a4. Addition of the C₂H₃ radical to the terminal oxygen atom results in the formation of P_a5 (CH₂CHO + N₂).

In addition, N₂O can abstract a hydrogen atom directly from the C₂H₃ radical to generate C₂H₂, as shown in Fig. 2. When the terminal nitrogen abstracts hydrogen from the CH₂ group, HN₂O is formed. Abstraction by the central nitrogen followed by hydrogen transfer can lead to either HN₂O or N₂ + OH. However, the transition states for these hydrogen transfers are associated with high energy barriers, with transition state energies of 60.9 and 63.7 kcal mol⁻¹ for migration to the O and N atoms, respectively. Species with T₁ diagnostic values greater than 0.045 are marked in red in Fig. 1 and 2. Since these species appear in both reaction channels, single-point energy calculations were performed using the CASPT2/cc-pVQZ method via Mokit software,³³ based on G4-optimized structures. An active space of 7 electrons in 7 orbitals was used for all TSs and intermediates. The CASPT2 energies are provided in Fig. S1 of the SM1.

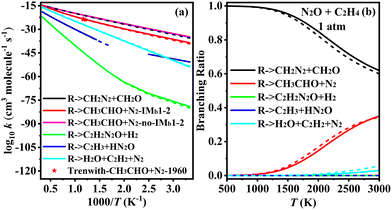
The PES for the reaction of N₂O with C₂H₄ is shown in Fig. 3, comprising five distinct reaction channels. In Fig. 3a, the first two, the two carbon atoms of C₂H₄ were added to the nitrogen and oxygen atoms of N₂O (via TS_b1), forming a five-membered ring intermediate, IM_b1. IM_b1 can either undergo concerted cleavage of the C–C and N–O bonds to form P_b1 (CH₂N₂ + CH₂O), or experience hydrogen transfer between the C–C bonds to form P_b2 (CH₃CHO + N₂). The latter channel corresponds to the reaction route proposed by Li et al. using the B3LYP/6-31++G** method.²⁵ At the G4 level, the energy barriers for TS_b1-1 and TS_b1-2 differ by only 1.2 kcal mol⁻¹, indicating both are kinetically accessible. The third channel involves a much higher energy barrier via TS_b1-3 (117.3 kcal mol⁻¹) and leads to the less favorable formation of P_b3 (C₂H₂N₂O and H₂). The IM_b1 can also undergo intramolecular hydrogen transfer, as shown in Fig. 3b, where a hydrogen atom on a CH₂ group migrates to the nitrogen atom, followed by bond cleavage to form P_b4. However, this pathway has a high product relative energy of 87.9 kcal mol⁻¹. In another reaction channel, C₂H₄ adds via its carbon atom to the terminal nitrogen of N₂O, while a hydrogen atom on the same carbon simultaneously transfers to the oxygen atom of N₂O, forming a five-membered ring transition state TS_b2. Subsequently, another hydrogen atom from the remaining carbon transfers to the oxygen atom, leading to the formation of H₂O + C₂H₂ + N₂ (P_b5). Compared to the first two channels, the last three pathways involve significantly higher energy barriers and are therefore less favorable under typical reaction conditions.

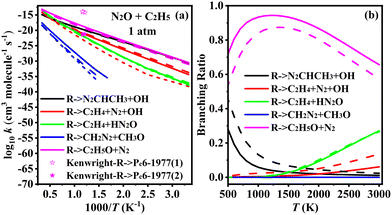
The PES for the N₂O + C₂H₅ reactions are illustrated in Fig. 4, encompassing ten distinct reaction channels. Four of these channels originate from the addition of the C₂H₅ radical to the terminal nitrogen atom of N₂O, as shown in Fig. 4(a) and (b). This addition forms the intermediate IM_c1 via a newly generated C–N bond. IM_c1 can undergo intra-molecular hydrogen transfer: either the H on the methylene group or the methyl group mitigates to the O atoms, forming IM_c1-1 and IM_c1-2, respectively. IM_c1-1 proceeds via N–O bond breaking to yield the product P_c1 (N₂CHCH₃ + OH), while IM_c1-2 undergoes C–N bond-breaking to form P_c2 (C₂H₄ + N₂ + OH). An alternative pathway involves transfer of a hydrogen atom from the methyl group to the adjacent nitrogen atom, followed by C–N bond breaking to form P_c3 (C₂H₄ + ON₂H). The transition state for this process, TS_c1-5, involves a four-membered ring and features a higher transition state energy of 48.0 kcal mol⁻¹. In addition, the possibility of methyl (CH₃) group transfer (the roaming process) via 1M_c1 is considered. This pathway entails an even higher transition state energy (59.0 kcal mol⁻¹), where the CH₃ group transfers to the oxygen atom, followed by N–O bond cleavage to form P_c4 (CH₂N₂ + CH₃O). The T₁ diagnostic value for the roaming transition state (TS_c-roaming) is notably high (0.061), indicating a significant multireference characteristic, and thus single-point energy calculations were performed using the CASPT2/cc-pVQZ//B3LYP/6-31G(2df,p) method. Similarly, since the product ON₂H in P_c3 also has a T₁ diagnostic value greater than 0.045, a multireference treatment was also applied to that pathway. For both channels, the transition states and intermediates were calculated with an active space of 7 electrons in 7 orbitals.

As shown in Fig. 4c, the C₂H₅ radical can also be added to either the central nitrogen or the terminal oxygen atom of N₂O. Addition at the central nitrogen forms the intermediate IM_c2, which subsequently undergoes hydrogen transfer between the methyl carbon and the oxygen atom, leading to the same product as P_c2, namely P_c5 (C₂H₄ + N₂ + OH). In contrast, addition to the oxygen atom follows a more straightforward pathway, directly forming P_c6 (C₂H₅O + N₂). Similar to the hydrogen abstraction reactions between N₂O and the C₂H₃ radical, N₂O can also abstract a hydrogen atom from the methyl group of the C₂H₅ radical to produce C₂H₄, as shown in Fig. 4d. All three atoms in N₂O are capable of abstracting a hydrogen atom. Among these, abstraction by the terminal nitrogen has the lowest energy barrier, followed by abstraction by the terminal oxygen. Abstraction by the central nitrogen, along with the subsequent hydrogen transfer process, exhibits the highest energy barrier.

3.2. Rate constants for N₂O + C₂H_3–5

Based on the above PESs studies, a further kinetic analysis of the reaction pathways for N₂O + C₂H_3–5 was performed to obtain the rate constants over the temperature range of 300 to 3000 K at 1–100 atm.

3.2.1. N₂O + C₂H₃. The reaction between N₂O and C₂H₃ is classified according to the product channels, with the rate constants and branching ratios of the different pathways presented in Fig. 5(a) and (b), respectively. The results of the rate constants obtained by the G4 method and the CASPT2/cc-pVQZ single-point energy calculation method performed based on the optimized structure of the G4 method are compared. The rate constants obtained by the G4 method are generally higher than those from the multi-reference methods. The difference in total rate constants between the two methods reaches its maximum of 12.55 at 400 K under 1 atm. As the temperature increases, the difference in total rate constants between the two methods decreases, and at 3000 K, their ratio is 97.92%. The N₂O and C₂H₃ reaction primarily produces four products, and the branching ratios among them show significant differences. The formation of C₂H₂ + N₂ + OH and C₂H₂ + HN₂O is minimal and can be considered negligible. At temperatures below 1300 K, the formation of CH₃CO + N₂ dominates, with a branching ratio exceeding 57% under the G4 method. At temperatures above 1300 K, the formation of CH₂CHO + N₂ becomes predominant, and with increasing temperature, its branching ratio reaches 97% at 3000 K.

3.2.2. N₂O + C₂H₄. The rate constants and branching ratios for the five reaction pathways of N₂O and C₂H₄ are given in Fig. 6(a) and 6(b), respectively. The rate constants obtained using the G4 and CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP methods are generally similar. Among them, P_b1 is the dominant reaction pathway across the entire temperature range. The structure and energy of IM_b1-2 are shown in Fig. 3. It can be seen that IM_b1-2 is a weakly interacting intermediate formed after the simultaneous cleavage of the C–N and O–N bonds in the five-membered ring structure. The energy of this structure differs between the G4 and CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP methods, being 71.0 and 73.5 kcal mol⁻¹, respectively. Under the G4 method, when the product complex (IM_b1-2) is not considered, the rate constants for the reaction pathways leading to P_b1 and P_b2 are similar, showing nearly identical values between 1100 and 1200 K. In contrast, when the formation of the IM_b1-2 is taken into account, the rate constants for the P_b2 pathway are lower than those for P_b1 under both theoretical methods, which is in general agreement with the experimental results of Trenwith.²⁴ The pathways leading to P_b3 and P_b4 have minimal rate constants, with branching ratios close to zero. The branching ratio for P_b5 is also near zero below 1200 K but increases with temperature, reaching approximately 3% at 3000 K.

3.2.3. N₂O + C₂H₅. Fig. 7(a) and (b) show the rate constants and branching ratios for different reaction pathways of N₂O and C₂H₅. The pathways for the species marked in red in Fig. 4 were all calculated using a multi-reference approach, and the rate constants obtained from the CASPT2/cc-pVQZ//B3LYP/6-31G(2df,p) method are presented, represented by short dashed lines in the left diagram. Upon observation, it can be seen that the reaction pathways corresponding to the multi-reference method are not the key pathways, with relatively low rate constants. Overall, the channel leading to the formation of P_c6 (C₂H₅O + N₂) is the most dominant across the entire temperature range of 300 to 3000 K. The formation of P_c1 (N₂CHCH₃ + OH) is the second most important path, but its contribution progressively diminishes as the temperature increases. We compared the current theoretical results with the experimental data of Kenwright and Trenwith²² obtained in the temperature range of 826–861 K and found that the rate constant for the formation of P_c6 derived from our theoretical calculations lies in between their two groups of experimental results. The channel leading to the formation of C₂H₄ + HN₂O shows increasing contribution with rising temperature, reaching 27.1% and 26.6% at 3000 K under the G4 and CCSD(T)/cc-pVQZ + ZPE methods, respectively. The branching ratio of the pathway producing C₂H₄ + N₂ + OH contributes less than 6.1% across the entire temperature range under the G4 method and less than 13.6% under the CCSD(T)/cc-pVQZ + ZPE method. The pathway forming CH₂N₂ + CH₃O has a very low rate constant and can be considered negligible.

3.3. Ignition delay time and sensitivity analysis

Next, the N₂O + C₂H_3–5 reaction rates developed in this work using the G4 method were incorporated with the N₂O–C₂ mechanism proposed by Zheng et al.¹⁸ The reactions C₂H₃ + N₂O → CH₃CO + N₂ and N₂O + C₂H₄ → C₂H₃ + HN₂O in ref. 18 were replaced with the 14 calculated direct N₂O–C₂H_3–5 reactions in this work. Ignition delay time (IDT) was selected to verify the optimized mechanism. That is because, for NOFBX rocket propellants, ignition reliability and ignition response speed are key indicators that determine the performance of the propulsion system, and IDT serves as a direct quantitative parameter to characterize these two indicators.

IDT of N₂O/C₂H₄ (diluted with Ar, equivalence ratio 0.5 and 4 atm pressure) were predicted using this combined model, which was compared with experimental results,^18,42 obtained from shock tube measurements) and simulations obtained using the original model in Fig. 8. The inclusion of the 14 calculated direct N₂O–C₂H_3–5 reactions improved the predictions of IDT, especially under low-temperature ranges. Similar improvement is also observed for the N₂O/C₂H₆ mixture (see Fig. S3 of the SM1) and other pressures. Moreover, there is a more pronounced change in the predicted fuel conversion rates with temperature when the 14 reactions are added, albeit no experimental data is available for comparison. As shown in Fig. S4 of SM1, the new model results in higher conversions by up to 1.8% at temperatures of ∼1050 K and 3.22% at ∼1200 K.

Finally, sensitivity analysis (SA) was performed using the new kinetic model comprising the 14 N₂O–C₂H_3–5 reactions and Zheng's model.¹⁸Fig. 9 shows the normalized sensitivity analysis coefficients of the top 5 most important reactions in the N₂O–C₂H_3–5 system for C₂H₄ in the temperature range of 850–1550 K. At all investigated temperatures, the reactions C₂H₄ + N₂O → CH₂N₂ + CH₂O and C₂H₄ + N₂O → CH₃CHO + N₂ are the most important among the 14 steps. At 850 K the system is under a weakly reacting state (i.e., before practical ignition, see Fig. S4), and hence no one among the 14 reactions are significant, as reflected by the small SA coefficients less than 0.1%. At this stage, C₂H₅ + N₂O → C₂H₅O + N₂ and C₂H₅ + N₂O → C₂H₄ + HN₂O have positive SA coefficients, indicating they are against the conversion of C₂H₄. Moreover, the SA coefficients gradually increase until ∼1200 K and then decrease with further increased temperatures. C₂H₅ + N₂O → C₂H₅O + N₂ also changes its SA to negative at 1200 K. This is consistent with the discrepancies in C₂H₄ conversion rates predicted by the new and original models, which is greatest at ∼1200 K, and suggests that the investigated N₂O–C₂H_3–5 reactions are the most significant in the medium temperature regime.

4. Conclusions

This work investigates the reactions of N₂O with C₂H₃, C₂H₄, and C₂H₅, using the G4 and CCSD(T)/cc-pVQZ//M06-2X(D3)/def2-TZVP methods, and provides a detailed study of the PESs and kinetics of these reactions. In the process of N₂O oxidizing CH components, the reaction typically proceeds through the addition of the CH component to either the N or O site, followed by subsequent reactions. Alternatively, the hydrogen abstraction reaction from the CH component by N₂O may occur first. The reaction paths of N₂O + C₂H₃ and N₂O + C₂H₅ are similar, where the radicals can add to any of the three atoms in the N₂O molecule, or undergo hydrogen abstraction from the radical to form stable CH-containing products. In contrast, the N₂O + C₂H₄ reaction primarily proceeds via the initial formation of a five-membered ring transition state, followed by subsequent reactions. Through kinetic studies, the rate constants and branching ratios of the N₂O + CH species are discussed in detail. In the N₂O + C₂H₃ reaction, the formation of CH₃CO + N₂ and CH₂CHO + N₂ corresponds to the dominant reaction pathways at low and high temperatures, respectively. In the N₂O + C₂H₄ reaction, the formation of CH₂N₂ + CH₂O dominates across the entire temperature range. In the N₂O + C₂H₅ reaction, the primary product is C₂H₅O + N₂. Comprehensive calculations of the rate constants updated the corresponding rate constant data, and 2 elementary reactions in a literature kinetic model were replaced with the herein theoretically calculated fourteen N₂O–C₂H_3–5 steps. By incorporating the current theoretical findings into the N₂O/C₂H₄ and N₂O/C₂H₆ models and comparing with experimental data, an improvement in the ignition delay times is observed. The new model also yields higher/lower fuel conversion rates at temperatures below/above 1000 K. Sensitivity analysis further revealed that upon ignition the herein calculated N₂O–C₂H_3–5 steps, which were missing from previous literature models, play a nonnegligible role promoting fuel conversion, which have a non-monotonic temperature dependence with the most pronounced impact at medium temperatures ∼1200 K. This study is hence beneficial for advancing the combustion mechanisms of N₂O and small hydrocarbons and models of green rocket propellants from a quantitative perspective.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03435c.

Acknowledgements

This work was supported by the National Key R&D Program of China (2024YFB410480101), the National Natural Science Foundation of China (52506001, 52576126), and the Dushi Project of Tsinghua University. The numerical calculations in this paper were carried out at the Hefei Advanced Computing Center.

References

1. A. S. Gohardani, J. Stanojev, A. Demairé, K. Anflo, M. Persson, N. Wingborg and C. Nilsson, Prog. Aeronaut. Sci., 2014, 71, 128–149.
2. V. Zakirov, A. Perera-Webb, R. Osborne, C. Milyaev, J. Anderson, S. Gwozdz and P. Ganapathiperumal, J. Br. Interplanet. Soc., 2021, 74, 223–233.
3. L. Werling and T. Hörger, Acta Astronaut., 2021, 189, 437–451.
4. L. Werling and P. Bätz, J. Propul. Power, 2022, 38, 254–266.
5. R. Ma, H. Zhang and W. Fan, Energy, 2024, 297, 131245.
6. W. Wang and H. Zhang, Combust. Flame, 2019, 202, 362–375.
7. C. Naumann, T. Kick, T. Methling, M. Braun-Unkhoff and U. Riedel, Int. J. Energetic Mater. Chem. Prop., 2019, 19, 65–71.
8. J. Koop and O. Deutschmann, Appl. Catal., B, 2009, 91, 47–58.
9. F. Normann, K. Andersson, B. Leckner and F. Johnsson, Prog. Energy Combust. Sci., 2009, 35, 385–397.
10. A. N. Hayhurst and A. D. Lawrence, Prog. Energy Combust. Sci., 1992, 18, 529–552.
11. S. Skeen, G. Yablonsky and R. Axelbaum, Combust. Flame, 2010, 157, 1745–1752.
12. W. K. Metcalfe, S. M. Burke, S. S. Ahmed and H. J. Curran, Int. J. Chem. Kinet., 2013, 45, 638–675.
13. H. Wang, X. You, A. V. Joshi, S. G. Davis, A. Laskin, F. Egolfopoulos and C. K. Law, URL: http://ignis.usc.edu/USC_Mech_II.htm, 2007.
14. S. Panigrahy, A. A. E.-S. Mohamed, P. Wang, G. Bourque and H. J. Curran, Proc. Combust. Inst., 2023, 39, 253–263.
15. N. E. Meagher and W. R. Anderson, J. Phys. Chem. A, 2000, 104, 6013–6031.
16. S. Liu, W. Fan, X. Wang, J. Chen and H. Guo, Energy, 2022, 247, 123445.
17. W. L. Wang and H. Q. Zhang, Combust. Flame, 2019, 202, 362–375.
18. D. Zheng, P. F. Xiong and B. J. Zhong, Acta Phys.-Chim. Sin., 2019, 35, 1241–1247.
19. A. A. Konnov, Combust. Flame, 2009, 156, 2093–2105.
20. F. Zhang, H. Y. Chen, J. C. Feng and D. Zheng, Fuel, 2021, 288, 119688.
21. A. R. Ravishankara, J. S. Daniel and R. W. Portmann, Science, 2009, 326, 123–125.
22. R. Kenwright, P. L. Robinson and A. B. Trenwith, J. Chem. Soc., 1959, 2079–2082.
23. R. Tang and S. Cheng, Energies, 2023, 16, 4967.
24. A. Trenwith, J. Chem. Soc., 1960, 3722–3726.
25. Y. Y. Li, R. P. Jiang, S. Xu and X. D. Gong, Propellants, Explos., Pyrotech., 2022, 47, e202200082.
26. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
27. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. H. Wang, C. Cao, S. Zheng and R. Sui, Combust. Sci. Technol., 2025, 197 DOI:10.1080/00102202.2025.2500503.
30. B. Chan, M. L. Coote and L. Radom, J. Chem. Theory Comput., 2010, 6, 2647–2653.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
32. H.-T. Guo, L. Yang, Z. Serinyel and C.-W. Zhou, Phys. Chem. Chem. Phys., 2025 10.1039/D5CP03515E.
33. J. Zou, Molecular Orbital Kit (MOKIT), https://gitlab.com/jxzou/mokit, 2024.
34. H. Werner, P. Knowles, G. Knizia, F. Manby, M. Schutz, P. Celani, W. Gyorffy, D. Kats, T. Korona and R. Lindh, MOLPRO, a package of ab initio programs, version 2015.1, University of Stuttgart, 2015.
35. K. Kohse-Höinghaus, J. Troe, J.-U. Grabow, M. Olzmann, G. Friedrichs and K.-D. Hungenberg, Phys. Chem. Chem. Phys., 2018, 20, 10561–10568.
36. Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154.
37. B. E. Poling, J. M. Prausnitz and J. P. O’connell, Properties of gases and liquids, McGraw-Hill Education, 2001.
38. J. Welty, G. L. Rorrer and D. G. Foster, Fundamentals of momentum, heat, and mass transfer, John Wiley & Sons, 2014.
39. L. Zhang, Q. Chen and P. Zhang, Proc. Combust. Inst., 2015, 35, 481–489.
40. F. Zhang and T. S. Dibble, Phys. Chem. Chem. Phys., 2011, 13, 17969–17977.
41. J. Bao, J. Zheng, I. Alecu, B. Lynch, Y. Zhao and D. Truhlar, https://comp.chem.umn.edu/freqscale/index.html, 2019.
42. F. Deng, Y. Pan, W. Sun, F. Yang and Y. Zhang, Energy Fuels, 2017, 31, 14116–14128.

---