Open Access Article
Open Access ArticleAn X-ray scattering and quasielastic neutron scattering study on the structure and dynamic properties of low-temperature methanol confined in ordered microporous carbon and mesoporous organosilica pores
Hongyan Liu a,
Zhuanfang Jing
a,
Zhuanfang Jing a,
Keke Chai
a,
Keke Chai ac,
Yongquan Zhou
ac,
Yongquan Zhou *a,
Koji Yoshida
*a,
Koji Yoshida b,
Takeshi Yamadad and
Toshio Yamaguchi
b,
Takeshi Yamadad and
Toshio Yamaguchi *ab
*ab
aKey Laboratory of Comprehensive and Highly Efficient Utilization of Salt Lake Resources, Key Laboratory of Salt Lake Resources Chemistry of Qinghai Province, Qinghai Institute of Salt Lakes, Chinese Academy of Sciences, Xining, Qinghai 810008, China. E-mail: yamaguch@fukuoka-u.ac.jp; yongqzhou@163.com
bDepartment of Chemistry, Faculty of Science, Fukuoka University, Nanakuma, Jonan, Fukuoka 814-0180, Japan
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
dNeutron Science and Technology Center, Comprehensive Research Organization for Science and Society, 162-1 Shirakata, Tokai 319-1106, Japan
First published on 19th November 2025
Abstract
We utilized large-angle X-ray scattering (LAXS) and quasielastic neutron scattering (QENS) to measure the structure and dynamic properties of methanol confined in ordered microporous carbon (OMC) and periodic mesoporous organosilica (PMO) materials with phenyl groups embedded in a silica matrix (Ph-PMO). The pore diameters of the OMC and Ph-PMO materials obtained by the nitrogen adsorption and desorption isotherm analysis are 18.7 Å and 30.0 Å, respectively. The LAXS data of the methanol molecules confined in the Ph-PMO pores at a low temperature (230 to 298 K) reveal that the structure of the capillary-condensed methanol molecules in the Ph-PMO pores consists of the monolayer of methanol on the surface and the hydrogen-bonded chains of the methanol molecules at the central part of the pores. As the temperature decreases, the methanol chains in the Ph-PMO pores gradually become ordered; however, the degree of this enhancement with temperature is not as significant as that for water in the Ph-PMO pores. The QENS spectra were analyzed using a jump-diffusion model to describe the motion of the methanol molecules. For the methanol molecules confined in the OMC pores, as the temperature decreases, the hydrogen-bonded axial chain structure of methanol in the pores is enhanced and the movement of the confined methanol molecules slows down. A comparison of the dynamic properties of the methanol and water molecules under the same conditions shows that the confinement effect has a greater impact on the dynamic characteristics of the methanol molecules than on the water molecules. For the methanol molecules confined in the amphiphilic Ph-PMO with a relatively large capillary pore, a kind of ‘bulk-like’ behavior was observed, especially at 315 K, which is in accord with the behavior of the water molecules in the Ph-PMO pores. In addition, similar to the case for the water molecules, we found evidence of the immobile and mobile fractions of the confined methanol molecules.
1. Introduction
Porous materials exhibit tremendous application potential in gas storage, molecular separation, catalytic reactions, and other fields due to their unique pore structures and excellent physicochemical properties. According to the definition by the International Union of Pure and Applied Chemistry (IUPAC), porous materials can be classified into three categories based on their pore size: microporous materials (pore size: <2 nm), mesoporous materials (pore size: 2–50 nm), and macroporous materials (pore size: >50 nm). This tunable pore structure endows porous materials with extremely high specific surface area and porosity, enabling their significant potential in multiple critical applications.1,2Methanol, as a crucial basic chemical feedstock and clean energy carrier, has long been a research focus, particularly its adsorption and diffusion behaviors in porous materials.3 In practical applications, the distribution structure and dynamic properties of the methanol molecules within the pores directly determine the material's adsorption capacity, selectivity, and mass-transfer efficiency for methanol. However, confined methanol molecules exhibit behaviors significantly distinct from their bulk-state counterparts due to the pronounced influence of pore size, geometry, and surface chemistry. Traditional experimental characterization techniques struggle to comprehensively and accurately obtain the structural and dynamic information of confined methanol molecules, necessitating more effective research methodologies.
Quasielastic neutron scattering (QENS) spectroscopy is a technique that allows for the observation of the microscopic dynamics of confined liquids, as long as they fall within the time scales of the QENS spectrometers.4 QENS can provide information on correlated particle motions in the case of coherent scattering and single-particle motions in the case of incoherent scattering. For hydrogen-rich materials, such as methanol and water, the total scattering cross-section is strongly dominated by the self-motions of hydrogen atoms because of their high incoherent scattering cross-section.5 Therefore, the QENS technique is well placed to gain an understanding of how the diffusion changes with temperature and the dynamic properties of methanol confined in porous materials.
At present, the research on methanol confined in porous materials mainly focuses on zeolite3,6–8 and MCM-41.9 Matam et al. used QENS to study the dynamic behavior of methanol in zeolites with different Si/Al ratios, showing that as the measurement temperature increased, the nature of the methanol dynamics changed from rotational to translational diffusion.3,7 The study of methanol diffusion and dynamics in zeolite H-ZSM-5 by QENS and classical molecular dynamics (MD) simulations provides comprehensive information on the effect of acid site density on the methanol dynamics in ZSM-5 pores and highlights the complementarity of QENS and MD and their advantages and limitations.6 Omojola et al. confirmed through the QENS method that methanol confined in H-ZSM-5 catalysts exhibited different molecular behaviors at various temperatures.8 The dynamics of methanol confined in MCM-41, as investigated by QENS, indicate the relatively high cooperativity of molecular motions in liquid methanol.9
Ordered microporous carbon (OMC)10 and mesoporous organosilica (Ph-PMO),11 as two representative types of porous materials, provide an ideal platform for studying liquid molecular behavior in confinement, owing to their precisely controllable pore dimensions and outstanding physicochemical stability. In the past three decades, X-ray and neutron scattering measurements have often been performed on water/methanol confined in porous materials to elucidate its structure and dynamics at the molecular level.12–18 In our previous work, using X-ray diffraction (XRD) and QENS, we found that the tetrahedral network structure of water confined in OMC pores is perturbed from the bulk water structure, and the translational diffusion is comparable to that of bulk water at 300 K and higher than that in MCM-41.12 The studies of Aso et al. suggested that the tetrahedral-like hydrogen-bonded structure of water is distorted in the Ph-PMO pores, and the QENS data showed that the translational diffusion coefficient, the residence time, and the rotational relaxation time of the water molecules in the Ph-PMO pores are comparable with those in bulk.13 Morishige and Kawano have investigated the freezing and melting behaviors of methanol confined in MCM-41 and SBA-15 with different pore sizes using the LAXS method.14 Based on the XRD patterns, they discussed a pore-size effect on the vitrification, crystallization, and phase transition of methanol in the pores. Takamuku et al. have confirmed through the LAXS method that the capillary-condensed methanol confined in MCM-41 forms the hydrogen bond chains of methanol molecules, and the hydrogen bonds between the methanol molecules in the pores are significantly distorted or partially broken.15 However, the structure of methanol in the pores has still been ambiguous at the molecular level. The in-depth exploration of the structure and dynamics of liquid molecules confined in these material channels not only helps reveal the interaction mechanisms between molecules and pore walls but also offers theoretical foundations for optimizing material performance and expanding applications.
In the present investigation, we have made LAXS measurements over a low temperature range from 230 to 298 K on methanol adsorbed under capillary-condensed conditions in Ph-PMO pores. The QENS measurements were carried out from 255 to 315 K on methanol adsorbed in OMC (monolayer conditions) and Ph-PMO (capillary-condensed conditions) pores. Based on the results, the structure and dynamics of the methanol confined in the OMC and Ph-PMO pores are discussed, along with the temperature and pore properties (hydrophilicity/hydrophobicity). The structural and dynamic differences between methanol and water confined in the same pores are discussed at the molecular level.
2. Experimental
2.1 Sample preparation
Periodic mesoporous organosilica (PMO) materials with phenyl groups embedded in a silica matrix (Ph-PMO) were prepared and characterized, as described in ref. 11. They have a highly ordered mesostructure with a well-defined hexagonal, uniform pore-size distribution and a high surface area whose interface consists of organic phenyl groups and vitreous silica. Ordered microporous carbon (OMC) materials were prepared via the direct carbonization of the periodically ordered nanocomposites of a thermosetting polymer and a thermally decomposable surfactant, according to the method by Tanaka et al.19,20 The OMC materials have an ordered hydrophobic pore wall channel structure, as described in ref. 12. The nitrogen adsorption and desorption isotherms of the Ph-PMO and OMC materials were measured at 77 K using an automatic gas adsorption apparatus, BELSORP-max (Microtrac BEL Corp.). A nitrogen adsorption analysis at liquid-N2 temperature was conducted on the Ph-PMO and OMC materials. To evaluate the pore diameter, specific surface area, and pore volume of the Ph-PMO and OMC materials, the corresponding values by the Brunauer–Emmett–Teller plot and the Dollimore and Heal method21 are summarized in Table 1. As shown in Table 1, the pore diameter of Ph-PMO, a mesoporous material, is 30.0 Å, while the pore diameter of OMC, a microporous material, is 18.7 Å.| Samples | Surface area (m2 g−1) | Pore diameter (Å) | Pore volume (cm3 g−1) |
|---|---|---|---|
| Ph-PMO | 735.0 | 30.0 | 0.54 |
| OMC | 583.4 | 18.7 | 0.27 |
To evaluate the adsorption of methanol into the Ph-PMO and OMC pores, adsorption and desorption isotherms at 298 K were measured by weighing the methanol adsorbed into the Ph-PMO and OMC pores with an electronic balance (BEL, Rubotherm) connected to a vacuum line, where methanol vapor pressure can be controlled. Fig. 1 shows the adsorption and desorption isotherms of methanol on the Ph-PMO and OMC pores, as a function of methanol vapor pressure. The black lines show no hysteresis between the adsorption and desorption isotherms for the Ph-PMO pores. Moreover, methanol is adsorbed into the Ph-PMO pores in two steps; the first one, below P/P0 of ∼0.4, corresponds to the formation of a monolayer of methanol on the pore surface, while the second one, above P/P0 of ∼0.5, shows the capillary condensation of methanol in the central part of the pores. The sharp jump at the second step reflects a very narrow distribution of the pore diameters for the synthesized Ph-PMO.13,22 The OMC material (blue lines in Fig. 1) exhibited a large amount of adsorption at the initial stage and showed a type I loop. That is, the characteristics of typical microporous materials include rapid adsorption saturation in the low-pressure region, a desorption curve that coincides with the adsorption curve, no obvious hysteresis loop, and only a single plateau, which conforms to Langmuir's monolayer adsorption model.
2.2 LAXS measurements
Ph-PMO powder was filled into a glass capillary (WJM-Glas MÜller GmBH) with an inner diameter and wall thickness of 2 mm and 0.01 mm, respectively, which was connected through a stainless-steel flange with a valve through a vacuum line to an in situ adsorption apparatus.23 The Ph-PMO powder samples were dried in a vacuum at 298 K for about 12 h and then gradually exposed to methanol vapor to reach P/P0 = 0.90, which is required for capillary condensation conditions. After the completion of methanol adsorption, the samples were contacted with N2 up to one atmosphere of pressure. The same method was used to adsorb methanol in the OMC powder; it was found that because of the hydrophobicity of the pore wall and the microporous property of the OMC materials, the adsorbed methanol content was very small; thus, the relevant LAXS experiments were not carried out.The LAXS intensities from the capillary condensation of the methanol in the Ph-PMO pores were measured at 298, 270, 250, 230, and 220 K with a rapid liquid X-ray diffractometer (BRUKER AXS, DIP301) using an imaging plate (IP) as a two-dimensional area detector, as described elsewhere.12,23 The X-rays were generated at a rotary Mo anode operated at 50 kV and 200 mA, then monochromatized with a flat graphite crystal to acquire Mo Kα radiation (the wavelength (λ) = 0.7107 Å). A dual-aperture collimator with an aperture diameter of 0.9 mm was used to obtain a parallel X-ray beam. The camera length and the effective area of IP were 150 mm and 200 × 400 mm2, respectively. The IP area spans the scattering angle (2θ) of 0°–109°, corresponding to an amplitude of the scattering vector (Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ) of 0–14.4 Å−1. The cooling of the sample was carried out using a specially designed cryostat that blew cold N2 gas from liquid N2 onto the capillary. The temperature of the sample was measured using a copper-constantan thermocouple and controlled within ±1 K by adjusting the blowing rate of N2 gas. The exposure time was one hour for measurement at each temperature. After the X-ray measurements for the Ph-PMO samples with adsorbed methanol, the tip of the capillary was opened again by breaking it. Moreover, to prepare the dried Ph-PMO samples, the adsorbed methanol was evaporated from the Ph-PMO pores by connecting the sample to the vacuum line. The X-ray scattering intensity of the dried Ph-PMO was then measured at the same temperatures as the methanol-doped sample. It should be noted that this measurement procedure has the advantage of subtracting the scattered intensity of a dry Ph-PMO from a methanol-absorbed sample (wet Ph-PMO) without moving the sample position. The experimental scattered intensities of the wet and dry Ph-PMO samples at different temperatures are shown in Fig. S1 of the SI. Details about the X-ray data analysis can be found in Part 2 of the SI and ref. 12 and 13.
θ/λ) of 0–14.4 Å−1. The cooling of the sample was carried out using a specially designed cryostat that blew cold N2 gas from liquid N2 onto the capillary. The temperature of the sample was measured using a copper-constantan thermocouple and controlled within ±1 K by adjusting the blowing rate of N2 gas. The exposure time was one hour for measurement at each temperature. After the X-ray measurements for the Ph-PMO samples with adsorbed methanol, the tip of the capillary was opened again by breaking it. Moreover, to prepare the dried Ph-PMO samples, the adsorbed methanol was evaporated from the Ph-PMO pores by connecting the sample to the vacuum line. The X-ray scattering intensity of the dried Ph-PMO was then measured at the same temperatures as the methanol-doped sample. It should be noted that this measurement procedure has the advantage of subtracting the scattered intensity of a dry Ph-PMO from a methanol-absorbed sample (wet Ph-PMO) without moving the sample position. The experimental scattered intensities of the wet and dry Ph-PMO samples at different temperatures are shown in Fig. S1 of the SI. Details about the X-ray data analysis can be found in Part 2 of the SI and ref. 12 and 13.
2.3 QENS measurements
According to the adsorption isotherms (Fig. 1), the samples of the methanol adsorbed in the Ph-PMO pores at a capillary condensation state were prepared at P/P0 = 0.90, as described in the previous sections. Then, a monolayer of the methanol sample was prepared by adsorbing methanol into the OMC powder. The powder samples were inserted into a double-cylinder aluminum cell. The diameters, thicknesses, and heights of the inner and outer cylinders were 14.0 mm, 0.25 mm, and 45 mm and 18.0 mm, 0.25 mm, and 50 mm, respectively. The thickness of the sample was 1 mm to ensure that the transmission of neutrons was more than 90% to avoid multiple scattering.The QENS measurements were conducted using the near-backscattering spectrometer, DNA, which was installed at the Japan Proton Accelerator Research Complex (J-PARC) Materials and Life Science Experimental Facility (MLF). The details of the spectrometer and its performance have been described elsewhere.24,25 The injected proton beam power incident on the neutron target was ∼200 kW. The energy resolution of the full width at half-height was 3.6 µeV using a Si(111) analyzer. The covered Q range was from 0.15 to 1.85 Å−1, where Q is the momentum transfer of neutrons by scattering. The energy transfer E was between −40 and +100 µeV. The QENS measurements of the samples were performed at 315, 300, 285, 270, and 255 K. A cylindrical vanadium was measured at 300 K to determine the instrument resolution. QENS data were collected for about 12 h at each temperature.
The QENS spectra I(Q, E) of the methanol molecules confined in the OMC and Ph-PMO pores were generally analyzed by a model of both translational and rotational motions,26,27 which can be expressed by eqn (1).
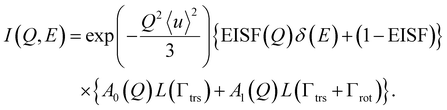 | (1) |
A0(Q) could be larger than A1(Q) in the present experimental Q range. In addition, since the energy range measured with the spectrometer, DNA, was very narrow, the spectra that originated from the rotational motion were much broader than the observable energy range of the spectrometer. Thus, the contribution of the molecular rotation should be treated as a background term. As a result, I(Q, E) was analyzed using a model of the translational diffusions of the methanol molecules as given by eqn (2),26–28
| I(Q, E) = [A(Q)δ(E) + (1 − A(Q))S(Q, E) + B(Q, E)]⊗R(Q, E), | (2) |
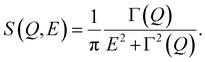 | (3) |
In the jump-diffusion model for translation, the HWHM of Γ(Q) is according to eqn (4).
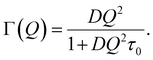 | (4) |
3. Results and discussion
3.1 LAXS measurements of the methanol molecules confined in the Ph-PMO pores
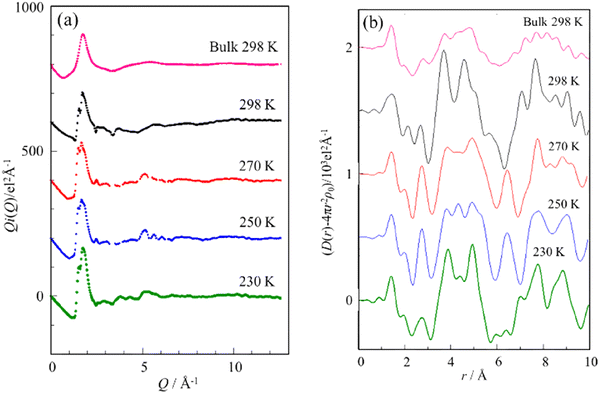
The Q-weighted structure functions (i(Q)) for the bulk methanol at 298 K and the capillary-condensed methanol in the Ph-PMO pores from a low temperature of 230–298 K are shown in Fig. 2(a). The corresponding radial distribution functions (RDFs) in the form of D(r) − 4πr2ρ0 are displayed in Fig. 2(b), which are obtained by the Fourier transformation of the structure functions, as shown in Fig. 2(a). The structure of the bulk methanol at 298 K has been reported in ref. 29–31; thus, we provide a brief description herein. As shown in Fig. 2(b), two peaks at 1.4 and 2.1 Å can be ascribed to the intramolecular interactions within a methanol molecule; the distinct peak at 1.4 Å is assigned to the C–O bond, and the small one at 2.1 Å originates from the nonbonding C⋯H(OH) and nonbonding O⋯H(CH3) interactions. The characteristic peak located at 2.8 Å belongs to the O⋯O hydrogen bond between the methanol molecules. The broad multiple peaks in the range of 3.5–5.5 Å are attributed to the intermolecular interactions between the first and second neighbors of the methanol molecules, such as C⋯C interaction at ∼3.7 Å and O⋯O and O⋯C interactions at ∼4.5 Å and ∼4.8 Å, respectively. The broad multiple peaks in the range of 6.5–9.5 Å are assigned to the third- and fourth-neighbor interactions of the methanol molecules. These features indicate that in the bulk methanol solution, four to five methanol molecules form a chain structure through hydrogen bonding.The RDF for the capillary-condensed methanol in the Ph-PMO pores at 298 K shows significant differences from those for the bulk methanol. The C–O intramolecular interaction peak at 1.4 Å did not show an obvious change. Furthermore, the nonbonding C⋯H(OH) and O⋯H(CH3) interaction peaks at 2.1 Å for the bulk methanol shift to 2.3 Å for the confined methanol molecules and become more notable, indicating that the confinement effect enhanced the intramolecular interactions of the methanol molecules. The O⋯O hydrogen bonding peak between the methanol molecules at 2.8 Å is also significantly enhanced and slightly shifted to 2.7 Å, indicating that the confinement effect enhances the intermolecular interactions of methanol. It should be noted here that the O⋯O peak also includes the short O⋯O hydrogen bonds between the methanol molecules and the silanol groups on the surface.
In the Ph-PMO pores, the first- and second-neighbor interaction peaks (3.5–5.5 Å) and the third- and fourth-neighbor interaction peaks (6.5–9.5 Å) in the methanol chains transformed from broad multiple peaks into several distinct sharp peaks. Particularly, the obvious sharp peak at 3.7 Å is attributed to the superposition peak of the interaction peak between the silanol groups on the surface of the Ph-PMO pores and methanol molecules (Si⋯OHCH3)13,15 and the C–C interaction peak between the methanol molecules. The peaks corresponding to the O–O and O–C interactions between the methanol molecules at 4.5 Å and 4.8 Å show significant enhancement. These features suggest that the methanol molecules still form hydrogen-bonded chains even within 30-Å-diameter Ph-PMO pores, with markedly strengthened intermolecular and intramolecular interactions. These results are consistent with the RDF analyses of methanol confined in MCM-4115 and water confined in Ph-PMO.13
Compared with the RDF of the capillary-condensed methanol in Ph-PMO at different temperatures, the intramolecular C–O interaction and nonbonding C⋯H(OH)/O⋯H(CH3) interaction peaks show no significant variations. As the temperature decreased from 298 K, the peaks at 2.7 Å and 4.8 Å showed significant enhancement, while the peak intensities at 3.7 Å and 4.5 Å decreased. Additionally, new peaks emerged at 4.3 Å and 6.4 Å. The peaks at 3.9 Å and 4.8 Å gradually evolved and sharpened as the temperature decreased to 230 K, suggesting that other interactions, which are sensitive to temperature, should be considered for the two peaks. It is highly probable that the interactions between the hydrogen-bonded methanol chains also contribute to these peaks, since the Ph-PMO pore diameter (30 Å) is approximately six times larger than the methanol molecular diameter (∼5 Å). This finding suggests the possible formation of two parallel methanol chains along the cylindrical pore axis, while maintaining a surface-adsorbed monolayer of methanol. This conclusion is consistent with the methanol structure confined in MCM-41.15
In Fig. 3, a plausible model of the structure for the capillary-condensed methanol is illustrated with important interatomic distances. In accordance with the van der Waals radius (2.0 Å) of the methyl group, the distance of the C⋯C interaction between two methanol chains is estimated to be 4.0 Å, and that of the C⋯O interaction between methyl C and hydroxyl O atoms is 4.9 Å. As shown in Fig. 3, there are also C⋯C and C⋯O interactions between the hydrogen-bonded methanol chains and the methanol molecules adsorbed on the Ph-PMO surface. Their distances are in good agreement with the 3.9- and 4.8-Å peaks, respectively, which are less than those of the 4.1- and 5.1-Å peaks of the methanol confined in MCM-41.15 A possible reason for the translational motion of the methanol chains in the Ph-PMO pores is strongly restricted is that the C⋯C and C⋯O interactions are strong in the RDF of methanol for the capillary condensation state but not significant for the bulk methanol. In contrast, for the bulk methanol, the methanol chains can freely undergo a three-dimensional translational motion, leading to relatively loose interactions between the chains. The model shown in Fig. 3 indicates that the interaction between the methanol layers is likely dominated by the van der Waals forces between the methyl groups rather than hydrogen bonds. Otherwise, the previous investigation showed that the hydrogen-bonded network of water is evolved even in the Ph-PMO pores.13 This difference between the methanol and water molecules confined in the Ph-PMO pores may originate from the relatively few hydrogen-bonding sites and the bulkiness of the methanol molecules. Moreover, as the temperature decreases, the O⋯O hydrogen bond peak at 2.7 Å gradually sharpens, indicating that the hydrogen bonds between the methanol molecules become increasingly ordered with temperature. The C⋯C and C⋯O interactions at 3.7 Å and 4.8 Å also intensify, suggesting that the van der Waals forces between the methyl groups of the methanol layers are strengthened and the movement of the methanol molecules in the pores is gradually restricted as the temperature decreases.
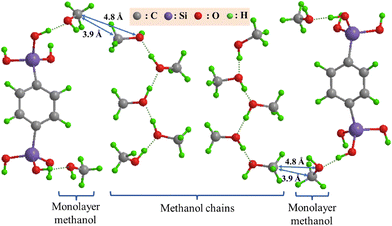 | ||
| Fig. 3 Structure model of the capillary-condensed methanol in the Ph-PMO pores. The dashed lines represent hydrogen bonds. | ||
3.2 QENS measurements
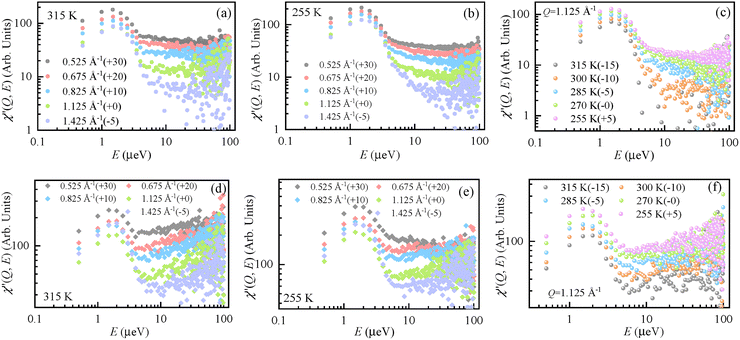
In Fig. 4, we plot a set of dynamical structure factors (S(Q, ω)) as a function of temperature at Q = 0.825 Å−1 (a, c) and 1.275 Å−1 (b, d) for the methanol molecules confined in the OMC and Ph-PMO pores. The spectrum measured at 300 K of vanadium (red lines in Fig. 4) was used for the instrument resolution of this spectrometer. The central peaks are broadened from the resolution function, characterizing the quasielastic scattering from the samples. The peak width gradually decreases as the temperature decreases, indicating that the motion of the methanol molecules is becoming relatively slow. Meanwhile, as shown in Fig. 4, the quasielastic scattering and its variation with the temperature of the methanol molecules confined in the OMC pores are more obvious than those in Ph-PMO, indicating that the smaller the pore size, the greater the influence of the confinement on the dynamic characteristics. Moreover, by comparing the QENS spectra of the water molecules confined in OMC12 with those of the methanol molecules, it is evident that the latter are broader, which means a faster dynamic process.
Furthermore, the QENS spectra can be analyzed by their representation as dynamic susceptibilities, as shown in Fig. 5. The dynamic susceptibility is a model-free presentation of the QENS signal normalized by the Bose occupation factor. The dynamic susceptibility as a function of energy transfer shows unique peaks corresponding to the relaxation process.5 The number of peaks and their positions represent the number of different relaxation processes and their energy/time scale in the sample, respectively. Generally, dynamic susceptibility (χ″) is inversely proportional to the Bose occupation number (nB(E, T)), that is, χ″ ∝ [I(Q, E)]/[nB(E, T)] and nB(E, T) ∝ [exp(E/kBT) − 1]−1. At room temperature, the Boson population factor can be simplified by Taylor series expansion. Therefore, the expression is given by eqn (5),
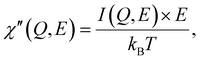 | (5) |
The dynamic susceptibility comparison of the methanol molecules confined in the OMC and Ph-PMO pores at 315 K (a, d) and 255 K (b, e) with different Q values and at Q = 1.125 Å−1 (c, f) with different temperatures, as displayed in Fig. 5, can help to validate any real dynamic representation. The dynamic susceptibilities of the methanol molecules confined in the OMC and Ph-PMO pores at 300 K, 285 K, and 270 K are given in Fig. S2 and S3. The most representative values of the susceptibility are the instrumental resolution and the signal associated with the relaxation processes, which are both captured and well separated. The broad peak observed at a relatively low energy (around 1–2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) µeV), as shown in Fig. 5, represents the elastic scattering, that is, the energy resolution of the instrument. In the 5–100
µeV), as shown in Fig. 5, represents the elastic scattering, that is, the energy resolution of the instrument. In the 5–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) µeV region, only one additional peak (besides the resolution peak) is observed, indicating that only one measurable relaxation process exists within the resolution and measured energy range of the instrument.
µeV region, only one additional peak (besides the resolution peak) is observed, indicating that only one measurable relaxation process exists within the resolution and measured energy range of the instrument.
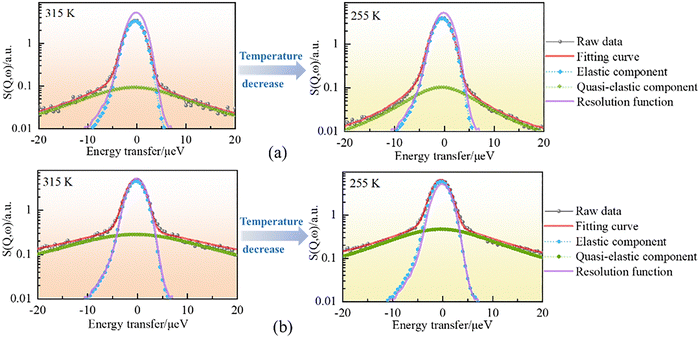
Fig. 7(a) and (d) show the Q2 dependence of Γ(Q). For the methanol molecules confined in the OMC and Ph-PMO pores, Γ(Q) initially increases and then plateaus at relatively high Q values, suggesting a translational diffusion process, such as jump-diffusion. As seen in Fig. 7(a) and (d), the experimental values fit quite well with this model, confirming that the jump-diffusion model is suitable for the methanol molecules, which remain in a specific site for a time (τ0) before they jump a distance (l) to another position. The HWHMs decrease as the temperature decreases, while the diffusive motion becomes slow. The solid lines represent the fits using the jump-diffusion model governed by eqn (4), from which the diffusion coefficient (D) is obtained,36 and the values for τ0 and l at different temperatures are summarized in Table 2. Also included in this table are similar data for the water molecules in the OMC pores under identical conditions to enable us to compare the binding behavior of some small molecules having similar size but different chemical structures. Fig. S6 and S7 in the SI show the nonlinear fitting of the Γ(Q) function at each temperature for the methanol molecules in the OMC and Ph-PMO pores, respectively.
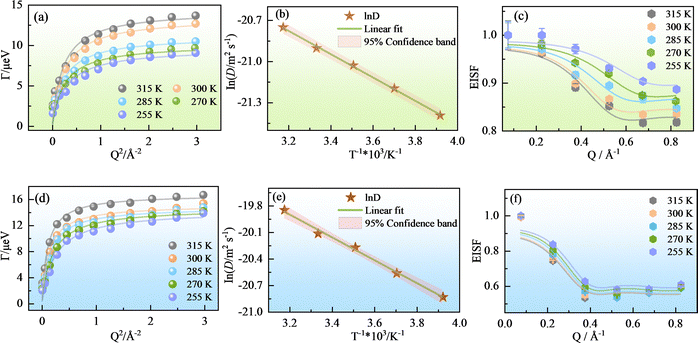 | ||
| Fig. 7 The HWHM (ball) of the QENS spectra for the methanol molecules confined in the OMC and Ph-PMO pores at 315, 300, 285, 270, and 255 K (a) and (d); the solid lines indicate a nonlinear fitting. Arrhenius plot of the diffusion coefficient of the methanol molecules confined in the OMC (b) and Ph-PMO (e) pores; the solid lines indicate a linear fitting. EISF for methanol at various temperatures measured in the OMC (c) and Ph-PMO pores (f); the solid lines represent the fittings of the EISF model described in eqn (7). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT)
exp(−Ea/kBT)
| T/K | D/×10−10 m2 s−1 | τ0/ps | l/Å | c | P0 | a/Å | Ea/kJ mol−1 |
|---|---|---|---|---|---|---|---|
| Methanol molecules confined in the OMC pores | |||||||
| 315 | 9.72 ± 1.74 | 45.94 ± 2.15 | 5.18 ± 0.47 | 0.969 | 0.151 ± 0.003 | 7.14 ± 0.03 | 7.08 ± 0.16 |
| 300 | 8.35 ± 1.32 | 48.99 ± 2.12 | 4.95 ± 0.41 | 0.972 | 0.149 ± 0.003 | 7.18 ± 0.04 | |
| 285 | 7.36 ± 1.40 | 55.40 ± 2.98 | 4.94 ± 0.50 | 0.977 | 0.147 ± 0.003 | 6.70 ± 0.04 | |
| 270 | 6.22 ± 1.24 | 65.08 ± 3.56 | 4.93 ± 0.51 | 0.981 | 0.132 ± 0.002 | 6.08 ± 0.03 | |
| 255 | 5.10 ± 0.90 | 68.50 ± 3.61 | 4.58 ± 0.44 | 0.986 | 0.118 ± 0.002 | 5.73 ± 0.03 | |
| Water molecules confined in the OMC pores12 | |||||||
| 300 | 20.77 ± 2.13 | 23.53 ± 0.71 | 5.42 ± 0.30 | 0.96 ± 0.01 | 0.19 ± 0.02 | 7.59 ± 0.03 | 12.0 ± 1.1 |
| 250 | 8.60 ± 0.84 | 49.64 ± 1.52 | 5.06 ± 0.28 | 0.96 ± 0.01 | 0.15 ± 0.02 | 5.01 ± 0.02 | |
| Methanol molecules confined in the Ph-PMO pores | |||||||
| 315 | 24.06 ± 3.13 | 39.23 ± 0.95 | 7.53 ± 0.42 | 0.880 ± 0.002 | 0.167 ± 0.003 | 10.00 ± 0.07 | 10.78 ± 0.46 |
| 300 | 18.41 ± 2.48 | 43.43 ± 1.16 | 6.93 ± 0.41 | 0.886 ± 0.002 | 0.159 ± 0.003 | 10.00 ± 0.07 | |
| 285 | 15.76 ± 2.20 | 44.48 ± 1.32 | 6.49 ± 0.42 | 0.901 ± 0.002 | 0.138 ± 0.002 | 10.00 ± 0.06 | |
| 270 | 11.76 ± 1.41 | 45.03 ± 1.30 | 5.64 ± 0.33 | 0.911 ± 0.001 | 0.130 ± 0.002 | 10.00 ± 0.05 | |
| 255 | 8.98 ± 1.11 | 46.12 ± 1.54 | 4.99 ± 0.32 | 0.924 ± 0.001 | 0.118 ± 0.002 | 9.84 ± 0.05 | |
The motion becomes faster at high temperatures, as shown in Fig. 7(a) and (d), and the Lorentzian component in the spectrum is wider than that at 255 K, as shown in Fig. 6. The obtained measured diffusion coefficients of the methanol molecules in the OMC and Ph-PMO pores listed in Table 2 are also shown in Fig. S8. For the methanol molecules confined in the OMC pores (pore diameter 18.7 Å), as the temperature decreases from 315 to 255 K, the diffusion coefficient progressively decreases from 9.72 × 10−10 to 5.10 × 10−10 m2 s−1. On comparing the D values given in Table 2 with those of the bulk methanol at 298 K (D = 2.4 or 2.6 × 10−9 m2 s−1),33 we can conclude that the translational motion of the methanol entrapped in the OMC pores is significantly slower than that of the bulk liquid methanol. This result is due to the methanol molecules confined in the hydrophobic OMC pores, forming a monolayer adsorption. As a result, the axial chain structure of methanol by the hydrogen bond in the pores is enhanced, while for the bulk methanol, the methanol chains can freely undergo three-dimensional translational motion, leading to relatively loose interactions between the chains. Therefore, at the same temperature, the motion of the methanol molecules confined in the OMC pores becomes slow.
For 300 K, the obtained diffusion coefficient of the methanol molecules in the OMC pores is 8.35 × 10−10 m2 s−1, while for the water molecules, it is 21 × 10−10 m2 s−1.12 For the bulk water and methanol, the diffusion coefficients are 2.3 × 10−9 m2 s−1 (ref. 28) and 2.4 or 2.6 × 10−9 m2 s−1,33 respectively. The diffusion rate of the bulk methanol is quite similar to that of the bulk water, while under the same confinement conditions, the diffusion rate of water is almost 2.5 times higher than that of methanol. This result may be due to the following reasons: (1) the dynamic diameter of the water molecules (about 3 Å) is smaller than that of the methanol molecules (about 5 Å), allowing water molecules to adjust more flexibly to pore geometry constraints in OMC, while the methyl group of methanol causes steric hindrance. (2) Although both methanol and water can form hydrogen bonds, the three-dimensional hydrogen bond network of water has a relatively high dynamic equilibrium. This result implies that the confinement effect has a greater impact on the dynamic characteristics of the methanol molecules than on the water molecules.
For the methanol molecules confined in the Ph-PMO (pore diameter 30.0 Å) pores, as the temperature decreases from 315 K to 255 K, the diffusion coefficient progressively decreases from 24.06 × 10−10 m2 s−1 to 8.98 × 10−10 m2 s−1, which is higher than that of the methanol molecules confined in the OMC pores, as described above. In principle, when the methanol molecules are confined in the OMC and Ph-PMO pores, the hydrophobic pore walls of OMC only form weak van der Waals interactions with the methanol molecules. In contrast, the amphiphilic pore walls of Ph-PMO contain silanol hydroxyl groups that establish relatively strong hydrogen bonding interactions with the methanol molecules. However, methanol exhibits a relatively high diffusion rate in Ph-PMO, indicating that the diffusion of methanol in the confining materials is not only dependent on the inherent properties of the pores but also correlated with the pore diameter. Moreover, the diffusion coefficient is 24.06 × 10−10 m2 s−1 at 315 K, which is almost equal to the bulk methanol of 24 × 10−10 m2 s−1.33,34 This result is due to the ‘‘bulk-like’’ behavior observed when liquid is contained in the large capillary pores, which is in accord with the behavior of the water molecules confined in the Ph-PMO pores.13 Furthermore, the tortuosity value, which is the relationship of Dbulk/Dpore, for the methanol molecules confined in the OMC pores is 2.87 larger than 1.30 for the methanol molecules confined in the Ph-PMO pores at 300 K, indicating a more significant variation in the diffusion coefficient for the methanol molecules confined in the OMC pores compared with that of the bulk methanol, and with smaller hydrophobic pores exhibiting more pronounced confinement effects.
The residence time (τ0) and jump length (l) for the methanol molecules in the OMC and Ph-PMO pores at different temperatures were also obtained, as listed in Table 2. The jump length decreases from 5.18 to 4.58 Å and from 7.53 to 4.99 Å, respectively, as the temperature decreases for the methanol molecules confined in the OMC and Ph-PMO pores. The change range of the former is significantly smaller than that of the latter, indicating that smaller confined spaces lead to shorter jump distances of the methanol molecules, with their dynamics becoming less sensitive to temperature variations. Correspondingly, the τ0 progressively increases, demonstrating that the motion of the methanol molecules confined in the porous material becomes slower as the temperature decreases.
Fig. 7(b) and (e) display the Arrhenius plot of the diffusion coefficients of the methanol molecules confined in the OMC and Ph-PMO pores, showing the Arrhenius type of temperature dependence. The solid lines in Fig. 7(b) and (e) best fit to D = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT). The extracted activation energies (Table 2), Ea = (7.08 ± 0.16) kJ mol−1 for the methanol molecules in the OMC pores, are less than those of the water molecules (12.0 kJ mol−1) under identical conditions.12 This phenomenon may be attributed to the fact that water forms tightly clustered structures through intermolecular hydrogen bonds, facilitating the formation of multi-layered hydrogen-bond networks within OMC pores, which restricts molecular motion. When water participates in reactions, more hydrogen bonds need to be broken than those in methanol, thereby increasing the activation energy. In contrast, methanol (CH3OH) contains only one hydroxyl group (–OH), and its intermolecular hydrogen bonds are weaker than those in water. Additionally, the hydrophobic effect of the methyl group (–CH3) can further weaken the hydrogen-bond network. Within the OMC pores, the methanol molecules are more likely to break free from the hydrogen-bond constraints, resulting in a low energy barrier to overcome during reactions. In addition, the extracted activation energies (Table 2), Ea = (10.78 ± 0.46) kJ mol−1, for the methanol molecules in the Ph-PMO pores are also lower than those of the water molecules (17.2 kJ mol−1)13 in the same pores; the reason for this is the same as mentioned above.
exp(−Ea/kBT). The extracted activation energies (Table 2), Ea = (7.08 ± 0.16) kJ mol−1 for the methanol molecules in the OMC pores, are less than those of the water molecules (12.0 kJ mol−1) under identical conditions.12 This phenomenon may be attributed to the fact that water forms tightly clustered structures through intermolecular hydrogen bonds, facilitating the formation of multi-layered hydrogen-bond networks within OMC pores, which restricts molecular motion. When water participates in reactions, more hydrogen bonds need to be broken than those in methanol, thereby increasing the activation energy. In contrast, methanol (CH3OH) contains only one hydroxyl group (–OH), and its intermolecular hydrogen bonds are weaker than those in water. Additionally, the hydrophobic effect of the methyl group (–CH3) can further weaken the hydrogen-bond network. Within the OMC pores, the methanol molecules are more likely to break free from the hydrogen-bond constraints, resulting in a low energy barrier to overcome during reactions. In addition, the extracted activation energies (Table 2), Ea = (10.78 ± 0.46) kJ mol−1, for the methanol molecules in the Ph-PMO pores are also lower than those of the water molecules (17.2 kJ mol−1)13 in the same pores; the reason for this is the same as mentioned above.
To further comprehend the concept of the dynamic states distinguished by the mobility of the methanol molecules, we calculated the elastic incoherent structure factor (EISF), which was derived from the elastic and quasielastic components of the experimental data. The EISF is defined as the fraction of elastic intensity in the QENS spectra (A(Q) in eqn (2)), and due to the fact that molecules are either completely immobilized within the time scale of the instrument (fraction P0) or confined (fraction 1 − P0), they can only diffuse within the effective confinement radius (a).35 In Fig. S9 and S10, we show the EISFs derived from the QENS measurements as a function of Q at different temperatures. The decrease in the EISF with an increase in the temperature suggests that the fraction of immobile H atoms decreases. As shown in Fig. 7(a) and (d), it is found that the behavior of HWHM is characteristic of the diffusion of the methanol protons confined in a volume assimilated to a sphere with confinement radius a, which was confirmed by the fitting of EISF. For such a situation, EISF can be given by
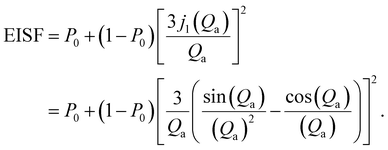 | (6) |
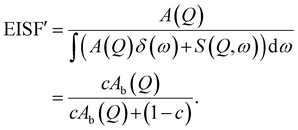 | (7) |
For the methanol molecules confined in the OMC and Ph-PMO pores, the values of c increase from 0.969 to 0.986 and 0.880 to 0.924, respectively, as the temperature decreases from 315 to 255 K, indicating that most of the methanol molecules in the microporous/mesoporous pores are in a bound state, with only a small portion of the methanol molecules being free. These bound methanol molecules participate in jump diffusion or fast dynamical processes, and the jump diffusion motion gradually becomes relatively slow as the temperature is decreased. The values of P0 (fraction of “immobile” hydrogen atoms) and a (confinement radius) for the methanol molecules in the OMC pores gradually decrease from 0.151 to 0.118 and 7.14 to 5.73 Å, respectively, implying that the jump diffusion motion of methanol molecules becomes slow and the jumping distance decreases. This result coincides well with the dynamic properties of the water molecules confined in the OMC pores. Conversely, the values of P0 for the methanol molecules in the Ph-PMO pores decrease from 0.167 to 0.118, revealing that the jump diffusion motion of the methanol molecules becomes slow. However, the values of the confinement radius (a) remain at 10.00 Å (approximately twice the diameter of methanol) until the temperature drops to 255 K, and then a decreases to 9.84 Å. This result suggests that in large pore mesoporous materials (30 Å), the confinement radius is only affected at relatively low temperatures (≤255 K), which is different from the situation when the methanol molecules are confined in the OMC pores.
In summary, based on the experimental phenomena described, we propose that the methanol molecules exhibit different dynamic behaviors in the OMC and Ph-PMO pores. Combining Fig. 5 and 6 reveals that, within the resolution range provided by the spectrometer, DNA, only one dynamic process is observable. This process proved jump diffusion based on the dependence of the HWHM of the Lorentzian fit, i.e., S(Q, E) in eqn (4). Any dynamic process that exceeds the time-domain or Q scale of the instrument will contribute to the elastic peak (A(Q) in eqn (2)) of the QENS spectrum. To investigate these processes, we analyzed an EISF. Although this method cannot obtain dynamic information, its Q dependence can be characterized as confined diffusion.5,37 By analyzing it, the confinement length and the fractions of the completely immobilized versus confined methanol molecules can be obtained. Theoretically, the EISF should approach one in the low-Q region, as processes in large-scale spaces are generally slow and only contribute to the elastic peak. However, as shown in Fig. 7(c) and (e), the EISF values in the low-Q region are less than one, indicating the presence of highly dynamic methanol molecules even at relatively large length scales.
4. Conclusions
The structure of capillary-condensed methanol molecules confined in Ph-PMO porous materials with phenyl groups embedded in a silica matrix (pore diameter 30.0 Å) at low temperatures (from 230 to 298 K) was obtained by LAXS measurements. The analysis results of the LAXS data showed that the structure of methanol consists of a monolayer of methanol on the surface and the hydrogen-bonded chains of methanol molecules at the central part of the pores. With a decrease in the temperature, the methanol chains in the Ph-PMO pores gradually become ordered; however, the degree of this enhancement with temperature is not as significant as that for the water molecules confined in the Ph-PMO pores. This result is achieved probably because the interaction between the methanol layers, such as the surface methanol monolayer and the methanol hydrogen-bonded chains in the pore center, mainly relies on the van der Waals forces between methyl groups rather than hydrogen bonds. In other words, the methanol structure cannot undergo three-dimensional evolution in the pores as the temperature decreases.The dynamics of the methanol molecules confined in the Ph-PMO (capillary-condensed conditions) and OMC (pore diameter 18.7 Å, monolayer conditions) pores at a low temperature (from 255 to 315 K) were characterized by QENS measurements. Comparing the dynamic properties of the methanol and water molecules under the same confinement conditions in the OMC pores shows that the confinement effect has a greater impact on the dynamic characteristics of the methanol molecules than on those of the water molecules. For the methanol molecules confined in the amphiphilic Ph-PMO of a large capillary pore, especially at 315 K, a “bulk-like” behavior was observed, which is in accord with the behavior of the water molecules confined in the Ph-PMO pores. Through the analysis of the jump length for the methanol molecules in the OMC and Ph-PMO pores, it was discovered that smaller confined spaces lead to shorter jump distances of the methanol molecules, with their dynamics becoming less sensitive to temperature variations. Correspondingly, the residence time progressively increases as the temperature decreases, demonstrating that the motion of the methanol molecules confined in the porous material becomes relatively slow. In addition, the plot of the diffusion coefficient of the methanol molecules confined in the OMC and Ph-PMO pores shows the Arrhenius type of temperature dependence. Owing to the different hydrogen-bond structures formed by the methanol and water molecules under the same confined conditions, the activation energies of the methanol molecules are lower than those of the water molecules. By analyzing the elastic incoherent structure factor, the confinement length and the fractions of the completely immobilized versus confined methanol molecules can be obtained. The mobile fraction exhibited jump diffusion, with a jump length consistent with a sphere having confinement radius a.
Author contributions
Hongyan Liu analyzed the data, wrote, and revised the manuscript. Zhuanfang Jing conceived the idea and revised the manuscript. Keke Chai revised the manuscript. Yongquan Zhou supervised the project and revised the manuscript. Koji Yoshida performed the LAXS experiments and revised the manuscript. Takeshi Yamada performed the QENS experiments and revised the manuscript. Toshio Yamaguchi conceived the idea, performed the LAXS and QENS experiments, analyzed the data, and revised the manuscript. All the authors discussed the results and contributed to the preparation of the manuscript.Conflicts of interest
The authors report no potential conflicts of interest.Data availability
The data supporting the findings of this study are available within the article and its supporting information (SI). Supplementary information: experimental X-ray scattering intensities, the details of LAXS data analysis, dynamic susceptabilities, fits of QENS spectra, fits of HWHM using the jump diffusion model, and diffusion coefficients of methanol in OMC and Ph-PMO. See DOI: https://doi.org/10.1039/d5cp03868e.Acknowledgements
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (CAS) (Grant No. XDB1130102), the Qinghai Provincial Science and Technology International Cooperation Special Project (Grant No. 2025-QY-813), the Fund for Young Team of the Qinghai Institute of Salt Lakes, CAS (Grant No. ISLJCTD-2022-04), and JSPS KAKENHI (Grant No. JP23550028). The neutron experiment at the J-PARC Materials and Life Science Experimental Facility was performed under a user program (Proposal No. 2013A0162). The authors thank the DNA spectrometer beamline scientists for their help with the experiments. We express our gratitude to Dr Yasutomo Goto and Dr Shinji Inagaki for providing the Ph-PMO samples.References
- T. D. Bennett, F. X. Coudert, S. L. James and A. I. Cooper, Nat. Mater., 2021, 20, 1179–1187 CrossRef CAS PubMed.
- Z. X. Wang, D. D. Wang, S. T. Wang and Y. Y. Song, Chin. J. Chromatogr., 2025, 43, 594–605 CrossRef CAS PubMed.
- S. K. Matam, C. A. Catlow, I. P. Silverwood and A. J. O’Malley, Top. Catal., 2021, 64, 699–706 CrossRef CAS.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- G. R. Acharya, M. Tyagi, E. Mamontov and P. M. Hoffmann, J. Phys. Chem. B, 2023, 127, 7384–7393 CrossRef CAS PubMed.
- S. K. Matam, I. P. Silverwood, L. Boudjema, A. J. O’Malley and C. A. Catlow, Philos. Trans. R. Soc., A, 2023, 381, 1–20 CrossRef PubMed.
- S. K. Matam, A. J. O’Malley, C. A. Catlow, S. Suwardiyanto, P. Collier, A. P. Hawkins, A. Zachariou, D. Lennon, I. Silverwood, S. F. Parker and R. F. Howe, Catal. Sci. Technol., 2018, 8, 3304–3312 RSC.
- T. Omojola, I. P. Silverwood and A. J. O’Malley, Catal. Sci. Technol., 2020, 10, 4305–4320 RSC.
- S. Takahara, S. Kittaka, T. Mori, Y. Kuroda, T. Takamuku and T. Yamaguchi, J. Phys. Chem. C, 2008, 112, 14385–14393 CrossRef CAS.
- K. Ito, A. Faraone, M. Tyagi, T. Yamaguchi and S. H. Chen, Phys. Chem. Chem. Phys., 2019, 21, 8517–8528 RSC.
- S. Inagaki, S. Guan, T. Ohsuna and O. Terasaki, Nature, 2002, 416, 304–307 CrossRef CAS PubMed.
- H. Liu, Z. Jing, Y. Zhou, T. Nagatoshi, K. Ito, K. Yoshida, T. Yamada and T. Yamaguchi, J. Mol. Liq., 2024, 415, 126316 CrossRef CAS.
- M. Aso, K. Ito, H. Sugino, K. Yoshida, T. Yamada, O. Yamamuro, S. Inagaki and T. Yamaguchi, Pure Appl. Chem., 2012, 85, 289–305 CrossRef.
- K. Morishige and K. Kawano, J. Chem. Phys., 2000, 112, 11023–11029 CrossRef CAS.
- T. Takamuku, H. Maruyama, S. Kittaka, S. Takahara and T. Yamaguchi, J. Phys. Chem. B, 2005, 109, 892–899 CrossRef CAS PubMed.
- T. Yamaguchi, K. Yoshida, P. Smirnov, T. Takamuku, S. Kittaka, S. Takahara, Y. Kuroda and M.-C. Bellissent-Funel, Eur. Phys. J.: Spec. Top., 2007, 141, 19–27 Search PubMed.
- T. Takamuku, M. Yamagami, H. Wakita, Y. Masuda and T. Yamaguchi, J. Phys. Chem. B, 1997, 101, 5730–5739 CrossRef CAS.
- S. Takahara, M. Nakano, S. Kittaka, Y. Kuroda, T. Mori, H. Hamano and T. Yamaguchi, J. Phys. Chem. B, 1999, 103, 5814–5819 CrossRef CAS.
- S. Tanaka, N. Nishiyama, Y. Egashira and K. Ueyama, Chem. Commun., 2005, 2125–2127 RSC.
- S. Tanaka, Y. Katayama, M. P. Tate, H. W. Hillhouse and Y. Miyake, J. Mater. Chem., 2007, 17, 3639–3645 RSC.
- E. P. Barret, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef.
- T. Yamaguchi, H. Sugino, K. Ito, K. Yoshida and S. Kittaka, J. Mol. Liq., 2011, 164, 53–58 CrossRef CAS.
- K. Yamanaka, T. Yamaguchi and H. Wakita, J. Chem. Phys., 1994, 101, 9830–9836 CrossRef CAS.
- K. Shibata, N. Takahashi, Y. Kawakita, M. Matsuura, T. Yamada, T. Tominaga, W. Kambara, M. Kobayashi, Y. Inamura, T. Nakatani, K. Nakajima and M. Arai, J. Phys. Soc. Conf., Proc., 2015, 8, 036022 Search PubMed.
- H. Seto, S. Itoh, T. Yokoo, H. Endo, K. Nakajima, K. Shibata, R. Kajimoto, S. Ohira-Kawamura, M. Nakamura, Y. Kawakita, H. Nakagawa and T. Yamada, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 3651–3660 CrossRef CAS PubMed.
- K. Yoshida, Y. Sanada, T. Yamaguchi, M. Matsuura, H. Tamatsukuri and H. Uchiyama, J. Mol. Liq., 2022, 366, 120218 CrossRef CAS.
- M. Bee, in Quasielastic neutron scattering: Principles and applications in solid state chemistry, biology, and material science, ed. A. Hilger, Bristol, 1988 Search PubMed.
- J. Teixeira, M. C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1913–1917 CrossRef CAS PubMed.
- X. J. Wu, Y. Y. Chen and T. Yamaguchi, J. Mol. Spectrosc., 2007, 246, 187–191 CrossRef CAS.
- T. Yamaguchi, K. Hidaka and A. K. Soper, Mol. Phys., 1999, 96, 1159–1168 CrossRef CAS.
- T. Yamaguchi, K. Hidaka and A. K. Soper, Mol. Phys., 1999, 97, 603–605 CrossRef CAS.
- M. Kardar, Statistical Physics of Fields, Cambridge University Press, 2007 Search PubMed.
- N. M. Gupta, D. Kumar, V. S. Kamble, S. Mitra, R. Mukhopadhyay and V. B. Kartha, J. Phys. Chem. B, 2006, 110, 4815–4823 CrossRef CAS PubMed.
- F. J. Bermejo, F. Batallan, E. Enciso, R. White, A. J. Dianoux and W. S. Howells, J. Phys.: Condens. Matter, 1990, 2, 1301–1316 CrossRef CAS.
- U. R. Shrestha, D. Bhowmik, J. R. Copley, M. Tyagi, J. B. Leão and X. Q. Chu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13886–13891 CrossRef CAS PubMed.
- K. Ito, K. Yoshida, M. C. Bellissent-Funel and T. Yamaguchi, Bull. Chem. Soc. Jpn., 2014, 87, 603–608 CrossRef CAS.
- J. Jacobsen, M. S. Rodrigues, M. T. Telling, A. L. Beraldo, S. F. Santos, L. P. Aldridge and H. N. Bordallo, Sci. Rep., 2013, 3, 2667 CrossRef PubMed.
| This journal is © the Owner Societies 2026 |