Deciphering competitive water–toluene adsorption mechanisms on oxide surfaces
Mouna Wissem
Guellil
 *,
Abderrahim
Choukchou-Braham
,
Chewki
Ziani-Cherif
and
Sanâa
El Korso
*,
Abderrahim
Choukchou-Braham
,
Chewki
Ziani-Cherif
and
Sanâa
El Korso
Laboratory of Catalysis and Synthesis in Organic Chemistry, Chemistry Department, University of Tlemcen, Tlemcen, Algeria. E-mail: wissemguellil.univtlm@gmail.com
First published on 18th November 2025
Abstract
Understanding how polar and nonpolar molecules compete for oxide surfaces is essential for controlling interfacial reactivity and hydrophobicity. Herein, we report the coupling of in situ FTIR spectroscopy with an extended IAST–Freundlich model to quantitatively probe water–toluene co-adsorption on SiO2, Al2O3, and TiO2. This integrated approach links vibrational fingerprints to thermodynamic parameters, revealing both site selectivity and surface restructuring under mixed-vapor conditions. Quantitative analysis shows that SiO2 exhibits the highest water uptake owing to its large surface area, while TiO2 features stronger but more localized hydroxyl interactions; Al2O3 displays intermediate, reversible adsorption governed by Lewis acidity. Spectral evolutions distinguish three competitive regimes: water displacement by toluene on SiO2, co-adsorption on Al2O3, and complete water-driven substitution on TiO2. The combined FTIR–IAST framework establishes a consistent hierarchy of adsorption affinities and offers a transferable strategy for quantitative spectroscopic evaluation of competitive adsorption on heterogeneous catalysts.
Introduction
Water rarely acts as a passive spectator in catalytic systems; it competes strongly with organic molecules for adsorption sites on oxide surfaces, reshaping interfacial equilibria at the molecular scale. Understanding this competition is essential for optimizing catalytic performance, selective separations, and the rational design of functional oxide materials.A persistent challenge in heterogeneous catalysis lies in the competitive adsorption between water and hydrocarbons, particularly under humid conditions where water can drastically modify adsorption equilibria and catalyst activity.1–8 Transition-metal oxides, such as SiO2, Al2O3, and TiO2, are widely employed due to their tunable acidity, hydrophilicity, and hydroxyl-group distribution.4–7 Similar Al2O3-based materials have been investigated for catalytic transformations, highlighting the importance of their surface chemistry and acid–base properties.9 However, the molecular mechanisms governing the competition between polar and nonpolar adsorbates remain poorly quantified, especially under realistic mixed-adsorbate environments.
The water/toluene pair provides an instructive model system: water forms strong hydrogen bonds with surface hydroxyls, whereas toluene interacts mainly through van der Waals forces with surface oxygen atoms.10 These contrasting adsorption modes enable the direct probing of site specificity, polarity effects, and surface restructuring phenomena.
Conventional techniques such as gravimetry and calorimetry10–12 provide only limited molecular insight. Fourier-transform infrared (FTIR) spectroscopy offers direct access to vibrational fingerprints of adsorbate–surface interactions,13–16 yet it lacks a quantitative thermodynamic framework to describe multicomponent equilibria. Comparable vibrational approaches have been applied to probe molecules and oxide interactions, including CO2 and methane activation on transition metal oxides.17
To address this gap, we have combined real-time FTIR spectroscopy with the ideal adsorbed solution theory (IAST) modeling to elucidate the competitive adsorption of water and toluene on SiO2, Al2O3, and TiO2. This integrated approach bridges spectroscopy and thermodynamics, providing quantitative insight into the hydrophilicity–hydrophobicity balance, surface site competition, and adsorption selectivity. Beyond the specific water–toluene system, the combined FTIR–IAST framework developed here can be readily extended to other hydrocarbon–water pairs and oxide supports relevant to liquid-phase oxidation, dehydration, or separation processes in industrial contexts,18–20 thereby guiding the design of catalysts and separation materials for humid or mixed-feed conditions.
Experimental
Materials
Tetraethyl orthosilicate (Si(OC2H5)4, Aldrich, 99.99%); aluminum tri-sec-butanolate (Al[OCH(CH3)C2H5]3, Aldrich, >99%); titanium propoxide (Ti[OCH(CH3)2]4, Sigma-Aldrich, 98%); nitric acid (HNO3, Aldrich, >99%); hydrochloric acid (HCl, 37%); acetic acid (CH3COOH, Aldrich, >99%); ethanol (CH3CH2OH, Aldrich, >99.99%); and 2-propanol (CH3–CHOH–CH3, Aldrich, >99%) were utilized without additional purification.Preparation
All catalysts were prepared through an acid-catalyzed sol–gel process, exemplified by the synthesis of SiO2 using the method outlined by Wang.21 In a beaker, 10.17 mL of tetraethyl orthosilicate (TEOS) was mixed with 7.85 mL of ethanol and 4 mL of nitric acid. The mixture was stirred for 15 minutes with the dropwise addition of 4.25 mL of nitric acid, and then stirring was continued for 2 hours. The resulting gel was dried in a sand bath at 60 °C for 12 hours. Subsequently, the product was further dried at 120 °C overnight and ultimately calcined at 400 °C for 4 hours with a heating rate of 5 °C min−1.Characterization of the catalysts
Diffractograms of the catalysts were obtained through X-ray diffraction (XRD) experiments performed on a Rigaku Mini Flex 600 diffractometer equipped with a copper anticathode (Cu Kα). The diffractograms were recorded at room temperature in the 2θ range between 10° and 80° with a step of 0.01° and an acquisition time of 2° min−1.The textural properties of the materials, including specific surface area, pore volume, and pore size, were determined using the nitrogen adsorption–desorption technique. Measurements were conducted using the NOVA 1000e device (Quantachrome Instruments).
The catalysts' acid sites, including type, number, and strength, were characterized by in situ IR spectroscopy using pyridine as a probe molecule. IR spectra were acquired using a Nicolet Magna 550 FTIR spectrometer (resolution: 4 cm−1, 128 scans). The sample, compressed into a disc (approximately 10–20 mg; 2 cm2), was activated under high vacuum (10−5 torr) at 400 °C for 2 hours and then cooled to room temperature. A saturating quantity of pyridine (∼0.5 torr) was introduced at this temperature for 10 minutes (equilibrium time). Subsequently, the temperature was gradually increased to desorb the pyridine, obtaining spectra that define the acid strength. Different spectra were generated by subtracting the spectra of the activated catalyst from the spectra obtained after pyridine adsorption (or desorption).
Pure gas adsorption: water/toluene
To evaluate the hydrophobic/hydrophilic properties of the oxides through the competitive adsorption of the gas mixture water/toluene, we first had to study the adsorption of pure components. To achieve this, a self-supporting material sample disk (2 cm2, approximately 15–20 mg) was subjected to mechanical compression (below 500 kg cm−2). Subsequently, this compressed disk was positioned within a quartz infrared cell for heating and vacuum treatment to activate the catalyst (at 450 °C overnight, under a pressure of 10−5 torr) and adsorb precise amounts of gases. Once the adsorption equilibrium was reached (15 min), various spectra obtained were subtracted from the spectrum of the activated catalyst. These spectra were collected to assist us in qualitatively studying the interactions of adsorbates with our materials and quantifying the adsorption of each gas on the surface of the oxides by measuring the intensity of the adsorption peaks.Complementary information regarding the preparation of self-supported pellets, calibration of absorbance intensities and estimation of experimental uncertainties is provided below to strengthen the quantitative accuracy of the FTIR data. Integrated absorbances were normalized to the specific surface area of each oxide to account for the large differences in textural properties among SiO2, Al2O3, and TiO2. The molar absorption coefficients (ε) used for the quantitative estimation of adsorbed species were taken from literature data for the selected vibrational bands (νOH for H2O and νCH or νCC for toluene).22,23 Repeated measurements performed on the same material showed excellent reproducibility in both band intensities and isotherm shapes. The FTIR cell was evacuated before each experiment, under secondary vacuum when the same probe molecule was reused, and through repeated pumping cycles when switching between H2O and toluene. Background spectra were systematically collected before adsorption, and all spectra were processed by subtraction of the pre-treated sample reference to eliminate any residual contributions from gas impurities (CO2, H2O). Considering the uncertainties associated with the literature ε values and baseline corrections, the estimated error on the absolute quantities adsorbed is within ±20%, which does not affect the relative comparison between samples.24
Theoretical models of adsorption
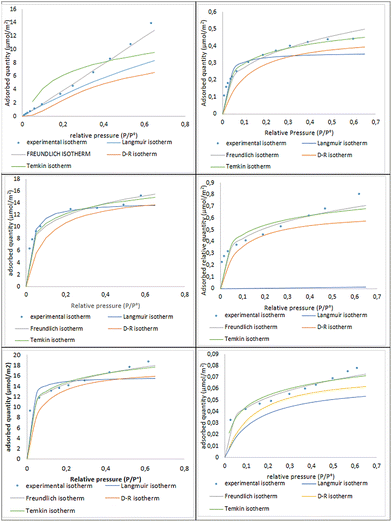
By fitting our experimental data to various theoretical models, we aimed to deepen the understanding of adsorption phenomena, guide the design of adsorbent materials, and facilitate the analysis and prediction of experimental results. Based on the nature of our adsorbents and the data collected from the experiments, we selected four two-parameter theoretical models, detailed below.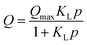 | (1) |
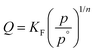 | (2) |
Q = QD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−BDε2) exp(−BDε2) | (3) |
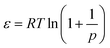 | (4) |
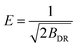 | (5) |
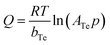 | (6) |
Competitive adsorption of water/toluene
The competitive adsorption experiment of water and toluene was conducted using the same experimental setup and under identical temperature and equilibrium time conditions as for pure component adsorption. The activated adsorbent was exposed to different partial pressures, allowing the observation of the influence of each adsorbate on the adsorption of the other. To achieve different partial pressures, we began by adsorbing approximately 15 torr of water. Once equilibrium was reached, the toluene valve was opened for adsorption, and the compartment valve was used to release some water, maintaining a total pressure close to 15 torr. This process increases the toluene amount as the water amount decreases. The same protocol was then applied in reverse, starting with toluene adsorption followed by water, resulting in an increase in water amount as the toluene amount decreased. After reaching equilibrium, spectra were collected, and each component was identified and quantified by integrating characteristic peaks.Mixture adsorption model predictions
Two types of behaviour can be encountered when presenting the adsorption isotherm in a binary mixture. Type 1 behaviour corresponds to weak preferential adsorption of component i relative to j, while type 2 behaviour represents strong preferential adsorption of component i relative to j. In the latter case, no classical form of the international union of pure and applied chemistry (IUPAC) classification adequately describes the isotherm of molecule j.In our study, we have used two theoretical models to describe the competitive adsorption of a binary mixture: the generalized Langmuir model and the ideal adsorbed solution theory (IAST), which, among other parameters, incorporates Freundlich parameters.
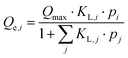 | (7) |
The widely recognized IAS theory has undergone comprehensive scrutiny in the literature.36 The theory posits that the adsorbed phase behaves as an ideal solution of the adsorbed components, and the reduced spreading pressure 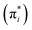 of all components in the mixture, in their standard states, is equivalent to the reduced spreading pressure of the adsorbed mixture (π*).
of all components in the mixture, in their standard states, is equivalent to the reduced spreading pressure of the adsorbed mixture (π*).
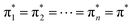 | (8) |
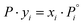 | (9) |
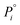 is the pressure of the pure component i at the same spreading pressure of the mixture, P is the total adsorptive pressure, and yi and xi are the mole fractions of component i in the gas (vapor) phase and in the adsorbed phase, respectively.37
is the pressure of the pure component i at the same spreading pressure of the mixture, P is the total adsorptive pressure, and yi and xi are the mole fractions of component i in the gas (vapor) phase and in the adsorbed phase, respectively.37
The following conditions38,39 were then applied to estimate the composition of the adsorbed phase:
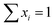 | (10) |
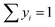 | (11) |
| ni = nT·xi | (12) |
Results and discussion
Characterization
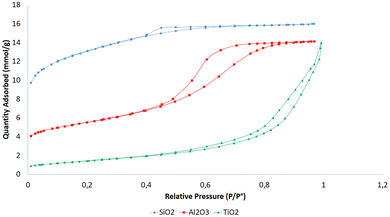
XRD patterns for SiO2, Al2O3, and TiO2 samples are depicted in Fig. 1. The SiO2 diffractogram displays a single broad peak around 2θ = 24°, indicating the amorphous nature of silica.41 The Al2O3 spectrum reveals the presence of boehmite AlO(OH), though it is not well-crystallized.42 Finally, the TiO2 spectrum exhibits characteristic peaks of the anatase phase at 2θ = 25°, 37°, 72°, 48.08°, 53.81°, 54.61°, 62.57° and 70.21°, corresponding to planes (101), (004), (200), (105), (211) (204), (116), and (220), respectively.43The textural properties of the samples were analyzed using N2 adsorption isotherms at −200 °C (Fig. 2). Specific surface areas, as well as micro-, meso-, and total pore volumes, are summarized in Table 1. The adsorption isotherms exhibit a type IV classification according to IUPAC standards,44 indicating mesoporous characteristics. TiO2 shows an H1-type hysteresis loop, suggesting a broad and uniform pore size distribution,45,46 whereas SiO2 and Al2O3 exhibit H2-type loops, characteristic of interconnecting mesopores.45
| SiO2 | Al2O3 | TiO2 | |
|---|---|---|---|
| A BET (m2 g−1) | 596 | 286 | 119 |
| D (nm) | 3.95 | 6.37 | 14.61 |
| V total (cm3 g−1) | 0.29 | 0.52 | 0.48 |
| Acidity of Lewis (µmol g−1) | 0 | 323 | 196 |
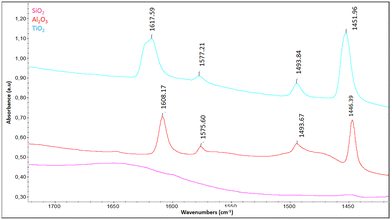
The analysis of the acidity of the mesoporous SiO2, Al2O3, and TiO2 materials via pyridine adsorption, followed by IR spectroscopy, revealed significant differences among these materials in terms of the nature and number of acidic sites. Fig. 3 illustrates the IR spectra of the materials after pyridine desorption at 150 °C, a temperature at which physisorbed pyridine is removed. The results show that for SiO2, no characteristic bands of Brønsted or Lewis acidity are observed, confirming that silica is a neutral material, as is widely reported in the literature.47 In contrast, the spectrum of Al2O3 exhibits four characteristic bands at 1448, 1492, 1576, and 1614 cm−1, attributed to Lewis sites, and potentially mixed Brønsted–Lewis sites around 1492 cm−1. The persistence of the bands at 1455 and 1623 cm−1 up to 250 °C suggests good thermal stability of the Lewis sites, with a possible contribution from a small amount of Brønsted sites. Quantitatively, alumina shows a high number of Lewis sites at 150 °C (323 µmol g−1), which decreases to 161 µmol g−1 at 250 °C, reflecting the progressive desorption of weakly bound pyridine molecules. It is worth noting that the calcination protocol strongly governs the surface chemistry of these oxides. The chosen treatment temperature ensures partial dehydroxylation without inducing structural phase transitions, thus maintaining comparable textural properties among samples. Calcination under more severe or milder conditions would modify the crystalline structure and the distribution of surface hydroxyls, leading to different proportions and strengths of acid sites.48,49 These results are consistent with reports on mesoporous alumina in the literature, where similar values have been observed.50
For TiO2, the spectrum displays characteristic bands at 1445, 1491, 1575, and 1604 cm−1, confirming the predominance of Lewis acid sites (Ti4+) and the possible coexistence of mixed Brønsted–Lewis sites near 1491 cm−1. Upon heating to 200 °C, these bands become less resolved, consistent with the desorption of weakly bound pyridine and spectral broadening effects. Quantitatively, TiO2 exhibits a Lewis acidity of 196 µmol g−1 at 150 °C, decreasing to 63 µmol g−1 at 250 °C, indicating lower thermal stability of its acidic sites compared with alumina.51
This attenuation in Lewis-band intensity agrees with DFT and FTIR studies reporting pyridine coordination to Ti4+ centers and their susceptibility to surface hydroxylation and carbonate contamination.47,52 However, the persistence of residual Ti4+–pyridine bands after calcination suggests that rehydroxylation does not fully neutralize Lewis acidity, reflecting a slightly higher thermal robustness in our TiO2 samples than typically observed for mesoporous titania.48
Thus, these results highlight a hierarchy in the acidity of the studied materials, with Al2O3 exhibiting the highest acidity, followed by TiO2, and finally SiO2, which is neutral, as shown in Table 1. The possible presence of mixed sites, suggested by the bands around 1490 cm−1, may contribute to specific catalytic properties, particularly for reactions where interactions with both Brønsted and Lewis sites are critical. Finally, the mesoporous nature of these materials enhances the accessibility of acidic sites, further increasing their appeal for catalytic applications, as confirmed by several studies.53
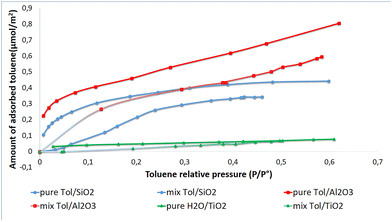
Adsorption of pure gases
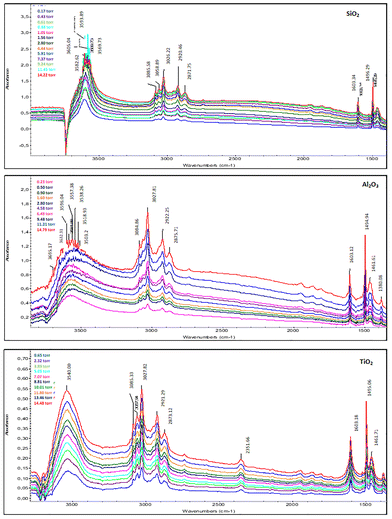
For SiO2, the OH stretching bands (νsym, νasym) between 3700 and 2600 cm−1 highlight diverse interactions, ranging from isolated silanols (sharp band at 3747 cm−1) to OH groups involved in extensive hydrogen-bonded networks.58 The progressive consumption of isolated silanols is evidenced by the marked decrease and red shift of the 3747 cm−1 band.59,60 Concurrently, the broadening of the νOH bands reflects increased hydrogen bonding. These findings confirm the strong hydrophilic nature of SiO2 and the formation of a dense hydrogen-bonded network under water vapor, consistent with earlier studies.61 The H2O bending band at 1635 cm−1 further supports the presence of molecularly adsorbed water, with its intensity increasing with humidity.
For Al2O3, bands in the 3500–3600 cm−1 region, characteristic of strongly bound OH vibrations, suggest water–surface interactions dominated by hydrogen bonding. Unlike SiO2, no distinct band corresponds to isolated hydroxyls, suggesting their absence or masking due to competitive interactions. The broad intensity observed in this region reflects a high water retention capacity,62 though the noisy and saturated spectra indicate interpretative complexity, potentially due to strong polarization effects of water molecules on acidic sites. The pronounced band at 1630–1640 cm−1 further confirms molecular water adsorption. These results align with the literature, where Al2O3 is described as an intermediate material,63,64 capable of significant water adsorption but with limited specificity in distinguishing interaction types.
For TiO2, the spectrum exhibits similarities to Al2O3 in the OH region but also reveals distinctive behaviors. A sharp band at 3800 cm−1, attributed to isolated hydroxyls on active sites, diminishes rapidly with increasing humidity, indicating the high reactivity of these sites toward water. Additionally, a broad band between 3200 and 3400 cm−1 illustrates the formation of hydrogen-bonded networks at higher humidity. Notably, the appearance of a band at 2380 cm−1, linked to asymmetric vibrations of confined CO2, signals residual interactions between the material and external molecules.65 This could indirectly indicate a partially modified or contaminated surface, a hypothesis frequently discussed in studies on TiO2.14 Finally, the 1640 cm−1 band indicates the bending of adsorbed water, with a more moderate intensity compared to Al2O3.
These findings underscore the pivotal role of surface chemistry in governing water adsorption. SiO2 facilitates hydrogen bonding through its silanol groups, while Al2O3 and TiO2 involve more complex interactions due to their acidic hydroxyls and active sites. The gradual evolution of spectral features with increasing water vapor pressure also highlights a transition from molecular adsorption to stronger interactions, and in some cases, localized capillary condensation, particularly for Al2O3. These observations align with existing literature while offering additional insights into the unique behaviors of each material.
The extent and nature of water adsorption are intrinsically linked to the textural and chemical properties of the oxides. The high surface area of SiO2 enhances its ability to form extensive hydrogen-bonded networks, whereas the larger pore diameters of Al2O3 and TiO2 influence both water retention and capillary condensation effects. Additionally, the presence of Lewis acid sites on Al2O3 and TiO2 introduces specific interactions, modifying the adsorption dynamics compared to the purely physisorptive behavior observed for SiO2. These combined effects contribute to the observed spectral variations, particularly in the OH stretching region, where differences in intensity and band broadening reflect distinct water–surface interactions across the materials.
Upon exposure to water vapor, dried surfaces engage in continuous interactions with gaseous molecules, leading to water condensation. The O–H stretching vibrations, forming a broad band around 3400 cm−1, reflect contributions from both isolated and hydrogen-bonded hydroxyl groups. This region is often challenging to interpret due to overlapping signals and contrasts with the sharper and more distinct H–O–H bending band at approximately 1645 cm−1. The latter offers a reliable measure for quantifying adsorbed water, reducing uncertainties inherent to the O–H stretching region.66,67
These differences are closely related to the textural and chemical properties of the materials. Despite its high specific surface area (596 m2 g−1) and narrow pores (3.95 nm), SiO2 exhibits limited adsorption, likely due to the absence of Lewis acid sites and its strong hydrophilicity, which preferentially interacts with polar molecules rather than toluene.73 In contrast, Al2O3, with a lower specific surface area (286 m2 g−1) but a high density of Lewis acid sites (323 µmol g−1), shows enhanced adsorption, as Lewis sites play a crucial role in interacting with the π-electrons of toluene.74,75 TiO2, despite having the lowest specific surface area (119 m2 g−1) and an intermediate density of Lewis acid sites (196 µmol g−1), still exhibits notable adsorption, likely facilitated by its wider pores (14.61 nm), which improve molecular accessibility.76
These findings align with literature reports, which emphasize that adsorption efficiency is governed not only by surface area but also by surface acidity and pore structure.77 While SiO2 features a mesoporous structure, its lack of Lewis acid sites limits strong interactions with toluene. Al2O3 benefits from pronounced surface acidity, enhancing adsorption through π-electron interactions. TiO2 highlights the critical role of molecular accessibility, as its larger pores facilitate the diffusion and interaction of adsorbates. Therefore, optimizing adsorption performance for applications in separation and catalysis requires a balanced design that integrates specific surface area, acidity, and pore accessibility.
To quantify adsorption from FTIR spectra, we used an adapted form of the Beer–Lambert law:
| A = ε·l·c | (13) |
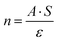 | (14) |
This methodological approach ensures robust and reproducible adsorption isotherms, minimizing uncertainties associated with overlapping signals. Such FTIR-based quantification techniques have been extensively validated in the literature for studying adsorption on porous materials and heterogeneous catalysts.79 The estimated uncertainty of ±20% in the absolute quantification, mainly arising from the use of literature ε values and baseline correction, does not affect the comparative trends observed among materials, as the same calibration and normalization procedures were systematically applied.
Table 2 summarizes the linearization parameters and statistical metrics of the different theoretical models studied.
| Parameters | Water | Toluene | ||||
|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | TiO2 | SiO2 | Al2O3 | TiO2 | |
| Langmuir model | ||||||
| Q max (µmol m−2) | 9.10 | 14.18 | 15.76 | 0.36 | 0.52 | 0.06 |
| K L (m2 µmol−1) | 0.62 | 42.87 | 85.77 | 52.74 | 0.04 | 7.17 |
| R 2 | 0.996 | 0.976 | 0.814 | 0.924 | 0.773 | 0.788 |
| RMSE | 2.14 | 0.65 | 1.59 | 0.05 | 0.49 | 0.02 |
| AIC | 22.23 | −2.67 | 12.33 | −74.28 | −10.03 | −77.25 |
| Freundlich model | ||||||
| K F (µmol m−2 kPa1/n) | 20.04 | 17.12 | 19.44 | 0.57 | 0.79 | 0.08 |
| N | 0.98 | 4.44 | 5.41 | 3.12 | 3.68 | 3.59 |
| R 2 | 0.998 | 0.965 | 0.984 | 0.988 | 0.966 | 0.951 |
| RMSE | 0.43 | 0.55 | 0.41 | 0.02 | 0.04 | 0.003 |
| AIC | −16.1 | −5.57 | −12.09 | −104 | −59.46 | −109.8 |
| Dubinin–Radushkevich model | ||||||
| Q D (µmol m−2) | 9.35 | 15.02 | 16.95 | 0.44 | 0.62 | 0.069 |
| E (kJ mol−1) | 3839 | 7593 | 8948 | 7004 | 7950 | 6798 |
| R 2 | 0.985 | 0.921 | 0.993 | 0.931 | 0.994 | 0.989 |
| RMSE | 2.92 | 2.68 | 2.31 | 0.08 | 0.12 | 0.01 |
| AIC | 29.73 | 19.80 | 19.07 | −62.45 | −38.20 | −86.28 |
| Temkin model | ||||||
| b T (J mol−1) | 42.58 | 947.77 | 1994.88 | 375.88 | 490.83 | 222.32 |
| A (KPa−1) | 864 | 1062 | 1008 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 027 027 |
173![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378 378 |
| R 2 | 0.776 | 0.982 | 0.944 | 0.990 | 0.872 | 0.880 |
| RMSE | 2.09 | 0.39 | 0.66 | 0.14 | 0.06 | 0.004 |
| AIC | 21.75 | −11.14 | −3.55 | −46.29 | −51.14 | −102.7 |
For toluene adsorption, SiO2 shows low capacity but high affinity,87 suggesting effective retention of toluene in limited quantities. This behavior can be ascribed to the weak polarity of toluene, which interacts primarily via van der Waals dispersion forces with non-functionalized silica surfaces.88,89 Conversely, Al2O3 exhibits the highest adsorption capacity but the lowest affinity,90 likely due to the presence of moderately polar Lewis sites that provide more available adsorption sites without strong specific interactions, thereby reducing overall affinity.12 TiO2, with its crystalline structure and pore distribution, demonstrates the lowest adsorption capacity and moderate affinity.
For toluene, KF values indicate that Al2O3 has the highest adsorption capacity, while TiO2 has the lowest. The N values suggest favorable adsorption across all oxides, with Al2O3 being slightly more favorable than SiO2 and TiO2. Notably, hydrophilicity is inversely proportional to the total pore volume (Table 1), highlighting the role of pore accessibility in water retention.93 The toluene adsorption trend (Al2O3 > SiO2 > TiO2) further confirms that oleophilicity does not necessarily correlate with hydrophobicity.94 Toluene adsorption on Al2O3 is enhanced by Lewis acid sites (Al3+),95 whereas SiO2 interacts mainly through van der Waals forces. TiO2, with its less interactive surface, exhibits the lowest toluene adsorption.
Statistical evaluation of isotherm fitting highlights the Freundlich model as the most suitable for the majority of materials. Higher R2 values indicate superior fit compared to Langmuir, and lower RMSE values, measuring the average deviation between experimental and predicted values, confirm better predictive accuracy, particularly for water adsorption. Akaike information criterion (AIC) values further support this trend, showing a stronger alignment with the Freundlich model. This is further illustrated in Fig. 6, where the experimental isotherms closely follow the Freundlich predictions, particularly at low and moderate pressures, while deviations are more pronounced for the Langmuir model at higher pressures.
 | ||
| Fig. 6 Theoretical models compared to experimental results for the adsorption isotherms of simple components, water and toluene, on oxides. | ||
For toluene, Freundlich again provides the best fit, as evidenced by lower RMSE and AIC values. In contrast, the Langmuir model exhibits limitations, especially for TiO2. The overall analysis suggests that the Freundlich model best describes adsorption on heterogeneous surfaces with variable site energies, unlike Langmuir's monolayer assumption. This indicates that the studied materials possess a diverse range of active sites, likely associated with cation coordination and accessible hydroxyl groups.
Competitive adsorption
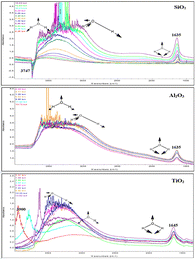
The competitive adsorption between water and toluene is strongly influenced by the surface properties of the oxides, particularly their hydrophilicity, porosity, and Lewis acidity. The FTIR spectral analysis (Fig. 7) highlights the critical role of adsorption affinity and the sequence of introduction in determining selective interactions. At the molecular scale, the evolution of the IR bands reflects both the competition for surface sites and the restructuring of the interfacial hydrogen-bond network upon displacement.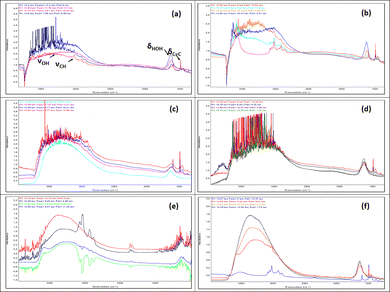 | ||
| Fig. 7 FTIR spectra of competitive adsorption: water-first (a), (c) and (e) vs. toluene-first (b), (d) and (f) on SiO2, Al2O3, and TiO2, respectively. | ||
For SiO2, the high specific surface area (Table 1) and the presence of silanol groups promote moderate water adsorption, despite its low affinity. This limited hydrophilicity, combined with the apolar nature of toluene, allows toluene to progressively replace water when introduced second. The corresponding attenuation of the νOH band and the growth of aromatic νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vibrations confirm the stepwise displacement of weakly bound water molecules by toluene. Conversely, when toluene is adsorbed first, the incomplete recovery of the νOH intensity upon water introduction demonstrates that water cannot fully reoccupy the same sites, revealing a strong site-blocking effect and limited reversibility. This behaviour aligns with the Freundlich isotherm, characteristic of weakly specific and reversible adsorption.101,102
C vibrations confirm the stepwise displacement of weakly bound water molecules by toluene. Conversely, when toluene is adsorbed first, the incomplete recovery of the νOH intensity upon water introduction demonstrates that water cannot fully reoccupy the same sites, revealing a strong site-blocking effect and limited reversibility. This behaviour aligns with the Freundlich isotherm, characteristic of weakly specific and reversible adsorption.101,102
In contrast, Al2O3 exhibits a more balanced competitive adsorption due to its moderate surface area and higher Lewis acidity. Persistent νOH bands after toluene introduction indicate strong interactions of water with Lewis sites, while the appearance of aromatic δC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bands suggests partial co-adsorption. This simultaneous presence of both signatures indicates that the two molecules can coexist on distinct but energetically coupled sites, implying limited displacement and local restructuring of the hydrogen-bond network around the coordinated water. Even when toluene is adsorbed first, water can effectively replace it, reflecting the polar nature of Al2O3 and moderate competition compared to SiO2.103,104
C bands suggests partial co-adsorption. This simultaneous presence of both signatures indicates that the two molecules can coexist on distinct but energetically coupled sites, implying limited displacement and local restructuring of the hydrogen-bond network around the coordinated water. Even when toluene is adsorbed first, water can effectively replace it, reflecting the polar nature of Al2O3 and moderate competition compared to SiO2.103,104
TiO2, despite its lower surface area and larger pore size, strongly favors water adsorption. FTIR spectra reveal negative toluene bands in competitive conditions, highlighting TiO2's high hydrophilicity and strong interaction with water via Lewis acid sites and a hydroxylated surface network. The concurrent recovery of intense νOH stretching bands is evidence of surface reorganization upon co-adsorption, where hydrogen-bonded networks are re-established and toluene is fully displaced. In the reverse sequence, water displaces toluene entirely, underscoring TiO2's selective adsorption of polar molecules. This complete spectral inversion illustrates a dynamic restructuring of the surface, confirming TiO2's strong preference for water and the instability of adsorbed toluene under humid conditions. In the reverse sequence, water displaces toluene entirely, underscoring TiO2's selective adsorption of polar molecules. Such reversible replacement and reformation of OH groups illustrate a molecular-level reorganization of the surface, typical of amphoteric oxides and consistent with recent spectroscopic investigations of molecule–oxide interactions.18
These molecular-scale spectral evolutions collectively demonstrate that the competitive behavior is not limited to adsorption strength but also involves site accessibility, hydrogen-bond rearrangement, and surface reorganization, which govern the observed selectivity trends among the three oxides.
To derive competitive adsorption isotherms from FTIR spectra, the contribution of gas-phase species was first subtracted to isolate the adsorbed fraction of each component. Quantification was then performed by integrating the characteristic bands of water (1760–1560 cm−1) and toluene (1514–1480 cm−1), carefully selecting regions to prevent spectral overlap. The resulting integrated absorbance values were converted into adsorbed amounts using the adapted Beer–Lambert relation (eqn (14)), allowing for the reliable estimation of surface coverage.
Fig. 8 and 9 further corroborate these findings through adsorption isotherm analysis. For water adsorption (Fig. 8), competitive isotherms generally show reduced uptake compared to pure-component adsorption, particularly on SiO2, where the isotherm transitions from linear to type III. This shift suggests a change in adsorption mechanisms that is likely driven by displacement or partial inhibition due to toluene co-adsorption.105 Conversely, Al2O3 and TiO2 exhibit increased water uptake under competitive conditions, which may result from the preferential adsorption of water over toluene on Lewis acid sites and possible exclusion effects that increase access to hydroxylated domains.106,107 This behavior might also reflect the limited accessibility of non-polar molecules like toluene to polar surface regions, indirectly favoring water adsorption.108
For toluene adsorption (Fig. 9), uptake decreases across all materials, reflecting strong competition with water for adsorption sites. The reduction is most pronounced on TiO2, with the maximum uptake decreasing by approximately 68% under competitive conditions, likely due to its strong hydrophilicity and high affinity for water,109 which hinders toluene access to active sites. On SiO2 and Al2O3, toluene uptake remains more significant but still declines under competitive conditions, likely due to partial site-sharing and surface polarity mismatch.
These observations emphasize the critical role of surface chemistry in governing competitive adsorption. On SiO2 and Al2O3, relatively reversible adsorption allows displacement between water and toluene depending on their partial pressures and surface affinities. In contrast, TiO2's strong hydration tendency and the stability of water adsorption make the replacement of water by toluene less favorable, leading to nearly irreversible water-dominated surface coverage. This complex interplay between adsorbate–adsorbent and adsorbate–adsorbate interactions determines adsorption selectivity and competition in mixed systems.
Mixture adsorption model predictions
In order to accurately study the competitive adsorption of water and toluene on SiO2, Al2O3, and TiO2, two theoretical prediction models were tested: the generalized Langmuir and the IAST–Freundlich model. The IAST–Freundlich model was selected due to its ability to incorporate the Freundlich isotherm. The latter was selected because it integrates the empirical Freundlich isotherm, previously identified as the best descriptor of pure-component adsorption.102 This approach combines the spreading pressure formalism of IAST with the heterogeneity of Freundlich adsorption. It thus offers a flexible representation of non-ideal competition on surfaces where adsorption sites are not uniform.110 The spreading pressure equation used in the calculations is as follows: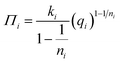 | (15) |
A graphical comparison between models and experiments (Fig. 10 and 11) confirms that the IAST–Freundlich model better reproduces the data. In contrast, the Langmuir model underestimates adsorption at higher pressures because it cannot represent multilayer adsorption or cooperative effects. This limitation is consistent with previous reports showing that Langmuir-type approaches fail to capture competitive adsorption when intermolecular interactions become significant.113
Some deviations persist for the H2O/Al2O3 system at low pressures, where the model overestimates adsorption. This discrepancy is attributed to the strong Lewis acidity of Al2O3, which enhances water interaction at low coverage.114 Similarly, the overestimation of toluene uptake on SiO2 and Al2O3 reflects the limited representativity of pure-component data under true competition. The FTIR spectra confirm that toluene adsorption is hindered by water occupying active sites—an effect that the model cannot fully capture.115
Although the IAST–Freundlich approach provides a convenient framework for describing competitive adsorption, it remains an empirical extension of the Freundlich formalism rather than a fully thermodynamic IAST treatment.115,116 In particular, it assumes site independence and neglects lateral interactions between adsorbed molecules, while representing the solid by smoothed single-component isotherms that overlook surface energy heterogeneity.117 Such simplifications may lead to deviations at high coverages or in confined mesoporous domains, where molecular orientation, pore accessibility, and trapping effects become significant. Despite these limitations, the model remains a valuable sensitivity tool for highlighting the interplay between chemical affinity and textural accessibility in determining apparent hydrophobicity.118
Ultimately, the IAST–Freundlich model demonstrates superior predictive capacity when compared to the Langmuir model, particularly for systems where competitive interactions and surface-specific effects play a dominant role. The combination of IR spectral data and theoretical modeling underscores the importance of considering molecular-level interactions for a better understanding of the adsorption dynamics in mixed systems. This integrative approach highlights the unique contribution of this study in bridging experimental and theoretical insights.119
To facilitate direct comparison between materials, Table 3 compiles the main qualitative and quantitative features of water and toluene adsorption on SiO2, Al2O3, and TiO2, under both pure and competitive conditions, highlighting the influence of surface chemistry on adsorption selectivity.
| Oxide | Water adsorption (pure) | Toluene adsorption (pure) | Competitive behaviour (water/toluene) | Dominant surface features |
|---|---|---|---|---|
| SiO2 | Moderate capacity (KF↑, N ≈ 1). Linear isotherm. Adsorption occurs mainly via hydrogen bonding on silanols. | Intermediate capacity (KF↑). Favorable adsorption via weak van der Waals and OH–π interactions. | – Toluene replaces weakly adsorbed H2O | High surface area; abundant silanols; no Lewis acidity. |
| – Shift from hydrophilic to oleophilic behaviour | ||||
| – Limited reversibility | ||||
| Al2O3 | Lower capacity (KF↓). L-type isotherm; strong interaction with Lewis acid sites (Al3+). | Highest capacity (KF↑↑). Strong Lewis–π and dispersion interactions. | – Co-adsorption regime: both molecules retained | Moderate surface area; mixed acidity; stable Lewis sites. |
| – Nearly balanced selectivity and reversible exchange | ||||
| TiO2 | High capacity (KF↑). L-type isotherm; strong H-bonding with surface hydroxyls. | Lowest capacity (KF↓). Weak physisorption on Ti–O–Ti domains. | – H2O completely displaces toluene | Amphoteric surface; highly hydroxylated; strong Lewis acidity. |
| – Shift to irreversible water selectivity | ||||
| – Surface rehydroxylation |
Conclusions
This study provides an in-depth analysis of water/toluene competitive adsorption on oxides commonly used in heterogeneous catalysis. Beyond the conventional characterization of adsorption properties, our work stands out by combining IR spectroscopy with advanced modeling (IAST), enabling a more refined understanding of adsorption mechanisms under competitive conditions. The spectroscopic approach offers direct experimental validation of theoretical models, highlighting the need to consider real interaction dynamics at catalytic surfaces.Our findings demonstrate that the strong hydrophilicity of TiO2 and Al2O3 may hinder their performance in humid environments, whereas SiO2 appears to be a more suitable support under such conditions. The successful application of the IAST model further underscores the necessity of moving beyond classical isotherms to accurately predict competitive adsorption. By integrating spectroscopic and modeling techniques, this study opens new avenues for the rational optimization of catalytic supports, ensuring greater stability and selectivity in real-world applications where water and hydrocarbons are simultaneously present. The integrated spectroscopic–modeling approach developed in this work thus offers a transferable framework for understanding and predicting competitive adsorption phenomena on oxide surfaces, with potential relevance to catalytic and separation operations involving other hydrocarbon–water systems.
Future work and perspectives
This study provides a detailed picture of competitive water–toluene adsorption on oxide surfaces; however, several aspects deserve further exploration. In future work, in situ FTIR spectroscopy under liquid-phase oxidation or dehydration reaction conditions, systems routinely investigated within our group, could directly reveal the evolution of surface species and the dynamic interplay between adsorbed molecules and active sites. Moreover, density functional theory (DFT) calculations will be pursued to predict IR spectra from realistic surface models, enabling a more rigorous assignment of vibrational features and a quantitative link between experimental and theoretical adsorption energies. Such combined in situ and computational approaches will provide a deeper, time-resolved understanding of competitive adsorption and site restructuring phenomena relevant to catalytic and separation processes.Author contributions
MWG: conceptualization, methodology, investigation, formal analysis, data curation, validation, visualization, writing – original draft, and writing – review & editing. ACB: conceptualization, supervision, project administration, funding acquisition, and writing – review & editing. CZC: supervision and resources. SE: validation and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Data availability
All data supporting the findings of this study are available within the article. Additional raw data are available from the corresponding author upon reasonable request.Acknowledgements
The authors sincerely thank Professor Arnaud Travert (Normandie University, ENSICAEN, CNRS, Laboratoire Catalyse et Spectrochimie, Caen, France) for his invaluable scientific support, and the Ministry of Higher Education and Scientific Research, Algeria, for the privilege of funding the Franco-Algerian Profas B+ program that enabled this work.Notes and references
- K. Tanabe and W. F. Hölderich, Appl. Catal., A, 1999, 181, 399–434 CrossRef CAS.
- M. Timofeeva, Appl. Catal., A, 2003, 256, 19–35 CrossRef CAS.
- R. Schlögl, Angew. Chem., Int. Ed., 2015, 54, 3465–3520 CrossRef PubMed.
- R. Lundy, C. Byrne, J. Bogan, K. Nolan, M. N. Collins, E. Dalton and R. Enright, ACS Appl. Mater. Interfaces, 2017, 9, 13751–13760 CrossRef CAS PubMed.
- A. I. Osman, J. K. Abu-Dahrieh, D. W. Rooney, J. Thompson, S. A. Halawy and M. A. Mohamed, J. Chem. Technol. Biotechnol., 2017, 92, 2952–2962 CrossRef CAS PubMed.
- J. C. Védrine, ChemSusChem, 2019, 12, 577–588 CrossRef PubMed.
- E. Bekhradinassab, M. Haghighi and M. Shabani, Fuel, 2025, 379, 132986 CrossRef CAS.
- C. H. Bolster and G. M. Hornberger, Soil Sci. Soc. Am. J., 2007, 71, 1796–1806 CrossRef CAS.
- M. M. Mohammed, N. S. M. Ali, H. A. Alalwan, A. H. Alminshid and H. Aljaafari, Results Chem., 2021, 3, 100249 CrossRef CAS.
- F. Göltl, A. Grüneis, T. Bučko and J. Hafner, J. Chem. Phys., 2012, 137, 114111 CrossRef.
- M. A. Gomez, L. R. Pratt, J. D. Kress and D. Asthagiri, Surf. Sci., 2007, 601, 1608–1614 CrossRef CAS.
- E. P. Hessou, L. A. Bédé, H. Jabraoui, A. Semmeq, M. Badawi and V. Valtchev, Molecules, 2021, 26, 5486 CrossRef CAS PubMed.
- S. U. Rege and R. T. Yang, Chem. Eng. Sci., 2001, 56, 3781–3796 CrossRef CAS.
- J. R. Brownson, M. I. Tejedor-Tejedor and M. A. Anderson, J. Phys. Chem. B, 2006, 110, 12494–12499 CrossRef CAS PubMed.
- T. Xiao, H. Yuan, Q. Ma, X. Guo and Y. Wu, Int. J. Biol. Macromol., 2019, 132, 1106–1111 CrossRef CAS.
- S. Alafnan, A. Awotunde, G. Glatz, S. Adjei, I. Alrumaih and A. Gowida, J. Pet. Sci. Eng., 2021, 207, 109172 CrossRef CAS.
- H. A. Alalwan, A. H. Alminshid, M. M. Mohammed and M. F. Mohammed, Part. Sci. Technol., 2023, 41, 653–660 CrossRef CAS.
- H. A. Alalwan, A. Alminshid, M. M. Mohammed and M. F. Mohammed, Chem. Eng. Technol., 2023, 46, 587–594 CrossRef CAS.
- H. H. Kristoffersen and J. H. Chang, Computational Photocatalysis: Modeling of Photophysics and Photochemistry at Interfaces, ACS Publications, 2019, pp. 225–238 Search PubMed.
- S. Melchers, J. Schneider, A. V. Emeline and D. W. Bahnemann, Catalysts, 2018, 8, 417 CrossRef.
- C.-B. Wang, R. G. Herman, C. Shi, Q. Sun and J. E. Roberts, Appl. Catal., A, 2003, 247, 321–333 CrossRef CAS.
- J.-P. Gallas, J.-M. Goupil, A. Vimont, J.-C. Lavalley, B. Gil, J.-P. Gilson and O. Miserque, Langmuir, 2009, 25, 5825–5834 CrossRef CAS PubMed.
- O. Veselý, H. Pang, S. M. Vornholt, M. Mazur, J. Yu, M. Opanasenko and P. Eliášová, Catal. Today, 2019, 324, 123–134 CrossRef.
- A. Gil, Catal. Today, 2023, 423, 114016 CrossRef CAS.
- K. Vijayaraghavan, T. Padmesh, K. Palanivelu and M. Velan, J. Hazard. Mater., 2006, 133, 304–308 CrossRef CAS.
- S. Kundu and A. K. Gupta, Chem. Eng. J., 2006, 122, 93–106 CrossRef CAS.
- A. W. Adamson and A. P. Gast, Physical chemistry of surfaces, Interscience Publishers, New York, 1967 Search PubMed.
- J. Zeldowitsch, Acta Physicochim. URSS, 1934, 1, 961–973 Search PubMed.
- F. Haghseresht and G. Lu, Energy Fuels, 1998, 12, 1100–1107 CrossRef CAS.
- M. Dubinin, Chem. Rev., 1960, 60, 235–241 CrossRef CAS.
- A. Günay, E. Arslankaya and I. Tosun, J. Hazard. Mater., 2007, 146, 362–371 CrossRef PubMed.
- A. Dąbrowski, Adv. Colloid Interface Sci., 2001, 93, 135–224 CrossRef.
- Y. Kim, C. Kim, I. Choi, S. Rengaraj and J. Yi, Environ. Sci. Technol., 2004, 38, 924–931 CrossRef CAS PubMed.
- C. Aharoni and M. Ungarish, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 456–464 RSC.
- J. A. Ritter, S. J. Bhadra and A. D. Ebner, Langmuir, 2011, 27, 4700–4712 CrossRef CAS PubMed.
- A. L. Myers and J. M. Prausnitz, AIChE J., 1965, 11, 121–127 CrossRef CAS.
- D. Pino, F. Plantier and D. Bessieres, J. Therm. Anal. Calorim., 2014, 117, 1469–1477 CrossRef CAS.
- J. Zhang, H. Wu, T. J. Emge and J. Li, Chem. Commun., 2010, 46, 9152–9154 RSC.
- V. Goetz, O. Pupier and A. Guillot, Adsorption, 2006, 12, 55–63 CrossRef CAS.
- H. R. Abid, G. H. Pham, H.-M. Ang, M. O. Tade and S. Wang, J. Colloid Interface Sci., 2012, 366, 120–124 CrossRef CAS PubMed.
- B. M. Reddy, P. Lakshmanan and A. Khan, J. Phys. Chem. B, 2004, 108, 16855–16863 CrossRef CAS.
- A. Khazaei, S. Nazari, G. Karimi, E. Ghaderi, K. Mansouri Moradian and Z. Bagherpor, Int. J. Nanosci. Nanotechnol., 2016, 12, 207–214 Search PubMed.
- H. M. Yang and S.-J. Park, J. Ind. Eng. Chem., 2016, 41, 33–39 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- D. H. Everett and F. S. Stone, The structure and properties of porous materials, Butterworths, 1958 Search PubMed.
- A. R. Keshavarz, M. Rezaei and F. Yaripour, Powder Technol., 2010, 199, 176–179 CrossRef CAS.
- M. I. Zaki, M. A. Hasan, F. A. Al-Sagheer and L. Pasupulety, Colloids Surf., A, 2001, 190, 261–274 CrossRef CAS.
- G. Busca, Advances in catalysis, Elsevier, 2014, vol. 57, pp. 319–404 Search PubMed.
- M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, J. Catal., 2002, 211, 1–5 CrossRef CAS.
- T. Onfroy, G. Clet and M. Houalla, Microporous Mesoporous Mater., 2005, 82, 99–104 CrossRef CAS.
- F. Can, X. Courtois and D. Duprez, Catalysts, 2021, 11, 703 CrossRef CAS.
- F. Elgayar, E. Jeanneau, P. Bargiela, A. Mesbah, N. Essayem and S. Mishra, Catal. Sci. Technol., 2025, 15, 6744–6756 RSC.
- I. E. Wachs and B. M. Weckhuysen, Appl. Catal., A, 1997, 157, 67–90 CrossRef CAS.
- W. Guo and J. R. Errington, J. Phys. Chem. C, 2019, 123, 19649–19658 CrossRef CAS.
- J. Yu, C. Y. Jimmy, W. Ho and Z. Jiang, New J. Chem., 2002, 26, 607–613 RSC.
- L. H. Little, A. V. Kiselev and V. I. Lygin, Infrared Spectra of Adsorbed Species, Academic Press, London–New York, 1966, 428 pp Search PubMed.
- D. D. Weis and G. E. Ewing, Anal. Chem., 1998, 70, 3175–3183 CrossRef CAS PubMed.
- A. Jentys, G. Warecka, M. Derewinski and J. A. Lercher, J. Phys. Chem., 1989, 93, 4837–4843 CrossRef CAS.
- Y.-T. Lin, G. Agnello, M. Link, Y. Guo, A. N. Zoba, A. Antony, N. J. Smith, J. Banerjee and S. H. Kim, Langmuir, 2024, 40, 1658–1665 CrossRef CAS.
- B. Morrow, I. Cody and L. S. Lee, J. Phys. Chem., 1976, 80, 2761–2767 CrossRef CAS.
- K. Hadjiivanov, Advances in Catalysis, Elsevier, 2014, vol. 57, pp. 99–318 Search PubMed.
- T. Richard, L. Mercury, F. Poulet and L. d'Hendecourt, J. Colloid Interface Sci., 2006, 304, 125–136 CrossRef CAS PubMed.
- H. A. Al-Abadleh and V. Grassian, Langmuir, 2003, 19, 341–347 CrossRef CAS.
- K. Hass, W. Schneider, A. Curioni and W. Andreoni, J. Phys. Chem. B, 2000, 104, 5527–5540 CrossRef CAS.
- M. Driessen and V. Grassian, J. Phys. Chem., 1995, 99, 16519–16522 CrossRef CAS.
- A. Goodman, E. Bernard and V. Grassian, J. Phys. Chem. A, 2001, 105, 6443–6457 CrossRef CAS.
- D. Eisenberg and W. Kauzmann, The structure and properties of water, OUP, Oxford, 2005 Search PubMed.
- G. Herzberg and B. L. Crawford Jr, J. Phys. Chem., 1946, 50, 288 CrossRef.
- N. Asprion, H. Hasse and G. Maurer, Fluid Phase Equilib., 2001, 186, 1–25 CrossRef CAS.
- R. L. Brinkley and R. B. Gupta, AIChE J., 2001, 47, 948–953 CrossRef CAS.
- W. Xu, N. Wang, Y. Chen, J. Chen, X. Xu, L. Yu, L. Chen, J. Wu, M. Fu and A. Zhu, Catal. Commun., 2016, 84, 61–66 CrossRef CAS.
- B. Athokpam, S. G. Ramesh and R. H. McKenzie, Chem. Phys., 2017, 488, 43–54 CrossRef.
- S. C. Ringwald and J. E. Pemberton, Environ. Sci. Technol., 2000, 34, 259–265 CrossRef CAS.
- A. Simon-Masseron, J. Marques, J. M. Lopes, F. R. Ribeiro, I. Gener and M. Guisnet, Appl. Catal., A, 2007, 316, 75–82 CrossRef CAS.
- Y. Li, M. Wei, L. Liu, Q. Xue and B. Yu, Sci. Total Environ., 2020, 740, 140104 CrossRef CAS PubMed.
- C.-K. Lee, S.-K. Fen, H.-P. Chao, S.-S. Liu and F.-C. Huang, Adsorption, 2012, 18, 349–357 CrossRef CAS.
- E. Sarti, T. Chenet, L. Pasti, A. Cavazzini, E. Rodeghero and A. Martucci, Minerals, 2017, 7, 22 CrossRef.
- M. Nagao and Y. Suda, Langmuir, 1989, 5, 42–47 CrossRef CAS.
- A. J. McCue, G. A. Mutch, A. I. McNab, S. Campbell and J. A. Anderson, Catal. Today, 2016, 259, 19–26 CrossRef CAS.
- Z. Z. Xia, C. J. Chen, J. K. Kiplagat, R. Z. Wang and J. Q. Hu, J. Chem. Eng. Data, 2008, 53, 2462–2465 CrossRef CAS.
- L. Zhuravlev, Colloids Surf., A, 2000, 173, 1–38 CrossRef CAS.
- A. M. Schrader, J. I. Monroe, R. Sheil, H. A. Dobbs, T. J. Keller, Y. Li, S. Jain, M. S. Shell, J. N. Israelachvili and S. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895 CrossRef CAS PubMed.
- Y. F. Shi, X. J. Liu, H. J. Nie and Y. S. Liu, Appl. Mech. Mater., 2012, 229, 100–104 Search PubMed.
- D. Coster, A. Blumenfeld and J. Fripiat, J. Phys. Chem., 1994, 98, 6201–6211 CrossRef CAS.
- K. Nakajima, R. Noma, M. Kitano and M. Hara, J. Phys. Chem. C, 2013, 117, 16028–16033 CrossRef CAS.
- V. Shapovalov and T. N. Truong, J. Phys. Chem. B, 2000, 104, 9859–9863 CrossRef CAS.
- W. Zhang, Z. Qu, X. Li, Y. Wang, D. Ma and J. Wu, J. Environ. Sci., 2012, 24, 520–528 CrossRef CAS PubMed.
- M. Hernández, J. Velasco, M. Asomoza, S. Solís, F. Rojas and V. Lara, Ind. Eng. Chem. Res., 2004, 43, 1779–1787 CrossRef.
- C. Vittoni, G. Gatti, I. Braschi, E. Buscaroli, G. Golemme, L. Marchese and C. Bisio, Materials, 2020, 13, 2690 CrossRef CAS PubMed.
- N. G. Mostafa, A. F. Yunnus and A. Elawwad, Adsorpt. Sci. Technol., 2022, 2022, 7582756 CrossRef.
- T. Morimoto, M. Nagao and J. Imai, Bull. Chem. Soc. Jpn., 1971, 44, 1282–1288 CrossRef CAS.
- M. T. Amin, A. A. Alazba and M. Shafiq, Sustainability, 2015, 7, 15302–15318 CrossRef CAS.
- Y. Xie, H. Fan, M. Che, Y. Liu, C. Liu, X. Hu and B. Teng, Molecules, 2024, 29, 5251 CrossRef CAS PubMed.
- M. Takeuchi, R. Kurosawa and J. Ryu, J. Raman Spectrosc., 2022, 53, 1793–1804 CrossRef CAS.
- J. Wang, H. Chen and Q. Li, React. Kinet. Catal. Lett., 2000, 69, 277–284 CrossRef CAS.
- Z. Zhao, Z. Li and Z. Zou, J. Phys. Chem. C, 2012, 116, 7430–7441 CrossRef CAS.
- T. A. Gordymova, A. A. Budneva and A. A. Davydov, React. Kinet. Catal. Lett., 1982, 20, 113–117 CrossRef CAS.
- J. Pires, M. Pinto, J. Estella and J. C. Echeverría, J. Colloid Interface Sci., 2008, 317, 206–213 CrossRef CAS PubMed.
- K. H. Chu, Ind. Eng. Chem. Res., 2021, 60, 13140–13147 CrossRef CAS.
- Q. Hu, R. Lan, L. He, H. Liu and X. Pei, J. Environ. Manage., 2023, 329, 117104 CrossRef PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- H. Freundlich, J. Phys. Chem., 1906, 57, 1100–1107 Search PubMed.
- K. Sing, Colloids Surf., A, 2001, 187, 3–9 CrossRef.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. Sing, Adsorption by powders and porous solids: principles, methodology and applications, Academic Press, 2013 Search PubMed.
- J. Farrell, C. Manspeaker and J. Luo, Microporous Mesoporous Mater., 2003, 59, 205–214 CrossRef CAS.
- W. Zhao, Y. Tang, Y. Wan, L. Li, S. Yao, X. Li, J. Gu, Y. Li and J. Shi, J. Hazard. Mater., 2014, 278, 350–359 CrossRef CAS PubMed.
- G. Yan and D. G. Vlachos, J. Phys. Chem. C, 2024, 128, 16996–17005 CrossRef CAS.
- S. Wang, P. Jiao, Z. Zhang and Q. Niu, Molecules, 2024, 29, 3745 CrossRef CAS PubMed.
- D. Taffa, M. Kathiresan and L. Walder, Langmuir, 2009, 25, 5371–5379 CrossRef CAS PubMed.
- J. Porter, G. McKay and K. Choy, Chem. Eng. Sci., 1999, 54, 5863–5885 CrossRef CAS.
- C. Luo, Z. D. Hood, A. B. Martinson and A. S. Hock, J. Phys. Chem. C, 2024, 128, 17038–17046 CrossRef CAS.
- B. Baumgartner, J. Hayden, A. Schwaighofer and B. Lendl, ACS Appl. Nano Mater., 2018, 1, 7083–7091 CrossRef CAS.
- Q. Jin, L. Huang, A. Li and A. Shan, Chemosphere, 2017, 185, 518–528 CrossRef CAS PubMed.
- A. P. Kulkarni and D. S. Muggli, Appl. Catal., A, 2006, 302, 274–282 CrossRef CAS.
- A. Amrutha, G. Jeppu, C. Girish, B. Prabhu and K. Mayer, Environ. Processes, 2023, 10, 38 CrossRef.
- A. Basu, S. S. Ali, S. S. Hossain and M. Asif, Processes, 2022, 10, 1154 CrossRef CAS.
- G. Fraux, A. Boutin, A. H. Fuchs and F.-X. Coudert, Adsorption, 2018, 24, 233–241 CrossRef CAS.
- X. Hou, Y. Zheng, X. Ma, Y. Liu and Z. Ma, Molecules, 2021, 26, 1130 CrossRef CAS PubMed.
- H. Ablat, X. Nurmamat, X. Ma, Q. Xie and Z. Zhao, Water Environ. Res., 2023, 95, e10867 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |