Open Access Article
Open Access ArticleStructural and chemical properties of Pt-rich PtxZry nanoalloys
Luis M.
Molina
 *a and
Julio A.
Alonso
*a and
Julio A.
Alonso
 ab
ab
aDepartamento de Física Teórica, Atómica y Optica, Universidad de Valladolid, E-47011 Valladolid, Spain. E-mail: lmolina@uva.es
bDonostia International Physics Center (DIPC), 20018 San Sebastián, Spain
First published on 19th November 2025
Abstract
Density functional theory (DFT) simulations have been performed to study the structure and physico-chemical properties of bimetallic PtxZry nanoclusters, for stoichiometries rich in platinum, and sizes ranging from Pt3Zr to Pt72Zr24. For each cluster, the search for the most stable structural conformations was performed using a mixed approach where a family of stable isomers was first determined by means of a genetic algorithm based on a modified Sutton–Chen semiempirical potential; subsequently, that family of conformations was relaxed by performing DFT calculations. This procedure results in cluster geometries which reproduce reasonably well the ordering and atomic packing present in the bulk Pt–Zr alloys. The binding energies and electronic structures were studied as a function of both stoichiometry and cluster size; as a result, we identified some clusters with enhanced stability, such as Pt5Zr2 or Pt9Zr3. The analysis of the densities of states and local reactivity indicators highlights the strong intermetallic character of the Pt–Zr bonding, with large charge transfer from Zr to Pt atoms. The Pt–Zr interaction also induces a sizable weakening of the ability of Pt sites to bind CO, making these bimetallic clusters less sensitive to poisoning by carbon monoxide.
1 Introduction
Bimetallic clusters have attracted significant attention due to their unique properties1–3 and novel potential applications in various fields, such as materials science, nanotechnology, and catalysis.4–8 The combination of two different chemical elements results in materials with new properties compared to their pure metal counterparts.9–11 An interesting case is platinum. This metal is widely used as the main catalyst in fuel cells,12,13 and for oxygen reduction, hydrogen oxidation, and hydrogen evolution reactions.14 One of the most problematic issues with platinum catalysts is their susceptibility to carbon monoxide poisoning,15 and therefore the development of new catalysts with improved resistance to poisoning by trace amounts of CO is highly recommended. An interesting way of overcoming these problems is the doping of platinum catalysts with other transition metals.16–19 Recent studies have shown that the addition of small amounts of 4d metal impurities results in important changes in the electronic properties of the host Pt nanoclusters, modifying the CO binding energies.20–23The modifications induced by alloying affect not only the adsorption of various reactants, but also a range of other cluster properties. Among the dopants which form stable intermetallic compounds when alloyed with platinum, Zr is an interesting case. At platinum-rich compositions, the Pt–Zr phase diagram shows the formation of several very stable intermetallic compounds;24 among these, the most stable is Pt3Zr, with a melting point well above 2200 °C, much higher than those of either pure Pt or Zr. The bulk Pt3Zr compound has been studied erlier.25–28 Bonding in this alloy and similar A3B compounds can be interpreted according to “Engel-Brewer” theories;29 the electronegativity difference between Pt and Zr30 induces a sizable electron transfer from Zr to Pt,31 with an associated increased filling of the platinum d states. These features result in interesting chemical properties for the surface of these intermetallic compounds. For example, compared to pure Zr, the surface of Pt3Zr is more inert towards water dissociation.32 Also, compared to pure Pt, the presence of Zr is expected to produce substantial changes in reactivity for oxidation reactions.
In contrast to the bulk case, no previous studies exist for small bimetallic Pt–Zr clusters. This has motivated us to perform an extensive theoretical study of the structure and properties of PtxZry clusters with sizes between 10 and 100 atoms, approximately, and platinum-rich concentrations around the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio where the very stable bulk Pt3Zr compound is formed. This allows to extract valuable information on the effects caused by Zr doping on the chemical properties of small-size platinum catalysts. As it is discussed in the next section, the first fundamental challenge of this type of studies is to find the most stable structural conformation in situations where the number of possible structural isomers and permutational homotopes grows exponentially with the number of atoms in the system. To address this issue, we employ an approach which combines the use of empirical potentials and genetic algorithms with DFT simulations, to obtain the lowest energy conformations with a reasonable degree of reliability. The results show that, although empirical potentials lead to structures different from the ones obtained by DFT, they are still useful to generate a set of initial conformations with structural properties similar to the most stable DFT isomers, thus providing substantial help to the complex problem of determining the true global minimum for these intermetallic nanoalloys. Besides, we have also analyzed a number of chemical properties of these clusters, namely electronic structure, binding energies, charge distribution and tolerance for CO poisoning. We found that these nanoalloys are highly stable (with large values for the mixing energies) and they also possess a strong intermetallic character, with a large charge transfer from zirconium to platinum atoms; in some cases, this leads to large HOMO–LUMO gaps. Finally, we have studied the process of CO accumulation in one selected case (Pt9Zr3), comparing it with a pure platinum cluster of similar size (Pt12). The results clearly demostrate that the presence of the zirconium impurities produces a strong decrease of the CO binding at the platinum sites, thus making more difficult the poisoning by CO of the bimetallic Pt–Zr clusters.
1 ratio where the very stable bulk Pt3Zr compound is formed. This allows to extract valuable information on the effects caused by Zr doping on the chemical properties of small-size platinum catalysts. As it is discussed in the next section, the first fundamental challenge of this type of studies is to find the most stable structural conformation in situations where the number of possible structural isomers and permutational homotopes grows exponentially with the number of atoms in the system. To address this issue, we employ an approach which combines the use of empirical potentials and genetic algorithms with DFT simulations, to obtain the lowest energy conformations with a reasonable degree of reliability. The results show that, although empirical potentials lead to structures different from the ones obtained by DFT, they are still useful to generate a set of initial conformations with structural properties similar to the most stable DFT isomers, thus providing substantial help to the complex problem of determining the true global minimum for these intermetallic nanoalloys. Besides, we have also analyzed a number of chemical properties of these clusters, namely electronic structure, binding energies, charge distribution and tolerance for CO poisoning. We found that these nanoalloys are highly stable (with large values for the mixing energies) and they also possess a strong intermetallic character, with a large charge transfer from zirconium to platinum atoms; in some cases, this leads to large HOMO–LUMO gaps. Finally, we have studied the process of CO accumulation in one selected case (Pt9Zr3), comparing it with a pure platinum cluster of similar size (Pt12). The results clearly demostrate that the presence of the zirconium impurities produces a strong decrease of the CO binding at the platinum sites, thus making more difficult the poisoning by CO of the bimetallic Pt–Zr clusters.
2 Computational setup
Density functional theory (DFT) calculations were carried out using the projector augmented-wave method, as implemented in the GPAW code.33,34 Depending on its size, each cluster was placed at the center of a large cubic cell, with sides ranging in length from 16 Å for the smaller sizes to 24 Å for the largest case, Pt72Zr24. The spacing of the real-space three-dimensional grid was set to 0.2 Å. This ensures a convergence of the total binding energy of the order of 0.01 eV. Exchange–correlation effects were modelled with the PBE functional.35,36 PAW pseudopotentials were used,37 and 10 and 12 valence electrons per atom for Pt and Zr, respectively, were included in the calculations. In the case of Pt, the pseudopotential includes scalar-relativistic effects. Spin-polarized calculations were carried out in all cases, to take into account magnetization of the Pt atoms. However, we found that the presence of Zr effectively quenches any magnetic moment on the Pt sites, and for all the clusters studied the total magnetization was zero, without any sizable spin polarization. The convergence threshold for the one-electron eigenstate energies was set to 5 × 10−7 eV. Structure optimization was carried out making use of the BFGS (Quasi-Newton) algorithm38 until forces on the atoms were below 0.01 eV Å−1.For binary clusters of medium and large sizes the search for the most stable structural conformation (Global Minimum, or GM) is an extremely complex problem. The number of local minima to be searched increases exponentially with cluster size, the presence of two different atomic species adding more complexity to the problem in the form of permutational isomers. In order to perform an extensive isomer search with good chances of locating the true GM, we have followed a two-stages procedure. In the first stage, we have used a Genetic Algorithm (GA)39–41 based on empirical embedded-atom potentials, to generate a large amount of different structures (up to 20–30, for small and intermediate cluster sizes). As we discuss below, this family of selected local minimum structures obtained with the empirical potentials needs to show a fair amount of structural variability. It is also important that the main structural features (degree of mixing, chemical ordering, symmetry) present in the empirical potential minima do resemble as much as possible the characteristics of the bulk alloy determined from experimental measurements. The second stage of the process involves relaxing with DFT the initial family of selected structures. As we will comment later, the use of DFT is mandatory to obtain reliable structures. In fact, relaxation with DFT of almost any local or global minimum structure obtained with the empirical potentials leads to different and more stable structures. That is, although a search of isomers with empirical potentials can lead to conformations which share common structural features with the DFT minima, these conformations do never actually coincide with the global minimum obtained with DFT. However, the use of a GA based on empirical-potentials as a generator of initial structures for the DFT step greatly improves the chances of finding the DFT global minimum structure with a moderate computational effort. For clusters with more than about 10 atoms, the computational cost of an isomer search with a fully DFT-based genetic algorithm would be prohibitive.
For the GA algorithm, we employed the empirical Sutton–Chen embedded atom potentials.42 The expression for the total energy of a system of N metal atoms of equal type is given by:
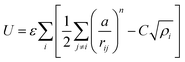 | (1) |
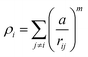 with parameters ε, a, C, n y m which are fitted to the bulk properties of a given metal.
with parameters ε, a, C, n y m which are fitted to the bulk properties of a given metal.
In the case of a binary alloy, such as Pt–Zr, the total potential energy will be an analogous sum extended over all the atoms, with different parameters ε, a, C, etc…, for each of the Pt–Pt, Zr–Zr of Pt–Zr interactions. However, whereas the parameters characterizing the interaction between atoms of the same kind are easy to obtain, it is more difficult to obtain an accurate description of the parameters for the interaction between unlike atoms. The usual approach consists in taking arithmetic or geometrical averages of the parameters for like-atoms, according to the expressions:
 | (2) |
After performing test simulations using such averages for the interaction parameters between unlike atoms (see the values of the parameters in Table 1), we noticed that the results were rather poor, with global minima in which the degree of mixing in the nanoalloys was highly underestimated. Fig. S2 in the SI shows the global minima found for some selected cases, with a marked preference for the formation of a core of close-packed platinum atoms surrounded by some Zr atoms in the surface. In contrast, as we will see later, the structures of these binary clusters are characterized by a strong tendency for the Zr atoms to be surrounded by Pt atoms. This is due to a sizable electronic charge transfer from Zr to Pt atoms (caused by a large electronegativity difference), which results in a strong tendency for chemical ordering in the alloys, an effect which takes place mainly for Pt-rich compositions. To take this effect into account, instead of introducing artificial modifications of the Sutton–Chen parameters εAB, CAB, etc…, we use a novel approach involving the introduction of an extra Coulomb term which accounts for the interaction between charged atoms in the nanoalloy. Therefore, the total interaction energy is written as the sum of the empirical Sutton–Chen interaction and an extra Couloumb interaction term between charged atoms, with the charges Q on each type of atom determined by a Bader analysis based on test DFT calculations
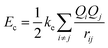 | (3) |
| ε | a | C | n | m | |
|---|---|---|---|---|---|
| Pt | 0.01983 | 3.92 | 34.41 | 10 | 8 |
| Zr | 0.00127 | 4.53 | 71.68 | 9 | 4 |
| Pt–Zr | 0.00502 | 4.225 | 53.04 | 9 | 6 |
For Pt-rich compositions (Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr ratio equal or over 3
Zr ratio equal or over 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the Bader charge analysis shows that each Zr atom transfers more than one electron to the surrounding Pt atoms, which become negatively charged sharing the charge donated by the Zr atoms. As the Pt
1), the Bader charge analysis shows that each Zr atom transfers more than one electron to the surrounding Pt atoms, which become negatively charged sharing the charge donated by the Zr atoms. As the Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr ratio decreases and tends towards 2
Zr ratio decreases and tends towards 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the extra electronic charge on each Pt atom decreases, and a value of approximately 0.8 electrons is reached. At the same time, the net positive charge on the Zr sites also decreases. To model the extra charge variations with changing concentrations in a simple way, we used the following partial charges for the Coulomb interation term within a PtxZry cluster:
1, the extra electronic charge on each Pt atom decreases, and a value of approximately 0.8 electrons is reached. At the same time, the net positive charge on the Zr sites also decreases. To model the extra charge variations with changing concentrations in a simple way, we used the following partial charges for the Coulomb interation term within a PtxZry cluster:
| if x/y ≥ 3 Q[Zr] = +1.2 Q[Pt] = −1.2y/x |
| if x/y < 3 Q[Zr] = +0.8x/y Q[Pt] = −0.80 |
The genetic algorithm employs various operations on the members of a given population, to produce the offspring for the next generation. In our customized GA, the following combination of mating and mutation operations are used:
• Mate: mating of two clusters using the Deaven–Ho45 cut-and-splice crossover operation. In this procedure, each one of the two clusters is cut in two pieces through a plane crossing the center of mass, and one half of each cluster is combined with one half of the other cluster into a new structure.
• Swap: for a given cluster structure, pairs of atoms of different elements exchange their nature (a Zr atom is transformed into Pt and vice versa; this is the same as exchanging their positions). For each call to the swap operator, we exchange the atom types of 20% of all the atoms within the cluster.
• Cartesian displacement operator (CDO): the position of each atom is randomly displaced by up to 15% of the value of the bond distance between that atom and its nearest neighbour.
• Angular operator (AO): 5% of the atoms in the cluster are randomly selected, and each of them is randomly displaced along the surface of a sphere centered in the cluster's center of mass, and with radius Ri equal to the distance between that atom and the center of mass.
• Twist: a plane with arbitrary orientation passing through the cluster's center of mass is randomly selected, thus dividing the cluster into two halves. Then, the atoms in one side are rotated by a random angle with respect to the atoms in the other side.
Each time that a mating or mutation operation is performed, it is important to check the resulting atomic coordinates. If any two atoms within the constructed structure are too close to each other (we chose a cutoff criteria of 2.2 Å), the numerical parameters for the mutation are changed, and this procedure is repeated until all the atoms are properly separated. This proves important for the next step in the algorithm, which is the relaxation of the new structures generated. At this stage, we have introduced an important modification to the standard method. Instead of simply relaxing each structure towards its closest local minimum, we performed a damped molecular dynamics simulation, using the velocity-Verlet algorithm46 with a time step of 1 femtosecond, and scaling down the modulus of the velocity of each atom by a factor of 0.08 every 5 steps. This procedure improves the speed of convergence towards a low energy minimum, while exploring secondary minima nearby, and preventing the structure to become stuck in one of them. As a result of this improvement, we have observed that, for small and medium cluster sizes, the genetic algorithm leads to a smaller family of different conformations, easily discarding in the final population the repetition of isomers with very similar energies and structures.
On each iteration of the GA, a population M ranging between 20 and 100 different isomers was considered, depending on cluster size. Then, after 2 M/3 mating and mutation operations, the M best conformations (those with lower energies) were selected for the next iteration. The operators were randomly selected according to the following probability distribution, which ensures a good degree of structural variation on the members of the population: Mate, 45%; Swap, 20%; CDO, 15%; AO, 10%; Twist, 10%. Typically, between 100 to 200 iterations were necessary to converge the GA.
Fig. 1 shows, for the Pt10Zr4 cluster, a comparison between the results obtained with the GA algorithm based on Sutton–Chen-Coulomb empirical potentials, and the final collection of isomers obtained after relaxing with DFT the initial structures obtained from the GA. Because of the tendency of embedded atom methods to favour close-packed geometries, all the Sutton–Chen-Coulomb conformations try to maximize atomic packing and have near spherical shapes. Inclusion of the extra Coulomb term leads to conformations where the Zr atoms maximize their mutual separation, with Pt atoms situated between them, forming a nanoalloy with a high degree of chemical order. The conformations obtained at the DFT level have some similarities with the empirical potential conformations (for example, the presence of chemical ordering) but also some differences: often, the global minimum and some of the isomers energetically close to it have a less packed structure, sometimes with a smaller degree of sphericity. At this point, it must be remarked that, although the family of Sutton–Chen-Coulomb energy minima provides a good starting point for the search of stable conformations at the DFT level, structural relaxation at the DFT level produces in general substantial distortions of the initial structures. In fact, it rarely happens (with the notable exception of the highly symmetrical Pt9Zr3 cluster) that the most stable Sutton–Chen-Coulomb minimum leads, after relaxation, to the most stable DFT minimum. Still, this mixed method using empirical-potential-based GA and subsequent DFT relaxation allows for a reasonably accurate search of low-energy conformations at a small computational cost. This is extremely important for clusters with medium or large sizes, especially if the cluster is bimetallic, because chemical ordering may be present. In this case, GA isomer search using exclusively DFT becomes prohibitive.
3 Results and discussion
We are interested on PtxZry clusters with stoichiometries rich in platinum, focussing on concentrations close to the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio corresponding to the Engel–Brewer-type Pt3Zr solid alloy. For clusters containing up to six Zr atoms, we have studied Pt
1 ratio corresponding to the Engel–Brewer-type Pt3Zr solid alloy. For clusters containing up to six Zr atoms, we have studied Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr relative concentrations ranging between the 2
Zr relative concentrations ranging between the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios. For larger clusters, the 3
1 ratios. For larger clusters, the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio was fixed and we have studied cluster sizes with 8, 12, 16 and 24 Zr atoms, in order to obtain a good understanding of the effects of cluster size. However, for the two largest clusters, Pt48Zr16 and Pt72Zr24, with 672 and 1008 valence electrons, respectively, the computational cost of the DFT simulations becomes quite high, and only the most stable Sutton–Chen-Coulomb isomer obtained with the genetic algorithm was relaxed using DFT.
1 ratio was fixed and we have studied cluster sizes with 8, 12, 16 and 24 Zr atoms, in order to obtain a good understanding of the effects of cluster size. However, for the two largest clusters, Pt48Zr16 and Pt72Zr24, with 672 and 1008 valence electrons, respectively, the computational cost of the DFT simulations becomes quite high, and only the most stable Sutton–Chen-Coulomb isomer obtained with the genetic algorithm was relaxed using DFT.
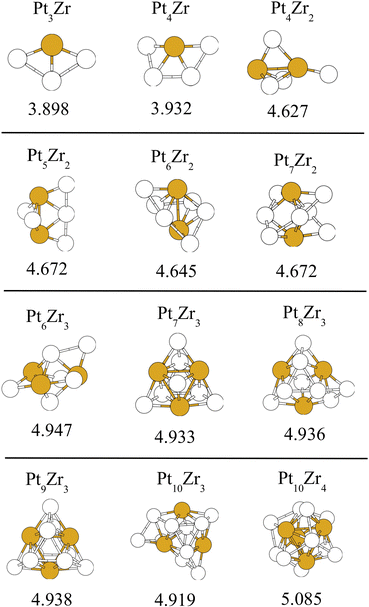
After relaxing with DFT a large collection of different isomers, the most stable structures obtained for each cluster composition are shown in Fig. 2 and 3 (see also the SI). Also, the corresponding binding energies per atom calculated for each PtxZry cluster as
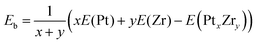 | (4) |
Comparing the structure of small Pt–Zr clusters with the Pt3Zr bulk alloy, some interesting effects can be noticed, associated to the small size of the clusters. In general, Pt–Zr bond distances for PtxZry clusters are slightly smaller than the bond distances in the bulk alloy: approximately 2.7 Å in the clusters, compared to 2.81 Å in the bulk.47 This is a typical cluster size effect for the interatomic distances.48 However, Zr–Zr distances are more sensitive to finite size effects. For instance, in Pt9Zr3, distances between Zr atoms are approximately 3.2 Å, much shorter than the value of 3.97 Å for the bulk Pt3Zr alloy. As the cluster size increases, such Zr–Zr distances gradually increase, being approximately 3.45 Å for Pt12Zr4, and between 3.6 and 4.0 Å for Pt36Zr12. We have also studied a few larger clusters, with sizes in the range 50–100 atoms. Because of the very demanding computational cost of the DFT calculations for these cluster sizes, only a few Sutton–Chen-Coulomb structures were relaxed using DFT. These calculations lead to amorphous structures with a quite uniform distribution of Zr atoms within such nanoparticles.
As we have studied clusters with varying numbers of either Zr or Pt atoms, it is possible to calculate DFT binding energies for individual atoms in the cluster. These are defined as the energy gained by the addition of a single Pt or Zr atom to the cluster, that is:
| Ebinding(Zr) = E(PtxZry−1) + E(Zr) − E(PtxZry) | (5) |
| Ebinding(Pt) = E(Ptx−1Zry) + E(Pt) − E(PtxZry) | (6) |
These binding energies are shown in Table 2. Several interesting features can be noticed. First, the binding of Zr atoms is much stronger (almost twice as strong) than the binding of Pt atoms. This is justified by the observation that the coordination of Zr atoms in the clusters is higher than the coordination of Pt atoms. Second, the Pt binding energies in some clusters are slightly larger compared to other clusters. This occurs for Pt9Zr3 in the PtxZr3 group, and for Pt12Zr4 in the PtxZr4 group, both clusters having 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. However, this is not the case for Pt6Zr2 in the PtxZr2 group. Instead, for clusters having two Zr atoms, the largest Pt binding energy occurs for Pt5Zr2.
1 stoichiometry. However, this is not the case for Pt6Zr2 in the PtxZr2 group. Instead, for clusters having two Zr atoms, the largest Pt binding energy occurs for Pt5Zr2.
| Cluster | Pt4Zr2 | Pt6Zr3 | Pt10Zr4 | Pt15Zr6 |
| E binding(Zr) | 8.105 | 7.359 | 7.242 | 8.163 |
| Cluster | Pt4Zr | Pt5Zr2 | Pt6Zr2 | Pt7Zr2 |
| E binding(Pt) | 4.065 | 4.943 | 4.458 | 4.885 |
| Cluster | Pt7Zr3 | Pt8Zr3 | Pt9Zr3 | Pt10Zr3 |
| E binding(Pt) | 4.809 | 4.959 | 4.970 | 4.680 |
| Cluster | Pt11Zr4 | Pt12Zr4 | Pt16Zr6 | |
| E binding(Pt) | 4.992 | 5.449 | 4.956 | |
To gain more insight into the stability of these Pt–Zr nanoalloys, we have also performed a systematic search for the most stable conformation of PtxZry clusters with a fixed total number of atoms (12), through the whole range of relative concentrations from pure Pt to pure Zr. To quantify the tendency towards alloying and formation of intermetallic compounds, we have calculated the mixing (or excess) energy Emixing, defined as the energy gain obtained when a bimetallic cluster PtxZry is formed, with respect to its pure Pt12 or Zr12 counterparts:
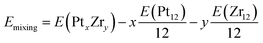 | (7) |
 | ||
| Fig. 4 Structures and mixing energies (in eV) for PtxZry clusters with a total of 12 atoms and varying Pt/Zr concentration. White spheres: Pt atoms. Orange spheres: Zr atoms. | ||
Fig. 5 shows the electronic density of states (DOS) for some selected clusters, and the DOS of all the studied clusters are shown in the SI. In all cases, the DOS is characterized by an almost filled platinum d-band. A large part of the contribution from Zr d-states lies above the Fermi energy, meaning that sizable electronic charge transfer from Zr to Pt atomos takes place; we later confirm this interpretation by analyzing Bader charges on the atoms. Also, one can notice the hybridization between Pt and Zr d-states, revealed by the presence of partial Zr d-character of the states at the bottom of the Pt d-band (energies around −8 eV). The electronic charge transfer from Zr to Pt atoms results in the increased filling of the Pt d-states, which become completely filled in general. In most small clusters, this results in the opening of HOMO–LUMO energy gaps with a magnitude of 1-0-1.5 eV. Interestingly, such gap opening occurs for Pt/Zr ratios including 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2.5
1, 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and also 3
1, and also 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Pt4Zr2, Pt5Zr2 and Pt6Zr2 illustrate this behaviour). In Table 3, we report the size of the HOMO–LUMO gap for all the clusters where a significant separation (higher than 0.1 eV) was found between those two energy levels.
1 (Pt4Zr2, Pt5Zr2 and Pt6Zr2 illustrate this behaviour). In Table 3, we report the size of the HOMO–LUMO gap for all the clusters where a significant separation (higher than 0.1 eV) was found between those two energy levels.
 | ||
| Fig. 5 Densities of electronic states (DOS) for some PtxZry clusters calculated by DFT. Blue lines show projections of the DOS over Zr orbitals. Dashed lines mark the location of the Fermi level. | ||
| Cluster | Pt3Zr | Pt4Zr | Pt4Zr2 | Pt5Zr2 |
| Gap size (eV) | 1.01 | 0.41 | 1.42 | 1.28 |
| Cluster | Pt6Zr2 | Pt7Zr2 | Pt6Zr3 | Pt7Zr3 |
| Gap size (eV) | 0.82 | 0.75 | 1.00 | 0.46 |
| Cluster | Pt8Zr3 | Pt9Zr3 | Pt10Zr3 | Pt10Zr4 |
| Gap size (eV) | 0.42 | 0.19 | 0.47 | — |
| Cluster | Pt11Zr4 | Pt12Zr4 | Pt15Zr5 | Pt15Zr6 |
| Gap size (eV) | 0.32 | — | 0.24 | 0.17 |
| Cluster | Pt16Zr6 | Pt18Zr6 | Pt24Zr8 | Pt36Zr12 |
| Gap size (eV) | — | 0.15 | 0.18 | — |
As the cluster size increases, the discrete distribution of electronic states evolves into a quasi-continuous distribution dominated by platinum d-states with a minor contribution from hybridization with Zr d-states. For the largest clusters, Pt24Zr8, Pt36Zr12, Pt48Zr16 and Pt72Zr24, a clear minimum in the DOS develops around the Fermi energy. All these facts indicate that the electronic structure of Pt–Zr nanoalloys with Pt/Zr content between 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 show special features, which may be caused by the intermetallic character of these alloys, with a strong charge transfer from Zr to Pt.
1 show special features, which may be caused by the intermetallic character of these alloys, with a strong charge transfer from Zr to Pt.
Fig. 6 gives the atomic Bader charges49 for some selected clusters. The results highlight the partial ionic character of these intermetallic nanoalloys, with the positive charge on the Zr atoms ranging from +1.6 to +1.9|e| (electrons). Interestingly, the charge lost by the Zr atoms does not depend too much on the relative concentration of Pt and Zr; similar values are found for Pt6Zr3 and Pt9Zr3 clusters, with 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries. On the other hand, the change in Pt
1 stoichiometries. On the other hand, the change in Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr ratio leads to a change in the average charge gained by the Pt atoms, varying from −0.85|e| to −0.6|e|, depending on the relative concentrations. For larger clusters (Pt18Zr6 and Pt24Zr8), the amount of charge gained by Pt atoms varies a lot with the Pt site, between −0.4 and −0.8|e|. In both cases, an interesting feature is observed: the most negatively charged Pt atom is placed at a central position inside the cluster; that charge is −1.40|e| in Pt18Zr6.
Zr ratio leads to a change in the average charge gained by the Pt atoms, varying from −0.85|e| to −0.6|e|, depending on the relative concentrations. For larger clusters (Pt18Zr6 and Pt24Zr8), the amount of charge gained by Pt atoms varies a lot with the Pt site, between −0.4 and −0.8|e|. In both cases, an interesting feature is observed: the most negatively charged Pt atom is placed at a central position inside the cluster; that charge is −1.40|e| in Pt18Zr6.
Next, we have analyzed the local reactivity of some of these clusters, by studying the spatial distribution of the Fukui functions (f+(r) and f−(r)), defined as:
| f+(r) = ρN+1(r) − ρN(r) | (8) |
| f−(r) = ρN(r) − ρN−1(r) | (9) |
By assuming a small distortion of the Kohn–Sham orbitals after addition or removal of one electron, the Fukui functions will resemble the electron densities of the frontier orbitals of the cluster (the HOMO and the LUMO orbitals); that is,
| f+(r) ≈ ρLUMO(r) f−(r) ≈ ρHOMO(r). | (10) |
 | ||
| Fig. 7 Three-dimensional plots showing the spacial distribution of the Fukui functions for Pt6Zr3, Pt15Zr5, and Pt36Zr12 clusters, according to eqn (5). Green spheres: Pt atoms. Pale red spheres: Zr atoms. Red and blue isosurfaces show regions with values of +0.03e− Å−3 and −0.03e− Å−3 for the density differences, respectively. | ||
Next, the vertical ionization potentials and electron affinities of some selected clusters (that is, calculated using the same geometry for the neutral and charged clusters) are plotted in Fig. 8 as a function of the number of atoms in the cluster. The ionization potentials vary between 7 and 6 eV for small clusters, with the changes becoming smaller when the cluster size is bigger than 15–20 atoms. Similar effects are found for the electron affinities, with values varying between 2 and 3 eV.
 | ||
| Fig. 8 Ionization potentials (IP) and electron affinities (EA) of PtxZry clusters as a function of cluster size. | ||
Finally, we have studied the chemical reactivity of these clusters towards CO adsorption. In order to make a direct comparison of these bimetallic clusters with the case of pure platinum, we have chosen Pt12 and Pt9Zr3 as a prototypical case. Then, for each of these clusters, we have studied the multiple adsorption of CO molecules until a saturation coverage is reached. For each additional CO molecule added to the cluster, various alternate conformations were tested with the CO molecules bonded to different sites. Panels (c) and (d) of Fig. 9 show the most stable isomer found for each coverage. It is important to comment that, for pure Pt12 with no CO molecules adsorbed, the structure shown in the figures (identical to Pt9Zr3, save for the substitution of three Pt atoms by Zr ones) is not the most stable isomer. We found, in agreement with other studies19,52 a more stable isomer with a structure having the shape of two stacked equilateral Pt6 triangles, around 0.7 eV lower in energy. However, we checked that upon addition of 2–3 CO molecules, such conformation is strongly destabilized in favour to the close-packed one shown in Fig. 9. Therefore, it makes sense to compare the reactivity of isomers with similar structural features, focussing on the effects caused by a change in stoichiometry.
In the case of pure Pt12, we found a preference towards CO binding on top of Pt atoms located at the top and bottoms triangles of the close-packed structure. On panels (a) and (b) of Fig. 9 we plot, respectively, the total and incremental CO binding energies, defined as either the total energy gained upon adsorption of N molecules:
| Ebinding = E(Pt12) + NE(CO) − E(CONPt12) | (11) |
| Eincrem = E(CON−1Pt12) + E(CO) − E(CONPt12) | (12) |
In the case of Pt9Zr3, the most stable conformations for various coverages of CO molecules are shown in panel (d) of Fig. 9. We found a marked preference for configurations where CO bridges two Pt atoms. We have also checked that, as it should be expected, binding of CO at Zr sites is much weaker, with a binding energy of only 0.7 eV. This means that, under a CO atmosphere, the CO adsorbates will exclusively be adsorbed at the Pt sites in Pt9Zr3. Such preference of CO for Pt sites at bimetallic clusters have already been reported for other metals, such as Pt–Ag, for example.19 The presence of the three Zr impurities results also in drastic changes in CO reactivity at the Pt sites themselves, in comparison with the pure Pt12 cluster; for up to 5 CO molecules, the incremental CO binding energies fluctuate around 2 eV, being 0.5 eV smaller that in the case of the pure platinum cluster. Then, for the sixth CO molecule the binding strength drops suddenly to values of the order of 1 eV. Finally, a saturation coverage seems to be reached at most with 8 CO molecules, since the next CO molecule only adsorbs with around 0.5 eV binding energy.
In conclusion, the results show that the presence of a number of Zr impurities in Pt-rich clusters leads to a strong weakening of the intrinsically high binding of CO at platinum atoms. However, it must be noted that such effect becomes apparent only when multiple CO adsorption at the cluster is considered; the adsorption of a single CO molecule at either Pt12 or Pt9Zr3 has very similar binding energy, between 2.0–2.5 eV.
4 Conclusions
The structure and chemical properties of small and medium-size bimetallic Pt–Zr clusters have been studied, focusing on concentrations rich in platinum. Due to the relatively large number of atoms, and the presence of two different species, the number of structural possibilities to consider, both in terms of geometrical and permutational isomers, becomes overwhelmingly large. In order to facilitate finding the lowest energy structures, we have explored the use of a Genetic Algorithm based on the semiempirical Sutton–Chen potential, which was modified with the addition of a Coulomb term to adequately reproduce the ordering and atomic packing in the mixed nanoalloy. In general, the Genetic Algorithm produces a family of isomers with structural features resembling the chemical ordering in the Pt3Zr bulk alloy. By relaxing afterwards the most stable conformations using DFT, substantial structural relaxations occur, leading in general to new structures. The lowest energy DFT structures are usually different from those obtained with the semiempirical potential. This is not unexpected, since this semiempirical potential only takes into account two-body effects and does not take into account some subtle bonding effects mediated by the d electrons. However, it must be recognized that by reproducing the chemical ordering in the nanoalloy, the family of isomers obtained with the semiempirical potential provides a very good start for the DFT search of the global minimum. In each case, relaxation of the collection of semiempirical local minima at the DFT level leads to a wide range of different structures. Therefore, in cases where the use of other search algorithms based solely on ab initio methods becomes prohibitively expensive due to the large cluster size (such as DFT-Basin-Hopping, etc…) this approach, which combines semiempirical calculations with subsequent DFT relaxation provides an interesting alternative to find stable conformations for transition metal nanoalloys. It is interesting to note that, in one case (Pt9Zr3) the semiempirical global minimum actually coincides with the one found at the DFT level. This can be understood because of the highly symmetrical and compact structure of this cluster.Our study, which is focussed on Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr concentrations around the 3
Zr concentrations around the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, allowed us to uncover several interesting structural effects. First, for clusters containing two or three Zr atoms, varying the amount of platinum results in growth patterns based on some highly stable symmetrical units decorated by platinum atoms. Second, by increasing the cluster size a transition takes place from highly symmetrical to amorphous-like structures. The transition occurs for clusters with 4–5 Zr atoms; that is, with a number of 15–20 atoms in the cluster. The calculated binding energies allowed us to obtain a rough estimate of relative stabilities for various clusters. Pt-rich compositions around the 3
1 stoichiometry, allowed us to uncover several interesting structural effects. First, for clusters containing two or three Zr atoms, varying the amount of platinum results in growth patterns based on some highly stable symmetrical units decorated by platinum atoms. Second, by increasing the cluster size a transition takes place from highly symmetrical to amorphous-like structures. The transition occurs for clusters with 4–5 Zr atoms; that is, with a number of 15–20 atoms in the cluster. The calculated binding energies allowed us to obtain a rough estimate of relative stabilities for various clusters. Pt-rich compositions around the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry result in some quite stable clusters, although clusters of some neighbouring compositions, such as Pt5Zr2, are also highly stable, due to a sizable electronic gap. The intrinsic stability of these clusters against segregation was also tested by calculating their mixing energies. The systematic study for 12-atom PtxZry clusters has shown that the alloying of Pt and Zr is very favourable for a broad range of relative concentrations, with mixing energies per atom of the order of 1 eV.
1 stoichiometry result in some quite stable clusters, although clusters of some neighbouring compositions, such as Pt5Zr2, are also highly stable, due to a sizable electronic gap. The intrinsic stability of these clusters against segregation was also tested by calculating their mixing energies. The systematic study for 12-atom PtxZry clusters has shown that the alloying of Pt and Zr is very favourable for a broad range of relative concentrations, with mixing energies per atom of the order of 1 eV.
The analysis of the electronic structure reveals a large electronic charge transfer from Zr to Pt atoms. At various relative Pt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr concentrations, the amount of charge donated by Zr is approximately constant, meaning that changing the stoichiometry results in a varying amount of extra negative charge on the Pt atoms. These effects influence the densities of states, which show hybridization between platinum d-states and Zr d states at the bottom of the valence band. The electronic structure of many small clusters shows a substantial HOMO–LUMO gap. For the largest clusters studied, with sizes in the range of 30–100 atoms, a minimum in the density of states develops at the Fermi level. This, undoubtedly, is a precursor of the character of the bulk alloy with the composition 3
Zr concentrations, the amount of charge donated by Zr is approximately constant, meaning that changing the stoichiometry results in a varying amount of extra negative charge on the Pt atoms. These effects influence the densities of states, which show hybridization between platinum d-states and Zr d states at the bottom of the valence band. The electronic structure of many small clusters shows a substantial HOMO–LUMO gap. For the largest clusters studied, with sizes in the range of 30–100 atoms, a minimum in the density of states develops at the Fermi level. This, undoubtedly, is a precursor of the character of the bulk alloy with the composition 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is an ordered intermetallic compound. Also, the local chemical reactivity of the surface of the PtxZry nanoalloys was studied by investigating the Fukui functions, which in general are evenly distributed around the platinum sites.
1, which is an ordered intermetallic compound. Also, the local chemical reactivity of the surface of the PtxZry nanoalloys was studied by investigating the Fukui functions, which in general are evenly distributed around the platinum sites.
Finally, the tolerance towards CO poisoning for these clusters was studied by comparing two clusters with the same number of atoms, namely Pt9Zr3 and Pt12. Our results show that the presence of Zr impurities has a sizable effect on the strength of the CO-Pt bond, effectively reducing the saturation coverage (very high por pure platinum clusters) to values well below the ratio of one CO molecule per surface platinum site. Overall, the results reported in this manuscript indicate that small PtxZry clusters around the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry possess interesting chemical properties, which could make them useful as potential new bimetallic catalysts for various reactions.
1 stoichiometry possess interesting chemical properties, which could make them useful as potential new bimetallic catalysts for various reactions.
Author contributions
Conceptualization: LMM, JAA; formal analysis: LMM, JAA; funding acquisition: LMM; visualisation: LMM; investigation: LMM, JAA; writing – original draft: LMM; writing – review & editing: LMM, JAA.Conflicts of interest
The authors have no conflicts to disclose.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Supplementary information (SI): Fig. S1 shows the lowest energy isomers of Pt10Zr4 using a genetic algorithm search based on Sutton–Chen-Coulomb empirical potentials. Fig. S2 shows the effect of omitting the Coulomb correction term. Fig. S3–S18 show the relaxed structures and relative energies of all isomers of each PtxZry cluster under study, calculated at the DFT level. Fig. S19–S23 show the projected densities of states (DOS) for the most stable isomers of each PtxZry cluster. See DOI: https://doi.org/10.1039/d5cp02864g.
Acknowledgements
Work supported by Ministerio de Ciencia e Innovación of Spain (Grant PID2022-138340OB-I00 funded by MCIN/AEI/10.13039/501100011033 and FSE+), Junta de Castilla y León (Apoyo a GIR, Project VA029G24), and University of Valladolid (GIR Nanostructure Physics). We also acknowledge networking within the COST Action CA21101 “Confined molecular systems: from a new generation of materials to the stars” (COSY) supported by COST (European Cooperation in Science and Technology).References
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CAS.
- H. Liu and E. S. Hernández, J. Nanosci. Nanotechnol., 2014, 14, 1533–1548 CAS.
- J. M. Montejano-Carrizales, M. P. Iñiguez and J. A. Alonso, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16649–16658 CAS.
- L. Liu and A. Corma, Chem. Rev., 2023, 123, 4855–4933 CAS.
- G. X. Pei, L. Zhang and X. Sun, Coord. Chem. Rev., 2024, 506, 215692 CAS.
- T. Kawawaki, Y. Imai, D. Suzuki, S. Kato, I. Kobayashi, T. Suzuki, R. Kaneko, S. Hossain and Y. Negishi, Chem. – Eur. J., 2020, 26, 16150 CAS.
- H. Mistry, A. Varela, S. Kühl, P. Strasser and B. Roldan-Cuenya, Nat. Rev. Mater., 2016, 1, 16009 CAS.
- G. Vinuesa, R. H. Aguilera-del-Toro and A. Vega, J. Magn. Magn. Mater., 2021, 524, 167636 CAS.
- L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Chem. Phys., 2008, 128, 134517 Search PubMed.
- N. Canestrari, D. Nelli and R. Ferrando, Nat. Commun., 2025, 16, 1655 CAS.
- Q. Zou, Y. Akada, A. Kuzume, M. Yoshida, T. Imaoka and K. Yamamoto, Angew. Chem., Int. Ed., 2022, 61, e202209675 CAS.
- M. K. Debe, Nature, 2012, 486, 43–51 CAS.
- O. T. Holton and J. W. Stevenson, Platinum Met. Rev., 2013, 57, 259 Search PubMed.
- A. A. J. Parker, G. Opletal and A. S. Barnard, J. Appl. Phys., 2020, 128, 014301 CrossRef CAS.
- J. Baschuk and X. Li, Int. J. Energy Res., 2001, 25, 695 CrossRef CAS.
- A. Álvarez-García, I. L. Garzón and L. M. Molina, Phys. Chem. Chem. Phys., 2025, 27, 11353–11364 RSC.
- F. R. Negreiros, A. Halder, C. Yin, A. Singh, G. Barcaro, L. Sementa, E. C. Tyo, M. J. Pellin, S. Bartling, K.-H. Meiwes-Broer, S. Seifert, P. Sen, S. Nigam, C. Majumder, N. Fukui, H. Yasumatsu, S. Vajda and A. Fortunelli, Angew. Chem., Int. Ed., 2018, 57, 1209–1213 CrossRef CAS PubMed.
- P. L. Rodríguez-Kessler, A. Muñoz-Castro and A. R. Rodríguez-Domíguez, Phys. Chem. Chem. Phys., 2021, 23, 7233–7239 RSC.
- P. L. Rodríguez-Kessler, A. Muñoz-Castro, P. A. Alonso-Dávila, F. Aguilera-Granja and A. R. Rodríguez-Domíguez, J. Alloys Compd., 2020, 845, 155897 CrossRef.
- P. Ferrari, L. M. Molina, V. E. Kaydashev, J. A. Alonso, P. Lievens and E. Janssens, Angew. Chem., Int. Ed., 2016, 55, 11059–11063 CAS.
- P. Ferrari, G. Libeert, N. M. Tam and E. Janssens, CrystEngComm, 2020, 22, 4807–4815 CAS.
- L. M. Molina, C. Arranz-Simón and J. A. Alonso, Mol. Catal., 2022, 533, 112749 CAS.
- A. Ugartemendia, J. M. Mercero, A. de Cózar, M. M. Melander, J. Akola and E. Jimenez-Izal, ChemCatChem, 2024, 16, e202301137 CAS.
- H. Okamoto, Pt–Zr (Platinum-Zirconium), J. Phase Equilb. Diffus., 2008, 29, 385 CAS.
- Y. Pan, S. Wang, L. Jia and X. Zhang, RSC Adv., 2017, 7, 54772–54778 CAS.
- M. Antlanger, W. Mayr-Schmölzer, J. Pavelec, F. Mittendorfer, J. Redinger, P. Varga, U. Diebold and M. Schmid, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035451 Search PubMed.
- Y. Pan, JOM, 2020, 72, 2419–2425 CAS.
- Y. Pan, Y. Lin, X. Wang, S. Chen, L. Wang, C. Tong and Z. Cao, J. Alloys Compd., 2015, 643, 49–55 CAS.
- W. Hume-Rothery, Prog. Mater. Sci., 1968, 13, 229–265 Search PubMed.
- J. A. Alonso and L. A. Girifalco, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 3889–3895 CAS.
- H. Wang and E. A. Carter, J. Am. Chem. Soc., 1993, 115, 2357–2362 CAS.
- J. S. Arellano, L. M. Molina, M. J. López and J. A. Alonso, Comput. Mater. Sci., 2024, 245, 113313 CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dulak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. A. L. Marques, M. J. T. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503 Search PubMed.
- R. L. Johnston, Dalton Trans., 2003, 4193–4207 RSC.
- J. M. C. Marques and F. B. Pereira, Chem. Phys. Lett., 2010, 485, 211–216 CrossRef CAS.
- J. A. Vargas, F. Buendía and M. R. Beltrán, J. Phys. Chem. C, 2017, 121, 10982–10991 CrossRef CAS.
- A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139 CrossRef.
- B. D. Todd and R. M. Lynden-Bell, Surf. Sci., 1993, 281, 191–206 CrossRef CAS.
- H.-J. Lee, Molecular Dynamics Studies of Metallic Glasses. (PhD Dissertation). California Institute of Technology, 2003 DOI:10.7907/ZE5V-VZ33.
- D. M. Deaven and K. M. Ho, Phys. Rev. Lett., 1995, 75, 288–291 CrossRef CAS PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- B. Predel, Pt–Zr (Platinum-Zirconium), in Springer Materials-The Landolt-Börnstein Database, ed. O. Madelung, 1998 Search PubMed.
- J. A. Alonso, Structure and Properties of Atomic Nanoclusters, World Scientific, 2012, 2nd edn Search PubMed.
- R. F. W. Bader, Atoms in Molecules: a Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989 Search PubMed.
- P. W. Ayers, R. C. Morrison and R. K. Roy, J. Chem. Phys., 2002, 116, 8731 CrossRef CAS.
- B.-N. Nguyen-Ha, M.-P. Pham-Ho, N. M. Tam and M. T. Nguyen, RSC Adv., 2025, 15, 19273–19286 RSC.
| This journal is © the Owner Societies 2026 |