 Open Access Article
Open Access ArticleShape modification of mineral inclusions in diamond: thermodynamic and kinetic considerations
M.
Bruno
 *,
S.
Ghignone
*,
S.
Ghignone
 ,
F.
Boero
and
D.
Aquilano
,
F.
Boero
and
D.
Aquilano

Dipartimento di Scienze della Terra, Università degli Studi di Torino, Via Valperga Caluso 35, 10125, Torino (TO), Italy. E-mail: marco.bruno@unito.it
First published on 20th November 2025
Abstract
The study of mineral inclusions in diamonds is attracting increasing interest among the scientific community of mineralogists and petrologists. A question that has recently been addressed is whether the shape of solid inclusions is immutable once trapped in the diamond or it can evolve over time until it manifests an equilibrium form. In this paper, we approach this topic by means of thermodynamic and kinetic considerations. The concept of equilibrium shape is revisited by inserting the Gibbs–Wulff theorem into a new perspective to fit the context of a mineral inclusion. We then demonstrate that it is currently not possible to determine the equilibrium shape of a mineral inclusion in a diamond, due to the large number of calculations that need to be performed. Successively, kinetic considerations on the formation of the equilibrium shape are made. It is shown that the shape evolution of an inclusion requires a significant amount of mass transfer at constant volume and the data currently at our disposal do not allow the estimation of the time needed to reach the equilibrium shape.
1. Introduction
In recent years, there has been a growing interest in the study of mineral inclusions in diamonds.1–16 In particular, many studies have been dedicated to clarifying whether the minerals that now reside as inclusions in the diamond are formed before the diamond hosting them (i.e., protogenetic inclusions) or grow simultaneously and through the same reaction (i.e., syngenetic inclusions; the inclusion should presumably be in equilibrium with the diamond-forming medium). A protogenetic inclusion can partly or completely re-equilibrate with the diamond-forming fluid (or melt) through intracrystalline diffusion and/or exchange reactions before (or during) its encapsulation in it; therefore, its current composition could be completely different from the original one. There are also epigenetic inclusions, which form along the fractures (or cleavage planes) of pre-formed diamonds.The identification of syngenetic inclusions is of fundamental importance in diamond studies. Since diamond behaves as an inert container, any geological information extracted from a syngenetic inclusion, such as pressure (P) and temperature (T) of formation, age, and geochemistry of the source medium (i.e., fluid or melt), should also be valid for the host diamond. It should be noted that the concept of syngenesis/protogenesis can be extended to any inclusion and host mineral. For example, garnet is a phase that is usually rich in inclusions but, historically, an in-depth analysis of its inclusions has never been performed. Therefore, the distinction between syngenesis and protogenesis is not a simple academic exercise, but a fundamental requirement for understanding geological phenomena.
The three most commonly described potential indicators of syngenesis are: (i) the morphological criterion (MC), when the diamond imposes its morphology on the inclusions;6,17–22 (ii) the growth zones criterion (GC), if the interruption of the diamond growth zones occurs by the diamond/inclusion contact;21 (iii) the epitaxial criterion (EC), when an epitaxial relationship sets up between the inclusion and its host.6,19,20,22,23
The purpose of this work is not to discuss the validity of the above criteria. They have already been extensively discussed,1,24,25 and their unreliability in discriminating between syngenesis and protogenesis was demonstrated. Instead, here we want to discuss in more detail, from both thermodynamic and kinetic points of view, what may be the mechanisms that lead a mineral inclusion to acquire a diamond-imposed morphology (i.e., the shape of a negative diamond crystal). The hypotheses proposed so far are the following:
(i) Diamond imposes its morphology on the mineral inclusion only when the diamond and inclusion are formed simultaneously (syngenesis), owing to diamond's much greater formation energy,20 also named the crystalloblastic force of diamond faces. As highlighted by Bruno et al.:24 “An ill-defined force is invoked to explain the morphology of the inclusions, a force whose origin does not exist in crystal growth theory, the relevance of which is not clear”.
(ii) Post-entrapment shape maturation process:14,26 the imposed morphology is not due to syngenesis, but developed after the entrapment of the inclusion. That is, a syngenetic or protogenetic inclusion trapped in the diamond develops successively a diamond-imposed morphology by minimizing the Gibbs energy of a closed system by rearranging the diamond/inclusion interfaces through diffusion processes.
(iii) The imposed morphology of a protogenetic inclusion is acquired during its entrapment:24 the diamond-imposed morphology is due to a low diamond growth rate associated with a low dissolution rate of the reabsorbed mineral; hence, the inclusion/diamond system can adapt to develop the lowest interface energy.
As reported by Cesare et al.,26 “the possibility of a change of shape of inclusions within their host would greatly impact the applications of elastic barometry, as well as all other approaches that require or assume inclusions to maintain a constant shape”. Furthermore, the ability to estimate the time required to observe a possible change in the shape of a solid inclusion could provide information on the P–T conditions experienced by the rock during its geological history.
In this regard, a brief review of previous articles addressing this topic will be carried out, but before the discussion, the concept of the equilibrium shape (ES) of a crystal is revisited to fit into the context of a mineral inclusion. Furthermore, some kinetic considerations on the formation of the equilibrium shape are made and a possible strategy to assess whether an inclusion is protogenetic or syngenetic is described.
2. Equilibrium shape of a mineral inclusion
The equilibrium shape (ES) of a crystal A included in a crystal B is ruled by the Gibbs–Wulff theorem:27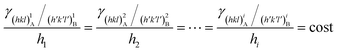 | (1) |
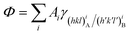 with the following constraints: (i) a mineral inclusion has a constant volume and (ii) the morphology of the inclusion is a convex polyhedron; Ai is the area of the i-th interface. The system inclusion/host will tend to lower its Gibbs energy by generating the interfaces allowing the minimum of Φ.
with the following constraints: (i) a mineral inclusion has a constant volume and (ii) the morphology of the inclusion is a convex polyhedron; Ai is the area of the i-th interface. The system inclusion/host will tend to lower its Gibbs energy by generating the interfaces allowing the minimum of Φ.
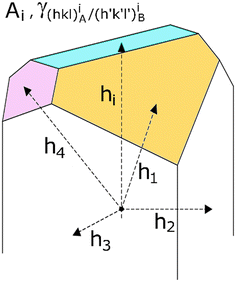 | ||
| Fig. 1 Equilibrium shape (ES) of a mineral inclusion A included in a crystal B determined through the Gibbs–Wulff theorem. The ES is calculated by tracing segments of length hi proportional to the surface tensions γi. All these segments start from an arbitrary central point and are perpendicular to the respective faces having area Ai. The smallest polyhedron obtained represents the ES. Modified from Aquilano et al.28 | ||
According to this theorem, mineral inclusions having different crystallographic orientation relationships (i.e., how the crystallographic axes of the inclusion are arranged with respect to those of the host phase; CORs hereinafter) will develop different ESs, to minimize the thermodynamic quantity Φ. Initially, when a mineral inclusion A is trapped in the hosting phase B, its morphology is far from that of equilibrium, and the value of the function Φ is not at a minimum. Only subsequently, assuming that the rock remains at a high temperature for a sufficient time, the inclusion can evolve towards the ES, by rearranging the (hkl)iA/(h′k′l′)iB interfaces until developing those that minimize Φ, i.e. Φ*(COR), for that peculiar COR. We must therefore expect that, independently by their volume, mineral inclusions with different CORs will develop different ESs, not being able to generate the same (hkl)iA/(h′k′l′)iB interfaces. We assume that the bulk structure of the mineral inclusion is not involved in this process of interface adjustment; consequently, the COR between the inclusion and host does not vary. We cannot rule out such a bulk structural modification a priori, but we believe it to be highly unlikely due to the high energetic cost and the very long time needed for it to occur. Moreover, we assume that there is no fluid between the inclusion and host; thus, we are dealing with dry interfaces.
To better explain this concept, let us suppose that two mineral inclusions of the phase A (tetragonal system; point group: 4/mmm; cell parameters: a0 = b0, c0 = 2a0) are hosted in the same phase B (cubic system; point group: m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with the following CORs:
m) with the following CORs:
(i) the directions of the crystallographic axes of the phases A and B coincide: [100]A ≡ [100]B, [010]A ≡ [010]B and [001]A ≡ [001]B (COR1 hereinafter; Fig. 2a);
(ii) the crystallographic axis yA coincides with yB, while the crystallographic axis zA is rotated by 45°, around the common direction [010]A ≡ [010]B, with respect to the crystallographic axis zB: [100]A ≡ [100]B, [010]A ≡ [010]B and [001]A ≡ [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01]B (COR2 hereinafter; Fig. 2b).
01]B (COR2 hereinafter; Fig. 2b).
We also suppose that the two mineral inclusions of phase A are not in contact with each other.
The two mineral inclusions of A cannot develop the same ES, but they are forced to generate different interfaces to reduce the Gibbs energy of the system inclusion/host. The ES of the mineral inclusion A with COR1 (corresponding to Φ*(COR1)) is composed of the following interfaces (Fig. 2a): (001)1A/(001)1B, (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B, (100)3A/(100)3B and (
)2B, (100)3A/(100)3B and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4A/(
00)4A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4B. According to the point groups considered in our example (i.e., 4/mmm for A and m
00)4B. According to the point groups considered in our example (i.e., 4/mmm for A and m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m for B), (00
m for B), (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B is equivalent by symmetry to (001)1A/(001)1B and, similarly, (
)2B is equivalent by symmetry to (001)1A/(001)1B and, similarly, (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4A/(
00)4A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4B is equivalent to (100)3A/(100)3B. This implies that γ(001)1A/(001)1B = γ(00
00)4B is equivalent to (100)3A/(100)3B. This implies that γ(001)1A/(001)1B = γ(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B and γ(100)3A/(100)3B = γ(
)2B and γ(100)3A/(100)3B = γ(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4A/(
00)4A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00)4B. Instead, the ES of the inclusion A with COR2 (corresponding to Φ*(COR2)) is composed of other interfaces (Fig. 2b): (102)1A/(001)1B, (
00)4B. Instead, the ES of the inclusion A with COR2 (corresponding to Φ*(COR2)) is composed of other interfaces (Fig. 2b): (102)1A/(001)1B, (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B, (
)2B, (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)3A/(0
02)3A/(0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)3B, (10
0)3B, (10![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )4A/(010)4B, (001)5A/(
)4A/(010)4B, (001)5A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)5B and (00
01)5B and (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6A/(10
)6A/(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6B. In this case, (102)1A/(001)1B, (
)6B. In this case, (102)1A/(001)1B, (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B, (
)2B, (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)3A/(0
02)3A/(0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)3B and (10
0)3B and (10![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )4A/(010)4B are equivalent by symmetry to each other, as well as the interfaces (001)5A/(
)4A/(010)4B are equivalent by symmetry to each other, as well as the interfaces (001)5A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)5B and (00
01)5B and (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6A/(10
)6A/(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6B. Thus, the following relations hold: γ(102)1A/(001)1B = γ(
)6B. Thus, the following relations hold: γ(102)1A/(001)1B = γ(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )2A/(00
)2A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )2B = γ(
)2B = γ(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 02)3A/(0
02)3A/(0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)3B = γ(10
0)3B = γ(10![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )4A/(010)4B and γ(001)5A/(
)4A/(010)4B and γ(001)5A/(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01)5B = γ(00
01)5B = γ(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6A/(00
)6A/(00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )6B.
)6B.
It is worth noting that COR1 and COR2 are only two of the infinite CORs that a protogenetic inclusion can acquire when entrapped in the hosting phase. We can associate an ES with each of these CORs and then we can state that the minimum of the quantity Φ is a function of the COR, Φ*(COR) (Fig. 3). Φ*(COR) is a continuous and bounded function: among all the possible CORs, there will be one (i.e., COR*) for which Φ*(COR) has the lowest value, Φ*(COR*) (the absolute minimum of the function Φ*(COR)), while there will be other CORs (e.g., COR1) that can be in a local minimum of Φ*(COR). In any case, the values of the function Φ*(COR) will be between Φ*(COR*) and a maximum value that will occur for a particular COR. In summary, for each inclusion/host system there exists only an absolute ES, corresponding to the absolute minimum of the function Φ*(COR) related to a specific orientation of the inclusion with respect to the host, but there are infinite ESs for all the other CORs.
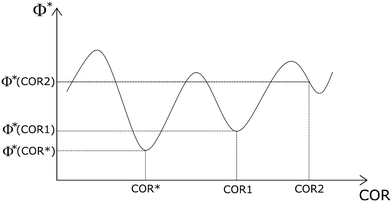 | ||
Fig. 3 Schematic diagram representing the function 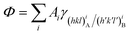 . On the abscissa axis, different orientations (COR1, COR2, etc.…) of the crystal relationships (CORs) are represented. On the y-axis, the corresponding functions Φ*(COR) have been drawn. It is worth remembering that each COR value represents only one of the infinite CORs that a protogenetic inclusion can acquire when entrapped in the hosting phase. The asterisk * indicates the minimum of the Φ quantity. Φ*(COR) is a continuous and bounded function: among all the possible CORs, there will be one (i.e., COR*) for which Φ*(COR) has the lowest value, Φ*(COR*) (the absolute minimum of Φ*(COR)), while there will be other CORs (e.g., COR1, COR2, etc.…,) that can be in a local minimum of Φ*(COR). See paragraph 2 to find the ES of a crystal system A/B, which is ruled by the Gibbs–Wulff theorem.27 . On the abscissa axis, different orientations (COR1, COR2, etc.…) of the crystal relationships (CORs) are represented. On the y-axis, the corresponding functions Φ*(COR) have been drawn. It is worth remembering that each COR value represents only one of the infinite CORs that a protogenetic inclusion can acquire when entrapped in the hosting phase. The asterisk * indicates the minimum of the Φ quantity. Φ*(COR) is a continuous and bounded function: among all the possible CORs, there will be one (i.e., COR*) for which Φ*(COR) has the lowest value, Φ*(COR*) (the absolute minimum of Φ*(COR)), while there will be other CORs (e.g., COR1, COR2, etc.…,) that can be in a local minimum of Φ*(COR). See paragraph 2 to find the ES of a crystal system A/B, which is ruled by the Gibbs–Wulff theorem.27 | ||
Based on the above, determining an ES for a given COR turns out to be a very difficult task, requiring the calculation of an unknown number of interfacial energies. For those interested in the calculation strategy to adopt for the determination of the interfacial energy at the quantum-mechanical or empirical level, we recommend reading the articles by Bruno's research group.29–32 To our knowledge, there are not theoretical estimates or experimental evidence of the mineral inclusions' ES.
The only estimates of interface energies between a mineral inclusion and a diamond host were provided by Bruno et al.,29,30 who carried out ab initio calculations on four diamond (D)/forsterite (Fo) interfaces: γ(111)D/(001)Fo = 6.459, γ(001)D/(021)Fo = 6.477 and γ(110)D/(101)Fo = 6.375 J m−2. The interfaces considered are related to the following CORs:
• (001)D/(001)Fo: [110]D ≡ [100]Fo, [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]D ≡ [010]Fo and [001]D ≡ [001]Fo
0]D ≡ [010]Fo and [001]D ≡ [001]Fo
• (111)D/(001)Fo: [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01]D ≡ [100]Fo, [0
01]D ≡ [100]Fo, [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1]D ≡ [110]Fo and [111]D ≡ [001]Fo
1]D ≡ [110]Fo and [111]D ≡ [001]Fo
• (001)D/(021)Fo: [110]D ≡ [100]Fo, [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]D ≡ [0
0]D ≡ [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2]Fo and [001]D ≡ ⊥(021)Fo
2]Fo and [001]D ≡ ⊥(021)Fo
• (110)D/(101)Fo: [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]D ≡ [010]Fo, [010]D ≡ [
]D ≡ [010]Fo, [010]D ≡ [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01]Fo and [110]D ≡ ⊥(101)Fo
01]Fo and [110]D ≡ ⊥(101)Fo
Interestingly, despite the different crystallographic orientations between diamond and forsterite, the values of the interface energy are very high and similar, being in the range of 6.105–6.477 J m−2. This is due to a very low chemical affinity between diamond and forsterite, which translates into a very low adhesion energy β(hkl)D/(h′k′l′)Fo (0.243–0.391 J m−2),30 a fundamental thermodynamic quantity related to the interface energy by means of Duprè's relation:27
| γ(hkl)D/(h′k′l′)Fo = γ(hkl)D + γ(h′k′l′)Fo − β(hkl)D/(h′k′l′)Fo | (2) |
Now, (i) supposing a low constant value of the adhesion energy for every diamond/forsterite interface (β(hkl)D/(h′k′l′)Fo = 0.300 J m−2), of the same order of magnitude of the values calculated by Bruno et al.,30 (ii) using the most accurate and reliable surface energy values of forsterite determined at the ab initio level by Demichelis et al.33 and (iii) the surface energy values of diamond calculated always at the ab initio level by De La Pierre et al.,34 we apply relation (2) to estimate all the diamond/forsterite interface energies listed in Table 1.
| Forsterite face | γ (h′k′l′)Fo | Diamond face | γ (hkl)D | Interface | γ (hkl)D/(h′k′l′)Fo |
|---|---|---|---|---|---|
| (010)Fo | 0.930 | (100)D | 4.825 | (100)D/(010)Fo | 5.455 |
| (111)D | 3.759 | (111)D/(010)Fo | 4.389 | ||
| (110)D | 5.539 | (110)D/(010)Fo | 6.169 | ||
| (101)Fo | 1.300 | (100)D | 4.825 | (100)D/(101)Fo | 5.825 |
| (111)D | 3.759 | (111)D/(101)Fo | 4.759 | ||
| (110)D | 5.539 | (110)D/(101)Fo | 6.539 | ||
| (111)Fo | 1.380 | (100)D | 4.825 | (100)D/(111)Fo | 5.905 |
| (111)D | 3.759 | (111)D/(111)Fo | 4.839 | ||
| (110)D | 5.539 | (110)D/(111)Fo | 6.619 | ||
| (001)Fo | 1.330 | (100)D | 4.825 | (100)D/(001)Fo | 5.855 |
| (111)D | 3.759 | (111)D/(001)Fo | 4.789 | ||
| (110)D | 5.539 | (110)D/(001)Fo | 6.569 | ||
| (110)Fo | 1.730 | (100)D | 4.825 | (100)D/(110)Fo | 6.255 |
| (111)D | 3.759 | (111)D/(110)Fo | 5.189 | ||
| (110)D | 5.539 | (110)D/(110)Fo | 6.969 | ||
| (120)Fo | 1.090 | (100)D | 4.825 | (100)D/(120)Fo | 5.615 |
| (111)D | 3.759 | (111)D/(120)Fo | 4.549 | ||
| (110)D | 5.539 | (110)D/(120)Fo | 6.329 | ||
| (021)Fo | 1.440 | (100)D | 4.825 | (100)D/(021)Fo | 5.965 |
| (111)D | 3.759 | (111)D/(021)Fo | 4.899 | ||
| (110)D | 5.539 | (110)D/(021)Fo | 6.679 |
We can observe from Table 1 that the surface energy values of diamond faces are much greater than those of forsterite: the average value of diamond surface energies, 〈γD〉 = 4.708 J m−2, is about three and a half times that of forsterite, 〈γFo〉 = 1.314 J m−2. Then, it is plausible to assume that the interface energy value of any forsterite/diamond interface is dominated by the diamond surface energy. Such a conclusion is probably true for all silicates included in diamond (e.g., garnet and pyroxene): it is reasonable to assume a very low chemical affinity between all of the silicates and diamond and, consequently, that the silicate/diamond interface energies are dominated by the diamond surface energy. This is also suggested by the surface energy value of the {001} form of pyrope [Mg3Al2(SiO4)3], 1.712 J m−2,35 which is of the same order of magnitude as the surface energy values of forsterite (Table 1).
3. Kinetic considerations on the formation of the equilibrium shape
As already specified in the paper by Bruno et al.,24 although thermodynamics allows for post entrapment modification of the inclusions, there is no information about the kinetics of the process. However, it is evident that the shape evolution of the inclusion requires a significant amount of mass transfer, both from the host and inclusions, which must occur at constant volume (i.e., closed system) by means of growth/dissolution processes occurring at the host/inclusion interface, coupled with grain boundary diffusion. In order to give an idea of the amount of matter involved in this process, let us consider an inclusion of a tetragonal mineral (A) in diamond (B) having edge lengths a* and c* and the following COR (Fig. 4): [100]A ≡ [100]B, [010]A ≡ [010]B and [001]A ≡ [001]B. Then, let us imagine that this inclusion will evolve at constant volume until reaching its ES defined by the edge lengths a and c, with a* > a and c* < c. If we suppose that the shape evolution occurs at a fixed centre of gravity, that is the centre of gravity of the mineral inclusion before and after the evolution is not changed, then the amount of matter of phases A (ΔmA; moles) and B (ΔmB; moles) involved in the shape evolution is easily determined by the relationship: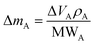 | (3) |
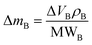 | (4) |
| ΔV = c*(a*2 − a2) | (5) |
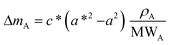 | (6) |
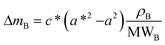 | (7) |
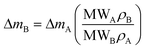 | (8) |
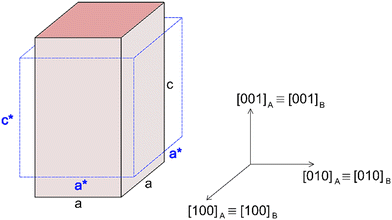 | ||
| Fig. 4 Schematic drawing representing a tetragonal mineral (A) in diamond (B) having edge lengths a* and c* and the following CORs: [100]A ≡ [100]B, [010]A ≡ [010]B and [001]A ≡ [001]B. | ||
If the forsterite/diamond interface is dry (i.e., no fluids separating the phases), in order to estimate the time required to move all this matter, it is necessary to know the grain boundary diffusion coefficients of the involved elements (Fe, Si, O and C) as a function of temperature and pressure; data not currently available. The rate of the morphological evolution of the inclusion will be limited by the element with the lowest mobility, the one with the lowest grain boundary diffusion coefficient.
Instead, if there is a fluid at the forsterite/diamond interface (wet interface), dissolution/growth processes of the phases must be considered to model the evolution of the inclusion morphology, together with the diffusion of elements within the fluid. It is highly probable that the presence of a thin fluid at the mineral/host interface accelerates the kinetics of the process, favouring more rapid evolution of the inclusion's shape towards equilibrium. However, to our knowledge there are no data that allow a reliable estimation of the time required to reach equilibrium. It is evident that the smaller the inclusion, the shorter the time needed to obtain the equilibrium morphology, since the amount of the material to be reorganized is smaller.
Recently, phase-field modelling has been used to analyse the shape evolution of crystals,36,37 but never for solid inclusions in minerals. This computational methodology could provide an estimation of the time required to reach the equilibrium shape defined by the Gibbs–Wulff theorem. However, the application of such advanced models always requires reliable data on intergranular diffusion coefficients, which are currently unknown for the silicate/diamond system.
4. A strategy to evaluate, through observation, the existence of post-entrapment modification
To evaluate whether the post-entrapment modification of an inclusion can occur in diamond, Bruno et al.24 proposed a strategy, described below, which is based on the morphological evolution of mineral inclusions.First of all, it is fundamental to find a diamond containing two or more mineral inclusions with the same crystallographic orientation and that exhibit both diamond-imposed and lobed morphologies; the same orientation ensures that the inclusions are relicts of an original monocrystal (i.e., protogenetic inclusions). The crystallographic orientations of the inclusions in diamond can be determined either by single-crystal X-ray diffraction or electron back scatter diffraction (EBSD). The coexistence of iso-oriented inclusions with both imposed and lobed morphologies in the same diamond suggests the following two possible hypotheses if we assume that they come from a single resorbed original crystal:
(i) The inclusion shape, once trapped in the diamond, is not modified. Then, their different morphologies should follow the growth and dissolution rates of the diamond and mineral undergoing resorption, respectively. Likely, low diamond growth, along with a low dissolution rate of the reabsorbed mineral, favours the inclusions with a diamond-imposed morphology to minimise the system energy, generating inclusion/diamond interfaces with the lowest interfacial energies. Conversely, both high diamond growth rates and high dissolution rates of the inclusion do not readjust the inclusion/diamond interfaces; thus, it is reasonable to expect crystals with a lobed morphology.
(ii) The inclusion shape can change, once trapped in the diamond, through thermally activated grain-boundary diffusion along dry (or wet) interphase boundaries, so generating a crystal habit which reflects that of the host diamond (ES of the inclusion, as described in paragraph 2). If this can occur, inclusions with both imposed and lobed morphologies mean that the maturation process has involved only some relicts of the partially resorbed single crystal. This can occur only when the inclusions have been trapped at different times; the first to be captured into the diamond are those that have a longer time to adjust their morphology. In practice, inclusions with an imposed morphology, more than those with the lobed one, should lie closer to the central growth zone of the diamond. Thus, it is crucial to associate the mineral inclusions with the growth sectors of the diamond to disprove or validate the post-entrapment shape maturation process.
Subsequently, it is essential to compare the inclusions' places with their position in the diamond growth sectors, which can be observed by means of cathodoluminescence (CL). These data being collected, two cases can be considered for the inclusion: (1) those with an imposed morphology are located closer to the central growth zone of the diamond than the lobed ones (Fig. 5a). Thus, one cannot establish whether such a morphology distribution is due to post-entrapment modification or if it is syngenetic to the growth of the host (i.e., a consequence of the growth and dissolution rates of the host and resorbing mineral, respectively); (2) the lobed ones are located closer to the central growth zone of the diamond than those with an imposed morphology (Fig. 5b). In the last case, one can state that post-entrapment modification did not occur. Indeed, since the first inclusions to be captured into the host (diamond or garnet) will be those having a longer time to fix their morphology, the lobed morphologies near the central growth zone cannot be explained by post-entrapment modification.
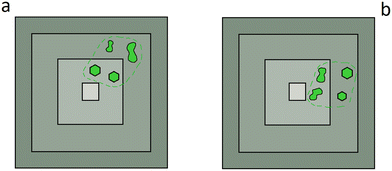 | ||
| Fig. 5 A schematic diagram representing two cases of mineral inclusions (green) in diamond (grey); growth sectors of diamond are represented by different shades of grey. (a) Inclusions with an imposed morphology are closer to the central growth zone of the host phase (diamond) than those with a lobed morphology: post-entrapment modification may have occurred; (b) inclusions with a lobed morphology are closer to the central growth zone of the host phase (diamond) than those with an imposed morphology: post-entrapment modifications cannot occur. The green dotted line marks the edge of the crystal before its resorption. Modified from Bruno et al.24 | ||
It is worth highlighting that this analysis must be done on inclusions of similar size. In fact, small inclusions require much less mass transfer (and then less time) than larger ones to adjust their shapes.
5. Conclusions
Within the present paper, we address a topic of great interest about the shape evolution of a mineral inclusion in diamond; this topic being approached through thermodynamic and kinetic considerations.First, the equilibrium shape (ES) of a crystal was revisited to fit into the context of a mineral inclusion. The Gibbs–Wulff theorem is described in detail and inserted in a new perspective. Then, we showed that determining the ES of a mineral inclusion is a very difficult task, since it requires the calculation of an unknown number of interfacial energies. It is currently not possible to say with certainty whether a given inclusion in a diamond has reached its ES.
Subsequently, kinetic considerations on the ES formation were made. The shape evolution of the inclusion requires a significant amount of mass transfer at constant volume (i.e., a closed system) by means of growth/dissolution processes occurring at the host/inclusion interface, coupled with grain boundary diffusion. Unfortunately, the data currently at our disposal do not allow the estimation of the time needed to reach the ES: as an example, intergranular diffusion coefficients and growth/dissolution rates of diamond and its inclusions at the T and P of interest are missing.
Finally, a method proposed by Bruno et al.24 to evaluate whether the post-entrapment modification of an inclusion can occur in diamond is described, which requires knowing: (i) how the crystal axes of the inclusion are arranged relative to those of the host phase and (ii) the position of the inclusions with respect to the diamond growth sectors.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
All the data are reported in the main text of the paper.Acknowledgements
We thank the reviewers for their comments, which have been useful to improve the quality of our manuscript.References
- F. Nestola, P. Nimis, R. J. Angel, S. Milani, M. Bruno, M. Prencipe and J. W. Harris, Olivine with diamond-imposed morphology included in diamonds: Syngenesis or protogenesis?, Int. Geol. Rev., 2014, 56, 1658–1667 CrossRef.
- F. Nestola, D. E. Jacob, M. G. Pamato, L. Pasqualetto, B. Oliveira, S. Greene, S. Perritt, I. Chinn, S. Milani, N. Kueter, N. Sgreva, P. Nimis, L. Secco and J. W. Harris, Protogenetic garnet inclusions and the age of diamonds, Geology, 2019, 47, 431–4349 CrossRef CAS.
- P. Nimis, F. Nestola, M. Schiazza, R. Reali, G. Agrosì, D. Mele, G. Tempesta, D. Howell, M. T. Hutchison and R. Spiess, Fe-rich ferropericlase and magnesiowüstite inclusions reflecting diamond formation rather than ambient mantle, Geology, 2018, 47, 27–30 CrossRef.
- P. Nimis, R. J. Angel, M. Alvaro, F. Nestola, J. W. Harris, N. Casati and F. Marone, Crystallographic orientations of magnesiochromite inclusions in diamonds: What do they tell us?, Contrib. Mineral. Petrol., 2019, 174, 29 CrossRef.
- L. Pasqualetto, F. Nestola, D. E. Jacob, M. G. Pamato, B. Oliveira, S. Perritt, I. Chinn, P. Nimis, S. Milani and J. W. Harris, Protogenetic clinopyroxene inclusions in diamond and Nd diffusion modelling-Implications for diamond dating, Geology, 2022, 50, 1038–1042 CrossRef CAS.
- D. F. Wiggers de Vries, M. R. Drury, D. A. M. de Winter, G. P. Bulanova, D. G. Pearson and G. R. Davies, Three-dimensional cathodoluminescence imaging and electron backscatter diffraction: Tools for studying the genetic nature of diamond inclusions, Contrib. Mineral. Petrol., 2011, 161, 565–579 CrossRef CAS.
- R. D. Neuser, H.-P. Schertl, A. M. Logvinova and N. V. Sobolev, An EBSD study of olivine inclusions in Siberian diamonds: Evidence for syngenetic growth?, Geol. Geofiz., 2015, 56, 321–329 Search PubMed.
- D. E. Jacob, S. Piazolo, A. Schreiber and P. Trimby, Redox-freezing and nucleation of diamond via magnetite formation in the Earth's mantle, Nat. Commun., 2016, 7, 11891 CrossRef CAS PubMed.
- S. Milani, F. Nestola, R. J. Angel, P. Nimis and J. W. Harris, Crystallographic orientations of olivine inclusions in diamonds, Lithos, 2016, 265, 312–316 CrossRef CAS.
- G. R. Davies, Q. van den Heuvel, S. Matveev, M. R. Drury, I. L. Chinn and M. U. Gress, A combined cathodoluminescence and electron backscatter diffraction examination of the growth relationships between Jwaneng diamonds and their eclogitic inclusions, Mineral. Petrol., 2018, 112, 231–242 CrossRef CAS.
- N. V. Sobolev, Y. V. Seryotkin, A. M. Logvinova, A. D. Pavlushin and S. S. Ugap'eva, Crystallographic orientation and geochemical features of mineral inclusions in diamonds, Geol. Geofiz., 2020, 61, 634–649 Search PubMed.
- M. G. Pamato, D. Novella, D. E. Jacob, B. Oliveira, D. G. Pearson, S. Greene, J. C. Afonso, M. Favero, T. Stachel, M. Alvaro and F. Nestola, Protogenetic sulfide inclusions in diamonds date the diamond formation event using Re-Os isotopes, Geology, 2021, 49, 941–945 CrossRef CAS.
- S. Lorenzon, M. Wenz, P. Nimis, S. D. Jacobsen, L. Pasqualetto, M. G. Pamato, D. Novella, D. Zhang, C. Anzolini, M. Regier, T. Stachel, D. G. Pearson, J. W. Harris and F. Nestola, Dual origin of ferropericlase inclusions within super-deep diamonds, Earth Planet. Sci. Lett., 2023, 608, 118081 CrossRef CAS.
- V. Afanasiev, S. Ugapeva and A. Logvinova, Shape Change of Mineral Inclusions in Diamond–The Result of Diffusion Processes, Minerals, 2024, 14, 594 CrossRef CAS.
- V. M. Kvasnytsya, Analyzing the polyhedral shape of mineral inclusions in diamond crystals using goniometric data, J. Superhard Mater., 2024, 46, 94–105 CrossRef.
- M. M. Wincott, S. C. Kohn and I. J. Parkinson, Six olivine inclusions in diamond are remnants of a syngenetic monocrystal, Lithos, 2025, 496–497, 107953 CrossRef CAS.
- J. W. Harris, The recognition of diamond inclusions. Pt. 1: Syngenetic inclusions, Ind. Diamond Rev., 1968, 28, 402–410 Search PubMed.
- S. I. Futergendler and V. A. Frank-Kamenetsky, Oriented inclusions of olivine, garnet and chrome-spinel in diamonds, Zap. Vses. Mineral. Obshch., 1961, 90, 230–236 Search PubMed.
- N. V. Sobolev, Deep-seated inclusions in kimberlites and the problem of the composition of the upper mantle, American Geophysical Union, Washington D.C, 1977 Search PubMed.
- J. W. Harris and J. J. Gurney, in Properties of diamond, ed. J. E. Field, Academic Press, London, 1979, pp. 555–591 Search PubMed.
- G. P. Bulanova, The formation of diamond, J. Geochem. Explor., 1995, 53, 1–23 CrossRef CAS.
- D. G. Pearson and S. B. Shirey, in Application of radiogenic isotopes to ore deposit research and exploration, ed. D. D. Lambert and J. Ruiz, Society of Economic Geologists, Michigan, 1999, pp. 143–171 Search PubMed.
- Y. L. Orlov, The mineralogy of the diamond, John Wiley & Sons, 1977 Search PubMed.
- M. Bruno, S. Ghignone, D. Aquilano and F. Nestola, Is the imposition of diamond morphology on mineral inclusions a syngenetic or post-genetic process with respect to diamond formation?, Cryst. Growth Des., 2023, 23, 5279–5288 CrossRef CAS.
- M. Bruno, S. Ghignone, D. Aquilano and F. Nestola, A critique of using epitaxial criterion to discriminate between protogenetic and syngenetic mineral inclusions in diamond, Sci. Rep., 2024, 14, 8674 CrossRef CAS PubMed.
- B. Cesare, M. Parisatto, L. Mancini, L. Peruzzo, M. Franceschi, T. Tacchetto, S. Reddy, R. Spiess, F. Nestola and F. Marone, Mineral inclusions are not immutable: Evidence of post-entrapment thermally-induced shape change of quartz in garnet, Earth Planet. Sci. Lett., 2021, 555, 116708 CrossRef CAS.
- B. Mutaftschiev, The Atomistic Nature in Crystal Growth, Springer Series in Materials Science, Springer-Verlag, Berlin, 2001 Search PubMed.
- D. Aquilano and G. Sgualdino, in Meccanismi della crescita cristallina: fondamenti e applicazioni, ed. D. Aquilano, G. Artioli and M. Moret, Università degli Studi di Milano, Milano, 2003, pp. 2–80 Search PubMed.
- M. Bruno, M. Rubbo, L. Pastero, F. R. Massaro, F. Nestola and D. Aquilano, Computational Approach to the Study of Epitaxy: Natural Occurrence in Diamond/Forsterite and Aragonite/Zabuyelite, Cryst. Growth Des., 2015, 15, 2979–2987 CrossRef CAS.
- M. Bruno, M. Rubbo, D. Aquilano, F. R. Massaro and F. Nestola, Diamond and its olivine inclusions: A strange relation revealed by ab initio simulations, Earth Planet. Sci. Lett., 2016, 435, 31–35 CrossRef CAS.
- M. Bruno, F. R. Massaro and M. Rubbo, A new computational approach to the study of epitaxy: the calcite/dolomite case, CrystEngComm, 2017, 19, 3939–3946 RSC.
- M. Bruno, L. Pastero, A. Cotellucci and D. Aquilano, Epitaxy: a methodological approach to the study of an old phenomenon, CrystEngComm, 2022, 24, 4165–4173 RSC.
- R. Demichelis, M. Bruno, F. R. Massaro, M. Prencipe, M. De La Pierre and F. Nestola, First-Principle Modelling of Forsterite Surface Properties: Accuracy of Methods and Basis Sets, J. Comput. Chem., 2015, 36, 1439–1445 CrossRef CAS PubMed.
- M. De La Pierre, M. Bruno, C. Manfredotti, F. Nestola, M. Prencipe and C. Manfredotti, The (100), (111) and (110) surfaces of diamond: an ab initio B3LYP study, Mol. Phys., 2014, 112, 1030–1039 CrossRef.
- R. F. Massaro, M. Bruno and F. Nestola, Analysis of the Configurations of a Crystal Surface. Pyrope (Mg3Al2Si3O12) as a Case Study, Cryst. Growth Des., 2014, 14, 2357–2365 CrossRef.
- R. S. Qin and H. K. D. H. Bhadeshia, Phase-field model study of the crystal morphological evolution of hcp metals, Acta Mater., 2009, 57, 3382–3390 CrossRef CAS.
- P. C. Bollada, P. K. Jimack and A. M. Mullis, Phase field modelling of hopper crystal growth in alloys, Sci. Rep., 2023, 13, 12637 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |

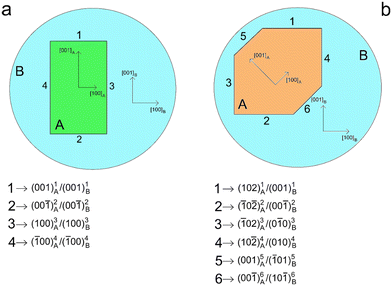
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) 01]B. In (b), [001]A is anticlockwise rotated by 45° around [010]A ≡ [010]B with respect to [001]B. In (a), the ES of the mineral inclusion A is defined by the interfaces: (001)1A/(001)1B, (00
01]B. In (b), [001]A is anticlockwise rotated by 45° around [010]A ≡ [010]B with respect to [001]B. In (a), the ES of the mineral inclusion A is defined by the interfaces: (001)1A/(001)1B, (00