Non-monotonic metastable zone-width behavior in cooling cocrystallization: a case study on the sulfamethazine-acetylsalicylic acid cocrystal system

Abstract

The metastable zone width (MSZW) during the cooling crystallization of sulfamethazine–acetylsalicylic acid (SMZ–ASA) cocrystal system in acetonitrile (ACN) exhibits different patterns with variations in coformer ratios and saturation temperatures. Studies were carried out at a fixed 0.3 °C min⁻¹ cooling rate in 20 mL with three agitation rates (100, 400, and 800 RPM), across a saturation temperature range of 15–35 °C with ASA/SMZ molar ratios ranging from 2.5–9.61. Polynomial surface fitting of the induction time data was employed to assess the dependence of MSZW on solute concentration and saturation temperature, where the concentration range was varied between 30–70 mM for SMZ and 100–400 mM for ASA. The results revealed that both coformers' composition and temperature strongly influence MSZW. Importantly, a non-monotonic trend was observed, with the MSZW broadening at higher saturation temperatures for fixed ASA/SMZ ratios, an atypical behavior compared to conventional cooling crystallization. These findings emphasize the system-specific complexity of cocrystal nucleation and the intertwined influence of solute composition and saturation temperature.

---

Introduction

Over the past couple of decades, rapid growth has occurred in the laboratory screening and identification of potential pharmaceutical cocrystals with enhanced physicochemical properties. Nonetheless, their translation to commercial manufacturing remains limited with only a handful of marketed drugs.^1–3 This gap partly arises from the challenges of reliably producing cocrystals at a larger scale while maintaining consistent critical quality attributes (CQAs) like phase purity, morphology, and particle size distribution. Pharmaceutical cocrystals can be produced by various techniques, including mechanochemical grinding, melt crystallization, and solution-mediated routes.⁴ Among these, solution-based methods, such as slurry conversion, cooling crystallization, and antisolvent addition, are particularly attractive for industrial-scale production, as they are compatible with existing crystallization equipment and easy real-time monitoring using established Process Analytical Technology (PAT) tools.^5–7 Cooling and combined cooling-antisolvent crystallization approaches enable precise modulation of different process parameters like supersaturation generation rate, solvent composition, and agitation rate, providing enhanced control over CQAs.⁸ For successful scale-up of such solution-mediated processes within a systematic Quality-by-Design (QbD) framework, it is necessary to investigate the underlying thermodynamic and kinetic factors governing nucleation and growth, as these directly influence the robustness and reproducibility of the final product.^9–11

One of the critical parameters essential for designing robust and reproducible cooling crystallization processes is the metastable zone width (MSZW) expressed as ΔT_max, defined as the interval between the saturation temperature (T₀) and the onset temperature for spontaneous nucleation (T_nuc).¹² A certain level of supersaturation, which is the driving force for nucleation, is required for the creation of new solid interfaces. This supersaturation level at which spontaneous nucleation begins is often referred to as supersolubility.¹³ By definition, the region between the solubility curve (at T₀) and the supersolubility curve (at T_nuc) in the concentration vs. temperature plot is the metastable zone. MSZW determination enables the selection of optimal seeding windows, minimization of uncontrolled nucleation, and control of particle size distribution. It can also provide insight into the solute–solvent interactions and the kinetic landscape of crystallization. The relationship between MSZW and process variables such as cooling rate, saturation temperature, agitation rate, and solution volume can guide process optimization and scale-up.¹⁴

While a few recent studies have examined nucleation pathways in cocrystal systems, these investigations have primarily focused on induction time measurements and mechanistic interpretation of nucleation^15–18 rather than systematic evaluation of the MSZW in cocrystal systems. The relationship between metastable zone width (MSZW) and saturation temperature is well established for single-component systems but studies focusing on MSZW behavior in cocrystal systems remain relatively limited. Among the reported studies, Boyd et al. investigated the benzoic acid–isonicotinamide cocrystal and highlighted the influence of solute–solute interactions, showing that increasing benzoic acid concentration led to a broader MSZW.¹⁹ Baldea et al. examined the ketoconazole–fumaric acid system, identifying optimal ketoconazole concentrations for high-yield crystallization in ethanol and acetone–water (4 : 6 v/v), though extensive parametric analysis was not conducted.²⁰ Zhao et al. conducted a more comprehensive study on the barbituric acid–urea cocrystal, analyzing MSZW dependence on both cooling rate and solute concentration. Their findings showed that MSZW increased with cooling rate and urea concentration, while interfacial energy and the MSZW decreased with rising saturation temperature.²¹

The current study systematically investigates the combined influence of coformer concentration ratios, saturation temperature, and stirring rate (RPM) on MSZW in a cocrystal system, using SMZ–ASA cocrystal in ACN under a constant cooling rate.

Results and discussions

To determine the MSZW, controlled cooling crystallization experiments were carried out at a constant cooling rate of 0.3 °C min⁻¹ in a magnetically stirred 20 mL system, using concentrations selected along the reported cocrystal stable-phase solubility line from TPDs at 15, 25, and 35 °C,⁹ across molar ratios ([ASA]/[SMZ]) ranging from 2.5 to 9.61, which lies between the two invariant points of the established TPDs. This ensured that all experiments were conducted within the stable-phase cocrystal region, so that the crystallized phase obtained would consistently be the 1 : 1 SMZ–ASA cocrystal. Nucleation onset was detected using a turbidity-based method, using three different stirring rates (100, 400 and 800 RPM), and each condition was repeated six times to systematically evaluate the effects of solute concentration, stirring rate, and saturation temperature on MSZW, as illustrated in Fig. 1. The reported MSZW values representing the mean of six independent measurements for each condition, with standard deviations (S.D.), are provided in Table S1 of SI. After 6–8 minutes of nucleation, once sufficient solid had formed, samples were withdrawn, filtered, dried, and subjected to PXRD analysis to confirm the solid phase. The PXRD patterns of the samples obtained at 400 RPM are provided in the SI (Fig. S1). It is evident from Fig. 1 that the MSZW is significantly narrower at 400 RPM compared to 100 RPM across all saturation temperatures and concentration ratios, which can be attributed to the improved diffusional transport and enhanced mass transfer with the increase in agitation rate.²² But again, on increasing the agitation rate to 800 RPM no specific trend or significant changes in MSZW were observed as compared to 400 RPM. It is reported that in some systems, the relationship between stirring rate and MSZW can exhibit an inflection point, depending on the solute, solvent, and other operational conditions.^23–25 In this system, the experimental results indicate that increasing the agitation rate beyond 400 RPM does not produce any significant change in the nucleation behavior or the corresponding MSZW. Accordingly, subsequent analysis was restricted to the 100 and 400 RPM datasets to evaluate the effects of composition and saturation temperature on MSZW.

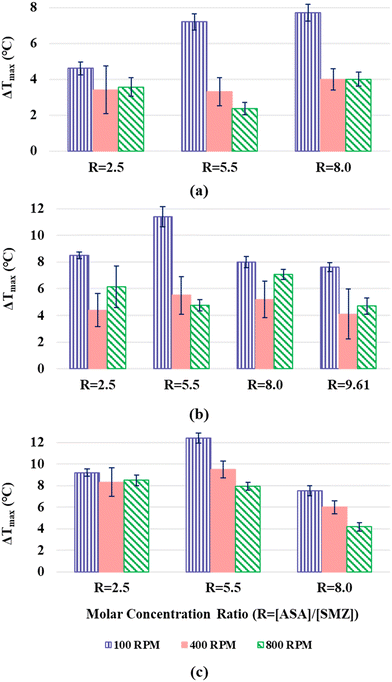Fig. 1 Effect of solute molar concentration ratio on the MSZW in ACN at saturation temperature of (a) 15 °C, (b) 25 °C and (c) 35 °C.

A second-degree polynomial surface fit (poly22, MATLAB R2024a) was applied to the solubility data within the cocrystal stability region, bounded by the TPD invariant points at 15, 25, and 35 °C, yielding the continuous blue surface in Fig. 2 that defines the equilibrium solubility limit as a function of SMZ and ASA concentrations. Similar surface fit of the experimentally observed nucleation onset temperatures is superimposed as the grey mesh surface in Fig. 2. The vertical distance between the two surfaces corresponds to the MSZW, indicative of the kinetic barrier to nucleation under each condition at 100 and 400 RPM. The polynomial surface fit equations are provided in the SI (Table S1). The high R-squared (R²), adjusted R-squared (Adj. R²), and low Root Mean Square Error (RMSE) values for each fit, detailed in SI (Table S2), confirm a strong correlation between the models and the experimental data. Thus, these equations provide a quantitative basis for comparing the effects of concentration on both the equilibrium solubility and the MSZW. The generated surfaces and their respective polynomial fits serve as a robust predictive tool for mapping the crystallization window under varying process conditions.

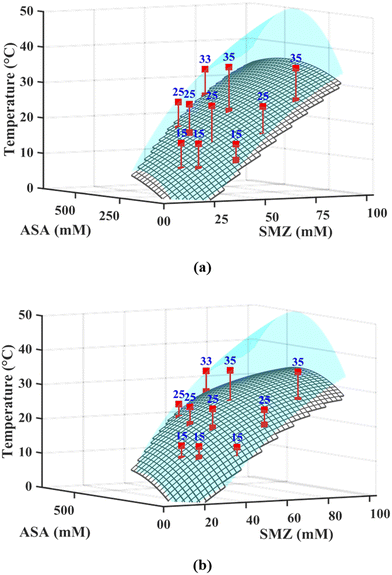Fig. 2 Solubility surface (blue) and supersolubility surface (grey mesh) for SMZ–ASA cocrystal at (a) 100 RPM and (b) 400 RPM.

The trends in Fig. 3(a–d) highlight the influence of solute composition on the MSZW, ΔT_max under different agitation rates. At a constant SMZ concentration Fig. 3(a and b), increasing ASA concentration initially broadens the MSZW, but beyond a specific ASA concentration (corresponding to an SMZ concentration), the MSZW begins to decrease. This behavior suggests that at higher ASA concentration beyond a threshold value, the nucleation kinetics become faster, and crystallization can occur at lower supersaturation, thereby narrowing the MSZW.

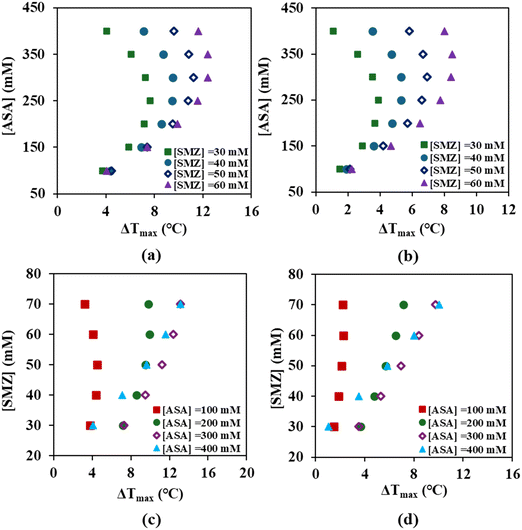Fig. 3 Effect of SMZ and ASA concentration on the MSZW, ΔT_max for the SMZ–ASA cocrystal at (a and c) 100 RPM and (b and d) 400 RPM.

Conversely, at constant ASA concentration Fig. 3(c and d), increasing SMZ concentration generally leads to a progressive broadening of the MSZW, reflecting slower nucleation kinetics in SMZ-rich environments where higher supersaturation is required to trigger nucleation. An exception is observed at very low ASA concentration (∼100 mM), where the MSZW remains nearly constant despite increase in SMZ concentration. In general, it may be concluded that as the concentration of the low solubility coformer (SMZ) increases, the MSZW increases, while high concentration of the high solubility coformer (ASA) decreases the MSZW. However, this behavior might be specific to the model system and hence may not be generalized until more data on other cocrystals are available. Nonetheless, the observations confirm that the concentrations of both the coformers and their ratios are critical factors that influences the MSZW in cocrystallization process. Overall, higher concentration of ASA, which exhibits higher solubility and nucleation rates than SMZ, favour faster nucleation and leads to a narrower MSZW.⁹

From the solubility and supersolubility curves presented in Fig. 4(a and b) and the experimental induction time data presented in Fig. 1, it can be observed that the MSZW exhibits a non-monotonic relationship with the coformer concentration and the MSZW broadens as T₀ increases. While single-component systems typically show a narrowing of the MSZW with increasing saturation temperature,^26,27 such trends may not always be applicable to multicomponent systems like cocrystals. In cocrystals, the MSZW becomes more system-specific, governed by the interplay between solute composition, their intermolecular interactions, and the kinetics of complex formation preceding nucleation.

Fig. 4 Solubility and supersolubility curve for the SMZ–ASA cocrystal (a) at constant SMZ concentration and (b) at constant ASA concentration.

The atypical observation of MSZW expansion with increasing temperature might be explained by a temperature-dependent reduction in hydrogen-bonding propensity between SMZ and ASA. Specifically, the 1 : 1 SMZ–ASA cocrystal is stabilized by acid–amide heterosynthon, which involves intermolecular hydrogen bonding between the carboxylic acid group of ASA and both the sulfonamide nitrogen and pyrimidine ring nitrogen of SMZ.²⁸ With elevated temperature, the strength and stability of hydrogen-bonded molecular clusters essential for nucleus formation are likely to decrease.²⁹ Consequently, a higher Gibbs free energy barrier may be needed to form stable critical nuclei for the cocrystal system, thus delaying nucleation onset and broadening the MSZW at elevated temperatures. This interpretation aligns with thermodynamic expectations for multicomponent systems where intermolecular interactions, especially hydrogen bonding, critically influence nucleation kinetics.³⁰ However, this proposed mechanism is a plausible hypothesis based on the observed macroscopic trends. Direct verification of this hypothesis at the molecular level through molecular dynamics simulations or experimental investigations to quantify the stability of specific hydrogen-bonded clusters as a function of temperature would be required for definitive proof and presents a valuable avenue for future investigation. These results demonstrate that the determination of MSZW in cocrystal systems is inherently complex and system-specific, being governed by the nucleation kinetics of the constituent molecules and the target cocrystal, and is therefore critical for robust process design, reliable scale-up, and enabling seeded crystallization strategies to control the CQAs of the final cocrystal product.

Conclusions

The MSZW for cocrystal nucleation in cooling crystallization was found to be highly sensitive to the relative concentrations of coformers and the saturation temperature. Relying on the concentration of a single coformer is insufficient to predict the cocrystal MSZW and may be influenced by system-specific characteristics such as intermolecular interactions. To capture this complex non-monotonic dependence, a polynomial curve fitting approach was applied, providing a good correlation with experimentally determined MSZW. It was observed that at the highest SMZ and ASA concentration values, the MSZW decreased by a factor of approximately 1.4 when the stirring rate was increased from 100 RPM to 400 RPM. Further increase in agitation to 800 RPM did not influence the MSZW significantly. In contrast, coformer composition played a more decisive role. At constant SMZ concentration, increasing ASA broadened the MSZW until a threshold concentration was reached, beyond which, the MSZW progressively narrowed. At constant ASA concentration, increasing SMZ increased the MSZW. However, low ASA concentration (∼100 mM) showed minimal impact on the MSZW to changing SMZ concentration. A particularly unconventional trend was observed where the MSZW broadened with increasing saturation temperature at similar [ASA]/[SMZ] ratios. This is likely due to reduced hydrogen-bonding propensity at elevated temperatures, influencing pre-nucleation clusters thereby increasing the nucleation barrier. Overall, this study demonstrates that the MSZW behavior in multicomponent systems like cocrystals may exhibit inconsistent trends compared to the more predictable patterns of single-component crystallization. This inherent complexity highlights that precise determination of MSZW is a prerequisite for robust process design for solvent-mediated cocrystallization strategies.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: PXRD data of the samples, summary of the MSZW under different conditions, and polynomial surface fits for the solubility and supersolubility surfaces are provided in the SI file. See DOI: https://doi.org/10.1039/d5ce00822k.

Acknowledgements

The authors gratefully acknowledge financial support from Anusandhan National Research Foundation (erstwhile Science and Education Research Board), Government of India (Grant number: CRG/2021/004299).

References

1. G. Bolla, B. Sarma and A. K. Nangia, Chem. Rev., 2022, 122, 11514–11603.
2. A. Saha, S. V. Dalvi, A. A. Dar and J. V. Parambil, Chem. Eng. Res. Des., 2024, 210, 71–81.
3. O. N. Kavanagh, D. M. Croker, G. M. Walker and M. J. Zaworotko, Drug Discovery Today, 2019, 24, 796–804.
4. M. Karimi-Jafari, L. Padrela, G. M. Walker and D. M. Croker, Cryst. Growth Des., 2018, 18, 6370–6387.
5. R. B. Chavan, R. Thipparaboina, B. Yadav and N. R. Shastri, Drug Delivery Transl. Res., 2018, 8, 1726–1739.
6. N. Pawar, A. Saha, N. Nandan and J. Parambil, Crystals, 2021, 11, 303.
7. A. Saha, A. A. Ahangar, A. A. Dar, S. Thirunahari and J. V. Parambil, Cryst. Growth Des., 2023, 23, 7558–7581.
8. E. Kougoulos, A. G. Jones and M. W. Wood-Kaczmar, Org. Process Res. Dev., 2006, 10, 739–750.
9. A. Saha, S. V. Dalvi, A. A. Dar and J. V. Parambil, Cryst. Growth Des., 2025, 25, 4521–4530.
10. S. Vedantam and V. V. Ranade, Sadhana, 2013, 38, 1287–1337.
11. A. A. Zlota, in Polymorphism in the Pharmaceutical Industry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2018, pp. 305–328.
12. J. Ulrich and C. Strege, J. Cryst. Growth, 2002, 237–239, 2130–2135.
13. G. Zeng, H. Li, S. Huang, X. Wang and J. Chen, Theor. Found. Chem. Eng., 2015, 49, 869–876.
14. H. Yang and A. J. Florence, CrystEngComm, 2017, 19, 3966–3978.
15. Z.-H. Li, G. Coquerel, B. J. Park and W.-S. Kim, Cryst. Growth Des., 2025, 25, 747–759.
16. H. McTague and Å. C. Rasmuson, Cryst. Growth Des., 2023, 23, 7053–7065.
17. P. Alinda, K. Shi and M. Li, Cryst. Growth Des., 2022, 22, 5215–5228.
18. H. McTague and Å. C. Rasmuson, Cryst. Growth Des., 2021, 21, 2711–2719.
19. S. Boyd, K. Back, K. Chadwick, R. J. Davey and C. C. Seaton, J. Pharm. Sci., 2010, 99, 3779–3786.
20. I. Baldea, R. Moldovan, A.-L. Nagy, P. Bolfa, R. Decea, M. O. Miclaus, I. Lung, A. M. R. Gherman, A. Sevastre-Berghian, F. A. Martin, I. Kacso and V. Răzniceanu, Int. J. Mol. Sci., 2024, 25, 13346.
21. J. Zhao, Q. Zhang, Y. Yan, Y. Xue and X. Zhang, J. Mol. Liq., 2023, 385, 122305.
22. K. R. J. W. Mullin, Nature, 1961, 190, 4772.
23. S. Z. Mohd Noor, D. M. Camacho, C. Yun Ma and T. Mahmud, Chem. Eng. Technol., 2020, 43, 1105–1114.
24. F. Mura and A. Zaccone, Phys. Rev. E, 2016, 93, 1–11.
25. J. Liu and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 4385–4394.
26. Z. Chen, R. Zhou, H. Yin and S. Yuan, J. Cryst. Growth, 2023, 601, 126941.
27. T. Zhou, C. Tu, Y. Sun, L. Ji, C. Bian, X. Lu and C. Wang, Chin. J. Chem. Eng., 2021, 31, 164–168.
28. M. R. Caira, J. Crystallogr. Spectrosc. Res., 1992, 22, 193–200.
29. M. Hu, J. Zhou, L. Jiang, Z. Wang, Y. Bao and S. Cui, J. Phys. Chem. B, 2025, 129, 4547–4557.
30. P. Cui, X. Zhang, Q. Yin and J. Gong, Ind. Eng. Chem. Res., 2012, 51, 13663–13669.

---