Optical field-induced mass transfer in plasmonic electrochemistry

Abstract

The relative contributions of different rate-enhancement mechanisms in plasmon-assisted electrochemical reactions remain debated. Here, we separate the photothermally-induced natural convection component of mass transfer from an optical field-mediated effect that depends on light intensity and wavelength.

---

Understanding how light interacts with electrochemical interfaces is key to harnessing plasmonic materials for relevant chemical transformations. When a plasmonic material absorbs light, collective electron oscillations give rise to strong electromagnetic fields, the formation of energetic (hot) charge carriers, and heat, localized to the plasmonic material's surface.^1–3 These phenomena affect chemical reactions in different ways, by altering the kinetics, the thermodynamics, and the mass transfer conditions. While hot charge carriers and the photothermal effect have been widely studied,^4–11 the impact of optical near-fields on mass transport remains less understood.

In our previous work,¹² we designed a simple system to separate the thermal from the non-thermal contributions of plasmon excitation to reaction rate enhancements. Using a nanostructured Au disk electrode and the outer-sphere redox couple [Ru(NH₃)₆]^3+/2+, we performed cyclic voltammetry under continuous-wave laser illumination at three visible light wavelengths while monitoring the electrode surface temperature using a custom-built working electrode. When the same electrode surface temperature was reproduced in the dark using a heating assembly that did not heat the electrolyte, the voltammograms closely matched those obtained under illumination. Finite-element simulations indicated that the light-induced temperature gradient across the electrode–electrolyte interface introduced convective flow orders of magnitude greater than diffusion or migration, even for surface temperature rises as low as 1.2 K. Nevertheless, illumination still produced a λ-dependent increase in the steady-state current density, which we attributed to a non-thermal component.

In this work, we sought to understand the non-thermal plasmonic enhancement in electrochemical reactions. We hypothesized that the excess current could originate from optical field-mediated enhancement of mass transfer near the electrode surface. Because the electric field amplitude depends both on wavelength and intensity, we systematically varied the incident light intensity at 473 and 532 nm and measured the steady-state current density using chronoamperometry. These wavelengths were selected due to their distinct form of interaction with Au: 473 nm primarily excites interband transitions, while 532 nm overlaps with the surface plasmon resonance.¹² To visualize the optical field enhancement, we simulated the electric field around a representative Au nanoparticle (r = 100 nm), chosen based on the average size of nanoscale Au features of an electrochemically roughened electrode (Fig. S1–S3). Fig. 1 shows the simulated electromagnetic field enhancement around a Au nanosphere in water under circularly polarized 473 or 532 nm illumination. The enhancement is higher at 532 nm for all simulated intensities, consistent with what would be expected from excitation of the localized surface plasmon resonance (Fig. S4 and S5). Accordingly, any optical field-mediated effects are expected to be more pronounced at 532 nm than at 473 nm.

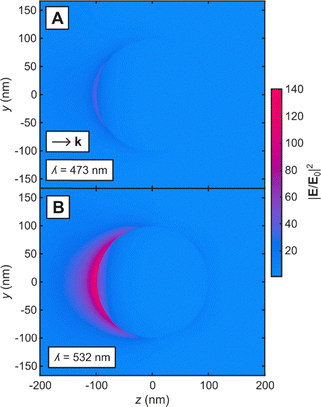Fig. 1 Simulated electromagnetic field enhancement in the vicinity of a 200 nm Au nanosphere in water under excitation of 2.38 W cm⁻² of (A) 473 and (B) 532 nm.

To test this hypothesis, we employed the same experimental configuration as in our previous work.¹² An aqueous 5 mM [Ru(NH₃)₆]³⁺ solution was used to serve as a model outer-sphere, non-catalytic redox couple, and a plasmonically-active roughened Au disk served as the working electrode. To monitor the surface temperature, the electrode assembly incorporated a thermocouple in contact with the Au disk but insulated from the solution (Fig. S6). Controlled heating was achieved using an aluminium block containing an embedded resistive element into which the electrode lead was inserted (Fig. S6). A potential of −0.45 V vs. Ag/AgCl (3 M KCl) was applied to the electrode to drive the one-electron reduction of [Ru(NH₃)₆]³⁺. A photograph of the experimental setup is shown in Fig. S7.

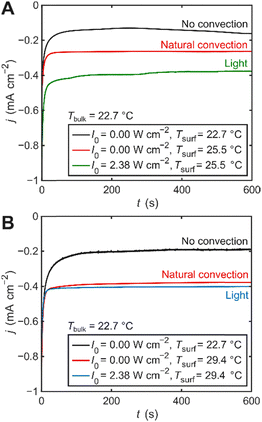
Fig. 2 shows chronoamperograms obtained under three different experimental conditions. The black curves correspond to the “dark” (no laser illumination) and isothermal condition, where the solution is nominally quiescent, and absent of natural convection. The green and blue curves were acquired under electrode illumination, whereby the electrode surface was irradiated by a circularly polarized laser with an intensity of 2.38 W cm⁻² of 532 or 473 nm, respectively. The temperature of the electrode surface was measured using the aforementioned embedded thermocouple (Tables S1 and S2). The red curves show the current density measured in the absence of illumination, but with the electrode surface selectively heated to the same temperature observed in the illuminated electrode experiments at each respective wavelength. This experimental condition serves as a control for photothermal effects resulting from light excitation of the Au electrode. Because non-isothermal systems commonly show hysteresis, ensuring stable temperature conditions helped minimize changes in the behaviour of convection. Chopped illumination experiments indicate a faster current increase under light excitation than current decrease when electrode illumination was blocked (Fig. S8). While a fast rise/drop in current density is typically attributed to enhanced electron-transfer rates, simulations of the same system suggest this is caused by the hysteretic behaviour of fluid velocity in relation to heating. Natural convection quickly develops when temperature gradients arise but take much longer to vanish as heating stops and the system slowly cools. Therefore, all measurements were performed after enough time was allowed for the system to thermally equilibrate.

Fig. 2 Experimental chronoamperograms collected at −0.45 V vs. Ag/AgCl (3 M KCl) on a roughened Au electrode, using a graphite rod as a counter electrode and 5 mM [Ru(NH₃)₆]³⁺ in a 0.1 M phosphate buffer (pH = 6) as the electrolyte. The curves show the measured current density under three different conditions: dark (black); dark with the Au electrode heated to the same temperature measured under illumination at (A) 532 or (B) 473 nm (red); laser illumination at (A) 532 or (B) 473 nm laser light (green and blue curves, respectively).

In the case of a heated electrode, a temperature gradient at the electrode–electrolyte interface results in a density gradient, generating buoyancy, which drives natural convection (Fig. 2).^12,13 The electrode surface temperature increases ca. 7 and 2 °C, resulting in a ca. 100 and 50% increase in current density, from excitation with 2.38 W cm⁻² of 473 and 532 nm light, respectively. Greater incident photon energies produce higher energy electron–hole pair excitations and a greater rise in electrode surface temperature following deexcitation. Thus, a larger temperature gradient is developed under 473 nm excitation, leading to greater convection and enhanced current density. In the case of Au electrode excitation with 473 nm light, the increase in current density can largely be attributed to natural convection induced by the photothermal effect (Fig. 2B). Interestingly, under 532 nm laser excitation, the steady-state current density observed exceeds the contribution from the photothermal effect (Fig. 2A), indicative of an additional, non-thermal enhancement to the reaction rate.

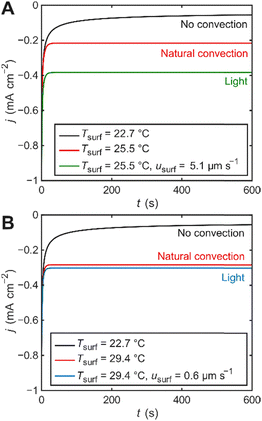
Several mechanisms are known to affect heterogeneous electron-transfer rates, including thermal effects (r ∝ T), electrostatic effects (changes in overpotential due to a photopotential,¹⁴ optical rectification,¹⁵ or double layer changes¹⁶), and direct plasmon-induced charge transfer.⁷ However, despite the fact that some or all of these effects might be present, they cannot explain the observed difference in current density between cases with electrode illumination and the corresponding photothermal control because the system operates in the mass-transfer-limited regime, where changes in k⁰ or η have negligible effect on the steady-state current. To estimate the magnitude of the mass transfer enhancement required to reproduce the experimental results, we conducted finite-element simulations of our electrochemical cell under three conditions corresponding to the experimental setup (Fig. S9 and Table S3). The difference between the simulated chronoamperograms under isothermal conditions (black, no convection) and with a heated electrode surface (red, natural convection) quantitatively resemble our experimental data (Fig. 3). Simulations also show that the direction of the heat flux vector (i.e., light excitation vs. resistive heater) negligibly impacts the electrode surface temperature (Fig. S10). We presume that the simulated current densities are overall lower because non-Faradaic contributions are unaccounted for. The green and blue curves represent simulations under the same conditions as the heated electrode case (red), with the addition of a fluid velocity vector with magnitude u_surf, applied at the electrode interface, serving to account for the non-thermal enhancement contribution. The value of u_surf was calculated to reproduce the experimentally observed difference in steady-state current density between the heated and illuminated electrode cases (red vs. blue/green). The calculated velocity required to match the experimental current density enhancement is in the order of µm s⁻¹, ca. 5.1 and 0.6 µm s⁻¹ for 532 and 473 nm illumination, respectively.

Fig. 3 Simulated chronoamperograms at −0.45 V vs. Ag/AgCl (3 M KCl) of a 5 mM [Ru(NH₃)₆]³⁺ solution. The curves show current density under three different conditions: isothermal (black); electrode surface at the same temperature measured under illumination at (A) 532 or (B) 473 nm (red); same as red but with an added fluid velocity at the electrode surface of (A) 5.1 or (B) 0.6 µm s⁻¹ to match the experimentally observed current density under electrode illumination.

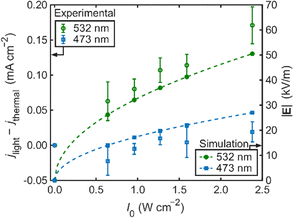
By accounting for the photothermal effect experimentally and with finite-element simulations, and due to the difference in optical near-fields generated under the two excitation wavelengths at a fixed intensity, we deduce that the non-thermal enhancement in current density is attributable to the influence of the local electromagnetic field at the surface of the nanostructured Au electrode. This is corroborated by experiments performed at different light intensities (Fig. S11–S26). Electrode illumination with 532 nm light shows an increase in the non-thermal steady-state current density enhancement (j_light – j_thermal) with light intensity, while the non-thermal current density enhancement at 473 nm excitation remains small or negligible within the experimental uncertainty (Fig. 4). These trends correlate with the simulated electric field magnitude, |E|, at the surface of the Au nanoparticle as a function of excitation intensity at 473 and 532 nm. As expected, the relationship follows the sublinear dependence 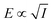.¹⁷ Several mass transfer phenomena involving electric fields are well established in the literature. The most common in the context of electrochemistry is migration, which applies to ionic transport in solution.¹⁸ Nevertheless, this mechanism can be largely ruled out in the present system. The high concentration of supporting electrolyte mostly negates this effect. Furthermore, the net ion flux due to migration is expected to be zero with an oscillating (AC) electric field. This points instead to mechanisms that depend on the time-averaged electric field or its gradient, rather than on the instantaneous electric field itself.

Fig. 4 Difference between plasmon and thermal current densities (left y-axis) and simulated magnitude of the electric field at the surface of the nanoparticle (right y-axis) as a function of the incident light intensity at 473 and 532 nm.

Other classes of mass transfer mechanisms that arise from AC electric fields are dielectrophoresis, optical tweezers,¹⁹ and AC electrokinetics, the latter which includes AC electroosmosis (ACEO) and AC electrothermal (ACET) flow.²⁰ In ACEO, a nonuniform alternating electric field drives flow tangential to the electrode surface.²¹ The component of the electric field normal to the electrode polarizes the electrical double layer (EDL), inducing an oscillating surface charge distribution, while the tangential component exerts a Coulombic force on these induced charges. Although both the field and the induced charges reverse sign each half cycle, the product qE remains positive, yielding a non-zero time-averaged force and thus net flow.²² Similarly, in dielectrophoresis, a nonuniform field exerts a force on the polarized EDL around a particle in solution, and the direction of flow depends on the field frequency.²³ However, the alternating electric fields in our system oscillate at optical frequencies (hundreds of THz), much faster than the EDL relaxation time constants.²⁴ This suggests that ACEO and dielectrophoresis cannot occur under optical excitation unless significant nonlinear effects arise at the interface. Particles can also experience forces when large optical intensity gradients exist, such as in optical or plasmonic tweezers.¹⁹ Still, the light intensities that manifest those effects are several orders of magnitude greater than in our study. ACET flow, on the other hand, originates from spatial variations in the fluid's electrical properties, specifically permittivity and conductivity, caused by temperature gradients within the electrolyte.²⁰ In such a case, spatial variations in temperature lead to changes in local permittivity, which induce an apparent free charge density within the fluid, generating a body force in the presence of an electric field. The driving force for this phenomenon scales as |E|²∇T. Assuming photothermal heating is mainly dissipated by conduction, and because power density scales as |E|², the resulting ACET force is expected to scale approximately as |E|⁴.

The total ACET body force consists of Coulombic and dielectric components that dominate in low- and high-frequency regimes, respectively. The dielectric force is proportional to an electric field gradient, ∇|E|², rather than |E|². Our finite-element simulations also show significant electric field gradients at the surface of the Au nanostructure, extending ca. 200 nm from the electrode surface (Fig. S27). The magnitude of ∇|E| depends on the excitation wavelength. Simulations of a Au dimer showed an increase in the electric field magnitude, as well as an enhanced difference between ∇|E| at 532 nm over 473 nm (Fig. S28). Because the roughened Au surface used in the experiments contains randomly distributed nanostructures spanning many sizes, the single-nanoparticle model likely underestimates the effect. Although the conditions and geometry of our system are far from those optimized for strong ACET flow, reported values in the literature range from tens to thousands of µm s⁻¹,^25,26 comparable to our simulated u_surf values, suggesting that even a much weaker manifestation of such effects could plausibly account for the magnitude of the enhanced mass transfer observed here.

The results presented here suggest that light–matter interactions at plasmonic electrodes can influence mass transfer in electrochemistry beyond photothermal effects. By separating the convective and non-convective components of the steady-state current response, we demonstrate that the enhancement under resonant excitation scales with the local electromagnetic field. The observed dependence of the non-thermal enhancement on intensity and wavelength implies that optical field-driven processes contribute to mass transfer at plasmonic surfaces under illumination. These findings highlight that plasmon-assisted electrochemistry cannot be described solely in terms of hot carriers, interfacial potentials, or photothermally induced temperature gradients. Instead, optical field-mediated mass transfer effects must be considered as a possible, and perhaps substantial, component of plasmonic enhancement.

Author contributions

J. V. H.: Simulation data curation, formal analysis, methodology, writing – original draft. M. A.: Experimental data curation, formal analysis, methodology, writing – original draft. A. J. W.: Conceptualization, funding acquisition, project administration, supervision, writing – original draft, review and editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the supplementary information (SI). Supplementary information includes finite-element simulations and methods, experimental set-up, electrode characterization, and unprocessed raw data. See DOI: https://doi.org/10.1039/d5cc06109a.

Acknowledgements

This work was supported in part by start-up funding provided by the University of Louisville, and in part by funding from the National Science Foundation (CHE-2441381).

References

1. G.-S. Park, K. S. Min, H. Kwon, S. Yoon, S. Park, J.-H. Kwon, S. Lee, J. Jo, M. Kim and S. K. Kim, Adv. Mater., 2021, 33, 2100653.
2. J. Zhao, S. Xue, R. Ji, B. Li and J. Li, Chem. Soc. Rev., 2021, 50, 12070–12097.
3. Z. Geng, Y. Yu and J. Liu, J. Phys. Chem. C, 2023, 127, 17723–17731.
4. K. Yue, J. Nan, X. Zhang, J. Tang and X. Zhang, Appl. Therm. Eng., 2016, 99, 1093–1100.
5. N. B. Schorr, M. J. Counihan, R. Bhargava and J. Rodríguez-López, Anal. Chem., 2020, 92, 3666–3673.
6. Y. Yu, V. Sundaresan and K. A. Willets, J. Phys. Chem. C, 2018, 122, 5040–5048.
7. Y. Zhang, L. Yan, M. Guan, D. Chen, Z. Xu, H. Guo, S. Hu, S. Zhang, X. Liu, Z. Guo, S. Li and S. Meng, Adv. Sci., 2022, 9, 2102978.
8. R. J. Dillon, T. N. Lewis, X. Dong, T. J. Gately, C. J. Bardeen, J. P. McClure and D. R. Baker, ACS Appl. Nano Mater., 2021, 4, 13196–13205.
9. T. P. Rossi, P. Erhart and M. Kuisma, ACS Nano, 2020, 14, 9963–9971.
10. C. Zhan, X.-J. Chen, J. Yi, J.-F. Li, D.-Y. Wu and Z.-Q. Tian, Nat. Rev. Chem., 2018, 2, 216–230.
11. M. Kim, M. Lin, J. Son, H. Xu and J.-M. Nam, Adv. Opt. Mater., 2017, 5, 1700004.
12. M. Al-Amin, J. V. Hemmer, P. B. Joshi, K. Fogelman and A. J. Wilson, Commun. Chem., 2024, 7, 70.
13. Md Al-Amin, J. V. Hemmer and A. J. Wilson, ACS Appl. Mater. Interfaces, 2025, 54816–54825.
14. A. J. Wilson, V. Mohan and P. K. Jain, J. Phys. Chem. C, 2019, 123, 29360–29369.
15. D. A. Nelson and Z. D. Schultz, J. Phys. Chem. C, 2018, 122, 8581–8588.
16. J. Sun and J. Wu, J. Phys. Chem. C, 2025, 129, 8946–8954.
17. E. Hecht, Optics, Pearson Education, Inc, Boston, 5 edn, 2017.
18. A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods, Wiley, 3rd edn, 2022.
19. M. Riccardi and O. J. F. Martin, Chem. Rev., 2023, 123, 1680–1711.
20. A. Salari, M. Navi, T. Lijnse and C. Dalton, Micromachines, 2019, 10, 762.
21. N. G. Green, A. Ramos, A. González, H. Morgan and A. Castellanos, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4011–4018.
22. A. Ramos, A. González, A. Castellanos, N. G. Green and H. Morgan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 056302.
23. Y.-W. Lu, C. Sun, Y.-C. Kao, C.-L. Hung and J.-Y. Juang, Nanomaterials, 2020, 10, 1364.
24. A. Greco, S. Imoto, E. H. G. Backus, Y. Nagata, J. Hunger and M. Bonn, Science, 2025, 388, 405–410.
25. R. H. Vafaie, H. B. Ghavifekr, H. Van Lintel, J. Brugger and P. Renaud, Electrophoresis, 2016, 37, 719–726.
26. M. Lian and J. Wu, Appl. Phys. Lett., 2009, 94, 064101.

---

Footnote

† Authors contributed equally to this work.

---