Open Access Article
Open Access ArticleImpact of thermally activated ionic dynamics on the trap-mediated current–voltage characteristics of a mixed-halide hybrid perovskite†
Manoj
Singh
a,
Lokesh Singh
Tanwar
a and
Rupak
Banerjee
 *ab
*ab
aDepartment of Physics, Indian Institute of Technology, Palaj, Gandhinagar 382355, India. E-mail: rupakb@iitgn.ac.in
bK C Patel Centre for Sustainable Development, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, India
First published on 11th June 2025
Abstract
Organic–inorganic metal halide perovskites (OIMHPs) are at the forefront of leading energy research. Therefore, it is pivotal to understand the effect of operating conditions like temperature, humidity, light exposure, etc. on these materials. The transient ionic dynamics and its effect on the steady-state J–V characteristics of an OIMHP, viz. FAPbBr2I, having a mixed halide composition, were investigated by temperature-dependent dielectric spectroscopy and temperature-dependent space charge limited current (SCLC) measurements in the temperature range of 305–454 K. The contribution of the resistance and capacitance of grains and grain boundaries to the total impedance at different temperatures has been interpreted by analyzing the Bode plots using the Maxwell–Wagner equivalent circuit model. The AC conductivity spectra demonstrate different behaviors in two different temperature regimes. In the low-temperature (LT) regime (323–381 K), the temperature response of ionic conductivity is only dependent on hopping frequency (the ionic carrier concentration factor being temperature-independent), leading to almost similar activation energies of ionic conduction (Ea) and hopping migration (Em), where Ea = Em = 0.30 ± 0.05 eV. However, in the high temperature (HT) regime (395–454 K), we observed a difference in Ea (0.74 ± 0.05 eV) and Em (0.50 ± 0.05 eV) values, which is attributed to the activation energy of mobile charge carrier formation (Ef = Ea − Em = 0.24 ± 0.05 eV). We propose that the trapped ions in the LT regime are now released by overcoming the barrier Ef in the HT regime, leading to a substantial increase in the mobile ion concentration. Furthermore, we have unveiled the effect of these mobile ions and trapped carriers on the J–V characteristics in both temperature regimes by analyzing the temperature-dependent SCLC J–V characteristics in the Ag/FAPbBr2I/Ag device configuration. The AC conductivity and electric modulus loss spectra scale to different master curves in the LT and HT regimes, further corroborating the observed thermally activated interplay of ionic conduction and hopping migration. The key findings of this work stimulate more such fundamental investigations of electrical transport in mixed halide OIMHPs and establish their potential in various energy storage applications like batteries, integrated PV-battery/supercapacitor systems, and others.
I. Introduction
The intriguing photo-physical and dielectric attributes of organic–inorganic metal halide perovskites (OIMHPs) have fascinated the scientific community. Specifically, the underlying mechanism of ion transport and relaxation dynamics is still elusive in such materials and warrants extensive investigation. Deeper insights into these mechanisms are imperative to identify the microscopic processes involved and correlate them with the performance and stability parameters of multifunctional devices based on halide perovskites, such as solar cells, high energy radiation (X-ray and γ-ray) detectors, piezoelectric nanogenerators, field effect transistors, memory devices, photo-catalysts and so on.1–12 The OIMHPs exhibit attractive optoelectronic properties, viz. strong optical absorption, large photoluminescence quantum yields, low exciton binding energy, high mobility and diffusion lengths of charge carriers, etc.13–15 The power conversion efficiencies (PCEs) of thin film-based solar cell devices of OIMHPs have reached up to ∼25.5% in only over a decade of research.16 However, one of the significant bottlenecks in the technological deployment of such devices is the creation of surface defects due to the prompt crystallization and grain boundary effects.17 Several other parameters, such as ion migration, carrier lifetime, mobility, etc., are also known to influence device performance and stability.Single crystalline materials of these halide perovskites have been recently explored due to their significantly low trap density (∼109 cm−3), higher diffusion length (up to ∼1 μm), and higher carrier mobilities and the absence of grain boundaries.18,19 Therefore, synthesizing high-quality single crystals (SCs) or highly epitaxial growth of these perovskite materials is the most feasible way forward for significant improvement in this field. However, integrating these SCs in solar cells and other energy-harvesting devices is still challenging. In the recent past, several approaches have been adopted to synthesize high-quality, large perovskite-based SCs, such as inverse temperature crystallization (ITC), anti-solvent vapor-assisted crystallization (AVC), seed crystal growth, Bridgeman method, and so on.20–23 Among these, the ITC method is the most common for synthesizing OIMHP-based SCs because of the fast growth rate of high-quality, shape-controlled, and large-sized crystals. Saidaminov et al. demonstrated the rapid crystallization (within minutes) of high-quality, size- and shape-controlled MAPbX3 (MA = CH3NH3 and X = Br or I) SCs by the ITC method.21 Consequently, FAPbX3 (FA = CH (NH2)2, X = Cl, Br, I) SCs were also studied, which demonstrated better thermal and moisture stability than the MA-based perovskite SCs.24 FA-based, mixed halide perovskite SCs (FAPbBr2I) have been used as a photodetector with stable performance. The fabricated device exhibited an excellent photo-response with a responsivity of ∼0.8 A W−1 and a detectivity of ∼1.81 × 1011 Jones for a visible laser (λ ∼ 376 nm).25
A formamidinium (FA) based hybrid lead halide perovskite, like FAPbI3, has an optimal band gap (∼1.48 eV) from the perspective of perovskite-based device performance and has been the focus of the scientific community to date.26–28 However, FAPbI3 is highly unstable and cannot sustain its photoactive cubic α-phase at room temperature, degrading immediately to a photo-inactive δ-phase. This degradation is often attributed to the iodide ion migration in various literature studies.29,30 Moreover, FA+ also gives more thermal stability to the FA-based perovskites compared to their methylammonium (MA+) based counterparts.31 The halide substitution, for instance, the substitution of iodide by bromide partially, is also reported to arrest the ion migration and provide structural stability.31,32 The replacement of iodide by bromide not only increases the bandgap, but also enhances the structural stability such that the bulk single crystalline samples could be stable in the cubic α-phase for months to even years under ambient conditions.33,34 Hence, the mixed halide compositions of OIMHPs have proved to be vital for the application versatility.
The OIMHPs are mixed ionic–electronic conducting materials, and the understanding of ionic transport and the strength of electron–lattice interaction related to the polaronic transport, ionic polarization strength, and defect tolerance2,35–38 is crucial for the efficient design of multifunctional energy storage and conversion devices based on such materials.39,40 Dielectric spectroscopy is an efficient, non-destructive, and reliable technique that is widely used to probe the ionic conduction, relaxation mechanisms, polaron dynamics, etc., in the OIMHPs. Several other techniques, such as blocking electrodes, Hall effect, and permeation studies, have also been employed to this end.41
Here, we report the synthesis of an FA-based mixed halide FAPbBr2I single crystal by the ITC method. The synthesized FAPbBr2I single crystal is characterized by X-ray diffraction (XRD), which establishes its cubic crystal structure with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The in situ temperature-dependent XRD, thermogravimetric analysis (TGA), and differential scanning calorimetry (DSC) demonstrate that there are no thermally induced structural changes in the FAPbBr2I SC up to 200 °C (473 K). Furthermore, the temperature-dependent (305–454 K) dielectric spectra of the FAPbBr2I sample have been investigated in a wide frequency range of 20 Hz to 10 MHz. The contribution of the resistance and capacitance of grains and the grain boundaries to the impedance is discussed quantitatively by fitting the Bode plots. The analysis of electric modulus loss spectra using the Havriliak–Negami (HN) and Kohlrausch–Williams–Watts (KWW) models and the AC conductivity spectra using the modified Jonscher's power law model at various temperatures indicates two different types of ionic conduction and hopping migration mechanisms in high-temperature (HT) and low-temperature (LT) regimes. In the LT regime (305–381 K), the DC ionic conductivity is exclusively dependent on the hopping frequency, resulting in almost similar activation energies (AEs) of ionic conduction (Ea = 0.28 ± 0.05 eV) and hopping migration (Em = 0.29 ± 0.05 eV), whereas in the HT regime (395–454 K), we observed differences in both the AEs (Ea = 0.73 ± 0.05 eV and Em = 0.49 ± 0.05 eV), which is attributed to the formation of mobile carriers, justified by the orders of magnitude increase in the carrier concentration factor. This difference in the AEs corresponds to the energy expended in forming these mobile carriers (Ef = Ea − Em = 0.24 ± 0.05 eV). The role of traps and the influence of mobile ions in the expected changes in the steady-state J–V characteristics is corroborated by the temperature-dependent space charge limited current (SCLC) measurements. The differences observed in the scaling behavior of the electric modulus and the AC conductivity spectra at different temperatures also justify the prevalence of different conduction mechanisms in both temperature regimes. These results offer vital insights into the dielectric attributes of the FAPbBr2I halide perovskite and assess its suitability for applications in optoelectronic and energy harvesting devices.
m space group. The in situ temperature-dependent XRD, thermogravimetric analysis (TGA), and differential scanning calorimetry (DSC) demonstrate that there are no thermally induced structural changes in the FAPbBr2I SC up to 200 °C (473 K). Furthermore, the temperature-dependent (305–454 K) dielectric spectra of the FAPbBr2I sample have been investigated in a wide frequency range of 20 Hz to 10 MHz. The contribution of the resistance and capacitance of grains and the grain boundaries to the impedance is discussed quantitatively by fitting the Bode plots. The analysis of electric modulus loss spectra using the Havriliak–Negami (HN) and Kohlrausch–Williams–Watts (KWW) models and the AC conductivity spectra using the modified Jonscher's power law model at various temperatures indicates two different types of ionic conduction and hopping migration mechanisms in high-temperature (HT) and low-temperature (LT) regimes. In the LT regime (305–381 K), the DC ionic conductivity is exclusively dependent on the hopping frequency, resulting in almost similar activation energies (AEs) of ionic conduction (Ea = 0.28 ± 0.05 eV) and hopping migration (Em = 0.29 ± 0.05 eV), whereas in the HT regime (395–454 K), we observed differences in both the AEs (Ea = 0.73 ± 0.05 eV and Em = 0.49 ± 0.05 eV), which is attributed to the formation of mobile carriers, justified by the orders of magnitude increase in the carrier concentration factor. This difference in the AEs corresponds to the energy expended in forming these mobile carriers (Ef = Ea − Em = 0.24 ± 0.05 eV). The role of traps and the influence of mobile ions in the expected changes in the steady-state J–V characteristics is corroborated by the temperature-dependent space charge limited current (SCLC) measurements. The differences observed in the scaling behavior of the electric modulus and the AC conductivity spectra at different temperatures also justify the prevalence of different conduction mechanisms in both temperature regimes. These results offer vital insights into the dielectric attributes of the FAPbBr2I halide perovskite and assess its suitability for applications in optoelectronic and energy harvesting devices.
II. Experimental
A. Chemicals
Formamidinium iodide (FAI) and lead(II) bromide (PbBr2) were procured from Sigma Aldrich. Gamma-butyrolactone (GBL) and N,N-dimethyl formamide (DMF) were purchased from Alfa-Aesar. All these analytical-grade reagents were used without any further purification.B. Synthesis of FAPbBr2I single crystals
The FAPbBr2I SCs were grown using the ITC synthesis technique. 1 mmol FAI and 1 mmol PbBr2 were dissolved in GBL at 60 °C. When the precursors are dissolved completely, a clear solution is formed. After that, the temperature is increased to 115 °C and kept as it is until the crystallization starts. The single crystals of FAPbBr2I then start to grow bigger within hours. The synthesis procedure and images of SCs are shown in Fig. S1(a) and (b) in the ESI.†C. Characterization of physicochemical properties of single crystals
The powder XRD patterns of the pulverized SCs of FAPbBr2I were measured using a 9 kW Multimode XRD system (SmartLab, Rigaku Corp., Japan) for structural analysis. The X-ray source used was copper Kα (λ = 1.54 Å), and the scan rate was maintained at 1° min−1 with a 2θ scan range of 10° to 45°. UV-visible reflectance spectroscopy was performed using a QE-R quantum efficiency measurement system (EnliTech, Taiwan) using an integrating sphere in the reflectance measurement module. The reflectance was calibrated using a reference barium sulphite standard sample. The bandgap of the synthesized samples was deduced from the reflectance data using the Tauc plots. The thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) of the pulverized FAPbBr2I sample were performed using the PerkinElmer TG analyzer and PerkinElmer differential scanning calorimeter, respectively. The temperature-dependent space charge limited current–voltage measurements on the Ag/FAPbBr2I SC/Ag device were carried out in an in-house temperature-controlled setup using the electrical source meter provided by Keithley Instruments Inc., Model: 2601B.D. Dielectric spectroscopy
For studying the dielectric response of the FAPbBr2I perovskite material, the electroding of the top and bottom surfaces of the FAPbBr2I pellet (pressed from the as-synthesized SCs) was done by the application of silver paste to achieve the Ag/FAPbBr2I/Ag device configuration. The Keysight Impedance Analyzer E4990 was utilized to acquire the conductance and capacitance at different temperatures in the frequency range 20 Hz–10 MHz under a 0 V DC potential with a small AC perturbation potential of 0.1 V. The conductance and capacitance data were used to extract the complex impedance Z*(ω), AC conductivity σ′(ω), complex dielectric constant ε*(ω), and complex electric modulus M*(ω). The digital image of the impedance analyzer with a PID temperature controller is also presented in Fig. S2 in the ESI.†III. Results and discussion
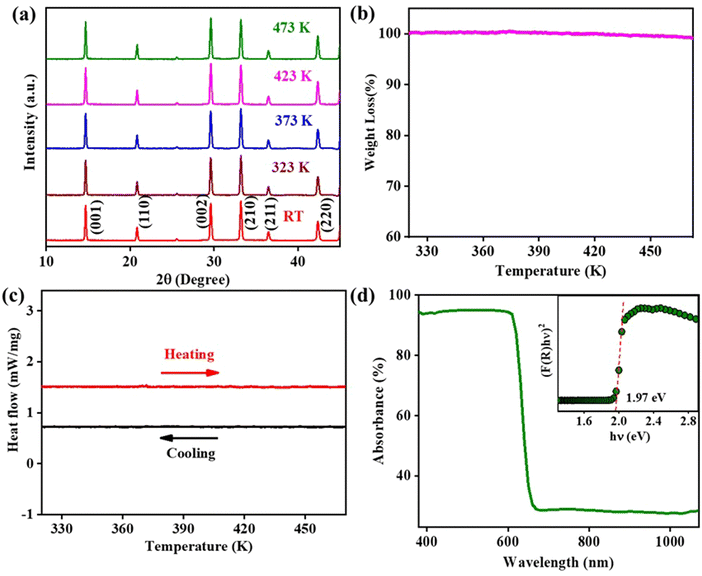
Fig. 1(a) depicts the XRD profile of the FAPbBr2I single crystal perovskite at room temperature (RT) and various other temperatures up to 473 K. The XRD profiles of the FAPbBr2I single crystal show diffraction peaks at 2θ = 14.69°, 20.81°, 25.54°, 29.57°, 33.19°, 36.46° and 42.35° corresponding to the (001), (110), (111), (002), (210), (211) and (220) lattice planes, respectively. The peak profile indicates that FAPbBr2I crystallizes in a cubic crystal system with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and is in agreement with previous reports on the FAPbX3 (where X = Cl, Br, I, or a mixed halide) crystal structure.25,42,43 The in situ temperature-dependent XRD of FAPbBr2I SC was also performed from RT to 200 °C (473 K) to examine the temperature-induced structural changes (if any) within the said temperature range. We do not observe any changes in the shape, size and number of diffraction peaks. Therefore, we conclude that there are no structural changes in the measured temperature range.
m space group and is in agreement with previous reports on the FAPbX3 (where X = Cl, Br, I, or a mixed halide) crystal structure.25,42,43 The in situ temperature-dependent XRD of FAPbBr2I SC was also performed from RT to 200 °C (473 K) to examine the temperature-induced structural changes (if any) within the said temperature range. We do not observe any changes in the shape, size and number of diffraction peaks. Therefore, we conclude that there are no structural changes in the measured temperature range.
Furthermore, to probe the thermal stability of FAPbBr2I SCs, we performed the TGA and DSC measurements from RT to 473 K. The TGA and DSC plots of FAPbBr2I are shown in Fig. 1(b) and (c). The TGA trace shows no significant weight loss up to 473 K, implying that the perovskite is thermally stable in this temperature range. The DSC trace also does not show any exothermic or endothermic anomalies, confirming the thermal stability of FAPbBr2I SCs. The optical absorption of FAPbBr2I SCs is explored by UV-visible spectroscopy in the wavelength range of 300 to 1100 nm. The absorbance versus wavelength plot is shown in Fig. 1(d), and its inset shows the Tauc plot. The Tauc plot between [F(R)hυ]1/η and hυ (where F(R) is known as the Kubelka–Munk function, hυ is the energy of the incident photon, and η is a parameter determining the type of bandgap transition) is obtained from the reflectance data according to the following equation
 | (1) |
Complex impedance spectroscopy (CIS) has proven to be a remarkable technique for investigating ion dynamics and relaxation mechanisms in dielectric materials. The halide perovskites, being highly dielectric in nature, have been recently probed extensively using the CIS technique to understand the underlying phenomena behind the dynamics of ion migration, trap states, and recombination of ions inside the bulk as well as the surface of the materials.44 Generally, the complex impedance spectra of dielectric materials can be understood by analyzing the individual contributions from grains, grain boundaries, and sample–electrode interfaces associated respectively with the high-frequency (HF), low to mid-frequency (MF), and ultra low-frequency (ULF) regions.44,45 The temperature-dependent CIS measurements of the Ag/FAPbBr2I/Ag device are manifested in the Bode plots expressed as frequency versus real (Z′(ω)) and imaginary (Z′′(ω)) parts of CI. The Bode plots of Z′′(ω) vs. ω at different temperatures (305–454 K) are shown in Fig. 2(a)–(d), and the equivalent circuit model to fit the data is shown in the insets. In our measurement configuration of the Ag/perovskite/Ag device, we have the perovskite in the polycrystalline pellet form composed of grains and grain boundaries (GBs). Hence, we can represent this system by a Maxwell–Wagner equivalent electrical circuit having two parallel RC circuits connected in series, each corresponding to a physical process happening in the grain and GBs. The real (Z′(ω)) and imaginary (Z′′(ω)) parts of impedance for such a model are given by:46
 | (2) |
 | (3) |
 | (4) |
 | (5) |
Fig. S3(a–j) (ESI†) also presents the fitted Bode plots of the real part of CI: Z′(ω) vs. ω at various temperatures. The values of Z′(ω) decrease with increasing temperature, indicating that FAPbBr2I follows a negative temperature coefficient of resistance, typical of semiconductors. At low frequencies (ω → 0), the impedance is very high (Z′(ω) → (R1 + R2), according to eqn (2)), and at high frequencies (ω → ∞), the circuit offers very low impedance (Z′(ω) → 0). Physically, inside our system, at LFs, the free ions are able to follow the applied AC field and move inside the system from grains towards GBs; hence, they experience a very high impedance contribution from both grains and GBs. Usually, at LFs, the resistors act as the short circuit path, and capacitors block DC; hence, the effective impedance is primarily the resistive contribution of grains and GBs. While at high frequencies, we know that resistances block AC field and capacitors act as short circuits and pass the AC signal; hence, the impedance falls significantly at higher frequencies with an inverse dependence on the frequency of the AC field (Z′(ω) ∼ 1/ω). This transition from high to low impedance should occur at the effective relaxation frequency (ωR) of the equivalent circuit. With the increment in temperature, this transition occurs at larger effective relaxation frequency, which is natural because the ionic movement is temperature activated and long-range motion persists more at higher temperatures.
The values of these parameters (R1, C1, and R2, C2) obtained by fitting the Bode plots of Z′′(ω) and Z′(ω) at all the measurement temperatures are presented in Table S1 in the ESI.† The resistance of GBs and grains and their difference (R2 − R1) is observed to decrease with the increment in temperature (Fig. S3(k) in the ESI†). The variation of grain and GB-capacitance with temperature is also shown in Fig. S3(l) in the ESI.†
We have calculated the DC conductivity (σdc) at different temperatures from the impedance data by using the relation:  , where t is the thickness, A is the area of the sample, and R is the total resistance offered by the sample. Here, the total resistance is a sum of grain and grain-boundary resistance, i.e., R = R1 + R2, t = 0.8 mm, and A = 8 mm2. The σdc obtained from impedance data as a function of 1000/T follows the Arrhenius relation shown in Fig. 2(e), and we observe two different activation energies (AEs) of ion conduction (Ea) obtained from the Arrhenius plots in two different temperature regions, which we designate as the low and high-temperature regions (LTR and HTR). The obtained values of activation energies in the LTR and HTR are 0.31 ± 0.05 eV and 0.74 ± 0.05 eV. Furthermore, we also calculated the effective relaxation frequencies (ωR) at all the measured temperatures from the impedance data. The expression of ωR is derived in the Note S1 (ESI†). Typically, ωR is the frequency value at which the imaginary impedance (Z′′(ω); representing relaxation) becomes maximum. The simplified expression of effective relaxation frequency is
, where t is the thickness, A is the area of the sample, and R is the total resistance offered by the sample. Here, the total resistance is a sum of grain and grain-boundary resistance, i.e., R = R1 + R2, t = 0.8 mm, and A = 8 mm2. The σdc obtained from impedance data as a function of 1000/T follows the Arrhenius relation shown in Fig. 2(e), and we observe two different activation energies (AEs) of ion conduction (Ea) obtained from the Arrhenius plots in two different temperature regions, which we designate as the low and high-temperature regions (LTR and HTR). The obtained values of activation energies in the LTR and HTR are 0.31 ± 0.05 eV and 0.74 ± 0.05 eV. Furthermore, we also calculated the effective relaxation frequencies (ωR) at all the measured temperatures from the impedance data. The expression of ωR is derived in the Note S1 (ESI†). Typically, ωR is the frequency value at which the imaginary impedance (Z′′(ω); representing relaxation) becomes maximum. The simplified expression of effective relaxation frequency is 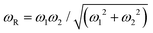 , where ω1 and ω2 are the relaxation frequencies corresponding to the grains (1/R1C1) and GBs (1/R2C2) using eqn (4) and (5). It is noteworthy that the term “effective relaxation frequency” should not be taken analogous to the single RC component, nor it is intended to imply a single relaxation mechanism. It arises from a combination of grain and GB relaxations and is used solely for plotting an Arrhenius relation to estimate activation energy. The plot of log(ωR) vs. 1000/T also follows the Arrhenius behavior since hopping is a temperature-activated phenomenon. The AEs of hopping migration (Em) in the LTR and HTR were estimated as 0.28 ± 0.05 eV and 0.53 ± 0.05 eV, respectively. The plausible reasons and the implications of observing two different AEs in LTR and HTR as well as differences in Ea and Em in the HTR are discussed later in the AC conductivity section.
, where ω1 and ω2 are the relaxation frequencies corresponding to the grains (1/R1C1) and GBs (1/R2C2) using eqn (4) and (5). It is noteworthy that the term “effective relaxation frequency” should not be taken analogous to the single RC component, nor it is intended to imply a single relaxation mechanism. It arises from a combination of grain and GB relaxations and is used solely for plotting an Arrhenius relation to estimate activation energy. The plot of log(ωR) vs. 1000/T also follows the Arrhenius behavior since hopping is a temperature-activated phenomenon. The AEs of hopping migration (Em) in the LTR and HTR were estimated as 0.28 ± 0.05 eV and 0.53 ± 0.05 eV, respectively. The plausible reasons and the implications of observing two different AEs in LTR and HTR as well as differences in Ea and Em in the HTR are discussed later in the AC conductivity section.
The coupled ionic–electronic behavior forms a complex problem in the halide perovskite materials because of the multiple physical processes manifesting in different types of dielectric polarization.2,49 While the impedance spectra help us understand how the system impedes the charge transport, the permittivity spectra shed light on the different polarization contributions in the system. The various physical processes include electronic, ionic, dipolar or orientational, and space charge (resulting from redistribution of free ions and electrons) polarizations, which contribute to the relative permittivity. All these components, due to the respective physical processes, occur at a diverse range of time scales ranging from femtoseconds to seconds. The real and imaginary parts of the frequency-dependent complex dielectric constant can be expressed as:
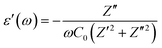 | (6) |
 | (7) |
The real part of the dielectric constant (ε′) vs. ω for the FAPbBr2I perovskite is plotted at various temperatures (305–454 K), shown in Fig. 3(a). The value of the dielectric constant is higher at LFs, as expected, due to the Maxwell–Wagner space charge effects.2 The ionic movement is a slow process, and at lower frequencies, the slow switching of the AC field does not affect the long-range ionic movements, and thus the ions move across long distances. Hence, they accumulate at the GB interfaces and contribute to the space charge polarization. That is why we observe high relative permittivity values at LFs, which fall off as the frequency is increased because long-range ionic motion is less significant as the frequency is increased. Typically, after the resonant frequency (corresponding to the relaxation of space charges), other contributions, viz. dipolar, atomic, and electronic polarizations, take over. Hence, physically, in our system, the ionic movement (at LFs) from grain towards GBs experiences the impedance from both grains and GBs and forms a space-charge layer at GB interfaces, which primarily contributes to the space charge polarization and hence the dielectric permittivity. Furthermore, the dielectric permittivity is observed to increase at LFs as we increase the temperature, further confirming the Maxwell–Wagner space charge polarization effect, which corresponds to the temperature activated ionic conduction and hopping transport.
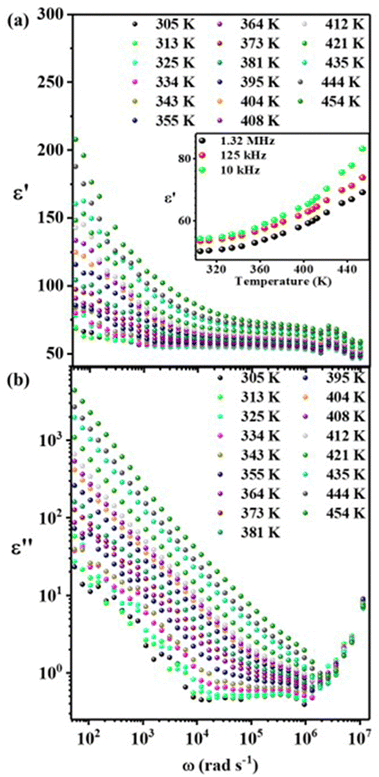 | ||
| Fig. 3 Temperature-dependent (305–454 K) dielectric (a) relative permittivity and (b) loss spectra of the FAPbBr2I perovskite. | ||
The room temperature (RT) value of ε′ for FAPbBr2I varies from 52 to 56 in the kHz to MHz frequency range and agrees with the reported values on various FAPbX3 perovskites.50 The temperature variation of ε′ in the HFs (1 kHz to 1.32 MHz) is also presented in the inset of Fig. 3(a). The ε′–T curve at HFs also shows temperature dependence (weaker dependence as compared to that at the LFs) and can be attributed to the dipolar relaxation of the reorienting FA+ dipoles. S. Govinda et al.51 also reported strong evidence of the MA+ dipole orientation in the tetragonal phase of MAPbX3 by observing a strong temperature dependence of ε′ compared to temperature-independent ε′ in CsPbBr3 at the kilohertz to megahertz frequencies. They also quantified the large contribution of MA+ dipoles and almost a negligible effect of Maxwell–Wagner space-charge polarization in this frequency range. Therefore, the temperature-dependency of ε′ (inset of Fig. 3(a)) in the case of the FAPbBr2I perovskite clearly suggests the role of FA+ dipolar contribution. Notably, the ε′–T dependency in our case is also observed to change with frequency but is not as strong as in the reported MAPbX3 perovskites, which were measured at temperatures lower than RT. Our range of temperatures are much higher (305–454 K), which induces extrinsic effects other than mere dipolar contributions.51 Additionally, FAPbBr2I exhibits the cubic phase, and FA+ possesses a lower dipole moment compared to MA+.52 The nature of the frequency-dependent dielectric loss ε′′(ω) spectra is shown in Fig. 3(b). The dielectric loss spectra are defined as17,53
 | (8) |
In accordance with the Jonscher power law (JPL), identified by σ′ = σdc + Aωs (σdc is the DC ionic-conductivity, A is a prefactor, and s is an exponent; 0 < s < 1),54 the expression (8) becomes:
 | (9) |
 in the LFs corresponding to the DC ionic conductivity and as
in the LFs corresponding to the DC ionic conductivity and as  in the dispersive or JPL region. In the LFs, we observed the DC region
in the dispersive or JPL region. In the LFs, we observed the DC region  at all temperatures, implying the long-range ionic conductivity of space charges. However, the dispersive region (kilohertz to megahertz) exhibits nearly constant loss (NCL) in the LTR (regions with almost constant ε′′), corresponding to s ≈ 1, and decreasing loss in the HTR (ε′′ decreases faster with ω as temperature increases), corresponding to a strongly decaying s with temperature. The s-values at different temperatures are also quantified in the analysis of the AC conductivity in a later section. The dielectric loss in a material decreases with an increment in the frequency of the applied AC field, because the contribution of space charge and dipolar polarization decreases significantly.55 In our observation of loss spectra of FAPbBr2I, in the LT and dispersive region (kHz–MHz), where we can find a region with s ≈ 1, the FA+-dipoles are able to reorient and dipolar polarization is still stronger to contribute to the NCL, whereas the Maxwell–Wagner polarization (MWP) will not be significant because the space charges will not have enough time to accumulate at the interfaces. In the HT and dispersive regions, where s decreases strongly with temperature, the contributions from both MWP and FA+-dipolar reorientation will be more insignificant and hence implies the faster decay of loss spectra as we increase the temperature.
at all temperatures, implying the long-range ionic conductivity of space charges. However, the dispersive region (kilohertz to megahertz) exhibits nearly constant loss (NCL) in the LTR (regions with almost constant ε′′), corresponding to s ≈ 1, and decreasing loss in the HTR (ε′′ decreases faster with ω as temperature increases), corresponding to a strongly decaying s with temperature. The s-values at different temperatures are also quantified in the analysis of the AC conductivity in a later section. The dielectric loss in a material decreases with an increment in the frequency of the applied AC field, because the contribution of space charge and dipolar polarization decreases significantly.55 In our observation of loss spectra of FAPbBr2I, in the LT and dispersive region (kHz–MHz), where we can find a region with s ≈ 1, the FA+-dipoles are able to reorient and dipolar polarization is still stronger to contribute to the NCL, whereas the Maxwell–Wagner polarization (MWP) will not be significant because the space charges will not have enough time to accumulate at the interfaces. In the HT and dispersive regions, where s decreases strongly with temperature, the contributions from both MWP and FA+-dipolar reorientation will be more insignificant and hence implies the faster decay of loss spectra as we increase the temperature.
The AC conductivity spectra of the Ag/FAPbBr2I/Ag device are also studied in detail to gain critical insights into the mechanisms behind thermally activated ionic conduction and hopping migration. The conductivity spectra σ′(ω) of FAPbBr2I at various temperatures (305–454 K) and the corresponding fits using the Almond–West model (a modified form of JPL) in terms of DC conductivity (σdc), hopping frequency (ωH) and power law exponent (s) with a limiting value of 0 ≤ s ≤ 1 are displayed in Fig. 4(a) and are given as54,56
 | (10) |
The fitting parameters (σdc, ωH and s) at different temperatures are compiled in Table SII in the ESI.† Generally, in a dielectric material, the LF region is dominated by the long-range transport of ions,37,45,57 which results in the successful hopping of these ions from one lattice site to another.58 We, therefore, observe a frequency-independent DC conductivity (σdc) in the LF region. The DC conductivity region then crosses over (at ω = ωH) to a frequency-dependent dispersive region at the HF region. The dispersive nature of conductivity at high frequencies can be explained by the time-evolution of correlated forward–backward hopping of ions, as formulated in Funke's Jump-Relaxation Model.58
The ionic conduction and hopping migration follow the Arrhenius law because they are thermally activated processes:
 | (11) |
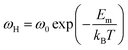 | (12) |
The general expression of the DC ionic conductivity of any given material is given as:59
 | (13) |
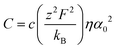 | (14) |
| σdcT = CωH | (15) |
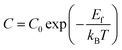 | (16) |
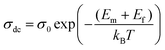 | (17) |
| Ea = Em + Ef | (18) |
In the case of FAPbBr2I, we calculated the values of the carrier concentration factor C at all temperatures using eqn (15) and fitted parameters (σdc, ωH). The C vs. T plot in the temperature range (305–454 K) is presented in Fig. 4(d). From the C–T plot, we clearly observe that C is almost constant in the LTR (305–381 K), justifying the similar values of AEs (Ea ≈ Em) obtained in this temperature regime. However, C increases by orders of magnitude in the HTR (395–454 K) and confirms the thermally activated mechanism where the concentration of mobile ions has increased substantially by overcoming the barrier Ef(Ea − Em ≈ 0.24 + 0.05 eV) and is responsible for the difference in the observed AEs.
We propose a plausible mechanism in which the traps play a crucial role in the thermally activated ionic conduction and hopping process. The traps formed in the MHPs are attributable to the presence of vacancies, interstitial, anti-site substitution defects, etc.61 The additional mobile ions might be generated via defect dissociation, ionization of neutral species, or any other relevant process. In other words, these ions were earlier trapped in the LTR because of insufficient thermal energy to overcome the potential well, whereas in the HTR, the thermal energy is sufficient to dissociate and make them free.59,62 The substantial increase in the ionic carrier concentration factor C with temperature (Fig. 4(d)) also indicates the crucial role of traps in ionic conduction. The barrier Ef for overcoming the formation of mobile ions corresponds here to the trap potential. Hence, the increase of ionic concentration leads to different activation barriers (Ea and Em) in the HTR (395–454 K).
Additionally, another pertinent question arises as to why Em itself would increase from 0.28 eV (in the LTR) to 0.49 eV (in the HTR). This can be addressed as follows: since the ion concentration is temperature-independent in the LTR, it suggests that the system has a constant defect population (e.g., intrinsic vacancies), which is synthetically created and cannot be avoided. This would predominantly lead to independent hopping of ions. However, when the ion concentration is temperature-dependent (as observed in the HTR), it suggests thermal generation of additional mobile ions. This would lead to increased ion–ion interactions and possibly enhanced correlated ionic hopping (rather than independent hopping across barriers), thus increasing the activation barrier. This idea is also supported by the observed temperature-dependent changes in the frequency exponent (s) as depicted in Fig. 4(e). In the LTR (305–381 K), the exponent (s) varies slightly from 0.96 (at 305 K) to 0.81 (at 381 K) and is close to 1, which indicates a nearly constant loss (NCL) or the hopping of each ion is independent of each other between localized sites,63 whereas in the HTR (395–454 K), s decreases significantly to lower values from 0.66 (at 395 K) to 0.46 (at 454 K) and a sudden jump from 0.81 (at 381 K) to 0.66 (at 395 K) is observed. This indicates that the ion hopping is no longer independent; rather, it is a correlated hopping of ions between localized sites64 due to enhanced ion–ion interactions via generation of additional free ions. This correlated ion transport would, more often than not, increase the energy barrier for hopping. Hence, the variation of s with temperature clearly indicates a sudden change of AEs in two different temperature regimes and direct implications can be made to correlate different kinds of ionic transport in different regions of temperature. For the broader context, we have also compared the activation energies associated with the hopping migration of various species (ions/vacancies) in the OIMHPs, estimated via a wide variety of experimental techniques (see Table 1).
| S. No. | Material composition | Migrating species | Activation energy (eV) | Technique | Ref. |
|---|---|---|---|---|---|
| 1 | MAPbI3 | I− | 0.17 | Nuclear quadrupole resonance (NQR) | 65 |
| 2 | MAPbI3 | I− | 0.29 ± 0.06 | Transient ion drift | 66 |
| 3 | MASnI3 | Iodide vacancy (VI) | 0.37 | Density functional theory (DFT) | 67 |
| Iodide interstitial (Ii) | 0.65 | ||||
| 4 | MASnBr3 | Br− | 0.44 | Solid-state nuclear magnetic resonance (NMR) | 68 |
| 5 | MAPbI3−xClx | I− | 0.55 | Impedance and intensity modulated photovoltage spectroscopy (IMVS) | 69 |
| 6 | FAPbI3 | I− | 0.222 ± 0.015 | Temperature-dependent J–V | 70 |
| 7 | MA0.5FA0.5PbI3 | I− | 0.296 ± 0.015 | Temperature-dependent J–V | 70 |
| 8 | FAPbBr2.9Cl0.1 | Br− | 0.58 | Temperature-dependent J–V | 71 |
| 9 | FAPbBr3 | Bromide vacancy (VBr) | 0.33 | Density functional theory (DFT) | 72 |
| Bromide interstitial (IBr) | 0.24 | ||||
| FA vacancy (VFA) | 0.39 | ||||
| FA interstitial (IFA) | 0.34 | ||||
| 10 | FAPbBr2I | Halide (Br/I) | 0.30 ± 0.05 (low temperature (305–381 K)) | Temperature-dependent impedance spectroscopy | This work |
| Not conclusive which halide | 0.50 ± 0.05 (high temperature (395–454 K)) |
To gain further insights into the role of trap states and trapped carriers in understanding the thermally activated ion conduction and hopping in FAPbBr2I perovskites, we have investigated the temperature-dependent space charge limited current–voltage characteristics. We have discussed the effect of mobile carrier formation at HT on influencing the corresponding steady-state SCLC characteristics. The presence of localized states in the sub-bandgap region, known as traps, is commonly observed due to the high degree of energetic and spatial disorders in the MHPs.61,73 Due to the presence of these trap-states, there is accumulation (or trapping) of charge species, and the current due to the free carriers is limited by these space charges. Usually, in a trap-free device, there are two regions, namely an ohmic region (J–V) at very low voltages dominated by background carrier density,74,75 followed by the space charge limited current (SCLC) region (J∼V2) after crossing a certain threshold voltage. The SCLC region occurs due to increased carrier density (due to the injection of charges after crossing the threshold voltage) compared to the background carrier density. The SCLC follows the Mott–Gurney Law:76
 | (19) |
 | (20) |
The experimentally determined log–log plots of J–V characteristics for the Ag/FAPbBr2I SC/Ag device configuration at different temperatures such as 100 °C (373 K), 120 °C (393 K), 140 °C (413 K) and 160 °C (433 K) are presented in Fig. 5. The digital images of the lateral device architecture of the Ag/FAPbBr2I SC/Ag device are presented in Fig. S4(a and b) in the ESI.† In the log–log plot, all the regions, viz. ohmic, TFL, and SCLC, are fitted separately in accordance with the generic scaling law of J–V, i.e., J∼Vβ in the respective regions. Several reports75,79,80 have demonstrated by the drift-diffusion (DD) simulation studies that mobile ions can strongly influence the typical SCLC characteristics because they can screen/negate the charge of trapped carriers (e− or h+). Hence the density of trapped carriers expressed by eqn (20) can be underestimated by orders of magnitude depending on the difference between mobile ion density and trapped carrier density. Duijnstee et al.75 showed that if the mobile ions are introduced then Vons shifts to lower values and when the value of ion density outnumbers the trapped carrier density, then the effect of traps is eventually overshadowed and we cannot observe the TFL region. In effect, if traps dominate, then the TFL region can be observed and if mobile ion density dominates the traps, then the TFL region could no longer be observed.
 | ||
| Fig. 5 Temperature-dependent space charge limited current–voltage (J–V) characteristics of the Ag/FAPbBr2I SC/Ag device configuration at temperature T = 373 K, 393 K, 413 K, and 433 K. | ||
Remarkably, from our observations of the ionic carrier concentration factor vs. temperature in the conductivity section, the value of C has increased significantly in the HTR (Fig. 4(d)). Moreover, this increase is also justified by the observance of an AE barrier of forming these carriers, as indicated in the Arrhenius plots of DC conductivity and hopping frequency (Fig. 4(b) and (c)). The onset voltage (Vons) is determined from the crossover point of the ohmic to the TFL region. The values of Vons at 100 °C (373 K) and 120 °C (393 K) from the J–V plots are found to be 1.57 V and 1.24 V, respectively. Notably, we cannot use Vons in eqn (20) for extracting trap density because the ion migration would lead to the hysteresis effect80,81 and this value of Vons would be different for forward and reverse scans. In this context, researchers have also introduced the pulsed-voltage SCLC technique for halide perovskites75,79,80 where one can measure the hysteresis-free J–V characteristics and extract these device parameters more reliably. Therefore, we only consider the forward scan J–V characteristics at all temperatures for extracting Vons for a qualitative comparison. In addition, our primary focus is on observing the changes in the nature of J–V characteristics from the LTR to the HTR, which would help us to interpret the effect of mobile ion dynamics on the nature of steady state J–V characteristics.
The values of Vons decrease as expected because the ion density increases with temperature, negating the charge of trapped carriers. Eventually, the ion density might have outnumbered the traps beyond a critical temperature of 395 K and hence we conclude that the large number of mobile carriers formed in the HTR by the temperature triggered mechanism is responsible for the absence of the TFL region at 413 K and 433 K. The slope of the TFL regime was also observed to increase from ∼2.84 at 373 K to ∼5.67 at 393 K. In this way, we have demonstrated that the effect of transient ionic mechanisms, viz. thermally activated formation of mobile ions and differences in the AEs of ionic conduction and hopping migration, is very well manifested in the nature of steady-state SCL J–V characteristics. In addition to the observation of the influence of mobile ions on the expected changes of the nature of J–V characteristics, the observed changes in the J–V characteristics also corroborate the role of traps in understanding the thermally activated interplay of ionic conduction and hopping migration in the mixed halide FAPbBr2I perovskite.
In order to investigate the relaxation mechanisms involved in the FAPbBr2I perovskites, the electric modulus loss spectra M′′(ω) are investigated in the temperature range of 305 K to 454 K. The electric modulus is expressed as the reciprocal of complex dielectric permittivity M*(ω) = 1/ε*(ω). The CEMS serves as a powerful tool to analyze relaxation phenomena, specifically in materials where electrode polarization or large DC conductivity may obscure bulk features in the permittivity or impedance spectra.82 As evident from the mathematical expression or formalism of electric modulus (reciprocal of complex permittivity), it suppresses the effects of large capacitance contributions (such as from interfacial regions of grain boundaries or electrodes) and emphasizes the bulk relaxation dynamics of charge carriers.82,83 In contrast to the impedance formalism, which highlights regions of high resistance (like grain boundaries), the modulus spectrum is more sensitive to regions of low capacitance, such as the grains or bulk.
The frequency dependence of M′′(ω) at different temperatures, presented in Fig. 6(a), shows distinctive relaxation peaks and is ascribed to the relaxation of space charges at the characteristic frequency of the material. These peaks are also indicative of the transition from long-range ionic motion at the LF region to localized, short-range motion at the HF region. The M′′(ω) peaks also shift towards the HF side, suggesting the thermally activated relaxation process. The M′′(ω) spectra of the FAPbBr2I perovskite show asymmetric relaxation peaks characteristic of the non-Debye type of relaxation.47 The imaginary part of the Havriliak–Nigami (HN) model is used to fit the asymmetric curves of M′′(ω) spectra observed for FAPbBr2I:84
 | (21) |
 | (22) |
The plot of log10τ vs. reciprocal temperature is shown in Fig. 6(b), and the activation energies obtained in the LTR and HTR are EHN1 = 0.29 ± 0.05 eV and EHN2 = 0.49 ± 0.05 eV respectively. These values are coherent with the AEs of hopping migration in the LTR and HTR, obtained from the Arrhenius plots of hopping frequency, validating different hopping mechanisms in LTR and HTR regions. The shape parameters are also plotted as a function of temperature in Fig. 6(c) and observed to follow complementary variations with temperature.
The experimentally observed relaxation behavior in the FAPbBr2I perovskite is also analyzed by the well-known time domain relaxation model, Kohlrausch–Williams–Watts (KWW) function, given by86,87
 | (23) |
The KWW function, ϕ(t), represents the decay of the applied electric field E(t) inside the material. The τKWW is the KWW relaxation time, and βKWW (0 ≤ βKWW ≤ 1) is the stretched exponent, typically used for the materials obeying slow relaxation dynamics.88βKWW is a very useful parameter that distinguishes the Debye- and non-Debye-types of relaxation of mobile ions. The Debye-type relaxation is indicated when βKWW obtains or tends to the value of 1. The values 0 < βKWW < 1 suggest the non-Debye relaxation, and βKWW = 0 for maximum dipole–dipole interaction.89 The values of βKWW for the FAPbBr2I perovskite were observed to vary from ∼0.61 at 305 K to ∼0.58 at 454 K with random increment or decrement in between the temperature range without any specific trend. The KWW relaxation function is calculated by using the M′′(ω) spectra, as90
 | (24) |
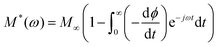 | (25) |
The KWW relaxation function for the FAPbBr2I perovskite in the temperature range 305–454 K was then calculated using the experimentally observed M′′(ω) data in eqn (24) and fitted by the KWW relaxation function defined in eqn (23). The fitted KWW function at various temperatures is shown in Fig. 6(d). The fitting parameters, τKWW and βKWW, obtained at all temperatures (305–454 K), are summarized in Table SIV in the ESI.† The KWW relaxation time also obeys the Arrhenius relation: 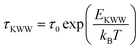 with the inverse temperature. The Arrhenius plot of the KWW relaxation time, shown in Fig. 6(e), also demonstrated the two activation energies, EKWW1 = 0.29 ± 0.05 eV and EKWW2 = 0.50 ± 0.05 eV in the LTR and HTR, respectively, further corroborating the values of AE of hopping migration obtained from the hopping frequency Arrhenius plot in both temperature regimes. Furthermore, we also verified the compliance of fitting the observed electric modulus data at various temperatures using both the HN and KWW formalisms. For this, the parameters of both HN and KWW models must obey the following relation:88
with the inverse temperature. The Arrhenius plot of the KWW relaxation time, shown in Fig. 6(e), also demonstrated the two activation energies, EKWW1 = 0.29 ± 0.05 eV and EKWW2 = 0.50 ± 0.05 eV in the LTR and HTR, respectively, further corroborating the values of AE of hopping migration obtained from the hopping frequency Arrhenius plot in both temperature regimes. Furthermore, we also verified the compliance of fitting the observed electric modulus data at various temperatures using both the HN and KWW formalisms. For this, the parameters of both HN and KWW models must obey the following relation:88
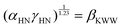 | (26) |
The scaling process of a physical quantity is employed to probe whether the dynamical processes associated with that quantity are affected by the external parameters, viz. temperature, composition, and others. The scaling of the AC conductivity and electric modulus loss spectra acquired at different temperatures to a master curve suggests the distinct physical mechanisms behind the ionic conduction and relaxation processes.91 Several parameters have been previously used to scale the AC conductivity and modulus loss spectra.91–95 For the FAPbBr2I perovskite, the temperature-dependent AC conductivity is scaled by scaling the conductivity (σ′) and frequency (ω) axes by σdc and ωH and is presented in Fig. 7(a). The electric modulus loss spectra are also scaled similarly, by scaling the modulus (M′′) and frequency (ω) axes by M′′max and ωmax respectively, as displayed in Fig. 7(b). The AC conductivity scaling plot (Fig. 7(a)) performed using the Pan and Ghosh model95 depicts a common master curve in the LTR (305–381 K, shown by green scatter plots), and a slightly different master-curve at the HTR (395–454 K, shown by red scatter plots). Additionally, the scaling plot of modulus loss spectra (Fig. 7(b)) also shows slightly different master curves in the LTR and HTR. The scaling of σdc and ωH thus are also indicative of two different ionic conduction and hopping relaxation mechanisms in the low-temperature and the high-temperature regimes.
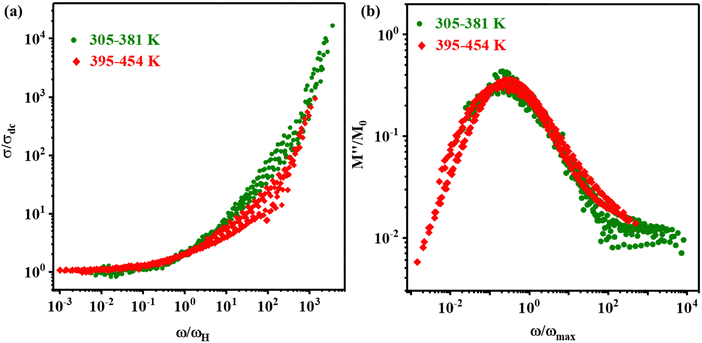 | ||
| Fig. 7 Scaling of (a) AC conductivity and (b) electric modulus loss spectra of the FAPbBr2I perovskite at different temperatures. | ||
IV. Conclusions
In summary, we have grown single crystals of FA-based mixed halide FAPbBr2I using the inverse temperature crystallization method. The structural and optical characterization was performed using XRD and UV-vis techniques. The XRD analysis rendered the cubic crystal structure of FAPbBr2I with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The ion conduction and relaxation dynamics at different temperatures (305–454 K) were probed by complex impedance spectroscopy, complex electric modulus spectroscopy, and AC conductivity. These spectra were analyzed using various theoretical models, viz. the Maxwell–Wagner equivalent circuit model, Havriliak–Negami (HN) and Kohlrausch–Williams–Watts (KWW) model, and modified Jonscher power law. The Nyquist plots obtained from the fits to the Maxwell–Wagner model were used to interpret the contributions of grains and grain boundaries to the total impedance. The HN model and JPL confirmed the presence of two regions of ionic conductivity. In the LTR (305–381 K), we observed almost similar values of AE of ionic conduction and hopping migration (Ea = Em = 0.30 ± 0.05 eV) since the temperature response of ionic conduction in this temperature range is dependent only on the hopping frequency. On the other hand, in the HTR, we observed a substantial increase in the number of mobile ions, facilitated by overcoming an activation energy barrier, Ef = 0.24 ± 0.05 eV of forming mobile ions, as evidenced by the differences in activation energies (Ea = 0.74 ± 0.05 eV and Em = 0.50 ± 0.05 eV). The temperature-dependent SCLC measurements on the Ag/FAPbBr2I SC/Ag device revealed that these mobile ions can significantly influence the nature of steady-state J–V characteristics and reaffirm the role of traps and mobile ions in understanding the observed thermally activated mechanism of ionic conduction and hopping migration. Lastly, the temperature scaling of the AC conductivity and complex electric modulus also validates the existence of different conduction and hopping mechanisms in low-temperature and high-temperature regions.
m space group. The ion conduction and relaxation dynamics at different temperatures (305–454 K) were probed by complex impedance spectroscopy, complex electric modulus spectroscopy, and AC conductivity. These spectra were analyzed using various theoretical models, viz. the Maxwell–Wagner equivalent circuit model, Havriliak–Negami (HN) and Kohlrausch–Williams–Watts (KWW) model, and modified Jonscher power law. The Nyquist plots obtained from the fits to the Maxwell–Wagner model were used to interpret the contributions of grains and grain boundaries to the total impedance. The HN model and JPL confirmed the presence of two regions of ionic conductivity. In the LTR (305–381 K), we observed almost similar values of AE of ionic conduction and hopping migration (Ea = Em = 0.30 ± 0.05 eV) since the temperature response of ionic conduction in this temperature range is dependent only on the hopping frequency. On the other hand, in the HTR, we observed a substantial increase in the number of mobile ions, facilitated by overcoming an activation energy barrier, Ef = 0.24 ± 0.05 eV of forming mobile ions, as evidenced by the differences in activation energies (Ea = 0.74 ± 0.05 eV and Em = 0.50 ± 0.05 eV). The temperature-dependent SCLC measurements on the Ag/FAPbBr2I SC/Ag device revealed that these mobile ions can significantly influence the nature of steady-state J–V characteristics and reaffirm the role of traps and mobile ions in understanding the observed thermally activated mechanism of ionic conduction and hopping migration. Lastly, the temperature scaling of the AC conductivity and complex electric modulus also validates the existence of different conduction and hopping mechanisms in low-temperature and high-temperature regions.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
Funding from the ANRF, Government of India, under Project No. CRG/2022/005258 is gratefully acknowledged. We also thank the Central Instrumentation Facility at IIT Gandhinagar for facilitating several measurements. We also acknowledge Mr Surya Pratap Singh Shekhawat from the Department of Applied Physics in Delhi Technological University for facilitating the impedance measurements.References
- R. Su, Z. Xu, J. Wu, D. Luo, Q. Hu, W. Yang, X. Yang, R. Zhang, H. Yu and T. P. Russell, Dielectric screening in perovskite photovoltaics, Nat. Commun., 2021, 12(1), 2479 CrossRef CAS.
- J. N. Wilson, J. M. Frost, S. K. Wallace and A. Walsh, Dielectric and ferroic properties of metal halide perovskites, APL Mater., 2019, 7(1), 010901 CrossRef.
- Y. He, M. Petryk, Z. Liu, D. G. Chica, I. Hadar, C. Leak, W. Ke, I. Spanopoulos, W. Lin and D. Y. Chung, CsPbBr3 perovskite detectors with 1.4% energy resolution for high-energy γ-rays, Nat. Photonics, 2021, 15(1), 36–42 CrossRef CAS.
- Z. Li, F. Zhou, H. Yao, Z. Ci, Z. Yang and Z. Jin, Halide perovskites for high-performance X-ray detector, Mater. Today, 2021, 48, 155–175 CrossRef.
- W.-J. Yin, J.-H. Yang, J. Kang, Y. Yan and S.-H. Wei, Halide perovskite materials for solar cells: a theoretical review, J. Mater. Chem. A, 2015, 3(17), 8926–8942 RSC.
- R. Ding, X. Zhang, G. Chen, H. Wang, R. Kishor, J. Xiao, F. Gao, K. Zeng, X. Chen and X. W. Sun, High-performance piezoelectric nanogenerators composed of formamidinium lead halide perovskite nanoparticles and poly (vinylidene fluoride), Nano Energy, 2017, 37, 126–135 CrossRef CAS.
- W. Yu, F. Li, L. Yu, M. R. Niazi, Y. Zou, D. Corzo, A. Basu, C. Ma, S. Dey and M. L. Tietze, Single crystal hybrid perovskite field-effect transistors, Nat. Commun., 2018, 9(1), 5354 CrossRef CAS PubMed.
- T. Paul, P. K. Sarkar, S. Maiti, A. Sahoo and K. K. Chattopadhyay, Solution-processed light-induced multilevel non-volatile wearable memory device based on CsPb2Br5 perovskite, Dalton Trans., 2022, 51(10), 3864–3874 RSC.
- M. Singh, J. Nama, T. Paul, N. H. Makani, A. Sahoo, S. Sharma and R. Banerjee, Photoelectrochemically Induced CO2 Reduction Using Halide-Tunable Lead-Free Perovskites, ACS Appl. Energy Mater., 2023, 6(6), 3566–3578 CrossRef CAS.
- T. Paul, A. Sahoo, S. Maiti, D. S. Gavali, R. Thapa and R. Banerjee, Halide Tunablility Leads to Enhanced Biomechanical Energy Harvesting in Lead-Free Cs2SnX6-PVDF Composites, ACS Appl. Mater. Interfaces, 2023, 15(29), 34726–34741 CrossRef CAS.
- A. Sahoo, T. Paul, A. Nath, S. Maiti, P. Kumar, P. Ghosh and R. Banerjee, Preferential Perovskite Surface-termination Induced High Piezoresponse in Lead-free in situ Fabricated Cs3Bi2Br9-PVDF Nanocomposites Promotes Biomechanical Energy Harvesting, Nanoscale, 2023, 15(27), 11603–11615 RSC.
- A. Sahoo, T. Paul, N. H. Makani, S. Maiti and R. Banerjee, High piezoresponse in low-dimensional inorganic halide perovskite for mechanical energy harvesting, Sustainable Energy Fuels, 2022, 6(19), 4484–4497 RSC.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Hybrid organic—inorganic perovskites: low-cost semiconductors with intriguing charge-transport properties, Nat. Rev. Mater., 2016, 1(1), 1–16 CrossRef.
- Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Electron-hole diffusion lengths> 175 μm in solution-grown CH3NH3PbI3 single crystals, Science, 2015, 347(6225), 967–970 CrossRef CAS PubMed.
- C. M. Sutter-Fella, Y. Li, M. Amani, J. W. Ager III, F. M. Toma, E. Yablonovitch, I. D. Sharp and A. Javey, High photoluminescence quantum yield in band gap tunable bromide containing mixed halide perovskites, Nano Lett., 2016, 16(1), 800–806 CrossRef CAS PubMed.
- P. Basumatary and P. Agarwal, A short review on progress in perovskite solar cells, Mater. Res. Bull., 2022, 149, 111700 CrossRef CAS.
- R. Kumar, P. Srivastava, T. Kumar and M. Bag, Electronic-Ionic Transport in MAPbBr3 Single Crystal: The Evidence of Super-Linear Power Law in AC Conductivity, J. Phys. Chem. C, 2022, 126(33), 14305–14311 CrossRef CAS.
- Y. Lei, Y. Chen and S. Xu, Single-crystal halide perovskites: opportunities and challenges, Matter, 2021, 4(7), 2266–2308 CrossRef CAS.
- Y. Cho, H. R. Jung and W. Jo, Halide perovskite single crystals: growth, characterization, and stability for optoelectronic applications, Nanoscale, 2022, 14(26), 9248–9277 RSC.
- H. Jiang and C. Kloc, Single-crystal growth of organic semiconductors, MRS Bull., 2013, 38(1), 28–33 CrossRef CAS.
- M. I. Saidaminov, A. L. Abdelhady, B. Murali, E. Alarousu, V. M. Burlakov, W. Peng, I. Dursun, L. Wang, Y. He and G. Maculan, High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization, Nat. Commun., 2015, 6(1), 7586 CrossRef PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger and K. Katsiev, Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals, Science, 2015, 347(6221), 519–522 CrossRef CAS.
- Y. Dang, Y. Liu, Y. Sun, D. Yuan, X. Liu, W. Lu, G. Liu, H. Xia and X. Tao, Bulk crystal growth of hybrid perovskite material CH3NH3PbI3, CrystEngComm, 2015, 17(3), 665–670 RSC.
- D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Hörantner, A. Haghighirad, N. Sakai, L. Korte and B. Rech, A mixed-cation lead mixed-halide perovskite absorber for tandem solar cells, Science, 2016, 351(6269), 151–155 CrossRef CAS.
- R. Gupta, V. Gupta, R. Datt, S. Arya, A. Pandey, A. Singh, S. Husale, R. Srivastava and S. Pathak, Enhanced photosensitive properties of a single-crystal formamidinium lead bromide iodine (FAPbBr2I) based photodetector, Mater. Adv., 2022, 3(4), 2089–2095 RSC.
- K. Sekar, R. Manisekaran, O. M. Nwakanma and M. Babudurai, Significance of Formamidinium Incorporation in Perovskite Composition and Its Impact on Solar Cell Efficiency: A Mini-Review, Adv. Energy Sustainability Res., 2024, 5(8), 2400003 CrossRef CAS.
- M. Li, R. Sun, J. Chang, J. Dong, Q. Tian, H. Wang, Z. Li, P. Yang, H. Shi and C. Yang, Orientated crystallization of FA-based perovskite via hydrogen-bonded polymer network for efficient and stable solar cells, Nat. Commun., 2023, 14(1), 573 CrossRef CAS PubMed.
- S. Sidhik, I. Metcalf, W. Li, T. Kodalle, C. J. Dolan, M. Khalili, J. Hou, F. Mandani, A. Torma and H. Zhang, Two-dimensional perovskite templates for durable, efficient formamidinium perovskite solar cells, Science, 2024, 384(6701), 1227–1235 CrossRef CAS PubMed.
- M. Que, Y. Li, H. Yuan, P. Zhong, B. Li, J. Wei, P. Hu, L. Gao, W. Huang and S. Liu, Surface Doping to Suppress Iodine Ion Migration for Stable FAPbI3 Perovskite Quantum Dot Solar Cells, Small, 2025, 21(4), 2406569 CrossRef.
- J. Kim, J. S. Park, G. Y. Kim and W. Jo, Autonomous Control of Ion Migration at α-FAPbI3 Heterointerfaces via Interfacial-Self-Assembled 2D Perovskite, Adv. Energy Mater., 2024, 14(40), 2402117 CrossRef CAS.
- Y. Liang, F. Li, X. Cui, T. Lv, C. Stampfl, S. P. Ringer, X. Yang, J. Huang and R. Zheng, Toward stabilization of formamidinium lead iodide perovskites by defect control and composition engineering, Nat. Commun., 2024, 15(1), 1707 CrossRef CAS PubMed.
- D. K. LaFollette, J. Hidalgo, O. Allam, J. Yang, A. Shoemaker, R. Li, B. Lai, B. Lawrie, S. Kalinin and C. A. Perini, Bromine Incorporation Affects Phase Transformations and Thermal Stability of Lead Halide Perovskites, J. Am. Chem. Soc., 2024, 146(27), 18576–18585 CrossRef CAS PubMed.
- O. Nazarenko, S. Yakunin, V. Morad, I. Cherniukh and M. V. Kovalenko, Single crystals of caesium formamidinium lead halide perovskites: solution growth and gamma dosimetry, NPG Asia Mater., 2017, 9(4), e373 CrossRef CAS.
- L. Chen, Y.-Y. Tan, Z.-X. Chen, T. Wang, S. Hu, Z.-A. Nan, L.-Q. Xie, Y. Hui, J.-X. Huang and C. Zhan, Toward long-term stability: single-crystal alloys of cesium-containing mixed cation and mixed halide perovskite, J. Am. Chem. Soc., 2019, 141(4), 1665–1671 CrossRef CAS PubMed.
- J. Berry, T. Buonassisi, D. A. Egger, G. Hodes, L. Kronik, Y. L. Loo, I. Lubomirsky, S. R. Marder, Y. Mastai and J. S. Miller, Hybrid organic–inorganic perovskites (HOIPs): Opportunities and challenges, Adv. Mater., 2015, 27(35), 5102–5112 CrossRef CAS.
- D. Ghosh, E. Welch, A. J. Neukirch, A. Zakhidov and S. Tretiak, Polarons in halide perovskites: a perspective, J. Phys. Chem. Lett., 2020, 11(9), 3271–3286 CrossRef CAS.
- N. H. Makani, A. Sahoo, P. Pal, T. Paul, L. S. Tanwar, M. Singh, A. Ghosh and R. Banerjee, Onset of vacancy-mediated high activation energy leads to large ionic conductivity in two-dimensional layered Cs2PbI2Cl2 Ruddlesden–Popper halide perovskite, Phys. Rev. Mater., 2022, 6(11), 115002 CrossRef CAS.
- C. G. Bischak, C. L. Hetherington, H. Wu, S. Aloni, D. F. Ogletree, D. T. Limmer and N. S. Ginsberg, Origin of reversible photoinduced phase separation in hybrid perovskites, Nano Lett., 2017, 17(2), 1028–1033 CrossRef CAS PubMed.
- W. Tress, Metal Halide Perovskites as Mixed Electronic–Ionic Conductors: Challenges and Opportunities□ From Hysteresis to Memristivity, J. Phys. Chem. Lett., 2017, 8(13), 3106–3114 CrossRef CAS PubMed.
- N. K. Tailor, N. Parikh, P. Yadav and S. Satapathi, Dielectric Relaxation and Polaron Hopping in Cs2AgBiBr6 Halide Double Perovskites, J. Phys. Chem. C, 2022, 126(24), 10199–10208 CrossRef CAS.
- G. Y. Kim, A. Senocrate, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Large tunable photoeffect on ion conduction in halide perovskites and implications for photodecomposition, Nat. Mater., 2018, 17(5), 445–449 CrossRef CAS PubMed.
- L.-C. Chen, K.-L. Lee, C.-H. Tien and H.-Y. Wei, FAPbBr3−xIx perovskite quantum dots red Light-Emitting diodes with double confinement layer structure, Mater. Sci. Eng.: B, 2021, 264, 114969 CrossRef CAS.
- R. Ding, H. Liu, X. Zhang, J. Xiao, R. Kishor, H. Sun, B. Zhu, G. Chen, F. Gao and X. Feng, Flexible piezoelectric nanocomposite generators based on formamidinium lead halide perovskite nanoparticles, Adv. Funct. Mater., 2016, 26(42), 7708–7716 CrossRef CAS.
- M. A. Afroz, C. A. Aranda, N. K. Tailor, Yukta, P. Yadav, M. M. Tavakoli, M. Saliba and S. Satapathi, Impedance spectroscopy for metal halide perovskite single crystals: Recent advances, challenges, and solutions, ACS Energy Lett., 2021, 6(9), 3275–3286 CrossRef CAS.
- M. Singh, T. Paul, P. Pal, A. Sahoo, L. S. Tanwar, N. H. Makani, A. Ghosh and R. Banerjee, High ionic conduction and polarity-induced piezoresponse in layered bimetallic Rb4Ag2BiBr9 single crystals, J. Phys. Chem. C, 2022, 126(51), 21810–21824 CrossRef CAS.
- M. Sajedi Alvar, P. W. Blom and G. J. A. Wetzelaer, Device model for methylammonium lead iodide perovskite with experimentally validated ion dynamics, Adv. Electron. Mater., 2020, 6(6), 1900935 CrossRef CAS.
- F. Borsa, D. Torgeson, S. W. Martin and H. K. Patel, Relaxation and fluctuations in glassy fast-ion conductors: wide-frequency-range NMR and conductivity measurements, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(2), 795 CrossRef CAS PubMed.
- M. E. Hajlaoui, R. Dhahri, N. Hnainia, A. Benchaabane, E. Dhahri and K. Khirouni, Conductivity and giant permittivity study of Zn0.5Ni0.5Fe2O4 spinel ferrite as a function of frequency and temperature, RSC Adv., 2019, 9(56), 32395–32402 RSC.
- A. Guerrero, J. Bisquert and G. Garcia-Belmonte, Impedance spectroscopy of metal halide perovskite solar cells from the perspective of equivalent circuits, Chem. Rev., 2021, 121(23), 14430–14484 CrossRef CAS PubMed.
- S. Govinda, B. P. Kore, D. Swain, A. Hossain, C. De, T. N. Guru Row and D. Sarma, Critical comparison of FAPbX3 and MAPbX3 (X = Br and Cl): how do they differ?, J. Phys. Chem. C, 2018, 122(25), 13758–13766 CrossRef CAS.
- S. Govinda, B. P. Kore, M. Bokdam, P. Mahale, A. Kumar, S. Pal, B. Bhattacharyya, J. Lahnsteiner, G. Kresse and C. Franchini, Behavior of methylammonium dipoles in MAPbX3 (X = Br and I), J. Phys. Chem. Lett., 2017, 8(17), 4113–4121 CrossRef CAS PubMed.
- D. Gets, G. Verkhogliadov, E. Danilovskiy, A. Baranov, S. Makarov and A. Zakhidov, Dipolar cation accumulation at the interfaces of perovskite light-emitting solar cells, J. Mater. Chem. C, 2020, 8(47), 16992–16999 RSC.
- D. Singh, K. Shahi and K. K. Kar, Superlinear frequency dependence of AC conductivity and its scaling behavior in xAgI-(1−x) AgPO3 glass superionic conductors, Solid State Ionics, 2016, 287, 89–96 CrossRef CAS.
- A. K. Jonscher, The ‘universal’dielectric response, Nature, 1977, 267(5613), 673–679 CrossRef CAS.
- C. Koops, On the dispersion of resistivity and dielectric constant of some semiconductors at audiofrequencies, Phys. Rev., 1951, 83(1), 121 CrossRef CAS.
- D. Almond and A. West, Anomalous conductivity prefactors in fast ion conductors, Nature, 1983, 306(5942), 456–457 CrossRef CAS.
- X. Zheng, S. Wang, J. Wang, W. Hua, J. Zhang and L. Liu, Long-range and short-range transport dynamics of Li ions in LiMn2O4, J. Phys. Chem. C, 2020, 124(46), 25254–25261 CrossRef CAS.
- K. Funke and R. Hoppe, Jump-relaxation model yields Kohlrausch-Williams-Watts behaviour, Solid State Ionics, 1990, 40, 200–204 CrossRef.
- S. Yang, S. Y. Kim and G. Chen, Halide Superionic Conductors for All-Solid-State Batteries: Effects of Synthesis and Composition on Lithium-Ion Conductivity, ACS Energy Lett., 2024, 9(5), 2212–2221 CrossRef CAS PubMed.
- D. Almond, G. Duncan and A. West, The determination of hopping rates and carrier concentrations in ionic conductors by a new analysis of ac conductivity, Solid State Ionics, 1983, 8(2), 159–164 CrossRef CAS.
- H. Jin, E. Debroye, M. Keshavarz, I. G. Scheblykin, M. B. Roeffaers, J. Hofkens and J. A. Steele, It's a trap! On the nature of localised states and charge trapping in lead halide perovskites, Mater. Horiz., 2020, 7(2), 397–410 RSC.
- D. Meggiolaro, E. Mosconi and F. De Angelis, Formation of surface defects dominates ion migration in lead-halide perovskites, ACS Energy Lett., 2019, 4(3), 779–785 CrossRef CAS.
- C. León, K. Ngai and A. Rivera, Correlation between ion hopping conductivity and near constant loss in ionic conductors, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(13), 134303 CrossRef.
- A. Rivera, C. León, J. Sanz, J. Santamaria, C. Moynihan and K. Ngai, Crossover from ionic hopping to nearly constant loss in the fast ionic conductor Li0.18La0.61TiO3, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(22), 224302 CrossRef.
- A. Senocrate, I. Moudrakovski, G. Y. Kim, T. Y. Yang, G. Gregori, M. Grätzel and J. Maier, The nature of ion conduction in methylammonium lead iodide: a multimethod approach, Angew. Chem., 2017, 129(27), 7863–7867 CrossRef.
- M. H. Futscher, J. M. Lee, L. McGovern, L. A. Muscarella, T. Wang, M. I. Haider, A. Fakharuddin, L. Schmidt-Mende and B. Ehrler, Quantification of ion migration in CH3NH3PbI3 perovskite solar cells by transient capacitance measurements, Mater. Horiz., 2019, 6(7), 1497–1503 RSC.
- T. Shi, H.-S. Zhang, W. Meng, Q. Teng, M. Liu, X. Yang, Y. Yan, H.-L. Yip and Y.-J. Zhao, Effects of organic cations on the defect physics of tin halide perovskites, J. Mater. Chem. A, 2017, 5(29), 15124–15129 RSC.
- D. J. Kubicki, D. Prochowicz, E. Salager, A. Rakhmatullin, C. P. Grey, L. Emsley and S. D. Stranks, Local structure and dynamics in methylammonium, formamidinium, and cesium tin(II) mixed-halide perovskites from 119Sn solid-state NMR, J. Am. Chem. Soc., 2020, 142(17), 7813–7826 CrossRef CAS PubMed.
- A. Pockett, G. E. Eperon, N. Sakai, H. J. Snaith, L. M. Peter and P. J. Cameron, Microseconds, milliseconds and seconds: deconvoluting the dynamic behaviour of planar perovskite solar cells, Phys. Chem. Chem. Phys., 2017, 19(8), 5959–5970 RSC.
- W. Li, M. U. Rothmann, Y. Zhu, W. Chen, C. Yang, Y. Yuan, Y. Y. Choo, X. Wen, Y.-B. Cheng and U. Bach, The critical role of composition-dependent intragrain planar defects in the performance of MA1–xFAxPbI3 perovskite solar cells, Nat. Energy, 2021, 6(6), 624–632 CrossRef CAS.
- Q. Zhang, X. Liu, X. Zhang, Z. Wang, B. Zhang, Y. Hao, A. Dubois, W. Jie and Y. Xu, Single nucleation of Cl-doped FAPbBr3 with inhibited ion migration for ambipolar radiation detection, J. Mater. Chem. A, 2024, 12(6), 3304–3310 RSC.
- A. Oranskaia, J. Yin, O. M. Bakr, J.-L. Brédas and O. F. Mohammed, Halogen migration in hybrid perovskites: the organic cation matters, J. Phys. Chem. Lett., 2018, 9(18), 5474–5480 CrossRef CAS PubMed.
- S. Rizvi, P. Mantri and B. Mazhari, Traps signature in steady state current-voltage characteristics of organic diode, J. Appl. Phys., 2014, 115(24), 244502 CrossRef.
- J. A. Röhr, T. Kirchartz and J. Nelson, On the correct interpretation of the low voltage regime in intrinsic single-carrier devices, J. Phys.: Condens. Matter, 2017, 29(20), 205901 CrossRef PubMed.
- E. A. Duijnstee, J. M. Ball, V. M. Le Corre, L. J. A. Koster, H. J. Snaith and J. Lim, Toward understanding space-charge limited current measurements on metal halide perovskites, ACS Energy Lett., 2020, 5(2), 376–384 CrossRef CAS.
- N. R. W. Mott Gurney Electronic Processes in ionic crystals, Clarendon, Oxford, 1948, vol. 12, p. 155 Search PubMed.
- M. A. Lampert, Simplified theory of space-charge-limited currents in an insulator with traps, Phys. Rev., 1956, 103(6), 1648 CrossRef CAS.
- A. Stoneham, Current Injection in Solids, IOP Publishing, 1970 Search PubMed.
- E. A. Duijnstee, V. M. Le Corre, M. B. Johnston, L. J. A. Koster, J. Lim and H. J. Snaith, Understanding dark current-voltage characteristics in metal-halide perovskite single crystals, Phys. Rev. Appl., 2021, 15(1), 014006 CrossRef CAS.
- V. M. Le Corre, E. A. Duijnstee, O. El Tambouli, J. M. Ball, H. J. Snaith, J. Lim and L. J. A. Koster, Revealing charge carrier mobility and defect densities in metal halide perovskites via space-charge-limited current measurements, ACS Energy Lett., 2021, 6(3), 1087–1094 CrossRef CAS PubMed.
- M. Sajedi Alvar, P. W. Blom and G.-J. A. Wetzelaer, Space-charge-limited electron and hole currents in hybrid organic-inorganic perovskites, Nat. Commun., 2020, 11(1), 4023 CrossRef CAS PubMed.
- F. Tian and Y. Ohki, Electric modulus powerful tool for analyzing dielectric behavior, IEEE Trans. Dielectr. Electr. Insul., 2014, 21(3), 929–931 CAS.
- Y. Ohki, Broadband complex permittivity and electric modulus spectra for dielectric materials research, IEEJ Trans. Electr. Electron. Eng., 2022, 17(7), 958–972 CrossRef CAS.
- S. Havriliak and S. Negami, A complex plane representation of dielectric and mechanical relaxation processes in some polymers, Polymer, 1967, 8, 161–210 CrossRef CAS.
- P. Pal and A. Ghosh, Ionic conduction and relaxation mechanisms in three-dimensional CsPbCl3 perovskite, J. Appl. Phys., 2021, 129(23), 234102 CrossRef CAS.
- F. Kohlrausch Kohlrausch, Poggendorff's Ann. Phys., 1863, 119, 352 Search PubMed.
- G. Williams and D. C. Watts, Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function, Trans. Faraday Soc., 1970, 66, 80–85 RSC.
- F. Alvarez, A. Alegra and J. Colmenero, Relationship between the time-domain Kohlrausch-Williams-Watts and frequency-domain Havriliak-Negami relaxation functions, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(14), 7306 CrossRef PubMed.
- A. Lukichev, Relaxation function for the non-Debye relaxation spectra description, Chem. Phys., 2014, 428, 29–33 CrossRef CAS.
- F. Howell, R. Bose, P. Macedo and C. Moynihan, Electrical relaxation in a glass-forming molten salt, J. Phys. Chem., 1974, 78(6), 639–648 CrossRef CAS.
- B. Roling, A. Happe, K. Funke and M. Ingram, Carrier concentrations and relaxation spectroscopy: new information from scaling properties of conductivity spectra in ionically conducting glasses, Phys. Rev. Lett., 1997, 78(11), 2160 CrossRef CAS.
- S. Summerfield, Universal low-frequency behaviour in the ac hopping conductivity of disordered systems, Philos. Mag. B, 1985, 52(1), 9–22 Search PubMed.
- N. Balkan, P. Butcher, W. Hogg, A. Long and S. Summerfield, Analysis of frequency-dependent loss data in amorphous silicon and germanium, Philos. Mag. B, 1985, 51(1), L7–L12 CAS.
- T. B. Schrøder and J. C. Dyre, Scaling and universality of ac conduction in disordered solids, Phys. Rev. Lett., 2000, 84(2), 310 CrossRef PubMed.
- A. Ghosh and A. Pan, Scaling of the conductivity spectra in ionic glasses: dependence on the structure, Phys. Rev. Lett., 2000, 84(10), 2188 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc02146d |
| This journal is © The Royal Society of Chemistry 2025 |