Realistic finite temperature simulations for the magnetic and transport properties of ferromagnets

Abstract

Spontaneous magnetization cannot be accurately estimated using the ordinary classical Heisenberg model because the quantization effects are neglected, especially in low-temperature regions where experimental observations follow Bloch's 3/2 power law driven by magnon thermal excitation. The spontaneous magnetization of body-centered cubic (bcc) iron (Fe) is elucidated based on first-principles calculations by considering phonon and magnon fluctuation effects. The magnetic exchange coupling constants (J_ij) are derived while incorporating thermal lattice vibration effects, achieving a more realistic temperature dependence of J_ij of bcc Fe. Our Monte Carlo simulations showed that thermal lattice vibration effects reduced the Curie temperature from 1503 K to 1060.9 K, closely matching the experimental value of 1043 K. The temperature dependence of spontaneous magnetization is significantly improved when the quantization effects are considered, using Bose–Einstein statistics for thermal spin fluctuation effects. The well-known discrepancies in spontaneous magnetization between the ordinary classical Heisenberg model and experimental results are resolved, particularly in the low-temperature regime. Additionally, we elucidated finite-temperature electronic structures by accounting for thermal lattice vibration and thermal spin fluctuation effects. The temperature dependence of electrical resistivity is well reproduced by using the Kubo–Greenwood formula as a linear response theory with thermal lattice vibration and thermal spin fluctuation effects. Our findings highlight the importance of considering both thermal lattice vibration and thermal spin fluctuation effects with Bose–Einstein statistics when modeling ferromagnetic materials, thus enabling more precise predictions of magnetic and transport properties at finite temperatures.

---

1 Introduction

Spontaneous magnetization in ferromagnetic materials, such as body-centered cubic (bcc) iron (Fe), is a fundamental characteristic that describes how magnetization fluctuates with temperature in the absence of an external magnetic field.^1,2 A comprehensive understanding and accurate modeling of this behavior are essential for various applications, including soft magnetic, hard magnetic, and spintronic materials, where spontaneous magnetization relates to exchange stiffness, spin wave stiffness, and magnetocrystalline anisotropy constants.^1,3,4 Experimentally, spontaneous magnetization is determined by extrapolating magnetization versus field (M–H) measurements to zero fields across different temperatures.^1,5 Theoretical simulations typically employ a multi-step approach: first, the electronic structure of the material is computed using density functional theory (DFT); next, magnetic exchange coupling constants (J_ij) are derived by using linear response theory to parameterize a classical Heisenberg model; finally, this model is solved through Monte Carlo simulations to predict temperature-dependent magnetic properties.⁶ The accuracy of these simulations is often assessed by comparing the calculated saturation magnetization and Curie temperature with experimental findings.⁷ While DFT can yield precise values for saturation magnetization, accurately reproducing the Curie temperature remains challenging because the electronic structures are ground states at absolute zero (0 K) with no finite temperature effects.⁷ Enhancing the accuracy of these simulations is crucial for developing materials with optimized magnetic performance for technological applications. Alternative approaches for calculating finite temperature magnetism, such as mean-field approximations or high-order Green's function methods.⁸

Furthermore, the temperature dependence of spontaneous magnetization in Monte Carlo simulations of the classical Heisenberg model, which has the critical behavior expressed as m(T)/m(0) = (1 −T/T_C)^β, diverges from experimental results,¹ except when temperatures are near the Curie temperature, as illustrated in Fig. 1. In the low-temperature regime, Monte Carlo simulations using the classical Heisenberg model tend to overestimate the reduction in the magnetization curve due to thermal excitation. This discrepancy arises because these simulations rely on Boltzmann distributions, whereas the thermal fluctuations of spin moments, represented as magnons, follow Bose–Einstein distributions.^2,9,10 In this context, experimental magnetization typically follows Bloch's 3/2 power law as m(0) − m(T) = a(1 − T/T_C)^3/2, which is obtained by applying Bose–Einstein distributions to the magnon density of states to quantify the thermal fluctuations affecting the magnetization curve. However, Bloch's 3/2 power law also fails to accurately represent the spontaneous magnetization observed in experiments within an intermediate temperature range. This failure of Bloch's law at intermediate and high temperatures might arise from the assumption that the magnon density of states remains unchanged at finite temperatures.

Fig. 1 Normalized spontaneous magnetization of body-centered cubic (bcc) Fe in experimental work as Kuz’min formula^1,5 (black color), Bloch law at low temperature (red color), and critical exponential or Landau theory near Curie temperature (blue color).

One approach to improving the magnetization curve at low temperatures is to employ the quantum Heisenberg model or Ising model instead of the classical Heisenberg model.^9–11 However, the quantum Heisenberg model is computationally intensive even for medium-sized systems and encounters sign problems when magnetic exchange coupling constants are frustrated.^9,10,12 The Ising model's restriction on the spin direction can create an energy barrier against thermal fluctuations in the spin system at low temperatures, resulting in a flattened magnetization curve that resembles frozen spins.^9–11 This artificial behavior contrasts with Bloch's 3/2 power law observed experimentally. The temperature dependence of spontaneous magnetization provides insight into thermal spin fluctuation effects. Comparing these calculated transport properties with experimental results allows us to validate the accuracy of our finite temperature model.^13–15 In such cases, both thermal lattice vibration and thermal spin fluctuation effects are essential for estimating the transport properties of ferromagnetic materials, such as electrical resistivity.^13–15

In this study, we investigate the magnetic and transport properties of bcc Fe by integrating first-principles calculations with Monte Carlo simulations. We compute the magnetic exchange coupling constants while incorporating thermal lattice vibrations, modeling multiple atomic displacements using the coherent potential approximation (CPA). By considering magnon quantization via the Bose–Einstein distribution, we obtain spontaneous magnetization in reasonable agreement with experiments. Additionally, we model the total specific heat of bcc Fe by incorporating quantum effects into the classical Heisenberg model. Notably, at 0 K, the equipartition theorem dictates that the heat capacity per atom in the classical Heisenberg model with a Boltzmann distribution equals the Boltzmann constant, a limitation we attempt to address in our approach.

For electrical resistivity and finite-temperature exchange coupling constants, we employ the SPR-KKR code, following methodologies similar to ref. 13 and 16. While previous studies, such as ref. 13, indicate that using classical Heisenberg model simulations for thermal spin fluctuations does not fully capture experimental resistivity values for bcc Fe below the Curie temperature, we explore possible improvements in spontaneous magnetization calculations.

In particular, we examine two key factors: incorporating finite-temperature exchange coupling constants (as in ref. 16) and implementing quantum fluctuation–dissipation relations (QFDRs). By including quantum effects through QFDRs, which accounts for Bose–Einstein statistics of magnons, we obtain a refined spontaneous magnetization curve and specific heat behavior. While our approach does not rely on experimental input such as spontaneous magnetization, we believe it provides useful insights into the magnetic and transport properties of bcc Fe.

2 Theory/calculation

The relaxation of the crystal structure of the bcc Fe is performed using the Vienna ab initio simulation package (VASP) code.^17–19 This calculation employed the generalized gradient approximation, specifically the Perdew–Burke–Ernzerhof (GGA-PBE) functional.²⁰ For optimal structural calculations, a k-point mesh of 24 × 24 × 24 was utilized alongside a plane-wave basis set cutoff energy of 500 eV. To compute the force constants, density functional perturbation theory was applied within the VASP framework,^17–19 employing supercells of varying sizes: 2 × 2 × 2, 3 × 3 × 3, and 4 × 4 × 4. The Phonopy code was used in creating these supercells.^21,22 The phonon dispersion curves and the phonon density of states were derived from the force constants by using the Phonopy code.^21,22 Additionally, the specific heat of the lattice is calculated using harmonic approximations in the Phonopy code.^21,22

The magnetic exchange coupling constants were evaluated using the Liechtenstein formula within the SPR-KKR code for a disordered local moment (DLM) as a reference state, which accounts for finite temperature effects using an analogy model.^13,16,23,24 To incorporate the effects of thermal lattice vibration, a variety of atomic displacement configurations were averaged using the coherent potential approximation (CPA),^13,16 which is shown in Fig. 2.^13–15 The connection between these displacement configurations and the thermal lattice vibration effects is modeled through the use of a discrete set of displacement vectors ΔR⃑_v(T_lattice) characterized by probabilities x_v for v = 1,…,N_v. This relationship is expressed as:^13,16

Fig. 2 Diagram illustrating thermal lattice vibration and thermal spin fluctuation effects used in finite temperature simulations, incorporating multiple atomic displacements and spin configurations through the coherent potential approximation (CPA).^13–15

Moreover, the temperature dependence of the root mean square displacement (〈u²〉_T)^1/2 is estimated using Debye's theory, formulated as:^13,15,16

In this equation, Φ(Θ_D/T_lattice) denotes the Debye function, with Θ_D, ħ, and k_B representing the Debye temperature, Planck's constant, and Boltzmann's constant, respectively. The term 1/4 is approximated as negligible under the assumption of a frozen potential for the displaced atoms. The magnetic exchange coupling constants at varying finite temperatures are subsequently determined by setting T_lattice = T. The Debye temperature is theoretically estimated from phonon calculations using a combination of VASP and Phonopy.

To model the magnetic interactions, the classical Heisenberg model with exchange interactions is employed, represented by:

Here, the exchange interaction constants J^m_ij(T_lattice) are computed over a temperature range from 0 K to 1600 K, with a step interval of 25 K.

For the Monte Carlo simulations of the spin system, the probability distribution of the spin configurations {S_i} follows the equation:^25,26

In this context, C is a normalization constant, E refers to the total energy of the spin system, and η(T) signifies the average thermal energy, which is temperature-dependent. For standard classical Monte Carlo simulations, the classical fluctuation–dissipation ratio is defined as η^c(T) = k_BT, ensuring adherence to the Boltzmann distribution. Conversely, for an accurate representation of the Bose–Einstein statistics of magnons, a quantum fluctuation–dissipation ratio η^qt(T) is utilized, expressed as:^25,26

In this equation, ω denotes the frequency of magnons, while g_m(ω,T) represents the magnon density of states.

To evaluate the magnetization and magnetic energy as a function of lattice temperature, we employed classical Monte Carlo simulations based on the classical Heisenberg model.^27,28 In our Monte Carlo simulations, the magnetic exchange coupling constants were considered up to a maximum interaction distance of four lattice constants. The simulations were conducted using an in-house Monte Carlo code, incorporating both the classical fluctuation–dissipation relation (CFDR) and the quantum fluctuation–dissipation relation (QFDR).^25,26 A system size of 40 × 40 × 40 unit cells, comprising 128 000 atoms, was simulated. Each simulation involved 1 600 000 steps for thermalization followed by an additional 1 600 000 steps for data collection. The temperature was varied from 0 K to 1600 K in increments of 25 K for the spontaneous magnetization and magnetic energy simulations. Meanwhile, the temperature step 1 K was used to estimate the Curie temperature. The magnetic specific heat was determined from the derivative of the magnetic energy obtained in the Monte Carlo simulations for both CFDR and QFDR approaches. The QFDR scheme incorporates the Bose–Einstein distribution for the magnon density of states to estimate the thermal energy of the spin system, accounting for quantization effects. In contrast, a purely classical approach, which relies on the Boltzmann distribution, fails to accurately describe the thermal energy of the spin system. By employing the QFDR scheme, the accuracy of both spontaneous magnetization and specific heat can be significantly improved.

The electrical conductivity tensor σ_μν for bcc Fe is assessed using linear response theory within the SPR-KKR code, utilizing the Kubo–Greenwood formula incorporating vertex corrections. The equation can describe the conductivity by considering thermal lattice vibration and thermal spin fluctuation effects with CPA:^29,30

In this expression, ĵ_μ and ĵ_ν represent the current density operators, while G⁺(ε_F) is the retarded Green's function at Fermi energy. The finite temperature effects are factored in through both thermal lattice vibration and thermal spin fluctuation effects, where the latter is informed by the magnetization data derived from the Monte Carlo simulations, as illustrated in Fig. 2.^13–15

3 Results and discussion

The energy as a function of lattice constants for bcc Fe in non-magnetic (NM), ferromagnetic (FM), and disordered local moment (DLM) states are shown in Fig. 3. The energy of the FM and DLM states reaches its lowest point at similar lattice constants, whereas the NM state exhibits a minimum energy at a smaller lattice constant. The energy differences at the local minima for the FM state compared to the DLM and NM states are 0.2414 eV per atom and 0.5035 eV per atom, respectively. According to mean-field theory (MFA), the Curie temperature can be estimated from the energy difference between the FM and DLM states using the formula T_C(MFA) = ⅔(E_DLM − E_FM), yielding a value of 1867.5 K for the Curie temperature. This value is significantly higher than the experimentally determined Curie temperature of bcc Fe, which is 1043 K.¹⁶ Although MFA is known to overestimate the Curie temperature, the substantial discrepancy between MFA and experimental results may be attributed to the absence of phonon effects, such as thermal lattice vibration effects, in the calculations.^7,16 The correlation effects are crucial in determining the correct magnetic moment and exchange splitting in bcc Fe. Standard DFT with local or semi-local functionals often underestimates these correlation effects, requiring more sophisticated approaches like DFT+U, dynamical mean-field theory (DMFT), or quantum Monte Carlo methods for accurate predictions.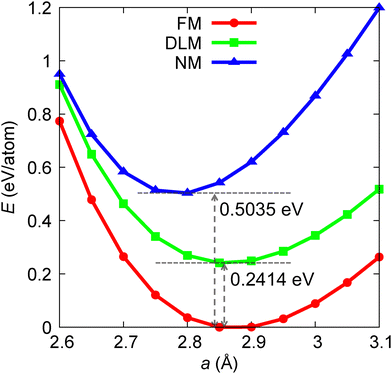

Fig. 3 Dependence of total energy on lattice parameters for bcc Fe in ferromagnetic (FM), disordered local moment (DLM), and non-magnetic (NM) states by using the SPR-KKR code.

The phonon dispersion and phonon density of states for bcc Fe are presented in Fig. 4. Utilizing density functional perturbation theory methods, we find that the phonon dispersion and density of states show minimal dependency on the cell size across 2 × 2 × 2, 3 × 3 × 3, and 4 × 4 × 4 configurations. The Debye temperature of bcc Fe, obtained from fitting the lattice-specific heat formula by Debye's theory to the results from the 4 × 4 × 4 supercell, is found to be Θ_D = 430 K. This value is slightly lower than the experimental measurement of 470 K and is also less than the Debye temperature calculated from the highest frequency in the phonon dispersions for the 4 × 4 × 4 supercell, which is 451 K.¹³

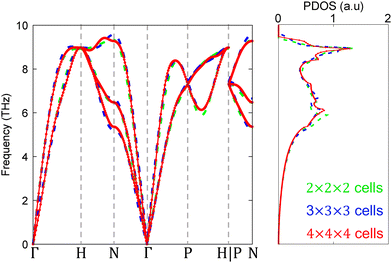Fig. 4 Phonon dispersion and phonon density of states (DOS) for bcc Fe, calculated for supercell sizes of 2 × 2 × 2, 3 × 3 × 3, and 4 × 4 × 4 by combining VASP and Phonopy codes.

The temperature dependence of the magnetic exchange coupling constants for Fe–Fe pairs in bcc Fe is illustrated in Fig. 5(a). The primary contribution to the high Curie temperature of bcc Fe originates from the first nearest neighbor within the Fe–Fe pair; however, this contribution significantly diminishes as thermal lattice vibration effects increase with an increase in the lattice temperature. The change in exchange coupling constants due to thermal lattice vibration effects is minimal when considering pairs at greater distances. Additionally, the exchange coupling constants for the second and fifth nearest neighbors show a slight increase as the lattice temperature increases. To accurately determine the Curie temperature in Monte Carlo simulations, all coupling constants within a cutoff radius of up to 4a – where a represents the lattice parameters, which are incorporated into these simulations.

Fig. 5 (a) Temperature dependence of magnetic exchange coupling constants J_ij for Fe–Fe pairs in bcc Fe, including the effects of thermal lattice vibration (T_lattice) by using the SPR-KKR code for the DLM state. (b) Curie temperature of bcc Fe as determined by Monte Carlo simulations, shown as a function of the amplitude of thermal lattice vibration effects (root mean square of lattice displacement, 〈u²〉^1/2 or T_lattice).

The Curie temperature of bcc Fe, which is influenced by the lattice temperature (T_lattice) or the root mean square of lattice displacements (〈u²〉^1/2), is illustrated in Fig. 5(b). This Curie temperature is determined through Monte Carlo simulations by analyzing the peak position of the magnetic susceptibility. When considering a scenario without thermal lattice vibration effects, where T_lattice = 0 K, the calculated Curie temperature is 1503 K. This value is lower than the 1867.5 K derived from mean-field approximations. The lower temperature obtained from the Monte Carlo simulations is justifiable, as mean-field approximations tend to overestimate the Curie temperature. Nevertheless, the resulting Curie temperature remains significantly higher than those reported in experimental studies. When the effects of thermal lattice vibration are included, the Curie temperature decreases due to the diminished first nearest neighbor of magnetic exchange coupling constants. To accurately estimate the Curie temperature in the presence of thermal lattice vibration effects, we identify the point where the diagonal line T_C = T_lattice intersects with the Curie temperature of the Monte Carlo simulation curve. This intersection occurs at T_C = T_lattice ≈ 1060.9 K, which aligns quite closely with the experimental value of 1043 K.^7,16 It means that the thermal lattice vibration effects are important factors in obtaining the correct Curie temperature in simulations for ferromagnet materials. It is noteworthy that our Curie temperature, calculated using the J_ij values from the GGA functional, is much closer to the experimental value compared to ref. 16, which reports a value of approximately 800 K using the LDA functional.

The spontaneous magnetization curves of bcc Fe as a function of temperature, derived from Monte Carlo simulations, alongside the lattice temperature on thermal lattice vibration effects in the classical Heisenberg model with the CFDR and QFDR, are presented in Fig. 6(a, b, e and f). The black curve represents the magnetization response calculated under the condition where the magnetic exchange coupling constants are defined by T_lattice = T. In the CFDR context, it is observed that the spontaneous magnetization at T_lattice = T demonstrates a subtle increase at intermediate temperatures when compared to the spontaneous magnetization obtained at a fixed lattice temperature. This behavior can be attributed to the reduction of the Curie temperature as the lattice temperature increases. However, it is important to note that this spontaneous magnetization remains lower than those observed in experimental studies, primarily due to the exclusion of quantum effects for magnons that follows Bose–Einstein distributions. In the analysis incorporating the QFDR, the spontaneous magnetization decreases slowly at lower temperatures due to the thermal excitation of magnons following a Bose–Einstein distribution. This behavior markedly contrasts with that observed in the Ising model, where the presence of an energy barrier for spin flipping results in a completely flat spontaneous magnetization curve, or a regime of frozen spin dynamics in the low-temperature domain.

Fig. 6 Temperature dependence of magnetization curves for bcc Fe at various lattice temperatures T_lattice using the classical Heisenberg model with the classical fluctuation–dissipation relation (CFDR) (a) and (e) and the quantum fluctuation–dissipation relation (QFDR) (b) and (f). Temperature dependence of magnetic energy for bcc Fe under similar conditions with the CFDR (c) and (g) and QFDR (d) and (h). The black curve represents the magnetization and magnetic energy calculated using finite temperature exchange coupling constants J_ij(T) as T_lattice = T.

Furthermore, the temperature dependence of the magnetic energy curves of bcc Fe for the classical Heisenberg model under both the CFDR and QFDR is illustrated in Fig. 6(c, d, g and h). In contrast to spontaneous magnetization, where the thermal lattice vibration effects predominantly contribute to a reduction in the Curie temperature, the magnetic moment from finite temperature exchange coupling calculations using the SPR-KKR code remains unchanged at 0 K, as there are no thermal lattice vibration effects at this temperature. Notably, at low-temperature regions, the absolute values of the magnetic energy curves diminish due to the reduced magnetic exchange coupling constants. However, the slope of the magnetic energy curves within the CFDR framework remains consistent with the thermal energy predictions of the classical model. When transitioning to the QFDR, the magnetic energy curves exhibit a flattening at low temperatures, converging towards the CFDR results above the Curie temperature, reflecting classical behavior in the high-temperature limit.

The density of states for bcc Fe under both ferromagnetic (FM) conditions and disordered local moment (DLM) configurations, without thermal lattice vibration effects, is presented in Fig. 7(a and d). In contrast, the density of states with the influences of thermal lattice vibration and thermal spin fluctuation effects are shown in Fig. 7(b, c, e and f). To account for the effects of thermal spin fluctuation at finite temperatures, we utilize magnetization curves derived from Monte Carlo simulations of the classical Heisenberg model, employing both the CFDR and QFDR for the thermal spin fluctuation effect.

Fig. 7 Density of states (DOS) for bcc Fe under ferromagnetic (FM) (a) and disordered local moment (DLM) (d) configurations at 0 K, without finite temperature effects, are calculated using the SPR-KKR code. The total DOS (black) and the d-orbital projected DOS (red) are shown for both FM and DLM states. The DOS of the FM state serves as the reference for evaluating thermal effects. Finite temperature effects, including thermal lattice vibrations and thermal spin fluctuations, are incorporated at 300 K (b), 600 K (c), 900 K (e), and 1200 K (f) using the SPR-KKR code. These effects are further illustrated by the magnetization curves derived from the classical Heisenberg model, using CFDR (blue) and QFDR (red) schemes.

The thermal spin fluctuation effects are incorporated using coherent potential approximations, where the spin distributions are mapped to magnetization values in the Monte Carlo simulations of the classical Heisenberg model. At absolute zero (0 K), the density of states for the FM configuration exhibits a pronounced peaky structure, contrasting with the smoother density of states observed in the DLM configuration at 0 K due to the spin–spin scattering effect. Upon incorporating thermal lattice vibration and thermal spin fluctuation effects at 300 K, the resultant density of states transitions from the FM state to a smoother form; however, the distinct structures characterized by three prominent peaks in both spin-up and spin-down configurations still remain. Notably, the QFDR curves for thermal spin fluctuation effects are sharper compared to the CFDR curves due to the comparatively lower magnetization value associated with the CFDR, leading to stronger spin–spin scattering effects in the CFDR compared with the QFDR. As the temperature increases to 600 K and 900 K, two of the three peaks in the spin-down density of states broaden and ultimately vanish, while the three peaks in the spin-up configuration remain intact. At 1200 K, which exceeds the Curie temperature of 1060.9 K as determined in this analysis, the density of states for both the CFDR and QFDR coincide, indicating that the magnetization reaches zero in both scenarios leading to the same thermal spin fluctuation effects. At this elevated temperature, the density of states exhibits similarities to the DLM state at 0 K, though it becomes smoother with broader peak profiles in both spin-up and spin-down configurations, attributable to the influence of thermal lattice vibration effects. It is important to note that the DLM state at 0 K contains the spin–spin scattering effects.

The temperature dependence of the electrical resistivity of bcc Fe is illustrated in Fig. 8(a). In this case, two sources of scattering mechanisms are considered: phonon and magnon scattering. When examining the case of only phonon scattering, it shows that electrical resistivity increases almost linearly with an increase in temperature, which contrasts with experimental results. This discrepancy arises because the effects of thermal lattice vibration, stemming from atomic displacements, increase almost linearly; however, the experimental data show a strong temperature-dependent curve shape. This occurs because the spontaneous magnetization curve, which is essential for determining magnon fluctuations, does not decline linearly as temperature increases. When accounting for both thermal lattice vibration and thermal spin fluctuation effects, the electrical resistivity in the case of the CFDR is higher than the experimental results at low temperatures up to the Curie temperature. This difference can be attributed to the spontaneous magnetization curve in the CFDR, which deviates from the experimental observations that follow Bloch's law in low-temperature regions. It might lead to stronger thermal spin fluctuation effects with higher resistivity in the CFDR case compared with experimental results from 0 K to the Curie temperature. Consequently, in such cases, the combined effects of thermal lattice vibration and thermal spin fluctuation with the QFDR yield a lower electrical resistivity compared to the CFDR, resulting in values that are much closer to the experimental results due to a more accurate temperature dependence of spontaneous magnetization in the QFDR.

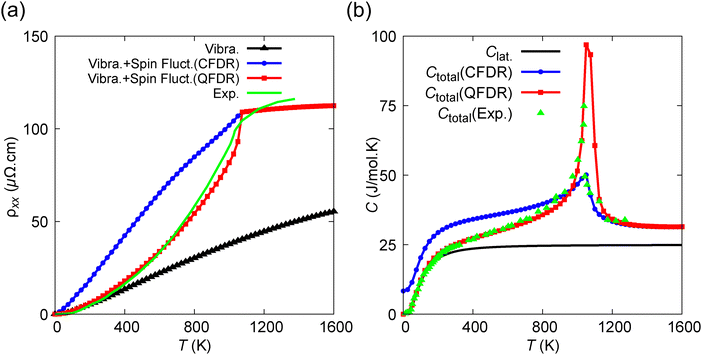Fig. 8 (a) Temperature dependence of electrical resistivity of bcc Fe by using the SPR-KKR code: comparison of experimental data,¹³ thermal lattice vibration effects only, and combined thermal lattice vibration and thermal spin fluctuation effects modeled with the classical Heisenberg model using the CFDR and QFDR. (b) Temperature dependence of the specific heat of bcc Fe: contributions from the lattice, electronic, and magnetic components, along with total specific heat derived from CFDR and QFDR models, compared to experimental data.³¹

The temperature dependence of the specific heat of bcc Fe is illustrated in Fig. 8(b). The total specific heat comprises lattice, electronic, and magnetic contributions. The specific heat attributed to the lattice is derived from the phonon spectrum using Bose–Einstein distributions. In contrast, the magnetic component is estimated based on the density of states at the Fermi level obtained from density functional theory (DFT) calculations. The specific heat related to the magnetic part is derived as a derivative of the magnetic energy obtained from Monte Carlo simulations for the classical Heisenberg model with the CFDR and QFDR, represented as black curves in Fig. 6(c and d). When the thermal lattice vibration effects on magnetic exchange coupling constants are not considered, the magnetic part's specific heat in Monte Carlo simulations using the CFDR will equate to 1.0 (k_B per atom per K) or 8.31 (J mol⁻¹ K⁻¹) as a gas constant R at 0 K based on the equipartition theorem, which contrasts with experimental findings at low temperatures. However, due to the reduction of magnetic exchange coupling constants induced by thermal lattice vibration effects, the specific heat of the magnetic part in the CFDR case, as illustrated by the derivative of the black curve in Fig. 6(c), is slightly above 1.0 (k_B per atom per K). Notably, the total specific heat, including the magnetic contribution calculated with the QFDR, aligns perfectly with the experimental results across a broad temperature range. Because the magnetic energy of the QFDR at high temperature (above the Curie temperature) approaches the magnetic energy of the CFDR, as can be seen in Fig. 6(c and d), a small magnetic specific heat of the QFDR at the low-temperature region leads to a sharper peak of specific heat at the Curie temperature.

4 Summary

In summary, this study explores a simulation approach that combines first-principles calculations with Monte Carlo simulations to investigate the magnetic and transport properties of ferromagnetic body-centered cubic (bcc) iron (Fe) at finite temperatures. By computing magnetic exchange coupling constants J_ij while incorporating thermal lattice vibration effects, we obtain a Curie temperature that better reflects the temperature dependence of J_ij. Our Monte Carlo simulations, which account for thermal spin fluctuations using Bose–Einstein statistics for magnons, yield a spontaneous magnetization curve that aligns more closely with experimental trends. This approach helps to address discrepancies in classical Heisenberg models, particularly in the low-temperature regime, where experimental observations follow the Blochs 3/2 power law. Furthermore, we examined the role of quantum effects in the classical Heisenberg model and found that incorporating these effects improves the description of electrical resistivity and specific heat. Our results highlight the importance of considering both the temperature dependence of thermal lattice vibrations and thermal spin fluctuations. While further refinements are needed, we believe that this approach offers useful insights for advancing the understanding of magnetic materials in technological applications. This scheme can be applied to other ferromagnets such as cobalt and nickel, where the spontaneous magnetization is not accurate in classical Monte Carlo simulations and can be improved with the quantum fluctuation–dissipation relation.

Author contributions

H. B. Tran: investigation and writing – original draft preparation. H. Li: writing – reviewing and editing.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Prof. T. Oguchi and Prof. K. Sato for their valuable discussions. This work was partially supported by JSPS KAKENHI as a Grant-in-Aid for Research Activity Start-up (Grant Number JP24K22847) and Grant-in-Aid for Early-Career Scientists (Grant Number JP25K17932). The computations for this work were performed on the supercomputers at the Institute for Solid State Physics, University of Tokyo, and the MASAMUNE-IMR system at the Center for Computational Materials Science, Institute for Materials Research, Tohoku University (Project No. 202412-SCKXX-0211 and 202412-SCKXX-0205).

Notes and references

1. M. D. Kuz’min, Shape of temperature dependence of spontaneous magnetization of ferromagnets: quantitative analysis, Phys. Rev. Lett., 2005, 94, 107204,  DOI:10.1103/PhysRevLett.94.107204.
2. S. V. Halilov, A. Y. Perlov, P. M. Oppeneer and H. Eschrig, Magnon spectrum and related finite-temperature magnetic properties: a first-principle approach, Europhys. Lett., 1997, 39, 91–96,  DOI:10.1209/epl/i1997-00319-x.
3. A. Hirohata, K. Yamada, Y. Nakatani, I. L. Prejbeanu, B. Diény, P. Pirro and B. Hillebrands, Review on spintronics: Principles and device applications, J. Magn. Magn. Mater., 2020, 509, 166711,  DOI:10.1016/j.jmmm.2020.166711.
4. J. M. D. Coey, Perspective and prospects for rare earth permanent magnets, Engineering, 2020, 6, 119–131,  DOI:10.1016/j.eng.2018.11.034.
5. J. Crangle and G. M. Goodman, The magnetization of pure iron and nickel, Proc. R. Soc. London, Ser. A, 1971, 321, 477,  DOI:10.1098/rspa.1971.0044.
6. I. Turek, J. Kudrnovský, V. Drchal and P. Bruno, Exchange interactions, spin waves, and transition temperatures in itinerant magnets, Philos. Mag., 2006, 86, 1713–1752,  DOI:10.1080/14786430500504048.
7. T. Tanaka and Y. Gohda, Prediction of the Curie temperature considering the dependence of the phonon free energy on magnetic states, npj Comput. Mater., 2020, 6, 184,  DOI:10.1038/s41524-020-00458-5.
8. R. Bastardis, U. Atxitia, O. Chubykalo-Fesenko and H. Kachkachi, Unified decoupling scheme for exchange and anisotropy contributions and temperature-dependent spectral properties of anisotropic spin systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 094415,  DOI:10.1103/PhysRevB.86.094415.
9. F. Körmann, A. Dick, T. Hickel and J. Neugebauer, Rescaled Monte Carlo approach for magnetic systems: ab initio thermodynamics of bcc iron, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 134425,  DOI:10.1103/PhysRevB.81.134425.
10. F. Körmann, A. Dick, T. Hickel and J. Neugebauer, Role of spin quantization in determining the thermodynamic properties of magnetic transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 165114,  DOI:10.1103/PhysRevB.83.165114.
11. F. Walsh, M. Asta and L. W. Wang, Realistic magnetic thermodynamics by local quantization of a semiclassical Heisenberg model, npj Comput. Mater., 2022, 8, 186,  DOI:10.1038/s41524-022-00875-8.
12. P. Henelius and A. W. Sandvik, Sign problem in Monte Carlo simulations of frustrated quantum spin systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 1102,  DOI:10.1103/PhysRevB.62.1102.
13. H. Ebert, et al., Calculating linear-response functions for finite temperatures on the basis of the alloy analogy model, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165132,  DOI:10.1103/PhysRevB.91.165132.
14. H. Shinya, S. Kou, T. Fukushima, A. Masago, K. Sato, H. Katayama-Yoshida and H. Akai, First-principles calculations of finite temperature electronic structures and transport properties of Heusler alloy Co2 MnSi, Appl. Phys. Lett., 2020, 117, 042402,  DOI:10.1063/5.0017862.
15. H. Shinya, T. Fukushima, K. Sato, S. Ohya and H. Katayama-Yoshida, Theoretical study on the origin of anomalous temperature-dependent electric resistivity of ferromagnetic semiconductor, APL Mater., 2023, 11, 111114,  DOI:10.1063/5.0165352.
16. S. Mankovsky, S. Polesya and H. Ebert, Exchange coupling constants at finite temperature, Phys. Rev. B, 2020, 102, 134434,  DOI:10.1103/PhysRevB.102.134434.
17. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558,  DOI:10.1103/PhysRevB.47.558.
18. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50,  DOI:10.1016/0927-0256(96)00008-0.
19. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169,  DOI:10.1103/PhysRevB.54.11169.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
21. A. Togo, L. Chaput, T. Tadano and I. Tanaka, Implementation strategies in phonopy and phono3py, J. Phys.: Condens. Matter, 2023, 35, 353001,  DOI:10.1088/1361-648X/acd831.
22. A. Togo, First-principles phonon calculations with phonopy and phono3py, J. Phys. Soc. Jpn., 2023, 92, 012001,  DOI:10.7566/JPSJ.92.012001.
23. H. Ebert, et al., The Munich SPR-KKR package, version 8.6, 2022, https://www.ebert.cup.uni-muenchen.de/sprkkr8/licenses.
24. H. Ebert, D. Ködderitzsch and J. Minár, Calculating condensed matter properties using the KKR-Green's function method-recent developments and applications, Rep. Prog. Phys., 2011, 74, 096501,  DOI:10.1088/0034-4885/74/9/096501.
25. C. H. Woo, H. Wen, A. A. Semenov, S. L. Dudarev and P. W. Ma, Quantum heat bath for spin-lattice dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104306,  DOI:10.1103/PhysRevB.91.104306.
26. L. Bergqvist and A. Bergman, Realistic finite temperature simulations of magnetic systems using quantum statistics, Phys. Rev. Mater., 2018, 2, 013802,  DOI:10.1103/PhysRevMaterials.2.013802.
27. H. B. Tran, H. Momida, Y. Matsushita, K. Sato, Y. Makino, K. Shirai and T. Oguchi, Effect of magnetocrystalline anisotropy on magnetocaloric properties of an AlFe2B2 compound, Phys. Rev. B, 2022, 105, 134402,  DOI:10.1103/PhysRevB.105.134402.
28. H. B. Tran, H. Momida, Y. Matsushita, K. Shirai and T. Oguchi, Insight into anisotropic magnetocaloric effect of CrI₃, Acta Mater., 2022, 231, 117851,  DOI:10.1016/j.actamat.2022.117851.
29. B. Velický, Theory of Electronic Transport in Disordered Binary Alloys: Coherent-Potential Approximation, Phys. Rev., 1969, 184, 614,  DOI:10.1103/PhysRev.184.614.
30. W. H. Butler, Theory of electronic transport in random alloys: Korringa-Kohn-Rostoker coherent-potential approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3260,  DOI:10.1103/PhysRevB.31.3260.
31. D. C. Wallace, P. H. Sidles and G. C. Danielson, Specific heat of high purity iron by a pulse heating method, J. Appl. Phys., 1960, 31, 168,  DOI:10.1063/1.1735393.

---