Open Access Article
Open Access ArticleNo strain, no piezoelectric gain: pushing piezoelectric boundaries via composition-dependent strain engineering in wurtzite scandium-doped aluminum nitride†
Zicong Marvin Wong ,
Gang Wu
,
Gang Wu ,
Yang Hao Lau
,
Yang Hao Lau ,
Teck Leong Tan
,
Teck Leong Tan *,
Fong Yew Leong
*,
Fong Yew Leong and
Hariharaputran Ramanarayan
and
Hariharaputran Ramanarayan *
*
Institute of High Performance Computing (IHPC), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, #16-16 Connexis, Singapore, 138632, Republic of Singapore. E-mail: hariharaputran@ihpc.a-star.edu.sg
First published on 10th July 2025
Abstract
This study presents an investigation of the structural and piezoelectric properties of scandium-doped aluminum nitride (Al1−xScxN) alloys over a wide composition range, using first-principles calculations. We explore compositions ranging from pure AlN to Al0.5Sc0.5N under various biaxial strain conditions, revealing the complex interplay between composition, strain, and piezoelectric response. Our findings demonstrate that the piezoelectric coefficient d33 of unstrained Al1−xScxN reaches a maximum at x = 0.4375, significantly surpassing that of pure AlN. Remarkably, we show that applying biaxial strain dramatically enhances d33, with values peaking at compositional-dependent critical strains. These peak values, ranging from 519.03 pC N−1 for strained AlN to an extraordinary 5121.58 pC N−1 for strained Al0.625Sc0.375N, represent improvements of over two orders of magnitude compared to their unstrained counterparts. We attribute this enhancement to a strain-induced phase transition from wurtzite to non-polar hexagonal layered structures, similar to the structural change observed with enhanced Sc concentration, accompanied by significant changes in elastic and piezoelectric constants. Notably, we demonstrate that this phenomenon can be exploited through changes in both tensile strain in Al-rich compositions and compressive strain in Sc-rich compositions, highlighting the exceptional tunability of Al1−xScxN. These insights provide a fundamental understanding of Al1−xScxN behavior and offer valuable guidance for optimizing its properties in next-generation piezoelectric devices.
1. Introduction
Piezoelectric materials, capable of converting mechanical stress into electrical charge and vice versa, play a crucial role in a wide range of technological applications, from sensors and actuators to energy harvesting devices.1–4 Among these materials, aluminum nitride (AlN) has garnered significant attention due to its prominent piezoelectric properties, high thermal conductivity, and compatibility with semiconductor processing.5–7 However, the quest for materials with enhanced piezoelectric performance has led researchers to explore alloying strategies, with scandium-doped aluminum nitride (Al1−xScxN) emerging as a promising candidate for next-generation piezoelectric applications.The incorporation of Sc into the AlN matrix has been shown to significantly enhance the piezoelectric response of the material. This enhancement is attributed to the larger atomic radius of Sc compared to Al, which induces structural distortions and increases the polarizability of the crystal lattice.8 Previous studies have demonstrated that the piezoelectric coefficient d33 of Al1−xScxN is several times higher than that of pure AlN, making it an attractive option for various applications, including surface acoustic wave devices, bulk acoustic resonators, and microelectromechanical systems (MEMS).9–11 However, the structural and piezoelectric properties of Al1−xScxN are highly dependent on both composition and strain state. As the Sc content increases, the material undergoes a transition from the polar wurtzite structure characteristic of AlN (space group: P63mc) to a non-polar hexagonal layered structure (space group: P63/mmc) resembling hexagonal boron nitride (hBN) at high Sc concentrations.12,13 This structural evolution, coupled with the effects of strain arising from lattice mismatch in thin film growth, significantly influences the piezoelectric response of the material.14 Understanding these complex relationships is therefore crucial for optimizing the performance of Al1−xScxN in practical applications.
In this study, we present a comprehensive investigation of the structural and piezoelectric properties of Al1−xScxN alloys across a range of compositions and under various biaxial strain conditions. Using first-principles calculations based on density functional theory (DFT) and the special quasi-random structure (SQS) approach to model the random alloys, we explore the intricate interplay between Sc concentration, strain, phase transitions, and piezoelectric response. We aim to provide fundamental insights into the behavior of Al1−xScxN and elucidate strategies for tailoring its properties to meet the diverse requirements of advanced piezoelectric devices.
2. Computational methodology
2.1 Cluster expansion (CE) method
To efficiently explore the configuration space of Al1−xScxN alloys, we employed the cluster expansion (CE) method.15–17 In this formalism, a particular alloy configuration on a fixed lattice is described using a set of occupational variables. For our Al1−xScxN system, we generated substitutional alloys on the metallic sublattice with varying Al and Sc percentages, while maintaining the fraction of N.We utilized the thermodynamic tool-kit (TTK) code18–20 to perform CE calculations. The process involved constructing an initial CE Hamiltonian by fitting the effective cluster interactions (ECIs) from a learning set of DFT-calculated mixing enthalpies ΔHmix of 861 alloy configurations with wurtzite, non-polar hexagonal layered, and rock-salt phases. ΔHmix of a given configuration σ at 0 K is calculated relative to the most stable wurtzite AlN and rock-salt ScN constituents:
| ΔHmix(Al1−xScxN, σ) = E(Al1−xScxN, σ) − (1 − x)E(wz-AlN) − xE(rs-ScN) | (1) |
We next screened over 3 × 106 alloy structures with unique configurations to obtain their corresponding CE energies. The CE was considered properly truncated when no new ground-states were predicted and/or CE ΔHmix were reproduced accurately within <0.005 eV atom−1. Using the ECIs, the CE-predicted ΔHmix of the Al1−xScxN solid solutions could then be determined.21
For the systematic selection of the disordered solid solution Al1−xScxN alloys for first-principles simulations, we utilized the special quasi-random structure (SQS) approach22 by sieving out from the 106 different wurtzite alloy configurations with x = 0.0000, 0.0625, 0.1250, 0.1875, 0.2500, 0.3125, 0.3750, 0.4375, 0.5000, consisting of 64-atom pseudo-orthorhombic supercells, and selecting those configurations with cluster correlations of two- and three-body interactions closest to those of a random alloy.23 While this supercell size may have limitations in capturing very long-range strain fields, it is adequate for modeling the critical local atomic distortions and competing structural motifs that drive the phase transition at high Sc concentrations.24
2.2 Density functional theory (DFT) calculations
First-principles calculations were performed using density functional theory (DFT)25 via the Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional based on the generalized gradient approximation (GGA)26,27 as implemented in the Vienna ab initio simulation package (VASP).28,29 The projector augmented wave (PAW) method30 was used to describe the electron–ion interactions, using the PAW potentials Al, Sc_sv, and N. Plane-wave cut-offs were set to 500 eV and an electronic convergence criterion of 10−8 eV was applied. All atomic coordinates were fully relaxed until the calculated Hellmann–Feynman force on each atom was less than 0.01 eV Å−1. Brillouin zone sampling was performed with Monkhorst–Pack (MP) k-point meshes31 inclusive of the Γ-point. A k-point mesh of 2 × 4 × 2 which translates to a density of around 20 k-points per Å−1 was used for the disordered solid solution Al1−xScxN alloy supercells.To investigate the effects of strain on the piezoelectric properties of Al1−xScxN, we applied biaxial strains ranging from −5% to +8% to our optimized structures in steps of 0.5%, with finer steps close to phase transitions, allowing for the study of phase transitions and their effects on piezoelectric properties. The strain was applied in the a–b plane while allowing relaxation along the c-axis. For each strained configuration, we calculated the elastic tensor elements Cij including ionic relaxations via the finite differences method32 and the piezoelectric tensor elements eij using density functional perturbation theory (DFPT).32 The piezoelectric coefficient d33 could then be estimated from the piezoelectric constants e33 and elastic constants C33 according to the relationship:8
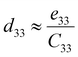 | (2) |
The elastic constants were obtained by applying small strains to the relaxed structures and calculating the resulting stress tensors. This approach allowed us to systematically study the evolution of piezoelectric properties as a function of both composition and strain state, with a focus on identifying the critical strain levels where d33 peaks.
3. Results and discussion
3.1 Phase properties of scandium-doped aluminum nitride Al1−xScxN alloys
Fig. 1 illustrates the relative stability of various Al1−xScxN alloy structures by examining the mixing enthalpies of wurtzite, rock-salt, and non-polar hexagonal layered phases, calculated using eqn (1). Our analysis reveals that the wurtzite phase exhibits a lower mixing enthalpy and greater thermodynamic stability compared to the rock-salt phase for compositions up to x = 0.6. This finding indicates that the wurtzite phase represents the ground-state structure for both pure AlN and Al-rich Al1−xScxN alloys. Our findings are in excellent agreement with both experimental and computational work. Talley et al. reported a wurtzite-to-rock-salt transition in Al1−xScxN between x = 0.4 and 0.65 via XRD measurements,13 while Höglund et al. showed that single-phase wurtzite films are achievable up to x = 0.6, above which the material phase-separates into wurtzite and rock-salt domains.33 Likewise, Zhang et al.'s first principles study located the same composition transition (x = 0.6) and found mixing enthalpies rising from 0 to 0.2 eV atom−1 at that point, using an approach analogous to ours.12A noteworthy observation is the behavior of the non-polar hexagonal layered phase. While it does not represent the ground-state for all compositions, its mixing enthalpies converge with those of the wurtzite phase under Sc-rich conditions. This convergence is consistent with the optimized structure of initial wurtzite ScN being similar to the non-polar hexagonal layered structure. Fig. S1 in the ESI† further elucidates this phenomenon, demonstrating that both the structural and absolute energy differences between Al1−xScxN configurations in wurtzite and non-polar hexagonal layered phases diminish with increasing Sc content, approaching zero for pure ScN.
The transformation from wurtzite to non-polar hexagonal layered structure can be attributed to the larger atomic size of Sc (1.60 Å) compared to Al (1.25 Å).34 As the Sc content increases, it induces an expansion in the crystalline volume of wurtzite Al1−xScxN. This expansion facilitates the structural transformation. The process likely involves a gradual distortion of the wurtzite lattice, with atomic rearrangements leading to the formation of the non-polar hexagonal layered structure.
This phase transition has profound implications for the material's piezoelectric response. The wurtzite structure is inherently polar (space group P63mc), with a spontaneous polarization along the c-axis. In contrast, the non-polar hexagonal layered structure with the presence of inversion center lacks this intrinsic polarization (space group P63/mmc). As we shall explore in the subsequent sections, the transition between these phases will lead to significant changes in the piezoelectric coefficients, which are directly related to the material's ability to convert mechanical stress into electrical charge and vice versa.
Given that extensive research has already been conducted on the structural and phase transitions of Al1−xScxN,12,13 the focus of the following section will be in providing a detailed description and analysis of the piezoelectric properties of both non-strained and strained Al1−xScxN alloys. This includes examining how these properties vary with Sc concentration and the associated phase transformations, providing a comprehensive understanding of the material's potential for piezoelectric applications.
3.2 Piezoelectric properties of non-strained and strained Al1−xScxN alloys
Using the 64-atom pseudo-orthorhombic special quasirandom structures (SQS) supercells of Al1−xScxN with Sc fractions ranging from 0 to 50% (0 ≤ x ≤ 0.5), we calculated the piezoelectric coefficients (d33) from the piezoelectric constants (e33) and elastic constants (C33) via eqn (2). As shown in Fig. 2a, for the non-strained Al1−xScxN alloys, the d33 value exhibits a strong dependence on the Sc concentration. It increases from 4.57 pC N−1 in pure AlN to a maximum of 29.88 pC N−1 when x = 0.4375, before falling to 13.36 pC N−1 at 50% Sc. This calculated peak d33 of 29.88 pC N−1 at x = 0.4375 aligns well with the reported experimental range, which varies from ∼25 pC N−1 (Teshigahara et al.)10 to over 30 pC N−1 (Lu et al.),11 with the minor deviation attributable to the ideal, defect-free nature of the SQS model compared to experimental films, which often contain performance-limiting defects, grain boundaries, and residual stress.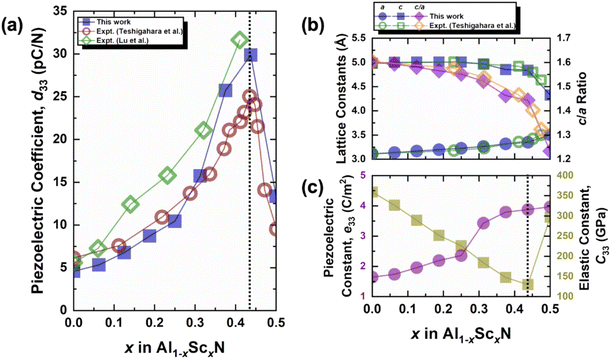 | ||
| Fig. 2 (a) Plot of piezoelectric coefficients, d33, versus different Sc fraction, x, for Al1−xScxN SQS supercells. The blue squares, red circles, and green diamonds, correspond to values obtained via simulation for this work, and experimental results by Teshigahara et al.10 and Lu et al.11 (b) Plot of lattice constants, a and c, and c/a ratio versus different Sc fraction, x, for Al1−xScxN SQS supercells. The filled symbols correspond to values calculated from optimized structures in this work, while the hollow symbols correspond to experimental data from Teshigahara et al.10 (c) Plot of piezoelectric constants, e33, and elastic constant, C33, versus different Sc fraction, x, for Al1−xScxN SQS supercells. The purple circles and olive squares correspond to e33 and C33, respectively. Vertical dotted lines at x = 0.4375 highlight how a significant increase in C33 results in a decrease in d33. | ||
To explain this behavior, we can examine the structural changes induced by Sc doping. Fig. 2b illustrates that increasing Sc content leads to a gradual increase in lattice parameter a, while lattice parameter c decreases, leading to the reduction in c/a ratio. The increase in a is primarily attributed to the larger atomic radius of Sc which expands the basal plane of the wurtzite structure. As the lattice structure becomes more planar-like, the axial Al/Sc–N bond weakens and causes an elastic softening and mechanical weakening of the structure along the axial or z-axis,35 reflected in the decrease in the elastic constant C33 in Fig. 2c. The reduction in C33 contributes to the increase in d33, as the piezoelectric coefficient is inversely proportional to the elastic constant. In addition to the changes in lattice parameters, the piezoelectric constant e33 also critically impacts the piezoelectric coefficient. As Sc concentration increases, e33 initially rises due to the enhanced polarization induced by the larger and more polarizable Sc atoms substituting for Al. The substitution leads to a stronger piezoelectric response in the crystal.
However, these trends for C33 and e33 do not continue indefinitely. Above 43.75% Sc, there is a notable decrease in c, resulting in the c/a ratio decreasing from ∼1.6 to ∼1.2, which is characteristic of the non-polar hexagonal layered phase. This shift signals a transition in Al1−xScxN from the wurtzite structure to a non-polar hexagonal layered crystalline structure at high scandium content. In the hexagonal layered phase, the structure becomes mechanically stiffer, resulting in an increase in C33 compared to the wurtzite phase. This is in stark contrast to just prior to the transformation, where the weakening of the axial Al/Sc–N bonds softens C33. Instead, once the structure transitions to the hexagonal layered phase, its planarity leads to more uniform axial interactions across atoms in adjacent layers, enhancing the stiffness of the lattice. The significant increase in C33 offsets the much smaller increase in e33, leading to a net reduction in d33. Here, assuming constant e33, an increase in C33 from ∼130 to ∼290 GPa corresponds to a decrease in d33 from ∼30 to ∼13 pC N−1, a 2.2-fold reduction.
It is noteworthy that our calculated values align well and are consistent with those measured experimentally from synthesized Al1−xScxN alloys,10,11 validating our chosen SQS supercells in representing the random alloy structure (see Fig. 2a). This agreement also underscores the predictive power of our computational approach in studying these complex alloy systems.
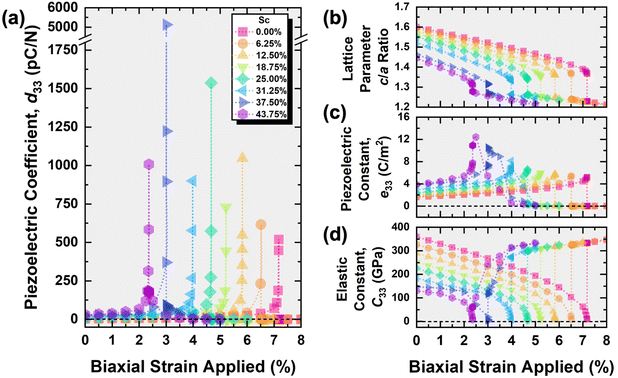
Typically, in deposited Al1−xScxN films, strain arises from lattice mismatch with the substrate and the incorporation of Sc atoms into the AlN matrix, significantly influencing piezoelectric properties. To investigate these effects, we have applied a series of in-plane biaxial (along the a and b directions) tensile strains on the Al1−xScxN SQS supercells (with 0 ≤ x ≤ 0.4375, and the structures begin in the wurtzite phase before being strained) as shown in Fig. 3 to assess their impact on the structural and piezoelectric properties. When positive (tensile) biaxial strain is applied, we observe a dramatic increase in the piezoelectric coefficient d33 of Al1−xScxN, which peaks at a specific biaxial tensile strain value for each Sc concentration before dropping abruptly to near zero. Remarkably, the peak d33 values range from 519.03 pC N−1 in strained AlN to an exceptionally high 5121.58 pC N−1 in strained Al0.625Sc0.375N, both at least two orders of magnitude larger than their unstrained counterparts. For context, commercial PZT (lead zirconate titanate) ceramics exhibit d33 values in the range of 300 to 1000 pC N−1, whereas BTO (barium titanate) ceramics typically lie in the few-hundred pC N−1 regime (e.g., 100 to 460 pC N−1 in BTO nanoparticles).1 Our peak d33 of 5121.58 pC N−1 in strained Al0.625Sc0.375N therefore exceeds these classic materials by more than an order of magnitude. Moreover, unlike PZT which contains toxic lead and is not compatible with standard CMOS back-end processes, and BTO which suffers from lower Curie temperature and integration challenges,1,36 Al1−xScxN is both lead-free and fully CMOS-compatible, making these exceptionally large d33 values particularly compelling for on-chip applications.
While these peak values occur at relatively high strain levels that may be challenging to achieve experimentally, the significant enhancement in d33 even at moderate strain levels provides valuable insights into the fundamental mechanisms of strain-enhanced piezoelectric response in these materials. Notably, as the Sc concentration increases, the amount of biaxial tensile strain required to achieve the maximum d33 value decreases from 7.18% in AlN to 2.37% in Al0.5625Sc0.4375N which indicates that the maximum piezoelectric coefficient is more easily attainable with less tensile strain as Sc content increases. To place these values in context, biaxial tensile strains in state-of-the-art epitaxial films are typically limited to 1% to 2.5% to avoid material degradation. For instance, tensile strains of ∼1% are common for AlN on Si and SiC substrates,37,38 while growth on a GaN template can induce a tensile strain of approximately 2.4%.39,40 Although the 7.18% strain required to maximize d33 in pure AlN is likely unattainable, the predicted 2.37% strain for Al0.5625Sc0.4375N is remarkedly close to what is practically achievable via heteroepitaxy on GaN. This suggests that near-maximal d33 enhancement in Sc-rich Al1−xScxN is a tangible goal for experimental realization. Furthermore, strain engineering via flexible substrates or in MEMS structures offers alternative pathways to apply the necessary mechanical loads to harness this predicted giant piezoelectric effect.41,42
Interestingly, at low biaxial strains, Al1−xScxN alloys with different Sc contents but the same x–y biaxial unit area coincidentally exhibit nearly identical d33 values (Fig. S2, ESI†). This behavior, though seemingly unexpected, suggests a dominant role of strain-induced polarization effects in the wurtzite structure that may momentarily override composition-dependent variations. This observation reinforces the robustness of strain as a tuning parameter and highlights a potential design strategy where targeted strain levels, rather than precise control over Sc content, can achieve a consistent enhancement of piezoelectric properties.
To understand the underlying mechanisms behind this behavior, we examine Fig. 3b–d, which illustrate the contributing factors to the piezoelectric coefficient. The observed trends can be rationalized by considering the interplay between structural changes, electronic polarization, and elastic properties as a function of both Sc concentration and applied strain:
(I) Structural evolution: as shown in Fig. 3b, the lattice parameter c/a ratio decreases in general with increasing strain for all concentrations of Sc. This is expected due to the Poisson effect, whereby the tensile strain leads to an expansion of in-plane lattice parameters a and b and corresponding compression in the out-of-plane lattice parameter c. This decrease is not linear, and for each Sc concentration, there is a steep abrupt decrease in the c/a ratio to ∼1.25. This abrupt change coincides with the respective value of biaxial tensile strain at which the d33 value peaks; it also marks the transition point between the wurtzite and non-polar hexagonal layered phase.
(II) Piezoelectric constants: Fig. 3c demonstrates that the piezoelectric constants, e33, increase with increasing biaxial tensile strain, peaking at the transition points before decreasing rather abruptly to close to zero. The maximum e33 values are higher with more Sc content (from 5.22 C m−2 in AlN to 12.44 C m−2 in Al0.5625Sc0.4375N), which can be attributed to the enhanced polarization induced by the larger and more polarizable Sc atoms substituting for Al.43 This increased polarization strengthens the piezoelectric response until the structural transition occurs.
(III) Elastic properties: in Fig. 3d, we observe drastic changes in the elastic constants, C33, at the transition points. Before reaching the critical biaxial tensile strain, C33 decreases with increasing strain, likely due to the elastic softening as the wurtzite structure becomes increasingly distorted under tensile stress. This softening leads to values between 1.4 to 10.1 GPa. However, after the transition to the non-polar hexagonal phase, C33 increases significantly to above 300 GPa, reflecting the increased mechanical rigidity of the new phase.
The changes in both e33 and C33 modify d33 following eqn (2), where d33 is the ratio of e33 to C33. As the structure approaches the phase transition, it becomes highly polarizable (high e33) and extremely compliant (low C33), resulting in the observed large values of d33 at the applied biaxial tensile strains at the transition points. The subsequent abrupt drop of d33 to near-zero is the definitive hallmark of this structural phase transition; it is a direct consequence of the system adopting the higher-symmetry, non-polar hexagonal layered structure (space group P63/mmc), which, as a centrosymmetric phase, forbids piezoelectricity. It is important to note that the actual peak values of d33 may be subject to estimation errors, particularly due to the small values and potential inaccuracies in determining C33 at the transition point. However, despite these uncertainties, we can assert that a significant increase in d33 values occurs as the applied biaxial tensile strain is increased just below its critical value.
Building on the observed transition between the wurtzite and non-polar hexagonal layered structures, we explored whether the piezoelectric properties of Al0.5Sc0.5N, which naturally adopts a non-polar hexagonal layered structure in its unstrained form, could be enhanced by applying biaxial compressive strain instead of tensile strain. Indeed, as shown in Fig. S3 (ESI†), applying compressive strain induces a polar, wurtzite-like character, resulting in a significant enhancement of the d33 value at a critical compressive strain of 1.69%. To clarify the nature of this change, this is not a formal phase transition back to the P63mc space group, but rather a strain-induced distortion of the disordered hexagonal structure. Interestingly, this strain-induced phase distortion in Al0.5Sc0.5N does not produce the same abrupt changes in the c/a ratio, e33, and C33 values as observed in Al1−xScxN alloys with x ≤ 0.4375 under tensile strain (Fig. 3). This can be attributed to the more inherently distorted structure of Al0.5Sc0.5N from its higher Sc content, where the larger Sc atoms create local structural irregularities and varying bond lengths throughout the crystal. These pre-existing distortions provide multiple avenues for structural accommodation of strain, allowing the material to respond more gradually to applied stress, rather than undergoing the sharp, collective transitions seen in the more uniform, less distorted structures of Al-rich compositions. This prevents a collective, abrupt symmetry change and instead, favors a progressive distortion towards a polar, wurtzite-like state. As for AlN and Al1−xScxN alloys with x ≤ 0.4375, compressive strains within our investigative range simply lead to a more rigid wurtzite structure, accompanied by reduced piezoelectric properties. This dichotomy in behavior between Sc-rich and Al-rich compositions highlights the complex interplay between composition, structure, and strain in determining the piezoelectric response of these alloys.
These findings lead to a crucial insight: regardless of the initial structure, if Al1−xScxN is subjected to either compressive or tensile strain, to the point of transition between the wurtzite and non-polar hexagonal layered phases, it becomes possible to greatly enhance the piezoelectric properties. This highlights the exceptional versatility of Al1−xScxN as a tunable piezoelectric material. By strategically engineering strain and modulating Sc composition, it is possible to tailor the structural and piezoelectric properties of Al1−xScxN to meet the diverse requirements of piezoelectric device applications, making Al1−xScxN alloys a promising candidate for next-generation piezoelectric materials.
4. Conclusion
Our comprehensive study of Al1−xScxN alloys reveals the exceptional tunability and versatility of this material system for piezoelectric applications. Through careful analysis of the structural, electronic, and piezoelectric properties across a range of compositions and strain states, we uncovered several key insights. First, we showed that the wurtzite phase is the ground-state structure for Al1−xScxN at low Sc concentrations, with a transition to a non-polar hexagonal layered phase occurring at moderate Sc concentration before transforming to rock-salt above 60% Sc. Second, we observed that the piezoelectric coefficient d33 of unstrained Al1−xScxN reaches a maximum at x = 0.4375, demonstrating a significant enhancement over pure AlN. More strikingly, we found that applying biaxial tensile strain can dramatically increase d33, with values peaking at specific critical strains for each composition. These peak values, ranging from 519.03 pC N−1 for strained AlN to an extraordinary 5121.58 pC N−1 for strained Al0.625Sc0.375N, represent improvements of at least two orders of magnitude over their unstrained counterparts.The observed enhancement in piezoelectric properties is intimately linked to the structural evolution of Al1−xScxN under strain, particularly the transition between the wurtzite and non-polar hexagonal layered phases. This phase transition, occurring at composition-dependent critical strain values, is accompanied by a significant softening of the elastic constant C33 and a peak in the piezoelectric constant e33. Importantly, we demonstrated that this phenomenon can be exploited not only through tensile strain in Al-rich compositions but also through compressive strain in Sc-rich compositions like Al0.5Sc0.5N. This bidirectional tunability underscores the remarkable adaptability of Al1−xScxN as a piezoelectric material, which opens up new avenues for material design and device optimization, potentially enabling the development of highly efficient and versatile piezoelectric devices for a wide range of applications, from high-frequency acoustics to sensitive pressure sensors and efficient micro-scale actuators.
Conflicts of interest
The authors declare no competing financial interest.Data availability
Data that supports the findings of this study are presented within figures and tables of the article and ESI.† Additional data that support the findings of this study are available from the corresponding author upon reasonable request.Acknowledgements
This work is supported by the Agency for Science, Technology and Research (A*STAR) of Singapore (Grant ID: A20G9b0135). The authors would like to acknowledge the use of high-performance computing facilities provided by the National Supercomputing Centre Singapore (NSCC) (Grant No. 13002487) and A*STAR Computational Resource Centre (A*CRC).References
- N. Sezer and M. Koç, A comprehensive review on the state-of-the-art of piezoelectric energy harvesting, Nano Energy, 2021, 80, 105567 CrossRef CAS.
- M. C. Sekhar, E. Veena, N. S. Kumar, K. C. B. Naidu, A. Mallikarjuna and D. B. Basha, A Review on Piezoelectric Materials and Their Applications, Cryst. Res. Technol., 2023, 58(2), 2200130 CrossRef CAS.
- K. Uchino and K. Uchino, The Development of Piezoelectric Materials and the New Perspective, in Woodhead Publishing in Materials, Woodhead Publishing, 2017, ch. 1, pp. 1–92 Search PubMed.
- S. D. Mahapatra, P. C. Mohapatra, A. I. Aria, G. Christie, Y. K. Mishra, S. Hofmann and V. K. Thakur, Piezoelectric Materials for Energy Harvesting and Sensing Applications: Roadmap for Future Smart Materials, Adv. Sci., 2021, 8(17), 2100864 CrossRef CAS PubMed.
- H. P. Loebl, C. Metzmacher, R. F. Milsom, P. Lok, F. van Straten and A. Tuinhout, RF Bulk Acoustic Wave Resonators and Filters, J. Electroceram., 2004, 12(1), 109–118 CrossRef CAS.
- S. T. Haider, M. A. Shah, D.-G. Lee and S. Hur, A Review of the Recent Applications of Aluminum Nitride-Based Piezoelectric Devices, IEEE Access, 2023, 11, 58779–58795 Search PubMed.
- R. M. R. Pinto, V. Gund, R. A. Dias, K. K. Nagaraja and K. B. Vinayakumar, CMOS-Integrated Aluminum Nitride MEMS: A Review, J. Microelectromech. Syst., 2022, 31(4), 500–523 CAS.
- F. Tasnádi, B. Alling, C. Höglund, G. Wingqvist, J. Birch, L. Hultman and I. A. Abrikosov, Origin of the Anomalous Piezoelectric Response in Wurtzite ScxAl1−xN Alloys, Phys. Rev. Lett., 2010, 104(13), 137601 CrossRef.
- M. Akiyama, T. Kamohara, K. Kano, A. Teshigahara, Y. Takeuchi and N. Kawahara, Enhancement of Piezoelectric Response in Scandium Aluminum Nitride Alloy Thin Films Prepared by Dual Reactive Cosputtering, Adv. Mater., 2009, 21(5), 593–596 CrossRef CAS PubMed.
- A. Teshigahara, K.-y. Hashimoto and M. Akiyama, Scandium aluminum nitride: Highly piezoelectric thin film for RF SAW devices in multi GHz range, in 2012 IEEE International Ultrasonics Symposium, 7-10 Oct. 2012, 2012, pp. 1–5.
- Y. Lu, M. Reusch, N. Kurz, A. Ding, T. Christoph, M. Prescher, L. Kirste, O. Ambacher and A. Žukauskaitė, Elastic modulus and coefficient of thermal expansion of piezoelectric Al1−xScxN (up to x = 0.41) thin films, APL Mater., 2018, 6(7), 076105 CrossRef.
- S. Zhang, D. Holec, W. Y. Fu, C. J. Humphreys and M. A. Moram, Tunable optoelectronic and ferroelectric properties in Sc-based III-nitrides, J. Appl. Phys., 2013, 114(13), 133510 CrossRef.
- K. R. Talley, S. L. Millican, J. Mangum, S. Siol, C. B. Musgrave, B. Gorman, A. M. Holder, A. Zakutayev and G. L. Brennecka, Implications of heterostructural alloying for enhanced piezoelectric performance of (Al,Sc)N, Phys. Rev. Mater., 2018, 2(6), 063802 CrossRef CAS.
- P. Daoust, M. Côté, P. Desjardins and R. A. Masut, Impact of applied biaxial stress on the piezoelectric, elastic, and dielectric properties of scandium aluminum nitride alloys determined by density functional perturbation theory, APL Advances, 2021, 11(9), 095017 CAS.
- J. W. D. Connolly and A. R. Williams, Density-functional theory applied to phase transformations in transition-metal alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27(8), 5169–5172, DOI:10.1103/PhysRevB.27.5169.
- J. M. Sanchez, F. Ducastelle and D. Gratias, Generalized cluster description of multicomponent systems, Phys. A, 1984, 128(1), 334–350, DOI:10.1016/0378-4371(84)90096-7.
- N. A. Zarkevich and D. D. Johnson, Reliable First-Principles Alloy Thermodynamics via Truncated Cluster Expansions, Phys. Rev. Lett., 2004, 92(25), 255702, DOI:10.1103/PhysRevLett.92.255702.
- T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, A Comprehensive Search for Stable Pt–Pd Nanoalloy Configurations and Their Use as Tunable Catalysts, Nano Lett., 2012, 12(9), 4875–4880, DOI:10.1021/nl302405k.
- T. L. Tan, L.-L. Wang, J. Zhang, D. D. Johnson and K. Bai, Platinum Nanoparticle During Electrochemical Hydrogen Evolution: Adsorbate Distribution, Active Reaction Species, and Size Effect, ACS Catal., 2015, 5(4), 2376–2383, DOI:10.1021/cs501840c.
- N. A. Zarkevich, T. L. Tan and D. D. Johnson, First-principles prediction of phase-segregating alloy phase diagrams and a rapid design estimate of their transition temperatures, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(10), 104203, DOI:10.1103/PhysRevB.75.104203.
- Z. M. Wong, T. L. Tan, S.-W. Yang and G. Q. Xu, Optimizing special quasirandom structure (SQS) models for accurate functional property prediction in disordered 2D alloys, J. Phys.: Condens. Matter, 2018, 30(48), 485402 CrossRef.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65(3), 353–356, DOI:10.1103/PhysRevLett.65.353.
- Z. M. Wong, H. Cheng, S.-W. Yang, T. L. Tan and G. Q. Xu, Computational Design of Perovskite BaxSr1–xSnO3 Alloys as Transparent Conductors and Photocatalysts, J. Phys. Chem. C, 2017, 121(47), 26446–26456, DOI:10.1021/acs.jpcc.7b08681.
- K. Furuta, K. Hirata, S. A. Anggraini, M. Akiyama, M. Uehara and H. Yamada, First-principles calculations of spontaneous polarization in ScAlN, J. Appl. Phys., 2021, 130(2), 024104, DOI:10.1063/5.0051557 (accessed 6/9/2025).
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138, DOI:10.1103/PhysRev.140.A1133.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett., 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396, DOI:10.1103/PhysRevLett.78.1396.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188–5192, DOI:10.1103/PhysRevB.13.5188.
- X. Wu, D. Vanderbilt and D. R. Hamann, Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(3), 035105, DOI:10.1103/PhysRevB.72.035105.
- C. Höglund, J. Bareño, J. Birch, B. Alling, Z. Czigány and L. Hultman, Cubic Sc1−xAlxN solid solution thin films deposited by reactive magnetron sputter epitaxy onto ScN(111), J. Appl. Phys., 2009, 105(11), 113517, DOI:10.1063/1.3132862 (accessed 6/9/2025).
- J. C. Slater, Atomic Radii in Crystals, J. Chem. Phys., 1964, 41(10), 3199–3204 CrossRef CAS.
- D. F. Urban, O. Ambacher and C. Elsässer, First-principles calculation of electroacoustic properties of wurtzite (Al,Sc)N, Phys. Rev. B, 2021, 103(11), 115204 CrossRef CAS.
- S. Xiaolei, C. Yigang, S. Weimin and W. Linjun, Study of high temperature piezoelectric scandium aluminum nitride thin films. Proc. SPIE, 2011, vol. 7995, p. 79951N DOI:10.1117/12.888228.
- M. Hu, P. Wang, D. Wang, Y. Wu, S. Mondal, D. Wang, E. Ahmadi, T. Ma and Z. Mi, Heteroepitaxy of N-polar AlN on C-face 4H-SiC: Structural and optical properties, APL Mater., 2023, 11(12), 121111, DOI:10.1063/5.0168970 (accessed 6/9/2025).
- H. Agrawal, Strain analysis for AlN thin-films on Si using high-resolution X-ray diffraction, University of California, Los Angeles, 2024 Search PubMed.
- A. Bourret, C. Adelmann, B. Daudin, J.-L. Rouvière, G. Feuillet and G. Mula, Strain relaxation in (0001) AlN/GaN heterostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(24), 245307, DOI:10.1103/PhysRevB.63.245307.
- A. V. Kuchuk, S. Kryvyi, P. M. Lytvyn, S. Li, V. P. Kladko, M. E. Ware, Y. I. Mazur, N. V. Safryuk, H. V. Stanchu and A. E. Belyaev, et al., The Peculiarities of Strain Relaxation in GaN/AlN Superlattices Grown on Vicinal GaN (0001) Substrate: Comparative XRD and AFM Study, Nanoscale Res. Lett., 2016, 11(1), 252, DOI:10.1186/s11671-016-1478-6.
- S. Petroni, C. L. Tegola, G. Caretto, A. Campa, A. Passaseo, M. D. Vittorio and R. Cingolani, Aluminum Nitride piezo-MEMS on polyimide flexible substrates, Microelectron. Eng., 2011, 88(8), 2372–2375, DOI:10.1016/j.mee.2011.02.080.
- T. Li and P. S. Lee, Piezoelectric Energy Harvesting Technology: From Materials, Structures, to Applications, Small Structures, 2022, 3(3), 2100128, DOI:10.1002/sstr.202100128 (accessed 2025/06/09).
- P. Schwerdtfeger and J. K. Nagle, 2018 Table of static dipole polarizabilities of the neutral elements in the periodic table, Mol. Phys., 2019, 117(9–12), 1200–1225 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Plot of structural difference versus absolute energy difference between wurtzite and non-polar hexagonal layered phases of Al1−xScxN of particular alloy configurations; plots of piezoelectric coefficients d33 versus biaxial unit area of Al1−xScxN SQS supercells; plots of piezoelectric coefficients d33, lattice parameter c/a ratio, piezoelectric constant e33, and elastic constant C33 versus biaxial strain applied for Al0.5Sc0.5 SQS supercell and AlN. See DOI: https://doi.org/10.1039/d5tc01075f |
| This journal is © The Royal Society of Chemistry 2025 |