Open Access Article
Open Access ArticleAnomalous resistivity and superconductivity in the polymorphs of (TiZrHf)95Sc5
Denver
Strong
 *,
Danrui
Ni
*,
Danrui
Ni
 ,
Xianghan
Xu
and
R. J.
Cava
*
,
Xianghan
Xu
and
R. J.
Cava
*
Department of Chemistry Princeton University, Princeton, NJ, USA. E-mail: dpstrong@princeton.edu; rcava@princeton.edu
First published on 25th June 2025
Abstract
Three polymorphs of (TiZrHf)95Sc5, one of which is glassy, are identified. The materials are the result of splat cooling arc melted samples. The temperature-dependent resistivities of the body centered cubic and amorphous materials are anomalous. Low temperature resistivity and heat capacity measurements indicate that superconducting transitions are present when the material has either a body centered cubic (TC ∼ 1.5 K) or hexagonal close packed (TC ∼ 0.8 K) crystal structure and the superconductivity of the amorphous phase below 0.65 K cannot be ruled out. We include evidence of a robust critical field in the body centered cubic material.
Introduction
High entropy and multicomponent alloys have become increasingly popular over the last decade, primarily due to the fact their stability can be attributed to their large mixing entropy, which can overcome an unfavorable mixing enthalpy.1 If the mixing entropy does not overcome the enthalpy, then precipitates or mixtures of intermetallic phases can form instead, compromising the possibility of a single solid solution. This high entropy concept has also been used to stabilize intermetallics made from widely different elements, where each site can host a solid solution with little to no atomic mixing between them.2–4 Furthermore, it has been used as an extension of chemical doping, where the crystal structure is entropically stabilized due to the number of “dopants” but the Fermi energy can be tuned.1,5,6 The “tunability” associated with multicomponent alloys has opened a vast avenue for studying new electronic and quantum states in materials.One important advantage of high entropy alloys (HEAs) is the fact that the competition between entropy and enthalpy can stabilize new phases. One path where exploration has been limited has been the study of polymorphs of the same composition with different physical and electronic structures. Due to the number of binary interactions at play, adjusting the temperature or pressure of a material with a single composition gives the field of materials physics access to study the consequences of polymorphism.7 One review paper emphasized the importance of elements, structure, and synthesis to compare materials one-to-one, and entropy stabilized materials offer a promising route to such control.8
For superconducting high entropy alloys in general, a few reports stand out as being relevant to the current work. First, are two series (Nb-Mo-Re-Ru-Rh and Mo-W-Re-Ru-Pd) where the relative concentrations can be changed to stabilize various crystal structures (α-Mn → Hexagonal Close Packed (HCP) and Body Centered Cubic (BCC) → σ → HCP, respectively).9,10 All were reported to show fully gapped superconducting states and a clear linear trend in the superconducting transition temperature (TC) even across structure types, indicating a subtle difference in their density of states at the Fermi energy. Closer to the current work is the explicit polymorphism in superconducting V-Nb-Mo-Al-Ga, comparing the as-cast body centered cubic solid solution and the annealed, ordered A15-type material - the latter of which superconducts below a Tc of 10 K while the as-cast body centered cubic version shows no sign of superconductivity above 2 K.11 Here we report the existence of multiple polymorphs, one of which is amorphous, of a single medium entropy alloy, and signs of very low temperature superconductivity in the crystalline materials.
Methods
Because the entropic contributions to the free energy are maximized at high temperature, high temperature synthesis and fast cooling were employed. The nominal formula for the hexagonal close packed (HCP) sample was (TiZrHf)95Sc5 while the beginning composition for body centered cubic (BCC) sample was (TiZrHf)90Sc10. The amount of material summed to 200 mg and 300 mg for the HCP and BCC samples respectively. Stoichiometric amounts of Ti, Zr, and Hf powders were compressed using a steel dye and Sc pieces were melted alongside the resulting pellet.The samples were placed in the arc melter alongside a Zr getter, which was heated to collect any residual oxygen in the chamber. The samples were originally melted with a low current to sinter the powders into a more robust pellet. The power was then increased to melt each sample into a button: I ≈ 50 A and V ≈ 480 V was usually sufficient. Once in the molten state, it was held there for 5–8 seconds. Each sample was melted 3–5 times and flipped in between to ensure homogeneity. Mass loss in the HCP sample was negligible and mass loss in the BCC sample neared 2.5%. Some of the Sc boiled away in the preparation of the BCC material due to the fact that temperatures exceeding 3100 °C were obtained.
Afterward, the resulting buttons were placed in a water-cooled copper well. Residual oxygen was once again collected with a Zr getter. The sample was heated for 5–8 seconds after reaching the molten state. Immediately after that time, the electrode was withdrawn from the well and a spring-loaded Cu plate was released to rapidly cool the sample. (i.e. splat cooling to maintain the high entropy state) The result was thin solidified sheets with variable morphology.
Since the samples were typically thin, powder X-ray diffraction (pXRD) measurements can be collected easily. Diffractograms were collected in the Bragg Brentano geometry on a Bruker D8 Advance ECO diffractometer using Cu Kα X-rays. Le Bail refinements were performed using GSAS-II to determine lattice parameters. A Quanta 200 FEG Environmental Scanning Electron Microscope (SEM) equipped with Energy-dispersive X-Ray spectroscopy (EDS) was also used to confirm the stoichiometry of select samples.
Physical property measurements were performed in a Quantum Design Physical Property Measurement System (PPMS) equipped with a 3He apparatus. Resistivity measurements were performed on a 4-probe resistivity puck between 0.3 K and 300 K. Heat capacity measurements were done between 0.65 K and 200 K.
Structure & morphology
Fig. 1 reports two crystalline structures arising from splat cooling. The first of which, hexagonal close packed (HCP), the structure-in-structure-out method predicts;1 however, the refined lattice parameters, a = 3.1468(2) A and c = 4.9864(2) A, are slightly larger than the weighted average of the individual elements’ lattice parameters. The other crystalline material is body centered cubic (BCC) with lattice parameter, a = 3.4067(2) A.High temperature BCC allotropes of the groups III and IV elements have been reported and a calculated phase diagram suggests the ternary TiZrHf BCC phase exists as well with a minimum suggested heating temperature of 1200 °C.12–16 The type of splat cooling used here is meant to stabilize high temperature and metastable phases by creating a thin sample, quenched between two plates that absorb heat quickly. General arc melting can exceed 3000 °C given by the fact it can reliably melt W and Re. Although the nominal composition of the BCC sample was (TiZrHf)90Sc10, the EDS measurements, shown in Fig. 2a, confirmed an actual composition of (TiZrHf)95Sc5 which is likely due to reaching temperatures exceeding 3100 °C for this sample.
The surface morphologies of the bulk pieces in Fig. 2 immediately indicate the quality of the splat, as the BCC sample is much smoother. The experimentally determined composition of (a) is Ti30.9Zr32.2Hf32.7Sc4.3 while the experimentally determined composition of (b) is Ti30.9Zr30.3Hf34.5Sc4.3. (The missing data for the HCP sample is due to the surface morphology where higher parts of the sample block the path between the sample and the detector.) Local spectra on the latter consistently returned scandium concentrations between 3.4% and 4.5% suggesting that the material is compositionally homogenous.
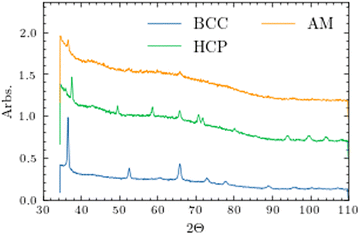
In order to perform the physical property measurements, small pieces (<2 mg) were broken off the edges of the bulk splats. Since these are high temperature phases, pXRD was run on every piece and, during this process, an additional amorphous phase was found in both samples, which contributed to the strong background shown in Fig. 3. Unfortunately, the splat cooling apparatus used here is not capable of isolating the three phases. With this in mind, EDS measurements were performed on any piece where physical property measurements were done to confirm its composition. While transmission electron microscopy (TEM) would be ideal for identifying each structure, it's difficult for the electron beam to pass through the bulk material. In previous work, we’ve used TEM on powder samples filed from the bulk and many of those particles were still too large due to the fact that HEAs are much harder than traditional metals.17
Discovering the amorphous component was a surprise; however, Zr- and Hf-based alloys tend to be reliable glass formers in conjunction with a later transition metal such as Ni or Cu.18–20 Ti-Zr-Hf has been included in other high entropy and bulk metallic glasses, but to the best of our knowledge, they have yet to be reported exclusively within the early transition metals.19,21–28 Many of these amorphous alloys are synthesized using melt spinning which has a lower cooling rate than the method used here.29,30
Since the samples reported here physically appear to be splatted in some form or another, it's obvious the Cu splat tip is impacting the material while it's still in the molten state. We suggest the following explanation for the formation of the polymorphs. If the impact occurs while the sample is at different temperatures, the viscosities of each will differ. An impact at a higher sample temperature where the molten liquid can flow more freely, will in turn increase the surface contact area, cooling the sample faster, stabilizing the high temperature state. We presume the amorphous component forms during the initial contact at the interface of the copper and sample explaining why there seems to be weaker crystalline peaks in the small pieces measured; however, a dedicated and systematic study of this mechanism would be beneficial.
Our work emphasizes the importance of two-tier cooling during this process. While in the molten state, the cooling should be “slow” to initialize a higher effective temperature after impact. One way to do this is by varying the mass of the melt. Larger samples cool slower, enhancing the quality of the splat after impact. This is the opposite of traditional arc melting considering smaller samples are often used to get the fastest cooling rate.
Resistivity
Superconductivity was observed in two of the three polymorphs discussed here, which is summarized in Fig. 4. The resistivity for the HCP variant is included in Fig. 4a and decreases with decreasing temperature before it flattens near 50 K. The residual resistivity ratio, ρ300 K/ρ2 K = 1.59, is on par with other concentrated alloys.31–33 It's interesting to note the values reported here are very similar to ScTiZrHf which was arc melted then annealed for 140 hours at 700 °C.31 This may suggest the microstructures, which can affect resistivity due to grain boundaries, are not very different between the two synthesis methods. The superconducting transition for our alloy can be seen near 1.0 K.Fig. 4b shows data for a piece of the BCC sample with a superconducting transition near 1.5 K. Above the transition, the shape of the resistivity curve is anomalous. The primary feature is decreasing resistivity with increasing temperature, indicated with the dashed line. This has been reported in other glassy materials with resistivities between 150–300 μΩ cm and arises because the mean free path of the electrons is on the order of the interatomic distances.34–36 This phenomenon, often called the Mooij rule, has been explained using weak localization effects.37,38 At this level, the intercarrier distance is on the order of the interatomic spacing. Here, the electrons are essentially ‘trapped’ near one atom and the material begins to act like an insulator. This is often seen in metallic glasses with a low carrier concentration and is being realized more in disordered glassy alloys.39–41
Of particular importance is why this anomalous curve is observed instead of the standard metallic behavior of BCC alloys. Since the BCC resistivity in Fig. 4d does go to zero, there is a complete superconducting path between the voltage leads – within experimental error. There's no evidence here or in the literature that this transition is associated with the amorphous phase, otherwise, a small superconducting signature would be present in the HCP sample as well. Often it is seen that the BCC structure has a lower resistivity than the HCP counterpart. This can be seen when comparing the group IV and V transition metals as well as a decrease in resistivity once Ti, Zr, and Hf undergo their structural change to BCC at high temperatures.42–44 Unfortunately, resistivity data for the BCC allotropes at 300 K could not be found for comparison.
While there are very few examples of crystalline metals displaying this type of behavior, it's well recorded that atomic disorder can contribute to a negative temperature dependence in resistivity.45,46 This may be one realization where high entropy alloys with very few carriers induce an anomalous effect, but measurements on BCC Ti, Zr, or Hf below 300 K are required to confirm this behavior is driven by disorder.
It's important to note the magnitude of the resistivity as well. At 585 μΩ cm, it is surprising there is not an underlying metallic behavior. Many HEAs have resistivities of 100–200 μΩ cm47–51 but there are reports of σ-phase HEAs reaching 400 μΩ cm and α-Mn types nearing 600 μΩ cm.48,52 While microstructure and grain boundaries can increase the resistance, another cause that cannot be ruled out is that the conduction path length is incorrect. This is particularly important in multiphase samples where the current may have to take many detours before reaching the other voltage lead. However, this is not expected to reverse the trend which is seen above 150 K.
Focusing on the superconducting transitions, in agreement with previous literature, the HCP phase has the lower transition temperature, (TC), plotted in Fig. 4c. At zero field, the 50% criterion indicates TC = 0.98 K whereas the BCC phase has a transition centered at 1.5 K (Fig. 4d.) Following this, an analysis to determine the critical field was done on each material.
We plot the superconducting temperatures at each applied field to estimate the upper critical field at 0 K, Hc2(0). We include additional points representing the absolute maximum field due to the Zeeman energy,53Hmax = 2.6TC, another for the Pauli paramagnetic limit,54HP = 1.84TC and finally the Werthamer–Helfand–Hohenberg (WHH) theory,55–59
 | (1) |
Two additional models are presented as well. Model 1 (red),2,60,61
 | (2) |
 | (3) |
The Zeeman splitting induced by a magnetic field is the primary mechanism to destroy superconductivity.53 However, an applied field also raises the energy of spin-down electrons. This means any carriers that were anti-aligned with the applied field will have some inclination to flip. This induces Pauli paramagnetism which is self-destructive to the superconducting state (i.e. The Pauli limit).54 We propose two hypotheses for the robust critical field, both of which require a more detailed theoretical analysis to confirm.
Hypothesis 1
Pauli paramagnetism is directly related to the density of states at the Fermi energy, χP = μB2g(EF), where μB is the Bohr magneton. It's reasonable to suggest there is a minimal number of carriers in these systems simply because the valence electron count (VEC) < 4. Without a substantial number of carriers, these materials minimize compounding effects from the self-induced magnetic field, pushing the boundaries of the Pauli limit.Hypothesis 2
It's been reported that transition metals want to maximize the spin of the system (Hund's rules).64 With such few total carriers, most of these electrons are already pointing the same direction and, in return, it takes very little energy to reorient the few orphan electrons. If nothing is reoriented, there are no self-destructive tendencies. As a follow up to this concept, the initial upward curvature in Fig. 4f is a fundamental feature of charged bosons.60 If it's taken that a cooper pair is a boson, but the correlated electrons are both spin up, the cooper pair in these materials are charged.It is important that we address the potential impact of the mixed phases on the superconducting properties. It's previously been reported that eutectic phases can influence the mechanical properties of high entropy alloys as well as increase their superconducting transition temperatures.65,66 This was related to the proximity effect but does not seem to be relevant to the superconducting phases reported here primarily because amorphous phases with low VECs have lower transition temperatures than their crystalline counterparts.67 However, the proximity effect may be relevant for the transition temperature of the amorphous phase if it does superconduct; which specific heat measurements would be required to confirm. Beyond this, eutectic phases have been shown to enhance the critical current compared to the bulk. This is because the critical current is intricately related to the microstructure as well as the nature of the eutectic phases.68 However, the literature suggests this enhanced critical current is not followed by an enhanced critical field because the underlying electronic structure is not significantly changed,69 indicating the enhanced critical fields are not trivial and more detailed work needs to be done on low VEC HEAs.
Heat capacity
Since previous measurements confirm the potential for multiphase pieces, specific heat measurements (Fig. 5) are used to identify an anomaly near the transition temperature, but a quantitative analysis of the superconducting jump would not be insightful without a pure phase.Data for the HCP sample is shown in Fig. 5a. A jump associated with the transition temperature occurs near 0.8 K, reasonably just below the transition in the resistivity. Since the transition temperature is near the reliable limit of the He3 apparatus, Quantum Design's dual slope analysis routine was used which gives more data points.
The results for the BCC material are reported in Fig. 5b. The well-defined peak of the anomaly near 1.5 K is consistent with resistivity measurements. Fitting the high temperature region to the Einstein model,
 | (4) |
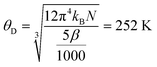 | (5) |
Conclusion
We’ve synthesized mixed phase HCP + amorphous and BCC + amorphous versions of the (TiZrHf)95Sc5 medium entropy alloy. We also showed the possibility of targeting polymorphs by splat cooling arc melted samples and taking advantage of a two-tiered cooling process. Superconducting signals were shown for the crystalline phases with the HCP phase at 0.98 K and the BCC phase at 1.5 K. The latter has a critical field that exceeds the Pauli limit. Superconductivity of the amorphous phase below 0.65 K cannot be ruled out. These results encourage further exploration of low VEC HEAs and the splat cooled arc melting technique may significantly expand the number of entropy-stabilized alloys that appear to display superconductivity.Author contributions
Conceptualization, synthesis, and limited structural and physical property characterizations were performed by Denver Strong. SEM measurements were done by Danrui Ni. Low temperature PPMS experiments were performed by Xianghan Xu. R. J. Cava funded and directed the work.Ethical approval
Not applicableData availability
Please reach out to the corresponding author for raw data. It's also available at https://github.com/dpstrong/Polymorph-Data_Ti-Zr-Hf-Sc.Conflicts of interest
There are no conflicts of interest.Acknowledgements
This research was funded by the Gordon and Betty Moore Foundation, grant number GBMF-9066, and by the Division of Basic Energy Sciences of the US Department of Energy, grant number DE-FG02-98ER-45706.References
- D. B. Miracle and O. N. Senkov, A critical review of high entropy alloys and related concepts, Acta Mater., 2017, 122, 448–511 CrossRef CAS.
- K. Stolze, J. Tao, F. O. Von Rohr, T. Kong and R. J. Cava, Sc–Zr–Nb–Rh–Pd and Sc–Zr–Nb–Ta–Rh–Pd High-Entropy Alloy Superconductors on a CsCl-Type Lattice, Chem. Mater., 2018, 30, 906–914 CrossRef CAS.
- B. Liu, et al., Superconductivity in Cubic A15-type V–Nb–Mo–Ir–Pt High-Entropy Alloys, Front. Phys., 2021, 9, 651808 CrossRef.
- A. Yamashita, et al., An efficient way of increasing the total entropy of mixing in high-entropy-alloy compounds: a case of NaCl-type (Ag,In,Pb,Bi)Te1−xSex (x = 0.0, 0.25, 0.5) superconductors, Dalton Trans., 2020, 49, 9118–9122 RSC.
- D. Strong and R. J. Cava, Superconductivity in the face-centered cubic W-M-Rh-Ir-Pt M = {Mo, Nb, Ta, Re} high-entropy alloy, J. Mater. Sci., 2024, 59, 10347–10356 CrossRef CAS.
- L. Zeng, et al., Superconductivity and non-trivial band topology in high-entropy carbonitride Ti0.2Nb0.2Ta0.2Mo0.2W0.2C1−xNx, Innovation Mater., 2023, 1, 100042 CrossRef.
- F. Zhang, et al., Polymorphism in a high-entropy alloy, Nat. Commun., 2017, 8, 15687 CrossRef CAS PubMed.
- T. Berry, N. Ng and T. M. McQueen, Tools and Tricks for Single Crystal Growth, Chem. Mater., 2024, 36, 4929–4944 CrossRef CAS.
- B. Liu, et al., Structural evolution and superconductivity tuned by valence electron concentration in the Nb–Mo–Re–Ru–Rh high-entropy alloys, J. Mater. Sci. Technol., 2021, 85, 11–17 CrossRef CAS.
- X. Xu, et al., Structural sequence and superconductivity in high-entropy Mo–W–Re–Ru–Pd alloys, Scr. Mater., 2024, 243, 115986 CrossRef CAS.
- J. Wu, et al., Polymorphism and superconductivity in the V-Nb-Mo-Al-Ga high-entropy alloys, Sci. China Mater., 2020, 63, 823–831 CrossRef CAS.
- W. Petry, et al., Phonon dispersion of the bcc phase of group-IV metals. I. bcc titanium, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 43, 10933–10947 CrossRef.
- A. Heiming, et al., Phonon dispersion of the bcc phase of group-IV metals. II. bcc zirconium, a model case of dynamical precursors of martensitic transitions, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 43, 10948–10962 CrossRef CAS PubMed.
- J. Trampenau, et al., Phonon dispersion of the bcc phase of group-IV metals. III. bcc hafnium, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 10963–10969 CrossRef CAS PubMed.
- C. Stassis, J. Zarestky and N. Wakabayashi, Lattice Dynamics of bcc Zirconium, Phys. Rev. Lett., 1978, 41, 1726–1729 CrossRef CAS.
- L. Lin, L. Delaey, O. Van Der Biest and P. Wollants, Calculation of isothermal sections of three ternary Ti–Zr–X systems, Scr. Mater., 1996, 34, 1411–1416 CrossRef CAS.
- A. J. Browne, D. P. Strong and R. J. Cava, Phase stability and possible superconductivity of new 4d and 5d transition metal high-entropy alloys, J. Solid State Chem., 2023, 321, 123881 CrossRef CAS.
- F. E. Luborsky, Amorphous metallic alloys, Elsevier Science, Kent, 2014 Search PubMed.
- R. Ristić, et al., Properties and atomic structure of amorphous early transition metals, J. Alloys Compd., 2010, 504, S194–S197 CrossRef.
- I. Bakonyi, Electronic properties and atomic structure of (Ti, Zr, Hf)(Ni, Cu) metallic glasses, J. Non-Cryst. Solids, 1995, 180, 131–150 CrossRef CAS.
- A. Pasko, et al., Crystallization of the amorphous phase and martensitic transformations in multicomponent (Ti,Hf,Zr)(Ni,Cu)-based alloys, J. Non-Cryst. Solids, 2007, 353, 3062–3068 CrossRef CAS.
- M. Hasiak, et al., Some Magnetic Properties of Bulk Amorphous Fe–Co–Zr–Hf–Ti–W–B–(Y) Alloys, IEEE Trans. Magn., 2008, 44, 3879–3882 CAS.
- L. Wang, C. Li and A. Inoue, Formation of Ti-Zr(Hf)-Ni-Cu Amorphous Alloys and Quasicrystal Precipitation upon Annealing, Mater. Trans., 2001, 42, 528–531 CrossRef CAS.
- Y. J. Huang, J. Shen, J. F. Sun and X. B. Yu, A new Ti–Zr–Hf–Cu–Ni–Si–Sn bulk amorphous alloy with high glass-forming ability, J. Alloys Compd., 2007, 427, 171–175 CrossRef CAS.
- R. Ristić, et al., Transition from high-entropy to conventional (TiZrNbCu)1−xCox metallic glasses, J. Appl. Phys., 2021, 130, 195102 CrossRef.
- A. Inoue, K. Kobayashi, M. Nose and T. Masumoto, Mechanical properties of (Fe, Co, Ni)-M-B (M = Ti, Zr, Hf, V, Nb, Ta AND Mo) amorphous alloys with low boron concentration, J. Phys., Colloq., 1980, 41, C8-831–C8-834 Search PubMed.
- H. Son, G. Yoo, Q. Mustaghfiroh, D.-H. Kim and H. Choi-Yim, Effect of Substituting Hf for Zr on Fe-Co-M-Nb-B (M = Zr, Hf) Amorphous Alloys with High Saturation Magnetization, Metals, 2021, 12, 12 CrossRef.
- R. Ristić, K. Zadro, D. Pajić, I. A. Figueroa and E. Babić, On the origin of bulk glass forming ability in Cu-Hf, Zr alloys, EPL Europhys. Lett, 2016, 114, 17006 CrossRef.
- K. Biljaković, et al., Electronic structure and properties of (TiZrNbCu)1−xNix high entropy amorphous alloys, J. Alloys Compd., 2017, 695, 2661–2668 CrossRef.
- I. A. Figueroa, et al., Properties of (TiZrNbCu)1−xNix metallic glasses, J. Alloys Compd., 2018, 745, 455–459 CrossRef CAS.
- S. Uporov, S. Kh Estemirova, V. A. Bykov, D. A. Zamyatin and R. E. Ryltsev, A single-phase ScTiZrHf high-entropy alloy with thermally stable hexagonal close-packed structure, Intermetallics, 2020, 122, 106802 CrossRef CAS.
- S. Marik, et al., Superconductivity in a new hexagonal high-entropy alloy, Phys. Rev. Mater., 2019, 3, 060602 CrossRef CAS.
- B. Liu, et al., Superconductivity in hexagonal Nb-Mo-Ru-Rh-Pd high-entropy alloys, Scr. Mater., 2020, 182, 109–113 CrossRef CAS.
- D. Korn, H. Pfeifle and G. Zibold, Electrical resistivity of amorphous alloys, Z. Für Phys, 1974, 270, 195–202 CrossRef CAS.
- K. Frobose and J. Jackle, On the temperature dependence of the electrical resistivity of amorphous metals, J. Phys. F: Met. Phys., 1977, 7, 2331–2348 CrossRef.
- S. R. Nagel, Temperature dependence of the resistivity in metallic glasses, Phys. Rev. B: Solid State, 1977, 16, 1694–1698 CrossRef CAS.
- J. H. Mooij, Electrical conduction in concentrated disordered transition metal alloys, Phys. Status Solidi A, 1973, 17, 521–530 CrossRef CAS.
- V. F. Gantmakher, Mooij rule and weak localization, JETP Lett., 2011, 94, 626–628 CrossRef CAS.
- V. F. Gantmakher and L. I. Man, Electrons and Disorder in Solids, Oxford University Press, 2005 DOI:10.1093/acprof:oso/9780198567561.001.0001.
- M. Park, K. Savran and Y. Kim, Weak localization and the Mooij rule in disordered metals, Phys. Status Solidi B, 2003, 237, 500–512 CrossRef CAS.
- S. Ciuchi, D. Di Sante, V. Dobrosavljević and S. Fratini, The origin of Mooij correlations in disordered metals, Npj Quantum Mater., 2018, 3, 44 CrossRef.
- W. C. Michels and S. Wilford, The Physical Properties of Titanium. I. Emissivity and Resistivity of the Commercial Metal, J. Appl. Phys., 1949, 20, 1223–1226 CrossRef CAS.
- A. Cezairliyan and F. Righini, Thermodynamic studies of the a? phase transformation in zirconium using a subsecond pulse heating technique, J. Res. Natl. Bur. Stand. Sect. Phys. Chem, 1975, 79A, 81 CrossRef CAS PubMed.
- P. D. Desai, T. K. Chu, H. M. James and C. Y. Ho, Electrical Resistivity of Selected Elements, J. Phys. Chem. Ref. Data, 1984, 13, 1069–1096 CrossRef CAS.
- T. Harmening, H. Eckert and R. Pöttgen, Defects in half-Heusler type antimonides ScTSb (T = Ni, Pd, Pt), Solid State Sci., 2009, 11, 900–906 CrossRef CAS.
- D. Gnida, K. Ciesielski and D. Kaczorowski, Origin of the negative temperature coefficient of resistivity in the half-Heusler antimonides LuNiSb and YPdSb, Phys. Rev. B, 2021, 103, 174206 CrossRef CAS.
- F. Von Rohr, M. J. Winiarski, J. Tao, T. Klimczuk and R. J. Cava, Effect of electron count and chemical complexity in the Ta–Nb–Hf–Zr–Ti high-entropy alloy superconductor, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E7144–E7150 CrossRef CAS PubMed.
- K. Stolze, F. A. Cevallos, T. Kong and R. J. Cava, High-entropy alloy superconductors on an α-Mn lattice, J. Mater. Chem. C, 2018, 6, 10441–10449 RSC.
- M.-H. Tsai, Physical Properties of High Entropy Alloys, Entropy, 2013, 15, 5338–5345 CrossRef CAS.
- J. Kitagawa, et al., Superconductivity and hardness of the equiatomic high-entropy alloy HfMoNbTiZr, J. Alloys Compd., 2022, 924, 166473 CrossRef CAS.
- S. Jangid, et al., Superconductivity with a high upper critical field in an equiatomic high-entropy alloy Sc–V–Ti–Hf–Nb, Appl. Phys. Lett., 2024, 124, 192602 CrossRef CAS.
- B. Liu, et al., Formation and Superconductivity of Single-Phase High-Entropy Alloys with a Tetragonal Structure, ACS Appl. Electron. Mater, 2020, 2, 1130–1137 CrossRef CAS.
- B. S. Chandrasekhar, A note on the Maximum critical field of high-field superconductors, Appl. Phys. Lett., 1962, 1, 7–8 CrossRef CAS.
- A. M. Clogston, Upper Limit for the Critical Field in Hard Superconductors, Phys. Rev. Lett., 1962, 9, 266–267 CrossRef.
- R. R. Hake, Paramagnetic Superconductivity in Extreme Type-II Superconductors, Phys. Rev., 1967, 158, 356–376 CrossRef CAS.
- E. Helfand and N. R. Werthamer, Temperature and Purity Dependence of the Superconducting Critical Field, Hc2II, Phys. Rev., 1966, 147, 288–294 CrossRef CAS.
- N. R. Werthamer, E. Helfand and P. C. Hohenberg, Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects, Phys. Rev., 1966, 147, 295–302 CrossRef CAS.
- R. R. Hake, Upper-critical-field limits for bulk type-II superconductors, Appl. Phys. Lett., 1967, 10, 189–192 CrossRef CAS.
- G. Cody, Critical fields of type II superconductors, RCA Laboratories Princeton, New Jersey, 1968, pp. 405–436 Search PubMed.
- R. Micnas, J. Ranninger and S. Robaszkiewicz, Superconductivity in narrow-band systems with local nonretarded attractive interactions, Rev. Mod. Phys., 1990, 62, 113–171 CrossRef CAS.
- A. B. Karki, et al., Physical properties of the noncentrosymmetric superconductor Nb0.18Re0.82, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 144525 CrossRef.
- G. Xiao, et al., Chemical composition effect on superconductivity in noncentrosymmetric β -Mn-type high-entropy alloys, J. Mater. Res. Technol., 2024, 28, 2516–2522 CrossRef CAS.
- G. Kim, et al., Strongly correlated and strongly coupled s-wave superconductivity of the high entropy alloy Ta1/6Nb2/6Hf1/6Zr1/6Ti1/6 compound, Acta Mater., 2020, 186, 250–256 CrossRef CAS.
- S. K. Riddle, T. R. Wilson, M. Rajivmoorthy and M. E. Eberhart, Principles Determining the Structure of Transition Metals, Molecules, 2021, 26, 5396 CrossRef CAS PubMed.
- J. Kitagawa, N. Ishizu and S. Hamamoto, Materials Research on High-Entropy Alloy Superconductors, in Advances in High-Entropy Alloys – Materials Research, Exotic Properties and Applications, ed., J. Kitagawa, IntechOpen, 2021 DOI:10.5772/intechopen.99693.
- Y. Lu, et al., A Promising New Class of High-Temperature Alloys: Eutectic High-Entropy Alloys, Sci. Rep., 2014, 4, 6200 CrossRef CAS PubMed.
- C. A. Shiffman, J. F. Cochran, M. Garber and G. W. Pearsall, Specific Heat Measurements and Proximity Effects in Tin-Lead Eutectic Alloys, Rev. Mod. Phys., 1964, 36, 127–130 CrossRef CAS.
- J. E. Evetts, A. M. Campbell and D. Dew-hughes, Flux instabilities in hard superconductors, Philos. Mag., 1964, 10, 339–343 CrossRef.
- S. A. Levy, Y. B. Kim and R. W. Kraft, Effect of Structure on the Superconducting Properties of Eutectic Alloys, J. Appl. Phys., 1966, 37, 3659–3665 CrossRef CAS.
- R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford University Press, Oxford, New York, 2005 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |