Open Access Article
Open Access ArticleFirst-principles study of metal and ligand substitution effects on EUV absorption and electron energy loss†
Florian
Brette
,
Vishal
Gupta
and
Geunsik
Lee
 *
*
Department of Chemistry, Center for Superfunctional Materials, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Republic of Korea. E-mail: gslee@unist.ac.kr
First published on 13th March 2025
Abstract
Secondary electrons play a vital role in extreme ultraviolet lithography (EUV-L), as low-energy electrons (LEEs) induce the solubility switch of the photoresist via electron-induced reactions. However, optimizing EUV absorption at 92 eV and addressing the relatively long inelastic mean free path (IMFP) of LEEs, which can lead to pattern blurring, remain critical challenges. Here, first-principles calculations based on time-dependent density functional theory (TDDFT) are conducted to evaluate how chemical substitutions in metal and ligand sites affect both EUV absorption and the energy loss function (ELF) of LEEs in oxalate systems. Results highlight that atomic cross-sections alone are insufficient for optimizing photoabsorption, and electronic structure effects must be considered. Analysis of the ELF of LEEs reveals that iodine-containing systems exhibit a higher ELF at low energies, suggesting a reduced IMFP. Additionally, iodine incorporation shows potential to lower the band gap, which may further reduce the IMFP of LEEs in photoresists. These findings underscore the significance of electronic structure effects in EUV-L and demonstrate the value of first-principles calculations in optimizing photoabsorption and electron behavior for next-generation lithography applications.
1. Introduction
As the demand for smaller feature size increases, extreme ultraviolet lithography (EUV-L) appears as the most promising technology to reach the targeted sub-20 nm resolution.1 EUV-L involves transferring of a pattern from a patterned mask onto a photosensitive material using exposure to EUV light. The interaction of EUV photons with a photoresist is a complex multi-step process, in which an absorbed photon has sufficient energy (92 eV) to ionize a molecule resulting in the emission of the primary photoelectron, which will thus further interact with the photoresist, generating more electrons (secondary electrons).2–5 The ejected electrons (primary and secondary) usually have a kinetic energy range from 0 to 80 eV, depending on the atoms and orbitals involved in the emission process.6 The absorption and emission events hence continue in a cascade manner with the total electron yield suggested to be 2–4 per EUV absorption.5 It is believed that the low-energy electrons (LEEs), with energies below ∼20 eV, are mostly responsible for the solubility switch that leads to nanopattern formation. They achieve this by inducing further ionization and bond scission, which can result in cross-linking.2,7–11 By this multiple processes, EUV-L faces challenges to find a EUV resist with optimal RLS (resolution, line edge roughness, sensitivity) trade-off, regarding EUV absorption and effects of LEEs, while conventional deep ultraviolet lithography seeks for resists with desirable photochemical property.Regarding the sensitivity of the photoresist, previous generation organic photoresists have low absorption cross-section at EUV wavelengths.12 Moreover, EUV contains a much smaller number of photons, less than ten times compared to deep UV of the same power, thus the associated photon shot noise can induce roughness of line pattern.11,13,14 One way to tackle the photon shot noise problem is by the direct utilization of more photons.15 Still, optimizing the absorption of the EUV photon appears critical to make EUV-L cost effective. The common strategy to enhance EUV absorption is simply to incorporate elements with higher atomic cross-section at 92 eV.11,16–22 However, this approach, or the Gelius model, is insufficient to explain the observed dependence on metal–ligand interactions or molecular structure.23 In addition, regarding LEEs for the solubility switch of EUV photoresists, their relatively long inelastic mean free path (IMFP) can contribute to image blur and loss of resolution.24 Assessing the IMFP of these LEEs is crucial for gaining a deeper understanding of EUV-L physics and optimizing future EUV photoresists. However, experimentally determining the IMFP of LEEs remains highly challenging.25–27 Theoretical calculation of IMFP might be helpful, but most are for pure elements.25,28,29 Since the IMFP can be significantly influenced by material-dependent electronic structure details, especially for low-energy below ∼30 eV corresponding to the minimum of the universal curve, it is essential to investigate material dependence beyond the elemental phase.30–34
In this paper, we study the impact of metal and ligand substitutions on the photoabsorption properties and IMFP of LEEs through first-principles calculations. We consider ML2(C2O4) (M = Zr or/and Sn; L = OH, F or/and I) as model systems for two key reasons. First, their crystal structure is relatively simple with two formula units per unit cell, making calculations that include quantum many-body effects feasible. Second, Zr(OH)2(C2O4) has already been synthesized.35 We present our calculation methods in Section 2, followed by our results and discussion in Section 3. Finally, we conclude in Section 4.
2. Calculation methods
The results presented in this work are based on first-principle simulations performed within the framework of density functional theory (DFT) as implemented in the WIEN2k code,36–38 and time-dependent density functional theory (TDDFT) as implemented in the Quantum espresso package (QE).39–43 In the following, the details of our calculations are presented in parallel for (i) electronic structures, (ii) photoelectron spectra (PES), (iii) dielectric functions, and (iv) ELF and IMFP. Prior to those calculations geometry optimization was performed with the projector augmented wave method, as implemented in the Vienna ab initio simulation package (VASP, see Section A.1 in ESI†).39,402.1. Electronic structures
In the framework of DFT, the calculations were performed with the all-electron full potential linearized augmented-plane-wave (FLAPW) using the WIEN2k code. The LAPW treatment implemented in WIEN2k is one of the most accurate methods for electronic structure calculations. Calculations presented in this paper were performed in the scalar relativistic framework. Exchange and correlation effects were treated in the generalized gradient approximation (GGA) using the PBE functional.44 As GGA is known to underestimate the band gap in semiconductor systems, the modified Becke Johnson (mBJ) exchange potential by Tran et al. was used too and the results were systematically compared to the PBE ones.45 The size of the basis set is determined by the product of the smallest atomic sphere radius (R) and the plane-wave cutoff parameter (Kmax), denoted as RKmax. For the calculations, the plane wave basis set was defined using a RKmax value of 4 for systems containing OH bonds (because of the short bond length) and 6.5 for the other cases. The Brillouin zone was sampled using the Monkhorst–Pack scheme,46 and converged calculations were obtained for 8 × a × 8 (with 6 ≤ a ≤ 8, function of the element substitution), k-grid. Bader charge analysis were conducted using the AIM program implemented in the WIEN2k code to quantitively estimate the charge transfers between the different species.47The TDDFT calculations were performed using the plane wave implementation of the QE package with the PBE variant of the GGA functional.42–44 The input files for QE were generated as described in the software manual.43 A plane-wave basis with energy and charge density cutoffs of 60 and 480 Ry, respectively, was used.48 The outermost shell for all species, and additional semi-core (4d for I and Sn, 4p for Zr) were treated as valence electrons. The Brillouin zone was sampled with a 10 × 12 × 12 Monkhorst–Pack grid. As already mentioned by some authors, even if the DFT calculations are over-converged with respect to the grid, a denser grid is necessary to obtain a smooth shape of the response functions.49
2.2. PES using atomic cross-sections
To study the photoabsorption properties of our model structures, we conducted simulations of the valence band spectra for photon energy of 100 eV, using the PES module as implemented in the WIEN2k code.50 The PES module calculates X-ray photoelectron spectra (XPS) by summing over all atomic-orbitals the product of the partial density of states (pDOStl) and excitation-energy-dependent atomic-orbital cross-sections (σtl) (from tables51,52):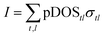 | (1) |
2.3. Dielectric functions
The dielectric function, ε, describes the dielectric responses of a medium to an external perturbation.53,54 For weak perturbations, the linear response function χ (ε = χ + 1) relates the changes of the interacting density to an external perturbation.55 It can be evaluated perturbatively from Kohn–Sham DFT by the solving the Dyson-like screening equation for this operator:49,55| χ = χ0 + χKχ0 | (2) |
Standard DFT is a ground-state theory, thus not strictly applicable to the calculation of excitation energies or other excited-state properties, as opposed to TDDFT which allows the calculation of a dynamic responses of electrons to a time-dependent external perturbation. Still, DFT is often used for the calculation of optical properties and reproduces quite well experimental observations.59,60 Hence, here, we compared the results of the complex dielectric function (ε) by two methods: in the IPA using the OPTIC package as implemented in the WIEN2k code, and TDDFT using the turboEELS code of the QE package.61,62
In the case of the WIEN2k code, using the OPTIC package, the dielectric tensor calculation is performed from the calculated electronic structure. The OPTIC package clearly distinguishes between the optically allowed and forbidden transitions in the IPA using dipole selection rules. It calculates the direct transition (conservating k) between occupied nk and unoccupied n′k states with the probabilities proportional to the square of the momentum matrix element. Hence, in this case, the calculation of optical properties does not go beyond the interpretation of the Kohn–Sham eigenvalues in terms of the band structure.37 The case n = n′ represents intraband optical transitions, while the case n ≠ n′ gives the interband contribution. This formalism is implemented into WIEN2k to compute the imaginary part of the optical dielectric function, ε2(0, ω). The real part, ε1(0, ω), is then determined by a Kramers–Kronig transformation,38,61 enabling the determination of the optical energy-loss function (ELF, q → 0).32
In the case of TDDFT, the conventional approach is to compute the independent-electron susceptibility and then solve the Dyson-like screening equation to obtain the full response function (see eqn (2)). However, this method is computationally expensive as it requires knowledge of many empty states, the inversion and multiplication of large matrices, and must be repeated for each frequency of interest. The turboEELS code of the QE package is based on linearized TDDFpT (time-dependent density functional perturbation theory) and address those drawbacks by expressing the response density matrix as the solution of the linearized quantum Liouville equation and Lanczos recursion algorithm.63–65 The implementations of the Liouville-lanczos approach to TDDFpT are described in the thesis of Rocca and Timrov and the papers associated with the turboTDDFT and turboEELS code.62,63,66,67
2.4. ELF and IMFP
The ELF, which describe the probability of energy-loss ω and momentum-transfer q of an electron traveling through a material, is obtained from the complex dielectric function:32,54,68 | (3) |
 | (4) |
3. Results and discussion
Fig. 1 shows the crystal structure of our system ML2(C2O4) (M = Zr or/and Sn; L = OH, F or/and I). There are four metals atoms and eight ligands in the conventional unit cell of ab face-centered monoclinic (C2/c). The neighboring metal–oxalate chains are linked by two ligands per metal along the c-direction. The lattice parameter and the M–L bond lengths do not notably vary when the metal species is changed, but they significantly increase when OH is substituted by I (see Table S1, ESI†). | ||
| Fig. 1 Crystal structures of ML2(C2O4) in the conventional unit of the monoclinic phase (C2/c), adapted from Thomas et al.35 The green, purple balls denote metal (M), ligand (L), respectively, while brown and red rods denote oxalate (C2O4). In the unit cell (dashed line), there are two kinds of metal–oxalate chains, M1-ox-M4 and M2-ox-M3, and two neighboring chains are linked by two ligands per metal atoms. For crystal structures with varying metal (M = Zr, Sn) and ligand (L = OH, F, I), refer to Fig. S1 (ESI†). For the lattice parameters and bond distances, refer to Table S1 (ESI†). | ||
3.1. Photoabsorption properties and electronic structures
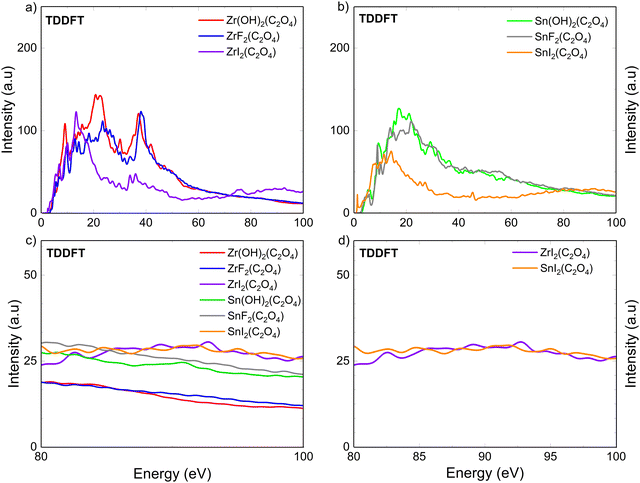
Fig. 2 presents the calculated optical absorption spectra of the Zr(OH)2(C2O4), ZrF2(C2O4), ZrI2(C2O4), Sn(OH)2(C2O4), SnF2(C2O4) and SnI2(C2O4) model systems, from 0 to 100 eV within TDDFT. The results in IPA using the WIEN2k code are shown in Fig. S2 in ESI.† These calculations showcase the influence of the substitution on the photoabsorption properties of our model systems, which can be extended to the analysis of EUV resist. The overall calculated optical absorptions (Fig. 2a and b) are remarkably similar respectively for Zr(OH)2(C2O4) and ZrF2(C2O4), Sn(OH)2(C2O4) and SnF2(C2O4), and ZrI2(C2O4) and SnI2(C2O4). This observation holds for the two levels of theory used (see Fig. S2 in ESI†). From 0 to 70 eV, the optical absorption of iodine containing systems exhibits a lower intensity than those of (OH) and F ligands. This is because the 2p orbitals of OH and F are spatially contracted towards the nuclei compared to the 5p orbitals of I, leading to suppressed cancellation among the dipole matrix elements near the ionization threshold, thus slower decay with increasing photon energy.23 However, for 80 to 100 eV, a clear increase in intensity is observed when iodine is introduced. This increase of intensity (for TDDFT) can be explained as follows. Generally, the absorption peaks are near the binding energy, however, for high value of angular momentum (l ≥ 2) delayed absorption maxima are observed.73 This phenomenon is discussed by Manson et al.74 in the non-Coulombic central potential model and has been theoretically explained as owing to the suppression of the d → f transitions near the threshold, which is caused by the centrifugal barrier potential superimposed on the attractive Coulomb potential.75–78 A systematic comparison between the two approaches reveals that while IPA captures the overall optical absorption trends, it significantly underestimates the delayed absorption maximum near 92 eV. In contrast, TDDFT accurately reproduces the enhanced absorption intensity attributed to the I-4d states. This improvement is evident in the pronounced peak at 92 eV observed in our TDDFT simulations (see Fig. S2 in ESI†). Those combined effects are the cause of the iodine 4d orbital high cross-section at around 90 eV, but are not well accounted for in the IPA (see Fig. S2 in ESI†). Hence, it justifies the need for TDDFT simulations for EUV absorption simulations. The expected maxima of absorption for iodine is experimentally reported at around 90 eV,73,79,80 in consistency with the TDDFT results, and iodine substitution is promising for EUV-L.In Fig. 2c, the absorption is plotted together for six cases for better comparison of the relative intensities. Zr(OH)2(C2O4) and ZrF2(C2O4) present the lowest intensity at 92 eV, followed by Sn(OH)2(C2O4) and SnF2(C2O4), and then ZrI2(C2O4) and SnI2(C2O4).
A common strategy to increase absorption properties is to incorporate elements with high cross-section at 92 eV as mentioned before.11,16–22 However, in Fig. 2c and d we observed that despite the higher cross-section of tin compared to zirconium, SnI2(C2O4) and ZrI2(C2O4) shows the same intensity at 92 eV. To explain the similarity between SnI2(C2O4) and ZrI2(C2O4) a deeper look into the electronic structure is relevant.
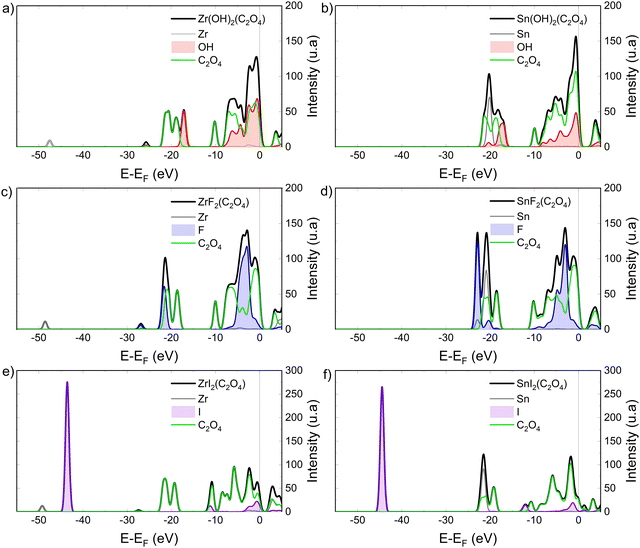
Fig. 3 presents the simulation of the valence band XPS spectra of Zr(OH)2(C2O4), Sn(OH)2(C2O4), ZrF2(C2O4), SnF2(C2O4), ZrI2(C2O4), and SnI2(C2O4), calculated with the PES module implemented in WIEN2k for an unpolarized beam of 100 eV.38,50–52 Density of states (DOS) in the valence band coupled with the energy-dependent cross-section energy, enables to study the electronic structure similarities and/or differences of these systems to better explain the optical absorption properties. First, only considering the F and (OH) ligand, in Fig. 3a–d for Zr(OH)2(C2O4), Sn(OH)2(C2O4), ZrF2(C2O4), SnF2(C2O4), the tin containing model systems present an overall slightly higher intensity. For Sn(OH)2(C2O4) and SnF2(C2O4), the Sn-4d states, at around −22 eV below the Fermi level, are responsible for the increase of optical absorption at around 55 eV in Fig. 2c, due to the same delayed maxima effect observed for the I-4d states.77
This phenomenon leads to the overall increase of the optical absorption intensity, compared to the Zr(OH)2(C2O4) and ZrF2(C2O4) systems. The peak at around −50 eV in the Zr containing systems is due to the Zr-4s semi-core states, and its intensity is far lower than the ones of the I-4d and Sn-4d states, reflecting the low sensitivity of Zr to EUV photons. The same observation can be made for the Zr-4p states at around 27 eV below Fermi level (see Fig. 3a–e).
Compared to the initial Zr(OH)2(C2O4) structure, the substitution of the (OH) groups by iodine leads to an increase of photoabsorption at 92 eV (see Fig. 2d). This is attributed to the I-4d orbital that appears at around −45 eV below Fermi level (Fig. 3e). The high intensity of this peak compared to the others features originates from the high DOS (five atomic orbitals) in this energy range (localized states) together with the high cross-section at 100 eV (∼92 eV). The same observation is made in Fig. 3f, for the SnI2(C2O4) systems. Still, the Sn-4d are present too at around −22 eV below Fermi level. Thus, an enhanced intensity at 92 eV for SnI2(C2O4) compared to ZrI2(C2O4) is expected when one considers only the atomic cross-section. To explain the unexpected phenomena of the comparable optical absorption intensity between ZrI2(C2O4) and SnI2(C2O4) (Fig. 2d) we discuss the Bader charge of the metal element in the model systems.
In Fig. 2, two main differences are observed for the optical absorption spectra between the iodine containing systems and the (OH)/F containing systems. First, below around 70 eV, the optical absorption intensities of ZrI2(C2O4) and SnI2(C2O4) are lower than those of the other four cases, especially above 15 eV. Second, the optical absorption above 80 eV, and particularly at 92 eV, seems to be only dependent on the iodine cross-section in ZrI2(C2O4) and SnI2(C2O4), as there are no differences of optical absorption intensity between the two (see Fig. 2d), whereas it depends on the nature of the metal element for the four other systems. Both observations are related to each other and originate from the effects of underlying geometrical and electronic structures. The lower optical absorption intensity for the iodinated systems, below 70 eV (Fig. 2a and c), may be related to the reduction of orbital overlap between iodine and tin (or zirconium), as compared to with (OH) or F ligands. Indeed, there is less charge transfer between the metallic element and I, than for (OH) and F, as evidenced by the calculated Bader charge in Table 1, which further supports this argument.81 Likewise, the similar optical absorption intensity of ZrI2(C2O4) and SnI2(C2O4) above 80 eV may be explained from charge transfer considerations. The shape resonance of the I-4d and Sn-4d states, which is characterized by an increase of cross-section, depends strongly upon the electronic configuration, the geometry and the chemical environment, all of which can, to some extent, be captured by the Bader charge description.23,82 Therefore, because the Sn atoms in SnI2(C2O4) have more electrons than those in Sn(OH)2(C2O4) and Sn(F)2(C2O4), we propose that the relatively similar response observed between the two iodine containing systems can, in part, be attributed to the reduced orbital overlap between Sn and I atoms in SnI2(C2O4). This explanation is in good agreement with the longer bond distance observed for Sn–I (see Table S1, ESI†) as well as the reduced Bader charge of the Sn atoms.
| ML2(C2O4) | PBE gap value (eV) | mBJ gap value (eV) | Bader charge of the metal element (qe) |
|---|---|---|---|
| Zr(OH)2(C2O4) | 3.31 [0.0%] | 4.72 [0.0%] | 2.67 |
| ZrF2(C2O4) | 3.19 [−3.6%] | 4.83 [+2.3%] | 2.79 |
| ZrI2(C2O4) | 2.24 [−32.2%] | 3.17 [−32.8%] | 2.26 |
| Sn(OH)2(C2O4) | 2.55 [−23%] | 4.58 [−3.0%] | 2.51 |
| SnF2(C2O4) | 2.33 [−29.6%] | 4.59 [−2.8%] | 2.66 |
| SnI2(C2O4) | 0.98 [−70.4%] | 1.82 [−61.4%] | 1.61 |
To illustrate this point, we conducted calculations in SnI2(C2O4) structure with atomic substitution of the I atoms by F atoms (without allowing the structure to relax). Thus, the Sn–F bond length of the substituted system, denoted as Sn[I− > F]2(C2O4), is greatly increased compared to the Sn(F)2(C2O4) (from an average of 2.12 Å to 2.93 Å). Hence the charge transfer between the Sn and F atoms is modified. The calculated Bader charge of the Sn atoms in Sn[I− > F]2(C2O4) is 1.83qe, which is lower than the 2.66qe Bader charge of the tin in Sn(F)2(C2O4), and more comparable to the Bader charge of the Sn atoms in SnI2(C2O4) (1.61qe see Table 1). This difference in charge transfer (or orbital overlap here), strongly influences the optical absorption spectra. The optical absorption spectra of Sn[I− > F]2(C2O4) is shown in Fig. S2 in ESI.† It is overall similar to the absorption spectra of SnI2(C2O4), minus the absorption enhancement by the I-4d states. Increasing the Sn–F bond length, which decreases the orbital overlap, drastically reduces the optical absorption. This effect is well accounted for using the Bader charge as descriptor. It confirms that the lower optical absorption in SnI2(C2O4) is mainly due to a decrease of the orbital overlap between Sn and I, in contrast that Sn(F)2(C2O4) exhibits clear hybridization between the Sn-p (and Sn-d) and F-p with substantial orbital overlap (see Fig. S3, ESI†).
TDDFT framework has been shown to accurately describe electronic structure effects, where IPA which ignores electron–electron interactions fails to describe it.83 For example, screening effects have been observed in optical absorption spectra of transition metal, with TDDFT calculations well reproducing the experimental data.84 The underlying process is known as the local field effect, and strongly support the use of TDDFT simulations in our work to account for many-body effects.
These results evidence that simply considering the atomic cross-section of the different elements of a system to optimize the optical absorption for EUV-L is insufficient. Interplay between chemical, structural and electronic structure, as well as the consideration of many-body effects, needs to be considered for the optimization of future EUV photoresist materials.
3.2. LEEs ELF analysis and qualitative IMFP discussion
Beside the optimization of the optical absorption at 92 eV, the travel of LEEs in the photoresist is of major importance. While LEEs are primordial to the electron-induced reaction in EUV-L their high IMFP may lead to blur in practical applications. Nevertheless, not much is said for very low-energy electrons for which the IMFP is known to drastically increase. This quantity is particularly important and it has been shown that the distribution of low energy electron inside the photoresist (for energy below the vacuum barrier), which is representative of the multiplication cascade of the low energy electrons, can exhibit faster increase than exponential with decreasing kinetic energy.85 While some Monte-Carlo simulation of the IMFP of low-energy electron exists, they suffer some drawback as they may not take into account all possible considerations to obtain reliable IMFP.86 Experimentally, it has been shown that for energy about below 100 eV, the elastic reflectivity from surface no longer agree quantitatively with atomic cross section.87 Thus while the cross-section defines the probability of a scattering event at a given energy, and may be the dominant factor for medium energy (>100 eV), considering the band structure appears indispensable at low energies. Hence, the dielectric functions in Zr(OH)2(C2O4), ZrF2(C2O4), ZrI2(C2O4), Sn(OH)2(C2O4), SnF2(C2O4) and SnI2(C2O4) were calculated within the DFT and the TDDFT frameworks, to study the ELF of LEEs in model systems, and thus infer possible trend on the IMFP dependence on the electron energy.We compared the ELF results by the IPA and the TDDFT (obtained using the QE code) methods, as shown in Fig. 4 in ESI,† and found that the overall shape is very similar between the two methods, in contrast with the calculated optical absorption at 92 eV. Here, we specifically focus on the low-energy region below 20 eV for two reasons; (i) the universal IMFP curve of Seah and Dench show that the minima for the IMFP are in the range of around 20 to 100 eV, and increase below.88 (ii) The low-energy electrons involved in electron-induced reaction possess on average an energy below 20 eV.9,24,89 The DFT calculated ELF with WIEN2k appears to present more detailed features, which is due to the ease of convergence compared to the TDDFT simulations. Still, as discussed below, the main features of the spectra are consistently observed for the two levels of theory. Therefore, here, despite DFT being a ground-state theory, and thus not strictly applicable to the calculation of excitations energies or other excited-state properties, the influence of the exchange–correlation kernel included in TDDFT is not significant in our ELF analysis. We note that the long-range Coulomb interaction is more important for energy loss.90 Thus, we discuss the ELF of LEEs from a standard DFT framework.41
Fig. 4a and b present the calculated ELF within the IPA using the WIEN2k code for the Zr and the Sn containing model systems, respectively.
From Fig. 4a, the optical absorption properties, Zr(OH)2(C2O4) and ZrF2(C2O4) show similar LEEs ELF spectra, while ZrI2(C2O4) is drastically different. The same holds for the Sn containing systems (Fig. 4b). For each of ZrI2(C2O4) and SnI2(C2O4), the ELF spectrum exhibits a shift to lower energy, owing to a reduced band gap (see Table 1), and an increase of intensity, as compared to the other four cases. Considering that the IMFP of electron in a medium is inversely proportional to the ELF, the fact that the EFL of ZrI2(C2O4) and SnI2(C2O4) are shifted to lower energy and higher in intensity, makes iodine quite interesting to reduce LEEs’ IMFP and thus enhance the resolution for EUV-L applications.
From the theoretical point of view, the ELF in the dielectric description reflects optical transition above the band gap. To study the origin of the desirable ELF feature of the iodinated systems a deeper look into the detail of the complex dielectric function and the project density of states (pDOS) near the Fermi level is relevant (see Fig. 5 and 6). The information about the real part and the imaginary part of the dielectric function can be very useful for the analysis of the ELF (see eqn (3)). The static dielectric function, ε(0), which corresponds to the value of the real part at 0 eV, is higher for the iodinated systems. It is relatively high for ZrI2(C2O4) compared to the other systems and is the greatest for SnI2(C2O4) (see Fig. 5) following an overall trend of higher static dielectric function for smaller band gap value.91
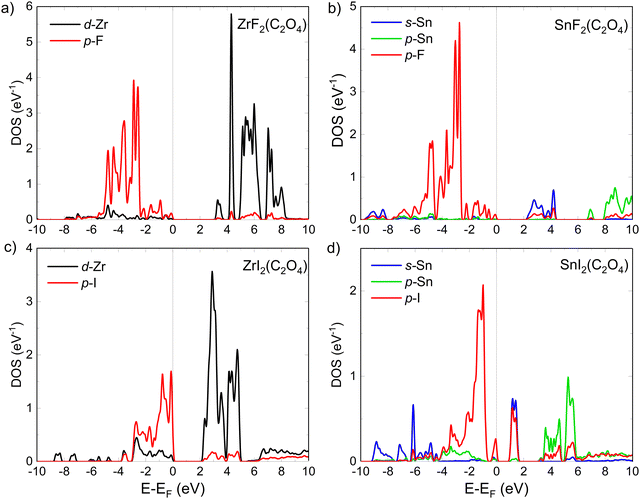 | ||
| Fig. 6 Relevant pDOS of (a) ZrF2(C2O4), (b) SnF2(C2O4), (c) ZrI2(C2O4) and (d) SnI2(C2O4) calculated with the WIEN2k code using the PBE exchange–correlation functional. | ||
The imaginary part of the complex dielectric function (blue lines in Fig. 5), describes the electronic transitions across the energy gap from the valence band to the conduction band.54 The intensity of the first (main) absorption peaks observed in Fig. 5 clearly correlate with the calculated band gap value in Table 1, where the peak intensity becomes stronger for the lower band gap. The imaginary part of the dielectric function exhibits dependence on the nature of the ligand groups in the systems. For the (OH) groups, it first presents a quite broad and flat region, from around 4 to 6 eV in Zr(OH)2(C2O4) and Sn(OH)2(C2O4), followed by a higher absorption region (especially for Zr(OH)2(C2O4)) between around 7 to 10 eV. The broad peak in the imaginary part of the dielectric function of Zr(OH)2(C2O4) (Fig. 5a) is clearly related to the broad peak in the ELF at around 10 eV (Fig. 4a). It is a well-known fact that the features in the imaginary part of the dielectric function and the ELF does not coincide, and this difference arises from the denominator of the ELF.53 It is however still possible to unambiguously identify features in the ELF from electronic transitions shown in the imaginary part of the dielectric function. The imaginary part of the dielectric function of ZrF2(C2O4) and SnF2(C2O4) (Fig. 5c and d) are less similar, but both present a higher first absorption peak compared to the (OH) systems. In the iodinated systems, the first absorption peak is the highest in intensity. ZrI2(C2O4) presents a broad and intense absorption peak at an energy matching the band gap, while SnI2(C2O4) presents a sharp peak. This sharp peak is clearly observed in the ELF of SnI2(C2O4) (see Fig. 4).
The low-energy loss region contains low-energy interband transitions of single electrons, and collective oscillation of the conduction electrons (i.e., plasmons).92,93 For the interband transition, the initial states of those are located close to the Fermi level. Thus, to get insights on what causes the differences in the complex dielectric function and the ELF between iodinated and fluorinated systems, we calculated the pDOS for our model structures (see Fig. 6).94 Because the photoabsorption properties as well as ELF of the LEEs are strongly similar between the systems with (OH) groups and F atoms, we reduced the comparison to fluorinated systems here. In ZrF2(C2O4), the first absorption peak of ε2 in Fig. 5c is associated with electronic transition from F-p to Zr-d states (Fig. 6a), while for SnF2(C2O4) the first absorption peak in Fig. 5d is attributed to the transition from F-p to Sn-s states (Fig. 6b). In both systems, in the valence band the F-p intensity are quite similar, however, in the conduction band the Sn-s intensity for SnF2(C2O4) are far lower than the Zr-d for ZrF2(C2O4). Despite this, the intensities of the absorption peaks (Fig. 5) are similar in both systems. This is because the electronic transitions calculated from the electronic structure or the joint DOS are weighted by the transition probability, thus only analyzing the pDOS is not enough to discuss the absorption peak intensity.95 Nevertheless, the intensity of the absorption peaks in Fig. 5 are strongly dependent on the band gap size.
Despite ZrF2(C2O4) presenting a higher intensity in the valence band from the F-p states, compared to the I-p states in ZrI2(C2O4), and with the conduction bands dominated by Zr-d in both cases, the absorption peaks are more intense in ZrI2(C2O4) (see Fig. 5c and e) exhibiting the smaller band gap (see Table 1). The same observation is made for SnI2(C2O4), where the pDOS intensity (only for Sn and I in Fig. 6d) in the valence and the conduction band is drastically smaller, but it presents the higher intensity of absorption peak (Fig. 5f), following a reduced band gap. Moreover, a strong hybridization between the I-p and Sn-s states in the conduction band of SnI2(C2O4) is noticed, which may contribute to the higher absorption peak intensity.96
In the Zr-based oxalate system, iodine substitution shifts the Fermi level upward, which reduces the band gap. At the same time, the Zr-d states in the valence band are shifted closer to the Fermi level, which correlates with an increased ELF at low energy. In the Sn-based oxalate system, a similar Fermi level shift and band gap reduction occur; however, the effect is further amplified by the mixing between the I-p and Sn-s orbitals in the conduction band. This additional hybridization, combined with the higher electron count in Sn relative to Zr, not only lowers the band gap further but also increases the density of conduction states available for low-energy transitions. As a result, the ELF at low energies is more enhanced in SnI2(C2O4) than in ZrI2(C2O4). These observations highlight the interplay between metal and ligand substitution and illustrate how ligand orbitals modify the conduction band, hence shaping the electronic structure and optical properties of these oxalate-based photoresists.
Table 1 presents the calculated gap value in our different model structures either using the PBE or the mBJ functional. First, regarding the effect of the exchange correlation functional used: as GGA PBE is known to underestimate the band gap in semiconductors, we observe a systematic increase of the band gap value using the mBJ functional. The use of the mBJ in this study is motivated by the fact that it had been shown to improve the band gap value for calculation specifically focused on optoelectronic properties in various semiconductors.97–104 Using the mBJ functional, Nakano and Sakai calculated the optical band gap of 70 semiconductors and determined that the calculated bandgaps and the optical constant agree well with the experimental value (to within 0.440 eV for the bandgaps), which strongly support the use of the mBJ functional in our study.105 Other studies suggest that on average the use of the mBJ does estimate band gap value better than other sophisticated theories, which are computationally orders of magnitude more expensive such as the HSE06 functional.45,106,107 We note that, while some confirm that mBJ is one of the most accurate functionals for band gap calculations, the mBJ functional underestimates bandwiths.108–110
For the Zr containing model systems, by the PBE functional, a decrease of the gap value is observed when (OH) groups are substituted by iodine, with ZrI2(C2O4) presenting the smallest gap value (Table 1). This trend is mainly due to the reduced difference in the electronegativity between the Zr cation and the ligand, consistent with the work of Zitouni et al. where a decrease of the band gap was observed for different percentage of iodine doping in CsPbBr3−x (x = 0, 22 and 33% of iodine).111 The same trend of band gap reduction is observed when Zr is substituted by Sn, which may be explained as a gradual filling of the sp hybrid orbitals with the increasing number of valence electrons, thus shifting the Fermi energy level to higher energy and therefore reducing the gap value. Consequently SnI2(C2O4) presents the smallest calculated band gap value. Using the mBJ functional, an increase of every band gap value is observed as compared to the PBE scheme, owing to a systematic shift of the band above the Fermi level to higher energy.112,113 The difference of band gap between the different model systems as a function of the substitution is however less significant with the mBJ functional. Particularly for Sn(OH)2(C2O4) and SnF2(C2O4) the differences in gap value are respectively of −23% and −29.6% in PBE and only −3.0% and −2.8% with the mBJ functional.
Moreover, the calculated Bader charge analysis provides an indirect measurement of the metal's reducibility. Although our study is limited to Zr and Sn-based oxalate systems, the calculated Bader charges correlate with the band gap values, with lower charges indicating a more readily reduced metal center. This finding is in qualitative agreement with the experimental observations of Grzeskowiak et al. who reported that metal oxalate resists with more easily reduced centers (i.e. Co as compared to Cr and Fe) exhibit significantly higher sensitivity, evidenced by enhanced CO2 outgassing, despite only minimal differences in EUV absorption (due to the low concentration of metal atoms).114 Thus, our results suggest that the reducibility of the metal center, as reflected by Bader charge analysis, might be important in determining the overall sensitivity of EUV resists.
The band gap value is of primordial importance for EUV-L application. From the physical point of view, a larger band gap means that electrons need more energy for transition from the valence to the conduction band, resulting in fewer available levels for inelastic scattering process. As a result a larger band gap typically leads to an increased IMFP.87 In this regards, the possibility to reduce the band gap by introducing iodine atoms thus seems promising for EUV-L.
Following our studies on the electronic structure and optical absorption properties of Zr(OH)2(C2O4), ZrF2(C2O4), ZrI2(C2O4), Sn(OH)2(C2O4), SnF2(C2O4) and SnI2(C2O4), we estimated the IMFP of LEEs using the optical ELF calculated with the mBJ functional. Here we used the formula  providing a qualitative interpretation of the substitution effects on the IMFP. As previously discussed, calculation of IMFP from the optical ELF implied to reconstruct the q dependent ELF, which lead to a lot of discrepancies in the literature. Moreover, as a first approximation it seems reasonable to assume that higher q value simply lowers the ELF intensity and shift the features to higher energy.71,115 Hereafter, we qualitatively discuss the IMFP to assess the substitution effects and decipher electronic structure effects. Fig. 7a presents an estimated qualitative ‘optical’ IMFP for the Zr containing systems. As the IMFP is proportional to the inverse of the ELF, observations made on the ELF still hold. Hence, with our approach it is observed that a smaller band gap value greatly reduces the IMFP of LEEs. In Fig. 7a, which presents qualitative IMFP of Zr(OH)2(C2O4), ZrF2(C2O4) and ZrI2(C2O4), the smaller band gap of the iodinated systems (Table 1) is responsible for the shift to lower energy, compared to the other two systems, thus reducing the IMFP of LEEs. This drastic effect is observed because the dependence of IMFP on ELF is greatly enhanced for low energy regions.
providing a qualitative interpretation of the substitution effects on the IMFP. As previously discussed, calculation of IMFP from the optical ELF implied to reconstruct the q dependent ELF, which lead to a lot of discrepancies in the literature. Moreover, as a first approximation it seems reasonable to assume that higher q value simply lowers the ELF intensity and shift the features to higher energy.71,115 Hereafter, we qualitatively discuss the IMFP to assess the substitution effects and decipher electronic structure effects. Fig. 7a presents an estimated qualitative ‘optical’ IMFP for the Zr containing systems. As the IMFP is proportional to the inverse of the ELF, observations made on the ELF still hold. Hence, with our approach it is observed that a smaller band gap value greatly reduces the IMFP of LEEs. In Fig. 7a, which presents qualitative IMFP of Zr(OH)2(C2O4), ZrF2(C2O4) and ZrI2(C2O4), the smaller band gap of the iodinated systems (Table 1) is responsible for the shift to lower energy, compared to the other two systems, thus reducing the IMFP of LEEs. This drastic effect is observed because the dependence of IMFP on ELF is greatly enhanced for low energy regions.
From around 7 to 10 eV, the IMFP of ZrI2(C2O4) becomes higher than the IMFP of Zr(OH)2(C2O4), ZrF2(C2O4). This observation is explained when one looks at the pDOS of ZrI2(C2O4) in Fig. 6c, and comes from the lack of I-p states below 4 eV. Thus, it provides direct correlation between the electronic structure and the IMFP. Overall, ZrI2(C2O4) shows a lower IMFP. The same observation is made for Sn(OH)2(C2O4), SnF2(C2O4) and SnI2(C2O4) in Fig. 7b, where the substitution by iodine atoms greatly reduces the gap value (Table 1). Thus, this proves once again the interest of iodine for the possible control of blur in EUV-L application, as it leads to reduced IMFP at low-energy.
3.3. Possible additional consideration below the band gap (electron–phonon coupling)
We note that at very low energy the scattering processes other than electron–electron interaction may need to be considered to obtain an accurate value of the electron mean free path.116,117 One possible mechanism at very low electron energies is the process of phonon creation.117 In addition to modifying the electron energy levels in solids, the electron–phonon interaction plays an important role in the optical properties of semiconductors and insulator, as it is responsible for phonon-assisted transitions.118 Combining the dielectric models associated with electron and photon scatterings, Bhattarai et al., showed that at very low-energy (less than 10 eV) the total IMFP may follow the path limited mainly by phonon excitation; i.e., a dramatic reduction of the IMFP would be observed.116It is to be noted, however, that for the IMFP of copper, calculations using DFT ELF reproduce well the one calculated from experimental ELF without the need to consider electron–phonon interaction.68 Moreover, the predicted drastic decrease of IMFP, when phonon creation process are considered, is not present in the experiments.88 Thus here these material specific effect were not considered, but should certainly be accounted for in practical EUV-L application.
4. Conclusions
As a summary, we have demonstrated the need of considering electronic structures for the development of new photoresist material in EUV-L applications. From the experimentally synthesized material Zr(OH)2(C2O4), we substituted metal Zr and ligand OH to obtain model systems (ZrF2(C2O4), ZrI2(C2O4), Sn(OH)2(C2O4), SnF2(C2O4) and SnI2(C2O4)) as a means to decipher electronic structures effects on optical properties, specifically the photoabsorption of EUV photon and the ELF of LEEs. Calculations were performed in the framework of DFT and TDDFT, using the PBE and the mBJ exchange correlation functional. For the optical absorption properties, we highlight the difference obtained in the IPA and in TDDFT, making the use of TDDFT mandatory for the simulation of optical absorption of EUV photons. We show that the optical absorption of EUV photon may not be predicted by atomic cross-section and that additional many-bodies effects (encompassed in TDDFT) should be considered. Optical absorption properties at 92 eV of ZrI2(C2O4) and SnI2(C2O4) are similar, despite the drastically higher cross-section at 92 eV of Sn compared to Zr. On the other side, for ELF of LEEs, we show that DFT calculations are sufficient to reproduce the TDDFT results in low energy range. This makes the WIEN2k code a tool of choice, as its full potential all electron approach is extremely precise for the determination of electronic density of states. We further discuss the calculated ELF by analyzing the complex dielectric function and the pDOS of the model systems. Lastly, we discuss the effect of iodine on the band gap value of our model systems, using the mBJ exchange correlation functional, well adapted for the calculation of band gap in semiconductors, and show a decrease of the gap value.Among the main results, iodine emerges as a promising candidate for EUV photoresists, as it enhances the photoabsorption, increases the ELF of LEEs, and reduces the band gap value. Thus, lowering the IMFP of LEEs, hence potentially reducing the blur in EUV-L applications. It is important to acknowledge that the present study focuses on bulk properties of the model oxalate-based materials. In practical EUV lithography, however, photoresists are typically employed as thin films that may experience surface oxidation, contamination, or other ambient effects, which can alter the dielectric function, ELF, and ultimately the IMFP. Future investigations should extend this computational framework to include slab models and explicit surface treatments to capture these phenomena, thereby enabling a more accurate prediction of performance under industrial conditions.
Beyond the element dependent results, these first-principles simulations of optical properties highlight the need to consider electronic structures for EUV photoresist design. Although commercial EUV resists typically consist of more complex metal–organic hybrids or inorganic clusters, the fundamental electronic structures effects discussed here are expected to persist in more complex materials. Thus, the trends observed in our model systems provide valuable guidelines that can be extrapolated to more industrially relevant EUV resists. Hence, our findings, which emphasize the physical perspective of EUV exposure, are particularly significant for optimizing new EUV photoresists in a field that has so far been primarily focused on the chemical aspects of the EUV-L process.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Research Foundation of Korea (2021M3H4A1A02055684, RS-2023-00257666, RS-2024-00508578) funded by the Korea government (MSIT). We acknowledge the supercomputing resources including technical support from the National Supercomputing Center KISTI (KSC-2024-CRE-0482, KSC-2024-CRE-0201).References
- R. Md, M. Hasan and X. Luo, Nanomanuf. Metrol., 2018, 1, 67–81 CrossRef.
- T. Kozawa and S. Tagawa, Jpn. J. Appl. Phys., 2010, 49, 030001 CrossRef.
- N. Mark, K. Cho and K. Petrillo, J. Photopol. Sci. Technol., 2012, 25, 87–94 CrossRef.
- C. K. Ober, F. Käfer and C. Yuan, Polymer, 2023, 280, 126020 CrossRef CAS.
- A. Narasimhan, L. Wisehart, S. Grzeskowiak, L. E. Ocola, G. Denbeaux and R. L. Brainard, J. Photopol. Sci. Technol., 2017, 30, 113–120 CrossRef CAS.
- R. Brainard, E. Hassanein, J. Li, P. Pathak, B. Thiel, F. Cerrina, R. Moore, M. Rodriguez, B. Yakshinskiy, E. Loginova, T. Madey, R. Matyi, M. Malloy, A. Rudack, P. Naulleau, A. Wüest and K. Dean, Proc. SPIE, 2008, 6923, 692325 CrossRef.
- I. Bespalov, Y. Zhang, J. Haitjema, R. M. Tromp, S. J. Van Der Molen, A. M. Brouwer, J. Jobst and S. Castellanos, ACS Appl. Mater. Interfaces, 2020, 12, 9881–9889 CrossRef CAS.
- J. Torok, R. D. Re, H. Herbol, S. Das, I. Bocharova, A. Paolucci, L. E. Ocola, C. Ventrice Jr., E. Lifshin, G. Denbeaux and R. L. Brainard, J. Photopol. Sci. Technol., 2013, 26, 625–634 CrossRef CAS.
- C. R. Arumainayagam, H.-L. Lee, R. B. Nelson, D. R. Haines and R. P. Gunawardane, Surf. Sci. Rep., 2010, 65, 1–44 CrossRef CAS.
- B. A. Naqvi, S. Enomoto, K. Machida, Y. Takata, T. Kozawa, Y. Muroya, S. De Gendt and D. De Simone, Chem. Mater., 2024, 36, 1459–1471 CrossRef CAS.
- G. Lim, K. Lee, S. Choi and H. J. Yoon, Coord. Chem. Rev., 2023, 493, 215307 CrossRef CAS.
- X. Wang, P. Tao, Q. Wang, R. Zhao, T. Liu, Y. Hu, Z. Hu, Y. Wang, J. Wang, Y. Tang, H. Xu and X. He, Mater. Today, 2023, 67, 299–319 Search PubMed.
- R. L. Brainard, P. Trefonas, J. H. Lammers, C. A. Cutler, J. F. Mackevich, A. Trefonas and S. A. Robertson, Proc. SPIE, 2004, 5374, 74 Search PubMed.
- H. J. Levinson, Jpn. J. Appl. Phys., 2023, 62, SG0802 CrossRef CAS.
- J. Stowers, J. Anderson, B. Cardineau, B. Clark, P. De Schepper, J. Edson, M. Greer, K. Jiang, M. Kocsis, S. Meyers, A. Telecky, A. Grenville, D. De Simone, W. Gillijns and G. Vandenberghe, Proc. SPIE, 2016, 9779, 977904 Search PubMed.
- K. D. Closser, D. F. Ogletree, P. Naulleau and D. Prendergast, J. Chem. Phys., 2017, 146, 164106 CrossRef PubMed.
- R. Fallica, J. Haitjema, L. Wu, S. C. Ortega, A. M. Brouwer and Y. Ekinci, J. Micro/Nanolithogr., MEMS, MOEMS, 2018, 17, 023505 Search PubMed.
- D. De Simone, Y. Vesters and G. Vandenberghe, Adv. Opt. Technol., 2017, 6, 163–172 CrossRef CAS.
- B. G. Ghule, M. Kim and J. Jang, Bull. Korean Chem. Soc., 2023, 44, 900–910 CrossRef CAS.
- S. M. Lewis, H. R. Alty, M. Vockenhuber, G. A. DeRose, A. Fernandez-Mato, D. Kazazis, P. L. Winpenny, R. Grindell, G. A. Timco, A. Scherer, Y. Ekinci and R. E. P. Winpenny, J. Micro/Nanolithogr., MEMS, MOEMS, 2022, 21, 041404 CAS.
- C. Luo, C. Xu, L. Lv, H. Li, X. Huang and W. Liu, RSC Adv., 2020, 10, 8385–8395 RSC.
- L. Wu, M. Tiekink, A. Giuliani, L. Nahon and S. Castellanos, J. Mater. Chem. C, 2019, 7, 33–37 Search PubMed.
- J. C. Green and P. Decleva, Coord. Chem. Rev., 2005, 249, 209–228 CrossRef CAS.
- W. F. Van Dorp, Frontiers of Nanoscience, Elsevier, 2016, vol. 11, pp. 115–133 Search PubMed.
- H. T. Nguyen-Truong, Appl. Phys. Lett., 2016, 108, 172901 CrossRef.
- J. D. Bourke and C. T. Chantler, Phys. Rev. Lett., 2010, 104, 206601 CrossRef CAS.
- R. Fallica, N. Mahne, T. Conard, A. Vanleenhove, D. De Simone and S. Nannarone, ACS Appl. Mater. Interfaces, 2023, 15, 35483–35494 CrossRef CAS.
- H. T. Nguyen-Truong, J. Electron Spectrosc. Relat. Phenom., 2014, 193, 79–85 CrossRef CAS.
- D.-N. Le and H. T. Nguyen-Truong, J. Phys. Chem. C, 2021, 125, 18946–18951 CrossRef CAS.
- C. T. Chantler and J. D. Bourke, Ultramicroscopy, 2019, 201, 38–48 CrossRef CAS.
- P. De Vera and R. Garcia-Molina, J. Phys. Chem. C, 2019, 123, 2075–2083 CrossRef CAS.
- J. D. Bourke and C. T. Chantler, J. Electron Spectrosc. Relat. Phenom., 2014, 196, 142–145 CrossRef CAS.
- D. Emfietzoglou, I. Kyriakou, R. Garcia-Molina and I. Abril, Surf. Interface Anal., 2017, 49, 4–10 CrossRef CAS.
- M. A. Flores-Mancera, J. S. Villarrubia and G. Massillon-JL, ACS Omega, 2020, 5, 4139–4147 Search PubMed.
- R. Thomas, P. Devaux, M. Rivenet, N. Henry and F. Abraham, ACS Omega, 2020, 5, 21260–21270 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 18 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 18 Search PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 Search PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- L. Lanzetta, T. Webb, N. Zibouche, X. Liang, D. Ding, G. Min, R. J. E. Westbrook, B. Gaggio, T. J. Macdonald, M. S. Islam and S. A. Haque, Nat. Commun., 2021, 12, 2853 CrossRef CAS.
- D. A. Leon, C. Elgvin, P. D. Nguyen, Ø. Prytz, F. S. Hage and K. Berland, arXiv, 2024, preprint, arXiv:2403.08385, https://arxiv.org/abs/2403.08385.
- M. Bagheri and P. Blaha, J. Electron Spectrosc. Relat. Phenom., 2019, 230, 1–9 CrossRef CAS.
- M. B. Trzhaskovskaya, V. K. Nikulin, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2006, 92, 245–304 CrossRef CAS.
- M. B. Trzhaskovskaya, V. I. Nefedov and V. G. Yarzhemsky, At. Data Nucl. Data Tables, 2001, 77, 97–159 CrossRef CAS.
- P. Schattschneider, Ultramicroscopy, 1989, 28, 1–15 CrossRef.
- H. Kuzmany, Solid-State Spectroscopy, Springer Berlin Heidelberg, Berlin, Heidelberg, 1998 Search PubMed.
- T. Sander and G. Kresse, J. Chem. Phys., 2017, 146, 064110 CrossRef PubMed.
- X. Blase, I. Duchemin and D. Jacquemin, Chem. Soc. Rev., 2018, 47, 1022–1043 RSC.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- V. Mauchamp, G. Hug, M. Bugnet, T. Cabioc’h and M. Jaouen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 035109 CrossRef.
- T. Bilyk, H.-W. Hsiao, R. Yuan, M. Benchakar, A. Habrioux, S. Célérier, J.-M. Zuo, J. Pacaud and V. Mauchamp, 2D Mater., 2022, 9, 035017 CrossRef CAS.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- I. Timrov, N. Vast, R. Gebauer and S. Baroni, Comput. Phys. Commun., 2015, 196, 460–469 CrossRef CAS.
- I. Timrov, Ecole Polytechnique X, 2013 Search PubMed.
- D. Rocca, R. Gebauer, Y. Saad and S. Baroni, J. Chem. Phys., 2008, 128, 154105 CrossRef.
- B. Walker and R. Gebauer, J. Chem. Phys., 2007, 127, 164106 CrossRef.
- D. Rocca, Scuola Internazionale Superiore di Studi Avanzati, 2007 Search PubMed.
- O. B. Malcıoğlu, R. Gebauer, D. Rocca and S. Baroni, Comput. Phys. Commun., 2011, 182, 1744–1754 CrossRef.
- C. T. Chantler and J. D. Bourke, J. Phys. Chem. A, 2014, 118, 909–914 CrossRef CAS PubMed.
- D. R. Penn, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 482–486 CrossRef CAS.
- B. Da, X. Liu, L. H. Yang, J. M. Gong, Z. J. Ding, H. Shinotsuka, J. W. Liu, H. Yoshikawa and S. Tanuma, J. Appl. Phys., 2022, 131, 175301 CrossRef CAS.
- H. T. Nguyen-Truong, J. Phys.: Condens. Matter, 2017, 29, 215501 CrossRef.
- H. T. Nguyen-Truong, B. Da, L. Yang, Z. Ding, H. Yoshikawa and S. Tanuma, Appl. Phys. Lett., 2020, 117, 033103 CrossRef CAS.
- L. Nahon, A. Svensson and P. Morin, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 2328–2337 CrossRef CAS.
- S. T. Manson and J. W. Cooper, Phys. Rev., 1968, 165, 126–138 CrossRef CAS.
- U. Fano and J. W. Cooper, Rev. Mod. Phys., 1968, 40, 441–507 CrossRef CAS.
- J. W. Cooper, Phys. Rev. Lett., 1964, 13, 762–764 CrossRef CAS.
- in Giant Resonances in Atoms, Molecules, and Solids, ed. J. P. Connerade, J. M. Esteva and R. C. Karnatak, Springer US, Boston, MA, 1987, vol. 151 Search PubMed.
- J. A. D. Matthew, Contemp. Phys., 1993, 34, 89–98 CrossRef CAS.
- F. J. Comes, U. Nielsen and W. H. E. Schwarz, J. Chem. Phys., 1973, 58, 2230–2237 CrossRef CAS.
- D. W. Lindle, P. H. Kobrin, C. M. Truesdale, T. A. Ferrett, P. A. Heimann, H. G. Kerkhoff, U. Becker and D. A. Shirley, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 239–244 CrossRef CAS.
- R. F. W. Bader, D. Bayles and G. L. Heard, J. Chem. Phys., 2000, 112, 10095–10105 CrossRef CAS.
- C. W. Clark and T. B. Lucatorto, in Giant Resonances in Atoms, Molecules, and Solids, ed. J. P. Connerade, J. M. Esteva and R. C. Karnatak, Springer US, Boston, MA, 1987, pp. 137–151 Search PubMed.
- in Fundamentals of Time-Dependent Density Functional Theory, ed. M. A. L. Marques, N. T. Maitra, F. M. S. Nogueira, E. K. U. Gross and A. Rubio, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, vol. 837 Search PubMed.
- M. Volkov, S. A. Sato, F. Schlaepfer, L. Kasmi, N. Hartmann, M. Lucchini, L. Gallmann, A. Rubio and U. Keller, Nat. Phys., 2019, 15, 1145–1149 Search PubMed.
- R. Fallica, S. J. Rezvani, S. Nannarone, S. Borisov, D. De Simone, S. Babin, G. Lorusso and G. Vandenberghe, in Advances in Patterning Materials and Processes XXXVI, ed. R. Gronheid and D. P. Sanders, SPIE, San Jose, United States, 2019, p. 8 Search PubMed.
- O. Y. Ridzel, V. Astašauskas and W. S. M. Werner, J. Electron Spectrosc. Relat. Phenom., 2020, 241, 146824 CrossRef CAS.
- W. S. M. Werner, Front. Mater., 2023, 10, 1202456 Search PubMed.
- M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11 CrossRef CAS.
- A. Rathore, M. Cipriani, C.-C. Huang, L. Amiaud, C. Dablemont, A. Lafosse, O. Ingólfsson, D. De Simone and S. De Gendt, Phys. Chem. Chem. Phys., 2021, 23, 9228–9234 RSC.
- E. Pavarini, E. Koch, J. van den Brink and G. Sawatzky, Institute for Advanced Simulation, and German Research School for Simulation Sciences, Eds., Quantum materials: experiments and theory: lecture notes of the Autumn School on Correlated Electrons 2016: at Forschungszentrum Jülich, 12-16 September 2016, Forschungszentrum, Zentralbibliothek, Jülich, 2016.
- R. Ravichandran, A. X. Wang and J. F. Wager, Opt. Mater., 2016, 60, 181–187 CrossRef CAS.
- Ø. Prytz, O. M. Løvvik and J. Taftø, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245109 CrossRef.
- L. H. Yang, B. Da, H. Yoshikawa, S. Tanuma, J. Hu, J. W. Liu, D. M. Tang and Z. J. Ding, Appl. Phys. Lett., 2021, 118, 053104 CrossRef CAS.
- Q.-J. Liu, Z.-T. Liu, L.-P. Feng and H. Tian, Phys. B, 2010, 405, 4032–4039 CrossRef CAS.
- M. Alouani, L. Brey and N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 1167–1179 CrossRef CAS.
- H. Bu, H. Zheng, H. Zhang, H. Yuan and J. Zhao, Sci. Rep., 2020, 10, 6808 CrossRef CAS.
- N. Erum, M. A. Iqbal and I. Bashir, Phys. Scr., 2021, 96, 025807 CrossRef CAS.
- H. M. Ghaithan, Z. A. Alahmed, S. M. H. Qaid and A. S. Aldwayyan, Materials, 2020, 13, 4944 CrossRef CAS.
- S. Azam, S. A. Khan and S. Goumri-Said, Mater. Sci. Semicond. Process., 2015, 39, 606–613 CrossRef CAS.
- M. R. Benam, J. Baedi and Z. Barmaki, Optik, 2020, 206, 164351 CrossRef CAS.
- R. Vettumperumal, J. R. Jemima, S. Kalyanaraman and R. Thangavel, Vacuum, 2019, 162, 156–162 CrossRef CAS.
- M. Bashi, H. A. R. Aliabad and M. Samsami, J. Mol. Model., 2021, 27, 274 CrossRef CAS PubMed.
- M. Samsami, B. Azadegan, H. A. Rahnamaye Aliabad and F. Amiri-Shookoh, J. Mol. Model., 2022, 28, 136 CrossRef CAS PubMed.
- M. I. Hussain, R. M. A. Khalil, F. Hussain, M. Imran, A. M. Rana and S. Kim, Mater. Sci. Semicond. Process., 2020, 113, 105064 CrossRef CAS.
- K. Nakano and T. Sakai, J. Appl. Phys., 2018, 123, 015104 CrossRef.
- J. A. Camargo-Martínez and R. Baquero, arXiv, 2013, preprint, arXiv:1208.2057, https://arxiv.org/abs/1208.2057.
- A. S. Milošević, M. V. Lalić, Z. S. Popović and F. R. Vukajlović, Opt. Mater., 2013, 35, 1765–1771 CrossRef.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- D. Waroquiers, A. Lherbier, A. Miglio, M. Stankovski, S. Poncé, M. J. T. Oliveira, M. Giantomassi, G.-M. Rignanese and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075121 CrossRef.
- D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134 CrossRef.
- H. Zitouni, N. Tahiri, O. El Bounagui and H. Ez-Zahraouy, J. Electron Spectrosc. Relat. Phenom., 2021, 247, 147043 CrossRef CAS.
- S. Samanta and S. M. Saini, J. Electron. Mater., 2014, 43, 3659–3665 CrossRef CAS.
- S. Samanta, Opt. Mater., 2015, 45, 141–147 CrossRef CAS.
- S. Grzeskowiak, A. Narasimhan, M. Murphy, L. Napolitano, D. A. Freedman, R. L. Brainard and G. Denbeaux, Proc. SPIE, 2017, 10146, 1014605 CrossRef.
- Y. G. Li, S. F. Mao and Z. J. Ding, in Applications of Monte Carlo Method in Science and Engineering, ed. S. Mordechai, InTech, 2011 Search PubMed.
- S. Bhattarai, A. R. Neureuther and P. P. Naulleau, Proc. SPIE, 2016, 9779, 97790B CrossRef.
- M. Dapor, J. Phys.: Conf. Ser., 2012, 402, 012003 CrossRef CAS.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5tc00441a |
| This journal is © The Royal Society of Chemistry 2025 |