Metal–organic frameworks built from a carborane linker isolating ideal one-dimensional large-spin chains of Co (S = 3/2) or Ni (S = 1)

Abstract

One-dimensional (1D) antiferromagnetic chains are fascinating because of their exotic quantum phenomena. However, isolating large-spin S chains remains challenging as even minimal interchain interaction J′ tends to drive unwanted long-range ordering. Here, we report on the synthesis, crystal structure, magnetism, optical, and electronic properties of two isostructural metal–organic frameworks (MOFs), [M₂(mCB-L)₂(μ₂-H₂O)₂(DMF)₄]_n·solv (M = Co(II) (mCB-Co) or Ni(II) (mCB-Ni)), which feature water-bridged Co (S = 3/2) or Ni (S = 1) spin chains that are effectively separated by bulky carborane linkers (1,7-di(4-carboxyphenyl)-1,7-dicarba-closo-dodecaborane, mCBLH₂). The temperature-dependent susceptibility reveals strong antiferromagnetic interactions with significant intrachain coupling, J_Co/k_B = −4.65 K (mCB-Co) and J_Ni/k_B = −23.36 K (mCB-Ni), yet confirm the absence of long-range order down to 0.3 K due to negligible interchain interactions, as corroborated by specific heat data. This indicates extremely small J′, with J′/J < 4.7 × 10⁻⁴ (3.7 × 10⁻⁵) for Co (Ni) MOFs, making these new materials nearly ideal 1D antiferromagnets. Additionally, optical band gaps were estimated via the Kubelka–Munk method, yielding an increase from 3.83 eV for mCB-Co to 4.20 eV for mCB-Ni, showcasing tunable electronic properties across the two MOFs.

---

Introduction

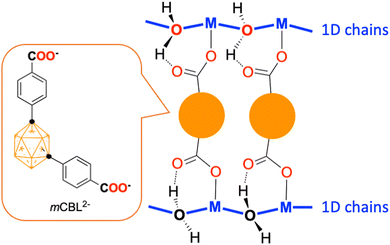
Low-dimensional magnetic systems, such as one-dimensional (1D) and two-dimensional (2D) spin networks, have attracted significant interest due to their rich magnetic properties and novel quantum phenomena.^1–3 The magnetic behavior of these systems is intricately shaped by various factors, including dimensionality, the spin magnitude, spin anisotropy, type of magnetic coupling (ferromagnetic or antiferromagnetic), and the interplay between the different interactions. Among low-dimensional magnetic systems, 1D spin chains play a foundational role in testing quantum magnetism theories and uncovering new magnetic phenomena.^4,5 Single-chain magnets (SCMs), for example, are composed of isolated chains of anisotropic magnetic units linked by strong ferromagnetic (FM) intrachain interactions, resulting in slow magnetization relaxation.^6,7 In contrast, 1D antiferromagnetic (AFM) spin chains and ladders reveal behaviors driven purely by quantum mechanics, such as spin-charge separation, spin-Peierls transitions,⁸ and ballistic thermal transport of spinons—phenomena that have no direct analogs in 3D systems. In particular, Heisenberg AFM spin chains have sparked strong interest for their ability to explore the transition between classical and quantum regimes of magnetism, and their connection to exotic quantum phases like quantum spin liquids (QSLs).⁹ These systems feature highly entangled spins and pronounced quantum fluctuations, resulting in unconventional magnetic behavior and the absence of long-range magnetic order, even at 0 K. A landmark theoretical prediction in this field is the Haldane conjecture,¹⁰ which states that integer-spin Heisenberg AFM chains have a gapped ground state, while half-integer spin chains are gapless. Experimental studies of Heisenberg AFM chains have largely focused on spin S = 1/2 systems, where quantum effects are particularly strong, and theoretical models exist to describe magnetization and heat capacity behaviors.^11–13 In contrast, studies on large-spin systems remains comparatively limited, in part due to the difficulty in isolating ideal Heisenberg AFM chains. Advances in synthetic strategies have enabled the creation and study of both integer and half-integer large-S Heisenberg AFM chains in inorganic materials (S = 1,¹⁴S = 5/2,^15–18S = 3/2^19–25) and hybrid inorganic–organic materials (S = 1,²⁶S = 2,^27–30S = 5/2^31,32). Despite this progress, stabilizing quantum phases and verifying the Haldane conjecture in large-S one-dimensional systems remains challenging, as even slight interchain coupling often leads to unwanted long-range magnetic ordering.

Notably, metal–organic frameworks (MOFs), composed of metal ions coordinated by organic linkers, offer promising platforms for hosting such ideal spin chains, though synthesizing such systems experimentally remains challenging.^33,34 MOFs provide flexible and highly ordered porous structures that can host different types of spin chains with precise control over magnetic interactions. By selecting specific magnetic cations, tailoring their coordination environment, and designing both intrachain and interchain linkers, it is possible to engineer a range of spin-S systems that behave as ideal 1D chains. An essential aspect of this design is the use of long organic ligands, which shield individual magnetic chains and reduce interchain interactions, thus preserving the desired low-dimensional quantum properties.

In previous work, we demonstrated that rare-earth ions combined with m-carborane ligands can form metal organic frameworks (mCB-MOFs) hosting 1D chains connected by the bulky carborane linkers (1,7-di(4-carboxyphenyl)-1,7-dicarba-closo-dodecaborane, mCBLH₂).^35–39 Carboranes (1,n-C₂B₁₀H₁₂ (n = 2, 7 or 12)) are a class of clusters composed of boron, carbon, and hydrogen atoms, known for their remarkable stability and unique structural features.^40–45 Their bulky, electron-rich frameworks can provide diverse coordination environments for metal ions, making them ideal candidates for creating robust, highly ordered architectures in transition metal MOFs.^46–53 Carboranes’ ability to stabilize metal centers while minimizing interactions between adjacent chains makes them particularly valuable in the design of 3D materials that exhibit 1D magnetic behavior. Building on these insights, we aimed to leverage the unique stabilizing properties of the carborane ligand, mCBLH₂, to create isolated 1D chains of transition metals with various large spin values, thereby achieving low-dimensional magnetism in MOFs.

In this work, we present two new mCB-MOFs that host ideal 1D antiferromagnetic chains of Co²⁺ (S = 3/2) or Ni²⁺ (S = 1) ions, effectively isolated by bulky carborane ligands. The resulting negligible interchain interactions prevent long-range ordering down to 0.3 K.

Results and discussion

Synthesis and chemical composition

Needle like crystals of [M₂(mCB-L)₂(μ₂-H₂O)₂(DMF)₄]_n·solv (M = Co (mCB-Co), Ni (mCB-Ni); Fig. 1(a) insets) were obtained by solvothermal reactions of M(NO₃)₂·6H₂O (M = Co, Ni), respectively, with mCB-H₂L (1,7-di(4-carboxyphenyl)-1,7-dicarba-closo-dodecaborane) in a molar ratio of ca. 5 : 4 in a mixture of N,N-dimethylformamide (DMF), methanol and H₂O (see the Experimental section for details). Powder X-ray diffraction (PXRD; Fig. 1(a)) revealed that both mCB-Co and mCB-Ni are isostructural. Fourier transform infrared (FTIR) spectroscopy (Fig. S1, ESI†) show characteristic B–H stretching bands, that for the carborane fragments appear at 2590–2592 cm⁻¹ and those for ν(COO⁻) stretching vibrations appear at 1589, 1543 and 1383 cm⁻¹ (mCB-Co) or 1587, 1541 and 1385 cm⁻¹ (mCB-Co).⁵⁴ Thermogravimetric (TGA; shown in Fig. S2, ESI†) demonstrate their robust thermal stability, with the frameworks remaining intact up to 400 °C. Notably, both mCB-Co and mCB-Ni exhibit good stability in neutral water and aqueous solutions across a broad pH range (3–11) for at least 24 h or in water for one week. PXRD traces of both materials, pre- and post-incubation in water within a closed vial, confirm the stability of the materials (Fig. S3, ESI†). This exceptional water stability can be attributed to the highly hydrophobic nature of the carborane moiety in our linker.^39,47,48,51

Fig. 1 PXRD profiles, SEM images (a) and XPS spectra (b) of mCB-Co and mCB-Ni.

We have studied the chemical composition and valence state of Co and Ni by X-ray photoelectron spectroscopy (XPS). The full range XPS spectra for both MOFs (mCB-Co and mCB-Ni; Fig. 1(b)), show the peaks of C 1s, O 1s, B 1s and N 1s and the corresponding metals (Co and or Ni). The high-resolution Co and Ni 2p spectra (Fig. S4, ESI†) are split into 2p_3/2 and 2p_1/2 doublets, due to the spin–orbit coupling, together with shakeup satellite peaks. Recent reports have questioned the use of the C 1s peak from adventitious carbon as a reference in XPS,⁵⁵ as well as the reliability of extracting accurate transition metal oxidation states from binding energies.⁵⁶ In our case, the X-ray structures, shown in the following section, confirm that both metals are in the divalent M²⁺ state.

Crystal structures

Single-crystal X-ray diffraction (SCXRD) confirm that both mCB-Co and mCB-Ni are isostructural (and crystallize in the monoclinic P2/c space group) (Fig. 2, Fig. S5, S6 and Table S1, ESI†). The comparison between the experimental PXRD patterns and those calculated from the SCXRD data show a very good match, confirming that the compounds crystallize as pure phases (Fig. S7, ESI†). The inorganic secondary building unit (SBU) in both compounds is formed by MO₆ polyhedra (M = Co or Ni) that share vertexes via one μ-O atom from a water molecule, providing the observed water-bridged 1D metal chains along the b axis (Fig. 2, Scheme 1 and Fig. S5, S6, ESI†). Two independent metal atoms are repeated to provide 1D inorganic chains that are bridged by the carborane linker to form the observed 3D structures (Fig. 2(c)). The two nonequivalent crystallographic Co^II cations in mCB-Co (Co1 and Co2, Fig. 2(a), left), show octahedral coordination, and with Co1⋯Co2 distances across the bridging water molecule of 3.8998(9) and 3.8194(9) Å. Identical octahedral coordination to that observed in mCB-Co is observed for the two nonequivalent crystallographic Ni^II cations in mCB-Ni (Fig. 2(a), right), with shorter and more regular metal to metal distances across the bridging water molecules (Ni1⋯Ni2; 3.765(1) and 3.783(1)). Two mCB-L²⁻ carboxylate anions are bonded to each M^II atom in a monodentate mode, with the remaining oxygen atom of the carboxylic group acting as hydrogen bond acceptors for one of the bridging water hydrogens (Fig. 2(a), Fig. S5, S6, ESI† and Scheme 1). The coordination spheres of each metal atom are completed by two DMF molecules (shown in orange color in Fig. 2(b)). Co–O and Ni–O distances (Table S2, ESI†) are within the ranges observed for related water-bridged 1D cobalt^57,58 or nickel⁵⁹ rod structures. The observed 3D packing results in non-interconnected voids, accounting for 6.0% and 8.4% of the unit cell volume when measured with a probe radius of 1.0 Å using Mercury software for mCB-Co and mCB-Ni, respectively (Fig. S8, ESI†).

Fig. 2 Crystal structures of mCB-Co (left) and mCB-Ni (right). (a) Coordination environment of the Co^II and Ni^II atoms, including intramolecular OH⋯O hydrogen bonds (see Fig. S5 and S6, ESI† for hydrogen bonding parameters). (b) Views of the coordination of mCB-L to the Co or Ni atoms showing the inorganic chains; oxygen atoms for DMF are colored in orange while the ligand and water oxygens are in red; metal to metal distances are indicated. (c) the extended 3D structures along the a axis; 1D chain to 1D chain distances are indicated. Parts of the ligands are omitted for clarity. Blue polyhedra represent the Co coordination spheres, green polyhedra represent the Ni ones and H atoms are omitted for clarity. Color code: Co, dark blue; Ni, green; O, red; C, gray; N, blue; B, pink.

Scheme 1 Schematic dicarboxylates bringing modes found in mCB-Co and mCB-Ni.

Schematic bonding of mCB-L in both MOFs is shown in Scheme 1 and individual and average bond distances and angles are listed in Table S2 (ESI†) and Table 1, respectively. The main structural difference between the two structures lies in the slightly shorter Ni–O distances compared to Co–O distances. This leads to significantly shorter Ni⋯Ni distances than Co⋯Co distances along the chains (Fig. 1(b) and Table 1). For the same reason, the coordination of the bulky, non-conjugated carborane ligand results in shorter Ni interchain distances (9.88 Å, 12.40 Å, and 17.77 Å; Fig. 2(c) and Fig. S6, ESI†) compared to the corresponding Co interchain distances (10.35 Å, 12.97 Å, 17.81 Å, and 17.96 Å; Fig. 2(c) and Fig. S5, ESI†). The M(μ₂-H₂O)M angles are slightly wider for Ni (128.8 Å) than for Co (127.5 Å). This can be explained by considering the combined effect of the different metal ion sizes (0.745 Å for Co²⁺ and 0.69 Å for Ni²⁺) and the hydrogen bonding strength between the coordinated water and the unbound carboxyl groups (Fig. 2, Scheme 1 and Table 1).

Table 1 Selected average distances and angles for mCB-Co and mCB-Ni

	mCB-Co	mCB-Ni
Distances (Å)
M–OCOR	2.023	1.996
M–O(DMF)	2.136	2.056
M–O(μ2-OH2)	2.152	2.093
M⋯M	3.860	3.774
HO–H⋯O=COR	1.79	1.73
Angles (°)
M–OH2–M	127.5	128.8

---

The two newly synthesized isostructural 3D MOFS, embedding well-isolated water-extended 1D chains of transition metals with different, high spin, Co^II (S = 3/2) and Ni^II (S = 1), offer an ideal platform to study and compare their magnetic properties.

Magnetic properties

The magnetic properties of mCB-Co and mCB-Ni in powder form were studied through static susceptibility, magnetization, and heat capacity measurements.

mCB-Co (S = 3/2)

The temperature dependence of the susceptibility, χ(T), reveals the low-dimensional nature of magnetism in the two synthesized transition metal MOFs. The χ(T) curves under zero-field cool (ZFC) and field-cooled (FC) conditions showed no divergence, ruling out the existence of spin-glass behavior (Fig. S9, ESI†). Fig. 3(a) shows the susceptibility measured for mCB-Co under an applied field of 0.1 T in the temperature range between 1.8–300 K. The χ(T) curve shows a Curie–Weiss behaviour at high temperatures, and exhibits a broad maximum at around T_max ≈ 14 K, indicating strong AFM intrachain interactions with short-range spin–spin correlations, which is a typical feature of low dimensional magnetism. Additionally, χ(T) includes a “Curie tail” at low temperatures, suggestive of weakly interacting or non-cooperative spins in the 1D chains, commonly observed in spin-chain compounds.^60,61 No magnetic long-range order is observed for T > 1.8 K.

Fig. 3 (a) Temperature-dependence of the magnetic susceptibility, χ(T), measured at 0.1 T for mCB-Co. The black line is the fit curve by the Bonner–Fisher model. The inset shows the χ⁻¹(T) curve and also the Curie–Weiss fit; (b) field-dependence of the magnetization per Co ion, M(H), measured for mCB-Co at different temperatures, 1.8 K, 15 K, 50 K, across T_max in the χ(T) curve; (c) χ(T) at 0.1 T for mCB-Ni, and fit curve by the Weng model. Inset: χ⁻¹(T) curve and Curie–Weiss fit from 100 to 300 K; (d) M(H), per Ni ion, measured for mCB-Ni at different temperatures (T = 1.8 K, 4.5 K, 50 K, 100 K).

The fit of the inverse susceptibility 1/χ(T) at high temperatures from 150–300 K by the Curie–Weiss law, χ = C/(T − θ) + χ₀, Fig. 3(a) (inset), yields a temperature independent susceptibility χ₀ = 1.9 × 10⁻³ emu mol_Co⁻¹, and Curie constant C = 2.87 emu K mol_Co⁻¹, from which we determined the gyromagnetic factor g = 2.47 and effective magnetic moment of the Co²⁺ ions μ_eff = 4.78μ_B. This value exceeds the expected spin-only contribution but falls within the typical range observed for most Co²⁺ in an octahedral environment (4.3–5.2μ_B).⁶² The increase is associated with the orbital contribution (L = 1) in the presence of significant spin–orbit coupling for this ion (−180 cm⁻¹). The obtained Weiss temperature is large and negative, θ = −26 K. This value can simply arise from the thermal depopulation of the ground state due to the orbital contribution but is also compatible with the existence of antiferromagnetic Co–Co interactions. The existence of AFM intrachain interactions is indeed confirmed and quantified below.

The appearance of a correlation maximum in the χ(T) curve is typical for linear AFM chain systems. The intrachain interaction may be first roughly estimated from this hump within the simplified nearest-neighbor exchange interaction model for a S = 3/2 Heisenberg chain (De John & Miedema⁶³), k_BT_max ≈ 4.75|J|/2, yielding J/k_B = −5.91 K. Note here that J is defined negative for AFM coupling within the exchange Hamiltonian .

To determine the intrachain interaction more precisely, the susceptibility curve was fitted in the entire temperature range to the equation, χ(T) = χ_chain(T) + χ_imp(T). Here, the AFM spin-chain for S = 3/2 was modelled by the Bonner–Fisher formula:⁶⁴

where α = |J|/k_BT (J is the intrachain interaction constant), N_A, μ_B and k_B are Avogadro, Bohr and Boltzmann constants, and the Curie term χ_imp(T) = C_imp/T was introduced to account for the impurity spins contribution. For fitting the susceptibility, the χ₀ and g-factor were fixed to the abovementioned values. The fit, shown in Fig. 3(a), yielded the intrachain AFM constant J_Co/k_B = −4.65 K, and a Curie component C_imp = 0.025 emu K mol_Co⁻¹, implying approximately 0.87% of “paramagnetic” spin-3/2 impurities.

Based on the crystal structure of mCB-Co, where the metal 1D chains are well-separated by the bulky carborane ligand (Fig. 2, left and Fig. S5, ESI†), interchain Co–Co interactions (J′) are expected to be much smaller than intrachain interactions (J). The interchain interactions J′ can be estimated by the model based on the Green function method:⁶⁵

where I(η) ≈ 0.633/(η^1/2), η = J′/J (for η ≪ 1). From heat capacity measurements (vide infra), no magnetic ordering is observed down to 0.4 K; thus T_N < 0.4 K, which gives a particularly small threshold value of J′/J = 4.74 × 10⁻⁴ and demonstrates the smallness of interchain interactions.

Fig. 3(b) shows the field-dependent magnetization of mCB-Co at different temperatures, T = 1.8, 15, 50 K, measured up to 5 T. Above 15 K, a linear M(H) dependence is observed, while at 1.8 K the magnetization exhibits a curvature that can be assigned to the paramagnetic contribution of impurities. The magnetization value is only 0.37μ_B per Co at 5 T, 1.8 K, which is far from the expected saturation value per Co^II (M_sat = gμ_BS = 5.82μ_B), supporting AFM interactions in this compound.

To further characterize the magneto-thermal properties of mCB-Co, the specific heat was measured in the temperature range between 0.4–300 K at different applied magnetic fields, between 0–5 T (Fig. 4(a)). The specific heat under H = 0 decreases with decreasing the temperature and no λ-like peak is observed down to 0.4 K, indicating the absence of AFM long-range ordering down to this temperature. The presence of short-range spin correlations along the chain, that results in the susceptibility maximum at T_max ≈ 14 K, is not reflected in the C_p(T), overshadowed by the dominant lattice contribution in this temperature range. Co²⁺ ion is a Kramers ion and exhibits at low temperatures an effective S* = 1/2 ground state doublet. Under the application of a magnetic field, the Zeeman splitting of this doublet gives rise to the observed Schottky anomaly in the heat capacity, mainly visible at 1 T, which shifts to higher temperatures as the field increases.

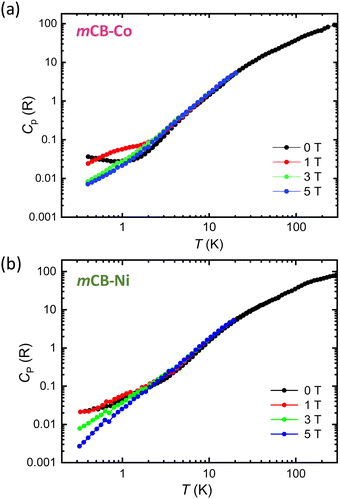Fig. 4 Specific heat as a function of temperature, per ion, measured at different applied magnetic fields between 0–5 T for (a) mCB-Co and (b) mCB-Ni.

mCB-Ni (S = 1)

The χ(T) curve measured for mCB-Ni compound, shown in Fig. 3(c), does not show a clear maximum, like the mCB-Co analogue, only a hump above the Curie–Weiss behavior is hinted. However, given the two compounds are isostructural, we hypothesize that the system also behaves as a chain antiferromagnet, in this case with S = 1. No magnetic long-range order is observed for T > 1.8 K.

The fit of the 1/χ(T) with the Curie–Weiss law, shown in Fig. 3(c) (inset), gives χ₀ = 7.4 × 10⁻⁴ emu mol⁻¹, and Curie constant C = 1.22 emu K mol⁻¹, thereby defining a g-factor g = 2.21 and an effective magnetic moment for the Ni²⁺ ions of μ_eff = 3.12μ_B, within the range reported for Ni²⁺ in an octahedral environment (2.9–3.3μ_B).^66,67 The Weiss temperature is negative, θ = −26.93 K, supporting the predominance of AFM interactions in mCB-Ni.

To determine the intrachain interaction, the susceptibility curve was fitted with the equation χ(T) = χ_chain(T) + χ_imp(T), where the AFM Heisenberg spin-chain susceptibility for S = 1 is given by the Weng model:⁶⁸

The fit, shown in Fig. 3(c), yielded the intrachain AFM constant J_Ni/k_B = −23.36 K, and C_imp = 0.2208 emu K mol_Ni⁻¹, implying approximately 18.11% spin-1 impurities. Using the simplified De Jongh & Miedema model with S = 1, where k_BT_max ≈ 1.35|J|/2, for J_Ni/k_B = −23.36 K, we would expect a correlation maximum at T_max = 31.54 K, which is compatible with the bump observed in the χ(T) curve.

The estimation of the inter- to intrachain coupling ratio, based on eqn (2) and the Néel temperature threshold T_N = 0.3 K obtained from heat capacity measurements (vide infra), yields J′/J < 3.71 × 10⁻⁵, demonstrating again the good isolation of the 1D chains facilitated by the carborane linkers.

The M(H) curves for mCB-Ni up to 5 T at different temperatures, T = 1.8, 4.5, 50 and 100 K, are shown in Fig. 3(c). The behavior of M(H) is qualitatively similar to that of mCB-Co, corresponding to an AFM linear chain, with additional contribution from paramagnetic impurities at 1.8 K. The magnetization at 5 T, M(1.8 K) ≈ 0.31μ_B per Ni, is much smaller than the expected saturation magnetization of Ni²⁺ ions, M_sat = gS = 2.25 μ per Ni. This result aligns with 1D Heisenberg AFM as well as Haldane systems, in which the saturation magnetization can often not be reached even in fields up to 40 T. At low temperatures (1.8 K, 4.5 K), M(H) exhibits non-linear behavior, which may be attributed to the paramagnetic impurities.

Fig. 4(b) shows the specific heat measurements for mCB-Ni conducted down to 0.3 K. Ni²⁺ is a non-Kramers ion (S = 1), so the main contribution to the heat capacity of mCB-Ni comes from the zero-field splitting (ZFS), which, although generally small, becomes apparent at low temperatures. When an external field is applied, the Zeeman effect further modulates the ZFS levels, resulting in the observed field-dependent C_p(T,H) trend that differs from the behavior observed for Co²⁺ Kramers ion. However, similar to the mCB-Co analogue, no evidence of AFM long-range ordering is observed down to the lowest tested temperature, allowing to set a threshold for the Néel temperature of T_N = 0.3 K.

Comparison with other Co (S = 3/2) and Ni (S = 1) linear spin chains

A variety of metal–organic architectures with diverse structural dimensionality include Co(II) or Ni(II) magnetic 1D chains. In the following, we discuss the distinct magnetic behavior of our two new carborane-based 3D MOFs, incorporating quasi-ideal 1D AFM Co(II) or Ni(II) chains, with previously reported materials, as summarized in Table S3 (ESI†).

Co(II) magnetic chains exhibit a rich variety of magnetic behaviors, depending on the interplay between ion anisotropy, intra- and interchain interactions. Single-chain magnet (SCM) behavior is often favored for chains of anisotropic Co(II) ions, in highly distorted coordination environments, strongly coupled through ferromagnetic (FM) intrachain interactions.⁶⁹ The spin reversal magnetic relaxation times are highly dependent on the bridging linkers, in both isolated Co(II) polymers and chains assembled in MOFs. Interchain magnetic interactions promote long-range magnetic ordering, which can however coexist with SCM dynamics.⁷⁰ Metamagnetism, revealed by the sigmoidal shape of the magnetization curve, has also been observed in strongly correlated AFM or weakly FM chains of highly anisotropic Co(II) ions,⁷¹ sometimes coexisting with SCM behavior.

The one-dimensional AFM behavior found in our mCB-Co is qualitatively similar to that found in water-bridged [Co(m-H₂tpta)(μ₂-H₂O)(H₂O)₂]_n (g = 2.41, J/k_B = −14.3 K),⁷² or isolated polymeric chains bridged by oxalate ligands. However, the later systems present stronger AFM interactions, such as {[Co(l-ox)(H₂O)₂]·2H₂O}_n (g = 2.51, J/k_B = −23.6 K),⁷³ {[Co(ox)(Htr)₂]·2H₂O}_n (ox = oxalate dianion; Htr = 1,2,4-triazole) (g = 2.64, J/k_B = −13.38 K),⁷⁴ Co(ox)(en) (g = 2.5, J/k_B = −16.98 K)⁷⁵ and Co(ox)(en)·2H₂O (g = 2.6, J/k_B = −14.82 K).⁷⁵ For water-extended Co(II) chains isolated by bulky 9-anthracenecarboxylato and 4-quinolinecarboxylato ligands, the different interchain interactions resulted in SCM behavior (Δ/k_B = 8.11 K, Δξ = 4.20 K) in the canted antiferromagnetic phase for {[Co(H₂O)₂(L)₂]·2H₂O}_n⁷⁶ while, in contrast, metamagnetism and SCM (Δ/k_B = 4.80 K, Δξ = 4.49 K) were observed in {[Co(H₂O)₂(L′)₂]·2H₂O}_n.⁷⁶

It is particularly intriguing that the related 3D coordination polymer, [Co₂(L)₂(μ₂-H₂O)₂(DMF)₄]_n, which also contains water-bridged Co²⁺ chains separated by a long, planar ligand (L = 3,3′-(1,3,6,8-tetraoxobenzol[lmn][3,8]-phenanthroline-2,7(1H,3H,6H,8H)-diyl)-di-benzoic acid), exhibits markedly different magnetic behavior compared to mCB-Co, which contains a bulky (3D), V-shaped carborane ligand. Despite their structural similarity, they exhibit markedly different magnetic behavior. [Co₂(L)₂(μ₂-H₂O)₂(DMF)₄]_n shows FM intrachain interactions (J/k_B = 33.22 K), leading to SCM behavior with an energy barrier of Δ/k_B = 21.65 K and correlation energy of Δξ/k_B = 6.44 K.⁷⁷

In the case of Ni(II), we have found an unique example of a 3D coordination polymer showing 1D AFM Ni(II) chains (Table S2, ESI†).⁷² This corresponds to {[Ni₂(p-pta)(μ₂-H₂O)₂(H₂O)₄]·2H₂O}, which shows somewhat larger AFM interactions (g = 2.19, J/k_B = −45.05 K) than mCB-Ni. The 1D coordination polymer [NiL₂-(μ-N₃)]_n(ClO₄)_n, composed of Ni(II) bridged by azido ligands, shows a quite similar 1D AFM behaviour (g = 2.20, J/k_B = −22.2 K)⁷³ to that of mCB-Ni.

Magnetic exchange interactions involving μ-water bridges are far less common in coordination polymers than μ-oxo-bridges.⁷⁴ Intrachain exchange couplings are basically dominated by the chain Co⋯Co distances and bridging Co–O_water–Co angles in these systems.⁷⁵ The different exchange behavior between mCB-Co (AFM) and [Co₂(L)₂(μ₂-H₂O)₂(DMF)₄]_n (FM) can be explained by the different Co⋯Co distances (3.860 and 4.199 Å, respectively) and bridging Co–O_water–Co angles (127.5 and 139.0 deg, respectively) within the chains of these two 3D coordination polymers. Consistently, the corresponding parameters for the also AFM bridged [Co(m-H₂tpta)(μ₂-H₂O)(H₂O)₂]_n (Co⋯Co: 3.910 Å; Co–O_water–Co: 130.6°) are comparable with those for mCB-Co. Ni⋯Ni distances and bridging Ni–O_water–Ni angles are also similar to the only other water-bridge {[Ni₂(p-pta)(μ₂-H₂O)₂(H₂O)₄]·2H₂O}, but also to the Co(II) coordination polymers described above, except for [Co₂(L)₂(μ₂-H₂O)₂(DMF)₄]_n.⁷⁶

It is also noteworthy to compare the results of mCB-Ni with prior attempts to create Ni(II) spin-1 AFM Haldane chains in other type of materials. Various hybrid compounds have been proposed for this purpose, including ANiCl₃ complexes composed of chains of NiCl₆ octahedra separated by organic cations of varying sizes and geometries. The intrachain AFM coupling in mCB-Ni is comparable to that in MANiCl₃ (MA = methylammonium, g = 2.27, J/k_B = −21.46 K).⁷⁷ In the organic–inorganic hybrid compound NiCl₃C₆H₅CH₂CH₂NH₃, the Ni²⁺ ions are isotropic (g = 2.25) and coupled AFM along the chain with an exchange constant of J/k_B = −25.5 K; however, interchain couplings in this compound lead to magnetic ordering at T_N = 10 K.⁷⁸ Additionally, several inorganic Ni compounds have been synthesized and put in the Haldane,^79–82 Z-AFM,^83,84 and XY-AFM¹⁴ sectors of the Sakai-Takahashi phase diagram (J′/J vs. D/J) for uniform spin-1 chains. Y₂BaNiO₅, a representative compound in the Haldane phase, consists of (NiO₅)_n isolated chains along the a-axis separated by Y and Ba atoms.⁷⁹ It behaves as a spin-1 Heisenberg chains with strong AFM coupling (J/k_B ≈ −285 K) and exhibits no long-range ordering down to 1.8 K, implying an inter-intrachain coupling ratio J'/J ≪ 10⁻¹. Although the AFM intrachain interaction in mCB-Ni is significantly weaker, its high degree of chain isolation (J'/J = 6.61 × 10⁻⁵) makes it an intriguing candidate for further investigation of quantum effects in 1D systems.

Optical and electronic properties

The diffuse reflectance (DR) UV-vis spectra of as synthesized mCB-Co and mCB-Ni are shown in Fig. 5. The spectra in the form of Reflectance versus wavelength are given in Fig. S10 (ESI†). The spectra are consistent with an octahedral coordination geometry for Co²⁺ and Ni²⁺. The adsorption bands in the range 200–300 nm are attributed to π* → π transitions of the aromatic rings in the mCB-L ligand.³⁹ Absorption bands at 450–550 nm (maxima at around 500 nm) and 650–670 nm (maxima at 660 nm) are associated with d–d transitions of octahedral Co²⁺ and Ni²⁺ sites, respectively.^85,86mCB-Co shows two absorption bands, one in the UV region (487 nm) and another in the Near Infrared (NIR) region (1131 nm), both corresponding to d–d transitions in octahedral Co²⁺.⁸⁷ The shoulder observed for the 662 nm band (Fig. 5) corresponds to the splitting of the band due to spin–orbit coupling, which mixes two different states that are very close in energy. The mCB-Ni spectrum exhibits three absorption bands, two at the UV region (388 and 662 nm) and one at the NIR region (1073 nm), which are also attributed to d–d transitions for Ni²⁺ sites.

Fig. 5 Normalized UV-vis absorbance spectra of mCB-Co and mCB-Ni.

The optical band gap energies (E_g) for mCB-Co and mCB-Ni were estimated using the Kubelka–Munk (KM) model combined with the Tauc plot method (see Experimental section and ESI† for details).^88,89 Plots for direct band gaps show a more clearly defined linear region than the corresponding indirect plots (Table S4 and Fig. S11, S12, ESI†), suggesting that our materials behave as direct semiconductors.⁸⁹ Thus, E_g values were estimated from direct plots and are in the range of 3.68–3.88 eV (mCB-Co) and 4.08–4.20 eV (mCB-Ni), all being consistent with the literature reports.^89,90Fig. 6 presents the plots of the F(R)² function versus energy, which has been recently suggested as the most appropriate approach for determining band gaps in MOF systems.⁸⁹ As shown in this figure, there is a steep, linear increase in light absorption with increasing photon energy, characteristic of semiconducting materials. The linear fit of this steep region intersects the hν axis, providing an estimate of E_g values for the MOFs.

Fig. 6 Direct band gap energy assessment using the Kubelka–Munk function for mCB-Co and mCB-Ni. The linear portion of the plot is extrapolated to the x-axis (red dotted arrows) to determine the band gap energies (see text for further discussion).

The ability to engineer the band gap of MOFs is crucial for optimizing their light absorption, as well as their electrical and photocatalytic properties.⁹¹ Band gap modulation can be achieved by modifying the organic linkers, incorporating guest molecules, or altering the metal nodes within the framework.^92–95 The choice of metal centers plays a fundamental role in determining the conduction band, thereby affecting the overall band gap. Among various strategies for tuning MOF electronic properties, metal substitution within isostructural frameworks has gained significant attention. Studies on MOF-74 have demonstrated that replacing Zn²⁺ with transition metals such as Co²⁺ or Cu²⁺ leads to a reduction in band gap, attributed to the presence of semi-occupied d orbitals that alter the conduction band.^96,97 Similarly, in the MFU-4 framework, substituting Zn²⁺ with Co²⁺ results in a material with a lower band gap, confirmed by both experimental and computational analyses.⁹⁸ The NNU-31-M series, which consists of Fe₂M clusters (M = Co, Ni, Zn), further highlights the impact of metal choice, with band gaps varying from 1.85 eV for Co to 1.82 eV for Ni and 1.53 eV for Zn. These findings underscore the critical role of metal nodes in band gap engineering.⁹⁹ However, although the precise and continuous tunability of band gaps by modifying metal nodes is highly desirable, obtaining target MOFs is challenging, as altering the metal nodes can easily result in a completely different architecture.⁹²

The isostructurality of our MOFs, with identical coordination geometries and atom types coordinated to the metal centers, allows us to attribute the observed differences in band gaps primarily to the nature of the transition metals. Ni²⁺ has a more filled 3d-orbital configuration ([Ar] 3d⁸) than Co²⁺ ([Ar] 3d⁷), leading to reduced overlap of the d-orbitals between the metal centers and the linkers. This decreased overlap in the case of nickel results in a greater separation between the valence and conduction bands, thereby increasing the band gap. Conversely, cobalt, with less filled d-orbital configuration, facilitate more extensive electronic interactions within the framework, lowering the energy difference between the valence and conduction bands and thus resulting in a smaller band gap.^95,100

Conclusions

We have successfully synthesized two new metal–organic frameworks (MOFs), [M₂(μ₂-H₂O)₂(mCB-L)₂(DMF)₄]_n·solv, incorporating water-bridged spin chains of Co^II (S = 3/2) or Ni^II (S = 1), by a solvothermal method. These MOFs, designated as mCB-Co and mCB-Ni, feature one-dimensional spin chains effectively isolated by the bulky carborane linkers mCBLH₂. Magnetic susceptibility measurements reveal a broad maximum at 14 K for mCB-Co and a bulge at ∼32 K for mCB-Ni, pointing to strong intrachain antiferromagnetic interactions (J_Co/k_B = −4.65 K and J_Ni/k_B = −23.36 K). No long-range magnetic ordering is observed, as confirmed by heat capacity results down to 0.3 K, due to the negligible interchain interactions provided by the bulky carborane ligands. This behavior highlights mCB-Co and mCB-Ni as promising high-spin one-dimensional antiferromagnetic chains, offering a unique platform for exploring quantum effects in well-isolated spin chains. The carborane-MOF strategy further opens possibilities to construct a variety of different spin, low-dimensional magnetic lattices. Additionally, both frameworks exhibit wide-band-gap semiconducting properties, with optical band gaps of 3.62 eV for mCB-Co and 3.84 eV for mCB-Ni. The increase in band gap upon substituting Co with Ni further underscores the tunability of electronic properties in these MOFs, suggesting potential applications in semiconductor technologies.

Experimental section

All chemicals were of reagent-grade quality. They were purchased from commercial sources and used as received. 1,7-Di(4-carboxyphenyl)-1,7-dicarba-closo-dodecaborane ligand (mCBH₂L) was synthesized by a slight modification of a literature procedure.³³

Synthesis of {[M₂(μ₂-H₂O)₂(mCB-L)₂(DMF)₄]_n·solv} (M = Co (mCB-Co) and Ni (mCB-Ni))

These materials were synthesized using solvothermal methods. In a typical preparation, mCBH₂L (0.04 mmol), the corresponding M(NO₃)₃ (0.05 mmol), DMF (1.0 mL), H₂O (0.8 mL), and methanol (0.35 mL) were added to an 8-dram vial. The mixture was then heated in an oven at 100 °C for 48 hours. During the synthesis, the reactants typically dissolved completely within 2 hours, and small particles began to form in the suspension after approximately 20 hours. No further changes were observed even with extended heating up to 6 days. Upon cooling the closed vials to room temperature over 4 hours, large pink (Co) or green (Ni) needles formed. The crystals were then collected and washed with DMF. (Yield based on the metal ions: 29% for mCB-Co and 33% for mCB-Ni). Elemental analyses (%): calculated for {[Co₂(μ₂-H₂O)₂(mCB-L)₂(DMF)₃(H₂O)]_n·2H₂O}: C 41.31, H 5.67, N 3.53; found: C 41.35, H, 5.42, N 3.62; calculated for {[Ni₂(μ₂-H₂O)₂(mCB-L)₂(DMF)₃(H₂O)]_n·2H₂O}: C 41.33, H 5.67, N 3.53; found: C 41.41, H 5.45, N 3.63.

Instruments and characterization

Attenuated total reflection Fourier transform infrared (ATR-FTIR) spectra were recorded using a PerkinElmer Spectrum One spectrometer equipped with a Universal ATR sampling accessory. Spectra were collected with 2 cm⁻¹ spectral resolution in the 4000–650 cm⁻¹ range. Elemental analyses were obtained by using a Thermo (Carlo Erba) Flash 2000 Elemental Analyser, configured for wt% CHN. Inductively Coupled Plasma – Mass Spectrometry (ICP-MS) measurements were carried out in an Agilent ICP-MS 7700× apparatus. Thermogravimetric Analysis (TGA) was performed in N₂, on an nSTA 449 F1 Jupiter instrument (heating rate: 10 °C min⁻¹; temperature range: 25 °C to 800 °C). Scanning Electron Microscopy (SEM) (QUANTA FEI 200 FEGESEM) and optical microscopy (Olympus BX52) were used to monitor the morphology and color changes at various conditions.

X-ray diffraction

A crystal suitable for single crystal X-ray diffraction (SCXRD) with dimensions 0.18 × 0.07 × 0.04 mm³ was selected and mounted on a MITIGEN holder with silicon oil on a ROD, Synergy Custom system, HyPix diffractometer. The crystal was kept at a steady T = 100(2) K during data collection. The analysis of the crystal structures has been carried out within the CCDC Mercury software.¹⁰¹ Powder X-ray Diffraction (PXRD) was recorded at room temperature on a Siemens D-5000 diffractometer with Cu Kα radiation (λ = 1.5418 Å, 35 kV, 35 mA, increment = 0.02°).

X-ray photoelectron spectra

XPS were acquired using SPECS PHOIBOS 150 hemispherical analyzer (SPECS GmbH, Berlin, Germany) with a base pressure of 5 × 10⁻¹⁰ mbar using monochromatic Al K-alpha radiation (1486.74 eV) as excitation source operated at 300 W. A low-energy charge neutralizer was used to remove the charge shifts during photoemission. Survey scans were recorded at a pass energy E_pass = 50 eV, in steps of 1 eV, and high-resolution spectra with 0.1 eV step and E_pass = 20 eV. Referencing the C 1s peak for charge correction in XPS measurements has been shown to be unreliable. Recent studies have demonstrated that using the C 1s peak from adventitious carbon is not a consistent or accurate method for determining binding energy (BE) references, as the BE of adventitious carbon can vary significantly depending on the sample and measurement conditions.^55,102,103 Thus, it is recommended to obtain the sample work function from UV photoelectron spectroscopy (UPS) for samples conducting enough. However, as this is not possible for poorly conductive or insulating samples (like ours), there is no reliable method to calibrate the BE and therefore we do not state any binding energy for a fact and focus instead on spectral changes within our family of isostructural materials.

Dc magnetometry

Magnetization and dc susceptibility measurements in the temperature range 1.8 to 300 K in applied magnetic fields up to 5 T were performed by using a Quantum Design MPMS SQUID magnetometer. Experiments were conducted on powdered samples embedded in Daphne oil to prevent grain orientation. A diamagnetic correction of −7.9 × 10⁻⁸ emu was applied to account for the diamagnetic contribution of the SQUID capsule, the Daphne oil and the organic compound.

Heat capacity

Heat capacity as a function of the temperature were measured between 0.3–300 K at different applied fields between 0–3 T on a pressed powder pellet fixed with Apiezon N grease, using a Quantum Design PPMS equipped with a ³He refrigerator.

Ac susceptibility

χ′, χ′′(f, T, H) measurements were performed using a Quantum Design PPMS susceptometer over a temperature range of 0.1–9.0 K, at H_ac = 4.1 × 10⁻⁴ T, dc magnetic field of H_dc = 0–2.5 T, and frequencies between f = 100–10 000 Hz. None of the studied TM-MOFs showed an out-of-phase component in the susceptibility, indicating the absence of magnetic relaxation.

Diffuse-reflectance UV-visible

(DR-UV-Vis) spectra were collected on a Varian CARY-500 Spectrophotometer equipped with a diffuse reflectance accessory in the wavelength range 200–1600 nm. The room temperature DR-UV-Vis spectra were measured using Spectralon white as a reference material and treated as explained in the main text for estimation of the optical band gap energies.

Author contributions

J. G. P. conceived the project concept. J. G. P., E. B., and X. B. L. designed the detailed project scope and the experiments. X. B. L. performed the sample preparation and conducted basic characterizations. M. E. L. conducted the X-ray diffraction measurements. A. A. and E. B. conducted the magnetic measurements. J. G. P. and E. B. analyzed the data and wrote the paper. A. A., and X. B. L. discussed the results and commented on the manuscript. All authors revised the manuscript and have given approval to the final version of the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.† The data includes: IR, TGA, SCXRD, PXRD, XPS, UV-vis DR and band gaps estimation details. CCDC 2267757 and 2341767.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Spanish “Ministerio de Ciencia, Innovacion y Universidades” (PID2022-136892NB-I00) and (PID2022-138492NB-I00), the Gobierno de Aragón (RASMIA E12-23R), the State Investigation Agency, through the Severo Ochoa Program for Centres of Excellence in R&D (CEX2023-001263-S and CEX2023-001286-S), and by the Generalitat de Catalunya (2021/SGR/00442). Xiao-Bao Li is enrolled in the UAB PhD program and acknowledges the China Scholarship Council (CSC) for his PhD grant (202106650003). Authors would like to acknowledge the use of Servicio General de Apoyo a la Investigación-SAI, Universidad de Zaragoza.

References

1. A. Vasiliev, O. Volkova, E. Zvereva and M. Markina, npj Quantum Mater., 2018, 3, 18.
2. Quantum Magnetism, ed. U. Schollwöck, J. Richter, D. J. J. Farnell and R. F. Bishops, Springer, 2004.
3. S. Sachdev, Quantum Phase Transitions, Cambridge, United Kingdom, 1999.
4. F. D. M. Haldane, Phys. Lett. A, 1983, 93, 464–468.
5. M. Hagiwara, L. P. Regnault, A. Zheludev, A. Stunault, N. Metoki, T. Suzuki, S. Suga, K. Kakurai, Y. Koike, P. Vorderwisch and J.-H. Chung, Phys. Rev. Lett., 2005, 94, 177202.
6. C. Coulon, H. Miyasaka and R. Clérac, in Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, pp. 163–206.
7. H. Miyasaka, M. Julve, M. Yamashita and R. Clérac, Inorg. Chem., 2009, 48, 3420–3437.
8. J. W. Bray, H. R. Hart, L. V. I. Jr., I. S. Jacobs, J. S. Kasper, G. D. Watkins, S. H. Wee and J. C. Bonn, Phys. Rev. Lett., 1975, 35, 744–747.
9. L. Savary and L. Balents, Rep. Prog. Phys., 2017, 80, 016502.
10. F. D. M. Haldane, Phys. Rev. Lett., 1983, 50, 1153.
11. J. C. Bonner and M. E. Fisher, Phys. Rev., 1964, 135, A640–A658.
12. S. Eggert, I. Affleck and M. Takahashi, Phys. Rev. Lett., 1994, 73, 332.
13. D. C. Johnston and A. Klümper, Phys. Rev. Lett., 2000, 84, 4701.
14. E. S. Kozlyakova, A. V. Moskin, P. S. Berdonosov, V. V. Gapontsev, S. V. Streltsov, M. Uhlarz, S. Spachmann, A. ElGhandour, R. Klingeler and A. N. Vasiliev, Sci. Rep., 2021, 11, 15002.
15. G. R. Wagner and S. A. Friedberg, Phys. Lett., 1964, 9, 11.
16. R. Dingle, M. E. Lines and S. L. Holt, Phys. Rev., 1969, 187, 643.
17. M. Liu, Z. Ouyang, X. Liu, J. Cao, T. Xiao, Z. Xia and Z. Wang, Inorg. Chem., 2022, 61, 15045–15050.
18. L. D. Sanjeewa, V. O. Garlea, M. A. McGuire, C. D. McMillen, H. Cao and J. W. Kolis, Phys. Rev. B, 2016, 93, 224407.
19. M. Niel, C. Cros, G. Le Flem, M. Pouchard and P. Hagenmuller, Physica B+C, 1977, 86–88, 702.
20. H. Mutka, C. Payen and P. Molini, Europhys. Lett., 1993, 21, 623.
21. C. Venkatesh, B. Bandyopadhyay, A. Midya, K. Mahalingam, V. Ganesan and P. Mandal, Phys. Rev. B, 2020, 101, 184429.
22. A. B. Christian, A. Rebello, M. G. Smith and J. J. Neumeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 174425.
23. S. Itoh, Y. Endoh, K. Kakurai, H. Tanaka, S. M. Bennington, T. G. Perring, K. Ohoyama, M. J. Harris, K. Nakajima and C. D. Frost, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 14406.
24. M. Hase, M. Soda, T. Masuda, D. Kawana, T. Yokoo, S. Itoh, A. Matsuo, K. Kindo and M. Kohno, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024416.
25. C. Venkatesh, B. Bandyopadhyay, A. Midya, K. Mahalingam, V. Ganesan and P. Mandal, Phys. Rev. B, 2020, 101, 184429.
26. F. Lipps, A. H. Arkenbout, A. Polyakov, M. Günther, T. Salikhov, E. Vavilova, H. Klauss, B. Büchner, T. Palstra and V. Kataev, Low Temp. Phys., 2017, 43, 1298.
27. J. Pitcairn, A. Iliceto, L. Cañadillas-Delgado, O. Fabelo, C. Liu, C. Balz, A. Weilhard, S. P. Argent, A. J. Morris and M. J. Cliffe, J. Am. Chem. Soc., 2023, 145, 1783–1792.
28. G. E. Granroth, M. W. Meisel, M. Chaparala, Th Jolicœur, B. H. Ward and D. R. Talham, Phys. Rev. Lett., 1996, 77, 1616.
29. G. E. Granroth, M. W. Meisel, M. Chaparala, Th Jolicœur, B. H. Talham and D. R. Ward, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 77, 1616.
30. A. Panja, N. Shaikh, P. Vojtısek, S. Gao and P. Banerjee, New J. Chem., 2002, 26, 1025–1028.
31. Y. Wang, P. Fu, H. Takatsu, C. Tassel, N. Hayashi, J. Cao, T. Bataille, H.-J. Koo, Z. Ouyang, M.-H. Whangbo, H. Kageyama and H. Lu, J. Am. Chem. Soc., 2024, 146, 8320–8326.
32. H. Lu, T. Yamamoto, W. Yoshimune, N. Hayashi, Y. Kobayashi, Y. Ajiro and H. Kageyama, J. Am. Chem. Soc., 2015, 137, 9804–9807.
33. P. Tin, M. J. Jenkins, J. Xing, N. Caci, Z. Gai, R. Jin, S. Wessel, J. Krzystek, C. Li, L. L. Daemen, Y. Cheng and Z.-L. Xue, Nat. Commun., 2023, 14, 5454.
34. J. Pitcairn, A. Iliceto, L. Cañadillas-Delgado, O. Fabelo, C. Liu, C. Balz, A. Weilhard, S. P. Argent, A. J. Morris and M. J. Cliffe, J. Am. Chem. Soc., 2023, 145, 1783–1792.
35. Z. Li, A. Arauzo, C. Roscini, J. G. Planas and E. Bartolomé, J. Mater. Chem. A, 2024, 12, 21971–21986.
36. Z. Li, A. Arauzo, J. Giner Planas and E. Bartolomé, Dalton Trans., 2024, 53, 8969–8979.
37. Z. Li, C. Roscini, R. Núñez, F. Teixidor, C. Viñas, E. Ruiz and J. G. Planas, J. Mater. Chem. C, 2024, 12, 2101–2109.
38. Z. Li, X.-B. Li, M. E. Light, A. E. Carrillo, A. Arauzo, M. Valvidares, C. Roscini, F. Teixidor, C. Viñas, F. Gándara, E. Bartolomé and J. G. Planas, Adv. Funct. Mater., 2023, 33, 2307369.
39. Z. Li, R. Núñez, M. E. Light, E. Ruiz, F. Teixidor, C. Viñas, D. Ruiz-Molina, C. Roscini and J. G. Planas, Chem. Mater., 2022, 34, 4795–4808.
40. J. Poater, C. Viñas, M. Solà and F. Teixidor, Nat. Commun., 2022, 13, 3844.
41. J. Poater, C. Viñas, I. Bennour, S. Escayola, M. Solà and F. Teixidor, J. Am. Chem. Soc., 2020, 142, 9396–9407.
42. J. Poater, M. Solà, C. Viñas and F. Teixidor, Angew. Chem., Int. Ed., 2014, 53, 12191–12195.
43. R. N. Grimes, Carboranes, 3rd edn, 2016.
44. M. Scholz and E. Hey-Hawkins, Chem. Rev., 2011, 111, 7035–7062.
45. J. Plesek, Chem. Rev., 1992, 92, 269–278.
46. L. Gan, M. T. Nord, J. M. Lessard, N. Q. Tufts, A. Chidambaram, M. E. Light, H. Huang, E. Solano, J. Fraile, F. Suárez-García, C. Viñas, F. Teixidor, K. C. Stylianou and J. G. Planas, J. Am. Chem. Soc., 2023, 145, 13730–13741.
47. L. Gan, E. Andres-Garcia, G. Mínguez Espallargas and J. G. Planas, ACS Appl. Mater. Interfaces, 2023, 15, 5309–5316.
48. Z. Li, D. Choquesillo-Lazarte, J. Fraile, C. Viñas, F. Teixidor and J. G. Planas, Dalton Trans., 2022, 51, 1137–1143.
49. J. Soldevila-Sanmartín, E. Ruiz, D. Choquesillo-Lazarte, M. E. Light, C. Viñas, F. Teixidor, R. Núñez, J. Pons and J. G. Planas, J. Mater. Chem. C, 2021, 9, 7643–7657.
50. Z. Li, J. Fraile, C. Viñas, F. Teixidor and J. G. Planas, Chem. Commun., 2021, 57, 2523–2526.
51. L. Gan, A. Chidambaram, P. G. Fonquernie, M. E. Light, D. Choquesillo-Lazarte, H. Huang, E. Solano, J. Fraile, C. Viñas, F. Teixidor, J. A. R. Navarro, K. C. Stylianou and J. G. Planas, J. Am. Chem. Soc., 2020, 142, 8299–8311.
52. S. Rodríguez-Hermida, M. Y. Tsang, C. Vignatti, K. C. Stylianou, V. Guillerm, J. Pérez-Carvajal, F. Teixidor, C. Viñas, D. Choquesillo-Lazarte, C. Verdugo-Escamilla, I. Peral, J. Juanhuix, A. Verdaguer, I. Imaz, D. Maspoch and J. Giner Planas, Angew. Chem., Int. Ed., 2016, 55, 16049–16053.
53. M. Y. Tsang, S. Rodríguez-Hermida, K. C. Stylianou, F. Tan, D. Negi, F. Teixidor, C. Viñas, D. Choquesillo-Lazarte, C. Verdugo-Escamilla, M. Guerrero, J. Sort, J. Juanhuix, D. Maspoch and J. Giner Planas, Cryst. Growth Des., 2017, 17, 846–857.
54. K. I. Hadjiivanov, D. A. Panayotov, M. Y. Mihaylov, E. Z. Ivanova, K. K. Chakarova, S. M. Andonova and N. L. Drenchev, Chem. Rev., 2021, 121, 1286–1424.
55. G. Greczynski and L. Hultman, Angew. Chem., 2020, 132, 5034–5038.
56. Q. Lu, ACS Nano, 2024, 18, 13973–13982.
57. X. Ma, Z. Zhang, W. Shi, L. Li, J. Zou and P. Cheng, Chem. Commun., 2014, 50, 6340–6342.
58. D. Chisca, L. Croitor, O. Petuhov, E. B. Coropceanu and M. S. Fonari, CrystEngComm, 2016, 18, 38–41.
59. M. Indrani, R. Ramasubramanian, F. R. Fronczek, N. Y. Vasanthacharya and S. Kumaresan, J. Mol. Struct., 2009, 931, 35–44.
60. R. Dingle, M. E. Ljnes, S. L. Hor T, A. J. Heeger, O. Beckman, A. M. Portis, P. Rev, D. T. Teanley, M. J. Freesen, R. W. H. Stevenson, R. J. Birgeneau, H. J. Guggenheim, G. Shirane, H. Forstat, N. D. Love, J. N. McElearney, P. Letters, D. Spence, J. A. Casey, V. Nagarajan, B. Am Phys Soc, G. K. Wertheim, H. J. Williams and D. N. E. Buchanan, Phys. Rev. J. Arch, 1962, 187, 643.
61. M. Liu, Z. Ouyang, X. Liu, J. Cao, T. Xiao, Z. Xia and Z. Wang, Inorg. Chem., 2022, 61, 15045–15050.
62. L. D. Sanjeewa, V. O. Garlea, M. A. McGuire, C. D. McMillen, H. Cao and J. W. Kolis, Phys. Rev. B, 2016, 93, 224407,  DOI:10.1103/PhysRevB.93.224407.
63. M. Niel, C. Cros, G. Le Flem, M. Pouchard and P. Hagenmuller, Magnetic behaviour of vanadiumII in one- and two-dimensional systems, Physica B+C, 1977, 86–88(Part 2), 702–704.
64. H. Mutka, C. Payen and P. Molinié, Europhys. Lett., 1993, 21, 623.
65. C. Venkatesh, B. Bandyopadhyay, A. Midya, K. Mahalingam, V. Ganesan and P. Mandal, Phys. Rev. B, 2020, 101, 184429,  DOI:10.1103/PHYSREVB.101.184429.
66. A. B. P. Lever, Inorg. Chem., 1965, 4, 763–764.
67. T. Lee, D. B. Straus, K. P. Devlin, X. Gui, P. Louka, W. Xie and R. J. Cava, Inorg. Chem., 2022, 61, 10486–10492.
68. M. Hase, M. Soda, T. Masuda, D. Kawana, T. Yokoo, S. Itoh, A. Matsuo, K. Kindo and M. Kohno, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024416.
69. M. Wang, X. Gou, W. Shi and P. Cheng, Chem. Commun., 2019, 55, 11000–11012.
70. C. Coulon, R. Clérac, W. Wernsdorfer, T. Colin and H. Miyasaka, Phys. Rev. Lett., 2009, 102, 167204.
71. K. S. Lim, W. R. Lee, H. G. Lee, D. W. Kang, J. H. Song, J. Hilgar, J. D. Rinehart, D. Moon and C. S. Hong, Inorg. Chem., 2017, 56, 7443–7448.
72. F. Su, S. D. Li, C. Han, L. T. Wu and Z. J. Wang, Chin. J. Inorg. Chem., 2022, 38, 1421–1432.
73. J. Ribas, M. Monfort, C. Diaz, C. Bastos, C. Mer and X. Solans, Inorg. Chem., 1995, 34, 4986–4990.
74. M. Wang, X. Gou, W. Shi and P. Cheng, Chem. Commun., 2019, 55, 11000–11012.
75. Y. Zhang, Z.-Y. Liu, H.-M. Tang, B. Ding, Z.-Y. Liu, X.-G. Wang, X.-J. Zhao and E.-C. Yang, Inorg. Chem. Front., 2022, 9, 5039–5047.
76. X. Ma, Z. Zhang, W. Shi, L. Li, J. Zou and P. Cheng, Chem. Commun., 2014, 50, 6340–6342.
77. T. Lee, D. B. Straus, K. P. Devlin, X. Gui, P. Louka, W. Xie and R. J. Cava, Inorg. Chem., 2022, 61, 10486–10492.
78. F. Lipps, A. H. Arkenbout, A. Polyakov, M. Guenther, T. Salikhov, E. Vavilova, H. Klauss, B.-H. Buechner, T. M. Palstra and V. Kataev, Low Temp. Phys., 2017, 4, 1298–1304.
79. J. Darriet and L. P. Regnault, Solid State Commun., 1993, 86, 409–412.
80. A. Zheludev, T. Masuda, B. Sales, D. Mandrus, T. Papenbrock, T. Barnes and S. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144417.
81. A. Zheludev, T. Masuda, I. Tsukada, Y. Uchiyama, K. Uchinokura, P. Böni and S.-H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8921.
82. A. K. Bera, B. Lake, A. T. M. N. Islam, B. Klemke, E. Faulhaber and J. M. Law, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224423.
83. R. M. Morra, W. J. L. Buyers, R. L. Armstrong and K. Hirakawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 543.
84. Z. Tun, W. J. L. Buyers, A. Harrison and J. A. Rayne, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13331.
85. A. Masala, J. G. Vitillo, F. Bonino, M. Manzoli, C. A. Grande and S. Bordiga, Phys. Chem. Chem. Phys., 2016, 18, 220–227.
86. X. Zhang, J. Luo, K. Wan, D. Plessers, B. Sels, J. Song, L. Chen, T. Zhang, P. Tang, J. R. Morante, J. Arbiol and J. Fransaer, J. Mater. Chem. A, 2019, 7, 1616–1628.
87. F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, Willey, New York, 6th edn, 1999.
88. J. B. Coulter and D. P. Birnie, Phys. Status Solidi B, 2018, 255, 1700393.
89. P. H. M. Andrade, C. Volkringer, T. Loiseau, A. Tejeda, M. Hureau and A. Moissette, Appl. Mater. Today, 2024, 37, 102094.
90. Y. Yan, C. Wang, Z. Cai, X. Wang and F. Xuan, ACS Appl. Mater. Interfaces, 2023, 15, 42845–42853.
91. N. Kolobov, M. G. Goesten and J. Gascon, Angew. Chem., Int. Ed., 2021, 60, 26038–26052.
92. X. Guo, L. Liu, Y. Xiao, Y. Qi, C. Duan and F. Zhang, Coord. Chem. Rev., 2021, 435, 213785.
93. Y. Yan, C. Wang, Z. Cai, X. Wang and F. Xuan, ACS Appl. Mater. Interfaces, 2023, 15, 42845–42853.
94. L. Á. Alfonso Herrera and H. I. Beltrán, Coord. Chem. Rev., 2024, 505, 215658.
95. J. Panda, D. Singha, P. K. Panda, B. Chandra Tripathy and M. K. Rana, J. Phys. Chem. C, 2022, 126, 12348–12360.
96. J. H. Choi, Y. J. Choi, J. W. Lee, W. H. Shin and J. K. Kang, Phys. Chem. Chem. Phys., 2009, 11, 628–631.
97. J. A. Botas, G. Calleja, M. Sánchez-Sánchez and M. G. Orcajo, Int. J. Hydrogen Energy, 2011, 36, 10834–10844.
98. P. Sippel, D. Denysenko, A. Loidl, P. Lunkenheimer, G. Sastre and D. Volkmer, Adv. Funct. Mater., 2014, 24, 3885–3896.
99. L. Dong, L. Zhang, J. Liu, Q. Huang, M. Lu, W. Ji and Y. Lan, Angew. Chem., 2020, 132, 2681–2685.
100. P. Sippel, D. Denysenko, A. Loidl, P. Lunkenheimer, G. Sastre and D. Volkmer, Adv. Funct. Mater., 2014, 24, 3885–3896.
101. C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
102. G. Greczynski and L. Hultman, J. Appl. Phys., 2022, 132, 011101.
103. G. Greczynski and L. Hultman, Prog. Mater. Sci., 2020, 107, 100591.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2267757 and 2341767. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5tc00280j

---